Cascade Prediction With Self-Exciting Point Process and Local User Influence Measurement

With the rise and large-scale applications of social networking service, the prediction of information cascades has attracted extensive attention of researchers. User influence is an important factor affecting the dissemination of posts in online social networks. However, current studies usually take the number of users’ neighbors as their influence, and do not accurately describe the role of participating users in information dissemination. In this paper, a prediction model of information cascades in social networks is established based on the Hawkes process, and the model considers three factors, i.e., post influence, user influence and users’ response time, to describe the occurrence probability of forwarding events. In order to utilize abundant information of local network topology, we present a new method of calculating user influence, combining with semi-local centrality and local clustering coefficients. Then, a regression tree algorithm is used to determine time correction coefficients to reveal dynamic post influence, and the popularity prediction of posts in social networks is realized. Comparison experiments of different models are carried out on real-world datasets to evaluate the effectiveness and prediction performance of the proposed model, and results show that our method outperforms other counterparts.

1 Introduction

With massive user-generated contents and closely intertwined user relationship networks, the phenomena of information cascades become more and more common [1–3], and the work of information cascade prediction has also received notable attention of researchers [4–6]. The cascade prediction focuses on the cascade of social networks, which aims to estimate the future information diffusion ways. The final size of an information cascade directly indicates the popularity and influence depth of the information, and it is the reflection of information importance. That is, the larger the final scale of an information cascade, the higher its popularity and the wider the influence. Taking Twitter as an example, users can express their views and opinions on this platform. When a user posts a tweet, some users who follow it may retweet the tweet because they like it or approve of it, and then, the users who follow those retweeters have an opportunity to see the tweet [7–9]. After the tweet is received, it may also be forwarded, and the retweeting process is repeated continuously, forming a cascade of information in the network.

Existing work on information cascade prediction can be generally divided into two aspects: prediction methods based on feature learning and those based on model generation. The basic idea of feature learning is to use related algorithms of machine learning to formalize information cascade prediction as a classification or regression problem, and to extract relevant features of user-generated contents and initial cascade process, such as information disseminator [10, 11], information contents [12–14], and network structure [15–17], etc. Then, this kind of methods use different algorithms to mine the extracted features, so as to establish a mapping relationship between correlated characteristics and the future size of an information cascade. Wang et al. [18] proposed a combined social media popularity prediction framework based on multimodal feature extraction, implemented feature generalization and temporal modeling, and adopted a sliding window average to model short-term dependency of each user among visual and textual features. Kong et al. [19] focused on predicting multiple stages of popularity such as outbreak, plateau, rise, and fall. They adopted a pattern matching method to predict the future popularity stage by extracting multiple dynamic factors such as the number of retweets, the number of users, and network structure features at the micro level, and extracting the overall evolution pattern of the popularity stage at the macro level. Zhang et al. [20] extracted the time, structure and content features from the diffusion process of embedded web pages in WeChat moments and predicted the growth of content popularity. The results showed that the popularity scale was strongly correlated with the initial network structure of the cascade. Due to the diversity of features in the process of information cascades, it is very difficult to extract the optimal feature set. How to minimize the calculation and optimize the dynamic feature extraction process is an urgent problem to be solved.

On the other side, the methods with model generation directly simulate the process of information diffusion in a network, and formalize the cascade process into a parameterized model by analyzing the factors that affect the diffusion. After the diffusion model is established, various parameters of the model are estimated according to the cascade data observed in the initial stage, so as to predict the future cascade [21–27]. Zhao et al. [28] used the time-varying tweet influence to measure the forwarding rate, and identified whether a cascade is in the supercritical state or in the subcritical state. Chen et al. [29] proposed a marked self-exciting point process model to capture the retweeting dynamics and predict the tweet popularity. They selected the specific parameter form of the function in the model by comparing the goodness of fit of retweet cascades in the training data set. Palmowski et al. [30] described moments method of estimation of the parameters of Hawkes point process by using the generator theory to analyze and model the cascade effect of forwarding in social networks. Srivathsan et al. [31] presented a detailed Bayesian model of the information by incorporating prior knowledge of unobserved user information, which removed the high influence of the first observed user behavior. The results show that users make weighted choices between adoption and rejection, but do not always choose the most likely option, and adding prior user information will delay the cascade effect. Due to various assumptions on many factors affecting propagation process in the modeling, compared with prediction methods based on feature learning, model generation methods do not have the learning process of cascading features, so their prediction performance may be limited to a certain extent. Therefore, model generation methods should be incorporated with feature learning to improve the expressions of propagation details.

Existing models of cascade prediction only consider the number of followers for each forwarding user, that is, the in-degree of a node, when modeling the arrival intensity of forwarding events. The number of user’s followers can indeed represent the influence of a user to a certain extent, but this measurement also has certain shortcomings. Users with more followers do not necessarily have higher activity. Higher activity of a user in social networks means that the user may frequently post or repost a message, contributing to the growth of the forwarding cascade. In addition, fake online users are often used to construct fake popularity of influencers. If a user has a large number of fake fans, its influence will be overestimated when only measured by the number of fans.

We mainly focus on the problem of information cascades formed by the diffusion of posts (tweets on Twitter) after the posts are published in social networks, and investigate the prediction method based on model generation. We analyze the factors which affect the spreading of posts, and take the final number of reposts to measure the size of a cascade. Then, we construct the cascade prediction model based on the Hawkes process (also known as a self-exciting point process) to explore the final scale and influence range of an information cascade. In addition, we integrate the model with feature learning by introducing a cascading parameter to reflect the timeliness of posts. The main work of this paper is as follows:

1) We model the forwarding times of posts as a counting process, and characterize the arrival intensity of forwarding events by three factors, i.e., the influence of posts themselves, the influence of forwarding users, and the response time of users. Finally, the prediction model of the final forwarding number is obtained by integrating the theory of a branching process.

2) We propose a method of calculating the influence of forwarding users and predict the influence of posts. Then, we use a regression tree algorithm to train the cascading parameter, and a prediction algorithm is realized to obtain the final forwarding numbers of posts.

3) We conduct performance evaluation and comparative analysis of the cascade prediction model on two datasets from real social networks, and confirm the effectiveness of our model.

The rest of the paper is structured as follows. Our cascade prediction method is presented in Section 2. Section 3 provides experiments and empirical results of the model. Our conclusions are presented in Section 4.

2 Methods

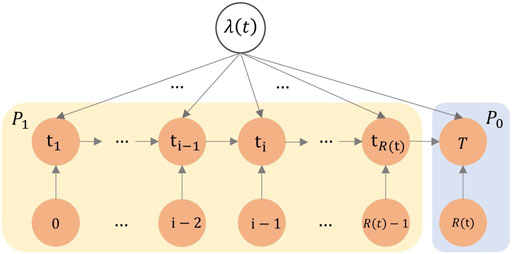
In this section, firstly, we describe the specific problem discussed in this paper, and introduce the goal of information cascade prediction. Then, in terms of the theory of a counting process, we model the arrival intensity of post forwarding events based on the Hawkes process. Finally, we combine our generative model with intergenerational characteristics of a branching process, and obtain the predicted value of the final forwarding number. Figure 1 illustrates the overview of our proposed model.

FIGURE 1

FIGURE 1. Overview of the proposed framework.

2.1 Problem Definition

We assume that the publishing time for a post is $t_0$. According to forwarding events of the post in the time period $\left[t_0,t\right]$ which include forwarding time and relevant information of forwarding users, we arrange these forwarding events in the order of forwarding time. The occurrence time of the $i$-th forwarding event is defined as $t_i$, and $u_i$ is used to represent the corresponding forwarding user. Then, the relevant information chain $\left\{\left(t_1,u_1\right),\left(t_2,u_2\right),\dots ,\left(t_i,u_i\right),\dots \right\}$ at the initial stage of the post forwarding cascade is obtained as known information. It is worth noting here that the relevant information of forwarding users is reflected by the user relationship network, and it is mainly used to extract the influence of users in the network. The influence determines the size of the user group that may take further forwarding behaviors. The counting process $R\left(t\right)$ as a representative of point process is used to describe the cumulative number of forwards obtained by the post in the time period [$t_0,t$]. Then, the task of information cascade prediction is to predict the final number of forwards $\widehat{R}\left(\infty \right)$ obtained by the post at the time $t$ according to the information chain $\left\{\left(t_1,u_1\right),\left(t_2,u_2\right),\dots ,\left(t_i,u_i\right),\dots \right\}$. Table 1 shows the notations involved in this paper.

TABLE 1

TABLE 1. Notations.

2.2 Forwarding Probability Modeling

Apparently, in the study of a counting process, how to characterize event arrival intensities in the process is a key problem. According to the features and growth mechanism of a forwarding cascade, each time a post is forwarded by a user, it may gain the attention of more users. Therefore, the number of potential users that may take forwarding behaviors increases due to forwarding events, and then more subsequent forwards are stimulated.

We characterize the probability of post forwarding events based on the intensity function of the Hawkes process. The intensity function of an event arrival in the classical Hawkes process is expressed as follows [32]:

$\mathit{\lambda }\left(\mathit{t},{\mathit{{\rm H}}}_{\mathit{t}}\right)=\mathit{\nu }+{\displaystyle \underset{-\infty }{\overset{\mathit{t}}{\int }}\mathit{\gamma }\left(\mathit{t}-\mathit{u}\right)\mathit{dR}\left(\mathit{t}\right)}(1)$

where ${\text{Η}}_t$ represents the historical data in the counting process $R\left(t\right)$ up to time $t$. $\nu$ indicates the external incentive intensity, which describes the impact of the post background on subsequent forwarding cascade. For instance, in the process of information dissemination, some emergencies in real world affect information cascades in the social network, and the influence belongs to external factors other than forwarding events themselves. $\gamma \left(t\right)$ is a self-excited kernel function, which characterizes the self-excited effect of historical forwarding events on the current event, i.e., the self-excited effect of the current event on subsequent forwarding cascade. In order to quantify the growth mechanism of an information cascade, the original Hawkes process is simplified to exclude the influence of external incentive factors, and the function of event arrival intensity in the cascade process is expressed as the linear sum of self-excited kernel functions over time. The intensity function is given as follows:

$\mathit{\lambda }\left(\mathit{t}\right)={\displaystyle \sum _{{\mathit{t}}_{\mathit{i}}\le \mathit{t}}\mathit{\gamma }\left(\mathit{t}-{\mathit{t}}_{\mathit{i}}\right)}(2)$

We refine the self-excited effect and decompose the self-excited kernel function in the intensity function $\lambda \left(t\right)$. Then, we obtain

$\mathit{\lambda }\left(\mathit{t}\right)=\mathit{p}\left(\mathit{t}\right){\displaystyle \sum _{{\mathit{t}}_{\mathit{i}}\le \mathit{t}}{\mathit{u}}_{\mathit{i}}\mathrm{\ast }\mathit{\Phi }\left(\mathit{t}-{\mathit{t}}_{\mathit{i}}\right),\mathit{t}\ge {\mathit{t}}_0}(3)$

where $p\left(t\right)$ represents the influence of the post itself, which quantifies the possibility of being forwarded for the post when it is observed by users at time $t$. $p\left(t\right)$ is time-dependent. For example, a post always gets more attention when it is just released. With the time elapsed, the attraction of the post decreases, and it will be crowded out by a large number of newly released information on the platform. In addition to the factor of timeliness, the influence of the post is also related to its content, release time and geographical location of the author. We synthesize all the relevant influencing factors of a post by $p\left(t\right)$. $u_i$ is the influence of forwarding user $i$, which quantifies the probability that the post will be forwarded when it is seen by users at time $t$ from the perspective of network topology. In another word, $u_i$ represents the set of users that may take forwarding behaviors in the future, and therefore, we should give more weights to nodes with greater influence. $\text{Φ}\left(t\right)$ is a memory kernel which indicates users’ reaction time. After a post is published, it will appear in the information flow of continuous post generation. After users see the post, they may wait for a certain time to decide whether to forward it. Therefore, $\text{Φ}\left(t\right)$ is just the function of quantifying the probability density distribution obeyed by this time interval.

Eq. 3 is the expression of the arrival intensity of post forwarding events in the information cascade, and $\lambda \left(t\right)$ describes the rate at which the post is forwarded. We have the following additional explanations of $\lambda \left(t\right)$. After the post is forwarded for the i time, users are affected by the influence of antecedent spreaders to consider participating in the diffusion. These users see the post in turn and decide whether to take forwarding behaviors according to $\text{Φ}\left(t\right)$ which characterizes a certain response time. Therefore, ${\displaystyle \sum _{t_i\le t}{u}_i\mathrm{\ast }\text{Φ}\left(t-t_i\right)}$ refers to the arrival intensity of the users who see the post in the subsequent user groups and may take forwarding behaviors when influenced by the cascade events until time $t$, and then, we can multiply the intensity of users by $p\left(t\right)$ to obtain the arrival intensity of forwarding events at time $t$. The arrival intensity means the probability of a forwarding event occurring in an infinitesimal time interval.

The arrival intensity of forwarded events $\lambda \left(t\right)$ includes three factors: the influence of the post itself, the influence of forwarding users and the response time of forwarding. The quantification and parameter estimation of these three factors will be introduced in detail below.

2.3 Tweet Attraction

The influence $p\left(t\right)$ of a post comprehensively involves many factors affecting the forwarding related to the post itself, but the forms of parameters in $p\left(t\right)$ are not determined in the modeling. Instead, we model the influence $p\left(t\right)$ in a nonparametric form, and then, and estimate the value of $p\left(t\right)$ according to the observed information chain at the initial stage of the forwarding cascade.

Firstly, we consider the case that $p\left(t\right)$ does not change with time, that is, $p\left(t\right)=p$ is a constant. The sample density of forwarding cascade process based on the intensity function $\lambda \left(t\right)$ is

$\mathit{P}\left\{\mathit{R}\left(\mathit{t}\right)=\mathit{r};{\mathit{t}}_{\mathbf{1}},\dots ,{\mathit{t}}_{\mathit{r}}\right\}={\text{Π}}_{\mathit{i}=\mathbf{1}}^{\mathit{R}\left(\mathit{t}\right)}\mathit{\lambda }\left({\mathit{t}}_{\mathit{i}}\right)\mathit{exp}\left(-{{\displaystyle \int }}_{{\mathit{t}}_{\mathbf{0}}}^{\mathit{t}}\mathit{\lambda }\left(\mathit{\tau }\right)\mathit{d\tau }\right)(4)$

In order to explain the process more clearly and concisely, the graphical expression of the model for the arrival process is shown in Figure 2. To simplify the representation of $\mathit{P}\left\{\mathit{R}\left(\mathit{t}\right)=\mathit{r};{\mathit{t}}_1,\dots ,{\mathit{t}}_{\mathit{r}}\right\}$, we roughly use variable $\mathit{P}$ with subscripts to denote the sample density at different times during the forwarding cascade process. The yellow area shows the initial cascading information chain, where the sample density at each moment is marked by $\mathit{P}$. ${\mathit{P}}_1$ indicates the density at the initial moment. The blue area indicates the sample density ${\mathit{P}}_{\mathit{T}}$ to be calculated of the current time T with known historical information.

FIGURE 2

FIGURE 2. Graphical representation of the model for the arrival process.

Eq. 4 also represents the likelihood function of $p\left(t\right)$ when the initial cascading information chain is given. Taking the derivative of the logarithmic function for Eq. 4 and combining with Eq. 2, the maximum likelihood estimation of $p\left(t\right)$ is

${\mathit{U}}_{\mathit{t}}^{\mathit{e}}={\displaystyle {\sum }_{\mathit{i}=\mathbf{0}}^{\mathit{R}\left(\mathit{t}\right)}{\mathit{u}}_{\mathit{i}}{{\displaystyle \int }}_{{\mathit{t}}_i}^{\mathit{t}}\mathit{\Phi }\left(\mathit{\tau }-{\mathit{t}}_{\mathit{i}}\right)\mathit{d\tau }}(5)$

$\widehat{\mathit{p}}\left(\mathit{t}\right)=\frac{\mathit{R}\left(\mathit{t}\right)}{{\mathit{U}}_{\mathit{t}}^{\mathit{e}}}(6)$

Here, $U_t^e$ can be understood as the sum of effective values for the influence of forwarding users until time $t$. It represents the users who have seen the post up to time $t$ among the users who are influenced and may take forwarding behaviors. Then, the estimated value of the influence of the post itself $\widehat{p}\left(t\right)$ can be explained as the proportion of the cumulative forwarding number of the post until time $t$ in the users who have seen the post.

In order to consider the time-varying characteristic of $p\left(t\right)$, the unilateral kernel function $K_t\left(s\right),s>0$ is introduced here to smooth $p\left(t\right)$ and weight different forwarding cascades. The weighted estimation value of $p\left(t\right)$ is obtained by using the observation information chain closer to time $t$ [28]:

$\widehat{\mathit{p}}\left(\mathit{t}\right)=\frac{{{\displaystyle \int }}_{{\mathit{t}}_{\mathbf{0}}}^{\mathit{t}}{\mathit{K}}_{\mathit{t}}\left(\mathit{t}-\mathit{s}\right)\mathit{dR}\left(\mathit{s}\right)}{{{\displaystyle \int }}_{{\mathit{t}}_{\mathbf{0}}}^{\mathit{t}}{\mathit{K}}_{\mathit{t}}\left(\mathit{t}-\mathit{s}\right)\mathit{d}{\mathit{U}}_{\mathit{s}}^{\mathit{e}}}=\frac{{\displaystyle {\sum }_{\mathit{i}=\mathbf{0}}^{\mathit{R}\left(\mathit{t}\right)}{\mathit{K}}_{\mathit{t}}\left(\mathit{t}-{\mathit{t}}_{\mathit{i}}\right)}}{{\displaystyle {\sum }_{\mathit{i}=\mathbf{0}}^{\mathit{R}\left(\mathit{t}\right)}{\mathit{u}}_{\mathit{i}}{{\displaystyle \int }}_{{\mathit{t}}_{\mathit{i}}}^{\mathit{t}}{\mathit{K}}_{\mathit{t}}\left(\mathit{t}-\mathit{s}\right)\mathit{\Phi }\left(\mathit{s}-{\mathit{t}}_{\mathit{i}}\right)\mathit{ds}}}(7)$

where the unilateral kernel function $K_t\left(s\right)$ is defined as $K_t\left(s\right)=max\left\{1-s/L,0\right\},s>0$. $L$ is the interval between the observation point and the prediction time, that is, the size of the observation cascade window. The data in the window is used for the prediction of the final cascade size. Here, we heuristically set $L$ to 0.5, and the latter half of the information chain in the initial stage of the forwarding cascade is used as the observation interval. In this way, the forwards earlier than $t/2$ will be ignored by the kernel function. The function gives more weights to the events closer to the prediction time $t$ in the window, and gradually reduces the weights of old forwarding events, so as to make the estimated value $\widehat{p}\left(t\right)$ closer to the real dynamic post influence.

In social networks, users’ forwarding behaviors have a certain delay time. After a post is published, users need a period of response time to notice the post and decide whether to forward it. The probability density distribution of response time is determined by the memory kernel function $\text{Φ}\left(t\right)$ in the Hawkes model, which characterizes the relaxation response of the system. In social networks, the probability density distribution of users’ response time obeys the heavy-tailed distribution [28], and therefore, the power-law memory kernel function is used here, as shown below:

$\mathit{\Phi }\left(\mathit{t}\right)=\{\begin{array}{cc}\mathit{c},& \mathbf{0}<\mathit{t}\le {\mathit{t}}_{\mathbf{0}}\\ \mathit{c}{(\mathit{t}/{\mathit{t}}_{\mathbf{0}})}^{-\left(\mathbf{1}+\mathit{\theta }\right)},& \mathit{t}\ge {\mathit{t}}_{\mathbf{0}}\end{array}(8)$

where $t_0=300s$, because it is observed that the memory kernel function remains unchanged for the first 5 min, and then it shows the characteristic of power-law attenuation. The deceleration rate is obtained as $\theta =0.242$ by fitting, which is obtained by experimentally fitting the distribution of the user’s forwarding time in the training set. In addition, we notice the truth that the probability density function is integrated as one on the whole integration interval $\left[0,+\infty \right)$, and then, we obtain the parameter $c=6.27\times {10}^{-4}$.

2.4 User Influence Modeling

We measure the influence of the ith forwarding user $u_i$ from the perspective of network topology. Figure 3 shows a simple network with 23 nodes and 37 edges. Obviously, node 1 has the largest number of nearest neighbors, but the posts published by node one do not necessarily generate a faster and wider cascade, because the degrees of its neighbor nodes are very small. In contrast, although node 23 does not have more nearest neighbors, the statuses of its neighbors may make it have more influence.

FIGURE 3

FIGURE 3. Illustration of user influence analysis.

Combined with two indicators of node influence, i.e., semi-local centrality [33] and local clustering coefficients, we expand the measurement of forwarding user influence by using more information of local network topology. The calculation method of semi-local centrality is as follows:

$\begin{array}{l}\mathbf{Q}\left(\mathbf{w}\right)={\displaystyle \sum _{\mathbf{u}\in \mathbf{N}\left(\mathbf{w}\right)}\left|\mathbf{\Gamma }\left(\mathbf{u}\right)\right|},\\ \mathbf{L}\mathbf{C}\left(\mathbf{i}\right)={\displaystyle {\sum }_{\mathbf{w}\in \mathbf{N}\left(\mathbf{i}\right)}\mathbf{Q}\left(\mathbf{w}\right)}\end{array}(9)$

Where $N\left(w\right)$ represents the set of nearest neighbor nodes (including in-degree and out-degree of node w), $\text{Γ}\left(u\right)$ represents the set of nearest neighbor and next nearest neighbor nodes of node u (i.e., the adjacent nodes of the nearest neighbor nodes), and $LC\left(i\right)$ is the semi-local centrality size of node i. This measurement method expands the range of involved neighbor nodes to within the fourth order neighbors, which is a trade-off between low correlation centrality measure and high time-consuming global measure. Therefore, it can not only improve the calculation accuracy, but also ensures low time complexity. However, this method ignores the influence of the connectivity between nodes in the local topology which reflects the clustering degree of nodes in the network. Therefore, considering the connectivity between neighbor nodes of a node can improve the measurement accuracy of node influence. The closer the relationships between the neighbors of a node are, the higher the degree of mutual influence will be, and the greater the influence of the node will be. The clustering coefficient is an indicator which measures the degree of connectivity between nodes. The local clustering coefficient reflects the degree of interactions between neighbor nodes of the current node. The formula is as follows:

${\mathit{c}}_{\mathit{i}}=\frac{{{\displaystyle \sum }}_{\mathit{j}}{\mathit{e}}_{\mathit{ij}}{{\displaystyle \sum }}_{\mathit{k},\mathit{k}\ne \mathit{j}}{\mathit{e}}_{\mathit{ik}}{\mathit{e}}_{\mathit{jk}}}{\left|\mathit{N}\left(\mathit{i}\right)\right|\left(\left|\mathit{N}\left(\mathit{i}\right)\right|-\mathbf{1}\right)/\mathbf{2}}(10)$

Where $e_{ij}$ indicates whether nodes j and k are connected, and $\left|N\left(i\right)\right|$ is the number of nearest neighbor nodes. Considering the two indicators of semi-local centrality and local clustering coefficients, the influence of user i is quantified as

$\begin{array}{l}{\mathit{u}}_{\mathit{i}}={\displaystyle \sum }_{\mathit{w}\in \mathit{N}\left(\mathit{i}\right)}\left(\mathit{\beta }\mathit{\ast }\left|\mathit{\Gamma }\left(\mathit{w}\right)\right|+\left(\mathbf{1}-\mathit{\beta }\right)\mathrm{\ast }{\displaystyle \sum _{\mathit{u}\in \mathit{\Gamma }\left(\mathit{w}\right)}{\mathit{c}}_{\mathit{u}}}\right)\\ =\mathit{\beta }\mathit{*}{\displaystyle {\sum }_{\mathit{w}\in \mathit{N}\left(\mathit{i}\right)}\left|\mathit{\Gamma }\left(\mathit{w}\right)\right|+\left(\mathbf{1}-\mathit{\beta }\right)}\mathrm{\ast }{\displaystyle {\sum }_{\mathit{w}\in \mathit{N}\left(\mathit{i}\right)}{\displaystyle {\sum }_{\mathit{u}\in \mathit{\Gamma }\left(\mathit{w}\right)}{\mathit{c}}_{\mathit{u}}}}\end{array}(11)$

Where $\beta$ ($0\le \beta \le 1$) is the balance parameter for user influence. For each nearest neighbor node w of node i, $\left|\text{Γ}\left(w\right)\right|$ is the sum of the number of w’s nearest neighbor and next nearest neighbor nodes. For each node $u\in \text{Γ}\left(w\right)$, $c_u$ is the local clustering coefficient of node u. The first part of Eq. 11 considers the number of nodes whose distances from the nearest neighbor node w of node i are within two steps, and the second part considers the connectivity between neighbor nodes of node u in $\text{Γ}\left(w\right)$. In other words, user influence represented by Eq. 11 considers not only the local influence of the nearest neighbor nodes, but also the degree of interactions between nodes in the local network. In addition, we consider both in-degrees and out-degrees of the nearest neighbor nodes, and this measurement makes up for the deficiency of considering only node in-degrees in a sparse directed network.

2.5 Predicting an Information Cascade

After the modeling and parameter estimation of the arrival intensity for post’s forwarding events, this section will discuss how to predict the final number of forwards, that is, the final size of an information cascade. We define $G_k$ as the total number of forwards formed by the descendants of the k-generation forwarding users, i.e., the users who may take forwarding behaviors driven by the influence of the k-generation forwarding users. If the cumulative forwarding users until time $t$ are treated as the first generation with the count $R\left(t\right)$, then $G_1$ represents the total number of forwards in the next generation affected by $R\left(t\right)$ users. Based on this scenario, the information cascade chain after time $t$ is obtained as $\left\{G_1,G_2,\dots G_k\right\}$.

The final scale of the information cascade to be predicted is expressed as

$\widehat{\mathit{R}}\left(\infty \right)=\mathit{R}\left(\mathit{t}\right)+{\displaystyle {\sum }_{\mathit{k}=\mathbf{1}}^{\infty }{\mathit{G}}_{\mathit{k}}}(12)$

We assume that the own influence of the post remains unchanged after the prediction time $t$ is $p\left(t\right)$, and the number of users that may take forwarding behaviors caused by user influence is expected to be $u_{\ast }$. Therefore, $u_{\ast }$ indicates the expected value of the forwarding user influence, which can be obtained from the dataset. Then, the branching factor of the cascade process is defined as $\rho =p{u}_{\ast }$. The branching factor represents the expected value of descendants’ forwarding events, so we have $G_k=\rho G_{k-1}$. When $\rho <1$, i.e., $p<1/u_{\ast }$, the final scale of the information cascade is always bounded, and the social system enters a subcritical state. The forwarding process will gradually slow down and finally stop, and the final forwarding number can be predicted. However, when $\rho >1$, the final scale of the information cascade is unbounded, and the system state is called a supercritical state. The forwarding process never stops, and the final forwarding number cannot be predicted. Obviously, this outcome is usually not in line with the actual situation. Therefore, when $\rho <1$, ${\displaystyle \sum _{k=1}^{\infty }{G}_k}$ can be regarded as the summation of geometric series, that is

${\displaystyle {\sum }_{\mathit{k}=\mathbf{1}}^{\infty }{\mathit{G}}_{\mathit{k}}}=\frac{{\mathit{G}}_{\mathbf{1}}}{\mathbf{1}-\mathit{\rho }}(13)$

Where $G_1$ represents the users who have seen the post and may forward it after time $t$. If $U_t$ represents the sum of the influence of forwarding users up to time $t$, we obtain

${\mathit{G}}_{\mathbf{1}}=\mathit{p}\left({\mathit{U}}_{\mathit{t}}-{\mathit{U}}_{\mathit{t}}^{\mathit{e}}\right)(14)$

Based on Eq. 14, the predicted final scale of the information cascade can be obtained, [28] that is, the final forwarding number is

${\widehat{\mathit{R}}}_{\infty }\left(\mathit{t}\right)=\mathit{R}\left(\mathit{t}\right)+{\displaystyle {\sum }_{\mathit{k}=\mathbf{1}}^{\infty }{\mathit{G}}_{\mathit{k}}}=\mathit{R}\left(\mathit{t}\right)+\frac{\mathit{p}\left({\mathit{U}}_{\mathit{t}}-{\mathit{U}}_{\mathit{t}}^{\mathit{e}}\right)}{\mathbf{1}-\mathit{p}{\mathit{u}}_{\mathit{\ast }}}(15)$

In order to eliminate the inaccurate assumption that $p\left(t\right)$ remains unchanged after time $t$, a distinct correction coefficient ${\mu }_t(0<{\mu }_t<1)$ is introduced for each post to adjust the predicted value of the final forwarding number. ${\mu }_t$ reflects the reduced influence of a post due to obsolescence, and we use a machine learning method to obtain dynamic ${\mu }_t$. The predicted value of the final forwarding cascade size is

${\widehat{\mathit{R}}}_{\infty }\left(\mathit{t}\right)=\mathit{R}\left(\mathit{t}\right)+{\mathit{\mu }}_{\mathit{t}}\frac{\widehat{\mathit{p}}\left(\mathit{t}\right)\mathrm{\ast }\left({\mathit{U}}_{\mathit{t}}-{\mathit{U}}_{\mathit{t}}^{\mathit{e}}\right)}{\mathbf{1}-\widehat{\mathit{p}}\left(\mathit{t}\right)\mathrm{\ast }{\mathit{u}}_{\mathit{\ast }}}(16)$

Eq. 16 is the final prediction model of an information cascade. We use the regression algorithm of a decision tree to solve and quantify ${\mu }_t$. The selection process of the feature set is as follows:

$\begin{array}{l}{\mathit{f}}_{\mathbf{1}}=\mathit{R}\left(\mathit{t}\right),\\ {\mathit{f}}_{\mathbf{2}}=\widehat{\mathit{p}}\left(\mathit{t}\right),\\ {\mathit{f}}_{\mathbf{3}}={\mathit{U}}_{\mathit{t}},\\ {\mathit{f}}_{\mathbf{4}}={\mathit{U}}_{\mathit{t}}^{\mathit{e}}.\end{array}(17)$

After selecting the feature set, we use the data in the training set to train the regression tree. In the test set, we input the feature set $\{f_1,f_2,f_3,f_4\}$ into the trained regression tree model so as to obtain the corresponding correction coefficient ${\mu }_t$. The whole algorithm of information cascade prediction is shown in

Algorithm 1. Final scale prediction of an information cascade

3 Experiment Results

We use two real-world datasets in the experiments. The first dataset was collected from the Twitter platform and disclosed by Zhao et al. [28] in their research on the prediction of tweet forwarding. This dataset contains all the posts published on Twitter and their forwarding information within 1 month from 7 October 2011. The information of each post includes its ID, publishing time, the ID and number of fans of the publisher, as well as a series of forwarding time and the forwarding users. However, this dataset does not contain the structure information of the forwarding network, that is, there is no relationship information between users. Therefore, we introduce only the correction coefficient ${\mu }_t$ on dataset one to advance the prediction model. In order to improve the efficiency, we select the posts with the forwarding numbers greater than 500 in the dataset for cascade prediction. We split the posts published in the first 8 days as the training set, and the test set contains the posts published in the next 7 days. The forwarding number formed in the remaining days is regarded as the final size of an information cascade. The second dataset was collected from Twitter available on the website¹, which not only contains related forwarding information of 3,553 posts, but also includes 1,731,658 relationships between 71,367 users. The purpose of introducing this dataset is to expand the measurement method of user influence in the original Hawkes process from the perspective of network topology. The descriptions of the datasets are shown in Table 2. In the experiments, we randomly select 1,000 posts as the research subset in which forwarding cascades of 723 posts are used as the training set.

TABLE 2

TABLE 2. Statistics of datasets.

We use the absolute percentage error (APE) and Kendall rank correlation coefficient as the evaluation metrics of prediction performance. APE is calculated as follows:

$\mathit{APE}=\frac{\left|{\widehat{\mathit{R}}}_{\infty }\left(\mathit{t}\right)-\mathit{R}\left(\infty \right)\right|}{\mathit{R}\left(\infty \right)}(18)$

Where ${\widehat{R}}_{\infty }\left(t\right)$ is the predicted value of the cascade size, and $R\left(\infty \right)$ is the real value. Obviously, smaller values of APE indicate higher prediction accuracy. The Kendall rank correlation is usually used to count the correlation of two attributes for $n$ objects, which is defined as follows

$\mathit{k}=\left(\mathbf{4}\mathit{P}/\mathit{n}\mathrm{\ast }\left(\mathit{n}-\mathbf{1}\right)\right)-\mathbf{1},\mathit{ }-\mathbf{1}<\mathit{k}<\mathbf{1}(19)$

Where $P$ represents the number of concordant pairs of objects between the predicted values and real values. In other words, we suppose that there are $n$ objects, each of which has two attributes, corresponding to the predicted value and the real value, respectively. Then, we sort the $n$ objects according to the predicted values and real values, respectively. If both the ranks of ${\widehat{R}}_{\infty }\left(t\right)$ and $R\left(\infty \right)$ for object i are larger than those for object j, the pair of i and j are called a concordant pair. Then, $P$ counts the number of concordant pairs of objects [34]. Obviously, the larger the value of $k$, the higher the matching degree between the predicted values and real values, so that the better prediction performance is achieved.

Here, we use the Hawkes model proposed by Zhao et al. [28] as the benchmark for experimental evaluation. The original Hawkes model uses the same correction coefficient for all posts, and the measurement of user influence only considers the number of users’ fans, so we address the role of our method of calculating user influence for the prediction performance. Note that the two datasets do not play the same role. We distinguish between two datasets to evaluate the impact of different modules on prediction performance. Dataset one does not have user relationships, so we validate on this dataset the effect on prediction performance of having different correction factors for different posts that we learned through machine learning without calculating user influence. Dataset 2 has user relationships, so influence can be calculated. We mainly extend the user influence on dataset two and verify the impact of this module on the prediction performance. For each post, 300s, 600s, 900s, 1,200s and 1,800s are selected as the prediction time to obtain the final sizes of forwarding cascades.

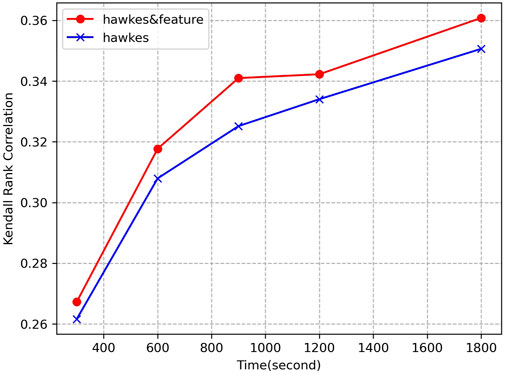
The comparison results on dataset one are shown in Figure 4 and Figure 5. In both figures, the curve ‘Hawkes’ represents the original Hawkes model, and the curve ‘Hawkesandfeature’ represents the model by introducing the idea of feature learning and using the regression tree algorithm to improve only correction coefficients. Figure 4A shows the evolutionary trend of the median of APE as a function of the prediction time $t$, and Figure 4B shows the evolutionary trend of the mean of APE with the prediction time $t$. As can be seen from Figure 4, different correction coefficients ${\mu }_t$ varying with time are generated for each post through the feature set of the initial cascade process, and the performance of Hawkesandfeature is improved both for the median or mean value of APE compared with the original model. Specifically, at time 300s, 600s, 900s, 1,200s and 1,800s, the improvement in median APE compared to the Hawkes process is 36.28%, 46.38%, 46.58%, 44.77% and 45.07%, respectively in Figure 4A. For the mean APE, the best improved performance reaches 36.70% in time 1800s compared to the Hawkes process Figure 4B. The value of APE decreases with the increase of prediction time $t$, indicating that when more historical cascade information is used, the performance of the prediction method will be improved.

FIGURE 4

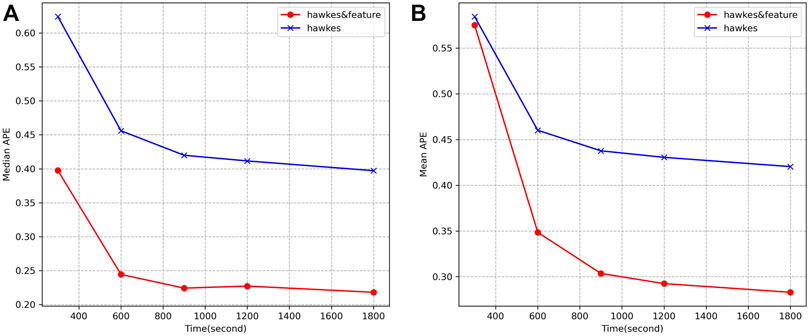
FIGURE 4. Comparison of APE of two models on dataset 1. (A) Evolutionary trend of the median APE with prediction time $t$, (B) Evolutionary trend of mean APE with prediction time $t$.

FIGURE 5

FIGURE 5. Comparison of Kendall rank correlation for two models on dataset 1.

Figure 5 shows the evolutionary trend of Kendall rank correlation for the above two models with prediction time $t$. It can be seen that the model Hawkesandfeature also performs better than the original process model in the correlation between the predicted values and real values, and the value of Kendall rank correlation also increases with time, indicating that the correlation between the predicted values and real values is also improved due to the use of more historical cascade information.

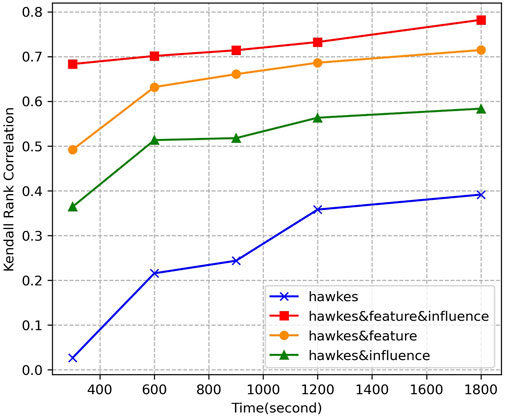
In the experiments on dataset 2, the measurement of user influence is expanded and the influence balance factor is set at $\beta =0.7$. The improved correction coefficients are also included. The relevant experimental results are shown in Figure 6. The curve ‘Hawkesandinfluence’ represents the model only expanding user influence measurement on the basis of the original process model, and the curve ‘Hawkesandfeature&influence’ represents our cascade prediction model which comprehensively improves the correction coefficients and expands user influence measurement. Figure 6A shows the evolutionary trend of the median of APE with the prediction time $t$, and Figure 6B shows that of the mean of APE. It can be seen that although the model Hawkes and influence which only expands user influence measurement has a certain performance improvement over the original process model, it is not as effective as the model Hawkesandfeature which only improves the correction coefficients. Therefore, the prediction method based on feature learning has more advantages in prediction accuracy than the method based on a generative model. Combining the improvement of correction coefficients and user influence, the final model Hawkesandfeature&influence has the smallest APE value, and its prediction performance is the best. For the median APE, the performance of final model improves 71.60% than Hawkes at time 300s in Figure 6A. For the mean APE, the performance improves 78.46% at time 300s in Figure 6B. With the increase of the prediction time, the median and mean of APE show an overall downward trend, which once again reveals the fact that using more historical cascade information can improve the prediction accuracy. Meanwhile, from Figure 4 and Figure 6, the decline rate of APE gradually slows down with the passage of the prediction time, indicating that the amount of historical information available at the initial stage of the forwarding cascade increases rapidly, and then the growth rate of cascade information slows down. This phenomenon to some extent shows the rapid dissemination in social networks and the timeliness of posts, that is, posts are easier to obtain more forwards not long after publication, and with the time elapsed, the propagation of the posts eventually becomes stable.

FIGURE 6

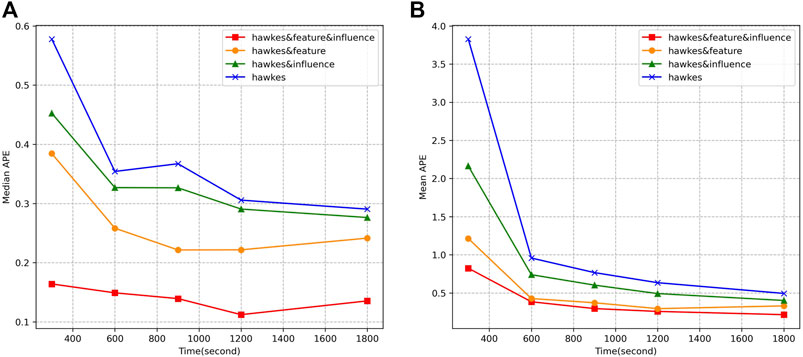
FIGURE 6. Comparison of APE of different models on dataset 2. (A) Evolutionary trend of the median APE with prediction time $t$, (B) Evolutionary trend of mean APE with prediction time $t$.

Figure 7 shows the evolution trend of Kendall rank correlation of the above four models with prediction time $t$. It can be seen from the figure that our model represented by Hawkesandfeature&influence has larger Kendall rank correlation, indicating that the correlation between predicted values and real values is the highest, and the prediction performance of the model is the best. The value of Kendall rank correlation increases with the passage of prediction time, and also reflect the fact that the prediction accuracy is improved with the increase of historical cascade information.

FIGURE 7

FIGURE 7. Comparison of Kendall rank correlation for different models on dataset 2.

We also notice that the performance of the models on the two datasets is slightly different. For instance, the mean APE of hawkesandfeature and Kendall rank correlation in dataset two are higher than it in dataset 1, which could be caused by the differences of the two networks. Dataset one contains a longer timeline of users’ actions, which leads to the better results.

Above all, through the experiments on real-world datasets, it can be concluded that our proposed method can effectively predict the final size of an information cascade, and has obvious performance improvement compared with the current process model.

4 Conclusion

Information cascades reflect a kind of user clustering behaviors, and the prediction of them has important theoretical significance and practical applications. In this paper, the prediction method based on model generation was proposed to solve the problem of cascade prediction. By analyzing the factors affecting information diffusion, we studied the growth mechanism of information cascades. On the basis of the Hawkes process, we modeled the arrival intensity of post forwarding process in combination with post attraction, forwarding user influence and users’ response time. We combined semi-local centrality with local clustering coefficients to measure the influence of forwarding users, and used the regression tree algorithm to improve the correction coefficients. Finally, the prediction model of the final number of forwards was obtained. The performance evaluation of the proposed method was carried out on real-world datasets, and results demonstrated that our method improves the prediction accuracy compared with representative models, indicating our method effectively realizes the prediction of information cascades.

In future, we will use deep learning methods to exploit forwarding paths and extract more latent features of information cascades, and incorporate deep learning with model generation methods. In addition, we will study the effective calculation methods of user influence in the propagation process, and investigate their roles in popularity prediction.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YZ designed the research and wrote the paper, CZ performed the experiments, and YZ conducted the validation and analyzed the results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://github.com/ShinyZC/dataset.

References

1. Davis JT, Perra N, Zhang Q, Moreno Y, Vespignani A. Phase Transitions in Information Spreading on Structured Populations. Nat Phys (2020) 16:590–596. doi:10.1038/s41567-020-0810-3

CrossRef Full Text | Google Scholar

2. Chen X, Wang R, Tang M, Cai S, Stanley HE, Braunstein LA. Suppressing Epidemic Spreading in Multiplex Networks with Social-Support. New J Phys (2018) 20:013007. doi:10.1088/1367-2630/aa9cda

CrossRef Full Text | Google Scholar

3. Velásquez-Rojas F, Ventura PC, Connaughton C, Moreno Y, Rodrigues FA, Vazquez F. Disease and Information Spreading at Different Speeds in Multiplex Networks. Phys Rev E (2020) 102:022312. doi:10.1103/PhysRevE.102.022312

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bao Q, Cheung WK, Zhang Y, Liu J. A Component-Based Diffusion Model with Structural Diversity for Social Networks. IEEE Trans Cybern (2017) 47(4):1078–1089. doi:10.1109/tcyb.2016.2537366

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Li D, Zhang S, Sun X, Zhou H, Li S, Li X. Modeling Information Diffusion over Social Networks for Temporal Dynamic Prediction. IEEE Trans Knowl Data Eng (2017) 29(9):1985–97. doi:10.1109/tkde.2017.2702162

CrossRef Full Text | Google Scholar

6. Cui P, Jin S, Yu L, Wang F, Zhu W, Yang S. Cascading Outbreak Prediction in Networks: a Data-Driven Approach. In: Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining; 2013 Aug 11-14; New York, USA. Association for Computing Machinery (2013). p. 901–909.

Google Scholar

7. Zhao J, Wu J, Xu K. Weak Ties: Subtle Role of Information Diffusion in Online Social Networks. Phys Rev E Stat Nonlin Soft Matter Phys (2010) 82:016105. doi:10.1103/PhysRevE.82.016105

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ma Z, Sun A, Cong G. On Predicting the Popularity of Newly Emerging Hashtags in Twitter. J Am Soc Inf Sci Tec (2013) 64:1399–1410. doi:10.1002/asi.22844

CrossRef Full Text | Google Scholar

9. Xiong F, Liu Y, Zhang Z, Zhu J, Zhang Y. An Information Diffusion Model Based on Retweeting Mechanism for Online Social media. Phys Lett A (2012) 376(30-31):2103–2108. doi:10.1016/j.physleta.2012.05.021

CrossRef Full Text | Google Scholar

10. Bakshy E, Hofman J, Mason W, Watts D. Everyone’s an Influencer: Quantifying Influence on Twitter. In: Proceedings of the Fourth ACM International Conference on Web Search and Data Mining; 2011 Feb 9-12; Hong Kong, China. ACM Press (2011). p. 65–74.

Google Scholar

11. Flamino J, Szymanski B. A Reaction-Based Approach to Information cascade Analysis. In: 28th International Conference on Computer Communication and Networks; 2019 Jul 29-Aug 1; Valencia, Spain. IEEE (2019). p. 1–9. doi:10.1109/icccn.2019.8847096

CrossRef Full Text | Google Scholar

12. Tsur O, Rappoport A. What’s in a Hashtag? : Content Based Prediction of the Spread of Ideas in Microblogging Communities. In: Proceedings of the Fifth ACM International Conference on Web Search and Data Mining; 2012 Feb 8-12; Seattle, Washington, USA. ACM Press (2012). p. 643–652.

Google Scholar

13. Bakshy E, Hofman JM, Mason WA, Watts DJ, Watts D. Everyone's an Influencer: Quantifying Influence on Twitter. In: Proceedings of the 4th ACM International Conference on Web Search & Web Data Mining; 2011 Feb 9-12; Hong Kong, China. ACM Press (2011). p. 65–74.

Google Scholar

14. Wang J, Li W, Weili W. Predicting Information Popularity Degree in Microblogging Diffusion Networks. Int J Multimedia Ubiquitous Eng (2014) 9(2):21–30. doi:10.14257/ijmue.2014.9.2.30

CrossRef Full Text | Google Scholar

15. Weng L, Menczer F, Ahn Y-Y. Virality Prediction and Community Structure in Social Networks. Sci Rep (2013) 3:2522. doi:10.1038/srep02522

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Tsugawa S. Empirical Analysis of the Relation between Community Structure and Cascading Retweet Diffusion. In: Proceedings of the Thirteenth International AAAI Conference on Web and Social Media; 2019 Jun 11-14; Münich, Germany. AAAI Press (2019). p. 493–504.

Google Scholar

17. Hong L, Dan O, Davison BD. Predicting Popular Messages in Twitter. In: Proceedings of the 20th International Conference Companion on World Wide Web; 2011 Mar 28-Apr 1; Hyderabad, India. ACM (2011). p. 57–58. doi:10.1145/1963192.1963222

CrossRef Full Text | Google Scholar

18. Wang K, Wang PH, Chen X, Huang Q, Mao Z, Zhang Y. A Feature Generalization Framework for Social Media Popularity Prediction. In: Proceedings of the 28th ACM International Conference on Multimedia (MM ’20); Seattle, WA; October 12–16, 2020. Association for Computing Machinery (2020). p. 4570–4574. doi:10.1145/3394171.3416294

CrossRef Full Text | Google Scholar

19. Kong Q, Mao W, Chen G, Zeng D. Exploring Trends and Patterns of Popularity Stage Evolution in Social Media. IEEE Trans Syst Man Cybern, Syst (2020) 50(10):3817–3827. doi:10.1109/tsmc.2018.2855806

CrossRef Full Text | Google Scholar

20. Zhang B, Wu Q, Chen X, Chen L. Information Cascades over Diffusion-Restricted Social Network: A Data-Driven Analysis. In: IEEE INFOCOM 2019 - IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS) (2019). 29 April 2019 - 02 May 2019, Paris, France, p. 151–156. doi:10.1109/infcomw.2019.8845264

CrossRef Full Text | Google Scholar

21. Crane R, Sornette D. Robust Dynamic Classes Revealed by Measuring the Response Function of a Social System. Proc Natl Acad Sci U.S.A (2008) 105(41):15649–15653. doi:10.1073/pnas.0803685105

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li Q, Wu Z, Yi L, N K, N. H, Ma X. WeSeer: Visual Analysis for Better Information cascade Prediction of WeChat Articles. IEEE Trans Vis Comput. Graphics (2020) 26:1399–1412. doi:10.1109/tvcg.2018.2867776

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Szabo G, Huberman BA. Predicting the Popularity of Online Content. Commun ACM (2010) 53:80–88. doi:10.1145/1787234.1787254

CrossRef Full Text | Google Scholar

24. Yu L, Cui P, Wang F, Song C, Yang S. From Micro to Macro: Uncovering and Predicting Information Cascading Process with Behavioral Dynamics. In: 2015 IEEE International Conference on Data Mining; 2015 Nov 14-17; Atlantic City, USA. IEEE (2015). p. 559–568. doi:10.1109/icdm.2015.79

CrossRef Full Text | Google Scholar

25. Zaman T, Fox EB, Bradlow ET. A Bayesian Approach for Predicting the Popularity of Tweets. Ann Appl Stat (2014) 8(3):1583–1611. doi:10.1214/14-aoas741

CrossRef Full Text | Google Scholar

26. Shen H, Wang D, Song C, Barabási AL. Modeling and Predicting Popularity Dynamics via Reinforced Poisson Processes. In: Proceedings of the 28th AAAI Conference on Artificial Intelligence; 2014 Jul 27-31; Québec, Canada. AAAI Press (2014). p. 291–297.

CrossRef Full Text | Google Scholar

27. Kobayashi R, Lambiotte R. TiDeH: Time-dependent Hawkes Process for Predicting Retweet Dynamics. In: the 10th International AAAI Conference on Web and Social Media; 2016 May 17-20; Cologne, Germany. AAAI Press (2016). p. 191–200.

Google Scholar

28. Zhao Q, Erdogdu MA, He HY, Rajaraman A, Leskovec J. SEISMIC: A Self-Exciting point Process Model for Predicting Tweet Popularity. In: Proceedings of the 21th International Conference on Knowledge Discovery and Data Mining; 2015 Aug 10-13; Sydney, Australia. ACM (2015). p. 1513–1522.

Google Scholar

29. Chen F, Tan WH. Marked Self-Exciting Point Process Modelling of Information Diffusion on Twitter. Ann Appl Stat (2018) 12(4):2175–2196. doi:10.1214/18-aoas1148

CrossRef Full Text | Google Scholar

30. Palmowski Z, Puchalska D. Modeling Social media Contagion Using Hawkes Processes. New York, NY: Cornell University (2020). ArXiv, abs/2010.14623.

Google Scholar

31. Srivathsan S, Cranefield S, Pitt J. A Bayesian Model of Information Cascades. New York, NY: Cornell University (2021). p. 03166. ArXiv, abs/2105.

Google Scholar

32. Hawkes AG, Oakes D. A Cluster Process Representation of a Self-Exciting Process. J Appl Probab (1974) 11(3):493–503. doi:10.2307/3212693

CrossRef Full Text | Google Scholar

33. Chen D, Lü L, Shang M-S, Zhang Y-C, Zhou T. Identifying Influential Nodes in Complex Networks. Physica A: Stat Mech its Appl (2012) 391(4):1777–1787. doi:10.1016/j.physa.2011.09.017

CrossRef Full Text | Google Scholar

34. van Doorn J, Ly A, Marsman M, Wagenmakers E-J. Bayesian Inference for Kendall's Rank Correlation Coefficient. The Am Statistician (2018) 72(4):303–308. doi:10.1080/00031305.2016.1264998

CrossRef Full Text | Google Scholar