- 1School of Electrical and Electronic Engineering, Anhui Science and Technology University, Bengbu, China
- 2Key Laboratory of Functional Materials and Devices for Informatics of Anhui Higher Education Institutes, Fuyang Normal University, Fuyang, China
- 3School of Physics and Optoelectronics Engineering, Anhui University, Hefei, China
Einstein–Podolsky–Rosen steering is a peculiar quantum nonlocal correlation and has unique physical characteristics and a wide application prospect. Even more importantly, multipartite steerable states have more vital applications in the future quantum information field. Thus, in this work, we explored the dynamics characteristics of both genuine multipartite steering (GMS) and genuine multipartite entanglement (GME) and the relations of both under an open tripartite system. Specifically, the tripartite decoherence system may be modeled by the three parties of a tripartite state that undergo the noisy channels. The conditions for genuine entangled and steerable states can be acquired for the initial tripartite state. The results showed that decoherence noises can degrade the genuine multipartite entanglement and genuine multipartite steering and even induce its death. Explicitly, GME and GMS disappear with the increase in the decoherence strength under the phase damping channel. However, GME and GMS rapidly decay to death with the increase in the channel-noise factor and then come back to life soon after in the bit flip channel. Additionally, the results indicate that GMS is born of GME, but GME does not imply GMS, which means that the set of genuine multipartite steerable states is a strict subset of the set of genuine multipartite entangled states. These conclusions may be useful for discussing the relationship of quantum nonlocal correlations (GME and GMS) in the decoherence systems.
Introduction
EPR steering and entanglement are two fundamental characteristics of quantum mechanics and that are inextricably linked. For the moment, the researchers believe that EPR steering stems from entanglement, but entanglement does not imply EPR steering [1, 2]. EPR entanglement characterizes quantum nonlocal correlations among remote parties that are totally forbidden within the classical regime. Moreover, multipartite entangled states have important applications in the field of quantum information. Utilizing and characterizing such quantum resources stemming from multipartite nonlocal correlations [3] are rather crucial for the applications of the information theory [4–10] and from foundational perspectives. A multipartite state is deemed to be genuinely multipartite entangled [11] if and only if the state may not be written as a convex linear combination of states, each of which is disentangled with reference to some partition.
One the other hand, the concept of EPR steering was first introduced by Schrödinger [12, 13] in the context of the EPR argument [14]. Conceptually, EPR steering describes a nontrivial trait of quantum mechanics that an observer can immediately “steer” a distant party by employing the local quantum measures. EPR steering can be detected by utilizing EPR steering inequalities [15–22]; the violation of EPR steering inequalities can indicate that EPR steering occurs. At first, Reid [23] derived an inequality for EPR steering based on Heisenberg uncertainty relation in 1989. Then, EPR steering was formally defined in 2007 [24]. Numerous EPR steering inequalities have since been given; however, most respect was given to detecting bipartite EPR steering [25]. Additionally, multipartite steerable states have vital applications in the future quantum information field. Consequently, the detection and investigation of multipartite EPR steering is more important and challenging. The concept of multipartite EPR steering was first introduced by He and Reid [26] and developed for Gaussian states by Kogias et al. [27]. Experiments were followed [28–32], which motivated research studies of the monogamy relationship of EPR steering [33, 34]. Moreover, Wang et al. [35] have optimized the collective EPR steering for the tripartite state within a particular optics-based system in 2014.
In a realistic world, a quantum system ineluctably suffers from the influence of the decoherence attributed to the mutual effect between the system and its external noises. Typically, noisy environments usually can be classified into two species, namely, non-Markovian and Markovian environments [36–40]. In detail, the Markovian noisy environment is featured by leading to the degeneration of quantum nonlocal correlations [40]. By contrast, as a normative non-Markovian noisy environment [41, 42], a dynamic characteristic of quantum nonlocal correlations can be discovered, which is the renewal of quantum nonlocal correlations after a finite time period of the entire disappearance [43]. As a consequence, in the course of quantum information processing, considering the external noisy environments is indispensable and significant under a realistic regime. However, in the past years, there have been only a few authors to examine the steerability of multipartite states in the local noisy environments [44–46]. Hence, we will concentrate on exploring the genuine multipartite steering (GMS) and genuine multipartite entanglement (GME) under the noise channels. We here mainly probed the dynamic characteristics of GME and GMS and the relationship between them under the noise channels.
The remainder of this article is organized as follows. In Section II, we introduced the measuring method of GME and GMS within the multi-body systems, respectively. Then, we investigated the dynamic behaviors of GMS for the initial tripartite state under two kinds of different noises in Section 3. In Section 4, we probed the characteristic of GME and compared it with GMS as the tripartite state under the two kinds of different noises. Finally, we ended up our article with a brief conclusion.
2 Measurements of GME and GMS
2.1 Measurement of GME
In the first place, a method to measure multi-body entanglement is introduced, viz., GME. N-partite entanglement is defined by its opposite, bi-separability. An N-partite state that cannot be written as an ensemble of bi-separable states is an N-partite entangled state. Employing the results of Ref. [47], for a multi-body quantum state
where
where Eq. 2 is a quantified expression for multi-body entanglement, and the range is zero to one. If the value of the GME is equal to zero, which means that the tripartite state does not have genuine multipartite entanglement, then the tripartite state is not a genuine tripartite entangled state. Furthermore, if the value of the GME is greater than zero and less than or equal to one, which means that the tripartite state does have genuine multipartite entanglement, the tripartite state is a genuine tripartite entangled state. Moreover, the value of the GME is equal to one, which means that the tripartite state is the maximal genuine entangled state.
2.2 Measurement of GMS
According to the method proposed by He and Reid [26], if the tripartite system is a three-qubit system, with the usual Pauli operators defined for each site, the uncertainty relation for spin implies
where
If the GMS inequality in Eq. 4 is violated, which is sufficient to show GMS, and the value of GMS inequality is smaller, it means that the steerability is stronger.
3 Dynamic Properties of GMS for the Initial Tripartite State Within the Two Kinds of the Different Noises
In this section, we assume that there are three parties and they share an initial three-qubit state in the form of [48, 49].
where
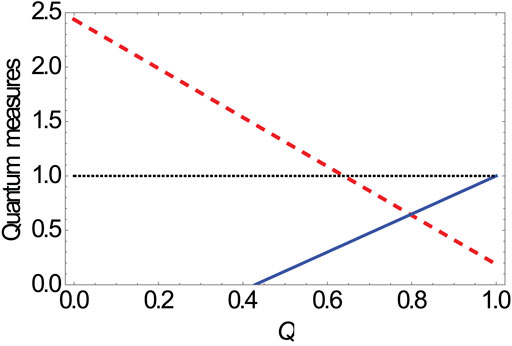
FIGURE 1. (Color online) Quantum measures {GME (blue solid line) and GMS inequality (red dashed line)} as a function of the state parameter Q, when
Next, we considered that the tripartite states each independently and locally interacts with a zero-temperature reservoir. Herein, the two kinds of different noisy channels were considered: the bit flip (BF) channel and phase damping (PD) channel, respectively. In this context, the system–environment interaction via the operator-sum representation formalism is utilized. Following the approach of the Kraus operators, the time-evolution of the initial three-qubit states under the local noisy environment can be expressed by the trace-preserving quantum operation
where one can call that d is the channel-noise factor and
where d is the decoherence strength, and
As a consequence, when three parties (all subsystem) of the three-qubit states suffer from the two different noisy environments, we then can obtain the non-zero elements of two kinds of the different final states,
To be precise, as three parties of the three-qubit states undergo the BF channel, the final state can be written as
Hence, we can obtain the non-zero elements of the final states
Then, as three parties of the three-qubit states, Eq. 5 suffers from the PD channel; the final state can be written as
and the non-zero elements of final states
Herein, by using Eqs 3, 4, one can gain an analytical expression of the GMS inequality for the initial state within the two kinds of different noisy channels, respectively. In accordance with the abovementioned analysis, one can draw the GMS inequality of the states
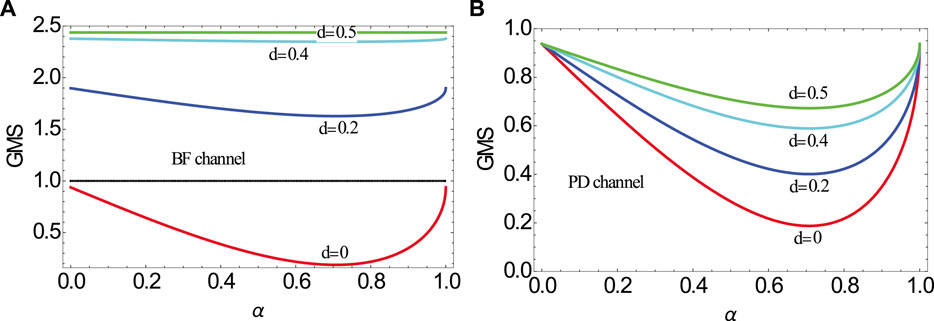
FIGURE 2. (Color online) GMS-inequality as a function of the state parameter
Then, in order to explore the influence of the state parameters
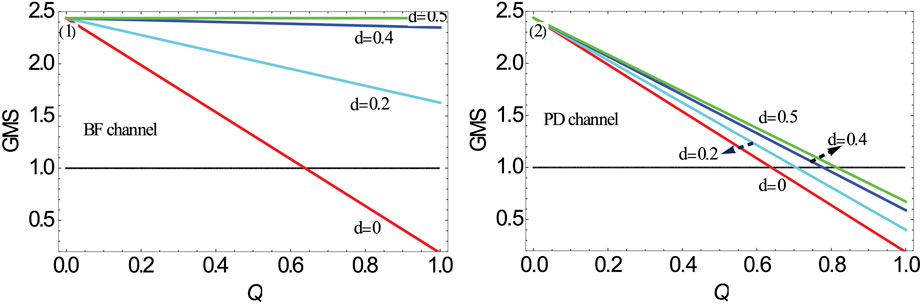
FIGURE 3. (Color online) GMS inequality as a function of the state parameter
Next, we considered the effects of the state parameters
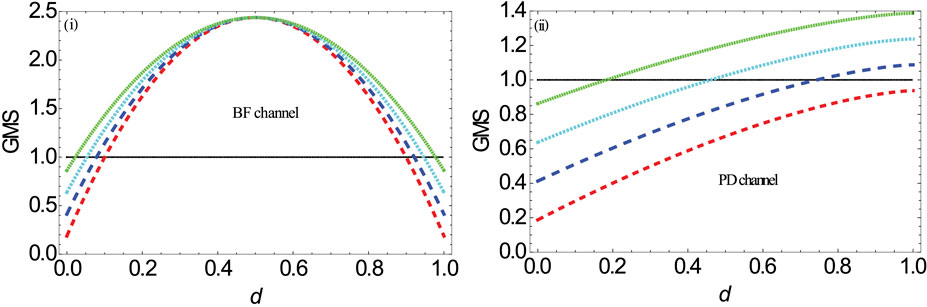
FIGURE 4. (Color online) GMS inequality as a function of the channel-noise factor d in terms of different state parameters
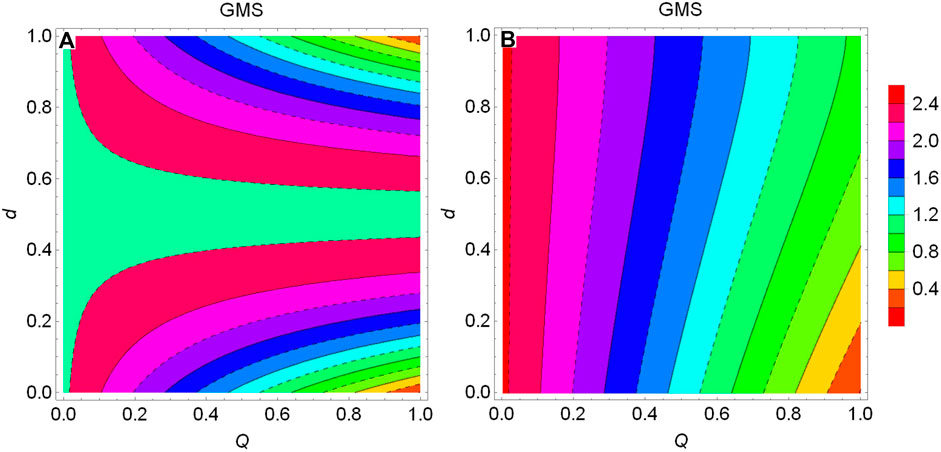
FIGURE 5. (Color online) Contour plot of GMS inequality versus the state parameter
Hence, we can conclude that the decoherence effect can destroy the steerability of quantum states or even completely disable the steerability. In order to more intuitively observe the influence of the three parameters (the channel-noise factor
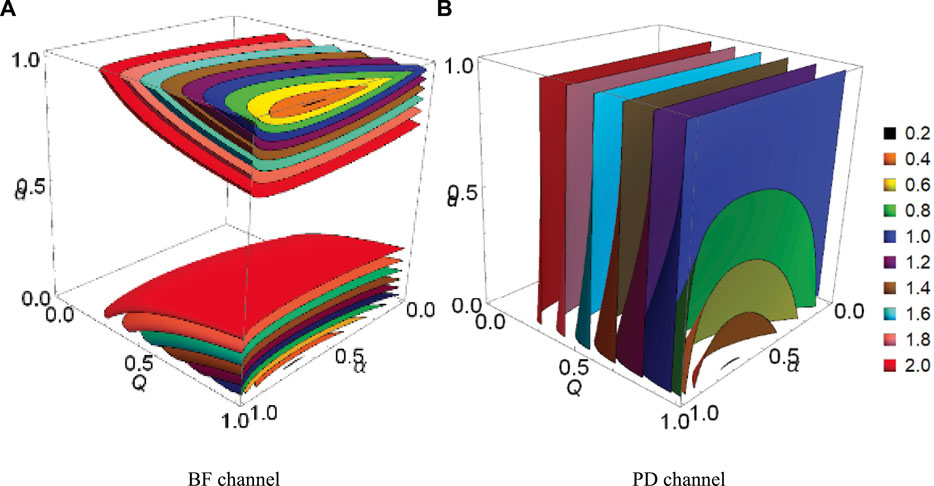
FIGURE 6. (Color online) 3D contour plot of GMS inequality versus the state parameters
4 Dynamic Characteristics of GME and Its Comparison With the GMS Under the Two Kinds of the Different Noises
It is generally acknowledged that quantum steering originates from quantum entanglement; however, entanglement does not imply steering, which means that the set of steerable states is a strict subset of the set of entangled states. In this section, we probed the dynamic characteristics of GME and then discussed the relationship between GMS and the GME under the two kinds of the noisy channels.
By employing Eq. 2, we can give the expressions of the GME as
and
under the BF and PD channels, respectively.
To begin with, we considered the influence of the state parameters
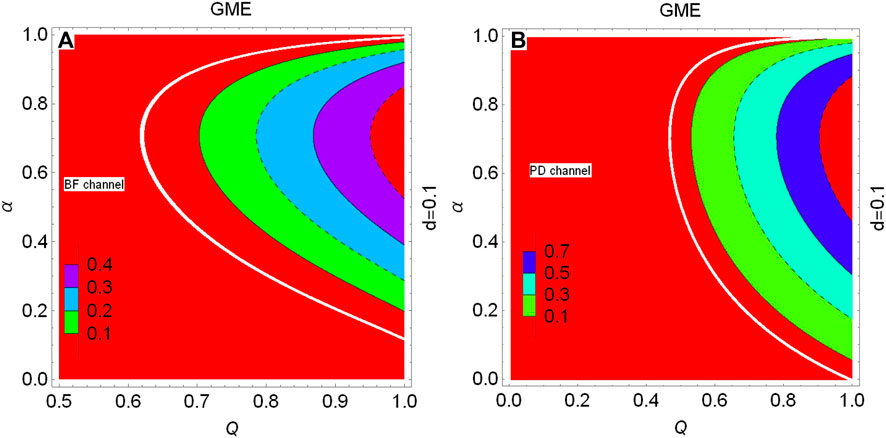
FIGURE 7. (Color online) Contour plot of GME versus the state parameters
Next, for comparing GME with GMS and the relationship between GMS and GME, we investigated the influence between the state parameters

FIGURE 8. (Color online) Variety of quantum measures (GME (dashed line) and GMS (solid line)) as a function of channel-noise factor d in terms of different state parameters
5 Conclusion
In this article, we mainly investigated the physical characteristic of GME and GMS within the two kinds of the different noisy channels. In contrast with our previous work [49], we used different initial states, and this state (see Eq. 5) is more general. In addition, here, we utilized different measurement methods for the multipartite quantum nonlocal correlation (GME) in this work. The anti-decoherence ability of GME is stronger than that of GMN. In the next place, a tripartite state is subjected to different decoherence noisy environments, but one is under curved spacetime (non-inertial frame) and one is without (this work). Consequently, in this study, we first discussed that the dynamic properties of GMS and GME for the initial tripartite state and the conditions for entangled and steerable states can be given. Then, the effect of BF and PD noises on the GMS is discussed, respectively. The results indicated that GMS is very flimsy under the influence of the decoherence. Specifically, GMS will perish with the increase in the channel-noise factor under the PD channel. However, GMS rapidly decays to death with the increase in the channel-noise factor and then come back to life soon in the BF channel. At the end, we studied the dynamic characteristics of GME and discussed the relationship between GME and GMS under decoherence noises. The decoherence noises can also degrade the GME and even induce its death. In addition, we can draw a conclusion that GMS originates from GME, but the GME does not imply GMS, which means that the set of genuine multipartite steerable states is a strict subset of the set of genuine multipartite entangled states. These conclusions may be useful for analyzing the relationship of quantum nonlocal correlations in the decoherence noises.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
W-YS contributed to the conception and design of the study. W-YS wrote the first draft of the manuscript. A Ding, H-TG, and JH wrote sections of the manuscript. All authors revised, read, and approved the submitted manuscript.
Funding
This work was supported by the Anhui Provincial Natural Science Foundation under the Grant No. 2008085QF328, and the Open Project Program of Key Laboratory of Functional Materials and Devices for Informatics of Anhui Higher Education Institutes (Fuyang Normal University) under Grant No. FSKFKT003, and the Talent Introduction Project of Anhui Science and Technology University under Grant Nos. DQYJ202005 and DQYJ202004, and also the Natural Science Foundation of Education Department of Anhui Province under Grant Nos. KJ2021A0865, KJ2021ZD0071 and KJ2021A0867.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Jones SJ, Wiseman HM, Doherty AC. Entanglement, Einstein-Podolsky-Rosen Correlations, Bell Nonlocality, and Steering. Phys Rev A (2007) 76:052116. doi:10.1103/physreva.76.052116
2. Wu S-M, Zeng H-S. Genuine Tripartite Nonlocality and Entanglement in Curved Spacetime. Eur Phys J C (2022) 82:4. doi:10.1140/epjc/s10052-021-09954-4
3. Bengtsson I, Zyczkowski K. A Brief Introduction to Multipartite Entanglement. arXiv preprint arXiv: 1612.07747 (2016). doi:10.48550/arXiv.1612.07747
4. Hillery M, Bužek V, Berthiaume A. Quantum Secret Sharing. Phys Rev A (1999) 59:1829–34. doi:10.1103/physreva.59.1829
5. Sørensen AS, Mølmer K. Entanglement and Extreme Spin Squeezing. Phys Rev Lett (2001) 86:4431. doi:10.1103/physrevlett.86.4431
6. Raussendorf R, Briegel HJ. A One-Way Quantum Computer. Phys Rev Lett (2001) 86:5188–91. doi:10.1103/physrevlett.86.5188
7. Chen K, Lo H-K. Multi-partite Quantum Cryptographic Protocols with Noisy GHZ States. Quan Inf. Comput (2007) 7:689–715. doi:10.26421/qic7.8-1
8. Briegel HJ, Browne DE, Dür W, Raussendorf R, Van den Nest M. Measurement-based Quantum Computation. Nat Phys (2009) 5:19–26. doi:10.1038/nphys1157
9. Toth G. Multipartite Entanglement and High-Precision Metrology. Phys Rev A (2012) 85:022322. doi:10.1103/physreva.85.022322
10. Dai TZ, Fan Y, Qiu L. Complementary Relation between Tripartite Entanglement and the Maximum Steering Inequality Violation. Phys Rev A (2022) 105:022425. doi:10.1103/physreva.105.022425
11. Gühne O, Seevinck M. Separability Criteria for Genuine Multiparticle Entanglement. New J Phys (2010) 12:053002. doi:10.1088/1367-2630/12/5/053002
12. Schrödinger E. Discussion of Probability Relations between Separated Systems. Proc Cambridge Philos Soc (1935) 31:555. doi:10.1017/s0305004100013554
13. Schrödinger E. Probability Relations between Separated Systems. Proc Cambridge Philos Soc (1936) 32:446. doi:10.1017/s0305004100019137
14. Einstein A, Podolsky B, Rosen N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys Rev (1935) 47:777–80. doi:10.1103/physrev.47.777
15. Cavalcanti EG, Jones SJ, Wiseman HM, Reid MD. Experimental Criteria for Steering and the Einstein-Podolsky-Rosen Paradox. Phys Rev A (2009) 80:032112. doi:10.1103/physreva.80.032112
16. Cavalcanti EG, Foster CJ, Fuwa M, Wiseman HM. Analog of the Clauser-Horne-Shimony-Holt Inequality for Steering. J Opt Soc Am B (2015) 32:A74. doi:10.1364/josab.32.000a74
17. Schneeloch J, Broadbent CJ, Walborn SP, Cavalcanti EG, Howell JC. Einstein-Podolsky-Rosen Steering Inequalities from Entropic Uncertainty Relations. Phys Rev A (2013) 87:062103. doi:10.1103/physreva.87.062103
18. Chen J-L, Ye X-J, Wu C, Su H-Y, Cabello A, Kwek LC, et al. All-versus-nothing Proof of Einstein-Podolsky-Rosen Steering. Sci Rep (2013) 3:2143. doi:10.1038/srep02143
19. Jevtic S, Hall MJW, Anderson MR, Zwierz M, Wiseman HM. Einstein-Podolsky-Rosen Steering and the Steering Ellipsoid. J Opt Soc Am B (2015) 32:A40. doi:10.1364/josab.32.000a40
20. Costa ACS, Angelo RM. Quantification of Einstein-Podolski-Rosen Steering for Two-Qubit States. Phys Rev A (2016) 93:020103. doi:10.1103/physreva.93.020103
21. Kogias I, Skrzypczyk P, Cavalcanti D, Acín A, Adesso G. Hierarchy of Steering Criteria Based on Moments for All Bipartite Quantum Systems. Phys Rev Lett (2015) 115:210401. doi:10.1103/physrevlett.115.210401
22. Zukowski M, Dutta A, Yin Z. Geometric Bell-like Inequalities for Steering. Phys Rev A (2015) 91:032107. doi:10.1103/physreva.91.049902
23. Reid MD. Demonstration of the Einstein-Podolsky-Rosen Paradox Using Nondegenerate Parametric Amplification. Phys Rev A (1989) 40:913–23. doi:10.1103/physreva.40.913
24. Wiseman HM, Jones SJ, Doherty AC. Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox. Phys Rev Lett (2007) 98:140402. doi:10.1103/physrevlett.98.140402
25. Uola R, Costa ACS, Nguyen HC, Gühne O. Quantum Steering. Rev Mod Phys (2020) 92:015001. doi:10.1103/revmodphys.92.015001
26. He QY, Reid MD. Genuine Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2013) 111:250403. doi:10.1103/physrevlett.111.250403
27. Kogias I, Lee AR, Ragy S, Adesso G. Quantification of Gaussian Quantum Steering. Phys Rev Lett (2015) 114:060403. doi:10.1103/PhysRevLett.114.060403
28. Cavalcanti D, Skrzypczyk P, Aguilar GH, Nery RV, Ribeiro PHS, Walborn SP. Detection of Entanglement in Asymmetric Quantum Networks and Multipartite Quantum Steering. Nat Commun (2015) 6:7941. doi:10.1038/ncomms8941
29. Armstrong S, Wang M, Teh RY, Gong Q, He Q, Janousek J, et al. Multipartite Einstein-Podolsky-Rosen Steering and Genuine Tripartite Entanglement with Optical Networks. Nat Phys (2015) 11:167–72. doi:10.1038/nphys3202
30. Kunkel P, Prüfer M, Strobel H, Linnemann D, Frölian A, Gasenzer T, et al. Spatially Distributed Multipartite Entanglement Enables EPR Steering of Atomic Clouds. Science (2018) 360:413–6. doi:10.1126/science.aao2254
31. Fadel M, Zibold T, Décamps B, Treutlein P. Spatial Entanglement Patterns and Einstein-Podolsky-Rosen Steering in Bose-Einstein Condensates. Science (2018) 360:409–13. doi:10.1126/science.aao1850
32. Opanchuk B, Rosales-Zárate L, Teh RY, Dalton BJ, Sidorov A, Drummond PD, et al. Mesoscopic Two-Mode Entangled and Steerable States of 40 000 Atoms in a Bose-Einstein-Condensate Interferometer. Phys Rev A (2019) 100:060102. doi:10.1103/physreva.100.060102
33. Deng X, Xiang Y, Tian C, Adesso G, He Q, Gong Q, et al. Demonstration of Monogamy Relations for Einstein-Podolsky-Rosen Steering in Gaussian Cluster States. Phys Rev Lett (2017) 118:230501. doi:10.1103/physrevlett.118.230501
34. Cheng S, Milne A, Hall MJW, Wiseman HM. Volume Monogamy of Quantum Steering Ellipsoids for Multiqubit Systems. Phys Rev A (2016) 94:042105. doi:10.1103/physreva.94.042105
35. Wang M, Gong Q, He Q. Collective Multipartite Einstein-Podolsky-Rosen Steering: More Secure Optical Networks. Opt Lett (2014) 39:6703. doi:10.1364/ol.39.006703
36. Zhang W-M, Lo P-Y, Xiong H-N, Tu MW-Y, Nori F. General Non-markovian Dynamics of Open Quantum Systems. Phys Rev Lett (2012) 109:170402. doi:10.1103/physrevlett.109.170402
37. Yin XL, Ma J, Wang XG, Nori F. Spin Squeezing under Non-markovian Channels by the Hierarchy Equation Method. Phys Rev A (2012) 86:012308. doi:10.1103/physreva.86.012308
38. Zhang J, Liu Y-X, Wu R-B, Jacobs K, Nori F. Non-Markovian Quantum Input-Output Networks. Phys Rev A (2013) 87:032117. doi:10.1103/physreva.87.032117
39. Xiong H-N, Lo P-Y, Zhang W-M, Feng DH, Nori F. Non-Markovian Complexity in the Quantum-To-Classical Transition. Sci Rep (2015) 5:13353. doi:10.1038/srep13353
40. Myatt CJ, King BE, Turchette QA, Sackett CA, Kielpinski D, Itano WM, et al. Decoherence of Quantum Superpositions through Coupling to Engineered Reservoirs. Nature (2000) 403:269–73. doi:10.1038/35002001
41. Lo Franco R, Bellomo B, Andersson E, Compagno G. Revival of Quantum Correlations without System-Environment Back-Action. Phys Rev A (2012) 85:032318. doi:10.1103/physreva.85.032318
42. Xu J-S, Sun K, Li C-F, Xu X-Y, Guo G-C, Andersson E, et al. Experimental Recovery of Quantum Correlations in Absence of System-Environment Back-Action. Nat Commun (2013) 4:2851. doi:10.1038/ncomms3851
43. Mazzola L, Maniscalco S, Piilo J, Suominen K-A, Garraway BM. Sudden Death and Sudden Birth of Entanglement in Common Structured Reservoirs. Phys Rev A (2009) 79:042302. doi:10.1103/physreva.79.042302
44. Wang M, Gong QH, Ficek Z, He QY. Role of thermal Noise in Tripartite Quantum Steering. Phys Rev A (2014) 90:023801. doi:10.1103/physreva.90.023801
45. Wang M, Xiang Y, He Q, Gong Q. Asymmetric Quantum Network Based on Multipartite Einstein-Podolsky-Rosen Steering. J Opt Soc Am B (2015) 32:A20. doi:10.1364/josab.32.000a20
46. Wang M, Xiang Y, He QY, Gong QH. Detection of Quantum Steering in Multipartite Continuous-Variable Greenberger-horne-zeilinger-like States. Phys Rev A (2015) 91:012112. doi:10.1103/physreva.91.012112
47. Rafsanjani SMH, Huber M, Broadbent CJ, Eberly JH. Genuinely Multipartite Concurrence of N-Qubit X Matrices. Phys Rev A (2012) 86:062303. doi:10.1103/physreva.86.062303
48. Ma XS, Wang AM, Cao Y. Entanglement Evolution of Three-Qubit States in a Quantum-Critical Environment. Phys Rev B (2007) 76:155327. doi:10.1103/physrevb.76.155327
49. Sun W-Y, Wang D, Ye L. Dynamics and Recovery of Genuine Multipartite Einstein-Podolsky-Rosen Steering and Genuine Multipartite Nonlocality for a Dissipative Dirac System via the Unruh Effect. Annalen Der Physik (2018) 530:1700442. doi:10.1002/andp.201700442
Keywords: open system, genuine multipartite steering, genuine multipartite entanglement, noise channel, uncertainty relation
Citation: Sun W-Y, Ding A, Gao H, Wang L, He J and Ye L (2022) Probing Genuine Multipartite Einstein–Podolsky–Rosen Steering and Entanglement Under an Open Tripartite System. Front. Phys. 10:941159. doi: 10.3389/fphy.2022.941159
Received: 11 May 2022; Accepted: 16 June 2022;
Published: 19 July 2022.
Edited by:
Jun Feng, Xi'an Jiaotong University, ChinaReviewed by:
Rui Qu, Xi'an Jiaotong University, ChinaLiming Zhao, Southwest Jiaotong University, China
Copyright © 2022 Sun, Ding, Gao, Wang, He and Ye. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wen-Yang Sun, c3d5XzMyOTlAMTYzLmNvbQ==
 Wen-Yang Sun
Wen-Yang Sun Amin Ding1
Amin Ding1 Liu Ye
Liu Ye