- Centre for Inertial Fusion Studies, The Blackett Laboratory, Imperial College, London, United Kingdom
Inertial confinement fusion (ICF) experiments create a unique laboratory environment in which thermonuclear fusion reactions occur within a plasma, with conditions comparable to stellar cores and the early universe. In contrast, accelerator-based measurements must compete with bound electron screening effects and beam stopping when measuring fusion cross sections at nucleosynthesis-relevant energies. Therefore, ICF experiments are a natural place to study nuclear reactions relevant to nuclear astrophysics. However, analysis of ICF-based measurements must address its own set of complicating factors. These include: the inherent range of reaction energies, spatial and temporal thermal temperature variation, and kinetic effects such as species separation. In this work we examine these phenomena and develop an analysis to quantify and, when possible, compensate for their effects on our inference. Error propagation in the analyses are studied using synthetic data combined with Markov Chain Monte Carlo (MCMC) machine learning. The novel inference techniques will aid in the extraction of valuable and accurate data from ICF-based nuclear astrophysics experiments.
1 Introduction
Inertial confinement fusion (ICF) experiments use implosions to reach thermonuclear conditions with high temperatures (T ≳ 1 keV) and densities (ρ ≳ 1 g/cc). The short-lived plasma is sufficiently hot that thermal ions can undergo fusion reactions, at typical densities plasma screening effects are currently modelled to be at the
The fusion cross section is canonically written in the following form:
where K is the reactants relative kinetic energy, S is the S-factor, and KB is the Coulomb barrier energy. By splitting terms in this form, the S-factor gives the nuclear physics dependent contribution to the cross section. As the Coulombic part is already known, cross section measurements aim to extract the value of the S-factor as a function of reaction energy.
The probability of a reaction is proportional to the product of the cross section and relative velocity, σv. The reactant species in a thermonuclear plasma have a range of velocities and thus the probability of reaction and number of fusion reactions depends on the average σv value. Mathematically, the volumetric reaction rate and yield of a reaction involving reactants labelled 1 and 2 are given by:
where n1 and n2 are the reactant number densities, ⟨σv⟩12 is the reactivity and δ12 is a Kronecker delta to account for double counting in homonuclear reactions. Extracting reactivity information from a yield requires knowledge of the number densities of the reactants and their burn time and volume. Instead, it is preferable to perform a differential measurement through a yield ratio. The yield ratio between reactions involving reactants 1,2 and 3,4 is given by:
Generally, one of the reactions considered has a well-known S-factor and acts as a reference from which the other target reaction S-factor can be measured. A temperature must also be measured to evaluate the reference reaction reactivity. The ion temperature is typically measured using fusion product spectroscopy [9–13]. However, in order to relate the yield ratio and temperature measurements to the underlying fusion cross section a number of approximations must be made. Listed below are the set of approximations commonly used to infer cross-sections from yield ratio measurements in ICF experiments:
1. Maxwellian reactant ion velocity distributions
2. No species separation, ni/ntot = constant
3. Uniform static temperature, T = constant
4. Narrow Gamow peak, S(K) ≃ constant
Approximations (1) and (2) can only be violated if ion kinetic effects are present, while approximation (3) is violated by spatial and/or temporal hydrodynamic temperature gradients. Finally, approximation (4) introduces errors even for a single temperature plasma–the Gamow peak is the range of relative kinetic energies over which the majority of fusion reactions occur, a more detailed description will be given in Section 2.
In this work we will examine the yield ratio measurement and the error associated with the common approximations made. This will provide both quantitative estimates of the error but also analysis techniques to reduce or remove the errors.
2 Gamow peak approximations
Within a local description of a plasma, ions have a range of velocities as determined by the distribution function. Therefore, there is an inherent range of relative velocities in the reactants. The number density of reactions at a given relative kinetic energy is given by:
where g(K) is the distribution of relative kinetic energy in the reactants, vr is the relative velocity and m12 is the reactants’ reduced mass. The cross section more than exponentially suppresses reactions a low K, while typical ion velocity distributions are decreasing functions of K. Therefore, the product of the cross section and vrg(K) define a peaked window of probable reaction energies known as the Gamow peak. For Maxwellian reactants at temperature T:
Integrating Eq. 5 over all energies gives rise to the following reactivity:
Yield ratios depend on these reactivities and we wish to relate them to the form of the cross section. Using the canonical form of cross section, we can separate the fast Coulomb barrier penetrability from the slow S-factor dependence. The product of the Coulomb barrier penetrability and the reactant K distribution is the primary determinant in the form of the Gamow peak. Now, the S-factor is sampled across the narrow Gamow peak giving an opportunity for an energy-resolved measurement. The problem is greatly simplified by working in the natural energy unit of the Gamow peak energy [14, 15], KG. At a given temperature, this is the most probable (modal) reaction energy.
where we include the definition of Clayton’s large dimensionless parameter [15], τ. Using this canonical variable transformation leads to a reactivity formula of the form:
If ϵ ≪ 1, then this reactivity formula is a Laplace-type integral and the saddlepoint method will give a good approximation [9]. A temperature-dependent effective S-factor can then be constructed which takes into account the finite width of Gamow peak, the energy dependence of the S-factor and the innate skew of the Gamow peak [14].
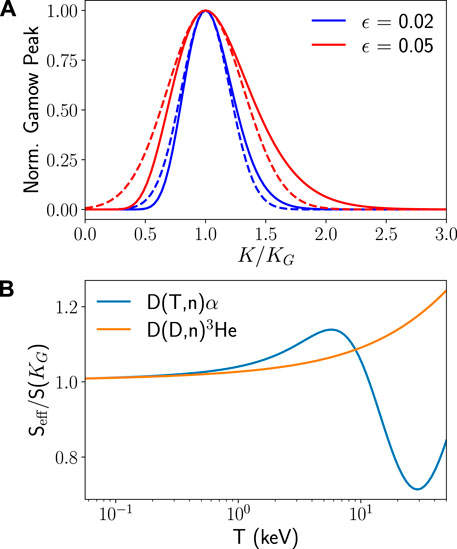
FIGURE 1. (A) The normalised Gamow peak for ϵ values of 0.02 and 0.05. The solid lines use the exact form and the dashed lines show the saddlepoint approximation, which is valid for ϵ ≪ 1. (B) The ratio of Seff (as defined in Eq. 13) to S(KG) for the resonant D (T,n)α and non-resonant D (D,n)3He reactions. These are evaluated using the Bosch-Hale cross section fit [8].
Similar to the saddlepoint approximation to the Gamow peak, the small parameter ϵ can be used as an expansion coefficient for the effective S-factor. This expansion will give a formula relating the effective S-factor to the nuclear S-factor [16]:
Full expressions for δA,n are given in Supplementary Appendix SA, these terms can be used to evaluate the accuracy of the Gamow peak approximation. As long as ϵ is sufficiently small to validate the expansion, these equations provide the relationship between effective and nuclear S-factors. As shown by Eq. 15, the value of the effective S-factor is sensitive to local behaviour of S(K) around the Gamow peak energy, beyond just the value of S(KG). For non-resonant reactions a linear or quadratic order expansion of S(K) will likely be sufficient. As shown in Figure 1, the deviation between effective and nuclear S-factors is larger for resonant reactions and therefore more expansion terms would be required to maintain accuracy; it is therefore preferable to use resonant reactions as reference reactions. At higher temperatures or ϵ, the Gamow peak will be broader and thus sample the S-factor over a larger range of energies. Consequently, more terms may be required for accuracy at higher ϵ.
As discussed in Section 1, yield ratio measurements are used to infer target reaction S-factors relative to a well-known reference reaction. If we permit ourselves to utilise approximations (1)–(3), this inference uses the following equation:
where:
where the target reaction involves species 1 and 2, and reference reaction species 3 and 4. The particle charges are Zi and the concentration fractions are fi. The exponent function χ(T) is set by the difference in the two reactions’ Coulomb barriers. These equations can be used to evaluate the target reaction Seff from knowledge of the reference reaction effective S-factor. For non-resonant reactions, we expect the effective S-factor to be closely related to the nuclear S-factor evaluated at the Gamow peak energy. More formally, we can define a ratio of these terms,
Accurately computing
Within the literature, a commonly studied non-resonant reference is D (D,n)3He—we will use this as a case study for errors introduced by approximations to
It is simple to show that the argument of S(K) above is the mean energy for the Gamow peak [17],
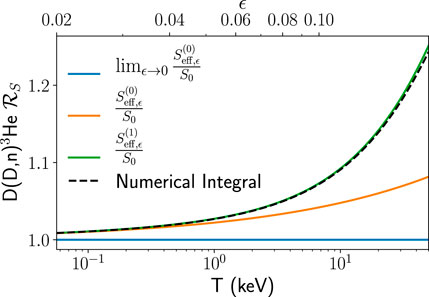
FIGURE 2. Plot showing the ratio of effective to nuclear S-factor,
It is important to make a distinction here between KG,
In summary, the nuclear S-factor can be inferred from a measured effective S-factor for non-resonant reactions with low error. This does require additional correction factors to be evaluated which will depend on the local behaviour of the nuclear S-factor about the Gamow peak. This complicates the inference as a-priori information on the S-factor is required. Avoiding this complication by assuming S(K) is linear or constant over the whole Gamow peak can introduce errors from a few percent to tens of percent depending on the temperature and reactions. It is therefore vitally important to consider the acceptable level of approximation and when necessary introduce a-priori information on the nuclear S-factor to improve the accuracy of the inference.
3 Hydrodynamic plasmas
3.1 Temperature variance
In the previous section we consider reactions from an isothermal fusion plasma. In ICF experiments the temperature rapidly varies in space and time. Therefore, there is an inherent range of temperatures in which fusion reactions are occurring. The reaction-weighted temperature distribution will have a mean temperature (T) and variance
Previous work by Kabadi et al. [18] derived a second order yield-temperature relation which included the effect of temperature variance. We can extend this work to the effective S-factor reactivity formalism by including a correction factor,
The second-order correction factor is then given by:
where s1 and s2 are functions of the target and reference reaction effective S-factors:
The temperature-dependent function ΓT can be used to explore fusion reactions’ sensitivity to temperature variance. As one might expect, yield ratios are sensitive to the local behaviour of the effective S-factor when there is a range of temperatures. As in the previous section, we must evaluate whether this sensitivity precludes an accurate inference of the target reaction S-factor. Separate to S-factor gradients, it is clear that a significant correction will arise from reaction pairs with large differences in Coulomb barrier penetrability. Figure 3 explores the temperature dependence of ΓT for the reaction pair 3He (D,p)α and D (D,n)3He. We find that a temperature variance correction including only the Coulomb barrier terms, i.e., s1 = s2 = 0, provides a good estimate of the effect on yield ratio for the reaction pair 3He (D,p)α and D (D,n)3He, for T
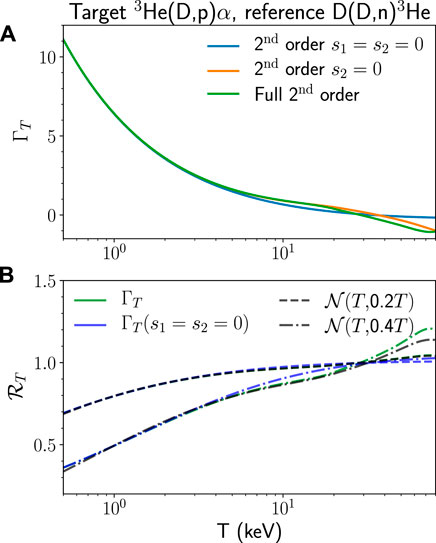
FIGURE 3. (A) Plot showing the temperature dependence of the second-order yield ratio temperature variance correction, ΓT. Including the effect of the effective S-factor temperature is shown. (B) Plot showing the
3.2 Synthetic data study
We will use synthetic data to illustrate the propagation of errors involved with both our assumptions and typical measurement uncertainties. We will use the non-resonant reactions p (D,γ)3He and D (D,n)3He as our first target/reference pair. This will allow a comparison to recent ICF-based measurements by Zylstra et al. [3].
We will use the Bosch-Hale [8] fit for D (D,n)3He and the Adelberger et al. [7] fit for p (D,γ)3He to create the synthetic data. These fits use accelerator-based data down to nucleo-synthesis relevant energies, additional modern data is available for these reactions [21–23]. For measurement uncertainties we assume: a 10% uncertainty in the yield ratio, 0.2 keV error in the spectral temperature [9], 1% uncertainty in the fuel fill fractions and 5% uncertainty in the D (D,n)3He S-factor. There are additional known unknowns which increase the uncertainty in our inference. The spectral temperature (Ts) is inflated above the burn-averaged temperature by fluid velocity effects [11–13], for D (D,n)3He this is given by
For the synthetic data study, we will also assume no a-priori information on the target reaction effective S-factor and thus we will drop the s1 and s2 terms in ΓT. The second part of the analysis is to extract the nuclear S-factor from the effective S-factor to allow comparison with accelerator data. This can be done using a 0th or 1st order approximation for

TABLE 1. A table summarising the Bayesian model and MCMC sampling statistics for the two synthetic data studies in this work.
Figure 4 shows the results of this synthetic data study. It is seen that the effects of fluid velocity and temperature variance introduce a systematic error of a similar order to the local behaviour of the S-factor around the Gamow peak. This systematic error will be increased for implosions with larger deviations from uniform conditions or for reactions with stronger sensitivity to temperature variance. It is also clear that the local behaviour of the S-factor around the Gamow peak is of equal importance. When these effects are properly accounted for, this synthetic data study suggests the analysis presented above can be highly accurate and remove much of the systematic error. This synthetic data study is directly comparable to the p (D,γ)3He measurement by Zylstra et al. [3]. Using a uniform model, Zylstra et al. found a S-factor above model values [7] and recent accelerator data [25]. Using the hydrodynamic model described here would improve agreement between the ICF and accelerator measurements. Improvements in experimental uncertainties, particularly for the yield ratio measurement, will be necessary to reduce the remaining random error in the inference. Simulation studies could also be used to improve our priors on temperature variance and spectral broadening by isotropic flows. Alternatively, experiments with multiple reference reactions could be used to measure these effects independently.
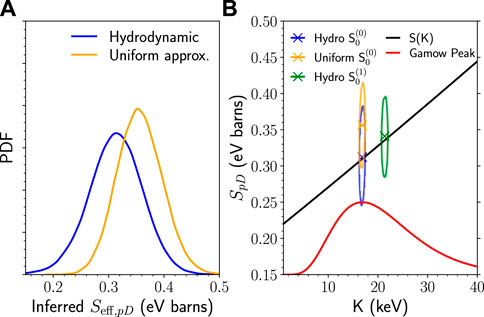
FIGURE 4. (A) Plot showing the probability distribution function (PDF) of the inferred p (D,γ)3He effective S-factor for two different sets of assumptions on plasma conditions. For the study: the burn-averaged and spectrally inferred temperatures were 5.40 and 5.65 keV, respectively, the temperature standard deviation was 1.62 keV and the p/D fuel fractions were 50/50. The associated uncertainties are given at the beginning of Section 3.2. (B) Plot showing the inferred and “true” [7] nuclear S-factors from the synthetic data study. The crosses denote the centroid of the PDF and they are surrounded by the 1σ contour, all inferences exhibit ∼ 18% error. The zeroth order estimates (
4 Kinetic plasmas
Shock-driven ICF implosions can operate in a regime where the ion mean free path is large compared to gradient length scales. This gives rise to ion kinetic effects which violate many of the approximations of hydrodynamics. In the following we will consider the effect of species separation, thermal decoupling and non-Maxwellian velocity distributions on fusion product based diagnostics.
4.1 Species separation
Ion kinetic effects can cause the concentration of reactants to spatially and temporally vary. This will have an effect on the yields by modifying the reactant number densities and therefore the yield ratio and subsequent S-factor measurements.
It is considerably easier to consider plasmas with only two reactants which have both hetero- and homo-nuclear fusion reactions, for example a DT mixture. The concentration fractions, denoted fi for species i, then satisfy
simplifying the dependence down to just a single variable, f1, for which we define:
where both
From Eqs 22–25, one can find the lowest order effect of fuel fractions on the associated yield ratios:
It is clear that even if the mean concentration remains fixed, increased variance in the concentration acts to increase the yield ratio of homo-to hetero-nuclear reactions (Y11/Y12). For the ratio of homo-nuclear reactions (Y22/Y11), if
4.2 Thermal decoupling
The second ion kinetic effect we will consider is thermal decoupling between the reactant species. This is where the different ion species have different temperatures but still maintain a Maxwellian distribution of velocities. Thermal decoupling is expected to occur as strong shocks deliver different amounts of energy to different ion species depending on their ion mass and charge [26, 27]. If inter-species equilibration times are longer than the fusion burn period then the separate species temperatures will affect fusion reactivity and spectra.
As shown in Eq. 5, the reaction rate and reactivity is determined by the distribution of relative kinetic energies. First we will consider a locally uniform thermally decoupled plasma. It can be shown [9, 28] that the reactivity for Maxwellians with separate temperatures is equal to the single temperature Maxwellian reactivity evaluated at a mass weighted temperature:
Separately, the spectral temperature, which determines the width of the fusion product spectra, depends on the average centre of mass kinetic energy [10]. When reactants have separate temperatures, this introduces correlation between the relative and centre of mass velocity. This modifies the relationship between thermal and spectral temperature due to the cross section weighting. The spectral temperature from a thermally decoupled plasma is then given by:
The second term in Eq. 29 is often neglected [29], it can however cause a significant increase in spectral temperature for large temperature separations. The superscript th is included to show that this is the spectral temperature without the effect of fluid velocity Doppler broadening. The average reaction energy, ⟨K⟩, can be calculated from the formula of Brysk [9] and Eq. 14:
where for thermally decoupled plasmas the above formula is evaluated at the reactivity temperature, Tr12.
Thermally decoupled ICF plasmas will also have spatial and temporally changes in temperature; potentially with species separation as well. Therefore, the effect of burn-averaging must also be considered. For the hetero-nuclear reactions, the spectral width will depend on the burn-averaged value of Eq. 29, making it non-trivial to extract reactivity temperatures from spectral measurements. It is more straightforward for the homo-nuclear reaction as the spectral temperature, ⟨Ts11⟩, is simply the burn-averaged temperature,
We will assume the thermal decoupling parameter, θ, is approximately constant over the burn volume and time. This allows us to use the same model as used for single temperature plasma with T1 expanded about homo-nuclear burn-averaged temperature,
To proceed we need estimates of θ,
It is clear from the form of ⟨Ts12⟩ that it will be sensitive to correlations of reactant concentration and temperature. Quantifying this correlation will introduce additional parameters. Instead, we consider the zeroth order effect of reactant concentration on the burn-averaging i.e., a multiplicative factor of
With the approximations applied above, the derived system is both under-determined and non-linear, with 6 unknowns (θ,
A synthetic data study can be used to explore S-factor inference in the presence of species separation and thermal decoupling. The reference reaction is taken as D (T,n)α and target D (D,n)3He such that neutron spectral measurements can be included in the analysis. While both of these reactions are well known, this study serves to test the efficacy of the model when complete spectral information is available. To provide a suitably generic set of test conditions, we consider a multivariate normal distribution of reaction rate weighted temperatures and concentrations:
on the domain TD, TT ∈ [Tmin, ∞] and fD ∈ [0, 1], where Tmin is chosen to be 0.5 keV. We expect strong positive correlation between TD and TT as the ion species are heated by the same processes and exchange energy through collisions. Correlations between species concentration and temperature are more difficult to predict. Thermo-diffusion models [32] suggest a negative correlation between the lighter species concentration and temperature in a “saturated” state. It is worth noting that the above model does not have constant value of θ. Given these physical insights, in this study the following fixed parameters are chosen for the model defined in Eqs 40–42:
while ⟨fD⟩ and
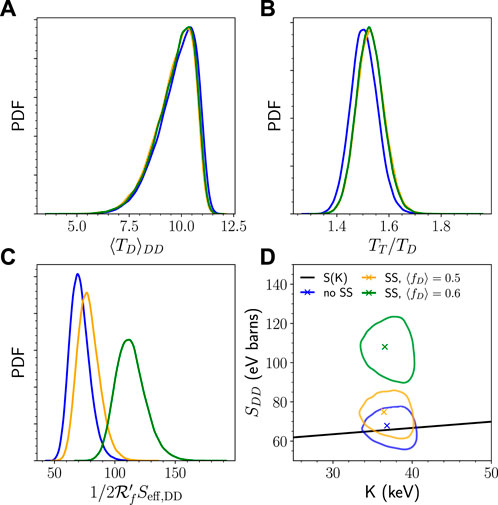
FIGURE 5. For all subplots: blue data includes no species separation (SS), orange data includes species separation with ⟨fD⟩ = 0.5 and
4.3 Non-Maxwellian velocity distributions
Once the reactant velocity distributions are non-Maxwellian we must revisit the definition of reactivity and the Gamow peak. Without a-priori knowledge of the form the velocity distributions, we have no known relationships between the yields, spectral measurements, effective S-factor and Gamow peak energy. This makes it difficult to relate the cross section to yield ratios. One possible approach is to introduce a model which can predict the kinetic ion velocity distributions in the experiment [33, 34]. Synthetic diagnostics of yield and spectra could be compared to experimental values [33] and sensitivity to varying model S-factors can be studied in this way. However, this cannot be used to infer an S-factor without making the assumption that the ion kinetic model had very accurately reproduced the reactant velocity distributions present in the experiment. In absence of a model, one can determine if the reactant velocity distributions have become non-Maxwellian via spectroscopy methods by comparison of the first two spectral moments to the Maxwellian prediction [35]. This suggests a future avenue of investigation into the relationship between reactivity and spectral moments to improve understanding of yields in highly kinetic experiments. This future work would be key in understanding cross section measurements in the presence of non-Maxwellian velocity distributions.
5 Discussion
Inertial confinement fusion (ICF) experiments create a unique laboratory environment in which thermonuclear fusion reactions occur within a plasma. Previous experiments have leveraged this environment to perform measurements of light ion fusion S-factors without the need for screening corrections [1–3]. However, to further increase the accuracy of ICF-based measurements requires an examination of the physical mechanisms affecting fusion yields and spectra. In this work we have discussed and analysed the effects of the inherent range of reaction energies, spatial and temporal thermal temperature variation, and kinetic effects such as species separation.
We showed that yield ratio measurements in an uniform Maxwellian plasma are directly related to the effective S-factors of the reactions. By considering expansions about the Gamow peak we were able to relate the effective and nuclear S-factors as well as provide the commonly used saddlepoint approximation to the reactivity ratio. It was seen that the local behaviour of the nuclear S-factor at the Gamow peak can affect its inference. In a hydrodynamic plasma, spatial and temporal temperature variation was seen to effect yield ratio measurements. The temperature variation has the largest effect on the yield ratio when the reactants have large differences in KB due to charge and/or mass. A synthetic data study was used to illustrate the propagation of errors in S-factor inference in hydrodynamic ICF plasmas. The results showed that using a more detailed model can remove systematic uncertainty present in previous, more approximate, analyses.
Finally, we considered the effect of notable ion kinetic behaviours, particularly species separation and thermal decoupling. To simplify the problem, only two species plasmas were considered. Then, the model developed for hydrodynamic plasmas was extended to include the ion kinetic effects. In order to constrain thermal decoupling, additional spectroscopic data was included via both hetero- and homo-nuclear spectral temperatures. The dominant effect of species separation was to alter the yield ratios. Again, a synthetic data study was used to investigate the efficacy of these models in handling these novel kinetic factors. It was found that thermal decoupling is well constrained by the spectral measurements but species separation can cause large changes in the yield ratios and hence large systematic uncertainty in the S-factor inference.
The synthetic data studies in this work give single examples of the inference process with chosen physical parameters and priors subject to bias. Future work should provide a more systematic approach to this data study. The proposed models of distributions of temperatures, velocities and concentrations should be compared to integrated hydrodynamic and kinetic simulations. This will ensure confidence in the conclusions drawn from these case studies.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
AC is the main author and contributed the main body of the work. IG-F performed the initial work on S-factor inference in hydrodynamic plasmas. BA provided knowledge and insights particularly in respect to ion kinetic effects in ICF implosions. JC supervised the work and provided an expert perspective on the hydrodynamics of ICF implosions.
Acknowledgments
The authors would like to thank G. Kagan for useful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.937972/full#supplementary-material
References
1. Casey DT, Sayre DB, Brune CR, Smalyuk VA, Weber CR, Tipton RE, et al. Thermonuclear reactions probed at stellar-core conditions with laser-based inertial-confinement fusion. Nat Phys (2017) 13(12):1227–31. doi:10.1038/nphys4220
2. Zylstra AB, Herrmann HW, Gatu Johnson M, Kim YH, Frenje JA, Hale G, et al. Using inertial fusion implosions to measure the T +3He fusion cross section at nucleosynthesis-relevant energies. Phys Rev Lett (2016) 117:035002. doi:10.1103/physrevlett.117.035002
3. Zylstra AB, Herrmann HW, Kim YH, McEvoy A, Frenje JA, Gatu Johnson M, et al. 2H(p, γ)3He cross section measurement using high-energy-density plasmas. Phys Rev C (2020) 101:042802. doi:10.1103/physrevc.101.042802
4. Otuka N, Dupont E, Semkova V, Pritychenko B, Blokhin AI, Aikawa M, et al. Towards a more complete and accurate experimental nuclear reaction data library (exfor): International collaboration between nuclear reaction data centres (nrdc). Nucl Data Sheets (2014) 120:272–6. doi:10.1016/j.nds.2014.07.065
5. Spitaleri C, Cognata ML, Lamia L, Pizzone RG, Tumino A. Astrophysics studies with the trojan horse method. Eur Phys J A (2019) 55(9):161–29. doi:10.1140/epja/i2019-12833-0
6. Chadwick MB, Obložinský P, Herman M, Greene NM, McKnight RD, Smith DL, et al. ENDF/B-VII.0: Next generation evaluated nuclear data library for nuclear science and technology. Nucl Data Sheets (2006) 107(12):2931–3060. Evaluated Nuclear Data File ENDF/B-VII.0. doi:10.1016/j.nds.2006.11.001
7. Adelberger EG, García A, Hamish Robertson RG, Snover KA, Balantekin AB, Heeger K, et al. Solar fusion cross sections. II. Theppchain and CNO cycles. Rev Mod Phys (2011) 83:195–245. doi:10.1103/revmodphys.83.195
8. Bosch H-S, Hale GM. Improved formulas for fusion cross-sections and thermal reactivities. Nucl Fusion (1992) 32(4):611–31. doi:10.1088/0029-5515/32/4/i07
9. Brysk H. Fusion neutron energies and spectra. Plasma Phys (1973) 15(7):611. doi:10.1088/0032-1028/15/7/001
10. Ballabio L, Allne JK, Gorini G. Relativistic calculation of fusion product spectra for thermonuclear plasmas. Nucl Fusion (1998) 38(11):1723–35. doi:10.1088/0029-5515/38/11/310
11. Appelbe B, Chittenden J. The production spectrum in fusion plasmas. Plasma Phys Control Fusion (2011) 53(4):045002. doi:10.1088/0741-3335/53/4/045002
12. Murphy TJ. The effect of turbulent kinetic energy on inferred ion temperature from neutron spectra. Phys Plasmas (2014) 21(7):072701. doi:10.1063/1.4885342
13. Munro DH. Interpreting inertial fusion neutron spectra. Nucl Fusion (2016) 56(3):036001. doi:10.1088/0029-5515/56/3/036001
14. John N. Bahcall. Non-resonant nuclear reactions at stellar temperatures. Astrophysical J (1966) 143:259–61.
15. Clayton DD. Principles of stellar evolution and nucleosynthesis. University of Chicago press (1983).
17. Williams MMR. A generalized energy exchange kernel for inelastic neutron scattering and thermonuclear reactions. J Nucl Energ (1971) 25(10):489–501. doi:10.1016/0022-3107(71)90029-3
18. Kabadi NV, Adrian PJ, Bose A, Casey DT, Frenje JA, Johnson MG, et al. A second order yield-temperature relation for accurate inference of burn-averaged quantities in multi-species plasmas. Phys Plasmas (2021) 28(2):022701. doi:10.1063/5.0032139
19. Foreman-Mackey D, Hogg DW, Lang D, Goodman J. emcee: The mcmc hammer. Publications Astronomical Soc Pac (2013) 125(925):306–12. doi:10.1086/670067
20. Goodman J, Weare J. Ensemble samplers with affine invariance. Comm App Math Comp Sci (2010) 5(1):65–80. doi:10.2140/camcos.2010.5.65
21. Mossa V, Stöckel K, Cavanna F, Ferraro F, Aliotta M, Barile F, et al. The baryon density of the universe from an improved rate of deuterium burning. Nature (2020) 587(7833):210–3. doi:10.1038/s41586-020-2878-4
22. Turkat S, Hammer S, Masha E, Akhmadaliev S, Bemmerer D, Grieger M, et al. Measurement of the 2H(p, γ)3He s factor at 265–1094 kev. Phys Rev C (2021) 103:045805. doi:10.1103/physrevc.103.045805
23. Leonard DS, Karwowski HJ, Brune CR, Fisher BM, Ludwig EJ. Precision measurements of 2H(d, p)3H and 2H(d, n)3He total cross sections at big bang nucleosynthesis energies. Phys Rev C (2006) 73:045801. doi:10.1103/PhysRevC.73.045801
24. Van Ravenzwaaij D, Cassey P, Brown SD. A simple introduction to Markov chain monte–carlo sampling. Psychon Bull Rev (2018) 25(1):143–54. doi:10.3758/s13423-016-1015-8
25. Casella C, Costantini H, Lemut A, Limata B, Bonetti R, Broggini C, et al. First measurement of the d(p, γ )3he cross section down to the solar gamow peak. Nucl Phys A (2002) 706(1):203–16. doi:10.1016/s0375-9474(02)00749-2
26. Rinderknecht HG, Rosenberg MJ, Li CK, Hoffman NM, Kagan G, Zylstra AB, et al. Ion thermal decoupling and species separation in shock-driven implosions. Phys Rev Lett (2015) 114:025001. doi:10.1103/physrevlett.114.025001
27. Kabadi NV, Simpson R, Adrian PJ, Bose A, Frenje JA, Gatu Johnson M, et al. Thermal decoupling of deuterium and tritium during the inertial confinement fusion shock-convergence phase. Phys Rev E (2021) 104:L013201. doi:10.1103/physreve.104.l013201
28. Bellei C, Rinderknecht H, Zylstra A, Rosenberg M, Sio H, Li CK, et al. Species separation and kinetic effects in collisional plasma shocks. Phys Plasmas (2014) 21(5):056310. doi:10.1063/1.4876614
29. Inglebert A, Canaud B, Larroche O. Species separation and modification of neutron diagnostics in inertial-confinement fusion. EPL (Europhysics Letters) (2014) 107(6):65003. doi:10.1209/0295-5075/107/65003
30. Hatarik R, Nora RC, Spears BK, Eckart MJ, Grim GP, Hartouni EP, et al. Using multiple neutron time of flight detectors to determine the hot spot velocity. Rev Scientific Instr (2018) 89(10):10I138. doi:10.1063/1.5039372
31. Mannion OM, Knauer JP, Glebov VY, Forrest CJ, Liu A, Mohamed ZL, et al. A suite of neutron time-of-flight detectors to measure hot-spot motion in direct-drive inertial confinement fusion experiments on omega. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2020) 964:163774. doi:10.1016/j.nima.2020.163774
32. Kagan G, Tang X-Z. Thermo-diffusion in inertially confined plasmas. Phys Lett A (2014) 378(21):1531–5. doi:10.1016/j.physleta.2014.04.005
33. Higginson DP, Ross JS, Ryutov DD, Fiuza F, Wilks SC, Hartouni EP, et al. Kinetic effects on neutron generation in moderately collisional interpenetrating plasma flows. Phys Plasmas (2019) 26(1):012113. doi:10.1063/1.5048386
Keywords: inertial confinement fusion (ICF), nuclear astrophysics, Bayesian inference, S factor, bare nuclear cross section, thermal reactivity, ion kinetic effects
Citation: Crilly AJ, Garin-Fernandez I, Appelbe BD and Chittenden JP (2022) Efficacy of inertial confinement fusion experiments in light ion fusion cross section measurement at nucleosynthesis relevant energies. Front. Phys. 10:937972. doi: 10.3389/fphy.2022.937972
Received: 06 May 2022; Accepted: 25 August 2022;
Published: 20 September 2022.
Edited by:
Mark Paris, Los Alamos National Laboratory (DOE), United StatesReviewed by:
Daniel Odell, Ohio University, United StatesCarlo G. Bruno, University of Edinburgh, United Kingdom
Copyright © 2022 Crilly, Garin-Fernandez, Appelbe and Chittenden. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. J. Crilly, YWMxMTZAaWMuYWMudWs=
 A. J. Crilly
A. J. Crilly I. Garin-Fernandez
I. Garin-Fernandez B. D. Appelbe
B. D. Appelbe J. P. Chittenden
J. P. Chittenden