Self-Assembly in Mixtures of Charged Lobed Particles

We report coarse-grained Langevin dynamics simulations of homogeneous mixtures of lobed colloidal particles with opposite charges. We show that dumbbell, trigonal planar, tetrahedral, square planar, trigonal bipyramidal, and octahedral shaped particles form distinct self-assemblies including chains, sheets, crystalline, and spherical structures. The dumbbell and square planar particles predominantly form chains and sheets while other particles form network-like self-assembled morphologies. At higher temperatures and lower charges, non-planar particles form three-dimensional aggregates. We further report on packing arrangements of particles which lead to differences in porosities within self-assembled morphologies. Our results show that the trigonal planar particles form larger porous structures. The self-assembled structures that we report are potentially useful in designing porous biomaterials for biomedical applications.

Introduction

Self-assembly is an approach where the components of a system spontaneously assemble without the application of external forces [1, 2]. The self-assembled structure gains its stability from the interactions among its constituents. Colloidal particles are one such class of materials which have been widely studied for their tendency to form larger clusters with distinct morphologies [3–5]. The interactions of significance in these assemblies include van der Waals interactions (vdW) [6], electrostatic interactions [7], steric effects [8], and solvation forces [9, 10]. Colloidal systems have served as models in understanding fundamental and applied problems including phase behavior [11], glass transition [12, 13], crystal nucleation [14, 15], and biomedical applications [16–18].

Self-assemblies of patchy colloidal particles are known for their distinct shapes and novel applications [19–22]. The placement of patches on colloidal particles leads to selective and tunable interactions that allow control over the morphologies of the structures formed via self-assembly [23, 24]. These patches can take the form of lobes that protrude from the surface of colloidal particles. As a result, the lobes can dictate the phase behavior and porosity of a given self-assembled structure due to their size, number, location, and inter-particle interactions, in addition to environmental conditions [25]. Our previous simulation studies have shown that the incorporation of lobes in colloidal particles results in the formation of structures with enhanced porosity due to an increase in the excluded volume created by the non-spherical shapes of particles [18, 25–29].

Interest in the synthesis and self-assembly of colloidal particles with lobes has been increasing in recent years [30–40]. A pioneering study by Wang et al. [31] reported the synthesis of colloidal particles with lobes in positions that mimic hybridized atomic orbitals, which provide three-dimensional bonding symmetries resulting in novel self-assembled structures. Liu and colleagues [32] have synthesized dumbbell-shaped particles and observed that when the particle lobes are DNA-coated, these particles self-assemble to form Kagome lattices, brick-wall-like lattices, or a co-existence of these two arrangements, based on the temperature of the system. Wolters et al. [39] synthesized two-lobed particles with a “Mickey Mouse” shape and reported that these particles self-assemble to form tube-like structures.

Simulations have also been conducted for studying the assemblies of tri-block patchy colloidal particles of tetrahedral and octahedral shapes which result in the formation of colloidal crystals of body centered cubic and cubic diamonds [41]. Simulations of dumbbell-shaped particles show the formation of micelles, vesicles or bilayers with a change in size ratio, separation between two dumbbell spheres and volume fraction [42]. Further, using experimental and computational approaches, dumbbell-shaped particles were shown to stabilize microspheres against aggregation [43]. Simulations of spherical patchy particles have highlighted the dependence of the interaction strength, patch coverage, and density as the key factors in forming two-dimensional self-assemblies [29, 44]. However, lobed patchy particles and their mixtures have been underexplored for the creation of porous colloidal self-assemblies.

We have previously reported simulation studies on the self-assembly of lobed colloidal particles [18, 25–28]. We considered different particle types, as in the current work (dumbbell, trigonal planar, square planar, tetrahedral, trigonal bipyramidal, and octahedral), and investigated their morphologies and porosities where the lobes of these particles are either neutral, charged, or functionalized. Many of these particle types have been successfully designed using experimental approaches, thereby highlighting the feasibility of creating larger lobes instead of patches [31, 34, 45–47]. However, in one of our previous studies in which the lobed particles with charges were studied [27], the positive and the negative charges are placed on different lobes of the same particle to have a net charge of zero on the particle, but experimentally designing lobed particles where different lobes on the same particle can be functionalized differently is significantly challenging. In contrast, it is conceivable that all lobes on a given particle can be functionalized uniformly to have complementary interactions between a pair of distinctly-functionalized particles.

In this work, we introduce a new design of lobed colloidal particles with uniformly-charged lobes where we assign either an overall positive or an overall negative charge to all lobes of a given type of particle (Figures 1A-F) to mimic complementary interactions between the lobes. For observing self-assembly due to complementary interactions, we studied 1:1 mixtures of the same type of particles where half of the particles in the mixture have positively-charged lobes and the other half have negatively-charged lobes, thus studying an overall electrically neutral system. Along with investigating the role of the particle design, charges, and temperature on the phase behavior and porosity, we also focus on packing modes of particles which lead to differences in porosities of the self-assembled structures.

FIGURE 1

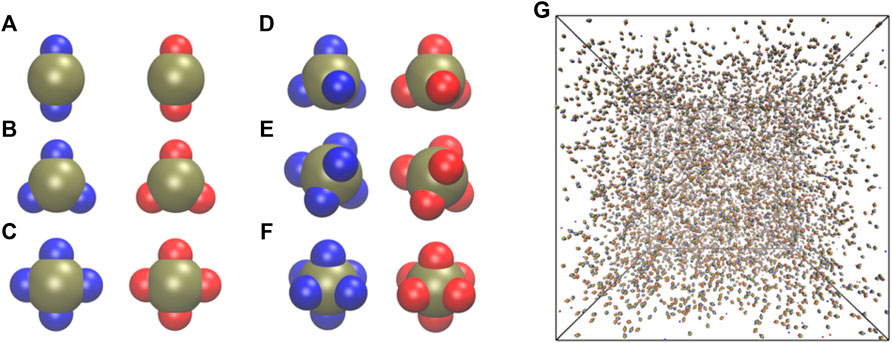
FIGURE 1. Snapshots of particle geometries studied in this work: (A) Dumbbell $(S_2^{DB})$, (B) Trigonal planar $(S_3^{TP})$, (C) Square Planar $(S_4^{SP})$, (D) Tetrahedral $(S_4^{TH})$, (E) Trigonal bipyramidal $(S_5^{TB})$, and (F) Octahedral $(S_6^{OC})$. The seeds are colored tan, the positively-charged lobes are colored blue, and the negatively-charged lobes are colored red. Two representations of each particle in the panels (A–F) indicate that a 1:1 mixture of the same type of particles was studied. (G) A snapshot of the simulation domain showing a typical randomized initial configuration.

Models and Methods

Model

We conducted Langevin molecular dynamics simulations to study the self-assembly behavior of six different types of lobed particles with oppositely-charged lobes. These particles with distinct shapes include dumbbell $(S_2^{DB})$, trigonal planar $(S_3^{TP})$, square planar $(S_4^{SP})$, tetrahedral $(S_4^{TH})$, trigonal bipyramidal $(S_5^{TB})$, and octahedral $(S_6^{OC})$ particles. We prepared six different homogeneous systems by mixing particles of the same type but with opposite charges on the lobes (Figures 1A-F). We used a seed (σ_S) to lobe (σ_L) diameter ratio of 2:1, respectively, with their masses (m_S and m_L) set as 1. The mixed system is prepared with the lobes on half of the particles having positive charges and on the remaining half of the particles having negative charges of equal magnitudes, thus, making an overall neutral system. Consistent with our previous study [27], we used charges on the lobes with magnitudes of 2, 4 and 6 units for each type of particle. We utilized reduced units for all parameters used in our simulations and used harmonic potentials to maintain the shape of the particles during simulations, as described in our previous studies [18, 25–28].

Non-Bonded Interactions

The self-assembly of charged colloidal particles is mediated by non-bonded short-range interactions short-range interactions as well as long-range electrostatic interactions [48]. The model used in our simulations accounts for both types of interactions. The seed-seed (S-S), lobe-lobe (L-L), and seed-lobe (S-L) non-bonded interactions are modeled by using the shifted Lennard-Jones (SLJ) potential (Eq. 1). The SLJ potential was chosen to model the non-bonded interactions because the diameters of the colloidal particles of interest are in the μm range. Therefore, the interactions are computed between the surfaces of the particles rather than between the centers of the particles [49].

$U_{\mathit{SLJ}}\left(r_{ij}\right)=4{ϵ}_{ij}\left[{\left(\frac{\sigma }{r_{ij}-\delta }\right)}^{12}-{\left(\frac{\sigma }{r_{ij}-\delta }\right)}^6\right](1)$

In this equation, ϵ_ij denotes the depth of the potential well for a pair of particles i and j, and σ denotes the distance of the closest approach. The equation is used to model the pairwise interaction potentials when r_ij < r_cut + δ. Here, r_cut signifies a cut-off distance and δ = (σ_i + σ_j)/2–1, where σ_i and σ_j are the particle diameters. When r_ij ≥ (r_cut + δ), non-bonded interactions are neglected, i.e., U_SLJ (r_ij) = 0. The depth of the pair-potential well for interactions between the positive and negative lobes is fixed as three in reduced units, while it was kept as one for all other pairs, similar to our previous work on particles with charges on the lobes [27]. The short-ranged repulsions are treated by setting the cut-off distance (r_cut) as $2^{\frac{1}{6}}\sigma$ for all pairs other than the negative lobe-positive lobe pairs, where an r_cut of 2.5σ is used to account for attractive interactions [49–53]. The σ values in the SLJ potential are set to 2.0, 1.5, and 1.0 for the seed-seed, seed-lobe, and lobe-lobe interactions, respectively. The electrostatic interactions are computed with the following equation, using a cut-off of 15σ_L [54].

$U_{\mathit{Elec}}\left(r_{ij}\right)=\frac{q_i{q}_j}{4\pi {ϵ}_0{ϵ}_r}\frac{1}{r_{ij}}(2)$

where, q_i and q_j are the charges on a pair of particles i and j, respectively, ϵ₀ is the permittivity of the free space, and ϵ_r the relative permittivity. For electrostatic screening, ϵ_r represents the dielectric permitivity of bulk water at ambient conditions (equal to 80).

Simulation Details

We conducted coarse-grained Langevin dynamics simulations for all systems using the HOOMD-Blue software [55]. We computed the electrostatic interactions by using the particle-particle-particle-mesh (PPPM) method [54, 56]. Each system is composed of 8,000 particles of the same type (4,000 each with positively-charged and negatively-charged lobes, respectively) and the length of the simulation domain is 160σ_L along each direction in all simulations. Overall, we simulated six distinct systems, each at four distinct temperatures and three distinct charge values. Specifically, we performed simulations of all six types of particles at four different temperature conditions (k_BT = 0.1, 0.4, 0.7, and 1.0, in reduced units) with three different magnitudes for the charges on the lobes (±2, ±4, and ±6 in reduced units). We note that k_BT = 1.0 corresponds to T = 298 K [22]. Therefore, k_BT = 0.1, 0.4, and 0.7 correspond to 29.8, 119.2, and 208.6 K, respectively.

We generated initial conditions for different systems by simulating each system for 10,000 steps at k_BT = 3.0, a sufficiently higher temperature to prevent any self-assembly at all conditions and to randomize the initial configurations (Figure 1G). In all simulations, we used an integration time-step of 0.005 and a simulation length of 5 × 10⁷ steps. We confirmed the stability of a given self-assembled structure by analyzing the convergence of the potential energy per particle and the total number of clusters (Supplementary Figure S1) as a function of the number of time-steps. The self-assembled clusters are formed by those particles whose centers of masses are within 3.25σ_L from each other. The cluster calculation was carried out using the freud software [57].

Pore Diameter and Interplanar Angle Measurements

We analyzed two types of pores in our self-assembled morphologies, the interstitial (Figure 2A) and the intra-network pores (Figure 2B). The interstitial pores arise in the system due to the formation of large three-dimensional self-assembled morphologies. The available spaces within these aggregates correspond to interstitial pores. The interstitial pore size is calculated by carving out a cube from a three-dimensional aggregate and the pores within the cube (zoomed view in Figure 2A) are characterized as representative of the self-assembled morphology. The intra-network pores exist due to the formation of interconnected structures (chains, sheets and random aggregates) within the simulation domain. We consider the entire simulation domain for capturing the sizes of intra-network pores formed from different types of particles. We used the Zeo++ software [58–60] to compute the pore size diameter by measuring the diameter of the largest free sphere (D_LFS) which can freely diffuse through a self-assembled porous structure. For this, we considered a probe radius equivalent to $\frac{1}{2}{\sigma }_L$, similar to our previous work [18, 25–28].

FIGURE 2

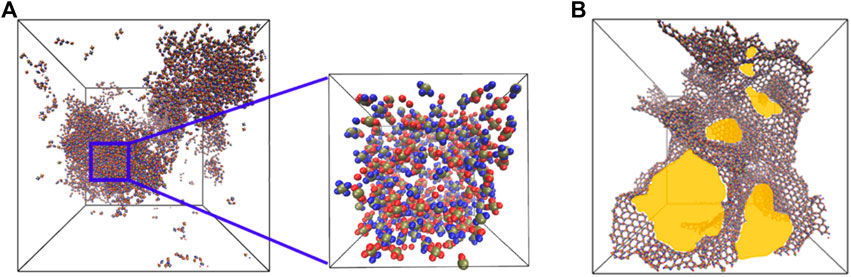
FIGURE 2. (A) A snapshot highlighting the interstitial pores formed in three-dimensional aggregates. The zoomed-view shows a cube carved out of larger aggregates and used in the calculation of the sizes of interstitial pores. (B) A snapshot highlighting the intra-network pores (yellow) observed in self-assembled structures.

To characterize the packing arrangements among particles in self-assembled morphologies, we also computed the distributions of the interplanar angles between the planes formed by S–L⁺–L⁻ and L⁺–L⁻–S groups of particles, where L⁺ and L⁻ denote the positively-charged and negatively-charged lobes, respectively, and S signifies the central seed particle on which the lobes are placed. The interplanar angle values span the range between -180° and +180° which correspond to the interior/exterior angles between the two planes.

Results and Discussion

We studied self-assembly for six different types of lobed particles which differ in their number of lobes (Figure 1) as well as their positions and charges. We systematically studied the effect of temperature (k_BT = 0.1, 0.4, 0.7, and 1.0) and charges (2, 4, or 6 units) on the lobes with a focus on homogeneous mixtures of particles where half of the particles have positively-charged lobes and the remaining half have negatively-charged lobes. The time-evolution of the potential energy per particle and the total number of clusters in each system for a given condition of q and k_BT are shown in Supplementary Figure S1. Similar convergence trends were observed for all systems. However, we note that patchy interactions may lead to the formation of kinetically trapped structures [61–63], especially at lower temperatures. Therefore, alternate methodologies [64, 65] could be explored in future studies to further probe such structures.

Self-Assembled Morphologies

We analyzed the final configurations obtained at the end of the simulations for each system according to their morphologies. In Figure 3, we summarize the phase behavior of different morphologies formed by these mixtures under all temperature and charge conditions.

FIGURE 3

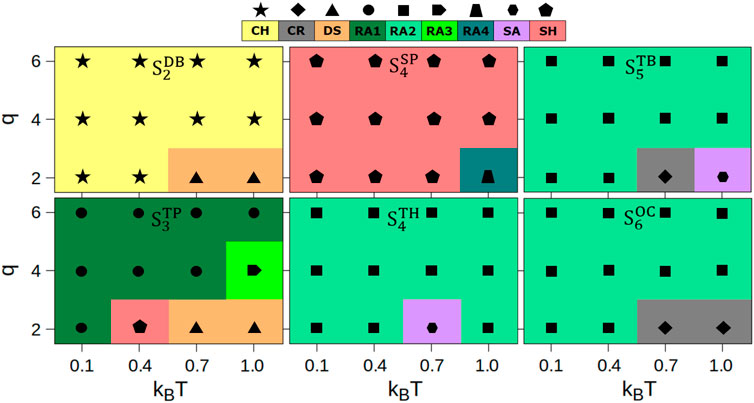
FIGURE 3. Phase behavior in homogeneous mixtures of charged lobed particles at all charge (q) and temperature (k_BT) conditions. Each type of morphology is color coded: chains (CH), crystalline self-assemblies (CR), random aggregates (RA1, RA2, RA3, RA4), sheets (SH), and spherical aggregates (SR). The conditions at which self-assembly is not observed are labeled as DS, the dissociated state.

These data reveal the formation of various types of network-like particle assemblies including chains (CH), different types of random aggregates (RA1, RA2, RA3, RA4), and two-dimensional sheets (SH), or three-dimensional clusters including crystalline (CR) and spherical aggregates (SA). The random aggregates termed RA1 and RA3 are formed by the planar particles $(S_3^{TP})$ with RA3 having the maximum porosity, RA2 are formed by the non-planar particles ($S_4^{TH}$, $S_5^{TB}$, $S_6^{OC}$), and RA4 are formed by the square planar $(S_4^{SP})$ particles. At some conditions (q = 2; k_BT = 0.7 and 1.0), $S_2^{DB}$ and $S_3^{TP}$ particles do not form any type of self-assembled structure, thereby remaining in a dissociated state (DS).

The relative occurrence of distinct phases in simulations of charged particles without mixing, as reported in our previous work [27], and homogeneous mixtures of charged particles from this work is shown in Supplementary Figure S2 (magenta bars, previous work; green bars, this work). The fractional occurrence (expressed as a percentage) is computed by comparing the formation of a specific phase with respect to the total number of phases formed in simulations. The homogeneous mixtures reported in this work have higher occurrences of some (CH, CR, RA1, RA2, and RA3) morphologies, and comparable occurrences of other (SA and SH) morphologies. The RA4 morphology is only observed in homogeneous mixtures albeit at a significantly lower fraction compared to other morphologies.

Structural Motifs in Self-Assembled Morphologies

For dumbbell-shaped particles with two lobes $(S_2^{DB})$, at most conditions of charges and temperatures, we observed the formation of linear chain-like (CH) arrangements (Figure 4A) that originate from the electrostatic interactions between the oppositely-charged lobes. However, at a lower charge (q = 2), the electrostatic interactions are weaker at higher temperatures (k_BT = 0.7 and 1.0), where only a dissociated state (DS) is observed. The linear shape of dumbbell-shaped particles accounts for the formation of extended chain-like (CH) networks. A zoomed view of these chains shows further chain coiling (highlighted in zoomed blue circles, Figure 4A), which leads to the formation of extended porous networks inside the simulation domain. The oppositely-charged lobes of a pair of particles in different chains can attract each other via electrostatic interactions causing elongated chain associations. In our previous study on functionalized lobed particles [18], the $S_2^{DB}$ particles also formed the CH phase. However, the overall morphology is different (Supplementary Figure S3) in comparison to the current configuration (Figure 4A). For example, only shorter chains without any extended network and non-porous self-assembled morphologies were observed in our previous work [18].

FIGURE 4

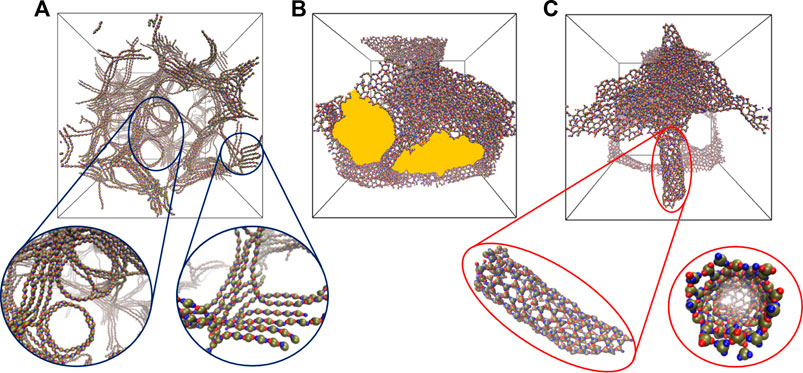
FIGURE 4. Snapshots highlighting self-assembled networks formed by the particles with two $(S_2^{DB})$ or three $(S_3^{TP})$ lobes. (A) Interconnected chain-like morphologies formed by the $S_2^{DB}$ particles; and (B,C) random aggregates and hollow cylindrical morphologies formed by the $S_3^{TP}$ particles. The blue and red circles show zoomed-in views, and a yellow patch (panel B) represents intra-network pore space.

As the number of lobes increases, as in the case of $S_3^{TP}$ particles, network-like assemblies arise from random aggregates (RA1 or RA3) or sheet-like (SH) morphologies. In Figures 4B,C and Supplementary Figure S4A, we show self-assemblies formed by $S_3^{TP}$ particles and the zoomed-views of the network-like morphology showing cylindrical organization of particles. We classify this network-like organization assisted by two-dimensional sheets and three-dimensional particle arrangements as RA1. These aggregates are predominantly observed in self-assemblies of $S_3^{TP}$ particles, and can be attributed to the existence of an additional lobe on the $S_3^{TP}$ particles in comparison to the $S_2^{DB}$ particles. In sheet-like morphologies formed by the $S_3^{TP}$ particles, we observed the formation of six-membered rings (Figure 5A) in which the oppositely-charged lobes interact via electrostatic interactions to form a network (Supplementary Figure S4A). This six-membered ring-like (“Kagome-lattice” type) arrangement is not present in our previous work on charged particles [27], where the existence of oppositely-charged lobes present on the same particle led to the formation of three-membered rings (Figures 5B and Supplementary Figure S4B). Similarly, our previous work on self-assemblies formed by uncharged but functionalized lobes of $S_3^{TP}$ particles favor the formation of honeycomb-like sheets with five or seven membered rings (Figure 5C).

FIGURE 5

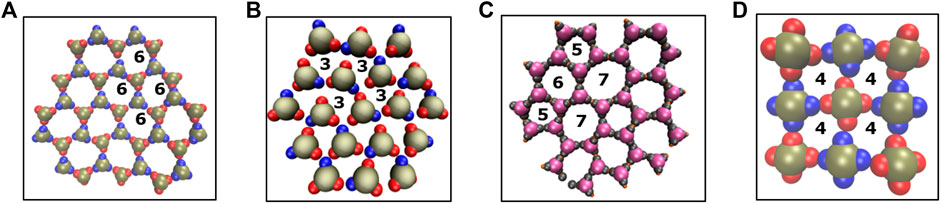
FIGURE 5. A comparison of structural motifs in sheet-like morphologies reported in this study and our previous work [18, 27]. (A–C) Ring-like arrangements of particles with three lobes are shown: six membered rings (panel A, current work), three membered rings (panel B, previous work [27]), and five or seven membered rings (panel C, previous work [18]). (D) Four membered rings formed by the square planar $(S_4^{SP})$ particles from our current work.

In Supplementary Figure S5, we show the systematic evolution of morphologies formed by the $S_3^{TP}$ particles from the current work, where the particles are initially randomly oriented within the simulation domain (Supplementary Figure S5A) but gradually reorganize and self-assemble into three-dimensional networks (Supplementary Figures S5B–D) made up of ring-like motifs (Figure 5A). At a lower charge and higher temperature (q = 2 at k_BT = 0.7 or 1.0), we do not observe self-assemblies due to higher thermal energies in comparison to electrostatic interactions, but at a moderate charge but similar temperature (q = 4, k_BT = 1.0), we observed porous networks with larger intra-network pores (highlighted by a yellow patch in Figure 4B).

Further, the particles with four lobes either have a square-planar $(S_4^{SP})$ or a tetrahedral $(S_4^{TH})$ geometry (Figures 1C,D). Due to the planar geometry of the $S_4^{SP}$ particles, they predominantly self-assembled into sheet-like (SH) morphologies (Figure 3). The two oppositely-charged lobes on these particles act as the connecting units responsible for a well-packed sheet-like structure where the inter-particle interaction form a four-membered ring-like structural motif (Figure 5D). This packing behavior of the $S_4^{SP}$ particles is similar to the one observed in our previous work [27]. At certain charge/temperature conditions (at q = 2, and k_BT = 1.0), we also observed the formation of three-dimensional random aggregates (termed RA4) that do not form an interconnected network of pores, but exist as three-dimensional clusters of random shapes. The available pore spaces in these self-assembled morphologies serve as interstitial pores (Figure 2A).

In contrast, the $S_4^{TH}$ particles having non-planar tetrahedral arrangement of four lobes do not form sheet-like configurations but form network-like assemblies originating from random interconnected networks (e.g., at q = 4 and 6; all T values; Figure 3). We classify these network-like assemblies from randomly organized particles as RA2. However, at a lower charge (q = 2), we identified the formation of spherical aggregates (SA) at k_BT = 0.7, which transition into random network-like assemblies (RA2-type) at a higher temperature (k_BT = 1.0) (Supplementary Figure S6).

Similar network-like morphologies originating from the RA2-type configurations are found in the assemblies of lobed particles with 5 or 6 lobes ($S_5^{TB}$ and $S_6^{OC}$) at all temperatures (e.g., at q = 4 or 6 and all T values; Figure 3). Additionally, $S_5^{TB}$ particles also form spherical aggregates (q = 2, k_BT = 1.0; Figure 3), and both types of particles form crystalline morphologies (q = 2, k_BT = 0.7; Figure 3). In Figure 6, we show the shape transitions among various morphologies for the $S_5^{TB}$ particles, where network-like configurations first switch to crystalline and then to spherical morphologies as temperature gradually increases (k_BT = 0.4, 0.7, and 1.0). This morphological transition is similar to the one observed in our previous study [27], where the $S_6^{OC}$ particles were observed to transition from random aggregates to crystalline structures and further to spherical aggregates with a temperature change from k_BT = 0.7 to 1.1. These transitions occur due to an intricate balance between the electrostatic interactions and thermal diffusive effects.

FIGURE 6

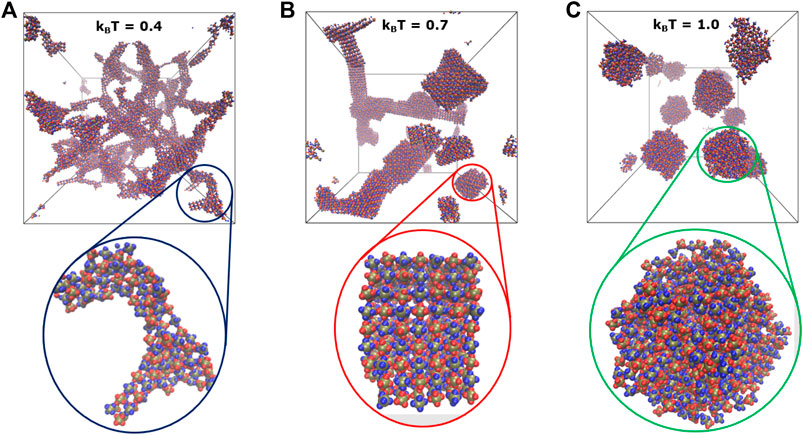
FIGURE 6. Shown are the snapshots highlighting temperature-dependent shape transitions in self-assemblies formed by the $S_5^{TB}$ particles: (A) porous network-like assemblies; (B) crystalline morphologies; and (C) spherical aggregates.

Interstitial and Intra-Network Pore Sizes

To probe the porosity of a given self-assembled structure, we computed the pore sizes (measured using the diameter of the largest free sphere D_LFS as a metric) for all assemblies at all conditions of charges and temperatures (Supplementary Figure S7). This analysis considered all particle shapes and the conditions responsible for the formation of pores of various diameters. The smaller pores originate from the interstitial space between particles in three-dimensional aggregates, while the larger pores originate from the intra-network void space in a given network-like morphology. Among all charge (q) and temperature values, the pore-sizes with larger diameters are observed for q = 4, k_BT = 0.7 and 1.0.

In Figure 7, we show the trends in pore sizes (D_LFS) for both interstitial and intra-network pores for self-assemblies formed by particles with three or more lobes ($S_3^{TP}$, $S_4^{SP}$, $S_4^{TH}$, $S_5^{TB}$, $S_6^{OC}$). The intra-network pores are an order of magnitude larger than the interstitial pores. For comparison, we also show the data from our previous study on charged lobed particles without mixtures [27] (magenta bars in Figure 7) along with the data from our current study where mixtures are studied (green/cyan bars in Figure 7). These data show that the interstitial pores are significantly larger in self-assemblies observed for $S_4^{SP}$, $S_5^{TB}$, and $S_6^{OC}$ particles studied in our current work (Figure 7A). This is attributed to larger porous sheets formed by the $S_4^{SP}$ particles (Figure 5D) or RA2-type random aggregates, crystalline, and spherical self-assembled morphologies formed by $S_5^{TB}$ and $S_6^{OC}$ particles. However, for self-assemblies formed by the $S_4^{TH}$ particles in our current work, we observed smaller interstitial pores in comparison to our previous study [27] indicating a tighter packing of particles in random and spherical aggregates formed by them.

FIGURE 7

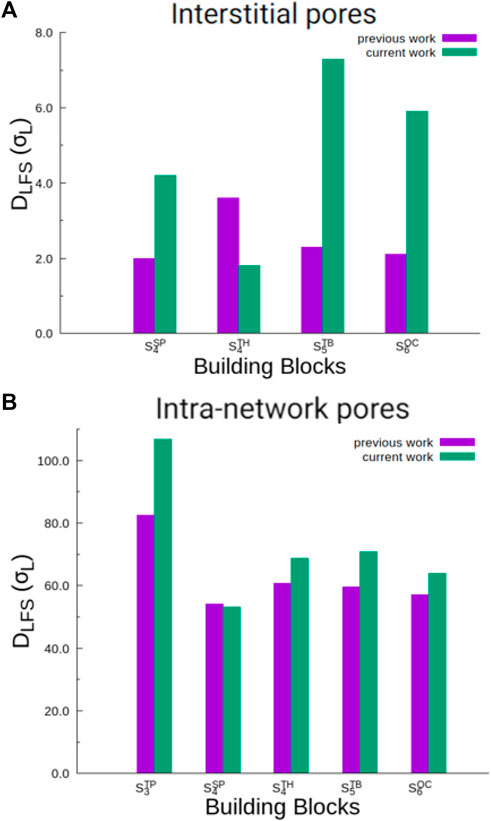
FIGURE 7. A comparison of interstitial pore diameters [panel (A)] and intra-network pore diameters [panel (B)], computed based on data from this study and our previous work on charged lobed particles [27]. Data are shown for only those particle types which form interstitial or intra-network pores in both studies. In Supplementary Figure S7, we also present pore diameters for self-assemblies of all particle types at all conditions from this study.

On comparing intra-network pores (Figure 7B), we find that the network-like self-assemblies formed by particle mixtures studied in our current work have larger pores in most cases except for the $S_4^{SP}$ particles where pores of similar size to our previous study [27] are observed. Overall, the intra-network pores are significantly larger than the interstitial pores. This is potentially relevant for applications of colloidal based systems in designing tissue engineering scaffolds in which interconnected larger pores are needed to allow cellular penetration and nutrient circulation [66]. The required sizes for the pores may vary according to the type of cells that are being targeted for growth in these scaffolds, but they typically range from ∼30–400 μm for human cells [67]. Our simulations show that the lobed particles form interconnected networks with significantly larger pores compared to the particle-size which could be suitable for applications in designing tissue engineering scaffolds.

Particle Packing Modes: Interplanar Angles

To further probe the correlation between the porosity and the packing arrangements of particles within self-assemblies, we computed the distributions of the inter-planar angles between the planes S−L⁺−L⁻ and L⁺−L⁻−S that are formed by the seed (S) and positively-charged as well as negatively-charged lobes (L⁺/L⁻) (Figure 8). The inter-planar angle distributions for the $S_2^{DB}$ (dumbbell) particles show the peaks near -180° and -180° (Figure 8A). This indicates a linear or head-to-head arrangement of particles within the porous networks where the particles organize themselves in a parallel or an anti-parallel arrangement to form chain-like configurations (Figure 4A). The angle distributions for the $S_3^{TP}$ particles (Figure 8B) show a broader range of inter-planar angle values in self-assemblies of these particles. For example, a broader distribution of the angle values exists in the range between −40° and −10°, while the distributions are sharply peaked at $\sim 30°$ and $\sim 180°$. These observations can be attributed to the planar shapes of the $S_3^{TP}$ particles which can arrange themselves in different modes including porous random aggregates (RA1, RA3; Figure 3) and porous sheets with six-membered ring-like motifs (Figure 5A).

FIGURE 8

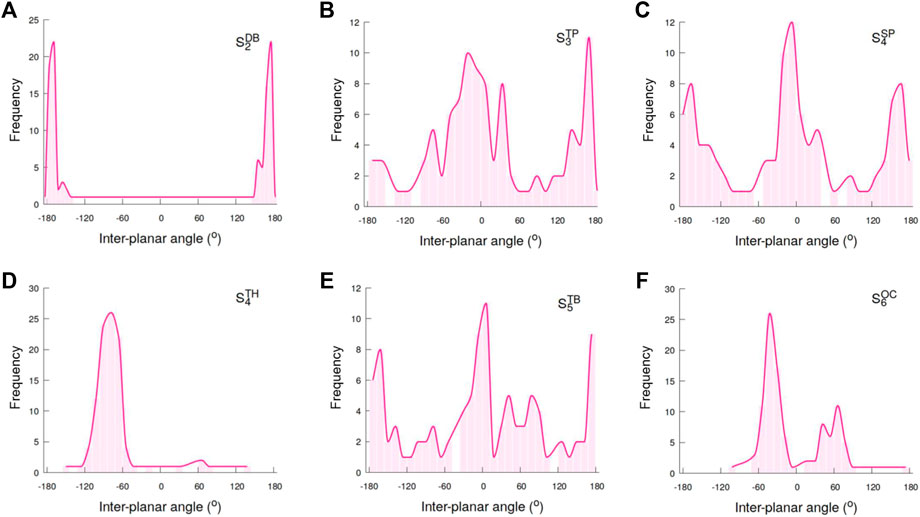
FIGURE 8. Shown are the distributions of the inter-planar angles in self-assemblies formed by (A) dumbbell, (B) trigonal planar (C) square planar, (D) tetrahedral, (E) trigonal bipyramidal, and (F) octahedral shaped particles.

The angle distributions for the $S_4^{SP}$ particles are reported in Figure 8C. These particles predominantly form sheet-like morphologies due to their planar structure. This feature is well captured from the interplanar angle distribution in which three peaks for the angle values −180°, 0°, 180° are observed. However, the non-planar $S_4^{TH}$ particles having the same number of lobes do not form any planar morphologies which is also reflected in their interplanar angle distributions (Figure 8D) showing that these particles align themselves by maintaining an angle of $\sim 90°$. Therefore, due to their non-planarity, these particles break the parallel or anti-parallel alignment as found in the planar $S_4^{SP}$ particles with the same number of lobes.

The trigonal bipyramidal particles with five lobes $(S_5^{TB})$ show several different types of interplanar angles (Figure 8E), similar to the $S_3^{TP}$ particles. This can be attributed to the planar equatorial framework within the $S_5^{TB}$ particles which resembles the $S_3^{TP}$ geometry and also due to a higher number of lobes leading to different packing modes, which leads to the $S_5^{TB}$ particles forming intra-network pores with the second largest sizes after the $S_3^{TP}$ particles. Finally, the distributions of the $S_6^{OC}$ particles are presented in Figure 8F. These particles do not show a wider range of angle values as in the case of $S_3^{TP}$ or $S_5^{TB}$ particles. Instead, the angle values are largely confined to ∼-40° or between $\sim 40°$ and $\sim 70°$. The restricted arrangements for these particles is attributed to the highest number of lobes to avoid several lobe-lobe replusions.

Conclusion

We studied self-assembly in homogeneous mixtures of particles with oppositely-charged lobes and probed their pore forming tendencies. In these mixtures, each particle has all the lobes either positively-charged or negatively-charged to resemble functionalized lobed particles with complementary interactions that are potentially experimentally realizable in comparison to the particles where the lobes on the same particle have different charges [27]. We observed the formation of morphologies with interstitial as well as intra-network pores, where the pores in the latter morphologies are an order of magnitude larger than in the former morphologies. Among all the particles studied, the $S_3^{TP}$ particles formed larger pores due to their smaller size, planar shape, and packing modes conducive to the formation of porous morphologies. We also observed that the mixtures of particles with oppositely-charged lobes have larger intra-network pores than the unmixed charged particles from our previous work [27]. Therefore, we suggest that the particle designs reported in our current work are suitable to applications in designing porous biomaterials for bioengineering and biomedical applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HV: conceptualization, supervision, funding acquisition, and draft editing. AS and BR: modeling, simulation, analysis, and draft preparation. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge the National Science Foundation (NSF) EPSCoR award (OIA-1757371; HV) for financial support as well as for providing the hetereogenous CPU/GPU supercomputing facility at the University of New Hampshire (UNH).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.936385/full#supplementary-material

References

1. Whitesides GM, Grzybowski B. Self-assembly at All Scales. Science (2002) 295:2418–21. doi:10.1126/science.1070821

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Sacanna S, Pine DJ, Yi G-R. Engineering Shape: the Novel Geometries of Colloidal Self-Assembly. Soft Matter (2013) 9:8096–106. doi:10.1039/c3sm50500f

CrossRef Full Text | Google Scholar

3. Matijevic E. Monodispersed Metal (Hydrous) Oxides - a Fascinating Field of Colloid Science. Acc Chem Res (1981) 14:22–9. doi:10.1021/ar00061a004

CrossRef Full Text | Google Scholar

4. Matijevic E. Preparation and Properties of Uniform Size Colloids. Chem Mater (1993) 5:412–26. doi:10.1021/cm00028a004

CrossRef Full Text | Google Scholar

5. Matijevic E. Uniform Inorganic Colloid Dispersions. Achievements and Challenges. Langmuir (1994) 10:8–16. doi:10.1021/la00013a003

CrossRef Full Text | Google Scholar

6. Vold MJ. The effect of adsorption on the van der waals interaction of spherical colloidal particles. J Colloid Sci (1961) 16:1–12. doi:10.1016/0095-8522(61)90057-5

CrossRef Full Text | Google Scholar

7. Moncho-Jordá A, Martínez-López F, González AE, Hidalgo-Álvarez R. Role of Long-Range Repulsive Interactions in Two-Dimensional Colloidal Aggregation: Experiments and Simulations. Langmuir (2002) 18:9183–91. doi:10.1021/la0258805

CrossRef Full Text | Google Scholar

8. Min Y, Akbulut M, Kristiansen K, Golan Y, Israelachvili J. The Role of Interparticle and External Forces in Nanoparticle Assembly. Nat Mater (2008) 7:527–38. doi:10.1038/nmat2206

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lotito V, Zambelli T. Approaches to Self-Assembly of Colloidal Monolayers: A Guide for Nanotechnologists. Adv Colloid Interf Sci (2017) 246:217–74. doi:10.1016/j.cis.2017.04.003

CrossRef Full Text | Google Scholar

10. van Dommelen R, Fanzio P, Sasso L. Surface Self-Assembly of Colloidal Crystals for Micro- and Nano-Patterning. Adv Colloid Interf Sci (2018) 251:97–114. doi:10.1016/j.cis.2017.10.007

CrossRef Full Text | Google Scholar

11. Lu PJ, Weitz DA. Colloidal Particles: Crystals, Glasses, and Gels. Annu Rev Condens Matter Phys (2013) 4:217–33. doi:10.1146/annurev-conmatphys-030212-184213

CrossRef Full Text | Google Scholar

12. Pham KN, Puertas AM, Bergenholtz J, Egelhaaf SU, Moussaïd A, Pusey PN, et al. Multiple Glassy States in a Simple Model System. Science (2002) 296:104–6. doi:10.1126/science.1068238

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition. Science (2000) 287:627–31. doi:10.1126/science.287.5453.627

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Schall P, Cohen I, Weitz DA, Spaepen F. Visualization of Dislocation Dynamics in Colloidal Crystals. Science (2004) 305:1944–8. doi:10.1126/science.1102186

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Schall P, Cohen I, Weitz DA, Spaepen F. Visualizing Dislocation Nucleation by Indenting Colloidal Crystals. Nature (2006) 440:319–23. doi:10.1038/nature04557

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ghosh Chaudhuri R, Paria S. Core/shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications. Chem Rev (2012) 112:2373–433. doi:10.1021/cr100449n

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Gao L, Gan H, Meng Z, Gu R, Wu Z, Zhang L, et al. Effects of Genipin Cross-Linking of Chitosan Hydrogels on Cellular Adhesion and Viability. Colloids Surf B: Biointerfaces (2014) 117:398–405. doi:10.1016/j.colsurfb.2014.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gorai B, Rocha BC, Vashisth H. Design of Functionalized Lobed Particles for Porous Self-Assemblies. JOM (2021) 73:2413–22. doi:10.1007/s11837-021-04715-w

CrossRef Full Text | Google Scholar

19. Ravaine S, Duguet E. Synthesis and Assembly of Patchy Particles: Recent Progress and Future Prospects. Curr Opin Colloid Interf Sci (2017) 30:45–53. doi:10.1016/j.cocis.2017.05.002

CrossRef Full Text | Google Scholar

20. Pawar AB, Kretzschmar I. Fabrication, Assembly, and Application of Patchy Particles. Macromol Rapid Commun (2010) 31:150–68. doi:10.1002/marc.200900614

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bharti B, Rutkowski D, Han K, Kumar AU, Hall CK, Velev OD. Capillary Bridging as a Tool for Assembling Discrete Clusters of Patchy Particles. J Am Chem Soc (2016) 138:14948–53. doi:10.1021/jacs.6b08017

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Long AW, Ferguson AL. Nonlinear Machine Learning of Patchy Colloid Self-Assembly Pathways and Mechanisms. J Phys Chem B (2014) 118:4228–44. doi:10.1021/jp500350b

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhang Z, Glotzer SC. Self-assembly of Patchy Particles. Nano Lett (2004) 4:1407–13. doi:10.1021/nl0493500

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kraft DJ, Groenewold J, Kegel WK. Colloidal Molecules with Well-Controlled Bond Angles. Soft Matter (2009) 5:3823. doi:10.1039/b910593j

CrossRef Full Text | Google Scholar

25. Paul S, Vashisth H. Self-assembly Behavior of Experimentally Realizable Lobed Patchy Particles. Soft Matter (2020) 16:8101–7. doi:10.1039/d0sm00954g

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Paul S, Vashisth H. Self-assembly of Lobed Particles into Amorphous and Crystalline Porous Structures. Soft Matter (2020) 16:1142–7. doi:10.1039/c9sm01878f

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Rocha BC, Paul S, Vashisth H. Enhanced Porosity in Self-Assembled Morphologies Mediated by Charged Lobes on Patchy Particles. J Phys Chem B (2021) 125:3208–15. doi:10.1021/acs.jpcb.0c11096

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Paul S, Vashisth H. Self-assembly of Porous Structures from a Binary Mixture of Lobed Patchy Particles. Front Phys (2021) 9:767623. doi:10.3389/fphy.2021.767623

CrossRef Full Text | Google Scholar

29. Mathews K RA, Mani E. Stabilizing Ordered Structures with Single Patch Inverse Patchy Colloids in Two Dimensions. J Phys Condens Matter (2021) 33:195101. doi:10.1088/1361-648x/abf0c0

CrossRef Full Text | Google Scholar

30. Blenner D, Stubbs J, Sundberg D. Multi-lobed Composite Polymer Nanoparticles Prepared by Conventional Emulsion Polymerization. Polymer (2017) 114:54–63. doi:10.1016/j.polymer.2017.02.080

CrossRef Full Text | Google Scholar

31. Wang Y, Wang Y, Breed DR, Manoharan VN, Feng L, Hollingsworth AD, et al. Colloids with Valence and Specific Directional Bonding. Nature (2012) 491:51–5. doi:10.1038/nature11564

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Liu M, Zheng X, Grebe V, He M, Pine DJ, Weck M. Two‐Dimensional (2D) or Quasi‐2D Superstructures from DNA‐Coated Colloidal Particles. Angew Chem Int Ed (2021) 60:5744–8. doi:10.1002/anie.202014045

CrossRef Full Text | Google Scholar

33. van Ravensteijn BGP, Kegel WK. Tuning Particle Geometry of Chemically Anisotropic Dumbbell-Shaped Colloids. J Colloid Interf Sci (2017) 490:462–77. doi:10.1016/j.jcis.2016.11.045

CrossRef Full Text | Google Scholar

34. Meester V, Verweij RW, van der Wel C, Kraft DJ. Colloidal Recycling: Reconfiguration of Random Aggregates into Patchy Particles. ACS Nano (2016) 10:4322–9. doi:10.1021/acsnano.5b07901

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Sacanna S, Pine DJ. Shape-anisotropic Colloids: Building Blocks for Complex Assemblies. Curr Opin Colloid Interf Sci (2011) 16:96–105. doi:10.1016/j.cocis.2011.01.003

CrossRef Full Text | Google Scholar

36. Liu M, Dong F, Jackson NS, Ward MD, Weck M. Customized Chiral Colloids. J Am Chem Soc (2020) 142:16528–32. doi:10.1021/jacs.0c07315

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Liu M, Zheng X, Grebe V, Pine DJ, Weck M. Tunable Assembly of Hybrid Colloids Induced by Regioselective Depletion. Nat Mater (2020) 19:1354–61. doi:10.1038/s41563-020-0744-2

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zheng X, Wang Y, Wang Y, Pine DJ, Weck M. Thermal Regulation of Colloidal Materials Architecture through Orthogonal Functionalizable Patchy Particles. Chem Mater (2016) 28:3984–9. doi:10.1021/acs.chemmater.6b01313

CrossRef Full Text | Google Scholar

39. Wolters JR, Avvisati G, Hagemans F, Vissers T, Kraft DJ, Dijkstra M, et al. Self-assembly of "Mickey Mouse" Shaped Colloids into Tube-like Structures: Experiments and Simulations. Soft Matter (2015) 11:1067–77. doi:10.1039/c4sm02375g

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Kraft DJ, Vlug WS, van Kats CM, van Blaaderen A, Imhof A, Kegel WK. Self-assembly of Colloids with Liquid Protrusions. J Am Chem Soc (2008) 131:1182–6. doi:10.1021/ja8079803

CrossRef Full Text | Google Scholar

41. Morphew D, Shaw J, Avins C, Chakrabarti D. Programming Hierarchical Self-Assembly of Patchy Particles into Colloidal Crystals via Colloidal Molecules. ACS Nano (2018) 12:2355–64. doi:10.1021/acsnano.7b07633

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Avvisati G, Vissers T, Dijkstra M. Self-assembly of Patchy Colloidal Dumbbells. J Chem Phys (2015) 142:084905. doi:10.1063/1.4913369

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Wolters JR, Verweij JE, Avvisati G, Dijkstra M, Kegel WK. Depletion-induced Encapsulation by Dumbbell-Shaped Patchy Colloids Stabilize Microspheres against Aggregation. Langmuir (2017) 33:3270–80. doi:10.1021/acs.langmuir.7b00014

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Sato M. Effect of the Interaction Length on Clusters Formed by Spherical One-Patch Particles on Flat Planes. Langmuir (2021) 37:4213–21. doi:10.1021/acs.langmuir.1c00102

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Sacanna S, Korpics M, Rodriguez K, Colón-Meléndez L, Kim SH, Pine DJ, et al. Shaping Colloids for Self-Assembly. Nat Commun (2013) 4:1688. doi:10.1038/ncomms2694

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Gong Z, Hueckel T, Yi G-R, Sacanna S. Patchy Particles Made by Colloidal Fusion. Nature (2017) 550:234–8. doi:10.1038/nature23901

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lin Y-C, Tripathi AK, Tsavalas JG. Tunable Multilobe Particle Geometry by Annealing-Assisted Emulsion Polymerization. ACS Appl Polym Mater (2022) 4:313–26. doi:10.1021/acsapm.1c01312

CrossRef Full Text | Google Scholar

48. Glotzer SC, Solomon MJ, Kotov NA. Self-assembly: From Nanoscale to Microscale Colloids. Aiche J (2004) 50:2978–85. doi:10.1002/aic.10413

CrossRef Full Text | Google Scholar

49. Marson RL, Phillips CL, Anderson JA, Glotzer SC. Phase Behavior and Complex crystal Structures of Self-Assembled Tethered Nanoparticle Telechelics. Nano Lett (2014) 14:2071–8. doi:10.1021/nl500236b

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Santos PHS, Campanella OH, Carignano MA. Brownian Dynamics Study of Gel-Forming Colloidal Particles. J Phys Chem B (2010) 114:13052–8. doi:10.1021/jp105711y

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Santos PHS, Campanella OH, Carignano MA. Effective Attractive Range and Viscoelasticity of Colloidal Gels. Soft Matter (2013) 9:709–14. doi:10.1039/c2sm26585k

CrossRef Full Text | Google Scholar

52. Chremos A, Jeong C, Douglas JF. Influence of Polymer Architectures on Diffusion in Unentangled Polymer Melts. Soft Matter (2017) 13:5778–84. doi:10.1039/c7sm01018d

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Liu T, VanSaders B, Keating JT, Glotzer SC, Solomon MJ. Effect of Particles of Irregular Size on the Microstructure and Structural Color of Self-Assembled Colloidal Crystals. Langmuir (2021) 37:13300–8. doi:10.1021/acs.langmuir.1c01898

PubMed Abstract | CrossRef Full Text | Google Scholar

54. LeBard DN, Levine BG, Mertmann P, Barr SA, Jusufi A, Sanders S, et al. Self-assembly of Coarse-Grained Ionic Surfactants Accelerated by Graphics Processing Units. Soft Matter (2012) 8:2385–97. doi:10.1039/c1sm06787g

CrossRef Full Text | Google Scholar

55. Anderson JA, Glaser J, Glotzer SC. Hoomd-blue: A python Package for High-Performance Molecular Dynamics and Hard Particle Monte Carlo Simulations. Comput Mater Sci (2020) 173:109363. doi:10.1016/j.commatsci.2019.109363

CrossRef Full Text | Google Scholar

56. Hockney RW, Goel SP, Eastwood JW. Quiet High-Resolution Computer Models of a Plasma. J Comput Phys (1974) 14:148–58. doi:10.1016/0021-9991(74)90010-2

CrossRef Full Text | Google Scholar

57. Ramasubramani V, Dice BD, Harper ES, Spellings MP, Anderson JA, Glotzer SC. Freud: A Software Suite for High Throughput Analysis of Particle Simulation Data. Comp Phys Commun (2020) 254:107275. doi:10.1016/j.cpc.2020.107275

CrossRef Full Text | Google Scholar

58. Willems TF, Rycroft CH, Kazi M, Meza JC, Haranczyk M. Algorithms and Tools for High-Throughput Geometry-Based Analysis of Crystalline Porous Materials. Microporous Mesoporous Mater (2012) 149:134–41. doi:10.1016/j.micromeso.2011.08.020

CrossRef Full Text | Google Scholar

59. Pinheiro M, Martin RL, Rycroft CH, Jones A, Iglesia E, Haranczyk M. Characterization and Comparison of Pore Landscapes in Crystalline Porous Materials. J Mol Graphics Model (2013) 44:208–19. doi:10.1016/j.jmgm.2013.05.007

CrossRef Full Text | Google Scholar

60. Pinheiro M, Martin RL, Rycroft CH, Haranczyk M. High Accuracy Geometric Analysis of Crystalline Porous Materials. CrystEngComm (2013) 15:7531–8. doi:10.1039/c3ce41057a

CrossRef Full Text | Google Scholar

61. Zhang J, Luijten E, Granick S. Toward Design Rules of Directional Janus Colloidal Assembly. Annu Rev Phys Chem (2015) 66:581–600. doi:10.1146/annurev-physchem-040214-121241

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Dias CS, Braga C, Araújo NAM, Telo da Gama MM. Relaxation Dynamics of Functionalized Colloids on Attractive Substrates. Soft Matter (2016) 12:1550–7. doi:10.1039/c5sm02754c

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Hagan MF, Elrad OM, Jack RL. Mechanisms of Kinetic Trapping in Self-Assembly and Phase Transformation. J Chem Phys (2011) 135:104115. doi:10.1063/1.3635775

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Nykypanchuk D, Maye MM, van der Lelie D, Gang O. DNA-Guided Crystallization of Colloidal Nanoparticles. Nature (2008) 451:549–52. doi:10.1038/nature06560

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Paquet E, Viktor HL. Molecular Dynamics, Monte Carlo Simulations, and Langevin Dynamics: A Computational Review. Biomed Res Int (2015) 2015:1–18. doi:10.1155/2015/183918

CrossRef Full Text | Google Scholar

66. O’brien FJ. Biomaterials & Scaffolds for Tissue Engineering. Mater Today (2011) 14:88–95.

Google Scholar

67. Loh QL, Choong C. Three-dimensional Scaffolds for Tissue Engineering Applications: Role of Porosity and Pore Size. Tissue Eng B: Rev (2013) 19:485–502. doi:10.1089/ten.teb.2012.0437

CrossRef Full Text | Google Scholar