Broadband Coherent Mid-Infrared Supercontinuum Generation in All-Chalcogenide Microstructured Fiber With All-Normal Dispersion

We demonstrated numerically the generation of broadband, coherent supercontinuum (SC) spectra in the mid-infrared region using dispersion-engineered all-chalcogenide microstructured fibers (MOFs). The 1-cm-long hexagonal fiber can be made with Ge_11.5As₂₄S_64.5 glass as a low-refractive-index material embedded in a Ge_11.5As₂₄Se_64.5 glass matrix. By optimizing the structural parameters, we determined a broad and flat all-normal-dispersion characteristic up to 14 μm. A highly coherent broadband SC with an intensity greater than −3 dB in the range from 5973 to 8695 nm is obtained when the fiber is pumped by a 7 μm laser with pulse duration of 50 fs and peak power of 6 kW. Flat-top SC of −30 dB level can be observed utilizing identical pump pulse parameters, covering wavelengths from 3823 to 13577 nm (>1.5 octaves). This broadband coherent MIR SC source can be applied in frequency metrology, optical coherence tomography, biomedical imaging, and few-cycle pulse compression.

Introduction

Supercontinuum (SC) generation in the mid-infrared (MIR) spectral region has great potential because it offers unique capabilities in molecule detection and identification [1]. The development of broadband coherent MIR SC sources has improved technologies such as trace gas spectroscopy and optical sensing [2, 3], and boosted studies and applications in frequency metrology, optical coherence tomography, and biomedical imaging [4–6]. To achieve a coherent SC output with the broadest spectra, a common way is to pump the fiber in its anomalous dispersion regime and close to the zero-dispersion wavelength (ZDW) [7]. However, since the spectral broadening mechanism here is dominated by soliton-related dynamics, the generated SC spectra are strongly sensitive to fluctuations of the pump pulse intensity and present considerable fine structure throughout the bandwidth [8, 9]. Modulation instability processes also have a significant influence on SC coherence, where the initial spectral broadening is seeded from noise when pumping occurs in the anomalous dispersion regime [10]. Alternatively, the use of all-normal dispersion (ANDi) fibers based on the adjustment of group velocity dispersion (GVD) offers an opportunity to generate highly coherent, single-pulsed, stable SC spectra, where the broadening mechanism is mainly self-phase modulation (SPM) and optical wave breaking (OWB) [11, 12]. The coherence of the output SC thus is almost the same as that of the pump source, attributed to the fact that the SPM and OWB processes are self-seeded [8]. Therefore, SC spectra with better shot-to-shot coherence and spectral flatness over the bandwidth could be obtained when optical fibers are engineered in all-normal dispersion, and the single pulse preserved in the time domain is also essential for applications in time-resolved measurements and few-cycle pulse compression [13, 14].

Coherent SC generation that covers up to the near-infrared region based on ANDi microstructured fibers (MOFs) has been investigated numerically and experimentally [14–18]. However, the transmission loss beyond 2.7 μm and the relatively weak nonlinearity of commonly used silica glass tremendously limit the silica fibers reaching the MIR region [12, 19–22]. Chalcogenide (ChG) fibers have been demonstrated to be promising candidates due to their high intrinsic nonlinearity and low photon energies [14, 18, 23], and the long-wave transmission edge can be up to about 14 μm when selenide-based materials are used [24–27]. Compared to standard step-index fibers, MOFs, or photonic crystal fibers (PCFs), are more attractive because of their ability to adjust the waveguide dispersion so that material dispersion is compensated. Combining ruggedness, compactness, and excellent beam quality of fiber-based light sources, an ANDi profile is achievable in MOFs with enhanced nonlinear effects, controllable mode area, and desirable GVD properties through dispersion engineering [28]. Among all MOFs, all-solid microstructured cladding could avoid holey structure deformation and environmental gas impurities during thermal processing in fiber fabrication [29]. Recently, the generation of broadband SC spectra in the MIR region through all-solid MOFs has been demonstrated both experimentally [15, 16, 18, 30] and numerically [31–33]. Klimczak et al. experimentally demonstrated a MIR SC extending to 2.3 μm with a soft glass PCF made of boron-silicate glass and silicate glass, pumped with 75-fs pulses at 1550 nm [16]. Liu et al. experimentally reported a coherent MIR SC generation covering up to 3.3 μm based on a 2-cm-long AsSe₂/As₂S₅ four-hole ChG MOF pumped by a 2.7 μm laser [15]. Ren et al. experimentally demonstrated a Ge₁₂As₂₄Se₆₄/Ge₁₀As₂₄S₆₆ MOF with an ultra-large mode area, generating MIR SC from 3.5 to 7.5 μm, pumped at 4 μm in the ANDi regime [30]. Yuan et al. experimentally reported a broadband coherent MIR SC generation up to 13.2 μm in an ANDi Te-based ChG MOF made from Ge₂₀As₂₀Se₂₀Te₄₀ and As₂S₃, under pumping at 5 μm [18]. Among the chalcogenide family, Ge_11.5As₂₄Se_64.5 has gained considerable interest not only due to its relatively high nonlinearity (about 2.5 times that of As₂S₃), but also due to its higher thermal, optical, and chemical stability under intense illumination [34, 35]. Karim et al. numerically showed MIR SC spectral broadening extending beyond 15 μm in a Ge_11.5As₂₄Se_64.5/Ge_11.5As₂₄S_64.5 triangular-core fiber, pumped at 4 μm in the anomalous dispersion regime [31]. Huang designed a ChG MOF composed of hexagonal rings using As₂Se₃ and Ge_11.5As₂₄Se_64.5, which supports SC generation from 3450 to 8015 nm when the fiber is pumped at 5 μm [32]. Medjouri et al. simulated a MIR SC with wavelengths ranging from 1.6 to 7 μm with an ANDi Ge₁₅Sb₁₅Se₇₀/Ge₂₀Se₈₀ MOF, pumped with pulses of 50 fs at 3 μm [33].

In this work, we numerically demonstrate broadband and coherent MIR SC generation in a dispersion-engineered all-solid MOF using Ge_11.5As₂₄Se_64.5 as the core embedded with low-refractive-index Ge_11.5As₂₄S_64.5 rods in its cladding. The lasers can then be confined and propagated in the core region of the MOF obeying the guidance mechanism similar to that of conventional fibers. By optimizing structural parameters, ChG MOF with broad and flat all-normal dispersion profiles from 4 to 14 μm can be achieved, supporting the generation of broadband SC covering up to the transparency limit wavelength (∼14 μm) of the GeAsSe glass with perfect coherence when pumped by wavelength-tunable femtosecond lasers with peak powers of no more than 6 kW. The generalized nonlinear Schrödinger equation is used to model the spectral broadening, and the output bandwidth and coherence are studied when various pump pulse and fiber characteristics are applied. To the best of our knowledge, this is the broadest coherent SC generation in the ANDi MOF where the broadening mechanism is mainly SPM and OWB effects.

Concept and Fiber Structure

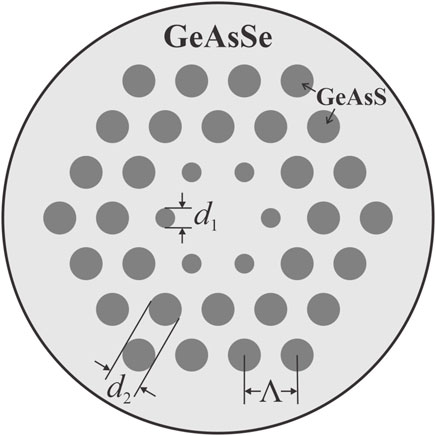
The schematic cross-section of the proposed all-chalcogenide MOF structure is depicted in Figure 1. In this study, we employed a three-ring hexagonal lattice all-solid MOF structure, which can be manufactured using the rod-in-tube drawing technique [36]. The gray regions denote low-index Ge_11.5As₂₄S_64.5 glass rods, and the background region denotes high-index Ge_11.5As₂₄Se_64.5 glass. The ChG MOF is modeled and optimized by varying the pitch $\text{Λ}$ and diameters of the innermost ring of GeAsS rods $d_1$ and outer rings of the rods $d_2$, through the CUDOS MOF Utilities package based on a multipole method [37, 38]. The waveguide characterizing parameters can then be calculated and optimized by investigating the structure of the MOF. The Sellmeier equations are used to determine the wavelength-dependent linear refractive index of the Ge_11.5As₂₄Se_64.5 and Ge_11.5As₂₄S_64.5 ChG glasses over the entire wavelength range [35]:

$\begin{array}{c}{n}_{{\text{Ge}}_{11.5}{\text{As}}_{24}{\text{Se}}_{64.5}}\left(\lambda \right)=\sqrt{1+\frac{5.78525{\lambda }^2}{{\lambda }^2-{0.28795}^2}+\frac{0.39705{\lambda }^2}{{\lambda }^2-{30.39338}^2}},\end{array}(1)$

$\begin{array}{c}{n}_{{\text{Ge}}_{11.5}{\text{As}}_{24}{\text{S}}_{64.5}}\left(\lambda \right)=\sqrt{1+\frac{4.18011{\lambda }^2}{{\lambda }^2-{0.31679}^2}+\frac{0.35895{\lambda }^2}{{\lambda }^2-{22.77018}^2}},\end{array}(2)$

where $\lambda$ is the wavelength in micrometers. By incorporating the material refractive index, the dispersion parameter of the MOF can be evaluated from the real part of the effective index $\mathrm{\Re }\left(n_{eff}\right)$[7, 39]:

$\begin{array}{c}D=-\frac{\lambda }{c}\frac{{\partial }^2\mathrm{\Re }\left(n_{eff}\right)}{\partial {\lambda }^2},\end{array}(3)$

where c denotes the light speed in the vacuum. On the other hand, the imaginary part of the effective index $\mathrm{\Im }\left(n_{eff}\right)$ is related to the confinement loss L in decibels per meter which results from the finite transverse extent of the confining structure through relation [39]:

$\begin{array}{c}L=\frac{20}{\text{ln}\left(10\right)}\frac{2\pi }{\lambda }\Im \left(n_{eff}\right)\times {10}^6,\end{array}(4)$

FIGURE 1

FIGURE 1. Schematic cross-section of the all-chalcogenide microstructured fiber.

To study MIR SC generation in the ANDi regime, the pulse spectral evolution inside the proposed MOF is modeled by solving the generalized nonlinear Schrödinger equation (GNLSE) [7] including two-photon absorption (TPA) [40]:

$\begin{array}{l}\frac{\partial }{\partial z}A\left(z, T\right)+\frac{\alpha }{2}A-{\displaystyle \sum }_{k\ge 2}\frac{i^{k+1}}{k!}{\beta }_k\frac{{\partial }^{k}A}{\partial T^k}\\ \begin{array}{c}=i\left(\gamma +i\frac{{\alpha }_2}{2A_{\text{eff}}}\right)\left(1+i{\tau }_{shock}\frac{\partial }{\partial T}\right)\times \left(A\left(z,T\right){{\displaystyle \int }}_{-\infty }^{\infty }R\left(T\right){\left|A\left(z,T-T^{\prime }\right)\right|}^{2}d{T}^{\prime }\right).\end{array}\end{array}(5)$

The left-hand side of Eq. 5 models linear propagation effects, where $A\left(z, T\right)$ indicates the slowly varying pulse envelope evolving along the length of the MOF structure in a retarded time frame with reference $T=t-{\beta }_{1}z$ moving at the group velocity $v_g=1/{\beta }_1$. $\alpha$ is the transmission loss, and${\beta }_k$’s are the k’s order dispersion coefficients associated with the Taylor series expansion of the propagation constant $\beta \left(\omega \right)$ around the carrier frequency ${\omega }_0$. The right-hand side of Eq. 5 models nonlinear effects: $\gamma ={\omega }_0{n}_2/\left(c{A}_{\text{eff}}\right)$ is the usual nonlinear coefficient, where $n_2$ is the nonlinear refractive index and $A_{\text{eff}}={\left({\displaystyle \iint {\left|E\right|}^2}dxdy\right)}^2/\left({\displaystyle \iint {\left|E\right|}^{4}dxdy}\right)$ is the mode effective area evaluated at ${\omega }_0$ with $E$ as the electric field intensity. The TPA coefficient is ${\alpha }_2=7.88\times {10}^{-14} \text{m}/\text{W}$ [41], and can be assumed to be negligible when pumping occurs below 8 μm in our case. Shock term ${\tau }_{shock}=1/{\omega }_0$ is included. The response function $R\left(T\right)=\left(1-f_R\right)\delta \left(t\right)+f_R{h}_R\left(t\right)$ includes both instantaneous Kerr response and delayed Raman contributions, where $h_R\left(t\right)$ can be expressed as [42].

$\begin{array}{c}{h}_R\left(t\right)=\frac{{\tau }_1^2+{\tau }_2^2}{{\tau }_1{\tau }_2^2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{t}{{\tau }_2}\right)\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{t}{{\tau }_1}\right).\end{array}(6)$

The coefficients $f_R=0.031,$ ${\tau }_1=15.5 \text{fs}$, and ${\tau }_2=230.5 \text{fs}$ are used to model the Raman response of our ChG material [40]. In our simulation, a hyperbolic secant-shaped pulse is used with the optical field in the form

$\begin{array}{c}A\left(0,T\right)=\sqrt{P_0}sech\frac{T}{T_0},\end{array}(7)$

where $P_0$ is the peak power, and $T_0$ is the pulse full width at half-maximum duration (FWHM). The complex degree of first-order coherence used to investigate coherence degradation is calculated at each wavelength in SC by [8, 9].

$\begin{array}{c}\left|{\text{g}}_{12}^{\left(1\right)}\left(\lambda ,t_1-t_2\right)\right|=\left|\frac{\langle E_1^{\ast }\left(\lambda ,t_1\right)E_2\left(\lambda ,t_2\right)\rangle }{\sqrt{\langle {\left|E_1\left(\lambda ,t_1\right)\right|}^2\rangle \langle {\left|E_2\left(\lambda ,t_2\right)\right|}^2\rangle }}\right|.\end{array}(8)$

Angular brackets denote an ensemble average over independently generated pairs of SC spectra $[E_1\left(\lambda ,t_1\right)$, $E_2\left(\lambda ,t_2\right)]$ and $t$ is the time measured at the scale of the temporal resolution of the spectrometer used to resolve these spectra. To focus on the wavelength dependence of the coherence, we calculate the $\left|{\text{g}}_{12}^{\left(1\right)}\right|$ at $t_1-t_2=0$.

Results and Discussion

Dispersion Engineering of Chalcogenide Fiber

The SC spectral evolution at the fiber output is significantly dependent on the dispersion optimization. To achieve coherent SC spectral broadening up to the MIR region, a flat GVD profile with a small magnitude spanning a wide wavelength range in the ANDi regime is a vital factor, which can be modified by varying the geometric parameters of the MOF [17]. To obtain suitable GVD curves for pumping in this regime, numerous simulations are carried out on the proposed MOF structure with variations in its pitch and rod diameters. Figures 2A–C illustrate the fundamental mode dispersion curves calculated from the mode effective index obtained by the CUDOS MOF Utilities package. The material dispersion curve of the core glass Ge_11.5As₂₄Se_64.5 is also given as a reference, where the slope of the curve changes abruptly around 4 μm, and the zero dispersion of the material wavelength is located at approximately 7.1 μm. When the cladding region is embedded with Ge_11.5As₂₄S_64.5 glass rods with a relatively low refractive index, the waveguide dispersion of the MOF can be significantly modified, and the ZDW of the fiber extends into the red spectral region. Figure 2A shows that for fixed rod diameters $d_1=0.3 \text{μm}$ and $d_2=1.0 \text{μm}$, larger pitch $\text{Λ}$ shifts the GVD curve closer to the material dispersion. This is because, for larger pitches, the waveguide effects are weaker due to the larger MOF core, and thus the GVD is dominated by the material dispersion. On the contrary, for smaller pitches, the waveguide dispersion becomes stronger to compensate for material dispersion, whereas the amplitude of the dispersion curve oscillations increases. When $\text{Λ}$ increases from 1.6 to 1.8 μm, the ZDW is blue-shifted from 14.5 to 13.8 μm. Figure 2B shows that for fixed rod diameter $d_1=0.3 \text{μm}$ and pitch $\text{Λ}=1.7 \text{μm}$, the curve oscillation amplitude is also affected by the variation in rod diameter $d_2$. When $d_2$ increases from 0.9 to 1.1 μm, the dispersion curve can be further flattened in the wavelength range between 4 and 14 μm, however, the ZDW is blue-shifted from 14.6 to 13.6 μm. Although Figures 2A,B look similar in the wavelength range we are concerned about, there are still some minor differences resulting from the change of waveguide dispersion. In Figure 2A, the wavelengths associated with the local maximum dispersion in the three cases are stagnant at around 8 μm because the pitch $\text{Λ}$ variation mainly influences the ZDW and oscillations of the dispersion, while in Figure 2B, the local maximum dispersion wavelength increases with the diameter $d_2$, which is the result of the competition between the material dispersion and the waveguide dispersion due to the mode confinement nature of the MOF [39]. The influence of diameter $d_2$ is also apparent in the short-wavelength region, where the behavior is similar to that of rod diameter $d_1$ in this region in Figure 2C. As the innermost ring of the rods, the diameter $d_1$ impacts more on the light at short wavelengths because for short waves, the fine structure of the MOF matters, resulting in a great concentration in the core region. For longer wavelengths, which is above 6 μm in our case, the structure tends to be uniform, and the effective index of the mode would be limited within the uniform refractive index of the structure, thus generating nearly the same dispersion curve at long wavelengths [39]. The results show that the MOF exhibits broad and flat all-normal dispersion profiles before 14.2 μm with optimized diameters of the innermost ring of rods ($d_1=0.3 \text{μm}$) and two outer rings of rods ($d_2=1.0 \text{μm}$), and the pitch of the rod lattice is $\text{Λ}=1.7 \text{μm}$. Flattened dispersion is observed from 4 to 14 μm with an oscillation amplitude of $\pm 12.6 \text{ps}/\text{nm}/\text{km}$, and a local maximum of $-8.8 \text{ps}/\text{nm}/\text{km}$ at 7.9 μm. For the optimized MOF structure, mode effective areas ($A_{\text{eff}}$) are obtained through the CUDOS MOF Utilities package and their corresponding nonlinear coefficients ($\gamma$) are calculated using $n_2=7.08\times {10}^{-18}{\text{m}}^2/\text{W}$ [41] as shown in Figure 2D. The confinement loss is calculated based on the multipole method, and by combining the material linear propagation loss of $0.5 \text{dB}/\text{cm}$[31, 35], the transmission losses $\alpha =4$.3, 34.2, 136.0, 339.7, and 663.7 $\text{dB}/\text{cm}$ at pumping wavelengths of 3–7 μm are considered for our proposed MOF throughout all the SC simulations, respectively. Besides, impurity absorption attributed to the S-H, Se-H, Ge-H, As-H, O-H, and Ge-O bonds located at corresponding 4.1, 4.6, 4.9, 5.0, 6.3, and 7.9 µm, also has a great impact on the output spectral smoothness [18, 43]. However, by adopting purification in further fiber fabrication processes and all-solid microstructured fiber structure, one may obtain an effective way to reduce impurity absorption and prevent water contamination in the air [18, 29]. The fiber length is kept as short as 1 cm to reduce long propagation loss. It is worth mentioning that the MOF may support multimode transmission, whereas higher-order modes experience confinement losses of more than 10 times that of the fundamental mode based on our calculation. Previous research suggests that the SC bandwidth generated remains unchanged for a pump pulse with femtosecond duration due to the temporal walk-off between modes, preventing Raman-induced energy transfer [44]. Therefore, the SC bandwidth at the output of the MOF is not affected by higher-order modes, since an ultrashort pump pulse with a duration shorter than 200 fs is considered for our proposed designs.

FIGURE 2

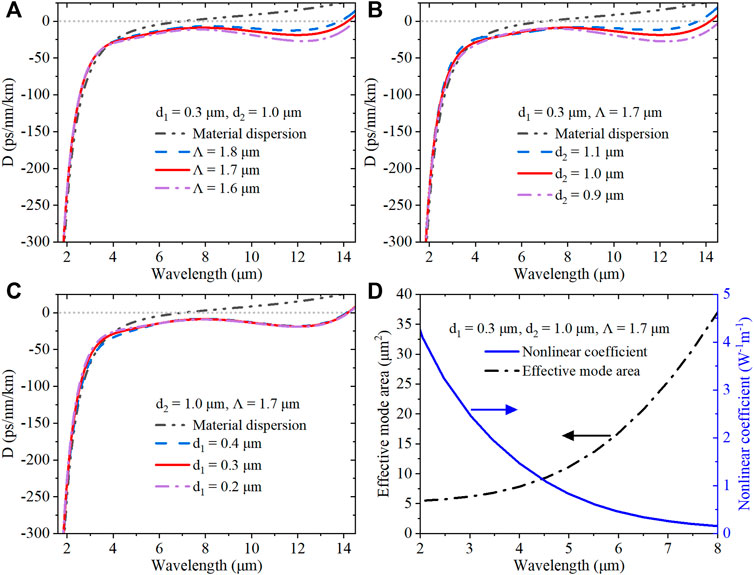
FIGURE 2. (A–C) Calculated material dispersion of GeAsSe glass and GVD characteristic curves of MOFs with various structural parameters. (D) Effective mode areas and their corresponding nonlinear coefficients for the MOF structure.

Broadband Coherent MIR Supercontinuum Generation

Pulse propagation in the proposed MOF is simulated using the split-step Fourier method to solve the GNLSE Eq. 5 through Python. Using the tunable pump source from 3 to 7 μm, the MIR SC spectral evolution in the ANDi regime is predicted using secant-shaped pulses of femtosecond duration in the MOFs with a low peak power of no more than 6 kW.

The spectral evolution on a logarithmic scale with the propagation distance in the fiber is shown in Figure 3A, where the pump pulse duration is 50 fs (FWHM) at 3 μm with a peak power of 1 kW. For a normal GVD pumping, the broadening process is initiated by the SPM, and the approximately symmetrical property is typical of what can be expected when SPM interacts with fiber’s normal dispersion [7]. The somewhat asymmetric SC spectral shapes are due to the influence of high-order dispersion, and the narrower spectrum bandwidth in the blue region is also the result of the much steeper GVD slope on this side of the pump as shown in Figure 2. The wave-breaking distance is introduced to calculate the propagation distance in fiber where the OWB starts to occur and spectral broadening begins to appear on both sides of the pump wavelength. For the secant-shaped pulse applied in our simulation, the estimated wave-breaking distance $Z_{wb}$ is given by [15, 45].

$\begin{array}{c}{Z}_{wb}={\left(\frac{3{\beta }_2}{2{\beta }_2+2\gamma P_0{T}_0^2}\right)}^{1/2}\frac{T_0^2}{{\beta }_2}.\end{array}(9)$

FIGURE 3

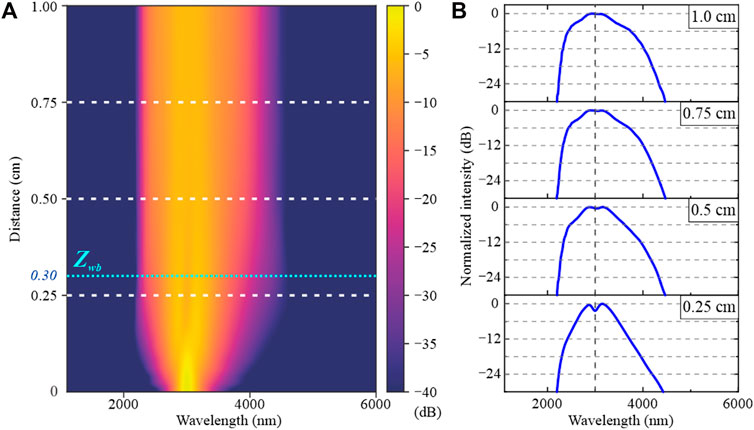
FIGURE 3. (A) Dependence of the spectrum evolution with the propagation distance. (B) Spectral profiles at different fiber propagation distances, with pump pulse wavelength at 3 μm marked as a vertical gray dashed line. The pump pulse duration and peak power are 50 fs and 1 kW, respectively.

The wave-breaking distance is 0.30 cm in this case as indicated in Figure 3A, which means that for fiber parameters and pumping conditions applied in our simulation, both OWB and SPM play a key role in the spectral broadening after 0.30 cm. Horizontal white dashed lines represent the fiber propagation distances where the spectral intensity profiles are investigated, as shown in Figure 3B, with every vertical interval divided by horizontal gray dashed lines representing a 6-dB variation in intensity. The pump pulse wavelength at 3 μm is marked as a vertical gray dashed line in Figure 3B. At a propagation distance of 0.25 cm, the spectrum bandwidth is narrow, and the peaks dominated by SPM are strong. After about 0.3 cm of propagation, sidelobes become apparent at both sides of the pump wavelength attributed to the effect of OWB, where the spectrum sidebands are obtained at the leading and trailing edges of the pulse by continually mixing the overlapping frequency components generated from SPM [11, 32]. Therefore, the spectral bandwidth is substantially maintained, and the spectral profile of the SC is well preserved during spectral broadening. At 0.5, 0.75, and 1.0 cm, the spectral profiles almost exhibit similar flatness and bandwidth, and a smoother profile is achieved with propagation. The spectral bandwidth with an intensity greater than −30 dB spans more than one octave, ranging from 2199 to 4465 nm.

The influence of pump pulse parameters on the spectral profiles is investigated to explore the spectral bandwidth and profiles of the generated SC. The spectral profiles of SC generation when pumping occurs at wavelengths tuning from 3 to 6 μm are shown in Figure 4A. The pulse FWHM and peak power are fixed at 50 fs and 1 kW, respectively. When pumping at 3 μm, the intensity in the short-wavelength region is slightly higher than that in the long-wavelength region due to the sharp increase in the magnitude of the dispersion below 3 μm, which generates an SC spectrum shifted toward the blue region. The spectral bandwidth with an intensity greater than −3 dB is 814 nm. As the pump wavelength moves further into the mid-infrared region, the spectral bandwidth becomes wider and more intensity is shifted toward the longer wavelength, and by combining a flat all-normal dispersion in this region, a spectral broadening with better smoothness is obtained. When pumping at 5 and 6 μm, the spectral bandwidth with an intensity greater than −3 dB achieves 1190 nm and 1180 nm, respectively. The relatively narrower 3-dB bandwidth when pumping occurs at 6 μm is due to the lower nonlinear coefficient and the smaller dispersion magnitude of the MOF at 6 μm, which induces more energy to be transferred to the far end of the spectrum by OWB. This process broadens the spectral bandwidth to 5.8 μm with an intensity greater than −30 dB when pumping at 6 μm. The impact of pump pulse duration on spectral profiles is investigated and shown in Figure 4B, when the pump pulse wavelength and peak power are fixed at 6 μm and 3 kW, respectively. In these cases, the broadest spectrum appears at the shortest pump duration of 50 fs. For longer pulse durations, a narrower bandwidth is generated with degraded flatness and smoothness, and peaks and dips emerge near the pump wavelength. This behavior can be attributed to the SPM effect at a longer pump pulse duration. As the wave-breaking distance is approximatively proportional to the pulse duration according to Eq. 9, OWB occurs later when longer pump pulses are employed, resulting in an SC spectrum with dips and peaks dominated by SPM. When the pump pulse with more peak power is applied, the SC spectrum becomes broader and extends to the transparency limit wavelength of the GeAsSe glass, as shown in Figure 4C, where the pulse wavelength and FWHM are fixed at 7 μm and 50 fs, respectively. By escalating pump pulse peak power from 3 to 6 kW, the spectra demonstrate better flatness and smoothness with increasing bandwidth. With higher peak power employed, more energy is transferred to new wavelengths at a broader spectral region due to the OWB effect. The spectral bandwidth with intensity above −30 dB achieves 9.8 μm, ranging from 3823 to 13577 nm, corresponding to more than 1.5 octaves. The 3-dB bandwidth is 2.7 μm, ranging from 5973 to 8695 nm. The generated broadband SC spectrum hence can be compressed to sub-cycle MIR pulses. Compared to previous works, including but not limited to [14–21, 32, 33], smooth SC spectra with a broader bandwidth are obtained from our proposed ANDi MOF with a relatively low pump peak power, based mainly on SPM and OWB effects. Such a broadband SC generation can be attributed to the combination of material nonlinearity and the optimized broad and flat all-normal dispersion profile. In all our simulations, the highest peak power density occurs when a 7 μm laser is applied with duration and peak power of 50 fs and 6 kW, respectively. Assuming the pump laser is focused on the MOF with a spot area the same as the mode area, which is 25.9 μm² under 7 μm pumping, the peak power density is 23 GW/cm², which is considered acceptable according to previous research [43, 46].

FIGURE 4

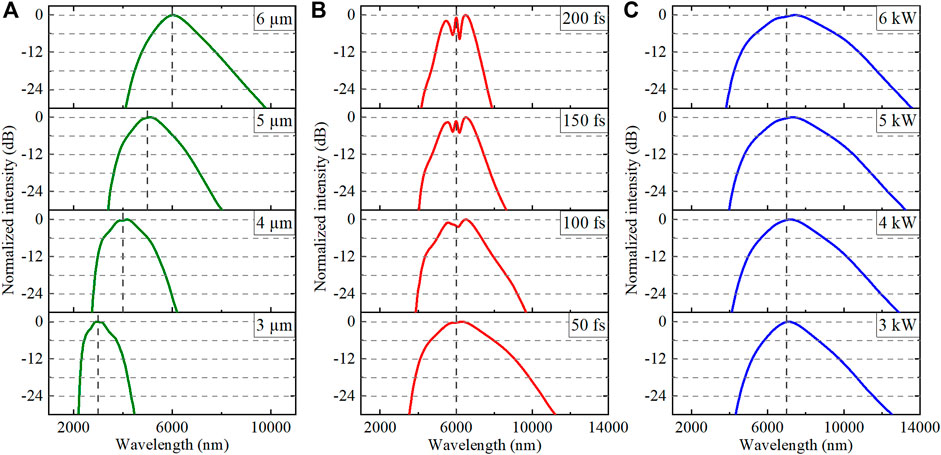
FIGURE 4. Supercontinuum generation in the 1-cm-long MOF with (A) pump wavelength from 3 to 6 μm, with a pulse FWHM of 50 fs and peak power of 1 kW; (B) pump pulse FWHM from 50 to 200 fs, with a pulse peak power of 3 kW at 6 μm; (C) pump pulse peak power from 3 to 6 kW, with a pulse FWHM of 50 fs at 7 μm. Pump pulse wavelengths are marked as vertical gray dashed lines.

The influence of the fiber parameters is also investigated since the deviation in geometric parameters usually occurs during fiber fabrication. Figures 5A–C show the SC output from the fibers with different pitch and rod diameters mentioned in Figure 2, where the pump pulse wavelength, FWHM, and peak power are fixed at 7 μm, 50 fs, and 6 kW, respectively. With a pitch deviation of $\pm 0.1 \text{μm}$, dispersion varies more in the long-wavelength region, and the spectral profile reflects this variation in this region, as shown in Figure 5A. For the increased pitch of the fiber, the generated spectral bandwidth greater than −30 dB becomes broader due to the smaller magnitude of the dispersion. The 3-dB bandwidth expects subtle changes as the pitch fluctuates. Figure 5B shows the influence of the rod diameter $d_2$ on the spectra profile. With this diameter increasing from 0.9 to 1.1 μm, the wavelength associated with the local maximum dispersion shifts toward the red region, and when it is located around the pump wavelength, a broader 3-dB bandwidth of the SC appears, which is the case where $d_2=1.0 \text{μm}$. The larger magnitude of the dispersion above 9 μm reduces the spectral bandwidth greater than −30 dB for smaller diameter $d_2$. The fluctuation of the rod diameter $d_1$ has a minute influence on the dispersion profile as shown in Figure 2C, the SC spectral profiles thus are almost invariable in this situation, as shown in Figure 5C. Therefore, for pump pulses with given parameters, the output spectral bandwidth and flatness can be compromised when nonlinearity and dispersion are balanced, which is the case when the ANDi MOF structure is engineered with the exact design parameters $d_1=0.3 \text{μm}$, $d_2=1.0 \text{μm}$, and $\text{Λ}=1.7 \text{μm}$. However, we can conclude from Figures 5A–C that the deviation of $\text{Λ},d_1,d_2\pm 0.1 \text{μm}$ is acceptable because within this range the spectra are still broad and smooth, and the spectral profiles remain without much change. Figure 5D shows the SC output spectrum for a pump pulse with the same parameter as in Figures 5A–C, with and without introducing an optical attenuation of 663.7 dB/cm, calculated from Eq. 4. Compared to the case without loss, the actual generated SC spectrum bandwidth with an intensity greater than −3 dB is reduced by 1.00 μm, and the 30-dB bandwidth is narrowed by 0.38 μm, attributed to the short fiber length used in our simulation.

FIGURE 5

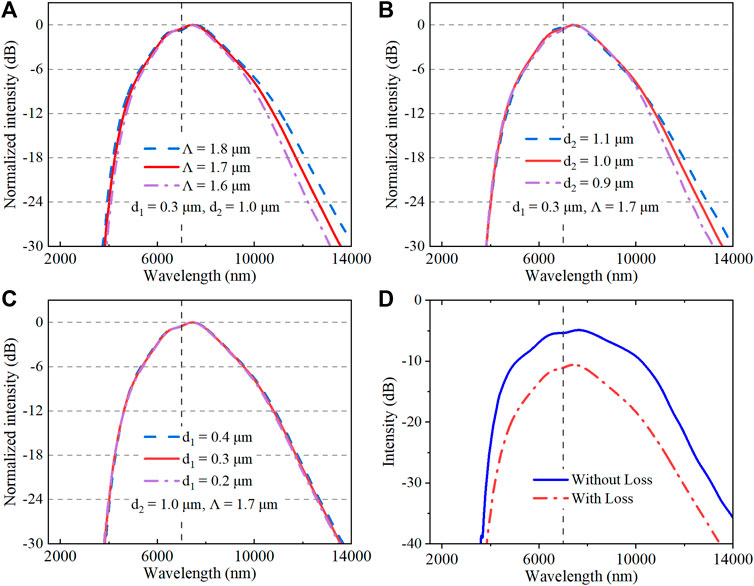
FIGURE 5. (A–C) Influence of the geometric parameters of the fiber on the spectral profiles. (D) SC generated with and without introducing transmission loss. The pump pulse wavelength (marked as vertical gray dashed lines), FWHM, and peak power are 7 μm, 50 fs, and 6 kW, respectively.

The coherence property of the SC generated is investigated according to Eq. 8 when the ChG MOF is pumped at 7 μm with 50 fs FWHM and 6 kW peak power. The SC spectrum is highly coherent over a broad bandwidth as shown in Figure 6, where zero denotes incoherent, and one is coherent on the scale bar. An ensemble average of over 200 pairs of independent SC spectra generated from input pulses with random quantum noise for the MOF structure of $\text{Λ}=1.7 \text{μm}$, $d_1=0.3 \text{μm}$, $d_2=1.0 \text{μm}$ is used to compute the modulus of the complex degree of coherence. The result indicates that highly coherent mid-infrared SC light expanding from 3.8 μm to the transparency limit of the GeAsSe glass is generated when pumped by a 7 μm laser. The relatively low coherence below 3.8 μm is due to the large magnitude of material dispersion, which significantly affects fiber GVD. Consequently, the SC output in this range involves a strong SPM, leading to the fluctuation of the output.

FIGURE 6

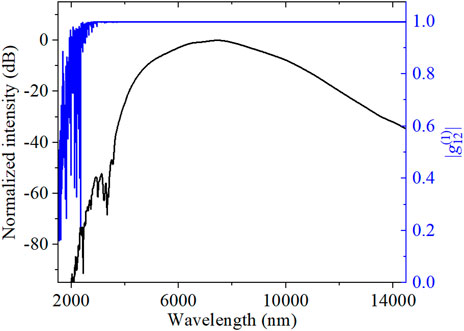
FIGURE 6. SC spectrum pumped at 7 μm with 50 fs FWHM and 6 kW peak power and its coherence property in all-chalcogenide MOF.

Conclusion

In this work, we propose a dispersion-engineered all-chalcogenide microstructured fiber, which could be fabricated using the rod-in-tube method. The optimized ChG fiber exhibits a broad and flat all-normal dispersion ranging from 4 to 14 μm, supporting the generation of a flat-top mid-infrared SC spectrum spanning over an octave. A highly coherent broadband SC in the range from 3.8 μm to the transparency limit of the material is generated from a 1-cm-long all-chalcogenide MOF pumped by a 7 μm laser. The influence of pump pulse wavelength, duration and peak power, and fiber geometric parameters on SC spectral profiles is systematically investigated. The results indicate that SC spectra from the near-infrared to MIR region with sufficient flatness can be obtained when the pump wavelength is tuned between 3 and 7 μm. The spectral bandwidth with an intensity greater than −3 dB and −30 dB achieves 2.7 and 9.8 μm when pumping at 7 μm, with the latter corresponding to more than 1.5 octaves. The broadband coherent SC spectra thus support compression to sub-cycle pulses at the MIR region. This work reveals the potential application of coherent, broadband laser sources in frequency metrology, optical coherence tomography, biomedical imaging, and few-cycle pulse compression.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

KX designed the fiber structure and simulated and analyzed the supercontinuum spectra; YY competed with the Python codes throughout the simulation; RM participated in the discussion of the mechanism of the broadband SC generation. All authors approve of the final version and agree to be responsible for all aspects of the work.

Funding

This work was supported by grants from the Basic and Applied Basic Research Foundation of Guangdong Province (2021A1515110310) and the Research Platform and Project of Guangdong Province (2021KQNCX268).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor SK declared a past co-authorship with the author RM.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sorokina IT, Vodopyanov KL. Solid-State Mid-infrared Laser Sources. Berlin, Heidelberg: Springer (2003).

Google Scholar

2. Grassani D, Tagkoudi E, Guo H, Herkommer C, Yang F, Kippenberg TJ, et al. Mid Infrared Gas Spectroscopy Using Efficient Fiber Laser Driven Photonic Chip-Based Supercontinuum. Nat Commun (2019) 10(1):1553. doi:10.1038/s41467-019-09590-3

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Jahromi KE, Pan Q, Høgstedt L, Friis SMM, Khodabakhsh A, Moselund PM, et al. Mid-infrared Supercontinuum-Based Upconversion Detection for Trace Gas Sensing. Opt Express (2019) 27(17):24469–80. doi:10.1364/oe.27.024469

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zheng S, Bai Y, Xu Z, Liu P, Ni G. Optical Coherence Tomography for Three-Dimensional Imaging in the Biomedical Field: A Review. Front Phys (2021) 9:744346. doi:10.3389/fphy.2021.744346

CrossRef Full Text | Google Scholar

5. Schliesser A, Picqué N, Hänsch TW. Mid-infrared Frequency combs. Nat Photon (2012) 6(7):440–9. doi:10.1038/nphoton.2012.142

CrossRef Full Text | Google Scholar

6. Hermes M, Morrish RB, Huot L, Meng L, Junaid S, Tomko J, et al. Mid-IR Hyperspectral Imaging for Label-free Histopathology and Cytology. J Opt (2018) 20(2):023002. doi:10.1088/2040-8986/aaa36b

CrossRef Full Text | Google Scholar

7. Agrawal GP. Nonlinear Fiber Optics. 5th ed. Oxford, UK; Waltham, MA: Academic Press (2013).

Google Scholar

8. Dudley JM, Genty G, Coen S. Supercontinuum Generation in Photonic crystal Fiber. Rev Mod Phys (2006) 78(4):1135–84. doi:10.1103/RevModPhys.78.1135

CrossRef Full Text | Google Scholar

9. Dudley JM, Coen S. Coherence Properties of Supercontinuum Spectra Generated in Photonic Crystal and Tapered Optical Fibers. Opt Lett (2002) 27(13):1180–2. doi:10.1364/ol.27.001180

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Corwin KL, Newbury NR, Dudley JM, Coen S, Diddams SA, Weber K, et al. Fundamental Noise Limitations to Supercontinuum Generation in Microstructure Fiber. Phys Rev Lett (2003) 90(11):113904. doi:10.1103/PhysRevLett.90.113904

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Tomlinson WJ, Stolen RH, Johnson AM. Optical Wave Breaking of Pulses in Nonlinear Optical Fibers. Opt Lett (1985) 10(9):457–9. doi:10.1364/ol.10.000457

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Heidt AM. Pulse Preserving Flat-Top Supercontinuum Generation in All-normal Dispersion Photonic crystal Fibers. J Opt Soc Am B (2010) 27(3):550–9. doi:10.1364/josab.27.000550

CrossRef Full Text | Google Scholar

13. Gu X, Xu L, Kimmel M, Zeek E, O’Shea P, Shreenath AP, et al. Frequency-resolved Optical Gating and Single-Shot Spectral Measurements Reveal fine Structure in Microstructure-Fiber Continuum. Opt Lett (2002) 27(13):1174–6. doi:10.1364/ol.27.001174

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Xing S, Kharitonov S, Hu J, Brès C-S. Linearly Chirped Mid-infrared Supercontinuum in all-normal-dispersion Chalcogenide Photonic crystal Fibers. Opt Express (2018) 26(15):19627–36. doi:10.1364/oe.26.019627

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Liu L, Cheng T, Nagasaka K, Tong H, Qin G, Suzuki T, et al. Coherent Mid-infrared Supercontinuum Generation in All-Solid Chalcogenide Microstructured Fibers with All-normal Dispersion. Opt Lett (2016) 41(2):392–5. doi:10.1364/ol.41.000392

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Klimczak M, Siwicki B, Skibiński P, Pysz D, Stępień R, Heidt A, et al. Coherent Supercontinuum Generation up to 2.3 μm in All-Solid Soft-Glass Photonic crystal Fibers with Flat All-normal Dispersion. Opt Express (2014) 22(15):18824–32. doi:10.1364/oe.22.018824

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Karim MR, Ahmad H, Rahman BMA. All-Normal Dispersion Chalcogenide PCF for Ultraflat Mid-infrared Supercontinuum Generation. IEEE Photon Technol Lett (2017) 29(21):1792–5. doi:10.1109/lpt.2017.2752214

CrossRef Full Text | Google Scholar

18. Yuan Y, Yang P, Peng X, Cao Z, Ding S, Zhang N, et al. Ultrabroadband and Coherent Mid-infrared Supercontinuum Generation in All-normal Dispersion Te-Based Chalcogenide All-Solid Microstructured Fiber. J Opt Soc Am B (2020) 37(2):227–32. doi:10.1364/josab.37.000227

CrossRef Full Text | Google Scholar

19. Heidt AM, Hartung A, Bosman GW, Krok P, Rohwer EG, Schwoerer H, et al. Coherent Octave Spanning Near-Infrared and Visible Supercontinuum Generation in All-normal Dispersion Photonic crystal Fibers. Opt Express (2011) 19(4):3775–87. doi:10.1364/oe.19.003775

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hooper LE, Mosley PJ, Muir AC, Wadsworth WJ, Knight JC. Coherent Supercontinuum Generation in Photonic crystal Fiber with All-normal Group Velocity Dispersion. Opt Express (2011) 19(6):4902–7. doi:10.1364/oe.19.004902

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Sukhoivanov IA, Iakushev SO, Shulika OV, Andrade-Lucio JA, Díez A, Andrés M. Supercontinuum Generation at 800 Nm in All-normal Dispersion Photonic crystal Fiber. Opt Express (2014) 22(24):30234–50. doi:10.1364/oe.22.030234

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Su N, Li P-X, Xiao K, Wang X-X, Liu J-G, Shao Y, et al. Supercontinuum Generation in Seven-Core Photonic crystal Fiber Pumped by a Broadband Picosecond Pulsed Fiber Amplifier. Chin Phys. B (2017) 26(7):074210. doi:10.1088/1674-1056/26/7/074210

CrossRef Full Text | Google Scholar

23. Yin K, Zhang B, Yao J, Cai Z, Liu G, Hou J. Toward High-Power All-Fiber 2-5 μm Supercontinuum Generation in Chalcogenide Step-Index Fiber. J Lightwave Technol (2017) 35(20):4535–9. doi:10.1109/jlt.2017.2749268

CrossRef Full Text | Google Scholar

24. Petersen CR, Møller U, Kubat I, Zhou B, Dupont S, Ramsay J, et al. Mid-infrared Supercontinuum Covering the 1.4-13.3 μm Molecular Fingerprint Region Using Ultra-high NA Chalcogenide Step-index Fibre. Nat Photon (2014) 8(11):830–4. doi:10.1038/nphoton.2014.213

CrossRef Full Text | Google Scholar

25. Cheng T, Nagasaka K, Tuan TH, Xue X, Matsumoto M, Tezuka H, et al. Mid-infrared Supercontinuum Generation Spanning 2.0 to 15.1 μm in a Chalcogenide Step-index Fiber. Opt Lett (2016) 41(9):2117–20. doi:10.1364/ol.41.002117

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Diouf M, Wague A, Zghal M. Numerical Investigation of an Ultra-broadband Coherent Mid-infrared Supercontinuum in a Chalcogenide AsSe₂-As₂S₅ Multimaterial Photonic crystal Fiber. J Opt Soc Am B (2019) 36(2):A8–A14. doi:10.1364/josab.36.0000a8

CrossRef Full Text | Google Scholar

27. Shiryaev VS, Churbanov MF. Recent Advances in Preparation of High-Purity Chalcogenide Glasses for Mid-IR Photonics. J Non-Crystalline Sol (2017) 475:1–9. doi:10.1016/j.jnoncrysol.2017.09.021

CrossRef Full Text | Google Scholar

28. Feng X, Monro T, Petropoulos P, Finazzi V, Hewak D. Solid Microstructured Optical Fiber. Opt Express (2003) 11(18):2225–30. doi:10.1364/OE.11.002225

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Toupin P, Brilland L, Mechin D, Adam J-L, Troles J. Optical Aging of Chalcogenide Microstructured Optical Fibers. J Lightwave Technol (2014) 32(13):2428–32. doi:10.1109/jlt.2014.2326461

CrossRef Full Text | Google Scholar

30. Ren H, Qi S, Hu Y, Han F, Shi J, Feng X, et al. All-solid Mid-infrared Chalcogenide Photonic Crystal Fiber with Ultralarge Mode Area. Opt Lett (2019) 44(22):5553–6. doi:10.1364/ol.44.005553

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Karim MR, Ahmad H, Rahman BMA. Design and Modeling of Dispersion-Engineered All-Chalcogenide Triangular-Core Fiber for Mid-infrared-region Supercontinuum Generation. J Opt Soc Am B (2018) 35(2):266–75. doi:10.1364/josab.35.000266

CrossRef Full Text | Google Scholar

32. Huang C, Bi W, Zheng B, Zhang C, Wang J, Zheng S. Ring-shaped Microstructured Chalcogenide Optical Fiber for Octave-Spanning Flat-Top Mid-infrared Supercontinuum Generation. Appl Opt (2020) 59(18):5391–8. doi:10.1364/ao.391564

CrossRef Full Text | Google Scholar

33. Medjouri A, Abed D. Modelling of All-Chalcogenide All-normal Dispersion Photonic Crystal Fiber for Ultraflat Mid-infrared Supercontinuum Generation. Opt Quant Electron (2021) 53(7):399. doi:10.1007/s11082-021-03027-2

CrossRef Full Text | Google Scholar

34. Bulla DAP, Wang RP, Prasad A, Rode AV, Madden SJ, Luther-Davies B. On the Properties and Stability of Thermally Evaporated Ge-As-Se Thin Films. Appl Phys A (2009) 96(3):615–25. doi:10.1007/s00339-009-5293-0

CrossRef Full Text | Google Scholar

35. Ma P, Choi D-Y, Yu Y, Gai X, Yang Z, Debbarma S, et al. Low-loss Chalcogenide Waveguides for Chemical Sensing in the Mid-infrared. Opt Express (2013) 21(24):29927–37. doi:10.1364/oe.21.029927

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Cheng T, Kanou Y, Xue X, Deng D, Matsumoto M, Misumi T, et al. Mid-infrared Supercontinuum Generation in a Novel AsSe₂-As₂S₅ Hybrid Microstructured Optical Fiber. Opt Express (2014) 22(19):23019–25. doi:10.1364/oe.22.023019

PubMed Abstract | CrossRef Full Text | Google Scholar

37. White TP, Kuhlmey BT, McPhedran RC, Maystre D, Renversez G, de Sterke CM, et al. Multipole Method for Microstructured Optical Fibers I Formulation. J Opt Soc Am B (2002) 19(10):2322–30. doi:10.1364/josab.19.002322

CrossRef Full Text | Google Scholar

38. Kuhlmey BT, White TP, Renversez G, Maystre D, Botten LC, de Sterke CM, et al. Multipole Method for Microstructured Optical Fibers II Implementation and Results. J Opt Soc Am B (2002) 19(10):2331–40. doi:10.1364/josab.19.002331

CrossRef Full Text | Google Scholar

39. Kuhlmey B, Renversez G, Maystre D. Chromatic Dispersion and Losses of Microstructured Optical Fibers. Appl Opt (2003) 42(4):634–9. doi:10.1364/ao.42.000634

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Karim MR, Rahman BMA, Agrawal GP. Dispersion Engineered Ge_11.5As₂₄Se_64.5 Nanowire for Supercontinuum Generation: A Parametric Study. Opt Express (2014) 22(25):31029–40. doi:10.1364/oe.22.031029

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Wang T, Gai X, Wei W, Wang R, Yang Z, Shen X, et al. Systematic Z-Scan Measurements of the Third Order Nonlinearity of Chalcogenide Glasses. Opt Mater Express (2014) 4(5):1011–22. doi:10.1364/ome.4.001011

CrossRef Full Text | Google Scholar

42. Blow KJ, Wood D. Theoretical Description of Transient Stimulated Raman Scattering in Optical Fibers. IEEE J Quan Electron. (1989) 25(12):2665–73. doi:10.1109/3.40655

CrossRef Full Text | Google Scholar

43. Zhang M, Li L, Li T, Wang F, Tian K, Tao H, et al. Mid-infrared Supercontinuum Generation in Chalcogenide Fibers with High Laser Damage Threshold. Opt Express (2019) 27(20):29287–96. doi:10.1364/OE.27.029287

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kubat I, Bang O. Multimode Supercontinuum Generation in Chalcogenide Glass Fibres. Opt Express (2016) 24(3):2513–26. doi:10.1364/oe.24.002513

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Anderson D, Desaix M, Lisak M, Quiroga–Teixeiro ML. Wave Breaking in Nonlinear-Optical Fibers. J Opt Soc Am B (1992) 9(8):1358–61. doi:10.1364/josab.9.001358

CrossRef Full Text | Google Scholar

46. Ma W, Wang L, Zhang P, Xu Y, Zhu L, Xu P, et al. Surface Damage and Threshold Determination of Ge-As-Se Glasses in Femtosecond Pulsed Laser Micromachining. J Am Ceram Soc (2020) 103(1):94–102. doi:10.1111/jace.16699

CrossRef Full Text | Google Scholar