Discriminative Monitoring of Seamless Rail Force by a High-Birefringence Effect-Based Fiber Optic Sensing Method

Nowadays, China has developed over 38,000-km high-speed railways (HSR). As one of the key elements in the HSR system, continuous welded rail (CWR) enables higher transportation efficiency, while demands for more robust inspection and maintenance techniques. The discrimination between longitudinal temperature force and longitudinal additional force is one of the main challenges in the rail health status evaluations. In this paper, the high-birefringence fiber Bragg grating (HB-FBG) is applied to reach the rail force discriminative measurement. By inscribing the Bragg grating on a high-birefringence fiber, two kinds of sensing modes can be generated and adopted to realize the discriminative measurement of longitudinal temperature force and longitudinal additional force. In the verification experiments, the longitudinal temperature and additional force are accurately measured with the error less than 1 kN. The accurate-measurement and easy-manufacture of the HB-fiber and HB-FBG make it possible to connect massive sensors in series to reach long-range monitoring of the rails on the land or cross-sea bridges.

Introduction

In current society, the transportation has become an important driving force for the development of economy, culture, and so on. As one of the main branches of the modern transportation, high-speed railway (HSR) has shown great advantages on safety, carrying capability, transport efficiency and sustainability. In contrast to the traditional seam rail, continuous welded rail (CWR) is widely deployed in the HSR system since it offers an almost continuous driving surface which enables a high rail track regularity. Higher track regularity brings better smoothness during the train moving. Therefore, higher running speed and traveling stability, lower vibration and noise, and longer rail service life can be achieved [1]. Nevertheless, since the CWR has no rail joints, the track regularity is highly sensitive to the longitudinal (temperature/additional) force resulting from the coupling effects of tracks and deformed superstructures, such as temperature effects, train braking/traction and track/bridge interaction [1–4]. To maintain a high track regularity, the track status should be timely and accurately adjusted according to the force conditions. However, it is still challenging to reach this goal presently since the commonly-used manual detection or track inspection car has a certain window period [1]. While the traditional electric sensors (such as resistance strain gages) are susceptible to the strong electromagnetic interference, corrosion, temperature and humidity variations along the railway lines [1]. As such, it is desired to find new techniques to acquire the rail force information precisely and continuously for reaching high-quality railway transportation. Fortunately, promising candidates have been appeared with the advance of fiber optic sensing technology.

The optical fiber sensors (OFS) take the optical fiber as the carrier and sense the outside physical quantities by interrogating the variations of light wave amplitude, phase, wavelength and polarization [5]. Therefore, the OFS has the advantages of high sensitivity, low loss, long sensing distance, smallness in size, immunity to external-electromagnetic interference and chemical inertness. Meanwhile, by exploring different mechanisms, the OFS has been developed into three main branches including discrete sensors [5], quasi-distributed sensors [6] and distributed sensors [7]. After decades efforts, the OFS technology has ripened relatively. At the current stage, the OFS application-investigations have begun and gradually shown advantages in multiple fields [8–13]. In the field of railway transportation, there are many impressive OFS application investigations being carried out in recent years [14]. For the rail track monitoring, the works can be divided into dynamic and static aspects. Firstly, lots of OFS-based methods are proposed to measure the dynamic response in the wheel-rail interaction since it contains a lot of useful information [14]. For instance, Yan et al. established a matched FBG pairs-based axle counting system which can acquire the real-time information of the train position and rail strain [15]. Yoon et al. proposed a real-time distributed strain monitoring system for measuring the rail strain distribution during the train movement [16]. Liu et al. developed a polarization-maintaining photonic crystal fiber interferometer-based accelerometer for train acceleration detection at a broad frequency range [17]. Apart from the dynamic aspect, the long-term static rail force monitoring shows a more far-reaching significance in terms of track regularity evaluation, rail status evolution investigation, track defect prevention and maintenance guideline. This promotes the development of OFS-based rail longitudinal force measurement methods. Wang et al. established a bi-directional FBGs pair-based longitudinal force measurement method. By installing two FBGs on the track in vertical and longitudinal directions, the FBGs have different responses to the longitudinal force. By subtracting the Bragg wavelengths corresponding to the two FBGs, the longitudinal force can be extracted [18]. Shao et al. developed a hetero-cladding FBGs sensor for the longitudinal force measurement. Two FBGs with different cladding thickness are fabricated through chemical etching and fixed along the neutral axis of the rail. Thanks to different strain sensitivities between the two FBGs, the longitudinal force can be measured [19]. Although these pioneering works have made remarkable progress for the rail force measurement, there are still certain limitations: as the FBGs in both schemes are physically separated, the measurement accuracy is susceptible to the rail condition differences (such as temperature, track material, deformation-degree, and so on) between the two installation points. In addition, the special layout and fiber microstructure fabrication of the two schemes increase the difficulty on manufacture and installation, which makes it hard to connect multiple sensors in serious for long-range rail force monitoring.

In this work, a simple rail longitudinal force measurement method based on the high-birefringence fiber Bragg grating (HB-FBG) is proposed and experimentally demonstrated. The topic of this work is the measurement of the longitudinal temperature force and longitudinal additional force, since the discrimination between the two force is crucial to analyze the coupling effects of the tracks and deformed superstructures [1]. Here, the Bragg grating with a certain period and length is inscribed on a high-birefringence fiber (HB-fiber) through UV photoetching, which gives rise to two kinds of sensing modes with different Bragg wavelengths and strain/temperature sensitivities [20]. By analyzing the responses of the two modes, the longitudinal (temperature/additional) force can be measured for the track status evaluation. In the experiment, longitudinal (temperature/additional) force are precisely measured with the error less than 1 kN. The method features the following advantages: 1) as the two sensing modes are in the same position, they will experience the same rail conditions, which guarantees the measurement accuracy and 2) multiple HB-FBGs can be easily inscribed one-by-one on one HB-fiber and directly installed on the rail, which makes it possible to monitor the longitudinal force distribution along the long railway lines or large-scale railway bridges, such as the cross-sea bridges.

Principle

The large-scale construction of the high-speed railway determines that the CWR will be built on variable geographical and geological environments, and be exposed to the complex and changeable atmospheric environment for a long time. The CWR is affected by combined impacts of the temperature changes, superstructure deformations and high-strength train loads and wear. Therefore, the geometric state of the CWR changes with temporal and spatial variations, and the requirement of high track regularity is severely challenged. The rail longitudinal force will affect the CWR status. According to the source of the force, the rail longitudinal force can be divided into 1) the inner stress or tension caused by temperature changes, collectively known as the rail longitudinal temperature force, and 2) the longitudinal additional force caused by the deformation of the superstructures (such as the temperature effects of large-span railway viaduct or suspension bridges, bridge–embankment transition areas, subgrade settlement and so on). Due to the joint action of the two force, the analysis of the rail force is complicated. The long-term discriminative monitoring of the longitudinal temperature force and longitudinal additional force along the railway lines plays a particularly positive role in the estimation of rail status, prevention and tracing of rail defects and maintenance guidance. For this goal, this work proposes a fiber optic discriminative rail longitudinal force measurement method bases on the HB-FBG.

The HB-FBG is fabricated by inscribing the Bragg grating on the HB-fiber through the UV photoetching technology [20–23]. The high birefringence of the HB-fiber is realized by the asymmetry of the fiber core, which is commonly achieved by introducing two stress bars into the fiber cladding (Panda or Bow-tie type) or directly designing the fiber core to ellipse. In the rail longitudinal force monitoring, a Panda-type HB-FBG is installed along the rail neutral axis with a pre-stress, as shown in Figure 1. When the rail temperature changes ∆T relative to the rail locking temperature, the rail in the free state will deform (expand or contract) due to its material characteristic. While this longitudinal temperature deformation is highly limited by the CWR fastener, which results in the cumulation of the longitudinal temperature force F_T inside the rail, as given by

$F_T=-E_R{A}_R{\alpha }_R\mathrm{\Delta }T(1)$

Where E_R is the rail young’s modulus, A_R is the track cross-sectional area and α_R is rail thermal expansion coefficient. At the same time, the rail may be also subjected to the longitudinal strain ∆ε caused by the longitudinal additional force F_A due to the deformation of the substructures, such as the bridges and transition areas. The relationship between the longitudinal additional force and track deformation is

$F_A=E_R{A}_R\Delta \epsilon (2)$

FIGURE 1

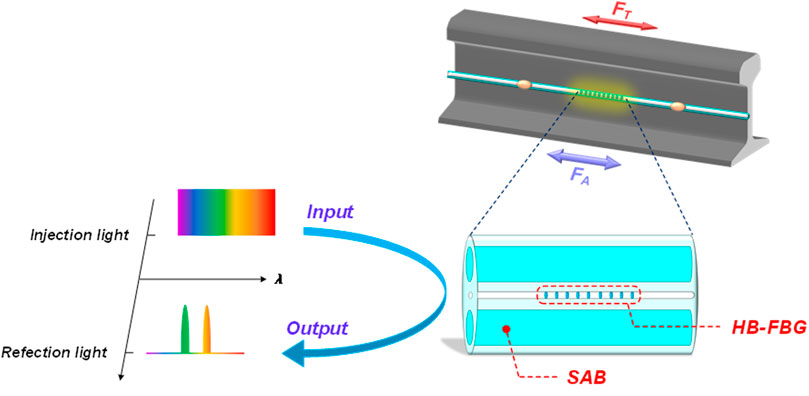
FIGURE 1. Schematic diagram of HB-FBG based CWR longitudinal rail force measurement. F_T: longitudinal temperature force, F_A: longitudinal additional force, SAB: stress applying bar, HB-FBG: high-birefringence fiber Bragg grating.

When the CWR experiences the variations of the temperature and longitudinal additional force, the HB-FBG [20] attached on the rail will sense them with two kinds of modes (fast and slow modes with different Bragg wavelengths and sensitivities) due to the high birefringence, which can be described as the following matrix form

$\left[\begin{array}{c}\mathrm{\Delta }{\lambda }_{fast}\\ \mathrm{\Delta }{\lambda }_{slow}\end{array}\right]=\left[\begin{array}{cc}\left(\alpha +{\zeta }_T^{fast}\right)& \left(1-{\zeta }_{\epsilon }^{fast}\right)\\ \left(\alpha +{\zeta }_T^{slow}\right)& \left(1-{\zeta }_{\epsilon }^{slow}\right)\end{array}\right]\left[\begin{array}{c}\text{Δ}T\\ \text{Δ}\epsilon -\alpha \text{Δ}T\end{array}\right]=K_s\left[\begin{array}{c}\text{Δ}T\\ \text{Δ}\epsilon -\alpha \text{Δ}T\end{array}\right](3)$

Where ∆λ_fast and ∆λ_slow are Bragg wavelength variations corresponding to the fast and slow modes, respectively. α is optical fiber thermal expansion coefficient. ${\zeta }_T^{fast}$ and ${\zeta }_T^{slow}$ are fiber thermo-optic coefficients (refractive index varies with the temperature) corresponding to the fast and slow modes, respectively. The difference between ${\zeta }_T^{fast}$ and ${\zeta }_T^{slow}$ depends on the birefringence and fiber annealing temperature [20]. ${\zeta }_{\epsilon }^{fast}$ and ${\zeta }_{\epsilon }^{slow}$ are fiber photo-elastic coefficients (refractive index changes with the strain) corresponding to the fast and slow modes, respectively. The difference between ${\zeta }_{\epsilon }^{fast}$ and ${\zeta }_{\epsilon }^{slow}$ is determined by the birefringence [20]. In the two modes’ responses, the rail longitudinal strain ∆ε is measured with a certain deviation -α∆T due to the fiber temperature deformation (expansion or contraction). From Eq. 3, it can be readily observed that, after acquiring the sensing matrix (K_s) and Bragg wavelength variations (∆λ_fast and ∆λ_slow), the measurands can be easily extracted by

$\left[\begin{array}{c}\mathrm{\Delta }T\\ \mathrm{\Delta }\epsilon -\alpha \mathrm{\Delta }T\end{array}\right]=K_s^{-1}\left[\begin{array}{c}\text{Δ}{\lambda }_{fast}\\ \text{Δ}{\lambda }_{slow}\end{array}\right](4)$

Where $K_s^{-1}$ means the inverse sensing matrix. Precisely retrieved ∆T and ∆ε-α∆T will compensate the deviation α_F∆T and obtaining the true value of ∆ε. As a result, the longitudinal additional force F_A and longitudinal temperature force F_T can be separately acquired according to the retrieved ∆ε and ∆T, respectively, which can be adopted to evaluate the rail status. In the following parts, the experiment is carried out to validate the HB-FBG based rail force discriminative measurement method.

Experimental Setup

Figure 2 shows the experimental setup for the validation of the HB-FBG based rail force discriminative measurement method. The stretched HB-FBG is installed on a polished test rail (E_R = 2.1 × 10¹¹Pa, A_R = 10.76 × 10⁻⁴ m², α_R = 1.18 × 10⁻⁵/^°C, L = 20 cm) with a pre-stress. The pre-stress is critical to ensure the HB-FBG to sense the rail shrink caused by the longitudinal additional pressure or low atmospheric temperature. In addition, the orientation of HB-FBG is an important point during the installation. Specifically, the HB-FBG should be as parallel as possible to the rail longitudinal direction, which enables the highest efficiency on the longitudinal force measurement. To accurately calibrate the sensing coefficient matrix and verify the performance of proposal, the experiment is implemented through the universal testing machine (UTM). The test rail is placed vertically in the middle of the upper and lower loading platforms of the UTM. The loading platform is capable to execute the pressure on the rail to generate the longitudinal additional force. Meanwhile, the longitudinal temperature force is fulfilled by varying the temperature around the rail by a temperature control box (TCB, control accuracy: 0.5°C). By controlling the loading platform and the TCB, the rail will experience the longitudinal temperature and additional force simultaneously for validating the HB-FBG based rail force discriminative monitoring scheme.

FIGURE 2

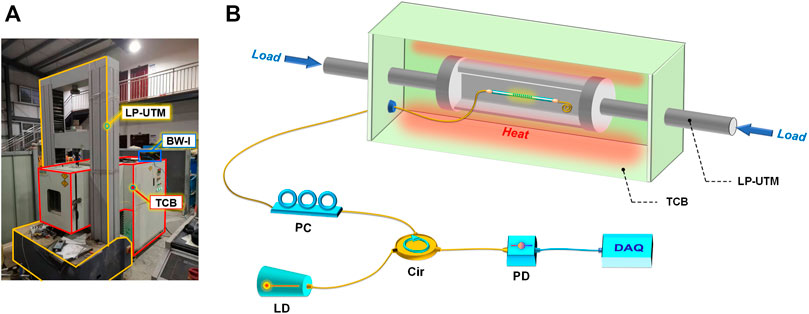
FIGURE 2. (A) test apparatus and (B) layout of validation experiment. UTM: universal testing machine, TCB: temperature control box, BW-I: Bragg wavelength interrogator, HB-FBG: high birefringence fiber Bragg grating, PC: polarization controller, LD: laser diode, Cir: circulator, PC: polarization controller, PD: photodiode, DAQ: data acquisition equipment.

The HB-FBG is fabricated by UV photoetching (248-nm excimer laser with phase mask method) the Bragg grating with a period of 531 nm and a length of 12 mm on the HB-fiber (birefringence: ∼5.85 · 10⁻⁴). As the HB-FBG is produced by the same process as that in the conventional FBG, its reproducibility is expected to be comparable with that of the FBG. The resulting Bragg wavelengths corresponding to the two sensing modes are ∼1,533.2 nm (slow mode, higher refractive index) and ∼1,532.6 nm (fast mode, lower refractive index), respectively. During the measurement, the laser diode (LD) inside a Bragg wavelength interrogator (BW-I) launches frequency-sweeping light waves into the HB-FBG with a period of 100 Hz. As the light wave will be reflected when its sweeping frequency falls within the two modes’ Bragg reflection spectrums, the Bragg wavelengths of the two modes can be interrogated through the intensities of the reflected light waves at different frequencies. Moreover, due to the polarization-dependence of the HB-fiber, the state of polarization of the input light should be adjusted by a polarization controller (PC) to ensure the light wave to be separated equally to the two main axis of the HB-fiber. As a result, the Bragg reflection spectrums of the two modes can have the same amplitudes and signal-to-noise ratios. In the following, the sensing matrix calibration and rail longitudinal force measurement will be demonstrated and discussed in detail.

Experimental Results

As mentioned above, the calibration of the sensing matrix K_s is crucial for the accuracy of longitudinal rail force measurement. Thus, the first step of the experiment is to calibrate the temperature sensitivity coefficients of the two modes. In this part, to avoid the influence of the additional strain, the HB-FBG is not yet installed on the rail and just placed in the TCB with the free state. The TCB temperature is gradually raised from 30 to 80°C with a step of 10°C. The acquisition of Bragg wavelengths at each step lasts 10 min. The relationship between the Bragg wavelengths and temperature variations is shown in Figure 3A. It can be seen that the Bragg wavelengths of the two modes increase linearly with the temperature raising. By cumulatively averaging the Bragg wavelengths at each step, the impact of the temperature fluctuation and random noise can be further reduced, which guarantees a higher calibration accuracy. Figure 3B illustrates the averaged Bragg wavelengths corresponding to the two modes at each step. By adopting linear fitting, the temperature sensitivity coefficients are calibrated to be 10.014 pm/°C (fast mode) and 10.696 pm/°C (slow mode). The fitting curve determination coefficients of the two modes are 0.9998 and 0.9999, respectively, indicating that the calibrated temperature sensitivity coefficients are reliable.

FIGURE 3

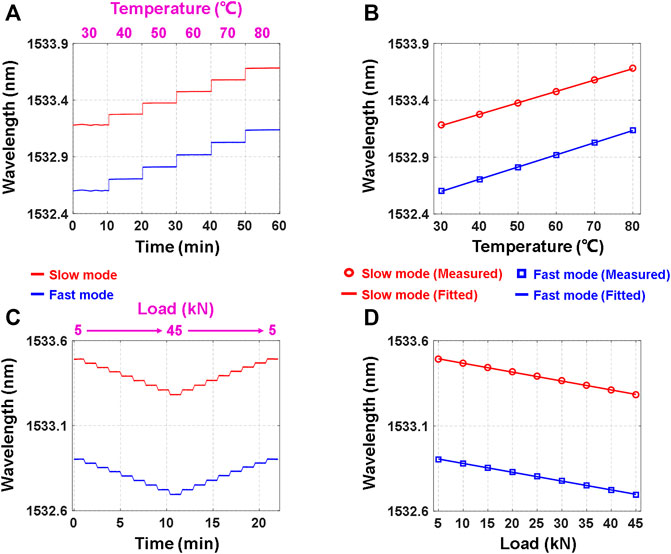
FIGURE 3. Real-time responses to (A) temperature and (C) force changes corresponding to the two sensing modes. Bragg wavelengths of the two sensing modes as a function of the (B) temperature and (D) force.

Subsequently, we move forward to calibrate the force (or strain as well) sensitivity coefficients of the two modes. In this case, the HB-FBG is installed along the rail neutral axis with a pre-stress. After that, the rail is placed vertically in the middle of the UTM loading platforms. The UTM executes the load on the rail from 5 to 45 kN with a step of 5 kN. The duration for acquiring the Bragg wavelengths at each load is ∼1 min since the UTM just takes a short time to shift and stabilize the load. During the wavelength acquisition, the rail temperature is kept constant by the TCB to avoid the impact of the temperature fluctuation. Figure 3C depicts the relationship between the load and Bragg wavelengths. With the increase of the load, the pressure on the rail enhances accordingly, which gives rise to the contraction of the HB-FBG. As a result, the Bragg wavelengths of the two modes decrease with the load increment. From the results in Figure 3C, the hysteresis ratio of the sensor is calculated to be 1.2% (fast mode) and 1.3% (slow mode), indicating that the hysteresis is quite low. Similarly, the Bragg wavelengths are further cumulatively averaged to increase the precision. The averaged Bragg wavelengths at each load together with the corresponding linear fitting curves are shown in Figure 3D. It can be seen that the Bragg wavelengths variations fit well with the linear curves. From the slopes of the two fitted curves, the force sensitivity coefficients are found to be 5.1769 pm/kN (fast mode) and 5.2238 pm/kN (slow mode). Notably, although the force sensitivity coefficient is adopted here for the sake of convenience, it can be directly switched to the strain sensitivity coefficient according to the Eq. 2. Moreover, the fitting curve determination coefficients of the two modes are 0.9996 and 0.9997, respectively. This means that the calibrated force sensitivity coefficients are perfectly usable.

After the calibration of the temperature and force sensitivity coefficients of the two modes, the sensing matric K_s can be constructed, as described in Eq. 3. By inversing the K_s, the K_s⁻¹ is calibrated as below

$K_s^{-1}={10}^6\times \left(\begin{array}{cc}0.001295913189543& -0.001284277753966\\ -2.484360462495554& 2.653485727678094\end{array}\right)(5)$

After the above key calibration works are completed, the HB-FBG is ready for the rail longitudinal force measurement. In the validation tests, various temperatures and additional force are executed on the rail simultaneously to verify the accuracy of the HB-FBG-based discriminative force measurement scheme. In detail, the rail temperature is gradually raised by 25°C with a step of 5°C. At each temperature point, the rail stress is increasingly strengthened to 45 kN with a step of 5 kN. As a result, the rail will experience 60 different temperature/force situations. The UTM loading processes at different temperature points are shown in Figure 4A. The measurement duration for each temperature/force situation is 1 min, and the measured Bragg wavelengths at each situation are cumulatively averaged to improve the signal-to-noise ratio. Figure 4B illustrates the measured Bragg Wavelengths of the two modes corresponding to different temperature/force situations. Clearly, the HB-FBG responses differently for different situations.

FIGURE 4

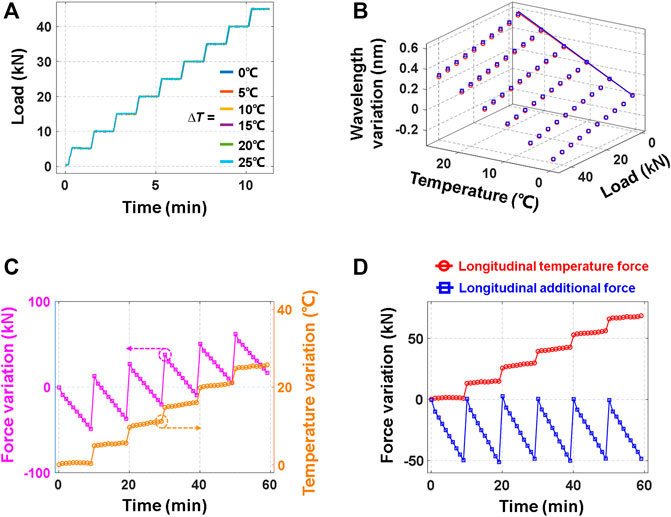
FIGURE 4. (A) Temperatures and additional force loaded on the rail. (B) Measured Bragg wavelengths corresponding to the two modes under different rail temperatures and additional force situations. (C) Temperatures and additional force extracted from the measured Bragg wavelengths. (D) Retrieved longitudinal temperature force and longitudinal additional force.

As described in Eq. 4, by multiplying the inverse sensing matrix K_s⁻¹ by the measured two modes’ Bragg wavelengths at each situation, the additional force and temperature values corresponding to different situations are retrieved and shown in Figure 4C. It can be seen that 1) the temperatures are extracted with a slight deviation which may be caused by the inaccuracy of the TCB temperature control and the measurement error of the HB-FBG, and 2) as the test rail is not constrained by the fastener and at the free state, the rail longitudinal temperature force F_T directly acts on HB-FBG. Thus, the measured longitudinal force F_m at each situation is a mixed value that contains the longitudinal temperature force F_T and longitudinal additional force F_A. Fortunately, the simultaneously measured temperature values can be used to calculate the longitudinal temperature force F_T and the fiber deformation-induced deviation −α∆T, as given by Eqs 1, 4. Therefore, by separating the F_m from the F_T and −α∆T, the longitudinal additional force F_A can be retrieved. Figure 4D illustrates the retrieved longitudinal temperature and additional force. Clearly, the discriminative measurement of the longitudinal temperature force and longitudinal additional force is validated. Notably, since the UTM’s force sensor starts to work until the loading platform completely contact with test specimen, the actual load at the initial stage is higher than the given load. As a result, the measured additional force at the initial phase (0 kN) is larger than the given step size (5 kN). Furthermore, the measurement accuracy is evaluated by comparing the adjacent additional force difference with the UTM load step size which is a certain value of 5 kN. By calculating all adjacent additional force variations (results at the initial loading phases are excluded), the minimum and maximum are found to be 4 and 5.78 kN, respectively. This means that the measurement error is lower than 1 kN and the measured force is close to the true value of the force. Moreover, the repeatability of the rail force measurement under different test situations is evaluated by calculating the standard deviation (SD) value of all adjacent additional force variations. The SD value turns out to be 0.42 kN, which means that 1) the measurement results concentrate at the mean value of 5.1 kN with the deviation of ±0.42 kN and 2) the results are repeatable.

Conclusion

In summary, a HB-FBG-based CWR longitudinal force discriminative measurement method is presented. Theorical analyses and experimental verifications are carried out. The results show that, by analyzing the dual sensing modes featured by the HB-FBG, the rail longitudinal temperature force and longitudinal additional force are retrieved accurately with the error lower than 1 kN. The proposed method offers a simple way to extract the rail longitudinal force and owns the potential to execute long-range measurement. Although the HB-fiber-based sensors (such as the HB-FBG [20], Brillouin dynamic grating [24]) and other new type fiber-based sensors (such as Polymer optical fiber Bragg grating [22, 23], two-core rectangular fiber Bragg grating [25]) have made significant technical progress in recent years, these advanced sensors have rarely been applied in the frontier application researches. This work demonstrates the feasibility of HB-FBG-based rail force discriminative measurement. While we believe that, in the future, more application investigations with these advanced OFS will be implemented to the high-speed railway system.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LY and YZ conceived and performed the papers and article writing. PW, RC, and JY were involved in the paper writing, ZL, WP, and BL were involved in the paper review and editing. All the authors contributed to the discussion on the results for this article.

Funding

The work was supported by the National Natural Science Foundation of China under Grant 61735015 and Sichuan International Science and Technology Innovation Cooperation Project under Grant 2021YFH0013.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang P, Xiao JL. Gaosu Tielu Guidao Pingshundu Jiance Guanjian Lilun Yu Jishu [Key Theory and Technology of High-Speed Railway Track Regularity Detection]. Shanghai: Shanghai kexue jishu chubanshe (2019). Print.

Google Scholar

2. Gao L. Gaosu Tielu Wufengxianlu Guangjian Jisu Yanjiu Yu Yingyong [Research and Application on Key Technology of Continuous Welded Rail in High-Speed Railway]. Beijing: Zhongguo tiedao chubanshe (2012). Print.

Google Scholar

3. Wang P. Gaosu Tielu Qiaoshang Wufengxianlu Jishu [Key Technology of Continuous Welded Rail on Bridge in High-Speed Railway]. Beijing: Zhongguo tiedao chubanshe (2016). Print.

Google Scholar

4. Kang C, Wenner M, Marx S. Background Investigation on the Permissible Additional Rail Stresses Due to Track/bridge Interaction. Eng Structures (2021) 228:111505. doi:10.1016/j.engstruct.2020.111505

CrossRef Full Text | Google Scholar

5. Lee B. Review of the Present Status of Optical Fiber Sensors. Opt Fiber Tech (2003) 9:57–79. doi:10.1016/s1068-5200(02)00527-8

CrossRef Full Text | Google Scholar

6. Li C, Tang J, Cheng C, Cai L, Yang M. FBG Arrays for Quasi-Distributed Sensing: A Review. Photonic Sens (2021) 11:91–108. doi:10.1007/s13320-021-0615-8

CrossRef Full Text | Google Scholar

7. Bao X, Chen L. Recent Progress in Distributed Fiber Optic Sensors. Sensors (2012) 12:8601–39. doi:10.3390/s120708601

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Schenato L, Palmieri L, Camporese M, Bersan S, Cola S, Pasuto A, et al. Distributed Optical Fibre Sensing for Early Detection of Shallow Landslides Triggering. Sci Rep (2017) 7:14686. doi:10.1038/s41598-017-12610-1

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Marra G, Clivati C, Luckett R, Tampellini A, Kronjäger J, Wright L, et al. Ultrastable Laser Interferometry for Earthquake Detection with Terrestrial and Submarine Cables. Science (2018) 361:486–90. doi:10.1126/science.aat4458

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhan Z, Cantono M, Kamalov V, Mecozzi A, Müller R, Yin S, et al. Optical Polarization-Based Seismic and Water Wave Sensing on Transoceanic Cables. Science (2021) 371:931–6. doi:10.1126/science.abe6648

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Leal-Junior AG, Frizera A, Marques C, Sánchez MRA, dos Santos WR, Siqueira AAG, et al. Polymer Optical Fiber for Angle and Torque Measurements of a Series Elastic Actuator’s Spring. J Lightwave Technol (2018) 36:1689–705. doi:10.1109/jlt.2017.2789192

CrossRef Full Text | Google Scholar

12. Leal-Junior AG, Díaz CR, Marques C, Pontes MJ, Frizera A. Multiplexing Technique for Quasi-Distributed Sensors Arrays in Polymer Optical Fiber Intensity Variation-Based Sensors. Opt Laser Tech (2019) 111:81–8. doi:10.1016/j.optlastec.2018.09.044

CrossRef Full Text | Google Scholar

13. Leitão C, Leal-Junior A, Almeida AR, Pereira SO, Costa FM, Pinto JL, et al. Cortisol AuPd Plasmonic Unclad POF Biosensor. Biotechnol Rep (2021) 29:e00587. doi:10.1016/j.btre.2021.e00587

CrossRef Full Text | Google Scholar

14. Du C, Dutta S, Kurup P, Yu T, Wang X. A Review of Railway Infrastructure Monitoring Using Fiber Optic Sensors. Sensors Actuators A: Phys (2020) 303:111728. doi:10.1016/j.sna.2019.111728

CrossRef Full Text | Google Scholar

15. Yan L, Zhang Z, Wang P, Pan W, Guo L, Luo B, et al. Fiber Sensors for Strain Measurements and Axle Counting in High-Speed Railway Applications. IEEE Sensors J (2011) 11:1587–94. doi:10.1109/jsen.2010.2086058

CrossRef Full Text | Google Scholar

16. Yoon HJ, Song KY, Choi C, Na HS, Kim JS. Real-time Distributed Strain Monitoring of a Railway Bridge during Train Passage by Using a Distributed Optical Fiber Sensor Based on Brillouin Optical Correlation Domain Analysis. J Sens (2016) 2016:10. doi:10.1155/2016/9137531

CrossRef Full Text | Google Scholar

17. Liu Z, Htein L, Gunawardena DS, Chung W-H, Lu C, Lee K-K, et al. Novel Accelerometer Realized by a Polarization-Maintaining Photonic crystal Fiber for Railway Monitoring Applications. Opt Express (2019) 27:21597–607. doi:10.1364/oe.27.021597

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wang P, Xie K, Shao L, Yan L, Xu J, Chen R. Longitudinal Force Measurement in Continuous Welded Rail with Bi-directional FBG Strain Sensors. Smart Mater Struct (2015) 25:015019. doi:10.1088/0964-1726/25/1/015019

CrossRef Full Text | Google Scholar

19. Shao L-Y, Zhang M, Xie K, Zhang X, Wang P, Yan L. The Longitudinal Force Measurement of CWR Tracks with Hetero-Cladding FBG Sensors: A Proof of Concept. Sensors (2016) 16:2184. doi:10.3390/s16122184

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Zhu M, Murayama H, Wada D, Kageyama K. Dependence of Measurement Accuracy on the Birefringence of PANDA Fiber Bragg Gratings in Distributed Simultaneous Strain and Temperature Sensing. Opt Express (2017) 25:4000–17. doi:10.1364/oe.25.004000

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Othonos A. Fiber Bragg Gratings. Rev Scientific Instr (1997) 68:4309–41. doi:10.1063/1.1148392

CrossRef Full Text | Google Scholar

22. Pospori A, Marques CAF, Bang O, Webb DJ, André P. Polymer Optical Fiber Bragg Grating Inscription with a Single UV Laser Pulse. Opt Express (2017) 25:9028–38. doi:10.1364/oe.25.009028

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Marques CAF, Min R, Junior AL, Antunes P, Fasano A, Woyessa G, et al. Fast and Stable Gratings Inscription in POFs Made of Different Materials with Pulsed 248 Nm KrF Laser. Opt Express (2018) 26:2013–22. doi:10.1364/oe.26.002013

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Song KY, Zou W, He Z, Hotate K. All-optical Dynamic Grating Generation Based on Brillouin Scattering in Polarization-Maintaining Fiber. Opt Lett (2008) 33:926–8. doi:10.1364/ol.33.000926

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Htein L, Gunawardena DS, Leong CY, Tam HY. Bragg Gratings in Two-Core Rectangular Fiber for Discrimination of Curvature, Strain, and Temperature Measurements. Trans Instru Meas (2021) 70:7001607. doi:10.1109/tim.2020.3035528

CrossRef Full Text | Google Scholar