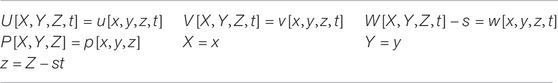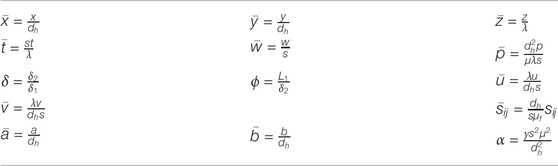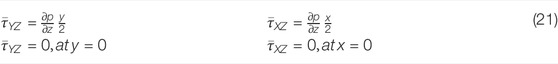- 1Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
- 2Research Centre, Future University in Egypt, New Cairo, Egypt
The current research is concerned with the mechanical characteristics of a Rabinowitsch fluid model that has been developed via an elliptic duct. If we study physiology or biomedicine, we will find that the Rabinowitsch fluid model in peristalsis is very useful because it is used to move blood around in the heart, lungs, sanitary fluid transport systems, transfer of corrosive fluids, and innovative pharmaceutical delivery systems. It is possible to get the elliptic domain for this duct model by using Cartesian coordinates, and in the boundary conditions for this duct, the equation of an ellipse is used to keep the elliptic cross-section for this duct in place. A mathematical model for an incompressible fluid is being created, and the mathematical issue is then transformed into its dimensionless form by using suitable transformations, including long-wavelength approximation. As soon as the problem is put into a dimensionless form, the partial differential equations for the velocity profile can be found. These partial differential equations are solved across elliptical cross-sections with the help of boundary conditions that are given, and accurate mathematical solutions are then found for them. This model is important because it shows three different types of flow: a dilatant fluid for
1 Introduction
Peristalsis is a mode of transport that involves the assimilation and propelling of materials during the contraction and expansion of a distensible tubes or channels, generated due to progressive waves that force the subjects forward alongside the channel. The term “peristalsis” is derived from the Greek word “peristaltikos,” which indicates “grabbing and crushing”. Peristalsis is the investigation of the movement of a fluid through the elliptic duct. The use of such a peristaltic flow phenomenon includes various physiological flow difficulties, such as the transportation of food through the digestive system, the transfer of urine to the bladder, and the circulation of blood in tiny blood arteries, among others. In physiology, this is important in a variety of situations, including food movement in the assimilation tract, urine transport, supply of blood in tiny blood arteries from the kidney to the bladder through the ureter, chyme movement in the gastrointestinal tract, and swallowing of food bolus via the esophagus. This mechanism may be found in roller pumping systems, finger pumping systems, cardiac machines, and blood-pumping machines, among other biomanufacturing devices. The relevance of this phenomenon may be seen not only in physiological processes but also in engineering and manufacturing, among other things. Peristalsis seems to be a critical instrument in the transit of chyme through the gastrointestinal tract, the passage of the ovum via the fallopian tube, and the circulation of blood through the heart chambers. Under this code, other biological equipment, such as the heart–lung machine, may operate. The pumping of poisonous and acidic fluids with the use of breaker and handle pumps, which exhibit peristaltic phenomena, is one of the most common industrial applications. A large number of experimental and theoretical efforts have been made to understand the peristaltic motion of Newtonian and non-Newtonian fluids in a variety of flow configurations.
When a nonlinear connection between shear stress and strain rate occurs, the Rabinowitsch fluid model is one of the fluid models that might be considered. This model is significant because it depicts the three primary kinds of the fluid for a variety of nonlinear factor values, each of which has a distinct relevance. Rabinowitsch fluids can address the complex physiological behaviors of the non-Newtonian model and also exhibit the characteristics of shear thinning or pseudoplastic (e.g., polymer solutions, blood plasma, latex paint, ketchup, and syrup), shear thickening or dilatant (e.g., oobleck, sand, and polyethylene glycol), and Newtonian behavior (e.g., air and water). In the literature, there have been many reports on the application of the Rabinowitsch fluid model [1–4]. This model has been examined by many researchers for the practical and theoretical examination of squeezing films, annular discs, externally pressured bearings, journal bearings, and pivoted curved slider bearings, among other types of bearings [5–7].
Anterograde peristalsis [8] is radially symmetrical contraction and relaxation of muscles that propagate as a wave down a tube in the opposite direction of the wave’s propagation direction. During peristalsis, the involuntary circular muscles in the lining of the gut contract and relax in a coordinated manner, which is preceded by a simultaneous contraction of the longitudinal muscle and relaxation of the circular muscle in the lining of the gut. The smooth muscle tissue contracts in succession in a digestive system, such as the human gastrointestinal tract, to generate a peristaltic wave, which pushes a ball of food (known as a bolus until it is turned into chyme in the stomach) through the tract. During the peristaltic movement, circular smooth muscles relax and then contract behind the chewed material to prevent it from traveling backward, and finally, longitudinal smooth muscles contract to drive the chewed material forward. To propel themselves around, earthworms use a system similar to this, and some contemporary technology is based on this concept [9, 10].
Mathematically, this phenomenon was initially explained and studied by Latham [11]. A series of analytical investigation studies on peristalsis have been produced following the innovative work published by [12–18], which is credited with laying the groundwork for peristaltic flows. A detailed mathematical analysis is performed with the non-Newtonian fluid models such as the Rabinowitsch fluid, which was studied by [19] in a two-dimensional channel, applying the suppositions of a low Reynolds number and a long wavelength. The experimental results of the Rabinowitsch model are studied by Wada and Hayashi [1]. This model is very important because it depends upon the combined relationship between shear stress and shear strain. In this relationship, the factor alpha is significant because of its effect. On this factor, we discuss the three types of the fluid, and the applications of the Rabinowitsch fluid are studied by [3]. Recently, flow through the elliptic duct has attracted scientists and engineers because of its wide range of applications. There are many research articles that deal with the peristaltic flow in a circle, rectangle, asymmetrical region, and so on. Here, we discuss the peristaltic flow through the elliptic duct. The peristaltic flow by using non-Newtonian fluid models such as the Jeffery model and Casson model is discussed, with the sinusoidal behavior of the peristaltic flow [20].
Non-Newtonian fluids contain several rheological characteristics that cannot be described by a single rheological model. In boundary layer flow, the importance of non-Newtonian fluid flows has grown. It is due to its numerous industrial and technological applications. For such flows, the mathematical description is generally complicated. Shear stress and strain rate cannot be evaluated in only one ingredient equation for these fluids. A mixed convective peristaltic flow of the methanol–Al2O3 nanofluid generates entropy owing to heat transfer and fluid friction. The Maxwell thermal conductivity model is employed. The entropy generation number is computed using velocity and temperature profiles [21]. This paper proposes a numerical solution for bioconvective nanofluid flow. An exponentially expanding vertical plate containing microorganisms in a tangent hyperbolic nanofluid is studied [22]. In the application of biological sciences and chemical and petroleum processes, non-Newtonian materials are used. Because of the logical examination of the kinetic energy law of liquid flows, the Eyring–Powell rheology of the non-Newtonian fluid is not an empirical method, but it is a realistic viscosity relaxing model because of the realistic viscosity relaxing model. Because of its vast range of applications, a growing number of researchers are becoming interested in investigating the behavior of this non-Newtonian fluid model in a variety of flow geometries. This paper devotes a significant portion of its literature review to the Eyring–Powell fluid flow in a circular pipe, with the purpose of obtaining accurate solutions for both the momentum and heat fields [23]. Mustafa is figuring out specific solutions for the boundary layer flow of certain nanofluids across porous stretching/shrinking surfaces with various topologies in his research lab at UC Berkeley. In order to achieve this goal, five different kinds of nanoparticles as well as water as the base fluid are being investigated: Ag, Cu, CuO, Al2O3, and TiO2 [24].
Many common liquids, like toothpaste and mayonnaise, exhibit non-Newtonian flows. The Maxwell fluid [25], Williamson fluid [26], Casson fluid [27], and Jeffrey fluid [28] and shear-thinning fluids are pseudoplastic fluids, for example, shampoo, ketchup, and slurries. With increased shear rate, these fluids’ viscosity decreases. Polymer solutions and related high-molecular weight solutions are examples of pseudoplastic fluids. Shear tension will occur in these liquids at low shear rates. Shear stress causes the rearranging of molecules to lower overall stress. This increase in fluid order decreases shear stress and causes the observed nonproportionality between shear rate and shear force. Shear-thickening fluids are dilatant fluids. These fluids’ viscosity increases with shear rate. Dilatant fluids are thick particle suspensions in liquids. If a shear rate is applied to these particles, they must rearrange to lessen the shear rate’s effect. This reduces the total shear force. Small shear rates allow particles to reorganize. If the shear rate is too fast, the particles do not have time to rearrange, and a large shear force builds up. A dilatant fluid is a water-corn starch suspension. Hand compression of such a suspension makes it virtually solid. By removing the pressure, the suspension reflows [29–31]. Long-wavelength peristaltic waves propagate [32] at the edges of small-width or small-diameter parts. Under the assumption of a long wavelength, the percentage of channel width to wavelength in the presented issue becomes insignificant. When compared to longitudinal flow amounts, transverse flow quantities become tiny and hence inconsequential. In the case of chyme transit in the small intestine, such validations remain valid. In the human ureter and reproductive systems, these approximations hold up well [33–36]. Under these conventions, the equations as well as boundary conditions are further simplified.
These microelements (e.g., bubbly liquids, lubricants, synovial fluids, some man-made liquids, physiological fluids, and polymeric suspensions) can completely change the rheological behavior of the resulting mixture according to micropolar constitutive laws by offering a substantial inertial effect with an increase in the effective viscosity of the medium due to the microscopic inertial effect. To accomplish these key aims, strong theories and assumptions are employed to accurately describe the fundamental conservation equations using Buongiorno’s model’s passive control. For realistic boundary conditions, the governing boundary layer equations are translated into a system of ordinary differential equations using the GDQLLM technique [37]. Researchers have been studying nanofluids’ thermal and rheological characteristics for decades. An impermeable horizontally electromagnetic surface (i.e., the Riga plate) heated convectively in the presence of a variable heat source was used in this numerical analysis to highlight the main renewable and mass transport appearances [38]. The numerical investigation of the peristaltic flow of a blood-based nanofluid is carried out with the help of the generalized differential quadrature technique [39]. An important part of this numerical study is that it shows how to do a unique computing analysis for steady-state magnetohydrodynamic (MHD) convective flow of radiative Casson fluids across a nonlinearly elongated elastic sheet with a nonuniform distribution of thickness [40]. Examination of steady mixed convection nanofluids flowing through an isothermal thin needle using metallic and metallic oxide nanoparticles was performed [41]. A detailed numerical investigation of thermodynamic irreversibilities in dissipative electromagnetodynamic (EMHD) fluid flows past a moving horizontal Riga plate was performed [42]. Blowing and suction effects on thermomagnetic convection in a narrow nanofluidic medium were studied [43]. The purpose of the current communication is to investigate the influence of the Cattaneo–Christov model and convective border on second-grade nanofluid flow in conjunction with a Riga pattern in a convective boundary. In order for the proportion of nanoparticles to retain their high retardation, zero mass flow must be accounted for at the solid surface of the Riga pattern on the solid surface. The research also considers the influence of Lorentz forces created by the Riga pate, which is a crucial part of the subject. Through the use of appropriately calibrated transformations, the controlling nonlinear issue is transformed into an ordinary problem. In order to identify solutions to nonlinear issues, the spectral local linearization approach has been included in the program [44].
The current model provides an explanation for the effects of the elliptic duct and changing liquid characteristics on the peristaltic transport of a Rabinowitsch fluid model. The current work has applications in the design of dialysis machines, roller–finger pumps, heart–lung machines, and other medical devices. The examination also provides a more in-depth understanding of the peristaltic system, which is responsible for the movement of chyme in the gastrointestinal tract and the flow of blood in tiny vessels. An elliptical cross-sectional duct has not yet been extensively studied in terms of its peristaltic flow dynamics. Peristaltic flow via an elliptical cross-sectioned duct is thus mathematically explored in this study. As a result, we use the Rabinowitsch fluid model. This study was motivated by the need for an understanding of the peristaltic flow mechanism inside an elliptic duct since the existing literature work only gives information on the peristalsis activity for cylindrical, rather than elliptic, ducts. Non-dimensional partial differential equations may be obtained from the governing equations after simplification, and the final form of the simplified equations is assessed in accordance with the corresponding applicable boundary conditions. Even more so, if we look at it from a biological standpoint, we can see that they are critical to the functioning of a wide range of biological propulsion processes. The precise solution part gives a thorough way for interpreting the analytical solution for velocity profiles, which may be found in the next section. This efficient and innovative technique yields accurate solutions to the partial differential equations that were generated in the course of this investigation. Finally, graphical representations of different peristaltic flow characteristics are used to show the solutions, and the visual findings are used to look at the streamlines.
1.1 Research Methodology
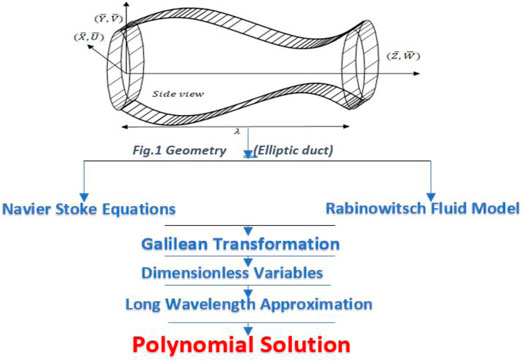
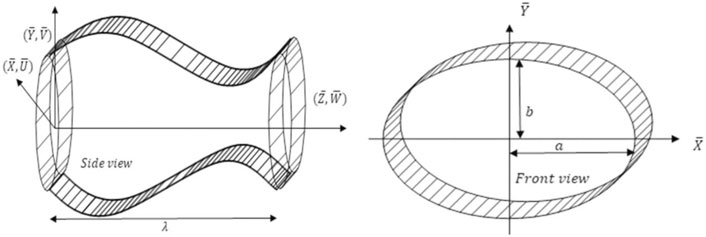
Researchers use a variety of research methodologies to find the ones that work best for their particular problem. The mathematical investigation of the peristaltic flow via a duct with an elliptic cross-section is presented Figure 1. The mathematical calculations are carried out using the Rabinowitsch fluid model, and an accurate mathematical answer is provided as a result. An elliptic domain is used in the solution to the issue. This elliptic duct features walls that oscillate sinusoidally, which causes the fluid to be propelled forward. In this geometry, Figure 1, the traveling wave may be observed to be present. After simplification, the controlling mathematical equations are transformed into dimensionless partial differential equations. A comparison of the final simplified version of the differential algorithms with regard to the required boundary conditions is performed, and a precise solution is obtained. Graphs are used to better explain the findings, and the many components of peristaltic flow phenomena are addressed in further detail. The lubrication theory is used to derive the dimensionless versions of the mathematical model that are
2 Mathematical Formulation
A mathematical model for the non-Newtonian Rabinowitsch fluid inside an elliptic domain is disclosed. Consider the flow of an incompressible peristaltic flow of the Rabinowitsch fluid in an elliptic duct of width
Deformable walls have a geometrical description that may be described by the sinusoidal equations shown below [44]
where
Here, U, V, and W are the components of the velocity in the direction of radial X, Lateral Y, and axial Z, respectively; P is the pressure; and
The dimensional form of boundary conditions of the above equations is given below
The Rabinowitsch fluid is included in the classification of pseudoplastic fluids (shear-thinning fluids), which include blood and other bodily fluids. This model accurately illustrates the influence of lubricant additives and is capable of fitting experimental data over a wide range of shear rates. Long-chain polymer solutions have been used successfully by tribologists for decades to improve the effectiveness of the stabilizing qualities of non-Newtonian lubricants by adding modest volumes of long-chain polymer solutions to the mix. The introduction of additives reduces the susceptibility of the lubricant to changes in the shearing strain rate during shearing operations. Moreover, because of the viscosity of these lubricants, there is a nonlinear connection between shearing stress and shearing strain rate when the shearing stress is increased. Here,
The Rabinowitsch fluid model [47] is defined as
2.1 Galilean Transformation
Galilean transformations, also known as Newtonian transformations, are a set of equations in classical physics that link the space and time coordinates of two systems that are traveling at a constant velocity relative to each other in the same direction. People who study things that happen at slower speeds than the speed of light can use Galilean transformations to talk about them. These transformations formally express the idea that space and time are absolute; that length, time, and mass are not affected by the relative motion of the observer; and that the speed of light is influenced by this motion.
Applying the Galilean transformations defined as [48]
Using the Galilean transformation in Eqs 2–5 gives the following equations in the wave frame (moving frame)
2.2 Dimensionless Variables
We introduce the following dimensionless variables in this section:Here,
e is called the eccentricity of the ellipse,
2.3 Long-Wavelength Approximation
Peristalsis with a long wavelength has traditionally been referred to as a regime in which the wavelength is enormous in comparison to the radius of the channel (when it is not disrupted), and this has been the case for many years. Because of the typical spacing between nonlinear parts that are dispersed across the channel, one obtains an extra length resulting from this scattering of elements. They may be highly significant in defining the flow–pressure relationship of the tube and, as a consequence, the operation of the biological system that they may depict, but they can also introduce complexity that makes an analytical approach difficult, so that is why they use long-wavelength approximation to make an easy analytical approach. After taking into consideration the restrictions of a long wavelength
2.4 Dimensionless Boundary Conditions
The corresponding dimensionless boundary conditions are
The expression of (1) takes the form
and expression (8) becomes
2.5 Exact Solution
Calculating the precise solution of the velocity profile may be done analytically with the aid of the polynomial that we specified for the given solution and the provided solution. This component is very crucial and plays a vital part in the solution of the velocity profile since it is constant in nature. Here, we get the solution of (17), The polynomial solution for
The constants of the above polynomial are
Replacing the values of constants, the above equation (22) becomes
The volumetric flow is calculated by integrating the velocity term over the elliptical cross-section; the dimensionless volumetric flow flux is written as follows:
The pressure gradient is in the term of
The pressure rise expression for the given flow is written as
3 The results of an investigation and conversations
3.1 Analysis of the Results
In this section, we analyze the results of various physical parameters with the help of the plotted figures. These graphs are plotted for volumetric flow rate, occlusion, aspect ratio, and following other parameters. We use a unique solution method to solve the complicated problem. Because of the polynomial solution and the way the graphs move, we can see that the boundary conditions are met and our solution for this elliptic duct is close to the correct answer.
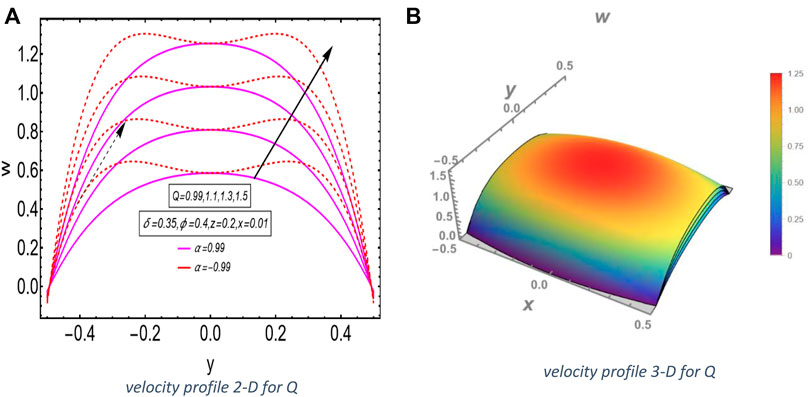
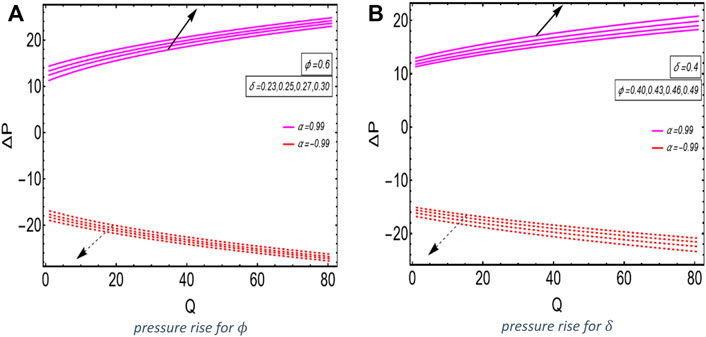
The analysis of the effect of the pseudoplasticity coefficient and the mean flow rate on the velocity of the fluid was performed. It has been shown that the magnitude of dimensionless velocity in the middle of the tube rises with the pseudoplasticity of the fluid and decreases with the dilatant nature of the fluid. On the elliptic duct, the opposite phenomenon is seen. Observers have analyzed that the pressure gradient exhibits an oscillatory characteristic. The trapping phenomena are also discussed in the context of the current fluid model for dilatant and pseudoplastic natures. The effect of the flow rate aspect ratio and various other parameters is analyzed for both cases, such as pseudoplasticity and the dilatant nature of the fluids. The Newtonian case is not studied in this section because at this condition, it is diverged.
3.2 Discussion of the Results
A graphical discussion of the precise solutions produced in the preceding section is shown here in order to offer a quality study of the mechanical behavior of the concerned fluid flow and the influence of the many factors involved in it. Using Mathematica 13.0, we created computer algorithms that enabled us to retrieve a set of data files, including information about the velocity, pressure gradient, and pressure rise. We discuss the graphical results of the velocity profile in 2-D and 3-D obtained by the polynomial solution method.
There are experiments to see from Figures 3A,B how the pseudoplasticity coefficient and the mean flow rate affect the fluid’s velocity. As has been seen, the dimensionless velocity in the center of the tube increases with pseudoplasticity and decreases with dilatation in the experiment. Case 1: The increasing volumetric flow rate causes an increase in velocity at the center of the channel, as shown in Figure 3A in 2-D. The velocity graph is plotted along to show the proper behavior of this profile with the increase of the value of the volumetric flow velocity profile, and it shows an increasing behavior for both the negative and positive values of the coefficient of pseudoplasticity
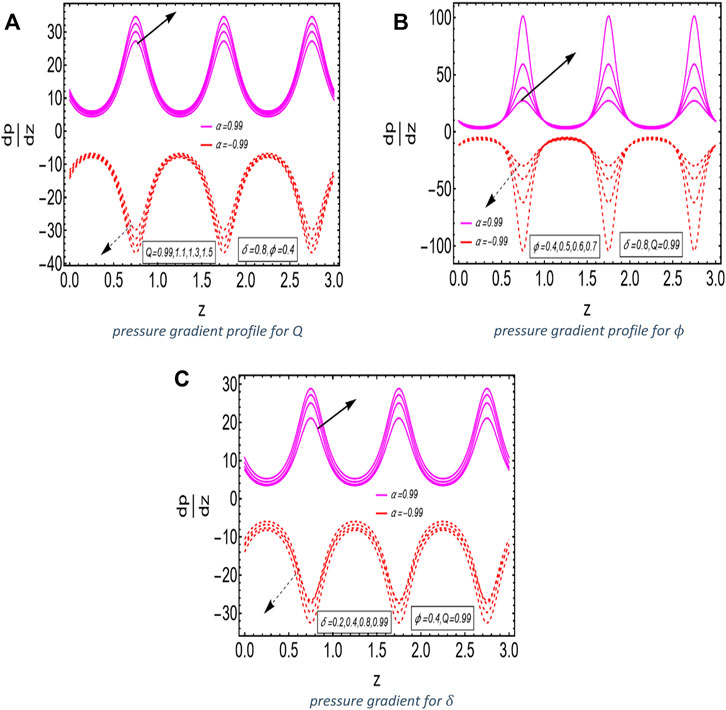
FIGURE 4. (A) Pressure gradient profile for Q. (B) Pressure gradient profile for
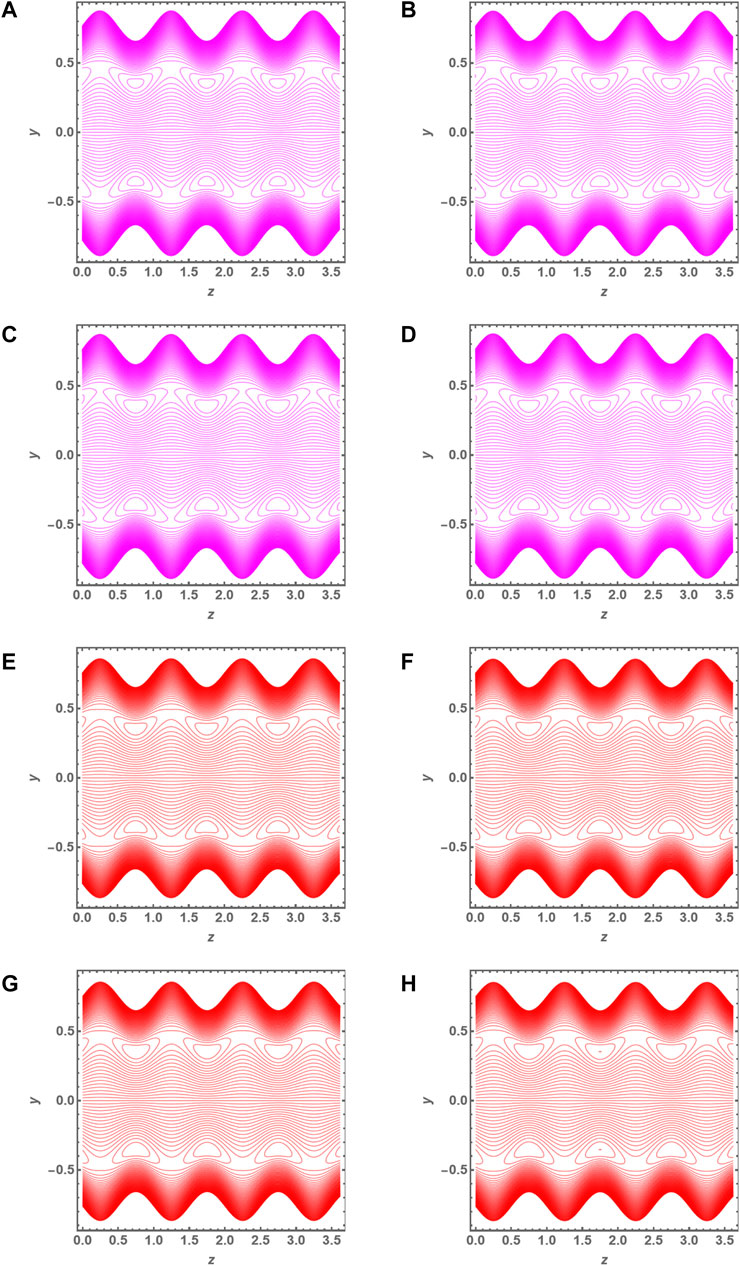
FIGURE 6. (A) Streamline for Q = 3.26 and
4 Conclusion
In this article, we analyzed the influence of the peristalsis flow of a Rabinowitsch fluid model passing via an elliptic duct. The dimensionless velocity is the greatest near the center of an elliptic duct, and in the case of pseudoplasticity, the magnitude of the dimensionless velocity rises and decreases with the dilatant nature of the fluid. It is seen that the duct wall exhibits the opposite behavior. As the mean flow rate increases, the velocity of the fluid increases as well. On closer inspection, it is seen that the pressure gradient exhibits oscillatory behavior like a sinusoidal wave. According to the streamlines of the velocity profile, it can be seen that the size of the trapping bolus for pseudoplastic and dilatant fluids is about the same. This research effort, which interprets the mathematical analysis of the flow, involves an elliptical duct with a non-Newtonian fluid flowing through it. In this article, we explore the unique analytical solution and applications of the peristaltic flow in different fields of life such as moving blood around in the heart, lungs, sanitary fluid transport systems, transfer of corrosive fluids, and innovative pharmaceutical delivery systems. A revolutionary mathematical approach for providing accurate exact solutions involving partial differential equations (PDEs) is described in detail. We give the unique solution method for this model; this solution is based on the polynomial solution. When it comes to fitting functions, polynomial models have traditionally been among the most commonly employed empirical models in history because they are popular, straightforward structures and commonly recognized. In physiology and biomedicine, since it is involved in the pumping of blood in heart/lung machines, the application of the Rabinowitsch fluid model to peristalsis is quite beneficial.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
SN is the supervisor and developed the problem. SA and JA have done the modeling and calculations. AM has drafted and proofread the article.
Funding
The authors will pay the charges.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
References
1. Wada S, Hayashi H. Hydrodynamic Lubrication of Journal Bearings by Pseudo-Plastic Lubricants : Part 2, Experimental Studies. Bull of JSME (1971) 14(69):279–86. doi:10.1299/jsme1958.14.279
2. Akbar NS, Nadeemb S. Application of Rabinowitsch Fluid Model in Peristalsis. Z für Naturforschung A (2014) 69(8-9):473–80. doi:10.5560/zna.2014-0034
3. Maraj EN, Nadeem S. Application of Rabinowitsch Fluid Model for the Mathematical Analysis of Peristaltic Flow in a Curved Channel. Z für Naturforschung A (2015) 70(7):513–20. doi:10.1515/zna-2015-0133
4. Sadaf H, Nadeem S. Analysis of Combined Convective and Viscous Dissipation Effects for Peristaltic Flow of Rabinowitsch Fluid Model. J Bionic Eng (2017) 14(1):182–90. doi:10.1016/s1672-6529(16)60389-x
5. Singh UP, Gupta RS, Kapur VK. On the Performance of Pivoted Curved Slider Bearings: Rabinowitsch Fluid Model. Tribology in industry (2012) 34(3):128.
6. Wells JC, Hung TTN. Longman Pronunciation Dictionary. RELC J (1990) 21(2):95–7. doi:10.1177/003368829002100208
7. Mittal R. Motor Function of the Pharynx, Esophagus, and its Sphincters. In Colloquium Ser on Integrated Syst Physiol From Molecule Funct (2011). Vol. 3, No. (3), pp. 1–84). Morgan & Claypool Life Sciences. doi:10.4199/c00027ed1v01y201103isp016
8. Stephen JAE, Choi US. Enhancing thermal Conductivity of Fluids with Nanoparticles. Dev and Appl of Non-Newtonian Flows (1995) 231:99–105.
9.WJ Minkowycz, EM Sparrow, and JP Abraham, editors. Nanoparticle Heat Transfer and Fluid Flow, 4. Florida, United States: CRC Press (2012).
10. Timofeeva EV, Routbort JL, Singh D. Particle Shape Effects on Thermophysical Properties of Alumina Nanofluids. J of applied Phys (2009) 106(1):014304. doi:10.1063/1.3155999
11. Latham TW. Fluid Motions in a Peristaltic Pump. Doctoral dissertation. Cambridge(US): Massachusetts Institute of Technology (1966).
13. Shapiro AH, Jaffrin MY, Weinberg SL. Peristaltic Pumping with Long Wavelengths at Low Reynolds Number. J Fluid Mech (1969) 37(4):799–825. doi:10.1017/s0022112069000899
14. Burns JC, Parkes T. Peristaltic Motion. J Fluid Mech (1967) 29(4):731–43. doi:10.1017/s0022112067001156
15. Zien T-F, Ostrach S. A Long Wave Approximation to Peristaltic Motion. J of Biomech (1970) 3(1):63–75. doi:10.1016/0021-9290(70)90051-5
16. Lew HS, Fung YC, Lowenstein CB. Peristaltic Carrying and Mixing of Chyme in the Small Intestine (An Analysis of a Mathematical Model of Peristalsis of the Small Intestine). J of Biomech (1971) 4(4):297–315. doi:10.1016/0021-9290(71)90036-4
17. Srivastava LM, Srivastava VP. Peristaltic Transport of a Power-Law Fluid: Application to the Ductus Efferentes of the Reproductive Tract. Rheol Acta (1988) 27(4):428–33. doi:10.1007/bf01332164
18. Carew EO, Pedley TJ. An Active Membrane Model for Peristaltic Pumping: Part I—Periodic Activation Waves in an Infinite Tube. J of Biochem Eng (1997) 119:66–76. doi:10.1115/1.2796066
19. Mishra M, Ramachandra Rao A. Peristaltic Transport of a Newtonian Fluid in an Asymmetric Channel. Z for Angew Mathematik Physik (Zamp) (2003) 54(3):532–50. doi:10.1007/s00033-003-1070-7
20. Saleem A, Akhtar S, Nadeem S, Alharbi FM, Ghalambaz M, Issakhov A. Mathematical Computations for Peristaltic Flow of Heated Non-Newtonian Fluid inside a Sinusoidal Elliptic Duct. Phys Scr (2020) 95(10):105009. doi:10.1088/1402-4896/abbaa3
21. Qasim M, Hayat Khan Z, Khan I, Al-Mdallal Q. Analysis of Entropy Generation in Flow of Methanol-Based Nanofluid in a Sinusoidal Wavy Channel. Entropy (2017) 19(10):490. doi:10.3390/e19100490
22. Shafiq A, Lone SA, Sindhu TN, Al-Mdallal QM, Rasool G. Statistical Modeling for Bioconvective tangent Hyperbolic Nanofluid towards Stretching Surface with Zero Mass Flux Condition. Scientific Rep (2021) 11(1):1–11. doi:10.1038/s41598-021-93329-y
23. Mustafa T. Eyring–Powell Fluid Flow through a Circular Pipe and Heat Transfer: Full Solutions. Int J of Numer Methods for Heat Fluid Flow (2020) 30:4765–74. doi:10.1108/HFF-12-2019-0925
24. Turkyilmazoglu M. Algebraic Solutions of Flow and Heat for Some Nanofluids over Deformable and Permeable Surfaces. Int J of Numer Methods for Heat Fluid Flow (2017) 27:2259–67. doi:10.1108/hff-09-2016-0358
25. Nadeem S, Ahmad S, Muhammad N, Mustafa MT. Chemically Reactive Species in the Flow of a Maxwell Fluid. Results in Phys (2017) 7:2607–13. doi:10.1016/j.rinp.2017.06.017
26. Nadeem S, Ashiq S, Ali M. Williamson Fluid Model for the Peristaltic Flow of Chyme in Small Intestine. Math Probl in Eng (2012) 2012:479087. doi:10.1155/2012/479087
27. Nadeem S, Ul Haq R, Lee C. MHD Flow of a Casson Fluid over an Exponentially Shrinking Sheet. Scientia Iranica (2012) 19(6):1550–3. doi:10.1016/j.scient.2012.10.021
28. Nadeem S, Zaheer S, Fang T. Effects of thermal Radiation on the Boundary Layer Flow of a Jeffrey Fluid over an Exponentially Stretching Surface. Numer Algor (2011) 57(2):187–205. doi:10.1007/s11075-010-9423-8
29. Ahmed SE, Arafa AAM, Hussein SA. MHD Ellis Nanofluids Flow Around Rotating Cone in the Presence of Motile Oxytactic Microorganisms. Int Commun in Heat and Mass Transfer (2022) 134:106056. doi:10.1016/j.icheatmasstransfer.2022.106056
30. Cao W, I.L. A, Yook S-J, V.A. O, Ji X. Simulation of the Dynamics of Colloidal Mixture of Water with Various Nanoparticles at Different Levels of Partial Slip: Ternary-Hybrid Nanofluid. Int Commun in Heat and Mass Transfer (2022) 135:106069. doi:10.1016/j.icheatmasstransfer.2022.106069
31. Animasaun IL, Shah NA, Wakif A, Mahanthesh B, Sivaraj R, Koriko OK. Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization. UK: Taylor and Francis Group (2022).
32. Radhakrishnamacharya G. Long Wavelength Approximation to Peristaltic Motion of a Power Law Fluid. Rheol Acta (1982) 21(1):30–5. doi:10.1007/bf01520703
33. Sher Akbar N. Influence of Magnetic Field on Peristaltic Flow of a Casson Fluid in an Asymmetric Channel: Application in Crude Oil Refinement. J of Magnetism and Magn Mater (2015) 378:463–8. doi:10.1016/j.jmmm.2014.11.045
34. Sher Akbar N, Raza M, Ellahi R. Influence of Induced Magnetic Field and Heat Flux with the Suspension of Carbon Nanotubes for the Peristaltic Flow in a Permeable Channel. J of magnetism and Magn Mater (2015) 381:405–15. doi:10.1016/j.jmmm.2014.12.087
35. Akbar NS. Entropy Generation and Energy Conversion Rate for the Peristaltic Flow in a Tube with Magnetic Field. Energy (2015) 82:23–30. doi:10.1016/j.energy.2014.12.034
36. Akbar NS, Nadeem S, Hayat Khan Z. Numerical Simulation of Peristaltic Flow of a Carreau Nanofluid in an Asymmetric Channel. Alexandria Eng J (2014) 53(1):191–7. doi:10.1016/j.aej.2013.10.003
37. Wakif A, Zaydan M, Alshomrani AS, Muhammad T, Sehaqui R. New Insights into the Dynamics of Alumina-(60% Ethylene Glycol+ 40% Water) over an Isothermal Stretching Sheet Using a Renovated Buongiorno's Approach: A Numerical GDQLLM Analysis. Int Commun in Heat and Mass Transfer (2022) 133:105937. doi:10.1016/j.icheatmasstransfer.2022.105937
38. Shah NA, Wakif A, El-Zahar ER, Ahmad S, Yook SJ. Numerical Simulation of a Thermally Enhanced EMHD Flow of a Heterogeneous Micropolar Mixture Comprising (60%)-ethylene Glycol (EG), (40%)-water (W), and Copper Oxide Nanomaterials (CuO). Case Stud in Therm Eng (2022) 35 102046. doi:10.1016/j.csite.2022.102046
39. Ashraf MU, Qasim M, Wakif A, Afridi MI, Animasaun IL. A Generalized Differential Quadrature Algorithm for Simulating Magnetohydrodynamic Peristaltic Flow of Blood‐based Nanofluid Containing Magnetite Nanoparticles: a Physiological Application. Numer Methods for Partial Differential Equations (2020) 38:666–92. doi:10.1002/num.22676
40. Wakif A. A Novel Numerical Procedure for Simulating Steady MHD Convective Flows of Radiative Casson Fluids over a Horizontal Stretching Sheet with Irregular Geometry under the Combined Influence of Temperature-dependent Viscosity and thermal Conductivity. Math Probl in Eng (2020) 2020:1675350. doi:10.1155/2020/1675350
41. Nayak MK, Wakif A, Animasaun IL, Alaoui MSH. Numerical Differential Quadrature Examination of Steady Mixed Convection Nanofluid Flows over an Isothermal Thin Needle Conveying Metallic and Metallic Oxide Nanomaterials: a Comparative Investigation. Arab J Sci Eng (2020) 45(7):5331–46. doi:10.1007/s13369-020-04420-x
42. Wakif A, Chamkha A, Animasaun IL, Zaydan M, Waqas H, Sehaqui R. Novel Physical Insights into the Thermodynamic Irreversibilities within Dissipative EMHD Fluid Flows Past over a Moving Horizontal Riga Plate in the Coexistence of wall Suction and Joule Heating Effects: a Comprehensive Numerical Investigation. Arab J Sci Eng (2020) 45(11):9423–38. doi:10.1007/s13369-020-04757-3
43. Zaydan M, Wakif A, Animasaun IL, Khan U, Baleanu D, Sehaqui R. Significances of Blowing and Suction Processes on the Occurrence of Thermo-Magneto-Convection Phenomenon in a Narrow Nanofluidic Medium: a Revised Buongiorno's Nanofluid Model. Case Stud in Therm Eng (2020) 22:100726. doi:10.1016/j.csite.2020.100726
44. Rasool G, Wakif A. Numerical Spectral Examination of EMHD Mixed Convective Flow of Second-Grade Nanofluid towards a Vertical Riga Plate Using an Advanced Version of the Revised Buongiorno's Nanofluid Model. J Therm Anal Calorim (2021) 143(3):2379–93. doi:10.1007/s10973-020-09865-8
45. Zeeshan A, Ijaz N, Bhatti MM, Mann AB. Mathematical Study of Peristaltic Propulsion of Solid-Liquid Multiphase Flow with a Biorheological Fluid as the Base Fluid in a Duct. Chin J of Phys (2017) 55(4):1596–604. doi:10.1016/j.cjph.2017.05.020
46. Akhtar S, McCash LB, Nadeem S, Saleem S, Issakhov A. Convective Heat Transfer for Peristaltic Flow of SWCNT inside a Sinusoidal Elliptic Duct. Sci Prog (2021) 104(2):00368504211023683. doi:10.1177/00368504211023683
47. Singh UP. On the Performance of Pivoted Curved Slider Bearings: Rabinowitsch Fluid Model. In Proceedings of National Tribology Conference (Vol. 2011). December 2011. (2011)
48. Saleem A, Akhtar S, Alharbi FM, Nadeem S, Ghalambaz M, Issakhov A. Physical Aspects of Peristaltic Flow of Hybrid Nano Fluid inside a Curved Tube Having Ciliated wall. Results in Phys (2020) 19:103431. doi:10.1016/j.rinp.2020.103431
49. Hayman WK, Shanidze ZG. Polynomial Solutions of Partial Differential Equations. Methods and Appl of Anal (1999) 6(1):97–108. doi:10.4310/maa.1999.v6.n1.a7
Nomenclature
Cartesian coordinate system
Half-axes of ellipse
Coefficient of pseudoplasticity
Eccentricity of ellipse
Occlusion
Electromagnetohydrodynamic (EMHD)
Velocity components
Wavelength
Velocity of propagation
Hydraulic diameter of ellipse
Fluid viscosity
Aspect ratio
Partial differential equations (PDEs)
Volumetric flow
Keywords: peristalsis, elliptical duct, Rabinowitsch fluid model, polynomial solution, exact solutions
Citation: Nadeem S, Abbas Haider J, Akhtar S and Mohamed A (2022) Insight Into the Dynamics of the Rabinowitsch Fluid Through an Elliptic Duct: Peristalsis Analysis. Front. Phys. 10:923269. doi: 10.3389/fphy.2022.923269
Received: 19 April 2022; Accepted: 19 May 2022;
Published: 06 July 2022.
Edited by:
Muhammad Mubashir Bhatti, Shandong University of Science and Technology, ChinaReviewed by:
Abderrahim Wakif, University of Hassan II Casablanca, MoroccoMustafa Turkyilmazoglu, Hacettepe University, Turkey
Qasem M. Al-Mdallal, United Arab Emirates University, United Arab Emirates
Copyright © 2022 Nadeem, Abbas Haider, Akhtar and Mohamed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sohail Nadeem, c29oYWlsQHFhdS5lZHUucGs=
 Sohail Nadeem
Sohail Nadeem Jamil Abbas Haider1
Jamil Abbas Haider1 Salman Akhtar
Salman Akhtar