Insight into the Significance of Viscous Dissipation and Heat Generation/Absorption in Magneto-Hydrodynamic Radiative Casson Fluid Flow With First-Order Chemical Reaction

This study is an attempt to explore two-dimensional magneto-hydrodynamic Casson fluid flow with heat generation or absorption, chemical reaction, and viscous dissipation under the effect of thermal radiation. Prescribed surface temperature (PST) and prescribed heat flux (PHF) cases have been taken into account to investigate the problem. The constitutive relations for Casson fluid incorporated with suitable boundary layer approximation theory have been utilized to achieve the flow model equations. The obtained highly non-linear partial differential equations cannot be solved analytically, so we transform them into first-order differential equations, then tackle them with the boundary value problem (BVP-4c) technique in Matlab. Radiation increment decreases primary and secondary velocity profiles abruptly in both cases. Heat generation and absorption augmentation decrease the thermal and momentum boundaries for both studied cases. The skin coefficient for PHF cases has decreased 80% when compared with PST cases. The increment in Casson parameter has enhanced the Nusselt number by 75% for the PST case, whereas the decline in Nusselt number has doubled for the PHF case with the increase in magnetic field. It is concluded that, with the increment in Casson fluid, magnetic, radiation, and permeability parameter the Nusselt number has significantly increased for the PST case. However, for these parameters, an abrupt decline in Nusselt number has been observed for the PHF case. Results reported in this study for shear stress and Sherwood number are in complete agreement with already published previous work.

1 Introduction

In chemical and material processing engineering, there are many fluid flow problems. Non-Newtonian is one of those flow patterns. These Non-Newtonian models include the Williamson model, Maxwell model, viscoelastic fluids, power law fluids, micro-polar fluids, and so on. The Casson fluid model, also known as the Casson fluid, is another non-Newtonian model. It basically demonstrates the attributes of yield stress. The Casson fluid model has a strange relationship between the yield stress and applied shear stress. It acts like a fluid and moves when the shear stress is less than the applied yield stress. It acts as a solid when the shear stress in the fluid system is higher than the applied yield stress. Polymer processing and biomechanics are major applications of Casson fluids. Jelly, tomato sauce, fruit juices and honey are fine examples of Casson fluids [1, 2].

Khalid et al. [3] examined magneto-hydrodynamics convection over a vertical permeable oscillating plate with Casson fluid. Recently, numerous studies have been conducted on Casson fluid under the applied external effects. Kodi et al. [4] investigated magneto-hydrodynamic Casson fluid with chemical reactions and thermal diffusion past a porous surface. Goud et al. [5] conducted free convection of Casson fluid employing FEM to study MHD flow under the external heat source over a vertically oscillating porous plate. Verma and Mondal [6] have provided a review of numerical methods used in the last decade to study Casson fluid. These include Rung-Kutta 4, Shooting Technique, Keller Box Method, and Spectral Method. Das et al. [7] examined the Newtonian heating effect on hydro-magneto Casson fluid for heat and mass transfer past a horizontal surface. Loganathan et al. [8] have provided an insight into Casson flow over a permeable Riga plate under electromagnetic and radiation effects. Raju et al. [9] have discussed heat and mass transfer of magneto-hydrodynamic Casson fluid over an exponentially permeable stretching surface. Casson fluid for vertical cone and plate for unsteady magneto-hydrodynamics and heat source/sink has been described in [10]. Loganathan et al. [11] investigated entropy optimization using third-grade fluid flowing across a convective surface. Loganathan et al. [12] have explored Cattaneo–Christov heat flux and Oldroyd-b fluid with convective heating under distinct externally applied effects of magneto-convection. Madhukesh et al. [13] studied hybrid Casson fluid induced by a Riga plate with thermophoretic particle disposition and for heat and mass transportation. Gowda et al. [14] have demonstrated Casson-Maxwell fluid through stretchable disks to examine slip flow [15–19]. and Arshad et al. [20–22] have extensively examined linear and exponential stretching surfaces with external applied effects for nano and hybrid nanofluids.

In fluid mechanics, the destruction of the velocity profile caused by applied viscous stress is called viscous dissipation. This phenomenon is regarded as the conversion of kinetic energy into internal energy of the respective fluid. Lund et al. [23] have investigated the stability, employing the dual solution technique to study the stagnation point flow of magneto-hydrodynamic Casson fluid under Rosseland radiation and dissipation effects. Reddy et al. [24] illustrated the unsteady natural convection of Casson fluid flow under viscous dissipation effect using the finite element approach. Pop and Sheremet [25] have studied Casson fluid under thermal radiation and dissipation effects to examine free convection in a square cavity. Qasim and Noreen [26] have explained the viscous dissipation effect in the boundary layer flow of Casson fluid for heat transfer over a shrinking permeable sheet. Mahanthesh and Gireesha [27] examined Casson fluid under thermal radiation, joule heating, and viscous dissipation for Marangoni convective two-phase flow. Kotha et al. [28] elaborated on the entropy generation on a convectively heated surface with a viscous dissipation effect for Casson fluid flow. Medikare et al. [29] focused their study on stagnation point flow of MHD Casson fluid over non-linear stretching with viscous dissipation. Khan et al. [30] have discussed the Casson fluid for Blasius and Sakiadis flows with viscous dissipation. Hayat et al. [31] have elaborated on magneto-hydrodynamic Casson fluid under variable properties and with viscous dissipation. Yusof et al. [32] discussed the exponentially slippery Riga plate with viscous dissipation in radiative boundary layer flow of Casson fluid. Loganathan and Rajan [33] have introduced optimization of the entropy of Williamson fluid with joule heating and zero mass flux of nano-particles. Loganathan et al. [34] have investigated the entropy optimization of third-grade fluid under slip influence with zero mass flux and non-Fourier heat flux. Kumar et al. [35] have utilized the KKL correlations to explore the impact of magnetic dipole on radiative nanofluid over a stretched sheet. Wang et al. [36] have proposed an applicable model for thermophoresis diffusion while examining the three-dimensional flow of Oldroyd-B fluid under magnetic field and radiative force.

A chemical reaction occurs when two components react together in the presence of a catalyst or enzyme to form a distinct product. There are two major kinds of chemical reactions, namely, reversible or irreversible chemical reactions. In a reversible chemical reaction, the formed product due to unfavorable conditions can return to its initial components, whereas in an irreversible reaction, the formed product would not convert into its initial states on its own. In principle, all chemical reactions are reversible, but they require very specific conditions. One of the major examples of a reversible reaction is the combustion of ammonium chloride. When heated, it converts into two constitutive components: ammonia gas and hydrogen chloride gas. But when cooled, they react together to form the initial product. On the other hand, the combustion of propane is a fine example of an irreversible reaction. A plethora of scientists have examined chemical reaction effects on different fluid models. Gowda et al. [37] have investigated the marangoni driven boundary layer flow for heat and mass transport analysis with chemical reaction and activation energy. Kumar et al. [38] have explored Casson fluid over a curved stretching surface under chemical reaction and magnetic field. Gowda et al. [39] have employed KKL correlations to examine nanofluid flow under magnetic dipole and chemical reaction over stretching surface. Manjunatha et al. [40] have discussed the influence of Stefan blowing over a curved surface for convective heat transportation of nanofluid under chemical reaction effect. Rotating nano and hybrid nanofluids over rotating vertical cones with externally applied effects have been discussed by [41–47] and Hassan et al. [48, 49]. They discovered and advised that the recently discovered phenomenon of hybrid nanofluids produces a higher heat transfer coefficient and lower shear stress.

Shehzad et al. [50] introduced the suction and chemical reaction effect to study the effect of mass transfer in magneto-hydrodynamic flow of Casson fluid. Auther et al. [51] have examined the effect of magnetic field and chemical reaction on Casson fluid over vertical porous plates. Khan et al. [52] have discussed homogeneous and heterogeneous effects on Casson fluid. Ramzan et al. [53] have described the Casson fluid past a porous medium with chemical reaction and Rosseland radiation. Reddy et al. [54] studied MHD Casson fluid over an exponentially stretching surface under thermal radiation and chemical reaction effects. Bejawada et al. [55] have elaborated on the radiation effects on Casson fluid in a porous medium with chemical reaction. Ramakrishana et al. [56] conducted a comparative analysis past an exponentially stretching plate to determine the effects of chemical reaction, Soret, and Lorentz forces on Casson fluid. Khan et al. [57] treated Casson fluid analytically to study chemical reaction attributes. Hayat et al. [58] have performed finite difference analysis on Casson fluid with thermo diffusion and diffusion thermo effects for optimization of entropy. Khan et al. [59] have conducted a mathematical simulation for magneto-hydrodynamic Casson fluid through a moving permeable wedge with chemical reaction. Loganathan et al. [60] have discussed the significance of Darcy–Forchheimer on third-grade fluid with entropy generation. Loganathan et al. [61] have examined Maxwell fluid over a thermally radiative convective sheet. Karthik et al. [62] have investigated the importance of zero and non-zero mass fluxes of bio-convection viscoelastic fluid on a three-dimensional Riga plate with swimming microorganisms. Loganathan et al. [63] have performed heat transfer analysis on a three-dimensional convectively heated Riga plate with the Cattaneo-Christov heat flux model. Grieehsa et al. [64] demonstrated heat and mass transfer in Casson fluid flow for a magneto-hydrodynamic boundary layer with a uniform heat source. Gowda et al. [65] have examined the magnetic dipole effect on ferrofluid over a stretching sheet. Gowda et al. [66] have investigated the modified Fourier heat flux model using KKL correlations for nanofluid over a curved surface. Sarada et al. [67] have discussed the non-Newtonian fluid flow for heat and mass transfer under the impact of magneto-hydrodynamics.

This present research is an attempt to discuss magneto-hydrodynamic radiative Casson fluid flow past a bidirectional permeable stretching surface, incorporating internal heat generation/absorption, viscous dissipation, and chemical reaction effects. The novelty of the present problem is to investigate a two-dimensional permeable stretching surface considering two distinct cases of prescribed surface temperature (PST) and prescribed heat flux (PHF) for Casson fluid with external applied effect under the influence of Rosseland radiation. The present study is focused on analyzing the aforesaid problem comparatively for prescribed surface temperature and prescribed heat flux cases. The above provided deep literature review describes the different numerical methods utilized to study miscellaneous Casson fluid problems. The boundary value problem technique (BVP-4c) is employed in this study to tackle the designed problem numerically and graphically. The convergence criterion, or tolerance, is set at 10^–07. The flow behavior characteristics of magneto-hydrodynamic Casson fluid are achieved graphically. The skin friction coefficients, Nusselt number, and Sherwood number are examined under increasing impressions of different study parameters. This study aims to obtain fruitful answers for both incorporated profiles, namely, prescribed surface temperature and prescribed heat flux cases. So, this investigation provides an answer to the following research questions designed for both aimed profiles.

1) What is the effect of raising the Casson fluid parameter on velocity profiles, temperature, and concentration profiles under Rosseland radiation impression?

2) What is the effect of magnetic force and high permeability on horizontal and vertical motion profiles and other distributions?

3) What impact do the distinct parameters have on (a) Grashof number for temperature, (b) chemical reaction, and (c) Schmidt number on concentration profile?

4) What effect does the high radiation influence produce? Does the heat generation/absorption and viscous dissipation produce a high heat transfer coefficient and reduced skin rates?

5) How do changes in different study parameters affect the Nusselt and Sherwood numbers, as well as the friction coefficient?

2 Basic Equations

The flow governing equation for viscous incompressible fluid in the presence of Rosseland radiation, viscous dissipation, and internal heat generation/absorption:

Equation of continuity

$\mathit{\nabla }.V=\mathrm{0}(1)$

Equation of Momentum

$\rho \left[\frac{\partial V}{\partial t}+\left(V.\mathit{\nabla }\right)V\right]=-\mathit{\nabla }p+\rho g+\mu {\mathit{\nabla }}^{\mathrm{2}}V-\left[\frac{\mu }{K_{\mathrm{0}}}\right]V(2)$

Energy equation

$\rho C_p\left[\frac{\partial T}{\partial t}+\left(V.\mathit{\nabla }\right)T\right]=k_f{\mathit{\nabla }}^{\mathrm{2}}T+k_f\left[{\left(\frac{\partial u}{\partial x}{)}^{\mathrm{2}}+(\frac{\partial v}{\partial y}\right)}^{\mathrm{2}}\right]-Q_{\mathrm{0}}\left(T-T_{\infty }\right)-\left[\frac{\partial }{\partial y}\left(q_r\right)\right](3)$

Concentration equation

$\frac{\partial C}{\partial t}+\left(V.\mathit{\nabla }\right)C=D_m{\mathit{\nabla }}^{\mathrm{2}}C+K_r\left(C-C_{\infty }\right)(4)$

All the physical quantities in the above Eqs 1–4 are defined in nomenclature.

3 Mathematical Formulation

Let us consider two-dimensional viscous incompressible radiative Casson fluid flow over a stretched permeable surface. Magnetic field $B_{\mathrm{0}}$ with viscous dissipation, internal heat generation/absorption $Q_{\mathrm{0}}$, and first-order chemical reaction $K_r$ are incorporated and discussed under the effect of Rosseland thermal radiation. The x-axis is taken in the horizontal direction and y-axis is considered along the vertical direction and incorporating bidirectional permeability $K_{\mathrm{0}}$ space. The flow is induced by the sheet being stretched linearly along the $x$-axis by the applied two equal and opposite forces simultaneously. Numerous studies have described the constitutive relations for Casson fluid [1, 2]. These relations are employed to obtain the flow governing equations with external applied effects.

Constitutive relation of Casson fluid [1, 2].

${\tau }_{ij}=\left({\mu }_B+\frac{p_y}{\sqrt{\mathrm{2}ϵ}}\right)\mathrm{2}{e}_{ij}ϵ>{ϵ}_c(5)$

${\tau }_{ij}=\left({\mu }_B+\frac{p_y}{\sqrt{\mathrm{2}{ϵ}_c}}\right)\mathrm{2}{e}_{ij},ϵ<{ϵ}_c(6)$

In these above relations, ${\mu }_B$ is plastic dynamic viscosity of the non-Newtonian fluid, $p_y$ is the fluid yield stress, $ϵ$ is the product of component of deformation rate with itself, that is $ϵ=e_{ij}\ast e_{ij}$, and ${ϵ}_c$ critical value of product of component of strain tensor rate with itself. The boundary layer approximations theory is utilized on the above constitutive relations of Casson fluids to obtain the flow governing equations.

3.1 Flow Governing Equations

The above constitutive relations of Casson fluid after applying suitable boundary layer approximation theory will give us the flow governing equations. The continuity, conservation momentum, energy, and concentration equations along with boundaries are given below [1, 2].

Equation of continuity

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=\mathrm{0}(7)$

Momentum Equations

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}={\nu }_f\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\frac{{\partial }^{\mathrm{2}}u}{\partial y^{\mathrm{2}}}-\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\frac{{\nu }_f}{K_{\mathrm{0}}}u-\frac{{\sigma }_f{B}_{\mathrm{0}}^{\mathrm{2}}}{{\rho }_f}u+g\beta \left(T-T_{\infty }\right)+g{\beta }^{\ast }\left(C-C_{\infty }\right)(8)$

$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}={\nu }_f\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\frac{{\partial }^{\mathrm{2}}v}{\partial y^{\mathrm{2}}}-\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\frac{{\nu }_f}{K_{\mathrm{0}}}v-\frac{{\sigma }_f{B}_{\mathrm{0}}^{\mathrm{2}}}{{\rho }_f}v(9)$

Energy Equation without $q_r$ relation

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_f}{{\left(\rho c_p\right)}_f}\left[\frac{{\partial }^{\mathrm{2}}T}{\partial y^{\mathrm{2}}}\right]+\frac{k_f}{{\left(\rho c_p\right)}_f}\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\left[{\left(\frac{\partial u}{\partial x}{)}^{\mathrm{2}}+(\frac{\partial v}{\partial y}\right)}^{\mathrm{2}}\right]-\frac{\mathrm{1}}{{\left(\rho c_p\right)}_f}\left[\frac{\partial }{\partial y}\left(q_r\right)\right]+\frac{Q_{\mathrm{0}}}{{\left(\rho c_p\right)}_f}\left(T-T_{\infty }\right)(10)$

Species continuity equation

$\frac{v\partial C}{\partial y}+\frac{u\partial C}{\partial x}=D_m\frac{{\partial }^{\mathrm{2}}C}{\partial y^{\mathrm{2}}}-K_r\left(C-C_{\infty }\right)(11)$

With boundary conditions for PST case as follows:

$u=U_w\left(x\right),v=V_w\left(x\right),C=C_w=C_{\infty }+cx,T=T_w=T_{\infty }+bx,aty=\mathrm{0},u\to \mathrm{0},v\to \mathrm{0},T\to T_{\infty },C\to C_{\infty },asy\to \infty (12)$

PHF case will have the boundary conditions as follow:

$u=U_w\left(x\right),v=V_w\left(x\right),C=C_w=C_{\infty }+cx,-k\frac{\partial T}{\partial y}=q=D_x,aty=\mathrm{0},u\to \mathrm{0},v\to \mathrm{0},T\to T_{\infty },C\to C_{\infty },asy\to \infty .(13)$

The radiative heat flux is defined as $q_r=-\frac{\mathrm{4}{\sigma }^{\ast }}{\mathrm{3}{K}^{\ast }}\frac{\partial T^{\mathrm{4}}}{\partial y}$. The temperature difference is small and the expansion of $T^{\mathrm{4}}$ in terms of $T_{\infty }$ using Taylor’s formula will give us:

$T^{\mathrm{4}}\approx T_{\infty }^{\mathrm{4}}-\mathrm{4}{T}_{\infty }^{\mathrm{3}}\left(T-T_{\infty }\right)+\mathrm{6}{T}_{\infty }^{\mathrm{2}}{\left(T-T_{\infty }\right)}^{\mathrm{2}}+.......(14)$

now, we’ll truncate the above Eq. 14 up to first degree and the order of truncation is O${\left((T-T_{\infty }\right)}^{\mathrm{2}}$, we arrive at:

$T^{\mathrm{4}}\approx \mathrm{4}T{T}_{\infty }^{\mathrm{3}}-\mathrm{3}{T}_{\infty }^{\mathrm{4}}(15)$

with this substitution our energy Eq. 10 will become:

$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_f}{{\left(\rho c_p\right)}_f}\left[\frac{{\partial }^{\mathrm{2}}T}{\partial y^{\mathrm{2}}}\right]+\frac{k_f}{{\left(\rho c_p\right)}_f}\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\left[{\left(\frac{\partial u}{\partial x}{)}^{\mathrm{2}}+(\frac{\partial v}{\partial y}\right)}^{\mathrm{2}}\right]+\frac{\mathrm{1}}{{\left(\rho c_p\right)}_f}\frac{\mathrm{16}{\sigma }^{\ast }{T}_{\infty }^{\mathrm{3}}}{\mathrm{3}{K}^{\ast }}\left[\frac{{\partial }^{\mathrm{2}}T}{\partial y^{\mathrm{2}}}\right]+\frac{Q_{\mathrm{0}}}{{\left(\rho c_p\right)}_f}\left(T-T_{\infty }\right).(16)$

Where $U_w=ax$ is stretched velocity, $a$ is positive constant, and $V_w$ is suction/blowing velocity at wall. The $V_w>\mathrm{0},$ correspond to suction and $V_w<\mathrm{0},$ to blowing.

3.2 Similarity Transformation

The stream function is defined as $\varphi \left(x,y\right)$ where, $u=\frac{\partial \varphi }{\partial y},andv=-\frac{\partial \varphi }{\partial x}$ and the set of similarity [65–67] is defined as follows:

$\eta ={\left(\frac{U_w}{v_{f}x}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}y,T-T_{\infty }=\left(T_w-T_{\infty }\right)\theta \left(\eta \right),C-C_{\infty }=\left(C_w-C_{\infty }\right)\phi \left(\eta \right),u=ax{f}^{\prime }\left(\eta \right),v=-\sqrt{v_{f}a}f\left(\eta \right),\varphi \left(x,y\right)={\left(U_{w}x{v}_f\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}f\left(\eta \right)(17)$

Where, $T_{\infty }$ and $T_w$ are ambient temperature and temperature at the wall, respectively. $C_w$ and $C_{\infty }$ denote the concentration at the wall and ambient concentration, respectively. For our own convenience we have assumed $f\left(\eta \right)$ as $\mathrm{g}\left(\eta \right)$ in second stream function $v=-\sqrt{v_{f}a}g\left(\eta \right)$. It is worth noting that we have defined temperature for PST case as $T-T_{\infty }=bx\theta \left(\eta \right)$ and for PHF case as $T-T_{\infty }=\frac{D_x}{k}{\left(\frac{v_f}{a}\right)}^{\mathrm{1}/\mathrm{2}}\theta \left(\eta \right)$.

3.3 Transformed Governing Equations

The flow governing equations of momentum, energy, and concentration (8–9, 16, and 11) respectively, after using the similarity transform, will take the following form along with boundary conditions:

$\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)f^{‴}=f^{{\prime }^{\mathrm{2}}}-g{f}^{″}-\frac{\mathrm{1}}{\mathrm{2}}\eta f^{\prime }{f}^{″}+\left(M^{\mathrm{2}}{f}^{\prime }+K\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\right)f^{\prime }-G_r\theta -G_C\phi (18)$

$\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)g^{″}=\left(M^{\mathrm{2}}+K\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\right)g-\frac{\mathrm{1}}{\mathrm{2}}\eta f^{\prime }{g}^{\prime }-g{g}^{\prime }(19)$

${\theta }^{″}\left(\mathrm{1}+Rd\right)=E_c\left[f^{{\prime }^{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{2}}{\eta }^{\mathrm{2}}{f}^{″}-\eta f^{\prime }{f}^{″}+g^{{\prime }^{\mathrm{2}}}\right]+\mathit{Pr}\left[\frac{\mathrm{1}}{\mathrm{2}}\eta f^{\prime }{\theta }^{\prime }+{\theta }^{\prime }g\right]+PrQ\theta (20)$

${\phi }^{″}=Sc\left[K_C\phi -\frac{\mathrm{1}}{\mathrm{2}}\eta {\phi }^{\prime }-g{\phi }^{\prime }\right](21)$

The boundary conditions for PST case are as follow:

$f^{\prime }\left(\eta \right)=\mathrm{1},g\left(\eta \right)=S,\theta \left(\eta \right)=\mathrm{1},\phi \left(\eta \right)=\mathrm{1},as\eta =\mathrm{0},{f\left(\eta \right)=\mathrm{0},f}^{\prime }\left(\eta \right)\to \mathrm{0},g\left(\eta \right)\to \mathrm{0},\theta \left(\eta \right)\to \mathrm{0},\phi \left(\eta \right)\to \mathrm{0}as\eta =\infty (22)$

The boundaries for PHF case are as follow:

$f^{\prime }\left(\eta \right)=\mathrm{1},g\left(\eta \right)=S,{\theta }^{\prime }\left(\eta \right)=-\mathrm{1},\phi \left(\eta \right)=\mathrm{1},as\eta =\mathrm{0},{f\left(\eta \right)=\mathrm{0},f}^{\prime }\left(\eta \right)\to \mathrm{0},g\left(\eta \right)\to \mathrm{0}\theta \left(\eta \right)\to \mathrm{0},\phi \left(\eta \right)\to \mathrm{0}as\eta =\infty (23)$

Where $K=\frac{v}{k_{\mathrm{0}}a}$ is permeability parameter, $\mathit{Pr}=\frac{{\left(\mu c_p\right)}_f}{k_f}$ is Prandtl number, $S=\frac{V_w\left(x\right)}{\sqrt{va}}$ suction/injection parameter, $M^{\mathrm{2}}=\frac{\sigma B_{\mathrm{0}}^{\mathrm{2}}}{\rho a}$ magnetic parameter, and $Sc=\frac{v}{D_m}$ Schmidt number. $G_r=\frac{g\beta \left(T_w-T_{\infty }\right)}{a^{\mathrm{2}}x}$ is Grashof number for temperature, $G_C=\frac{g{\beta }^{\ast }\left(C_w-C_{\infty }\right)}{a^{\mathrm{2}}x}$ is Grashof number for concentration, $E_c=\frac{v_{f}a}{{\left(\rho C_p\right)}_f\left(T_w-T_{\infty }\right)}$ is Eckert number, $Rd=\frac{\mathrm{16}{\sigma }^{\ast }{T}_{\infty }^{\mathrm{3}}}{{\mathrm{3}K}^{\ast }{k}_f}$ is radiation parameter, $Q=\frac{Q_{\mathrm{0}}}{a{\left(\rho C_p\right)}_f}$ is internal heat generation/absorption parameter, and denotes $K_C=\frac{K_r}{a}$ chemical reaction.

4 Numerical Solution of Problem

Numerical methods used in numerous studies carried out on Casson fluid regimes reported by Verma and Mondal [6] include Rung-Kutta 4, Shooting Methods, Keller Box Method, and Spectral Method. Hayat et al. [58] conducted their study using a finite difference scheme. Moreover, Goud et al. [5] examined the Casson fluid problem with the finite element method. In this study, the boundary value problem technique is employed in Matlab to tackle the problem numerically and achieve the graphical and tabulated results for the designed problem.

4.1 Technique Procedure

The boundary value problem technique involves a process of converting highly non-linear partial differential equations into first-order ordinary differential equations using the newly defined set of variables of our own choice. The boundaries are also transformed using similar suppositions; minimal convergence criterion or tolerance is set to achieve more accurate results. The set of first-order differential equations for both PST and PHF cases is given below, along with a newly defined set of variables.

The set of newly defined variables:

$f=y_{\mathrm{1}},f^{\prime }=y_{\mathrm{2}},f^{″}=y_{\mathrm{3}},f^{‴}=y_{\mathrm{3}}^{\prime },g=y_{\mathrm{4}},g^{\prime }=y_{\mathrm{5}},g^{″}=y_{\mathrm{5}}^{\prime },\theta =y_{\mathrm{6}},{\theta }^{\prime }=y_{\mathrm{7}},{\theta }^{″}=y_{\mathrm{7}}^{\prime },\phi =y_{\mathrm{8}},{\phi }^{\prime }=y_{\mathrm{9}},{\phi }^{″}=y_{\mathrm{9}}^{\prime }.(24)$

Transformed differential equations are:

$y_{\mathrm{1}}^{\prime }=y_{\mathrm{2}}(25)$

$y_{\mathrm{2}}^{\prime }=y_{\mathrm{3}}(26)$

$\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)y_{\mathrm{3}}^{\prime }=y_{\mathrm{2}}^{\mathrm{2}}-y_{\mathrm{4}}{y}_{\mathrm{3}}-\frac{\mathrm{1}}{\mathrm{2}}\eta y_{\mathrm{2}}{y}_{\mathrm{3}}+\left(M^{\mathrm{2}}{y}_{\mathrm{2}}^{\prime }+K\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\right)y_{\mathrm{2}}-G_r{y}_{\mathrm{7}}-G_C{y}_{\mathrm{8}},(27)$

$y_{\mathrm{5}}^{\prime }=y_{\mathrm{4}}(28)$

$\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)y_{\mathrm{5}}^{\prime }=\left(M^{\mathrm{2}}+K\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)\right)y_{\mathrm{4}}-\frac{\mathrm{1}}{\mathrm{2}}\eta y_{\mathrm{2}}{y}_{\mathrm{5}}-y_{\mathrm{4}}^{\prime }{y}_{\mathrm{5}},(29)$

$y_{\mathrm{6}}^{\prime }=y_{\mathrm{7}}(30)$

$y_{\mathrm{7}}^{\prime }\left(\mathrm{1}+Rd\right)=E_c\left[y_{\mathrm{2}}^{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{\eta }^{\mathrm{2}}{y}_{\mathrm{3}}-\eta {y_{\mathrm{2}}y}_{\mathrm{3}}+y_{\mathrm{4}}^{\mathrm{2}}\right]+\mathit{Pr}\left[\frac{\mathrm{1}}{\mathrm{2}}\eta y_{\mathrm{2}}{y}_{\mathrm{7}}+y_{\mathrm{7}}{y}_{\mathrm{4}}\right]+PrQ{y}_{\mathrm{6}},(31)$

$y_{\mathrm{8}}^{\prime }=y_{\mathrm{9}}(32)$

$y_{\mathrm{9}}^{\prime }=Sc\left[K_C{y}_{\mathrm{8}}-\frac{\mathrm{1}}{\mathrm{2}}\eta y_{\mathrm{9}}-y_{\mathrm{4}}{y}_{\mathrm{9}}\right].(33)$

Transformed boundary conditions for PST case:

$y_{\mathrm{2}}\left(\mathrm{0}\right)=\mathrm{1},y_{\mathrm{4}}\left(\mathrm{0}\right)=S,y_{\mathrm{6}}\left(\mathrm{0}\right)=\mathrm{1},y_{\mathrm{8}}\left(\mathrm{0}\right)=\mathrm{1},y_{\mathrm{1}}\left(\infty \right)\to \mathrm{0}{y}_{\mathrm{2}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{4}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{6}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{8}}\left(\infty \right)\to \mathrm{0}.(34)$

Boundaries for PHF case:

$y_{\mathrm{2}}\left(\mathrm{0}\right)=\mathrm{1},y_{\mathrm{4}}\left(\mathrm{0}\right)=S,y_{\mathrm{7}}\left(\mathrm{0}\right)=-\mathrm{1},y_{\mathrm{8}}\left(\mathrm{0}\right)=\mathrm{1},y_{\mathrm{1}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{2}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{4}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{6}}\left(\infty \right)\to \mathrm{0},y_{\mathrm{8}}\left(\infty \right)\to \mathrm{0}.(35)$

4.2 Quantities of Physical Interest

The Skin coefficient $\left(C_f\right)$ and Nusselt $\left(Nu\right)$ and Sherwood $\left(Sh\right)$ numbers are quantities of physical importance. Surface sheer stress ${\tau }_w$, surface heat flux $q_w$, and mass flux $m_w$ will be utilized to solve these quantities in dimensional form.

$C_f=\frac{\mu {\left(\frac{\partial u}{\partial y}\right)}_{y=\mathrm{0}}}{\rho U_w^{\mathrm{2}}},Nu=\frac{-{\left(\frac{\partial T}{\partial y}\right)}_{y=\mathrm{0}}}{\left(T_w-T_{\infty }\right)},Sh=\frac{-{\left(\frac{\partial C}{\partial y}\right)}_{y=\mathrm{0}}}{\left(C_w-C_{\infty }\right)},(36)$

The dimensionless form of these quantities for PST case will take the following form:

${Re}_x^{-\mathrm{1}/\mathrm{2}}{C}_f=\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)f^{″}\left(\mathrm{0}\right),{\left(R{e}_x\right)}^{-\frac{\mathrm{1}}{\mathrm{2}}}Sh=-{\phi }^{\prime }\left(\mathrm{0}\right),{\left(R{e}_x\right)}^{-\frac{\mathrm{1}}{\mathrm{2}}}Nu=-{\theta }^{\prime }\left(\mathrm{0}\right).(37)$

These quantities for PHF case in dimensionless form can be written as:

${Re}_x^{-\mathrm{1}/\mathrm{2}}{C}_f=\left(\mathrm{1}+\frac{\mathrm{1}}{\gamma }\right)f^{″}\left(\mathrm{0}\right),{\left(R{e}_x\right)}^{-\frac{\mathrm{1}}{\mathrm{2}}}Sh=\frac{\mathrm{1}}{{\phi }^{\prime }\left(\mathrm{0}\right)},{\left(R{e}_x\right)}^{-\frac{\mathrm{1}}{\mathrm{2}}}Nu=\frac{\mathrm{1}}{{\theta }^{\prime }\left(\mathrm{0}\right)}.(38)$

5 Results and Discussion

In this section, magneto-hydrodynamic Casson fluid flow characteristics over permeable plates are analyzed. The Casson fluid behavior under the influence of different study parameters is elaborated on primary and secondary velocity profiles, temperature, and concentration profiles. Table 1 shows the results obtained for skin and Nusselt and Sherwood numbers for PST case under the influence of different study parameters. Table 2 describes the skin and Nusselt and Sherwood numbers under increasing study parametric impression. Table 3, 4 present the comparison of obtained outcomes of shear stress and Sherwood number under suction and blowing influence with varying Casson fluid parameter, respectively.

TABLE 1

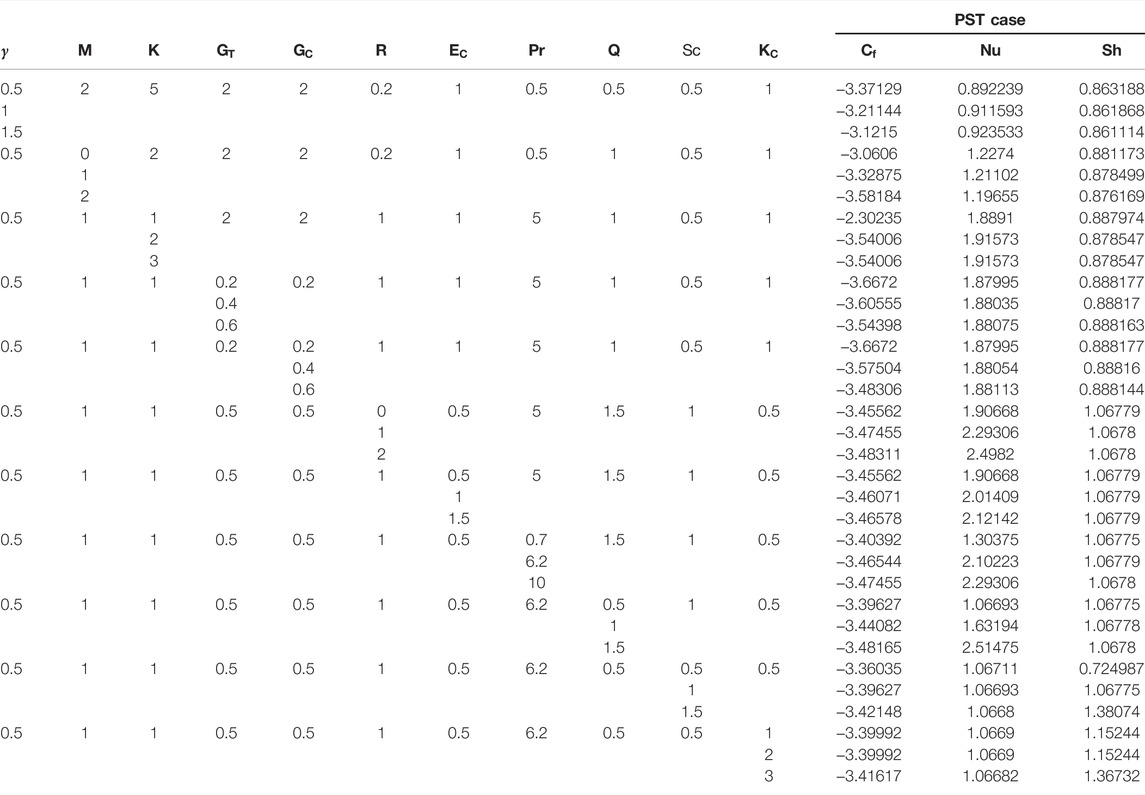
TABLE 1. Results of skin friction and Nusselt and Sherwood number for Prescribed surface temperature (PST) case under varying influence of distinct parameters.

TABLE 2

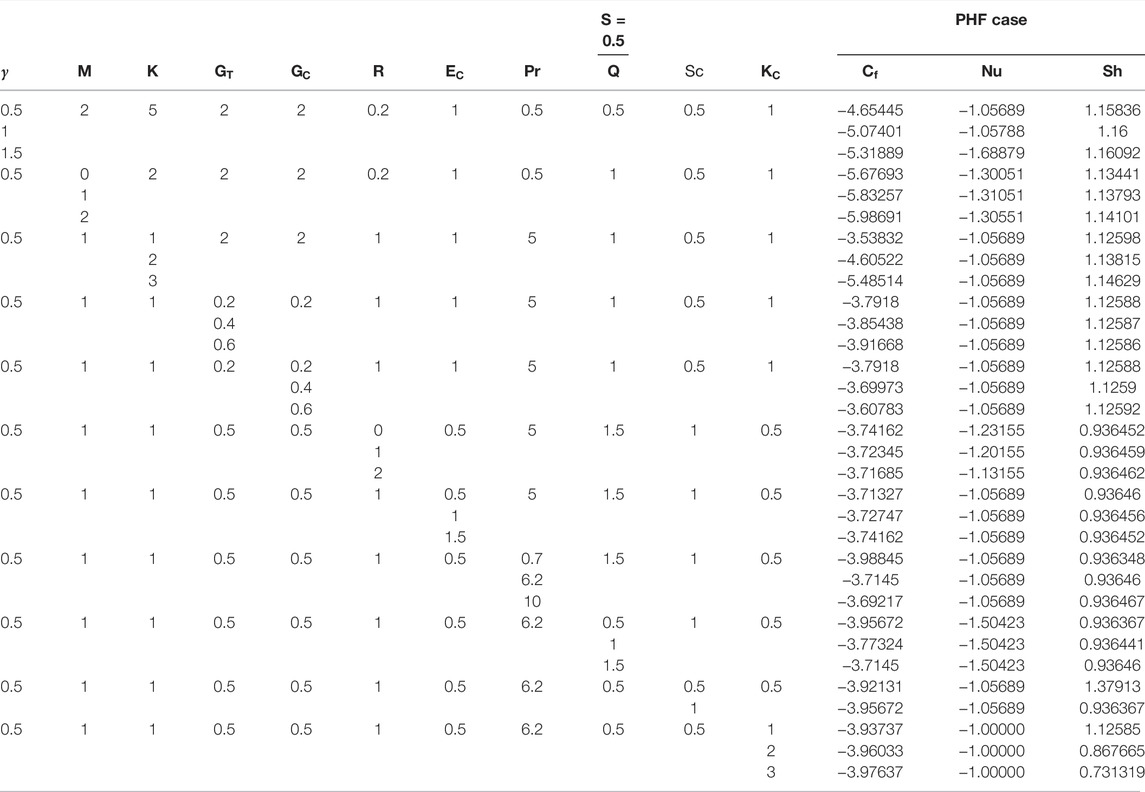
TABLE 2. Results of skin friction and Nusselt and Sherwood number for Prescribed heat flux (PHF) case under varying influence of distinct parameters.

TABLE 3

TABLE 3. Comparison of skin coefficient for varying Casson fluid parameters with already published work [64].

TABLE 4

TABLE 4. Comparison of Sherwood number for varying Casson fluid parameters with already published work [64].

5.1 Effect of Casson Fluid Parameter

In Figures 1B–D, 2A, the primary velocity profile is depicted under distinct study parameters. Figure 1B shows the impact of Casson fluid parameter on primary velocity for both PST and PHF case. In the prescribed surface temperature case, the increment in Casson fluid parameter has decreased the primary velocity profile sharply in comparison with prescribed heat flux case. Also, the associated momentum boundary has decreased more dramatically in the case of surface temperature case. This suggests that, as Casson fluid parameter is increased, the viscosity starts to increase, consequently, the free motion of fluid slows down. Moreover, a smooth decline is observed in motion of Casson fluid for both profiles. Figure 1C describes the impact of Casson fluid parameter on secondary profile. Contraction in momentum boundary layer of secondary velocity profile has been observed for surface temperature case and heat flux case with increments in Casson fluid parameter. Additionally, the viscosity gets thicker as the Casson fluid parameter is increased.

FIGURE 1

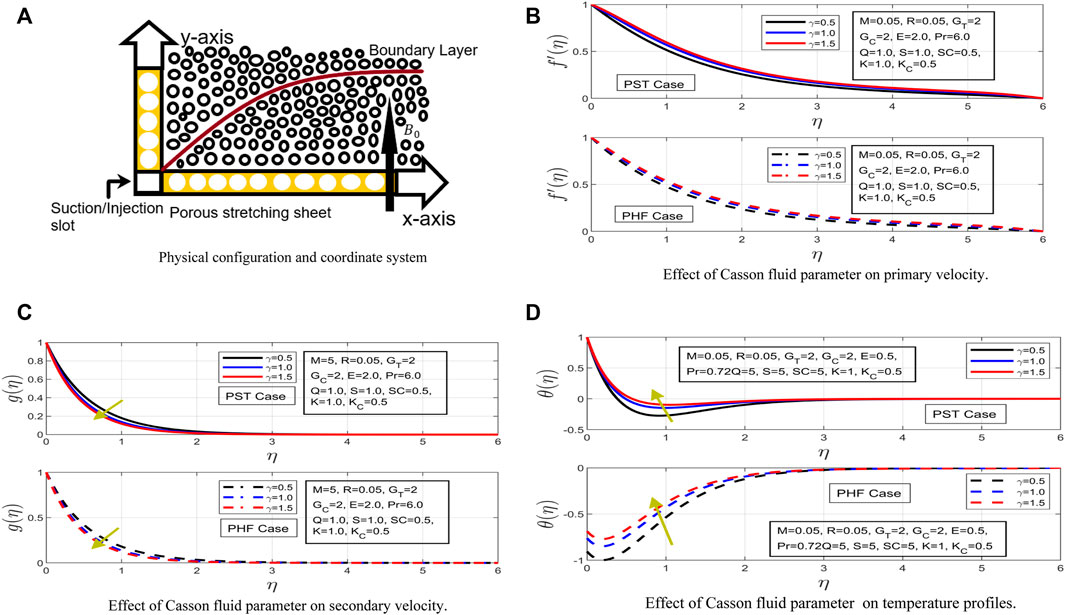
FIGURE 1. (A) Physical configuration and coordinate system (B) Effect of Casson fluid parameter on primary velocity. (C) Effect of Casson fluid parameter on secondary velocity. (D) Effect of Casson fluid parameter on temperature profiles.

FIGURE 2

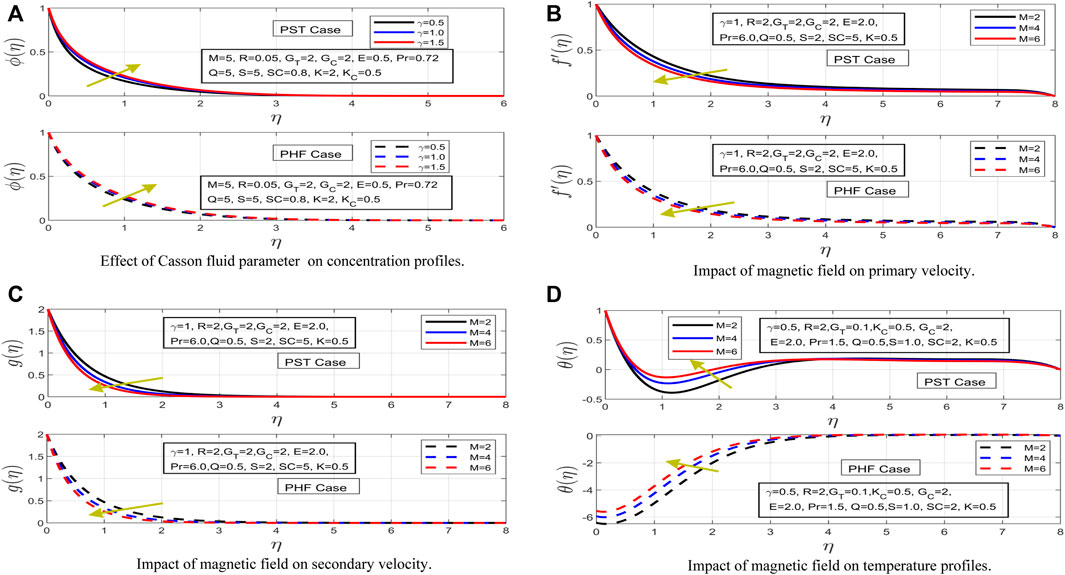
FIGURE 2. (A) Effect of Casson fluid parameter on concentration profiles. (B) Impact of magnetic field on primary velocity. (C) Impact of magnetic field on secondary velocity. (D) Impact of magnetic field on temperature profiles.

Figure 1D depicts the impression of Casson fluid parameter on temperature profile. The temperature profile has shown a very distinct behavior for both cases under incremental change of Casson fluid parameter. In the prescribed surface temperature case, the temperature profile has decreased with increases in Casson fluid parameter. This results in a contraction in the thermal boundary of the fluid. Moreover, the thickness of the thermal boundary has declined. Now, in the prescribed heat flux case, the temperature profile starts upsurging. It is interesting to note here that the thermal boundary has expanded for the prescribed heat flux case. Figure 2A illustrates the behavior of Casson fluid parameter on concentration profile. The result of an increase in Casson fluid parameter on concentration profile has contracted the concentration boundary layer drastically for both examined cases. This contraction phenomenon has occurred for both thermal and concentration layers; this impact resulted from the presence of a strong magnetic field and internal heat absorption parameter. The higher magnetic force generates a strong Lorentz force, which acts as a resistive force in free motion of Casson fluid. This effect has caused a contraction in thermal and concentration boundary layers. Furthermore, the thickness of the concentration layer associated with both PST and PHF cases has decreased. In prescribed heat flux case, more contraction is observed in the thermal layer and thickness of fluid.

5.2 Effect of Magnetic Field

The effect of increasing the magnetic field is examined on different study profiles in this sub-section. Figure 2B shows the outcome of the magnetic field on primary velocity profile for both PST and PHF cases. Primary velocity profile decreases slowly with increases in magnetic field. Even with high generated Lorentz force, which acts as a resistive force in the motion of fluid with the boundary layer, the primary velocity has decreased very smoothly. In other words, the primary velocity profile has gradually decreased even when experiencing a strong resistive force. Figure 2C depicts the impact of magnetic field on secondary velocity profile for PST and PHF cases. In the secondary velocity profile case, the increment in magnetic parameter has expanded momentum boundary for both cases. It is worth noting that, with a very slight difference, the momentum boundaries for both cases have decreased.

The increase in magnetic force has shown opposite impacts for both cases on temperature profile (See Figure 2D). Temperature profile in the case of prescribed surface has shown a downfall as the magnetic field is increased. It is worth noting that, even with presence of a strong resistive force, the temperature profile has decreased and expansion is observed in the thermal boundary layer for the prescribed surface temperature case. The temperature profile for heat flux case has upsurged. This illustrates the fact that in the prescribed surface temperature case, the temperature condition at initial position becomes surface temperature, while in heat flux case the initial temperature becomes surface heat flux. The thermal boundary has also expanded in the PHF case. Figure 3A describes the impact of magnetic field on concentration profile. It can be clearly observed that the thickness of concentration boundary layer has decreased for both cases under an incremental change in magnetic field. The resistive force generated within the electrically conducting fluid has caused contraction in concentration boundary layer of Casson fluid. Additionally, chemical reaction parameter also plays a significant role in the downfall of concentration profile and contraction in concentration layer for both cases under discussion.

FIGURE 3

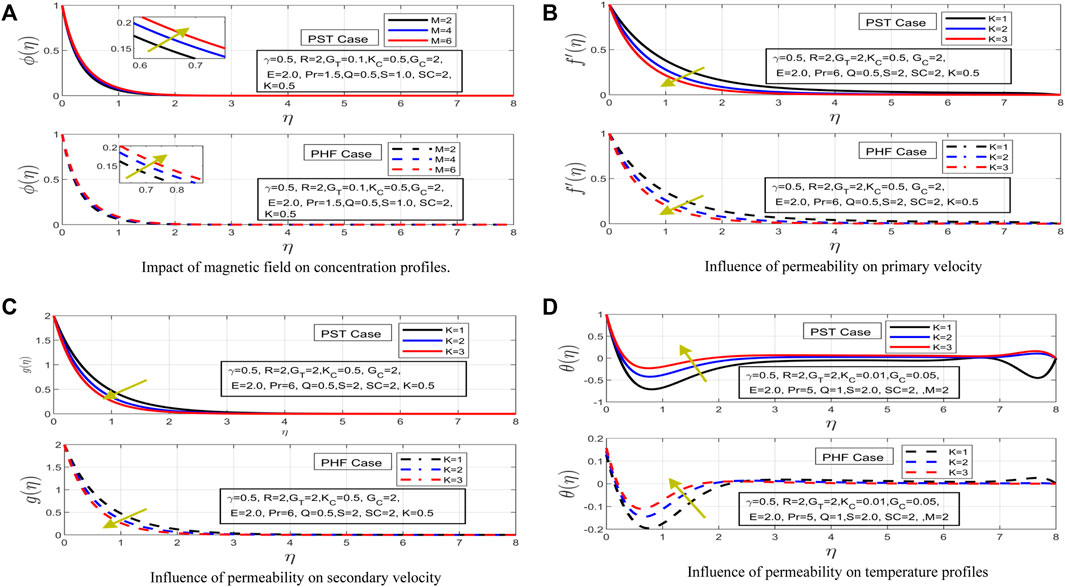
FIGURE 3. (A) Impact of magnetic field on concentration profiles. (B) Influence of permeability on primary velocity (C) Influence of permeability on secondary velocity (D) Influence of permeability on temperature profiles.

5.3 Effect of Permeability Parameter

Figure 3B shows the impact of increases in permeability parameter on primary velocity. The increment in permeability parameter generates free space for free movement of Casson fluid. The primary velocity profile has decreased with increases in permeability; consequently, the associated momentum boundary of the prescribed surface temperature case has sharply decreased. The influence of increasing permeability has decreased the primary velocity with a very slight difference for both surface temperature and heat flux cases. In another sense, the momentum boundary layer has also expanded rapidly for both cases with increases in availability of free space. The high permeability parameter has decreased the resistive force generated as the result of high applied magnetic force. Figure 3C depicts the permeability impact on secondary velocity profile. In both PST and PHF profiles, the secondary velocity profile has decreased sharply. Moreover, it is worth noting here that momentum boundary expands with high porosity increment. The extended computational domain provides the contrasting behavior of PST and PHF cases for secondary velocity profile.

Figure 3D describes the temperature profile under the influence of the permeability parameter for both PST and PHF cases. The expansion in domain has changed the overall behavior of the temperature profile under high permeability. In PST case, the temperature profile has increased and even with the presence of a high resistive force and internal heat absorption/generation the thermal boundary layer has expanded. The PHF case shows that, as the availability of free space increases, the thermal boundary expands and the temperature of Casson fluid increases. Figure 4A shows the impact of the permeability parameter on concentration profile. The concentration profile has decreased for both PST and PHF cases. The increment in permeability parameter has shown a decline in overall concentration profile. It is worth noting that even the concentration profile that decreased the concentration layer for PST and PHF cases has contracted. The presence of a high resistive force and high suction influence are major contributors to the contraction of the concentration layer.

FIGURE 4

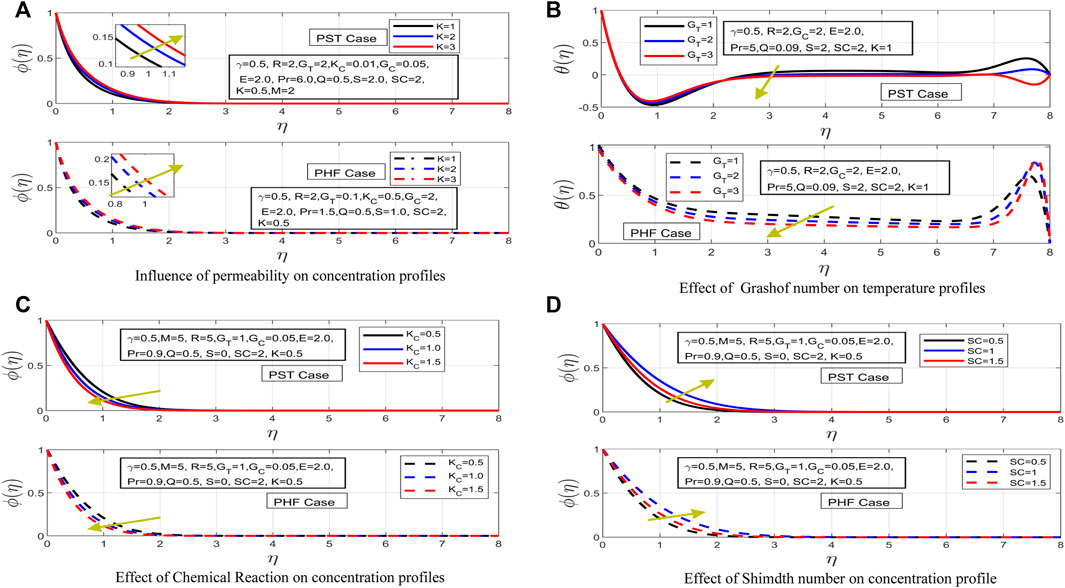
FIGURE 4. (A) Influence of permeability on concentration profiles (B) Effect of Grashof number on temperature profiles (C) Effect of Chemical Reaction on concentration profiles (D) Effect of Shimdth number on concentration profile.

5.4 Effect of Different Parameters

The increased Grashof number due to the small temperature difference and thermal expansion has been examined on temperature profile in Figure 4B. More generally, it determines the ratio of buoyancy forces to viscous force present in the fluid. Here, the temperature profile has decreased for PST case. The associated thickness of thermal boundary layer has dramatically decreased. Moreover, it is observed that the increment in Grashof number for temperature has decreased the temperature profile more rapidly for PST as compared to PHF case. In the case of PHF, the thermal boundary layer has been observed to be expanding when increasing the Grashof number. Although the temperature profile has decreased, it has decreased sharply for PST case when compared with PHF case.

The impact of the increase in the chemical reaction parameter is obtained on concentration profile for both cases, as seen in Figure 4C. The concentration profile has decreased for both PST and PHF cases under an incremental change in chemical reaction parameter. The concentration layer has shown a more rapid downfall for PST case as compared to PHF case. It is worth noting that a high magnetic force and radiation parameter do not impact the performance of chemical reaction parameter on the concentration profile for both discussed cases. Furthermore, the thickness of the concentration layer for both cases has increased.

Figure 4D describes the impact of Sherwood number on concentration profile for both cases. The concentration profile for both cases has decreased under the incremental influence of Sherwood number. The associated concentration boundary has increased for PHF case with the increase in Sherwood number. Whereas the concentration boundary layer has decreased for PST under an increase in Sherwood number.

5.5 Effect of Radiation

The change in radiation is observed on primary and secondary velocities as well as temperature profile in Figures 5A–C. The impact of radiation is illustrated in Figure 5A on primary velocity of profile for both cases. The motion of Casson fluid has decreased with the increment in radiation parameter. In PST case, the thickness of the momentum boundary has decreased. Additionally, the momentum boundary has contracted for PST case. In the PHF case, the primary velocity has decreased but it is quite significant to note here that the momentum boundary layer has expanded in PHF case. Moreover, momentum boundary has expanded more rapidly in PHF case as compared to PST case. Figure 5B shows the impact of radiation on the secondary velocity profile. It is interesting to observe that momentum boundary has contracted for both cases under high increment in radiation parameter. In both PST and PHF cases, the secondary velocity has decreased dramatically, consequently decreasing the thickness of momentum layer.

FIGURE 5

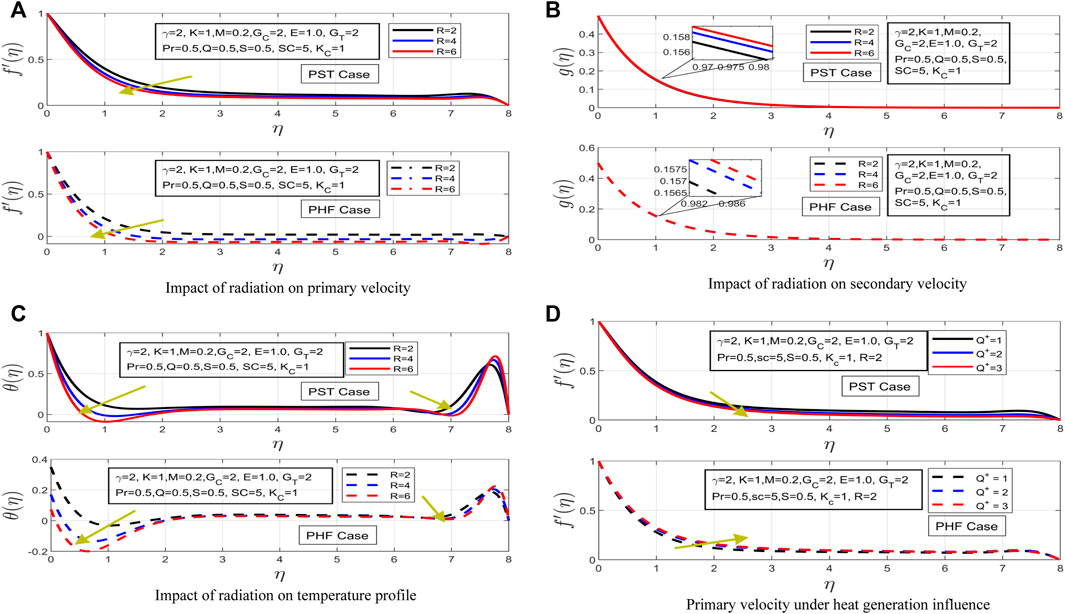
FIGURE 5. (A) Impact of radiation on primary velocity (B) Impact of radiation on secondary velocity (C) Impact of radiation on temperature profile (D) Primary velocity under heat generation influence.

Figure 5C demonstrates the influence of radiation on temperature profile. The temperature profile has been observed to be decreasing for examined cases. In PST case, the temperature profile has decreased. Furthermore, the thermal boundary has increased, and it is worth noting that the temperature profile for PST case towards the end experiences a bounce. This shows the thermal boundary expands and then satisfies the boundary conditions for said case. As the radiation parameter increases, the temperature profile has decreased for PHF. Maximum expansion in thermal boundary layer has been observed for PHF case when compared with PST case.

5.6 Effect of Heat Generation/Absorption

The impact of internal heat generation/absorption on Casson fluid flow system is determined in Figures 5D, 6A–C–C) on primary velocity and temperature profiles, respectively.

FIGURE 6

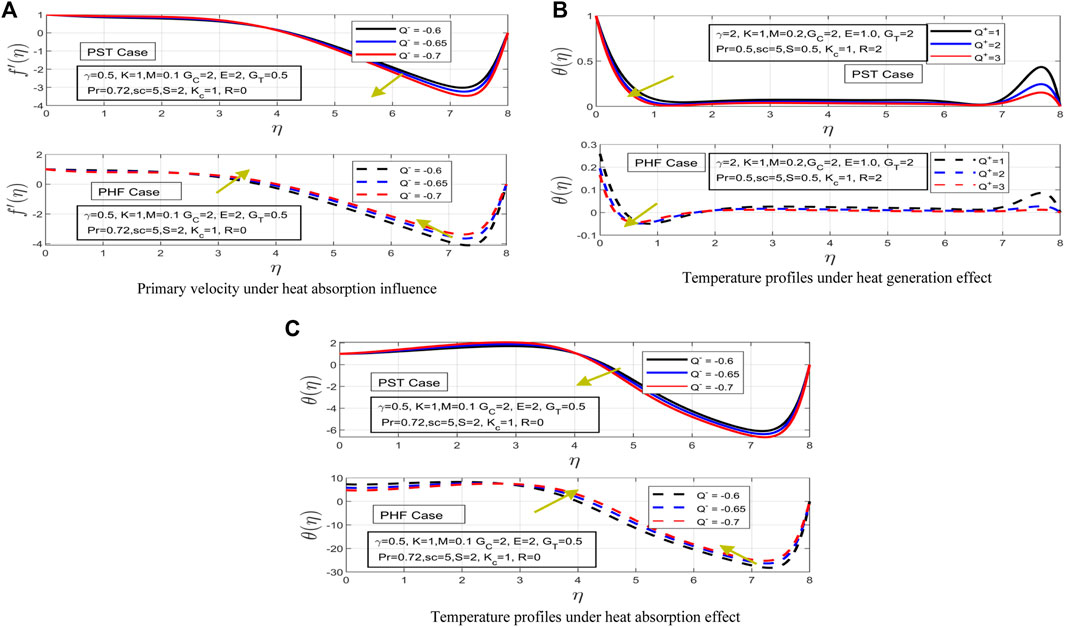
FIGURE 6. (A) Primary velocity under heat absorption influence (B) Temperature profiles under heat generation effect (C) Temperature profiles under heat absorption effect.

Figure 5D shows the impact of heat generation on primary velocity. The heat generation increment has decreased the primary velocity for both PST and PHF cases. In PST case, the momentum boundary has contracted and velocity profile has shown a more sharp decline. The velocity profile for PHF case has also decreased and severe contraction is observed in the momentum layer of Casson fluid. The impact of internal heat absorption parameter is examined on the primary velocity profile in Figure 6A. In PST case, the primary velocity has decreased smoothly, whereas a linear decreasing pattern has been observed in the case of PHF. The associated momentum layer has shown expansion for both cases under increments in heat absorption parameter. Moreover, in both heat generation and absorption, the PST and PHF cases have behaved in the exact same manner. The increment in heat generation/absorption parameter shows that, for PST, the primary velocity profile shows a decreasing behavior. While for PHF, the increase in heat generation/absorption parameter shows an increasing behavior for the primary velocity profile.

Figures 6B,C illustrate the impact of heat generation and absorption on the temperature profile for both PST and PHF cases, respectively. Figure 6B shows the influence of increment in heat generation parameter on temperature profile. It is interesting to observe that, with an increment in heat generation parameter, the temperature profile for PST case has decreased while it has decreased abruptly for PHF. Moreover, the PHF profile is associated with temperature condition at boundary, so as the result the temperature profile dramatically upsurged. Thermal boundary has expanded sharply for PHF case when compared with PST case (See Figure 6B). The impact of heat absorption parameter is depicted in Figure 6C, where the temperature profile has decreased and increased for PST and PHF cases, respectively, with an increment in heat absorption parameter.

6 Conclusion

In this study, magneto-hydrodynamic radiative Casson fluid flow incorporating internal heat generation/absorption, viscous dissipation, and first-order chemical reaction past the doubly permeable linearly stretching sheet is investigated. The achieved outcomes of different study parameters are discussed for primary and secondary velocity profiles as well as temperature and concentration profiles. The boundary value problem technique is utilized in Matlab and criterion of convergence is set at 10^–07. PST and PHF cases are examined comparatively under distinct parametric influence, and obtained outcomes are analyzed for both cases. The major results achieved are as follows:

6.1 Results for PST Case

1) The thickness of boundary layers has decreased with augmentation in Casson fluid parameter under fixed values of miscellaneous parameters.

2) Concentration profile decreases while thermal profile and motion in respective paths accelerates with increases in magnetic field.

3) Increment in permeability results in expansion of boundary layers of Casson fluid. Grashof number causes reduction in the thickness of thermal and concentration layers.

4) An expansion in concentration layer of Casson fluid is observed with augmentation in Schmidt number and chemical reaction parameter.

5) Increment in radiation produces an abrupt reduction in momentum boundary in secondary velocity profile and enhances the thickness of thermal layer.

6) Increment in heat generation/absorption expands thermal and momentum boundary layers.

7) Nusselt and Sherwood numbers have enhanced with augmentation in Prandtl number and chemical reaction, respectively. Reduced shear stress rates were obtained.

6.1 Results for PHF Case

1) Thermal boundary expands, while thickness of momentum layer has contracted with increases in Casson fluid parameter.

2) The horizontal motion of Casson fluid decreases smoothly, whereas the momentum boundary layer experiences an abrupt decline with high augmentation in magnetic field.

3) The increment in magnetic force increases temperature profile and expands associated thermal boundary of fluid.

4) The availability of free space increases the fluid motion in respective directions and enhances the thickness of thermal layer. Furthermore, concentration layer contracts.

5) Augmentation in Grashof number increases the thickness of thermal boundary layer. Chemical reaction and Schmidt number increment decrease the concentration profile.

6) The radiation impression expands temperature profiles while it decreases velocity profiles under fixed constraint.

7) The thickness of thermal boundary increases with increment in heat generation/absorption. The momentum layer experiences contraction with increases in heat generation/absorption.

8) Contrary to PST, Nusselt number decreases with varying study constraints and Sherwood number increases. The skin friction rates reduce to an all-time minimal.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptulization: AHa and AHu, writing original draft, Methodology and Formal Analysis: AHa, Formal Analysis: MA, FMA, and SG, validation and sources: JA and AMG, Validation and Funding Acquisition: SG, AMG, and FMA, Investigation: SE and AHa, Writing Review and Editing: AHa, Supervision: AHa and AHu.

Acknowledgments

The corresponding author would like to extend his appreciation to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R184), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia for funding this work.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rajakumar KVB, Balamurugan KS, Reddy MU, Murthy CVR. Radiation, dissipation and Dufour effects on MHD free convection Casson fluid flow through a vertical oscillatory porous plate with ion-slip current. Int J Heat Technol (2018) 36(2):494–508. doi:10.18280/ijht.360214

CrossRef Full Text | Google Scholar

2. Obalalu AM. Chemical entropy generation and second-order slip condition on hydrodynamic casson nanofluid flow embedded in a porous medium: A fast convergent method. J Egypt Math Soc (2022) 30(1):6–25. doi:10.1186/s42787-022-00140-3

CrossRef Full Text | Google Scholar

3. Khalid A, Khan I, Khan A, Shafie S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng Sci Technol Int J (2015) 18(3):309–17. doi:10.1016/j.jestch.2014.12.006

CrossRef Full Text | Google Scholar

4. Kodi R, Mopuri O, Sree S, Konduru V. Investigation of MHD Casson fluid flow past a vertical porous plate under the influence of thermal diffusion and chemical reaction. Heat Trans (2022) 51(1):377–94. doi:10.1002/htj.22311

CrossRef Full Text | Google Scholar

5. Goud BS, Kumar PP, Malga BS. Effect of Heat source on an unsteady MHD free convection flow of Casson fluid past a vertical oscillating plate in porous medium using finite element analysis. Partial Differential Equations Appl Maths (2020) 2:100015. doi:10.1016/j.padiff.2020.100015

CrossRef Full Text | Google Scholar

6. Verma VK, Mondal S. A brief review of numerical methods for heat and mass transfer of Casson fluids. Partial Differential Equations Appl Maths (2021) 3:100034. doi:10.1016/j.padiff.2021.100034

CrossRef Full Text | Google Scholar

7. Das M, Mahato R, Nandkeolyar R. Newtonian heating effect on unsteady hydromagnetic Casson fluid flow past a flat plate with heat and mass transfer. Alexandria Eng J (2015) 54(4):871–9. doi:10.1016/j.aej.2015.07.007

CrossRef Full Text | Google Scholar

8. Loganathan P, Deepa K. Electromagnetic and radiative Casson fluid flow over a permeable vertical Riga-plate. J Theor Appl Mech (2019) 57:987–98. doi:10.15632/jtam-pl/112421

CrossRef Full Text | Google Scholar

9. Raju CSK, Sandeep N, Sugunamma V, Babu MJ, Reddy JR. Heat and mass transfer in magnetohydrodynamic Casson fluid over an exponentially permeable stretching surface. Eng Sci Technol Int J (2016) 19(1):45–52. doi:10.1016/j.jestch.2015.05.010

CrossRef Full Text | Google Scholar

10. Jasmine Benazir A, Sivaraj R, Makinde OD. Unsteady magnetohydrodynamic Casson fluid flow over a vertical cone and flat plate with non-uniform heat source/sink. In: International journal of engineering research in africa, Vol. 21. Freienbach, Switzerland: Trans Tech Publications Ltd (2016). p. 69–83.

Google Scholar

11. Loganathan K, Mohana K, Mohanraj M, Sakthivel P, Rajan S. Impact of third-grade nanofluid flow across a convective surface in the presence of inclined Lorentz force: An approach to entropy optimization. J Therm Anal Calorim (2021) 144(5):1935–47. doi:10.1007/s10973-020-09751-3

CrossRef Full Text | Google Scholar

12. Loganathan K, Sivasankaran S, Bhuvaneswari M, Rajan S. Second-order slip, cross-diffusion and chemical reaction effects on magneto-convection of Oldroyd-B liquid using Cattaneo–Christov heat flux with convective heating. J Therm Anal Calorim (2019) 136(1):401–9. doi:10.1007/s10973-018-7912-5

CrossRef Full Text | Google Scholar

13. Madhukesh JK, Alhadhrami A, Naveen Kumar R, Punith Gowda RJ, Prasannakumara BC, Varun Kumar RS. Physical insights into the heat and mass transfer in Casson hybrid nanofluid flow induced by a Riga plate with thermophoretic particle deposition. Proc Inst Mech Eng E: J Process Mech Eng (2021) 2021:095440892110393. doi:10.1177/09544089211039305

CrossRef Full Text | Google Scholar

14. Gowda RJ, Rauf A, Naveen Kumar R, Prasannakumara BC, Shehzad SA. Slip flow of Casson–Maxwell nanofluid confined through stretchable disks. Indian J Phys (2021) 96:2041–9. doi:10.1007/s12648-021-02153-7

CrossRef Full Text | Google Scholar

15. Hussain A, Arshad M, Rehman A, Hassan A, Elagan SK, Ahmad H, et al. Three-dimensional water-based magneto-hydrodynamic rotating nanofluid flow over a linear extending sheet and heat transport analysis: A numerical approach. Energies (2021) 14(16):5133. doi:10.3390/en14165133

CrossRef Full Text | Google Scholar

16. Hussain A, Elkotb MA, Arshad M, Rehman A, Sooppy Nisar K, Hassan A, et al. Computational investigation of the combined impact of nonlinear radiation and magnetic field on three-dimensional rotational nanofluid flow across a stretchy surface. Processes (2021) 9(8):1453. doi:10.3390/pr9081453

CrossRef Full Text | Google Scholar

17. Hussain A, Arshad M, Hassan A, Rehman A, Ahmad H, Baili J, et al. Heat transport investigation of engine oil based rotating nanomaterial liquid flow in the existence of partial slip effect. Case Stud Therm Eng (2021) 28:101500. doi:10.1016/j.csite.2021.101500

CrossRef Full Text | Google Scholar

18. Hussain A, Arshad M, Rehman A, Hassan A, Elagan SK, Alshehri NA. Heat transmission of engine-oil-based rotating nanofluids flow with influence of partial slip condition: A computational model. Energies (2021) 14(13):3859. doi:10.3390/en14133859

CrossRef Full Text | Google Scholar

19. Hussain A, Alshbool MH, Abdussattar A, Rehman A, Ahmad H, Nofal TA, et al. A computational model for hybrid nanofluid flow on a rotating surface in the existence of convective condition. Case Stud Therm Eng (2021) 26:101089. doi:10.1016/j.csite.2021.101089

CrossRef Full Text | Google Scholar

20. Arshad M, Hussain A, Hassan A, Khan I, Badran M, Mehrez S, et al. Heat transfer analysis of nanostructured material flow over an exponentially stretching surface: A comparative study. Nanomaterials (2022) 12(7):1204. doi:10.3390/nano12071204

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Arshad M, Hussain A, Shah SAGA, Wróblewski P, Elkotb MA, Abdelmohimen MA, et al. Thermal energy investigation of magneto-hydrodynamic nano-material liquid flow over a stretching sheet: Comparison of single and composite particles. Alexandria Eng J (2022) 61(12):10453–62. doi:10.1016/j.aej.2022.03.069

CrossRef Full Text | Google Scholar

22. Arshad M, Hussain A, Hassan A, Haider Q, Ibrahim AH, Alqurashi MS, et al. Thermophoresis and brownian effect for chemically reacting magneto-hydrodynamic nanofluid flow across an exponentially stretching sheet. Energies (2021) 15(1):143. doi:10.3390/en15010143

CrossRef Full Text | Google Scholar

23. Lund LA, Omar Z, Khan I, Baleanu D, Nisar KS. Dual similarity solutions of MHD stagnation point flow of casson fluid with effect of thermal radiation and viscous dissipation: Stability analysis. Sci Rep (2020) 10(1):15405–13. doi:10.1038/s41598-020-72266-2

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Reddy GJ, Raju RS, Rao JA. Influence of viscous dissipation on unsteady MHD natural convective flow of Casson fluid over an oscillating vertical plate via FEM. Ain Shams Eng J (2018) 9(4):1907–15. doi:10.1016/j.asej.2016.10.012

CrossRef Full Text | Google Scholar

25. Pop I, Sheremet M. Free convection in a square cavity filled with a Casson fluid under the effects of thermal radiation and viscous dissipation. Int J Numer Methods Heat Fluid Flow (2017) 27:2318–32. doi:10.1108/hff-09-2016-0352

CrossRef Full Text | Google Scholar

26. Qasim M, Noreen S. Heat transfer in the boundary layer flow of a Casson fluid over a permeable shrinking sheet with viscous dissipation. Eur Phys J Plus (2014) 129(1):7–8. doi:10.1140/epjp/i2014-14007-5

CrossRef Full Text | Google Scholar

27. Mahanthesh B, Gireesha BJ. Scrutinization of thermal radiation, viscous dissipation and Joule heating effects on Marangoni convective two-phase flow of Casson fluid with fluid-particle suspension. Results Phys (2018) 8:869–78. doi:10.1016/j.rinp.2018.01.023

CrossRef Full Text | Google Scholar

28. Kotha G, Chamkha AJ, P MS. Entropy generation on convectively heated surface of casson fluid with viscous dissipation. Phys Scr (2020) 95(11):115203. doi:10.1088/1402-4896/abbaf2

CrossRef Full Text | Google Scholar

29. Medikare M, Joga S, Chidem KK. MHD stagnation point flow of a Casson fluid over a nonlinearly stretching sheet with viscous dissipation. Am J Comput Maths (2016) 6(01):37–48. doi:10.4236/ajcm.2016.61005

CrossRef Full Text | Google Scholar

30. Khan SI, Khan U, Ahmed N, Jan SU, Waheed A, Mohyud-Din ST. Effects of viscous dissipation and convective boundary conditions on Blasius and Sakiadis problems for Casson fluid. Natl Acad Sci Lett (2015) 38(3):247–50. doi:10.1007/s40009-014-0331-7

CrossRef Full Text | Google Scholar

31. Hayat T, Khan MI, Waqas M, Yasmeen T, Alsaedi A. Viscous dissipation effect in flow of magnetonanofluid with variable properties. J Mol Liquids (2016) 222:47–54. doi:10.1016/j.molliq.2016.06.096

CrossRef Full Text | Google Scholar

32. Yusof NS, Soid SK, Illias MR, Abd Aziz AS, Nasir NAAM. Radiative boundary layer flow of casson fluid over an exponentially permeable slippery Riga plate with viscous dissipation. J Adv Res Appl Sci Eng Technol (2020) 21(1):41–51. doi:10.37934/araset.21.1.4151

CrossRef Full Text | Google Scholar

33. Loganathan K, Rajan S. An entropy approach of Williamson nanofluid flow with Joule heating and zero nanoparticle mass flux. J Therm Anal Calorim (2020) 141(6):2599–612. doi:10.1007/s10973-020-09414-3

CrossRef Full Text | Google Scholar

34. Loganathan K, Muhiuddin G, Alanazi AM, Alshammari FS, Alqurashi BM, Rajan S. Entropy optimization of third-grade nanofluid slip flow embedded in a porous sheet with zero mass flux and a non-Fourier heat flux model. Front Phys (2020) 8:250. doi:10.3389/fphy.2020.00250

CrossRef Full Text | Google Scholar

35. Naveen Kumar R, Suresha S, Gowda RJ, Megalamani SB, Prasannakumara BC. Exploring the impact of magnetic dipole on the radiative nanofluid flow over a stretching sheet by means of KKL model. Pramana - J Phys (2021) 95(4):180–9. doi:10.1007/s12043-021-02212-y

CrossRef Full Text | Google Scholar

36. Wang Y, Kumar RN, Gouadria S, Helmi MM, Gowda RP, El-Zahar ER, et al. A three-dimensional flow of an Oldroyd-B liquid with magnetic field and radiation effects: An application of thermophoretic particle deposition. Int Commun Heat Mass Transfer (2022) 134:106007. doi:10.1016/j.icheatmasstransfer.2022.106007

CrossRef Full Text | Google Scholar

37. Punith Gowda RJ, Naveen Kumar R, Jyothi AM, Prasannakumara BC, Sarris IE. Impact of binary chemical reaction and activation energy on heat and mass transfer of marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes (2021) 9(4):702. doi:10.3390/pr9040702

CrossRef Full Text | Google Scholar

38. Varun Kumar RS, Gunderi Dhananjaya P, Naveen Kumar R, Punith Gowda RJ, Prasannakumara BC. Modeling and theoretical investigation on Casson nanofluid flow over a curved stretching surface with the influence of magnetic field and chemical reaction. Int J Comput Methods Eng Sci Mech (2022) 23(1):12–9. doi:10.1080/15502287.2021.1900451

CrossRef Full Text | Google Scholar

39. Punith Gowda RJ, Naveen Kumar R, Jyothi AM, Prasannakumara BC, Nisar KS. KKL correlation for simulation of nanofluid flow over a stretching sheet considering magnetic dipole and chemical reaction. ZAMM - J Appl Maths Mech/Z Angew Mathematik Mechanik (2021) 101(11):e202000372. doi:10.1002/zamm.202000372

CrossRef Full Text | Google Scholar

40. Manjunatha PT, Chamkha AJ, Punith Gowda RJ, Naveen Kumar R, Prasannakumara BC, Naik SM. Significance of stefan blowing and convective heat transfer in nanofluid flow over a curved stretching sheet with chemical reaction. j nanofluids (2021) 10(2):285–91. doi:10.1166/jon.2021.1786

CrossRef Full Text | Google Scholar

41. Hussain A, Hassan A, Mdallal QA, Ahmad H, Sherif ESM, Rehman A, et al. Comsolic solution of an elliptic cylindrical compressible fluid flow. Sci Rep (2021) 11(1):20030–12. doi:10.1038/s41598-021-99138-7

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Hussain A, Hassan A, Al Mdallal Q, Ahmad H, Rehman A, Altanji M, et al. Heat transportation enrichment and elliptic cylindrical solution of time-dependent flow. Case Stud Therm Eng (2021) 27:101248. doi:10.1016/j.csite.2021.101248

CrossRef Full Text | Google Scholar

43. Hussain A, Hassan A, Al Mdallal Q, Ahmad H, Rehman A, Altanji M, et al. Heat transport investigation of magneto-hydrodynamics (SWCNT-MWCNT) hybrid nanofluid under the thermal radiation regime. Case Stud Therm Eng (2021) 27:101244. doi:10.1016/j.csite.2021.101244

CrossRef Full Text | Google Scholar

44. Hussain A, Hassan A, Arshad M, Rehman A, Matoog RT, Abdeljawad T. Numerical simulation and thermal enhancement of multi-based nanofluid over an embrittled cone. Case Stud Therm Eng (2021) 28:101614. doi:10.1016/j.csite.2021.101614

CrossRef Full Text | Google Scholar

45. Hussain A, Haider Q, Rehman A, Ahmad H, Baili J, Aljahdaly NH, et al. A thermal conductivity model for hybrid heat and mass transfer investigation of single and multi-wall carbon nano-tubes flow induced by a spinning body. Case Stud Therm Eng (2021) 28:101449. doi:10.1016/j.csite.2021.101449

CrossRef Full Text | Google Scholar

46. Hussain A, Haider Q, Rehman A, Abdussattar A, Y Malik M. A new heat dissipation model and convective two-phase nanofluid in brittle medium flow over a cone. Math Probl Eng (2021) 2021:1–11. doi:10.1155/2021/6688747

CrossRef Full Text | Google Scholar

47. Hussain A, Haider Q, Rehman A, Malik MY, Nadeem S, Hussain S. Heat transport improvement and three-dimensional rotating cone flow of hybrid-based nanofluid. Math Probl Eng (2021) 2021:11. doi:10.1155/2021/6633468

CrossRef Full Text | Google Scholar

48. Hassan A, Hussain A, Arshad M, Haider Q, Althobaiti A, Elagan SK, Abdelmohimen MA. Heat transport investigation of hybrid nanofluid (Ag-CuO) porous medium flow: Under magnetic field and Rosseland radiation. Ain Shams Eng J (2022) 13(5):101667.

CrossRef Full Text | Google Scholar

49. Hassan A, Hussain A, Arshad M, Alanazi MM, Zahran HY. Numerical and thermal investigation of magneto-hydrodynamic hybrid nanoparticles (swcnt-Ag) under Rosseland radiation: A prescribed wall temperature case. Nanomaterials (2022) 12(6):891. doi:10.3390/nano12060891

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Shehzad SA, Hayat T, Qasim M, Asghar S. Effects of mass transfer on MHD flow of Casson fluid with chemical reaction and suction. Braz J Chem Eng (2013) 30:187–95. doi:10.1590/s0104-66322013000100020

CrossRef Full Text | Google Scholar

51. Arthur EM, Seini IY, Bortteir LB. Analysis of Casson fluid flow over a vertical porous surface with chemical reaction in the presence of magnetic field. J Appl Maths Phys (2015) 03(06):713–23. doi:10.4236/jamp.2015.36085

CrossRef Full Text | Google Scholar

52. Khan MI, Waqas M, Hayat T, Alsaedi A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J Colloid Interf Sci (2017) 498:85–90. doi:10.1016/j.jcis.2017.03.024

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Ramzan M, Bilal M, Chung JD. Numerical simulation of magnetohydrodynamic radiative flow of Casson nanofluid with chemical reaction past a porous media. J Comput Theor Nanosci (2017) 14(12):5788–96. doi:10.1166/jctn.2017.7013

CrossRef Full Text | Google Scholar

54. Reddy PBA. Magnetohydrodynamic flow of a Casson fluid over an exponentially inclined permeable stretching surface with thermal radiation and chemical reaction. Ain Shams Eng J (2016) 7(2):593–602. doi:10.1016/j.asej.2015.12.010

CrossRef Full Text | Google Scholar

55. Bejawada SG, Reddy YD, Jamshed W, Nisar KS, Alharbi AN, Chouikh R. Radiation effect on MHD Casson fluid flow over an inclined non-linear surface with chemical reaction in a Forchheimer porous medium. Alexandria Eng J (2022) 61(10):8207–20. doi:10.1016/j.aej.2022.01.043

CrossRef Full Text | Google Scholar

56. Ramakrishna SB, Nl R, Kumar Thavada S. Effects of chemical reaction, Soret and Lorentz force on casson fluid flow past an exponentially accelerated vertical plate: A comprehensive analysis. Heat Trans (2022) 51(2):2237–57. doi:10.1002/htj.22398

CrossRef Full Text | Google Scholar

57. Khan KA, Jamil F, Ali J, Khan I, Ahmed N, Andualem M, et al. Analytical simulation of heat and mass transmission in casson fluid flow across a stretching surface. Math Probl Eng (2022) 2022.

CrossRef Full Text | Google Scholar

58. Hayat T, Khan SA, Momani S. Finite difference analysis for entropy optimized flow of Casson fluid with thermo diffusion and diffusion-thermo effects. Int J Hydrogen Energ (2022) 47:8048–59. doi:10.1016/j.ijhydene.2021.12.093

CrossRef Full Text | Google Scholar

59. Khan Z, Rasheed HU, Khan I, Abu-Zinadah H, Aldahlan MA. Mathematical simulation of casson MHD flow through a permeable moving wedge with nonlinear chemical reaction and nonlinear thermal radiation. Materials (2022) 15(3):747. doi:10.3390/ma15030747

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Loganathan K, Alessa N, Tamilvanan K, Alshammari FS. Significances of Darcy–Forchheimer porous medium in third-grade nanofluid flow with entropy features. Eur Phys J Spec Top (2021) 230(5):1293–305. doi:10.1140/epjs/s11734-021-00056-6

CrossRef Full Text | Google Scholar

61. Loganathan K, Alessa N, Namgyel N, Karthik TS. MHD flow of thermally radiative Maxwell fluid past a heated stretching sheet with Cattaneo–Christov dual diffusion. J Maths (2021) 2021:1–10. doi:10.1155/2021/5562667

CrossRef Full Text | Google Scholar

62. Karthik TS, Loganathan K, Shankar AN, Carmichael MJ, Mohan A, Kaabar MK, et al. Zero and nonzero mass flux effects of bioconvective viscoelastic nanofluid over a 3D riga surface with the swimming of gyrotactic microorganisms. Adv Math Phys (2021) 2021:1–13. doi:10.1155/2021/9914134

CrossRef Full Text | Google Scholar

63. Loganathan K, Alessa N, Kayikci S. Heat transfer analysis of 3-D viscoelastic nanofluid flow over a convectively heated porous riga plate with Cattaneo-Christov double flux. Front Phys (2021) 9. doi:10.3389/fphy.2021.641645

CrossRef Full Text | Google Scholar

64. Gireesha BJ, Mahanthesh B, Rashidi MM. MHD boundary layer heat and mass transfer of a chemically reacting Casson fluid over a permeable stretching surface with non-uniform heat source/ sink. Int J Ind Maths (2015) 7.

Google Scholar

65. Gowda RP, Kumar RN, Prasannakumara BC, Nagaraja B, Gireesha BJ. Exploring magnetic dipole contribution on ferromagnetic nanofluid flow over a stretching sheet: An application of Stefan blowing. J Mol Liquids (2021) 335:116215. doi:10.1016/j.molliq.2021.116215

CrossRef Full Text | Google Scholar

66. Gowda RP, Al-Mubaddel FS, Kumar RN, Prasannakumara BC, Issakhov A, Rahimi-Gorji M, et al. Computational modelling of nanofluid flow over a curved stretching sheet using Koo–Kleinstreuer and Li (KKL) correlation and modified Fourier heat flux model. Chaos, Solitons & Fractals (2021) 145:110774. doi:10.1016/j.chaos.2021.110774

CrossRef Full Text | Google Scholar

67. Sarada K, Gowda RJP, Sarris IE, Kumar RN, Prasannakumara BC. Effect of magnetohydrodynamics on heat transfer behaviour of a non-Newtonian fluid flow over a stretching sheet under local thermal non-equilibrium condition. Fluids (2021) 6(8):264. doi:10.3390/fluids6080264

CrossRef Full Text | Google Scholar

Nomenclature

$f,g$ Primary and secondary velocity profile in dimensionless form

$\theta ,\varphi$ Temperature and concentration profile in dimensionless form

$u,v$ Velocities components in respective direction (m/s)

$v_f$ Casson fluid’s kinematic viscosity

$\gamma$ Casson fluid parameter

${\rho }_f,{\sigma }_f$ Density and electric conductivity of Casson fluid (kg/m³, W/(m∗K))

${\left(\rho c_p\right)}_f$ Volumetric heat capacity (J/kg∗K)

$B_{\mathrm{0}}$ Magnetic field

$q_r$ Rosseland Radiation Relation

$Rd$ Radiation parameter

$U_W$ Stretching velocity parameter

$PST$ Prescribed Surface temperature

$\mathit{Pr}$ Prandtl number

$G_r,G_C$ Grashof number for temperature and concentration, respectively

$K_C$ Dimensionless Reaction parameter

$Sc$ Schmidt or Sherwood number

${\mu }_B$ Plastic dynamic viscosity

$P_y$ Fluid yield stress

$ϵ=e_{ij}\ast e_{ij}$ Self product of deformation rate

${ϵ}_c$ Critical value of component of strain tensor with itself

$K_{\mathrm{0}}$ Permeability of free space in dimensional form

$\beta ,{\beta }^{\ast }$ Thermal expansion due to temperature and concentration, respectively

$T,C$ Temperature $\left(K\right)$ and Concentration profile

$\eta$ Similarity variable

$T_{\infty },C_{\infty }$ Ambient temperature $\left(K\right)$ and Concentration, respectively

$D_m$ Mass Diffusivity

$V_W$ Suction/Blowing parameter

$PHF$ Prescribed heat flux

$M,K$ Dimensionless Magnetic and Permeability parameter

$Q_{\mathrm{0}},Q$ Dimensional and dimensionless Internal Heat generation/Absorption parameter, respectively

$S$ Suction/Blowing ratio

$E_C$ Eckert number