
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 15 June 2022
Sec. Condensed Matter Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.919784
This article is part of the Research TopicNematicity in Iron-Based SuperconductorsView all 10 articles
We analyze theoretically the magnetic anisotropy in the nematic phase of FeSe by computing the spin and the orbital susceptibilities from the microscopic multiorbital model. In particular, we take into account both the xz/yz and the recently proposed non-local xy nematic ordering and show that the latter one could play a crucial role in reproducing the experimentally-measured temperature dependence of the magnetic anisotropy. This provides a direct fingerprint of the different nematic scenarios on the magnetic properties of FeSe.
Iron-based superconductors offer the opportunity to explore the interplay between electronic nematicity, magnetism and superconductivity. While the broad studies on cuprates already provide insights into the competition between magnetism and superconductivity [1, 2], the role of the still enigmatic nematic state is of particular interest. Since anisotropy arises in crystal structure, orbital and spin degrees of freedom, it is intricate to decipher the underlying mechanism [3, 4]. In most of the iron pnictides the structural transition precedes or coincides with the magnetic transition at TN, below which long-range antiferromagnetic order sets in [5], supporting the idea that nematicity (spin nematicity) is driven by magnetic interactions [6]. Note that the spin-nematic scenario can also lead to an effective orbital ordering once one takes the orbital content of the spin fluctuations within the so-called orbital-selective spin-fluctuation scenario into account [7–9].
Among various iron-based superconductors, FeSe with a simple crystal structure of the stacked FeSe layers has a rather unique behavior due to the presence of a marked nematic (structural) transition at TS = 90 K and a transition to superconductivity below Tc = 9 K, while magnetic order is absent [10–15]. Consequently, orbital degrees of freedom have also been proposed as the underlying mechanism for nematic order in FeSe [16–22]. The small lattice distortion contrasts with strong in-plane anisotropy of resistivity, magnetic susceptibility, electronic structure and orbital and momentum structure of the superconducting gap [23–34]. The phase diagram of FeSe is rich and sensitive to the application of hydrostatic pressure or chemical substitution [35–38]. Furthermore, various exotic superconducting states have been recently reported in this compound [15].
Recent experiments have overcame the intricacies of the formation of orthorombic domains in FeSe by applying uniaxial strain [39–43]. Using this technique, the in-plane anisotropy of resistivity, uniform magnetic susceptibility and the Knight shift have been found to exhibit the opposite sign of the anisotropy as compared to iron-pnictides [24, 25, 44–46]. Moreover, carefully avoiding eddy-current heating, a slight suppression of the Knight shift in the superconducting state has been measured recently, while superconductivity and nematicity seem to coexist [47–49]. This agrees with direct magnetization measurements [25].
From the experimental point of view the systematic investigation of the band-structure of FeSe by means of ARPES and quantum oscillations revealed a sizeable deformation of the Fermi surface, that can be described by the interplay of the dxz, dyz and dxy orbitals, their spin-orbit coupling and the nematic order [50–53]. Concerning the nematic order there is general understanding about the existence of a xz/yz splitting that changes sign in going from the Brillouin-zone center to momenta around QX = (π, 0) and QY = (0, π) points of the 1-Fe-unit cell Brillouin Zone (BZ) (both folded onto the M-point of the folded BZ with 2-Fe ions per unit cell). This can be represented by a nematic order parameter
This possibility to have a non-local nematic ordering of the dxy states was previously outlined in the literature [60–62] but assumed to be small in the models having on-site interaction terms only. However, an inclusion of the nearest-neighbor interaction terms (such as nearest neighbor exchange or Coulomb interaction) would change this picture. Note, recent NMR [63] and ARPES [41, 42] have also suggested that the dxy orbital may be strongly affected by the onset of the nematic state.
In this manuscript we investigate the consequences of the non-local dxy-nematic scenario for the magnetic susceptibility taking into account spin and orbital contributions. We analyze its temperature and doping dependencies and compare the results to the available experiments. We show that the non-local nematicity is responsible for the non-monotonic temperature dependence of the susceptibility and predict how it evolves with doping in FeSe1−xSx. Finally we studied how the magnetic anisotropy is affected in the superconducting state.
We adopt the low energy model for FeSe, previously employed in Ref. [56], and fitted to the available ARPES experiments [40, 45, 64]. It is based on the generalized low-energy effective model for iron-based superconductors, formulated by Cvetkovic and Vafek [65].
In particular, to describe the tetragonal state of FeSe, we start by describing the low-energy states near the corresponding symmetry points of the BZ. In particular, near the Γ point of the BZ there are two Fermi surface pockets formed by the hybridized xz- and yz-orbitals. For completeness we also take the xy-orbital band into account which is located approximately 50 meV below the Fermi level [64]. Its inclusion allows to treat correctly the spin-orbit coupling (SOC) within the t2g manifold. The states can be described by the spinor
where
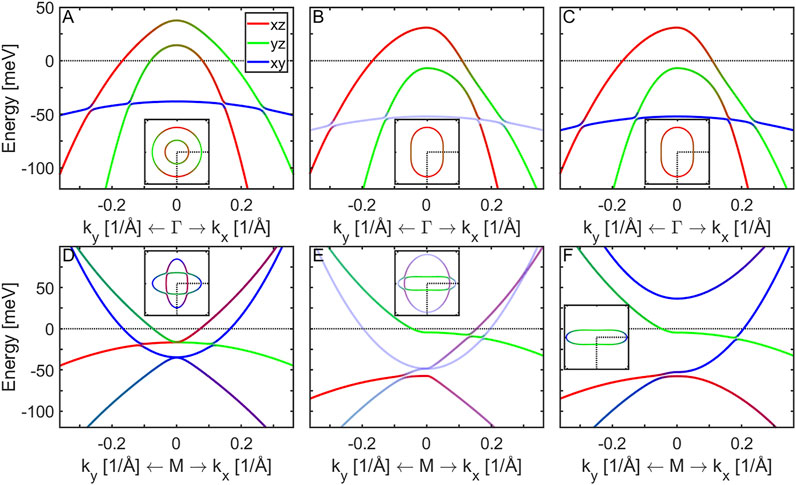
FIGURE 1. The band structure of the 2-Fe Brillouin zone around the Γ and the M point is presented comparing the tetragonal state and scenarios A and B for the nematic state in FeSe as described in the text. Panels (A)–(C) show the energy dispersion near the Γ point in the tetragonal state (A) and two nematic states without (Scenario A) (B) and with (C) non-local dxy nematicity (Scenario B). Panels (D–F) display the corresponding band structure near the M point. Red, green and blue colors illustrate the orbital weights of the dxz, dyz and dxy Fe-orbitals, respectively. The insets show the corresponding Fermi surface and demonstrate the cuts performed. Shading according to the dxy orbital weight in panels (B) and (E) reflects the Z-factors used in [44].
To describe the electronic states near the M-point of the 2-Fe unit cell we introduce the spinors
and the elements are
The orbitals are coupled by the in-plane SOC λ2
The band dispersion for the tetragonal state near the M point is shown in the bottom panel of the Figure 1D. Note the value of SOC is taken different if the orbitals originate from the same sublattice in the 1-Fe unit cell, λ1 = 23 meV or from the two different sublattices, λ2 = 4 meV [66]. This agrees with the experimental ARPES observation, which measured different values of the SOC near different symmetry points of the BZ [67, 68].
To describe the nematic state in FeSe, which forms below the TS = 90 K, we add the nematic order to the Hamiltonian in a phenomenological fashion. We assumed the nematic order parameters follow a mean-field temperature dependence
In particular, the xz/yz nematic order parameter near the Γ point can be described as:
For a given value of the SOC λ1, adding a nematic order parameter yields a Lifshitz transition such that one of the Fermi surface pockets near the Γ point sinks below the Fermi level as shown in panels 1B and 1C for Φh(10 K) = 15 meV. Near the M point the xz/yz nematic order has opposite sign to Φh and we also include an additional non-local dxy-nematic order [56]:
In the conventional scenario of nematicity (Scenario A), only Φe(10 K) = −26 meV is included and the resulting band structure near the M point is illustrated in Figure 1E. Observe two electron pockets at the M point, which exist for all temperatures. To connect Scenario A with experimental ARPES results in the nematic state, which do not observe the larger electron pocket, orbital-selective quasiparticle weights are introduced in various works [26, 30, 44, 54, 69], see also for a recent review Ref. [70]. Within this scenario the quasiparticle weight of the dxy orbital is claimed to be much smaller than that of the dyz/dxz orbitals. This would lead to a suppression of the quasiparticle weight of the dxy dominated bands and especially of the outer electron pocket at M point, making dxy- rbital states invisible in the ARPES experiment. This is illustrated in panels 1B and 1E by orbital-selective shading. The idea of orbital-selective spectral weights is motivated also by the previous results of the dynamical mean-field theory calculations [71]. This scenario was claimed to be in agreement with STM measurements of the electronic structure [69], the superconducting gap properties [30], and the magnetic susceptibility measured by inelastic neutron scattering [26]. A problem of this scenario is that both in the tetragonal and the nematic state of FeSe, bands of dxy orbital character have been identified around the M point [28]. Although dxy orbital appears indeed to exhibit a larger effective mass renormalization than the other two orbitals, it is not sufficiently large to mask dxy spectral weight completely in the ARPES experiments [64].
Within the Scenario B one introduces the non-local nematic order within the xy-orbital: Φxy(10 K) = 45 meV and Δϵxy(10 K) = 40 meV and the resulting band structure is shown in Figure 1F. As the band structure evolves from the tetragonal to the nematic state, an additional Lifshitz transition occurs around 70 K, leaving a single electron Fermi surface pocket at 10 K. The Scenario B assumes that the nematic ordering near the M point does not cause a minor perturbation of the electronic structure, but can lift an entire electron pocket away from the Fermi level. Its consequences for various experiments were reviewed in Ref. [59] and present an alternative description of the nematicity in FeSe. The chemical potential μ is renormalized to fulfill the Luttinger theorem and is set to zero at 10 K [56].
It was argued in the past that within both the Scenario A and the Scenario B the superconducting order parameter and its angular dependence on the Fermi surface pockets can be equally well described within a microscopic description [54, 56]. This indicates that superconductivity just adopts the existing electronic structure in the nematic state without further significant feedback on the nematicity. So within Scenario B we use the microscopic description of Ref. [56]. In particular, below the superconducting transition at Tc = 8 K, we additionally include superconducting gaps in the dxz and dyz orbitals and use previously found values from a microscopic calculations describing an extended s-wave gap structure [56]. The values are obtained solving the gap equations at T = 0 K focusing on the bands crossing the Fermi surface. Possible dxy contributions to the pairing interaction are neglected. To describe the temperature dependence we assume a typical BCS form
with
with
Within random phase approximation (RPA) analysis of the magnetic susceptibility χ [72–74] the bare part of the susceptibility is given by a combination of normal and anomalous contributions (GG and FF-terms)
where G and F denote the single-particle normal and anomalous Green’s functions and the FF-term vanishes above Tc. We use the short hand notations k = (k, iωn) and η = (μ, σ) denoting orbital and spin degrees of freedom. The sum of Matsubara frequencies is carried out analytically and yields a Lindhard-type expression for the bare susceptibilities. Further details can be found in the Supplementary Material S1.
Within RPA we include the local interactions from a Hubbard-Hund Hamiltonian
In what follows we set the intraorbital Coulomb repulsion interaction U = 1 eV. For the interorbital Coulomb repulsion U′, the residual Hund interaction J and the pair hopping J′ terms we use the standard spin-rotational relations U′ = U − 2J and J = J′ and set J/U = 1/6 similar to previous studies [26, 44].
The RPA treatment yields a Dyson type equation with a symbolic solution
The interaction matrix
The magnetic susceptibility tensor component χab results from the contraction of the external spin and orbital indices of the solution with the a-th and b-th component of the operator. We can separate the spin χspin, the orbital χorb and mixed χmix components of the susceptibility. In this manuscript we focus on the static limit of uniform susceptibility χab(q → 0) and further details of the calculation can be found in the Supplementary Material S1.
In the following we present the results for the magnetic susceptibility χ(q → 0) and its anisotropy following Scenario B. Note that within Scenario A the behavior of the magnetic susceptibility was considered in Ref. [44]. One of the main findings of this study was that in order to reproduce the correct sign of the magnetic anisotropy at low temperatures, i.e. χyy < χxx, the quasiparticle weight of various orbitals has to fulfil Zxy < Zxz < Zyz. Within Scenario B this assumption is not necessary as the dxy orbital is weakly present at the Fermi level and this should yield in principle the right sign of the magnetic anisotropy. We show in the Supplementary that further factors can affect the signs of the anisotropy as well and the situation depends on the details of the electronic structure in both Scenarios. In addition, in our case we find the dominance of the spin component of the susceptibility χmix < χorb < χspin, which is a consequence of the low-energy model we used. Moreover, we find that RPA primarily amplifies the spin contribution. Including the whole 3d state manifold would increase the temperature-independent orbital contribution to the susceptibility, which can be treated as a constant.
Nevertheless, one of the interesting questions is how to distinguish between both scenarios and whether one is able to identify an additional Lifshitz transition associated with the removal of the second electron pocket from the Fermi level at the M point both theoretically and experimentally. To do so we calculate the temperature dependence of the static uniform susceptibility and compare our results with experimental data of Ref. [25] where the standard notations x∥a, y∥b and z∥c are used.
The temperature dependence of the static uniform susceptibility is shown in Figure 2A. For comparison we also display the experimental data from Ref. [25] in the inset. Above the nematic transition the magnetic anisotropy is governed by the spin-orbit coupling and shows an easy-plane anisotropy χxx = χyy > χzz. Below TS, one observes two characteristic features. First we find that χxx becomes progressively larger than χyy as a result of the nematic order and the splitting between them increases continuously upon decreasing temperature. At the same time all three components of the magnetic susceptibility show a non-monotonic temperature dependence characterized by a rapid decrease below TS and a plateau-like behavior, which starts around 60 K. Both, a continuous increase of the anisotropy upon lowering temperature and the non-monotonic temperature dependence of the susceptibilities agree well with the available experimental data of Ref. [75], shown in the inset.
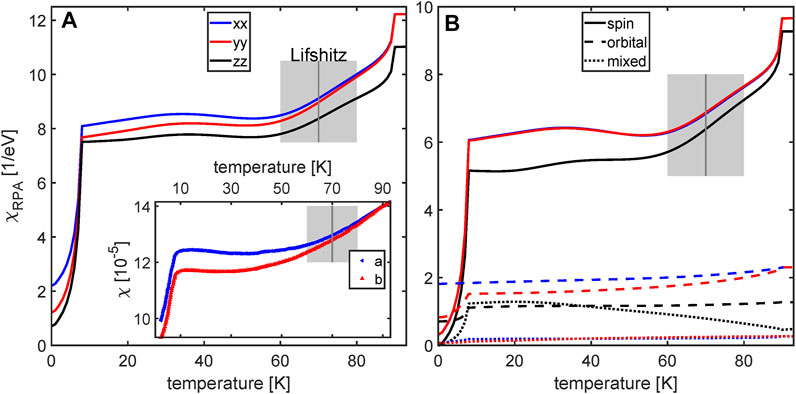
FIGURE 2. Calculated temperature dependence of the magnetic susceptibility χ(q → 0) calculated with an RPA approach. In (A) the total diagonal components χxx, χyy and χzz of the susceptibility calculated for scenario B are presented as blue, red and black curves, respectively. The corresponding spin, orbital and mixed contributions to the different components are shown in (B) as solid, dashed and dotted curves, respectively. The inset in (A) shows the experimental data extracted from [25] for comparison. The markers do not represent data points from the experiment. The gray boxes illustrate the decrease in susceptibility due to the Lifshitz transition of the Y-band. The boxes are centered around the Lifshitz transition temperature (dark gray line). Notice that the blue solid curve for the
To understand better the origin of these effects we show in Figure 2B the spin, the orbital, and the mixed susceptibilities. Note, the spin component of the magnetic susceptibility is the largest in magnitude and its non-monotonic temperature dependence is connected to the Lifshitz transition within Scenario B. In this scenario, the non-local dxy nematic order parameter induces the shift of the larger electron pocket away from the Fermi level, which occurs in the temperature interval 60 K
We also note that in the iron pnictides, where nematicity coexists with the antiferromagnetic order an in-plane anisotropy of the magnetic susceptibility would give a corresponding feedback on the magnetic order parameter and also enhance the anisotropy of the spin susceptibility below the magnetic transition temperature, see for example Ref. [76]. However, as the magnetic transition in FeSe appears only upon applying pressure and bearing in mind that the in-plane anisotropy we found is only few percent of the total magnitude of the spin susceptibility, the anisotropy of the orbital susceptibility will be the main origin of the magnetic anisotropy in FeSe.
To complete the analysis we also computed the change of the uniform superconductivity in the superconducting state. Due to the spin singlet superconducting order parameter in FeSe we see a sharp drop in the uniform susceptibility upon entering the superconducting state, see Figure 2A. This is due to the strong reduction of the spin component of the susceptibility, as evident from Figure 2B. Note the small admixture of the spin-triplet component of the superconducting gap due to the finite spin-orbit coupling does not affect much the magnetic anisotropy in the spin part. The residual contribution to the magnetic susceptibility stems largely from the orbital part of the susceptibility and corresponds to inter-orbital contributions, which is slightly affected by the onset of superconductivity. The decrease in
To make a qualitative prediction on the evolution of the uniform susceptibility and its in-plane magnetic anisotropy in Figure 3, we present our calculations for the susceptibility in the doped FeSe1−xSx compounds, following previous analysis of superconductivity and nematicity [56]. In particular, we show χxx and χyy for x = 0, x = 0.085 and x = 0.135 in panels 3A-3C, respectively. The doping evolution of the nematic order parameters is modeled with a mean-field dependence
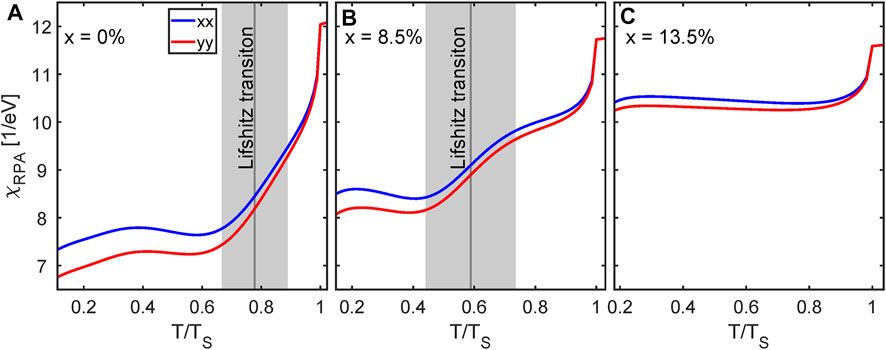
FIGURE 3. Calculated effect of sulphur doping of FeSe1−xSx on temperature dependence of the magnetic susceptibility χ(q → 0). The panels (A)–(C) compare the doping values x = 0, x = 0.085 and x = 0.135. As in 2, the gray boxes illustrate the Lifshitz transition region of the Y-band. For x = 13.5, the Lifshitz transition is absent.
Our calculated results for the uniform magnetic susceptibility within the non-local dxy nematicity agree well with experimental observations including the Knight shift measurements [16, 21, 25, 47, 48, 75]. Within this scenario there is no necessity to use orbital-selective quasiparticle weights. Furthermore, this scenario can also successfully explain the non-monotonic temperature dependence of the uniform susceptibility as resulting from the Lifshitz transition of the larger electron pocket, which rapidly shifts away from the Fermi level within 60 K
Our studies suggest that both spin and orbital contributions and their temperature dependencies are important in describing the uniform magnetic susceptibility or the Knight shift. While the spin part provides the main contribution to the temperature dependence, the orbital part is crucial for a sizeable in-plane anisotropy as observed in experiments. The temperature dependence of the spin part fits very well to the scenario of a Lifshitz transition at Y-point, which appears due to the inclusion of the non-local dxy-nematicity. The finite temperature dependence of the orbital susceptibility breaks linear relation between the bulk magnetic susceptibility and the Knight shift and naturally explains the observed Knight shift anomaly [47, 75]. We note further that the orbital contribution can be in fact larger if one includes larger energy window for the considered model. This should result in the larger in-plane anisotropy but will not affect the non-monotonic temperature dependence of the spin susceptibility.
Our results for the superconducting state also agree qualitatively with recent measurements. The decrease below Tc is seen in measurement of the static, uniform bulk susceptibility [25, 75] and also in the Knight shift measurements [47, 48]. Moreover, in agreement with our results, a slight enhancement of in-plane anisotropy is observed [47].
In summary, we have studied the uniform magnetic susceptibility for a model of FeSe and FeSe1−xSx compounds with particular attention on the consequences of non-local dxy-nematicity. We associate the corresponding Lifshitz transition of a Y-electron pocket with a sharp decrease of the spin component of the magnetic susceptibility, whereas large in-plane anisotropy of the magnetic susceptibility is linked to the orbital susceptibility. The hierarchy of the anisotropy depend on orbital structure of the electronic bands at and away from the Fermi level where the orbital selective quasiparticle weights could be only one potential factor affecting the anisotropy.
We further note that the nematicity also affects the anisotropy of the spin fluctuations at the antiferromagnetic momentum near (π, 0) or (0, π) wavevectors. This anisotropy we also found in our calculations by computing the spin response at large momenta (not shown). This behavior is quite similar in both scenarios of nematicity, while we expect a different temperature dependence of the uniform magnetic susceptibility at q = 0 in both cases.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
SB made the analytical and numercial calculations under the supervision of IE, both discussed the obtained results and wrote the manuscript.
This work was supported by a joint NSFC-DFG grant (ER 463/14-1).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We are thankful to Jakob Böker and Luke Rhodes for fruitful discussions. We also acknowledge support by the Open Access Publication Funds of the Ruhr-Universität Bochum.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.919784/full#supplementary-material
1. Kastner MA, Birgeneau RJ, Shirane G, Endoh Y. Magnetic, Transport, and Optical Properties of Monolayer Copper Oxides. Rev Mod Phys (1998) 70:897–928. doi:10.1103/RevModPhys.70.897
2. Tranquada JM, Xu G, Zaliznyak IA. Superconductivity, Antiferromagnetism, and Neutron Scattering. J magnetism Magn Mater (2014) 350:148–60. doi:10.1016/j.jmmm.2013.09.029
3. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors? Nat Phys (2014) 10:97–104. doi:10.1038/nphys2877
4. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in Fese. J Phys Condensed Matter (2017) 30:023001.
5. Dai P. Antiferromagnetic Order and Spin Dynamics in Iron-Based Superconductors. Rev Mod Phys (2015) 87:855–96. doi:10.1103/revmodphys.87.855
6. Fernandes RM, Schmalian J. Manifestations of Nematic Degrees of freedom in the Magnetic, Elastic, and Superconducting Properties of the Iron Pnictides. Supercond Sci Technol (2012) 25:084005. doi:10.1088/0953-2048/25/8/084005
7. Fanfarillo L, Cortijo A, Valenzuela B. Spin-orbital Interplay and Topology in the Nematic Phase of Iron Pnictides. Phys Rev B (2015) 91:214515. doi:10.1103/PhysRevB.91.214515
8. Fanfarillo L, Mansart J, Toulemonde P, Cercellier H, Le Fèvre P, Bertran F, et al. Orbital-dependent Fermi Surface Shrinking as a Fingerprint of Nematicity in Fese. Phys Rev B (2016) 94:155138. doi:10.1103/PhysRevB.94.155138
9. Fanfarillo L, Benfatto L, Valenzuela B. Orbital Mismatch Boosting Nematic Instability in Iron-Based Superconductors. Phys Rev B (2018) 97:121109. doi:10.1103/PhysRevB.97.121109
10. Hsu FC, Luo JY, Yeh KW, Chen TK, Huang TW, Wu PM, et al. Superconductivity in the Pbo-type Structure α-fese. Proc Natl Acad Sci (2008) 105:14262–4. doi:10.1073/pnas.0807325105
11. McQueen T, Williams A, Stephens P, Tao J, Zhu Y, Ksenofontov V, et al. Tetragonal-to-orthorhombic Structural Phase Transition at 90 K in the Superconductor Fe 1.01 Se. Phys Rev Lett (2009) 103:057002. doi:10.1103/PhysRevLett.103.057002
12. Bendele M, Amato A, Conder K, Elender M, Keller H, Klauss HH, et al. Pressure Induced Static Magnetic Order in Superconducting Fese1−x. Phys Rev Lett (2010) 104:087003. doi:10.1103/PhysRevLett.104.087003
13. Gallais Y, Paul I. Charge Nematicity and Electronic Raman Scattering in Iron-Based Superconductors. Comptes Rendus Physique (2016) 17:113–39. Iron-based superconductors /Supraconducteurs à base de fer. doi:10.1016/j.crhy.2015.10.001
14. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of Fese. Annu Rev Condensed Matter Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137
15. Shibauchi T, Hanaguri T, Matsuda Y. Exotic Superconducting States in Fese-Based Materials. J Phys Soc Jpn (2020) 89:102002. doi:10.7566/jpsj.89.102002
16. Baek SH, Efremov D, Ok J, Kim J, Van Den Brink J, Büchner B. Orbital-driven Nematicity in Fese. Nat Mater (2015) 14:210–4. doi:10.1038/nmat4138
17. Su Y, Liao H, Li T. The Form and Origin of Orbital Ordering in the Electronic Nematic Phase of Iron-Based Superconductors. J Phys Condensed Matter (2015) 27:105702. doi:10.1088/0953-8984/27/10/105702
18. Mukherjee S, Kreisel A, Hirschfeld PJ, Andersen BM. Model of Electronic Structure and Superconductivity in Orbitally Ordered Fese. Phys Rev Lett (2015) 115:026402. doi:10.1103/PhysRevLett.115.026402
19. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in Fese. Phys Rev B (2016) 93:115138. doi:10.1103/PhysRevB.93.115138
20. Yamakawa Y, Onari S, Kontani H. Nematicity and Magnetism in Fese and Other Families of Fe-Based Superconductors. Phys Rev X (2016) 6:021032. doi:10.1103/physrevx.6.021032
21. Böhmer A, Arai T, Hardy F, Hattori T, Iye T, Wolf T, et al. Origin of the Tetragonal-To-Orthorhombic Phase Transition in Fese: A Combined Thermodynamic and Nmr Study of Nematicity. Phys Rev Lett (2015) 114:027001. doi:10.1103/PhysRevLett.114.027001
22. Xing RQ, Classen L, Khodas M, Chubukov AV. Competing Instabilities, Orbital Ordering, and Splitting of Band Degeneracies from a Parquet Renormalization Group Analysis of a Four-Pocket Model for Iron-Based Superconductors: Application to Fese. Phys Rev B (2017) 95:085108. doi:10.1103/PhysRevB.95.085108
23. Margadonna S, Takabayashi Y, McDonald MT, Kasperkiewicz K, Mizuguchi Y, Takano Y, et al. Crystal Structure of the New Fese 1- X Superconductor. Chem Commun (2008) 5607–9. doi:10.1039/b813076k
24. Tanatar MA, Böhmer AE, Timmons EI, Schütt M, Drachuck G, Taufour V, et al. Origin of the Resistivity Anisotropy in the Nematic Phase of Fese. Phys Rev Lett (2016) 117:127001. doi:10.1103/physrevlett.117.127001
25. He M, Wang L, Hardy F, Xu L, Wolf T, Adelmann P, et al. Evidence for Short-Range Magnetic Order in the Nematic Phase of Fese from Anisotropic In-Plane Magnetostriction and Susceptibility Measurements. Phys Rev B (2018) 97:104107. doi:10.1103/physrevb.97.104107
26. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic Spin Fluctuations in Detwinned Fese. Nat Mater (2019) 18:709–16. doi:10.1038/s41563-019-0369-5
27. Lu X, Zhang W, Tseng Y, Liu R, Tao Z, Paris E, et al. Spin-excitation Anisotropy in the Nematic State of Detwinned Fese (2021). arXiv preprint arXiv:2108.04484.
28. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of Fese. Annu Rev Condensed Matter Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137
29. Xu H, Niu X, Xu D, Jiang J, Yao Q, Chen Q, et al. Highly Anisotropic and Twofold Symmetric Superconducting gap in Nematically Ordered Fese 0.93 S 0.07. Phys Rev Lett (2016) 117:157003. doi:10.1103/physrevlett.117.157003
30. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of Orbital-Selective cooper Pairing in Fese. Science (2017) 357:75–80. doi:10.1126/science.aal1575
31. Rhodes LC, Watson MD, Haghighirad AA, Evtushinsky DV, Eschrig M, Kim TK. Scaling of the Superconducting gap with Orbital Character in Fese. Phys Rev B (2018) 98:180503. doi:10.1103/physrevb.98.180503
32. Kushnirenko Y, Fedorov A, Haubold E, Thirupathaiah S, Wolf T, Aswartham S, et al. Three-dimensional Superconducting gap in Fese from Angle-Resolved Photoemission Spectroscopy. Phys Rev B (2018) 97:180501. doi:10.1103/physrevb.97.180501
33. Liu D, Li C, Huang J, Lei B, Wang L, Wu X, et al. Orbital Origin of Extremely Anisotropic Superconducting gap in Nematic Phase of Fese Superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/physrevx.8.031033
34. Hashimoto T, Ota Y, Yamamoto HQ, Suzuki Y, Shimojima T, Watanabe S, et al. Superconducting gap Anisotropy Sensitive to Nematic Domains in Fese. Nat Commun (2018) 9:1–7. doi:10.1038/s41467-017-02739-y
35. Huh S, Lu Z, Kim YS, Kim D, Liu S, Ma M, et al. Cu Doping Effects on the Electronic Structure of Fe1-Xcuxse (2021). arXiv preprint arXiv:2110.14463.
36. Mizuguchi Y, Tomioka F, Tsuda S, Yamaguchi T, Takano Y. Substitution Effects on Fese Superconductor. J Phys Soc Jpn (2009) 78:074712. doi:10.1143/jpsj.78.074712
37. Schoop LM, Medvedev SA, Ksenofontov V, Williams A, Palasyuk T, Troyan IA, et al. Pressure-restored Superconductivity in Cu-Substituted Fese. Phys Rev B (2011) 84:174505. doi:10.1103/physrevb.84.174505
38. Medvedev S, McQueen T, Troyan I, Palasyuk T, Eremets M, Cava R, et al. Electronic and Magnetic Phase Diagram of β-fe1. 01se with Superconductivity at 36.7 K under Pressure. Nat Mater (2009) 8:630–3. doi:10.1038/nmat2491
39. Shimojima T, Suzuki Y, Sonobe T, Nakamura A, Sakano M, Omachi J, et al. Lifting of Xz/yz Orbital Degeneracy at the Structural Transition in Detwinned Fese. Phys Rev B (2014) 90:121111. doi:10.1103/PhysRevB.90.121111
40. Watson MD, Haghighirad AA, Rhodes LC, Hoesch M, Kim TK. Electronic Anisotropies Revealed by Detwinned Angle-Resolved Photo-Emission Spectroscopy Measurements of Fese. New J Phys (2017) 19:103021. doi:10.1088/1367-2630/aa8a04
41. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in Fese. Phys Rev X (2019) 9:041049. doi:10.1103/physrevx.9.041049
42. Huh S, Seo J, Kim B, Cho S, Jung JK, Kim S, et al. Absence of Y-Pocket in 1-fe Brillouin Zone and Reversed Orbital Occupation Imbalance in Fese. Commun Phys (2020) 3:1–7.
43. Pfau H, Yi M, Hashimoto M, Chen T, Dai PC, Shen ZX, et al. Quasiparticle Coherence in the Nematic State of Fese. Phys Rev B (2021) 104:L241101. doi:10.1103/physrevb.104.l241101
44. Zhou R, Scherer DD, Mayaffre H, Toulemonde P, Ma M, Li Y, et al. Singular Magnetic Anisotropy in the Nematic Phase of Fese. npj Quan Mater (2020) 5:1–9. doi:10.1038/s41535-020-00295-1
45. Watson MD, Kim TK, Haghighirad AA, Davies NR, McCollam A, Narayanan A, et al. Emergence of the Nematic Electronic State in Fese. Phys Rev B (2015) 91:155106. doi:10.1103/PhysRevB.91.155106
46. Chu JH, Analytis JG, De Greve K, McMahon PL, Islam Z, Yamamoto Y, et al. In-plane Resistivity Anisotropy in an Underdoped Iron Arsenide Superconductor. Science (2010) 329:824–6. doi:10.1126/science.1190482
47. Vinograd I, Edwards S, Wang Z, Kissikov T, Byland J, Badger J, et al. Inhomogeneous Knight Shift in Vortex Cores of Superconducting Fese. Phys Rev B (2021) 104:014502. doi:10.1103/physrevb.104.014502
48. Li J, Kang B, Zhao D, Lei B, Zhou Y, Song D, et al. Se 77-nmr Evidence for Spin-Singlet Superconductivity with Exotic Superconducting Fluctuations in Fese. Phys Rev B (2022) 105:054514. doi:10.1103/physrevb.105.054514
49. Pustogow A, Luo Y, Chronister A, Su YS, Sokolov D, Jerzembeck F, et al. Constraints on the Superconducting Order Parameter in Sr2ruo4 from Oxygen-17 Nuclear Magnetic Resonance. Nature (2019) 574:72–5. doi:10.1038/s41586-019-1596-2
50. Zhang P, Qian T, Richard P, Wang XP, Miao H, Lv BQ, et al. Observation of Two Distinct Dxz/dyz Band Splittings in Fese. Phys Rev B (2015) 91:214503. doi:10.1103/PhysRevB.91.214503
51. Suzuki Y, Shimojima T, Sonobe T, Nakamura A, Sakano M, Tsuji H, et al. Momentum-dependent Sign Inversion of Orbital Order in Superconducting Fese. Phys Rev B (2015) 92:205117. doi:10.1103/PhysRevB.92.205117
52. Zhang Y, Yi M, Liu ZK, Li W, Lee JJ, Moore RG, et al. Distinctive Orbital Anisotropy Observed in the Nematic State of a Fese Thin Film. Phys Rev B (2016) 94:115153. doi:10.1103/PhysRevB.94.115153
53. Watson MD, Haghighirad AA, Takita H, Mansuer W, Iwasawa H, Schwier EF, et al. Shifts and Splittings of the Hole Bands in the Nematic Phase of Fese. J Phys Soc Jpn (2017) 86:053703. doi:10.7566/JPSJ.86.053703
54. Kreisel A, Andersen BM, Sprau PO, Kostin A, Davis JS, Hirschfeld P. Orbital Selective Pairing and gap Structures of Iron-Based Superconductors. Phys Rev B (2017) 95:174504. doi:10.1103/physrevb.95.174504
55. Hu H, Yu R, Nica EM, Zhu JX, Si Q. Orbital-selective Superconductivity in the Nematic Phase of Fese. Phys Rev B (2018) 98:220503. doi:10.1103/physrevb.98.220503
56. Rhodes LC, Böker J, Müller MA, Eschrig M, Eremin IM. Non-local D Xy Nematicity and the Missing Electron Pocket in Fese. npj Quan Mater (2021) 6:1–14. doi:10.1038/s41535-021-00341-6
57. Islam KR, Böker J, Eremin IM, Chubukov AV. Specific Heat and gap Structure of a Nematic Superconductor: Application to Fese. Phys Rev B (2021) 104:094522. doi:10.1103/physrevb.104.094522
58. Marciani M, Benfatto L. Resistivity Anisotropy from Multiorbital Boltzmann Equation in Nematic Fese (2022). arXiv preprint arXiv:2202.12070.
59. Rhodes LC, Eschrig M, Kim TK, Watson MD. Fese and the Missing Electron Pocket Problem. Frontiers in Physics (2022) 10:859017. doi:10.3389/fphy.2022.859017
60. Fernandes RM, Vafek O. Distinguishing Spin-Orbit Coupling and Nematic Order in the Electronic Spectrum of Iron-Based Superconductors. Phys Rev B (2014) 90:214514. doi:10.1103/PhysRevB.90.214514
61. Classen L, Xing RQ, Khodas M, Chubukov AV. Interplay between Magnetism, Superconductivity, and Orbital Order in 5-pocket Model for Iron-Based Superconductors: Parquet Renormalization Group Study. Phys Rev Lett (2017) 118:037001. doi:10.1103/PhysRevLett.118.037001
62. Christensen MH, Fernandes RM, Chubukov AV. Orbital Transmutation and the Electronic Spectrum of Fese in the Nematic Phase. Phys Rev Res (2020) 2:013015. doi:10.1103/PhysRevResearch.2.013015
63. Li J, Lei B, Zhao D, Nie LP, Song DW, Zheng LX, et al. Spin-orbital-intertwined Nematic State in Fese. Phys Rev X (2020) 10:011034. doi:10.1103/PhysRevX.10.011034
64. Watson M, Kim T, Haghighirad A, Davies N, McCollam A, Narayanan A, et al. Emergence of the Nematic Electronic State in Fese. Phys Rev B (2015) 91:155106. doi:10.1103/physrevb.91.155106
65. Cvetkovic V, Vafek O. Space Group Symmetry, Spin-Orbit Coupling, and the Low-Energy Effective Hamiltonian for Iron-Based Superconductors. Phys Rev B (2013) 88:134510. doi:10.1103/physrevb.88.134510
66. Scherer DD, Jacko A, Friedrich C, Şaşıoğlu E, Blügel S, Valentí R, et al. Interplay of Nematic and Magnetic Orders in Fese under Pressure. Phys Rev B (2017) 95:094504. doi:10.1103/physrevb.95.094504
67. Borisenko S, Evtushinsky DV, Liu ZH, Morozov I, Kappenberger R, Wurmehl S, et al. Direct Observation of Spin–Orbit Coupling in Iron-Based Superconductors. Nat Phys (2015) 12:311. doi:10.1038/nphys3594
68. Day RP, Levy G, Michiardi M, Zwartsenberg B, Zonno M, Ji F, et al. Influence of Spin-Orbit Coupling in Iron-Based Superconductors. Phys Rev Lett (2018) 121:076401. doi:10.1103/PhysRevLett.121.076401
69. Kostin A, Sprau PO, Kreisel A, Chong YX, Böhmer AE, Canfield PC, et al. Imaging Orbital-Selective Quasiparticles in the Hund’s Metal State of Fese. Nat Mater (2018) 17:869. doi:10.1038/s41563-018-0151-0
70. Kreisel A, Hirschfeld PJ, Andersen BM. On the Remarkable Superconductivity of Fese and its Close Cousins. Symmetry (2020) 12. doi:10.3390/sym12091402
71. Yin ZP, Haule K, Kotliar G. Kinetic Frustration and the Nature of the Magnetic and Paramagnetic States in Iron Pnictides and Ironchalcogenide. Nat Mater (2018) 10:932. doi:10.1038/nmat3120
72. Maier T, Graser S, Scalapino D, Hirschfeld P. Neutron Scattering Resonance and the Iron-Pnictide Superconducting gap. Phys Rev B (2009) 79:134520. doi:10.1103/physrevb.79.134520
73. Graser S, Maier T, Hirschfeld P, Scalapino D. Near-degeneracy of Several Pairing Channels in Multiorbital Models for the Fe Pnictides. New J Phys (2009) 11:025016. doi:10.1088/1367-2630/11/2/025016
74. Kemper AF, Maier TA, Graser S, Cheng HP, Hirschfeld P, Scalapino D. Sensitivity of the Superconducting State and Magnetic Susceptibility to Key Aspects of Electronic Structure in Ferropnictides. New J Phys (2010) 12:073030. doi:10.1088/1367-2630/12/7/073030
75. Li J, Lei B, Zhao D, Nie L, Song D, Zheng L, et al. Spin-orbital-intertwined Nematic State in Fese. Phys Rev X (2020) 10:011034. doi:10.1103/physrevx.10.011034
76. He M, Wang L, Ahn F, Hardy F, Wolf T, Adelmann P, et al. Dichotomy between In-Plane Magnetic Susceptibility and Resistivity Anisotropies in Extremely Strained Bafe2as2. Nat Commun (2017) 8. doi:10.1038/s41467-017-00712-3
Keywords: iron-based superconductors, nematic ordering, magnetic susceptibility, uniform susceptibility, spin-orbit coupling
Citation: Bötzel S and Eremin IM (2022) Feedback of Non-Local dxy Nematicity on the Magnetic Anisotropy in FeSe. Front. Phys. 10:919784. doi: 10.3389/fphy.2022.919784
Received: 13 April 2022; Accepted: 11 May 2022;
Published: 15 June 2022.
Edited by:
Laura Fanfarillo, International School for Advanced Studies (SISSA), ItalyReviewed by:
Belén Valenzuela, Institute of Materials Science of Madrid (CSIC), SpainCopyright © 2022 Bötzel and Eremin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ilya M. Eremin, SWx5YS5FcmVtaW5AcnViLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.