Janus van der waals equations for real molecules with two-sided phase transitions

We obtained families of generalized van der Waals equations characterized by an even number n = 2, 4, 6 and a continuous free parameter, which is tunable for a critical compressibility factor. Each equation features two adjacent critical points which have a common critical temperature T_c and arbitrarily two close critical densities. The critical phase transitions are naturally two-sided: the critical exponents are ${\alpha }_P={\gamma }_P=\frac{2}{3}$ and ${\beta }_P={\delta }^{-1}=\frac{1}{3}$ for T > T_c and ${\alpha }_P={\gamma }_P=\frac{n}{n+1}$ and ${\beta }_P={\delta }^{-1}=\frac{1}{n+1}$ for T < T_c. In contrast with the original van der Waals equation, our novel equations all reduce consistently to the classical ideal gas law in the low-density limit. We tested our formulas against the NIST data for 11 major molecules and showed agreements better than the original van der Waals equation, not only near to the critical points but also in low-density regions.

Introduction

Two-sided phase transitions are rather out of the ordinary critical phenomena as their critical exponents take different values in the higher-and the lower-temperature phases. When the general renormalization group argument, e.g. [1], might appear to suppress such an unusual bilateral critical behavior, they have been reported to occur in various systems, such as the isotropic ferromagnet [2], XY-Heisenberg model [3], complex Sachdev–Ye–Kitaev models [4], and liquid–gas transitions of real molecules [5]. To explain the two-sided critical phase transitions while respecting the analyticity of the canonical partition function of a finite system, it was hypothesized that there may exist not a single but double critical points, which should be quite close to each other [5].

It is the dual purpose of the present article to modify the van der Waals equation toward the description of the two-sided phase transitions and to test our novel formulas against the NIST reference data (RRID:SCR_006452) [6], specifically for 11 real molecules. Our proposed equation of state, which we dub Janus van der Waals equations,¹ is characterized by extremely adjacent two critical points. The two critical points share strictly the same critical temperature, T_c, but, remarkably, the critical pressure, P_c, and the critical volume per particles, v_c, differ by arbitrarily small amounts, such that the two distinct critical points can appear practically indistinguishable.

The (original) van der Waals equation of state,

$\left(P_r+\frac{3}{v_r^2}\right)\left(v_r-\frac{1}{3}\right)=\frac{8}{3}{T}_r,(1)$

was meant to be an improvement of the classical ideal gas law, i.e.,

$Pv=k_{\text{B}}T\iff P_r{v}_r=\chi T_r:\chi =\frac{k_{\text{B}}{T}_c}{P_c{v}_c},(2)$

by attempting to take into account the finite volume of molecules and intermolecular attractions. In (1) and (2), and henceforth, P_r = P/P_c, T_r = T/T_c, and v_r = v/v_c are the reduced pressure, temperature, and volume per particle, respectively, while χ = k_BT_c/(P_cv_c) denotes the inverse of the critical compressibility factor which is dimensionless. The critical point is given by P_r = T_r = v_r = 1, such that the van der Waals Eq. 1 contains the critical point as $(1+3)(1-\frac{1}{3})=\frac{8}{3}$ and may describe the near critical behavior. However, in a large volume or low-density limit, Eq. 1 gives

$Pv\simeq \left(\frac{8P_c{v}_c}{3T_c}\right)T\ne k_{\text{B}}T.(3)$

Thus, unless $\chi =\frac{8}{3}$ by chance, the van der Waals Eq. 1 cannot be reduced to the classical ideal gas law (2) in the low-density limit and accordingly fails to describe real gases at low densities. In fact, the experimental real values of χ are typically around 3.5 larger than $\frac{8}{3}$. In contrast, our proposed Janus van der Waals equations are going to be consistent with the classical ideal gas law (2) at low densities. They are not particularly motivated by the finite volume or intermolecular effects. Instead, we addressed directly the definition of the critical point in thermodynamics: for a given equation of state, a critical point can be identified as a stationary inflection point in the constant temperature line on a pressure versus volume diagram. Specifically for a certain natural number greater than or equal to two, n_c ≥ 2, we have at the critical point,

$\begin{array}{c}\frac{{\partial }^{k}P\left(T_c,v_c\right)}{\partial v^k}=0\text{for}1\le k\le n_c,\hfill \end{array}(4)$

while the next higher-order derivative having k = n_c + 1 is nontrivial. In particular for van der Waals Eq. 1, the number takes the minimal value n_c = 2, and its spinodal curve, that is, by definition the lowest order k = 1 in (4), is given by

$T_r=1-\frac{{\left(v_r-1\right)}^2\left(4v_r-1\right)}{4v_r^3}.(5)$

This expression shows clearly that on the spinodal curve, the temperature is locally maximal at the critical point. In general, the characteristic number n_c can differ from two and may be used to classify the critical points, being dubbed as ‘critical index’ [5]. Thoroughly from (4), both the critical isobar of P_r ≡ 1, and the spinodal curve satisfies simple power-law behaviors around the critical point:

$\begin{array}{c}T-T_c\propto {\left(v-v_c\right)}^{1+n_c}:\text{critical\hspace{0.17em}isobar},T-T_c\propto {\left(v-v_c\right)}^{n_c}:\text{spinodal\hspace{0.17em}curve}.\hfill \end{array}(6)$

Combined with the analyticity of the underlying canonical partition function, this result fixes the (isobaric) critical exponents [8], ${\alpha }_P={\gamma }_P=\frac{n_c}{1+n_c}$ and ${\beta }_P={\delta }^{-1}=\frac{1}{1+n_c}$. These satisfy Rushbrooke and Widom scaling laws. Since n_c ≥ 2, the two curves of (6) are actually tangent to each other at the critical point.

The main result of [5] was that the NIST reference data on 20 major molecules [6] are indeed consistent with the analytic prediction of the critical exponents and, moreover, that the critical phase transitions are remarkably two-sided: for T > T_c the critical index is 2 universally, yet for T < T_c it varies as n ≡ 2, 3, 4, 5, 6 depending on each molecule, collectively denoted by a pair of critical indices, n_c ⇒ (n₊, n₋) = (2, n). In this work, we present Janus van der Waals equations characterized by a pair of adjacent critical points with indices (n₊, n₋) = (2, n) for n = 2, 4, 6 (even). With one continuous input parameter, which will be chosen to match the critical compressibility, they are shown to describe all the real molecules remarkably well with even critical indices identified in [5]. They are cyclopentane (C₅H₁₀) for n = 2; nitrogen (N₂), argon (Ar), methane (CH₄), ethylene (C₂H₄), ethane (C₂H₆), propylene (C₃H₆), propane (C₃H₈), butane (C₄H₁₀), and isobutane (C₄H₁₀) for n = 4; and helium-4 (⁴He) for n = 6.

Ansatz and derivation

Our Janus van der Waals equations assume an ansatz,

$\left(P_r+\chi f_n\left(v_r\right)\right)\left(v_r-b\right)=\chi T_r,(7)$

where f_n (v_r) is supposed to be a polynomial in $v_r^{-1}$, and $\chi =\frac{k_{\text{B}}{T}_c}{P_c{v}_c}$ is the (experimentally determinable) genuine free parameter which will guarantee the consistency with the classical ideal gas law (2) in the large-volume limit, hence resolving the inconsistency of the original van der Waals Eq. 3. Each molecule will have its own Janus van der Waals equation characterized by two input parameters, χ (continuous) and n = 2, 4, 6 (discrete).

With four constants {a, b, s, t}, which will be determined shortly, we require the spinodal curve to meet

$T_r=-{\left(v_r-b\right)}^2\frac{\text{d}{f}_n\left(v_r\right)}{\text{d}{v}_r}=1-\frac{{\left(v_r-a\right)}^n{\left(v_r-1\right)}^2\left(v_r^2-s{v}_r+t\right)}{v_r^{n+4}}.(8)$

When the first equality comes from the definition of the spinodal curve, crucially the second generalizes the van der Waals case (5) and gives rise to two distinct critical points:

$\begin{array}{c}\left(n_c,P_r,T_r,v_r\right)=\left(n,1+ϵ,1,a\right)\text{and}\left(\mathrm{2,1,1,1}\right).\hfill \end{array}(9)$

At each critical point, in view of (6), we clearly have

$T_r-1\propto \left\{\begin{array}{ccc}\hfill {\left(v_r-a\right)}^n\hfill & \hfill \text{as}\hfill & \hfill v_r\to a\hfill \\ \hfill {\left(v_r-1\right)}^2\hfill & \hfill \text{as}\hfill & \hfill v_r\to 1\hfill \end{array}.\right.(10)$

Their critical indices, pressure, and volume per particle may differ, but the critical temperature is the same, i.e., T_r = 1. For this, it is necessary to set 0 < a < 1 and s² ≠ 4t. We also put n to be even, n = 0, 2, 4, 6, ⋯, such that the critical temperature is (locally) maximal on the spinodal curve, which is the case with the van der Waals fluid (5), a relativistic ideal Bose gas [8] (Figures 2, 6 therein), and supposedly real molecules. Accordingly, the spinodal curve (8) has “twin peaks” in temperature, as depicted in Figure 1. Moreover, in order to be consistent with the realistic molecules for which only one critical point has been usually assumed, we shall let a be close to 1⁻, and then, from ϵ ∝ (1 − a)ⁿ⁺³, which we shall derive later in (17), the two critical pressure values, P_r = 1 and P_r = 1 + ϵ, will be practically indistinguishable from each other.

FIGURE 1

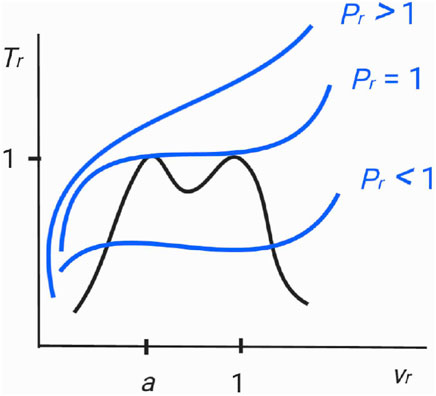
FIGURE 1. Schematic zoomed-in diagram of a spinodal curve (black colored) and three isobar curves (blue colored). There are two adjacent critical points on a spinodal curve at v_r = a and at v_r = 1. When P_r < 1, the isobar crosses the spinodal curve twice at v_r < a and at v_r > 1. When P_r > 1, the isobar does not meet the spinodal curve. When P_r = 1, with negligible ϵ, the critical isobar touches the spinodal curve at the two critical points. Specifically, along the critical isobar, as the temperature increases from T_r < 1 to T_r = 1⁻, the critical point at v_r = a with the critical index of n_c = n = 2, 4, 6 is relevant. On the other hand, as the temperature decreases from T_r > 1 to T_r = 1⁺, the dominant critical point is at v_r = 1 with n_c = 2. Between the two peaks on the spinodal curve, there is a local minimum which may be also identified as a “critical point” of which the critical temperature is less than T_c. This third critical point is sandwiched by the two extremely adjacent critical points and plays an inconsiderable role in our analysis. The diagram generalizes the single-peaked spinodal curve of a relativistic ideal Bose gas, depicted in Figure 1 of Ref. [8], to twin-peaks, and furthermore will be confirmed through a concrete example as in Figure 2.

From the fact that the last expression in (8) should be divisible by ${(v_r-b)}^2$, two constraints arise:

$\begin{array}{c}{\left(b-1\right)}^2{\left(b-a\right)}^n\left(b^2-sb+t\right)=b^{n+4};\frac{2}{b-1}+\frac{n}{b-a}+\frac{2b-s}{b^2-sb+t}=\frac{n+4}{b},\hfill \end{array}(11)$

which subsequently determine s and t in terms of a and b,

$\begin{array}{c}s=2b+\left(\frac{\left(n+2\right)ab-\left(n+4\right)a+4b-2b^2}{{\left(b-1\right)}^3{\left(b-a\right)}^{n+1}}\right)b^{n+3};t=b^2+\left(\frac{\left(n+1\right)ab-\left(n+3\right)a+3b-b^2}{{\left(b-1\right)}^3{\left(b-a\right)}^{n+1}}\right)b^{n+4}.\hfill \end{array}(12)$

With these identifications, the second equality of (8) fixes the function f_n (v_r):

$f_n\left(v_r\right)=\frac{1}{b^5}\sum _{l=0}^{n+1}\frac{c_l}{n+3-l}{\left(\frac{b}{v_r}\right)}^{n+3-l},(13)$

where the coefficients are given, with (12), by ²:

$c_l=\sum _{j=0}^l\left(j-l-1\right)\left[\left(\genfrac{}{}{0.0pt}{}{n}{j-4}\right)a^4+\left(\genfrac{}{}{0.0pt}{}{n}{j-3}\right)\left(2+s\right)a^3+\left(\genfrac{}{}{0.0pt}{}{n}{j-2}\right)\left(1+2s+t\right)a^2+\left(\genfrac{}{}{0.0pt}{}{n}{j-1}\right)\left(s+2t\right)a+\left(\genfrac{}{}{0.0pt}{}{n}{j}\right)t\right]{\left(-\frac{a}{b}\right)}^{n-j}.(14)$

It should be noted that the binomial coefficient $\left(\genfrac{}{}{0.0pt}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$ should be trivial if k or n − k is negative.

The remaining two constants a, b are then determined by requiring that the reduced critical pressure P_r should take the aforementioned values of 1 + ϵ and 1 at the two critical points of v_r = a and v_r = 1 (9):

$\begin{array}{c}\chi \left[\frac{1}{a-b}-f_n\left(a\right)\right]=1+ϵ;\chi \left[\frac{1}{1-b}-f_n\left(1\right)\right]=1.\hfill \end{array}(15)$

We obtained from the latter

$\chi =\frac{\left(n+3\right){\left(1-b\right)}^{n+3}}{{\left(1-b\right)}^{n+3}+b^{n+3}},(16)$

and by subtracting the latter from the former, we obtained

$ϵ=\frac{2\chi {\left(1-a\right)}^{n+3}\left[{\left(1-b\right)}^3{\left(a-b\right)}^{n+1}+\left\{\left(n+1\right)a-b+3\right\}{b}^{n+3}\right]}{\left(n+3\right)\left(n+2\right)\left(n+1\right)a^3{\left(1-b\right)}^3{\left(a-b\right)}^{n+1}}.(17)$

Inverting (16), we solve for b in terms of the physically measurable compressibility factor,

$b=\frac{{\left(n+3-\chi \right)}^{\frac{1}{n+3}}}{{\left(n+3-\chi \right)}^{\frac{1}{n+3}}+{\chi }^{\frac{1}{n+3}}}.(18)$

Clearly from (17), ϵ becomes small ϵ ∝ (1 − a)ⁿ⁺³ as the constant a gets close to unity from below. In fact, ϵ is positive when 0 < a < 1 and 0 < χ < n + 3. This confirms that the two critical points (9) can be indeed extremely adjacent and experimentally indistinguishable. Naturally, the limit a → 1⁻ does not match the exact value of a = 1: the former is still bi-critical, while the latter is mono-critical with the enhanced critical index n_c = n + 2. However, away from the critical points in the phase diagram, we may practically put

$a\approx 1,(19)$

and obtain approximate Janus van der Waals equations, which we shall test against the NIST reference data [6].

Figure 2 is the diagram of a spinodal curve (8) for the choice of n = 4, a = 0.99, and χ = 3.4556 as for nitrogen (N₂). It follows from (18) b = 0.5009 and subsequently (12) fixes s, t. The curve confirms the anticipated two adjacent critical points at a = 0.99 and 1.00. Spinodal curves for other molecules can be obtained by the same method.

FIGURE 2

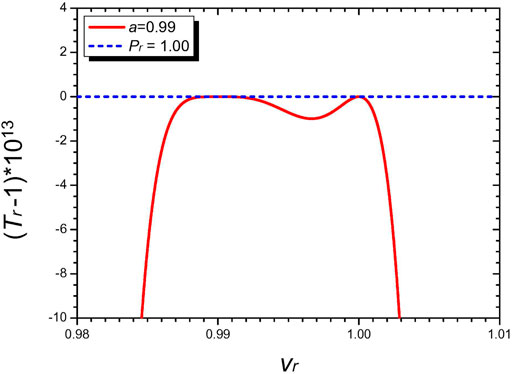
FIGURE 2. Diagram featuring the spinodal curve (red colored) and the critical isobar (blue colored) of the n = 4 Janus van der Waals equation with the two adjacent critical points at v_r = a = 0.99 and v_r = 1.00. We have set χ = 3.4556 as for nitrogen (N₂). Since ϵ = 6.0846 × 10^–15 (17), the two critical isobars P_r = 1 and P_r = 1 + ϵ are indeed practically indistinguishable. The (common) critical isobar then touches both the critical points, as anticipated in Figure 1. The local minimum value of T_r sandwiched by the twin critical points is lower than 1 by a small amount (<10^–12) and is thus also experimentally hard to detect.

Theoretical result: Janus van der waals equations

We now spell our modified van der Waals equations for each case of n = 0 (mono-critical) and n = 2, 4 (bi-critical/Janus) explicitly.

n = 0: Mono-critical generalization

When n = 0, the parameter a becomes irrelevant as there is only one critical point. Consequently, (7) reduces to a one-parameter generalization of the van der Waals equation,

$\left[P_r+\frac{\left[{\chi }^{\frac{1}{3}}-{\left(\chi -3\right)}^{\frac{1}{3}}\right]\left[{\chi }^{\frac{2}{3}}-{\left|\chi -3\right|}^{\frac{2}{3}}\right]}{v_r^2}+\frac{2-\chi +{\chi }^{\frac{1}{3}}{\left|\chi -3\right|}^{\frac{2}{3}}}{v_r^3}\right]\left[v_r-\frac{{\left(\chi -3\right)}^{\frac{1}{3}}}{{\left(\chi -3\right)}^{\frac{1}{3}}-{\chi }^{\frac{1}{3}}}\right]=\chi T_r.(20)$

The critical compressibility factor is at our disposal. Choosing $\chi =\frac{k_{\text{B}}{T}_c}{P_c{v}_c}=\frac{8}{3}$, one recovers the original van der Waals Eq. 1.

Among the 11 major molecules we examined, cyclopentane is exceptional as its critical phase transition is not two-sided: n_c = 2 universally for the temperature T > T_c and T < T_c [5]. Logically, it can be either mono-critical with n = 0 or bi-critical with n = 2. To examine which is correct with the NIST data, we put χ = 3.5572 as for the value of cyclopentane and prepared an n = 0 equation from (20):

$\left(P_r+\frac{1.1632}{v_r^2}-\frac{0.52356}{v_r^3}\right)\left(v_r+1.1694\right)=3.5572T_r.(21)$

The plus sign in the second bracket (which is generically the case for χ > 3) is in contrast with the negative sign in the original van der Waals Eq. 1.

n = 2 equation for cyclopentane (C₅H₁₀)

For n = 2, in the limit a → 1⁻ or a ≈ 1 (19), we have

$\begin{array}{ccc}\chi f_{n=2}\left(v_r\right)\hfill & \approx \hfill & \frac{{\chi }^{\frac{1}{5}}{\left(5-\chi \right)}^{\frac{1}{5}}\left[{\chi }^{\frac{1}{5}}-{\left(5-\chi \right)}^{\frac{1}{5}}\right]\left[{\chi }^{\frac{2}{5}}+{\left(5-\chi \right)}^{\frac{2}{5}}\right]+4\chi -10}{v_r^2}+\frac{{\chi }^{\frac{1}{5}}{\left(5-\chi \right)}^{\frac{2}{5}}\left[{\chi }^{\frac{2}{5}}-2{\chi }^{\frac{1}{5}}{\left(5-\chi \right)}^{\frac{1}{5}}+3{\left(5-\chi \right)}^{\frac{2}{5}}\right]-6\chi +20}{v_r^3}\hfill \\ +\frac{{\chi }^{\frac{1}{5}}{\left(5-\chi \right)}^{\frac{3}{5}}\left[{\chi }^{\frac{1}{5}}-3{\left(5-\chi \right)}^{\frac{1}{5}}\right]+4\chi -15}{v_r^4}\hfill \\ +\frac{{\chi }^{\frac{1}{5}}{\left(5-\chi \right)}^{\frac{4}{5}}-\chi +4}{v_r^5}.\end{array}(22)$

Letting χ = 3.5572, we obtain an n = 2 Janus van der Waals equation for C₅H₁₀ (cyclopentane),

$\left(P_r+\frac{5.0608}{v_r^2}+\frac{2.1811}{v_r^3}-\frac{3.8860}{v_r^4}+\frac{2.1710}{v_r^5}\right)\left(v_r-0.45500\right)\approx 3.5572T_r.(23)$

As we shall see in the following section, the NIST data on cyclopentane are better described by this bi-critical equation rather than the mono-critical one (21).

n = 4 equations for nitrogen (N₂), argon (Ar), methane (CH₄), ethylene (C₂H₄), ethane (C₂H₆), propylene (C₃H₆), propane (C₃H₈), butane (C₄H₁₀), and isobutane (C₄H₁₀)

For n = 4 with $b=\frac{{(7-\chi )}^{\frac{1}{7}}}{{(7-\chi )}^{\frac{1}{7}}+{\chi }^{\frac{1}{7}}}$ and a ≈ 1 (19), we have

$\begin{array}{c}\chi f_{n=4}\left(v_r\right)\approx \frac{21-140b+392b^2-588b^3+490b^4-196b^5}{\left[b^7+{\left(1-b\right)}^7\right]v_r^2}+\frac{-35+245b-728b^2+1176b^3-1078b^4+490b^5}{\left[b^7+{\left(1-b\right)}^7\right]v_r^3}\hfill \\ \hfill & \hfill & +\frac{35-245b+735b^2-1218b^3+1176b^4-588b^5}{\left[b^7+{\left(1-b\right)}^7\right]v_r^4}+\frac{-21+147b-441b^2+735b^3-728b^4+392b^5}{\left[b^7+{\left(1-b\right)}^7\right]v_r^5}\hfill \\ \hfill & \hfill & +\frac{7-49b+147b^2-245b^3+245b^4-140b^5}{\left[b^7+{\left(1-b\right)}^7\right]v_r^6}+\frac{-1+7b-21b^2+35b^3-35b^4+21b^5}{\left[b^7+{\left(1-b\right)}^7\right]v_r^7}.\hfill \end{array}(24)$

Choosing χ from the experimental data, we obtained n = 4 Janus van der Waals equations for nine molecules,

$\left(P_r+\frac{k_2}{v_r^2}+\frac{k_3}{v_r^3}+\frac{k_4}{v_r^4}+\frac{k_5}{v_r^5}+\frac{k_6}{v_r^6}+\frac{k_7}{v_r^7}\right)\left(v_r-b\right)\approx \chi T_r,(25)$

of which the coefficients are listed in Table 1.

TABLE 1

TABLE 1. Coefficients of the n = 4 Janus van der Waals equations for nine molecules.

n = 6 equation for helium-4 (⁴He)

For n = 6 with $b=\frac{{(9-\chi )}^{\frac{1}{9}}}{{(9-\chi )}^{\frac{1}{9}}+{\chi }^{\frac{1}{9}}}$ and a ≈ 1 (19), we have

$\begin{array}{cc}\chi f_{n=6}\left(v_r\right)\approx \hfill & \frac{36-315b+1215b^2-2700b^3+3780b^4-3402b^5+1890b^6-540b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^2}\hfill \\ \hfill & +\frac{-84+756b-3015b^2+6975b^3-10260b^4+9828b^5-5922b^6+1890b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^3}\hfill \\ \hfill & +\frac{126-1134b+4536b^2-10575b^3+15795b^4-15552b^5+9828b^6-3402b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^4}\hfill \\ \hfill & +\frac{-126+1134b-4536b^2+10584b^3-15867b^4+15795b^5-10260b^6+3780b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^5}\hfill \\ \hfill & +\frac{84-756b+3024b^2-7056b^3+10584b^4-10575b^5+6975b^6-2700b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^6}\hfill \\ \hfill & +\frac{-36+324b-1296b^2+3024b^3-4536b^4+4536b^5-3015b^6+1215b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^7}\hfill \\ \hfill & +\frac{9-81b+324b^2-756b^3+1134b^4-1134b^5+756b^6-315b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^8}\hfill \\ \hfill & +\frac{-1+9b-36b^2+84b^3-126b^4+126b^5-84b^6+36b^7}{\left[b^9+{\left(1-b\right)}^9\right]v_r^9}.\hfill \end{array}(26)$

Letting χ = 3.2991, we get an n = 6 Janus van der Waals equation for helium-4,

$\begin{array}{c}\left(P_r-\frac{10.671}{v_r^2}+\frac{97.188}{v_r^3}-\frac{259.53}{v_r^4}+\frac{393.69}{v_r^5}-\frac{366.57}{v_r^6}+\frac{210.75}{v_r^7}-\frac{69.112}{v_r^8}+\frac{10.066}{v_r^9}\right)\left(v_r-0.51519\right)\approx 3.2991T_r.\hfill \end{array}(27)$

Comparison with NIST reference data

Henceforth, we look into isochoric, isobaric, and isothermal cases for real molecules, which will demonstrate that our Janus van der Waals equations represent excellent agreements with the NIST data, better than the original van der Waals equation. By construction, the Janus van der Waals equations reflect the previously reported two-sided critical phenomena [5] and at the same time reduce consistently to the classical ideal gas law in the low-density limit far away from the critical point at v_r = 1.

First, we focused on the n = 2 case to which only the cyclopentane molecule (C₅H₁₀) belongs to.

Figure 3 shows the isochoric curves of the cyclopentane molecule at 1/v_r = 0.02 (A), 1/v_r = 0.5 (B), 1/v_r = 1.0 (C), and 1/v_r = 1.5 (D), respectively. They are drawn by the NIST data and further by the three equations: the n = 2 Janus van der Waals Eq. 23, the mono-critical equation (n = 0) (21), the original van der Waals Eq. 1, and the classical ideal gas law (2). The n = 2 Janus van der Waals equation fits best with the NIST data while consistently reducing to the classical ideal gas law in the low-density limit.

FIGURE 3

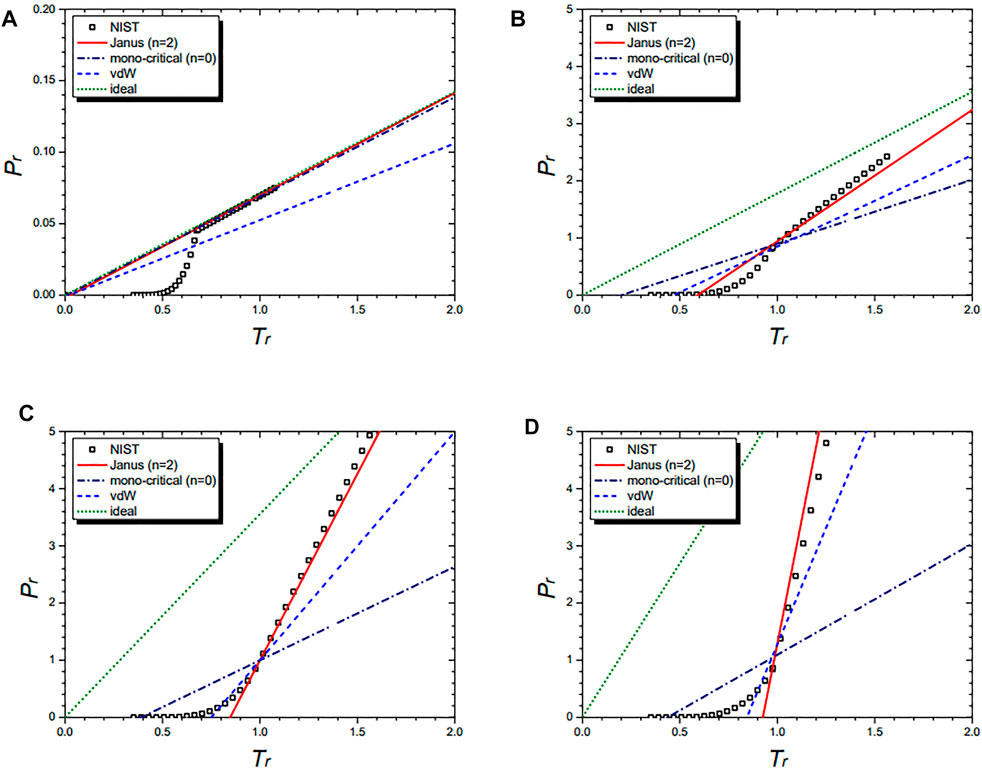
FIGURE 3. Isochoric curves of cyclopentane (C₅H₁₀) at 1/v_r = 0.02 (A), 1/v_r = 0.5 (B), 1/v_r = 1.0 (C), and 1/v_r = 1.5 (D),respectively. Boxes are from the NIST data. The red solid line is drawn from the n = 2 Janus van der Waals Eq. 23 and is better fitted than the three other equations: the n = 0 mono-critical Eq. 21, the original van der Waals Eq. 1, and the classical ideal gas law (2).

Figure 4 shows the isobaric curves of the cyclopentane molecule (C₅H₁₀) at P_r = 1.5 (A), P_r = 1.0 (B), and P_r = 0.5 (C), respectively. They are drawn by the NIST data and further by the four equations: the n = 2 Janus van der Waals Eq 23, the mono-critical equation (n = 0) (21), the original van der Waals Eq. 1, and the classical ideal gas law (2). The n = 2 Janus van der Waals equation is in excellent agreement with the NIST data, especially at the liquid–vapor coexistence region near P_r = 1 and at the supercritical region of P_r > 1.

FIGURE 4

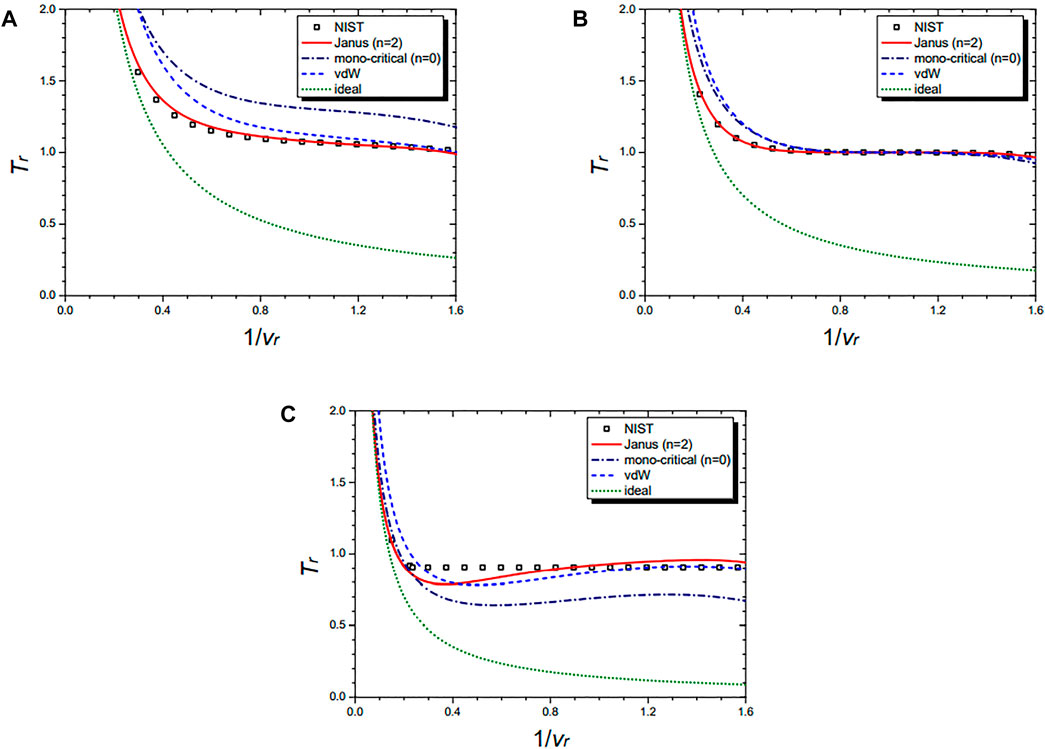
FIGURE 4. Isobaric curves of cyclopentane (C₅H₁₀) at P_r = 1.5 (A), P_r = 1.0 (B), and P_r = 0.5 (C), respectively. Boxes are from the NIST data. The red solid line is drawn from the n = 2 Janus van der Waals Eq. 23 and is better fitted than the n = 0 mono-critical Eq. 21, the original van der Waals Eq. 1, or the classical ideal gas law (2).

Figure 5 shows the isothermal curves of the cyclopentane molecule (C₅H₁₀) at T_r = 1.01 (A), T_r = 1.00 (B), and T_r = 0.99 (C), respectively. They are drawn by the NIST data and further by the four equations: the n = 2 Janus van der Waals Eq. 23, the mono-critical equation (n = 0) (21), the original van der Waals Eq. 1, and the classical ideal gas law (2). The Janus van der Waals equation shows the enhanced sigmoid shape compared to the original van der Waals equation when T_r is lower than 1.

FIGURE 5

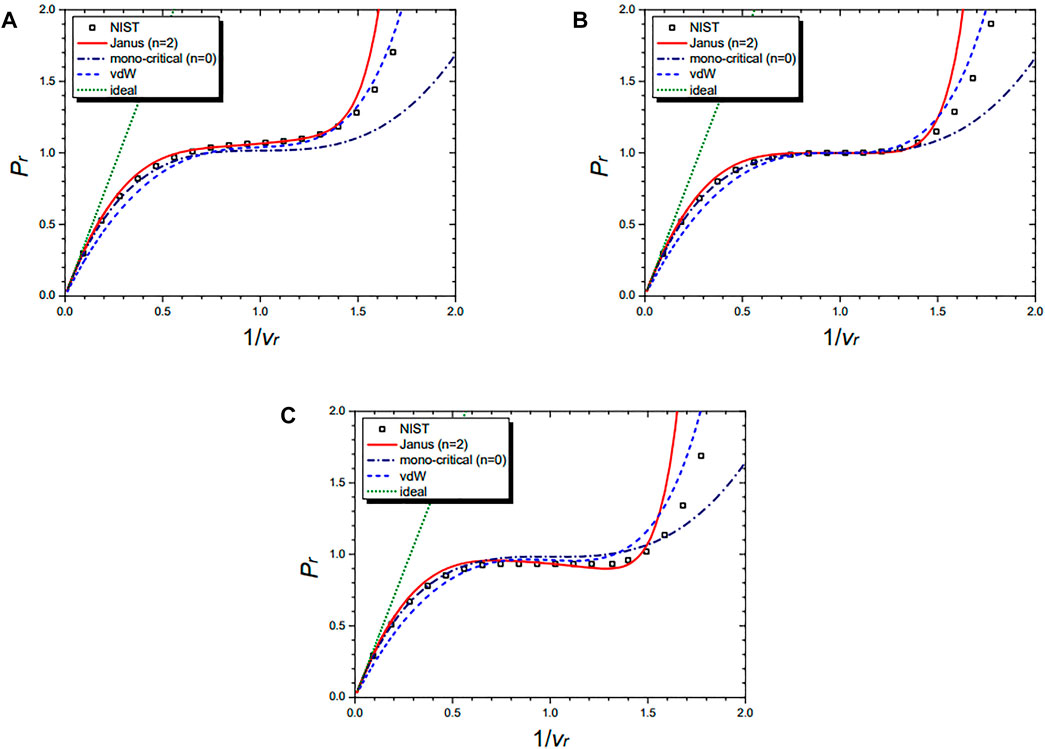
FIGURE 5. Isothermal curves of cyclopentane (C₅H₁₀) at T_r = 1.01 (A), T_r = 1.00 (B), and T_r = 0.99 (C), respectively. Boxes are from the NIST data. The red solid line is drawn from the n = 2 Janus van der Waals Eq. 23 and is better fitted than the n = 0 mono-critical Eq. 21, the original van der Waals Eq. 1, or the classical ideal gas law (2).

Figure 6 shows the three-dimensional P_r − v_r − T_r phase diagram of the exact n = 2 Janus van der Waals Eq. 7 with (13), as for cyclopentane molecule (C₅H₁₀). The red line shows the spinodal curve (8), i.e., ∂_vP (T, v) = 0, of the Janus van der Waals equation with the choice of a = 0.99.

FIGURE 6

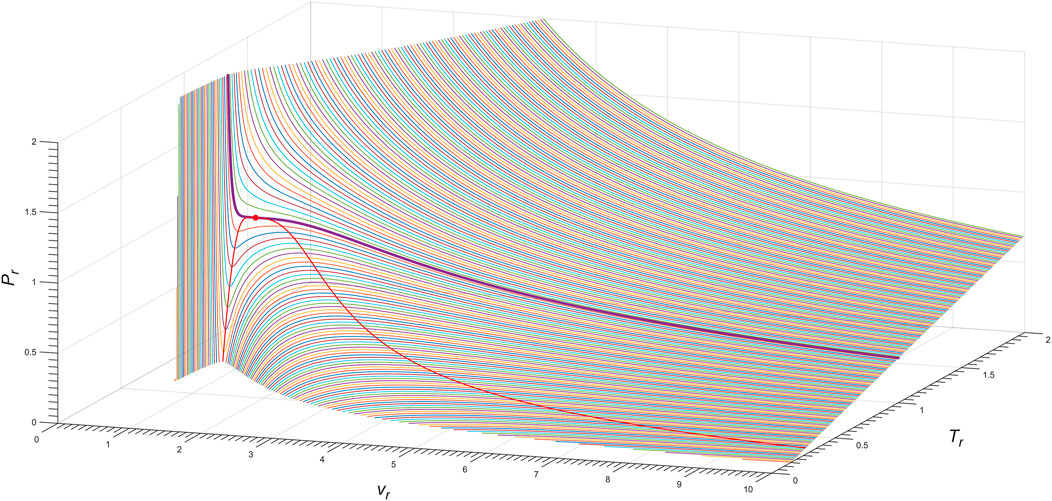
FIGURE 6. Three-dimensional P_r − v_r − T_r phase diagram of the exact n = 2 Janus van der Waals Eq. 7, as for the cyclopentane molecule (C₅H₁₀). The bold purple line corresponds to the isotherm of T_r = 1.00, as depicted in Figure 5B; the red line is the Janus van der Waals spinodal curve with a = 0.99; and the red dot is the critical point.

Now, we turn to the case of n = 4 where the following nine molecules belong to: nitrogen (N₂), argon (Ar), methane (CH₄), ethylene (C₂H₄), ethane (C₂H₆), propylene (C₃H₆), propane (C₃H₈), butane (C₄H₁₀), and isobutane (C₄H₁₀). Here, we chose nitrogen as a representative example. The other eight molecules and the n = 6 case to which only the helium-4 molecule belongs to are dealt in the Supplementary Material separately.

Figure 7 shows the isochoric curves of nitrogen (N₂) at 1/v_r = 0.02 (A), 1/v_r = 0.5 (B), 1/v_r = 1.0 (C), and 1/v_r = 1.5 (D), respectively. They are drawn by the NIST data and further by the four equations: the Janus van der Waals equation for n = 4 (25), the original van der Waals Eq. 1, and the classical ideal gas law (2). The Janus van der Waals equation fits best with the NIST data, especially at the region of T_r > 1 better than the original van der Waals equation. Again, we confirmed that the n = 4 Janus van der Waals equation reduces to the classical ideal gas law in the low-density limit.

FIGURE 7

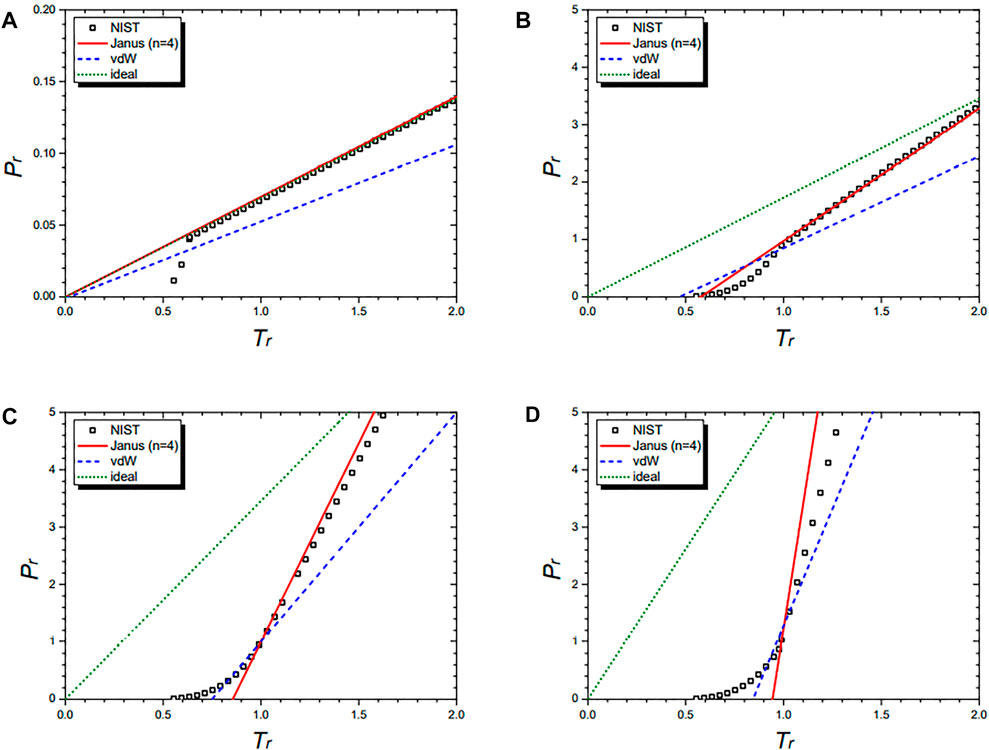
FIGURE 7. Isochoric curves of nitrogen (N₂) at 1/v_r = 0.02 (A), 1/v_r = 0.5 (B), 1/v_r = 1.0 (C), and 1/v_r = 1.5 (D), respectively. Boxes are from the NIST data. The red solid line is drawn from the n = 2 Janus van der Waals Eq. 23 and is better fitted than the original van der Waals Eq. 1 or the classical ideal gas law (2).

Figure 8 shows the isobaric curves of nitrogen (N₂) at P_r = 1.5 (A), P_r = 1.0 (B), and P_r = 0.5 (C), respectively. They are drawn by the NIST data and further by the three equations: the Janus van der Waals equation for n = 4 (25), the original van der Waals Eq. 1, and the classical ideal gas law (2). The n = 4 Janus van der Waals equation is in excellent agreement with the NIST data, especially at the liquid–vapor coexistence region near P_r = 1 and at the supercritical region of P_r > 1.

FIGURE 8

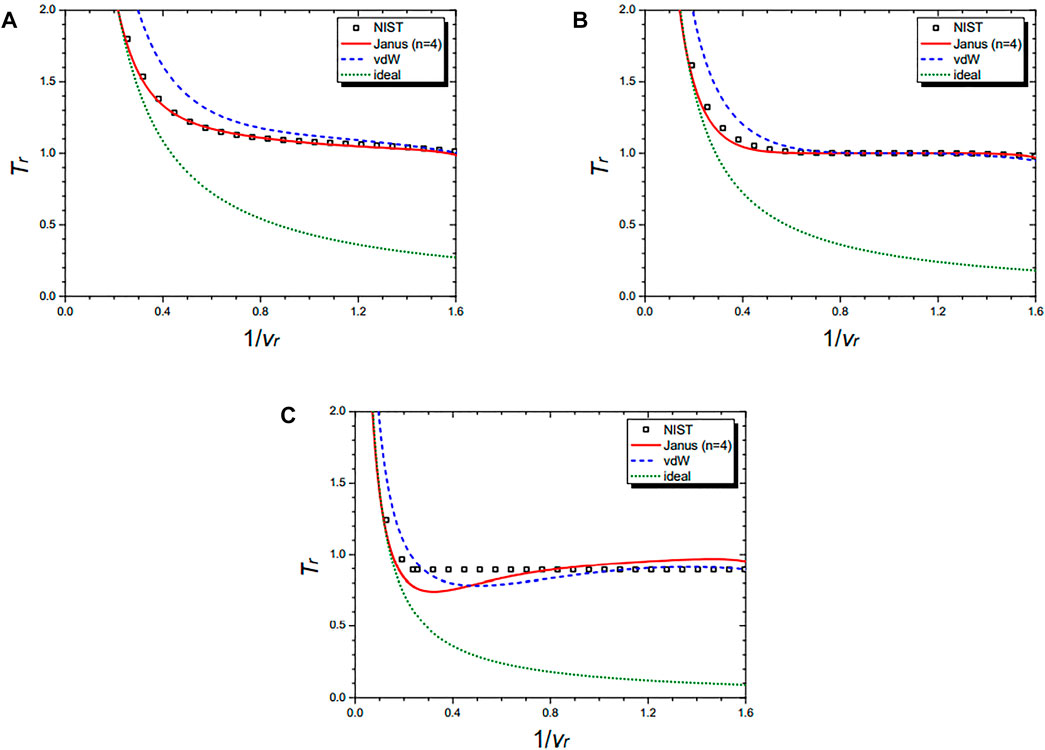
FIGURE 8. Isobaric curves of nitrogen (N₂) at P_r = 1.5 (A), P_r = 1.0 (B), and P_r = 0.5 (C), respectively. Boxes are from the NIST data. The red solid line is drawn from the n = 4 Janus van der Waals Eq. 25 and is better fitted than the original van der Waals Eq. 1 or the classical ideal gas law (2).

Figure 9 shows the isothermal curves of nitrogen (N₂) at T_r = 1.01 (A), T_r = 1.00 (B), and T_r = 0.99 (C), respectively. They are drawn by the NIST data and further by the three equations: the n = 4 Janus van der Waals Eq. 25, the original van der Waals Eq. 1, and the classical ideal gas law (2). The Janus van der Waals equation shows the enhanced sigmoid shape compared to the original van der Waals equation when T_r is lower than 1.

FIGURE 9

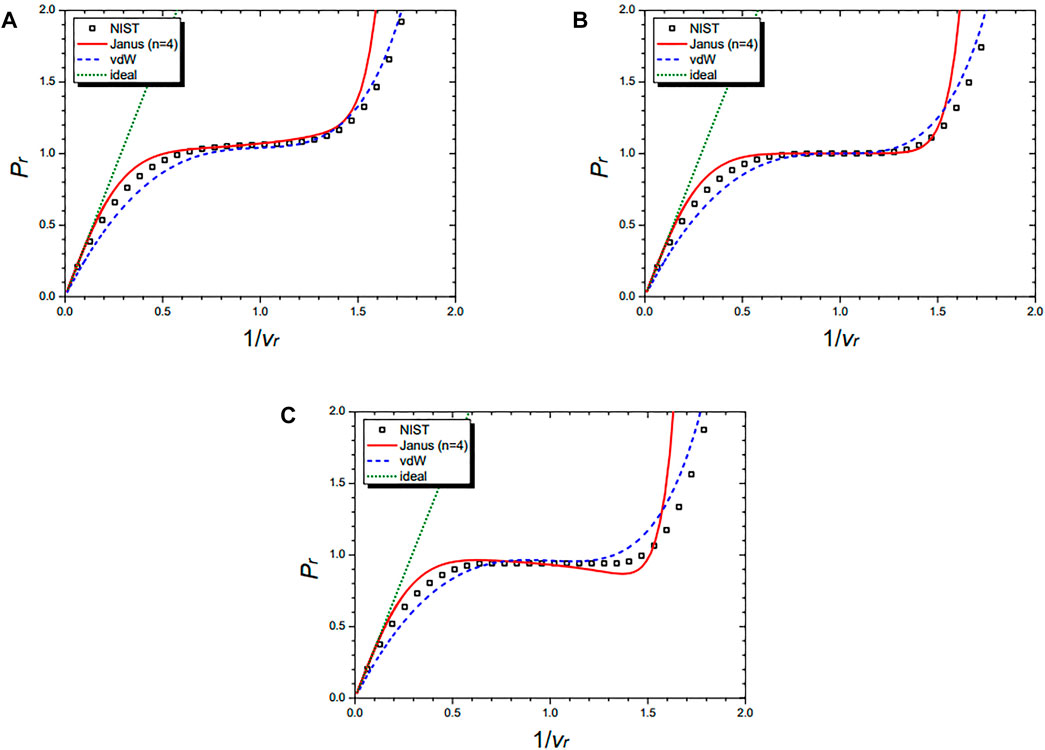
FIGURE 9. Isothermal curves of nitrogen (N₂) at T_r = 1.01 (A), T_r = 1.00 (B), and T_r = 0.99 (C), respectively. Boxes are from the NIST data. The red solid line is drawn from the n = 4 Janus van der Waals Eq. 25 and is better fitted than the original van der Waals Eq. 1 or the classical ideal gas law (2).

Figure 10 shows the three-dimensional P_r − v_r − T_r phase diagram of the exact n = 4 Janus van der Waals Eq. 7 with (13), as for nitrogen (N₂). The red line shows the spinodal curve (8), i.e., ∂_vP (T, v) = 0, of the Janus van der Waals equation with the choice of a = 0.99.

FIGURE 10

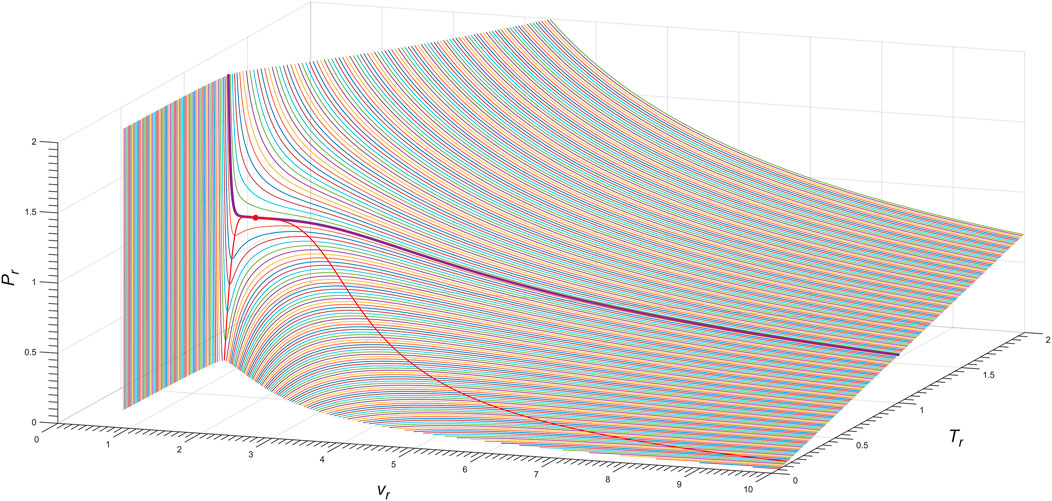
FIGURE 10. Three-dimensional P_r − v_r − T_r phase diagram of the exact n = 4 Janus van der Waals Eq. 7, as for nitrogen (N₂). The bold purple line corresponds to the isotherm of T_r = 1.00, as depicted in Figure 9B; the red line is the Janus van der Waals spinodal curve with a = 0.99; and the red dot is the critical point.

Discussion

Our Janus van der Waals equations may appear somewhat similar to the other known equations of state, such as an earlier modified van der Waals equation (9) or the virial equation of state [10], a typical example of series expansion. Irrespective of the similarity of appearance to other equations, Janus van der Waals equations differ significantly from others as the starting point is directly from statistical physics itself at the quantum level: in other words, the partition function of any finite system should be analytic. Alternative to the conventional thermodynamic limit [11, 12], if we persistently take the analyticity of a partition function for granted [8, 13–17], it becomes the spinodal curve itself that draws the liquid–gas phase diagram where a critical point is identified as the extremum of the spinodal curve, see [8] and Figure 6 therein. One surprising result of the previous work by two of us [5] was the possibility of having more than one critical point which should be very close to each other. The uncertainty in the measurement of the temperature is typically the order of magnitude smaller than that of the density [18], for example, around the critical point of nitrogen (N₂), we have the temperature uncertainty ΔT_r ≲ 0.0079%, which is 16 times smaller than that of the density Δ(1/v_r) ≲ 0.13% [6, 19]. This has motivated us to conceive the ansatz (8) which modifies the original van der Waals equation and realizes the idea of multi-critical points in a simple manner, where the two distinct critical points assume the same temperature.³ We have restricted to even critical indices, n_c = n = 2, 4, 6 for T < T_c and n_c = 2 for T > T_c, or following the notation of [5], (n₊, n₋) = (2, n). Our proposed van der Waals equations then naturally explain the two-sided phase transitions reported in [5] and provided the overall effective descriptions of real molecules, in particular better than the original van der Waals equation and the classical ideal gas law.

In Figure 11, we have compared the NIST co-existence curve data on the cyclopentane molecule (C₅H₁₀) with the Janus van der Waals spinodal curve (8) of n = 2, a = 0.99 and also with the original van der Waals spinodal curve (5). The Janus van der Waals spinodal curve fits well the NIST co-existence curve data in a wider range near the critical point, although not perfect. Further modifications of the present Janus van der Waals equations to match the spinodal curves with the co-existence curves of real molecules will lead to more realistic and improved equations of state. Such modifications may require more than the two critical points, generalizing the ansatz (8):

$T_r=-{\left(v_r-b\right)}^2\frac{\text{d}{f}_{\vec{n}}\left(v_r\right)}{\text{d}{v}_r}=1-\prod _{i=1}^N\frac{{\left(v_r-a_i\right)}^{n_i}}{v_r}.(28)$

Here, n_is are natural numbers, and particularly, those a_is with n_i ≥ 2 (even as well as odd) correspond to multi-critical points. The largest value of such a_is should be exactly in unity with the critical index 2 as the NIST data suggest [5], while the smallest one should be still close to unity. Furthermore, the former should be a local maximum of T_r, while the latter should be either a local maximum as in Figure 1 if the critical index is even or an inflection point if it is odd. We leave the construction of this kind of multi-critical Janus van der Waals equations for future work.

FIGURE 11

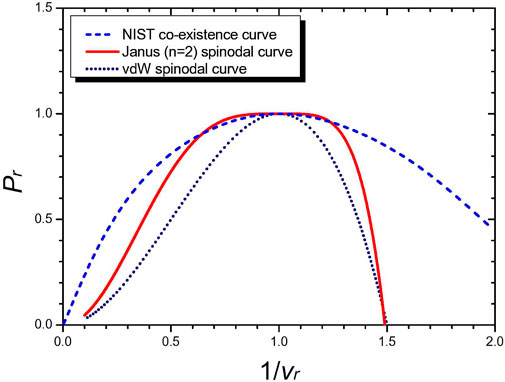
FIGURE 11. Comparison of the NIST co-existence curve data on cyclopentane (C₅H₁₀) (blue colored) with the Janus van der Waals spinodal curve (red colored, a = 0.99) and with the original van der Waals spinodal curve (dotted black line). It is a conjecture of Ref. [8] that the liquid–gas co-existence curve should actually coincide with the spinodal curve. Improving our proposed Janus van der Waals equations further, this may be realizable.

The three Janus van der Waals Eqs 23, 25, and 27 have been obtained after taking the limit a → 1⁻. Thus, the formulas should not be used to see the two-sided critical phase transitions for which the exact formula (7) with (13) must be taken and zoomed in sufficiently. When zoomed out, or moderately away from the two critical points, the two powers, ${(v_r-a)}^n$ and ${(v_r-1)}^2$ in (8) may appear converging to ${(v_r-1)}^{n+2}$ and mimic an enhanced critical index n_c = n + 2. This implies the critical exponents ${\alpha }_P={\gamma }_P=\frac{n+2}{n+3}$ and ${\beta }_P={\delta }^{-1}=\frac{1}{n+3}$ and also explains the ‘flatness’ of the top of the spinodal curve in Figure 11. The three formulas (23), 25, and 27 are for such effective descriptions. The NIST data analyses of [5], in particular Figures 2–4 therein, seem to agree with this enhancement moderately away from the critical points.

Having Janus van der Waals equations completely determined, it is worthwhile to recall

$P_r=\chi T_r\frac{\partial \ln Z\left(T_r,v_r\right)}{\partial v_r},(29)$

and to obtain the underlying partition function (per particle),

$\ln Z=\ln \left[\left(v_r-b\right)T_r^{3/2}\right]+\sum _{l=0}^{n+1}\frac{c_l{\left(b/v_r\right)}^{n+2-l},}{\left(n+3-l\right)\left(n+2-l\right)b^4{T}_r},(30)$

where the constant of integration $\frac{3}{2}\ln T_r$ has been added to ensure the isochoric specific heat $c_v=\frac{3}{2}{k}_{\text{B}}$ at high temperature.

Given the good agreement of the Janus van der Waals equation and the NIST reference data, which we report in this work, we call for further investigation of the multi-critical points and the analyticity of partition functions questioning the (rather dogmatic) thermodynamic limit.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

J-HP proposed the research and derived the formulas. JK contributed the NIST reference data handling and analysis. D-HK led the interpretation of the data. D-HK and J-HP wrote the manuscript.

Funding

This work was supported by the Basic Science Research Program through the National Research Foundation of Korea Grants, NRF-2016R1D1A1B01015196 and NRF-2020R1A6A1A03047877 (Center for Quantum Space Time).

Acknowledgments

The authors thank KyuHwan Lee for technical help at the early stage of the project.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.917453/full#supplementary-material

References

1. Zinn-Justin J. Quantum field theory and critical phenomena. 2nd ed. New York: Oxford University Press (1993). p. 610.

Google Scholar

2. Nelson DR. Coexistence-curve singularities in isotropic ferromagnets. Phys Rev B (1976) 13:2222–30. doi:10.1103/physrevb.13.2222

CrossRef Full Text | Google Scholar

3. Léonard F, Delamotte B. Critical exponents can Be different on the two sides of a transition: A generic mechanism. Phys Rev Lett (2015) 115(20):200601. [arXiv:1508.07852 [cond-mat.stat-mech]]. doi:10.1103/PhysRevLett.115.200601

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Azeyanagi T, Ferrari F, Schaposnik Massolo FI. Phase diagram of planar matrix quantum mechanics, tensor, and sachdev-ye-kitaev models. Phys Rev Lett (2018) 120(6):061602. arXiv:1707.03431 [hep-th]]. doi:10.1103/PhysRevLett.120.061602

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cho W, Kim D-H, Park J-H. Isobaric critical exponents: Test of analyticity against NIST reference data. Front Phys (2018) 6:112. arXiv:1612.06532 [cond-mat.stat-mech]]. doi:10.3389/fphy.2018.00112

CrossRef Full Text | Google Scholar

6. Lemmon EW, Huber ML, McLinden MO. NIST reference fluid thermodynamic and Transport Properties Database (REFPROP): Version 9.1. Gaithersburg: National Institute of Standards and Technology (NIST), Standard Reference Data Program (2013). Available at: https://www.nist.gov/srd/refprop.

Google Scholar

7. Bak D, Gutperle M, Hirano S. A Dilatonic deformation of AdS(5) and its field theory dual. J High Energ Phys (2003) 0305:072. doi:10.1088/1126-6708/2003/05/072

CrossRef Full Text | Google Scholar

8. Park J-H, Kim S-W. Existence of a critical point in the phase diagram of the ideal relativistic neutral Bose gas. New J Phys (2011) 13:033003. doi:10.1088/1367-2630/13/3/033003

CrossRef Full Text | Google Scholar

9. Schmidt G, Wenzel H. A modified van der Waals type equation of state. Chem Eng Sci (1980) 35:1503–12. doi:10.1016/0009-2509(80)80044-3

CrossRef Full Text | Google Scholar

10. Dymond JD, Marsh KN, Wilhoit RC. Virial coefficients of pure gases and mixtures. Heidelberg: Springer Berlin (2003).

Google Scholar

11. Yang CN, Lee TD. Statistical theory of equations of state and phase transitions. I. Theory of condensation. Phys Rev (1952) 87:410.

CrossRef Full Text | Google Scholar

12. Kadanoff LP. More is the same; phase transitions and mean field theories. J Stat Phys (2009) 137:777–97. doi:10.1007/s10955-009-9814-1

CrossRef Full Text | Google Scholar

13. Park J-H, Kim S-W. Thermodynamic instability and first-order phase transition in an ideal Bose gas. Phys Rev A (Coll Park) (2010) 81:063636. doi:10.1103/physreva.81.063636

CrossRef Full Text | Google Scholar

14. Jeon I, Kim S-W, Park J-H. Isobars of an ideal Bose gas within the grand canonical ensemble. Phys Rev A (Coll Park) (2011) 84:023636. doi:10.1103/physreva.84.023636

CrossRef Full Text | Google Scholar

15. Park J-H. How many is different? Answer from ideal Bose gas. J Phys : Conf Ser (2014) 490:012018. [arXiv:1310.5580 [cond-mat.stat-mech]], c.f. [17]. doi:10.1088/1742-6596/490/1/012018

CrossRef Full Text | Google Scholar

16. Cho W, Kim SW, Park J-H. Two-dimensional Bose-Einstein condensate under pressure. New J Phys (2015) 17(1):013038. [cond-mat.quant-gas]]. doi:10.1088/1367-2630/17/1/013038

CrossRef Full Text | Google Scholar

17. Anderson PW. More is different. Science (1972) 177:393–6. doi:10.1126/science.177.4047.393

PubMed Abstract | CrossRef Full Text | Google Scholar

18. McLinden MO. Densimetry for primary temperature metrology and a method for the in situ determination of densimeter sinker volumes. Meas Sci Technol (2006) 17:2597–612. doi:10.1088/0957-0233/17/10/011

CrossRef Full Text | Google Scholar

19. Span R, Lemmon EW, Jacobsen RT, Wagner W, Yokozeki A. A reference equation of state for the thermodynamic Properties of nitrogen for temperatures from 63.151 to 1000 K and pressures to 2200 MPa. J Phys Chem Reference Data (2000) 29:1361–433. doi:10.1063/1.1349047

CrossRef Full Text | Google Scholar

Footnotes

¹“Janus” is a Roman god who has two faces. Our nomenclature is inspired partially by [7].

²Essentially, the coefficients (14) stem from a recurrence relation c_l − 2c_l−1 + c_l−2 = h_l for some h_l, whose solution reads in general $c_l={\sum }_{j=0}^l(l+1-j)h_j$.

³This is for practical purpose. We do not exclude the possibility that the temperatures of the neighboring critical points may differ by an insignificant amount.