Abstract
In this article, the thermal flow effects of inclined magnetohydrodynamics ferrofluid filled in a wavy cavity are studied by adopting the finite element method (FEM). The non-dimensional governing equations and model for different parameters are evaluated. The system of non-linear algebraic equations is computed by adopting the Newton method. A space involving quadratic polynomials () has been selected to compute for the velocity profile, while the pressure and temperature profiles are approximated by linear () finite element space of functions. The discrete systems of non-linear algebraic equations are computed by utilizing the Newton method. The vertical walls are considered cold, whereas the bottom wavy surface is considered hot and the top wavy surface is insulated. The effect of the pertinent parameters, like , volume fraction inclination angle , and amplitude of the wavy surface is investigated. Computational results are addressed as streamlines out, isotherms, and proper graphs for substantial amounts of interest. Increasing Hartmann number ( leads to an increase in Bejan number , while opposite behavior can be observed in the case of viscous, magnetic, and thermal irreversibility, that is, curves are decreased by increasing . Under the influence of an inclined magnetic field, the mathematical structuring of the problem is manifested by continuity, momentum, and energy equations. These equations are solved by using the finite element method computation. The graphs of velocity and isotherm are compared to the relevant parameters. To predict the flow characteristics at different locations, cross-sectional lines representing the velocity field in the horizontal and vertical directions are also drawn. Magnetization’s impact on flow control, heat transfer, and various irreversibilities are also discussed. The progressively declined with the enhancement in the amplitude of the wavy surface .
Introduction
Within the computational fluid dynamics field, lid-driven cavity flow is widely researched. Since the geometry of cavity flow is simple, the algorithm can be coded easily and boundary conditions can be applied. Despite the way that the issue shows up simple in many regards, the flow in a cavity holds all of the fluid mechanics, with counter-turning vortices showing up at the cavity’s corners [1]. Cavities with wavy walls can be found in many engineering applications, such as heat exchangers, solar panels, and buildings. A few specialized applications, like cooling of electronic parts and fixed electrical or electronic boxes, cooling or heating rooms, heat exchanger plans, and sunlight-based energy authority plans, are keen on regular convection heat move from wavy surfaces. When considering all of these factors, natural convection heat transmission becomes quite important [2]. K. S. Mushate [3] has numerically examined natural convection thermal flow within a square cavity with two wavy sides. [4] considered the complex wavy walls and offered important knowledge into imminent answers for further developing convection heat move execution inside encased depressions with wavy wall (complex) surfaces. R. C. Mohapatra [5] tackled the natural convection issue in a cavity with three flat walls and a right upward wall with one undulation and three undulations. H. R. Ashorynejad [6] utilized the lattice Boltzmann method (LBM) to investigate the thermal flow of uniformly magnetized hybrid nanofluid within a wavy cavity. K. Javaherdeh [7] conducted a numerical study to research the thermal flow properties in a wavy enclosure inside the nanomaterials.
[8] conducted research and utilized 3D numerical simulation to determine the impact of a magnetized ferrofluid and thermal flow in a wavy channel. [9] used a unique approach to explore the behavior of ferrofluid inside a permeable district when presented to an electric field. [10] employed computational study of thermal flow peculiarities in a kerosene-based ferrofluid. [11] considered a numerical study of ferrofluid-filled lid-driven cavity for various heater configurations numerically.
Within the sight of an isothermally heated corner, a numerical investigation of MHD natural convection in a wavy open permeable tall cavity loaded up with a Cu–water nanofluid was researched by [12]. [13] used local thermal non-equilibrium conditions to investigate magnetize hybrid nanomaterial in a wavy porous media. [14] implemented a finite volume approach to analyze the magnetohydrodynamic non-Newtonian ferrofluid to better understand the properties of heat transfer in a duct. [15] studied the entropy-based characteristics of thermal flow rate in a cavity having a rotating obstacle. Furthermore, in everyday life, thermal conductivity has a basic impact on re-scaling the thermal flow characteristics of fluids. In this regard, [16–23] mention some new modifications, addressing major physical aspects and computational techniques. Selimefendigil and Öztop [24] have investigated the characteristics of thermal enhancement through MHD nanofluid in a cavity. Furthermore, they have explored the magnetic field is imposed and its strength is steadily raised, it reduces heat transmission and convective fluid motion. [25] analyzed the effects of heat transfer and a phase change material (PCM) inside the cavity in the presence of nanofluid via finite element computation. In addition, they have considered a lower PCM height and a better thermal conductivity ratio result in enhanced local and average temperature distribution. [26] investigated the influence of entropy generation and MHD nanofluid inside the permeable cavity. The fluctuation of the local Nusselt number for the corrugated wall is affected by the triangle wave’s imposed frequency. The corrugation frequency near the heated wall has a big impact on velocity and temperature implementations.
The objective of the present article is to elucidate the entropy generation process by including the magnetic field and natural convection process. A wide range of irreversibility types have been discussed including the irreversibilities of heat transfer, viscous effects, and magnetic field.
Problem Description
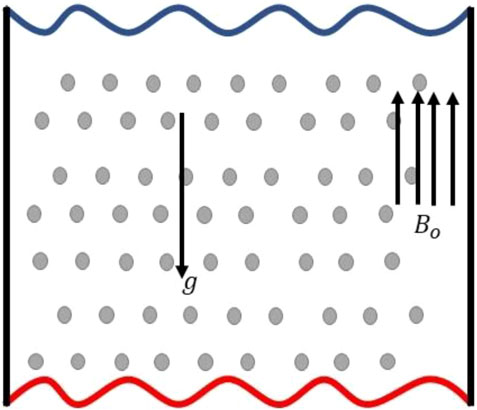
The wavy surface is considered here in this problem and the physical diagram of the problem is portrayed in Figure 1. In a cavity, represents temperature of the hot wall, while denotes the temperature of the cold wall, and the top wavy wall is insulated.
FIGURE 1
Schematic diagram of the problem.
The non-dimensional mathematical description of ferrofluid flow governed by the conservation law of mass, momentum, and energy are given as [
14]
where symbols have been established in the nomenclature portion. The boundary conditions are given as follows:
i) = 1, at the lower wavy surface.
ii) = 0, at all sides of the cavity.
iii) = 0, at the upper wavy surface.
iv) , at the vertical walls.
Thermophysical Features of Nanofluid
The effective equations for the thermophysical characteristics of the nanoparticle employed in this investigation. Table 1 also takes into account the ferrofluid’s thermophysical characteristics [14].
| Density |
| Thermal diffusivity |
| Electrical conductivity: |
| Specific heat |
| Thermal conductivity |
| Thermal expansion coefficient |
| Dynamic viscosity |
| Average Nusselt number |
TABLE 1
| 997.1 | 4,179 | 0.613 | 21E-5 | |
| 5,200 | 670 | 6 | 1.18E-5 |
Description of the base fluid and nanoparticles properties.
Entropy Generation
The measurement of local entropy production derived by adding conjugated fluxes and produced forces is referred to as irreversibility analysis. The non-dimensional local entropy production in a convective process and under the effect of a magnetic field is given by [14]:where
Here, , and represent the local entropy generation, entropy generation due to heat transfer ), irreversibility of viscous , and the irreversibility of magnetic field. In Eq. 5, the formula for distribution irreversibility ratio () is given in Eq. 10.
Here, represents the average temperature, that is, .
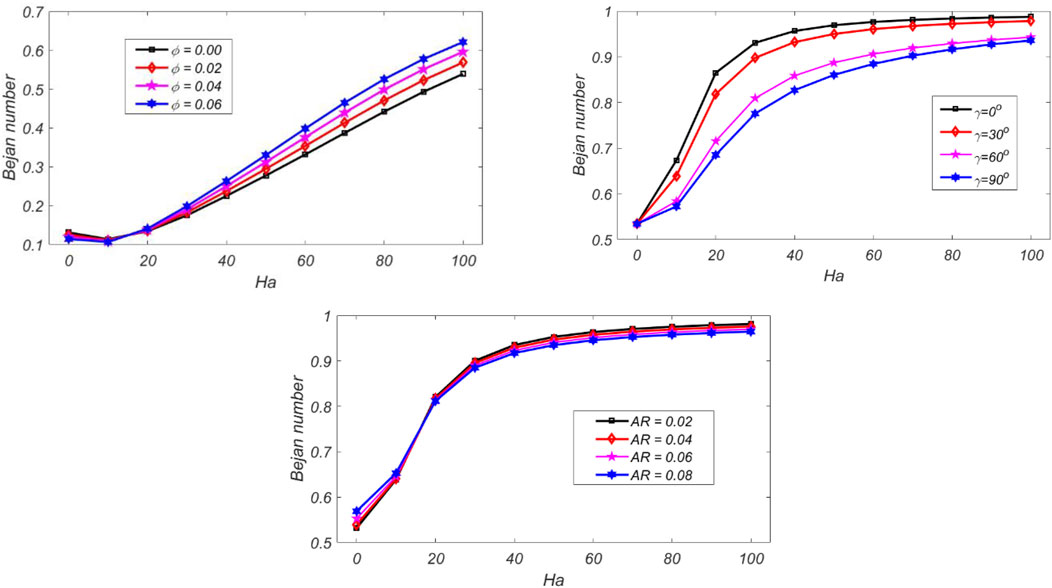
In addition, the non-dimensional Bejan number is described as the ration of thermal entropy and local entropy , which is found as , respectively.
Numerical Procedure
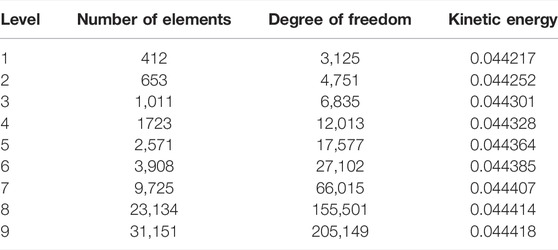
Because of the non-linearity and coupling of the governing Eqs 1–4, the continuity, momentum, and energy equations cannot be solved with analytical solution techniques, so we executed the solution using numerical approach, namely, FEM. The computational grid on a coarse level is shown in Figure 2 where a hybrid meshing is performed to capture the flow dynamics accurately near the boundaries. A space involving the quadratic polynomials () has been selected to compute for the velocity profile, while the pressure and temperature profiles are approximated by linear () finite element space of functions. The discrete systems of non-linear algebraic equations are computed by utilizing the Newton method and the linearized inner system with a direct solver PARDISO. There are many benefits of using the PARDISO solver (see [27–34] for further information). The PARDISO solver uses LU factorization and reduces the number of cycles required for the desired level of convergence.
FIGURE 2
Computational grid of the domain.
For various grid levels, the kinetic energy is determined. As the refinement level is increased, the percentage of an error lowers. The eighth refinement level is employed during findings because the difference between levels 8 and 9 is the smallest (Table 2).
TABLE 2
| Level | Number of elements | Degree of freedom | Kinetic energy |
|---|---|---|---|
| 1 | 412 | 3,125 | 0.044217 |
| 2 | 653 | 4,751 | 0.044252 |
| 3 | 1,011 | 6,835 | 0.044301 |
| 4 | 1723 | 12,013 | 0.044328 |
| 5 | 2,571 | 17,577 | 0.044364 |
| 6 | 3,908 | 27,102 | 0.044385 |
| 7 | 9,725 | 66,015 | 0.044407 |
| 8 | 23,134 | 155,501 | 0.044414 |
| 9 | 31,151 | 205,149 | 0.044418 |
Grid convergence test for kinetic energy.
Results and Discussion
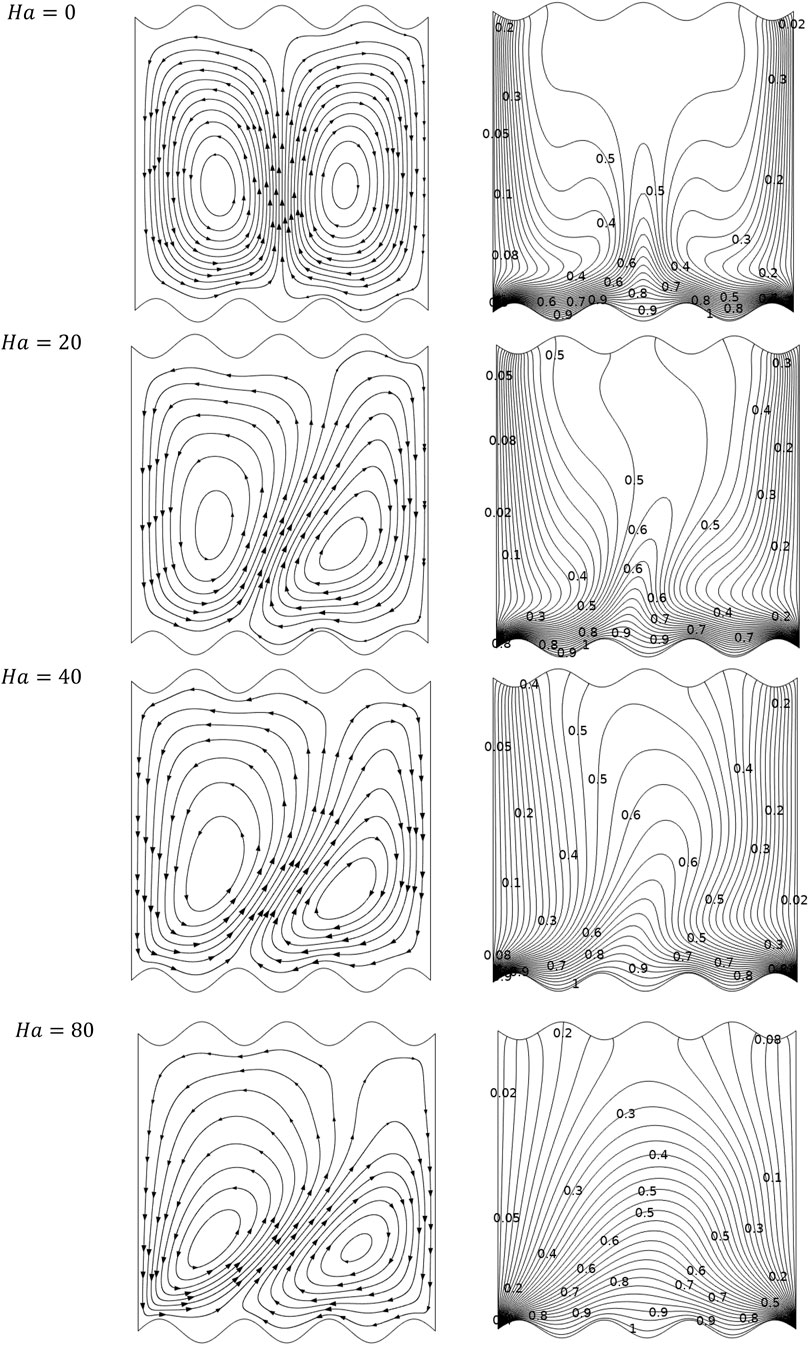
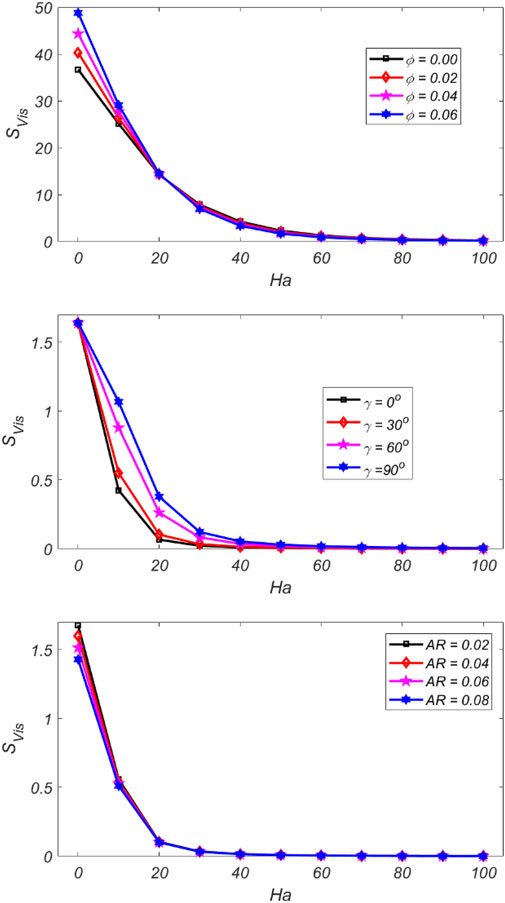
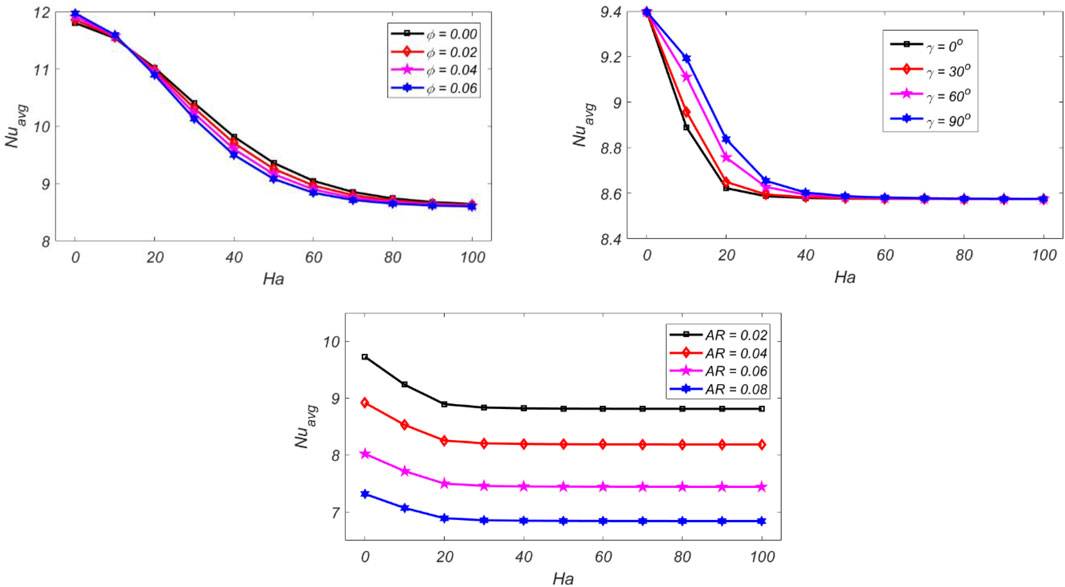
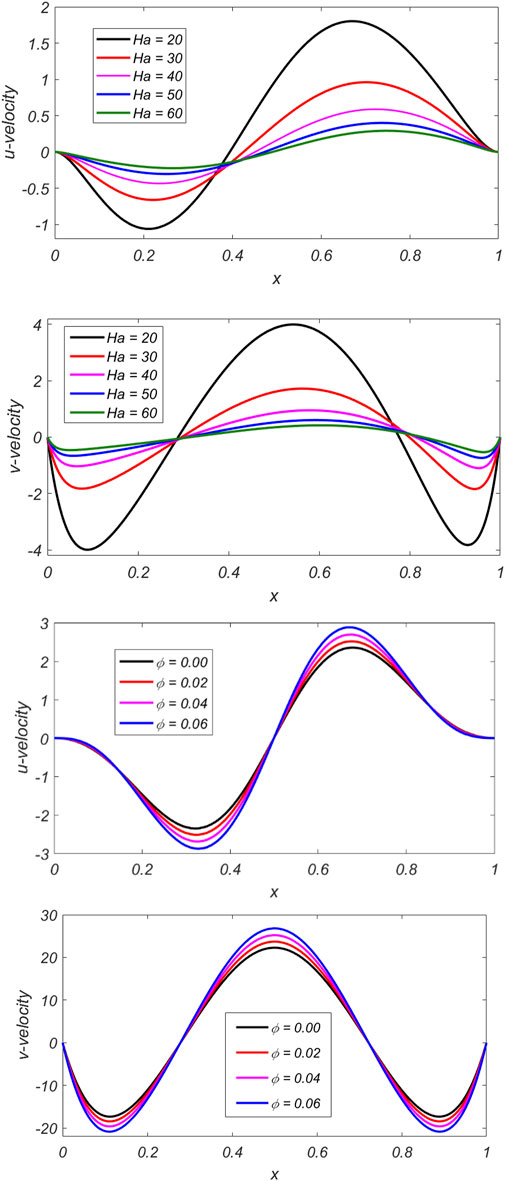
In this section, we present the flow features pertaining to different ranges of the involved physical parameters. Figure 3 shows the impact of on streamline (left) and isotherm contour (right) with Rayleigh number and = 0.04 in a wavy cavity. A couple of counter-rotating cells is shaped in the left and right portions of the enclosure. This fig shows a configuration of flow defined by two thermally convective cells that are symmetrical around the mid-plane . Compared to the left cell, the right one is squeezed and smaller as a result of the present undulation; however, it has considerably less impact on the left cell. The isotherms for higher concentrate near the bottom wall because the advection mode of the heat transfer dominates over conduction. At the point when is expanded, the compression of isotherms relaxes, this, in turn, reduces the amount of heat transmitted through hot vertical walls.
FIGURE 3
Impacts of on streamline (left) and isotherm contour (right) with and.
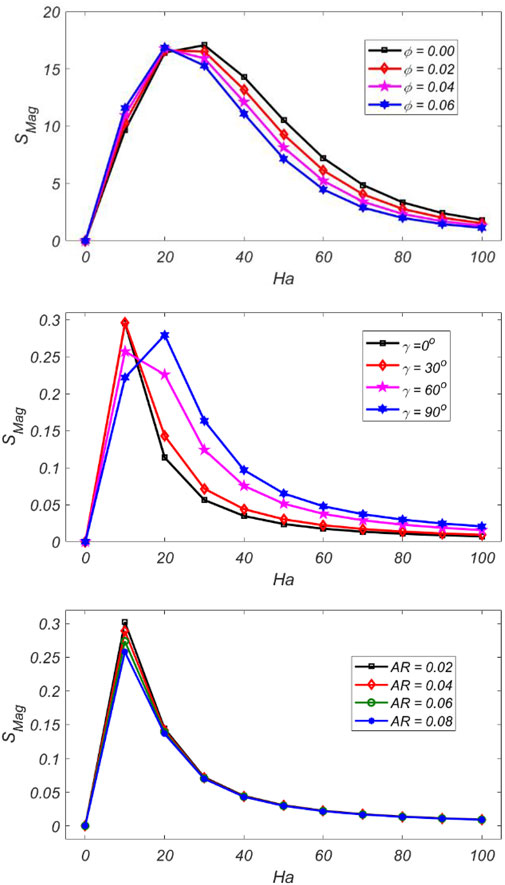
Figure 4 shows the variation of the production with for three different parameters, that is, volume fraction ( ), angle of inclination ( and amplitude of wavy surface (AR). It is noteworthy that thermal entropy generation in case of and has the highest numerical value when is low and afterward diminishes as is expanded and the curve is symmetrical in case of .
FIGURE 4
Impacts of on for various parameters.
Figure 5 depicted viscous irreversibility, which is related to for different parameters. When we increase , we can easily see that the generation of decreases. This decrease is caused by a decrease in natural convection as a result of the Lorentz force’s latent impact. It can also be examined that in the case of and the curves are decreasing until and after that the values of and are equal for a large value of .
FIGURE 5
Impacts of on for various parameters.
While in case of inclination angle () attains the maximum value at = and minimum value at . Figure 6 shows the impact on magnetic irreversibility against for different parameters. It is analyzed that in case and all curves at first increase then steadily decline as increases due to the Lorentz force. The curves show a similar trend in the case of AR. Figure 7 shows the impact on against for different parameters. It can be noted that in the case of volume fraction and amplitude of the wavy surface the curves are initially decreasing up to certain values of and after that the curves increase by increasing . Figure 8 illustrates the variation of with for different parameters. It can be noted that the curves continuously decrease as the value of increase. The curves are symmetrical in the case of Figure 9 shows the impact of velocity components on Ha and . The velocity profile has the peak values at the middle and least values near the wavy surface.
FIGURE 6
Impacts on against for different parameters.
FIGURE 7
Impacts on against for different parameters.
FIGURE 8
Impacts on against for different parameters.
FIGURE 9
Impacts of velocity components on Hartman number (Ha) and volume fraction.
Conclusion
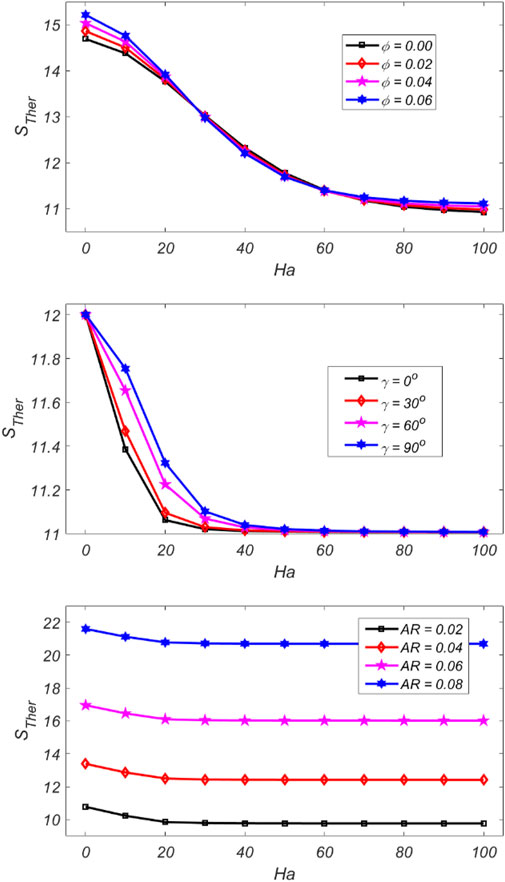
In this study, the thermal flow effects of inclined MHD ferrofluid filled in a wavy cavity are studied by adopting the FEM. The study has been considered by varying parameters, like
, volume fraction
inclination angle
, and amplitude of the wavy surface
by maintaining the Prandtl number (
) fixed. The results have been illustrated using graphs to show the physical repercussions. Magnetic, viscous, and thermal entropies are the three types of entropy variations that are evaluated. The primary goal of our current effort is to reveal variation in entropy generation in enclosures and to make predictions about factors that influence entropy measurements. The main findings of the aforementioned study are summarized as follow:
• is decreased with an increase in , while it is pronounced with an increase in .
• displayed an increasing trend with .
• Increasing leads to a decrease in viscous, thermal, and magnetic irreversibilities due to the Lorentz force.
• progressively declined with the enhancement in the amplitude of the wavy surface .
• A forward flow is observed via the horizontal component of the velocity in the upper half of the cavity while a backward flow in the lower half, with a strength directly proportional to the volume fraction .
• The vertical component of the velocity is enhanced in the central region of the cavity with an increase in the volume fraction
• For all cases of and , viscous irreversibility is dominated by the thermal irreversibility at low .The influence of corrugation amplitude, various corrugation types, different nanofluid types, and transient flow effects could all be addressed as extensions of this work.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YK has carried out modeling and computing data. RM has supervised us. AM and NR have written a complete manuscript. AA and NF have performed revisions and re-wrote the manuscript.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research, University of Hafr Al Batin for funding this work through the research group project no. (0033-1443-S).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
Specific heat
Hartmann number
Magnetic field
Cavity height
Prandtl number
Rayleigh number
Pressure
Thermal entropy
Magnetic entropy
Viscous entropy
Temperature
Non-dimensional velocities
Non-dimensional coordinates
Volume fraction
Temperature of the hot wall
Temperature of the cold wall
Density
Temperature gradient
Dynamic viscosity
Bejan number
Thermal diffusivity
Expansion coefficient
Distribution irreversibility ratio
Thermal conductivity
Amplitude of wavy surface
Average Nusselt number
Nomanclature
Abbreviations
Specific heat Hartmann number Magnetic field Cavity height Prandtl number Rayleigh number Pressure Thermal entropy Magnetic entropy Viscous entropy Temperature Non-dimensional velocities Non-dimensional coordinates Volume fraction Temperature of the hot wall Temperature of the cold wall Density Temperature gradient Dynamic viscosity Bejan number Thermal diffusivity Expansion coefficient Distribution irreversibility ratio Thermal conductivity Amplitude of wavy surface Average Nusselt number
References
1.
Erturk E . Discussions on Driven Cavity Flow. Int J Numer Meth Fluids (2009) 60:275–94. 10.1002/fld.1887
2.
Singh S Bhargava R . Numerical Study of Natural Convection within a Wavy Enclosure Using Meshfree Approach: Effect of Corner Heating. Scientific World J (2014) 2014:1–18. 10.1155/2014/842401
3.
Mushate KS . CFD Prediction of Natural Convection in a Wavy Cavity Filled with Porous Medium. Glob J Res Eng (2011) 11(2):29–42.
4.
Cho C-C Chen C-L Chen Co.-K . Natural Convection Heat Transfer Performance in Complex-Wavy-wall Enclosed Cavity Filled with Nanofluid. Int J Therm Sci (2012) 60:255–63. 10.1016/j.ijthermalsci.2012.05.001
5.
Mohapatra RC . Study on Natural Convection in a Square Cavity with Wavy Right Vertical wall Filled with Viscous Fluid. Iosr Jmce (2017) 14(01):32–9. 10.9790/1684-1401023239
6.
Ashorynejad HR . Natural Convection of Hybrid Nanofluid in an Open Wavy Cavity. Results Phys (2018) 9:440–55. 10.1016/j.rinp.2018.02.045
7.
Javaherdeh K Moslemi M Shahbazi M . Natural Convection of Nanofluid in a Wavy Cavity in the Presence of Magnetic Field on Variable Heat Surface Temperature. J Mech Sci Technol (2017) 31(4):1937–45. 10.1007/s12206-017-0342-7
8.
Mousavi SM Biglarian M Darzi AAR Farhadi M Afrouzi HH Toghraie D . Heat Transfer Enhancement of Ferrofluid Flow within a Wavy Channel by Applying a Non-uniform Magnetic Field. J Therm Anal Calorim (2020) 139(5):3331–43. 10.1007/s10973-019-08650-6
9.
Saleem S Shafee A Nawaz M Dara RN Tlili I Bonyah E . Heat Transfer in a Permeable Cavity Filled with a Ferrofluid under Electric Force and Radiation Effects. AIP Adv (2019) 9(9):095107. 10.1063/1.5120439
10.
Jafari A Tynjälä T Mousavi SM Sarkomaa P . Simulation of Heat Transfer in a Ferrofluid Using Computational Fluid Dynamics Technique. Int J Heat Fluid Flow (2008) 29(4):1197–202. 10.1016/j.ijheatfluidflow.2008.01.007
11.
Rabbi KM Saha S Mojumder S Rahman MM Saidur R Ibrahim TA . Numerical Investigation of Pure Mixed Convection in a Ferrofluid-Filled Lid-Driven Cavity for Different Heater Configurations. Alexandria Eng J (2016) 55(1):127–39. 10.1016/j.aej.2015.12.021
12.
Sheremet MA Oztop HF Pop I Al-Salem K . MHD Free Convection in a Wavy Open Porous Tall Cavity Filled with Nanofluids under an Effect of Corner Heater. Int J Heat Mass Transf (2016) 103:955–64. 10.1016/j.ijheatmasstransfer.2016.08.006
13.
Raizah Z Aly AM Alsedais N Mansour MA . MHD Mixed Convection of Hybrid Nanofluid in a Wavy Porous Cavity Employing Local thermal Non-equilibrium Condition. Sci Rep (2021) 11(1):1–22. 10.1038/s41598-021-95857-z
14.
Afsana S Molla MM Nag P Saha LK Siddiqa S . MHD Natural Convection and Entropy Generation of Non-newtonian Ferrofluid in a Wavy Enclosure. Int J Mech Sci (2021) 198(2020):106350. 10.1016/j.ijmecsci.2021.106350
15.
Alsabery AI Tayebi T Roslan R Chamkha AJ Hashim I . Entropy Generation and Mixed Convection Flow inside a Wavy-Walled Enclosure Containing a Rotating Solid cylinder and a Heat Source. Entropy (2020) 22(6):606. 10.3390/E22060606
16.
Karimipour A Hemmat Esfe M Safaei MR Toghraie Semiromi D Jafari S Kazi SN . Mixed Convection of Copper-Water Nanofluid in a Shallow Inclined Lid Driven Cavity Using the Lattice Boltzmann Method. Phys A Stat Mech Its Appl (2014) 402:150–68. 10.1016/j.physa.2014.01.057
17.
Achard F . James Clerk maxwell, a Treatise on Electricity and Magnetism. Math (1873) 1640-1940:564–87. Landmark Writings West. 10.1016/B978-044450871-3/50125-X
18.
Sheikholeslami M Gorji-Bandpy M Ganji DD . Numerical Investigation of MHD Effects on Al2O3-Water Nanofluid Flow and Heat Transfer in a Semi-annulus Enclosure Using LBM. Energy (2013) 60:501–10. 10.1016/j.energy.2013.07.070
19.
Alinia M Ganji DD Gorji-Bandpy M . Numerical Study of Mixed Convection in an Inclined Two Sided Lid Driven Cavity Filled with Nanofluid Using Two-phase Mixture Model. Int Commun Heat Mass Transf (2011) 38(10):1428–35. 10.1016/j.icheatmasstransfer.2011.08.003
20.
Alinia M . Numerical Study of Mixed Convection in an Inclined Two Sided Lid Driven Cavity Filled with Nanofluid Using Two-phase Mixture Model. Eur J Mech B/fluids (2014) 38(6):564–87. 10.1016/j.physa.2014.01.057
21.
Arshad M Hussain A Hassan A Haider Q . Thermophoresis and Brownian Effect for Chemically Reacting Magneto-Hydrodynamic Nanofluid Flow across an Exponentially Stretching Sheet. Energies (2022) 15(1):154. 10.3390/en15010143
22.
Frivaldsky M Pavelek M . Indirect electro-thermal Model semiconductor diode using non-linear Behav volt-ampere characteristic Energies. Energies (2022) 15(1):154. 10.3390/en15010154
23.
Nazir U Sohail M Hafeez MB Krawczuk M Askar S Wasif S et al An Inclination in thermal Energy Using Nanoparticles with Casson Liquid Past an Expanding Porous Surface. Energies (2021) 14(21):7328. 10.3390/en14217328
24.
Selimefendigil F Öztop HF . Role of Magnetic Field and Surface Corrugation on Natural Convection in Ananofluid Filled 3D Trapezoidal Cavity. Int Commun Heat Mass Transfer (2018) 95:182–96. 10.1016/j.icheatmasstransfer.2018.05.006
25.
Selimefendigil F Oztop H Chamkha AJ . Natural Convection in a CuO–Water Nanofluid Filled Cavity Underthe Effect of an Inclined Magnetic Field and Phase Change Material (PCM) Attached to its Vertical wall. J Therm Anal Calorim (2019) 135:1577–94. 10.1007/s10973-018-7714-9
26.
Chamkha AJ Selimefendigil F . MHD Free Convection and Entropy Generation in a Corrugated Cavity Filledwith a Porous Medium Saturated with Nanofluids. Entropy (2018) 20:846. 10.3390/e20110846
27.
Majeed AH Mahmood R Abbasi WS Usman K . Numerical Computation of MHD Thermal Flow of Cross Model over an Elliptic Cylinder: Reduction of Forces via Thickness Ratio. Math Probl Eng (2021) 2021:1–13. 10.1155/2021/2550440
28.
Bilal S Mahmood R Majeed AH Khan I Nisar KS . Finite Element Method Visualization about Heat Transfer Analysis of Newtonian Material in Triangular Cavity with Square cylinder. J Mater Res Technol (2020) 9(3):4904–18. 10.1016/j.jmrt.2020.03.010
29.
Mahmood R Bilal S Majeed AH Khan I Sherif ESM . A Comparative Analysis of Flow Features of Newtonian and Power Law Material: A New Configuration. J Mater Res Technol (2020) 9(2):1978–87. 10.1016/j.jmrt.2019.12.030
30.
Mahmood R Bilal S Majeed AH Khan I Nisar KS . Assessment of Pseudo-plastic and Dilatant Materials Flow in Channel Driven Cavity: Application of Metallurgical Processes. J Mater Res Technol (2020) 9(3):3829–37. 10.1016/j.jmrt.2020.02.009
31.
Majeed AH Jarad F Mahmood R Saddique I . Topological Characteristics of Obstacles and Nonlinear Rheological Fluid Flow in Presence of Insulated Fins: A Fluid Force Reduction Study. Math Probl Eng2021:15. 10.1155/2021/9199512
32.
Ahmad H Mahmood R Hafeez MB Hussain Majeed A Askar S Shahzad H . Thermal Visualization of Ostwald-De Waele Liquid in Wavy Trapezoidal Cavity: Effect of Undulation and Amplitude. Case Stud Therm Eng (2021) 29:101698. 10.1016/j.csite.2021.101698
33.
Mahmood R Majeed AH Ain QU Awrejcewicz J Khan I Shahzad H . Computational Analysis of Fluid Forces on an Obstacle in a Channel Driven Cavity: Viscoplastic Material Based Characteristics. Materials (2022) 15:529. 10.3390/ma15020529
34.
Majeed AH Afzal A Mahmood R . Numerical Investigation of Viscous Fluid Flow and Heat Transfer in the Closed Configuration Installed with Baffles. Int J Emerging Multidiciplinaries: Maths (2022) 1:49–57. 10.54938/ijemdm.2022.01.2.28
Summary
Keywords
FEM computation, MHD, ferrofluid, wavy cavity, Bejan number, entropy generation
Citation
Mahmood R, Khan Y, Rahman N, Majeed AH, Alameer A and Faraz N (2022) Numerical Computations of Entropy Generation and MHD Ferrofluid Filled in a Closed Wavy Configuration: Finite Element Based Study. Front. Phys. 10:916394. doi: 10.3389/fphy.2022.916394
Received
09 April 2022
Accepted
10 June 2022
Published
06 July 2022
Volume
10 - 2022
Edited by
Kh S. Mekheimer, Al-Azhar University, Egypt
Reviewed by
A. M. Rashad, Aswan University, Egypt
Fatih Selimefendigil, Celal Bayar University, Turkey
Updates
Copyright
© 2022 Mahmood, Khan, Rahman, Majeed, Alameer and Faraz.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Afraz Hussain Majeed, chafrazhussain@gmail.com; Y. Khan, yasirmath@yahoo.com
This article was submitted to Statistical and Computational Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.