Research on Quantum Annealing Integer Factorization Based on Different Columns

The majority of scholars believe that Shor’s algorithm is a unique and powerful quantum algorithm for RSA cryptanalysis, so current postquantum cryptography research has largely considered only the potential threats of Shor’s algorithm. This paper verifies the feasibility of deciphering RSA public key cryptography based on D-Wave, which is the second most effective RSA attack method after Shor’s algorithm. This paper proposes the influence of different column methods on the final integer factorization, puts forward a new dimension reduction formula, simplifies the integer factorization model based on quantum annealing, simulates it with the qbsolv quantum computing software environment provided by D-Wave, and factors the integer 1630729 (an 11-bit prime factor multiplied by an 11-bit prime factor). The research results show that choosing an appropriate number of columns and column width in the binary integer factorization multiplication table is very important for studying the optimization ability of the quantum annealing algorithm. In fact, Science, Nature, IEEE Spectrum, and the National Academies of Sciences (NAS) are consistent in asserting that the practical application of general-purpose quantum computers is far in the future. Therefore, although D-Wave computers were initially mainly purchased by Lockheed Martin, Google, etc., for purposes such as image processing, machine learning, combinatorial optimization, and software verification, post quantum cryptography research should further consider the potential of the D-Wave quantum computer in deciphering RSA cryptosystems in the future, and a discussion of this potential is one of the contributions of this paper.

Introduction

Quantum computers are mainly of two types: general-purpose quantum computers invented by Google, IBM and other institutions and dedicated D-Wave quantum computers. Since Peter Shor [1] proposed the prime factorization algorithm for large numbers in 1994, the development of quantum computing has posed a severe challenge to existing public key cryptosystems. The degree of difficulty in factoring large integers is the basis for the security of RSA public key cryptography. The core foundation of RSA security lies in the factorization of large numbers, in which a large integer $N$ is factored as $N=p\times q$. Under the conditions of quantum computing, the problem of the prime factorization of large numbers can be solved in polynomial time. This poses a potential threat to the security of the RSA public key cryptosystem widely used in governmental, financial and other important institutions.

Researchers have completed theoretical verification experiments on Shor’s algorithm based on various methods, such as nuclear magnetic resonance, optical quantum computing, and Josephson charges [2–5]. At present, the universal quantum Shor’s algorithm that can be realized in physics can only factor large numbers up to the integer 85 (combined with the properties of Fermat numbers). Shor’s algorithm can complete theoretical decoding through the quantum Fourier transform, which cannot be achieved by traditional methods and requires high-precision physical devices; the construction of general physical devices develops slowly. Classical computing simulation of Shor’s algorithm can simulate the matrix product state of Shor’s algorithm for up to 60 qubits by using supercomputing resources, but it is also limited by classical computing resources [6].

It is worth noting that, due to the current quantum computer qubit scale, error correction ability, control precision, anti-interference and other problems, the development of hardware is slow, and the practical general-purpose quantum computer still needs time to develop. In fact, Science [7, 8], Nature [9], IEEE Spectrum [10], and the National Academies of Sciences (NAS) are consistent in asserting that the practical application of general-purpose quantum computers is far in the future. For example, Google’s 72-qubit chip Bristlecone (Bristlecone), launched in 2018, could not achieve actual computing power due to problems such as Surface Code, and in 2019, Google’s quantum hegemony chip (Sycamore) could not be used for cryptographic deciphering [11].

In 2018, engineering and physical sciences, the National Academies of Science, the Academy of Medicine, and the Academy of Engineering jointly issued a report entitled “Quantum Computing: Progress and Prospects” [12]. This report clearly pointed out that making a quantum computer with practical capabilities that is capable of deciphering 2048-bit RSA or similar public key cryptosystems based on discrete logarithms is very unlikely within the next 10 years. As Shor’s algorithm has difficulty reducing the device requirements of qubits, Shor’s algorithm based on general quantum circuits is still in the theoretical stage for deciphering public key cryptography. Therefore, it is urgent to explore new quantum computing algorithms and computing architectures (dedicated quantum computers) in addition to Shor’s algorithm.

On the other hand, Canada’s D-Wave quantum computer has cooperated with many world-class companies and universities and is widely used in materials science, finance, biology, medicine, artificial intelligence, machine learning and other fields. It is expected to become a breakthrough point for the commercialization of dedicated quantum computing. The core principle of the D-Wave quantum computer is the quantum annealing algorithm. With its unique quantum tunnelling effect, the quantum annealing algorithm avoids being trapped in local extrema and thus approximates or achieves the global optimum in exponential solution search problems.

In addition to integer factorization based on Shor’s algorithm, there are two types of integer factorization methods based on the quantum adiabatic algorithm. One is the integer factorization method based on a nuclear magnetic resonance (NMR) quantum processor, which is used to realize small quantum computer technology. Due to the limitation of the number of qubits of the NMR platform, integer factorization based on NMR is not scalable, and the method is not universal [13, 14]. The other method is integer factorization based on the principle of the D-Wave quantum computer—the quantum annealing algorithm. The integer factorization method based on the D-Wave quantum annealing principle has more realistic attack power, and this method has versatility and scalability.

Lockheed Martin researcher Warren RH proposed a general framework for factoring all integers up to 1000. The largest integer factored by the D-Wave 2000 qubit processor is 7781 [15]. This model uses a large number of logical qubits, has a large parameter range, and requires high accuracy. Moreover, the constructed model has qubit redundancy. It is difficult for an actual quantum computer to meet these requirements. Riccardo et al. chose the block multiplication table method to test the performance and limitations of the low-noise D-Wave 2000Q quantum annealing machine. The low-noise D-Wave 2000Q can correctly factor all integers below 103459 [16]. Mashiyat et al. proposed PyQUBO to construct quadratic unconstrained binary optimization (QUBO) problems based on objective functions and constraints. These researchers introduced the characteristics of PyQUBO and its applications in integer factorization using binary multipliers [17]. Researchers at Shanghai University [18, 19] proposed using the target value information, structure information, carry information and an optimized dimensionality reduction formula in the columns of the binary multiplication table to reduce the number of required carry variables and the number of representation variables to reduce the number and parameter range of the auxiliary variables required for integer factorization problems. However, this does not take into account the influence of the column division of the binary integer factorization multiplication table on the accuracy of integer factorization.

Based on the method of Jiang et al. [20] at Purdue University, this paper will analyse the influence of different column methods on the final integer factorization. Based on the qbsolv quantum computing software environment provided by D-Wave, the experiment is carried out and compared with the method of Jiang et al. The feasibility of D-Wave in factoring large numbers and the potential of its deciphering RSA are verified, and D-Wave is found to have more realistic attack power than Shor’s algorithm.

Background

Quantum Annealing

Quantum annealing (QA) is the principle of the D-Wave quantum computer. Its unique quantum tunnelling effect can overcome the defect of the traditional search algorithm that it is easily trapped in local minima. In flight control software testing, image recognition, protein folding, financial analysis, quantum biochemistry, transportation, and inversion problems in Earth science and other fields, it has achieved good results. Further expansion of evolutionary cryptography has also been achieved in the field of cryptographic design and analysis [21].

In 1998, H. Nishimori and T. Kadowaki [22] proposed that by introducing a transverse magnetic field to construct quantum fluctuations, particles could achieve a quantum tunnelling effect and thus have the ability to penetrate a high and narrow potential barrier to overcome the defect that simulated annealing can only cross a low potential barrier.

As shown in Figure 1, simulated annealing can only reach the global minimum from a local minimum by crossing a barrier, while the quantum annealing algorithm can directly reach it from a local minimum with its quantum tunnelling effect. It is precisely because of the quantum tunnelling effect that the quantum annealing algorithm has better performance than the simulated annealing algorithm in some problems.

FIGURE 1

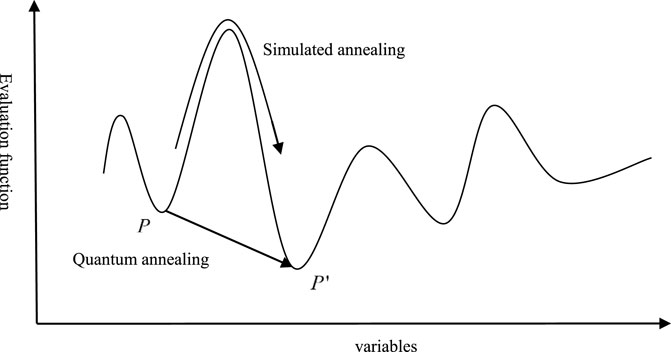
FIGURE 1. Comparison of the working principle of the simulated annealing algorithm and quantum annealing algorithm [23].

This simulation is based on the quantum computing software environment qbsolv. qbsolv is a metaheuristic or partition solver. It solves a potentially large QUBO problem by dividing it into blocks that are solved on D-Wave systems or by classical tabu solvers. For more information on the qbsolv software (provided by D-Wave), please refer to (http://github.com/dwavesystems/qbsolv).

Related Works

Quantum annealing uses the quantum effect produced by quantum fluctuations to determine the global optimal solution of an objective function. The integer factorization problem is converted into a combinatorial optimization problem that can be processed by the quantum annealing algorithm, and the minimum energy value is output through the quantum annealing algorithm. The minimum value is then the successful solution of integer factorization.

As the core algorithm of the D-Wave quantum computer, quantum annealing shows the potential to approach or even reach the global optimum in the exponential solution space, corresponding to the quantum evolution of the ground state of the Hamiltonian of the problem. Table 1 takes the binary multiplication table of the integer 143 as an example. The integer 143 is factored into three columns, the width of each column is 2, and the column method is expressed as [2, 4, 6]. The objective function of each column is expressed as the following equation:

$\left(p_2+p_1{q}_1+q_2-\left(c_2\times 4+c_1\times 2\right)\right)\times 2+\left(p_1+q_1\right)={\left(11\right)}_2=3.(1)$

$\left(q_1+p_2{q}_2+p_1+c_2-\left(c_4\times 4+c_3\times 2\right)\right)\times 2+\left(1+p_2{q}_1+p_{1}q{}_2+1+c_1\right)={\left(01\right)}_2=1.(2)$

$\left(1+c_4\right)\times 2+\left(q_2+p_2+c_3\right)={\left(100\right)}_2=4.(3)$

TABLE 1

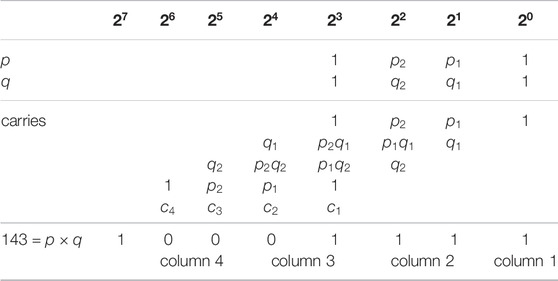
TABLE 1. Column binary multiplication table of 143 = 11 × 13 [20].

The objective function is defined as the sum of the squares of all columns:

$f={\left(2p_2+2p_1{q}_1+2q_2-8c_2-4c_1+p_1+q_1-3\right)}^2+{\left(2q_1+2p_2{q}_2+2p_1+2c_2-8c_4-4c_3+p_2{q}_1+p_1{q}_2+c{}_1+1\right)}^2+{\left(q_2+p_2+c_3+2c_4-2\right)}^2.(4)$

As can be seen from the above objective function, the minimum energy value of the final system after annealing should be 0. After expanding Formula 4, the energy of the objective function includes the observation energy value and constant term of quantum annealing. Since the sum of the two is 0, the absolute value of the observed quantum annealing energy can be regarded as the Hamiltonian energy of integer factorization.

The simulation steps for D-Wave to decipher RSA public key cryptography based on quantum annealing are as follows:

Step 1. Divide the binary multiplication table of any integer into columns (usually divided by column widths of 1, 2, 3, 4 or 5) and determine the carry variable.

Step 2. Construct the objective function of the integer binary multiplication table after column division and simplify the objective function with different column division methods according to the squared item attributes $p_i^2=p_i$, $q_i^2=q_i$, and $c_i^2=c_i$ and the dimension reduction formula.

Step 3. Perform variable substitution on the objective function of each column with $x_i=\left(1-s_i\right)/2$, $i$ = 1, 2, 3, · · ·, so that the value range is changed from {0, 1} to {−1, 1}. Single-term quadratic coefficients and quadratic-term quadratic coefficients of each column objective function are extracted as a local field coefficient matrix $h$ and a coupled term coefficient matrix $J$ to transform the integer factorization problem into an Ising model that can be handled by the qbsolv software environment.

Step 4. Input the final local field coefficient matrix $h$ and coupling term coefficient matrix $J$ of each column of the objective function into the quantum computing qbsolv software environment to perform the quantum annealing process. After sufficient slow adiabatic evolution, the final Hamiltonian of the system will be the ground state of the Ising model, namely, the factors produced by integer factorization.

In this paper, we propose two optimization methods (Method 1 and Method 2) to analyze the impact of different partition designs and new dimensionality reduction methods on integer factorization (including the number of qubits, parameter coefficients, success rate, and running time).

Methods

Method 1

Table 2 shows a parameter comparison of the factorization of 143 in different column methods adopted by Method 1.

TABLE 2

TABLE 2. Different ways of dividing the integer 143.

Table 1 shows that different column methods will affect the number of qubits required to factor the integer 143 and the range of the model parameters. When column splitting is performed [3, 6], we find that the number of qubits needed is reduced, but the corresponding parameter range is increased. The column partitioning methods [2–4, 6] and [2–6] have the same parameter range for the final model coefficient, but the number of qubits needed to factor the integer is different. The more columns there are, the more qubits are needed. As seen from Table 2, the greater the number of columns is, the smaller the minimum energy value of integer factorization. In a real D-wave quantum environment, the parameter range and energy value will affect the stability and accuracy of annealing.

The more columns there are, the greater the number of bits required to factor an integer because more columns are used, which leads to more objective functions for the entire binary multiplication table (each column corresponds to an objective function); the final integer factorization represents the sum of the squares of the objective functions of all columns. After the model is simplified, there will be more polynomials larger than the second degree (cubic terms or quartic terms). Since D-Wave quantum annealing can only handle the interaction of two variables at most, it is necessary to reduce the dimension of polynomials larger than the second degree, which requires the introduction of new variables, eventually leading to an increase in the number of qubits. Therefore, within the corresponding control range, we can choose fewer columns to reduce the quantum hardware requirements of the final model.

Table 3 shows the quantum simulation of factoring the integer 59989 based on different column methods. We find that the fewer columns are used, the fewer qubits are needed, but this does not mean that the fewer the number of columns, the better. For example, when the column is [6, 12], the model coefficients are already as high as [−84628, 98345.5] and [−90640, 44824], and the minimum energy is 1541132. The coupling strength between the quantum spin Ising models in D-Wave quantum computer topology is limited. When the parameter range of the Ising model is too large, the stability of some physical qubit chains may not be guaranteed, and the chains may appear to “break,” which will eventually lead to the inconsistency of physical qubits flipping, which will affect the stability of the annealing process and directly affect the accuracy of the quantum hardware in solving the actual combinatorial optimization problem. Comparing [3, 8, 12] and [4, 8, 12], the width of the second column of [3, 8, 12] is 5, and the width of the second column of [4, 8, 12] is 4. The width of the middle column ([4, 8, 12]) is smaller, which can greatly reduce the parameter range of the model, but the column width is not as small as possible.

TABLE 3

TABLE 3. Different column methods for the integer 59989.

For example, comparing [3, 5, 7, 9, 12] and [4, 5, 7, 9, 12], it is found that the width of the second column of [3, 5, 7, 9, 12] is 2, and the width of the second column of [4, 5, 7, 9, 12] is 1, but the parameter coefficient range and minimum energy value for the column width of 1 are larger. Similarly, compared with [3, 5–9, 12] and [4–9, 12], when the second column width of [3, 5–9, 12] is 2 and the second column width of [4–9, 12] is 1, the range of the coefficient and the minimum energy value of 1 are higher. Therefore, choosing an appropriate column width is crucial to the stability of quantum annealing. Based on the above discussion, it is found that the column width value 3 for the low column and the high column is the most appropriate, and the column width of the middle column is 2 or 3. Table 4 shows the quantum simulation of factoring the integer 376289 based on different column methods. The number of qubits increases as the number of columns increases.

1) When the column method uses [6, 10, 16], the number of qubits required to factor the integer 376289 is 89, and the number of qubits required to factor the integer 376289 by the method of Jiang et al. is 94; the column method uses five fewer qubits than Jiang et al., which can reduce hardware requirements.

2) When the column method uses [3, 6, 8, 10, 12, 14, 16], compared with the algorithm of Jiang et al., the number of columns increases, and although the number of qubits increases, the model coefficient can be greatly reduced. This is helpful in improving the stability of the factorization model of large numbers and improving the accuracy of the integer factorization problem. Therefore, the number of columns can be appropriately increased within a certain controllable range.

TABLE 4

TABLE 4. Different column methods for the integer 376289.

In summary, the selection of the number of columns and the width of the columns has a certain impact on the number of qubits required for factoring integers and the range of the model parameters. Values that are too large or too small will affect the final result. Too many columns can reduce the range of the model coefficients but increase the number of qubits needed. Too small or too large a number of columns will also affect the range of the model parameters. Therefore, seeking the appropriate number of columns and the appropriate column width to balance the number of qubits and the model parameters required for integer factorization has important research significance in studying the accuracy of quantum annealing in the D-Wave system.

Method 2

Although Jiang et al. introduced a method to simplify 3 local terms into 2 local terms in Ref. [20], the parameter value and coupling strength of the local field coefficient increased due to the coefficient “2,” especially for large integers. In the integer factorization problem based on quantum annealing, the reduction of model parameters is helpful for reducing the hardware requirements and precision of quantum annealing. To further simplify 3 local terms into 2 local terms, inspired by Ref. [19] and Ref. [15], a new dimension reduction method was proposed on the basis of further column optimization, as shown in the formula

$\{\begin{array}{l}{x}_1{x}_2{x}_3=\underset{x_4}{\min }\left(x_4{x}_3+x_1{x}_2-x_1{x}_4-x_2{x}_4+x_4\right)\\ -x_1{x}_2{x}_3=-\underset{x_4}{\min }\left(x_4{x}_3+x_1{x}_2-2x_1{x}_4-2x_2{x}_4+3x_4\right)\end{array}(5)$

By using the dimensionality reduction method, the minimum solution problem for quartic and cubic local terms can be transformed into a problem of quadratic local terms that the Ising model can handle. Compared with the methods of Ref. [19] and Ref. [20], this method can further reduce the coupling strength, local field coefficient and minimum energy so that the theoretical model can describe the original problem more accurately. This is of great significance for solving integer factorization problems by quantum annealing in real D-wave systems. The following gives a comparison of Method 1, Method 2, and the work of Jiang et al.

It can be seen from Table 5 that, compared with Jiang et al.’s method, Method 2 can further reduce the coupling strength, local field coefficient and minimum energy when the same column method is selected when the integer 143 is factored. Compared with Method 1, the new dimension reduction method can further improve the operational stability of D-Wave quantum annealing and thus improve the quantum annealing accuracy.

TABLE 5

TABLE 5. Comparison of different methods of factoring the integer 143.

It can be seen from Table 6 that compared with Jiang et al.’s method, Method 2 can further reduce the coupling strength, local field coefficient and minimum energy when the same column method is selected to factor 59989. Compared with that of Method 1, the dimension reduction method of Method 2 can further reduce the weight of the qubit and the range of the strength of the coupler involved in integer factorization. The reduction of the parameter value range can reduce the precision required to control the hardware bits, which is beneficial to the stability of the operation of a real D-Wave quantum computer to a certain extent, and it improves the integer factorization of large-scale cases in a real D-Wave computer.

TABLE 6

TABLE 6. Different methods of factoring the integer 59989.

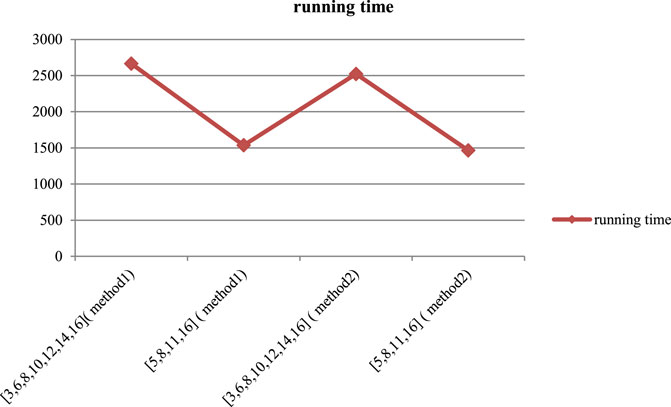
Figure 2 shows the comparison of the running time of the integer 376289 factored by the two optimization algorithms in different column ways (3000 experimental runs). As can be seen from the figure, both optimization methods show that the more columns there are, the longer the operation time will be. This also shows from the side, the more columns, the more quantum bits needed, the more difficult the factorization, so the running time is longer. Method 2 has a slight advantage over method 1 in running time in the same column, but the difference is not significant. From the perspective of running time, the impact of column on running time is far more than that of dimension reduction.

FIGURE 2

FIGURE 2. Comparison of running time of two optimization algorithms for factoring integer 376289.

Table 7 shows the factorization of 1630729 = 1277 × 1277. The running time of factorizing 1630729 is 7359 s, and the experiment is run 7000 times. Figure 3 shows the energy distribution of the factored integer 1630729 (1277 × 1277). The minimum energy value after quantum annealing is 39881 (the red part in the figure), and the minimum energy corresponds to the solution of the integer factorization.

TABLE 7

TABLE 7. Factorization of 1630729 = 1277 × 1277.

FIGURE 3

FIGURE 3. Observed energies for the integer 1630729 after quantum annealing.

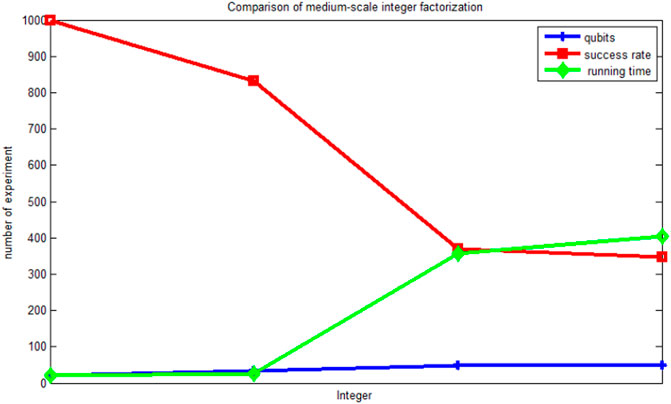
In addition, we analysed the accuracy of medium-scale integer factorization (493 = 17 × 29, 1649 = 17 × 97, 9409 = 97 × 97, 12319 = 97 × 127). Figure 4 shows a comparison of the number of bits required by different integer factorization methods, the accuracy of quantum annealing and the running time (run 1000 times).

FIGURE 4

FIGURE 4. Comparison of medium-scale integer factorization cases.

As shown in Figure 4, the number of bits, parameter range and running time required for factorization gradually increase with the increasing scale of integer factorization. The success rate of integer factorization decreases with the increase in the scale of integer factorization. This illustrates that as the scale of integer factorization increases, the difficulty of integer factorization also increases, and the model of the integer factorization problem represented by quantum annealing becomes more complicated.

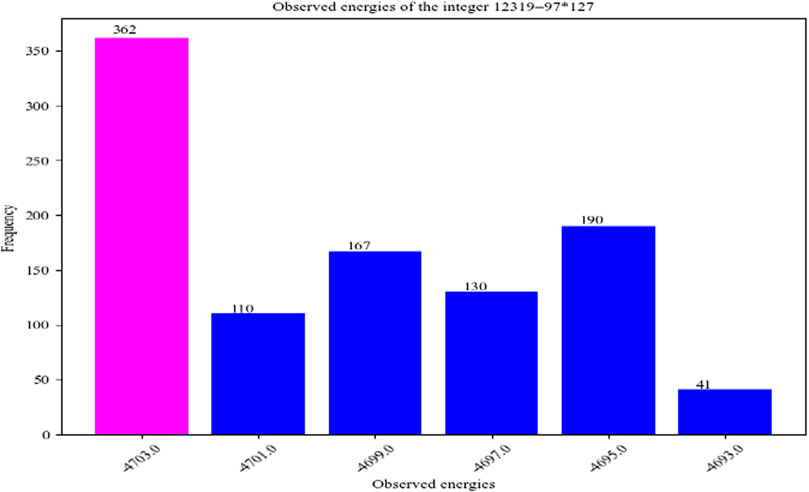
Figure 5 shows the energy distribution of the factorization 12319 = 97 × 127. The experiment was run 1000 times, the minimum energy value was 4703, and the number of successful factorizations was 362. In this paper, the integer factorization problem is transformed into a combinatorial optimization problem that can be handled by a quantum annealing algorithm. Here, the minimum energy (the red part in the figure) output by the quantum annealing algorithm corresponds to a successful integer factorization solution.

FIGURE 5

FIGURE 5. Observed energies of 12319 = 97 × 127 after quantum annealing.

Discussion and Future Work

Based on the algorithm of Jiang et al., this paper proposes two optimization algorithms to analyse the influence of different column methods of different integer multiplication tables on the final integer factorization model based on quantum annealing; that is, we propose a deeper exploration of the effect of different column methods on the number of qubits and model coefficients. The simulation results show that choosing the appropriate number of columns and the appropriate column width is essential for balancing the number of qubits and model coefficients. Finding a way to balance the column splitting method, the number of qubits, and the model coefficients to give full play to the optimization ability of the quantum annealing algorithm is very meaningful work.

Due to the slow development of universal quantum devices, the decomposable integer scale of Shor’s algorithm (based on the universal quantum circuit mode) is limited. The NMR platform based on quantum adiabatic annealing has no expansibility, and the method is not universal, as shown in Figure 5 for the energy distribution of the integer 12319 = 97 × 127 after the quantum annealing limitation of the qubit number of the platform. Existing D-Wave work is limited, so a general and extensible structure based on D-Wave is essential.

It has long been believed that Shor’s algorithm is the only effective quantum computing algorithm for attacking RSA and that Shor’s algorithm requires the support of high-precision quantum equipment. In fact, quantum annealing machines such as D-Wave are more likely to be able to decode RSA than Shor’s algorithm. According to a paper published by Google in January 2018, Shor’s algorithm needs $2n$ qubits to factor $n$ -bit large integers [24]. The algorithm in this paper requires ${\rm O}\left(lo{g}^2\left(N\right)\right)$ quantum bits in total, and $N$ is an integer to be factored. Although the complexity of the algorithm in this paper is not as good as Shor’s algorithm, Shor’s algorithm is highly dependent on hardware devices.

To realize the factorization of the maximum factored integer 1630729 (21-bit integer) in this paper, Shor’s algorithm needs at least 42 more quantum bits, and to factor the actual 1024 bits of public key password RSA. More than 2000 logical quantum bits are required, and the required physical quantity bits and quantum bit precision are far beyond the current hardware level. Therefore, the theoretical research proposed in this study that the factorization scale of large numbers can be achieved by sacrificing part of the physical qubit resources, which is more than several orders of magnitude larger than the general quantum computer is of great exploration value. In the future, anti-quantum cryptography needs to consider not only the potential threats from Shor’s general-purpose quantum computers, but also the potential threats of dedicated quantum computers.

It should be clarified that the current D-Wave computer is far from being able to decipher the 1024-bit RSA, nor can it achieve quantum supremacy. It makes sense to achieve large number factorization that is several orders of magnitude higher than that in general use with slightly more qubit resource consumption. Compared with the general Shor’s algorithm, D-Wave can be mixed and enhanced with classics, and it has the potential to achieve the modular distributed decryption of large numbers. It can be combined with classic computers in limited equipment to yield a large-scale distributed large number factorization framework.

Purdue University researchers used the D-Wave 2000Q (2000 qubits) real quantum computer to map the Hamiltonian to a hardware graph [20]. The implementation resolves the maximum integer 376289 by 1070 physical qubits representing 94 logical qubits (multiple physical qubits representing one logical bit). Due to the extreme topological connection limitation of D-Wave quantum hardware interconnection diagram, the Hamiltonian of larger integer problem cannot be mapped directly, and this integer is also the limit of D-Wave 2000Q factorization. The current D-Wave quantum computing platform uses the new Pegasus™ topology technology to improve the interconnection performance of qubits over 5000 qubits. When the scale of factorized integers increases further, two situations will occur: 1) Chimera graph cannot be mapped effectively, that is, the built-in algorithm cannot find an effective mapping method; 2) In the case that the quantum Chimera graph can be mapped effectively, the floating range of the coupling strength between the quantum bits (that is, the coefficient in the model) is very large, which will also increase the difficulty of the successful quantum annealing experiment, and the optimal solution may not be found. If the integer 1630729 is to be factored in a real quantum computer, the above two challenges need to be further solved, which is also the future research direction of this study.

The feasible directions of research on general frameworks for large number factorization in the future are as follows:

1) Construct a new objective function by using the target value restriction information in the column multiplication table (such as the relationship between $p$ and $q$).

2) Research the structure information and carry information of the multiplication table to further reduce the number of carry variables needed.

3) Construct a general multiplication table specifically for large numbers, such as a general multiplication table specifically for $11\times 11$, aiming to factor larger-scale integers.

There are three main types of mathematical problems in constructing public key cryptography: prime factorization problems based on large integers, discrete logarithm problems on multiplicative groups of finite fields, and discrete logarithm problems on elliptic curves (ELGamal algorithm). General-purpose quantum computers have not yet provided effective attacks on the latter two types of public key cryptography. Therefore, it is necessary to further explore the feasibility of D-Wave quantum computer attacks on discrete logarithms and elliptic curve discrete logarithms.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the grant of Shanghai Sailing Plan of “Science and Technology Innovation Action Plan” of China (No. 21YF1415100).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Shor P. W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In: Proceedings of the 35th Annual IEEE Symposium on the Foundations of Computer Science; 20-22 Nov. 1994; Santa Fe, NM, USA. IEEE (1994). p. 124–34. doi:10.1109/SFCS.1994.365700

CrossRef Full Text | Google Scholar

2. Vandersypen L. M., Steffen M., Breyta G., Yannoni C. S., Sherwood M. H., Chuang I. L. Experimental Realization of Shor's Quantum Factoring Algorithm Using Nuclear Magnetic Resonance. Nature (2001) 414(6866):883–7. doi:10.1038/414883a

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lu C. Y., Browne D. E., Yang T., Pan J. W. Demonstration of a Compiled Version of Shor's Quantum Factoring Algorithm Using Photonic Qubits. Phys Rev Lett (2007) 99(25):250504. doi:10.1103/PhysRevLett.99.250504

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lucero E., Barends R., Chen Y. Computing Prime Factors with a Josephson Phase Qubit Quantum Processor. Nat Phys (2012) 8(10):719–23. doi:10.1038/nphys2385

CrossRef Full Text | Google Scholar

5. Michael R. G., Zhou Z. Y. Factoring 51 and 85 with 8 Qubits. Scientific Rep (2012) 3:3023. doi:10.1038/srep03023

CrossRef Full Text | Google Scholar

6. Dang A., Hill C. D., Hollenberg L. C. L. Optimising Matrix Product State Simulations of Shor’s Algorithm. Quan Phys (2017) 1712. doi:10.48550/arXiv.1712.07311

CrossRef Full Text | Google Scholar

7. Brainard J. What’s Coming up in 2018. Science (2018) 359:10–2. doi:10.1126/science.359.6371.10

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Cho A. DOE Pushes for Useful Quantum Computing. Science (2018) 359(6372):141–2. doi:10.1126/science.359.6372.141

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Gibney E. Physics: Quantum Computer Quest. Nature (2014) 516(7529):24–6. doi:10.1038/516024a

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dyakonov M. The Case against Quantum Computing. IEEE Spectr Mar. (2019) 24:23–28. Available at: https://www.researchgate.net/publication/333816791.

Google Scholar

11. Arute F., Arya K., Babbush R., Bacon D., Bardin J. C., Barends R., et al. Quantum Supremacy Using a Programmable Superconducting Processor. Nature (2019) 574(7779):505–10. doi:10.1038/s41586-019-1666-5

PubMed Abstract | CrossRef Full Text | Google Scholar

12.National Academies of Sciences, Engineering, and Medicine. Quantum Computing: Progress and Prospects. Washington: National Academies Press (2019).

Google Scholar

13. Dattani N. S., Bryans N. Quantum Factorization of 56153 with Only 4 Qubits. Computer Science (2014) 11:1–6. doi:10.48550/arXiv.1411.6758

CrossRef Full Text | Google Scholar

14. Li Z. K., Dattani N. S., Chen X., Liu X. High-fidelity Adiabatic Quantum Computation Using the Intrinsic Hamiltonian of a Spin System: Application to the Experimental Factorization of 291311. Quant Phys (2017):1–6. doi:10.48550/arXiv.1706.08061

CrossRef Full Text | Google Scholar

15. Warren R. H. Factoring on a Quantum Annealing Computer. Quan Inf Comput (2019) 19:0252–61. doi:10.26421/qic19.3-4-5

CrossRef Full Text | Google Scholar

16. Mengoni R, Ottaviani D, Iorio P. Breaking RSA Security with A Low Noise D-Wave 2000Q Quantum Annealer: Computational Times, Limitations and Prospects. Quant Phys (2020):1–8. doi:10.48550/arXiv.2005.02268

CrossRef Full Text | Google Scholar

17. Zaman M., Tanahashi K., Tanaka S. PyQUBO: Python Library for Mapping Combinatorial Optimization Problems to QUBO Form. Quan Phys (2021) 2103–01708v2. doi:10.48550/arXiv.2103.01708

CrossRef Full Text | Google Scholar

18. Wangchun P., Baonan W., Feng H., YunJiang W., XianJin F., XingYuan C. Factoring Larger Integers with Fewer Qubits via Quantum Annealing with Optimized Parameters. Sci China-phys Mech Astron (2019) 62(6):060311. doi:10.1007/s11433-018-9337-5

CrossRef Full Text | Google Scholar

19. Baonan W, Feng H, Haonan Y, Chao W. Prime Factorization Algorithm Based on Parameter Optimization of Ising Model. Scientific Rep (2020) 10(1):1–10. doi:10.1038/s4159802062802-5

CrossRef Full Text | Google Scholar

20. Jiang S., Britt K. A., Mccaskey A. J., Humble T. S., Kais S. Quantum Annealing for Prime Factorization. Sci Rep (2018) 8(No. 1):17667. doi:10.1038/s41598-018-36058-z

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hu F., Lamata L., Sanz M., Chen X., Chen X., Wang C., et al. Quantum Computing Cryptography: Finding Cryptographic Boolean Functions with Quantum Annealing by a 2000 Qubit D-Wave Quantum Computer. Phys Lett A (2020) 384(10):126214. doi:10.1016/j.physleta.2019.126214

CrossRef Full Text | Google Scholar

22. Tadashi K., Hidetoshi N. Quantum Annealing in the Transverse Ising Model. Phys Rev E (1998) 58:5355–63. doi:10.1103/PhysRevE.58.5355

CrossRef Full Text | Google Scholar

23. Johnson M. W., Amin M. H., Gildert S., Lanting T., Hamze F., Dickson N., et al. Quantum Annealing with Manufactured Spins. Nature (2011) 473(7346):194–8. doi:10.1038/nature10012

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Gidney C. Factoring with N+2 Clean Qubits and N-1 Dirty Qubits. Quant Phys (2018):1–14. doi:10.48550/arXiv.1706.07884

CrossRef Full Text | Google Scholar