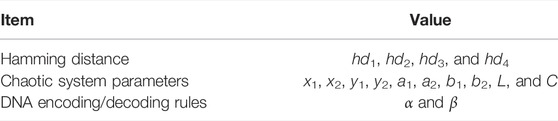A Chaos-Based Image Encryption Scheme Using the Hamming Distance and DNA Sequence Operation

In this study, we introduced a new memristive chaotic system with the rich dynamic behavior, and then we proposed a chaotic-based image encryption scheme which is based on the permutation–confusion–substitution structure. In our scheme, the Hamming distance is used to design a plain-related chaotic system initial condition, and the generated chaotic sequences are assigned to permutation, diffusion, and substitution stages. In the permutation stage, an effect pixel confusion is implemented through a new permutation approach, which is a double-ended select-swap scrambling strategy. In the diffusion stage, DNA XOR operation is implemented followed by DNA triploid mutation which is introduced to enhance the strength of our encryption system. A number of experiments and extensive safety analysis have been carried out and the results fully justify that our scheme not only ensures desirable security but also has superior efficiency.

1 Introduction

With the advent of the Internet and multimedia, the network plays a vital role in transmitting text, images, and video files as a medium. Therefore, the need to ensure the secure transmission of information on the network has become the focus of attention in the field of secure communications. Compared with text and video files, images with the visual information have many advantages in communication and transmission, such as large amount of information, small storage space occupation, and convenient transmission, so they are the most widely used [1]. However, images without special processing face the danger of being eavesdropped and crawled by some criminals using some special tools and means and image encryption came into being in this scenario [2, 3].

In recent years, image encryption technology has been developed one after another. Previous image encryption strategies that treated the image as a stream of a binary bit such as text information and then encrypted using the well-known AES and DES technologies have not been proven to use image files [4, 5]. This is due to the large amount of image data compared to adjacent pixels which are highly correlated and so on compared to text information. In contrast, compressive sensing [6, 7], DNA operation, and [8, 9] chaos theory [10, 11] are more suitable for image encryption. Among them, the chaotic image encryption algorithm is the most popular, which is due to the internal characteristics of chaos, such as initial value sensitivity; also, nonlinear behavior can ensure that the processed image has a higher security level [9, 12–23]. For instance, Hua et al. [24] presented a gray image encryption scheme based on a 2D Logistic-Sine-coupling map. The chaotic system was generated by coupling the Logistic and Sine map. In [12], Chai et al. exploited a secure cipher image scheme using the preprocessing-permutation–diffusion structure. In this cryptosystem, the key streams were generated from a memristive hyperchaotic system. In [25], Li et al. suggested an optical cryptosystem, in which the laser hyperchaotic system was presented in a fractional-order form to improve the complexity of the chaotic sequences.

For the chaotic image cryptosystem, the security performance of the processed ciphertext is composed of many factors. One is whether the structure of the algorithm is safe enough, that is, whether to use architectures like to use the classic permutation–diffusion, permutation–substitution [26–30, 42]. Whether the initial value of the second cryptosystem is designed to be related to the plaintext image to resist known-plaintext and chosen plaintext attacks [31, 32]. Third, in the development of chaos theory, various chaotic systems are developed and they are introduced into image encryption. However, these chaotic systems are not all suitable for the field of secure communication, which may be due to their low key space and due to fewer parameters [33, 34]. In addition, the weak chaotic performance will also become the main reason to threaten the security of cryptographic systems [35–37]. Therefore, using a high-performance chaotic system to design a cryptographic scheme with a secure structure and an efficient algorithm becomes an urgent requirement [30, 38–41].

In order to improve the security and enhance the efficiency of the chaotic image cryptosystem, a memristive system with better chaos performance has been designed by our team [42], and it was introduced for image encryption in this study. First, the chaotic system with complex chaotic behavior was demonstrated through the phase diagram, Lyapunov exponents (LEs), and Lyapunov dimensions (LEs). Then, the chaotic sequences were generated for the encryption phase. Before the confusion procedure, the DNA encoding rule was provided for the image, and then a new permutation approach was designed and implemented at the DNA level. Next, we used the DNA XOR operation to perform the diffusion operation. Finally, DNA triploid mutation with superior efficiency was carried out so as to enhance the system security. The experiment results and extensive safety analysis fully justify that our cryptosystem is suitable for practical secure images due to high-security level and satisfactory encryption efficiency.

The remaining part of the study is organized as follows. In Section 2, we introduced a memristive chaotic system, and its dynamic behavior is evaluated by the phase diagram and Lyapunov exponent. Section 3 shows the proposed encryption methodology. Section 4 presents the simulation results of different size images. Section 5 reports the security level of our encryption scheme. Section 6 summarizes the content of this study.

2 The Novel Chaotic Circuit Based on Two Memristors

Recently, a novel four-dimensional chaotic system based on memristors (4D-CMM) is proposed by our team [42] and an image cryptosystem is introduced to generate pseudo-random sequences in this study. The 4D-CMM model is defined as follows:

$\{\begin{array}{l}{\dot{i}}_L=\frac{1}{L}\cdot v-\frac{1}{L{a}_1}\cdot \frac{i_L}{z_1},\\ \dot{v}=-\frac{1}{C}\cdot i_L-\frac{a_2}{C}\cdot z_{2}v,\\ {\dot{z}}_1={\left(\frac{i_L}{a_1{z}_1}\right)}^2-b_1,\\ {\dot{z}}_2=v^2-b_2,\end{array}(1)$

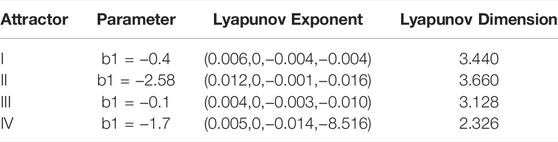
where a₁, a₂, b₁, b₂, L, and C represent system parameters. The set initial conditions of the system are (−1, 3, 1, and −0.7). There are four kinds of attractors with different parameter values of b₁ are shown in Figure 1 when a₁ = 5, a₂ = 0.825, b₂ = 10, L = 0.025, and C = 0.025. In addition, Lyapunov exponents (LEs) and Lyapunov dimensions (LDs) with the different parameter values of b₁ are listed in Table 1 to prove that the rich dynamic chaotic behavior exists in 4D-CMM. The results present that the 4D-CMM is chaotic and has rich dynamic behavior. Consequently, it can be introduced into the image encryption system as a key stream generator.

FIGURE 1

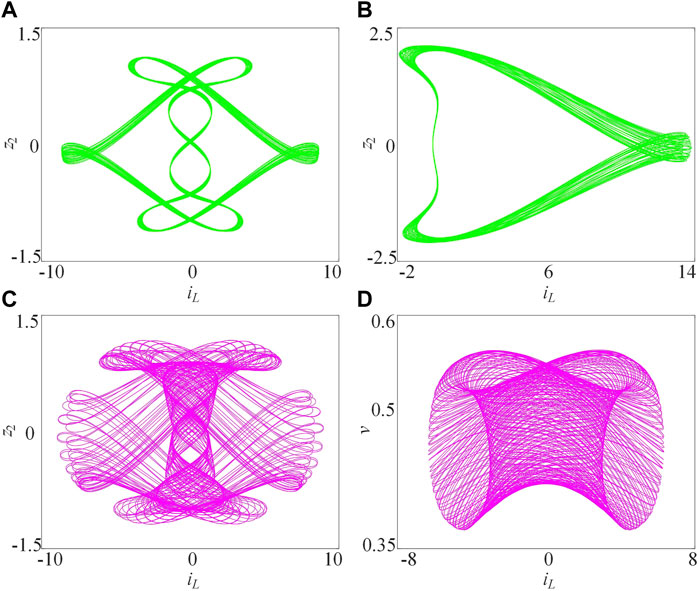
FIGURE 1. Four kinds of attractors with different parameter values b₁ [42]: (A) b₁ = −0.4, (B) b₁ = −2.58, (C) b₁ = −0.1, and (D) b₁ = −1.7.

TABLE 1

TABLE 1. LE and LD values with different chaotic attractors.

3 Image Encryption Algorithm

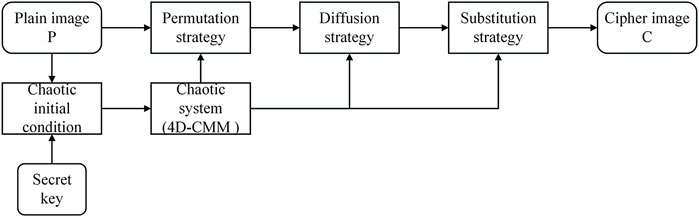
In this section, the proposed encryption scheme flow is presented, as shown in Figure 2, where the structure mainly consists of four parts, namely, initial condition generation, permutation, diffusion, and substitution, where encryption operations are performed at the DNA level The whole encryption process is as follows: a plain image and key are input and the latter is used to design the initial conditions of the chaotic system to initialize the chaotic system (4D-CMM). The three pseudo-random matrices generated by 4D-CMM are used as a key steam element for the encryption process. After that, P was transformed through the permutation procedure. The diffusion and substitution procedure are carried out, in turn, finally. Next, the implementation details in the encryption process will be described.

FIGURE 2

FIGURE 2. Proposed encryption scheme flow chart.

3.1 4D-CMM Initial Conditions

Based on the Hamming distance, we designed a plain pixel–related 4D-CMM initial conditions in this subsection. The Hamming distance is derived as follows:

$\{\begin{array}{l}H(x,y)={\displaystyle \sum _{i=1}^{n}h(x_i,y_i),}\\ {\displaystyle \sum _{i=1}^{n}h(x_i,y_i)}\{\begin{array}{l}0,x_i=y_i,\\ 1,x_i\ne y_i,\end{array}\end{array}(2)$

where x and y can be interpreted as two sequences and it can be obtained from the bit plain of image P (b₁, b₂, b_3, b₄, b₅,b₆,b₇, and b₈).

Assume that bit plain (b₁, b₂), (b_3, b₄), (b_5, b₆), and (b_7, b₈) represent W₁, W₂, W₃, and W₄, respectively. The Hamming distance hd₁ = H(W₁, W₂), hd₂ = H(W₁, W₃), hd₃ = H(W₁, W₄), and hd₄ = H(W₂, W₃). The initial conditions of 4D-CMM are obtained as follows:

$\{\begin{array}{l}{i}_L\left(0\right)=x_1+0.5\times h{d}_1/r,\\ v\left(0\right)=y_1+0.6\times h{d}_2/r,\\ z_1\left(0\right)=x_2+0.6\times h{d}_3/r,\\ z_2\left(0\right)=y_2+0.5\times h{d}_4/r,\end{array}(3)$

where x₁, x₂, y₁, and y₂ are secret keys and r = M×N is the number of pixels in the image P. Note that if the pixels in the image change, we can use the Hamming distance to capture the change. This means that two images can have different initial values even if they are slightly different. This feature ensures that the proposed cryptosystem can resist known-plaintext and select-plaintext attacks.

3.2 Permutation Strategy

In the permutation stage, we proposed a two-way confusion strategy to enhance the efficiency and effect of image permutation. In our scheme, the two starting points of permutation start from the head and the tail of the image, respectively, and the permutation process is similar to the floating process of bubbles, which is a nonlinear pixel swapping operation.

In the confusion process, the plain image with a size of M×N is encoded using DNA coding rule α, and then treated as a one-dimensional array P=(P (1), P (2), …, P (4MN)) by scanning the DNA-encoded image P in a Z-like mode. The head (positive direction) and tail (negative direction) of the image P are taken as the starting point of the two exchanges, and the exchange operation is carried out alternately in the positive and negative directions. One element is placed in the final position for each swap operation, which means that the swapped element must be in the position between the two most recently identified elements in the opposite direction. Assume that T is the position of the current element in positive exchange and T₀ represents the position to be swapped one, T₀ is obtained according to Eqs 4, 5.

$T_0=T+kn\left(T\right),(6)$

$kn\left(T\right)=mod(floor\left(abs(un\left(T\right)\times {10}^{12})\right),4MN-T),(7)$

where kn(T) is the key stream element used to generate confusion position T and un = [i_L, v, z_1, and z₂] is the chaotic sequence by iterating Eq. 1 MN times. The element swapping procedure is performed according to Eq. 6.

$\{\begin{array}{l}C\left(X\right)=P\left(T_0\right)=P(T+kn\left(T\right)),\\ P\left(T_0\right)=P\left(T\right),\end{array}(8)$

where C(X) is the confused element. Analogously, R = MN-T and R₀ represent the current element and the swapped one in the negative direction. The confused element is obtained by Eq. 7. In addition, it can get relaxed and can be concluded that T + R = 4 MN.

$\{\begin{array}{l}{R}_0=R+kn\left(R\right),\\ C\left(R\right)=C(4MN-T)=P\left(R_0\right),\\ P\left(R_0\right)=P\left(R\right),\\ kn\left(R\right)=mod(floor\left(abs(un\left(R\right)\times {10}^6)\right),4MN-R).\end{array}(9)$

When the positive and negative scrambling operations are performed at the same time, the scrambled image C is obtained after 2MN operations.

3.3 Diffusion Strategy

In the diffusion phase, we need to change the pixel value and transfer the current pixel value to other pixel values as much as possible to improve the concealment of the pixel. In our scheme, DNA XOR operations are introduced first and its calculation formula is shown as follows:

$S\left(i\right)=D\left(i\right)\oplus K_1\left(i\right)\oplus S(i-1),(10)$

where D(i) represents the pixel to be processed currently, and K₁(i) represents the key stream, which can be deduced from Eq. 9. S(i) represents the current modified pixel value, and S (i-1) represents the previous modified pixel value. When i = 1, S (0) = D(n), and n = MN.

$K_1\left(i\right)=\mathrm{mod}(un,256)+1.(11)$

3.4 Substitution Strategy

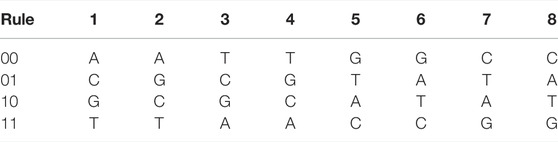
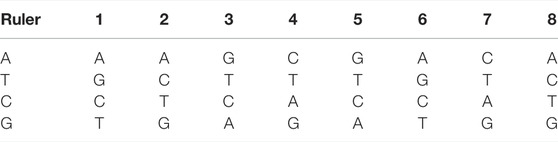
In order to improve the security of ciphertext, we designed a new DNA mutation rule based on the triploid mutation, which is used for the diffusion result. In triploid organisms, one DNA strand can replicate three identical DNA strands. Taking advantage of this property, new types of DNA mutations can be designed to obtain mutated single strands by adding the binary representations of the three DNAs. Assume that the current DNA single strand is “ACGT,” and its binary representation is “00100111” using the coding rule 2 in Table 2. After DNA replication, three identical DNA strands “ACGT,” “ACGT,” and “ACGT” are generated. Then the mutated DNA single strand obtained is “ACTG.” Similarly, when DNA coding rule 4 is used, DNA represented by “00100111″ is “TCGA”, and the mutated DNA single strand obtained is “GCTA.” It is pointed out that eight kinds of DNA mutation rules can be obtained under eight kinds of DNA coding rules as shown in Table 3, and they are in line with the principle of base complementary pairing. Note that for different four bases, triploid mutation changes only two bases at a time, but the mutated bases are represented differently under different coding rules. As a result, it is an efficient way to mutate.

TABLE 2

TABLE 2. DNA encoding and decoding rules.

TABLE 3

TABLE 3. DNA triploid mutation rules.

The DNA mutation based on triploid is carried out as follows:

$\kappa \left(i\right)=\mathrm{mod}(K_1\left(i\right),8)+1,(12)$

where κ (i) is the selected DNA mutation rule, and K₁ (i) is the key stream. After mutation was completed, the cipher E image was obtained using decoding rule β.

4 Simulation Results

In this section, a variety of images are selected and they are mainly from the USC-SIPI database [43]. The simulation environments are as follows: Intel Core i5-4210U CPU 1.70 GHz, Memory 4.00 G, MATLAB 2019a, and Windows 10 operation platform.

An efficient cryptographic system should be able to meet the security requirements of different types of images in secure communication. The grayscale images with different sizes are shown in Figure 3 [43], in which the first column is the original image, the second column is the histogram of the original image, the third column is the cipher, the fourth column is the histogram of the cipher image, and the fifth is the restored image. One can observe that after all the original images are encrypted, their ciphertext images are noisy and chaotic without any visual information, which can be proved by the histogram changes of the original image during the encryption process. In addition, the original image can be accurately restored when decrypted with the correct key, as shown in Figure 3E. In addition, we have also conducted experiments on color images, and the satisfactory results are shown in Figure 4 [43].

FIGURE 3

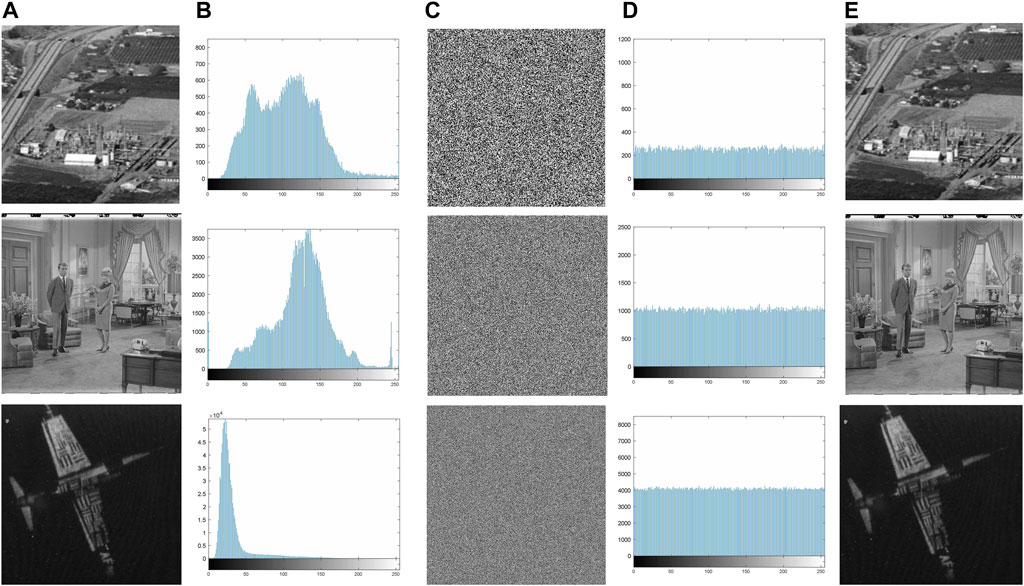
FIGURE 3. Gray image [43] simulation results:(A) plain images, (B) histograms for (A), (C) encrypted images, (D) histograms for (B), and (E) decrypted images.

FIGURE 4

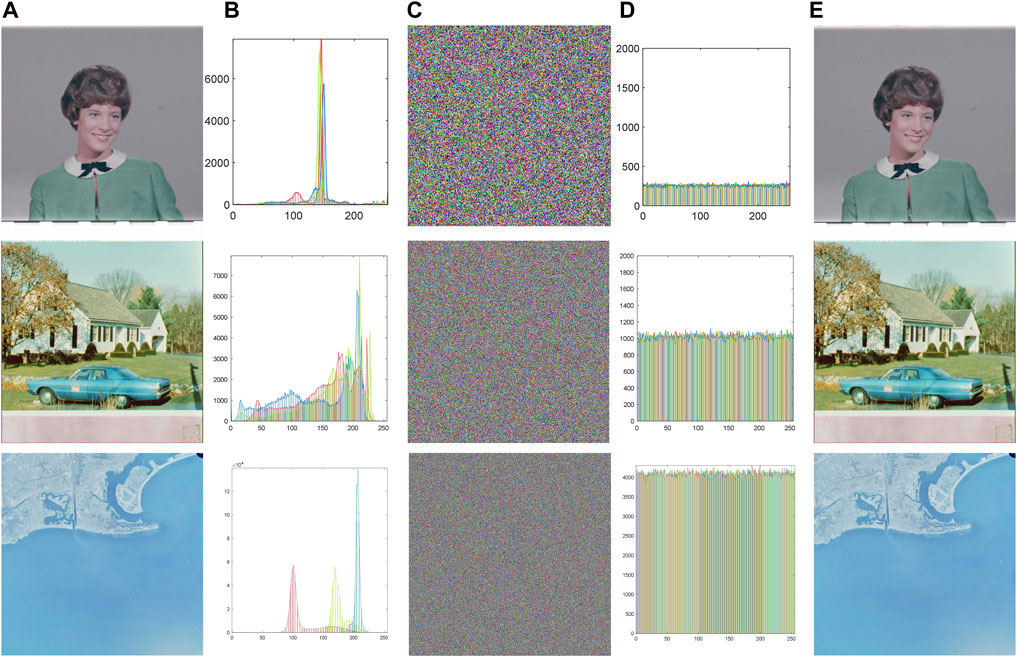
FIGURE 4. Color image [43] simulation results: (A) plain images, (B) histograms for (A), (C) encrypted images, (D) histograms for (B), and (E) decrypted images.

5 Security Analyses

5.1 Key Space Analysis

The key space consists of all the legal key combinations that can be used in the cryptosystem for encryption/decryption. A secure cryptographic system should have a large enough key space to preclude illegal decryption by implementing the brute-force attack. Table 4 lists all the keys that appear in the proposed cryptosystem. When the precision of the computer reaches 10¹⁵, the key space of the proposed cryptosystem is about 10^15×16 ≈ 2⁷⁹⁷, which is much larger than the key space 2¹⁰⁰ recommended by cryptography experts. Accordingly, the proposed cryptographic system can adequately cope with violent attacks.

TABLE 4

TABLE 4. Key during encryption set.

5.2 Key Sensitivity

In general, key sensitivity needs to be evaluated through both encryption and decryption processes. In the encryption process, first we get the cipher using the key K and then compare it with the cipher using the key K with a weakly change t = 10⁻¹⁵. In the decryption process, we also make the same adjustment to the decryption key K. In the decryption process, we also make the same adjustments to the decryption key K, and compare the differences between different decoded images. Figure 5 [43] and Figure 6 [43] show the key sensitivity test results in the encryption and decryption process, respectively. According to the difference in images, the corresponding images of different keys differ greatly, which enables our scheme to pass the key sensitivity test.

FIGURE 5

FIGURE 5. Key sensitivity test in the ciphering stage [43].

FIGURE 6

FIGURE 6. Key sensitivity test in the deciphering stage [43].

5.3 Correlation of Two Adjacent Pixels

Correlation analysis is a branch of statistical analysis, which is a quantitative analysis of the relationship between adjacent pixels in an image. The correlation r_xy can be derived by the following formulas:

$r_{xy}=\frac{\mathrm{cov}(x,y)}{\sqrt{D\left(x\right)D\left(y\right)}},(13)$

$\mathrm{cov}(x,y)=E\left\{\left[x-E\left(x\right)\right]\left[y-E\left(y\right)\right]\right\},(14)$

$E\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i},(15)$

$D\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[x_i-E\left(x\right)\right]}^2}.(16)$

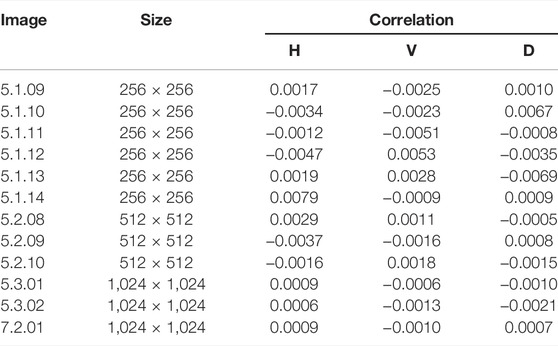
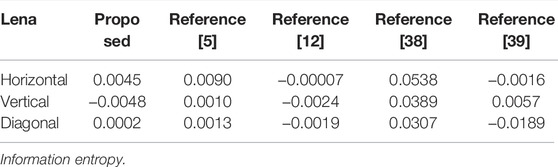
Figure 7 [43] presents 3,000 pairs of pixel values that are taken from the three directions of the plain and its cipher, namely, horizontal (H), vertical (V), and diagonal (D) directions, which constitute the distribution of coordinate points in the rectangular coordinate system. Meanwhile, we have also calculated the correlation in three channels, namely, red, green, and blue and the comparison results are presented in Table 5. Compared with Refs. [5, 12, 38, 39] in Table 6, our algorithm can more efficiently de-correlate the pixel correlation.

FIGURE 7

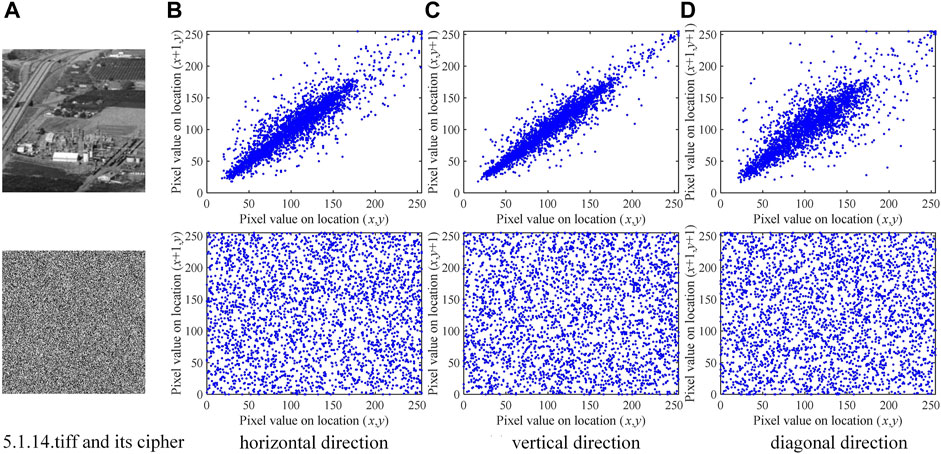
FIGURE 7. Correlation test of image 5.1.14.tiff [43] and its cipher in three directions.

TABLE 5

TABLE 5. Correlation of adjacent pixels in different cipher images.

TABLE 6

TABLE 6. Correlation comparison with different scheme results using the Lena image.

Information entropy (IE) can be used to measure the degree of pixel clutter and it is calculated by the following formula:

$H\left(m\right)=-{\displaystyle \sum _{i=0}^{255}p\left(m_i\right){\log }_{2}p\left(m_i\right)}.(17)$

For an ideal cryptographic system, the degree to which the IE calculated by the aforementioned formula approaches 8 can be used to evaluate the security of the system.

In addition, local Shannon entropy (LSE) is often used in recent years and its calculation formula is deduced as follows:

$H_{k,T_b}\left(s\right)={\displaystyle \sum _{i=1}^b\frac{H\left(s_i\right)}{b}},(18)$

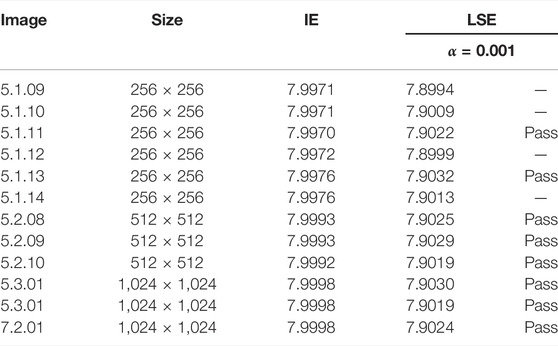
where the image is divided into b blocks with size T_b and H(s) is the current block IE. When significance level α = 0.001, IE should fall into the intervals (7.901515698 and 7.903422936).

Table 7 lists the IE and LSE values of different size images. The IE values of all images approach 8 and the LSE test is passed by almost all images. In addition, we implemented the algorithm comparison using image Lenna, and the compared results in Table 8 fully certify that highly chaotic cipher images can be obtained by our algorithm.

TABLE 7

TABLE 7. Information entropy (IE) and local entropy (LSE) with different images.

TABLE 8

TABLE 8. Comparison results of IE values with different scheme.

5.4 Speed Analysis

In real-time communications, the speed at which algorithms process images is critical. A superior cryptographic system should not only have high security, but also have fast encryption and decryption ability. In our algorithm, the implementation of each scramble operation can simultaneously confuse two pixels, which come from the front and rear of the image. The time complexity is reduced from O (4MN) to O (2MN), so the running efficiency of our algorithm is improved compared with the scrambling operation of a single pixel. In addition, only the two bases are mutated during the process of mutation and the two bases can represent any two bits under different coding rules, which demonstrate the efficiency of mutation operation to a certain extent.

In the test of running speed, standard gray image Lena with the size of 512 × 512 is involved and 100 tests are carried out on it. Table 9 shows the average of the test results through our encryption scheme and compares it with Refs. [34, 38, 39]. The experimental results show that the proposed scheme has an excellent running speed.

TABLE 9

TABLE 9. Running time compared to the relevant encryption systems (unit: second).

6 Conclusion

In this study, we introduced a memristor chaotic system for a chaotic-based secure communication field. The rich dynamic behavior is analyzed prior to encryption. In the process of encryption, the initial conditions of the chaotic system designed by the Hamming distance are used to enhance the plaintext correlation of cryptosystem and provide a secure key stream for encryption. In the permutation stage, we used a chaotic sequence to generate two random positions of pixels to be swapped at the beginning and end of the image to shuffle the pixel, which can enhance the pixel’s confusion effect and permutation speed to a certain extent. In the diffusion stage, DNA XOR operation is implemented followed by DNA mutation is introduced to generate high-quality ciphertext images. Simulation experiments and security analysis fully show that our scheme not only ensures security but also has high efficiency.

Data Availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

YS designed and carried out experiments, analyzed data, and wrote the manuscript. FB provided the theoretical guidance for this manuscript. LW carried out the experiment. HJ improved the algorithm. All authors reviewed the manuscript.

Funding

This work was supported by the Dalian Young Stars of Science and Technology Project (NO.2021RQ088).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Talhaoui MZ, Wang X, Talhaoui A. A New One-Dimensional Chaotic Map and its Application in a Novel Permutation-Less Image Encryption Scheme. Vis Comput (2020) 37(7):1757–68. doi:10.1007/s00371-020-01936-z

CrossRef Full Text | Google Scholar

2. Chai X, Zhi X, Gan Z, Zhang Y, Chen Y, Fu J. Combining Improved Genetic Algorithm and Matrix Semi-tensor Product (STP) in Color Image Encryption. Signal Process. (2021) 183:108041. doi:10.1016/j.sigpro.2021.108041

CrossRef Full Text | Google Scholar

3. Movafegh Ghadirli H, Nodehi A, Enayatifar R. Color Image DNA Encryption Using mRNA Properties and Non-adjacent Coupled Map Lattices. Multimed Tools Appl (2020) 80(6):8445–69. doi:10.1007/s11042-020-10014-4

CrossRef Full Text | Google Scholar

4. Khan JS, Ahmad J, Ahmed SS, Siddiqa HA, Abbasi SF, Kayhan SK. DNA Key Based Visual Chaotic Image Encryption. Ifs (2019) 37(2):2549–61. doi:10.3233/JIFS-182778

CrossRef Full Text | Google Scholar

5. Mondal B, Kumar P, Singh S. A Chaotic Permutation and Diffusion Based Image Encryption Algorithm for Secure Communications. Multimed Tools Appl (2018) 77(23):31177–98. doi:10.1007/s11042-018-6214-z

CrossRef Full Text | Google Scholar

6. Wang X, Su Y. Image Encryption Based on Compressed Sensing and DNA Encoding. Signal Processing: Image Commun (2021) 95:116246. doi:10.1016/j.image.2021.116246

CrossRef Full Text | Google Scholar

7. Ye G, Pan C, Dong Y, Shi Y, Huang X. Image Encryption and Hiding Algorithm Based on Compressive Sensing and Random Numbers Insertion. Signal Process. (2020) 172:107563. doi:10.1016/j.sigpro.2020.107563

CrossRef Full Text | Google Scholar

8. Patro KAK, Prasanth Jagapathi Babu M, Pavan Kumar K, Acharya B. Dual-Layer DNA-Encoding-Decoding Operation Based Image Encryption Using One-Dimensional Chaotic Map. Adv Data Inf Sci Springer (2020) 94 67–80. doi:10.1007/978-981-15-0694-9_8

CrossRef Full Text | Google Scholar

9. Wang X, Su Y, Liu L, Zhang H, Di S. Color Image Encryption Algorithm Based on Fisher-Yates Scrambling and DNA Subsequence Operation. Vis Comput (2021). doi:10.1007/s00371-021-02311-2

CrossRef Full Text | Google Scholar

10. Luo Y, Zhou R, Liu J, Qiu S, Cao Y. An Efficient and Self-Adapting Colour-Image Encryption Algorithm Based on Chaos and Interactions Among Multiple Layers. Multimed Tools Appl (2018) 77(20):26191–217. doi:10.1007/s11042-018-5844-5

CrossRef Full Text | Google Scholar

11. Wu X, Wang K, Wang X, Kan H, Kurths J. Color Image DNA Encryption Using NCA Map-Based CML and One-Time Keys. Signal Process. (2018) 148:272–87. doi:10.1016/j.sigpro.2018.02.028

CrossRef Full Text | Google Scholar

12. Chai X, Fu J, Zhang J, Han D, Gan Z. Exploiting Preprocessing-Permutation-Diffusion Strategy for Secure Image Cipher Based on 3D Latin Cube and Memristive Hyperchaotic System. Neural Comput Applic (2021) 33(16):10371–402. doi:10.1007/s00521-021-05797-y

CrossRef Full Text | Google Scholar

13. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Du S. FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys. B (2022) 31(2):020505. doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

14. Zhang X, Li C, Dong E, Zhao Y, Liu Z. A Conservative Memristive System with Amplitude Control and Offset Boosting. Int J Bifurcation Chaos (2022) 32(04):2250057. doi:10.1142/S0218127422500572

CrossRef Full Text | Google Scholar

15. Li Y, Li C, Zhao Y, Liu S. Memristor-type Chaotic Mapping. Chaos (2022) 32(2):021104. doi:10.1063/5.0082983

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Li Y, Li C, Zhang S, Chen GR, Zeng Z. A Self-Reproduction Hyperchaotic Map with Compound Lattice Dynamics. IEEE Trans Ind Electron (2022) 69(10):10564–10572. doi:10.1109/TIE.2022.3144592

CrossRef Full Text | Google Scholar

17. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Jin J, et al. Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic Radiation. Front Phys (2021) 9:690651. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

18. Yu F, Shen H, Zhang ZZZ, Huang Y, Cai S, Du S. A New Multi-Scroll Chua's Circuit with Composite Hyperbolic tangent-cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011

CrossRef Full Text | Google Scholar

19. Li C, Yang Y, Yang X, Zi X, Xiao F. A Tristable Locally Active Memristor and its Application in Hopfield Neural Network. Nonlinear Dyn (2022) 108:1697–717. doi:10.1007/s11071-022-07268-y

CrossRef Full Text | Google Scholar

20. Li C, Li H, Xie W, Du J. A S-type Bistable Locally Active Memristor Model and its Analog Implementation in an Oscillator Circuit. Nonlinear Dyn (2021) 106(1):1041–58. doi:10.1007/s11071-021-06814-4

CrossRef Full Text | Google Scholar

21. Yu F, Kong X, Chen H, Yu Q, Cai S, Huang Y, et al. A 6D Fractional-Order Memristive Hopfield Neural Network and its Application in Image Encryption. Front Phys (2022) 10:109. doi:10.3389/fphy.2022.847385

CrossRef Full Text | Google Scholar

22. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100(3):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

23. Li X, Mou J, Cao Y, Banerjee S. An Optical Image Encryption Algorithm Based on a Fractional-Order Laser Hyperchaotic System. Int J Bifurcation Chaos (2022) 32(03):2250035. doi:10.1142/S0218127422500353

CrossRef Full Text | Google Scholar

24. Hua Z, Jin F, Xu B, Huang H. 2D Logistic-Sine-Coupling Map for Image Encryption. Signal Process. (2018) 149:148–61. doi:10.1016/j.sigpro.2018.03.010

CrossRef Full Text | Google Scholar

25. Li X, Mou J, Xiong L, Wang Z, Xu J. Fractional-order Double-Ring Erbium-Doped Fiber Laser Chaotic System and its Application on Image Encryption. Opt Laser Techn (2021) 140(3):107074. doi:10.1016/j.optlastec.2021.107074

CrossRef Full Text | Google Scholar

26. Hua Z, Zhu Z, Yi S, Zhang Z, Huang H. Cross-plane Colour Image Encryption Using a Two-Dimensional Logistic Tent Modular Map. Inf Sci (2021) 546:1063–83. doi:10.1016/j.ins.2020.09.032

CrossRef Full Text | Google Scholar

27. Gan Z-h., Chai X-l., Han D-j., Chen Y-r. A Chaotic Image Encryption Algorithm Based on 3-D Bit-Plane Permutation. Neural Comput Applic (2018) 31(11):7111–30. doi:10.1007/s00521-018-3541-y

CrossRef Full Text | Google Scholar

28. Li CL, Zhou Y, Li HM. Image Encryption Scheme with Bit-Level Scrambling and Multiplication Diffusion[J]. Multimedia Tools Appl (2021) 80:18479–18501. doi:10.1007/s11042-021-10631-7

CrossRef Full Text | Google Scholar

29. Zhou Y, Li C, Li W, Li H, Feng W, Qian K. Image Encryption Algorithm with circle index Table Scrambling and Partition Diffusion. Nonlinear Dyn (2021) 103:2043–61. doi:10.1007/s11071-021-06206-8

CrossRef Full Text | Google Scholar

30. Zhou S, Wang X, Wang M, Zhang Y. Simple Colour Image Cryptosystem with Very High Level of Security. Chaos, Solitons & Fractals (2020) 141:110225. doi:10.1016/j.chaos.2020.110225

CrossRef Full Text | Google Scholar

31. Chen J-x., Zhu Z-l., Fu C, Yu H, Zhang L-b. A Fast Chaos-Based Image Encryption Scheme with a Dynamic State Variables Selection Mechanism. Commun Nonlinear Sci Numer Simulation (2015) 20(3):846–60. doi:10.1016/j.cnsns.2014.06.032

CrossRef Full Text | Google Scholar

32. Xiong L, Yang F, Mou J, An X, Zhang X. A Memristive System and its Applications in Red-Blue 3D Glasses and Image Encryption Algorithm with DNA Variation. Nonlinear Dyn (2022) 107(3):2911–33. doi:10.1007/s11071-021-07131-6

CrossRef Full Text | Google Scholar

33. Yang F, An X, Xiong L. A New Discrete Chaotic Map Application in Image Encryption Algorithm. Phys Scr (2022) 97(3):035202. doi:10.1088/1402-4896/ac4fd0

CrossRef Full Text | Google Scholar

34. Sha Y, Cao Y, Yan H, Gao X, Mou J. An Image Encryption Scheme Based on IAVL Permutation Scheme and DNA Operations. IEEE Access (2021) 9:96321–36. doi:10.1109/access.2021.3094563

CrossRef Full Text | Google Scholar

35. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022) 108(1):613–36. doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar

36. Gao X, Mou J, Banerjee S, Cao Y, Xiong L, Chen X. An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud Univ - Comp Inf Sci (2022) 34(4):1535–51. doi:10.1016/j.jksuci.2022.01.017

CrossRef Full Text | Google Scholar

37. Talhaoui MZ, Wang X, Midoun MA. Fast Image Encryption Algorithm with High Security Level Using the Bülban Chaotic Map. J Real-time Image Proc (2020) 18(1):85–98. doi:10.1007/s11554-020-00948-1

CrossRef Full Text | Google Scholar

38. Yuan X, Zhang L, Chen J, Wang K, Zhang D. Multiple-image Encryption Scheme Based on Ghost Imaging of Hadamard Matrix and Spatial Multiplexing. Appl Phys B (2019) 125(9):125. doi:10.1007/s00340-019-7286-9

CrossRef Full Text | Google Scholar

39. Ye H-S, Zhou N-R, Gong L-H. Multi-image Compression-Encryption Scheme Based on Quaternion Discrete Fractional Hartley Transform and Improved Pixel Adaptive Diffusion. Signal Process. (2020) 175:107652. doi:10.1016/j.sigpro.2020.107652

CrossRef Full Text | Google Scholar

40. Xiong L, Zhang X, Teng S, Qi L, Zhang P. Detecting Weak Signals by Using Memristor-Involved Chua's Circuit and Verification in Experimental Platform. Int J Bifurcation Chaos (2020) 30(13):2050193. doi:10.1142/S021812742050193X

CrossRef Full Text | Google Scholar

41. Zhou S, Wang X, Zhang Y. A Novel Image Encryption Cryptosystem Based on True Random Numbers and Chaotic Systems. Multimedia Syst (2022) 1–18. doi:10.1007/s00530-021-00803-8

CrossRef Full Text | Google Scholar

42. Ma X, Mou J, Xiong L, Banerjee S, Cao Y, Wang J. A Novel Chaotic Circuit with Coexistence of Multiple Attractors and State Transition Based on Two Memristors. Chaos, Solitons & Fractals (2021) 152:111363. doi:10.1016/j.chaos.2021.111363

CrossRef Full Text | Google Scholar

43.USC-SIPI. USC-SIPI Image Database. Los Angeles, CA: Signal and Image Processing Institute, University of Southern California (2013). [EB/OL]. Available at: http://sipi.usc.edu/database/ (Accessed February, 2022).

Google Scholar