Folded Resonator for Glucose Solution Density Detection Based on Airy Beam Arrays

We presented an investigation on the evolution properties of the finite Airy beam array (FAiBA) in metamaterial’s slab system constituting of right-handed materials and double negative materials combining the generalized Huygens–Fresnel integral equation and the light transfer matrix. The beam intensity distribution on the receiver plane and its side transmission view on the (z, x) plane are demonstrated numerically with several array numbers. Moreover, we put forward a kind of folded resonator to detect glucose solution density based on the derived principle and conclusion; the influence of curvature radius on the emerging beam’s evolution characteristics is discussed, and the empirical formula between FAiBA’s received power and glucose solution density is derived by using the fit linear analysis. We hope that the present concept and the derived conclusions can be employed for monitoring in the environmental field, as well as the biomedical and food safety detection.

Introduction

The novel pseudo-non-diffracting beam named the finite Airy beam (FAiB) has been of particular interest since it was first confirmed by Siviloglou et al. in 2007. They theoretically deduced the acceleration dynamics of this beam in both one- and two-dimensional configurations [1] and experimentally introduced how to generate the phase masks that were used to generate the Airy beam through the computer-generated hologram technique (Airy hologram masks) [2]. From then on, a lot of exciting applications based on FAiB have been proposed and implemented, such as light bullets, curved plasma channel generation, optical routing, optical interconnection, and image signal transmission [3–6]. However, the asymmetry of the transmission trajectory and faint optical power signals limit the application of FAiB in some fields [7–9], such as optical shearing and laser energy enhancement. It appears necessary to generate multiple Airy beams in the radial symmetry to overcome those defects; therefore, the finite Airy beam array (FAiBA) comes into existence [10].

Meanwhile, the multilayer slab systems, such as thin films, with axial step or gradient index variation are widely applied in precision optical micromanipulation, optical micro-cavity, filters, and optical communications, among which one-dimensional photonic crystal (PC) is a typical device of these metamaterials [11]. In 2018, Li et al. constructed a PC sensor to measure the refractive index and concentration of the sucrose solution [12]. Before long, an effective mixed liquid concentration PC sensor is proposed by Yimiti et al. to detect the water-acetic acid and water-methanol mixed liquids with different concentrations [13]. These PC sensors are dielectric or metallic periodical structures in which the ordinary materials with a positive refractive index are usually used. However, an increasing amount of attention has been paid to the double negative material (DNM) due to its beam focusing and phase compensation properties. It is discovered that PC with DNM results in a novel photonic zero-ϕ_eff band gap [14], which is omnidirectional and insensitive to the incident angle and polarization of the incident wave; meanwhile, it can be widened by adjusting the ratio of the thickness of the two materials, while the center of the band gap remains nearly constant, which is wholly different from band gaps induced by Bragg scattering in the traditional PCs. Due to the local resonance mechanism, this novel PC is also independent of the scale of lattice constant and rarely affected by the lattice disorder [15]. In 2018, Taya et al. proposed a ternary PC for sensing applications, which is composed of an air layer as an analyte sandwiched between two DNM layers [16]. A one-dimensional PC microring resonator based on a grooved optical waveguide was also put forward in order to make the refractive index sensor having a high quality factor and high sensitivity in 2020 [17].

The FAiBA transmission characteristics in masses of alignment optical systems, such as atmospheric turbulence [18], nonlinear media [19], and gradient refractive index media [20], were investigated extensively not long ago. In 2021, Lei et al. generated the Airy beam arrays in real and K spaces based on a dielectric meta-surface [21]. In the meantime, a lot of interest has focused on the FAiB and derivative beams transmitting in the multilayer slab systems [22–26] to explore the application of optical control in precision detection. To the best of our knowledge, however, the propagation rule and intensity distribution of the FAiBA in the metamaterial constituting of right-handed material (RHM) and DNM have not been reported in other studies. The discussion of a different number of FAiBA’s evolution characteristics in this periodic slab system may contribute new features and activities to the subject area of self-accelerating beams.

In the current study, we studied the FAiBA’s emerging intensity distribution on several cross sections of the metamaterial’s slab system, and the beam side intensity view on (z, x) plane is also demonstrated when the FAiBA penetrates in this slab system model. In Section 2, the general propagation formula of the FAiBA cutting through the periodic optical system is calculated in a space domain based on the generalized Huygens–Fresnel integral equation and the light transfer matrix. In Section 3, the intensity profiles of the FAiBA changed with array number in different positions of the metamaterial’s slab system are explored in detail by numerical examples. A folded resonator with a periodic metamaterial’s slab system is also put forward to detect the glucose solution density, the effect of curvature radius on the emerging beam’s evolution characteristics is discussed, and the empirical formula between FAiBA’s received power and glucose solution density is derived by using the fit linear analysis for this optical sensor. A concise conclusion is outlined in Section 4.

Physical Model and Formula

In the Cartesian coordinate system, the electric field distribution of a single Airy beamlet at the source plane can be written in the following form [1, 27]:

$E_1\left(x_0,y_0,z=0\right)=A_i\left(\frac{x_0}{{\omega }_{x0}}\right)\times \exp \left(a_0\frac{x_0}{{\omega }_{x0}}\right)·A_i\left(\frac{y_0}{{\omega }_{y0}}\right)\times \exp \left(a_0\frac{y_0}{{\omega }_{y0}}\right),(1)$

where x₀ and y₀ are the transverse coordinates at the original plane; ω_x0 and ω_y0 are the transverse beam spot sizes; here, we fix ω_x0 = ω_y0 = ω₀, with ω₀ being the incident beam waist radius, and a₀ is the truncation parameter to ensure the Airy beam carrying finite energy. The symbol A_i(●) is the Airy function governed by the following integral function [28]:

$A_i\left(x\right)=\frac{1}{2\pi }\times {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\exp \left[i\frac{u^3}{3}+iux\right]du}.(2)$

Generally, the symmetrical FAiBA is made up of four beamlets; the lobes of each finite Airy beam can be directed to the array by changing the phases of four Airy functions; hence, the expression of the incident FAiBA is gained,

$E_2\left(x_0,y_0,z=0\right)=E_1\left(x_0,y_0,0\right)+E_1\left(-x_0,y_0,0\right)+E_1\left(x_0,-y_0,0\right)+E_1\left(-x_0,-y_0,0\right).(3)$

For any number of the incident FAiBA, its mathematical expression reads

$E_3\left(x_0,y_0,z=0\right)={\displaystyle \sum _{n=0}^{N-1}{A}_i\left(J\right)\times \exp \left(a_{0}J\right)·A_i\left(K\right)\times \exp \left(a_{0}K\right)}(4)$

with

$J=\frac{\cos \left[n\times \left(\frac{2\pi }{N}\right)\right]x_0+\sin \left[n\times \left(\frac{2\pi }{N}\right)\right]y_0}{{\omega }_0},(5)$

$K=\frac{\cos \left[n\times \left(\frac{2\pi }{N}\right)+\frac{\pi }{2}\right]x_0+\sin \left[n\times \left(\frac{2\pi }{N}\right)+\frac{\pi }{2}\right]y_0}{{\omega }_0},(6)$

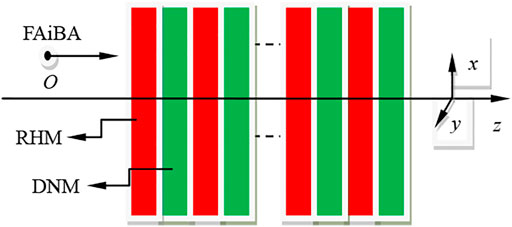
where N is the array number. As shown in Figure 1, our periodic metamaterial’s system model contains two different kinds of textures. The left layer with red color is RHM, and the right green one is the DNM. The Drude model is used to elucidate the relative permittivity and permeability characteristics of DNM when the wave traverses the metamaterials [29],

${\epsilon }_r\left(\omega \right)=1-\frac{{\omega }_{pe}^2}{{\omega }^2},(7)$

${\mu }_r\left(\omega \right)=1-\frac{{\omega }_{pm}^2}{{\omega }^2},(8)$

where ω_pe and ω_pm are the electric and magnetic plasma frequencies, respectively, and ω is the angular frequency of the input wave. The theory of electromagnetics shows that the DNM’s refractive index depends on the following expression:

$n_1=-\sqrt{{\epsilon }_r\left(\omega \right)\cdot {\mu }_r\left(\omega \right)}.(9)$

FIGURE 1

FIGURE 1. Schematic representation of the periodic slab system.

The thicknesses of DNM and RHM are L and R, respectively, n_r is the RHM refractive index, and these parameters are unchanged in the following analysis unless explicitly stated.

When the FAiBA passes through the metamaterial’s slab system, its output electric field distribution E(x, y, and z) can be determined by the generalized Huygens–Fresnel integral equation within the paraxial approximation as the following form [30]:

$E\left(x,y,z\right)=\left(\frac{-i}{\lambda B}\right){\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{E}_3\left(x_0,y_0,0\right){\mathrm{e}}^{\left(\frac{ik}{2B}\left[A\left(x_0^2+y_0^2\right)+D\left(x^2+y^2\right)-2\left(x{x}_0+y{y}_0\right)\right]\right)}d{x}_{0}d{y}_0}},(10)$

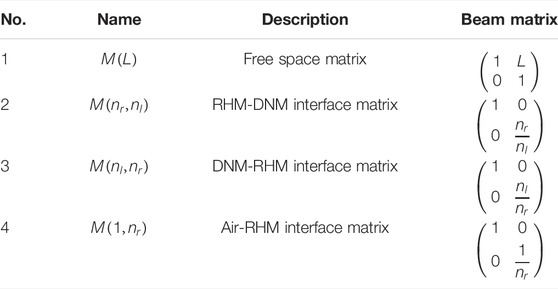
where λ is the wavelength of the input FAiBA, with k = 2π/λ being the wave number. The thickness of each unit is L (i.e., L = R). A, B, C, and D are the elements of the transfer matrix T for the beam evolution in an alignment slab system [31],

$T=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)=M\left(n_l,1\right)M\left(L\right)M\left(n_r,n_l\right)M\left(L\right)M\left(1,n_r\right).(11)$

Here, we introduced some matrix representations for several optical elements in Table 1.

TABLE 1

TABLE 1. Matrix representations for several optical elements.

Substituting Eq. 4 and Eq. 11 into Eq. 10 and after some calculations, the closed-form solution of the FAiBA through the metamaterial’s slab system in the space domain turns out to be

$E\left(x,y,z\right)={\displaystyle \sum _{n=0}^{N-1}{E}_n\left(x,y,z\right)},(12)$

where

$\begin{array}{l}{E}_n\left(x,y,z\right)=\left(\frac{1}{2\pi }\right){\left(\frac{1}{A}\right)}^{\frac{1}{2}}\exp \left[\frac{ikD}{2B}\left(J^2+K^2\right)\right]\times \\ \mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{1}{96}\frac{1}{{\left(\frac{ikA}{2B}\right)}^3{\omega }_0^6}\right]\exp \left[\frac{{\left(\frac{a_0}{{\omega }_0}+\frac{ikJ}{B}\right)}^{2}B}{2ikA}\right]\exp \left[\frac{1}{8}\frac{\left(\frac{a_0}{{\omega }_0}+\frac{ikJ}{B}\right)}{{\omega }_0^3{\left(\frac{ikA}{2B}\right)}^2}\right]\times \mathrm{e}\mathrm{x}\mathrm{p}\left[\frac{1}{96}\frac{1}{{\left(\frac{ikA}{2B}\right)}^3{\omega }_0^6}\right]\exp \left[\frac{{\left(\frac{a_0}{{\omega }_0}+\frac{ikK}{B}\right)}^{2}B}{2ikA}\right]\exp \left[\frac{1}{8}\frac{\left(\frac{a_0}{{\omega }_0}+\frac{ikK}{B}\right)}{{\omega }_0^3{\left(\frac{ikA}{2B}\right)}^2}\right]\times A_i\left[\frac{\left(\frac{a_0}{{\omega }_0}+\frac{ikJ}{B}\right)}{2{\omega }_0\left(\frac{ikA}{2B}\right)}+\frac{1}{16}\frac{1}{{\left(\frac{ikA}{2B}\right)}^2{\omega }_0^4}\right]\times A_i\left[\frac{\left(\frac{a_0}{{\omega }_0}+\frac{ikK}{B}\right)}{2{\omega }_0\left(\frac{ikA}{2B}\right)}+\frac{1}{16}\frac{1}{{\left(\frac{ikA}{2B}\right)}^2{\omega }_0^4}\right].\end{array}(13)$

The FAiBA optical field intensity at the receiver plane can be expressed approximately as

$I=\frac{n_0}{2c{\mu }_0}{\left|E\left(x,y,z\right)\right|}^2\infty {\left|E\left(x,y,z\right)\right|}^2,(14)$

where the constant coefficient n₀/(2cμ₀) is in connection with the refractive index of vacuum n₀, the speed of light c, and the free-space permeability μ₀.

Results and Discussion

FAiBA Evolution Properties

In order to clarify the FAiBA evolution properties in the metamaterial slab system, some numerical findings and interesting results are demonstrated in Figure 2. The calculation parameters are chosen as follows: λ = 1.55μm and ω_pe = ω_pm = 3.16πν, where ν = c/λ = 4.74×10² THz, resulting in n_l = -1.50 and ω₀ = 0.1mm; the FAiBA’s Rayleigh length is Z₀ = πω₀²/λ = 0.02m, R = L = 10Z₀, n_r = 1.50, and N = 4. As can been seen in the initial plane from Figures 2A and B, the factor a₀ leads to the tails of each Airy beam weakened rapidly, and the bigger the a₀ is, the more the energy is concentrated on the main lobes of the incident Airy beam array. During propagation in the RHM, each beamlet of FAiBA self-bends and maintains non-diffracting property in a short distance, as well as that of the FAiB. By observing the beam transmission side view in Figure 2C, it is discovered that they converge toward the center and meet together at a certain point, and this largest intensity enhancement position is called the focusing point. In the following process, the FAiBA continues to transmit independently and does not affect each other. Subsequently, the peak intensity of the FAiBA decreases, and its profile divides into four main lobes on the emerging RHM cross section, as shown in Figure 2D. As a result, the shape of the FAiBA evolves into a quadrangle with a number of side lobes arising around the main lobes. Because the DNM can make a perfect lens to remodel beam’s shape [32], the FAiBA undergoes an inverse parabolic curve in the DNM propagation (Figure 2E), and the emerging FAiBA returns to the original contour ultimately (i.e., the profiles of input and output beams are almost the same before and after FAiBA passes through the whole slab system) if there is no dielectric loss (Figure 2F).

FIGURE 2

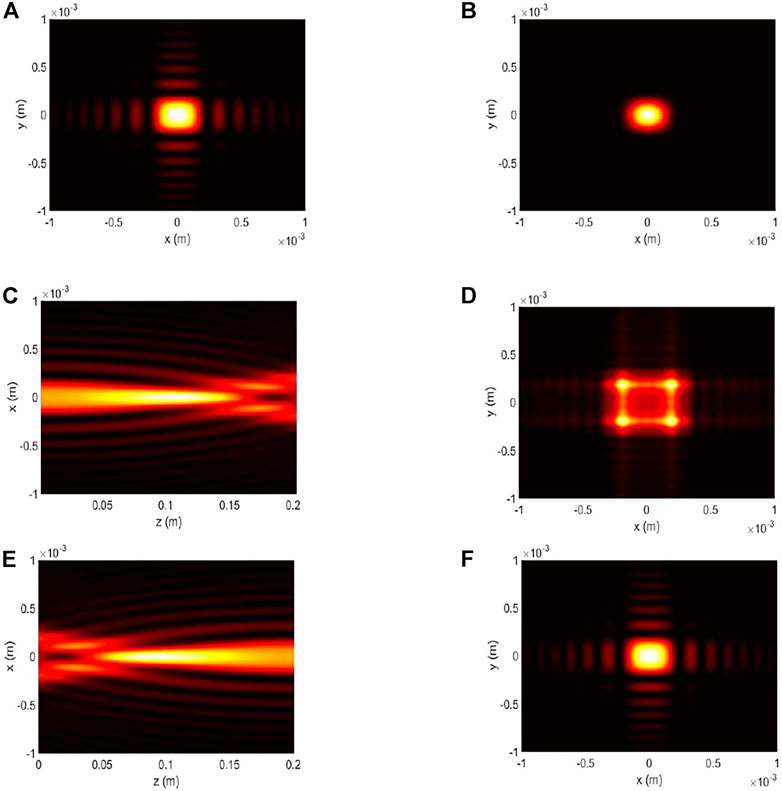
FIGURE 2. Incident FAiBA of (A) a₀ = 0.1 and (B) a₀ = 0.5. (C) Beam transmission side view in RHM. (D) Beam intensity distribution on z = 10Z₀. (E) Beam transmission side view in DNM. (F) Beam intensity distribution on z = 20Z₀. (C–F) a₀ = 0.1.

In order to verify the results of the designing method being universal significance, we delve into the FAiBA with different array numbers N threading this metamaterial slab system, and its intensity distribution profiles on the RHM-DNM interface and emerging plane are delineated in Figure 3. It is revealed that the evolution mechanism of all kinds of FAiBAs’ self-bending, acceleration, inverse parabolic curve, and convergence properties is pretty much the same except that their silhouettes are affected by N (see Figure 3A–F), that is to say, the obtained closed-form expression and achievement can be generalized to explore any number of FAiBA’s evolution property in this metamaterial slab system.

FIGURE 3

FIGURE 3. Transverse intensity profile of various FAiBAs threading the metamaterial’s slab system. (A) N = 3 and z = 10Z₀. (B) N = 3 and z = 20Z₀. (C) N = 6 and z = 10Z₀. (D) N = 6 and z = 20Z₀. (E) N = 8 and z = 10Z₀. (F) N = 8 and z = 20Z₀.

Design and Analysis of the Folded Cavity

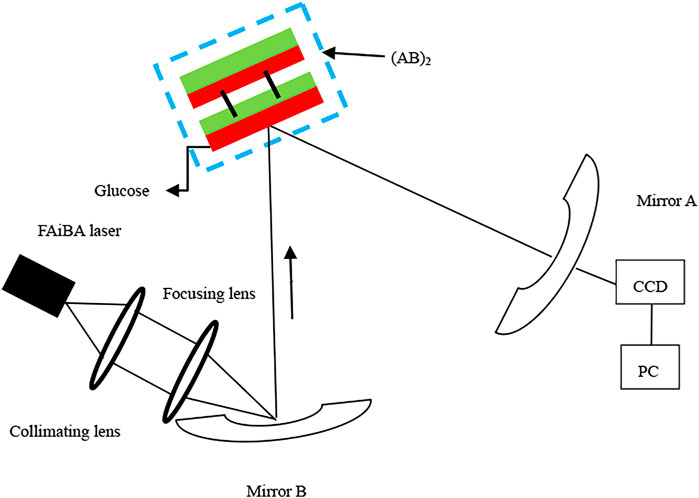
In this sub-section, based on the previously derived conclusions, we presented a folded resonator with the periodic metamaterial slab system model to detect the glucose solution density ρ. The experimental realization of the FAiBA laser depends on a computer-generated hologram technique, of which the key point is the broad Gaussian beam being reflected from the front facet of the liquid crystal spatial light modulator (SLM) [33]. One can use the Fourier transformation to elaborate the desired laser beam array so long as the cubic phase modulation is loaded into the SLM. Then, a linearly polarized light illuminating on the SLM is modulated and further shaped into the FAiBA in the focal plane of a lens through a Fourier transformation. The schematic diagram of this solution density detector is depicted in Figure 4. Two concave mirrors A and B with curvature radius r form a symmetric confocal resonator to meet the stability condition of the measurement:

$0<{\left(1-\frac{l}{r}\right)}^2<1,(15)$

where l = 0.2m for the purpose of matching the size of the single cavity. The periodic metamaterial slab system is installed on the other side of the regular triangle with R = L = Z₀ and the number of layers n = 10. The red color containers are filled with glucose solution, and the green color textures are the DNMs with n_l = -1.50 fixed. The incident FAiBA with a₀ = 0.1 can be imported into the optical cavity by using the collimating and focusing lens. The produced FAiBA passing through the whole folded resonator is then imaged on a carefully aligned CCD camera through a microscope objective. The intensity distribution of this beam array can then be recorded as a function of glucose solution density by translating the imaging apparatus.

FIGURE 4

FIGURE 4. Schematic diagram of the folded resonator with the periodic metamaterial slab system.

The transfer matrix for the beam reflecting off a concave mirror is expressed as

$M\left(f\right)=\left[\begin{array}{cc}1& 0\\ -\frac{1}{f}& 1\end{array}\right],(16)$

where f = r/2 denotes the focal length of the concave mirror. The effect of curvature radius r on the emerging beam’s evolution can be explored by adding the aforementioned matrix into Eq. 11, and the results are portrayed in Figure 5, where N = 8, and other parameters are the same as those in Figure 2. One can clearly see from Figures 5A,B that the beam profile quality and main lobe’s intensity are getting better with the decreasing value of r because the concave mirror’s focusing ability is strengthened in small curvature radius situation. The results in Figure 5A and Figure 3F are almost the same, indicating that the plane mirror can only change the path of light and reflect the wave to the objective plane. However, very small curvature radius might lead to the loss of the stability condition in Eq. 15, which is bad for signal detection. Thus, it is necessary to consider every factor comprehensively in the design process.

FIGURE 5

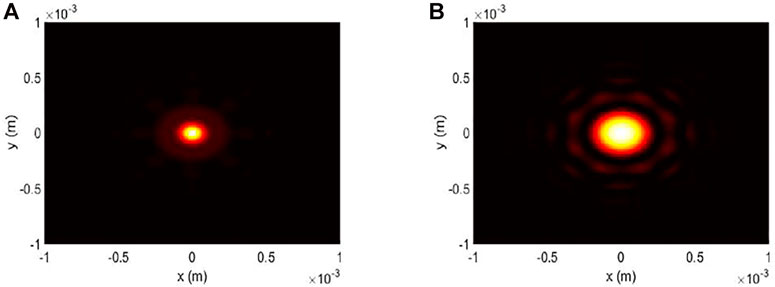
FIGURE 5. Influence of curvature radius on the emerging FAiBA’s intensity distribution. (A) r = 100 m and (B) r→∞.

When the wave emitted by the FAiBA source passes through the whole resonator circle, the output beam profile for different densities of glucose solution is depicted in Figure 6; here, we set r = 100 m, the solution temperature T = 40°C, and the other parameters are the same as those in Figure 5. Comparing Figure 6A with Figure 6B, it reveals that the relative maximum beam intensity shifts gradually as the glucose solution density ρ changes, and the central maximum intensity adds up to 0.68 a. u. when the solution density equals to 1.2235 g/ml, which can be confirmed by the color bar in the right side of Figure 6B.

FIGURE 6

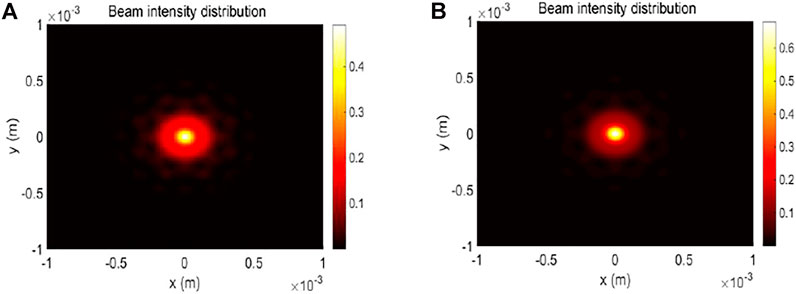
FIGURE 6. Emerging beam profile for several densities of glucose solution. (A) ρ = 0.9918 g/ml. (B) ρ = 1.2235 g/ml.

It remains to investigate the received power of the transmitted beam as a function of the glucose solution density ρ. As far as is known, the quantitative relationship among glucose solution density, concentration, and refractive index are expressed as [34-35].

$N_0=0.0009C+1.3294(17)$

and

$\rho =0.0046C+0.9918,(18)$

where N₀ is the glucose solution refractive index, and C is the solution concentration. Therefore, the quantitative correlation between the solution density and its refractive index is gained

$\rho =5.1111N_0-\mathrm{5.8029.}(19)$

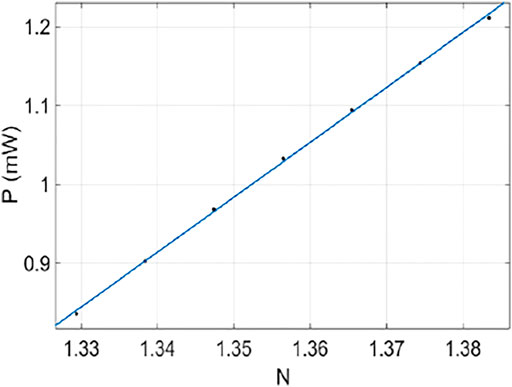
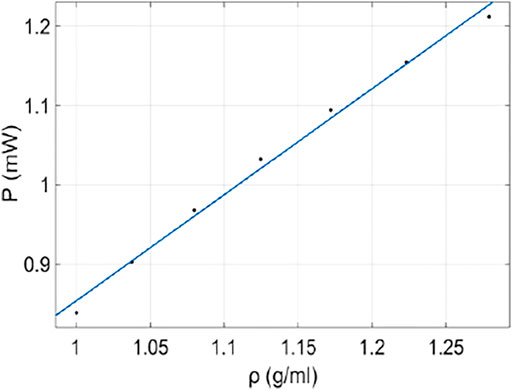
Figure 7 demonstrated the fitting curve between received power and glucose solution refractive index in the folded resonator. It is shown that each discrete point in the picture is very close to the straight line, manifesting that the sensor can offer a remarkable linear response. To go further, the received power value graph as a function of glucose solution density is depicted in Figure 8. The empirical formula is obtained by using the fit linear analysis as

$P=1.334\rho -0.4798,(20)$

where P expresses the emerging beam received power. The R-square (value range from 0 to 1) is 0.9927. This parameter describes the extent to which the input variables explain the output variables; in the univariate linear regression, the larger the R-square is, the better the fitting degree and precision are. It is obvious that the optical sensing technique exhibits the characteristics of simple design principle, high precision, and good linearity. We also made sure that the proposed folded resonator with the periodic metamaterial slab system can be applied to the detection of other transparent liquids as long as the coefficients in Eq. 20 are revised.

FIGURE 7

FIGURE 7. Refractive index fitting graph.

FIGURE 8

FIGURE 8. Density fitting graph.

Conclusion

In conclusion, we discussed the transmission characteristics of the FAiBA through the periodic metamaterial slab system formed by alternating the layers of RHM and DNM based on the light transfer matrix and the generalized Huygens–Fresnel integral equation. The emerging beam intensity distribution and side transmission view changed with different array numbers are studied in detail. We discovered that each beamlet of FAiBA self-bends and maintains non-diffracting property during propagation in the RHM; hence, the FAiBA converges toward the center and meets together at a focusing point in the beginning; then, it continues to transmit independently and do not affect each other; as a result, the shape of FAiBA evolves into a quadrangle with a number of side lobes arising around the main lobes on the emerging RHM cross section. Because the DNM can make a perfect lens to remodel beam’s shape, the FAiBA undergoes an inverse parabolic curve in the DNM propagation, and the emerging FAiBA returns to the original contour ultimately if there is no dielectric loss. It is also verified that the evolution mechanism of all kinds of FAiBAs’ self-bending, acceleration, inverse parabolic curve, and convergence properties is pretty much the same except that their silhouettes are affected by the array number N. In addition, we proposed one kind of folded resonator with the periodic metamaterial slab system to detect the glucose solution density based on the previously derived conclusions, the effect of curvature radius on the emerging beam evolution characteristics is discussed, and it reveals that the beam profile quality and main lobe’s intensity are getting better with the smaller curvature because the concave mirror’s focusing ability is strengthened in the small curvature radius situation, but it should be noted that very small curvature radius might lead to the loss of the stability condition for the cavity, which is bad for signal detection. The empirical formula between FAiBA’s received power and glucose solution density is derived by using the fit linear analysis. We hope that the derived analytical formulae and the corresponding conclusions might be useful for the researchers and designers working in the optical sensing technique area, especially in biomedical and food safety detection.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

LJ conceived the idea, performed the numerical simulations, wrote part of the manuscript, and determined the contents. YX drew the physical structures, prepared the figures, and revised the manuscript. All authors have given approval to the final version of the manuscript.

Funding

The authors gratefully acknowledge the financial support from the Hubei Provincial Department of Education in China (Grant No. D20201803).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Siviloglou G. A., Christodoulides D. N.. Accelerating Finite Energy Airy Beams. Opt Lett (2007) 32:979–81. doi:10.1364/ol.32.000979

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Siviloglou G. A., Broky J., Dogariu A., Christodoulides D. N.. Observation of Accelerating Airy Beams. Phys Rev Lett (2007) 99:213901. doi:10.1103/physrevlett.99.213901

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Polynkin P., Kolesik M., Moloney J. V., Siviloglou G. A., Christodoulides D. N.. Curved Plasma Channel Generation Using Ultraintense Airy Beams. Science (2009) 324:229–232. doi:10.1126/science.1169544

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wiersma N., Marsal N., Sciamanna M., Wolfersberger D.. All-optical Interconnects Using Airy Beams. Opt Lett (2014) 39:5997–6000. doi:10.1364/ol.39.005997

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Rose P., Diebel F., Boguslawski M., Denz C.. Airy Beam Induced Optical Routing. Appl Phys Lett (2013) 102:101101–7. doi:10.1063/1.4793668

CrossRef Full Text | Google Scholar

6. Liang Y., Hu Y., Song D., Lou C., Zhang X., Chen Z, et al. Image Signal Transmission with Airy Beams. Opt Lett (2015) 40:5686–9. doi:10.1364/ol.40.005686

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ren Z., Wu Q., Shi Y., Chen C., Wu J., Wang H.. Production of Accelerating Quad Airy Beams and Their Optical Characteristics. Opt Express (2014) 22:15154–64. doi:10.1364/oe.22.015154

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhang Z., Ye Z., Song D., Zhang P., Chen Z.. Repositioning and Steering Laser Beam Power via Coherent Combination of Multiple Airy Beams. Appl Opt (2013) 52:8512–7. doi:10.1364/ao.52.008512

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wu P., Ke X., Song Q.. Realization of Experiment on Auto-Focusing Array Airy Beam. Chin J Lasers (2018) 45:0605002. doi:10.3788/cjl201845.0605002

CrossRef Full Text | Google Scholar

10. Gu Y., Gbur G.. Scintillation of Airy Beam Arrays in Atmospheric Turbulence. Opt Lett (2010) 35:3456–8. doi:10.1364/ol.35.003456

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Mekis A., Chen J. C., Kurland I., Fan S., Villeneuve P. R., Joannopoulos J. D.. High Transmission through Sharp Bends in Photonic Crystal Waveguides. Phys Rev Lett (1996) 77:3787–3790. doi:10.1103/physrevlett.77.3787

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li X.-F., Liu Y.-Y., Zhao Y.-L.. Measurement of Refractive Index and Concentration of Solution Based on Photonic Crystal Sensor. J Lumin (2018) 39:1157–1162. doi:10.3788/fgxb20183908.1157

CrossRef Full Text | Google Scholar

13. Yimiti A, Abudurexiti A. Photonic crystal Liquid Concentration Sensor. Opt Tech (2019) 45:58–62.

Google Scholar

14. Jiang H., Chen H., Li H., Zhang Y., Zhu S.. Omnidirectional gap and Defect Mode of One-Dimensional Photonic Crystals Containing Negative-index Materials. Appl Phys Lett (2003) 83:5386–5388. doi:10.1063/1.1637452

CrossRef Full Text | Google Scholar

15. Quan X, Yang X. Band Rules for the Frequency Spectra of Three Kinds of Aperiodic Photonic Crystals with Negative Refractive index Materials. Chin Phys B (2009) 18:5313–25.

Google Scholar

16. Taya S. A., Alkanoo A. A., Ramanujam N. R., Mahalakshmi P., Vigneswaran D.. Photonic crystal with Epsilon Negative and Double Negative Materials as an Optical Sensor. Opt Quant Electron (2018) 50:222. doi:10.1007/s11082-018-1487-z

CrossRef Full Text | Google Scholar

17. Liu C., Sang C., Wu X., Mu Z., Cai J., Jia W.. One-dimensional Photonic crystal Groove Microring Resonators and its Sensing Characteristics. Acta Optica Sinica (2020) 40:2413002. doi:10.3788/aos202040.2413002

CrossRef Full Text | Google Scholar

18. Lu Q., Gao S., Sheng L., Wu J., Qiao Y.. Generation of Coherent and Incoherent Airy Beam Arrays and Experimental Comparisons of Their Scintillation Characteristics in Atmospheric Turbulence. Appl Opt (2017) 56:3750–7. doi:10.1364/ao.56.003750

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lu Z.-Y., Li L.-Y., Hu X.-D., Li Z.. Propagation Properties of Ring Airy Beams Array in a Nonlinear media. Phys Lett A (2021) 411:127552. doi:10.1016/j.physleta.2021.127552

CrossRef Full Text | Google Scholar

20. Jin L, Fu Y. Evolution of Finite Array Airy Beams in Gradient Refractive index Medium. Semiconductor Optoelectronics (2021) 42:66–71.

Google Scholar

21. Lei S., Zhang X., Zhu S., Geng G., Li X., Li J, et al. Generation of Airy Beam Arrays in Real and K Spaces Based on a Dielectric Metasurface. Opt Express (2021) 29:18781–90. doi:10.1364/oe.424056

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Liang G., Li J., Luo Z., Luo J., Chen Y., Deng D.. Propagation Properties of Radially and Azimuthally Polarized Chirped Airy-Gaussian Vortex Beams through Slabs of Right-Handed Materials and Left-Handed Materials. J Opt Soc Am A (2019) 36:2060–7. doi:10.1364/josaa.36.002060

CrossRef Full Text | Google Scholar

23. Hong S, Xie J, Yang X, Ye F, Wang G, Liu H, et al. Effects of the Multi-Order and off-axis Vortex on Quadratically Chirped Airy Beams in the Right-Handed and Left-Handed Materials Slabs. Opt Commun (2018) 437:160–7.

Google Scholar

24. Zhong T, Zhan J, Feng L, Pang Z, Wang L, Deng D. Propagation Properties of Radially and Azimuthally Polarized Chirped-Airy Vortex Beams through Slabs of Right-Handed Materials and Left-Handed Materials. J Opt Soc America B: Opt Phys (2017) 35:1354–61.

Google Scholar

25. Huang J., Liang Z., Deng F., Yu W., Zhao R., Chen B, et al. Propagation Properties of Right-Hand Circularly Polarized Airy-Gaussian Beams through Slabs of Right-Handed Materials and Left-Handed Materials. J Opt Soc Am A (2015) 32:2104–19. doi:10.1364/josaa.32.002104

CrossRef Full Text | Google Scholar

26. Xu S, Feng Y. Study on Propagation Properties of Airy Beams through Negative Index Medium. Acta Photonica Sinica (2015) 44:0208002. doi:10.3788/gzxb20154402.0208002

CrossRef Full Text | Google Scholar

27. Jin L., Zhang X.. Propagation Properties of Airy Beam through Periodic Slab System with Negative index Materials. Int J Opt (2018) 2018:1–7. doi:10.1155/2018/9478483

CrossRef Full Text | Google Scholar

28. Varlamov V.. Differential and Integral Relations Involving Fractional Derivatives of Airy Functions and Applications. J Math Anal Appl (2008) 348:101–115. doi:10.1016/j.jmaa.2008.06.052

CrossRef Full Text | Google Scholar

29. Shadrivov I. V., Sukhorukov A. A., Kivshar Y. S.. Beam Shaping by a Periodic Structure with Negative Refraction. Appl Phys Lett (2003) 82:3820–3822. doi:10.1063/1.1579849

CrossRef Full Text | Google Scholar

30. Xu S. Study on Propagation Properties of Airy Beams through One-Dimensional Photonic crystal. J Zhejiang Univ Sci Technology (2019) 31:1–4.

Google Scholar

31. Lin H, Pu J. Propagation of Airy Beams from Right-Handed Material to Left-Handed Material. Chin Phys B (2012) 21:221–6. doi:10.1088/1674-1056/21/5/054201

CrossRef Full Text | Google Scholar

32. Pendry J. B.. Negative Refraction Makes a Perfect Lens. Phys Rev Lett (2000) 85:3966–3969. doi:10.1103/physrevlett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Zhang Z, Liu J. J., Zhang P, Ni P.-G., Prakash J, Hu Y, et al. Generation of Autofocusing Beams with Multi-Airy Beams. Acta Phys Sin (2013) 62:034209. doi:10.7498/aps.62.034209

CrossRef Full Text | Google Scholar

34. Luo W, Sun F, Liu J, Hou J, Wang B, Huang X. Matrix Measurement of Glucose Concentration Based on Surface Plasmon Resonance Sensor. Spectrosc Spectralanalysis (2018) 38:1982–6.

Google Scholar

35. Chao H, Zhu Z, Zhu J. Using Light Beat Method Study on the Relationship between Density and Refractive Index of the Glucose Solution. Phys Exp Coll (2012) 25:3–5.

Google Scholar