
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Phys. , 13 June 2022
Sec. Optics and Photonics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.902133
This article is part of the Research Topic Nonlinear and Quantum Optics in Micro-Nano Structures View all 5 articles
Asymmetric quantum steering generated by the triple-photon down-conversion process in an injected signal optical cavity is investigated. The triple-photon down-conversion process can be realized in an optical superlattice by quasi-phase-matching technology. Asymmetric quantum steering can be obtained in this triple-photon down-conversion process. The direction of asymmetric quantum steering can be controlled by adjusting the parameters of the nonlinear process. The generation of asymmetric quantum steering in the present scheme has potential applications in quantum secret sharing and quantum networks.
As an extension of the Einstein–Podolsky–Rosen (EPR) paradox [2], Schrödinger found the phenomenon of quantum steering in 1935 [1]. Quantum steering is a sufficient condition for quantum entanglement and a necessary condition for Bell nonlocality [3]. Wiseman et al. [4] gave a mathematically operable definition for quantum steering in 2007. In addition, they raised the question of whether there is asymmetric quantum steering, that is, A can steer B, but conversely B cannot steer A. According to Reid’s quantum steering criteria [5], this question was quickly answered both theoretically [6, 7] and experimentally [8]. The research shows that asymmetric quantum steering is a universal property, which does not depend on Gaussian measurement [9]. Intracavity second harmonic generation [10] and atomic Bose–Hubbard chain [11, 12] can produce asymmetric quantum steering based on continuous variables. The asymmetric quantum steering in four-mode cluster states was measured experimentally [13]. An optical parametric oscillator (OPO) is used in many quantum optical experiments [14]. For example, it can produce three-color entanglement [15, 16]. By using the two down-converted optical fields of a nondegenerate OPO, Ou et al. proposed that EPR steering was experimental feasible [17]. For both degenerate [18] and nondegenerate [19] cases, the nonlinear conversion efficiency can be improved by injecting signals into the low-frequency mode. He and Reid confirmed the existence of N-partite EPR steering and developed the concept of genuine N-partite EPR steering, and put forward the criteria for genuine multipartite EPR steering [20]. A scheme is proposed for experimental generation of a highly versatile and flexible repository of multipartite steering using an optical frequency comb and ultrafast pulse shaping [21]. Collective multipartite EPR steering can be generated by cascaded four-wave mixing of rubidium atoms [22]. The research on multipartite quantum steering has attracted much attention [23–28]. Olsen [29] used a nondegenerate parametric oscillator with an injected signal to show how the directionality and extent of the steering can be readily controlled for output modes. Wang and Li analyzed theoretically and experimentally bichromatic entanglement between the signal and the idle [30]. Kalaga and Leoński analyzed the relations between entanglement and steering for a two-mode mixed state [31] and three qubit system [32], respectively. Cao and Guo [33] not only provided the mathematical basis and characterization for Bell delocalization and EPR steering but also derived a sufficient condition to judge whether the state can be steered. Recently, the hybrid ferrimagnet–light system of two macroscopic magnons has made a huge breakthrough. Zheng et al. [34] found that entanglement can be significantly enhanced and strong two-way asymmetric quantum steering appears between two magnons.
Rojas González et al. [35] gave the first theoretical demonstration of continuous-variable triple-photon state quantum entanglement. They also found that quantum entanglement among the three modes disappeared in the case of spontaneous parametric triple-photon generation. However, the genuine triple-photon entanglement can be obtained in the case of injection signal [35]. Agustí et al. [36] showed that the state generated by a three-mode spontaneous parametric down-conversion (SPDC) was the non-Gaussian state, and the states that were generated by superconducting-circuit implementation of the three-mode SPDC had tripartite entanglement based on the criteria built from three-mode correlation functions. However, the quantum steering correlation, especially the asymmetric quantum steering correlation, in the triple-photon down-conversion process has not been studied. In this article, the asymmetric quantum steering generated by the triple-photon down-conversion process with two injected signals is investigated. We demonstrate that the asymmetric quantum steering can be generated by this nonlinear process and also show how to control the asymmetry of quantum steering by adjusting the intensity of the injected signals. Similar to quantum key distribution, in quantum secret sharing [37–39], the confidentiality of shared information does not depend on computational assumptions, but on the uncertainty and non-cloning of quantum mechanics. Xiang et al. [23] designed a protocol based on EPR steering and extended the protocol to three-user scenarios to distribute richer steerability properties including one-to-multimode steering and collective steering that can be used for one-sided device-independent quantum secret sharing. We think that the present scheme of the generation of asymmetric quantum steering has potential applications in quantum secret sharing and quantum networks.
The system consists of a nondegenerate OPO that is driven by an external coherent pump field with the frequency of ω0. Triple-photon SPDC can be achieved in the optical cavity by using the quasi-phase-matching (QPM) technology [40]. The frequencies of the three parametric optical fields are ω1, ω2, and ω3, respectively, which satisfies the energy conservation relationship ω0 = ω1 + ω2 + ω3. The phase mismatch in this nonlinear process is compensated by the reciprocal lattice vector provided by the optical superlattice. The interaction Hamiltonian for the triple-photon SPDC can be written as
where κ represents the effective nonlinearity of optical superlattice that can be taken as real [41].
where ϵ0 is the amplitude of pump. ϵ1 and ϵ2 represent the injected signal fields, and they are also considered to be real. If ϵ1 = ϵ2 = 0, it is the case of spontaneous down-conversion. Because there is no quantum correlation among the output optical fields in the spontaneous down-conversion case [35], in this work, we will study the asymmetric quantum steering characteristics among the output optical fields with two injected signals. We assume that all the optical fields are resonant in the cavity. Following the description of Lindblad superoperator, the losses of the optical fields in the cavity can be written as
where γi (i = 0, 1, 2, 3) represents the cavity loss of the optical field with the frequency ωi.
One can obtain the Fokker–Planck equation in the positive-P representation for studying the characteristics of quantum steering [42, 43]. The third-order derivatives can be reasonably negligible. Then, the Fokker–Planck equation can be given as
Following the normal processing, the equations of motion of the cavity modes can be obtained as
The aforementioned eight coupled stochastic differential equations can be solved by the linearization method. One can expand the positive-P variables into their steady-state expectation values plus delta-correlated Gaussian fluctuation terms as αi = Ai + δαi (i = 0, 1, 2, 3) with δαi ≪ Ai. Ai is the steady-state solution of the cavity mode
The resulting equations can be written for the vector of fluctuation terms as
where A is the drift matrix, B is the noise term that contains the steady-state solutions, and dW is a vector of Wiener increments [43]. The drift matrix A is obtained as
Equation 8 can be solved via the Fourier transform. Then, one can obtain the intracavity spectra as
where ω is the Fourier analysis frequency and I is the identity matrix. According to the standard input–output relationship [44], the output spectra can be calculated through Eq. 10. The quadrature amplitude and phase can be defined as
where
EPRjk is the product of the
Because asymmetric quantum steering between the other optical fields are not obvious enough, we only investigate the asymmetric quantum steering characteristics between the optical fields
Figure 1 depicts the values of EPRjk and EPRkj versus the normalized analysis frequency ω/γ0. One can see that EPR01 = 1, while EPR10 < 1 in the whole range of the normalized analysis frequency, which shows that the output fields
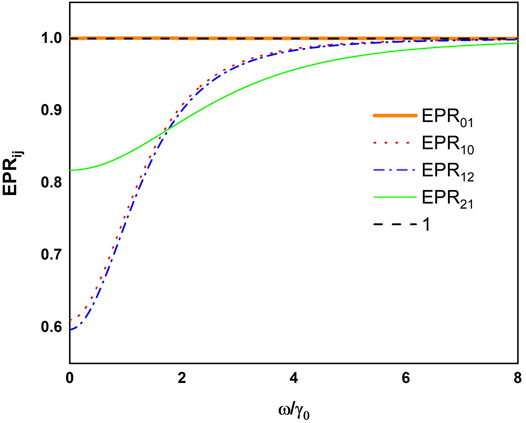
FIGURE 1. Values of EPRjk and EPRkj versus the normalized Fourier analysis frequency ω/γ0 with γ0=0.01, γ1=2γ0, γ2=4γ0, γ3=3γ0, κ =0.01, ϵ0=0.45, ϵ1=0.1, and ϵ2=0.2.
Figure 2 plots EPRjk and EPRkj versus 1) ϵ1/ϵ0 and 2) ϵ2/ϵ0 with ω = 8γ0, γ0 = 0.01, γ1 = 0.02, γ2 = 0.04, γ3 = 0.03, and κ = 0.01. We found that by changing the amplitude of the injected signal ϵ1or ϵ2, one can control whether there is asymmetric quantum steering between the output modes. As shown in Figure 2A, EPR21 is less than 1 and EPR12 is more than 1 when ϵ1/ϵ0 < 0.13, which shows that the output fields
Figure 3 shows the quantum steering of the output field
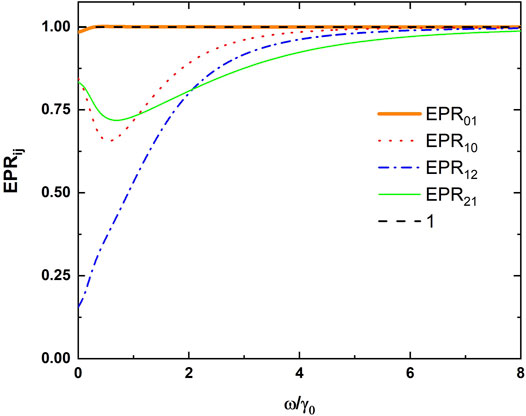
FIGURE 3. Values of EPRjk and EPRkj versus the Fourier analysis frequency ω with γ0=0.1, γ1=2γ0, γ2=4γ0, γ3=0.3γ0, κ =0.01, ϵ0=0.45, ϵ1=0.1, and ϵ2=0.2.
Asymmetric quantum steering produced by the triple-photon down-conversion process with two injected signals is investigated. Asymmetric quantum steering can be obtained in some parameter regimes between optical fields
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
TC wrote the manuscript. YY designed and directed the study. CX, KP, and AC contributed to the discussion and edited the manuscript.
This work is supported by the National Natural Science Foundation of China (No. 61975184) and the Science Foundation of Zhejiang Sci-Tech University (No. 19062151-Y).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Schrödinger E. Discussion of Probability Relations between Separated Systems. Proc Cambridge Philos Soc (1935) 31:555.
2. Einstein A, Podolsky B, Rosen N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys Rev (1935) 47:777–80. doi:10.1103/physrev.47.777
4. Wiseman HM, Jones SJ, Doherty AC. Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox. Phys Rev Lett (2007) 98:140402. doi:10.1103/physrevlett.98.140402
5. Reid MD. Demonstration of the Einstein-Podolsky-Rosen Paradox Using Nondegenerate Parametric Amplification. Phys Rev A (1989) 40:913–23. doi:10.1103/physreva.40.913
6. Olsen MK, Bradley AS. Bright Bichromatic Entanglement and Quantum Dynamics of Sum Frequency Generation. Phys Rev A (2008) 77:023813. doi:10.1103/physreva.77.023813
7. Midgley SLW, Ferris AJ, Olsen MK. Asymmetric Gaussian Steering: When Alice and Bob Disagree. Phys Rev A (2010) 81:022101. doi:10.1103/physreva.81.022101
8. Händchen V, Eberle T, Steinlechner S, Samblowski A, Franz T, Werner RF, et al. Observation of One-Way Einstein-Podolsky-Rosen Steering. Nat Photon (2012) 6:596. doi:10.1038/NPHOTON.2012.202
9. Bowles J, Vértesi T, Quintino MT, Brunner N. One-way Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2014) 112:200402. doi:10.1103/physrevlett.112.200402
10. Olsen MK. Asymmetric Gaussian Harmonic Steering in Second-Harmonic Generation. Phys Rev A (2013) 88:051802. doi:10.1103/physreva.88.051802
11. Olsen MK. Spreading of Entanglement and Steering along Small Bose-Hubbard Chains. Phys Rev A (2015) 92:033627. doi:10.1103/physreva.92.033627
12. Olsen MK. Asymmetric Steering in Coherent Transport of Atomic Population with a Three-Well Bose-Hubbard Model. J Opt Soc Am B (2015) 32:A15. doi:10.1364/josab.32.000a15
13. Deng X, Xiang Y, Tian C, Adesso G, He Q, Gong Q, et al. Demonstration of Monogamy Relations for Einstein-Podolsky-Rosen Steering in Gaussian Cluster States. Phys Rev Lett (2017) 118:230501. doi:10.1103/physrevlett.118.230501
15. Coelho AS, Barbosa FAS, Cassemiro KN, Villar AS, Martinelli M, Nussenzveig P. Three-Color Entanglement. Science (2009) 326:823–6. doi:10.1126/science.1178683
16. Yu YB, Wang HJ, Zhao JW. Analysis of Directly Produce Pump, Signal, and Idler Three-Color Continuous-Variable Entanglement. Eur Phys J D (2012) 66:18. doi:10.1140/epjd/e2011-20248-3
17. Ou ZY, Pereira SF, Kimble HJ, Peng KC. Realization of the Einstein-Podolsky-Rosen Paradox for Continuous Variables. Phys Rev Lett (1992) 68:3663–6. doi:10.1103/physrevlett.68.3663
18. Olsen MK, Dechoum K, Plimak LI. Degenerate Intracavity Parametric Processes with Injected Signal. Opt Commun (2003) 223:123–35. doi:10.1016/s0030-4018(03)01645-6
19. Coutinho dos Santos B, Dechoum K, Khoury AZ, da Silva LF, Olsen MK. Quantum Analysis of the Nondegenerate Optical Parametric Oscillator with Injected Signal. Phys Rev A (2005) 72:033820. doi:10.1103/physreva.72.033820
20. He QY, Reid MD. Genuine Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2013) 111:250403. doi:10.1103/physrevlett.111.250403
21. Cai Y, Xiang Y, Liu Y, He QY, Treps N. Versatile Multipartite Einstein-Podolsky-Rosen Steering via a Quantum Frequency Comb. Phys Rev Res (2020) 2:032046(R). doi:10.1103/physrevresearch.2.032046
22. Liu Y, Cai Y, Luo BS, Jin Y, Niu MQ, Li F, et al. Collective Multipartite Einstein-Podolsky-Rosen Steering via Cascaded Four-Wave Mixing of Rubidium Atoms. Phys Rev A (2021) 104:033704. doi:10.1103/physreva.104.033704
23. Xiang Y, Su XL, Mišta L, Adesso G, He QY. Multipartite Einstein-Podolsky-Rosen Steering Sharing with Separable States. Phys Rev A (2019) 99:010104(R). doi:10.1103/physreva.99.010104
24. Hao ZY, Sun K, Wang Y, Liu ZH, Yang M, Xu JS, et al. Demonstrating Shareability of Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2022) 128:120402. doi:10.1103/physrevlett.128.120402
25. Gupta S, Das D, Majumdar AS. Distillation of Genuine Tripartite Einstein-Podolsky-Rosen Steering. Phys Rev A (2021) 104:022409. doi:10.1103/physreva.104.022409
26. Teh RY, Gessner M, Reid MD, Fadel M. Full Multipartite Steering Inseparability, Genuine Multipartite Steering, and Monogamy for Continuous-Variable Systems. Phys Rev A (2022) 105:012202. doi:10.1103/physreva.105.012202
27. Xiang Y, Liu Y, Cai Y, Li F, Zhang YP, He QY. Monogamy Relations within Quadripartite Einstein-Podolsky-Rosen Steering Based on Cascaded Four-Wave Mixing Processes. Phys Rev A (2020) 101:053834. doi:10.1103/physreva.101.053834
28. Liu Y, Liang SL, Jin GR, Yu YB, Chen AX. Einstein-Podolsky-Rosen Steering in Spontaneous Parametric Down-Conversion Cascaded with a Sum-Frequency Generation. Phys Rev A (2020) 102:052214. doi:10.1103/physreva.102.052214
29. Olsen MK. Controlled Asymmetry of Einstein-Podolsky-Rosen Steering with an Injected Nondegenerate Optical Parametric Oscillator. Phys Rev Lett (2017) 119:160501. doi:10.1103/physrevlett.119.160501
30. Wang N, Li Y. Quantum Analysis and Experimental Investigation of the Nondegenerate Optical Parametric Oscillator with Unequally Injected Signal and Idler. Phys Rev A (2016) 93:013831.
31. Kalaga JK, Leoński W. Quantum Steering Borders in Three-Qubit Systems. Quan Inf Process (2017) 16:175. doi:10.1007/s11128-017-1627-6
32. Kalaga JK, Leoński W, Peřina JJ. Einstein-Podolsky-Rosen Steering and Coherence in the Family of Entangled Three-Qubit States. Phys Rev A (2018) 97:042110. doi:10.1103/physreva.97.042110
33. Cao H, Guo Z. Characterizing Bell Nonlocality and EPR Steering. Sci China Phys Mech Astron (2019) 62:30311. doi:10.1007/s11433-018-9279-4
34. Zheng SS, Sun FX, Yuan HY, Ficek Z, Gong QH, He QY. Enhanced Entanglement and Asymmetric EPR Steering between Magnons. Sci China Phys Mech Astron (2021) 64:210311. doi:10.1007/s11433-020-1587-5
35. Rojas González EA, Borne A, Boulanger B, Levenson JA, Bencheikh K. Continuous-Variable Triple-Photon States Quantum Entanglement. Phys Rev Lett (2018) 120:043601. doi:10.1103/PhysRevLett.120.043601
36. Agustí A, Sandbo Chang CW, Quijandría F, Johansson G, Wilson CM, Sabín C. Tripartite Genuine Non-gaussian Entanglement in Three-Mode Spontaneous Parametric Down-Conversion. Phys Rev Lett (2020) 125:020502. doi:10.1103/PhysRevLett.125.020502
37. Gottesman D. Theory of Quantum Secret Sharing. Phys Rev A (2000) 61:042311. doi:10.1103/physreva.61.042311
38. Dou Z, Xu G, Chen XB, Liu X, Yang YX. A Secure Rational Quantum State Sharing Protocol. Sci China Inf Sci (2018) 61:022501. doi:10.1007/s11432-016-9151-x
39. Wang Y, Tian CX, Su Q, Wang MH, Su Xl. Sci China Inf Sci (2019) 62:072501. doi:10.1007/s11432-018-9705-x
40. Zhu SN, Zhu YY, Ming NB. Quasi-Phase-Matched Third-Harmonic Generation in a Quasi-Periodic Optical Superlattice. Science (1997) 278:843–6. doi:10.1126/science.278.5339.843
41. Ferraro A, Paris MGA, Bondani M, Allevi A, Puddu E, Andreoni A. Three-mode Entanglement by Interlinked Nonlinear Interactions in Optical χ^(2) media. J Opt Soc Am B (2004) 21:1241. doi:10.1364/josab.21.001241
42. Drummond PD, Gardiner CW. Generalised P-Representations in Quantum Optics. J Phys A: Math Gen (1980) 13:2353–68. doi:10.1088/0305-4470/13/7/018
Keywords: quantum steering, EPR steering, asymmetric quantum steering, cascaded nonlinear, quasi-phase-matching
Citation: Chen TH, Pan KY, Xiao C, Yu YB and Chen AX (2022) Asymmetric Quantum Steering Generated by Triple-Photon Down-Conversion Process With Injected Signals. Front. Phys. 10:902133. doi: 10.3389/fphy.2022.902133
Received: 22 March 2022; Accepted: 02 May 2022;
Published: 13 June 2022.
Edited by:
Liangliang Lu, Nanjing Normal University, ChinaCopyright © 2022 Chen, Pan, Xiao, Yu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Y. B. Yu, eWJ5dUB6c3R1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.