Abstract
In order to accommodate multiple types of image encryption, a multi-image encryption algorithm for 2D and 3D images is designed in this paper. After recording the type and number of images, the pixels/coordinates of multiple images are stored in a cube block and are subjected to confusion and diffusion operations. The confusion step uses the random length sequence position swapping method to swap a row (column) vector of variable length with another row (column) vector of the same length at a random position. The diffusion is done by Exclusive OR to combine pixels/coordinates at different locations with different chaotic matrices. Finally, the cipher images are output one by one. Experimental simulations and security analysis verify the effectiveness and security of the algorithm.
Introduction
Image transmission has become more convenient with the development of the Internet, but also faces greater risk. Whether in life, medical, military or commercial fields, effective image encryption is needed to guarantee the secure transmission of various images [1–6]. In addition, since the development of 3D printing technology, image transmission has been extended from 2D images to 3D images [7]. Both 2D and 3D images are being transmitted in large quantities in all corners of the network. Common single-image encryption (SIE) methods are simple and effective, but cannot handle multiple images at the same time. In order to meet the demand of images being encrypted and transmitted in large capacity, multi-image encryption (MIE) algorithms are investigated [8].
Chaotic systems have characteristics such as sensitivity to initial values, pseudo-randomness, and are suitable for use in cryptography [9–14], so there are many SIE and MIE algorithms based on chaotic systems [15–18]. The sensitivity to the initial value guarantees that the image encryption algorithm will not be easily broken when it is perturbed. The pseudo-randomness brings a rich operation to the image encryption algorithm [19–25]. Since chaotic systems play a great advantage in image encryption, using chaotic systems to design image encryption algorithms has become a popular research topic [26, 27]. In previous work on image encryption, there are many classical 1D chaotic maps and 2D chaotic systems used for image encryption. However, with the improvement of computer performance and the development of mathematics and other theories, the simple structure of 1D maps and 2D chaotic systems can be predicted by methods such as nonlinear prediction, so we are also pursuing higher dimensional, more complex and secure chaotic systems to design image encryption algorithms. In the proposed scheme, a three-dimensional memristive neuron chaotic system is used for image encryption [28]. The system is simple in structure but rich in dynamical behavior and is very suitable for use in image encryption.
Multi-image encryption algorithms have been studied since 2012 or even earlier. Most early implementations of multi-image encryption used optical methods, such as Kong et al. used wavelet transform and fractional order Fourier transform in encryption of multiple images [29, 30]; Chen et al. combined optical wavelet transform and compression sensing to compress and encrypt multiple images [31]; Huang et al. used a two-dimensional linear canonical transformation and combined it with a chaotic system to encrypt multiple images [32]. Later, chaotic maps and chaotic systems were used for multi-image encryption, and once they were used, they were widely popularized. Singh uses chaotic maps to generate chaotic random phase masks for encryption of multiple images [33]. Santo Banerjee uses a chaotic laser system to achieve simultaneous encryption of multiple images [34]. Ye combines multiple plain images with a chaotic system to obtain encrypted images, and the security of the algorithm is improved [17]. However, there are multi-image encryption algorithms dedicated to two-dimensional images or three-dimensional images, and few scholars have focused on multi-image encryption algorithms that are applicable to both two-dimensional images and three-dimensional images. In order to follow the development of 3D printing technology and the progress of communication technology, an algorithm based on chaotic system, which is applicable to both 2D multi-image encryption and 3D multi-image encryption, is proposed. In the designed encryption mechanism, either single 2D/3D image or multiple 2D/3D images can be encrypted and decrypted. The encryption algorithm uses an Fridrich-structure and uses a confusion-diffusion encryption strategy [35]. In the confusion phase, each row/column vector of each encrypted plane is split into two row/column vectors of random length to be exchanged with row/column vectors at other locations. The pseudo-randomness of the chaotic sequences guarantees that the pixels of the 2D images or the coordinates of the 3D images are sufficiently disordered. In the diffusion phase, the chaotic sequences of diffusion are determined by the pixel positions/coordinates. The chaotic sequences transformation operation greatly enhances the security of the algorithm.
The paper structure is listed hereafter. Chaotic System introduces the chaotic system used by the proposed algorithm. Encryption Algorithm and Decryption Algorithm provides a detailed description of the encryption algorithm. Simulation Results verifies the effectiveness of the encryption algorithm with simulation results. Security Analysis proves the security of the proposed algorithm using security analysis. Conclusion concludes the multi-image encryption algorithm work.
Chaotic System
In the designed encryption scheme, a 3D memristive neuron model is used to generate chaotic sequences. The model is described as:where α is a positive value, A is the stimulus amplitude, F is the stimulus frequency, and k is the inductive strength of the memductance. When (α, A, k, F, x0, y0, z0) = (4.3, 0.24, 0.428, 1.1, 0.5, 1.55, −2), the phase trajectory of the non-autonomous chaotic system is exhibited in Figure 1. From Figure 1, chaotic system has very complex trajectories of action, indicating that this system can be applied in image encryption algorithms.
FIGURE 1
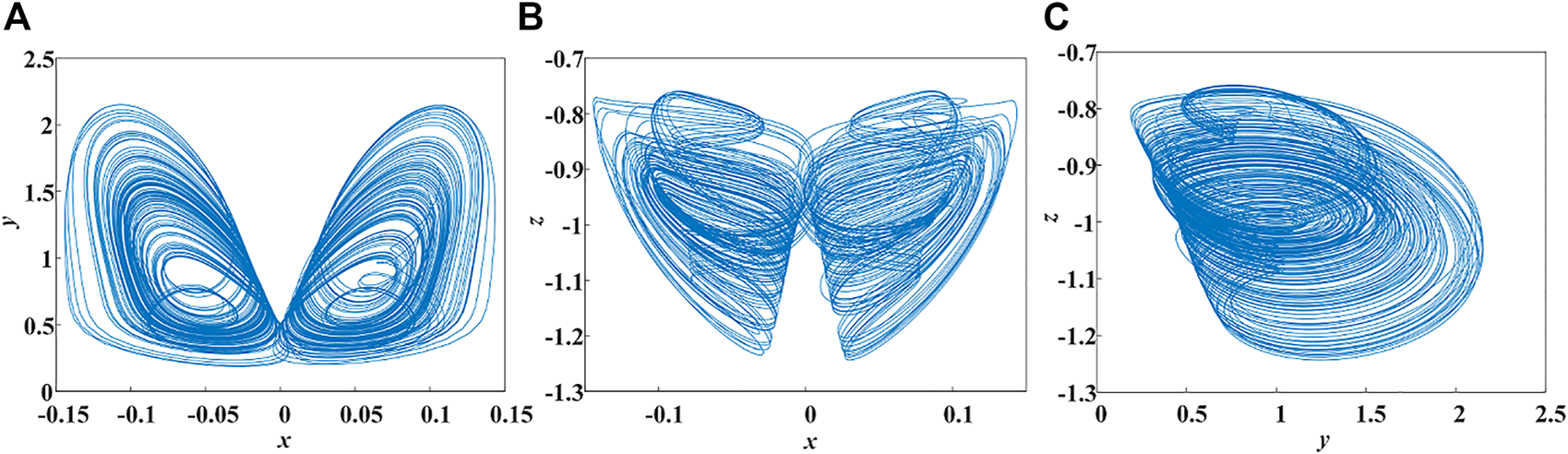
Phase trajectories of the chaotic system (A)x-y plane (B)x-z plane (C)y-z plane.
Encryption Algorithm and Decryption Algorithm
Encryption Algorithm
The encryption scheme as a whole adopts the encryption strategy of scrambling first and then diffusing. In the scrambling phase, the image data is intercepted at random lengths and swapped at random locations. During the diffusion phase, pixels or coordinates are converted using a combination of dynamic chaotic data blocks and image data blocks. After scrambling and diffusion, multiple 3D cipher images or multiple 2D cipher images are output. The encryption flowchart is displayed in Figure 2. The detailed encryption procedures are listed.
FIGURE 2
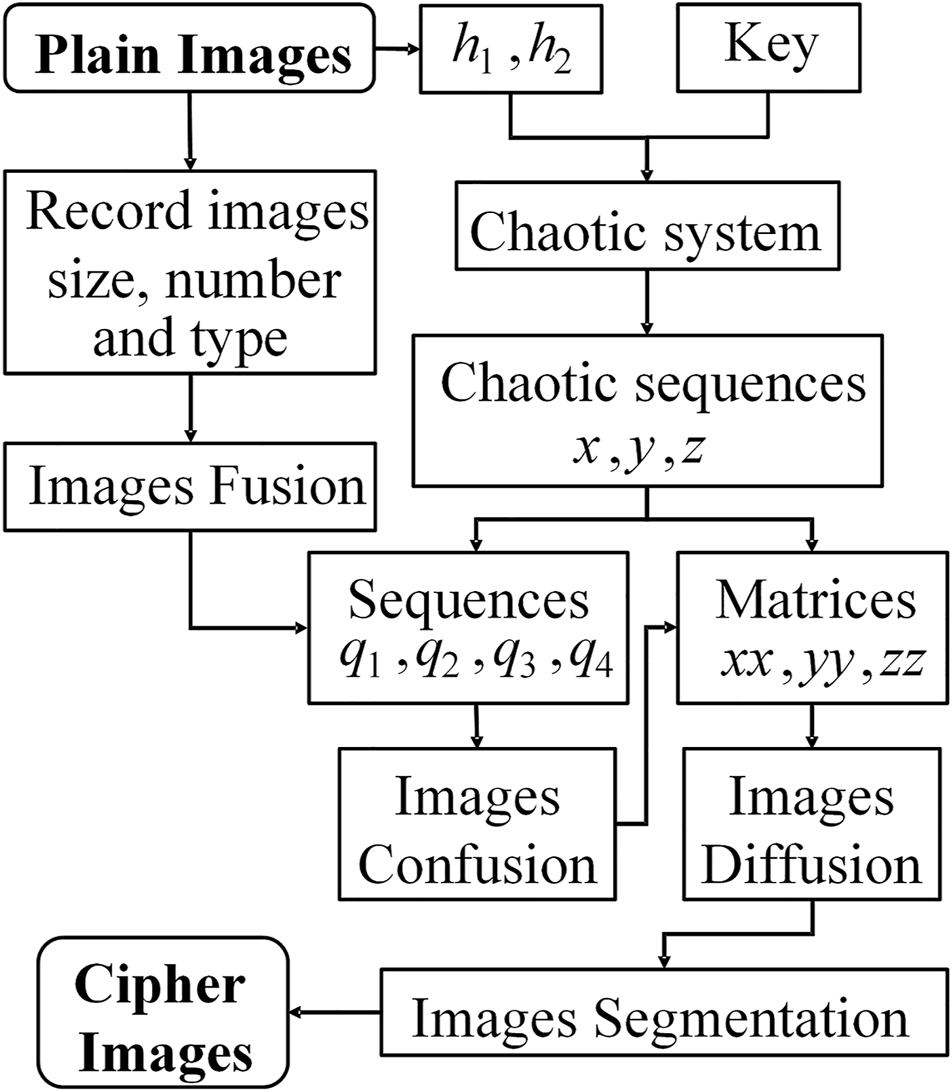
Encryption flowchart.
Step 1:Input several images of the same type and determine whether they are 2D or 3D images. If they are 2D images go to step 2, if they are 3D images go to step 3.
Step 2:The pixels of all 2D images are stored in vector V. The sizes of each 2D image are logged.
Step 3:The 3D image position coordinates are divided into an integer part and a fractional part. The fractional part is stored as a quotient and a remainder. All position coordinates are converted to integers and stored as vector V. The sizes of each 3D image are also logged.
Step 4:Convert the vector V into a cube C. Place the cube in space and mark the orientation of the cube with the x-y-z axis. The altitude of z-axis is denoted as L. The width and height of x-y plane are denoted as W and H. Taking (W, H) = (256, 256) (it can also be any other appropriate value), the length of the vector V as Le, the height of the cube C can be calculated aswhere ceil(a) is rounding a up.
Step 5:Cube C is summed and fed into Hash 256 to obtain a 64-bit hash value h. The hash value h is converted into a sequence of decimal numbers hd. Two parameters h1 and h2 associated with the plain images are obtained by processing the hd.where sl is the size of hd, bmod(a) yields the remainder of b divided by a.
Step 6:The parameters h1, h2, α, A, k, F, and the initial values x0, y0, z0 are input into the chaotic system, and the chaotic sequences are obtained by iteration. After quantizing the chaotic sequences, the sequences x, y and z are obtained.
Step 7:Four sequences q1, q2, q3 and q4 are obtained using three chaotic sequences.where beta is the maximum of W, H, and L.
Step 7.1:The value of the sequence q1 is adjusted to limit it to the interval H/4 to 3H/4.
Step 7.2:Cube C is scrambled along the rows from top to bottom. Swap the positions C(i, 1:q1(j), k) and C(q2(i×k mod(W)+1), 1:q1(j), q3(i×k mod(L)+1)), and swap the positions of C(i, q1(j)+1:H, k) and C(q3(i×k mod(W)+1), q1(j)+1:H, q4(i×k mod(L)+1)), i = 1, …, W; j = 1, …, H; k = 1, …, L.
Step 7.3:Cube C is scrambled along the columns in order from left to right. Swap the positions of C(1:q1(i)mod(W), j, k) and C(1:q1(i)mod(W), q3(j×k mod(H)+1), q4(j×k mod(L)+1)), and swap the positions of C(q1(i)mod(W)+1:W, j, k) and C(q1(i)mod(W)+1:W, q4(j×k mod(H)+1), q2(j×k mod(L)+1)). The cube after permutation is marked as C1.
Step 8:Three chaotic matrices xx, yy and zz of size W×H are obtained by chaotic sequences x, y, z.
Step 9.1Combining the cube C1 and the chaotic matrices, the first row and column of every plane are diffused. The diffused cube is denoted as C2.
Step 9.2Diffusion is performed on the remaining part of the cube.
Step 10Based on the image size recorded in step 2 or step 3, the cube C2 is split and output to obtain the cipher images.
Decryption Algorithm
The process of image decryption is to flip the encryption process. The cipher images and the keys are input to the decryption system, and the chaotic sequences and chaotic matrices are generated by the chaotic system for the inverse diffusion and inverse permutation of the decryption. All cipher images are fused into a cipher cube, and the exclusive OR operation is performed in the order of points, rows, columns, and planes. The inverse diffused cube is reverse permuted from right to left along the columns and from bottom to top along the rows. The decrypted images are obtained by re-partitioning the cube after the inverse permutation and reorganizing them according to the sizes and types of the original images. The specific decryption flow chart is shown in Figure 3.
FIGURE 3
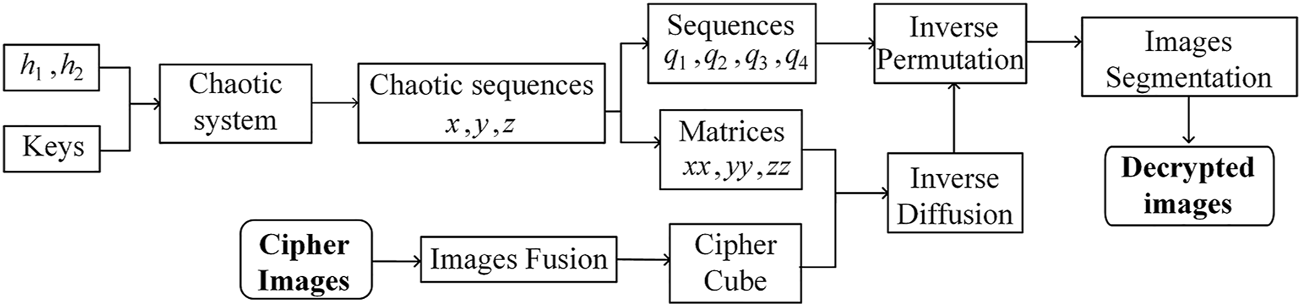
Decryption flowchart.
Simulation Results
In order to verify whether the encryption and decryption algorithms are effective, a set of 3D images and a set of 2D images are used for encryption and decryption tests respectively, and the results are presented in Figures 4, 5. In Figure 4, the three 3D plain images (Air picket, Boeing 747, BMW car) are shown in (A), the cipher images obtained by encryption are shown in (B), and the decrypted results are exhibited in (C). In Figure 5, the multiple 2D plain images (Water, Boat, 5.1.11, Crowd, Kodimo2, 2.2.11), the cipher images and the decrypted results are displayed in (A), (B) and (C). It can be observed from Figure 4 and Figure 5 that the decrypted images are consistent with the original images, while no information related to the original images is visible in the cipher images. Figure 4 and Figure 5 together verify that the designed multiple-image encryption scheme can encrypt the images to be protected and the decryption scheme can successfully recover the cipher images.
FIGURE 4
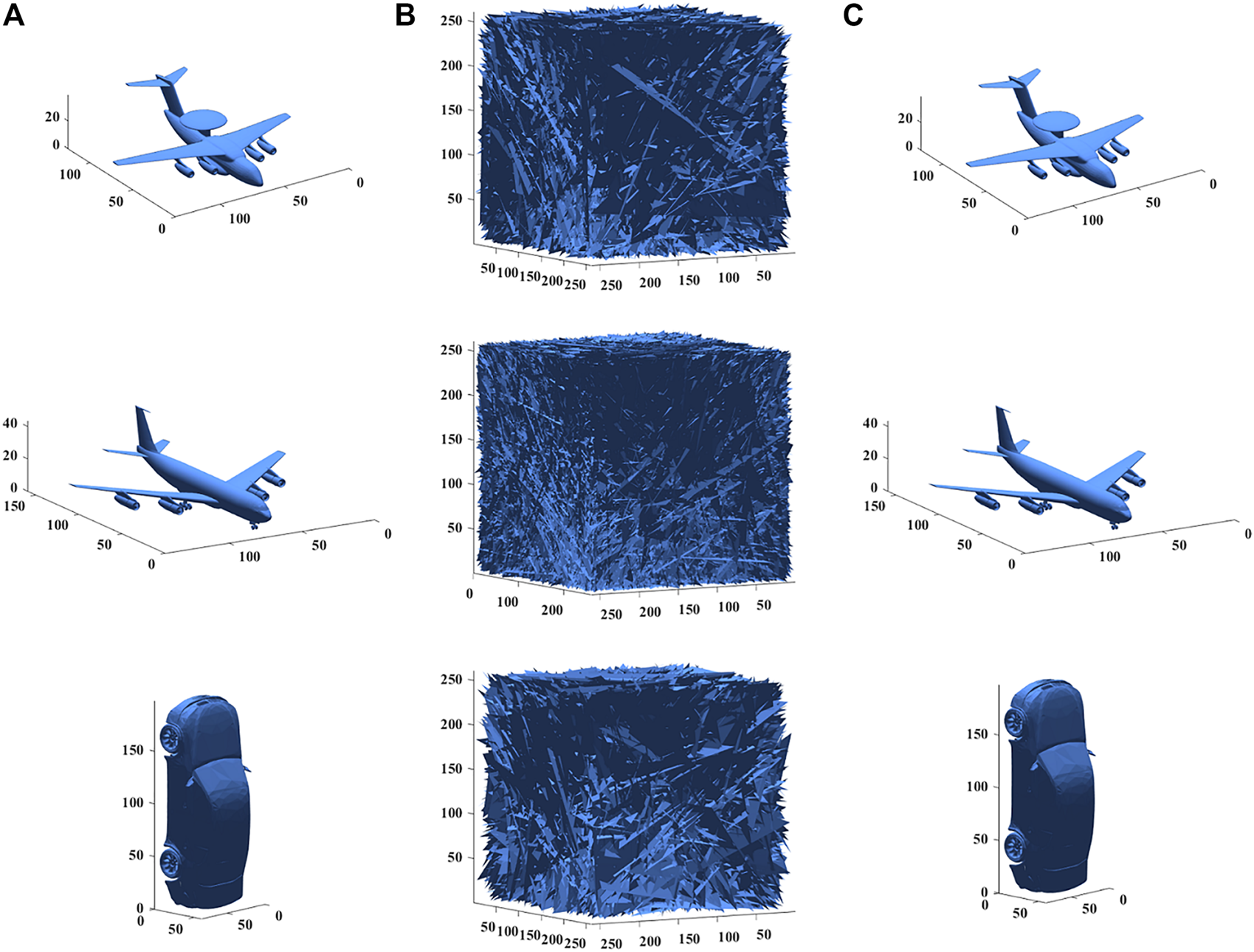
Simulation results of 3D images (A) Plain images (Air picket, Boeing 747, BMW car) (B) Cipher images (C) Decrypted images.
FIGURE 5

Simulation results of 2D images (A) Plain images (Water, Boat, 5.1.11, Crowd, Kodimo2, 2.2.11) (B) Cipher images (C) Decrypted images.
Security Analysis
Key Space and Key Sensitivity
It takes a very long time for an attacker to break the algorithm using a brute force attack when the key space is relatively large. Therefore, the probability of the encryption algorithm being breached decreases as the key space increases. When the key space is greater than 2,100, the encryption algorithm can be considered resistant to brute-force attacks [36]. The key consists of two parts: the parameters associated with the plain images and chaotic system parameters. The key sensitivity is tested by applying a small perturbation to each parameter, so that the key space for each parameter can be obtained. For example, the key remains unchanged during encryption and a perturbation of 10–15 is applied to parameter α during decryption, the decrypted images are observed to be noise-like images and the key space of parameter α can be determined to be 1015. The key space for each parameter is tested so that the total key space is obtained, and the test results are listed in Table 1. From Table 1, the key space is obviously larger than the minimum value, so the designed encryption algorithm will not be breached by brute force attacks.
TABLE 1
| Parameter | Key space | Parameter | Key space |
|---|---|---|---|
| α | 1015 | y 0 | 1015 |
| A | 1014 | z 0 | 1015 |
| k | 1014 | h 1 | 1014 |
| F | 1014 | h 2 | 1014 |
| x 0 | 1016 | Total | 10131≈2435 |
Key space of encryption scheme.
Testing of key sensitivity can be divided into encryption process and decryption process. When the encryption key is slightly changed, the obtained cipher image is CC2(i) (i = 1, 2, …, n, n is the total number of plain images) and the cipher images obtained from the original key encryption is C2(i). Let CC(i) = |C2(i)-CC2(i)|, if the obtained image CC(i) is a black 2D image or a blank 3D image, it means that the encryption process of the encryption algorithm is not sensitive enough. If the obtained image CC(i) is a noise-like 2D image or a cluttered 3D image, it means that the encryption algorithm has a strong encryption process key sensitivity. When the key is slightly changed during the decryption process and then the correct decrypted image is not available, then the encryption scheme is sensitive to the key during the decryption process. The results of the key sensitivity test are shown in Figures 6, 7. As can be seen in Figure 6, the cipher images obtained after the key is slightly perturbed during the encryption process are very different. As can be seen in Figure 7, the slight alteration of the decryption key leads to the inability to obtain the correct decrypted images. The sensitivity of the encryption scheme to the key is demonstrated in Figures 6, 7.
FIGURE 6

Encryption process key sensitivity (A) 3D models (B) 2D images.
FIGURE 7

Decryption process key sensitivity(A) 3D models (B) 2D images.
Statistical Properties
Histogram and χ2 Test
Histogram and χ2 test are commonly used to check whether the image pixels are evenly distributed. The histogram represents the distribution of light and dark in the image, the brighter the image the more the histogram crest tends to the right. Usually, the histograms of the plain images are irregularly distributed, and the histograms of the cipher images, where the pixel distribution information is hidden, are uniformly distributed. The χ2 test is used to test whether the assumption of uniform distribution of cipher images pixels holds. If the χ2 test results are less than the theoretical value (χ20.01 (255) = 310.4574, χ20.05 (255) = 293.2478, χ20.1 (255) = 284.3359) at different test levels, the hypothesis is valid. To check whether the proposed encryption algorithm can hide the light and dark information of the images, the histogram and χ2 test are presented in Figure 8 and Table 2. From Figure 8, the histograms of plain images vary, but the histograms of cipher images are uniformly distributed. The data in Table 2 verify the findings in Figure 8. Combined with Figure 8 and Table 2, the proposed encryption scheme can well hide the light and dark information of the images and avoid the statistical information of the images from being exploited by attackers.
FIGURE 8
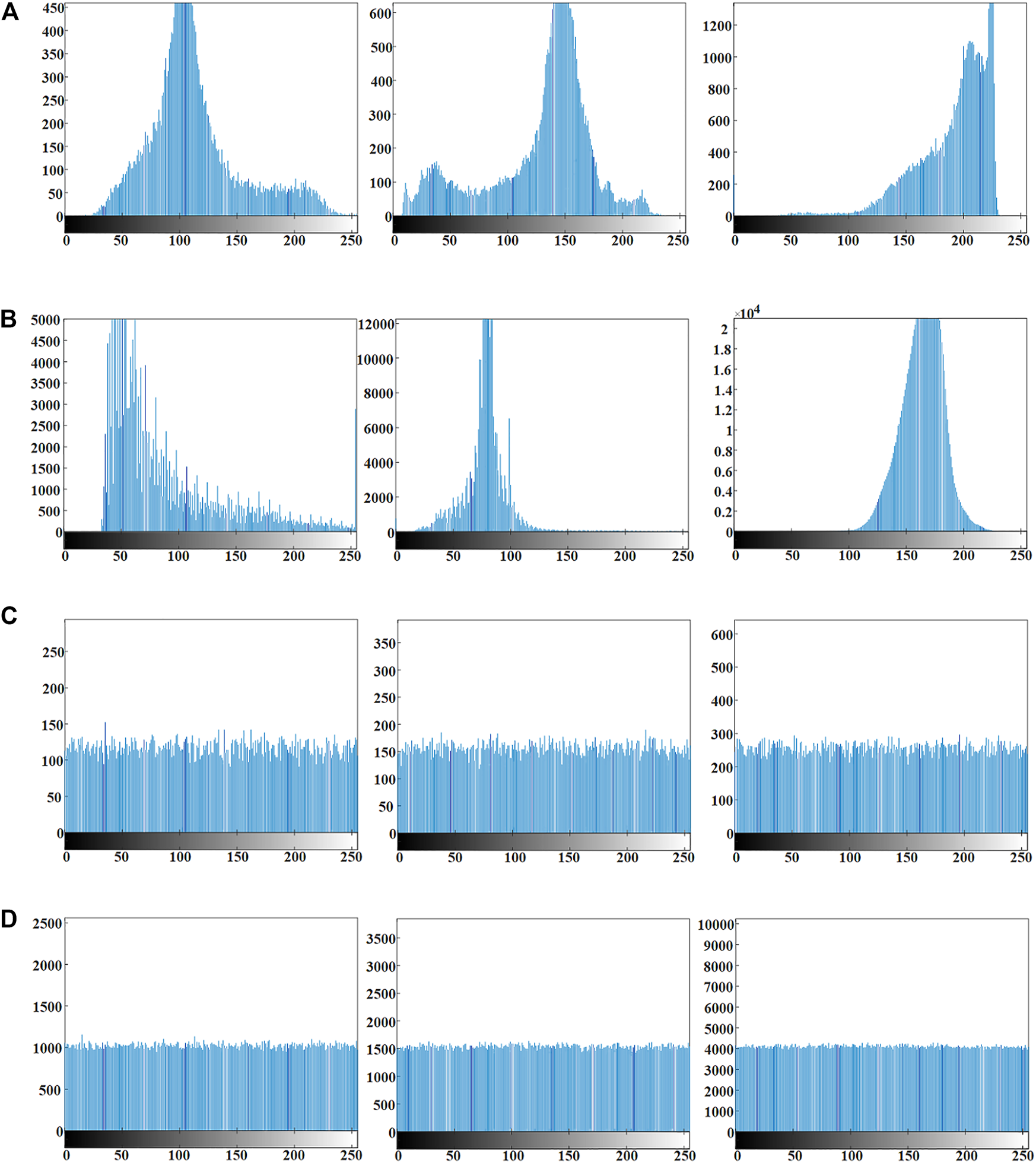
Histogram of encryption and decryption images (A,B) Histogram of plain images (Water, Boat, 5.1.11, Crowd, Kodimo2, 2.2.11) (C,D) Histogram of cipher images.
TABLE 2
| Image | χ2 Value | Result | |||
|---|---|---|---|---|---|
| Plain image | Cipher image | χ20.01 (255) | χ20.05 (255) | χ20.1 (255) | |
| Water | 43758.6176 | 252.1685 | Pass | Pass | Pass |
| Boat | 63497.6288 | 229.3504 | Pass | Pass | Pass |
| 5.1.11 | 220848.6796 | 231.4259 | Pass | Pass | Pass |
| Crowd | 740064.1758 | 275.8242 | Pass | Pass | Pass |
| Kodimo2 | 3605450.7031 | 283.7227 | Pass | Pass | Pass |
| 2.2.11 | 3352937.8725 | 246.2635 | Pass | Pass | Pass |
χ2 test results.
Correlation and Correlation Coefficient
Correlation generally refers to the adjacent pixel correlation of an image, mainly for 2D images. For 3D images, it is used to detect the correlation between adjacent coordinates. The encryption algorithm should have the ability to break the correlation between the adjacent pixels of the 2D images or the adjacent coordinates of the 3D images, so that the adjacent pixel/coordinates cipher images tend to be uncorrelated with each other. The correlation and correlation coefficients of the plain cube and cipher cube are tested. The test results are presented in Figure 9 and Table 3. As can be seen in Figure 9, the 2D plain image shows strong correlation with the distribution of adjacent pixels on a straight line with slope of 1. The 3D plain image also shows strong correlation. The adjacent pixels/coordinates of cipher image spread irregularly over the whole area and show no correlation. The correlation coefficients in Table 3 verify the adjacent pixel/coordinate distributions in Figure 9, where the correlation coefficients are larger for plain images and significantly reduced and very close to 0 for cipher images. It can be concluded from Figure 9; Table 3 that the presented image encryption scheme can effectively hide the correlation of the plain images.
FIGURE 9
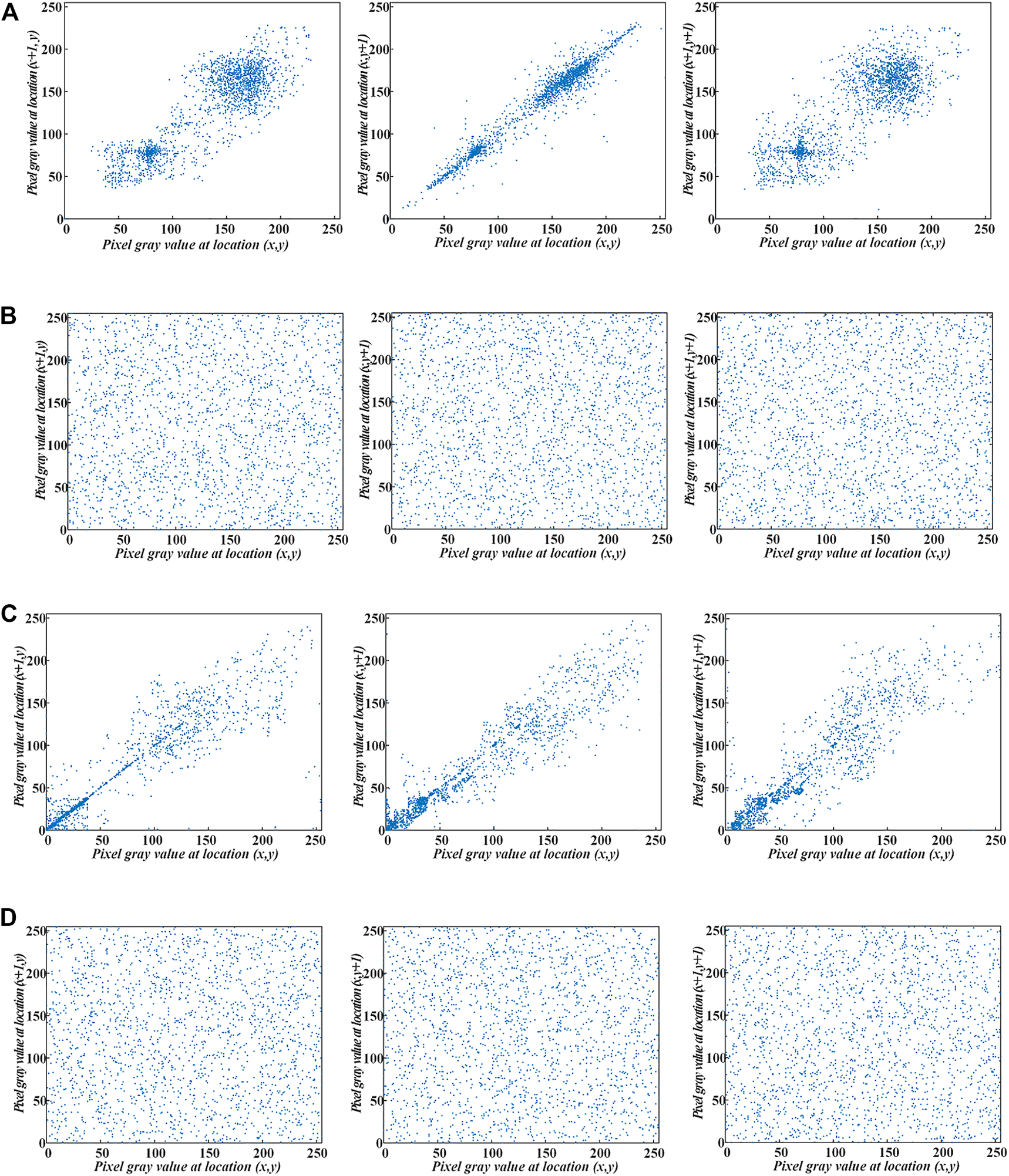
Correlation of different images (A) Correlation of 2D images plain cube (B) Correlation of 2D images cipher cube (C) Correlation of 3D images plain cube (D) Correlation of 3D images cipher cube.
TABLE 3
| Image | 2D images cube | 3D images cube | ||
|---|---|---|---|---|
| Plain | Cipher | Plain | Cipher | |
| Horizontal | 0.7288 | −0.0243 | 0.6703 | −0.0055 |
| Vertical | 0.9750 | 0.0072 | 0.6608 | −0.0027 |
| Diagonal | 0.6928 | 0.0035 | 0.6618 | −0.0031 |
Correlation coefficient of the plain images and cipher images.
Information Entropy and Local Entropy
Information entropy is used to measure the amount of information carried by an image. The greater the information entropy of an image, the greater the amount of information it carries, and then the more confusing the image is from a visual point of view. The local entropy of an image can reflect the local features of the image. The information entropy and local entropy are calculated as in Eq. 13, and the test results are shown in Table 4. From Table 4, it can be seen that the information entropy of the cipher images is significantly increased compared to that of the plain images, which are close to the theoretical value of 8. When the test level is 0.5, the theoretical range of local entropy is (7.901515698, 7.903037329) [37]. In Table 4, the local entropy of the cipher images all fall within the theoretical range. The comparison between the proposed algorithm and other algorithms regarding information entropy and local entropy is listed in Table 5 [17, 26, 38–46]. From Tables 4, 5, the designed encryption algorithm is able to mask the effective information of the plain images so that the cipher images do not contain readable information.where p(i) is the probability of gray value i, H(STB, L) is the information entropy of the non-overlapping image block STB, L is the image gray level, k = 30 is the number of image blocks, and TB = 1936 is the pixels of each image block.
TABLE 4
| Entropy | Image | Plain cube | Cipher cube |
|---|---|---|---|
| Information entropy | 2D images | 7.0985 | 7.9999 |
| 3D images | 7.1736 | 7.9999 | |
| Local entropy | 2D images | 6.8302 | 7.9028 |
| 3D images | 7.5172 | 7.9030 |
Information entropy and local entropy test results.
TABLE 5
| Algorithm | Information entropy | Algorithm | Local entropy |
|---|---|---|---|
| Reference [38] | 7.9998 | Reference [40] | 7.9034 |
| Reference [39] | 7.9993 | Reference [42] | 7.9025 |
| Reference [40] | 7.9973 | Reference [17] | 7.9125 |
| Reference [26] | 7.9998 | Reference [44] | 7.9028 |
| Reference [41] | 7.9994 | Ref. 7 [45] | 7.9028 |
| Reference [43] | 7.9992 | Reference [46] | 7.9029 |
| Proposed | 7.9999 | Proposed | 7.9029 |
Comparison with other algorithms on entropy.
Differential Attack
A differential attack is an attacker who analyzes the change in the cipher images caused by a change in the plain images to attack the encryption algorithm. The number of pixels change rate (NPCR) and the unified average changing intensity (UACI) are used as differential attack test metrics. The plain images are encrypted normally to get a set of original cipher images, and the plain images are slightly changed to get a new set of cipher images. The difference between the two sets of cipher images is measured by NPCR and UACI. The theoretical values of NPCR and UACI are calculated to be 99.6094 and 33.4635%, respectively [47]. A suitable encryption algorithm should have an NPCR greater than or equal to 99.6094% and the larger the better, and the UACI should be close to 33.4635%. To check the ability of the proposed encryption algorithm to resist the differential attack, NPCR and UACI are shown in Table 6. From Table 6, it can be seen that both 2D images and 3D images are used for encryption and the proposed algorithm is resistant to differential attacks. The differential test results of different algorithms are presented in Table 7 [17, 38, 40, 41, 43], where the proposed encryption algorithm is as good as other algorithms in resisting differential attacks.
TABLE 6
| Image | NPCR(%) | UACI(%) |
|---|---|---|
| Air picket | 99.6133 | 33.4674 |
| Boeing 747 | 99.6150 | 33.4625 |
| BMW car | 99.6144 | 33.4863 |
| Water | 99.6449 | 33.4898 |
| Boat | 99.6191 | 33.4528 |
| 5.1.11 | 99.6262 | 33.4709 |
| Crowd | 99.6159 | 33.4506 |
| Kodimo2 | 99.6156 | 33.4620 |
| 2.2.11 | 99.6144 | 33.4525 |
| Average | 99.6199 | 33.4661 |
Differential attack test results.
Conclusion
In this paper, an encryption scheme that can be used for both 2D multiple images and 3D multiple images is proposed. The proposed encryption and decryption algorithm can successfully encrypt and decrypt images regardless of whether the input images are multiple 2D images or multiple 3D images, and regardless of whether the input images are of the same size. The length of the chaotic system iteration is determined by the total size of the multiple images, and the chaotic sequences used for diffusion are determined by the position index of the images. In the algorithm design, the characteristics of the three-dimensional chaotic system are fully utilized, and all chaotic sequences are mobilized to fully participate into the encryption operation. The simulation results of multi-image encryption and decryption verify the ability of the proposed algorithm to encrypt and decrypt images. At the same time, the strong key sensitivity provides a guarantee for the algorithm to resist brute force attacks; the statistical test results demonstrate the ability of the algorithm to resist statistical attacks; the test results of differential attack and the comparison results illustrate that the encryption algorithm can effectively resist the differential attack. The experimental simulations and security tests together prove the effectiveness and practicality of the proposed encryption scheme, which has great application potential.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
XG provided the idea of algorithm, carried out the simulations, arranged the architecture and drafted the manuscript. MM and XC supervised the work and revised the manuscript. Both authors read and approved the final manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
Zhou S Wang X Zhang Y Ge B Wang M Gao S . A Novel Image Encryption Cryptosystem Based on True Random Numbers and Chaotic Systems. Multimedia Syst (2022) 28(1):95–112. 10.1007/s00530-021-00803-8
2.
Yu F Kong X Chen H Yu Q Cai S Huang Y et al A 6D Fractional-Order Memristive Hopfield Neural Network and its Application in Image Encryption. Front Phys (2022) 10, 847385. (in English). 10.3389/fphy.2022.847385
3.
Xiong L Yang F Mou J An X Zhang X . A Memristive System and its Applications in Red-Blue 3D Glasses and Image Encryption Algorithm with DNA Variation. Nonlinear Dyn (2022) 107(3):2911–33. 10.1007/s11071-021-07131-6
4.
Zhou Y Li C Li W Li H Feng W Qian K . Image Encryption Algorithm with circle index Table Scrambling and Partition Diffusion. Nonlinear Dyn (2021) 103(2):2043–61. 10.1007/s11071-021-06206-8
5.
Yu F Zhang Z Shen H Huang Y Cai S Du S . FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys. B (2022) 31:020505. 10.1088/1674-1056/ac3cb2
6.
Yu F Shen H Zhang Z Huang Y Cai S Du S . A New Multi-Scroll Chua's Circuit with Composite Hyperbolic tangent-cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. 10.1016/j.vlsi.2021.05.011
7.
Xu J Zhao C Mou J , "A 3D Image Encryption Algorithm Based on the Chaotic System and the Image Segmentation," IEEE Access (2020) 8, 1–13. 10.1109/access.2020.3005925
8.
Zhou S Wang X Wang M Zhang Y . Simple Colour Image Cryptosystem with Very High Level of Security. Chaos, Solitons Fractals (2020) 141:110225. 10.1016/j.chaos.2020.110225
9.
Ma C Mou J Li P Liu T . Dynamic Analysis of a New Two-Dimensional Map in Three Forms: Integer-Order, Fractional-Order and Improper Fractional-Order. Eur Phys J Spec Top (2021) 230(7):1945–57. 10.1140/epjs/s11734-021-00133-w
10.
Ma X Mou J Liu J Ma C Yang F Zhao X . A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100(3):2859–76. 10.1007/s11071-020-05601-x
11.
Liu T Banerjee S Yan H Mou J . Dynamical Analysis of the Improper Fractional-Order 2D-SCLMM and its DSP Implementation. The Eur Phys J Plus (2021) 136(5):1–17. 10.1140/epjp/s13360-021-01503-y
12.
Ma C Mou J Xiong L Banerjee S Han X . Dynamical Analysis of a New Chaotic System: Asymmetric Multistability, Offset Boosting Control and Circuit Realization. Nonlinear Dyn (2021) 103(6):1–14. 10.1007/s11071-021-06276-8
13.
Li C Yang Y Yang X Zi X Xiao F . A Tristable Locally Active Memristor and its Application in Hopfield Neural Network. Nonlinear Dyn (2022) 108(2):1697–717. 10.1007/s11071-022-07268-y
14.
Xiong L Zhang X Teng S Qi L Zhang P . Detecting Weak Signals by Using Memristor-Involved Chua's Circuit and Verification in Experimental Platform. Int J Bifurcation Chaos (2020) 30(13):2050193. 10.1142/s021812742050193x
15.
Hua Z Zhang K Li Y Zhou Y . Visually Secure Image Encryption Using Adaptive-Thresholding Sparsification and Parallel Compressive Sensing. Signal Process. (2021) 183:107998. 10.1016/j.sigpro.2021.107998
16.
Yousif B Khalifa F Makram A Takieldeen A . A Novel Image Encryption/decryption Scheme Based on Integrating Multiple Chaotic Maps. AIP Adv (2020) 10(7):075220. 10.1063/5.0009225
17.
Ye H-S Zhou N-R Gong L-H . Multi-image Compression-Encryption Scheme Based on Quaternion Discrete Fractional Hartley Transform and Improved Pixel Adaptive Diffusion. Signal Process. (2020) 175:107652. 10.1016/j.sigpro.2020.107652
18.
Tang Z Song J Zhang X Sun R . Multiple-image Encryption with Bit-Plane Decomposition and Chaotic Maps. Opt Lasers Eng (2016) 80:1–11. 10.1016/j.optlaseng.2015.12.004
19.
Li X Mou J Cao Y Banerjee S . An Optical Image Encryption Algorithm Based on a Fractional-Order Laser Hyperchaotic System. Int J Bifurcation Chaos (2022) 32(03):2250035. 10.1142/s0218127422500353
20.
Yang F An X xiong L . A New Discrete Chaotic Map Application in Image Encryption Algorithm. Phys Scr (2022) 97(3):035202. 10.1088/1402-4896/ac4fd0
21.
Zhang X Li C Dong E Zhao Y Liu Z . A Conservative Memristive System with Amplitude Control and Offset Boosting. Int J Bifurcation Chaos (2022) 32(04):2250057. 10.1142/s0218127422500572
22.
Li Y Li C Zhao Y Liu S . Memristor-type Chaotic Mapping. Chaos (2022) 32(2):021104. 10.1063/5.0082983
23.
Li Y Li C Zhang S Chen G Zeng Z . A Self-Reproduction Hyperchaotic Map with Compound Lattice Dynamics. IEEE Trans Ind Electron (2022) 69:10564–72. 10.1109/TIE.2022.3144592
24.
Yu F Zhang Z Shen H Huang Y Cai S Jin J et al Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic RadiationEnglish). Front Phys (2021) 9:690651. 10.3389/fphy.2021.690651
25.
Li C Li H Xie W Du J . A S-type Bistable Locally Active Memristor Model and its Analog Implementation in an Oscillator Circuit. Nonlinear Dyn (2021) 106(1):1041–58. 10.1007/s11071-021-06814-4
26.
Sahasrabuddhe A Laiphrakpam DS . Multiple Images Encryption Based on 3D Scrambling and Hyper-Chaotic System. Inf Sci (2021) 550:252–67. 10.1016/j.ins.2020.10.031
27.
Rakheja P Vig R Singh P . Double Image Encryption Using 3D Lorenz Chaotic System, 2D Non-separable Linear Canonical Transform and QR Decomposition. Opt Quant Electron (2020) 52(2):103. 10.1007/s11082-020-2219-8
28.
Bao BC Zhu YX Jun MA Bao H Huagan WU Chen M . Memristive Neuron Model with an Adapting Synapse and its Hardware Experiments. SCIENCE CHINA Technol Sci (2021) 64(5):11. 10.1007/s11431-020-1730-0
29.
Kong Dezhao 孔. Shen Xueju 沈. Lin Chao 林. Gao Yuchen 高. Multi-Image Encryption Based on Wavelet Transform and Fractional Fourier Transform. 激光与光电子学进展 (2013) 50(9):091002. 10.3788/lop50.091002
30.
Kong D Shen X Xu Q Xin W Guo H . Multiple-image Encryption Scheme Based on Cascaded Fractional Fourier Transform. Appl Opt (2013) 52(12):2619–25. 10.1364/ao.52.002619
31.
Chen X-D Liu Q Wang J Wang Q-H . Asymmetric Encryption of Multi-Image Based on Compressed Sensing and Feature Fusion with High Quality Image Reconstruction. Opt Laser Tech (2018) 107:302–12. 10.1016/j.optlastec.2018.06.016
32.
Huang Z-J Cheng S Gong L-H Zhou N-R . Nonlinear Optical Multi-Image Encryption Scheme with Two-Dimensional Linear Canonical Transform. Opt Lasers Eng (2020) 124:105821. 10.1016/j.optlaseng.2019.105821
33.
Singh N Sinha A . Chaos Based Multiple Image Encryption Using Multiple Canonical Transforms. Opt Laser Tech (2010) 42(5):724–31. 10.1016/j.optlastec.2009.11.016
34.
Banerjee S Mukhopadhyay S Rondoni L . Multi-image Encryption Based on Synchronization of Chaotic Lasers and Iris Authentication. Opt Lasers Eng (2012) 50(7):950–7. 10.1016/j.optlaseng.2012.02.009
35.
Aparna H Bhumijaa B Santhiyadevi R Vaishanavi K Sathanarayanan M Rengarajan A et al Double Layered Fridrich Structure to Conserve Medical Data Privacy Using Quantum Cryptosystem. J Inf Security Appl (2021) 63:102972. 10.1016/j.jisa.2021.102972
36.
Gao X Mou J Banerjee S Cao Y Xiong L Chen X . An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud Univ - Comp Inf Sci (2022) 34:1535–51. 10.1016/j.jksuci.2022.01.017
37.
Wu Y Zhou Y Saveriades G Agaian S Noonan JP Natarajan P . Local Shannon Entropy Measure with Statistical Tests for Image Randomness. Inf Sci (2013) 222:323–42. 10.1016/j.ins.2012.07.049
38.
Zhang X Hu Y . Multiple-image Encryption Algorithm Based on the 3D Scrambling Model and Dynamic DNA Coding. Opt Laser Tech (2021) 141:107073–88. 10.1016/j.optlastec.2021.107073
39.
Gao X Mou J Xiong L Sha Y Yan H Cao Y . A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022) 108:613–36. 10.1007/s11071-021-07192-7
40.
Zarebnia M Parvaz R . Dynamical 2D and 3D Image Encryption Method by Hybrid System Based on Cat Map and Wavelet Transform. Optik (2020) 219:165148. 10.1016/j.ijleo.2020.165148
41.
Patro KAK Acharya B . An Efficient Dual-Layer Cross-Coupled Chaotic Map Security-Based Multi-Image Encryption System. Nonlinear Dyn (2021) 104(3):2759–805. 10.1007/s11071-021-06409-z
42.
Huang W Jiang D An Y Liu L Wang X , "A Novel Double-Image Encryption Algorithm Based on Rossler Hyperchaotic System and Compressive Sensing, IEEE Access (2021) 9, 41704–16. 10.1109/access.2021.3065453
43.
Zhang L Zhang X . Multiple-image Encryption Algorithm Based on Bit Planes and Chaos. Multimedia Tools Appl (2020) 79(29-30):20753–71. 10.1007/s11042-020-08835-4
44.
Xian Y Wang X . Fractal Sorting Matrix and its Application on Chaotic Image Encryption. Inf Sci (2021) 547:1154–69. 10.1016/j.ins.2020.09.055
45.
Alawida M Teh JS Samsudin A Alshoura WH . An Image Encryption Scheme Based on Hybridizing Digital Chaos and Finite State Machine. Signal Process. (2019) 164:249–66. 10.1016/j.sigpro.2019.06.013
46.
Hua Z Zhou Y . Image Encryption Using 2D Logistic-Adjusted-Sine Map. Inf Sci (2016) 339:237–53. 10.1016/j.ins.2016.01.017
47.
Yue W Noonan JP Sos Agaian. NPCR and UACI Randomness Tests for Image Encryption. J Selected Areas Telecommunications (2011) 1(2):31–38.
Summary
Keywords
multi-image, 2D and 3D images, chaotic system, confusion, diffusion
Citation
Gao X, Miao M and Chen X (2022) Multi-Image Encryption Algorithm for 2D and 3D Images Based on Chaotic System. Front. Phys. 10:901800. doi: 10.3389/fphy.2022.901800
Received
22 March 2022
Accepted
11 May 2022
Published
13 June 2022
Volume
10 - 2022
Edited by
Shaobo He, Central South University, China
Reviewed by
Junxin Chen, Northeastern University, China
Zhongyun Hua, Harbin Institute of Technology, China
Updates
Copyright
© 2022 Gao, Miao and Chen.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miao Miao, miaomiao@dlpu.edu.cnmailto:miaomiao@dlpu.edu.cn
This article was submitted to Interdisciplinary Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.