Novel Global Asymptotic Stability and Dissipativity Criteria of BAM Neural Networks With Delays

In this article, issues of both stability and dissipativity for a type of bidirectional associative memory (BAM) neural systems with time delays are investigated. By using generalized Halanay inequalities and constructing appropriate Lyapunov functionals, some novelty criteria are obtained for the asymptotic stability for BAM neural systems with time delays. Also, without assuming boundedness and differentiability for activation functions, some new sufficient conditions for proving the dissipativity are established by making use of matrix theory and inner product properties. The received conclusions extend and improve some previously known works on these problems for general BAM neural systems. In the end, numerical simulation examples are made to show the availability of the theoretical conclusions.

1 Introduction

The BAM neural network model, proposed by Kosko in [1], consists of neurons in two layers, the x-layer and the y-layer. The neurons of the same layer are sufficiently interconnected to the neurons arranged in the other layer, but neurons do not interconnect among the same layer. A useful feature of BAM is its ability to invoke stored pattern pairs in the case of noise. For detailed memory structure and examples of the BAM neural network, please refer to [2]. In recent years, BAM neural systems have received significant attention due to their wide applications in a lot of fields such as pattern recognition, image processing, signal processing, associative memories, optimization problems, and other engineering areas [3–6].

In general, due to the limited switching speed and signal propagation speed of neuron amplifiers, the implementation of a neural network will inevitably have a time delay. We also know that using a delayed version of the neural network is very important to solve some motion-related optimization problems. However, research shows that time delay may lead to divergence, oscillation, and instability, which may be bad for BAM neural systems [7, 8]. Therefore, these applications of the BAM neural systems with delays greatly rely on the dynamical behavior of the neural systems. For these reasons, it is necessary to study the dynamical behavior of the neural systems with delays, and it has been widely studied by a great number of researchers [9, 10].

In the design and analysis of neural networks, stability analysis is a very important and essential link. As small as a specific control system or as large as a social system, financial system, and ecosystem, it is always carried out under various accidental or continuous disturbances. After bearing this kind of interference, it is very important whether the system can keep running or working without losing control or swinging. For neural networks, because the output of the network is a function of time, for a given input, the response of the network may converge to a stable output, oscillate, increase infinitely, or follow a chaotic mode. Therefore, if a neural network system wants to play a role in engineering, it must be stable.

The notion of global dissipativity proposed in the 1970s is a common notion in dynamical systems, and it is applied in the fields of chaos and synchronization theory, stability theory, and robust control and system norm estimation [11–14]. Hence, it is a special and interesting problem to study the dissipativity of dynamical networks. Up to now, the dissipativity for several classes of simple neural networks with delays has begun to attract initial interest in investigation, and some sufficient conditions have been received [15–17]. Yet, to our knowledge, only a few articles have not been used for Lyapunov–Krasovskii functionals or Lyapunov functionals [18–22]. In this study, a few dissipativity conclusions have been received for BAM neural networks with varying delays via inner product properties and matrix theory, which are different from the neural systems’ model investigated in [23, 24].

Inspired by the previous discussion, the global asymptotic stability and dissipativity of BAM neural systems with time delays are investigated. Some new criteria to ensure the dissipation and stability of the BAM neural system are received. Compared with the previous results, our main results are more general and less conservative. The innovations of the study are at least the following aspects.

1) The BAM neural network model studied in this article has a time-varying delay.

2) In our article, the nonlinear activation functions we assumed are not differentiable and bound.

3) In this article, the sufficient conditions for the dissipativity of BAM neural networks with time-varying delay are obtained by using only the inner product property and matrix theory.

4) Moreover, the global attraction sets, namely, positive invariant sets, are obtained.

The structure of the article is organized in the following. The model description and some preliminary knowledge with some necessary definitions and lemmas are given in Section 2. In Section 3, by constructing Lyapunov functionals, we discussed the global asymptotic stability for the equilibrium point of delayed BAM neural systems. Some sufficient criteria are obtained and discussed to guarantee the global dissipativity by using inner product properties in Section 4. Two examples and their simulation conclusions are provided in Section 5. In the end, some results are reached in Section 6.

2 Preliminaries

Notations: In this article, let Rⁿ be a Euclidean space with the inner product $<x,y>=y^{T}x$ and the norm $\Vert x{\Vert }_2=\sqrt{<x,x>}$, where $x={(x_1,x_2,\dots ,x_n)}^{T}andy={(y_1,y_2,\dots ,y_n)}^T\in R^n$. The matrix norm is $\Vert A{\Vert }_2=\sqrt{{\lambda }_{\max }(A^{T}A)}$ for A ∈ R^n×n, where λ_max(A^TA) denotes the maximum eigenvalue of A^TA. λ_min(A) denotes the minimum eigenvalue of A. A > 0 denotes that matrix A is symmetric positive definite. E is a unit matrix.

In this article, the model of delayed BAM neural networks is investigated.

$\left\{\begin{array}{c}\dot{x}\left(t\right)=-Ax\left(t\right)+Cf\left(y\left(t\right)\right)+\tilde{C}f\left(y\left(t-\tau \right)\right)+I,\hfill \\ \dot{y}\left(t\right)=-By\left(t\right)+Dg\left(x\left(t\right)\right)+\tilde{D}g\left(x\left(t-\sigma \right)\right)+J,\hfill \end{array}\right.(1)$

for t > 0, $x(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T$ represents neuron in the first layer at time t, and $y(t)={(y_1(t),y_2(t),\dots ,y_n(t))}^T$ represents neuron in the second layer at time t; A = diag (a₁, a₂, …, a_n) and B = diag (b₁, b₂, …, b_n), in which a_i > 0 and $b_j>0(i,j\in \mathcal{I}=\{\mathrm{1,2},\dots ,n\})$ denote passive decay rates, respectively; $C={(c_{ij})}_{n\times n},D={(d_{ij})}_{n\times n},\tilde{C}={({\tilde{c}}_{ij})}_{n\times n},and\tilde{D}={({\tilde{d}}_{ji})}_{n\times n}$ are synaptic connection strengths; $f(y(t))={(f_1(y_1(t)),f_2(y_2(t)),\dots ,f_n(y_n(t)))}^T$ and $g(x(t))={(g_1(x_1(t)),g_2(x_2(t)),\dots ,g_n(x_n(t)))}^T$ denote nonlinear activation functions; $I={(I_1,I_2,\dots ,I_n)}^T,J={(J_1,J_2,\dots ,J_n)}^T$ represents the external inputs to the neurons; $\tau ={({\tau }_1,{\tau }_2,\dots ,{\tau }_n)}^T,\sigma ={({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)}^T$ which are required for axonal transmission and neural processing of signals are time delays.

In this study, we considered the following continuous activation functions:

(H₁): $\forall x,y\in R,x\ne y,i,j\in \mathcal{I}$, activation functions f_j(⋅) and g_i(⋅) satisfy f_j(0) = g_i(0) = 0, and there exist constants l_j, m_i > 0 such that

$0\le \frac{f_j\left(x\right)-f_j\left(y\right)}{x-y}\le l_j,0\le \frac{g_i\left(x\right)-g_i\left(y\right)}{x-y}\le m_i.$

Remark 1:. The hypothesis of activation function H₁ in this study has been widely used in some references. In particular, when discussing the stability, synchronization, and dissipation of neural networks, H₁ is a common assumption. In the study, the activation function is Lipschitz continuous, so it is monotonously increasing. But it may not be differentiable or bounded. However, in [8, 13], the activation function should not only satisfy the hypothesis H₁ of this study but also satisfy the boundedness. In [15], the derivative of the activation function also satisfies boundedness. In this study, the activation function only needs to satisfy the hypothesis H₁. Compared with [8, 13, 15], the assumption of excitation function in this study is more general.The initial condition of the system (1) is considered as

$\left\{\begin{array}{c}x\left(s\right)=\phi \left(s\right),s\in \left[-\alpha +t_0,t_0\right],\hfill \\ y\left(s\right)=\psi \left(s\right),s\in \left[-\alpha +t_0,t_0\right],\hfill \end{array}\right.$

where $\bar{\tau }=\underset{j\in \mathcal{I}}{\max }\{{\tau }_j\},\bar{\sigma }=\underset{i\in \mathcal{I}}{\max }\{{\sigma }_i\},\alpha =\max \{\bar{\tau },\bar{\sigma }\},$ and φ(s), ψ(s) ∈ C[(− α + t₀, t₀), Rⁿ].

Definition 1:. [25]. The neural system (1) is globally dissipative if there exists a compact set S ⊆ R²ⁿ, such that ∀z₀ ∈ S, ∃ T(z₀) > 0, when t ≥ t₀ + T(z₀), z(t, t₀, z₀) ⊆ S, in which z(t, t₀, z₀) represents the solution for (1) from initial time t₀ and initial state z₀. A set S is said to be forward invariant if ∀z₀ ∈ S indicates z(t, t₀, z₀) ⊆ S for t ≥ t₀.

Definition 2:. [26]. The point ${({x^{*}}^T,{y^{*}}^T)}^T$ with $x^{*}={(x_1^{*},x_2^{*},\dots ,x_n^{*})}^{T}and{y}^{*}={(y_1^{*},y_2^{*},\dots ,y_n^{*})}^T$ is the equilibrium of system (1) if

$\left\{\begin{array}{c}-A{x}^{*}+Cf\left(y^{*}\right)+\tilde{C}f\left(y^{*}\right)+I=0,\hfill \\ -B{y}^{*}+Dg\left(x^{*}\right)+\tilde{D}g\left(x^{*}\right)+J=0.\hfill \end{array}\right.$

Lemma 1:. [27]. For every positive k > 0 and every a, b ∈ Rⁿ,

$2a^{T}b\le k{a}^{T}Xa+k^{-1}{b}^T{X}^{-1}b$

holds, in which X > 0.

Lemma 2:. (Generalized Halanay inequalities) [28]. If V(t) ≥ 0, t ∈ (−∞, + ∞) and

$D^{+}V\left(t\right)\le \gamma \left(t\right)+\xi \left(t\right)V\left(t\right)+\eta \left(t\right)\underset{t-\tau \left(t\right)\le s\le t}{\sup }V\left(s\right),t\ge t_0,$

for t ∈ [t₀, + ∞), in which γ(t) ≥ 0, η(t) ≥ 0, and ξ(t) ≤ 0 are continuous functions and τ(t) ≥ 0, and there exists α > 0 such that

$\xi \left(t\right)+\eta \left(t\right)\le -\alpha ,fort\ge t_0.$

Then,

$V\left(t\right)\le \frac{{\gamma }^{*}}{\alpha }+\left(\underset{-\infty \le s\le t_0}{\sup }V\left(s\right)-\frac{{\gamma }^{*}}{\alpha }\right)\cdot e^{-{\mu }^{*}\left(t-t_0\right)},$

where ${\gamma }^{*}=\underset{t_0\le t\le \infty }{\sup }\gamma (t),{\mu }^{*}=\underset{t\ge t_0}{\inf }\{\mu (t):\mu (t)+\xi (t)+\eta (t)e^{\mu (t)\tau (t)}=0\}$, and the upper-right Dini derivative $D^{+}y(t)=\overline{\underset{h\to 0^{+}}{\lim }}\frac{y(t+h)-y(t)}{h}$.

3 Global Asymptotic Stability for BAM Neural Networks

First of all, under condition (H₁), neural system (1) always at least has an equilibrium point. In the following, the asymptotic stability of the equilibrium point will be proved. For simplicity, we transformed the equilibrium point of system (1) to the origin. We assumed that $z^{*}={(x_1^{*},x_2^{*},\dots ,x_n^{*},y_1^{*},y_2^{*},\dots ,y_n^{*})}^T$ is an equilibrium of neural system (1). By the transformation $u_i(\cdot )=x_i(\cdot )-x_i^{\ast },w_j(\cdot )=y_j(\cdot )-y_j^{*}$, one can transform system (1) into the system as follows:

$\left\{\begin{array}{c}\dot{u}\left(t\right)=-Au\left(t\right)+C\tilde{f}\left(w\left(t\right)\right)+\tilde{C}\tilde{f}\left(w\left(t-\tau \right)\right),\hfill \\ \dot{w}\left(t\right)=-Bw\left(t\right)+D\tilde{g}\left(u\left(t\right)\right)+\tilde{D}\tilde{g}\left(u\left(t-\sigma \right)\right),\hfill \end{array}\right.(2)$

where $\tilde{f}(w(t))={({\tilde{f}}_1(w_1(t)),{\tilde{f}}_2(w_2(t)),\dots ,{\tilde{f}}_n(w_n(t)))}^T,\tilde{g}(u(t))={({\tilde{g}}_1(u_1(t)),{\tilde{g}}_2(u_2(t)),\dots ,{\tilde{g}}_n(u_n(t)))}^T$, in which ${\tilde{f}}_j(w_j(t))=f_j(w_j(t)+y_j^{*})-f_j(y_j^{*}),and{\tilde{g}}_i(u_i(t))=g_i(u_i(t)+x_i^{\ast })-g_i(x_i^{\ast })$. Functions f_j(⋅), g_i(⋅) satisfy the condition (H₁); hence, ${\tilde{f}}_j(\cdot ),{\tilde{g}}_i(\cdot )$ satisfy

$\left\{\begin{array}{c}{\tilde{f}}_j^2\left(w_j\left(\cdot \right)\right)\le l_j{w}_j\left(\cdot \right){\tilde{f}}_j\left(w_j\left(\cdot \right)\right),\hfill \\ {\tilde{f}}_j^2\left(w_j\left(\cdot \right)\right)\le l_j^2{w}_j^2\left(\cdot \right),{\tilde{f}}_j\left(0\right)=0,\hfill \end{array}\right.(3)$

$\left\{\begin{array}{c}{\tilde{g}}_i^2\left(u_i\left(\cdot \right)\right)\le m_i{u}_i\left(\cdot \right){\tilde{g}}_i\left(u_i\left(\cdot \right)\right),\hfill \\ {\tilde{g}}_i^2\left(u_i\left(\cdot \right)\right)\le m_i^2{u}_i^2\left(\cdot \right),{\tilde{g}}_i\left(0\right)=0.\hfill \end{array}\right.(4)$

Remark 2:. It is easy to verify that systems (1) and (2) have the same stability. Therefore, to prove the stability of the equilibrium point z* of the system (1), it is sufficient to prove the stability of the trivial solution of the system (2).

Theorem 1:. Under condition (H₁), if there exist positive definite diagonal matrices P = {p_i} ∈ R^n×n, N = {n_i} ∈ R^n×n and constants ς₁, ς₂, β₁, β₂ > 0 such that

$-2PA+{\varsigma }_1^{-1}P\tilde{C}{N}^{-1}{\tilde{C}}^{T}P+{\beta }_1^{-1}PC{C}^{T}P+{\beta }_2{M}^2+{\varsigma }_{2}P{M}^2<0,$

$-2NB+{\varsigma }_2^{-1}N\tilde{D}{P}^{-1}{\tilde{D}}^{T}N+{\beta }_2^{-1}ND{D}^{T}N+{\beta }_1{L}^2+{\varsigma }_{1}N{L}^2<0,$

where M = diag{m₁, …, m_n}, L = diag{l₁, …, l_n}; then the zero solution of neural system (2) is a unique equilibrium point and is globally asymptotically stable. Proof. Now, we chose Lyapunov functional.

$V\left(u\left(t\right),w\left(t\right)\right)=\sum _{i=1}^n{p}_i{u}_i^2\left(t\right)+{\varsigma }_1\sum _{j=1}^n{\int }_{t-{\tau }_j}^t{n}_j{\tilde{f}}_j^2\left(w_j\left(s\right)\right)ds+\sum _{j=1}^n{n}_j{w}_j^2\left(t\right)+{\varsigma }_2\sum _{i=1}^n{\int }_{t-{\sigma }_i}^t{p}_i{\tilde{g}}_i^2\left(u_i\left(s\right)\right)ds.$

Then,

$\begin{array}{ll}\hfill \dot{V}\left(u\left(t\right),w\left(t\right)\right)& =2\sum _{i=1}^n{p}_i{u}_i\left(t\right){\dot{u}}_i\left(t\right)+{\varsigma }_1\sum _{j=1}^n{n}_j\left[{\tilde{f}}_j^2\left(w_j\left(t\right)\right)-{\tilde{f}}_j^2\left(w_j\left(t-{\tau }_j\right)\right)\right]\hfill \\ \hfill & +2\sum _{j=1}^n{n}_j{w}_j\left(t\right){\dot{w}}_j\left(t\right)+{\varsigma }_2\sum _{i=1}^n{p}_i\left[{\tilde{g}}_i^2\left(u_i\left(t\right)\right)-{\tilde{g}}_i^2\left(u_i\left(t-{\sigma }_i\right)\right)\right]\hfill \\ \hfill & =2u^T\left(t\right)P\dot{u}\left(t\right)+{\varsigma }_1{\tilde{f}}^T\left(w\left(t\right)\right)N\tilde{f}\left(w\left(t\right)\right)-{\varsigma }_1{\tilde{f}}^T\left(w\left(t-\tau \right)\right)N\hfill \\ \hfill & \times \tilde{f}\left(w\left(t-\tau \right)\right)+2w^T\left(t\right)N\dot{w}\left(t\right)+{\varsigma }_2{\tilde{g}}^T\left(u\left(t\right)\right)P\tilde{g}\left(u\left(t\right)\right)\hfill \\ \hfill & -{\varsigma }_2{\tilde{g}}^T\left(u\left(t-\sigma \right)\right)P\tilde{g}\left(u\left(t-\sigma \right)\right)\hfill \\ \hfill & =2u^T\left(t\right)P\left(-Au\left(t\right)+C\tilde{f}\left(w\left(t\right)\right)+\tilde{C}\tilde{f}\left(w\left(t-\tau \right)\right)\right)+{\varsigma }_1{\tilde{f}}^T\left(w\left(t\right)\right)N\hfill \\ \hfill & \times \tilde{f}\left(w\left(t\right)\right)-{\varsigma }_1{\tilde{f}}^T\left(w\left(t-\tau \right)\right)N\tilde{f}\left(w\left(t-\tau \right)\right)+2w^T\left(t\right)N\left(-Bw\left(t\right)\right.\hfill \\ \hfill & +\left.D\tilde{g}\left(u\left(t\right)\right)+\tilde{D}\tilde{g}\left(u\left(t-\sigma \right)\right)\right)+{\varsigma }_2{\tilde{g}}^T\left(u\left(t\right)\right)P\tilde{g}\left(u\left(t\right)\right)\hfill \\ \hfill & -{\varsigma }_2{\tilde{g}}^T\left(u\left(t-\sigma \right)\right)P\tilde{g}\left(u\left(t-\sigma \right)\right).\hfill \end{array}(5)$

By Lemma 1, we obtained

$-{\varsigma }_1{\tilde{f}}^T\left(w\left(t-\tau \right)\right)N\tilde{f}\left(w\left(t-\tau \right)\right)+2u^T\left(t\right)P\tilde{C}\tilde{f}\left(w\left(t-\tau \right)\right)\le {\varsigma }_1^{-1}{u}^T\left(t\right)P\tilde{C}{N}^{-1}{\tilde{C}}^{T}Pu\left(t\right),(6)$

$-{\varsigma }_2{\tilde{g}}^T\left(u\left(t-\sigma \right)\right)P\tilde{g}\left(u\left(t-\sigma \right)\right)+2w^T\left(t\right)N\tilde{D}\tilde{g}\left(u\left(t-\sigma \right)\right)\le {\varsigma }_2^{-1}{w}^T\left(t\right)N\tilde{D}{P}^{-1}{\tilde{D}}^{T}Nw\left(t\right).(7)$

From Eqs 6, 7, then

$\begin{array}{ll}\hfill \dot{V}\left(u\left(t\right),w\left(t\right)\right)& \le -2u^T\left(t\right)PAu\left(t\right)+2u^T\left(t\right)PC\tilde{f}\left(w\left(t\right)\right)+{\varsigma }_1^{-1}{u}^T\left(t\right)P\tilde{C}{N}^{-1}{\tilde{C}}^{T}Pu\left(t\right)\hfill \\ \hfill & +{\varsigma }_1{\tilde{f}}^T\left(w\left(t\right)\right)N\tilde{f}\left(w\left(t\right)\right)-2w^T\left(t\right)NBw\left(t\right)+2w^T\left(t\right)ND\tilde{g}\left(u\left(t\right)\right)\hfill \\ \hfill & +{\varsigma }_2^{-1}{w}^T\left(t\right)N\tilde{D}{P}^{-1}{\tilde{D}}^{T}Nw\left(t\right)+{\varsigma }_2{\tilde{g}}^T\left(u\left(t\right)\right)P\tilde{g}\left(u\left(t\right)\right)\hfill \\ \hfill & \le -2u^T\left(t\right)PAu\left(t\right)+{\beta }_1^{-1}{u}^T\left(t\right)PC{C}^T{P}^{T}u\left(t\right)+{\beta }_1{\tilde{f}}^T\left(w\left(t\right)\right)\tilde{f}\left(w\left(t\right)\right)\hfill \\ \hfill & +{\varsigma }_1^{-1}{u}^T\left(t\right)P\tilde{C}{N}^{-1}{\tilde{C}}^{T}Pu\left(t\right)+{\varsigma }_1{w}^T\left(t\right)N{L}^{2}w\left(t\right)-2w^T\left(t\right)NBw\left(t\right)\hfill \\ \hfill & +{\beta }_2^{-1}{w}^T\left(t\right)ND{D}^T{N}^{T}w\left(t\right)+{\beta }_2{\tilde{g}}^T\left(u\left(t\right)\right)\tilde{g}\left(u\left(t\right)\right)\hfill \\ \hfill & +{\varsigma }_2^{-1}{w}^T\left(t\right)N\tilde{D}{P}^{-1}{\tilde{D}}^{T}Nw\left(t\right)+{\varsigma }_2{u}^T\left(t\right)P{M}^{2}u\left(t\right)\hfill \\ \hfill & =u^T\left(t\right)\left(-2PA+{\varsigma }_1^{-1}P\tilde{C}{N}^{-1}{\tilde{C}}^{T}P+{\beta }_1^{-1}PC{C}^{T}P+{\beta }_2{M}^2+{\varsigma }_{2}P{M}^2\right)u\left(t\right)\hfill \\ \hfill & +w^T\left(t\right)\left(-2NB+{\varsigma }_2^{-1}N\tilde{D}{P}^{-1}{\tilde{D}}^{T}N+{\beta }_2^{-1}ND{D}^{T}N+{\beta }_1{L}^2\right.\hfill \\ \hfill & +\left.{\varsigma }_{1}N{L}^2\right)w\left(t\right)\hfill \\ \hfill & <0,\forall u\left(t\right)\ne 0,w\left(t\right)\ne 0.\hfill \end{array}(8)$

This implies that the origin solution of system (2) is asymptotically stable. So the equilibrium point of system (1) is asymptotically stable.

Corollary 1:. Under condition (H₁), suppose L = M = E, ς₁ = ς₂ = β₁ = β₂ = 1, if there exist positive definite diagonal matrices P = {p_i} ∈ R^n×n, N = {n_i} ∈ R^n×n such that

$-2PA+P\tilde{C}{N}^{-1}{\tilde{C}}^{T}P+PC{C}^{T}P+E+P<0,$

$-2NB+N\tilde{D}{P}^{-1}{\tilde{D}}^{T}N+ND{D}^{T}N+E+N<0,$

then, the origin solution of network (2) is a unique equilibrium point, and it is globally asymptotically stable.

4 Global Dissipativity for BAM Neural Networks

In this part, the global dissipativity for the BAM neural system (1) is considered.

Theorem 2:. Under assumption (H₁), suppose $z(t)={(x_1(t),\dots ,x_n(t),y_1(t),\dots ,y_n(t))}^T$ is a solution of system (1) and

$\xi \left(t\right)+\eta \left(t\right)\le -\alpha <0,$

then for any given ɛ > 0, there exists T such that for all t ≥ T

$\Vert z\left(t\right){\Vert }_2\le \sqrt{\frac{{\gamma }^2}{\alpha }+\epsilon }.$

So, network (1) is dissipative, and the closed ball $E=E(0,\sqrt{\frac{{\gamma }^2}{\alpha }+\epsilon })$ is an absorbing set, where $\gamma ={\delta }_3\Vert I{\Vert }_2^2+{\rho }_3\Vert J{\Vert }_2^2,\xi (t)=\max \{-2{\lambda }_{\min }(A)+{\delta }_1^{-1}+{\delta }_2^{-1}+{\rho }_1{m}^2\Vert D{\Vert }_2^2+{\delta }_3^{-1},-2{\lambda }_{\min }(B)+{\rho }_1^{-1}+{\rho }_2^{-1}+{\delta }_1{l}^2\Vert C{\Vert }_2^2+{\rho }_3^{-1}\},$ $\eta (t)=\max \{{\delta }_2{l}^2\Vert \tilde{C}{\Vert }_2^2,{\rho }_2{m}^2\Vert \tilde{D}{\Vert }_2^2\},{\delta }_1,{\delta }_2,{\delta }_3,{\rho }_1,{\rho }_2,{\rho }_3>0,l=\underset{j\in \mathcal{I}}{\max }\{l_j\},andm=\underset{i\in \mathcal{I}}{\max }\{m_i\}$. Proof. The Lyapunov functional should be considered:

$\begin{array}{c}V\left(t\right)=\Vert x\left(t\right){\Vert }_2^2+\Vert y\left(t\right){\Vert }_2^2.\hfill \end{array}(9)$

Then,

$\begin{array}{ll}\hfill \dot{V}\left(t\right)& =2<x\left(t\right),\dot{x}\left(t\right)>+2<y\left(t\right),\dot{y}\left(t\right)>\hfill \\ \hfill & =2<x\left(t\right),-Ax\left(t\right)>+2<x\left(t\right),Cf\left(y\left(t\right)\right)>+2<x\left(t\right),\tilde{C}f\left(y\left(t-\tau \right)\right)>\hfill \\ \hfill & +2<x\left(t\right),I>+2<y\left(t\right),-By\left(t\right)>+2<y\left(t\right),Dg\left(x\left(t\right)\right)>\hfill \\ \hfill & +2<y\left(t\right),\tilde{D}g\left(x\left(t-\sigma \right)\right)>+2<y\left(t\right),J>\hfill \\ \hfill & \le -2{\lambda }_{\min }\left(A\right)\Vert x\left(t\right){\Vert }_2^2+2f^T\left(y\left(t\right)\right)C^{T}x\left(t\right)+2f^T\left(y\left(t-\tau \right)\right){\tilde{C}}^{T}x\left(t\right)+2I^{T}x\left(t\right)\hfill \\ \hfill & -2{\lambda }_{\min }\left(B\right)\Vert y\left(t\right){\Vert }_2^2+2g^T\left(x\left(t\right)\right)D^{T}y\left(t\right)+2g^T\left(x\left(t-\sigma \right)\right){\tilde{D}}^{T}y\left(t\right)+2J^{T}y\left(t\right).\hfill \end{array}(10)$

By $<x,y>=y^{T}x$, (H₁), and Lemma 1, there exists σ₁, σ₂, σ₃, ρ₁, ρ₂, ρ₃ > 0 such that

$\begin{array}{ll}\hfill 2f^T\left(y\left(t\right)\right)C^{T}x\left(t\right)& \le {\delta }_1{f}^T\left(y\left(t\right)\right)C^{T}Cf\left(y\left(t\right)\right)+{\delta }_1^{-1}{x}^T\left(t\right)x\left(t\right)\hfill \\ \hfill & \le {\delta }_1{\lambda }_{\max }\left(C^{T}C\right)\Vert f\left(y\left(t\right)\right){\Vert }_2^2+{\delta }_1^{-1}\Vert x\left(t\right){\Vert }_2^2\hfill \\ \hfill & \le {\delta }_1{\lambda }_{\max }\left(C^{T}C\right)l^2\Vert y\left(t\right){\Vert }_2^2+{\delta }_1^{-1}\Vert x\left(t\right){\Vert }_2^2\hfill \\ \hfill & \le {\delta }_1{l}^2\Vert C{\Vert }_2^2\Vert y\left(t\right){\Vert }_2^2+{\delta }_1^{-1}\Vert x\left(t\right){\Vert }_2^2,\hfill \end{array}(11)$

$\begin{array}{ll}\hfill 2f^T\left(y\left(t-\tau \right)\right){\tilde{C}}^{T}x\left(t\right)& \le {\delta }_2{f}^T\left(y\left(t-\tau \right)\right){\tilde{C}}^T\tilde{C}f\left(y\left(t-\tau \right)\right)+{\delta }_2^{-1}{x}^T\left(t\right)x\left(t\right)\hfill \\ \hfill & \le {\delta }_2{\lambda }_{\max }\left({\tilde{C}}^T\tilde{C}\right)\Vert f\left(y\left(t-\tau \right)\right){\Vert }_2^2+{\delta }_2^{-1}\Vert x\left(t\right){\Vert }_2^2\hfill \\ \hfill & \le {\delta }_2{\lambda }_{\max }\left({\tilde{C}}^T\tilde{C}\right)l^2\Vert y\left(t-\tau \right){\Vert }_2^2+{\delta }_2^{-1}\Vert x\left(t\right){\Vert }_2^2\hfill \\ \hfill & \le {\delta }_2{l}^2\Vert \tilde{C}{\Vert }_2^2\Vert y\left(t-\tau \right){\Vert }_2^2+{\delta }_2^{-1}\Vert x\left(t\right){\Vert }_2^2,\hfill \end{array}(12)$

$\begin{array}{ll}\hfill I^{T}x\left(t\right)& \le {\delta }_3{I}^{T}I+{\delta }_3^{-1}{x}^T\left(t\right)x\left(t\right)\hfill \\ \hfill & \le {\delta }_3\Vert I{\Vert }_2^2+{\delta }_3^{-1}\Vert x\left(t\right){\Vert }_2^2.\hfill \end{array}(13)$

Similar to Eqs 11–13, then

$\begin{array}{c}2g^T\left(x\left(t\right)\right)D^{T}y\left(t\right)\le {\rho }_1{m}^2\Vert D{\Vert }_2^2\Vert x\left(t\right){\Vert }_2^2+{\rho }_1^{-1}\Vert y\left(t\right){\Vert }_2^2,\hfill \end{array}(14)$

$\begin{array}{c}2g^T\left(x\left(t-\sigma \right)\right){\tilde{D}}^{T}y\left(t\right)\le {\rho }_2{m}^2\Vert \tilde{D}{\Vert }_2^2\Vert x\left(t-\sigma \right){\Vert }_2^2+{\rho }_2^{-1}\Vert y\left(t\right){\Vert }_2^2,\hfill \end{array}(15)$

$\begin{array}{c}{J}^{T}y\left(t\right)\le {\rho }_3\Vert J{\Vert }_2^2+{\rho }_3^{-1}\Vert y\left(t\right){\Vert }_2^2.\hfill \end{array}(16)$

By using Eqs 11–16 in Eq. 10, it is easy to obtain

$\begin{array}{ll}\hfill \dot{V}\left(t\right)& \le \left(-2{\lambda }_{\min }\left(A\right)+{\delta }_1^{-1}+{\delta }_2^{-1}+{\rho }_1{m}^2\Vert D{\Vert }_2^2+{\delta }_3^{-1}\right)\Vert x\left(t\right){\Vert }_2^2\hfill \\ \hfill & +\left(-2{\lambda }_{\min }\left(B\right)+{\rho }_1^{-1}+{\rho }_2^{-1}+{\delta }_1{l}^2\Vert C{\Vert }_2^2+{\rho }_3^{-1}\right)\Vert y\left(t\right){\Vert }_2^2\hfill \\ \hfill & +{\delta }_2{l}^2\Vert \tilde{C}{\Vert }_2^2\Vert y\left(t-\tau \right){\Vert }_2^2+{\rho }_2{m}^2\Vert \tilde{D}{\Vert }_2^2\Vert x\left(t-\sigma \right){\Vert }_2^2\hfill \\ \hfill & +{\delta }_3\Vert I{\Vert }_2^2+{\rho }_3\Vert J{\Vert }_2^2\hfill \\ \hfill & \le \gamma +\xi \left(t\right)\left(\Vert x{\Vert }_2^2+\Vert y{\Vert }_2^2\right)+\eta \left(t\right)\left(\Vert x\left(t-\sigma \right){\Vert }_2^2+\Vert y\left(t-\tau \right){\Vert }_2^2\right)\hfill \\ \hfill & \le \gamma +\xi \left(t\right)V\left(t\right)+\eta \left(t\right)\underset{t-\max \left\{\bar{\tau },\bar{\sigma }\right\}\le s\le t}{\sup }V\left(s\right).\hfill \end{array}(17)$

Then, by Lemma 2, we obtain

$\Vert z\left(t\right){\Vert }_2^2\le \Vert x\left(t\right){\Vert }_2^2+\Vert y\left(t\right){\Vert }_2^2=V\left(t\right)\le \frac{{\gamma }^{*}}{\alpha }+\left(\underset{-\infty \le s\le 0}{\sup }V\left(s\right)-\frac{{\gamma }^{*}}{\alpha }\right)e^{-{\mu }^{*}t},$

where ${\mu }^{*}=\underset{t\ge 0}{\inf }\{\mu (t):\mu (t)+\xi (t)+\eta (t)e^{\mu (t)\max \{\bar{\tau },\bar{\sigma }\}}=0\}$.So, for the given sufficient small ɛ > 0, there exists T ≥ 0 such that

$\Vert z\left(t\right){\Vert }_2\le \sqrt{\frac{{\gamma }^{*}}{\alpha }+\epsilon },\forall t\ge T,$

where ɛ > 0 is sufficiently small. □

Corollary 2:. If taking δ₁, δ₂, δ₃, ρ₁, ρ₂, ρ₃ = 1, under assumptions (H₁), suppose that $z(t)={(x_1(t),\dots ,x_n(t),y_1(t),\dots ,y_n(t))}^T$ is a solution of network (1) and

$\xi \left(t\right)+\eta \left(t\right)\le -\alpha <0,$

then network (1) is dissipative, and the closed ball $E=E(0,\sqrt{\frac{{\gamma }^2}{\alpha }+\epsilon })$ is an absorbing set for any ɛ > 0, where $\gamma =\Vert I{\Vert }_2^2+\Vert J{\Vert }_2^2,\xi (t)=\max \{-2{\lambda }_{\min }(A)+m^2\Vert D{\Vert }_2^2+3,-2{\lambda }_{\min }(B)+l^2\Vert C{\Vert }_2^2+3\},\eta (t)=\max \{l^2\Vert \tilde{C}{\Vert }_2^2,m^2\Vert \tilde{D}{\Vert }_2^2\}$.

Corollary 3:. Under assumptions (H₁), suppose that $z(t)={(x_1(t),\dots ,x_n(t),y_1(t),\dots ,y_n(t))}^T$ is a solution of network (1), if

$\xi \left(t\right)+\eta \left(t\right)\le -\alpha <0$

and

$\overline{\underset{t\ge 0}{\lim }}\left\{{\delta }_3\Vert I{\Vert }_2^2+{\rho }_3\Vert J{\Vert }_2^2\right\}=0,$

then system (1) is globally stable, where $\gamma ={\delta }_3\Vert I{\Vert }_2^2+{\rho }_3\Vert J{\Vert }_2^2,\xi (t)=\max \{-2{\lambda }_{\min }(A)+{\delta }_1^{-1}+{\delta }_2^{-1}+{\rho }_1{m}^2\Vert D{\Vert }_2^2+{\delta }_3^{-1},-2{\lambda }_{\min }(B)+{\rho }_1^{-1}+{\rho }_2^{-1}+{\delta }_1{l}^2\Vert C{\Vert }_2^2+{\rho }_3^{-1}\},$$\eta (t)=\max \{{\delta }_2{l}^2\Vert \tilde{C}{\Vert }_2^2,{\rho }_2{m}^2\Vert \tilde{D}{\Vert }_2^2\},{\delta }_1,{\delta }_2,{\delta }_3,{\rho }_1,{\rho }_2,{\rho }_3>0$.

Remark 3:. In the existing articles, a lot of researchers studied the qualitative behaviors of neural systems via the Lyapunov function with linear matrix inequality techniques [26, 29, 30]. However, in this article, some new sufficient criteria of dissipativity of BAM neural networks with time delays are given by only using the property of matrix theory and inner product.

5 Numerical Simulations

In the part, two examples are presented to show the effectiveness.

Example 1. Investigation of the delayed BAM neural network model.

$\left\{\begin{array}{c}\dot{x}\left(t\right)=-Ax\left(t\right)+Cf\left(y\left(t\right)\right)+\tilde{C}f\left(y\left(t-\tau \right)\right)+I,\hfill \\ \dot{y}\left(t\right)=-By\left(t\right)+Dg\left(x\left(t\right)\right)+\tilde{D}g\left(x\left(t-\sigma \right)\right)+J,\hfill \end{array}\right.(18)$

in which $x(t)={(x_1(t),x_2(t))}^T$ and $y(t)={(y_1(t),y_2(t))}^T$. Let τ₁ = 1, τ₁ = 0.9, σ₁ = 0.8, σ₂ = 0.7, A = B = E, I = J = 0 and

$C=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0.2\hfill \\ \hfill -0.2\hfill & \hfill 0.1\hfill \end{array}\right),\tilde{C}=\left(\begin{array}{cc}\hfill 0.1\hfill & \hfill 0.2\hfill \\ \hfill 0\hfill & \hfill -0.1\hfill \end{array}\right),D=\left(\begin{array}{cc}\hfill 0.2\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0.4\hfill \end{array}\right),\tilde{D}=\left(\begin{array}{cc}\hfill 0.2\hfill & \hfill 0.5\hfill \\ \hfill 0\hfill & \hfill -0.1\hfill \end{array}\right).$

Choose f_j(y_j) = (|y_j + 1| + |y_j − 1|)/2, g_j(x_j) = (|x_j + 1| + |x_j − 1|)/2, j = 1, 2, l₁ = l₂ = m₁ = m₂ = L = M = β₁ = β₂ = ς₁ = ς₂ = 1.

By computing, we can get

$-2PA+{\varsigma }_1^{-1}P\tilde{C}{N}^{-1}{\tilde{C}}^{T}P+{\beta }_1^{-1}PC{C}^{T}P+{\beta }_2{M}^2+{\varsigma }_{2}P{M}^2<0,$

$-2NB+{\varsigma }_2^{-1}N\tilde{D}{P}^{-1}{\tilde{D}}^{T}N+{\beta }_2^{-1}ND{D}^{T}N+{\beta }_1{L}^2+{\varsigma }_{1}N{L}^2<0.$

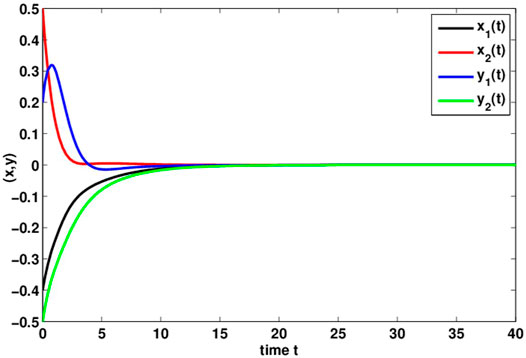
So, from Theorem 1, network (18) has a unique equilibrium, and it is globally asymptotically stable. By MATLAB, a unique equilibrium of network (18) (0,0,0,0)^T is given, and the simulation results are given in Figure 1.

FIGURE 1

FIGURE 1. Trajectories of system (18) for [x(0), y(0)]^T = (−0.4, 0.5, 0.2, −0.5)^T.

Example 2. The BAM neural model with delays is considered as (Eq. 18), where $x(t)={(x_1(t),x_2(t))}^T$, $y(t)={(y_1(t),y_2(t))}^T$ and x(0) = (−1, 1.5)^T, y(0) = (0.8, −1.5)^T. Let τ₁ = 0.9, τ₂ = 0.9, σ₁ = 0.8, σ₂ = 0.8, A = B = E, I = (1, 0.5)^T, J = (2.5, 0.5)^T and

$C=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0.2\hfill \\ \hfill -0.2\hfill & \hfill 0.1\hfill \end{array}\right),\tilde{C}=\left(\begin{array}{cc}\hfill 0.1\hfill & \hfill 0.2\hfill \\ \hfill 1\hfill & \hfill -0.1\hfill \end{array}\right),D=\left(\begin{array}{cc}\hfill 0.2\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0.4\hfill \end{array}\right),\tilde{D}=\left(\begin{array}{cc}\hfill 0.2\hfill & \hfill 0.5\hfill \\ \hfill 1\hfill & \hfill -0.1\hfill \end{array}\right).$

Choose f_j(y_j) = (|y_j + 1| + |y_j − 1|)/2, g_j(x_j) = (|x_j + 1| + |x_j − 1|)/2, j = 1, 2 and l₁ = l₂ = m₁ = m₂ = l = m = δ₁ = δ₂ = δ₃ = ρ₁ = ρ₂ = ρ₃ = 1.

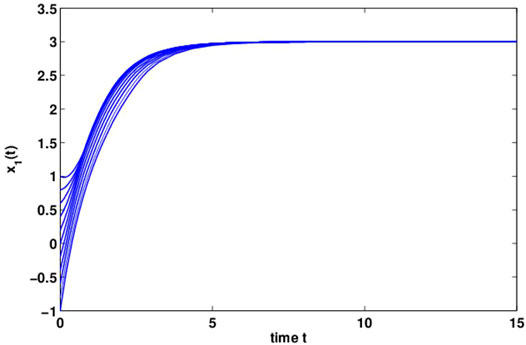
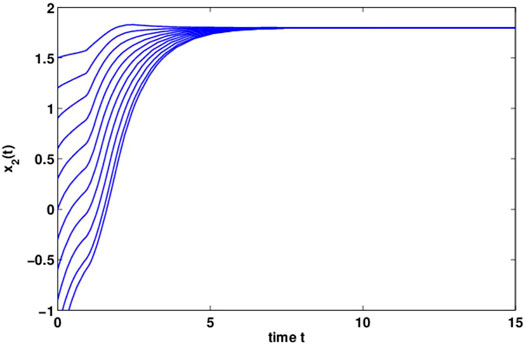
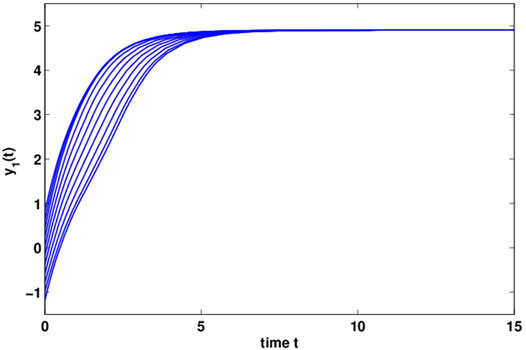
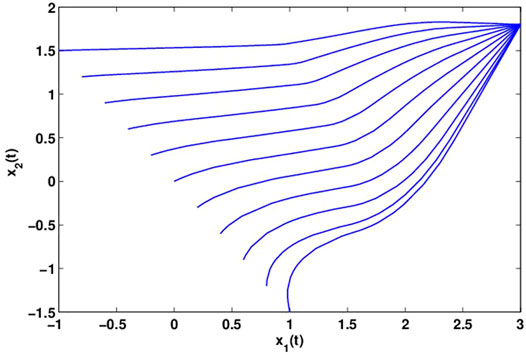
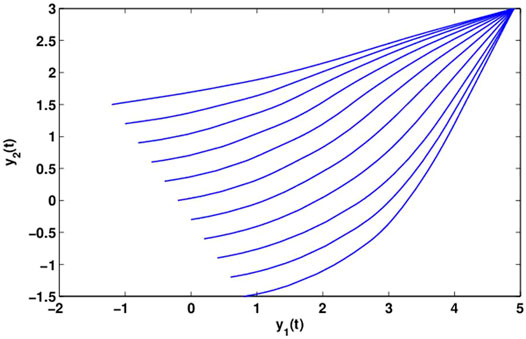
By computing, we can get γ = 7.75, ξ(t) = 2.703, η(t) = 1.04. Let α = 4, ɛ = 0.98, it follows from Theorem 2 and is observed that system (18) is global dissipativity. Figures 2, 3 reflect the behaviors for the states x₁(t) and x₂(t) with different initial conditions. Figures 4, 5 show the phase plane behaviors of y₁(t) and y₂(t) with different initial conditions. Figures 6, 7 demonstrate the behaviors of the time domain for the states x₁(t), x₂(t) and y₁(t), y₂(t) with different initial conditions. System (18) is globally dissipative from the numerical simulations.

FIGURE 2

FIGURE 2. Time response of the state variable x₁(t) with different initial values.

FIGURE 3

FIGURE 3. Time response of the state variable x₂(t) with different initial values.

FIGURE 4

FIGURE 4. Time response of the state variable y₁(t) with different initial values.

FIGURE 5

FIGURE 5. Time response of the state variable y₂(t) with different initial values.

FIGURE 6

FIGURE 6. Time response of the state variable x₁(t) and x₂(t) with different initial values.

FIGURE 7

FIGURE 7. Time response of the state variable y₁(t) and y₂(t) with different initial values.

Remark 4. : In the numerical simulation part of [13], the author only gives the simulation diagram of the BAM neural network model with one node. This article presents the simulation diagram of the BAM neural network model with two nodes. Moreover, in [13], the values of σ(t) and τ(t) are all 1, while the values of σ₁(t), σ₂(t), τ₁(t), and τ₂(t) in this study are different. Therefore, in numerical simulation, this study is more general in the value of the model and time delay. In addition, the unique equilibrium point (0,0,0,0)^T of the system (18) is obtained by MATLAB. Figure 1 shows an image which is globally asymptotically stable of the system (18) under initial conditions ${(x_1(t),x_2(t),y_1(t),y_2(t))}^T={(-0.4,0.5,0.2,-0.5)}^T$. Figures 2–5 show the state diagram of x₁(t), x₂(t), y₁(t), and y₂(t) under different initial conditions with respect to time t. Figures 6, 7 show the state diagrams of x₁(t), x₂(t) and y₁(t), y₂(t) under different initial conditions with respect to time t. The previous figures given in this study can more intuitively reflect the stability and dissipation of the BAM neural network model.

6 Conclusion

In this study, by using matrix theory, inner product properties, generalized Halanay inequalities, and constructing appropriate Lyapunov functionals, novel sufficient criteria of the global asymptotic stability of the system and the global dissipativity of the equilibrium point have been derived for a type of BAM neural systems with delays. The given results might have an impact on investigating the instability, the existence of periodic solutions, and the stability of BAM neural networks. A comparison between the results and the correspondingly previous works implies that the derived criteria are less conservative and more general through numerical simulations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

ML established the mathematical model, theoretical analysis, and wrote the original draft; HJ provided modeling ideas and analysis methods; CH checked the correctness of theoretical results; BL and ZL performed the simulation experiments. All authors read and approved the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grants No. 62003380).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to the editors and referees for their valuable suggestions and comments, which greatly improved the presentation of this article.

References

1. Kosko B. Adaptive Bidirectional Associative Memories. Appl Opt (1987) 26:4947–60. doi:10.1364/ao.26.004947

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Rajivganthi1 C, Rihan FA, Lakshmanan S. Dissipativity Analysis of Complex Valued BAM Neural Networks with Time Delay. Neural Comput. Applic. (2019). 31:127–137. doi:10.1007/s00521-017-2985-9

CrossRef Full Text | Google Scholar

3. Kosko B. Bidirectional Associative Memories. IEEE Trans Syst Man Cybern (1988) 18(10):49–60. doi:10.1109/21.87054

CrossRef Full Text | Google Scholar

4. Hopfield JJ. Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc Natl Acad Sci U.S.A (1982) 79:2554–8. doi:10.1073/pnas.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hopfield JJ. Neurons with Graded Response Have Collective Computational Properties like Those of Two-State Neurons. Proc Natl Acad Sci U.S.A (1984) 81:3088–92. doi:10.1073/pnas.81.10.3088

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Kosto B. Neural Networks and Fuzzy Systems-A Dynamical System Approach Machine Intelligence. Englewood Cliffs, NJ: Prentice-Hall (1992).

Google Scholar

7. Abdurahman A, Jiang H. Nonlinear Control Scheme for General Decay Projective Synchronization of Delayed Memristor-Based BAM Neural Networks. Neurocomputing (2019) 357:282–91. doi:10.1016/j.neucom.2019.05.015

CrossRef Full Text | Google Scholar

8. Xu G, Bao H. Further Results on Mean-Square Exponential Input-To-State Stability of Time-Varying Delayed BAM Neural Networks with Markovian Switching. Neurocomputing (2020) 376:191–201. doi:10.1016/j.neucom.2019.09.033

CrossRef Full Text | Google Scholar

9. Liu J, Jian J, Wang B. Stability Analysis for BAM Quaternion-Valued Inertial Neural Networks with Time Delay via Nonlinear Measure Approach. Mathematics Comput Simulation (2020) 174:134–52. doi:10.1016/j.matcom.2020.03.002

CrossRef Full Text | Google Scholar

10. Priya B, Ali MS, Thakur GK, Sanober S, Dhupia B. Pth Moment Exponential Stability of Memristor Cohen-Grossberg BAM Neural Networks with Time-Varying Delays and Reaction-Diffusion. Chin J Phys (2021) 74:184–94. doi:10.1016/j.cjph.2021.06.027

CrossRef Full Text | Google Scholar

11. Fang T, Ru T, Fu D, Su L, Wang J. Extended Dissipative Filtering for Markov Jump BAM Inertial Neural Networks under Weighted Try-Once-Discard Protocol. J Franklin Inst (2021) 358:4103–17. doi:10.1016/j.jfranklin.2021.03.009

CrossRef Full Text | Google Scholar

12. Yan M, Jiang M. Synchronization with General Decay Rate for Memristor-Based BAM Neural Networks with Distributed Delays and Discontinuous Activation Functions. Neurocomputing (2020) 387:221–40. doi:10.1016/j.neucom.2019.12.124

CrossRef Full Text | Google Scholar

13. Wu Z-G, Shi P, Su H, Lu R. Dissipativity-Based Sampled-Data Fuzzy Control Design and its Application to Truck-Trailer System. IEEE Trans Fuzzy Syst (2015) 23:1669–79. doi:10.1109/tfuzz.2014.2374192

CrossRef Full Text | Google Scholar

14. Xu C, Aouiti C, Liu Z. A Further Study on Bifurcation for Fractional Order BAM Neural Networks with Multiple Delays. Neurocomputing (2020) 417:501–15. doi:10.1016/j.neucom.2020.08.047

CrossRef Full Text | Google Scholar

15. Yan M, Jian J, Zheng S. Passivity Analysis for Uncertain BAM Inertial Neural Networks with Time-Varying Delays. Neurocomputing (2021) 435:114–25.

CrossRef Full Text | Google Scholar

16. Li R, Cao J. Passivity and Dissipativity of Fractional-Order Quaternion-Valued Fuzzy Memristive Neural Networks: Nonlinear Scalarization Approach. IEEE Trans Cybern (2022) 52 (99) 2821–2832. doi:10.1109/tcyb.2020.3025439

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li Y, He Y. Dissipativity Analysis for Singular Markovian Jump Systems with Time-Varying Delays via Improved State Decomposition Technique. Inf Sci (2021) 580:643–54. doi:10.1016/j.ins.2021.08.092

CrossRef Full Text | Google Scholar

18. Zhou L. Delay-dependent Exponential Stability of Cellular Neural Networks with Multi-Proportional Delays. Neural Process Lett (2013) 38(3):321–46. doi:10.1007/s11063-012-9271-8

CrossRef Full Text | Google Scholar

19. Zhou L, Chen X, Yang Y. Asymptotic Stability of Cellular Neural Networks with Multiple Proportional Delays. Appl Maths Comput (2014) 229(1):457–66. doi:10.1016/j.amc.2013.12.061

CrossRef Full Text | Google Scholar

20. Zhou L. Global Asymptotic Stability of Cellular Neural Networks with Proportional Delays. Nonlinear Dyn (2014) 77(1):41–7. doi:10.1007/s11071-014-1271-y

CrossRef Full Text | Google Scholar

21. Zhou L. Delay-dependent Exponential Synchronization of Recurrent Neural Networks with Multiple Proportional Delays. Neural Process Lett (2015) 42(3):619. doi:10.1007/s11063-014-9377-2

CrossRef Full Text | Google Scholar

22. Cong Z, Li N, Cao J. Matrix Measure Based Stability Criteria for High-Order Networks with Proportional Delay. Neurocomputing (2015) 149:1149. doi:10.1016/j.neucom.2014.09.016

CrossRef Full Text | Google Scholar

23. Zhang T, Li Y. Global Exponential Stability of Discrete-Time Almost Automorphic Caputo-Fabrizio BAM Fuzzy Neural Networks via Exponential Euler Technique. Knowledge-Based Syst (2022) 246:108675. doi:10.1016/j.knosys.2022.108675

CrossRef Full Text | Google Scholar

24. Wang S, Zhang Z, Lin C, Chen J. Fixed-time Synchronization for Complex-Valued BAM Neural Networks with Time-Varying Delays via Pinning Control and Adaptive Pinning Control. Chaos, Solitons & Fractals (2021) 153:111583. doi:10.1016/j.chaos.2021.111583

CrossRef Full Text | Google Scholar

25. Cai Z, Huang L. Functional Differential Inclusions and Dynamic Behaviors for Memristor-Based BAM Neural Networks with Time-Varying Delays. Commun Nonlinear Sci Numer Simulation (2014) 19:1279–300. doi:10.1016/j.cnsns.2013.09.004

CrossRef Full Text | Google Scholar

26. Zhou L. Novel Global Exponential Stability Criteria for Hybrid BAM Neural Networks with Proportional Delays. Neurocomputing (2015) 161:99–106. doi:10.1016/j.neucom.2015.02.061

CrossRef Full Text | Google Scholar

27. Ren F, Cao J. LMI-based Criteria for Stability of High-Order Neural Networks with Time-Varying Delay. Nonlinear Anal Real World Appl (2006) 7:967–79. doi:10.1016/j.nonrwa.2005.09.001

CrossRef Full Text | Google Scholar

28. Bo Liu B, Wenlian Lu W, Tianping Chen T. Generalized Halanay Inequalities and Their Applications to Neural Networks with Unbounded Time-Varying Delays. IEEE Trans Neural Netw (2011) 22(9):1508–13. doi:10.1109/tnn.2011.2160987

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang Z, Huang L. Global Stability Analysis for Delayed Complex-Valued BAM Neural Networks. Neurocomputing (2016) 173:2083–9. doi:10.1016/j.neucom.2015.09.086

CrossRef Full Text | Google Scholar

30. Rajchakit G, Saravanakumar R, Ahn CK, Karimi HR. Improved Exponential Convergence Result for Generalized Neural Networks Including Interval Time-Varying Delayed Signals. Neural Networks (2017) 86:10–7. doi:10.1016/j.neunet.2016.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar