Time and Quantum Clocks: A Review of Recent Developments

In this review we present the problem of time in quantum physics, including a short history of the problem and the known objections about considering time as a quantum observable. The need to deal with time as an observable is elaborated through some unresolved problems. The lack of a consistent theory of time is currently hindering the formulation of a full-fledged theory of quantum gravity. It is argued that the proposal set forth by several authors of considering an intrinsic measurement of quantum time, besides having the conventional external time, is compelling. Recently several suggestions have been put forward to revive the proposal of Page and Wootters (1983), elaborating and resolving some of the main ambiguities of the original proposal and opening new scope for understanding its content. The approach followed in these new contributions exposes the need to go beyond the limitations enforced by the conventional approach of quantum physics. The attitude of covariant loop quantum gravity, in which it is called to completely ignore time, is also discussed. This review could be a step forward in an endeavour to reform our outlook of the unification of the theory of relativity and quantum physics by furnishing the conceptual ground needed for this goal. Intentionally, some technical details are avoided since we aim to present the approaches to resolve the problem in a simple way with the clearest possible outlook. These can be looked up in the original references provided.

1 Introduction

The concept of time has long been the subject of philosophical contemplation as well as physical judgement for its role in defining the dynamics of systems. For Aristotle, time was a measure of motion: it is a number of change [1]. If there is no change there is no time; that is to say time exist whenever events exist. Even if there is no external change, the psychological time for Aristotle is a form of change within ourselves. This makes space, motion and matter constitute the arena in which time is realized. In this view the Universe was assumed to be eternal, with no beginning, and therefore time was thought to always exist. The Algerian Christian theologian and philosopher St. Augustine of Hippo (356-430 C.E.) presented a different notion of time, adopting the assumption that the Universe originally had a beginning. Although he considered time in relation with events as it was in the Aristotelean conception, he confessed that time did not exist before the creation of the Universe. A beautiful and meaningful explanation for eternity is given in his book “confessions” [2]. Abu Hamid Al-Ghazali (1058-1111 C.E.), the Muslim theologian and philosopher, elaborated further on the notion of time being related to the occurrence of events. Like Augustine, he believed that the Universe had a beginning with time. Furthermore, Al-Ghazali called to deal with space and time on equal footing, and recognized that the “time extension”, as he called it, must be treated on an equal footing as the space extension. In his own words: “Similarly, it will be said that just as spatial extension is a concomitant of body, temporal extension is a concomitant of motion.” [3]. Time according to Al-Ghazali can only be recognized in relationships to other events; there is no before or after except relative to another reference. He says: “There is no difference between temporal extension that in relation [to us] divides verbally into before and after and spatial extension that in relation [to us] divides into above and below. If, then, it is legitimate to affirm an above that has no above, it is legitimate to affirm a before that has no real before, except an estimative imaginary [one] as with the above. Clearly, no absolute time existed according to these two philosophers.

Isaac Newton adopted a completely different concept of time in which time is considered as an “absolute flow” that exists independent of the events and the observers; time is always there, marking the history of events. Newton recognized that a kind of “true time” exists that passes independently of things and of their changes [4]. Determining the dynamics of motion and change, the time t is always measured by an external clock which has its reference in the eternal astronomical motion. As it is paraphrased by the Stanford Encyclopedia of Philosophy, Newton stipulated that “Absolute, true, and mathematical time, and from its own nature, passes equably without relation to anything external, and thus without reference to any change or way of measuring time (e.g., the hour, day, month, or year).” [5]. Time is uniform and endless with no start nor an end, referred to by the ephemeris universal time. The transformation laws that maintain invariance of the laws of Newtonian mechanics are the Galilean transformations, which express the relationships between the positions of events, while time is left to be an unanimous parameter. The relative velocity of the frame of reference is the only coupling factor between the different frames of reference. In a sophisticated formulation, the dynamics is usually described by the Hamiltonian theory in which time plays a fundamental role in the evolution of the system. Changes that take place in accordance with the effects of the involved forces, and within which space and time are independent variables, are well-defined by this dynamics.

In the theory of relativity, different observers measure time differently, depending on their relative velocity or the strength of the gravity at their position: time dilates due to the relative speed of the frame of reference and due to gravity, manifested by the gravitational redshift effect [6]. In special relativity both space and time are considered as variables of the transformation laws describing the relationship between different frames of reference. These are the Lorentz transformations which maintain the invariance of the laws of electrodynamics. Both space and time are treated on equal footing, and the only universal invariant is the spacetime interval ds² = g_μυdx^μdx^υ (sum over repeated indices apply). For this reason and to maintain the invariance of the laws of physics, the notion of “proper time” was established. The proper time is common to all observers, since it is a co-moving measurement, like the wrist-watch time which is the same for all.

In the theory of general relativity, gravity plays a crucial role in defining time. Gravity is described by curved spacetime manifolds, and this description has imposed a fundamental change on our view of time. As in special relativity, time is relative and depends not only on the state of relative motion of the observer, but on their position in the gravitational field. Two different notions of time within the formalism of general relativity can be distinguished. Specifically, we have the coordinate time t that appears as the argument of the field variable, for instance in g_μυ(x, t), and the proper time s measured along a given world line W = W^μ(τ) parameterized by the variable τ and defined by [6].

$s=\underset{W}{\int }d\tau \sqrt{g_{\mu \upsilon }\frac{d{W}^{\mu }}{d\tau }\frac{d{W}^{\upsilon }}{d\tau }}.(1)$

The Einstein field equations are the equations of motion in the theory of general relativity, which can be seen as second order evolution equations in t. While the proper time maintains the covariance of the dynamics, the coordinate time t in these equations plays the same role as an evolution parameter of the equations of motion and is the same as the ordinary non-relativistic time. However, the physical interpretation of t is very different from the interpretation of the variable in the non-relativistic theory. While non-relativistic time is the observable quantity measured (or approximated) by physical clocks, relativity clocks measure, in general, the proper time s along their worldline, not t. The relativistic coordinate t is a freely chosen label with no direct physical interpretation. This is a well-known consequence of the covariance of the Einstein equations under general coordinate transformations. It is important to remind the reader that the theory of relativity suggests that the Universe is closed, and accordingly time wise it is blocked.

In the standard formulation of quantum physics time is considered a parameter measured by an external clock and is independent of the observer and the system [7]. This is the same as the Newtonian time. The role of time in the canonical formulation of the quantum dynamics is like its role in the classical Hamilton–Jacobi formulation. In Schrödinger’s formulation of quantum physics, the dynamics of a system is described in terms of the evolution of the state in time and follows the equation |ψ(t)⟩ = e^−iHt/ℏ|ψ(0)⟩ in which the Hamiltonian of the system is driving the temporal evolution unitarily. Alternatively, the Heisenberg equation of motion describes the evolution of the measurement in time where $i\hslash \partial A(t)/\partial t=\left[A(t),H\right]$, here it is the observable, more accurately the observation, which is evolving in time. In the particular case that the observable commutes with the Hamiltonian, the system will be represented by stationary states. James Hartle [8] has shown that in both formulations there is a need for a preferred Newtonian time. In the Schrödinger formulation a preferred time enters centrally into the formulation of the notion of the state and in the evolutionary laws of that state, whereas in the Heisenberg formulation the need for preferred time appears in order to define the ordering of the projections upon calculating the conditioned probabilities of an event in multi-time measurements. This requirement of preferred time for ordering the projections reflects the fact that the Heisenberg formulation is describing states that do not evolve in time, rather it is the process of observation which is evolving in time. For this reason the projections in the Heisenberg formulation are not trivially ordered as it is the case of the Schrödinger picture. In comparison with the sum-over-history formulation, Hartle finds that time does not enter the formalism for computing the probabilities in such a central way. This finding of Hartle is important for the realization of the role of time in both pictures. We will see later how the situation changes on considering another basic formulation and on adopting a different equation of motion.

But is the notion of time presented in the standard formulations of quantum physics an inevitable property, or can there be an alternative? According to Hartle [9] the answer is negative. After thorough analysis of the role of time in non-relativistic quantum cosmologies, in which part of the system functions approximately as an ideal quantum clock, Hartle suggests that our familiar notion of time in quantum physics is not an inevitable property of a general quantum framework but an approximate feature of specific initial conditions. This allows for an alternative formulation of quantum physics taken in a wider scope in which time may play a different role.

The Stone-von Neumann uniqueness theorem implies that any pair of canonically conjugate observables is essentially the canonical Schrödinger pair, i.e. the position operator and the momentum operator [10]. In particular both operators are necessarily unbounded from above and below. Then, from the non-relativistic form of the Hamiltonian, it follows that if the potential V is bounded from below, then the energy observable is also bounded from below. Therefore, the energy observable cannot have a canonical conjugate observable represented by a self-adjoint operator. This implies the nonexistence of a self-adjoint operator representing the time observable. Furthermore, Wolfgang Pauli [11] argued against considering time as a dynamical variable. His argument says that if the Hamiltonian is the generator of time translations as suggested by the Schrödinger equation, then this implies that any reasonable definition of the time operator must be conjugate to the Hamiltonian. Consequently, both time and energy must have the same spectrum since conjugate operators are unitarily equivalent. Clearly this is not always true; normal Hamiltonians have a lower bounded spectrum and often only have discrete eigenvalues whereas we typically require that time can take any real value from − ∞ to + ∞. Accordingly, Pauli concluded that constructing a general time operator is impossible.

However, time measurements are quite common experimentally, therefore a theoretical representation for them in quantum physics should exist. For this reason and for many other arguments, several approaches to define quantum time and quantum clocks to measure it were suggested. In this article we will present the most prominent of the recent suggestions for quantum time and for quantum clocks that can be used to measure it. The article is arranged as follows: in Section 2 we present several prominent cases where the definition and measurement of time stands as a problem. In Section 3 we present the early proposals to construct a quantum clock. In Section 4 we discuss the motivations to have a formulation for quantum time measurement and, in this context, we discuss the need for adopting the Wheeler-DeWitt constraint on the Hamiltonian. In Section 4 we present the recent formulations for dealing with quantum time, both for continuous and discrete energy scales. Meanwhile the resolution of the criticisms raised against the early proposals are presented and assessed. Finally in Section 5 we present a discussion of some open questions.

2 Problems Involving Quantum Time

The problem of time in quantum physics is related to several unresolved questions and paradoxes. These include the question of how much time is spent in tunnelling through a potential barrier in what is known as the Hartman effect, the electronic transition time, the quantum Zeno effect and the travel or arrival time. The reason for presenting these problems here is to show that the problem of time in quantum physics is not exclusively related to quantum gravity but is more general than that. These widely discussed controversial issues are intimately connected with time measurements.

2.1 Tunnelling Time

Tunnelling through potential barriers is one of the most stunning and non-intuitive phenomenon predicted by quantum physics, and physicists have been calculating and measuring tunnelling times for a long time now. In 1962, Hartman [12] studied the dynamics of a wave packet tunnelling through a rectangular potential barrier. He derived an analytical expression for the time spent by a non-relativistic particle inside the barrier and found that it is independent of the thickness of the barrier and less than the time required for the particle to travel the same distance in free space. This phenomenon is called the “Hartman effect” and has been verified experimentally many times, using both photons and massive particles, under various circumstances and employing different techniques [13–22]. Many controversial interpretations are given to these experimental results. Some authors suggest that the superluminal speed implies a violation of causality [20, 23–27]. Others conclude that the superluminal effect does not violate causality. The problem is complicated further as it involves the question of time measurement and a sizable amount of work was done to identify the correct definition and measurement of the “arrival time”. For example, Winful [28–33] negates the possibility of superluminal speed through tunneling, arguing that the “apparent” superluminal speed is caused by using certain confusing definitions for the transit time, proposing that the group delay in tunneling is not a transit time but a lifetime and hence should not be used to assign a speed of barrier traversal. Other authors [34] argue that the wave packet spread in momentum space will be so great as to invalidate the conventional spacetime description of the event; accordingly they conclude that an actual measurement of an anomalously short traversal time cannot be made.

Going through the most recent contributions regarding the time of tunneling through potential barriers mentioned above, one finds that the problem is far from being solved and from being fully understood. It is not even clear whether the tunneling particles are actually going through the potential barrier or not. This question might be answered by an experiment using a single shot with a particle that leaves a verifiable non-interacting trace within the barrier. Generally, under certain considerations, one would expect the particle to be at any time anywhere in the region surrounding the barrier. It is only the measurement of the flux of particles in different regions that selects which path the particle is following, a target which cannot be achieved under quantum indeterminism. Consequently, one would expect that the resolution of this problem may be found by considering the time of arrival in the context of the quantum measurement of time. Foden and Stevens [35] considered calculating the tunneling time using a primitive quantum clock coupled to the quantum system, but their calculations ran into difficulties. The reason, we think, is due to coupling the clock in their calculation to the quantum system, a situation which ought to lead to the inseparability of the Hamiltonian, and therefore the Hilbert space in consideration. Similar difficulties faced the work of Peres [36], as we will see below, who devised a clock coupled to the quantum system causing large disturbances of the results.

2.2 The Quantum Zeno Effect

If the wave function collapse interpretation is to be taken as an empirical fact and not just a pictorial presentation, then a continuous measurement of an excited state will prevent it from making a transition. This is known as the “quantum Zeno effect” [37]. As it is said, “a watched kettle never boils.” This is another effect which has been predicted theoretically and is related to the measurement of time. The effect is explained in the conventional context of the Copenhagen school by the collapse postulate, where it is understood that the continuous measurement of the energy will cause the wave function to be in a situation under continuous collapse to the same state preventing any transition from taking place. For a detailed account of the quantum Zeno effect see for example the extensive review by Facci and Pascazio [38].

Peres [39] considered the quantum Zeno effect (QZE) in the context of studying the effect of the measuring apparatus on the dynamical properties of the quantum system, particularly its decay law. He considered analyzing this problem away from the argument based on quantum measurement theory. Peres finds that under a very tight monitoring the decay is usually slowed down and can even be halted. However, he also found that the Zeno paradox arises directly from the Schrödinger equation, which means that it is not a result of measurement. This undermines the assumption of the wave function collapse. However, Peres considered again this question in a second paper [36] trying a resolution through measuring time by a quantum clock which he proposed, as we will see later in Section 5, affirming again that the QZE is not an effect of measurement. Nevertheless, analyzing the results of Itano et al.’s experiment [40], Beige and Hegerfeldt [41] have shown analytically that for a wide range of parameters, the short laser pulse acts as an effective level measurement to which the usual projection postulate applies with high accuracy, thus concluding that the projection postulate is an excellent pragmatic tool for a quick and simple understanding of the slow-down of time evolution in experiments of this type. They also recognize that the corrections to the ideal reductions and their accumulation over n pulses must be included, and a complete freezing does not seem possible because of the finite duration of measurements. Indeed this is correct once we know that the Zeno effect is exposed exclusively in measurements on a time scale comparable to the Zeno time, as shown below.

Another question which arises in this context is the question of the duration of a quantum jump, a problem which has been considered by Cook [42] and later by Schulman [43–44]. Analyzing the duration of a quantum jump, Schulman obtained an expression for what he calls the “Zeno time” which is a measure for the duration of the measurement slowing the transition. It is given by

$t_z=\frac{\hslash }{\sqrt{⟨\psi |{\left(H-E_{\psi }\right)}^2|\psi ⟩}}(2)$

where E_ψ = ⟨ψ|H|ψ⟩. The transition probability calculated by Schulman is

$P_{\mathit{interrupted}}\simeq \exp \left(-t\mathrm{\Delta }t/t_z^2\right),(3)$

where Δt is the duration between two successive measurements. Obviously, as t_z → 0, the transition gets halted. In this context time is taken to be a continuous, external and absolute coordinate as it is in standard quantum physics. Here this might be well justified for events taking place on atomic and molecular time scales, but when the Zeno time is as in Eq. 2 above, a quantum clock is needed to measure time, otherwise the exponential decay law cannot be verified [39].

2.3 Arrival Time in Quantum Mechanics

The detection of a particle usually happens once the particle interacts with the detector, which is normally located at a finite distance from its source. The moment of detection is called arrival time. Theoreticians find that the designation of an arrival time is a problematic part of the measurement in quantum mechanics since it is related to the indeterminacy of the position and momentum of the particle [45–47].

Perhaps Allcock [48] was the first to present a rigorous proof that the ordinary Hilbert space of a freely moving particle does not contain a set of measurement eigenstates of the arrival time. This proof depends on extending the frequency spectrum of the wave function to cover both positive and negative values, while at the same time the spatial domain of the wave function is halved. Delgado and Muga [49] (also see [50] for an updated account) find that a self-adjoint operator with dimensions of time can be explicitly constructed, and it is shown that its complete and orthonormal set of eigenstates can be used to define consistently a probability distribution of the time of arrival at a spatial point. However, we should note that this does not contradict the argument of Allcock about extending the spectrum to cover the positive and negative energy range. All in all, the formalism used by Delgado and Muga using the energy eigenstates |E, ±⟩ and the momentum projection operator $\mathrm{\Theta }(\pm \stackrel{\wedge }{P})$ along with the self-adjoint operator sgn$(\stackrel{\wedge }{P})=\mathrm{\Theta }(\stackrel{\wedge }{P})-\mathrm{\Theta }(-\stackrel{\wedge }{P})$ confirms again the essential need to cover the positive and the negative frequency ranges for the solutions of the eigenvalue equation in order to circumvent the Pauli objection. Here we might need to be careful about accounting for the negative energy in terms of the negative frequency. Both may have effectively the same contribution in some cases, but to generalize this might need further investigation. As we will see below, a more advanced and less involved account for the arrival time has recently been considered by authors using calculations depending on a quantum clock which measures the intrinsic time. This affirms again the necessity for a quantum clock.

2.4 Time in Quantum Gravity

Unifying quantum physics and the theory of relativity was the dream of Albert Einstein and many others. In fact, as early as 1916 Einstein expected that quantum theory will modify his theory of gravitation and is quoted saying “…it appears that quantum theory would have to modify not only electrodynamics, but also the new theory of gravitation” [51]. A theory which unifies quantum physics and gravity would provide a comprehensive framework to explain the physical phenomena on all scales, from the microscopic to the macroscopic level. However, this goal faces great conceptual and technical difficulties. The problem of time is one of the main obstacles in devising such a theory. One facet of the problem is the conflicting concepts of time in quantum physics and relativity theory, the conflict between the absolute and the relative, the external and the local. For these reasons there are several approaches to quantum gravity (for a comprehensive presentation of these approaches see [52]). The other facet of the problem arises in maintaining the unitarity required by the main equation of motion in quantum physics, the Schrödinger equation.

Over the decades several approaches to quantum gravity were suggested, many of those dropped short of achieving the goal and others are still surviving. In two seminal reviews published in the early 1990s Isham [53] and Kuchar [54] formalized a deep analysis of the discrepancies between the different approaches that were available at the time. Here we are not considering such an analysis of the present approaches since our main focus is on quantum time.

The problem of time in quantum gravity originates from the fundamental conflict between the way the concept of time is used in quantum theory, and the role it plays in a diffeomorphism-invariant theory like general relativity. Many authors recognized that observable time can only be defined intrinsically [55–73]. The affirmation of these authors and the examples given in their cited articles confirm that having the time operator corresponding to a quantum observable would require that time be treated intrinsically. Consequently this has a fundamental implication on the philosophy of accounting for a global system (called a Universe) which includes the clock and the quantum system under consideration. This would be in agreement with the notion of the block Universe implied by the theory of relativity.

Rovelli [74] argues that the theory of general relativity has fundamentally changed the way we deal with the dynamics of physical systems. Instead of having a time that passes with the ticking of an external cosmic clock, general relativity has adopted the relative evolution of observable quantities, not the evolution of quantities, as functions of time. According to him this summarizes the problem of time for a quantum gravity approach. After suggesting some technical alternatives, he concludes that “in order to build a quantum theory of gravity the most effective strategy is to forget the notion of time all together, and to define a quantum theory capable of predicting the possible correlations between partial observables.” This argument is found in many of his articles [75]. Along the same line of thought we find Julian Barbour who presents the “end of time” [76]. At first this might sound fine, but in fact we soon find that forgetting the notion of time altogether would make it difficult for us to regain time as we go on to consider the real world as we conceive it empirically. The statistical notion of thermodynamic time requires an ensemble of states and this might not always be available.

Dynamics is all about changes under the field of force, and a change can only be recognized with reference to two states, the one before and the one after. However, in order to generalize tracking the change in other states, to determine the dynamics involved, knowing how fast changes are occurring relatively, we need to have a measure that can be applied to all the changes taking place; such a measure should be a reference for comparison. This measure, which is independent of all the states, is what is called the intrinsic or internal time. This means that we cannot completely forget about time, but perhaps we should assign it to an internal clock which measures the change with reference to any two states and consider that as a basic measure for the change. In this way we can have a reliable reference by which we can regain the external coordinate time.

The quest for quantum gravity certainly needs some sort of quantization of time for a quantum picture of the spacetime to become possible. Applications of the quantum picture of time are not limited to the above, since it is expected that the new formalism of discrete time will have serious implications in areas of quantum computing and related subjects [77,78].

2.5 Pauli’s Objection Revisited

Recently, several suggestions were made to circumvent Pauli’s argument against the possible construction of a general time operator [79, 80]. In many of these the negative energy states, which are a result of the relativistic treatment, play a vital role. The wave function describing the state of the system is a complex function of space and time, both of which are considered in the Newtonian sense of being independent and absolute. For example Aguillon et al. [80] showed that Lorentz invariance, Born’s reciprocity invariance and the canonical quantization of special relativity can provide, among other things, the existence of a self-adjoint time operator that circumvents Pauli’s objection. Leon and Maccone [79] showed that Pauli’s argument fails when we use an internal clock for time measurement allowing for time to be represented by an operator which is conjugate to the clock Hamiltonian, not the system’s Hamiltonian. The total Hamiltonian includes the clock and the system. However, we find that this argument of the internal measurement of time, though providing a way to consider a time operator conjugate to the clock Hamiltonian, is insufficient to revoke Pauli’s objection since the system Hamiltonian may stay bound from below. The proper approach to overcome Pauli’s objection is to have a dynamical Hamiltonian which is unbound from below. The approach of Hodgson and collaborators [81, 82] on quantization of the electromagnetic field in position space provides such a dynamical Hamiltonian and, therefore, may provide a better argument to circumvent Pauli’s objection within the context of a more general theory of field quantization.

Moreover, Khorasani [83] showed that Dirac’s equation could be modified to allow discrete time, an exact self-adjoint 4 × 4 relativistic time operator for spin 1/2 particles is found and the time eigenstates for the non-relativistic case are then obtained. The result confirms that particles can indeed occupy negative energy levels with vanishingly small but non-zero probability, contrary to the general expectation from classical physics. This work is a better confirmation of the possibility to have the Hamiltonian unbounded from below since, for massive spin 1/2 particles, the results confirm the quantum mechanical speculation that particles can indeed occupy negative energy levels with vanishingly small but non-zero probability, contrary to the general expectation from classical physics. Accordingly, Pauli’s objection regarding the existence of a self-adjoint time operator is resolved.

3 Early Proposals for Quantum Time

In this section we present some important historical approaches to formulate the quantum measurement of time using a quantum clock. Despite the fact that these early proposals are outdated now, to present them here is important for justifying the later proposals which have been put forward during the last 5 years or so. The reader will observe the necessity of the diversion from the old approaches and for this reason the shortcomings of those early approaches are exposed. Nevertheless, the story of quantum time may not be complete until we see the empirical outcome of the recent approaches.

3.1 Wigner-Salecker Proposal

Wigner demonstrated that there are limitations of spacetime measurements due to the quantum nature of test particles [84], and it was in this context that Salecker and Wigner [85] introduced the idea of a quantum clock. They proposed to use clocks only for measuring spacetime distances and avoided using measuring rods which are essentially macro-physical objects. Their approach might be of value for some quantum applications, however the Salecker and Wigner program of quantum measurement of time went into difficulties as soon as the target tuned out to find the minimum mass of the clock and the minimum uncertainty involved in the measurement of time. An alternative less muddy consideration would be to consider the measurement of probabilities.

3.2 The Peres Clock

Peres [36] proposed another method of constructing a clock telling quantum time. At first Peres digitizes the time measurement by assuming a number of angular momentum states N designated by j such that N = 2j + 1. The states are prescribed by the wavefunctions:

${\varphi }_m\left(\theta \right)={\left(2\pi \right)}^{-1/2}{e}^{im\theta },0\le \theta <2\pi ,(4)$

where m = −j, …. + j. Another orthogonal basis is given by

$v_k\left(\theta \right)=\frac{1}{\sqrt{N}}\sum _m{e}^{2\pi ikm/N}{\varphi }_m\left(\theta \right).(5)$

For large N we have a sharp peak at θ = 2πk/N. This can be visualized as pointing to the kth hour with an angle uncertainty of ± π/N.

Peres defines the projection as P_kv_m = δ_kmv_m and defines the clock-time operator as T_c = τ∑kP_k, where τ is the time resolution of the clock (re-creation time). Accordingly the eigenvectors of T_c are v_k and the eigenvalues are taken as t_k = kτ with k = 0, … , N − 1 obtained as follows:

$T_c{v}_k=\tau \sum _{n}n{P}_n{v}_k=\sum _{n}n{\delta }_{kn}{v}_k=\tau k{v}_k=t_k{v}_k,(6)$

where the initial state of the clock is always taken as v₀. Now, measuring the time by this clock, T_c, will give an approximate discrete approximation to the true time, just like reading a digital watch. This means that the system is defining its own time. This time is so defined by the Hamiltonian causing the unitary development of the system.

Peres then introduces the Hamiltonian of the clock as H_c = ωJ with J = −iℏ∂/∂θ and with the eigenvalues of the clock given by H_cϕ_m = mℏωϕ_m. This is then incorporated with the system whence the total Hamiltonian becomes H = H_c + H_s. In this formulation the effect of the measuring device is incorporated into the quantum system and [T_c, H_c] = iℏ. However, this will lead to difficulties as we shall see below.

Peres’ quantum clock would interfere with the system and therefore a quantum clock with higher resolution, despite being more classical, will cause a greater disturbance in the system. For this reason the clock measurements run into difficulties upon considering some applications, which include the time of flight (arrival time) where he finds that his clock can only deal with the case $E\gg \left|V\right|$ upon considering the problem of barrier penetration. While in the case of Schrödinger’s cat, viewed as a decay time problem, and upon considering using the clock for measuring the spin precession under controlled switching times, Peres finds that his clock readings will be overwhelmed by its coupling to the device which it is supposed to control.

The work of Peres taught us that the clock must not interact with the system, otherwise the precession of the clock will be limited and a higher choice of the precession will lead to clock-system interference which would limit the usage of such a clock. However, the sentence spoken by Peres on the invalidity of differential calculus when dealing with quantum physics is very important and is calling for the use of a different mathematical construction to deal with physical systems. In fact, the adopted equation of motion has an important role to play too, as will be shown below. In Peres’s words “It thus seems that the Schrödinger wave function ψ(t)…is an idealization rooted in classical theory. It is operationally ill-defined (except in the limiting case of stationary states) and should give way to a more complicated dynamical formalism, perhaps one non-local in time.“However, we are not sure whether a more complicated or less complicated dynamical formalism is needed, but certainly further developments in this field show that a quantum clock adopting a different understanding of the dynamics and a different philosophy of time could offer a better alternative as we will see below.

Perhaps a better choice for an alternative mathematical construct for quantum gravity is to consider non-commutative spacetimes. Since it is known that different non-commutative spacetimes arise very naturally in most current approaches to quantum gravity, Addazi et al. [86] published a condensed and elegant review of such spacetimes exposing their main features and citing related experimental analyses in connection with the gravitational waves (GW) signal GW 150914 (see [87, 88]). Incidentally, such an analysis of GW signals looking for the traces of non-commutative spacetimes is necessary since effects from non-commutative spacetimes are expected to be found in the GW spectrum as it was the case when QED effects were discovered in the spectra of the atoms.

3.3 The Page and Wootters Approach

Page and Wootters (PW) [89] have placed several arguments and premises for their proposal on constructing a quantum clock for measuring time. First, influenced by the proof of Strocci and Wightman [90], which showed that the long-range Coulomb field causes the local charge operator to commute with all quasi-local observables, they find that a superselection rule should exist for gravitational energy. The observables in quantum systems should only be those that commute with the Hamiltonian of the system. Accordingly, the operator of time becomes stationary. This argument is placed to justify dealing with the clock states as stationary ones and enables them to overcome, at least partially, the problems faced by Peres when constructing a quantum clock which led to his disappointment. They also argue that in the Schrödinger equation the time t is an external parameter, and hence has no place in the quantum theory if the system is truly closed. This argument is placed to justify adopting the block Universe proposal which the theory of relativity is suggesting. Accordingly, they find that the temporal behaviour of the observer in quantum systems depends on some internal clock time, not on an external coordinate time. The clock system is decomposed into states of definite clock times. The observed temporal behaviour of the closed quantum system is found through the dependence of these component states on the time labelling them. So we have the quantum clock measuring the internal time and we have the values of the observables of the quantum system correlated with those markings by the clock, see Figure 1.

FIGURE 1

FIGURE 1. System observables correlated with the clock readings.

The proposal of PW has been criticized by several authors [54, 91, 92]. Kuchar [54] argues that their quantum clock cannot be used to construct a two-time propagator. In his view the PW quantum clock is unable to make two moves, it will be frozen after the first move. To overcome this, Gambini et al. [93] used Rovelli’s evolving constants of motion [75], parametrized by an arbitrary parameter which is then averaged over to yield the correct propagators, thus saving the PW clock. Although the end result matches the quantum predictions [94], Giovannetti et al. [95] find that the averaging which has been used by Gambini amounts to a statistical averaging, which is usually reserved to unknown physical degrees of freedom rather than to parameters with no physical significance. So, the question of the two-time propagator in the PW approach remains open. On the other hand, Unruh and Wald [92] argue that the “conditional probability interpretation” requires one to pick out a “preferred time variable”, or preferred class of such variables, from among the dynamical variables. Furthermore, these authors seem to resort again to Pauli’s objection claiming that in Schrödinger’s quantum physics for a system with a Hamiltonian bounded from below no dynamical variable can correlate monotonically with the Schrödinger time parameter t, and thus the role of t in the interpretation of Schrödinger quantum physics cannot be replaced by that of a dynamical variable. Obviously this is true for a Hamiltonian which is bound from below, but the argument is ruled out in case the Hamiltonian is unbound from both sides as will be shown below. Albrecht and Iglesias [96] raised some conceptual problems, since there are several, inequivalent choices of the clock which then appear to produce an ambiguity in the laws of physics for the rest of the Universe: different choices of the clock lead to different Hamiltonians, each corresponding to radically different dynamics in the rest of the Universe. So, it seems that the logic of the timeless approach cannot be applied as directly as in classical physics, because it does not lead to a unique Schrödinger equation for the rest of the Universe. This clock ambiguity has also been considered by Marletto and Vedral [97] and will be discussed below.

4 Quantum Measurement of Time

Recent presentations of the quantum time and constructions of quantum clocks have adopted the view of a “block Universe”. This construction is guaranteed by considering the total Hamiltonian composed of two parts: the clock Hamiltonian and the quantum system Hamiltonian. Accordingly, a joint Hilbert space is formed out of the direct product of these two parts. Furthermore, a Hamiltonian constraint is used to guarantee that the whole system forms a block Universe in which quantum states are stationary.

4.1 Why do We Need a Quantum Clock?

There are two main reasons for that. First, we need to quantize time to have it in harmony with the rest of the quantum structure. For this to be achieved we need to deal with time as a quantum observable and not as a parameter. Second, we need time to be an observer-dependent variable so that it would be in harmony with the requirements of the theory of relativity, otherwise we cannot obtain a construction for quantum gravity. For this goal to be achieved we need to have time measured internally within the quantum system. The clock must be separated from the quantum system, otherwise the quantum activity of the clock may strongly interfere with the system’s dynamics, causing high disturbances as shown by Peres [36]. The quantum clock is a generator of time eigenstates which are correlated with the quantum system’s states.

4.2 Why do We Need a Hamiltonian Constraint?

Generally, Schrödinger’s equation does not satisfy the requirements imposed by Einstein’s relativity theory in respect to treating space and time on an equal footing. Furthermore, relativity theory implies the notion of a “block Universe” where the past, present and the future all simultaneously exist in the Universe described by relativity theory. The before and the after have no absolute status but are known relatively in a relational description. This requires that the observables become stationary in this Universe. Such a requirement can be properly satisfied by applying a constraint on quantum states in the form of an equation which is sometimes called the Wheeler-DeWitt equation (98).

$H|\mathrm{\Psi }\rangle =0.(7)$

This equation is setting a constraint on the global state of the Universe (sometimes called the wavefunction of the Universe). Its physical meaning may be figured by saying that the global state |Ψ⟩ (sometimes written as double ket |Ψ⟩⟩) is a representation of a collection of all stationary states contained in the Universe (see Figure 2).

FIGURE 2

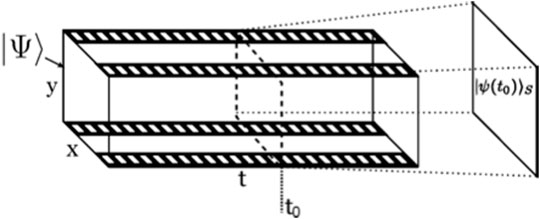
FIGURE 2. Pictorial representation of the projection of the global state |Ψ⟩ onto a given moment of time t₀ depicted here as a strip of a movie reel.

5 Recent Developments

The way in which PW presented their construction of quantum time was not as clear as we have made it seem. Many questions and ambiguities were posed, and for this reason perhaps the proposal did not attract enough attention for many decades. In this section the PW approach is described for both continuous and discrete spectra, as done in recent presentations. Presenting the PW formalism in this way clarifies many apparent ambiguities and mysteries of the PW approach. First, we briefly present the case for continuous spectra and then offer more details for the case of discrete spectra as we find it more suitable for the formulation of a discrete time measured by a quantum clock.

Recent studies of the quantum measurement of time and the assignment of a quantum clock [89, 95, 97, 99, 100] have adopted the constraint in Eq. 7 as a basic prescription in order to assure the independence of the clock which needs to behave as a subsystem belonging to a global system represented by the state |Ψ⟩. This means that the dynamics of the conventional formulation of quantum physics is replaced by this constraint equation where the total Hamiltonian H is given by

$H=H_c\otimes \mathbf{1}+\mathbf{1}\otimes H_s.(8)$

This Hamiltonian acts on the joint Hilbert space ${\mathcal{H}}_c\otimes {\mathcal{H}}_s$ which is a direct product of the two Hilbert spaces ${\mathcal{H}}_c$ and ${\mathcal{H}}_s$, where ${\mathcal{H}}_c$ is spanned by the basis states of the clock and where ${\mathcal{H}}_s$ is spanned by the basis states of the quantum system. Taking $H_c=-i\hslash \frac{\partial }{\partial t_c}$ as the clock Hamiltonian, one finds that

$\left(H_s+H_c\right)|\mathrm{\Psi }\rangle =\left(H_s-i\hslash \frac{\partial }{\partial t_c}\right)|\mathrm{\Psi }\rangle =0.(9)$

In this scheme the conventional formulation of quantum physics arises from conditioning the reference time to t. This can be done by projecting the global state |Ψ⟩ onto a state |t⟩ associated with the time t,

$|\psi \left(t\right)\rangle =⟨t|\mathrm{\Psi }⟩,(10)$

which yields the state |ψ(t)⟩ of the system at time t. The above is the basic structure of the formalism used in recent works for devising a quantum clock which reads the time in correlation with the states of the quantum system.

The solutions of Eq. 7 take different forms. Some authors describe them in terms of a continuous formulation, whereas others adopt a discrete formulation. The concern in these approaches is to get the probability of happenstance of a state. This usually can be obtained using the Born rule with the understanding that the calculated probability is conditional [89, 98]. In other words, the happenstance of a given state of the system is conditioned on the time t in the Schrödinger picture (In the Heisenberg picture the conditioning is on the observables.) Then a simple Bayes conditioning of the Born rule probability of the joint state would allow one to recover the full distribution of the time measurement [99]. According to [98] the conditional probability P(A|B) of a result A given a testable condition B is

$P\left(A|B\right)=\frac{Tr\left(P_A{P}_B\rho P_B\right)}{Tr\left(P_B\rho P_B\right)}(11)$

where ρ is the density matrix.

5.1 Continuous Spectra

Giovannetti et al. [95], and later Maccone and Sacha [99], renovated the PW approach and elaborated the main features of this approach in an elegant way, yet the basic arguments remain the same. Many problems faced by previous proposals for measuring the time of arrival at a given position are bypassed within their presentation. This enabled the authors to have a generic calculation method that covers situations beyond the time of arrival that other proposals could not treat [50, 101–103]. The particle is described by a state |ψ(t)⟩ with the time reference being a continuous quantum degree of freedom in the Hilbert space ${\mathcal{H}}_c$ of the clock. In this scheme we have a global state denoted by |Ψ⟩ which represents all the states at once as explained above. This is now given by

$|\mathrm{\Psi }\rangle =\frac{1}{\sqrt{T}}{\int }_{T}dt|t\rangle |\psi \left(t\right)\rangle .(12)$

Note here that the apparent entanglement in the above equation is not a result of the clock-system dynamics, since both are isolated from each other as required by the PW approach, but the result of having |Ψ⟩ satisfying the constraint Eq. 7. The states |ψ(t)⟩ of the quantum system are obtained by projecting |Ψ⟩ on t; that is |ψ(t)⟩ = ⟨t|Ψ⟩.

Extending the Born rule using the global state |Ψ⟩ which sums up the history of all the states of the system at all times, Maccone and Sacha [99] choose to construct a positive operator-valued measurement (POVM) of the time of arrival with the help of the projectors

${\mathrm{\Pi }}_t=|t\rangle \langle t|\otimes P_d\text{and}{\mathrm{\Pi }}_{na}=1-\int dt{\mathrm{\Pi }}_t.(13)$

If the particle is at the detector D then the projector is P_d ≡∫_Ddx|x⟩⟨x|. The projective POVM returns the value t of the clock if the particle is in D or the value na (not arrived) if it is not, if the arrival observable A is devised as

$A=\int dtt|t\rangle \langle t|\otimes P_d+\mathbf{1}\otimes \mathit{\lambda }{\int }_{x\notin D}dx|x\rangle \langle x|(14)$

where λ is an arbitrary eigenvalue of A that signals that the particle has not arrived. Using the Born rule, one obtains the joint probability that the particle is at x ∈ D and that the clock shows the time of arrival is t as

$p\left(t,x\in D\right)=Tr\left[|\mathrm{\Psi }\rangle \langle \mathrm{\Psi }|{\mathrm{\Pi }}_t\right]=\frac{1}{T}{\int }_{x\in D}dx|\psi \left(x|t\right){|}^2.(15)$

The time of arrival is recovered from the joint probability through the Bayes rule as

$p\left(t|x\in D\right)=\frac{{\int }_{x\in D}dx|\psi \left(x|t\right){|}^2}{{\int }_{T}dt{\int }_{x\in D}dx|\psi \left(x|t\right){|}^2}(16)$

which is effectively averaging over t through the whole period of the clock time.

5.2 Discrete Spectra

Discrete energy spectra need a slightly modified prescription. Pegg [104] recognized that the time representation of the clock’s Hamiltonian with $-i\hslash \frac{\partial }{\partial t_c}\to H_c$ would be correct only if H_c has a continuous unbound spectrum. In such a case the Hermitian time operator in the energy representation can be written as $\widehat{T}=-i\hslash \frac{\partial }{\partial E_c}$. If one would consider an isolated physical system of finite size then the introduction of an unbounded Hamiltonian with continuous spectrum would not be possible. This implies that a Hermitian time operator written in a differential form as above cannot be introduced within the standard approaches according to Pauli’s objection [11]. To overcome this dilemma, Pegg suggested constructing a Hermitian operator named “Age” as a complement of a lower-bounded Hamiltonian with equally spaced energy eigenvalues. His idea was to consider a Hamiltonian with an energy cut-off, to calculate the quantities of interest and to eventually remove the cut-off by allowing the upper bound to go to infinity. As such “Age” becomes a generator of energy shifts while the Hamiltonian is the generator of translation in time.

Favalli and Smerzi [100] introduced the prescription of Pegg into a PW formalism and found that the “Age” can be interpreted as a proper Hermitian time operator conjugate to a good clock Hamiltonian. With this amended approach they could deal with equally spaced energy spectra as well as with unequally-spaced spectra. Here we present this formalism since we feel that its details present the case of quantum time measurement in a more suitable way as both the energy representation and the clock readings are expressed in discrete variables. Again, the Hamiltonian is described to contain two parts, the system Hamiltonian H_s and the clock Hamiltonian H_c and is structured as in Eq. 8 above. The system is constrained by the Wheeler-DeWitt equation as in (9) and the global wave function |Ψ⟩ for a discrete system is of the form

$|\mathrm{\Psi }\rangle =\frac{1}{\sqrt{T}}\sum _n{a}_n|t_n\rangle |\psi \left(t_n\right)\rangle .(17)$

Here the quantum states of the system at time t_n are represented by |ψ(t_n)⟩. Furthermore, the wave function ψ(x|t_n) can be obtained by projecting |ψ(t_n)⟩ on the position eigenbasis ⟨x|ψ(t_n)⟩. A pictorial representation of the projection of the states is shown in Figure 2.

5.2.1 Eigenstates of the Clock

Following Pegg’s prescription [104], as elaborated by Favalli and Smerzi [100], a good clock is defined by a physical system governed by a lower-bounded Hamiltonian with discrete equally-spaced energy levels (for example, a simple quantum harmonic oscillator)

$H_c=\sum _{n=0}^s{E}_n|E_n{\rangle }_{cc}\langle E_n|(18)$

where d_c = s + 1 is the dimension of the Hilbert space ${\mathcal{H}}_c$ of the clock and the E_n and |E_n⟩_c are its energy eigenvalues and eigenstates. The Hermitian time-operator of the system can then be defined as

$\widehat{\tau }=\sum _{m=0}^s{\tau }_m|{\tau }_m{\rangle }_{cc}\langle {\tau }_m|(19)$

with the time eigenstates |τ_m⟩ given by

$|{\tau }_m{\rangle }_c=\frac{1}{\sqrt{s+1}}\sum _{n=0}^p{e}^{-i{E}_n{\tau }_m/\hslash }|E_n{\rangle }_c(20)$

with the orthogonality condition and completeness relationship

${}_c\langle {\tau }_m|{\tau }_{m^{\prime }}\rangle _c={\delta }_{m{m}^{\prime }}\mathrm{a}\mathrm{n}\mathrm{d}\sum _{m=0}^s|{\tau }_m{\rangle }_{cc}\langle {\tau }_m|={\mathbf{1}}_c.(21)$

It is easy to show that the above clock Hamiltonian H_c is a generator of transitions in time (see [36, 100, 104]) and hence conjugate to H_c. The eigenvalues of $\widehat{\tau }$ of a clock with equally-spaced levels can be written as

${\tau }_m={\tau }_0+m\left(\frac{T}{s+1}\right)(22)$

where T is the time it takes the clock to return to its initial state (full cycle). For example, for E_n = E₀ + ℏnω and

$T=\frac{2\pi }{\omega },(23)$

we automatically have |τ_m=s+1⟩_c = |τ_m=0⟩_c which is a property of the clock. Conversely, the smallest time interval measured by the clock is

$\mathrm{\Delta }\tau =\frac{2\pi }{\left(s+1\right)\omega }.(24)$

5.2.2 Dynamics

The global Hilbert space of the Universe (i.e. of the system and the clock) is $\mathcal{H}={\mathcal{H}}_c\otimes {\mathcal{H}}_s$ with ${\mathcal{H}}_c$ having the dimension d_c = s + 1 and ${\mathcal{H}}_s$ having the dimension d_s = p + 1. In order to cover the whole range of states of the system with clock readings we should always have d_c ≫ d_s. A general state of the whole system (the Universe) can then be written as

$|\mathrm{\Psi }\rangle =\sum _{n=0}^s\sum _{k=0}^p{c}_{n,k}|E_n{\rangle }_c\otimes |E_k{\rangle }_s(25)$

where the |E_k⟩_s denote the energy eigenstates of the system. On imposing condition H|Ψ⟩ = 0 and under the assumption of having a sufficiently dense clock spectrum one finds that the possible states |Ψ⟩ in the above equation reduce to states of the form

$|\mathrm{\Psi }\rangle =\sum _{k=0}^p{c}_k|E=-E_k{\rangle }_c\otimes |E_k{\rangle }_s,(26)$

where ∑_k|c_k|² = 1. Using Eq. 21, the global state of the Universe can be written as a superposition of direct products of clock and the system energy eigenstates [100],

$|\mathrm{\Psi }\rangle =\frac{1}{\sqrt{s+1}}\sum _{m=0}^s|{\tau }_m{\rangle }_c\otimes |{\psi }_m{\rangle }_s,(27)$

where the |ψ_m⟩_s are the states of the system related to the global state |Ψ⟩ by

$|{\psi }_m{\rangle }_s=\left(s+1\right)⟨{\tau }_m|\mathrm{\Psi }⟩(28)$

which are the states of subsystem S conditioned on the clock C being in |τ_m⟩. As such, the time development of |ψ_m⟩_s follows

$|{\psi }_m{\rangle }_s=e^{-i{H}_s\left({\tau }_m-{\tau }_0\right)/\hslash }|{\psi }_0{\rangle }_s.(29)$

Expressed in terms of the unitary operator $U_s({\tau }_m-{\tau }_0)=e^{-i{H}_s\left({\tau }_m-{\tau }_0\right)/\hslash }$, the state of the Universe can now be written as

$|\mathrm{\Psi }\rangle =\frac{1}{\sqrt{s+1}}\sum _{m=0}^s|{\tau }_m{\rangle }_c\otimes U_s\left({\tau }_m-{\tau }_0\right)|{\psi }_0{\rangle }_s.(30)$

Hence the conditional probability of obtaining outcome α for system S when measuring the observable A at a certain clock time τ_m is

$P\left(\alpha \text{\hspace{0.17em}on\hspace{0.17em}}S|{\tau }_m\text{\hspace{0.17em}on\hspace{0.17em}}C\right)=|⟨\alpha |U_s\left({\tau }_m-{\tau }_0\right)|{\psi }_0⟩{|}^2(31)$

according to the Born rule.

5.2.3 Unequally Spaced Energy Levels

Suppose a quantum system has p + 1 non-degenerate energy eigenstates |E_i⟩_s with eigenenergies E_i which are unequally-spaced but have rational energy differences. These energies can be written as

$E_i=E_0+r_i\frac{C_i}{B_i}=E_0+r_i\frac{2\pi \hslash }{T}(32)$

where C_i and B_i are natural numbers, as is the case of a free particle in a rigid box. Here T = 2πr₁/(E₁ − E₀) and r_i = r₁C_i/B_i with r₀ = 0. In such a case it is not possible to define a Hermitian operator for time, but Pegg [104] managed to identify a probability measure for such quantum systems with quantum clock states that are defined in a similar fashion to the case of equally-spaced energy levels. However, the rational ratio of the energy differences now describes a ladder of time measurements with a distribution of clock states along the unequally-spaced energy eigenstates of the system as shown in Figure 3. Using the clock states |α_m⟩_c of an associated quantum system with equal level spacing in a higher-dimensional Hilbert space, the probability of obtaining an outcome a for system S with unequal level spacing when measuring the observable A at a certain time α_m is again given by the Born rule as

$P\left(a\text{\hspace{0.17em}on\hspace{0.17em}}S|{\tau }_m\text{\hspace{0.17em}on\hspace{0.17em}}C\right)=|⟨a|U_s\left({\alpha }_m-{\alpha }_0\right)|{\psi }_0⟩{|}^2(33)$

for certain times τ_m = α_m and for a sufficiently large dimension s + 1 of the clock and a sufficiently large T [104].

FIGURE 3

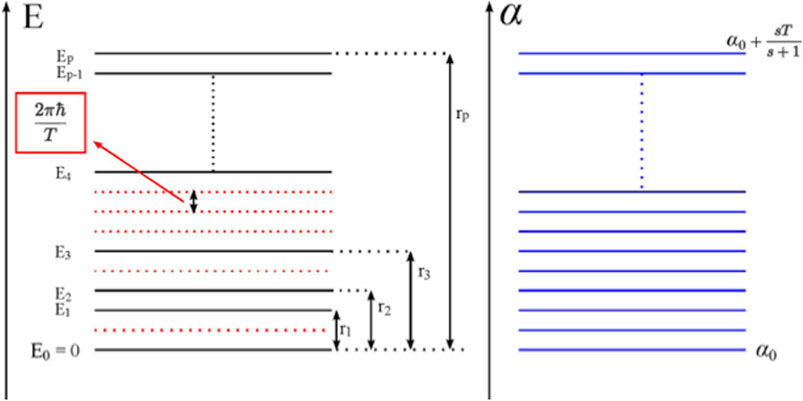
FIGURE 3. Shows the distribution of the energy levels for unequal energy levels (left) and for equal ones (right).

5.3 Clock Ambiguity

Since quantum theory provides infinitely many non-equivalent ways of partitioning the total Hilbert space of the Universe into a tensor-product structure, there are several choices of the clock by which unitary evolution can arise in the rest of the Universe. In other words, given the same global state |Ψ⟩ describing the Universe, the PW approach leads to completely different dynamics on the rest of the Universe. This is the clock ambiguity which has been nicely presented and discussed in [80]. Clock ambiguity has also been thoroughly discussed by Marletto and Vedral [97] who claim that there is no ambiguity in the PW formalism, but there is something else worth elaborating here. They provide some convincing arguments suggesting that the unitarity of the quantum system safeguards the equivalence of the dynamics generated by different clocks watching the same system. Indeed, their observation is analogous to the equivalence of the inertial frames of reference in the theory of special relativity. However, there is yet a need for a unifying reference for the choices of different times generated through different partitionings of the Hilbert space. Some attempts to resolve this question under linearized gravity have been carried out by Giacomini [105], but their consideration of the problem in a perturbative regime may undermine this attempt and turn it into an exercise rather than a viable solution. Until a metric defining a proper time is formulated we cannot talk about the equivalence of dynamics. This question remains an issue for further development of the program of quantum time formulation.

5.4 The Flow of Time

In the PW approach the flow of time arises in the correlation (entanglement) between the quantum degrees of freedom and the rest of the system, a correlation that is present in the global, time-independent state |Ψ⟩. An internal observer will see such a state describing normal time evolution; as we said earlier, the familiar system state |ψ(t)⟩ at time t arises by conditioning |Ψ⟩ via the projection ⟨t|Ψ⟩. Effectively there is no flow of time in the PW scheme. The clock measures the time correlated with the occurrence of the states according to the given probability [95]. This constructs a history as illustrated in Figure 2, where the global state |Ψ⟩ is projected onto space while the dotted frame translates along the horizontal axis representing t, just like the unfolding of a movie reel. The recorded movie frames are stationary states within a volume represented by |Ψ⟩ which constitutes a memory. Each frame stands for a given state of the system and as the time selects a frame by a measurement of the clock it gets projected onto a Schrödinger state |ψ(t)⟩.

Marletto and Vedral [97] describe this by saying that we have the observer, the observed and a sequence of ancillas. The elaboration given by Marletto and Vedral for the flow of time in the PW approach through counting the sequence of ancillas is analogous to the translation in a space-like Universe. In such a Universe, time is not time flowing independent of events but closely linked to spatial landmarks through which we can construct a sequence of correlations. From their own perspective, an observer does not notice anything different in the direction of the sequence of the occurrence of the events. Nevertheless, there is a meaning for the before and the after, marked by the order of the state “before” and the state “after” So, there is a meaning for a change in a local sense. As correctly remarked by [97], this is because an observer does not notice any sense of directivity, their state only contains information about the previous times. Our remark here is on constructing a memory; it is hard to understand how the observer can construct a memory in a Universe of stationary states except through different spatial locations. But if the spatial locations are not known then there will be no memory except for the last location, the one before the transition is made.

Hence, we conclude that the treatment of the transition from one state to the next could perhaps be presented using Hidden Quantum Markov Models [106]. In such a treatment the full scope of transitions would be presented as a correlation out of the set of possible states of the system and the corresponding states of the clock. This again is an issue that is worth further research. In a description based on Hidden Quantum Markov Models, the order of time and the concept of causality would be altered to become a correlation between cause and effect, thereby preserving causal order and causal relationships; however, no causal determinism can be strictly identified. This brings in the role of causal sets into the play of the exposed dynamics. For example, Zych et al. [107] considered such a question in a time-like context.

6 Discussion and Conclusion

The above approaches to the introduction of quantum time into the structure of quantum physics are certainly important steps towards dealing with time as an operator corresponding to a quantum observable, thereby targeting the role of time in quantum gravity. The quantization of spacetime, once having considered the bearing of the dynamics of events, is necessary for accurately describing natural phenomena. Relativistic effects are observed only in some extreme cases of high speed or strong gravity. While the dominating approach to quantum gravity, namely the covariant loop quantum gravity, tends to ignore the conventional spacetime background, the quantum time approach aims at quantizing time by considering it an internal degree of freedom which is observer dependent. In this respect the quantum time approach may face less difficulties in unifying relativity theory with quantum physics since it would be an difficult task to compile physical phenomena on the macroscopic level without regard to space and time [108]. In another article [109], which gives a beautiful account for when quantum effects are significant, the picture of a classically Evolving Block Universe (EBU), in his words, cedes place to one of a Crystallizing Block Universe (CBU) which reflects this quantum transition from indeterminacy to certainty, while nevertheless resembling the EBU on large enough scales. This issue is quite worth consideration.

Starting from an overall quantum description of two entangled but non-interacting systems, one of which is counted as a clock, Foti et al. [110] take the classical limit of the clock and only obtain the Schrödinger equation in this limit. Upon taking the classical limit for both the clock and the evolving system, they obtain Hamilton’s equation of motion. In their opinion, this shows that there is not a “quantum time”which is possibly opposed to a “classical” one; there is only one time and it is a manifestation of entanglement. These results can be easily explained by knowing that the time in Schrödinger’s equation is continuous and consequently recovering the equation is expected. The Hamiltonian of the global system is formed of the clock Hamiltonian and the system Hamiltonian, and upon taking the classical limit of both systems, the clock Hamiltonian gets dissolved and we are left with Hamilton’s equation of motion. Indeed, there are now two types of time, a discrete quantized time and a classical continuous time.

Considering a closed quantum system with a state that is perfectly distinguishable from all past or future states, Stoica [111, 112] shows that for any change that happens the Hamiltonian must be $H=-i\hslash \frac{\partial }{\partial \tau }$. Indeed, this is no surprise as this Hamiltonian is expressing the presence of a quantum clock as in the construction presented in this article [104], where τ is the time identified with the clock time correlated with change in the limit of vanishing energy level spacing. However, the value of this concise result comes from its explanation of the essence of the WD equation expressed as a Hamiltonian constraint as in Eq. 9 and its connection with the irreversibility of events. This is a result that might be taken further within the context of describing the causal order in a block Universe.

Notice that the constructed quantum clocks do not interact with the quantum system for which the time is being measured. This is an important condition to avoid the complications of having the clock disturbing the performance of the system as shown by Peres [36]. This is true as long as the clock is not physically related to the quantum system itself; however, the constraint of the WD equation in (9) establishes the conjugation between the clock and the system. The conditional probability is an important correlation link between the system and the clock. Nevertheless, there still seems to be several outstanding problems with the construction proposed by PW and other variants that followed. To resolve such problems we may need to add a fundamentally new postulate to the standard formulation of quantum physics which should provide us with a comprehensive resolution of other basic questions regarding the interpretation of quantum physics, like its range of validity and the problem of quantum measurement in general. We need to clarify, once and for all, the concepts we are dealing with. We need to clarify the physical meaning of the WD equation and its important role in fulfilling the requirement of the theory of relativity. We need to produce some quantum effects in the relation between the clock and the quantum system that is monitored. In this respect the question of entanglement needs to be further studied since the consideration of Marletto and Vedral [97] is by no means exhaustive. Moreover, we may need to add another postulate relating the changes in the value of observables to the probability of occurrence of the states, otherwise the clock may freeze after the first reading. These are some of the open questions that remain to be answered by a full theory of quantum time.

The identification of the WD constraint as a necessary prescription for the dynamics of isolated quantum systems is certainly an important step towards facilitating the adoption of the new philosophy of the relational role of time in connecting stationary states. However, again this approach is by no means complete. There seems to be more fundamental implications that need to be recognized for the full picture to become plausible. Such implications get uncovered, for example, in attempts of quantizing fields in position space. An example is offered in [81, 82], where it is shown that the full range of positive and negative frequencies is needed to represent electrodynamics. The role of the negative frequency solutions is very important and, as the solutions of the Dirac equation for the electron has shown, the treatment of space and time on equal footing as required by the theory of relativity has various implications that cannot be ignored. The existence of anti-particles and the negative energy states in vacuum is certainly strong evidence of such contributions brought out by the Dirac equation.

If the quantum dynamics is to be described as shown in Figure 2 and if the time and the dynamics is to emerge through correlations between the quantum clock and the system as described through an analogy with a movie reel, a question then arises about the speed of such an unfolding of events (states). Basically, it is the Hamiltonian which drives the time development of the system (as is the case in the Schrödinger equation). This is one strong reason for relating the clock to the system Hamiltonian, and done in a self-contained fashion by the Hamiltonian constraint in Eq. 9. To illustrate this and show that a hypothetical external observer would see the Universe as static whereas an internal observer will see it developing with time Moreva et al. [94] suggested an experimental set up using an entangled polarization state of two photons with one photon being used as a clock to measure the evolution of the second. They have shown that in their experiment an internal observer that becomes correlated with the photon taken as the clock will see the other photon evolve. However an external observer who only observes the global properties of the two photons sees it as static. Their scheme is an elegant illustration of the PW mechanism.

One important feature of quantum clocks arises once we have several equivalent quantum clocks measuring time. Due to the multiple partitionings of the Hilbert space, we would expect that time simultaneity is lost. This resembles what happens in the theory of special relativity; different observers measure different times of occurrence for the same event. We therefore need to establish a metric for the quantum measurement of time, or perhaps we need not. This remains an open question. Some proposals for quantum time in an interacting clock-system formulation are available (see for example [113]); however, the ambiguity of the disturbance caused by such an interacting model remains questionable. As it seems, the relatival description of the relation between the frames of reference and the question of perspectives, which is bound to satisfy certain symmetry requirements, is usually discussed in the context of the relativity of quantum states [114–116]. Specifically, a basic and straight forward description is given by Giacomini [105] in which the notion of the quantum reference frame (QRF) associated with a quantum particle is used. In this proposal the proper time of the particle is taken as a QRF and the evolving parameters of the rest of the quantum system under consideration coincides with it. Such QRF allows us to treat space and time on equal footing, safeguarding the Lorentz covariance of space and time measurements since we are dealing with the proper time. However, if we go back to the above formulations of quantum time, which are based on the PW scheme, we can see that this QFR is already built in the mechanism and is represented by the quantum clock. The author correctly remarked on this connection between their construction and the PW mechanism for non-interacting clocks when the external degrees of freedom are neglected.

PW [89] have remarked that because an infinite ensemble is needed to determine conditional probabilities, no prediction of quantum physics can ever be completely verified by quantum-mechanical observers within the Universe, for whom the theory can only make statistical predictions. This may sound discouraging to some extent since it implies that the observational verification of the quantum measurement of time may not be practically tenable. However, certainly there could be other approaches for chasing the detection of quantum time effects. One example of the precise measurement of quantum time effects could be through using the photometric effects of phase shifts [117].

At this stage it seems that the formulation of a consistent scheme of quantum time has already reached an advanced stage and has already overcome many fundamental difficulties. The formulations presented above are consistent and beautiful. However, the question whether the internal time measured by quantum clocks is affirming the philosophical choice of relatival time (that needs changes to exist) or substantival time (that does not need changes to exist) remains an open question [118].

Author Contributions

MBA conceived and led the project and wrote the paper. AB and DH contributed to the theoretical background and understanding and helped with the writing of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

MA would like to thank Alessandro Coppo, Tommaso Favalli, Flaminia Giacomini, Philipp A. Höhn, Lorenzo Maccone, Alexander Smith, Ovidiu Cristinel Stoica and Vlatko Vedral for useful discussions. Tommaso Favalli provided Figure 3 shown in the text. DH acknowledges financial support form the United Kingdom Engineering and Physical Sciences Research Council EPSRC (Award Ref. Nr. 2130171).

References

1.Aristotle. Physics, Trans. Robin Waterfield, with an Introduction and Notes by David Bostock. Oxford OX1 2JD, United Kingdom: Oxford University Press (1999):105.

Google Scholar

2.Augustine. Confessions, Translated by R. S. Pine-Coffin. Harmondsworth, Middlesex, Book XI: Penguin Books (1961):398.

Google Scholar

3.Al-Ghazali. The Incoherence of the Philosophers, Translated by Michael Marmura. Utah: Brigham Young University Press (2000):33.

Google Scholar

4. Smith G. Newton’s Philosophiae Naturalis Principia Mathematicain Varieties of Capitalism. The Institutional Foundations of Comparative Advantage. Winter 2008 Edn, Editor E. N. Zalta. Available at: https://plato.stanford.edu/archives/win2008/entries/newton-principia/. (Accessed May 09, 2020). (2007).

Google Scholar

5. Rynasiewicz R. Newton’s Views on Space, Time, and Motion. In: EN Zalta, editor. The Stanford Encyclopedia of Philosophy (2014). (Summer 2014 Edition). Available from: <https://plato.stanford.edu/archives/sum2014/entries/newton-stm/>. (Accessed February 21, 2022).

Google Scholar

6. Weinberg S. Gravitation and Cosmology. New York: Wiley (1972).

Google Scholar

7. Peres A. Quantum Theory: Concepts and Methods, 57. New York: Kluwer academic publishers (2002).

Google Scholar

8. Hartle JB. Quantum Kinematics of Spacetime. I. Nonrelativistic Theory. Phys Rev D (1988) 37:2818–32. doi:10.1103/physrevd.37.2818

CrossRef Full Text | Google Scholar

9. Hartle JB. Quantum Kinematics of Spacetime. II. A Model Quantum Cosmology with Real Clocks. Phys Rev D Part Fields (1988) 38:2985–99. doi:10.1103/physrevd.38.2985

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Holevo AS. Probabilistic and Statistical Aspects of Quantum Theory, 1. Springer (2011).

Google Scholar

11. Pauli W. General Principles of Quantum Mechanics. Berlin Heidelberg: Springer (1980).

Google Scholar

12. Hartman TE. Tunneling of a Wave Packet. J Appl Phys (1962) 33:3427–33. doi:10.1063/1.1702424

CrossRef Full Text | Google Scholar

13. Haibel A, Nimtz G. Universal Relationship of Time and Frequency in Photonic Tunnelling. Ann Phys (2001) 10:707–12. doi:10.1002/1521-3889(200108)10:8<707::aid-andp707>3.0.co;2-r

CrossRef Full Text | Google Scholar

14. Eckle P, Pfeiffer AN, Cirelli C, Staudte A, Dorner R, Muller HG, et al. Attosecond Ionization and Tunneling Delay Time Measurements in Helium. Science (2008) 322:1525–9. doi:10.1126/science.1163439

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Balcou P, Dutriaux L. Dual Optical Tunneling Times in Frustrated Total Internal Reflection. Phys Rev Lett (1997) 78:851–4. doi:10.1103/physrevlett.78.851

CrossRef Full Text | Google Scholar

16. Mugnai D, Ranfagni A, Ronchi L. The Question of Tunneling Time Duration: A New Experimental Test at Microwave Scale. Phys Lett A (1998) 247:281–6. doi:10.1016/s0375-9601(98)00628-8

CrossRef Full Text | Google Scholar

17. Yang S, Page JH, Liu Z, Cowan ML, Chan CT, Sheng P. Ultrasound Tunneling through 3D Phononic Crystals. Phys Rev Lett (2002) 88:104301. doi:10.1103/physrevlett.88.104301

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Robertson WM, Ash J, McGaugh JM. Breaking the Sound Barrier: Tunneling of Acoustic Waves through the Forbidden Transmission Region of a One-Dimensional Acoustic Band gap Array. Am J Phys (2002) 70:689–93. doi:10.1119/1.1477430

CrossRef Full Text | Google Scholar

19. Stahlhofen AA, Nimtz G. Evanescent Modes Are Virtual Photons. Europhys Lett (2006) 76:189–95. doi:10.1209/epl/i2006-10271-9

CrossRef Full Text | Google Scholar

20. Enders A, Nimtz G. On Superluminal Barrier Traversal. J Phys France (1992) 2:1693–8. doi:10.1051/jp1:1992236

CrossRef Full Text | Google Scholar

21. Steinberg AM, Kwiat PG, Chiao RY. Measurement of the Single-Photon Tunneling Time. Phys Rev Lett (1993) 71:708–11. doi:10.1103/physrevlett.71.708

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Spielmann C, Szipöcs R, Stingl A, Krausz F. Tunneling of Optical Pulses through Photonic Band Gaps. Phys Rev Lett (1994) 73:2308–11. doi:10.1103/physrevlett.73.2308

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Enders A, Nimtz G. Evanescent-mode Propagation and Quantum Tunneling. Phys Rev E (1993) 48:632–4. doi:10.1103/physreve.48.632

CrossRef Full Text | Google Scholar

24. Nimtz G. On Virtual Phonons, Photons, and Electrons. Found Phys (2009) 39:1346–55. doi:10.1007/s10701-009-9356-z

CrossRef Full Text | Google Scholar

25. Heitmann W. Superluminal Photonic Tunnelling and Quantum Electronics. Prog Quan Electronics (1997) 21:81.

Google Scholar

26. Aichmann H, Nimtz G. On the Traversal Time of Barriers. Found Phys (2014) 44:678–88. doi:10.1007/s10701-014-9804-2

CrossRef Full Text | Google Scholar

27. Nimtz G, Aichmann H. Zero-Time Tunneling - Revisited. Z für Naturforschung A (2017) 72:881–4. doi:10.1515/zna-2017-0172

CrossRef Full Text | Google Scholar

28. Winful HG. Tunneling Time, the Hartman Effect, and Superluminality: A Proposed Resolution of an Old Paradox. Phys Rep (2006) 436:1–69. doi:10.1016/j.physrep.2006.09.002

CrossRef Full Text | Google Scholar

29. Winful HG. Delay Time and the Hartman Effect in Quantum Tunneling. Phys Rev Lett (2003) 91:260401. doi:10.1103/physrevlett.91.260401

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Winful HG. Nature of "superluminal" Barrier Tunneling. Phys Rev Lett (2003) 90:023901. doi:10.1103/PhysRevLett.90.023901

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Winful HG. The Meaning of Group Delay in Barrier Tunnelling: a Re-examination of Superluminal Group Velocities. New J Phys (2006) 8:101. doi:10.1088/1367-2630/8/6/101

CrossRef Full Text | Google Scholar

32. Winful H. Energy Storage in Superluminal Barrier Tunneling: Origin of the Hartman Effect. Opt Express (2002) 10:1491. doi:10.1364/oe.10.001491

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Winful HG. Mechanism for 'superluminal' Tunnelling. Nature (2003) 424:638. doi:10.1038/424638a

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Low FE, Mende PF. A Note on the Tunneling Time Problem. Ann Phys (1991) 210:380–7. doi:10.1016/0003-4916(91)90047-c

CrossRef Full Text | Google Scholar

35. Foden C, Stevens KWH. Tunneling Times and a Quantum Clock. IBM J Res Dev (1988) 32:99–102. doi:10.1147/rd.321.0099

CrossRef Full Text | Google Scholar

36. Peres A. Measurement of Time by Quantum Clocks. Am J Phys (1980) 48:552–7. doi:10.1119/1.12061

CrossRef Full Text | Google Scholar

37. Misra B, Sudarshan ECG. The Zeno's Paradox in Quantum Theory. J Math Phys (1977) 18:756–63. doi:10.1063/1.523304

CrossRef Full Text | Google Scholar

38. Facchi P, Pascazio S. Quantum Zeno and Inverse Quantum Zeno Effects. Prog Opt (2001) 42:147–217. doi:10.1016/s0079-6638(01)80017-2

CrossRef Full Text | Google Scholar

39. Peres A. Zeno Paradox in Quantum Theory. Am J Phys (1980) 48:931–2. doi:10.1119/1.12204

CrossRef Full Text | Google Scholar

40. Itano WM, Heinzen DJ, Bollinger JJ, Wineland DJ. Quantum Zeno Effect. Phys Rev A (1990) 41:2295–300. doi:10.1103/physreva.41.2295

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Beige A, Hegerfeldt GC. Projection Postulate and Atomic Quantum Zeno Effect. Phys Rev A (1996) 53:53–65. doi:10.1103/physreva.53.53

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Cook RJ. What Are Quantum Jumps? Phys Scr (1988) T21:49–51. doi:10.1088/0031-8949/1988/t21/009

CrossRef Full Text | Google Scholar

43. Schulman LS, Ranfagni A, Mugnai D. Characteristic Scales for Dominated Time Evolution. Phys Scr (1994) 49:536. doi:10.1088/0031-8949/49/5/005

CrossRef Full Text | Google Scholar

44. Schulman LS. How Quick Is a Quantum Jump. In: D Mugnai, editor. Proc. Of the Adriatico Research Conf.:Tunneling and its Implications. Singapore: World Sci. (1997).

Google Scholar

45. Grot N, Rovelli C, Tate RS. Time of Arrival in Quantum Mechanics. Phys Rev A (1996) 54:4676–90. doi:10.1103/physreva.54.4676

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Leon J, Julve J, Pitanga P, de Urríes FJ. Time of Arrival in the Presence of Interactions. Phys Rev A (2000) 61:062101. doi:10.1103/physreva.61.062101

CrossRef Full Text | Google Scholar

47. Galapon EA. Theory of Quantum Arrival and Spatial Wave Function Collapse on the Appearance of Particle. Proc R Soc A (2009) 465:71–86. doi:10.1098/rspa.2008.0278

CrossRef Full Text | Google Scholar

48. Allcock GR. The Time of Arrival in Quantum Mechanics I. Formal Considerations. Ann Phys (1969) 53:253–85. doi:10.1016/0003-4916(69)90251-6

CrossRef Full Text | Google Scholar

49. Delgado V, Muga JG. Arrival Time in Quantum Mechanics. Phys Rev A (1997) 56:3425–35. doi:10.1103/physreva.56.3425

CrossRef Full Text | Google Scholar

50. Muga G, Sala Mayato R, Egusquiza IL. Time in Quantum Mechanics, Lecture Notes in Physics, 72. Berlin, New York: Springer (2002).

Google Scholar

51. Einstein A. Eine neue Formale Deutung der Maxwellschen Feldgleichungen der Elektrodynamik. Berlin (1916):688. (the quote appears on p. 696).

Google Scholar

52. Oriti D. Approaches to Quantum Gravity: Towards a New Understanding of Space, Time and Matter. S. B. Preuss Akad. Wiss. VII, 18488. Available at: https://echo.mpiwgberlin.mpg.de/ECHOdocuView?url=/permanent/echo/einstein/sitzungsberichte/8Y09B7KH/index.meta. (2009).

Google Scholar

53. Isham CJ. An Introduction to General Topology and Quantum Topology. In: HC Lee, editor. Physics, Geometry and Topology. New York: Plenum Press (1990). p. 129–89. doi:10.1007/978-1-4615-3802-8_5

CrossRef Full Text | Google Scholar

54. Kuchar KV. Time and Interpretation of Quantum Gravity. In: G Kunstatter, D Vincent, and J Williams, editors. Proceedings of the 4th Canadian Conference on General Relativity and Relativistic Astrophysics. Singapore: World Scientific (1992):69.

Google Scholar

55. Baierlein RF, Sharp DH, Wheeler JA. Three-Dimensional Geometry as Carrier of Information about Time. Phys Rev (1962) 126:1864–5. doi:10.1103/physrev.126.1864

CrossRef Full Text | Google Scholar

56. Misner CW. Absolute Zero of Time. Phys Rev Lett (1969) 186:1328–074. doi:10.1103/PhysRev.186.1328

CrossRef Full Text | Google Scholar

57. DeWitt BS. Quantum Theory of Gravity. I. The Canonical Theory. Phys Rev (1967) 160:1113–48. doi:10.1103/physrev.160.1113

CrossRef Full Text | Google Scholar

58. Wheeler JA. Battelle Rencontres, Lectures in Mathematics and Physics. In: CM DeWitt, and JA Wheeler, editors. New York: Benjamin (1968). p. 242–307.

Google Scholar

59. Kuchar K. Canonical Quantization of Cylindrical Gravitational Waves. Phys Rev (1971) D 4:955. doi:10.1103/PhysRevD.4.955

CrossRef Full Text | Google Scholar

60. Kuchar K. General Relativity: Dynamics without Symmetry. In: CJ Isham, R Penrose, and DW Sciama, editors. Quantum Gravity 2: A Second Oxford Symposium. Oxford): Clarendon (1981). p. 329–76.

Google Scholar

61. Misner CW. Mixmaster Universe. Phys Rev Lett (1969) 22:1071. doi:10.1103/physrevlett.22.1071

CrossRef Full Text | Google Scholar

62. York JW. Gravitational Degrees of Freedom and the Initial-Value Problem. Phys Rev Lett (1971) 26:1656–1658. doi:10.1103/physrevlett.26.1656

CrossRef Full Text | Google Scholar

63. Wheeler JA. Problems in the Foundations of Physics, Proceedings of the, International School of Physics ”Enrico Fermi, ” Course 72. In: G Toraldo di Francia, editor. Amsterdam: North-Holland (1979). p. 395–497.

Google Scholar

64. Rovelli C. Quantum Mechanics without Time: a Model. Phys Rev D (1991) 42:2638. doi:10.1103/PhysRevD.42.2638

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Rovelli C. Quantum Evolving Constants. Reply to "Comment on `Time in Quantum Gravity: An Hypothesis' ". Phys Rev (1991) D 44:1339. doi:10.1103/PhysRevD.44.1339

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Rovelli C. What Is Observable in Classical and Quantum Gravity? Class Quan Gravity (1991) 8:297. doi:10.1088/0264-9381/8/2/011

CrossRef Full Text | Google Scholar

67. Rovelli C. Quantum Reference Systems. Quan Gravity (1991) 8:p. 317. doi:10.1088/0264-9381/8/2/012

CrossRef Full Text | Google Scholar

68. Rovelli C, Ashtekar A, Stachel J. Time in Quantum Gravity: An Hypothesis. In: Conceptual Problems of Quantum Gravity. New York: Birkhauser (1991).

CrossRef Full Text | Google Scholar

69. Rovelli C. Analysis of the Different Meaning of the Concept of Time in Different Physical Theories. Nuovo Cimento (1995) 110B:81. doi:10.1007/BF02741291

CrossRef Full Text | Google Scholar

70. Rovelli C. Partial Observables. Phys Rev (2002) A 65:124013. doi:10.1103/PhysRevD.65.124013

CrossRef Full Text | Google Scholar

71. Reisenberger M, Rovelli C. Spacetime States and Covariant Quantum Theory. Phys Rev D (2002) 65:124013–456. doi:10.1103/PhysRevD.65.125016

CrossRef Full Text | Google Scholar

72. Marolf D, Rovelli C. Relativistic Quantum Measurement. Phys Rev D (2002) 66:023510. doi:10.1103/PhysRevD.66.023510

CrossRef Full Text | Google Scholar

73. Kuchar K. Ground State Functional of the Linearized Gravitational Field. J Math Physica (1970) 11:3322. doi:10.1063/1.1665133

CrossRef Full Text | Google Scholar

74. Rovelli C. "Forget Time". Found Phys (2011) 41(9):1475–90. doi:10.1007/s10701-011-9561-4

CrossRef Full Text | Google Scholar

75. Rovelli C. Time in Quantum Gravity: an Hypothesis. Phys Rev D (1991) 43:442. doi:10.1103/physrevd.43.442

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Barbour J. The End of Time: The Next Revolution in Physics. Oxford: Oxford University Press (2001).

Google Scholar

77. Bauer M, Aguillon CA. Second Quantization of Time and Energy in Relativistic Quantum Mechanics. arXiv preprint arXiv:2102.01042 (2021).

Google Scholar

78. Boette A, Rossignoli R, Gigena N, Cerezo M. System-time Entanglement in a Discrete-Time Model. Phys Rev A (2016) 93(6):062127. doi:10.1103/physreva.93.062127

CrossRef Full Text | Google Scholar

79. Leon J, Maccone L. The Pauli Objection. Found Phys (2017) 47(12):1597–608. doi:10.1007/s10701-017-0115-2

CrossRef Full Text | Google Scholar

80. Aguillón CA, Bauer M, García GE. Time and Energy Operators in the Canonical Quantization of Special Relativity. Eur J Phys (2020) 41:035601. doi:10.1088/1361-6404/ab67d6

CrossRef Full Text | Google Scholar

81. Hodgson D, Southall J, Purdy R, Beige A. Quantising One-Dimensional Electromagnetic fields in Position Space. arXive preprint arXiv:2104.04499 (2021).

Google Scholar

82. Hodgson D, Burgess C, Altaie MB, Beige A, Purdy R. An Intuitive Picture of the Casimir Effect. arXive preprint arXiv:2203.14385 (2022).

Google Scholar

83. Khorasani S. Time Operator in Relativistic Quantum Mechanics. Commun Theor Phys (2017) 68:35. doi:10.1088/0253-6102/68/1/35

CrossRef Full Text | Google Scholar

84. Wigner EP. Relativistic Invariance and Quantum Phenomena. Rev Mod Phys (1957) 29:255–68. doi:10.1103/revmodphys.29.255

CrossRef Full Text | Google Scholar

85. Salecker H, Wigner EP. Quantum Limitations of the Measurement of Space-Time Distances. Phys Rev (1957) 109:571. doi:10.1007/978-3-662-09203-3_15

CrossRef Full Text | Google Scholar

86. Addazi A. Quantum Gravity Phenomenology at the Dawn of the Multi-Messenger Era: A Review. Prog Part Nucl Phys (2022) 103948. doi:10.1016/j.ppnp.2022.103948

CrossRef Full Text | Google Scholar

87. Kobakhidze A, Lagger C, Manning A. Constraining Noncommutative Spacetime from GW150914. Phys Rev D (2016) 94:064033. doi:10.1103/physrevd.94.064033

CrossRef Full Text | Google Scholar

88. Bhattacharyya S, Gangopadhyay S, Saha A. Footprint of Spatial Noncommutativity in Resonant Detectors of Gravitational Wave. Class Quan Grav. (2019) 36:055006. doi:10.1088/1361-6382/ab008a

CrossRef Full Text | Google Scholar

89. Page DN, Wootters WK. Evolution without Evolution: Dynamics Described by Stationary Observables. Phys Rev D (1983) 27:2885–92. doi:10.1103/physrevd.27.2885

CrossRef Full Text | Google Scholar

90. Strocchi F, Wightman AS. Proof of the Charge Superselection Rule in Local Relativistic Quantum Field Theory. J Math Phys (1974) 15:2198–224. doi:10.1063/1.1666601

CrossRef Full Text | Google Scholar

91. Kuchar KV. Time and Interpretations of Quantum Gravity. Int J Mod Phys D (2011) 20:3. doi:10.1142/S0218271811019347

CrossRef Full Text | Google Scholar

92. Unruh WG, Wald RM. Time and the Interpretation of Canonical Quantum Gravity. Phys Rev D (1989) 40:2598–614. doi:10.1103/physrevd.40.2598

CrossRef Full Text | Google Scholar

93. Gambini R, Porto RA, Pullin J. A Relational Solution to the Problem of Time in Quantum Mechanics and Quantum Gravity: a Fundamental Mechanism for Quantum Decoherence. New J Phys (2004) 6:45. doi:10.1088/1367-2630/6/1/045

CrossRef Full Text | Google Scholar

94. Moreva E, Brida G, Gramegna M, Giovannetti V, Maccone L, Genovese M. Time from Quantum Entanglement: an Experimental Illustration. Phys Rev A (2014) 89:052122. doi:10.1103/physreva.89.052122

CrossRef Full Text | Google Scholar

95. Giovannetti V, Lloyd S, Maccone L. Quantum Time. Phys Rev D (2015) 92:045033. doi:10.1103/physrevd.92.045033

CrossRef Full Text | Google Scholar

96. Albrecht A, Iglesias A. Clock Ambiguity and the Emergence of Physical Laws. Phys Rev D (2008) 77:063506. doi:10.1103/physrevd.77.063506

CrossRef Full Text | Google Scholar

97. Marletto C, Vedral V. Evolution without Evolution and without Ambiguities. Phys Rev D (2017) 95:043510. doi:10.1103/physrevd.95.043510

CrossRef Full Text | Google Scholar

98. Page DN. Clock Time and Entropy. In: JJ Halliwell, J Perez-Mercader, and WH Zurek, editors. Physical Origins of Time Asymmetry. Cambridge: Cambridge University Press (1994).

Google Scholar

99. Maccone L, Sacha K. Quantum Measurements of Time. Phys Rev Lett (2020) 124:110402. doi:10.1103/physrevlett.124.110402

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Favalli T, Smerzi A. Time Observables in a Timeless Universe. Quantum (2020) 4:354. doi:10.22331/q-2020-10-29-354

CrossRef Full Text | Google Scholar

101. Ruschhaupt A, Werner RF. Quantum Mechanics of Time. In: P Blanchard, and J Fröohlich, editors. The Message of Quantum Science – Attempts towards a Synthesis, Lecture Notes in Physics. Springer (2015). doi:10.1007/978-3-662-46422-9_14

CrossRef Full Text | Google Scholar

102. Muga JG, Sala R, Palao JP. The Time of Arrival Concept in Quantum Mechanics. Superlattices and microstructures (1998) 23:833–42. doi:10.1006/spmi.1997.0544

CrossRef Full Text | Google Scholar

103. Mielnik B. The Screen Problem. Found Phys (1994) 24:1113–29. doi:10.1007/bf02057859

CrossRef Full Text | Google Scholar

104. Pegg DT. Complement of the Hamiltonian. Phys Rev A (1998) 58:4307–13. doi:10.1103/physreva.58.4307

CrossRef Full Text | Google Scholar

105. Giacomini F. Spacetime Quantum Reference Frames and Superpositions of Proper Times. Quantum (2021) 5:508. doi:10.22331/q-2021-07-22-508

CrossRef Full Text | Google Scholar

106. Monras A, Beige A, Wiesner K. Hidden Quantum Markov Models and Non-adaptive Read-Out of many-body States. Appl Math Comput Sci (2011) 3:93. doi:10.48550/arXiv.1002.2337

CrossRef Full Text | Google Scholar

107. Zych M, Costa F, Pikovski I, Brukner Č. Bell's Theorem for Temporal Order. Nat Commun (2019) 10:3772. doi:10.1038/s41467-019-11579-x

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Ellis GFR. Physics in the Real Universe: Time and Spacetime. Gen Relativ Gravit (2006) 38:1797–824. doi:10.1007/s10714-006-0332-z

CrossRef Full Text | Google Scholar

109. Ellis GFR, Rothman T. Time and Spacetime: The Crystallizing Block Universe. Int J Theor Phys (2010) 49:988–1003. doi:10.1007/s10773-010-0278-5

CrossRef Full Text | Google Scholar

110. Foti C, Coppo A, Barni G, Cuccoli A, Verrucchi P. Time and Classical Equations of Motion from Quantum Entanglement via the Page and Wootters Mechanism with Generalized Coherent States. Nat Commun (2021) 12:1787. doi:10.1038/s41467-021-21782-4

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Stoica OC. The Problem of Irreversible Change in Quantum Mechanics. arXiv preprint arXiv:2204.02270 (2022).

Google Scholar

112. Stoica OC. Versatility of Translational Quantum Dynamics. arXiv preprint arXiv:2204.01426 (2022).

Google Scholar

113. Smith ARH, Ahmadi M. Quantum Clocks Observe Classical and Quantum Time Dilation. Nat Commun (2020) 11:5360. doi:10.1038/s41467-020-18264-4

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Loveridge L, Busch P, Miyadera T. Relativity of Quantum States and Observables. Europhysics Lett (2017) 117:40004. doi:10.1209/0295-5075/117/40004

CrossRef Full Text | Google Scholar

115. Giacomini F, Castro-Ruiz E, Brukner Č. Quantum Mechanics and the Covariance of Physical Laws in Quantum Reference Frames. Nat Commun (2019) 10:494. doi:10.1038/s41467-018-08155-0

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Vanrietvelde A, Hoehn PA, Giacomini F, Castro-Ruiz E. A Change of Perspective: Switching Quantum Reference Frames via a Perspective-Neutral Framework. Quantum (2020) 4:225. doi:10.22331/q-2020-01-27-225

CrossRef Full Text | Google Scholar

117. Zych M, Costa F, Pikovski I, Brukner Č. Quantum Interferometric Visibility as a Witness of General Relativistic Proper Time. Nat Commun (2011) 2:505. doi:10.1038/ncomms1498

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Strelchuk S, Woods MP. Measuring Time with Stationary Quantum Clocks. arXiv preprint arXiv:2106.07684 (2021).

Google Scholar