- School of Physics, Sun Yat-Sen University, Guangzhou, China
We study single-photon scattering of an artificial giant Λ-type atom coupled to a superconducting quantum interference device (SQUID) chains waveguide at two points. In this circuit, the single-photon scattering rates are dependent on the atom-waveguide coupling strengths and the phase accumulated between two coupling points. By modulating the flux-dependent phase velocity in the SQUID-chain waveguide, the photon’s traveling time is changed, and the accumulating phase is adjusted simultaneously. We investigate the relationship between the scattering effect and the flux bias, which allows us to explore novel phenomena with the tunable traveling time in both Markovian and non-Markovian regimes, and to design novel quantum technologies such as quantum storage.
1 Introduction
In the last decades, research on superconducting quantum circuits has gone far forwards [1,2]. The superconducting quantum circuit is blessed with scalability, integrability, and flexibility interacting with other systems, making it a prospective platform for carrying on the quantum information and quantum compution missions [3-5]. The superconducting qubit can play a role as an artificial atom and then strongly coupled to microwave photons in circuit quantum electrodynamics (cQED) [6-17]. One can make the artificial atom’s scale comparable to wavelengths so that it goes beyond the dipole approximation [18]. Moreover, the artificial atoms can also couple with the field confined in a waveguide at several points, which behave as a giant atom [18]. In recent years, a giant atom system has been experimentally realized for the first time in an acoustic system, where a superconducting qubit coupled to a surface acoustic wave (SAW) via an interdigital transducer acts as a giant atom [19,20], the photonic version following [21,22]. In such giant atom systems, many striking effects were discovered [18]. For example, strongly frequency-dependent coupling between giant atoms and bosonic modes can be designed for realizing interference effects [23-26] between coupling points, which enables electromagnetically induced transparency (EIT) in a ladder configuration [27]. When the distance of the coupling points is too large, the Markovian approximation can no longer be applied to the whole system. The so-called non-Markovian effect [28] induced by the non-negligible travel time can cause some novel phenomena in giant-atom systems [29], such as non-exponential decay [30] and bound state in a continuum [31,32].
Waveguide quantum electrodynamics (wQED) [33] studies the interaction between an atom and continuum of electromagnetic modes confined in a 1D waveguide. WQED uses the transmission and reflection spectrum of the incident field to reveal the dynamics of the whole system and supports a theoretical basis for quantum networks. Because of recent experimental advances on giant atoms [19,20], wQED setups based on giant atoms have attracted considerable attention. For example, Ref. [34] proposed a decoherence-free waveguide with multiple giant atoms. In addition, an effective single-photon frequency conversion rate via a giant Λ-type atom can approach a unit combining with the Sagnac interferometer [35]. Compared to the two-level atom, the Λ-type three-level atom has two transition paths, which provide additional tunable spaces. Meanwhile, the circuit Λ-type atom has been demonstrated good tunability in experiments, as shown in Refs [36,37]. The combination of Λ-type atoms and giant atoms could be a promising way for quantum information processing, which will be explored in this paper. Very recently, Ref. [32] proposed tunable chiral bound states in a system composed of superconducting giant atoms and a Josephson photonic-crystal waveguide [38-42].
In this paper, we present a circuit giant Λ-type atom couples to the SQUID-chain waveguide. In contrast to previous works with a fixed length between two coupling points, we replace a typical SQUID-chain waveguide instead of a standard transmission line and achieve the in-situ tunability of traveling time. This tunability stems from the flux-dependent phase velocity of the SQUID-chain waveguide. By studying single-photon scattering in this system, we can understand the unique dynamics of the giant atom. Then, the tunable group velocity of this particular waveguide can be utilized to realize the tunable scattering rate. Furthermore, taking advantage of the tunability of this circuit, we explore the novel physical phenomena from Markovian to non-Markovian regimes and propose a promising protocol to store quantum information.
The paper is structured as follows. We begin in Section 2 with a brief introduction of the Hamiltonian of the whole system before turning to the detailed calculation of the single-photon process in the SQUID-chain waveguide in Section 3. Then, distinguishing scattering properties of this system from Markovian to Non-Markovian regimes and an application in quantum storage are discussed in Section 4. At last, we end with a conclusion in Section 5.
2 Model
We consider a giant Λ-type atom interacting with a 1D waveguide at two coupling points, as depicted in Figure 1. The Hamiltonian H is defined as
where
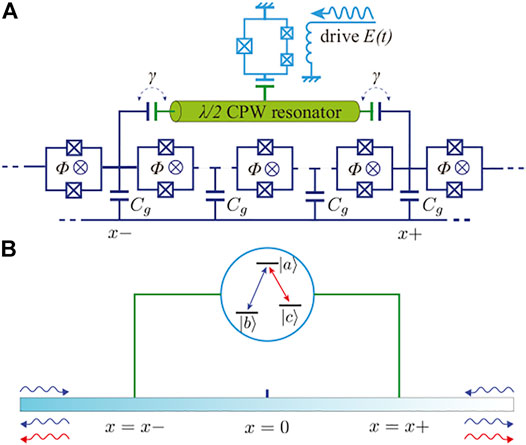
FIGURE 1. (A) Sketch of the circuit, a SQUID-chain waveguide (deep blue) capacitively coupled to a giant atom consisting of a flux qubit and a λ/2 CPW resonator at x± two points, γ denoting coupling strength. (B) Schematic illustration of the whole system. The giant atom is Λ-type three-level system consisting of exicting state |a⟩, ground state |b⟩ and substable state |c⟩.
Hw describes a bidirectional waveguide where photons propagate equally in two directions. In our setup, the waveguide is a superconducting transmission line composed of identical SQUID loops. The interval between adjacent loops equals d0, and a homogeneous magnetic field is applied vertically through every SQUID loop. The SQUID loop can be viewed as an effective inductance LJ parallel to the Josephson capacitance CJ. The Hamiltonian of SQUID chains can be quantized as [39]:
For the effective inductance of SQUID, LJ is flux dependent, the photon’s group velocity vg = dω/dk in the waveguide is, therefore, a tunable parameter. Assuming the waveguide length L → ∞, we obtain the continuum form of the Hamiltonian
Hint represents the coupling of two circuit systems and has the form,
Although the whole system may reach the non-Markovian regime originating from two distant coupling points, the Markovian approximation is still valid at each local coupling point x±. Consequently, the total Hamiltonian for the whole system can be written as
The terms on the right-hand side of the first line are the atom and field modes free energy, where |i⟩ and ωi are the eigenstates of the atomic system and their energies, respectively.
3 Single-Photon Process in SQUID-Chain Waveguides
3.1 Dynamics of the Giant Atom
Firstly, the motion equations of the giant atom limited in the single-photon subspace can be studied by using the similar method introduced in Ref [29]. The total state of a Λ-type giant atom and the microwave field in the waveguide can be described by
where |0⟩ represents the vacuum state of the microwave filed in the SQUID-chain waveguide. The integral terms describe the state of a single photon propagating in the waveguide towards right α = 1 or left α = 2, with the giant atom in the ground state |b⟩ (or substable state |c⟩). Using the Schrödinger equation iℏ∂/∂t|Φ(t)⟩ = H|Φ(t)⟩, we obtain the differential equations for coefficients: Ca(t) being the probability amplitude of the giant atom in exicted state |a⟩, Cb1(2)k and Cc1(2)q denoting the photon spectrums in the transmission line with the giant atom staying in the ground state |b⟩ and the substable state |c⟩, respectively. The time evolution of Ca(t) is then turned to
The first term denotes free evolution. The following two terms show the atom relaxing process with γ1,2 and feedback effect with Ca (t − T), where T = L/vg is the delay time. Here, Θ(•) is the Heaviside step function showing the time-delay feedback between the coupling points. We introduced the notion
Ca(t) can be analytically solved and finally has the spectrum form expansion (details in Appendix A)
where
3.2 Single-Photon Scattering
To study scattering properties of the giant atom, we set a right-propagating photon incident into the waveguide, whose frequency is centered at ωk (Cb1k0 ≠ 0), with the giant atom initially being in the ground state. The dynamical evolution equation of the giant atom is then derived from Eq. 7,
In the long-time limit, the emission spectrum of outgoing photons can be obtained (details in Appendix B):
where the ground state energy is set to zero ωb = 0 with variable substitution ωk = ωq + ωc. Then, we obtain the transmission rate Tk, the reflection rate Rk, and the forward conversion rate Tq,
In contrast to small atoms, Eqs 12–14 imply that the giant atom has the corrected transition frequency Ωa = ωa + γ1 sin(ωkT) + γ2 sin(ωqT) and decay rate Γ1(2) = γ1(2)(1 + cos(ωk(q)T)) [43]. From Eq. 13, the conditions for total reflection, Rk = 1, can be obtained directly
There are two ways to make the second condition satisfied. One is γ2 = 0, which means the transition path |a⟩ → |c⟩ directly turned off. The other one is ωqT = 2 (n + 1)π, which infers that the decay channel of |a⟩ → |c⟩ is suppressed by the destructive interference between coupling points [35]. Either of these two cases can cause that the Λ configuration atom could be reduced to a simple two-level atom. However, the first solution is trivial and will not be considered in our case. Then the two conditions in Eq. 15 can be rewritten as ωk − ωa = γ1 sin (ωcT) and ωqT = 2 (n + 1)π. Here, we introduce the detuning, Δ = ωk − ωa, of the incident photon from the |a⟩ − |b⟩ transition. The total reflection conditions are written as Δ = γ1 sin (ωcT) and Δ = ωc − ωa + 2 (n + 1)π/T.
While the total transmission, Tk = 1 and Rk = Tq = 0, happens in the case of ωkT = (2n + 1)π, no matter with ωcT. Because of the nondirectional decay process of the excited atom, the forward nonelastic scattering photon strength is equal to the backward one. Thus, it is reasonable to set the frequency conversion rate to be twice the forward conversion rate, Tc = 2Tq. The fundamental source affecting the conversion rate is the ratio of the decay rates, i.e., γ1/γ2. For simplicity, we set γ1/γ2 = 1 and use γ regardless of the subscript in the context.
In Figure 2, we plot the scattering rates as the function of the scaled detuning Δ/γ and the scaled substable level frequency ωc/γ, for ωaT = 2000π, where ωa/γ = 10,000 and T = 0.2π/γ. Figure 2A,B depict the reflection rates for the Markovian (γT = 0.2π) and non-Markovian (γT = 3π) regimes, respectively. Compared with Figure 2A,B shows two different features. First, there are additional small peaks at two sides of the primary maximum for the certain ωc. Second, the frequency band of the total reflection is broadened. The giant atom can provide a wide spectrum window for the strong reflection in the non-Markovian regime. Figure 2C,D represent the single-photon transmittance and the frequency conversion rate, respectively, of the giant atom in the Markovian regime.
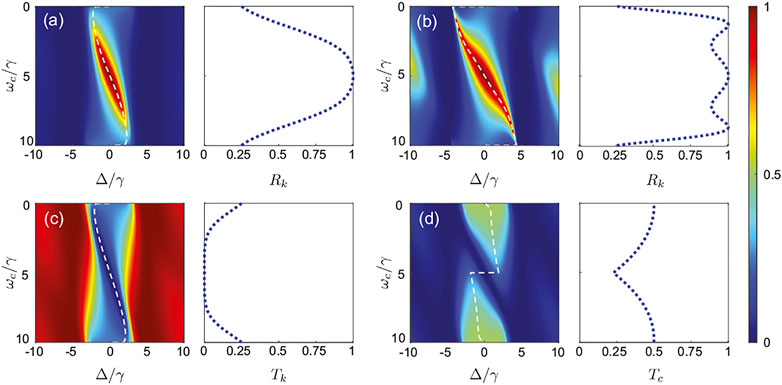
FIGURE 2. Scattering rates. (A), (C) and (D) depict the reflectance, transmittance, and frequency conversion rate of the incident ωk photon, respectively, as a function of the normalized detuning Δ/γ and the substable state frequency ωc/γ for γT = 0.2π. (B) shows the reflectance for γT = 3π. The white dashed curves in the colormaps depict trajectories of max [Rk(Δ)], min [Tk(Δ)], and max [Tc(Δ)] versus ωc/γ, respectively, while the right plots show the maximum or minimun value of the corresponding rate versus ωc/γ.
3.3 Tunable Traveling Time T
Based on the above investigation, it is clear that the single-photon scattering effect of the Λ-type giant atom is intensely affected by the two crucial phases, ωkT and ωcT. These phases are dependent on the atom’s energy level structure and the coupling points separation distance. Therefore, it is intuitive to control the spatial length between the coupling points for coherently tuning the phase. However, the spatial length is fixed once the circuit sample is fabricated. Here, we introduce the SQUID-chain transmission line, in which the photon’s phase velocity is flux-dependent. Although the spatial distance of two points in the waveguide is determined, changes in the photon’s phase velocity will change the cost time T for photons traveling between two fixed points, equivalent to the effective length and accumulated phase. Consequently, the effect will affect the dynamical evolution of this Λ-type giant atom as well as the scattering properties.
In addition to infinite length condition L → ∞, if the superconducting transmission line also satisfies following conditions [32]:
the dispersion relation Eq. 2 can be reduced to
i.e., the phase velocity is
The change in phase velocity leads to the change of the traveling time of photons propagating between two points, so does the accumulating phase. We set the separation distance of the two coupling points as d = nd0, i.e., n SQUIDs constituting the waveguide between the coupling points. Then, the traveling time of a photon is
By modulating the photon’s traveling time between two coupling points, we can explore some interesting applications that will be discussed in Section 4.
3.4 Experimental Feasibility
The linear dispersion relation (17) of the SQUID-chain waveguide is valid over a wide frequency domain ωk < 10 GHz, when the circuit parameters are taken as [32]; [41,40]: L0 = 0.2 nH, Cg = 0.4 fF, CJ = 90 fF, d0 = 1 μm. The transition frequencies of the circuit Λ-type atom can be set to fall within the frequency domain. For example, we can take these parameters: ωac/2π = 6.4828 GHz, ωab/2π ≈ 6.48452 GHz under a driving field with the frequency ωd/2π = 5.6466 GHz and the coupling strength Ωd/2π = 1.46 MHz [37], where ωab(c) = ωa − ωb(c) is the transition frequency between |a⟩ and |b(c)⟩. The original traveling time now is T0 ≈ 10–9 s without the magnetic field. With normal reliable decay rates γ (∼MHz) for the capacitive coupling, we can realize γT changing from the regime of γT ≪ 1 to γT ≈ 1 theoretically. In other words, the whole system can transit to the non-Markovian regime from the Markovian regime gradually. Thus, taking advantage of this setup, we can study novel physical phenomena in both Markovian and Non-Markovian regimes. It also allows fine-grained operations.
4 Discussions
4.1 From Markovian to Non-markovian
For the sake of intuitively seeing the tunable scattering effects, we substitute Eq. 19 into Eq. 12–14 and obtain the relationship between the scattering rates and the flux bias as:
where the corrected transition frequency
First, we demonstrate the giant atom’s scattering characteristics Rk, Tk and Tc as the function of the external scaled magnetic flux Φ/Φ0 and the scaled detuning from the excited state frequency Δ/γ in Figures 3A–C. The decay rates and the energy level structure of the giant atom are set to γ1 = γ2 = ωc/10 = ωa/10000. The original traveling time of the photon is set as T0 = 0.001/γ. Figures 3A–C clearly show that the scattering rate is a single value around zero flux. While the flux is increasing, the frequency band of the rates is broadened, as discussed in Section 3.2. Continue to increase magnetic flux approaching 0.5Φ0, the scattering rates begin violently oscillating, which implies γT > 1 in the non-Markovian regime. Then, the detailed scattering rates of the system near the white dashed line in Figures 3A–C are shown in Figures 3D–F. The shape of scattering rates spreading out like a water wave demonstrates their periodicity, which originates from the cosine function of the magnetic flux. The flux Φa along the white dashed line satisfies
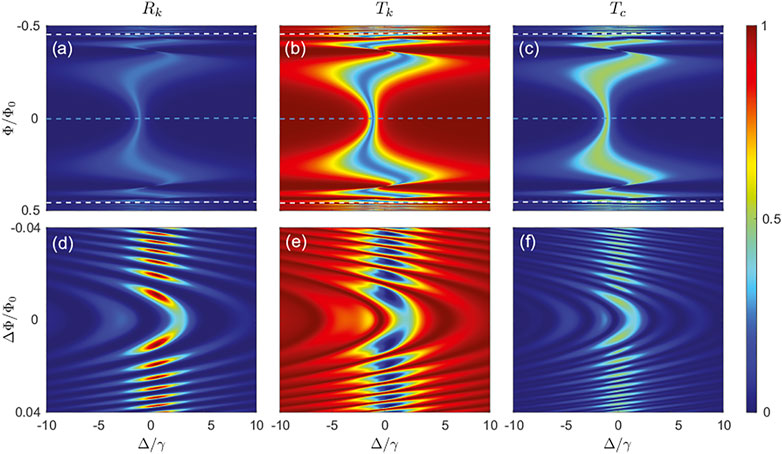
FIGURE 3. Density plots showing the single-photon (A,D) reflection rate Rk (B,E) transmission rate Tk, and (C,F) frequency conversion rate Tc as a function of the detuning Δ/γ and flux Φ/Φ0. In (A–C), the variation range of Φ is setted to be −0.5Φ0 ∼ 0.5Φ0 while (D–F) is −0.04Φ0 + Φa ∼ 0.04Φ0 + Φa with Φa satisfying
Figures 4A–C show the scattering rates Rk, Tk and Tc along the cuts of dashed lines in Figures 3A–C versus the normalized detuning Δ/γ. Here, the red curve describes the scattering rates for γT = 1 (the cut of white dashed lines), and the blue dashed curve describes the scattering rates for γT = 0.001 (the cut of blue dashed lines). The reflection rate and the transmission rate are significantly affected by the traveling time T with the maximum reflection rate increasing and the minimum transmission rate decreasing, respectively, as shown in Figures 4A,B . Apart from the main peak around the zero detuning, some small peaks arise on two sides of the resonance point. In contrast, the peaks of the frequency conversion rates for two cases only exhibit a slight shift, as shown in Figure 4C.
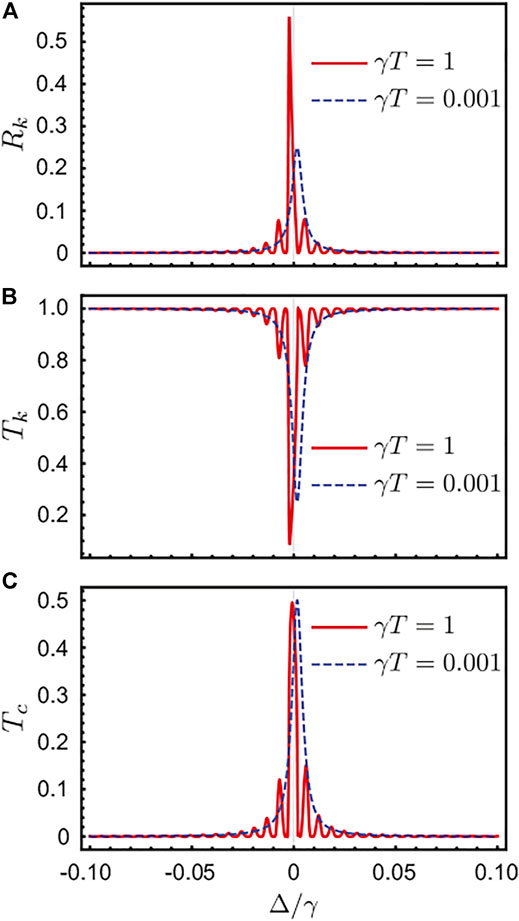
FIGURE 4. The scatting process described by the reflectance Rk (A), transmittance Tk (B), and frequency conversion rate Tc (C) versus normalized detuning Δ/γ with γT = 0.001 (dashed bule line) and γT = 1 (solid red line).
Based on the facts presented in Figures 3, 4, we find that the maximum reflection rate in the non-Markovian regime is much bigger than the corresponding rate in the Markovian regime with a narrower peak width. Giant atoms prefer to intensely interact with the photon modes with certain frequencies because these photon modes were selected out in a “cavity” formed by the two coupling points of the artificial giant atom, which acts as resonant mirrors [44].
Distinguishing scattering properties in both Markovian and non-Markovian regimes can serve future quantum technologies. Excitingly, all of these are now implemented by using one setup, in which we only need to change the external magnetic field through the SQUID loops. In addition, our circuit allows observing the transition between these two regimes by only modulating the external field gradually from one to the other.
4.2 Application: Quantum Storage
The tunable traveling time in our Λ-type giant atom can also be used to store quantum information. Because the corrected decay rates Γi depend on the phases, we can find an unusual phase ωcT, with which Γ2 can reach the maximum value as well as Γ1 at its minimum value. These tunable decay rates enable one to realize state transition between |b⟩ and |c⟩ in our system. For example, |b⟩ → |a⟩ → |c⟩ transitions can be achieved by switching off the decay Γ1, when the atom is excited by an incident ωk photon.
Recalling Eq. 7 with the initial values, Ca (0) = 1, Cbs (0), and Ccs(0) = 0, we obtain the atomic excitation
The emission spectrum of outgoing photons in the long-time limit is
When the phases satisfy the conditions, ωkT1 = ωabT1 = (2n + 1)π and ωqT1 = ωacT1 = 2nπ, the resonant photon with frequency ωab [Cbαk (∞)] vanishes corresponding to extreme depression of the decay path |a⟩ → |b⟩, while the conversion photon with frequency ωac [Ccαq (∞)] reaches the maximum corresponding to the enhancement of the decay from |a⟩ → |c⟩.
Using Residue theorem, we can derive
Interestingly, when sn is a purely imaginary number sn = iωs, there will be a mode sn without decay which can survive in the-long time limit. Therefore, we have the stationary solution
which yields a dark state decoupled with the open transmission line.
If the giant atom is initially prepared in the excited state and the transition frequencies between levels satisfy ωac = ωab = (2n + 1)π/T, a dark-state mode, sn = −iωa,
which are referring to continuum bound states [31,32]; [46,47]. Unlike the bound state protected by the energy gap [48-55], it derives from the destructive interference among the coupling points of the giant atom. Particularly, it can be created and relieved after introducing the adjustable traveling time. This method of preserving quantum information in an atom-waveguide bound state could be widely applied in quantum storage.
5 Conclusion
In this paper, we investigate a driven resonator-qubit giant Λ-type atom coupling to a SQUID-chain waveguide. By studying the scattering effect of individual photons on this giant atomic system, we explore both Markovian and non-Markovian phenomena caused by the interference effect between two coupling points. Due to the adjustable group velocity of the waveguide, the scattering effect of this artificial giant Λ-type atom to the incident microwave photon can show significant variation when we control the external magnetic field applied on SQUID loops in this particular waveguide. This in-situ modulation brings convenience to adjust the transmission of quantum information and provides more possibilities in future quantum technologies. Moreover, this setup can be realized in experiments using current state-of-the-art technologies for superconducting circuits [30]; [21,22]; [56].
6 APPENDIX
6.1 Derivation of the Giant Atom System
6.1.1 Artificial Λ-type Three-Level Atom
The artificial Λ-type giant atom can be realized in the design of the system of Ref. [36] in addition to one more coupling point in the waveguide-CPW resonator interface as shown in Figure 1A. The Hamiltonian of the qubit-resonator system is given by
where σi are the pauli operators of the flux qubit with frequency ωq. a†(a) is the creation (annihilation) operator of the resonator ωr photon. g denotes the coupling constant of the qubit and the resonator, while Ω is the Rabi frequency representing the amplitude of driving field E(t). This system has a set of polarition states |1⟩, |2⟩, |3⟩, and |4⟩, which can be approximated as [37]:
where the mixing angles θ0 and θ1 are given by tan (θ0) = Ωd/[(ωq − χ) − ωd] and tan (θ1) = Ωd/[ωd − (ωq − 3χ)], respectively. And we use the set of polariton states |1⟩, |2⟩ and |3⟩ to form a Λ-type system with the Hamiltonian
6.1.2 SQUID-Chain Waveguide
The SQUID-chain microwave transmission line model, as shown in Figure 1, can be described by the Hamiltonian
where the charge and phase vectors have the form,
and
respectively. The charge-density operator at the antinode position Q can be approximately, in the linear limit CJ = 0 [32], expressed as
Ct = NCg is the total capacitance of SQUID chains.
6.1.3 Coupling Between SQUID-Chain Waveguides and Artificial Λ-type Giant Atoms
The resonator-part Hamiltonian in the resonator-qubit system is written as
Qr and Φr are the charge operator and the flux operator of the resonator, while C and L are the circuit characteristic capacitance and inductance, respectively. When a microwave field is incident, the Hamiltonian of the circuit resonator can be rewritten as
From Eq. 35, we know that the charge induced by the incident field is
Expanding Eq. 37 as
we obtain the radiative decay rate κ from the resonator to the waveguide,
Consequently, the total Hamiltonian of the system including the SQUID-chain waveguide and artificial Λ-type giant atom can be obtained as
where
6.2 Derivation of the Single-Photon Process
In this part, we briefly derive the photon distruibution and time evolution of the single-photon process. From the single-excitation wave function Eq. 5, we can substitute the state formula into the Schröndinger equation and obtain the dynamical equation for the giant atom
The propogating photon fields in the transmission line can be written as
By integrating above equations, we can obtain Eq. 6. Then taking Laplace transform
Here we set the right-propagating incident photon field Cb1k (0) ≠ 0, which frequency band is around ωab. With the giant atom initially being in the ground state, the probability amplitude of the exctied state is given by
From Eq. 42, we obtain the solutions of the forward-scattered field
and the backward-scattered fields
where
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Z-LX initiated and supervised the project. J-PZ and Z-LX developed the theoretical model. J-PZ and R-YG performed the numerical plots. J-PZ and Z-LX wrote the draft. All authors contributed to the theoretical discussions, numerical plots analysis, and manuscript writing.
Funding
The National Natural Science Foundation of China (Grant No. 11874432), and the National Key R&D Program of China (Grant No. 2019YFA0308200).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. You JQ, Nori F. Atomic Physics and Quantum Optics Using Superconducting Circuits. Nature (2011) 474:589–97. doi:10.1038/nature10122
2. Xiang Z-L, Ashhab S, You JQ, Nori F. Hybrid Quantum Circuits: Superconducting Circuits Interacting with Other Quantum Systems. Rev Mod Phys (2013) 85:623–53. doi:10.1103/RevModPhys.85.623
3. Clarke J, Wilhelm FK. Superconducting Quantum Bits. Nature (2008) 453:1031–42. doi:10.1038/nature07128
5. Ladd TD, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien JL. Quantum Computers. Nature (2010) 464:45–53. doi:10.1038/nature08812
6. Blais A, Huang R-S, Wallraff A, Girvin SM, Schoelkopf RJ. Cavity Quantum Electrodynamics for Superconducting Electrical Circuits: An Architecture for Quantum Computation. Phys Rev A (2004) 69:062320. doi:10.1103/PhysRevA.69.062320
7. Wallraff A, Schuster DI, Blais A, Frunzio L, Huang RS, Majer J, et al. Strong Coupling of a Single Photon to a Superconducting Qubit Using Circuit Quantum Electrodynamics. Nature (2004) 431:162–7. doi:10.1038/nature02851
8. Johansson J, Saito S, Meno T, Nakano H, Ueda M, Semba K, et al. Vacuum Rabi Oscillations in a Macroscopic Superconducting QubitLCOscillator System. Phys Rev Lett (2006) 96:127006. doi:10.1103/PhysRevLett.96.127006
9. Astafiev O, Inomata K, Niskanen AO, Yamamoto T, Pashkin YA, Nakamura Y, et al. Single Artificial-Atom Lasing. Nature (2007) 449:588–90. doi:10.1038/nature06141
10. Abdumalikov AA, Astafiev O, Nakamura Y, Pashkin YA, Tsai J. Vacuum Rabi Splitting Due to strong Coupling of a Flux Qubit and a Coplanar-Waveguide Resonator. Phys Rev B (2008) 78:180502. doi:10.1103/PhysRevB.78.180502
11. Hofheinz M, Wang H, Ansmann M, Bialczak RC, Lucero E, Neeley M, et al. Synthesizing Arbitrary Quantum States in a Superconducting Resonator. Nature (2009) 459:546–9. doi:10.1038/nature08005
12. Niemczyk T, Deppe F, Huebl H, Menzel EP, Hocke F, Schwarz MJ, et al. Circuit Quantum Electrodynamics in the Ultrastrong-Coupling Regime. Nat Phys (2010) 6:772–6. doi:10.1038/nphys1730
13. Astafiev O, Zagoskin AM, Abdumalikov AA, Pashkin YA, Yamamoto T, Inomata K, et al. Resonance Fluorescence of a Single Artificial Atom. Science (2010) 327:840–3. doi:10.1126/science.1181918
14. Paik H, Schuster DI, Bishop LS, Kirchmair G, Catelani G, Sears AP, et al. Observation of High Coherence in Josephson junction Qubits Measured in a Three-Dimensional Circuit Qed Architecture. Phys Rev Lett (2011) 107:240501. doi:10.1103/PhysRevLett.107.240501
15. Blais A, Grimsmo AL, Girvin SM, Wallraff A. Circuit Quantum Electrodynamics. Rev Mod Phys (2021) 93:025005. doi:10.1103/RevModPhys.93.025005
16. Koch J, Yu TM, Gambetta J, Houck AA, Schuster DI, Majer J, et al. Charge-insensitive Qubit Design Derived from the cooper Pair Box. Phys Rev A (2007) 76:042319. doi:10.1103/PhysRevA.76.042319
17. Barends R, Kelly J, Megrant A, Sank D, Jeffrey E, Chen Y, et al. Coherent Josephson Qubit Suitable for Scalable Quantum Integrated Circuits. Phys Rev Lett (2013) 111:080502. doi:10.1103/PhysRevLett.111.080502
18. Frisk Kockum A. Quantum Optics with Giant Atoms-The First Five Years. In: T Takagi, M Wakayama, K Tanaka, N Kunihiro, K Kimoto, and Y Ikematsu, editors. International Symposium on Mathematics, Quantum Theory, and Cryptography. Singapore: Springer Singapore (2021). p. 125–46. doi:10.1007/978-981-15-5191-8_12
19. Gustafsson MV, Aref T, Kockum AF, Ekström MK, Johansson G, Delsing P. Propagating Phonons Coupled to an Artificial Atom. Science (2014) 346:207–11. doi:10.1126/science.1257219
20. Manenti R, Kockum AF, Patterson A, Behrle T, Rahamim J, Tancredi G, et al. Circuit Quantum Acoustodynamics with Surface Acoustic Waves. Nat Commun (2017) 8:975. doi:10.1038/s41467-017-01063-9
21. Guimond P-O, Vermersch B, Juan ML, Sharafiev A, Kirchmair G, Zoller P. A Unidirectional On-Chip Photonic Interface for Superconducting Circuits. Npj Quan Inf (2020) 6:32. doi:10.1038/s41534-020-0261-9
22. Kannan B, Ruckriegel MJ, Campbell DL, Frisk Kockum A, Braumüller J, Kim DK, et al. Waveguide Quantum Electrodynamics with Superconducting Artificial Giant Atoms. Nature (2020) 583:775–9. doi:10.1038/s41586-020-2529-9
23. Frisk Kockum A, Delsing P, Johansson G. Designing Frequency-dependent Relaxation Rates and Lamb Shifts for a Giant Artificial Atom. Phys Rev A (2014) 90:013837. doi:10.1103/PhysRevA.90.013837
24. Zhao W, Wang Z. Single-photon Scattering and Bound States in an Atom-Waveguide System with Two or Multiple Coupling Points. Phys Rev A (2020) 101:053855. doi:10.1103/PhysRevA.101.053855
25. Yu H, Wang Z, Wu J-H. Entanglement Preparation and Nonreciprocal Excitation Evolution in Giant Atoms by Controllable Dissipation and Coupling. Phys Rev A (2021) 104:013720. doi:10.1103/PhysRevA.104.013720
26. Yin X-L, Liu Y-H, Huang J-F, Liao J-Q. Single-photon Scattering in a Giant-Molecule Waveguide-Qed System. arXiv:2203.07812v1 (2022). doi:10.48550/ARXIV.2203.07812
27. Andersson G, Ekström MK, Delsing P. Electromagnetically Induced Acoustic Transparency with a Superconducting Circuit. Phys Rev Lett (2020) 124:240402. doi:10.1103/PhysRevLett.124.240402
28. de Vega I, Alonso D. Dynamics of Non-markovian Open Quantum Systems. Rev Mod Phys (2017) 89:1. doi:10.1103/RevModPhys.89.015001
29. Guo L, Grimsmo A, Kockum AF, Pletyukhov M, Johansson G. Giant Acoustic Atom: A Single Quantum System with a Deterministic Time Delay. Phys Rev A (2017) 95:053821. doi:10.1103/PhysRevA.95.053821
30. Andersson G, Suri B, Guo L, Aref T, Delsing P. Non-exponential Decay of a Giant Artificial Atom. Nat Phys (2019) 15:1123–7. doi:10.1038/s41567-019-0605-6
31. Guo L, Kockum AF, Marquardt F, Johansson G. Oscillating Bound States for a Giant Atom. Phys Rev Res (2020) 2:043014. doi:10.1103/PhysRevResearch.2.043014
32. Wang X, Liu T, Kockum AF, Li H-R, Nori F. Tunable Chiral Bound States with Giant Atoms. Phys Rev Lett (2021) 126:043602. doi:10.1103/PhysRevLett.126.043602
33. Sheremet AS, Petrov MI, Iorsh IV, Poshakinskiy AV, Poddubny AN. Waveguide Quantum Electrodynamics: Collective Radiance and Photon-Photon Correlations. arXiv e-prints, arXiv:2103.06824 (2021).
34. Kockum AF, Johansson G, Nori F. Decoherence-free Interaction between Giant Atoms in Waveguide Quantum Electrodynamics. Phys Rev Lett (2018) 120:140404. doi:10.1103/PhysRevLett.120.140404
35. Du L, Li Y. Single-photon Frequency Conversion via a Giant Λ -type Atom. Phys Rev A (2021) 104:023712. doi:10.1103/PhysRevA.104.023712
36. Inomata K, Koshino K, Lin ZR, Oliver WD, Tsai JS, Nakamura Y, et al. Microwave Down-Conversion with an Impedance-MatchedΛSystem in Driven Circuit QED. Phys Rev Lett (2014) 113:063604. doi:10.1103/PhysRevLett.113.063604
37. Long J, Ku HS, Wu X, Gu X, Lake RE, Bal M, et al. Electromagnetically Induced Transparency in Circuit Quantum Electrodynamics with Nested Polariton States. Phys Rev Lett (2018) 120:083602. doi:10.1103/PhysRevLett.120.083602
38. Rakhmanov AL, Zagoskin AM, Savel’ev S, Nori F. Quantum Metamaterials: Electromagnetic Waves in a Josephson Qubit Line. Phys Rev B (2008) 77:144507. doi:10.1103/PhysRevB.77.144507
39. Weißl T, Küng B, Dumur E, Feofanov AK, Matei I, Naud C, et al. Kerr Coefficients of Plasma Resonances in Josephson junction Chains. Phys Rev B (2015) 92:104508. doi:10.1103/PhysRevB.92.104508
40. Krupko Y, Nguyen VD, Weißl T, Dumur É, Puertas J, Dassonneville R, et al. Kerr Nonlinearity in a Superconducting Josephson Metamaterial. Phys Rev B (2018) 98:094516. doi:10.1103/PhysRevB.98.094516
41. Puertas Martínez J, Léger S, Gheeraert N, Dassonneville R, Planat L, Foroughi F, et al. A Tunable Josephson Platform to Explore many-body Quantum Optics in Circuit-Qed. Npj Quan Inf (2019) 5:19. doi:10.1038/s41534-018-0104-0
42. Planat L, Ranadive A, Dassonneville R, Puertas Martínez J, Léger S, Naud C, et al. Photonic-crystal Josephson Traveling-Wave Parametric Amplifier. Phys Rev X (2020) 10:021021. doi:10.1103/PhysRevX.10.021021
43. Shen JT, Fan S. Coherent Photon Transport from Spontaneous Emission in One-Dimensional Waveguides. Opt Lett (2005) 30:2001–3. doi:10.1364/OL.30.002001
44. Mirhosseini M, Kim E, Zhang X, Sipahigil A, Dieterle PB, Keller AJ, et al. Cavity Quantum Electrodynamics with Atom-like Mirrors. Nature (2019) 569:692–7. doi:10.1038/s41586-019-1196-1
45. Guo S, Wang Y, Purdy T, Taylor J. Beyond Spontaneous Emission: Giant Atom Bounded in the Continuum. Phys Rev A (2020) 102:033706. doi:10.1103/PhysRevA.102.033706
46. Hsu CW, Zhen B, Stone AD, Joannopoulos JD, Soljačić M. Bound States in the Continuum. Nat Rev Mater (2016) 1:16048. doi:10.1038/natrevmats.2016.48
47. Calajó G, Fang Y-LL, Baranger HU, Ciccarello F. Exciting a Bound State in the Continuum through Multiphoton Scattering Plus Delayed Quantum Feedback. Phys Rev Lett (2019) 122:073601. doi:10.1103/PhysRevLett.122.073601
48. Longo P, Schmitteckert P, Busch K. Few-photon Transport in Low-Dimensional Systems: Interaction-Induced Radiation Trapping. Phys Rev Lett (2010) 104:023602. doi:10.1103/PhysRevLett.104.023602
49. Shahmoon E, Kurizki G. Nonradiative Interaction and Entanglement between Distant Atoms. Phys Rev A (2013) 87:033831. doi:10.1103/PhysRevA.87.033831
50. Calajó G, Ciccarello F, Chang D, Rabl P. Atom-field Dressed States in Slow-Light Waveguide Qed. Phys Rev A (2016) 93:033833. doi:10.1103/PhysRevA.93.033833
51. Liu Y, Houck AA. Quantum Electrodynamics Near a Photonic Bandgap. Nat Phys (2017) 13:48–52. doi:10.1038/nphys3834
52. González-Tudela A, Cirac JI. Markovian and Non-markovian Dynamics of Quantum Emitters Coupled to Two-Dimensional Structured Reservoirs. Phys Rev A (2017) 96:043811. doi:10.1103/PhysRevA.96.043811
53. González-Tudela A, Cirac JI. Quantum Emitters in Two-Dimensional Structured Reservoirs in the Nonperturbative Regime. Phys Rev Lett (2017) 119:143602. doi:10.1103/PhysRevLett.119.143602
54. Sundaresan NM, Lundgren R, Zhu G, Gorshkov AV, Houck AA. Interacting Qubit-Photon Bound States with Superconducting Circuits. Phys Rev X (2019) 9:011021. doi:10.1103/PhysRevX.9.011021
55. Leonforte L, Carollo A, Ciccarello F. Vacancy-like Dressed States in Topological Waveguide Qed. Phys Rev Lett (2021) 126:063601. doi:10.1103/PhysRevLett.126.063601
Keywords: quantum optics, waveguide QED, superconducting circuit, giant atom, non-markovian dynamics
Citation: Zou J-P, Gong R-Y and Xiang Z-L (2022) Tunable Single-Photon Scattering of a Giant Λ-type Atom in a SQUID-Chain Waveguide. Front. Phys. 10:896827. doi: 10.3389/fphy.2022.896827
Received: 15 March 2022; Accepted: 07 April 2022;
Published: 27 April 2022.
Edited by:
Zhihai Wang, Northeast Normal University, ChinaReviewed by:
Re-Bing Wu, Tsinghua University, ChinaChang-Sheng Hu, Huazhong University of Science and Technology, China
Copyright © 2022 Zou, Gong and Xiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ze-Liang Xiang, eGlhbmd6bGlhbmdAbWFpbC5zeXN1LmVkdS5jbg==
 Jian-Ping Zou
Jian-Ping Zou Rui-Yang Gong
Rui-Yang Gong Ze-Liang Xiang
Ze-Liang Xiang