Generation of Neutral Chemically Reactive Species in Low-Pressure Plasma

The surface finish of organic and inorganic materials treated by gaseous plasma usually depends on the fluxes and fluencies of chemically reactive species such as molecular radicals. In low-pressure plasmas, the dissociation of molecules to parent atoms depends on the production rate in the gas phase and on the loss rate on surfaces. The processing will be efficient if the loss rate is minimized. The methods for minimizing the loss rate and thus increasing the processing efficiency are presented and discussed. The dissociation fraction of simple molecules exceeds 10% providing the plasma-facing materials are smooth with a low coefficient for heterogeneous surface recombination. The density of atoms in a plasma reactor increases with increasing pressure reaching a maximum and decreases with further pressure increase, which is explained by two competing processes. The energy efficiency also exhibits a maximum, which may be as high as 30% if plasma is sustained by electrodeless high-frequency discharges. Optimization of energy efficiency is not only beneficial for the costs of material processing but also for the prevention of excessive heating of treated materials. The latter is particularly important for organic materials because the surface functional groups are not stable but decay with increasing surface temperature.

Highlights

- The surface finish of solid materials depends on the fluxes and/or fluences of plasma-generated species.

- Neutral reactive species such as atoms of molecular gases are often the major reactants, especially when treating organic materials.

- Despite several methods for measuring the density and fluxes of neutral reactive species, the evolution of the surface properties versus fluences is rarely reported.

- The density of neutral species in a low-pressure plasma reactor depends on the surface loss by heterogeneous recombination and also on effective pumping speed.

- The energy efficiency of atom production in plasma is optimal in glass discharge tubes where plasma is sustained by electrodeless discharges.

- Gradients in atom density are unavoidable in large, industrial-size reactors.

Introduction

Interaction of reactive gaseous plasma with surfaces of solid materials has been a subject of extensive research in the past decades due to unsolved scientific issues and technological applications. Reactive gaseous plasma contains reactive species capable of interacting chemically on the surface of plasma-facing materials. Plasma technologies based on the chemical reactivity of gaseous species are nowadays applied in microelectronics [1], electro-catalysis [2], photocatalysis [3], air purification [4], wastewater treatment [5], combustion devices [6], super-capacitors [7], tissue engineering [8], cancer treatment [9], sterilization [10], food industry [11], agriculture [12], farming [13], seed treatment [14] and even for inactivation of viruses [15]. Chemically reactive gaseous species are created in gaseous plasma either because of the high gas temperature (thermal plasmas) or dissociative reactions at the collisions with energetic particles, usually free electrons (non-equilibrium plasma). A significant concentration of reactive species in thermal plasmas is achieved at high gas temperatures, usually several 1,000 K. Most materials degrade at high temperatures, so non-equilibrium plasmas are preferred sources of reactive species for tailoring surface properties of solid materials, in particular organic materials like polymers [16]. The gas temperature in non-equilibrium plasma is often just above room temperature, but the temperature of free electrons is usually several 10,000 K. Other temperatures have been reported in non-equilibrium plasmas, like vibrational [17] and rotational [18] temperatures. Non-equilibrium plasma is sustained at various pressures, but commonly only in the pressure range from about 0.1 to 100 Pa (low-pressure plasma) or at atmospheric pressure (around 10⁵ Pa = 1 bar). An essential difference in the behavior of reactive gaseous species in low- and atmospheric-pressure plasmas is reactive species’ lifetime. It is often as low as a microsecond at atmospheric pressure and could be over a second at low pressure [19]. At atmospheric pressure, the primary loss mechanic is homogeneous reactions in the gas phase, whereas, at low pressure, it is heterogeneous surface reactions [20].

The surface finish of materials exposed to gaseous plasma obviously depends on the material’s properties, (surface) temperature of the material, fluxes of reactive gaseous species onto the treated material, and treatment time. As long as fluxes and temperatures are constant, the surface finish will depend on the fluence of reactive species (product of fluxes and treatment time). The reactive species formed in plasma include positively charged ions, neutral molecular fragments in the ground electronic state, neutral species in metastable states, and radiation in the range of wavelengths where the photon energy is higher than the binding energy between atoms in the surface layer of the treated material. Non-equilibrium gaseous plasma is usually a rich radiation source in the vacuum ultraviolet (VUV) range [21, 22]. Figure 1 represents a spectrum of weakly ionized highly reactive oxygen plasma at the electron temperature of 3 eV and density of 1 × 10¹⁶ m⁻³. The spectrum was calculated using the NIST database [23] The literature on exact mechanisms of interaction between chemically reactive species and organic material on the atomic scale is scarce, so surface reactions on the atomic scale are yet to be elaborated.

FIGURE 1

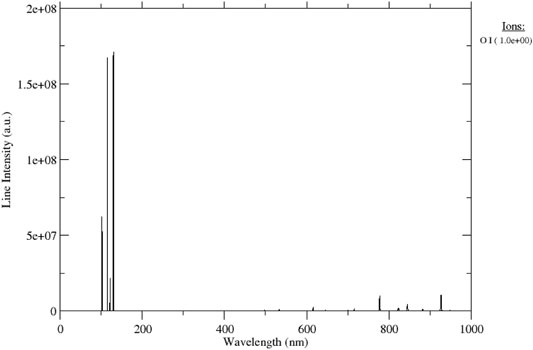
FIGURE 1. The spectrum of oxygen plasma with electron temperature 3 eV and density 1 × 10¹⁶ m⁻³ [23].

Significant are reactive neutral species because their interaction with solid material is purely potential; their kinetic energy is negligible. An excellent paper was recently published by Longo et al. [24]. The authors used density functional theory to study the chemical interaction of neutral oxygen atoms on a simple polymer (polystyrene, in particular) surface and identified almost 20 pathways. Their theoretical predictions were confirmed by carefully designed experiments where the O-atom fluence was varied systematically in a broad range between 10¹⁹ and 10²⁴ m⁻² [25]. The source of O-atoms was weakly ionized oxygen plasma, but the polymer treatment was performed in the flowing afterglow in order to exclude any contribution of other reactive species or VUV radiation on the surface finish. The flux of O-atoms onto the polymer surface was about 1 × 10¹⁹ m⁻²s⁻¹. Theoretical and experimental results presented in the above-cited articles clearly show that the surface finish in the case of a simple polymer, like polystyrene, actually depends on the fluence of O-atoms and not other parameters, as long as the surface temperature is kept constant. The same observation was reported by Recek et al. [26] for the case of corn seeds. Recek et al. used various plasmas sustained at different conditions but proved that the surface finish (in this case, the wettability) depended only on the fluence of neutral oxygen atoms.

The mechanisms of physicochemical interactions between the O-atoms and the solid surface were also elaborated by Uchida et al. [27]. Unlike Longo et al. [24], Uchida took into account also the various kinetic energies of impinging O-atoms. They found no chemical interaction with organic matter for atoms of kinetic energy 0.1 eV. The interaction of an O-atom of kinetic energy 1 eV resulted in surface functionalization, but the kinetic energy of 10 eV to etching. These results indicate that only the O-atoms in the high-energy tail of the Boltzmann distribution are capable of chemical interaction with the organic matter. The results reported by Uchida may explain a very low reaction coefficient reported for thermal O-atoms at room temperature. For example, Vesel et al. [28] found the probability of etching polyethylene terephthalate thin films by neutral oxygen atoms in the late-flowing afterglow of oxygen plasma as low as 1.4 × 10^–6. It should be stressed that the experiment with monochromatic O-atoms is challenging to perform, so the experimental confirmation of Uchida’s theory is yet to be reported.

This article aims to present the frontiers in understanding the fundamental mechanisms governing the density of neutral reactive plasma species focusing on the O-atoms in the ground state. The considerations are also valid for other atoms often used for tailoring surface properties of organic materials like hydrogen and nitrogen. Methods for optimization of energy efficiency are explained, and a practical example is illustrated.

Concentrations of Chemically Reactive Atoms in a Gaseous Plasma

The neutral reactive species play a dominant role in the surface modification of heat-sensitive materials. The density of these reactants in the gas phase depends on production and loss rates, which, in turn, depend on the peculiarities of the experimental setup. A valuable approach for determining the density of reactive particles is a theoretical one. Guerra et al. [29] provided detailed calculations of gas-phase and surface phenomena in oxygen, nitrogen, and O₂/N₂ plasmas sustained in a cylindrical tube in a recent comprehensive paper. They considered numerous reactions and explained electron, vibrational, chemical, and surface kinetics. While collisional cross sections in the gas phase were adequately determined decades ago, surface coefficients are still lacking, particularly coefficients for the accommodation of molecular oxygen metastables. Several channels for surface recombination of neutral oxygen atoms on perfectly smooth silica were considered by Guerra et al. [29]. The authors found the O-atom loss coefficient linearly increasing with the increasing flux, at least for the range of O-atom densities between 4 × 10²¹ and 2.5 × 10²² m⁻³. Their calculations were valid for a fixed density of O₂ molecules of 5 × 10²³ m⁻³. The surface recombination of O-atoms was found to follow the Langmuir-Hinshelwood model, i.e., two O-atoms accommodated on the surface associate to a parent molecule and desorb from the surface. The influence of kinetic energy of oxygen atoms and molecules impinging the surface was stressed–the authors clearly showed that the kinetic gas temperature near the wall would be probably higher than the wall temperature. The higher kinetic energy will stimulate surface mobility and thus enhance the recombination via the Langmuir-Hinshelwood pathway, according to [29].

Suppose the energy dissipated on the surface stimulates the recombination of atoms to parent molecules. In that case, the recombination coefficient will also depend on the energy released by other mechanisms, so the coefficient would increase with increasing ion flux and/or kinetic energy of positively charged ions impinging the walls. In fact, Booth et al. [30] provided experimental evidence for increasing recombination coefficient with increasing discharge current (and thus increasing the supply of energy to the surface of a glass tube). However, they explained the behavior of the recombination coefficient with the Eley-Rideal (ER) mechanism, i.e., incident O atoms recombine with both chemisorbed and more weakly bonded physisorbed atoms on the glass surface. The exact mechanisms of surface recombination of atomic radicals to parent molecules on the atomic scale upon plasma conditions are far from being known in detail and represent a scientific challenge for future theoretical and experimental research.

The theoretical predictions are best illustrated in Figure 2, which shows the density of neutral reactive plasma species versus the pressure in the discharge chamber. The parameter is the discharge power P, meaning that P₁ < P₂ < P₃ < P₄. All curves in Figure 2 exhibit maxima. The density below the maximum often increases linearly with increasing pressure. Linearity is explained by the linear increase of the density of molecules with increasing pressure at a constant temperature following the Equation.

$n_{\text{M}}=\frac{p}{k_{\text{B}}T}(1)$

where p is the gas pressure, k_B Boltzmann constant, and T is the neutral gas kinetic temperature.

FIGURE 2

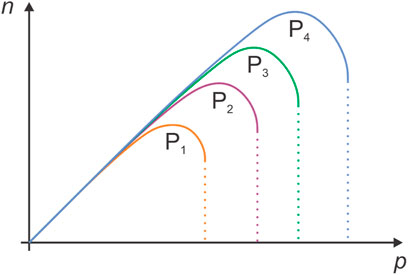
FIGURE 2. The density of neutral reactive plasma species versus pressure in the discharge chamber. The parameter is the discharge power with P₁ < P₂ < P₃ < P₄.

The slope of the curves in Figure 2 at low pressure (well before the maximum is reached) depends on the loss of atoms on the walls, i.e., the recombination coefficient. If the coefficient is 0, the atoms do not associate to parent molecules on a surface, so the dissociation should be complete taking into account negligible loss in the gas phase. In the approximation of zero-surface recombination, the density of atoms can be calculated from the measured pressure. For two-atom molecules such as O₂, N₂, H₂ etc., the atom density in the approximation of the zero-surface recombination is

$n_{\text{A}}=2n_{\text{M}}=\frac{2p}{k_{\text{B}}T}(2)$

The pressure (p) in Eq. 2 should be measured before the discharge is turned on. In practice, complete dissociation of molecules in plasma reactors does not appear at reasonable discharge power even at low pressures because of different reasons. The trivial one is the finite value of the surface recombination coefficient. Although many materials are regarded as inert for atoms like O, N, or H, both the theoretical [29] and experimental [30] studies showed finite values of the surface recombination, typically of about 10^–3 for inert materials.

Another deviation from the density as in Eq. 2 arises because most users employ flowing systems, i.e., gas is introduced continuously into the discharge chamber at one side and pumped out on the other. Such flowing systems ensure appropriate purity of gas during processing of materials because any volatile products of the interaction between plasma species and processed materials are removed from the discharge chamber. On the other hand, such a flowing regime also causes pumping atoms from the discharge chamber, so actually, the pump duct is also a sink for atoms. The loss of reactive atoms by pumping depends on the pump duct cross-section at the effective pumping speed at the cross-section between the discharge chamber and the pump duct. The flux of atoms onto the pump duct inner surface is

$j_{\text{ther}}=\frac{1}{4}{n}_{\text{A}}\langle v\rangle (3)$

and the flux of atoms removed due to pumping is

$j_{\text{drift}}=n_{\text{A}}v(4)$

Here, j_ther is the random (thermal) flux and <v> is the average thermal velocity, i.e.,

$v=\sqrt{\frac{8k_{\text{B}}T}{\pi m}}(5)$

The j_drift is the drift flux of atoms through the pump duct, and v is the average drift velocity at the beginning of the pump duct. The entrance to the pump duct, therefore, acts as a virtual surface with the recombination coefficient defined as

${\gamma }_{\text{pump}}=\frac{n_{\text{A}}v}{\frac{1}{4 }{n}_{\text{A}}\langle v\rangle }(6)$

The recombination coefficient is defined as the ratio between the number of atoms lost on the surface area in a unit of time and the number of atoms reaching the surface in a unit of time. In the approximation when v << <v>, n_A v is the number of atoms pumped from the chamber (flux of O-atoms because of the chamber pumping), and ¼ n_A <v> is the flux of atoms into the pump duct. Namely, not all atoms arriving at the pump duct by drifting the gas will be actually pumped from the chamber. The virtual recombination coefficient of the pump duct as calculated from Eq. 6 is shown versus the drift velocity in Figure 3. The values of random velocity were taken for neutral O-atoms (<v> = 630 m/s at room temperature). Typically, the plasma reactors are pumped with pumps which enable pumping with the drift velocity of the order of m/s. The drift velocity is calculated from the vacuum equation

$v=\frac{{\text{Φ}}_{\text{V}}}{A}(7)$

where Φ_V is the effective pumping speed (volume flow) at the cross-section of the pump duct and the plasma reactor, and A is the geometrical cross-section of the pump duct. The effective pumping speed can be estimated from the known pumping speed of the vacuum pump at a given pressure and the conductance of any vacuum element between the pump and the discharge vessel at a given pressure. By definition, the effective pumping speed is always smaller than the pumping speed of the pump. Experimentalists often operate their systems at an effective pumping speed several times smaller than the pumping speed of the pump.

FIGURE 3

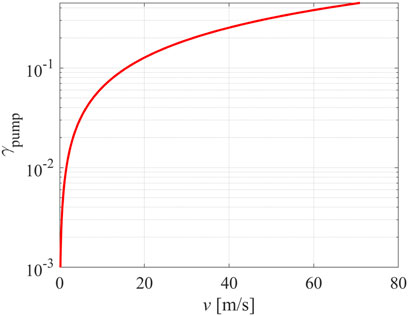
FIGURE 3. Virtual recombination coefficient of the pump duct versus the drift velocity of oxygen atoms at room temperature.

By definition, the virtual recombination coefficient at the drift velocity v = 0 m/s (no pumping) is zero because the residence time of the gas in the discharge chamber is infinite. The virtual recombination coefficient is 0.002 (a typical value for inert materials) at the drift velocity of 0.3 m/s. At a drift velocity of 1 m/s it is about 0.006, and at 10 m/s it becomes as large as 0.06. As mentioned earlier, experimentalists often operate their systems at a drift velocity of the order of 1 m/s, so pumping may well be a significant reason for the loss of radicals and thus deviation of the atom density from Eq. 2.

Eq. 6 is just a rough but valuable approximation. It is impractical at high drift velocities, especially when the drift velocity is comparable to the maximal achievable value, i.e., sound velocity (about 340 m/s). In practice, plasma systems suitable for surface modification of materials do not operate under such extreme conditions, so Eq. 6 is a good approximation to estimate the loss of neutral reactive plasma species in plasma reactors made from inert materials.

The virtual recombination due to pumping becomes insignificant when the plasma reactor is not made from an inter material but materials of significant recombination coefficient. In such cases, the curves before the maxima in Figure 2 will not be steep, and the achievable density of atoms will depend predominantly on the discharge power. The power lost on the surface because of the heterogeneous surface recombination of atoms to parent molecules will be

$P_{rec}=\frac{1}{4}{n}_{\text{A}}\langle v\rangle W_{\text{D}}{A}_{\text{tot}}\gamma (8)$

Here, W_D is the dissociation energy of a molecule (for oxygen 5.2 eV), A_tot is the sum of areas of any plasma-facing object, including to-be-treated materials, and γ is the recombination coefficient. Power versus surface area is plotted in Figure 4 for the limiting case of total surface recombination, i.e., γ = 1, moderately large surface recombination, i.e., 0.1, and low total surface recombination at γ = 0.01 and 0.001 at the atom density of 10²⁰ m⁻³. This atom density is appropriate for the surface functionalization of many materials. From Figure 4, one can establish that only powerful discharges can sustain plasma with a reasonably large atom density in reactors made from non-inert materials. The recombination coefficient of 1 is the limiting case when the surfaces exhibit rich morphology [31], while coefficients between about 0.1 and 0.3 are typical for many metals of smooth morphology [32, 33].

FIGURE 4

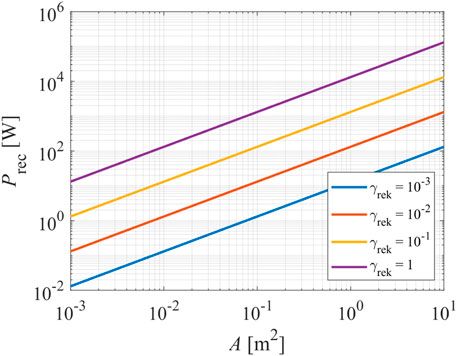
FIGURE 4. The power dissipated on the non-inert surfaces of a plasma reactor versus the geometrical area of any plasma-facing materials. The calculations are credible for O-atoms of the density of 10²⁰ m⁻³.

Rearranging Eq. 8 and explicitly expressing the atom density n_A, one can calculate the maximal achievable atom density in a plasma reactor versus the discharge power. The maximum density is plotted in Figure 5 for the case of oxygen atoms and a fully recombinative surface (γ = 1). Considerable discharge powers are needed when the plasma-facing materials exhibit a recombination coefficient of 1. Indeed, large densities of neutral reactive plasma species are not achievable at a reasonable discharge power if the materials facing plasma represent a perfect sink for the species.

FIGURE 5

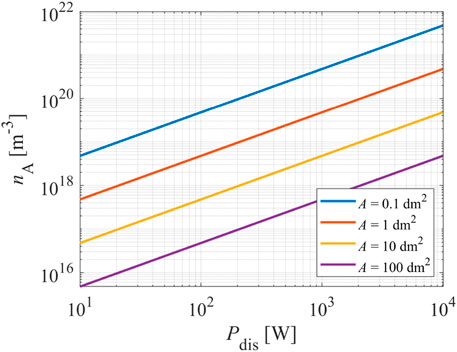
FIGURE 5. The theoretically achievable O-atom density in a plasma reactor of fully recombinative surfaces of surface area 0.1, 1, 10, 100 dm² versus the discharge power.

Eq. 8 and the corresponding graphs in Figures 4, 5 represent the theoretically minimal discharge power needed to sustain plasma of a specific density of neutral atoms. Namely, it was taken into account that all the discharge power is spent to dissociate gaseous molecules. This is not the case in practice because a part of the discharge power is used for ionization and some for radiation. Radiation from plasmas of hydrogen and oxygen is practically only in the VUV range (not visible to standard spectrometers), so it contributes significantly to the energy balance [22]. In a very rough approximation, the flux of VUV radiation from low-pressure gaseous plasma is of the same order as the flux of ions on the surface of plasma-facing materials [21, 22]. Therefore, the numerical values of the discharge power deduced from Figure 5 are underestimated but represent helpful guidance for constructing plasma reactors.

Furthermore, a significant recombination coefficient of a material treated by oxygen plasma will cause a gradient of O-atoms next to the surface. The gradients were elaborated in [34]. In fact, the gradients next to the catalytic materials will suppress the loss of atoms on surfaces, so the achievable O-atom density in the center of the plasma reactor will be more significant than is shown in Figure 5. The results shown in Figure 5 are therefore only for rough guidance.

Right from the maxima in Figure 2, the density of atoms decreases with increasing pressure. Solid lines terminate at a specific pressure where gaseous plasma can no longer be ignited or sustained using a given discharge power. More extensive power will generally expand the operable pressure range to higher values, but the dependence is not linear. At first, the density of atoms right from the maxima in Figure 2 decreases rather slowly, but when the pressure approaches the critical value, the decrease is rapid, and finally, the discharge is extinguished if the pressure is further increased. Therefore, the pressures right from the maxima are not very useful for practical applications. Here, it is worth mentioning that pressure in a plasma reactor may increase non-intentionally, for example, by desorption of volatile molecules from the surface of any material facing the plasma. Such desorption may cause the extinguishing of the discharge because the pressure has risen over the critical value. The power needed for igniting the discharge at a given pressure right from the maxima in Figure 2 is always larger than the power needed for sustaining plasma. If plasma cannot be ignited at the selected pressure, it is advisable to ignite the discharge at lower pressure and then increase pressure to the desired value. The plasma will probably shrink to a small volume at elevated pressure, but the O-atom density will still be reasonably large. The dissociation fraction, however, will decrease significantly with increasing pressure [35].

The absolute values of the atom density in a plasma reactor depend on numerous parameters. Figure 2 indicates that the density will increase monotonously with increasing discharge power. The peak value (at the maxima) can be estimated using rough theoretical estimations summarized in Equations 2, 6, 8 and Figures 3–5. In practice, however, it is advisable to measure the density of neutral reactive plasma species. The methods for measuring the O-atom density include actinometry [36], NO titration [37], NO₂ titration [38], VUV absorption spectroscopy [39], laser absorption spectroscopy [40], and catalytic probes [41].

Optimization of Plasma Reactors

The considerations presented in the upper text will be helpful at any attempt to construct a plasma reactor of the appropriate density of non-condensable molecular fragments such as neutral atoms. Usually, one seeks a reactor with the density of atoms as large as possible at the lowest possible discharge power. Best conditions are certainly met at the transition from the linearity before the maxima in Figure 2. The operation at the maximum gives some flexibility; if, for any reason, the pressure changes, the atom density should not change much in order to keep the processing parameters within the prescribed range.

Considering the results of Figure 3, it is evident that too much pumping will be detrimental to energy efficiency. As long as the interaction of atoms with the treated material is not extensive, it may be more beneficial to operate a plasma system at a moderate or relatively low effective pumping speed. On the other hand, if the neutral radicals interact chemically with the plasma-processed materials, they may be lost at the surface reactions and should be replaced by the continuous introduction of processing gas on one side of the reactor and pumping on the other. In such cases, more significant effective pumping speeds are needed to minimize the residence time in the discharge chamber and ensure rapid removal of the volatile reaction products.

The peak values in the curves of Figure 2 are often achieved in the pressure range from a few 10 Pa to a few 100 Pa. The pressure range dictates the selection of vacuum pumps. High vacuum pumps with maximal allowable pressure of a few Pa are ineffective unless a pressure reducer is mounted between the pump duct and the vacuum pump. The pressure reducer will suppress the effective pumping speed, so the high-vacuum pumps are not the best option. Pumps of ultimate pressure below, say, 1 Pa, and optimal pumping speed in the pressure range between a few 10 Pa to a few 100 Pa are a better and cost-efficient solution.

Considering Figures 4, 5, it is evident that plasma reactors should be constructed from inert materials to avoid excessive loss of atoms by heterogeneous surface recombination. One of the best materials are fluorinated polymers with a recombination coefficient as low as 10^–4 [42]. Polymers, however, are not the best materials used for building reactors, so they are rarely used in plasma technologies. A better choice is different types of glass and ceramic. Among glass, one of the best materials is fused silica (silicon dioxide), which is inert for many atoms except for some halogens. The recombination coefficient should be between 10^–4 and 10^–3 [30]. Soft glass may also be suitable, but the recombination coefficient for H-atoms on Pyrex increases significantly with increasing surface temperature, representing a definite detraction [43]. Likewise, ceramics are regarded as inert [44], but large reactors are rarely made from ceramics because of the surface roughness (which causes an increase in the surface loss of atoms) and porosity. Also, ceramics are opaque, preventing plasma monitoring by optical techniques such as spectroscopy and actinometry. One should avoid metals because the recombination coefficient is usually orders of magnitude larger than on inert materials. For example, the coefficient for most commonly used metal (stainless steel) is as large as 0.07 [32].

All inert materials are electrical insulators, limiting the type of discharges used to sustain gaseous plasmas. The best choice is an application of electrodeless radiofrequency discharges. Figure 6 represents a photo of a plasma reactor made from glass using such a discharge. The discharge tube length is 2 m, and the outer diameter is 20 cm. The pump duct is on the left side of the photo in Figure 6 (position 0 cm in Figure 7). Plasma is inductively coupled through a coil connected to the generator via a matching network. The matching network enables the adjustment of impedances between plasma and generator, and thus optimization of the energy efficiency. The density of oxygen atoms in such a reactor is plotted in Figure 7. The pressure was fixed to 44 Pa at the discharge forward power of 2.5 kW. Two curves are shown in Figure 7: one for the case of the continuous flow of oxygen at the rate of 300 sccm and the other without pumping and gas leakage (0 sccm). The density is relatively constant within the RF coil, i.e., in the range of distances between 50 and 150 cm, irrespective of pumping, because the effective pumping speed was only 40 m³/h and the drift velocity (Eq. 7) about 2 m/s. The constant density also persists in the volume between the coil and the pump duct. The virtual recombination coefficient of the pump duct was only 10^–2, so the O-atom density is not affected much by pumping under these conditions. The reason for the constant O-atom density outside the RF coil, i.e., at distances between 50 and 0 cm in Figure 7, is negligible loss of atoms by heterogeneous surface recombination on the glass tube.

FIGURE 6

FIGURE 6. A modern 2-m long plasma reactor powered with an inductively coupled RF discharge. Plasma is sustained in the air at the pressure of 20 Pa, and the discharge power of 3.5 kW.

FIGURE 7

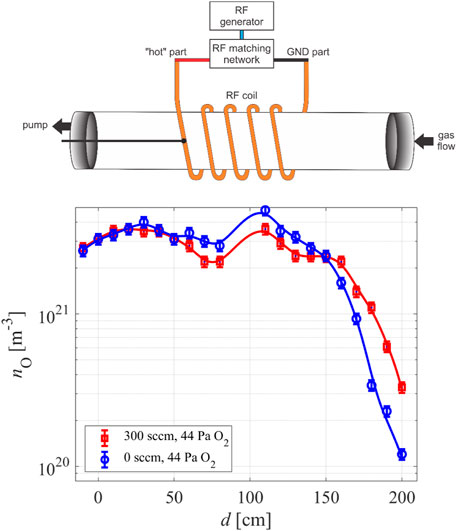
FIGURE 7. The density of O-atoms versus probe position in the reactor of Figure 6 with a schematic of the reactor (not to scale).

Surprisingly, the O-atom density at the positions between 150 and 200 cm in Figure 7 decreases with increasing distance, while this effect is not observed between positions 0 and 50 cm. The main reason is the capacitive coupling between the coil and flanges, which terminate the discharge tube. The capacitive coupling is rarely on both flanges. In our particular case, it appears between the hot part of the RF coil and the flange of the pump duct. On the other side, i.e., between the hot part of the RF coin and the flange where the gas inlet is mounted, the capacitive coupling is not effective enough to sustain the plasma, so the O-atom density decreases with increasing distance from the coil.

Conclusion

Neutral reactive plasma species play an important role in modifying the surface chemistry of solid materials. Apart from chemical reactions (surface functionalization, chemical etching), neutral reactive particles also tend to associate to form stable molecules. The surface association of atoms to parent molecules is called recombination. The probability depends on the type of material facing plasma, and it governs the density of atoms in the plasma reactor. If the recombination coefficients were zero, the density of atoms in the reactor would have been governed by the density of molecules in the source gas before igniting the discharge. Deviations from total dissociation of molecules are either due to the finite value of the recombination coefficient or pumping of the plasma reactor since the entrance to the pump ducts represents a virtual surface of the recombination coefficient, which depends on the gas drift velocity. The real recombination coefficients depend on the type of plasma-facing material and the surface finish, particularly the morphology. Reactors made from inert materials exhibit high atom density with a high dissociation fraction of source molecules and thus an optimal efficiency in terms of energy consumption. The electrodeless discharges are most effective for sustaining plasma of high atom density at moderate power. The density within the coil is reasonably constant, but in the volume between the coil and the flanges, it depends on the capacitive component of the coupling.

Author Contributions

GP conceived the manuscript, performed measurements, and wrote and reviewed the article.

Funding

This research was funded by the Slovenian Research Agency, project No. L2-9235 (Innovative configuration of inductively coupled gaseous plasma sources for up-scaling to industrial-size reactors) and core funding P2‐0082 (Thin‐film structures and plasma surface engineering).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Marchack N, Buzi L, Farmer DB, Miyazoe H, Papalia JM, Yan H, et al. Plasma Processing for Advanced Microelectronics beyond CMOS. J Appl Phys (2021) 130:080901. doi:10.1063/5.0053666

CrossRef Full Text | Google Scholar

2. Son H, Kim S, Lee JH, Li OL. Dye-synthesized N, S Co-doped Carbon via Plasma Engineering as Metal-free Oxygen Reduction Reaction Electrocatalysts. J Phys D: Appl Phys (2022) 55:074001. doi:10.1088/1361-6463/ac30ff

CrossRef Full Text | Google Scholar

3. Lin Y-C, Liang F-y., Fu C-k., Chang K-L. Removal of Isopropanol by Synergistic Non-thermal Plasma and Photocatalyst. J Hazard Mater (2022) 424:126874. doi:10.1016/j.jhazmat.2021.126874

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Liu B, Ji J, Zhang B, Huang W, Gan Y, Leung DYC, et al. Catalytic Ozonation of VOCs at Low Temperature: A Comprehensive Review. J Hazard Mater (2022) 422:126847. doi:10.1016/j.jhazmat.2021.126847

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Attri P, Tochikubo F, Park JH, Choi EH, Koga K, Shiratani M. Impact of Gamma Rays and DBD Plasma Treatments on Wastewater Treatment. Sci Rep (2018) 8:2926. doi:10.1038/s41598-018-21001-z

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Li F, Yang H, Ye Y, Jiang L, Zeng X, Zhao D, et al. One Zirconia-Based Ceramic Coating Strategy of Combustion Stabilization for Fuel-Rich Flames in a Small-Scale Burner. Fuel (2022) 310:122306. doi:10.1016/j.fuel.2021.122306

CrossRef Full Text | Google Scholar

7. Dong D, Zhang Y, Xiao Y, Wang T, Wang J, Gao W. Oxygen-enriched Coal-Based Porous Carbon under Plasma-Assisted MgCO3 Activation as Supercapacitor Electrodes. Fuel (2022) 309:122168. doi:10.1016/j.fuel.2021.122168

CrossRef Full Text | Google Scholar

8. Kawasaki T, Mitsugi F, Koga K, Shiratani M. Local Supply of Reactive Oxygen Species into a Tissue Model by Atmospheric-Pressure Plasma-Jet Exposure. J Appl Phys (2019) 125:213303. doi:10.1063/1.5091740

CrossRef Full Text | Google Scholar

9. Packer JR, Hirst AM, Droop AP, Adamson R, Simms MS, Mann VM, et al. Notch Signalling Is a Potential Resistance Mechanism of Progenitor Cells within Patient‐derived Prostate Cultures Following ROS‐inducing Treatments. FEBS Lett (2020) 594:209–26. doi:10.1002/1873-3468.13589

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Shaw P, Kumar N, Kwak HS, Park JH, Uhm HS, Bogaerts A, et al. Bacterial Inactivation by Plasma Treated Water Enhanced by Reactive Nitrogen Species. Sci Rep (2018) 8:11268. doi:10.1038/s41598-018-29549-6

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sruthi NU, Josna K, Pandiselvam R, Kothakota A, Gavahian M, Mousavi Khaneghah A. Impacts of Cold Plasma Treatment on Physicochemical, Functional, Bioactive, Textural, and Sensory Attributes of Food: A Comprehensive Review. Food Chem (2022) 368:130809. doi:10.1016/j.foodchem.2021.130809

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Puač N, Škoro N, Spasić K, Živković S, Milutinović M, Malović G, et al. Activity of Catalase Enzyme in Paulownia Tomentosa Seeds during the Process of Germination after Treatments with Low Pressure Plasma and Plasma Activated Water. Plasma Process Polym (2018) 15:1700082. doi:10.1002/ppap.201700082

CrossRef Full Text | Google Scholar

13. Attri P, Ishikawa K, Okumura T, Koga K, Shiratani M. Plasma Agriculture from Laboratory to Farm: A Review. Processes (2020) 8:1002. doi:10.3390/pr8081002

CrossRef Full Text | Google Scholar

14. Attri P, Koga K, Okumura T, Shiratani M. Impact of Atmospheric Pressure Plasma Treated Seeds on Germination, Morphology, Gene Expression and Biochemical Responses. Jpn J Appl Phys (2021) 60:040502. doi:10.35848/1347-4065/abe47d

CrossRef Full Text | Google Scholar

15. Filipić A, Dobnik D, Tušek Žnidarič M, Žegura B, Štern A, Primc G, et al. Inactivation of Pepper Mild Mottle Virus in Water by Cold Atmospheric Plasma. Front Microbiol (2021) 12:12. doi:10.3389/fmicb.2021.618209

CrossRef Full Text | Google Scholar

16. Saloum S, Abou Shaker S, Alwazzeh M, Hussin R. Polymer Surface Modification Using He/O 2 RF Remote Low‐pressure Plasma. Surf Interf Anal (2021) 53:754–61. doi:10.1002/sia.6976

CrossRef Full Text | Google Scholar

17. Foucher M, Marinov D, Carbone E, Chabert P, Booth J-P. Highly Vibrationally Excited O2molecules in Low-Pressure Inductively-Coupled Plasmas Detected by High Sensitivity Ultra-broad-band Optical Absorption Spectroscopy. Plasma Sourc Sci. Technol. (2015) 24:042001. doi:10.1088/0963-0252/24/4/042001

CrossRef Full Text | Google Scholar

18. Wijaikhum A, Schröder D, Schröter S, Gibson AR, Niemi K, Friderich J, et al. Absolute Ozone Densities in a Radio-Frequency Driven Atmospheric Pressure Plasma Using Two-Beam UV-LED Absorption Spectroscopy and Numerical Simulations. Plasma Sourc Sci. Technol. (2017) 26:115004. doi:10.1088/1361-6595/aa8ebb

CrossRef Full Text | Google Scholar

19. Zaplotnik R, Primc G, Paul D, Mozetič M, Kovač J, Vesel A. Atomic Species Generation by Plasmas. In: Plasma Applications for Material Modification. New York: Jenny Stanford Publishing (2021). p. 107–76. doi:10.1201/9781003119203-4

CrossRef Full Text | Google Scholar

20. Booth J-P, Mozetič M, Nikiforov A, Oehr C. Foundations of Plasma for Surface Functionalisation of Polymers for Industrial and Bio Applications. Plasma Sourc Sci Technol (2022). in press.

Google Scholar

21. Niemi K, O'Connell D, de Oliveira N, Joyeux D, Nahon L, Booth JP, et al. Absolute Atomic Oxygen and Nitrogen Densities in Radio-Frequency Driven Atmospheric Pressure Cold Plasmas: Synchrotron Vacuum Ultra-violet High-Resolution Fourier-Transform Absorption Measurements. Appl Phys Lett (2013) 103:034102. doi:10.1063/1.4813817

CrossRef Full Text | Google Scholar

22. Fantz U, Briefi S, Rauner D, Wünderlich D. Quantification of the VUV Radiation in Low Pressure Hydrogen and Nitrogen Plasmas. Plasma Sourc Sci. Technol. (2016) 25:045006. doi:10.1088/0963-0252/25/4/045006

CrossRef Full Text | Google Scholar

23. Kramida A, Ralchenko Y, Reader J. Atomic Spectra Database, NIST Standard Reference Database 78 (2021). version 5.9. doi:10.18434/T4W30F

CrossRef Full Text | Google Scholar

24. Longo RC, Ranjan A, Ventzek PLG. Density Functional Theory Study of Oxygen Adsorption on Polymer Surfaces for Atomic-Layer Etching: Implications for Semiconductor Device Fabrication. ACS Appl Nano Mater (2020) 3:5189–202. doi:10.1021/acsanm.0c00618

CrossRef Full Text | Google Scholar

25. Vesel A, Zaplotnik R, Mozetič M, Primc G. Surface Modification of PS Polymer by Oxygen-Atom Treatment from Remote Plasma: Initial Kinetics of Functional Groups Formation. Appl Surf Sci (2021) 561:150058. doi:10.1016/j.apsusc.2021.150058

CrossRef Full Text | Google Scholar

26. Recek N, Vesel A, Zaplotnik R, Paul D, Primc G, Gselman P, et al. Hydrophilization of Corn Seeds by Non-equilibrium Gaseous Plasma. Chem Biol Technol Agric (2021) 8:1–11. doi:10.1186/s40538-021-00231-w

CrossRef Full Text | Google Scholar

27. Uchida S, Yoshida T, Tochikubo F. Numerical Simulation of Physicochemical Interactions between Oxygen Atom and Phosphatidylcholine Due to Direct Irradiation of Atmospheric Pressure Nonequilibrium Plasma to Biological Membrane with Quantum Mechanical Molecular Dynamics. J Phys D: Appl Phys (2017) 50:395203. doi:10.1088/1361-6463/aa84ee

CrossRef Full Text | Google Scholar

28. Vesel A, Kolar M, Doliska A, Stana-Kleinschek K, Mozetic M. Etching of Polyethylene Terephthalate Thin Films by Neutral Oxygen Atoms in the Late Flowing Afterglow of Oxygen Plasma. Surf Interf Anal. (2012) 44:1565–71. doi:10.1002/sia.5064

CrossRef Full Text | Google Scholar

29. Guerra V, Tejero-del-Caz A, Pintassilgo CD, Alves LL. Modelling N2-O2 Plasmas: Volume and Surface Kinetics. Plasma Sourc Sci. Technol. (2019) 28:073001. doi:10.1088/1361-6595/ab252c

CrossRef Full Text | Google Scholar

30. Booth JP, Guaitella O, Chatterjee A, Drag C, Guerra V, Lopaev D, et al. Oxygen (3P) Atom Recombination on a Pyrex Surface in an O2 Plasma. Plasma Sourc Sci. Technol. (2019) 28:055005. doi:10.1088/1361-6595/ab13e8

CrossRef Full Text | Google Scholar

31. Mozetic M, Vesel A, Stoica SD, Vizireanu S, Dinescu G, Zaplotnik R. Oxygen Atom Loss Coefficient of Carbon Nanowalls. Appl Surf Sci (2015) 333:207–13. doi:10.1016/j.apsusc.2015.02.020

CrossRef Full Text | Google Scholar

32. Mozetič M, Zalar A. Recombination of Neutral Oxygen Atoms on Stainless Steel Surface. Appl Surf Sci (2000) 158:263–7. doi:10.1016/S0169-4332(00)00007-6

CrossRef Full Text | Google Scholar

33. Cauquot P, Cavadias S, Amouroux J. Thermal Energy Accommodation from Oxygen Atoms Recombination on Metallic Surfaces. J Thermophys Heat Transfer (1998) 12:206–13. doi:10.2514/2.6323

CrossRef Full Text | Google Scholar

34. Primc G, Mozetič M. Neutral Reactive Gaseous Species in Reactors Suitable for Plasma Surface Engineering. Surf Coat Tech (2019) 376:15–20. doi:10.1016/j.surfcoat.2018.11.103

CrossRef Full Text | Google Scholar

35. Liu Z, Li S, Chen Q, Yang L, Wang Z. Measurement of the O2Dissociation Fraction in RF Low Pressure O2/Ar Plasma Using Optical Emission Spectrometry. Plasma Sci Technol (2011) 13:458–61. doi:10.1088/1009-0630/13/4/14

CrossRef Full Text | Google Scholar

36. Booth JP, Sadeghi N. Oxygen and Fluorine Atom Kinetics in Electron Cyclotron Resonance Plasmas by Time‐resolved Actinometry. J Appl Phys (1991) 70:611–20. doi:10.1063/1.349662

CrossRef Full Text | Google Scholar

37. Ricard A, Gaillard M, Monna V, Vesel A, Mozetic M. Excited Species in H2, N2, O2 Microwave Flowing Discharges and post-discharges. Surf Coat Tech (2001) 142-144:333–6. doi:10.1016/S0257-8972(01)01276-2

CrossRef Full Text | Google Scholar

38. Den S, O'Keeffe P, Hayashi Y, Ito M, Hori M, Goto T. Development and Characterization of a New Compact Microwave Radical Beam Source. Jpn J Appl Phys (1997) 36:4588–92. doi:10.1143/JJAP.36.4588

CrossRef Full Text | Google Scholar

39. Matsushima K, Ide T, Takeda K, Hori M, Yamashita D, Seo H, et al. Densities and Surface Reaction Probabilities of Oxygen and Nitrogen Atoms during Sputter Deposition of ZnInON on ZnO. IEEE Trans Plasma Sci (2017) 45:323–7. doi:10.1109/TPS.2016.2632124

CrossRef Full Text | Google Scholar

40. Baeva M, Luo X, Pfelzer B, Repsilber T, Uhlenbusch J. Experimental Investigation and Modelling of a Low-Pressure Pulsed Microwave Discharge in Oxygen. Plasma Sourc Sci. Technol. (2000) 9:128–45. doi:10.1088/0963-0252/9/2/305

CrossRef Full Text | Google Scholar

41. Babič D, Poberaj I, Mozetič M. Fiber Optic Catalytic Probe for Weakly Ionized Oxygen Plasma Characterization. Rev Scientific Instr (2001) 72:4110–4. doi:10.1063/1.1409567

CrossRef Full Text | Google Scholar

42. Zaplotnik R, Vesel A, Mozetič M. Atomic Oxygen and Hydrogen Loss Coefficient on Functionalized Polyethylene Terephthalate, Polystyrene, and Polytetrafluoroethylene Polymers. Plasma Process Polym (2018) 15:1800021. doi:10.1002/ppap.201800021

CrossRef Full Text | Google Scholar

43. Mozetic M, Vesel A, Drenik A, Poberaj I, Babic D. Catalytic Probes for Measuring H Distribution in Remote Parts of Hydrogen Plasma Reactors. J Nucl Mater (2007) 363-365:1457–60. doi:10.1016/j.jnucmat.2007.01.206

CrossRef Full Text | Google Scholar

44. Li N, Hu P, Xing PF, Ke B. Catalytic Properties of ZrB2-SiC-W Ultra-high Temperature Ceramics at Moderate Temperatures. IOP Conf Ser Mater Sci Eng (2019) 479:012067. doi:10.1088/1757-899X/479/1/012067

CrossRef Full Text | Google Scholar