Electric Field Enhancement Effect of Aluminum Grating With Nanosecond Pulsed Laser Irradiation

Aluminum grating has wide applications in laser systems and photoelectric equipment. Research on the laser damage characteristics of aluminum grating has guiding significance and application value for improving the laser damage resistance. The aim of this study is to investigate the characteristics of damage induced by nanosecond pulsed lasers on the aluminum grating. To better understand the laser damage characteristics of aluminum grating, herein, Maxwell’s equations were numerically solved according to the finite difference time-domain method, and the electric field model of 1,064 nm Gaussian laser damage aluminum grating was established. The simulation results showed that the light field is modulated by the grating; furthermore, the maximum value of the electric field occurred at the ridge of the grating when the laser is irradiated vertically. Analysis suggested that the electric field distribution is in accordance with the laser energy distribution, and the distribution region of the maximum electric field is a vulnerable location. To further verify the local electric field enhancement effect, based on the 1-on-1 laser damage measurement method, an experimental study of the nanosecond laser (@1,064 nm, 6.5 ns) damage to the aluminum grating was carried out. Moreover, the damage morphology was analyzed using a scanning electron microscope (SEM), and the simulation results showed good agreement with the experimental results.

1 Introduction

In recent years, with the development of high-peak intensity laser technology [1–4], the interaction between laser and film materials has become an important topic for scholars [5–10]. On the one hand, the diffraction gratings are an important pulse compression element in the high-peak power laser system [11–13], and its laser-induced damage threshold (LIDT) limits the laser energy output and affects the operational cost of refurbishment or replacement of the optics. On the other hand, the gratings whose general structure is to deposit films on a glass substrate with regular grooves on the surface of the film play a critical role in spectroscopy equipment. In laser systems and photoelectric imaging equipment, to achieve an optimal design of gratings and the practical value for high-power laser systems, it is highly important to study the laser damage characteristic and mechanism of gratings.

For thin film structure materials, the electric field enhancement effect could easily induce frequent damage at some locations, such as the nodule defects [14], impurities, contaminations [15], and the interface between the substrate and the thin film, which will generally expand the damaged area. The influence of these factors will significantly decrease the LIDT of the thin film. Compared to the thin film, the grating is a surface relief structure formed on the surface of the thin film. Ignoring the contamination and defects introduced in the processing, the periodic structure of the grating itself has a modulation effect on the light field; meanwhile, the redistribution of the light field also determines the position where damage is more likely to occur during laser irradiation. Many studies have focused on the multilayer dielectric gratings in the fs [14, 16, 17] or ps regimes [18, 19]. For ultrashort pulsed lasers, initially, the back edges of the grating pillar, which is in correspondence with the electric field intensity maximum, incurred damage [20]. However, there are few reports on the damage characteristics of nanosecond pulsed laser on the aluminum grating. In addition, the incident angle between the laser and the material has an important influence on LIDT, which is closely related to the maximum value of the electric field [21]. Previous studies have shown that when the laser is incident obliquely, the electric field of the grating is stronger at the gate ridge opposite to the incident direction [20, 22], forming a burr structure [23]. In the practical application process, the situation of the normal incidence of the laser must also be considered. It is crucial to explore the influence of the redistribution of the optical field of the grating and the damage characteristics by the electric field induced by the gratings under the condition of the normal incidence of the laser. Furthermore, the characteristics of laser damage induced by electric field enhancement of aluminum film grating need to be further clarified.

In this work, to study the damage characteristics of the aluminum grating irradiated by laser, we used the finite difference time-domain (FDTD) method to solve Maxwell’s equation and numerically simulated the electric field distribution of the aluminum grating. To verify the simulation result, the single pulse damage induced by the nanosecond laser (@1,064 nm, 6.5 ns) on the aluminum grating was experimentally studied; the experimental damage morphology was found to be in good agreement with the simulated electric field distribution.

2 Simulation Method

Nanosecond pulsed laser damage of aluminum grating involves complex damage mechanisms. It is difficult to reveal damage mechanism and characteristics of aluminum grating only through experimental research. A laser is a type of electromagnetic wave; the distribution of the electric field, which determines the energy distribution of the laser to some extent, is modulated by the periodic structure of the grating when the grating is irradiated. Therefore, to deepen the understanding of damage characteristics of an aluminum film by laser @1,064 nm, in this section, we simulated the electric field distribution of 1,064 nm Gaussian laser irradiating the aluminum grating from a microscopic point of view and explored the influence of laser field on the grating damage characteristics.

2.1 Electric Field Model

Based on the FDTD method, we simulate the electric field of 1,064 nm Gaussian laser-irradiated aluminum film grating. Before we started modeling, we made the following assumptions: 1) the grating is ideal without considering defects, impurities, pollution, etc.; 2) the grating ridge is rectangular; and 3) the Gaussian beam waist radius is set to 300 um, and the grating line density is 1800 gr/mm. Owing to the size difference between the spot diameter and the grating period of the order of 10³, it is computationally intensive to completely simulate the entire region of laser action. Thus, from a microscopic point of view, we only simulate the electric field distribution of four grating ridges in the laser action center to reveal the influence of grating electric field distribution on laser damage morphology.

The three-dimensional model of the aluminum grating irradiated by 1,064 nm Gaussian laser is established, as shown in Figure 1, which only calculated the 3D model of four grids to save computer resources. Based on our actual grating samples (introduced in the third section), the grating period is 555 nm, the duty cycle is 0.7, the remaining layer thickness is 20 nm, and the ridge height is 105 nm. Because the real substrate thickness of gratings is 6 mm, the sum of the heights of the residual layers and ridges is 125 nm. Owing to the difference in thickness, on the one hand, the original scale modeling is inconvenient to show the results. On the other hand, as we focus on damage to the grating structure, the gratings could be considered as functionally damaged, and the use of the original proportional modeling results in wastage of computing resources. Therefore, we only calculate and simulate the electric field distribution of the substrate film interface and grating structure. The (n, k) parameters of air and the aluminum film are (1,0) and (1.3763, 10.245) @1064 nm [24], respectively. The parameters of the K9 glass are taken from the material library of CDGM H-K9L. Next, boundary conditions are set as shown in Figure 1. The periodic boundary conditions (PBS) are set in the x and y directions to simulate the periodic structure. The perfect matching layer (PML) is set in the z-direction; the boundary of the perfect matching layer is at least half a wavelength away from the object. At the top of the grating, the laser is incident vertically, and the beam waist radius of the Gaussian beam is 300 μm; the laser action position is (0, 0, 6000125 nm), and the grid element and precision are 2 nm and 8, respectively.

FIGURE 1

FIGURE 1. Electric field model of the grating.

Furthermore, Maxwell’s equations are solved numerically based on FDTD, as shown in Eq. 1, and vector E represents the electrical field; μ_r and ε_r are the relative permittivity and the relative permeability, respectively; and k₀ is the wavenumber of free space, and its expression is shown in Eq. 2, where ω, ε₀, and μ₀ are the angular frequency, permittivity of free space, and permeability of free space, respectively. c₀ is the speed of the wave in free space.

$\frac{\nabla \mathit{E}}{{\mu }_r}-k_0^2{\epsilon }_r\mathit{E}=0,(1)$

$k_0=\frac{\omega }{c_0}=\omega \sqrt{{\epsilon }_0{\mu }_0}.(2)$

2.2 Simulation Results

The calculation results are shown in Figure 2. Figures 2A,C are the x-z sections of |E| and |E|² along the y = 0 direction, respectively. Figures 2B,D are the x-y sections of |E| and |E|² on the grating surface, respectively. It can be seen from Figure 2 that the maximum value of the |E| or |E|² appeared at the ridge angle of the grid ridge. The simulation results of the electric field distribution show that the grating modulates and distributes the light field when the laser is irradiated vertically on the surface of the grating, which results in local electric field enhancement at the ridge corner of the aluminum grating. The position of the maximum electric field represents the position of the maximum light intensity, which implies that damage is most likely to occur at the ridge corner of the grating.

FIGURE 2

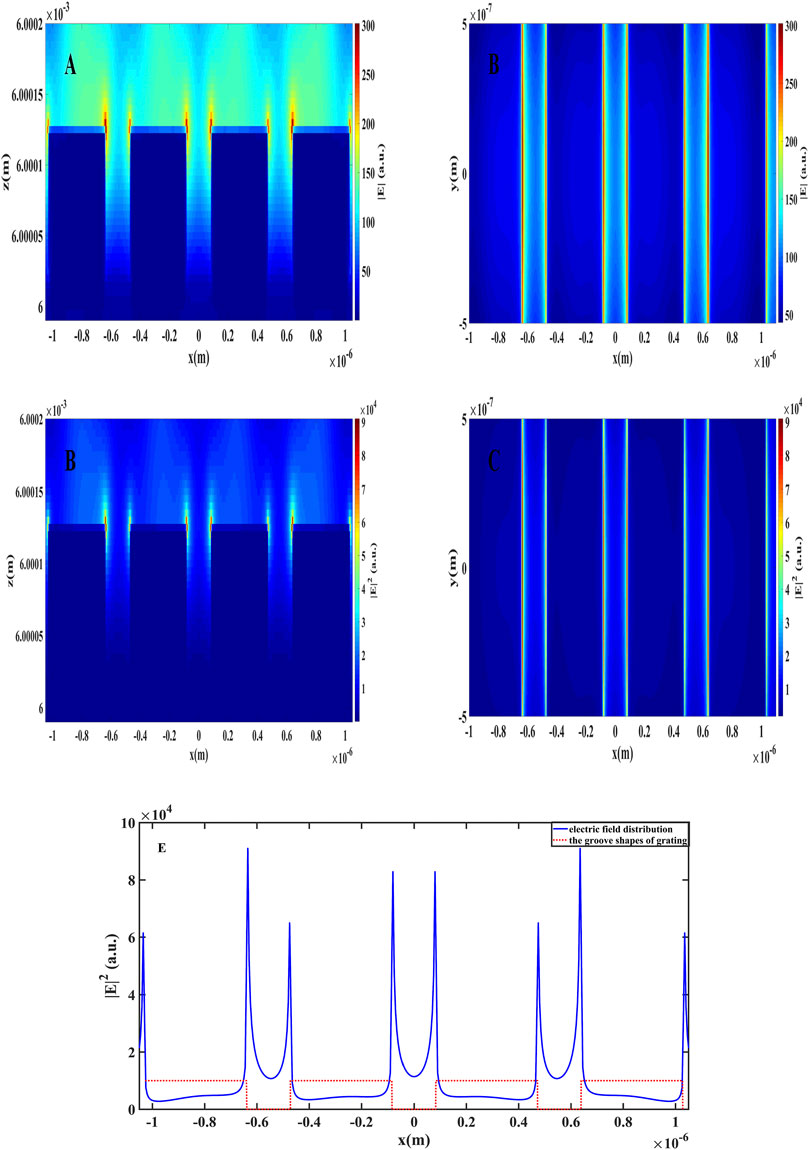
FIGURE 2. Electric field distribution of aluminum grating: (A) electric field of the x-z plane (y = 0); (B) electric field of the x-y plane (z = 6000125 nm); (C) |E|² distribution of the x-z plane; (D) |E|² distribution of the x-y plane (z = 6000125 nm); and (E) |E|² distribution in the x direction (y = 0 nm, z = 6000125 nm).

Figure 2E shows the electric field distribution of the four ridges in the center of the top layer of the grating along the x-axis. The solid blue line shown in Figure 2E represents the change in the electric field of the ridge along the x-direction, and the red dashed line represents the raster ridge outline. It shows that the curve of |E|² is axisymmetrically distributed at the center of laser action x = 0, representing the same electric field at the same position from the laser center. With the periodic structure of the grating, the electric field is distributed periodically, and the square of the electric field mode at the edge of the grating ridge is significantly larger than that in the middle region of the grid. This indicates a significant electric field enhancement at the ridge corner that is consistent with the results given in Figures 2A–D.

As a Gaussian electromagnetic wave, the electric field distribution in the optical structure of the laser reflects the energy distribution of the laser. The relation between the laser intensity and the electric field amplitude of the incident laser can be expressed as Eq. 3 [25].

$I\left(t\right)=\frac{1}{2}c{n}_0{\epsilon }_0{\left|\mathit{E}\left(t\right)\right|}^2,(3)$

where n₀ is the refractive index of the dielectric at the central frequency of the incident laser and ε₀ is the permittivity of free space.

3 Experiment

3.1 Experimental Setup

To verify the electric field model and explore the damage characteristics of the aluminum grating with nanosecond pulsed laser irradiation, we carried out an experimental study. The experimental device is shown in Figure 3.

FIGURE 3

FIGURE 3. Diagram of the experimental setup of nanosecond laser damage to the gratings.

The nanosecond pulsed laser system (@1,064 nm, 6.5 ns, 10 Hz, maximum single pulse energy 900 mJ) produced by Beamtech Optronics Co., Ltd. in China was used; this system has an energy stability (RMS) of ≤1%. The emitted laser energy is adjusted by an attenuator consisting of a half-wave plate and a polarizer. The reflected beam split by the beam splitter reaches the energy meter (Ophir, PE50-DIF-C), which is used for the real-time monitoring of energy to the target vertically. The transmitted beam is focused at the center of the target surface through the plane convex lens (f = 100 mm). Using the knife-edge method test, the waist radius of the nanosecond Gaussian beam is found to be 300 μm. The gratings are placed on a three-dimensional displacement platform (1 μm accuracy), and the position of laser action can be precisely controlled by a computer. Damage is monitored by online plasma flash detection and a charge-coupled device (CCD). The dust from the surface of the sample is cleaned before the experiment begins. The experiment was carried out in the air under 10000-level laboratory conditions. Based on the 1-on-1 damage threshold test method, the damage morphology was tested at 10 points under the same energy density. The laser fluence was gradually increased, and the damage morphology was observed using a Nomarski microscope (EB-4, produced by Taiwan Yiye International Co., LTD., with a total magnification of 200X) and SEM (S-4800, produced by HITACHI, Japan, maximum magnification is 20000X). The definition of LIDT is according to LIDT ISO 21254 standards [26]. Damage is defined to be a visible change in the surface morphology under the offline microscope. Here, owing to the uncertainties in laser energy measurement and facula effective area measurement, the relative error of the damage threshold by measurement is assessed closer to 3%.

3.2 Aluminum Grating

The aluminum gratings were designed to have a groove density of 1800 gr/mm and were produced by the National Engineering Research Center for Diffraction Gratings Manufacturing and Application in China. A resin glue of 30 μm thickness was spun onto 40 × 40 × 6 mm³ K9 glass substrates. A 125-nm-thick aluminum film of 99.9999% purity was used to fabricate the surface relief grating structure using E-beam evaporation. The photo-resistant material was spun onto the aluminum film, a photo-resistant grating structure was manufactured using a holographic method, and the structures of the photo-resistant gratings were transferred to the aluminum film layer by reactive ion beam etching. Finally, gratings with a diffraction efficiency of 70% were made. It can be seen that the grid lines in Figure 4 are clear and continuous.

FIGURE 4

FIGURE 4. SEM image of aluminum film grating.

3.3 Experimental Results

To analyze the damage morphology under different laser energy densities, we carried out a parametric scan of the laser energy density based on the experimental research in Section 3. With the change in the energy density of the single pulse of the applied laser, the grid incurred different degrees of damage. The damage probability is 100% at 0.67 J/cm² and 0% at 0.63 J/cm². The continued reduction of the laser resulted in no damage to the energy density.

In this section, to verify the effectiveness of the model and reveal the influence of the electric field enhancement effect on laser damage, the damage morphologies were compared and analyzed based on the experimental research in Section 3. To study the grid damage, we focused on the damage morphology of 0.67 J/cm², as shown in Figure 5.

FIGURE 5

FIGURE 5. Damage morphology of aluminum grating under a laser energy density of 0.67 J/cm².

Figure 5 shows the micro-damage morphology of grating ridges, which was measured experimentally. Figure 5A is the overall damage morphology measured at a laser energy density of 0.67/cm². Figures 5B and C are the SEM images that are magnified 5000X from the central and the edge of the damaged region in Figure 5A. Figure 5D is magnified 20000X of the marginal damaged area. Comparing Figures 5B and C, it can be found that owing to the energy distribution of the Gaussian laser, the degree of damage to the grid in the damaged area is reduced from the center to the edge. Figure 5D from right to left indicates the direction away from the laser action position, and it can be found that damage can easily occur at the corner of the ridge. Furthermore, the damage morphology at the gate ridge was observed, and it was found that the main damage mechanism of nanosecond laser damage to the aluminum grating was thermal-induced film peeling and ablation. The electric field distribution determines the energy distribution of the laser in the grating, and it leads to preferential ablation at the corner of the grid ridge.

4 Discussion

In this section, we will compare the experimental and simulation results to verify the local electric field enhancement effect of the grating ridge. Figure 4 shows the grating without laser damage, and it shows that the grating has clear and regular grid lines. Compared with the damaged morphology vertically irradiated by the laser, as shown in Figure 5D, it can be found that the grating grid was damaged. The grid damage was more serious in areas closer to the center of the laser spot; the damage location was at the edge of the grid ridge. This morphology is consistent with the conclusion given in Figure 2 of the electric field simulation results. The main reason for damage is that when the laser irradiates the grating surface vertically, the Gaussian distribution of the laser light field is modulated by the grating structure. Consequently, the electric field is locally enhanced at the ridge angle of the grating, and the distribution of the electric field represents the distribution of laser energy. Therefore, the density of laser energy is high at the ridge angle of the grating. Under the same irradiation conditions, the ridge corner area of the grid ridge preferentially reaches the melting point of the material, which results in the occurrence of ablation and spalling.

To achieve high diffraction efficiency, there is an optimal incidence angle of grating in the process of grating design and research. For the research of grating laser damage, more emphasis has been placed on the oblique incidence of laser; however, the vertical incidence of laser is also important in the process of practical application. Laurent Gallais et al. conducted an electrical simulation on the grating waveguide structure irradiated by laser and found that when the laser is in oblique incidence, it is easy to form a burr structure at the rear edge of the excitation incidence direction owing to the electric field enhancement effect [23]. Lingyun Xie studied the laser oblique incidence rectangular multilayer dielectric grating and clearly verifies that damage initiates at the edge of the grating pillars where the maximum EFI exists [20]. These studies show that the grating ridge area could be easily damaged by the laser, and the maximum value of the electric field corresponds to the position of LIDT, which is similar to the conclusion given in this study. The result of this study is that when the laser is vertically incident, there is the maximum value of the electric field at the ridge angle of the grating ridge, which makes it highly prone to laser damage. Therefore, compared to existing research, the present research work is credible and meets the requirements for practical applications.

5 Conclusion

The aim of this study was to explore the characteristics of damage induced by nanosecond pulsed laser on the aluminum grating. First, FDTD was used to numerically solve the electric field distribution of nanosecond laser-irradiated aluminum grating, wherein it was found that the local electric field enhancement effect occurred in corner of the ridges of the grating. Second, to verify the local enhancement effect at the corner of the grating ridge, an experimental study of nanosecond laser (@1,064 nm, 6.5 ns) damage to the aluminum grating was carried out based on the 1-on-1 laser damage measurement method. The results suggest that damage could easily occur at the grating ridges. The reason for analysis is that the modulation of the electric field by the grating makes the laser energy redistribute on the surface of the grating, which makes the film layer highly prone to ablation and peeling at the ridge angle of the gate ridge. It has good consistency with the electric field simulation of the aluminum grating. Our research results have guided significance for the design of grating and military application. This method will be further developed by considering more influencing factors, such as impurity, defects, and contamination.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

JW was the main author and was responsible for the first draft of the manuscript. All authors provided reviews and comments on the subsequent versions of the manuscript. JW was responsible for a theoretical simulation, acquisition of theoretical data, and analysis of results. CZ analyzed and guided the experiment. FC contributed to the writing and structure of the thesis. KZ, JY, YZ, and YJ explained the results and provided suggestions to improve the manuscript. GJ, WZ, and WL provide guidance on grating and grating theory knowledge. All of the authors read and approved the final manuscript.

Funding

The study was supported by the Major Innovation Project of CIOMP, CAS (E10302Y3M0), Fund project of the State Key Laboratory of Laser-Matter Interaction (SKLLIM1904), National Natural Science Foundation (61904178), Member of the Youth Innovation Promotion Association of the Chinese Academy of Sciences (2020227), and Funding of “Xuguang Talents” from CIOMP, National Natural Science Foundation of China (General Program 62075216).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors also gratefully acknowledge the National Engineering Research Center for Diffraction Gratings Manufacturing and Application to support the samples.

References

1. Salamin YI, Carbajo S. A Simple Model for the fields of a Chirped Laser Pulse with Application to Electron Laser Acceleration. Front Phys (2019) 7:2. doi:10.3389/fphy.2019.00002

CrossRef Full Text | Google Scholar

2. Qi P, Luo Y, Shi B, Li W, Liu D, Zheng L, et al. Phonon Scattering and Exciton Localization: Molding Exciton Flux in Two Dimensional Disorder Energy Landscape. eLight (2021) 1:2. doi:10.1186/s43593-021-00006-8

CrossRef Full Text | Google Scholar

3. Liu X, Ma Y. Sensitive Carbon Monoxide Detection Based on Light-Induced Thermoelastic Spectroscopy with a Fiber-Coupled Multipass Cell [Invited]. Chin Opt Lett (2022) 20(3):031201. doi:10.3788/COL202220.031201

CrossRef Full Text | Google Scholar

4. Strickland D. Nobel Lecture: Generating High-Intensity Ultrashort Optical Pulses. Rev Mod Phys (2019) 91(3). doi:10.1103/RevModPhys.91.030502

CrossRef Full Text | Google Scholar

5. Lozhkarev VV, Freidman GI, Ginzburg VN, Katin EV, Khazanov EA, Kirsanov AV, et al. 200 TW 45 Fs Laser Based on Optical Parametric Chirped Pulse Amplification. Opt Express (2006) 14(1):446–54. doi:10.1364/OPEX.14.000446

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Hitaishi VP, Mazurenko I, Vengasseril Murali A, de Poulpiquet A, Coustillier G, Delaporte P, et al. Nanosecond Laser-Fabricated Monolayer of Gold Nanoparticles on ITO for Bioelectrocatalysis. Front Chem (2020) 8:431. doi:10.3389/fchem.2020.00431

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Xie C, Meyer R, Froehly L, Giust R, Courvoisier F. In-situ Diagnostic of Femtosecond Laser Probe Pulses for High Resolution Ultrafast Imaging. Light Sci Appl (2021) 10(1):1–13. doi:10.1038/s41377-021-00562-1

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Jiang L, Wang A-D, Li B, Cui T-H, Lu Y-F. Electrons Dynamics Control by Shaping Femtosecond Laser Pulses in Micro/nanofabrication: Modeling, Method, Measurement and Application. Light Sci Appl (2018) 7(2):17134. doi:10.1038/lsa.2017.134

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Nakamura A, Mizuta T, Shimotsuma Y, Sakakura M, Otobe T, Shimizu M, et al. Picosecond Burst Pulse Machining with Temporal Energy Modulation [Invited]. Chin Opt Lett (2020) 18(12):123801. doi:10.3788/COL202018.123801

CrossRef Full Text | Google Scholar

10. Zhang W, Fu S, Kong W, Wang G, Xing F, Zhang F, et al. Review of Pulse Compression Gratings for Chirped Pulse Amplification System. Opt Eng (2021) 60(2):020902. doi:10.1117/1.Oe.60.2.020902

CrossRef Full Text | Google Scholar

11. Zhou C. Chirped Pulse Amplification: Review and Prospective from Diffractive Optics [Invited]. Chin Opt Lett (2020) 18(11):110502. doi:10.3788/COL202018.110502

CrossRef Full Text | Google Scholar

12. Lang Z, Qiao S, Ma Y. Acoustic Microresonator Based In-Plane Quartz-Enhanced Photoacoustic Spectroscopy Sensor with a Line Interaction Mode. Opt Lett (2022) 47(6):1295–8. doi:10.1364/OL.452085

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ma Y, Hu Y, Qiao S, Lang Z, Liu X, He Y, et al. Quartz Tuning forks Resonance Frequency Matching for Laser Spectroscopy Sensing. Photoacoustics (2022) 25:100329. doi:10.1016/j.pacs.2022.100329

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zou X, Kong F, Jin Y, Chen P, Chen J, Xu J, et al. Influence of Nodular Defect Size on Metal Dielectric Mixed Gratings for Ultra-short Ultra-high Intensity Laser System. Opt Mater (2019) 91:177–82. doi:10.1016/j.optmat.2019.02.027

CrossRef Full Text | Google Scholar

15. Liu F, Jiao H, Ma B, Paschel S, Balasa I, Ristau D, et al. Influence of the Surface and Subsurface Contaminants on Laser-Induced Damage Threshold of Anti-reflection Sub-wavelength Structures Working at 1064 Nm. Opt Laser Technology (2020) 127:106144. doi:10.1016/j.optlastec.2020.106144

CrossRef Full Text | Google Scholar

16. Xu J, Zou X, Chen J, Zhang Y, Wang Y, Jin Y, et al. Metal Dielectric Gratings with High Femtosecond Laser Damage Threshold of Twice as Much as that of Traditional Gold Gratings. Opt Lett (2019) 44(11):2871–4. doi:10.1364/OL.44.002871

CrossRef Full Text | Google Scholar

17. Kong F, Chen S, Liu X, He K, Jin Y, Liu S, et al. Femtosecond Laser Damage of All-Dielectric Pulse Compression Gratings. Laser Phys (2014) 24(10):106101. doi:10.1088/1054-660x/24/10/106101

CrossRef Full Text | Google Scholar

18. Hoffman BN, Kozlov AA, Liu N, Huang H, Oliver JB, Rigatti AL, et al. Mechanisms of Picosecond Laser-Induced Damage in Common Multilayer Dielectric Gratings. Opt Express (2020) 28(17):24928–36. doi:10.1364/oe.395197

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Garasz K, Kocik M. Experimental Investigations on Laser Ablation of Aluminum in Sub-picosecond Regimes. Appl Sci (2020) 10(24):8883. doi:10.3390/app10248883

CrossRef Full Text | Google Scholar

20. Xie L, Zhang J, Zhang Z, Ma B, Li T, Wang Z, et al. Rectangular Multilayer Dielectric Gratings with Broadband High Diffraction Efficiency and Enhanced Laser Damage Resistance. Opt Express (2021) 29(2):2669–78. doi:10.1364/OE.415847

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Neauport J, Lavastre E, Razé G, Dupuy G, Bonod N, Balas M, et al. Effect of Electric Field on Laser Induced Damage Threshold of Multilayer Dielectric Gratings. Opt Express (2007) 15(19):12508–22. doi:10.1364/OE.15.012508

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen J, Huang H, Zhang Y, Wang Y, Kong F, Wang Y, et al. Reducing Electric-Field-Enhancement in Metal-Dielectric Grating by Designing Grating with Asymmetric ridge. Sci Rep (2018) 8(1):1–6. doi:10.1038/s41598-018-22479-3

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Gallais L, Rumpel M, Moeller M, Dietrich T, Graf T, Abdou Ahmed M. Investigation of Laser Damage of Grating Waveguide Structures Submitted to Sub-picosecond Pulses. Appl Phys B (2020) 126(4):1–8. doi:10.1007/s00340-020-07419-2

CrossRef Full Text | Google Scholar

24. Rakić AD. Algorithm for the Determination of Intrinsic Optical Constants of Metal Films: Application to Aluminum. Appl Opt (1995) 34(22):4755–67. doi:10.1364/AO.34.004755

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chen S, Zhu M, Li D, He H, Zhao Y, Shao J, et al. Effects of Electric Field Distribution and Pulse Duration on the Ultra-short Pulse Laser Damage Resistance of Laser Coatings. Int Soc Opt Photon (2010) 7842:78420D. Effects of electric field distribution and pulse duration on the ultra-short pulse laser damage resistance of laser coatings[C]//Laser-Induced Damage in Optical Materials: 2010. doi:10.1117/12.867225

CrossRef Full Text | Google Scholar

26.ISO. Lasers and Laser-Related Equipment—Test Methods for Laser-Induced Damage Threshold—Part 2. International Organization for Standardization (ISO): Geneva, Switzerland (2011). I.J.I.O.f.S. 21254-2: 2011.

Google Scholar