The Contours of a Cliophysics. How Can Econophysics Enrich Cliometrics? Case Studies in Debt Issues and Global Capital Markets

In this article we illustrate what the contours of “Cliophysics” are. The term was coined by the “Cliometrics and Complexity” (CAC) team, composed of economists and physicists, and hosted by the Complex Systems Institute of ENS Lyon (IXXI). Cliophysics consists in the application of methodological tools from Complexity and Econophysics to the field of Economic history. More precisely, this new scientific challenge aims at combining Cliometrics, i.e. the application of economic modelling and econometrics to the field of Economic history, together with Complexity analysis and Econophysics. In this article, we highlight how using statistical signal processing, topological analysis and network analysis can enrich Cliometrics. To that end, we present three case studies taken from the research agenda developed within the CAC Team: 1) An original research in Cliophysics involving coïncidence analysis based on symbolic time series, aiming to revisit the classical standards of the link between public debt and economic growth in Economic history; 2) An approach in Cliophysics involving topological representations of asset markets networks, aiming to detect homogeneous eras of international monetary regimes; 3) An approach in Cliophysics involving the segmentation of multivariate time series derived from assets returns, aiming to allow for the identification of the structural breaks in the history of global capital markets. We provide evidence that Cliophysics 1) reveals new stylized facts in Economic history, 2) unveils key moments in the history of capital flows, different from the conventional view, and 3) fills a gap in historical analysis, by focusing on “structure matters in Economic history”.

1 Introduction

The work carried out jointly by physicists and economists [1–3] within the framework of the CAC team (hosted by IXXI, Institut Rhône Alpin des Systémes Complexes of ENS de Lyon) aims at renewing the methodological approach to major cliometric subjects: the public debt - growth relationship over history [1]; the development of financial globalization [3]; and the detection of major events in global capital markets [2]. On these three topics, the dating and/or identification of homogeneous periods is a major challenge of the empirical approach. The use of signal processing methods, in particular recurrence plots and multivariate segmentation methods by denoising, is consistent with the theoretical literature in Economic history (absence of recurrence hypothesis of non-contingent regimes) and adapted to the specific characteristics of historical data (incomplete and heterogeneous coverage depending on the countries).

Applied to time series of debt [1], global asset prices correlations [2] and graph indicators based on correlations [3], these signal processing methods shed light on central controversies. In particular, this work shows, for the post-World War II period, that the debt growth relationship cannot be considered in its sole domestic dimension [1]; that decisions of market operators are the main cause of major breaks in the dynamics of financial globalization [3]; and that the dependence of asset price time series allows for a satisfactory dating of major events in global capital markets [2].

Other work carried out within the framework of CAC by economists is largely inspired by Complexity methods, and in particular the comparative dynamics of sub-graphs within global economic and financial networks. These methods are applied to the long dynamics of financial integration [4]; to the characterisation in terms of graphs of path dependence [5], convergence [6], and the impact of regulatory shocks [7]; and more recently, to macroeconomic dynamics during a pandemic [8].

In this article we wish to illustrate what are the contours of Cliophysics, a term coined by the CAC team, which is characterized by the application of the methodological tools from Complexity and Econophysics (statistical signal processing, topological analysis, network analysis) to Economic and financial history. This new scientific approach which combines Cliometrics (the application of economic modelling and econometrics to the field of Economic history), Complexity and Econophysics expands the frontiers of both Physics and Cliometrics. We choose to illustrate what these “contours of Cliophysics” are through three types of case studies taken from the research agenda developed within the Team CAC: 1) An approach in Cliophysics involving coïncidence analysis based on symbolic time series allows to revisit classical standards of the link between public debt and economic growth in history; 2) An approach in Cliophysics involving topological representations of asset markets networks provides a quantitative framework for the analysis of homogeneous eras of the structure of financial globalization over history; 3) An approach in Cliophysics involving the segmentation of the descriptors of the distributions allows for the identification of the major events which have punctuated the history of global capital markets.

2 The Debt-Growth Relationship, and Coincidence Analysis Based on Symbolic Time Series

2.1 Cliometric Controversies About the Debt - Growth Relation in History

The work of Reinhardt and Rogoff (RR) has generated considerable controversy about how Economic history can be used to deliver policy recommendations today. RR’s seminal papers and book [9–13] lent credence to the idea that a simple, purely empirical and descriptive Economic history, letting the data speak and eschewing econometrics and economic modelling, was sufficient to uncover the characteristics of major financial crises and their recurrence in history. The authors’ lack of analytical method, as well as the resulting economic policy proposals, have given rise to an abundant critical literature, including [14–17]. All these critical analyses call into question RR empirical findings as a guide for policy recommendations. RR [10] identified a “threshold effect” that they turn into a “debt intolerance ratio” at the 90% level and their implicit suggestion is that governments should respect this limit to public indebtedness. This is undoubtedly a very questionable “pro” austerity message.

[18] established that [10] delivered a false picture, due to calculations errors with post WW2 averages. Indeed, in [10] an entire subset of countries was excluded from dataset. RR [19] published an “Errata to Growth in a Time of Debt” they present as “an erratum to their former publication, but not a response to critique”. They admit coding errors (5 countries have being excluded of the sample: Australia, Austria, Belgium, Canada and Denmark) and the means and medians for debt and growth were reported for 15 countries only (Finland, France, Germany, Greece, Ireland, Italy, Japan, Netherlands, New Zealand, Norway, Portugal, Spain, Sweden, United Kingdom, US. Amazingly, RR lessen the impact of their coding error: Once corrected, they contend they find outcomes of “comparable magnitude”, which is highly questionable since, once corrected, the countries with a debt to GDP ratio above 90% experienced in average over the post WW2 period a 2.2% rate of growth, instead of -0.1%…). Once corrected, the contraction in economic growth is no longer so apparent with regards to countries experiencing a debt to GDP ratio comprised between 60% and 90% and henceforth there is no statistically significant difference between the average growth rates of the last two regimes of public debt.

[15] explore the relevance of the exogenous threshold of 90% of debt to GDP ratio highlighted by RR (2010) by running a Panel Smooth Threshold Regression (PSTR) method [20] measuring the effect of debt on growth, depending on the debt level and thresholds of public debt-to-GDP ratios. They find for post WW2 episodes an endogenously-estimated threshold around a debt-to-GDP ratio of 115%, above which the negative debt-growth link even changes sign. For a longer historical period of 130 years (1880–2009) they identify a threshold for a public debt-to-GDP ratio around 130%, above which the correlation becomes positive, as well. This positive correlation corresponds in particular to major growth episodes in history, “30 glorieuses”, “Belle Epoque” and the “Roaring Twenties”. During these episodes, a quarter of the whole sample (France, Belgium, Italy, Spain and United Kingdom) experienced remarkably high economic growth rates in a context of elevated public debt ratios. Moreover countries characterized by a public debt-to-GDP ratio above 130%, presented on average growth rates that were comparable to the growth rates of countries with significantly lower public debt ratios, between 60 and 90%.

From the presence of nonlinearities in the effect of debt on growth for high debt ratios, [15] infer that a unique threshold does not make sense in history. Yet, the erroneous, mythical, and fanciful threshold of 90% has been used to justify austerity policies after the global financial crisis. The historical lesson of this nonlinear econometric analysis is that the existence of non negligeable peculiarities in history cannot be disregarded and impose caution and accountability in economic policy recommendation. Further economic evidence is needed before suggesting any policy recommendations regarding the presumed growth effects of fiscal policy in high debt regimes. In the next section we highlight that symbolic analysis is a way to deepen the analysis of the complex nonlinearities that characterize the debt/growth relationship all along with the history of capitalism.

2.2 Symbolic Time Series and Coïncidence Indicators of Databases With Outliers

To demonstrate the relevance of Complexity tools in Cliometrics, in what follows we will present one of the first fruits of this type of work [1]. Our approach highlights the complexity of the relationship between debt and growth and allows us to see the work of [11] in a different light. These scholars’ assertion that there have been inescapable thresholds in the debt-growth relationship throughout history has influenced policy decisions. According to their work, analysis of historical data shows that growth falls sharply when the debt-to-GDP ratio exceeds a threshold of 90%. Apart from shortcomings in the way they handled the data, their approach is based on an over-simplified description that reduces the data to their mean or median.

Our approach aims to conserve the full richness of the data, by not discarding any items and by keeping their four dimensions of growth, debt, country and year. This is a departure from the traditional econometric approach, which tends to eliminate atypical data items in order to retain only so-called “robust” results. For example, R&R’s data show that for a large proportion of the countries studied, the dynamics of the debt/GDP ratio has exhibited a U-shaped curve since the Second World War (Figure 1).

FIGURE 1

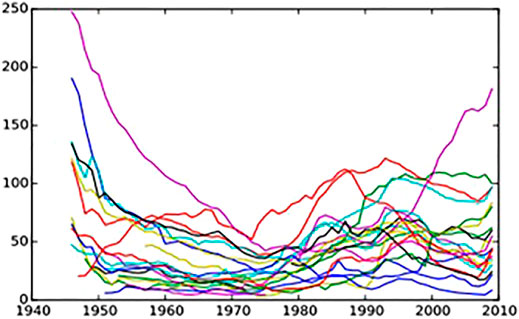
FIGURE 1. Debt-to-GDP ratio (in %) by year: each country is represented by a different colored line.

We have developed a method for studying these correlated changes, which is able to relate the changes in each country’s debt and growth to those occurring in the others. Our work also goes beyond that of [21], who adopted a temporal perspective similar to ours, and grouped countries together according to their growth or debt levels, but who confined themselves to observing heterogeneity between countries. We have shown that this heterogeneity does not prevent us from finding similarities between the different countries in the trends exhibited by the debt/GDP ratio. We have adapted recent developments in time series causality analysis (see in particular 22) to the same debt and GDP series in order to detect synchronization phenomena between different countries, which are seen as instantaneous causalities. We have discretized the real series by replacing them with symbolic series in which the increases are coded as “1” and the decreases as “0”, in order to overcome the problem of data imprecision. This allows us to compare the changes in the debt-to-GDP ratios of different countries by focusing on coincident increases or decreases. Figure 2 provides an overall picture of this, showing the sum of the symbolic growth series for the 20 countries in the sample. It reveals that the changes in different countries coincide to a very high degree, giving an overall indicator that is close to 20 over long time periods. Changes in the debt-to-GDP ratio are more complex, with values that are at times considerably above the median (the peaks in 1977, 1984, 1993 and 2009) as well as other periods with low values (e.g. 1957, 1966, 2000 and 2007).

FIGURE 2

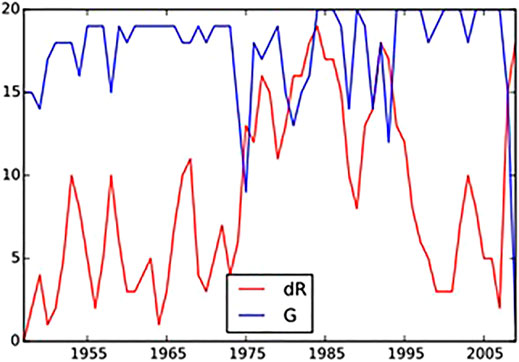
FIGURE 2. The sum of the discrete growth indicators (G) and the debt to GDP ratio indicators (dR) according to the year. For a given date, the indicators are calculated as the sum of the number of countries for which the direction of change coincides. A low value therefore indicates heterogeneous overall dynamics and a value close to the sample size indicates homogeneous overall dynamics.

2.3 Symbolic Time Series and Directed Indicators of Temporal Coincidence

To better quantify the presence of coincidence between the debt/GDP values of different countries, we developed a novel indicator, derived from Granger’s causality measure [23, 24] and Granger’s causality graphs [25] as later modified by [22] and linked to directed information measures. The idea is to quantify the error - based on the observation of a binary series x, taken as a series of “words u = (x_i, x_i+1, … , x_i+l) - that occurs when predictions are made of another series y (which is also binary) coded in the form w = (y_i+d, y_i+1+d, … , y_i+m+d) at time i + d (where d is a possible lag in the influence of one series on the other); the lengths of the words u and w may be different. The frequentist prediction strategy involves, when a specific word u is observed in x, retaining the word w which occurs most often in y at the same time (with a possible lag d). If we repeat this for all the observations, we estimate the error for this prediction strategy. Since we are not interested in causal prediction but in the quantification of temporal coincidence, the prediction strategy is applied to all observations, past and future. The error is then interpreted as a measure of the random differences between the two series. From this error, we obtain a directed relationship indicator (which is not simply a classical correlation but the outcome of the temporal coincidence of changes) of the temporal changes in the debt/GDP ratios in the pairs of studied countries.

The outcome of this study is that the dynamics of the different countries debt-to-GDP ratios mainly reflect coincident changes, as measured by the instantaneous causalities between these ratios for the different countries, rather than correlations with country-specific macroeconomic domestic characteristics, here summarized by domestic growth. In response to RR, for whom a country’s growth is determined by its level of debt, we find that growth is explained (in terms of a measure of shared information) primarily by the growth and debt-to-GDP ratio of all the countries. It therefore seems more accurate to state that it is the global macroeconomic context that dictates changes in the public debts of individual countries. Our results suggest that a country’s debt-to-GDP ratio is thus determined by those of other countries, which poses a problem for the economic interpretation proposed by RR. If each country’s debt-to-GDP dynamics are mainly determined by those of other countries, where does this leave RR’s clear-cut view that it is the level of domestic debt that determines domestic growth? The scientific basis for their economic policy recommendation is thus severely weakened.

3 Financial Globalization and Asset Markets Networks

Financial globalization is a central topic in contemporary financial macroeconomics. In particular, the existing literature investigates the measurement, dynamics, and drivers of the process. In addition, the standard cliometric perspective takes account of the long-term dynamics, in particular those at play since the so-called “first era” of modern globalization in the late 19th century. The “Cliophysics” perspective we aim to implement involves assessing these long-term dynamics using topological network representations and measures from the Econophysics literature. In what follows we present the reference cliometric literature, our methodological choices and the main results of two original studies carried out in this perspective.

3.1 Globalization in the Standard Cliometric Literature

The Cliometrics of financial globalization is first and foremost focused on the question of measurement. The standard Cliometrics literature contains two usual types of indicators of financial globalization. These are, first, stocks and flows of investment indicators and, second, price indicators. Stocks and flows of investment indicators (foreign assets to GDP ratios, foreign liabilities to GDP ratios, gross foreign investment, net foreign investment, etc.) appear to be affected, in particular, by the equity home bias reflecting the size of domestic asset markets. Indeed, the “Feldstein and Horioka” relationship [26] between domestic savings and domestic investment is persistently strong over history [27, 28]. As for quantity indicators, [27] find price criteria (covered nominal interest rate parity, real interest rate convergence, purchasing power parity, etc.) not to be free of bias either, mostly because of the possibility that international convergence would result from simultaneous national structural shifts. They nevertheless agree that “price criteria based on interest differentials may appear more persuasive than the quantity criteria” (p. 121).

All the indicators used in the Cliometrics literature corroborate the stylized fact that financial globalization after the late 19th century has followed a “U shape” (Obstfeld and Taylor, 2004). The left-hand side of the U-shape corresponds to the first modern era of global finance, from the end of the 19th century to World War I. The central part corresponds to the interwar disintegration of global capital markets. Finally, the right-hand side of the U-shape, which forms the second modern era of global finance, corresponds to the contemporary period. The main differences between the first and second eras are not in the level of globalization but in the range of market segments which are affected [29, 30]. However, as emphasized by [31], the structure of the first and second globalizations is different. In the first globalization, creditor countries were exporters of capital to the periphery, while in the second globalization, the United States has become the main debtor nation.

This conclusion is consistent with the so-called “Lucas Paradox” [32], i.e. the observation of persistently low levels of capital flows into developing economies in the post-colonial era in spite of markedly positive yield differentials compared to advanced economies. However, from the late 1980s onwards, some Asian and South American economies no longer seem to have been constrained by the Lucas paradox. This observation is the subject of a specific literature, in which the Lucas paradox, which contrasts advanced and developing economies, becomes an “allocation puzzle” where the contrast is between the relatively integrated emerging economies, and all the other developing economies which remain isolated from global capital flows [33, 34]. The group of emerging economies itself is not homogeneous. [35,36] highlight the gradual and heterogeneous spread of financial globalization from the core to the periphery, with East Asia experiencing the fastest change and Latin America experiencing a more cyclical dynamic.

This finding of a heterogeneous dynamic is shared throughout the cliometric literature on financial globalization, including the crucial debates on the configurations of convergence in [37] or extensive margins of globalization in [31]. The notion of extensive margins of financial globalization is derived from an analogy with international trade in which the intensive margins correspond to a high level of globalization within an unchanged core of economies, while the extensive margins correspond to a progressive inclusion of the present periphery. In this perspective, a topological approach has the advantage of providing a wide range of indicators that make it possible to assess both the structure of globalized capital markets (connectivity and assortativity indicators) and the strength of the relationships (distance indicators), their dispersion and their dynamics. In particular, topological representations of equity markets allow measurements to be made over time of different types of local or global distances that are particularly suitable for the analysis of convergence.

3.2 Topological Representations of Asset Markets Networks

The Minimum Spanning Tree (MST) [38] is the most widely used representation in the Econophysics literature. The ground-breaking papers of [39–43] show that correlations between individual equity prices identified by the MST reveal economically meaningful network structures. [41] shows that “the hierarchical organization found through the minimal spanning tree […] is of great interest from an economic point of view. In particular, by assuming this kind of topology [one is] able to isolate groups of stocks which make sense from an economic point of view by starting from the information carried by the time series of prices only” (p. 194–195). [44,45] extend this result to MSTs of national equity markets.

In parallel, other complex network models are being applied in finance, including planar maximal filtered graphs which contain the MST (developed in particular by [46]), or threshold networks (see, for example [47–49]). On the one hand, these graph models allow for loops analysis (and thus clustering measures) that the acyclic MST does not. On the other hand, some of their properties are less suitable for cliometric analysis than those of the MST. In particular, precisely because they are not acyclic, the planar maximal filtered graph and the threshold network do not have unique paths between pairs of nodes, and therefore do not allow us to compare the dynamics of local and global distances. The example of European integration over the last 6 decades shows that differences in speed are a major fact of financial globalization. As a result, the local distances take very different values depending on the local parts of the graph. Threshold networks (even with endogenous thresholds [49]) which by definition are filtered by a single threshold do not capture this stylized fact.

All these works developing correlations-based graphs have taken place in a context where the Econophysics literature on world equity markets shows that while short term correlations between national equity markets are caused by idiosyncratic events, long term correlations can be attributed to the dynamics of globalization [50], and that correlations, cointegration and Granger causality indicators of national equity markets all exhibit the same convergence of price dynamics in times of crisis [51]. Thus, while the existing Econophysics literature does not assess the structures of global equity markets over the course of history, its main findings create the conditions that make it possible.

From the very first work on the topic, the MST has been transdisciplinary in nature. For example [52], present it as “a method of determining the shortest polygonal line whose vertices are at the points of a finite set, given in advanc” (p. 1). [38] describe it as “a lower bound on the cost of an optimum tour” in a theoretical traveling-salesman problem including sixty-four cities, which they define as follows: “A tour is a cycle passing through each vertex exactly once. The traveling-salesman problem seeks a tour of minimum weight” (p. 7). In the more modern terms of graph theory, the MST is the acyclic, connected subgraph of minimum weight for a complete graph. In the case of equity markets, this complete graph is obtained by transforming the correlation matrix of a price indicator into a distance matrix. The MST therefore allows us to identify the connections and distances which link relatively homogeneous classes of assets. In a way that complements this, Econophysics makes wide use of the hierarchical tree (HT), which is a representation of the hierarchy of distances within the MST. The hierarchical tree constructed by the single linkage or nearest neighbor method has the same branchings as the MST, which itself is unique [53].

The Econophysics literature refers to portfolio management as the main application of the results obtained with this methodology. In our Cliophysics approach, this methodology is used to compute new tools for the measurement of financial globalization through history. Indeed, the structure of topological representations of complex systems evolves with the environment, and may even show phase transitions [54, 55]. In a cliometric perspective, this finding leads to the presumption that long-term changes in, for example, the economic, financial, political and regulatory environments of equity markets may result in distortions in the structure of their topological representations. By dating these distortions, we are able to identify the boundaries between the different eras of globalization. In particular, the sequence of this dating allows us to explore two main hypotheses: the boundaries are mainly the result of optimization choices made by the market (private economic agents) versus public regulatory decisions shape the history of international monetary relations.

To capture this temporal dimension, which is crucial to the cliometric approach, equity markets are represented as dynamic graphs obtained by applying successive windows to historical series of asset prices. The structure of these dynamic graphs is then described by the time series of a set of network topological indicators of distances and connectivity. These indicators, which constitute the standard approach for the characterization of network representations and are therefore generalizable to the history of financial globalization, have the advantage of being eminently suited to the cliometric interpretation. Distances are measured by three different indicators: distance to the nearest neighbors, average path length, and eccentricity. The first measures the distances in local parts of the network, the second the total distances within the network, and the third the distance of the longest path.

These three measures can be interpreted directly in terms of the heterogeneity of the process of financial globalization: for example, when heterogeneity increases, local distances within the core of the network (advanced economies) may still decrease, while the average path length and, especially, the eccentricity of the nodes located in the core, which measures their distance to the periphery (developing and emerging economies), increase. In addition to these distance measures, connectivity is measured by two indicators which also serve to trace the progressive and heterogeneous spreading of the globalization process. It is thus possible to observe how a node evolves within the network, from the periphery (low degree of the node itself and its closest neighbors) to the core (increase in the degree of the nearest neighbors) and finally to the status of a local or global hub (high degree of the node itself). By that way, Cliophysics innovates by assessing the network structure of globalization and identifying eras of financial globalization.

The two next sections relate respectively to the network structure of financial globalization over a century (section 3.3) and to identifying endogenous eras of globalization on the basis of homogeneous structures (section 3.4).

3.3 The Network Structure of Financial Globalization Over a Century

[4] revisit conventional wisdom on the dynamics of financial integration. Their sample includes monthly data on 17 national equity markets from 1913 to 2017 (source: Global Financial Data). A first major conclusion is that the U-shaped curve of financial globalization is in general validated, but with many reservations. First, at the network level, local distance measures (to the nearest neighbors) and global distance (average path length and eccentricity) do not always evolve in a similar way, reflecting structural distortions. In the beginning of the study period, global distance measures replicate the U-shaped curve, but local distance measures do not. Secondly, they obtain an asymmetric U-shaped curve, showing a strong acceleration of globalization over the last 20 years.

There is a longstanding debate in the Cliometrics literature about whether the first era or the contemporary period was the most intensive period of globalization. The dynamics of distance measures within world equity market networks clearly indicate that the contemporary period is the most globalized, particularly with regards to local distance measures. In the first era, the globalization of equity markets was merely based on strong connectivity (star network) rather than low local distance measures. Indeed, at the end of the first era of globalization, the peaks of connectivity indicators reached values which are comparable to those of the end of the 1990s. Finally, the U-shaped curve of financial globalization measured by distance indicators within equity market networks reveals notable peculiarities (a sharp temporary drop in all distance indicators) of similar magnitude around the major crises of 1929 and 2008. Interestingly, works using threshold networks also show specific properties of the graphs at the time of the 2008 crisis, in particular disconnections of regional subgroups for the highest threshold levels [48].

The second important conclusion relates to the heterogeneity of the dynamics of globalization. At the country level, network indicators help reveal the similarity or, on the contrary, the divergence of countries’ trajectories within the overall dynamics of financial globalization. The outcomes reached at the country level provide grounds for making network indicators systematic indicators of financial globalization. Indeed, they provide a richer and more nuanced view than standard Cliometrics about the evolution of financial globalization. In general, the heterogeneous spreading of the globalization process is very clear. The trend for local distances to decrease has not occurred at the same rate everywhere. While in the case of the United States and Japan the decreases in distances were immediate with a first sudden drop in the 1950s (United States) or 1960s (Japan) and a second in the 2000s, in the case of the European economies (France, Germany and the United Kingdom) the decrease was gradual and progressive.

Under these conditions, the hierarchical classification of distances within the network changes over time, revealing the disruption resulting from the European integration process to have been a major event. While during the interwar and Bretton Woods periods the United States and Canada were the closest pair of countries, this no longer applied in the contemporary period. Germany, the Netherlands and France, which belong to the hard core of European integration, are henceforth connected by very short distances compared to the rest of the network. Finally, this approach using dynamic equity market graphs helps characterize the process of financial globalization as a long trend affected by heterogeneity and local singularities, and whose very forms have evolved over the course of history. This outcome on the heterogeneous dynamics of globalization over a century puts the debate on the irreversible process of economic convergence into perspective.

3.4 Statistical Signal Processing to Identify Eras of Financial Globalization

To identify endogenous areas of globalization based on homogeneous structures, [3] use a sample including monthly data on 32 national equity markets from 1960 to 2018 (source: OECD). The identification of endogenous eras is based on signal processing to segment the time series of network indicators into stationary periods. In comparison to the usual methods of multivariate time series segmentation in the field of macro-econometrics, these methods have the advantage of not requiring any prior assumption about the regimes resulting from segmentation, nor about the existence of a finite number of regimes. The transitions and parameters of the distributions of the corresponding sub-periods are both endogenously determined by the signal processing method. The denoising method of [56] has been applied to delineate periods, corresponding here to eras of globalization characterized by stable network structures, during which the different time series of network indicators are simultaneously piecewise constant.

In signal processing, the segmentation of multivariate time series based on the covariance structure is the subject of a considerable literature, including work on asset price data [57]. The reference Econophysics literature shows that the MST derived from correlations reveals the underlying economic relationships (in particular, 41), which is also true in the case of networks of national equity market indices [44, 45]. This property of the MST, combined with the transparent economic interpretation of distance and connectivity indicators with regards to the spreading of the financial globalization process, makes it possible to segment, instead of the full covariance structure, only the multivariate signal present in the time series of the distance and connectivity indicators mentioned above. In other words, this segmentation does not require the stability of weak links within the entire network, but only the overall stability of the MST structure.

This segmentation methodology is therefore applied to the following multivariate time series at the network level: average distance to the nearest neighbors, average path lengths, eccentricity, standard deviation of degrees, average degree of the nearest neighbors. Three eras separated by two key dates, in 1983 and 2007, are apparent during the period of study (1960–2018). Both dates of separation coincided with major events that affected global financial markets. The first date marked the beginnings of the debt crisis of developing economies in the 1980s, and the second the beginnings of the global financial crisis. In terms of overall capital flows, the pre-1983 period corresponded to a North-South movement of global savings, the 1983–2007 period to a refocusing on predominant North-North flows, and the post-2007 to the return of investments to emerging economies in a context of a major crisis in the North. The dates of regulatory shocks or crises in international monetary relations, in particular what occurred in the 1970s due to the end of the Bretton Woods regime, appear only as determinants of a sub-segmentation, when the parameter of the denoising procedure takes on a low value tending to produce more segments.

Thus, the structure of the dynamic networks described by the time series to which the denoising procedure was applied supports the interpretation that the globalization eras are predominantly related to the optimization choices of private economic agents on asset markets and, in particular, to global movements of savings. This interpretation is reinforced by differentiated changes in the segmented indicators. During the period 1983–2007, eccentricity decreased less than the other distance indicators, and the centrality of the United States increased, showing a slowing in the convergence of developing and emerging economies. In contrast, after 2007, eccentricity decreased as much as the other distance measures, and the structure of the MST became more polycentric, with a specific part of the branching composed of developing and emerging economies, which were no longer located in the periphery of advanced economies. These results, obtained by combining dynamic graphs and statistical signal processing approaches, are methodologically original in that the delimitation of the eras does not presuppose that the globalization dynamics are necessarily characterized by a recurrence of similar regimes, but appear to be fundamentally heterogeneous.

4 Events, Crises and Segmentation of the Descriptors of Distributions

In [2], the authors study the changes in the correlation structure of multivariate series of log-return of world-wide equity markets, on the period 1960–2018. The goal is to analyse from endogenous data what are the different segments of international financial integration and to this end to identify the events that condition the changes in the structure of the correlations. It is approached by a signal method because what is sought is an endogenous segmentation method. That is to say, the method starts from measurements of correlations between returns, in a cliometric approach, by taking an interest in working over long times while starting from measurements over time with data-informed methods. For that, the authors consider different possible features describing the time evolving correlations and leverage a denoising method for multivariate piecewise constant signals so as to obtain segmentations for analysis. This method aims to denoise multivariate signals that are assumed to be piecewise constant with small numbers of jumps at the same locations (possibly without jumps for some series).

Contrary to classical covariance segmentation approaches (for example, in the case of financial data [57]), the authors work on global indicators describing the evolution of the distributions of the pairwise correlations between the stock returns of a set of countries. In fact, these methods generally assume piecewise stationarity of the correlation matrix itself. However, this is not really appropriate here since a country or a group of countries may not follow the same trends at all. The other difficulty lies in the nature of the data: they are left-censored for various reasons (absence of a reference financial centre, absence of informed data, etc.).

First, the return series are made sufficiently stationary over short times to estimate their Pearson correlations over sliding windows. The time series constituted by these correlations are then considered pairwise individually, without exploiting the matrix structure. The intuitively guiding development is that of Figure 3C) showing the sliding histogram of correlations: periods of financial integration result in a reasonably time-invariant distribution of these correlations. The method used will aim to segment this representation, as it appears through its histogram.

FIGURE 3

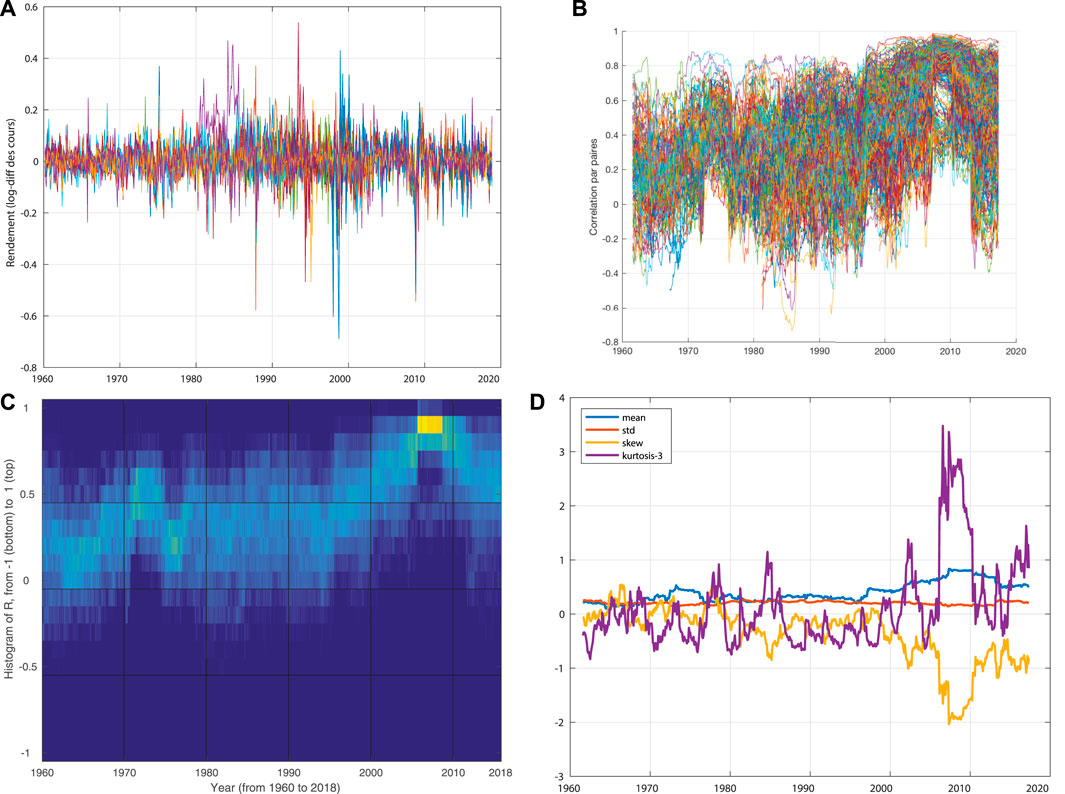
FIGURE 3. Visualisation of (A) the corrected and log-differentiated series (log returns), (B) the pairwise correlations, (C) the histogram over time of these correlations and (D) the indicators mean μ, standard deviation σ, skewness s, and kurtosis γ, at each t.s.

Three possibilities are tested: 1. Use the set of pairwise correlations directly. One difficulty is to properly handle missing data, in addition to having a fairly high dimensional problem. 2. Use the normalized histograms of these correlations; for example, as in Figure 3C. 3. Retain only the first descriptors of the distributions of the correlations: their mean μ, standard deviation σ, skewness s, and normalized kurtosis γ. The advantage is to have a stable number of series, while having less arbitrariness than in the case of the histogram since one does not have to choose the sampling.

Denoising is done by minimising a functional that reflects a balance between an attachment to the data and a term that favours a piecewise constant signal with a parsimonious number of jumps in all signals at the same times. A penalty parameter regulates this trade-off. The minimization of this non-smooth convex problem is done by a primal-dual proximal algorithm described in [56], adapted from the algorithm of [58]. For the three possible choices of indicators, this same denoising method is applied. The most meaningful segmentations are presented in Figure 4.

FIGURE 4

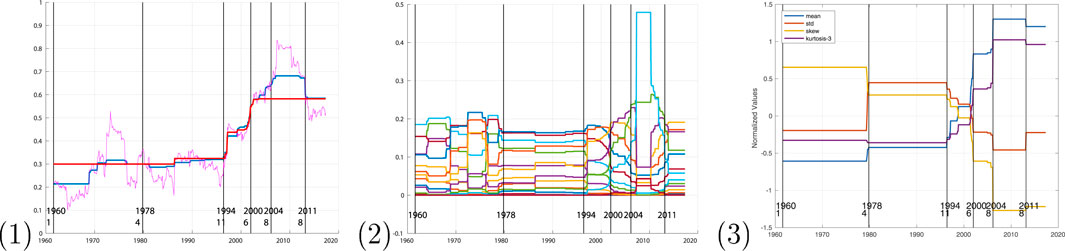
FIGURE 4. Visualisation of the segmentations obtained starting from [1]: all 96 series R_ij(t) (where we have represented two choices of the penalization parameter) [2]; standardised histograms of these correlations (each series being one of the 21 classes) or [3] indicators X(t) = [μ(t), σ(t), s(t), γ(t)]. The vertical black bars show the limits of the periods proposed by the segmentation of the indicators [3] (note that the shift with the axes is only apparent: the data are centred in the middle of the 3-years windows, so the bar in 1978/4 is then almost displayed in 1980 since the 1980/01 window starts in 1978/7).

The direct segmentation of the correlation returns the dominant mode related mainly to the mean alone, but does not capture the effects of convergence or bi-polarisation modification effects. By segmenting on the histogram, choice [2], one struggles to obtain segmentations with many segments. On the other hand, the segmentation on the first descriptors of the distributions finds and quantifies the evolutions that we see qualitatively (Figure 4).

Methodologically, the contribution is to show that the segmentation of a correlation matrix can be explored, even with missing data, based on denoising of descriptors of the correlation distribution. Signal analysis appears here as an interesting cliometric tool to detect tool for detecting structural distortions of correlations over long periods of time.

We have illustrated above that a method such as the segmentation of the descriptors of the distributions makes it possible to precisely date reversals and modifications in the correlation matrix, which is very useful from a cliometric perspective because it makes it possible to analyse economic phenomena such as contagion and the propagation of shocks from clearly identified dates and to identify truly systemic crises, i.e. those that affect the entire matrix. We have deliberately stayed at the level of the matrix of correlations of stock returns in the world, because with statistical signal processing we have a new method for refining the diagnosis of the phenomena of transmission of crises, and more generally how any shock to returns somewhere in the world affects the structure of correlations of returns in the world. This is a considerable cliometric enrichment. In this section, we wanted to highlight the power of this tool, which reveals the information content of the correlation matrix and provides information on the mechanisms of stock market interdependence and interconnection at work in world financial history.

5 Conclusion

In this article, we illustrate three major contributions in Cliophysics:

• Combining Cliometrics and Econophysics makes it possible to restore the dimension of heterogeneity in Economic history better than econometrics can do. Including all outliers in the study of the relationships between economic growth and public debt enables to revisit conventional wisdom that discards the diversity and heterogeneity of this relationships in historical perspective. These findings help questioning policy recommendations drawn from a too schematic approach á la Reinhardt and Rogoff.

• Network analysis helps identifying new features of financial globalization, that of dynamic structures of capitalism.

• Combining Econophysics and Cliometrics undoubtedly helps identifying a new historical dating and explanation of international monetary regimes: as an unexpected outcome, statistical signal processing gives evidence that international monetary regimes are a sub-segmentation of market capital movements and market infrastructures.

In these examples of applications we have so far considered the contribution of Econophysics, as a methodology, to Cliometrics, as a field. Conversely, Cliometrics can be the source of research questions and potential contributions in the field of Econophysics, in particular in the domain of asset communities on international equity markets. For example, the clear persistence of the historical importance of Dutch equity markets and the disruption of the hierarchy of distances within equity market networks resulting from European integration are both outcomes whose identification and exploitation are based on quantitative Economic history. Far from being specific to work spanning long periods of time, these results also appear in studies on contemporary equity markets, whose findings may be enriched by the highlighting and consideration of a historical dimension.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://stats.oecd.org/.

Author Contributions

Conceptualization: PA, CB, and AP. 1st case study: PB, PJ, and AP. 2nd case study: PA, CB, PB, PJ, and AP. 3rd case study: PA, CB, PB, PJ, and AP. Supervision: AP. Writing—original draft: CB and AP. Writing—review and editing: PA, CB, PB, PJ, and AP.

Funding

This research was co-financed by grants ANR Project DARLING ANR-19-CE48-0002; CHIST-ERA GRAPHNEX project ANR-21-CHR4-0009; and CRISHIS21_22 (U. Toulon, Pôle ESMED).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Guinard B. Public Debt and Economic Growth through History: Explorations with Complexity Tools,” Master’s Thesis. In: Complex Systems, under the Supervision of Pierre Borgnat, Pablo Jensen and Antoine Parent (2015).

Google Scholar

2. Borgnat P, Bastidon C, Jensen P, Abry P, Parent A. Segmentation de corrélations par débruitage pour explorer l’intégration financière internationale. In: GRETSI 2019-XXVIIème Colloque francophonede traitement du signal et des images (2019).

Google Scholar

3. Bastidon C, Parent A, Jensen P, Abry P, Borgnat P. Graph-based Era Segmentation of International Financial Integration. Physica A: Stat Mech its Appl (2020) 539:122877. doi:10.1016/j.physa.2019.122877

CrossRef Full Text | Google Scholar

4. Bastidon C, Bordo M, Parent A, Weidenmier M. Towards an Unstable Hook: The Evolution of Stock Market Integration since 1913. NBER Working Pap Ser (2019) 2019:26166. doi:10.3386/w26166

CrossRef Full Text | Google Scholar

5. Bastidon C, Parent A. Cliometrics of World Stock Markets Networks. Econophysics Colloquium (2018) 539:122877.

Google Scholar

6. Bastidon C, Parent A. Institutional Change and China Capitalism: Frontier of Cliometric and its Application to China. In: Vol. 539, Ch. Cliometrics of World Stock Markets Networks. Singapore: World Scientific Publishing (2018).

Google Scholar

7. Bastidon C, Jawadi F. The Network Structure of French Equity Markets. Dyn Socio-Economic Sci (2018) 539:122877.

Google Scholar

8. Bastidon C, Parent A. La modélisation économique à l’appui du choix public dans l’urgence de la pandémie de covid-19. Revue de l’OFCE (2021) 173:3.

Google Scholar

9. Reinhart CM, Rogoff KS. This Time Is Different: Eight Centuries of Financial Folly. Princeton, NJ, USA: Princeton University Press (2009).

Google Scholar

10. Reinhart CM, Rogoff KS. Growth in a Time of Debt. Am Econ Rev (2010) 100(2):573–8. doi:10.1257/aer.100.2.573

CrossRef Full Text | Google Scholar

11. Reinhart CM, Rogoff KS. The Aftermath of Financial Crises. Am Econ Rev (2009) 99(2):466–72. doi:10.1257/aer.99.2.466

CrossRef Full Text | Google Scholar

12. Reinhart CM, Rogoff KS. Is the 2007 Us Sub-prime Financial Crisis So Different? an International Historical Comparison. Am Econ Rev (2008) 98(2):339–44. doi:10.1257/aer.98.2.339

CrossRef Full Text | Google Scholar

13. Reinhart CM, Rogoff KS. This Time Is Different: A Panoramic View of Eight Centuries of Financial Crises. In: Tech. Rep. Cambridge, MA, USA: National Bureau of Economic Research (2008). doi:10.3386/w13882

CrossRef Full Text | Google Scholar

14. Parent A. Jadis et Naguère, la vision des crises financières dans l'histoire, selon Reinhart et Rogoff. Revue économique (2011) 62(6):1095–104. doi:10.3917/reco.626.1095

CrossRef Full Text | Google Scholar

15. Minea A, Parent A. Is High Public Debt Always Harmful to Economic Growth? Reinhart and Rogoff and Some Complex Nonlinearities (2012).

Google Scholar

16. Parent A. A Critical Note on "This Time Is Different". Cliometrica (2012) 6(2):211–9. doi:10.1007/s11698-011-0066-3

CrossRef Full Text | Google Scholar

17. Jensen P, Parent A. Dette publique et croissance: des erreurs bien choisies (2014).

Google Scholar

18. Herndon T, Ash M, Pollin R. Does High Public Debt Consistently Stifle Economic Growth? a Critique of Reinhart and Rogoff. Cambridge J Econ (2014) 38(2):257–79. doi:10.1093/cje/bet075

CrossRef Full Text | Google Scholar

19. Reinhart CM, Rogoff KS. Errata: ’growth in a Time of Debt’ (2010).

Google Scholar

20. Gonzalez A, Teräsvirta T, Van Dijk D, Yang Y. Panel Smooth Transition Regression Models (2017).

Google Scholar

21. Amann J, Middleditch P. Revisiting Reinhart and Rogoff after the Crisis: a Time Series Perspective. Cambridge J Econ (2020) 44(2):343–70. doi:10.1093/cje/bez009

CrossRef Full Text | Google Scholar

22. Amblard P-O, Michel O. Causal Conditioning and Instantaneous Coupling in Causality Graphs. Inf Sci (2014) 264:279–90. doi:10.1016/j.ins.2013.12.037

CrossRef Full Text | Google Scholar

23. Granger CWJ. Testing for Causality. J Econ Dyn Control (1980) 2:329–52. doi:10.1016/0165-1889(80)90069-x

CrossRef Full Text | Google Scholar

24. Granger CW. Some Recent Development in a Concept of Causality. J Econom (1988) 39(1-2):199–211. doi:10.1016/0304-4076(88)90045-0

CrossRef Full Text | Google Scholar

25. Eichler M. Granger Causality and Path Diagrams for Multivariate Time Series. J Econom (2007) 137(2):334–53. doi:10.1016/j.jeconom.2005.06.032

CrossRef Full Text | Google Scholar

26. Feldstein M, Horioka C. Domestic Savings and International Capital Flows. In: Tech. Rep. Cambridge, MA, USA: National Bureau of Economic Research (1979). doi:10.3386/w0310

CrossRef Full Text | Google Scholar

27. Obstfeld M, Taylor AM. Global Capital Markets: Integration, Crisis, and Growth. Cambridge: Cambridge University Press (2004).

Google Scholar

28. Ford N, Horioka CY. The 'real' Explanation of the PPP Puzzle. Appl Econ Lett (2017) 24(5):325–8. doi:10.1080/13504851.2016.1186790

CrossRef Full Text | Google Scholar

29. Bordo MD, Eichengreen B, Kim J. Was There Really an Earlier Period of International Financial Integration Comparable to Today? NBER working paper (1998) 1998:w6738.

Google Scholar

30. Bordo MD, Eichengreen B, Irwin DA, Frankel J, Taylor AM. Is Globalization Today Really Different from Globalization a Hundred Years Ago?. In: Brookings Trade Policy Forum. Washington, DC: National Bureau of Economic Research (1999).

Google Scholar

31. Williamson JG. Global Capital Markets in the Long Run: A Review of Maurice Obstfeld and Alan Taylor's Global Capital Markets. J Econ Lit (2007) 45(2):400–9. doi:10.1257/jel.45.2.400

CrossRef Full Text | Google Scholar

32. Lucas RE. Why Doesn’t Capital Flow from Rich to Poor Countries? Am Econ Rev (1990) 80(2):92–6.

Google Scholar

33. Gourinchas P-O, Obstfeld M. Stories of the Twentieth century for the Twenty-First. Am Econ J Macroeconomics (2012) 4(1):226–65. doi:10.1257/mac.4.1.226

CrossRef Full Text | Google Scholar

34. Prasad ES, Rajan RG, Subramanian A. Foreign Capital and Economic Growth. NBER Working Paper Ser (2007) 13619:64. doi:10.3386/w13619

CrossRef Full Text | Google Scholar

35. Bekaert G, Harvey CR. In: Tech. Rep. Cambridge, MA, USA: National Bureau of Economic Research (1998).Capital Flows and the Behavior of Emerging Market Equity Returns,”

Google Scholar

36. Bekaert G, Harvey CR, Lumsdaine RL. Dating the Integration of World Equity Markets. J Financial Econ (2002) 65(2):203–47. doi:10.1016/s0304-405x(02)00139-3

CrossRef Full Text | Google Scholar

37. O’Rourke KH, Williamson JG. Globalization and History (1999).

Google Scholar

38. Held M, Karp RM. The Traveling-Salesman Problem and Minimum Spanning Trees. Operations Res (1970) 18(6):1138–62. doi:10.1287/opre.18.6.1138

CrossRef Full Text | Google Scholar

39. Bonanno G, Lillo F, Mantegna RN. High-frequency Cross-Correlation in a Set of Stocks (2001).

Google Scholar

40. Bonanno G, Vandewalle N, Mantegna RN. Taxonomy of Stock Market Indices. Phys Rev E (2000) 62:R7615–R7618. doi:10.1103/physreve.62.r7615

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Mantegna RN. Hierarchical Structure in Financial Markets. Eur Phys J B (1999) 11(1):193–7. doi:10.1007/s100510050929

CrossRef Full Text | Google Scholar

42. Tumminello M, Coronnello C, Lillo F, Miccichè S, Mantegna RN. Spanning Trees and Bootstrap Reliability Estimation in Correlation-Based Networks. Int J Bifurcation Chaos (2007) 17(07):2319–29. doi:10.1142/s0218127407018415

CrossRef Full Text | Google Scholar

43. Tumminello M, Lillo F, Mantegna RN. Correlation, Hierarchies, and Networks in Financial Markets. J Econ Behav Organ (2010) 75(1):40–58. doi:10.1016/j.jebo.2010.01.004

CrossRef Full Text | Google Scholar

44. Sandoval L. Pruning a Minimum Spanning Tree. Physica A: Stat Mech its Appl (2012) 391(8):2678–711. doi:10.1016/j.physa.2011.12.052

CrossRef Full Text | Google Scholar

45. Kumar S, Deo N. Correlation and Network Analysis of Global Financial Indices. Phys Rev E Stat Nonlin Soft Matter Phys (2012) 86(2):026101. doi:10.1103/PhysRevE.86.026101

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Tumminello M, Aste T, Di Matteo T, Mantegna RN. A Tool for Filtering Information in Complex Systems. Proc Natl Acad Sci U.S.A (2005) 102(30):10421–6. doi:10.1073/pnas.0500298102

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Lin W-L, Engle RF, Ito T. Do bulls and Bears Move across Borders? International Transmission of Stock Returns and Volatility. Rev Financ Stud (1994) 7(3):507–38. doi:10.1093/rfs/7.3.507

CrossRef Full Text | Google Scholar

48. Lee JW, Nobi A. State and Network Structures of Stock Markets Around the Global Financial Crisis. Comput Econ (2018) 51(2):195–210. doi:10.1007/s10614-017-9672-x

CrossRef Full Text | Google Scholar

49. Ha G-G, Lee JW, Nobi A. Threshold Network of a Financial Market Using the P-Value of Correlation Coefficients. J Korean Phys Soc (2015) 66(12):1802–8. doi:10.3938/jkps.66.1802

CrossRef Full Text | Google Scholar

50. Song DM, Tumminello M, Zhou WX, Mantegna RN. Evolution of Worldwide Stock Markets, Correlation Structure, and Correlation-Based Graphs. Phys Rev E Stat Nonlin Soft Matter Phys (2011) 84:026108. doi:10.1103/PhysRevE.84.026108

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Chen Y, Mantegna RN, Pantelous AA, Zuev KM. A Dynamic Analysis of S&P 500, FTSE 100 and EURO STOXX 50 Indices under Different Exchange Rates. PLOS ONE (2018) 13:e0194067–40. doi:10.1371/journal.pone.0194067

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Florek K, Å ukaszewicz J, Perkal J, Steinhaus H, Zubrzycki S. Sur la liaison et la division des points d’un ensemble fini. Colloquium Mathematicum (1951) 2(3-4):282–5. doi:10.4064/cm-2-3-4-282-285

CrossRef Full Text | Google Scholar

53. Gower JC, Ross GJS. Minimum Spanning Trees and Single Linkage Cluster Analysis. Appl Stat (1969) 18(1):54–64. doi:10.2307/2346439

CrossRef Full Text | Google Scholar

54. May RM, Levin SA, Sugihara G. Ecology for Bankers. Nature (2008) 451(7181):893–4. doi:10.1038/451893a

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Gao J, Barzel B, Barabási A-L. Universal Resilience Patterns in Complex Networks. Nature (2016) 530(7590):307–12. doi:10.1038/nature16948

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Frecon J, Pustelnik N, Abry P, Condat L. On-the-fly Approximation of Multivariate Total Variation Minimization. IEEE Trans Signal Process (2016) 64(9):2355–64. doi:10.1109/tsp.2016.2516962

CrossRef Full Text | Google Scholar

57. Xuan X, Murphy K. Modeling Changing Dependency Structure in Multivariate Time Series. In: ICML. New York, NY, USA: ACM (2007). p. 1055–62. doi:10.1145/1273496.1273629

CrossRef Full Text | Google Scholar

58. Condat L. A Direct Algorithm for 1-D Total Variation Denoising. IEEE Signal Process Lett (2013) 20(11):1054–7. doi:10.1109/lsp.2013.2278339

CrossRef Full Text | Google Scholar