- Departamento de Física, Universidade Federal de Viçosa (UFV), Viçosa, Brazil
This mini-review highlights recent advances on computational approaches that have been used in the characterisation of the viscoelastic response of semiflexible filamentous biomaterials. Special attention is given to the multiscale and coarse-grained approaches that might be used to model the mechanical properties of systems which involve biopolymer assemblies, for instance, actin, collagen, vimentin, microtubules, DNA, viruses, silk, amyloid fibrils, and other protein-based filaments. Besides the basic features of the most commonly used models for semiflexible filaments, I present a brief overview of the numerical approaches that can be used to extract the viscoelasticity of dilute and concentrated solutions, as well as systems with cross-linked networks. Selected examples of simulations that attempt to retrieve the complex shear moduli at experimentally relevant time and length scales, i.e., including not only the fully formed filaments and networks but also their self-assembly kinetics, are also considered.
1 Introduction
Solutions of semiflexible filaments formed from the self-assembly of biomolecules are ubiquitous in living organisms [1, 2]. Understanding how their viscoelastic properties emerge is crucial not only for a better comprehension about the transport and structural properties of fluids and hydrogels at the cellular level [3–6], but also because they seem to play a significant role in many disruptive processes, like cell invasion in several types of cancer [7] and protein aggregation in tens of proteinopathies [8].
Besides being a highly interdisciplinary problem [9], the characterisation of the viscoelastic response of self-assembled molecular systems involves time and length scales that span several orders of magnitude [10], with the typical building blocks at length scales of a few nanometers (10−9 m) forming structures of micrometers (10−6 m) to centimeters (10−2 m) along time scales that range from nanoseconds (10−9 s) to hours (104 s). Experimentally, the mechanical properties of biomolecular systems and their building constituents have been probed at different scales mostly with aid of single-molecule [11] and microrheological techniques [12], and now, more than ever, multiscale and coarse-grained computational simulations [13] are becoming also a valuable tool in testing and validating modelling concepts in order to both understand and predict the viscoelastic behaviour of solutions of semiflexible filaments.
From the practical point-of-view, one aims to understand how the molecular information can be used to design the kind of response the biomaterial will display, e.g., liquid-like or solid-like [14], as well as to estimate the characteristic time scales that determine their viscoelastic behaviour. Figure 1 illustrates the typical viscoelastic responses that are obtained from rheology and microrheology experiments for three different types of solutions of semiflexible filaments. Liquid-like solutions, for instance, are primarily characterised by the value of their viscosity at low frequencies, i.e., η0 = limω→0η′(ω), with the frequency-dependent viscosity η′(ω) being associated to the loss modulus G′′(ω) as η′(ω) = G′′(ω)/ω. As shown in Figure 1A, the loss modulus displays a characteristic linear dependence on the frequency, i.e., G′′(ω) ≈ η0ω, while the storage modulus displays a quadratic behaviour, i.e., G′(ω) ∝ ω2, which are the expected low-frequency behaviours that one would obtain theoretically from the constitutive Maxwell and Rouse models [15]. Figures 1B,C illustrate the typical viscoelastic responses observed for solutions containing entangled and cross-linked semiflexible filaments, respectively. In both cases the solutions will display a semisolid/gel-like behaviour, and the interesting quantities are the entanglement modulus Ge, i.e., where G′(ω) displays a plateau-like regime (Figure 1B), and the low-frequency storage modulus G0 = limω→0G′(ω) (Figure 1C). In all cases one might want to predict both the exponents α and the corresponding frequency ranges of the power law regimes, i.e., where G′(ω) ∝ ωα and/or G′′(ω) ∝ ωα.
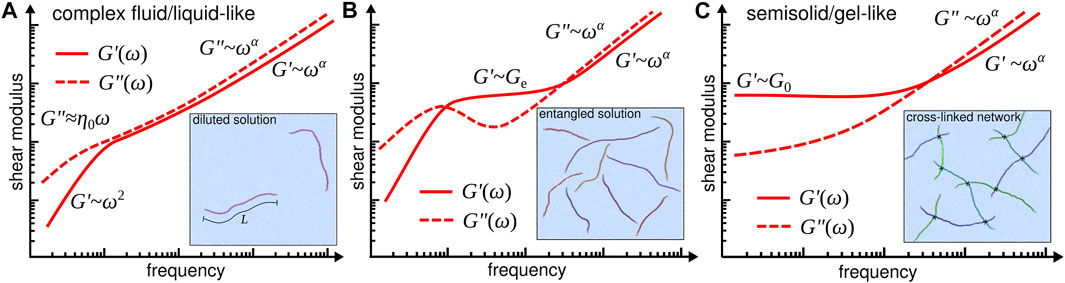
FIGURE 1. Typical viscoelastic responses characterised by the shear moduli G′(ω) and G′′(ω) for (A) complex fluid/liquid-like, (B) entangled, and (C) semisolid/gel-like solutions of semiflexible filaments. Inset drawings illustrate the configurations of the semiflexible filaments and their interactions in solution. Besides the identification of the distinct viscoelastic behaviours, the frequency-dependent shear moduli are often determined by experimentalists to provide a lower bound for the stiffness of the polymer biomaterials at different time scales [12].
In this mini-review I will focus mainly on simulations that have been used to study the aforementioned behaviours illustrated in Figure 1, including the effective modelling approaches of single semiflexible filaments, and the numerical methods used to describe entangled and cross-linked filament networks. Also, whenever it is pertinent, I will include information about the related self-assembly processes.
2 Modelling Approaches
2.1 Viscoelasticity and Relaxation Spectrum
As discussed in Ref. [16], polymer solutions are generally composed of structures that span several length scales so that they should contain many relaxation modes that can be characterised by a distribution of characteristic times τ, which is also known as the relaxation spectrum [17] H(τ). As extensively discussed in Ref. [17], one can relate the different mechanical responses illustrated in Figure 1 to different spectra H(τ) by assuming that the system is in the linear viscoelastic (LVE) response regime. Usually, the LVE regime is attained for small strains γ where the integrity of the biomolecular filaments (and, possibly, of the network structures) in the system is maintained during the whole measurement [12]. Although this might exclude drastic phenomena as those involved in shear banding and fracture experiments, situations that include the self-assembly of filaments (and networks) can be still studied if the time scales involved in the macroscopic reorganisation of the structures are greater than the time scales probed by the oscillatory or microrheology experiments. In practice, this means that the relaxation spectrum H(τ) or, equivalently, the stress relaxation modulus [17] G(t), does not change during the observation time [18], and one can evaluate the shear moduli in the LVE through a one-sided Fourier-Laplace transform [15, 17] as
For solutions, one might consider to perform nonequilibrium simulations and implement shear flow conditions through driven, e.g., Lees-Edwards [19], boundary conditions and similar approaches (see Figure 2A). Alternatively, in order to obtain the response of the system in the LVE, one may avoid working with transient behaviours by considering simulations at equilibrium [20–22], and evaluate the relaxation modulus G(t) from the stress-stress autocorrelation (see Figure 2B). This kind of approach has been used not only to demonstrate the characteristic high-frequency regime where G′ ∝ G′′ ∝ ω3/4 for dilute solutions of semiflexible filaments, but also in the evaluation of the plateau (i.e., entanglement) modulus Ge in entangled solutions [23–26]. Although in the highly entangled regime it is not always easy to determine the relevant characteristic length scales (i.e, the entanglement length Le) and the interactions that significantly contribute to the stress tensor [27], an alternative modelling approach based on primitive path analysis [28] (see Figure 2B) has been successfully used to obtain values for Ge [29, 30].
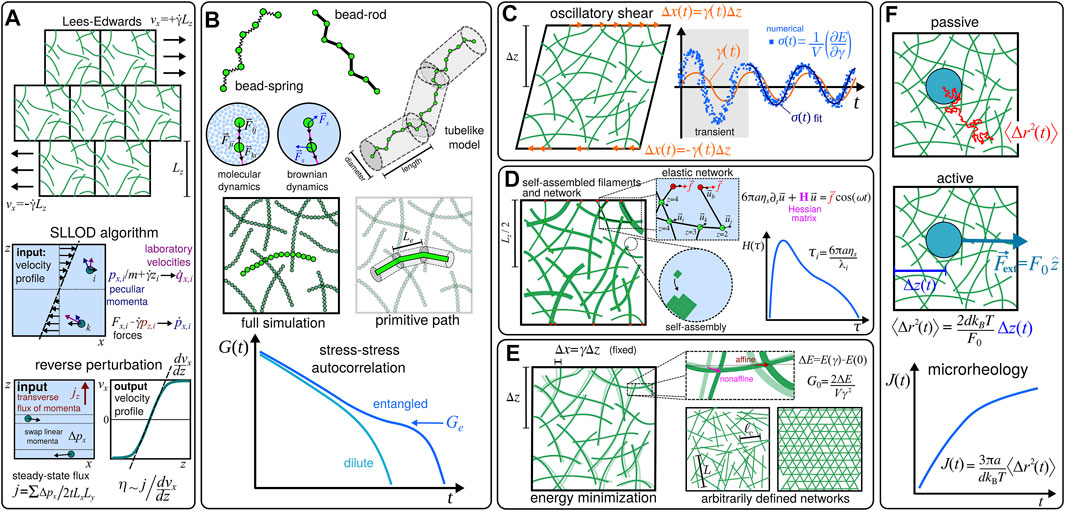
FIGURE 2. Examples of computational particle-based methods used to estimate the mechanical properties of biopolymer materials. (A) Shear flow conditions can be implemented through Lees-Edwards [19] driven boundary conditions [40], and other related methods, e.g., the SLLOD algorithm [40, 41], and the reverse perturbation method [42, 43], in order to evaluate the viscosity η0 at low shear rates
When the system present a percolating network one can, in principle, implement simulations based on oscillatory setups which are similar to experiments in rheology [14], and evaluate G*(ω) by direct means. For instance, in Ref. [31] the authors studied a network of cross-linked semiflexible filaments placed in a finite volume V by imposing a strain γ(t) = γ0 sin (ωt) and measuring the shear stress as1
It is worth mentioning that one can also consider the compliance function J(t) that is usually obtained from creep experiments to evaluate G*(ω), since G(t) is also related to J(t) through a convolution integral [12, 17]. In fact, since the compliance can be related to the mean-squared displacement (MSD) ⟨Δr2(t)⟩ of probe particles with radius a in d dimensions as [18] J(t) = (3πa/dkBT)⟨Δr2(t)⟩, one can also use approaches based on microrheology (see Figure 2F). In some cases it might be even possible to speed up the simulations by considering active, i.e., externally driven, approaches that are based on fluctuation-dissipation relations [39], where the equilibrium fluctuations in the position of the probe particles can be estimated from their displacement Δz in the direction of the external force
2.2 Coarse-Grained Models
Ideally, a full bottom-up modelling approach would have to incorporate all information about the molecular structures of the system, including not only the chemically specific features of the building blocks of the filaments but also additional solvent-specific details (Figure 2B). However, due to the intrinsic multiscale character of the viscoelastic behaviour, such atomistic-based approaches are only considered in a complementary manner, and mesoscopic (i.e., coarse-grained) modelling approaches are usually inevitable [26, 51, 52].
2.2.1 Self-Assembly of Filaments
In fact, even when simulating just the formation of filaments one may need to resort to coarse-grained models, which generally attempt to describe the folding and self-assembly processes of the biomolecules in an implicit solvent using effective interactions [53]. Unfortunately, there are not many studies in the literature that explore coarse-grained approaches to describe the self-assembly processes of semiflexible filaments [54, 55], and their computational implementation correspond to a challenge itself, as it might involve nucleation pathways that usually requires special rare-event sampling techniques [56]. Alternatively, one may resort to multiscale modelling approaches like the one introduced in Ref. [38], where a lattice model with anisotropic interactions was used to simulate the formation of the fibers, and the resulting network structure was considered as the input configuration for an effective elastic model (see Figure 2D).
2.2.2 Models for Single Semiflexible Filaments
Accordingly, in order to obtain the viscoelasticity of solutions at experimentally relevant time and length scales, one has to rely on coarse-grained models even at the single filament level. In that case, the individual filaments are usually described by discrete chains where N beads are connected through springs or rods (see Figure 2B). The simplest potential for the springs is the hookean, or harmonic, potential,
Finally, it is worth noting that, besides the already mentioned excluded volume and bending effective interactions, implicit effects on the bending rigidity of the filaments may also occur due to other sources. For instance, interactions between charged beads in the filament (and possibly) with ions in solution can be incorporated through bare (or screened) Coulomb potentials [65, 66]. In addition, at the coarse-grained level, hydrodynamics effects might be also modelled as “hydrodynamic interactions” between beads [51, 59].
2.3 Numerical Simulations
In the following I will describe additional approaches that are generally used in computational simulations, including a few selected examples that illustrate how the methods and models mentioned in the previous sections can be used to extract the viscoelastic responses of solutions like those displayed in Figure 1.
2.3.1 Dilute Solutions of Semiflexible Filaments
Since the intrinsic relaxation modulus [20] [G(t)] can be retrieved from the stress-stress autocorrelation function (Figure 2B), one can use the dynamics of a single filament to obtain the intrinsic shear moduli [G*(ω)] for an infinitely dilute solution. In that case one might estimate the actual modulus of dilute solutions by multiplying the intrinsic modulus by the number density of the filaments nf [15]. Usually, the dynamics of single filaments is obtained either from molecular dynamics [45] (MD) or from stochastic mesoscale approaches [40] (see Figure 2B). In particular, Ref. [43] includes results obtained for the shear-dependent viscosity
2.3.2 Solutions of Entangled Semiflexible Filaments
In principle, models for entangled solutions can be obtained simply by including a large number M of filaments in a simulation box with volume V, so that nf = M/V. In that case, the dynamics of a system with several entangled chains can be also obtained from full simulations [26] (see Figure 2B). However, as detailed in Ref. [47], this kind of approach might face limitations as the molecular weight of the filaments exceeds a “critical” value, and alternative methods may be required2. As mentioned in Section 2.1, simulations based on primitive path analysis (see Figure 2B) have been successfully used to obtain the plateau moduli Ge of entangled solutions which are consistent with the values that were experimentally determined for many polymer melts [29, 30]. In that case, the semiflexible filaments are described by the so-called Kremer-Grest model, which includes UFENE, UWCA, and bending Ub,θ potentials (see Section 2.2.2).
2.3.3 Cross-Linked Networks
Unfortunately, without many bottom-up approaches that incorporate the self-assembly of filaments (see, e.g., Figure 2D), it is sometimes difficult to generate and equilibrate systems with disordered cross-linked networks. Even so, a few procedures have been developed so that generic features of fully formed networks can be systematically studied. In this context, protocols for constructing ad hoc configurations (Figure 2E) include, e.g., (i) erasing a fraction p of the bonds of pre-established regular networks [37, 68, 69], and (ii) placing line segments in the system at random until the required crosslinking density is reached [35, 36, 70]. It is worth noting that Monte Carlo-based schemes [71–73] have been conveniently used to equilibrate networks generated with the protocol (ii). Besides the number density of filaments nf, the contour length L, and the persistence length Lp, useful quantities that can be used to characterise cross-linked networks of semiflexible filaments are the mean distance between crosslinks ℓc (Figure 2E), which also defines a crosslinking density ρc = 1/ℓc, and the mean network connectivity ⟨z⟩ (Figure 2D). In particular, the systematic studies presented in Refs. [36, 37] computed the plateau modulus G0 to obtain L-vs-ρc and z-vs-Lp phase diagrams, respectively. Interestingly, those studies indicated the presence of nonaffine and bending-dominated viscoelastic responses at small values of ⟨z⟩ and ρc, which have been also observed for heterogeneous networks [38]. In Ref. [38], the cross-linked networks were generated through a self-assembly process using a lattice model (Figure 2D), and were also explored in Ref. [34]. In the latter reference one can find the method based on the Hessian of the elastic energy (see Section 2.1), which allows one to assess the contributions of both affine and nonaffine deformations (Figure 2E) to the shear moduli G′(ω) and G′′(ω). In addition, Refs. [34, 38] considered a generalisation of the freely-hinged model used in Ref. [37] that incorporates the influence of heterogeneous structures (see Figure 2D), i.e., filaments with thickness-dependent stretching and bending constants, into the effective elastic energy E. As discussed in Ref. [33], semiflexible filaments are less prone to entangle than the flexible ones, so the viscoelastic response of their networks might rely much more on the cross-linker properties. For instance, the role of the flexibility of cross-linkers has been investigated in Ref. [74] in arbitrarily generated networks, with the value G0 computed from the derivatives of the total elastic energy of the system. In addition, the study in Ref. [75] investigated the effects of transient cross-linkers on the viscoelasticity of networks of stiff biopolymers, showing that they can lead to a wide distribution H(τ) yielding the power law behaviour observed for the shear moduli at low frequencies.
3 Outlook and Challenges
There are still many challenges to the physics-based computational approaches involving multiscale simulations that attempt to evaluate the viscoelastic response of solutions of semiflexible filamentous biomaterials. Although generic coarse-grained polymer models have been developed to describe the self-assembly processes of filaments [54, 55], there are only a few computational studies on the association of fully formed semiflexible filaments [61, 76], indicating the feasibility of large scale simulations using mesoscopic models to compute the LVE response. Coarse-grained models seem to be unavoidable when performing simulations in those cases, and besides systematic coarsening modelling approaches [26, 51, 56], one could also explore simple heuristic models which take into account specific details of real biomolecules [77]. Additionally, one can consider the dynamics of probe particles obtained from simulations like the one presented in Ref. [78] to estimate the shear moduli from microrheological approaches [18]. While the entanglement modulus have been successfully determined from simulations of models based on primitive path analysis [29], it might be interesting to verify whether this and other approaches can be used to investigate issues related to dependence of Ge on the persistence length Lp for solutions in the tightly entangled regime [79]. As discussed in Ref. [27], it might be important to assess how significant are the correlations between different chains in entangled solutions, but only recently such large scale simulations have been reported for semiflexible filaments [80], even though their viscoelastic properties were not computed. Finally, it is worth mentioning that this mini-review focused on isotropic disordered biomaterials, but one can further explore solutions of semiflexible filaments which display nematic phases [81], and where anisotropic viscoelastic responses are expected. Also, it should be noted that, although configurations of filaments and their cross-linked networks have been mostly defined in an arbitrary manner (see, e.g., Figure 2E), experimentally-revelant mesoscopic information about semiflexible filamentous biomaterials are now becoming more available [82–84], and those may provide a strong driven-force in the implementation of novel physics-based computational simulations.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
The author acknowledges the financial support of the Brazilian agencies CNPq (Grant No. 426570/2018-9 and 312999/2021-6) and FAPEMIG (Process APQ-02783-18).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1It is worth noting that, in general, there should be also an entropic contribution to the shear stress [32], i.e., −(T/V)(∂S/∂γ). Even so, semiflexible biopolymers are usually described as athermal filaments [33], which mean that their shapes are practically not affected by thermal fluctuations.
2Generally, Monte Carlo (MC) methods provide the most efficient ways to equilibrate complex polymer systems [67].
References
1. Burla F, Mulla Y, Vos BE, Aufderhorst-Roberts A, Koenderink GH. From Mechanical Resilience to Active Material Properties in Biopolymer Networks. Nat Rev Phys (2019) 1:249–63. doi:10.1038/s42254-019-0036-4
2. Patteson AE, Carroll RJ, Iwamoto DV, Janmey PA. The Vimentin Cytoskeleton: When Polymer Physics Meets Cell Biology. Phys Biol (2021) 18:011001. doi:10.1088/1478-3975/abbcc2
3. Bausch AR, Kroy K. A Bottom-Up Approach to Cell Mechanics. Nat Phys (2006) 2:231–8. doi:10.1038/nphys260
4. Huber F, Schnauß J, Rönicke S, Rauch P, Müller K, Fütterer C, et al. Emergent Complexity of the Cytoskeleton: From Single Filaments to Tissue. Adv Phys (2013) 62:1. doi:10.1080/00018732.2013.771509
5. Corominas-Murtra B, Petridou NI. Viscoelastic Networks: Forming Cells and Tissues. Front Phys (2021) 9:666916. doi:10.3389/fphy.2021.666916
6. Osada Y, Kawamura R, Sano KI. Hydrogels of Cytoskeletal Proteins: Preparation, Structure, and Emergent Functions. Switzerland: Springer International Publishing (2016).
7. Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ. Scaling the Microrheology of Living Cells. Phys Rev Lett (2001) 87:148102. doi:10.1103/physrevlett.87.148102
8. Knowles TPJ, Vendruscolo M, Dobson CM. The Amyloid State and its Association with Protein Misfolding Diseases. Nat Rev Mol Cell Biol. (2014) 15:384. doi:10.1038/nrm3810
9. Picu C, Ganghoffer JF. Mechanics of Fibrous Materials and Applications: Physical and Modeling Aspects. Springer (2020).
10. Mak M, Kim T, Zaman MH, Kamm RD. Multiscale Mechanobiology: Computational Models for Integrating Molecules to Multicellular Systems. Integr Biol (2015) 7:1093. doi:10.1039/c5ib00043b
11. Lavery R, Lebrun A, Allemand JF, Bensimon D, Croquette V. Structure and Mechanics of Single Biomolecules: Experiment and Simulation. J Phys Condens Matter (2002) 14:R383. doi:10.1088/0953-8984/14/14/202
12. Rizzi LG, Tassieri M. Microrhelogy of Biological Specimens. In: RA Meyers, editor. Encyclopedia of Analytical Chemistry. John Wiley & Sons (2018). p. 1–24. doi:10.1002/9780470027318.a9419
13. Gong B, Wei X, Qian J, Lin Y. Modeling and Simulations of the Dynamic Behaviors of Actin-Based Cytoskeletal Networks. ACS Biomater Sci Eng (2019) 5:3720. doi:10.1021/acsbiomaterials.8b01228
16. Danielsen SPO, Beech HK, Wang S, El-Zaatari BM, Wang X, Sapir L, et al. Molecular Characterization of Polymer Networks. Chem Rev (2021) 121:5042. doi:10.1021/acs.chemrev.0c01304
18. Rizzi LG. Microrheological Approach for the Viscoelastic Response of Gels. J Rheol (2020) 64:969. doi:10.1122/8.0000034
19. Lees AW, Edwards SF. The Computer Study of Transport Processes Under Extreme Conditions. J Phys C: Solid State Phys (1972) 5:1921. doi:10.1088/0022-3719/5/15/006
20. Pasquali M, Shankar V, Morse DC. Viscoelasticity of Dilute Solutions of Semiflexible Polymers. Phys Rev E (2001) 64:020802. doi:10.1103/PhysRevE.64.020802
21. Dimitrakopoulos P, Brady JF, Wang ZG. Short- and Intermediate-Time Behavior of the Linear Stress Relaxation in Semiflexible Polymers. Phys Rev E (2001) 64:050803. doi:10.1103/PhysRevE.64.050803
22. Shankar V, Pasquali M, Morse DC. Theory of Linear Viscoelasticity of Semiflexible Rods in Dilute Solution. J Rheol (2002) 46:1111. doi:10.1122/1.1501927
23. Likhtman AE, Sukumaran SK, Ramirez J. Linear Viscoelasticity from Molecular Dynamics Simulation of Entangled Polymers. Macromolecules (2007) 40:6748. doi:10.1021/ma070843b
24. Ramanathan S, Morse DC. Simulations of Dynamics and Viscoelasticity in Highly Entangled Solutions of Semiflexible Rods. Phys Rev E (2007) 76:010501. doi:10.1103/PhysRevE.76.010501
25. Hou JX, Svaneborg C, Everaers R, Grest GS. Stress Relaxation in Entangled Polymer Melts. Phys Rev Lett (2010) 105:068301. doi:10.1103/PhysRevLett.105.068301
26. Padding JT, Briels WJ. Systematic Coarse-Graining of the Dynamics of Entangled Polymer Melts: The Road from Chemistry to Rheology. J Phys Condens Matter (2011) 23:233101. doi:10.1088/0953-8984/23/23/233101
27. Likhtman AE. Whither Tube Theory: From Believing to Measuring. J Non-Newton Fluid Mech (2009) 157:158. doi:10.1016/j.jnnfm.2008.11.008
28. Everaers R, Sukumaran SK, Grest GS, Svaneborg C, Sivasubramanian A, Kremer K. Rheology and Microscopic Topology of Entangled Polymeric Liquids. Science (2004) 303:823. doi:10.1126/science.1091215
29. Svaneborg C, Everaers R. Characteristic Time and Length Scales in Melts of Kremer-Grest Bead-Spring Polymers with Wormlike Bending Stiffness. Macromolecules 2020 (2020) 53:1917. doi:10.1021/acs.macromol.9b02437
30. Everaers R, Karimi-Varzaneh HA, Fleck F, Hojdis N, Svaneborg C. Kremer-Grest Models for Commodity Polymer Melts: Linking Theory, Experiment, and Simulation at the Kuhn Scale. Macromolecules (2020) 53:1901. doi:10.1021/acs.macromol.9b02428
31. Huisman EM, Storm C, Barkema GT. Frequency-Dependent Stiffening of Semiflexible Networks: A Dynamical Nonaffine to Affine Transition. Phys Rev E (2010) 82:061902. doi:10.1103/PhysRevE.82.061902
32. Yoshikawa Y, Sakumichi N, i Chung U, Sakai T. Negative Energy Elasticity in a Rubberlike Gel. Phys Rev X (2021) 11:011045. doi:10.1103/physrevx.11.011045
33. Broedersz C, MacKintosh F. Modeling Semiflexible Polymer Networks. Rev Mod Phys (2014) 86:995. doi:10.1103/revmodphys.86.995
34. Rizzi L, Auer S, Head D. Importance of Non-Affine Viscoelastic Response in Disordered Fibre Networks. Soft Matter (2016) 12:4332. doi:10.1039/c6sm00139d
35. Head DA, Levine AJ, Mackintosh FC. Deformation of Cross-Linked Semiflexible Polymer Networks. Phys Rev Lett (2003) 91:108102. doi:10.1103/physrevlett.91.108102
36. Head DA, Levine AJ, Mackintosh FC. Distinct Regimes of Elastic Response and Deformation Modes of Cross-Linked Cytoskeletal and Semiflexible Polymer Networks. Phys Rev E (2003) 68:061907. doi:10.1103/PhysRevE.68.061907
37. Broedersz CP, Mao X, Lubensky TC, MacKintosh FC. Criticality and Isostaticity in Fibre Networks. Nat Phys (2011) 7:983. doi:10.1038/nphys2127
38. Rizzi LG, Head DA, Auer S. Universality in the Morphology and Mechanics of Coarsening Amyloid Fibril Networks. Phys Rev Lett (2015) 114:078102. doi:10.1103/PhysRevLett.114.078102
39. Duarte LKR, Teixeira AVNC, Rizzi LG. Microrheology of Semiflexible Filament Solutions Based on Relaxation Simulations. Soft Matter (2021) 17:2920. doi:10.1039/d0sm01976c
41. Evans DJ, Morriss GP. Statistical Mechanics of Nonequilibrium Liquids. Canberra, Australia: ANU Press (2007).
42. Müller-Plathe F. Reversing the Perturbation in Nonequilibrium Molecular Dynamics: An Easy Way to Calculate the Shear Viscosity of Fluids. Phys Rev E (1999) 59:4894.
43. Nikoubashman A, Howard MP. Equilibrium Dynamics and Shear Rheology of Semiflexible Polymers in Solution. Macromolecules (2017) 50:8279. doi:10.1021/acs.macromol.7b01876
44. Larson RG. The Rheology of Dilute Solutions of Flexible Polymers: Progress and Problems. J Rheol (2005) 49:1. doi:10.1122/1.1835336
45. Frenkel D, Smit B. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press (2002).
46. Gompper G, Ihle T, Kroll D, Winkler R. Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids. In: C. Holm,, and K. Kremer, editors. Advanced Computer Simulation Approaches for Soft Matter Sciences III, 221. Springer-Verlag (2009). p. 1–87. Adv. Polym. Sci..
47. Likhtman AE. 1.06 - Viscoelasticity and Molecular Rheology. In: K. Matyjaszewski,, and M. Möller, editors. Polymer Science: A Comprehensive Reference, 1. Elsevier (2012). p. 133–79. doi:10.1016/b978-0-444-53349-4.00008-x
48. Guénolé J, Nöhring WG, Vaid A, Houllé F, Xie Z, Prakash A, et al. Assessment and Optimization of the Fast Inertial Relaxation Engine (FIRE) for Energy Minimization in Atomistic Simulations and its Implementation in LAMMPS. Comput Mater Sci (2020) 175:109584.
49. Picu RC. Mechanics of Random Fiber Networks - A Review. Soft Matter (2011) 7:6768. doi:10.1039/c1sm05022b
50. Azevedo TN, Rizzi LG. Microrheology of Filament Networks from Brownian Dynamics Simulations. J Phys Conf (2020) 1483:012001. doi:10.1088/1742-6596/1483/1/012001
51. Li Y, Abberton BC, Kröger M, Liu WK. Challenges in Multiscale Modeling of Polymer Dynamics. Polymers (2013) 5:751. doi:10.3390/polym5020751
52. Gartner TE, Jayaraman A. Modeling and Simulations of Polymers: A Roadmap. Macromolecules (2019) 52:755. doi:10.1021/acs.macromol.8b01836
53. Zierenberg J, Marenz M, Janke W. Dilute Semiflexible Polymers with Attraction: Collapse, Folding and Aggregation. Polymers (2016) 8:333. doi:10.3390/polym8090333
54. Auer S, Dobson CM, Vendruscolo M, Maritan A. Self-Templated Nucleation in Peptide and Protein Aggregation. Phys Rev Lett (2008) 101:258101. doi:10.1103/physrevlett.101.258101
55. Auer S, Kashchiev D. Phase Diagram of α-Helical and β-Sheet Forming Peptides. Phys Rev Lett (2010) 104:168105. doi:10.1103/physrevlett.104.168105
56. Morriss-Andrews A, Shea JE. Computational Studies of Protein Aggregation: Methods and Applications. Annu Rev Phys Chem (2015) 66:643. doi:10.1146/annurev-physchem-040513-103738
57. Grest GS, Kremer K. Molecular Dynamics Simulation for Polymers in the Presence of a Heat Bath. Phys Rev A (1986) 33:3628. doi:10.1103/physreva.33.3628
58. Weeks JD, Chandler D, Andersen HC. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J Chem Phys (1971) 54:5237. doi:10.1063/1.1674820
59. Nikoubashman A, Milchev A, Binder K. Dynamics of Single Semiflexible Polymers in Dilute Solution. J Chem Phys (2016) 145:234903. doi:10.1063/1.4971861
60. Frigori RB, Rizzi LG, Alves NA. Microcanonical Thermostatistics of Coarse-Grained Proteins with Amyloidogenic Propensity. J Chem Phys (2013) 138:015102. doi:10.1063/1.4773007
61. Myung JS, Winkler RG, Gompper G. Self-Organization in Suspensions of End-Functionalized Semiflexible Polymers Under Shear Flow. J Chem Phys (2015) 143:243117. doi:10.1063/1.4933368
62. Pritchard RH, Huang YYS, Terentjev EM. Mechanics of Biological Networks: From the Cell Cytoskeleton to Connective Tissue. Soft Matter (2014) 10:1864. doi:10.1039/c3sm52769g
63. Meng F, Terentjev EM. Theory of Semiflexible Filaments and Networks. Polymers (2017) 9:52. doi:10.3390/polym9020052
64. Koslover EF, Spakowitz AJ. Multiscale Dynamics of Semiflexible Polymers from a Universal Coarse-Graining Procedure. Phys Rev E (2014) 90:013304. doi:10.1103/PhysRevE.90.013304
65. Muthukumar M. 50th Anniversary Perspective: A Perspective on Polyelectrolyte Solutions. Macromolecules (2017) 50:9528. doi:10.1021/acs.macromol.7b01929
66. Rizzi LG, Levin Y. Influence of Network Topology on the Swelling of Polyelectrolyte Nanogels. J Chem Phys (2016) 144:114903. doi:10.1063/1.4943981
67. Mavrantzas VG. Using Monte Carlo to Simulate Complex Polymer Systems: Recent Progress and Outlook. Front Phys (2021) 9:661367. doi:10.3389/fphy.2021.661367
68. Yucht MG, Sheinman M, Broedersz CP. Dynamical Behavior of Disordered Spring Networks. Soft Matter (2013) 9:7000. doi:10.1039/c3sm50177a
69. Head D, Storm C. Nonaffinity and Fluid-Coupled Viscoelastic Plateau for Immersed Fiber Networks. Phys Rev Lett (2019) 123:238005. doi:10.1103/physrevlett.123.238005
70. Hatami-Marbini H, Shriyan V. Topology Effects on Nonaffine Behavior of Semiflexible Fiber Networks. Phys Rev E (2017) 96:062502. doi:10.1103/PhysRevE.96.062502
71. Huisman EM, van Dillen T, Onck PR, der Giessen EV. Three-Dimensional Cross-Linked F-Actin Networks: Relation Between Network Architecture and Mechanical Behavior. Phys Rev Lett (2007) 99:208103. doi:10.1103/physrevlett.99.208103
72. Huisman EM, Storm C, Barkema GT. Monte Carlo Study of Multiply Crosslinked Semiflexible Polymer Networks. Phys Rev E (2008) 78:051801. doi:10.1103/PhysRevE.78.051801
73. Huisman EM, Lubensky TC. Internal Stresses, Normal Modes, and Nonaffinity in Three-Dimensional Biopolymer Networks. Phys Rev Lett (2011) 106:088301. doi:10.1103/PhysRevLett.106.088301
74. Heidemann KM, Sharma A, Rehfeldt F, Schmidt CF, Wardetzky M. Elasticity of 3d Networks with Rigid Filaments and Compliant Crosslinks. Soft Matter (2015) 11:343. doi:10.1039/c4sm01789g
75. Broedersz CP, Depken M, Yao NY, Pollak MR, Weitz DA, MacKintosh FC. Cross-Link-Governed Dynamics of Biopolymer Networks. Phys Rev Lett (2010) 105:238101. doi:10.1103/physrevlett.105.238101
76. Groot RD. Mesoscale Simulation of Semiflexible Chains. II. Evolution Dynamics and Stability of Fiber Bundle Networks. J Chem Phys (2013) 138:224904. doi:10.1063/1.4808200
77. Škrbić T, Maritan A, Giacometti A, Rose GD, Banavar JR. Building Blocks of Protein Structures: Physics Meets Biology. Phys Rev E (2021) 104:014402. doi:10.1103/PhysRevE.104.014402
78. Nahali N, Rosa A. Nanoprobe Diffusion in Entangled Polymer Solutions: Linear vs. Unconcatenated Ring Chains. J Chem Phys (2018) 148:194902. doi:10.1063/1.5022446
79. Tassieri M. Dynamics of Semiflexible Polymer Solutions in the Tightly Entangled Concentration Regime. Macromolecules (2017) 50:5611. doi:10.1021/acs.macromol.7b01024
80. Lang P, Frey E. Disentangling Entanglements in Biopolymer Solutions. Nat Commun (2018) 9:494. doi:10.1038/s41467-018-02837-5
81. Jordens S, Isa L, Usov I, Mezzenga R. Non-Equilibrium Nature of Two-Dimensional Isotropic and Nematic Coexistence in Amyloid Fibrils at Liquid Interfaces. Nat Commun (2013) 4:1917. doi:10.1038/ncomms2911
82. Licup AJ, Münster S, Sharma A, nadJawerth LMMS, Fabry B, Weitz DA, et al. Stress Controls the Mechanics of Collagen Networks. Proc Natl Acad Sci USA (2015) 112:9573. doi:10.1073/pnas.1504258112
83. Usov I, Mezzenga R. Fiberapp: An Open-Source Software for Tracking and Analyzing Polymers, Filaments, Biomacromolecules, and Fibrous Objects. Macromolecules (2015) 48:1269. doi:10.1021/ma502264c
Keywords: semiflexible filaments, computational simulations, viscoelastic biomaterials, microrheology, coarse-grained models
Citation: Rizzi LG (2022) Physics-Based Computational Approaches to Compute the Viscoelasticity of Semiflexible Filamentous Biomaterials. Front. Phys. 10:893613. doi: 10.3389/fphy.2022.893613
Received: 10 March 2022; Accepted: 02 May 2022;
Published: 20 June 2022.
Edited by:
Marco Laurati, University of Florence, ItalyReviewed by:
Jose Manuel Ruiz Franco, Wageningen University and Research, NetherlandsElena Koslover, University of California, San Diego, United States
Copyright © 2022 Rizzi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: L. G. Rizzi , bGVyaXp6aUB1ZnYuYnI=
 L. G. Rizzi
L. G. Rizzi