- 1Departament de Física Quàntica i Astrofísica and Institut de Ciències Del Cosmos (ICCUB), Universitat de Barcelona, MartÍ i Franqués, Barcelona,, Spain
- 2Max-Planck-Institut für Gravitationsphysik, Potsdam, Germany
- 3International Solvay Institutes ULB-Campus Plaine , Brussels, Belgium
Kinematic algebras can be realised on geometric spaces and constrain the physical models that can live on these spaces. Different types of kinematic algebras exist and we consider the interplay of these algebras for non-relativistic limits of a relativistic system, including both the Galilei and the Carroll limit. We develop a framework that captures systematically the corrections to the strict non-relativistic limit by introducing new infinite-dimensional algebras, with emphasis on the Carroll case. One of our results is to highlight a new type of duality between Galilei and Carroll limits that extends to corrections as well. We realise these algebras in terms of particle models. Other applications include curvature corrections and particles in a background electro-magnetic field.
1 Introduction
Relativistic and non-relativistic systems are usually distinguished by their kinematic algebras. Classifications of possible kinematic algebras (for point particles) have been obtained in four space-time dimensions in Refs. 1, 2 and in different dimensions for instance in Refs. 3, 4. The Poincaré algebra constrains relativistic systems in flat space, while non-relativistic systems of particles are subjected for example to Galilean or Carrollian algebras.1 In a given system, there is typically a physical quantity that can be combined with the speed of light c to form a dimensionless quantity whose limit to zero (or to infinity) defines the non-relativistic limit of the system. The prototypical example is the speed of a particle v and then the dimensionless quantity can be taken as v/c. In gravitational systems there is additionally the Newton constant to form dimensionless parameters and multiple limits can be considered in such cases [5, 6]. Similarly, for extended objects one can consider non-relativistic limits, but the extended nature of the world-volume allows for a variety of different limits [7–10].
The kinematic algebras do not contain the dimensionful quantity of a given physical system but only fundamental constants, for example c in the case of the Poincaré algebra although it is usually not explicit since it is absorbed in the definition of the generators. One can still consider non-relativistic limits of the algebras by formally scaling the parameters. This process, first performed for obtaining the Galilei algebra from the Poincaré algebra, is known as a (Inönü–Wigner) contraction of a Lie algebra [11]. The limit c → ∞ considered there implicitly assumes that all particle velocities that can arise are small compared to the speed of light. The similar contraction c → 0 giving the Carroll algebra [12, 13] makes the assumption that all particle velocities are large compared to the speed of light. We shall review these cases in detail in Section 2.1.
The non-relativistic symmetries obtained by Inönü–Wigner contractions are the strict limits of the scaling parameter, e.g., c → ∞ or c → 0. However, the inclusion of relativistic corrections is desirable for many systems such as their contributions to the fine structure of atoms. While many relativistic equations can be expanded in the small parameters, the resulting equations do not exhibit symmetries beyond the contracted algebra. It is one of the aims of this contribution to explain how to formulate a framework of kinematic algebras for these corrections. The main method we will use is to enlarge the space on which the symmetry acts and thereby allow for extensions of the contracted algebra.
One can construct systematically kinematic algebras that include perturbative corrections in a parameter (like 1/c) by deforming the contracted algebra, in this way performing something like the inverse of a Lie algebra contraction. This process adds new generators to the original algebra and thus enlarges it. Considering all-order expansions in the small parameter we obtain infinite-dimensional algebras and there are different ways of arriving at them.
One is to view the deformation problem as a cohomology problem such that one is asking for the most general non-trivial commutator of generators that commute in the contracted algebra. For instance, in the Galilei algebra one has famously that spatial translations Pi and Galilean boosts Bj commute while their most general commutator would be
A second way of obtaining a systematic perturbative extension of a kinematic algebra is the method of Lie algebra expansion [17–22]. This method can be described in its simplest form by starting with an algebra and tensoring it with a commutative semigroup. An example of a commutative semigroup is given by
The two constructions are not unrelated. This can be seen in the Galilean example with free Lie algebra commutator
There is furthermore a connection of the two constructions to (Borel subalgebras of) affine Kac–Moody algebras. Affine Kac–Moody algebras are obtained by tensoring a finite-dimensional algebra
There are many variations of these constructions one can consider, depending on the algebra one starts with and the precise expansion or quotient of a free Lie algebra one takes. The physical interpretation of the parameter λ depends on the context one considers and is by no means restricted to non-relativistic limits. It can also be viewed as a curvature parameter when one wants to describe deviations from flat space isometries as we shall review. Another arena is where higher powers of λ correspond to more and more complicated electro-magnetic backgrounds in Minkowski space, where the kinematic algebra becomes a generalisation of the Maxwell algebra [26–29].
The above methods provide a plethora of kinematic algebras of finite or even infinite dimension. Our next aim will be to describe a space on which they can act in the same way that the Poincaré algebra acts on flat Minkowski space. Such a space is not hard to find using a non-linear realisation [30–35] approach with a suitable coset. It is of higher dimension than usual space-time and we present many examples with different physical interpretations. Once a generalised space is defined we strive to probe it using a physical model. The simplest instance is that of a free particle moving in it and there are canonical constructions of associated particle models that we shall go through.5 One could also consider using higher-dimensional objects as probes but we shall not pursue this here.
As we shall demonstrate, these particle models give rise systematically to relativistic (or similar) corrections to the dynamics associated with the truncated algebra. Particular emphasis will be put on the case of Carroll particles, both of ordinary [38, 39] and of tachyonic [40] type. The reason for this is that they have featured prominently in recent studies, including applications to cosmology [40–44]. Formally, the Carroll limit is also related to the Belinsky–Khalatnikov–Lifshitz limit [45, 46] where temporal derivatives dominate over spatial derivatives ∂t ≫ c∂x and so formally c → 0. We shall also exhibit a new type of duality between (corrections to) Galilei and Carroll particle actions in Section 4.3.
The structure of this contribution is as follows. We first explain the basic algebraic constructions of kinematic algebras and their interrelations in Section 2. Then we present generalised space-times on which the kinematic algebras can act in Section 3. To probe the set-up we then consider free particle actions in Section 4 where we deduce non-relativistic and similar corrections. Some concluding comments are given in Section 5.
2 Algebraic Constructions
We present various methods for constructing kinematic algebras and how they are related to one another.
2.1 Contractions and Extensions of Kinematic Algebras
As an illustrative starting point we choose the Poincaré algebra in D = d + 1 space-time dimensions
where small Roman indices from the beginning of the alphabet are fundamental
which is an invertible change of basis for any λ > 0 and the algebra becomes
We see that we can take the limit λ → 0 smoothly and obtain a new algebra in that limit. This so-called contracted algebra is the non-relativistic Galilei algebra (c → ∞) where now Galilean boosts commute among themselves and with translations. This is the most famous example of an Inönü–Wigner contraction of a Lie algebra [11]. As is usual, the contracted algebra is no longer isomorphic to the algebra with λ > 0. The square root in Eq. 2.2 arises since we think of λ as 1/c2.6 For future reference we write the resulting contracted Galilei algebra
An alternative contraction of the algebra is obtained by formally interchanging the roles of time and space directions for the translation generators, i.e., letting [12]
and contracting again λ → 0. This leads to the Carroll algebra
This contraction of the Poincaré algebra is also known as the Carroll limit in which the speed of light tends to zero (c → 0). We see from Eqs 2.2 and 2.5 that there is a duality between the Galilean and the Carrollian contraction that simply exchanges the role of space and time translations in the contraction. Thinking of the time direction as the longitudinal direction of the world-line of a (massive) particle and the space directions as the transverse directions, makes it clear that a similar duality between longitudinal and transverse directions will be present for contractions related to extended objects as was discussed in more detail in Ref. 10.
Let us now formalise the contraction process. We start from an algebra
One approach to undoing the contraction perturbatively requires the knowledge of the original algebra
where the offset n0(α) can depend on the generator, we construct an infinite-dimensional algebra of the generators
Let us exemplify this in the case of the Galilei algebra Eq. 2.4. We define for n ≥ 0
where the offsets are taken in accordance with Eq. 2.2. The associated Lie algebra is
Since all commutators of generators at levels m and n generate only terms of level at least m + n, we can consistently quotient out all generators above a fixed level N. This leads to a finite-dimensional algebra. Retaining only the generators of level 0 leads to the Galilei algebra that is obtained by contraction. Keeping all generators up to level N then gives a perturbative approximation to the Poincaré algebra up to that order. The algebra Eq. 2.9 was given in Ref. 48, see also Refs. 49–52.
Repeating the same construction for the Carroll contraction Eq. 2.5 one can start with
We note that, when comparing Eq. 2.8 for the expanded Galilei algebra with Eq. 2.10 for the Carroll algebra, there is a duality between the two algebras where the λ1/2 is changed from P0 to Pi. This is a generalisation of the type of duality that has been noted before in Refs. 10, 24, 53.
The definition Eq. 2.10 leads to the infinite-dimensional algebra
We note that comparing this formula to Eq. 2.9, there are subtle but important differences in the shifts of the indices by + 1 on the right-hand sides which are due to the placements of λ1/2 in the definitions of the algebra, and so ultimately to the physical meaning of the contractions.
The above procedure can also be viewed as a variant of the method of Lie algebra expansions that was originally introduced in Refs. 17–22. For a Lie algebra expansion in its formulation given in Ref. 20 one requires an abelian semi-group S whose elements we call λi and the S-expanded Lie algebra
and commutativity of the product on S ensures the Jacobi identity of the expanded algebra. A simple example of a semi-group is given by
The element λN+1 serves as a substitute for zero in the multiplication. Tensoring this semi-group with the real numbers corresponds to taking the quotient of the polynomial rings
A more refined version of the Lie algebra expansion method can be obtained when the original Lie algebra has a decomposition. We here restrict to the case when8
(We use different letters here for the graded pieces in order to avoid confusion with the contracted algebra
with the obvious Lie brackets. It is this refined version of a Lie algebra expansion that makes direct contact with Eq. 2.7. A simple example of the refined expansion would be to take the Poincaré algebra Eq. 2.1 and write it as
The expansion with
with new non-trivial commutators
in the expanded algebra.
The algebra obtained by expanding with
2.2 Free Algebras, Cohomology and Quotients
We now turn to the discussion of free Lie algebras. General references for this are Refs. 54 and 55 and we follow the exposition in Refs. 16 and 29.
A free Lie algebra on a (finite) set of D = d + 1 generators
is obtained by considering all possible multi-commutators of the generators Pa only subject to anti-symmetry and the Jacobi identity. There is a natural grading of the free Lie algebra by the number of times the generators Pa appear in the multi-commutator.9 The infinite-dimensional free Lie algebra
with for example
being of dimension
The full structure of
that leads for example to
With ⊖ we mean the removal of a vector space from the tensor product, so that for
Free Lie algebras as defined above are graded consistently with Eq. 2.20, i.e., they satisfy
The elements in
The free Lie algebra can also be viewed as a successive extension of the real commutative Lie algebra
but the Zab are central in this extended algebra. Thus one has obtained a graded Lie algebra
As suggested by the notation (Eq. 2.19), we wish to think of the elements of
to begin with. As a Lie algebra this is a semi-direct sum since
Free Lie algebras
1. Level truncation: Due to the grading (Eq. 2.24), the space
is a Lie algebra ideal inside
consists of all elements up to level ℓ (as a vector space) and commutators going beyond the truncation are set to zero.
2. Row truncation: Referring back to the representation (Eq. 2.25) of elements of
which is an ideal of
3. Derivative truncation: The row truncation above can be refined by considering the ideal
The corresponding quotient
then consists only of those generators of
with an arbitrary number of boxes in the first row. Why we refer to this quotient as the derivative truncation will become clear in Section 4.6 below.
Yet another common quotient is described by Serre relations and this arises for Kac–Moody algebras [25, 58] as we shall review in Section 2.3 below.
2.2.1 Maxwell Free Lie algebra
Let us illustrate the free Lie algebra construction in the simplest case where
where Zab = Z[ab] is a basis of
Under the Lorentz generators Mab all elements transform as tensors in the way that their indices dictate.
The antisymmetric element Zab arose first in studies of the extension of the Poincaré algebra in the presence of a constant electro-magnetic field [1, 26, 27] when one co-rotates the constant field Fab under Lorentz [27, 28]. The extension including the generators Yab,c was also considered in Ref. 28 where it was linked to linearly varying electro-magnetic backgrounds: Fab ∼ Yab,cxc (in Cartesian coordinates) and the Young irreducibility (Eq. 2.35) is equivalent to the Bianchi identity
We note that one can also consider non-relativistic limits of the relativistic Maxwell algebra and there are different limits that arise depending on the scaling of the electric and magnetic fields. The corresponding algebras can be called electric, magnetic and pulse Maxwell algebras [16, 59].
2.2.2 Galilean Free Lie algebra
A second instance of the free Lie algebra construction can be obtained by starting from the Galilei algebra (Eq. 2.4) and letting [16]
Note that this assignment of generators to levels is different from that that would be inherited directly from the Poincaré case in the previous section. However, this assignment is consistent with the grading due to the contracted commutation relations (Eq. 2.4). A consequence of Eq. 2.36 is that the translation generator Ti occurs at level two in the free Lie algebra via the commutator
The free Lie algebra generated from Eq. 2.36 was called the magnetic Galilei algebra in Ref. 16 and it is the only case we consider here. Due to the presence of the rotation-invariant H inside
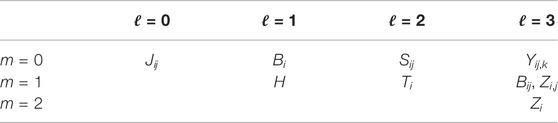
TABLE 1. The first few levels of the free Lie algebra generated by the (magnetic) Galilean choice (Eq. 2.36). The double-grading (ℓ, m) is explained in the text. A similar table has appeared in Ref. 16.
The notation in the table is such that indices that are separated with commas are in separate columns of a Young diagram while unseparated ones are in the same column. For instance, the commutator between the Galilean boost Bi and translation Ti is
The symmetric tensor Zi,j can be traced using the Euclidean metric δij and the corresponding scalar M under rotations is nothing but the Bargmann central extension [Bi, Tj] ∝ δijM.
However, the free Lie algebra methods provides many further extensions of interest that are discussed in more detail in Ref. 16.
2.2.3 Carrollian Free Lie algebra
In the same way as for the Galilei algebra above one can also construct a free Lie extension of the Carroll algebra (Eq. 2.6). By applying the duality P0 ↔ Pi between the Carroll and Maxwell case discussed in Section 2.1 one is led to starting from
that should be compared to Eq. 2.36.
Running the free Lie algebra construction (Eq. 2.23) then produces as next generators the result shown in Table 2, where we also introduced a second grading m to distinguish the generators Ki and Ti. Some commutators defining the elements in the table are written explicitly as
where Zi,j is symmetric while all the other rank two tensors Sij, Bij and Tij are anti-symmetric. The Carroll Hamiltonian K (see Eq. 2.6) is obtained as the trace of the symmetric tensor:
where we recall that d is the number of spatial dimensions.

TABLE 2. The first few levels of the free Lie algebra generated by Carroll. The double-grading (ℓ, m) is explained in the text, as is the relation between Young diagrams and comma-separated index notation.
We can recover the infinite Carroll algebra (Eq. 2.11) from the free Lie algebra construction by following steps similar to Ref. 16. By restricting to anti-diagonal lines (of fixed ℓ − m) in Table 2, restricting further to m ∈ {0, 1} and keeping only generators of vector and scalar type under rotations, we obtain an infinity of generators
2.3 Connection to Kac–Moody Algebras
In this final section on algebraic constructions we would like to make a brief comment on the relation to (affine) Kac–Moody algebras. For any finite-dimensional Lie algebra
of Laurent polynomials in λ with values in
The relation to the constructions above becomes transparent by restricting to the parabolic subalgebra of polynomials
The parabolic subalgebra
3 Geometric Realisations
Suppose we have a kinematic algebra
Let xa denote a set of local coordinates of M on which there is a faithful action of
With this we mean that
with an appropriate offset n(a) depending on the coordinate and restricted to n = 0 carries a faithful action of
to be dimensionless which means that the scaling of
3.1 Post-Galilean Space-Time
For the Poincaré algebra (Eq. 2.1) the space M is Minkowski space in D dimensions with coordinates xa of dimension L = length. The faithful action of the Poincaré algebra can described as follows. Let
be an arbitrary element of the Poincaré algebra. Its action on the coordinate xa is given by
For the Lorentz part
For the Galilean contraction (Eq. 2.2) we split space and time a = (0, i) and let
Here, the dimensions of t(n) and
The action of an element
of the algebra (Eq. 2.9) on a (dimensionless) coordinate element
is then given by the commutator of the two elements, leading to
We see that restricting to only level 0 this becomes the usual action on the Galilean coordinates (t, zi) with t = t(0) and
which is the lowest order term of the Lorentz boost. Note that in our conventions the parameter v(0) has dimension of L/T as a velocity, but we recall that
In order to see the systematic higher order expansion of the Lorentz boost encoded in Eq. 3.5, we follow [48] and define collective coordinates formally by
as well as the collective boost parameter
The transformation of the collective coordinates (Eq. 3.11) under such a collective boost then works out as
the usual expression for an infinitesimal relativistic Lorentz boost with rapidity Θi. However, the difference is that now the boost parameter and the coordinate are collective.
If one imposes that
for some scalar v and spatial unit vector ni, i.e., δijninj = 1, then the transformations (Eq. 3.13) become for λ = c−2
which are the expansions of the infinitesimal Lorentz boost with parameter θi = θni, where tanh θ = v/c for v/c ≪ 1.
At this point we should comment on the geometrical meaning of the collective coordinates (Eq. 3.11). These define a hyperspace of co-dimension D within the infinite-dimensional generalised Minkowski space with coordinates (Eq. 3.5). Since the sums are infinite and we are not making any assumptions about convergence here, the expressions are formal but the formal expansion parameter λ is introduced in such a way as to render meaningful expressions at any finite order in the expansion. What the transformation (Eq. 3.13) then describes is a transformation from one hyperspace to another one, so we obtain a description of ordinary Minkowski space as a family of hyperspaces inside generalised Minkowski space. We shall see that a similar picture applies to all other expansions considered in this paper.
3.2 Post-Carrollian Space-Time
For the case of the Carroll algebra, we use “Carroll time” s = Cx0 introduced in Refs. 12, 39. The contraction limit in these variables is C → ∞. Morally, we can think of C as being related to the inverse of the speed of light, so that the speed of light goes to zero. However, the dimension of C is that of a velocity. The expansion parameter λ = C−2, so that s(0) = x0 ⊗ C is the Carroll time of Refs. 12, 39.
For the Carrollian contraction (Eq. 2.5) we proceed analogously to the generalised Galilei space-time and define
where the difference to Eq. 3.5 that the constant shift has moved from the space to the time translations. The dimensions of the coordinates implied by these definitions are [s(n)] = L2n+2/T2n+1 and
A dimensionless element
of the expanded Carroll algebra (Eq. 2.11) then acts on the coordinates by
Especially, restricting to lowest order we obtain for the Carrollian time coordinate s = s(0) and
the well-known expression for this boost, see, e.g., Refs. 12, 39. In particular, an ordinary particle at rest cannot be Carroll boosted to one in motion: it is effectively stationary in any frame.
We now turn to corrections to this classical statement as contained in the infinite-dimensional algebra (Eq. 2.11). We introduce the collective coordinates
as well as the collective boost parameter
The transformation then becomes
just as in Eq. 3.13 and thus formally resembles the usual infinitesimal Lorentz boost with parameter Θi. With λ = C−2 we can now specialise to
to arrive at
This is the correct expansion of a Lorentz boost in Carroll parametrisation where
3.3 Conformal Post-Galilean Space-Time
The relativistic conformal algebra in D > 2 dimensions is
A non-relativistic Galilean version of this algebra can be obtained by considering the contraction (λ = c−2)
that extends the Galilean contraction (Eq. 2.2) from Poincaré to the conformal algebra. The resulting contracted algebra is known as the Galilei conformal algebra and has been studied for example in Refs. 61–65, see also Refs. 66, 67 for a recent extension to higher spin algebras.
The two lines of Eq. 3.27 also define spaces V0 and V1 satisfying (Eq. 2.14), so that an infinite expanded algebra undoing the contraction can be defined, exactly in the same way as for the previous cases. An infinite generalised space-time on which the infinite expanded Galilei conformal algebra can act is then defined by introducing coordinates
The action of the algebra on these coordinates can be worked out in the same way as in the previous cases, with the additional feature that the action of the special conformal transformation is non-linear in the coordinates due to the relativistic expressions
extending the Poincaré transformations (Eq. 3.4).
Collectives coordinates are defined by
exactly as for the non-conformal Galilei case (Eq. 3.11). Under special conformal transformations (Eq. 3.29), the lowest order coordinates transform as
where we have expanded the parameter of the transformation as
3.4 Post-Minkowski Space-Time
The small parameter can also be taken to be the curvature of space-time in appropriate dimensions. This was considered in Ref. 68 and leads to corrections to Minkowski space-time towards (Anti-)de Sitter space when the starting point is the (A)dS algebra that differs from the Poincaré algebra (Eq. 2.1) by the non-trivial commutator
among the translations. The sign σ = +1 is the AdS algebra
Following our usual expansion method we define the generators
where now λ = R−2 is to be thought of as the curvature scale of the (A)dS space-time. For R → ∞ we obtain the Poincaré algebra (Eq. 2.1) as a contraction of the (A)dS algebra similar to the non-relativistic cases in Section 2.1.
One can now similarly consider an extended space-time with coordinates
The transformations formula for these coordinates is now more complicated since the underlying translations no longer commute due to Eq. 3.33. Since we do not rely on them in the following, we refer the reader to Ref. 68. In Section 4.5 we shall study a particle model based on this generalised space-time.
3.5 Minkowski–Maxwell Space-Time
In the case of the Maxwell extension of Poincaré we also deal with non-commuting translations Pa, the basic commutator is Eq. 2.26, where Zab is a new generator unlike in the case of the (A)dS algebra.
The most general algebra that we can construct when starting from the Poincaré algebra is the Maxwell free Lie algebra that was introduced in Section 2.2.1. An associated generalised space-time can be defined by considering the Pa and all their free commutators as translation generators. This means that one has coordinates for each of them [28, 29]
The generalised space-time defined by these coordinates has non-abelian translations
where the higher-level coordinates are also affected by the translations of all lower levels.
In Section 4.6, we consider a particle model on the associated space-time and how it relates to the motion of charged particle in an electro-magnetic background field. We also note that one can consider various non-relativistic limits of Maxwell algebras and space-times [16, 59, 69].
4 Free Actions
In this section, we consider particle actions for free spinless particles in the various generalised space-times constructed in the previous section. We shall discuss in particular how they can be used to reproduce the corrections to the usual relativistic free particles. The case of the Carrollian generalisation will be discussed in most detail since it is less well-covered in the literature but has recently attracted attention in the context of cosmology and gravity [40–44]. We shall consider both tachyonic and ordinary particles and the resulting corrections in the case of Carroll are new to the best of our knowledge. In general, we shall parametrise the world-lines of particles using a parameter τ and denote derivatives with respect to this parameter by dots. The dimension of this parameter will be that of time (T) for Galilei but that of Carroll time (L2/T) for Carroll.
4.1 Particle in Post-Galilean Space-Time
The starting point for all actions comes from the expansion of the relativistic invariant metric using the collective coordinates (Eq. 3.11)
where the factor of λ in front of the spatial metric is crucial.
We shall first consider the usual massive relativistic particle, corresponding to a time-like norm of the velocity vector, and its Galilean limit. Then we shall consider the same procedure for a relativistic tachyon whose velocity vector is space-like and whose Galilean limit is a massless Galilean particle. The intuitive reason for this is that massless propagation in Newtonian physics is instantaneous which corresponds to space-like trajectories in Minkowski space. Galilean limits of relativistic light-like particles will not be considered in the context of post-Galilean space-time but in its conformal extension in Section 4.4.
4.1.1 Massive Galilean Particle
Perturbative actions for a massive particle can be obtained by expanding the reparametrisation invariant configuration space action
in powers of λ = c−2 with the result
This was given in Ref. 48 up to the fact that the dimensions of the variables here differ from there by a factor of c.
The actions written in Eq. 4.3 have global symmetries associated with the expanded algebras from Section 2.1 up to the order in the expansion. In particular, the action S(2) has more symmetries than the usual Galilei (or Bargmann) invariance. In addition, the actions have gauge symmetries generated by first-class constraints [48]. Gauge-fixing these symmetries one still retains enhanced global symmetries that are realised non-linearly. As we shall describe next, we will also identify the space coordinates
The first action S(0) is a total derivative and does not describe any non-trivial local dynamics. The existence of this term is nevertheless significant and related to the possibility of centrally extending the Galilei algebra to the Bargmann algebra [70].
The next action S(1) becomes the usual non-relativistic
in order to obtain conventional dimensions, but we emphasise that this step is not fixing a gauge symmetry but breaks symmetries [48].
For the next order term S(2), we similarly gauge-fix
and choose a slice as
This choice of slice is dictated by the relation (Eq. 3.5) between Minkowski and generalised Minkowski space. Plugging this into Eq. 4.3 leads to (using vector notation for the spatial components for simplicity)
Working out the energy of the particle associated with this action leads to
which agrees with the expansion of the relativistic energy
to the order given. Such an analysis can be performed to any desired order. Similarly, the momentum can be worked out as
which are the first two terms in the large-c expansion of
There is an ambiguity in interpreting the actions (Eq. 4.3) in terms of which space they are defined on. Since we started with an action on Minkowski space it is natural to view the actions as being defined on generalised Minkowski space to the same order in λ for both time and space variables. This means for example that we would like to view
to depend also formally on x(0) although x(0) does not enter the action at all. Taking this point of view implies that there are two canonical constraints associated to the action S(0), namely
The second constraint
4.1.2 Massless Galilean Particle
The massless Galilean particle [71] can be obtained as the non-relativistic limit of the relativistic tachyon [72]. From the point of view of the kinematic algebra the massless Galilean particle has vanishing Bargmann central charge. We will work out the first correction starting from a phase form of the action, starting from
where we have introduced the “colour” k2 = m2c2 [71]. The lowest order term in the limit c → ∞ removes the energy from the mass-shell constraint, leading to the action [72]
Here, we have used the expansions (λ = c−2)
These expansions are consistent with Eq. 3.11 except for an adjustment of dimensions. The variables
One thing we can immediately deduce from Eq. 4.14 is that
The next order action in S = ∑n≥0S(n) with S(n) of order λn then is
We note that the expansion of the momenta and coordinates always leads to a symplectic structure where the components are paired from opposite ends. The action enforces the constraints
Moreover, the action (Eq. 4.16) gives the constraint
similar to the constraint
The expanded actions S(N) derived from phase space always feature the same number N + 1 of t(n) and
As we shall see later, there is an interesting connection of this constraint structure to that of particles in Carroll space-time and that we comment on in Section 4.3. The special role played by the final pair of canonical variables as well as the unconventional symplectic structure will be seen to enter in the connection.
An important observation here is that we have now transitioned to a phase space action. In the case of configuration space actions we could recover corrections to relativistic actions by combining a gauge choice with a choice of a slice condition, see for instance Eqs 4.5 and 4.6. We are not aware of a similar construction for phase space.
4.2 Particles in Post-Carrollian Space-Time
In this section we study the Carrollian limits of relativistic particles, using the post-Carrollian space-time introduced in Section 3.2.
4.2.1 Massive Carroll Particle
In order to obtain the Carrollian expansion of a time-like Carroll particle we will start by considering the canonical action of a time-like massive relativistic particle given by the Lagrangian
We also use the Carrollian expansion of the collective coordinates (Eq. 3.21)
The first few terms of these expansions are explicitly
The expansion for the space-time momenta is given by
In order to expand (Eq. 4.19) we also need the expansion of the einbein
and also the rescaling (recall λ = C−2)
that defines a new mass M. The relativistic action then becomes
The first terms of the expansion are
which agrees with the one of Refs. 38, 39, and
This action derived from phase space also has the unconventional symplectic structure already encountered in Section 4.1.2. If we integrate out the auxiliary variables (E(0), E(1), e(0), e(1)) from this action we obtain
The equations of motion obtained from this action by varying the
The
4.2.2 Tachyonic Carroll Particle
In the strict Carroll limit, where the speed of light tends to zero, all moving particles have to be tachyonic as just argued. We therefore consider the action of a tachyonic particle that is constructed from the invariant metric
where we used (Eq. 3.16). The tachyonic configuration space action to be expanded is then
where the difference to the massive Galilean particle (Eq. 4.2) is that the sign inside the square-root has changed since we are now dealing with a tachyon. Moreover, we express the mass of the tachyon as
and higher order terms can be obtained easily. The action S(0) has already been studied in Ref. 40.
In order to elucidate the nature of these further actions, we now analyse them canonically.
4.2.2.1 Lowest Order Carroll Tachyon
From the action S(0) in Eq. 4.32 one finds the canonical momentum (using λ−1/2 = C)
where
This mass-shell constraint is first-class and generates the gauge transformations
in phase space. If one considers the action to formally also depend on the lowest order Carroll time s(0) we also get E(0) = 0 as a constraint since the variable
The extended Hamiltonian action is
The gauge symmetry (Eq. 4.35) can be gauge-fixed by setting for instance the first spatial component
There is a choice of square root when solving the constraint ϕ1 = 0. The Hamiltonian is no longer invariant under the full rotation group SO(d) but only under an SO(d − 1) subgroup. Moreover, the energy is not bounded from below or above. A similar phenomenon has been observed for the Galilean string [73].
4.2.2.2 First Correction to Carroll Tachyon
From the action S(1) in Eq. 4.32 we deduce the following conjugate momenta (setting
and the two primary, first-class constraints
Similar to the discussion at the end of Section 4.1.1 above, we could complement this by
by thinking of the theory as depending on both space and (Carroll) time coordinates to second order by including s(1). There are no further constraints. The first-class constraints (Eq. 4.39) generate the gauge transformations
and
The constraints can be gauge-fixed by setting s(0) = 0 (for ϕ1) and
The dynamics implied by this action is that
4.2.2.3 Configuration Space Actions and Choice of Slice
As for the Galilean particle in Eq. 4.5, we can now consider a gauge-fixing in configuration space. Here, we use the freedom to think of the world-line parameter τ to be of the same dimension as Carroll time, meaning it has dimension L2/T. Then the gauge choice we make is
Moreover, and similar to Eq. 4.6, we make the choice of slice
That this gauge choice is admissible can be checked using the gauge symmetries exhibited above. Substituting these conditions into Eq. 4.32 we obtain
This is to be compared to the large-C expansion of the relativistic tachyon action (Eq. 4.31), now rewritten as (x0 = s/C)
whose gauge-fixed form with s = τ agrees with the actions above.
4.3 Relation Between the Expanded Galilean and Carrollian Particle Actions
There is a close relationship between the Galilean and Carrollian particle actions discussed in Sections 4.1 and 4.2. This can be seen by comparing for instance the constraints implied by the various actions in canonical form and the connection is illustrated in Figure 1. In the figure we have also illustrated whether or not the particle was obtained starting from phase space or configuration space in the preceding sections.
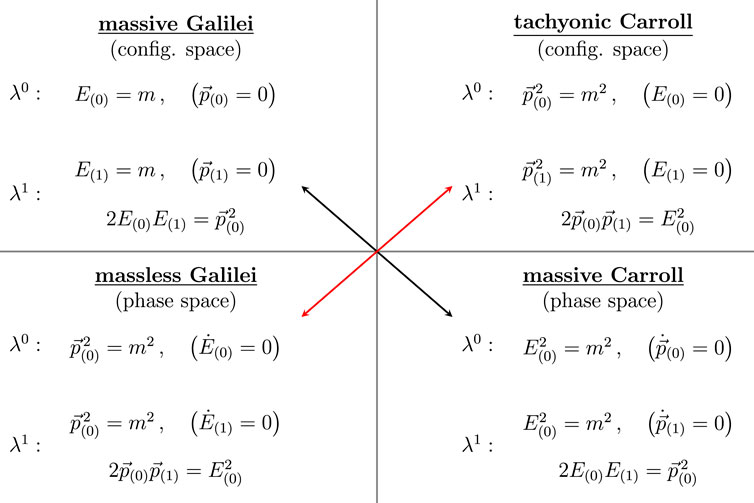
FIGURE 1. Diagram showing schematically the relation between the different non-relativistic limits for different types of particles. The focus is here on the constraints obeyed by the canonical variables. We have used the letter m for all types of masses that appear. In the case of the massless Galilei particle this corresponds to the colour k, see Eq. 4.14. The conditions shown in parentheses correspond to the ones that arise from using the same number of time and space variables as explained in the text.
A special role is played by the conditions in parentheses. These arise as constraints for configuration space from considering the action to formally depend also on one more variable, namely
There is a known duality between Galilei and Carroll limits [10] that acts horizontally in the diagram in each row. The duality was mentioned in the algebraic context in Section 2.1 and it exchanges morally the spatial and temporal translations.14 This duality relates massive to tachyonic particles because of the interchange of the associate physical quantities
On top of this, there is new relationship between Galilei and Carroll limits that acts across the diagonals, with only small differences. If one disregards the conditions in parentheses one can construct maps between the other constraints across diagonals as follows. At order λN for the NW-SE diagonal (black arrow) one exchanges E(n) ↔ E(N−n) and p(n) ↔ p(N−1−n). The reason for treating the E(n) and p(n) slightly differently is due to the fact that p(N) appears in the special condition in parentheses. Since we only allow for positive energies in the massive Galilei case by construction, the constraints there contain a choice of square of the constraints in the massive Carroll case.
Similarly, the SW-NE diagonal (red arrow) corresponds to the map E(n) ↔ E(N−1−n) and p(n) ↔ p(N−n) where now E(N) is treated in a special way since it enters the special constraints. The special condition in parentheses at lowest order is related to the energy of the particle. The zero energy condition was important in recent cosmological applications [40]. For the massless Galilei the condition follows from the equation of motion only requires the energy to be a constant but does not determine this constant and is thus weaker. Intriguingly, the dynamics in the reduced phase space is identical in both cases.15
We have verified explicitly that the maps indicated above also hold at the next order in λ and from the construction of the actions it seems clear that this correspondence will to any order.
We note that a feature of both types of dualities (horizontal and across the diagonal) is that the number of degrees of freedom is not preserved. As an example in D = 3 + 1, the order λ0 of massive Galilei has no degrees of freedom as there are four first-class constraints for eight phase space variables. By contrast, the horizontally mapped tachyonic Carroll has only two first-class constraints for eight variables and therefore four degrees of freedom in phase space, corresponding to the direction of the motion of the tachyon. Going across the diagonal to massive Carroll at order λ0, one finds six degrees of freedom in phase space that correspond the arbitrary position of the Carroll particle and the components of
4.4 Particle in Conformal Galilean Space-Time
Massless relativistic particles in Minkowski space enjoy more symmetries than massive ones in that the global symmetry is extended from the Poincaré algebra to the conformal algebra. This can be seen by looking at the action
and checking invariance of the equations under the transformations (Eq. 3.29). For this one has to also consider the relativistic transformation
Expanding this action expressed in terms of the collective coordinates (Eq. 3.30) leads to S = S(0) + S(1) + ⋯ with
where we have also expanded the einbein according to e = ∑n≥0e(n)λn. For the expanded components this implies the following transformations under special conformal transformations
One can verify that these transformations, together with Eq. 3.31, leave the actions S(0) and S(1) invariant.
In order to see the physical degrees of freedom of S(0) and S(1) we do the Hamiltonian analysis. The momenta are
and the canonical Hamiltonian is
We have two first-class constraints
Again, there are irregular constraints the true effective constraints are
The number of physical degrees of freedom is different from zero this time, and we are left with two degrees in phase space, namely t(0) and E(0). The fact that the number of degrees of freedom changes with the order in the expansion also occurs in the other cases prior to the choice of a slice. Once a slice condition is applied the number of degrees of freedom is unchanged.
4.5 Particle in Curved Background
We now study massive particle dynamics that are invariant under the extended algebra with generators (Eq. 3.34). As shown in Ref. 68, expanding the usual (A)dS invariant particle metric using the coordinates (Eq. 3.35) can be done in a way similar to non-relativistic cases and leads at lowest orders to the following actions
where m is the mass of the particle and all contractions are done with the Minkowski metric ηab. The
Putting now together the equation of motion for the collective coordinate
we find from the individual equations of motion (when evaluated at a given fixed order) that
This equation can be checked to agree with the expansion of the geodesic equation of a massive particle on an (A)dS background for large radius of curvature R [68], written in appropriate coordinates where the metric takes the form
where r = σxaηabxb and
4.6 Particle in Electro-Magnetic Background
Particles in electric-magnetic backgrounds are subject to the Lorentz force, where the relativistic equation of motion can be written as
where we have set the electric charge of the massive particle to one. When the electro-magnetic field is constant, the Poincaré symmetry is broken to translations Pa and FabMab as well as ɛabcdFabMcd in D = 4 [1]. If one considers the space of all constant electro-magnetic fields Fab with the obvious action of the Lorentz algebra one can maintain the whole Poincaré algebra. One can also consider constant shifts of Fab by introducing a new generator Zab and the resulting system then is invariant under the Maxwell algebra where Zab = [Pa, Pb] [27].
In order to describe varying electro-magnetic fields one has to consider an even further extension of the Maxwell algebra as shown originally in Ref. 28. Here, we recall how this works in a free Lie algebra language [29], where we use the free Lie algebra discussed in Section 2.2.1.
The starting point is a non-linear realisation of the Maxwell free Lie algebra where the local symmetry is just the Lorentz symmetry. This means that we are considering a coset element whose gauge-fixed form is
using the coordinates introduced in Eq. 3.36. The corresponding Maurer–Cartan form
has an expansion in terms of the levels of the free Lie algebra generated by the Pa.
We then consider the particle action given by the Lagrangian
where the various Ωa, Ωab, Ωab,c are the pull-backs of the components of the Maurer–Cartan form (Eq. 4.61) in an obvious way. The fields fab, fab,c are new dynamical quantities whose transformation under the Lorentz symmetry is dual to that of the components of the Maurer–Cartan form. Note that the first component Ωa has been treated differently, namely in such a way that it would just give a free massive Poincaré particle.
The equations of motion implied by Eq. 4.62 are such that one always has [29]
resembling the Lorentz force equation. While this equation is universal, the dynamical field fab is obeying its own equation of motion that needs to be solved. However, the Lagrangian also implies equations for the other fields that, in the truncation to level ℓ ≤ 3 as shown in Eq. 4.62, lead to
The evolution of the extra coordinates θab and ξab,c is therefore determined16 by that of the lowest coordinate xa. The form of this dependence resembles a multipole expansion of a system of particles [76]. By contrast, the first line introduces other integration constants for the dynamical f-fields. In the truncation shown we can solve the corresponding equations and arrive at
where the superscript 0 indicates an integration constant. In the previous equation we recognise the beginning of a Taylor expansion of an electro-magnetic field in Minkowski coordinates. Therefore, the extended Maxwell space-time has the potential to accommodate arbitrary electro-magnetic fields.
This can be made more precise by considering the next level in the expansion [28, 29]. This reveals that the full free Maxwell Lie algebra has too many generators compared to the Taylor expansion. In particular, there are generators that result in non-integrable contributions to fab, meaning that the field does not satisfy the Bianchi identity
One can guarantee integrable field strengths by restricting the Maxwell free Lie algebra consistently to a quotient, namely the derivative quotient shown in Eq. 2.33 [29]. We note that this kind of expansion is similar to what arises in unfolded dynamics [77, 78]. An open problem is the precise connection of the behaviour of the higher coordinates θab, ξab,c and so on to multipole moments [76]. Moreover, in the analysis above the electro-magnetic field was a background field and it would be interesting to extend the analysis such that it becomes dynamical, i.e., such that the Maxwell equations also emerge.
5 Conclusion
In this paper, we have studied the algebraic structures of corrections to kinematic algebras, using the methods of Lie algebra expansions and free Lie algebras. This has allowed us to describe several physically interesting situations starting from generalised configuration spaces and by considering particle actions associated with them. From these we could recover systematically corrections to strict (non-relativistic, flat space, field free) limits. We paid particular to attention Carroll limits and their relation to Galilei. It would be interesting to exploit the Galilei/Carroll dualities and relations put forward in Section 4.3 for applications such as gravity or hydrodynamics.
There are several avenues opened up by our approach. The first one is to extend our construction of generalised configuration spaces to that of generalised phase spaces and to see which conditions are needed to recover systematically corrections in phase space language. Besides particle actions one could also consider extended objects as probes. There are typically many more kinematic set-ups available due to the extended nature of the object [7–10, 53]. We anticipate a similar multitude of generalised configuration spaces.
The particle actions considered in this paper were obtained either geometrically, using the invariant metrics of the expanded algebras, or from their corresponding phase space versions. An alternative approach to particle actions is given by non-linear realisations [30–35] whose generalisation to our infinite-dimensional algebras would be interesting to explore in detail. Non-linear realisations are also tied closely to the method of co-adjoint orbits that have not been studied for expanded algebras to the best of our knowledge.17
Another interesting possibility to explore could be the possible interaction among tachyonic Carroll particles. Let us first consider two free tachyonic Carroll particles with spatial positions
where
where V is a scalar function under spatial rotations. The action for the interacting model is given by Eq. 5.1 with the substitution
There is also the secondary constraint
Our analysis was restricted to particle models and it would be interesting to generalise it to field theory. A bridge in that direction might be provided by world-line descriptions of field theory processes, see for instance [83–85]. Among other things this requires a quantisation and generalisation of our considerations to interacting systems. Different non-relativistic limits of field theories can be studied by considering limits of the ratio between the “electric” and “magnetic” contributions to a field’s Hamiltonian energy, see for instance [43]. The electric contribution is the one due to time derivatives of the field while the magnetic one stems from space derivatives. As these two are related by the speed of light, making one larger than the other can also be thought of as a limit in the speed of light and therefore directly suggests to identify the electric limit as the Carroll limit and the magnetic limit as the Galilei limit. Whether this intuitive picture holds up to a more detailed study when applying the world-line picture to field theory is left to future work.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The work of JG has been supported in part by MINECO FPA2016-76005-C2-1-P and PID2019-105614GB-C21 and from the State Agency for Research of the Spanish Ministry of Science and Innovation through the Unit of Excellence Maria de Maeztu 2020-203 award to the Institute of Cosmos Sciences (CEX2019-000918-M). Open access provided through Max Planck Digital Library.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Jakob Palmkvist, Diederik Roest and Patricio Salgado-Rebolledo for very enjoyable collaborations that underlie some of the results presented here. We are grateful to E. A. Bergshoeff, R. Casalbuoni, J. Figueroa-O’Farrill, H. Godazgar, M. Godazgar, M. Henneaux, C. N. Pope and P. K. Townsend for discussions.
Footnotes
1In this paper we use “non-relativistic” generally to refer to any system that does not have Poincaré symmetry.
2The trace δijZi,j is proportional to the Bargmann extension associated with massive representations of the Galilei algebra. The general symmetric Zi,j can be thought of as the anisotropic mass mij of a particle [14, 15].
3In our construction, it will be the semi-direct product of a manifest covariance algebra (e.g., spatial rotations) with a free Lie algebra. This is why we only say “includes”.
4The algebra with [Pi, Bj] = δijZ is known as the Bargmann central extension of the Galilei algebra [23].
5In the case of gravity, 1/c2 corrections have been considered already for example in Refs. 36 and 37.
6The same contraction can also be achieved when replacing the second line of Eq. 2.2 by Ti = Pi and H = λ−1/2P0. The two choices are related by an overall scaling of the translation generators Pa ↔ λ1/2Pa in the Poincaré algebra which, for λ > 0 is an invertible basis redefinition. For λ1/2 = c−1 this includes changing the dimension of the translation generators.
7In the construction, we are assuming for simplicity that we have a basis of
8More general cases can be found in Refs. 20 and 21.
9In later applications we shall also consider a refined double
10In this case a relation of the Galilean construction to the
11Our considerations will be purely local and leave out questions of topology of the spaces.
12The AdS algebra in D dimensions is famously isomorphic to the conformal algebra in D − 1 dimensions. Since we use the indices a to run over the space-time dimension, the range of indices in this section and Section 3.3 is different although they are based on the same types of algebra. However, they also address different contractions and expansions.
13If one wanted to keep the dimensions of Pa at L−1 this would require keeping an explicit 1/R2 on the right-hand side of the commutator (Eq. 3.33), where R is the (A)dS radius.
14It is an exact duality in 1 + 1 dimensions, in higher dimensions it is only heuristic since vector and scalar quantities are being interchanged.
15The massless Galilean particle has also appeared in the context of the optical Hall effect [74] where the appropriate Galilean coadjoint orbits were used.
16up to integration constants that reflect the global Maxwell symmetry.
17For the case of affine algebras, studies of co-adjoint orbits can be found for example in Refs. 79 and 80.
References
1. Bacry H, Lévy‐Leblond JM. Possible Kinematics. J Math Phys (1968) 9:1605–14. doi:10.1063/1.1664490
2. Bacry H, Nuyts J. Classification of Ten‐Dimensional Kinematical Groups With Space Isotropy. J Math Phys (1986) 27(10):2455–7. doi:10.1063/1.527306
3. Figueroa-O’Farrill JM. Kinematical Lie Algebras via Deformation Theory. J Math Phys (2018) 59(6):061701. arXiv:1711.06111 [hep-th].
4. Figueroa-O’Farrill J, Prohazka S. Spatially Isotropic Homogeneous Spacetimes. J High Energy Phys (2019) 01:229. arXiv:1809.01224 [hep-th].
5. Buonanno A, Damour T. Effective One-Body Approach to General Relativistic Two-Body Dynamics. Phys Rev D (1999) 59:084006. arXiv:gr-qc/9811091. doi:10.1103/physrevd.59.084006
6. Blanchet L. Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries. Living Rev Relativ (2014) 17:2. arXiv:1310.1528 [gr-qc]. doi:10.12942/lrr-2014-2
7. Brugues J, Curtright T, Gomis J, Mezincescu L. Non-Relativistic Strings and Branes as Non-Linear Realizations of Galilei Groups. Phys Lett B (2004) 594:227–33. arXiv:hep-th/0404175. doi:10.1016/j.physletb.2004.05.024
8. Andringa R, Bergshoeff E, Gomis J, de Roo M. ‘Stringy' Newton-Cartan Gravity. Class Quan Grav (2012) 29:235020. arXiv:1206.5176 [hep-th]. doi:10.1088/0264-9381/29/23/235020
9. Batlle C, Gomis J, Not D. Extended Galilean Symmetries of Non-Relativistic Strings. J High Energ Phys (2017) 02049. arXiv:1611.00026 [hep-th]. doi:10.1007/jhep02(2017)049
10. Barducci A, Casalbuoni R, Gomis J. Nonrelativistic k-Contractions of the Coadjoint Poincaré Algebra. Int J Mod Phys A (2020) 35(04):2050009. arXiv:1910.11682 [physics.gen-ph]. doi:10.1142/s0217751x20500098
11. Inönü E, Wigner EP. On the Contraction of Groups and Their Representations. Proc Natl Acad Sci U.S.A (1953) 39:510–24. doi:10.1073/pnas.39.6.510
12. Lévy-Leblond J-M. Une nouvelle limite non-relativiste du groupe de Poincaré. Ann de l’I.H.P. Physique théorique (1965) 3(1):1–12. http://archive.numdam.org/item/AIHPA_1965__3_1_1_0/ (Accessed August 12, 2021).
13. Sen Gupta ND. On an Analogue of the Galilei Group. Nuov Cim A (1966) 44(2):512–7. doi:10.1007/bf02740871
14. Bogoslovsky GY. On the Local Anisotropy of Space-Time, Inertia and Force Fields. Nuovo Cim B (1983) 77:181–90. doi:10.1007/bf02721483
15. Bonanos S, Gomis J. A Note on the Chevalley-Eilenberg Cohomology for the Galilei and Poincaré Algebras. J Phys A: Math Theor (2009) 42:145206. arXiv:0808.2243 [hep-th]. doi:10.1088/1751-8113/42/14/145206
16. Gomis J, Kleinschmidt A, Palmkvist J. Galilean Free Lie Algebras. J High Energ Phys (2019) 2019:109. arXiv:1907.00410 [hep-th]. doi:10.1007/jhep09(2019)109
17. Hatsuda M, Sakaguchi M. Wess-Zumino Term for the AdS Superstring and Generalized Inonu-Wigner Contraction. Prog Theor Phys (2003) 109:853–67. arXiv:hep-th/0106114. doi:10.1143/ptp.109.853
18. Boulanger N, Henneaux M, Nieuwenhuizen Pv. Conformal (Super)Gravities with Several Gravitons. J High Energ Phys (2002) 2002:035. arXiv:hep-th/0201023. doi:10.1088/1126-6708/2002/01/035
19. de Azcárraga JA, Izquierdo JM, Picón M, Varela O. Generating Lie and Gauge Free Differential (Super)Algebras by Expanding Maurer-Cartan Forms and Chern-Simons Supergravity. Nucl Phys B (2003) 662:185–219. arXiv:hep-th/0212347.
20. Izaurieta F, Rodríguez E, Salgado P. Expanding Lie (Super)Algebras Through Abelian Semigroups. J Math Phys (2006) 47:123512. arXiv:hep-th/0606215. doi:10.1063/1.2390659
21. de Azcárraga JA, Izquierdo JM, Picón M, Varela O. Expansions of Algebras and Superalgebras and Some Applications. Int J Theor Phys (2007) 46:2738–52. arXiv:hep-th/0703017. doi:10.1007/s10773-007-9385-3
22. Bergshoeff E, Izquierdo JM, Ortín T, Romano L. Lie Algebra Expansions and Actions for Non-Relativistic Gravity. J High Energy Phys (2019) 08:048. arXiv:1904.08304 [hep-th]. doi:10.1007/jhep08(2019)048
23. Bargmann V. On Unitary Ray Representations of Continuous Groups. Ann Maths (1954) 59:1–46. doi:10.2307/1969831
24. Barducci A, Casalbuoni R, Gomis J. Confined Dynamical Systems with Carroll and Galilei Symmetries. Phys Rev D (2018) 98(8):085018. arXiv:1804.10495 [hep-th]. doi:10.1103/physrevd.98.085018
25. Kac VG. Infinite-Dimensional Lie Algebras. 3rd ed. Cambridge: Cambridge University Press (1990).
26. Bacry H, Combe P, Richard JL. Group-Theoretical Analysis of Elementary Particles in an External Electromagnetic Field. Nuov Cim A (1970) 67:267–99. doi:10.1007/bf02725178
27. Schrader R. The Maxwell Group and the Quantum Theory of Particles in Classical Homogeneous Electromagnetic Fields. Fortschr Phys (1972) 20:701–34. doi:10.1002/prop.19720201202
28. Bonanos S, Gomis J. Infinite Sequence of Poincaré Group Extensions: Structure and Dynamics. J Phys A: Math Theor (2010) 43:015201. arXiv:0812.4140 [hep-th]. doi:10.1088/1751-8113/43/1/015201
29. Gomis J, Kleinschmidt A. On Free Lie Algebras and Particles in Electro-Magnetic Fields. J High Energy Phys (2017) 07:085. arXiv:1705.05854 [hep-th]. doi:10.1007/jhep07(2017)085
30. Coleman S, Wess J, Zumino B. Structure of Phenomenological Lagrangians. I. Phys Rev (1969) 177:2239–47. doi:10.1103/physrev.177.2239
31. Callan CG, Coleman S, Wess J, Zumino B. Structure of Phenomenological Lagrangians. II. Phys Rev (1969) 177:2247–50. doi:10.1103/physrev.177.2247
32. Salam A, Strathdee J. Nonlinear Realizations. I. The Role of Goldstone Bosons. Phys Rev (1969) 184:1750–9. doi:10.1103/physrev.184.1750
33. Isham CJ, Salam A, Strathdee J. Nonlinear Realizations of Space-Time Symmetries. Scalar and Tensor Gravity. Ann Phys (1971) 62:98–119. doi:10.1016/0003-4916(71)90269-7
35. Ogievetsky VI. Non-Linear Realizations of Internal and Spacetime Symmetries. In: Proceedings of the 10th Karpacz Winter School (1974). vol. 207 of Acta Univ. Wratislaviensis. Wroclaw: University of Wroclaw. Available at: https://www.imperial.ac.uk/media/imperial-college/research-centres-and-groups/theoretical-physics/msc/current/smb/other-resources/Ogievetsky---Karpacz-nonlinear-realization-lectures.pdf.
36. Dautcourt G. On the Newtonian Limit of General Relativity. Acta Phys Polon B (1990) 21(10):755–65.
37. Van den Bleeken D. Torsional Newton-Cartan Gravity from the Large c Expansion of General Relativity. Class Quan Grav (2017) 34(18):185004. arXiv:1703.03459 [gr-qc]. doi:10.1088/1361-6382/aa83d4
38. Bergshoeff E, Gomis J, Longhi G. Dynamics of Carroll Particles. Class Quan Grav (2014) 31(20):205009. arXiv:1405.2264 [hep-th]. doi:10.1088/0264-9381/31/20/205009
39. Duval C, Gibbons GW, Horváthy PA, Zhang PM. Carroll versus Newton and Galilei: Two Dual Non-Einsteinian Concepts of Time. Class Quan Grav (2014) 31:085016. arXiv:1402.0657 [gr-qc]. doi:10.1088/0264-9381/31/8/085016
40. de Boer J, Hartong J, Obers NA, Sybesma W, Vandoren S. Carroll Symmetry, Dark Energy and Inflation (2021). arXiv:2110.02319 [hep-th].
41. Bergshoeff E, Gomis J, Rollier B, Rosseel J, ter Veldhuis T. Carroll versus Galilei Gravity. JHEP (2017) 03:165. arXiv:1701.06156 [hep-th]. doi:10.1007/jhep03(2017)165
42. Gomis J, Kleinschmidt A, Palmkvist J, Salgado-Rebolledo P. Newton-Hooke/Carrollian Expansions of (A)dS and Chern-Simons Gravity. JHEP (2020) 02009. arXiv:1912.07564 [hep-th]. doi:10.1007/jhep02(2020)009
43. Henneaux M, Salgado-Rebolledo P. Carroll Contractions of Lorentz-Invariant Theories. J High Energ Phys (2021) 2021:180. arXiv:2109.06708 [hep-th]. doi:10.1007/jhep11(2021)180
44. Hansen D, Obers NA, Oling G, Søgaard BT. Carroll Expansion of General Relativity (2021). arXiv:2112.12684 [hep-th].
45. Belinsky VA, Khalatnikov IM, Lifshitz EM. Oscillatory Approach to a Singular Point in the Relativistic Cosmology. Adv Phys (1970) 19:525–73.
46. Damour T, Henneaux M, Nicolai H. Cosmological Billiards. Class Quan Grav (2003) 20:R145–R200. arXiv:hep-th/0212256. doi:10.1088/0264-9381/20/9/201
47. Aldaya V, de Azcárraga JA. Cohomology, Central Extensions, and (Dynamical) Groups. Int J Theor Phys (1985) 24(2):141–54. doi:10.1007/bf00672649
48. Gomis J, Kleinschmidt A, Palmkvist J, Salgado-Rebolledo P. Symmetries of Post-Galilean Expansions. Phys Rev Lett (2020) 124(8):081602. arXiv:1910.13560 [hep-th]. doi:10.1103/PhysRevLett.124.081602
49. Khasanov O, Kuperstein S. (In)finite Extensions of Algebras from Their İnönü-Wigner Contractions. J Phys A: Math Theor (2011) 44:475202. arXiv:1103.3447 [hep-th]. doi:10.1088/1751-8113/44/47/475202
50. Hansen D, Hartong J, Obers NA. Action Principle for Newtonian Gravity. Phys Rev Lett (2019) 122(6):061106. arXiv:1807.04765 [hep-th]. doi:10.1103/PhysRevLett.122.061106
51. Ozdemir N, Ozkan M, Tunca O, Zorba U. Three-Dimensional Extended Newtonian (Super)Gravity. JHEP (2019) 05130. arXiv:1903.09377 [hep-th]. doi:10.1007/jhep05(2019)130
52. Hansen D, Hartong J, Obers NA. Gravity Between Newton and Einstein. Int J Mod Phys D (2019) 28(14):1944010. arXiv:1904.05706 [gr-qc]. doi:10.1142/s0218271819440103
53. Bergshoeff E, Izquierdo JM, Romano L. Carroll versus Galilei from a Brane Perspective. JHEP (2020) 10:066. arXiv:2003.03062 [hep-th]. doi:10.1007/jhep10(2020)066
54. Bourbaki N. Lie Groups and Lie Algebras. Chapters 1–3. Elements of Mathematics (Berlin). Berlin: Springer-Verlag (1998). Translated from the French, Reprint of the 1989 English Translation.
55. Viennot G. Bases des algèbres de lie libres, in Algèbres de Lie Libres et Monoïdes Libres. Lecture Notes in Mathematics. Berlin: Springer (1978). Vol. 691. doi:10.1007/BFb0067952
56. Cederwall M, Palmkvist J. Superalgebras, Constraints and Partition Functions. JHEP (2015) 08:036. arXiv:1503.06215 [hep-th]. doi:10.1007/jhep08(2015)036
57. Gomis J, Kleinschmidt A, Palmkvist J. Symmetries of M-Theory and Free Lie Superalgebras. JHEP (2019) 03160. arXiv:1809.09171 [hep-th]. doi:10.1007/jhep03(2019)160
58. Gabber O, Kac VG. On Defining Relations of Certain Infinite-Dimensional Lie Algebras. Bull Amer Math Soc (1981) 5(2):185–9. doi:10.1090/s0273-0979-1981-14940-5
59. Barducci A, Casalbuoni R, Gomis J. Contractions of the Maxwell Algebra. J Phys A: Math Theor (2019) 52(39):395201. arXiv:1904.00902 [hep-th]. doi:10.1088/1751-8121/ab38f0
60. Salgado P, Salgado S. 𝔰𝔬(D−1, 1) ⊗ 𝔰𝔬(D−1, 2) Algebras and Gravity. Phys Lett B (2014) 728:5–10. doi:10.1016/j.physletb.2013.11.009
61. Negro J, Del Olmo MA, Rodríguez-Marco A. Nonrelativistic Conformal Groups. J Math Phys (1997) 38(7):3786–809. doi:10.1063/1.532067
62. Henkel M. Local Scale Invariance and Strongly Anisotropic Equilibrium Critical Systems. Phys Rev Lett (1997) 78:1940–3. arXiv:cond-mat/9610174. doi:10.1103/physrevlett.78.1940
63. Lukierski J, Stichel PC, Zakrzewski WJ. Exotic Galilean Conformal Symmetry and its Dynamical Realisations. Phys Lett A (2006) 357:1–5. arXiv:hep-th/0511259. doi:10.1016/j.physleta.2006.04.016
64. Bagchi A, Gopakumar R. Galilean Conformal Algebras and AdS/CFT. JHEP (2009) 07:037. arXiv:0902.1385 [hep-th]. doi:10.1088/1126-6708/2009/07/037
65. Duval C, Horváthy PA. Conformal Galilei Groups, Veronese Curves and Newton-Hooke Spacetimes. J Phys A: Math Theor (2011) 44:335203. arXiv:1104.1502 [hep-th]. doi:10.1088/1751-8113/44/33/335203
66. Ammon M, Pannier M, Riegler M. Scalar Fields in 3D Asymptotically Flat Higher-Spin Gravity. J Phys A (2021) 54(10):105401. arXiv:2009.14210 [hep-th]. doi:10.1088/1751-8121/abdbc6
67. Campoleoni A, Pekar S. Carrollian and Galilean Conformal Higher-Spin Algebras in Any Dimensions (2021). arXiv:2110.07794 [hep-th].
68. Gomis J, Kleinschmidt A, Roest D, Salgado-Rebolledo P. A Free Lie Algebra Approach to Curvature Corrections to Flat Space-Time. JHEP (2020) 09:068. arXiv:2006.11102 [hep-th]. doi:10.1007/jhep09(2020)068
69. Le Bellac M, Lévy-Leblond JM. Galilean Electromagnetism. Nuovo Cim B (1973) 14:217–34. doi:10.1007/bf02895715
70. Lévy-Leblond J-M. Group-Theoretical Foundations of Classical Mechanics: the Lagrangian Gauge Problem. Commun Math Phys (1969) 12(1):64–79. doi:10.1007/bf01646436
71. Souriau J-M. Structure of Dynamical Systems: A Symplectic View of Physics. Cham: Birkhäuser (1997). (Translated by C. H. Cushman-de Vries), Vol. 139 of Progress in Mathematics.
72. Batlle C, Gomis J, Mezincescu L, Townsend PK. Tachyons in the Galilean Limit. J High Energ Phys (2017) 2017:120. arXiv:1702.04792 [hep-th]. doi:10.1007/jhep04(2017)120
73. Gomis J, Townsend PK. The Galilean Superstring. J High Energ Phys (2017) 2017:105. arXiv:1612.02759 [hep-th]. doi:10.1007/jhep02(2017)105
74. Duval C, Horváth Z, Horváthy PA. Geometrical Spinoptics and the Optical Hall Effect. J Geometry Phys (2007) 57:925–41. arXiv:math-ph/0509031. doi:10.1016/j.geomphys.2006.07.003
75. Miskovic O, Zanelli J. Dynamical Structure of Irregular Constrained Systems. J Math Phys (2003) 44:3876–87. arXiv:hep-th/0302033. doi:10.1063/1.1601299
76. Dixon WG. Description of Extended Bodies by Multipole Moments in Special Relativity. J Math Phys (1967) 8:1591–605. doi:10.1063/1.1705397
77. Vasiliev MA. Actions, Charges and Off-Shell fields in the Unfolded Dynamics Approach. Int J Geom Methods Mod Phys (2006) 03:37–80. arXiv:hep-th/0504090. doi:10.1142/s0219887806001016
78. Boulanger N, Sundell P, West P. Gauge Fields and Infinite Chains of Dualities. J High Energ Phys (2015) 2015:192. arXiv:1502.07909 [hep-th]. doi:10.1007/jhep09(2015)192
79. Reyman AG, Semenov-Tian-Shansky MA. Reduction of Hamiltonian Systems, Affine Lie Algebras and Lax Equations. Invent Math (1979) 54(1):81–100. doi:10.1007/bf01391179
80. Khesin B, Wendt R. The Geometry of Infinite-Dimensional Groups. In: A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Berlin: Springer-Verlag (2009). Vol. 51 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge.
81. Kamimura K. Elimination of Relative Time in Bilocal Model. Prog Theor Phys (1977) 58:1947–53. doi:10.1143/ptp.58.1947
82. Dominici D, Gomis J, Longhi G. A Lagrangian for Two Interacting Relativistic Particles. Nuov Cim B (1978) 48:152–66. doi:10.1007/bf02743639
83. Feynman RP. Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction. Phys Rev (1950) 80:440–57. doi:10.1103/physrev.80.440
84. Casalbuoni R, Gomis J, Longhi G. The Relativistic Point Revisited in the Light of the String Model. Nuov Cim A (1974) 24:249–58. doi:10.1007/bf02821992
Keywords: free Lie algebras, Carrollian dynamics, Kac-Moody algebras, particle actions, non-relativistic corrections, kinematic algebras
Citation: Gomis J and Kleinschmidt A (2022) Infinite-Dimensional Algebras as Extensions of Kinematic Algebras. Front. Phys. 10:892812. doi: 10.3389/fphy.2022.892812
Received: 09 March 2022; Accepted: 28 March 2022;
Published: 06 July 2022.
Edited by:
Jan Rosseel, University of Vienna, AustriaReviewed by:
Evelyn Rodríguez, Catholic University of the Most Holy Conception, ChileStefan Prohazka, University of Edinburgh, United Kingdom
Copyright © 2022 Gomis and Kleinschmidt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Axel Kleinschmidt, YXhlbC5rbGVpbnNjaG1pZHRAYWVpLm1wZy5kZQ==
 Joaquim Gomis1
Joaquim Gomis1 Axel Kleinschmidt
Axel Kleinschmidt