- 1Jiangsu Key Lab of Opto-Electronic Technology, School of Physics and Technology, Nanjing Normal University, Nanjing, China
- 2National Astronomical Observatories/Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences, Nanjing, China
- 3CAS Key Laboratory of Astronomical Optics & Technology, Nanjing Institute of Astronomical Optics & Technology, Nanjing, China
- 4College of Physics and Electronic Engineering, Heze University, Heze, China
- 5Shandong Provincial Engineering and Technical Center of Light Manipulations & Shandong Provincial Key Laboratory of Optics and Photonic Device, School of Physics and Electronics, Shandong Normal University, Jinan, China
- 6School of Physical Science and Technology, Soochow University, Suzhou, China
In this work, the controllable self-focusing behavior is first investigated by manipulating the state of polarization (SoP), that is, the phase difference between two polarized components at the initial optical field, which can be used to realize the three-dimensional manipulation of self-focusing behavior. Furthermore, the properties of self-focusing propagation (including intensity distribution, propagation dynamics, and Stokes parameters) are researched in detail, which are beneficial to select the reasonable initial SoP for further theoretical and experimental exploration. Particularly, the radially polarized beam as a laser source not only prolongs the self-focusing length but also improves the power density of self-focusing spots on the target. These findings may have potential in the multidimensional optical manipulation, the optical information transmission, the high-power long-range laser atmospheric propagation, and related applications.
Introduction
In recent decades, filamentation propagation in the transparent medium [1], which can generate long plasma channels with very high intensities, has sparked extensive interest, owing to its wide application in many fields [2–5], such as lightening control, remote diagnostics, and LIDAR. In general, the filament length of laser pulse in the air is in the order of several meters to kilometers. In particular, the self-focusing length (SFL) plays a crucial role in high-power and long-range propagation [6–10] because it can make the length of filament steerable. Until now, the known methods for controlling the position of the filamentation domain are as follows: modulating the laser pulse power [6], adjusting the divergence angle of the initial laser [7], launching negatively chirped ultrashort pulses [8, 9], and double-lens setup [10]. Recently, the U.S. Naval Research Laboratory has investigated the SFL in atmospheric turbulence with theoretical and numerical methods [11, 12].
The vector optical field was proposed in 1961 [13]. Since 2000, this kind of optical field has been reappearing in sight due to its tight-focusing property [14]. The vector optical field with spatially inhomogeneous SoP at the field cross section has attracted immense attention, which can be widely used in nonlinear optics [15], optical tweezers [16], optical micro-manipulation [17], super-resolution microscopy [18], optical information transmission [19], and atmospheric propagation [20–25]. In recent years, to conveniently control the space-variant polarization state of a light beam, the optical arrangements containing spatial light modulators have been widely presented [26–38]. Due to the axial-symmetry breaking of optical field by the designable hybrid polarization structure, i.e., azimuthally-variant hybrid-polarized (AVHP) vector field, the controllable self-focusing spots of the vector optical field and multiple filamentation have been achieved [36–38], which may provide an alternative solution to control the SFL. It is well-known that the SFL for a Gaussian beam is relevant with the input power, which can be described by the semi-empirical Marburger formula [9, 39, 40]. Due to the changeable intensity profile in propagation for a hollow beam (e.g., hollow Gaussian beam (HGB)), it is difficult to derive a formula to characterize the relation between the SFL and input power. As a typical kind of hollow beam, the radially polarized beam (RPB) has been studied extensively in both the theory and experiment, owing to its interesting and unique focusing properties [41–44]. Thus, a new method to achieve the controllable SFL of other common beams is worthy of further exploration as well.
In this work, based on the SoP manipulation, the influence of the phase difference at the initial optical field on the self-focusing propagation is researched. It is found that self-focusing behavior can be controlled by adjusting the phase difference, enabling a three-dimensional (3D) manipulation of the SFL. Furthermore, characteristics of self-focusing are investigated in detail by means of three specific beams (HGB, RPB, and AVHP). Results show that RPB have a predominant advantage in the controllable SFL and high optical power density on the target, and it may have practical application significance in the multidimensional optical manipulation, optical information transmission, high-power long-range laser atmospheric propagation, and related areas.
Theory
We discussed the monochromatic (or continuous) regime for which the intensity of the laser does not depend on time. The propagation nonlinear dynamics of a high-power laser beam in the Kerr medium is researched by using nonlinear Schrödinger (NLS) equations. Under the slowly varying amplitude approximation, the NLS equation is given as follows[45, 46].
where
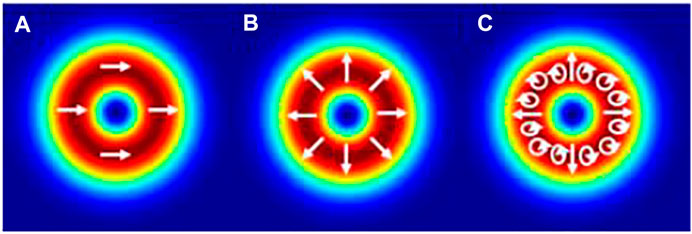
The azimuthally varying distribution of SoP at the initial optical field cross section can be expressed as follows [26, 35, 37].
where
i) when
(ii) when
(iii) when
The vector NLS equation can be divided into a pair of coupled NLS equations for two orthogonal components,
where
The SoP of the optical field cross section can be described by a set of Stokes parameters. Stokes polarization parameters are expressed as follows [48]:
where the positive and negative
Three-Dimensional Manipulation of Self-Focusing Behavior via SOPS
In the numerical calculation, the initial parameters are chosen as follows: wavelength
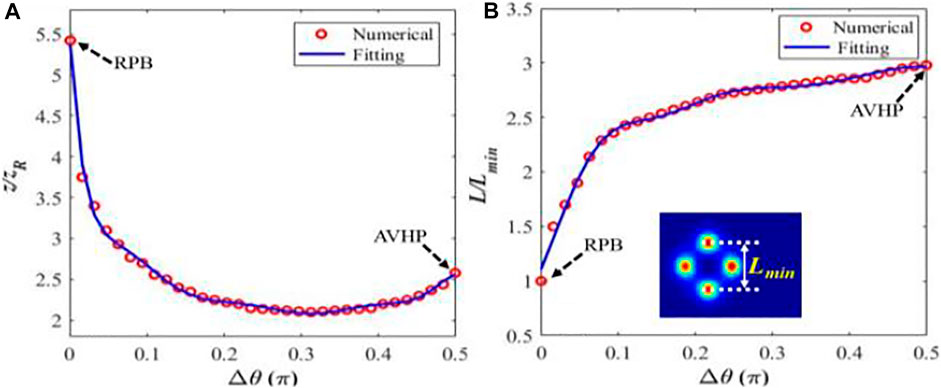
It is known that adjusting the input power is a common method to manipulate the SFL for a Gaussian beam [6]. For three hollow beams, the numerical relation of the SFL the with input power is shown in detail in Supplementary Material S1. However, in the practical experimental scenario, as an alternative or combination regimen to the input power manipulation, the approach to achieve the controllable SFL at the fixed input power is still a great challenge, which may greatly extend the manipulation dimensionality. As an intrinsic nature of light, polarization is of great importance to serve as a degree of freedom for manipulating light. With the aid of SoPs, herein, the manipulation of beam collapse under fixed input power is explored, that is, input power
Next, the spacing of symmetric self-focusing spots at the collapse plane is investigated. Herein, the minimum value
The intensity distribution of self-focusing spots is illustrated in Figure 3, where the phase differences are changed in two regions, i.e.,

FIGURE 3. Intensity distribution of self-focusing spots with various phase differences: (A)
Based on the variation of the phase difference, the fine manipulation of self-focusing spots (including the length, spacing, number, and orientation) can be achieved. It is found that manipulation of SoPs can be controlled not only in the axial dimensionality (i.e., the SFL) but also in radial (i.e., the spacing of self-focusing spots) and azimuthal (i.e., the number and orientation of self-focusing spots) dimensionalities. To the best of our knowledge, this is the first time to achieve three-dimensional (3D) manipulation of self-focusing behavior simultaneously by changing the phase difference. Meanwhile, the extension of this concept to other initial parameters (i.e., the input power, beam waist, wavelength, and nonlinear refractive index) is straightforward, and the limitations will be discussed in Conclusion and Discussion. Combining the manipulation of the input power and phase difference, it may enrich the multidimensional manipulation for self-focusing, which may provide a new approach to realizing the 3D manipulation of the optical field, enhancing the optical information transmission capacity, improving the high-power long-range atmospheric shooting on the target, and related areas.
Characteristics of Self-Focusing
To analyze the physical mechanism of the self-focusing propagation, the characteristics of the self-focusing spot for three specific beams are investigated in detail with the help of the intensity distribution, propagation dynamics, and Stokes parameters. The parameters in numerical calculation are the same as the aforementioned section.
The intensity distribution at different propagation planes and propagation dynamics of three optical fields are shown in Figure 4. At the source plane
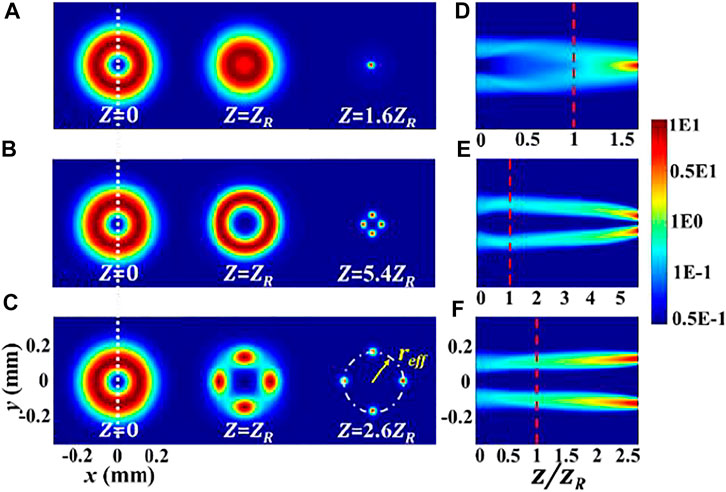
FIGURE 4. Intensity distribution located at various propagation planes for three optical fields (A) HGB, (B) RPB, and (C) AVHP and the corresponding propagation dynamics (D–F), respectively.
Stokes parameters for three models at the source plane (Figures 5A–C) and the corresponding spot plane (Figure 5D–F) are depicted, which benefits to analyze the physical mechanism of the self-focusing behavior. Stokes parameters for the HGB are shown in Figure 5A,D; it is seen that
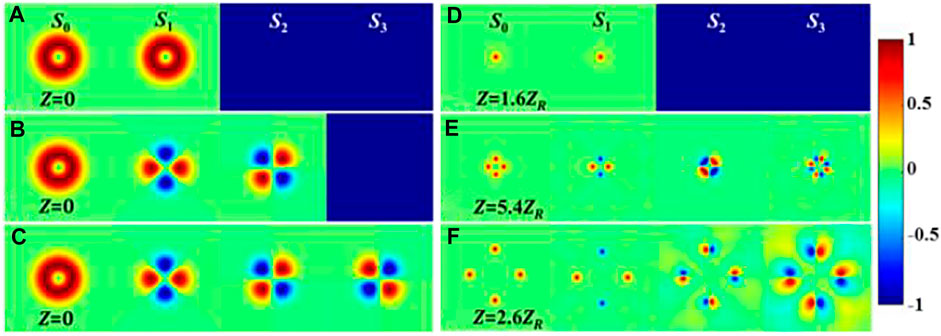
FIGURE 5. Stokes polarization parameters for three beam models at the source plane (i.e., (A) HGB, (B) RPB, and (C) AVHP) and at the corresponding focusing spot (i.e., (D) HGB (
Conclusion and Discussion
Based on the phase difference between two polarized components at the initial optical field cross section, the influence of the phase difference on self-focusing behavior is investigated. It is found that the length, spacing, number, and orientation of self-focusing spots can be controlled by adjusting the phase difference. In particular, it is of practical significance for realizing the 3D manipulation of self-focusing behavior simultaneously by changing the phase difference. In addition, properties of the SFL are investigated in detail with three specific models (i.e., HGB, RPB, and AVHP). It is revealed that the SFL of three cases satisfies the following relation: RPB > AVHP > HGB. In addition, two characteristics for the RPB should be mentioned: 1) self-focusing spots appear at a relatively long-range propagation distance; 2) the target optical power density of the RPB is larger than that of the AVHP at the receiver plane due to the effective beam radius focusing. Therefore, the RPB as a laser source may not only prolong the SFL but also improve the power density on the target. Based on the multidimensional controllable manipulation by changing the SoPs, it may open a new window for realizing the applications, such as 3D manipulation of the optical field, the optical information transmission, and the high-power long-range atmospheric propagation.
An extension of these results to other initial parameters (i.e., the input power, beam waist, wavelength, and nonlinear refractive index) is straightforward with reasonable limitations on some parameters. When the input power of the laser is much greater than the critical power, the beam may break up into multiple spots, forming its own filament with the critical power [37, 50, 51]. In our work, we discussed the relation of the SFL with moderate input power and the input power, which can generate four spots for the vector optical field that should be at least larger than four times of critical power:
For the conventional physical mechanism of multiple filamentation (MF), when the input peak power is far above the critical power for self-focusing, the modulational instability breaks up the beam into a large number of filaments [1]. These filaments, which grow from the small fluctuations in the beam intensity profile, can be seemingly randomly distributed in a given transverse plane or organized into specific patterns, and the number of filaments cannot be accurately predicted [1]. For the multiple spots induced by SoPs, a prerequisite is that the optical field should be axial-symmetry breaking in and of itself. Polarization, as an intrinsic and fundamental nature of light, plays an indispensable role in the interaction of light with matter. The self-focusing spot formation mechanism is axial-symmetry breaking [36, 37] due to the inhomogeneous state of polarization at the initial optical field cross section or the induction of the propagation process. With the input power changed, the distribution of spots is predictable, and the number also can be determined. Thus, these theoretical and numerical findings may be achieved by the controllable self-focusing behavior, and it may have practical application significance in 3D optical manipulation, optical information transmission, high-power long-range laser atmospheric propagation, and so on.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge the National Key Research and Development Project of China (2019YFA0705000), the National Natural Science Foundation of China (12192254, 91750201, 11974218, 11804234, 11903062, and 11904087), the Innovation Group of Jinan (2018GXRC010), and the Local Science and Technology Development Project of the Central Government (YDZX20203700001766).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.892581/full#supplementary-material
References
1. Couairon A, Mysyrowicz A. Femtosecond Filamentation in Transparent Mediafilamentation in Transparent media. Phys Rep (2007) 441:47–189. doi:10.1016/j.physrep.2006.12.005
2. Kasparian J, Rodriguez M, Méjean G, Yu J, Salmon E, Wille H, et al. White-light Filaments for Atmospheric Analysis. Science (2003) 301:61–4. doi:10.1126/science.1085020
3. Houard A, D’Amico C, Liu Y, André YB, Franco M, Prade B, et al. High Current Permanent Discharges in Air Induced by Femtosecond Laser Filamentation. Appl Phys Lett (2007) 90:171501. doi:10.1063/1.2734396
4. D’Amico C, Houard A, Franco M, Prade B, Mysyrowicz A, Couairon A, et al. Conical Forward THz Emission from Femtosecond-Laser-Beam Filamentation in Air. Phys Rev Lett (2007) 98:235002. doi:10.1103/PhysRevLett.98.235002
5. Amico CD, Houard A, Akturk S, Liu Y, Le Bloas J, Franco M, et al. Forward THz Radiation Emission by Femtosecond Filamentation in Gases: Theory and experiment. New J Phys (2008) 10:013015. doi:10.1088/1367-2630/10/1/013015
6. Houard A, Franco M, Prade B, Durécu A, Lombard L, Bourdon P, et al. Femtosecond Filamentation in Turbulent Air. Phys Rev A (2008) 78:033804. doi:10.1103/physreva.78.033804
7. Jin Z, Zhang J, Xu MH, Lu X, Li YT, Wang ZH, et al. Control of Filamentation Induced by Femtosecond Laser Pulses Propagating in Air. Opt Express (2005) 13(25):10424–30. doi:10.1364/opex.13.010424
8. Wöste L, Wedekind C, Wille H, Rairoux P, Stein B, Nikolov S, et al. Femtosecond Atmospheric Lamp. Laser und Optoelektronik. AT specialist Publisher (1997).
9. Sprangle P, Peñano JRB, Hafizi B. Propagation of Intense Short Laser Pulses in the Atmosphere. Phys Rev E Stat Nonlin Soft Matter Phys (2002) 66:046418. doi:10.1103/PhysRevE.66.046418
10. Fibich G, Sivan Y, Ehrlich Y, Louzon E, Fraenkel M, Eisenmann S, et al. Control of the Collapse Distance in Atmospheric Propagation. Opt Express (2006) 14(12):4946–57. doi:10.1364/oe.14.004946
11. Stotts LB, Peñano J, Urick VJ. Engineering Equation for Filamentation Self-Focusing Collapse Distance in Atmospheric Turbulence. Opt Express (2019) 27(11):15159–71. doi:10.1364/oe.27.015159
12. DiComo G, Helle M, Kaganovich D, Schmitt-Sody A, Elle J, Peñano J. Nonlinear Self-Channeling of High-Power Lasers through Controlled Atmospheric Turbulence. J Opt Soc Am B (2020) 37(3):797–803. doi:10.1364/josab.384137
13. Snitzer E. Cylindrical Dielectric Waveguide Modes*. J Opt Soc Am (1961) 51(5):491–8. doi:10.1364/josa.51.000491
14. Youngworth KS, Brown TG. Focusing of High Numerical Aperture Cylindrical-Vector Beams. Opt Express (2000) 7(2):77–87. doi:10.1364/oe.7.000077
15. Ciattoni A, Crosignani B, Di Porto PA, Yariv A. Azimuthally Polarized Spatial Dark Solitons: Exact Solutions of Maxwell's Equations in a Kerr Medium. Phys Rev Lett (2005) 94(7):073902. doi:10.1103/PhysRevLett.94.073902
16. Kawauchi H, Yonezawa K, Kozawa Y, Sato S. Calculation of Optical Trapping Forces on a Dielectric Sphere in the ray Optics Regime Produced by a Radially Polarized Laser Beam. Opt Lett (2007) 32(13):1839–41. doi:10.1364/ol.32.001839
17. Lou K, Qian S-X, Wang X-L, Li Y, Gu B, Tu C, et al. Two-dimensional Microstructures Induced by Femtosecond Vector Light fields on Silicon. Opt Express (2012) 20(1):120–7. doi:10.1364/oe.20.000120
18. Xie X, Chen Y, Yang K, Zhou J. Harnessing the point-spread Function for High-Resolution Far-Field Optical Microscopy. Phys Rev Lett (2014) 113:263901. doi:10.1103/physrevlett.113.263901
19. Gao X-Z, Pan Y, Zhao M-D, Zhang G-L, Zhang Y, Tu C, et al. Focusing Behavior of the Fractal Vector Optical fields Designed by Fractal Lattice Growth Model. Opt Express (2018) 26(2):1597–614. doi:10.1364/oe.26.001597
20. Cai Y, Lin Q, Eyyuboglu HT, Baykal Y. Average Irradiance and Polarization Properties of a Radially or Azimuthally Polarized Beam in a Turbulent Atmosphere. Opt Express (2008) 16(11):7665–73. doi:10.1364/oe.16.007665
21. Cheng W, Haus JW, Zhan Q. Propagation of Vector Vortex Beams through a Turbulent Atmosphere. Opt Express (2009) 17(20):17829–36. doi:10.1364/oe.17.017829
22. Wei C, Wu D, Liang C, Wang F, Cai Y. Experimental Verification of Significant Reduction of Turbulence-Induced Scintillation in a Full Poincaré Beam. Opt Express (2015) 23(19):24331–41. doi:10.1364/oe.23.024331
23. Cox MA, Rosales-Guzmán C, Lavery MPJ, Versfeld DJ, Forbes A. On the Resilience of Scalar and Vector Vortex Modes in Turbulence. Opt Express (2016) 24(16):18105–13. doi:10.1364/oe.24.018105
24. Lavery MPJ, Peuntinger C, Günthner K, Banzer P, Elser D, Boyd RW, et al. Free-space Propagation of High-Dimensional Structured Optical fields in an Urban Environment. Sci Adv (2017) 3(10):e1700552. doi:10.1126/sciadv.1700552
25. Yu J, Huang Y, Wang F, Liu X, Gbur G, Cai Y. Scintillation Properties of a Partially Coherent Vector Beam with Vortex Phase in Turbulent Atmosphere. Opt Express (2019) 27:26676. doi:10.1364/oe.27.026676
26. Han W, Yang Y, Cheng W, Zhan Q. Vectorial Optical Field Generator for the Creation of Arbitrarily Complex fields. Opt Express (2013) 21(18):20692–706. doi:10.1364/oe.21.020692
27. Han W, Cheng W, Zhan Q. Design and Alignment Strategies of 4f Systems Used in the Vectorial Optical Field Generator. Appl Opt (2015) 54(9):2275–8. doi:10.1364/ao.54.002275
28. Wan C, Zhan Q. Generation of Exotic Optical Polarization Möbius Strips. Opt Express (2019) 27(8):11516–24. doi:10.1364/oe.27.011516
29. Stirling S, Hend S, Kamel A, Zhan Q, Andrew F. General Design Principle for Structured Light Lasers. Opt Express (2020) 28(23):35006–17. doi:10.1364/oe.410963
30. Liu S, Qi S, Zhang Y, Li P, Wu D, Han L, et al. Highly Efficient Generation of Arbitrary Vector Beams with Tunable Polarization, Phase, and Amplitude. Photon Res (2018) 6(4):228–33. doi:10.1364/prj.6.000228
31. Ma C, Di J, Zhang Y, Li P, Xiao F, Liu K, et al. Reconstruction of Structured Laser Beams through a Multimode Fiber Based on Digital Optical Phase Conjugation. Opt Lett (2018) 43(14):3333–6. doi:10.1364/ol.43.003333
32. Ma C, Di J, Dou J, Li P, Xiao F, Liu K, et al. Structured Light Beams Created through a Multimode Fiber via Virtual Fourier Filtering Based on Digital Optical Phase Conjugation. Appl Opt (2020) 59(3):701–5. doi:10.1364/ao.380058
33. Chen Z, Zeng T, Qian B, Ding J. Complete Shaping of Optical Vector Beams. Opt Express (2015) 23(14):17701–10. doi:10.1364/oe.23.017701
34. Li L, Chang C, Yuan C, Feng S, Nie S, Ren Z-C, et al. High Efficiency Generation of Tunable Ellipse Perfect Vector Beams. Photon Res (2018) 6(12):1116–23. doi:10.1364/prj.6.001116
35. Wang H-T, Wang X-L, Li Y, Chen J, Ding C-SJ, Wang H. A New Type of Vector fields with Hybrid States of Polarization. Opt Express (2010) 18:10786–95. doi:10.1364/oe.18.010786
36. Li S-M, Li Y, Wang X-L, Kong L-J, Lou K, Tu C, et al. Taming the Collapse of Optical Fields. Sci Rep (2012) 2:1007. doi:10.1038/srep01007
37. Chen R-P, Zhong L-X, Chew K-H, Zhao T-Y, Zhang X. Collapse Dynamics of a Vector Vortex Optical Field with Inhomogeneous States of Polarization. Laser Phys (2015) 25:075401. doi:10.1088/1054-660x/25/7/075401
38. Li S-M, Ren Z-C, Kong L-J, Qian S-X, Tu C, Li Y, et al. Unveiling Stability of Multiple Filamentation Caused by Axial Symmetry Breaking of Polarization. Photon Res (2016) 4:B29–B34. doi:10.1364/prj.4.000b29
39. Marburger JH, Dawes E. Dynamical Formation of a Small-Scale Filament. Phys Rev Lett (1968) 21:556–8. doi:10.1103/physrevlett.21.556
40. Peñano J, Hafizi B, Ting A, Helle M. Theoretical and Numerical Investigation of Filament Onset Distance in Atmospheric Turbulence. J Opt Soc Am B (2014) 31(5):963–71. doi:10.1364/josab.31.000963
41. Wu G, Wang F, Cai Y. Coherence and Polarization Properties of a Radially Polarized Beam with Variable Spatial Coherence. Opt Express (2012) 20(27):28301–18. doi:10.1364/oe.20.028301
42. Wang F, Cai Y, Dong Y, Korotkova O. Experimental Generation of a Radially Polarized Beam with Controllable Spatial Coherence. Appl Phys Lett (2012) 100:051108. doi:10.1063/1.3681802
43. Zhu S, Wang J, Liu X, Cai Y, Li Z. Generation of Arbitrary Radially Polarized Array Beams by Manipulating Correlation Structure. Appl Phys Lett (2016) 109:161904. doi:10.1063/1.4965705
44. Ping C, Liang C, Wang F, Cai Y. Radially Polarized Multi-Gaussian Schell-Model Beam and its Tight Focusing Properties. Opt Express (2017) 25(26):32475–90. doi:10.1364/oe.25.032475
45. Menyuk CR. Stability of Solitons in Birefringent Optical Fibers II Arbitrary Amplitudes. J Opt Soc Am B (1988) 5(2):392–402. doi:10.1364/josab.5.000392
46. Park Q-H, Shin HJ. Painlevé Analysis of the Coupled Nonlinear Schrödinger Equation for Polarized Optical Waves in an Isotropic Medium. Phys Rev E (1999) 59(2):2373–9. doi:10.1103/physreve.59.2373
47. Cai Y, Lu X, Lin Q. Hollow Gaussian Beams and Their Propagation Properties. Opt Lett (2003) 28:1084–6. doi:10.1364/ol.28.001084
49. Dubietis A, Gaižauskas E, Tamošauskas G, Di Trapani P. Light Filaments without Self-Channeling. Phys Rev Lett (2004) 92:253903. doi:10.1103/physrevlett.92.253903
50. Wang D, Liu G-G, Lü J-Q, Li P-P, Cai M-Q, Zhang G-L, et al. Femtosecond Polarization-Structured Optical Field Meets an Anisotropic Nonlinear Medium. Opt Express (2018) 26(21):27726–47. doi:10.1364/oe.26.027726
51. Braun A, Korn G, Liu X, Du D, Squier J, Mourou G. Self-channeling of High-Peak-Power Femtosecond Laser Pulses in Air. Opt Lett (1995) 20:73–5. doi:10.1364/ol.20.000073
52. Liu Y, Chen Y, Chen Y, Wang F, Cai Y, Liang C, et al. Robust Far-Field Imaging by Spatial Coherence Engineering. Opto-Electron. Adv (2021) 4:210027. doi:10.29026/oea.2022.210027
53. Zhang X, Chen Y, Wang F, Cai Y. Scattering of Partially Coherent Vector Beams by a Deterministic Medium Having Parity-Time Symmetry. Photonics (2022) 9:140. doi:10.3390/photonics9030140
54. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical Coherence Encryption with Structured Random Light. PhotoniX (2021) 2:6. doi:10.1186/s43074-021-00027-z
55. Moll KD, Gaeta AL, Fibich G. Self-Similar Optical Wave Collapse: Observation of the Townes Profile. Phys Rev Lett (2003) 90:203902. doi:10.1103/physrevlett.90.203902
Keywords: self-focusing length, state of polarization, 3D manipulation, propagation characteristics, Stokes parameters
Citation: Lu L, Wang Z, Lin R and Cai Y (2022) Three-Dimensional Manipulation for Self-Focusing Behavior via the State of Polarization. Front. Phys. 10:892581. doi: 10.3389/fphy.2022.892581
Received: 09 March 2022; Accepted: 30 March 2022;
Published: 09 May 2022.
Edited by:
Shiyao Fu, Beijing Institute of Technology, ChinaReviewed by:
Xianfeng Chen, Shanghai Jiao Tong University, ChinaJianming Wen, Kennesaw State University, United States
Copyright © 2022 Lu, Wang, Lin and Cai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yangjian Cai, eWFuZ2ppYW5jYWlAc3VkYS5lZHUuY24=
†These authors have contributed equally to this work
 Lu Lu
Lu Lu Zhiqiang Wang
Zhiqiang Wang Rong Lin4
Rong Lin4 Yangjian Cai
Yangjian Cai