Electric Field Tuned Dipolar Interaction Between Rydberg Atoms

We demonstrated a tuned dipole interaction between Rydberg atoms by employing a controllable electric field in a cold cesium ensemble. The |nP_3/2⟩ (n = 38–40) Rydberg pairs are prepared with a three-photon scheme and detected via the state-selective field ionization technique. A weak DC electric field is used to tune the Rydberg pair interaction from the van der Waals interaction regime to the dipole–dipole interaction regime. The Förster resonant interaction and an adiabatic resonance energy transfer between the nP and nS Rydberg states are attained by precisely tuning the electric field. Rydberg excitation blockade with and without the electric field is investigated by changing the excitation pulse duration, which demonstrates that the dipole interaction–induced blockade effect is stronger than the van der Waals interaction–induced blockade effect. The precise control of the Rydberg interaction is of great significance to the coherent interaction in many-body systems and non-radiative collision processes.

1 Introduction

Rydberg atom, one electron placed in a highly energetic excited state is a kind of exotic atom that has attracted more and more attention in atomic and molecular physics in recent years. A Rydberg atom has a huge orbital radius ( ∝ n², n is the principal quantum number), a large polarizability (∝ n⁷), a strong interaction between Rydberg atoms (∝ n¹¹) [1], and so on. Due to these properties, the Rydberg atom is very popular both for investigation of the blockade effect and single photon source [2,3] and single photon transistor [4] and for the microwave field measurement and the field sensor [5–10].

In addition, Rydberg levels can be tuned by the external field to the Förster resonant regime, where the Rydberg atoms display strong dipole–dipole interaction and dipole blockade [11,12]. At the Förster resonance, the non-radiative redistribution of the electronic state between two particles coupled by the dipole–dipole interaction is of great importance for a variety of phenomena. For the Rydberg pair state, the initial prepared Rydberg atom can adiabatically transfer to a nearby state without a change in the kinetic energy, which is called the resonance energy transfer (RET). The dipole interaction and the RET play a very important role in atomic and molecular dynamics and multi-body interactions [13]. This kind of resonant interaction has been studied extensively, for example, the strong interaction between Rydberg atoms under an electric field [14–17], the exploration, and analysis of the multi-body [13] and the few-body interaction [18,19], an optical nonlinearity in cold atom systems [20], and an atomic interference [21]. In recent years, the resonant dipole interaction between neutral pairs of atoms, particularly the dipole interaction between Rydberg atoms, has been used to investigate quantum gates [22–24], quantum simulation, and computing [25,26].

In this work, we prepared the |nP_3/2⟩ (n = 38–40) Rydberg pair with the three-photon scheme in the cold cesium atoms. A weak DC electric field is used to tune the Rydberg pair interaction from the van der Waals interaction regime to the dipole–dipole interaction regime. At the Förster resonance, we achieved an adiabatic resonance energy transfer between the nP and nS Rydberg states by means of controlling the dipolar interaction tuned by an electric field. Rydberg excitation with and without the DC field and the blockade effect are investigated by changing the excitation pulse duration, which demonstrates that the dipole interaction–induced blockade effect is stronger than the van der Waals interaction–induced blockade effect.

2 Interactions Between Rydberg Atoms

As mentioned earlier, the Rydberg atom has a strong long-range interaction and a large dipole transition matrix element because of its huge polarizability. Considering a pair of Rydberg atoms, the Hamiltonian can be expressed as,

$H=H_0+{\widehat{V}}_{int},(1)$

where, H₀ = H_A + H_B is the Hamiltonian of the bare atoms A and B, ${\widehat{V}}_{int}$ is the interaction potential between atoms. The interaction potential can be written as a Laurent series with the atomic distance R,

${\widehat{V}}_{int}=-\sum _{n=1}^{\infty }\frac{C_n}{R^n},(2)$

with C_n as the dispersion coefficient. We assumed that two atoms are initially in the same Rydberg state |2⟩, as shown in Figure 1A. The state |2⟩ can transition to the state |1⟩ (|3⟩) by emitting (absorbing) a photon. The energy level is E_i (i = 1,2,3), and the energy defect of the atomic pair is defined as ΔE = 2E₂ − (E₁ + E₃). We take the pair state of {|2⟩|2⟩} (|nP⟩|nP⟩) and {|1⟩|3⟩} (|nS⟩|n′S⟩) as our basis vectors and further diagonalize the Hamiltonian to obtain the eigen energy,

$E_{\pm }=-\frac{\mathrm{\Delta }E}{2}\pm \sqrt{\left(\frac{\mathrm{\Delta }E}{2}\right)+{\left(\frac{{\vec{\mu }}_1\cdot {\vec{\mu }}_2}{R^3}\right)}^2},(3)$

where ${\vec{\mu }}_1$ $({\vec{\mu }}_2)$ represents the transition dipole moment of |2⟩ → |1⟩ (|2⟩ → |3⟩). Usually, 1) when |ΔE|≫|μ₁μ₂/R³|, the Rydberg pair mainly displays the van der Waals interaction, and the related interaction potential is V_vdW = C₆/R⁶ (C₆ ∼ n¹¹)(Figure 1A). 2) When |ΔE|≪|μ₁μ₂/R³|, the Rydberg pair shows the strong dipole–dipole interaction, and the interaction potential is V_dd = C₃/R³ (Figure 1B). For |38P_3/2, m_j = 3/2 (1/2)⟩ state used in this work, the calculated C₃ = 0.56 (0.37) GHz ⋅ μm³ and the mean of C₆ in all directions are 1.62 (1.40) GHz ⋅ μm³, respectively. Both the van der Waals and the dipole–dipole interaction of Rydberg atoms can block further excitation of the nearby atom, resulting in the blockade effect. Under the condition of ΔE = 0 (E₃ − E₂ = E₂ − E₁), one initial atom in |2⟩ state can transfer to |3⟩ state by absorbing a photon that is emitted by the |2⟩ → |1⟩ transition of the other atom, which is called the resonance energy transfer (RET).

FIGURE 1

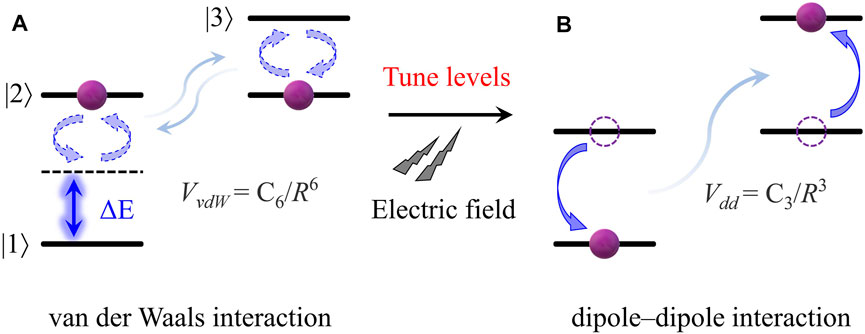
FIGURE 1. (color online). (A) Scheme of the van der Waals interaction between Rydberg atomic pairs. Two atoms initially prepared in the same Rydberg state |2⟩, |1⟩, and |3⟩ are the dipole allowed near states. ΔE indicates the energy defect between |3⟩ − |2⟩ and |2⟩ − |1⟩. For the case of ΔE ≠ 0, the Rydberg pair displays the van der Waals interaction, which scales as R⁻⁶. (B) Scheme of the dipole–dipole interaction. The weak DC electric field is used to tune the Rydberg level to the Förster resonance. For the case of ΔE = 0, the Rydberg pair displays the dipole–dipole interaction, which scales as R⁻³.

In view of Rydberg wave functions and parity conservation, the selection rules of Δl = ±1 (l, the orbital quantum number) and Δm_j = 0, ±1 (m_j, the total angular momentum quantum number) for the electric dipole moment operator are considered. For a cesium atom in this work, we chose the initial |nP_3/2⟩ state excited by the three-photon excitation; the form of resonance energy transfer is usually expressed as

$n{\mathrm{P}}_{3/2}+n{\mathrm{P}}_{3/2}\to n{\mathrm{S}}_{1/2}+\left(n+1\right){\mathrm{S}}_{1/2}.(4)$

Based on the Stark shift and splitting of the Rydberg state, we tuned the Rydberg level by applying the external DC electric field to obtain ΔE = 0 and the RET condition. Following Zimmerman’s method [27], we numerically resolved the radial equation of the cesium atom and obtained the Stark map of the cesium Rydberg atom. From the Stark map, we extracted the Stark shift of |nS_1/2⟩ and |nP_3/2⟩ levels and obtained the energy defect of the Rydberg pair and, further, the Förster resonant electric field. For details, refer Section 4.

3 Experiment Scheme and Setup

Our experiment is performed in a standard magneto-optical trap (MOT), where a cold cloud of Cs atoms is trapped in the center of a metal MOT with a density of 10¹⁰ cm⁻³. The |nP_3/2⟩ Rydberg state is excited by the three-photon excitation scheme. The experimental setup and three-photon excitation are displayed in Figure 2. Three photons at 852 nm, 1,470 nm and 780 nm lasers are used to realize the Rydberg transition of |6S_1/2⟩ → |6P_3/2⟩ → |7S_1/2⟩ → |nP_3/2⟩. The first photon couples the lower transition of |6S_1/2(F = 4)⟩ → |6P_3/2(F′ = 5)⟩ with the detuning of δ = +110 MHz and the Rabi frequency of Ω₈₅₂ = 2π × 45 MHz; the second photon drives the intermediate transition of |6P_3/2(F′ = 5)⟩ → |7S_1/2(F′′ = 4)⟩ with the Rabi frequency of Ω₁₄₇₀ = 2π × 80 MHz, while the third photon achieves the Rydberg transition of |7S_1/2⟩ → |nP_3/2⟩ with the Rabi frequency of Ω₇₈₀ = 2π × 10 MHz.

FIGURE 2

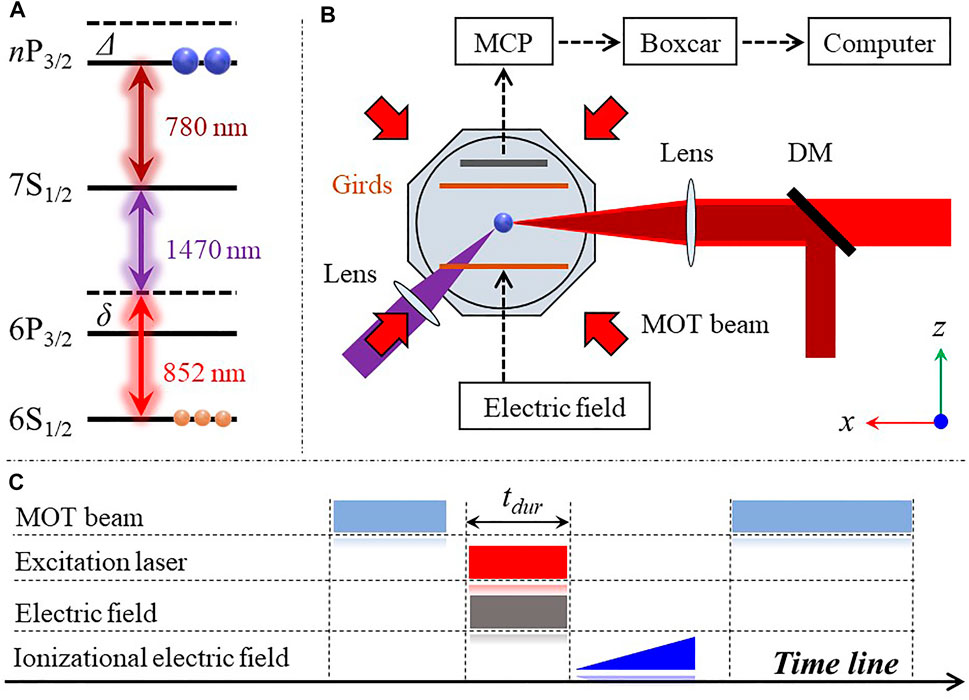
FIGURE 2. (color online). (A) Three-photon excitation diagram of the Rydberg state. The first photon from the 852 nm (red) laser drives the lower transition |6S_1/2⟩ → |6P_3/2⟩, whose frequency is blue detuned δ from the intermediate state. The second photon, 1,470-nm (dark purple) laser couples the intermediate transition of |6P_3/2⟩ → |7S_1/2⟩. The third photon, 780-nm (dark red) laser achieves the Rydberg state via the up transition |7S_1/2⟩ → |nP_3/2⟩. Yellow and blue balls represent the ground and Rydberg state atoms, respectively. (B) Schematic diagram of the experiment. Three excitation lasers cross through the MOT center. The ions of Rydberg atoms are detected with a MCP detector, analyzed with a boxcar, and recorded by a computer. The ramp (DC) electric field is applied to the grids located in the z direction for the field ionization (the manipulation of the Rydberg interaction). Other grids in x − and y − directions are not shown here. (C) Timing sequence. After switching off the MOT beam, the Rydberg excitation pulse with duration of 6 μs is switched on for preparing Rydberg atoms. During the Rydberg excitation, a weak DC electric field is applied to tune the interaction between Rydberg atoms. After the Rydberg excitation, a ramp electric field is applied that is used to selectively ionize the Rydberg atoms. DM: dichroic mirror.

The experimental setup is shown in Figure 2B. Cesium atoms are trapped in the center of a metal MOT via the laser cooling and trap technique. The MOT density is measured with the shadow image. The first photon, 852 nm, and the third photon, 780 nm, lasers with a waist of ∼ 80 μm are co-propagated through the MOT center along the x-axis after being combined by a dichroic mirror (DM), whereas, the second photon 1,470 nm lasers with a beam waist of 800 μm is crossed with the first photon laser at the center of the atom cloud, forming the cylindrical excitation region. Three pairs of girds (only one pair of grid is shown in Figure 2) are placed on either side of the MOT along three directions, which are used to apply the electric field for the state-selective field ionization of Rydberg atoms and compensate for the stray electric field. The resultant Rydberg ions are accelerated to the microchannel plate (MCP) detector. The Rydberg signal the MCP detects is analyzed with a boxcar and recorded with a computer.

The experiment is performed within 100 μs, during which the cooling light is turned off, see the timing sequence of Figure 2C. During the Rydberg excitation, we apply a weak DC electric field to tune the Rydberg level and further the interaction between Rydberg atoms. After the Rydberg excitation, we apply a ramp electric field for the state selective field, ionizing the initial prepared Rydberg atoms and the production due to the RET process.

4 Experimental Results

In the experiment, we used the three-photon scheme to excite the |nP_3/2⟩ Rydberg state; refer Figure 2A. The frequencies of the first (852 nm) and the second (1,470 nm) lasers are locked with a method of a saturated absorption spectrum (SAS) and an optical-optical double-resonance spectrum (OODRS), respectively. The frequency of the third (780 nm) laser is scanned at a speed of 4 mHz. In Figure 3, we present the time of flight (TOF) spectra of the |38P_3/2⟩ state without (Figure 3A) and with (Figure 3B) an electric field of 1.74 V/cm. The peak at 0.5 μs comes from the initially excited |38P_3/2⟩ state, which is marked with the blue gate. In Figure 3B, we clearly observed that the small peak appears at later time, marked with the yellow gate, which mainly comes from the |38S_1/2⟩ state. The |38S_1/2⟩ state is produced due to the RET process as the |38S_1/2⟩ state can only be populated at an external field of ∼ 1.74 V/cm, where the energy defect is ΔE ≈ 0. It should be noted that |39S_1/2⟩ would accompany the |38S_1/2⟩ state during the RET process and appear before the blue gate. However, in Figure 3B, we can see the variation of the front wing of the TOF spectrum but not a clear |39S_1/2⟩ signal due to our ramp electric field with a fast ramp time. In addition, it is also seen that in the presence of the electric field, the signal of the |38P_3/2⟩ state in the blue gate is about 50% of the field free signal; we attribute the decrease of the signal of the |38P_3/2⟩ state to the dipole blockade effect due to the strong dipole interaction at the Förster resonance. It is noted that the small peaks before the blue gate may be attributed to auto-ionization during the Rydberg excitation and the high angular momentum Rydberg states, which are beyond the scope of this work.

FIGURE 3

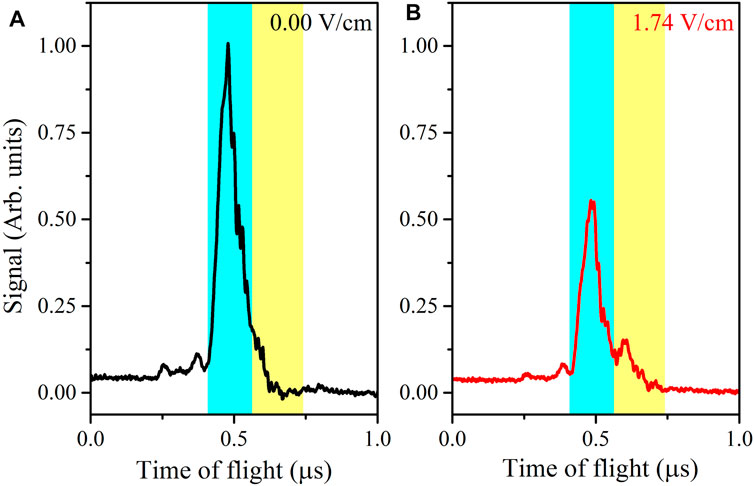
FIGURE 3. (color online). Time of flight spectrum of the |38P_3/2⟩ state with a DC field of 0 V/cm (A) and 1.74 V/cm (B). The blue and yellow shadows mark the positions of the |38P_3/2⟩ and |38S_1/2⟩ states, respectively. The initial |38P_3/2⟩ atoms transfer to |38S_1/2⟩ due to the Förster resonant dipole interaction within the electric field of 1.74 V/cm.

To better understand the RET process and qualitative analysis of the observed signals, in Figure 4A, we present the Stark map near n = 34, 35 manifolds including |38P_3/2⟩, |38S_1/2⟩, |39S_1/2⟩ states for |m_j| = 1/2 (red solid line) and 3/2 (blue solid line). The vertical dashed lines mark the Förster resonance electric fields, 1.60 V/cm for m_j = 1/2 and 1.74 V/cm for m_j = 3/2, where the energy defect ΔE ≃ 0. Therefore, although the dipole interaction can couple |38P_3/2⟩ to a bunch of states, the Förster resonance process occurs only for the specific pair of states under the specific electric field value. The signal of |38S_1/2⟩ in the yellow gate of Figure 3B is generated from the |38P_3/2⟩ Förster resonant transfer. We conducted a series of measurements and recorded the |38S_1/2⟩ signal in the yellow gate by changing the frequency of the 780 nm laser and DC electric fields. In Figure 4B, we present a contour plot of the |38S_1/2⟩ state transferred from |38P_3/2⟩ as a function of the DC electric field and the 780 nm laser detuning Δ₇₈₀. It is shown that the |38S_1/2⟩ signal is very small and reaches maximum only at the field of ∼ 1.58 ± 0.01 V/cm and 1.74 ± 0.01 V/cm, showing good agreement with the calculations with a deviation of less than 2%.

FIGURE 4

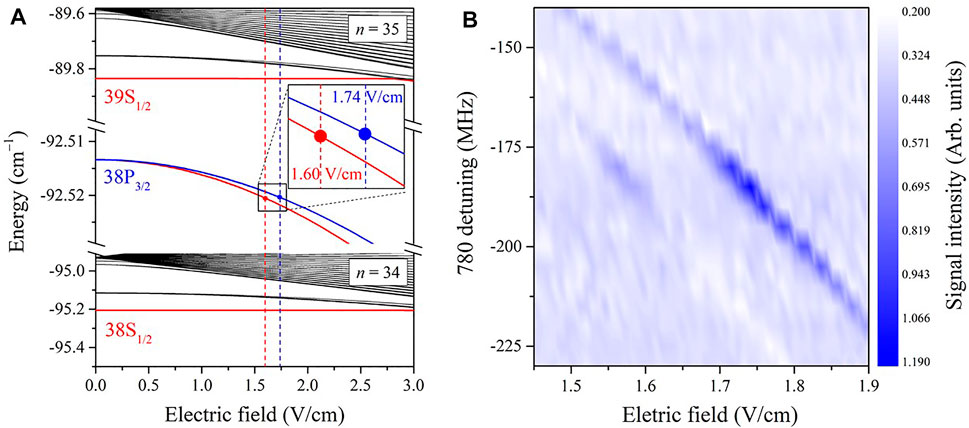
FIGURE 4. (color online). (A) Calculations of the Stark map near n = 34 and 35 manifolds. In the electric field, the |38P_3/2⟩ state shifts and splits into two Stark lines, forming two Förster resonant points at the electric field 1.60 V/cm and 1.74 V/cm, respectively, as shown with the black square. The inset shows the enlargement of the square marked region. (B) Contour plot of the |38S_1/2⟩ state transferred from the initial |38P_3/2⟩ state as a function of the DC electric field and the 780-nm laser detuning Δ₇₈₀. The signal of the |38S_1/2⟩ state can be observed at the electric fields of 1.58 ± 0.01 V/cm and 1.74 ± 0.01 V/cm, respectively.

As mentioned earlier, the strong interaction between Rydberg atoms can block further excitation of nearby atoms. In the following experiment, we will investigate the blockade effect with and without the electric field. The blockade effect is attained by varying the laser power [11,28] or the excitation pulse duration. In contrast to the previous literature, we changed the duration of the excitation pulse in this work. To observe the blockade effect, we recorded all the signals, including the signals in the blue and yellow gates. In Figure 5, we present the measured Rydberg ions of the |40P_3/2⟩ state as a function of the excitation pulse duration with (red circles) and without (blue squares) the DC electric field. The dashed line displays the Rydberg signal that linearly increases with the excitation duration without any blockade effect.

FIGURE 5

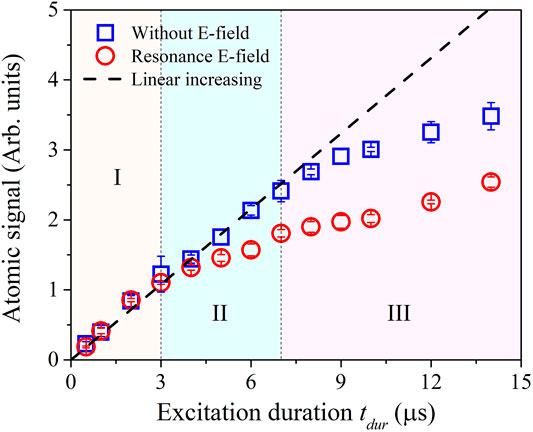
FIGURE 5. (color online). Measured field ionization signal of |40P_3/2⟩ Rydberg state as a function of the excitation duration with (red circles) and without (blue squares) the DC electric field. The black dashed line displays the linear increasing with the excitation duration without any blockade effect. It is seen that blockade behavior is stronger due to the dipole interaction than that due to the van der Waals interaction.

Close inspection of Figure 5 reveals that the Rydberg excitation process can be divided into three regions. I) The first linear region for the excitation duration t_dur < 3μs, where the excited Rydberg signals are almost same and lie in the dashed line, displaying linear increase with the excitation duration for both cases. II) The second region for the excitation duration of 3μs ≲ t_dur ≲ 7μs, where the measured Rydberg signal without the DC field still lies in the dashed line, displaying the linear increase, but the Rydberg signal with the DC field begins to deviate from the dashed line when t_dur > 3μs, and the difference between the signal with and without the DC field increases with the excitation duration. This behavior proves that the dipole interaction (1/R³)–induced blockade effect is much larger than the van der Waals interaction (1/R⁶)–induced blockade effect. III) The third blockade region for the excitation duration t_dur ≳ 7μs, where the Rydberg signal in the absence of the DC field also begins to deviate from the dashed line, showing the blockade effect. In this region, the difference between the signals with and without the DC field does not change much when we increase the excitation duration further because they are both in the blockade region.

Due to the large polarizability, the energy level of the Rydberg state is easily tuned with the external electric field to the Förster resonance, where Rydberg atoms display the strong dipole interaction. The electric field tuned dipole interaction has lots of applications in the non-radiative energy exchange [29], the collective effect [30], the engineering quantum states of matter [31], and so on. The tuning of coherent interactions in many-body systems with an external field has been a promising method. The cold Rydberg gases provide an ideal platform for the quantum simulation of complex many-body problems due to their controllable interactions.

5 Conclusion

To conclude, in this work, we have investigated the interaction between |nP_3/2⟩ (n = 38–40) Rydberg pairs, excited by the three-photon scheme in the cold cesium atoms. The Rydberg level is tuned by the weak DC field and the resonant energy transfer spectrum due to the Förster resonance is observed. The |38S_1/2⟩ state due to the resonant energy transfer as a function of the excitation frequency and the electric field has been obtained and the extracted Förster electric field for |38P_3/2⟩ Rydberg atom agrees with the calculated field value. Finally, the blockade effects induced by the van der Waals interaction and the dipole interaction between Rydberg pairs have been studied by changing the excitation duration, which demonstrates that the dipole interaction–induced blockade effect is stronger than the van der Waals interaction–induced blockade effect. Considering the flexible and controllable nature of the electric field, the field tuned dipole interaction plays an important role in the coherent interactions in many-body systems and non-radiative collision processes and collective effects and engineering quantum states of matter.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.

Author Contributions

JZ designed the study. YJ and JB collected and analyzed the data and wrote the original manuscript. RS, SB, and SJ contributed to the manuscript revision. All authors provided review and comment on the subsequent versions of the manuscript.

Funding

This study was supported by the National Key Research and Development Program of China (2017 YFA0304203), the National Natural Science Foundation of China (12120101004, 61835007, and 62175136), the Changjiang Scholars and Innovative Research Team in University of Ministry of Education of China (IRT 17R70), the Graduate Education Innovation Project of Shanxi Province (2021Y017), the Shanxi 1331 Project, and the Scientific and Technological Innovation Program of Higher Education Institutions in Shanxi Province (2020L0479).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Gallagher TF. Rydberg Atoms. New York, NY, USA: Cambridge University Press (1994).

Google Scholar

2. Ornelas-Huerta DP, Craddock AN, Goldschmidt EA, Hachtel AJ, Wang Y, Bienias P, et al. On-demand Indistinguishable Single Photons from an Efficient and Pure Source Based on a Rydberg Ensemble. Optica (2020) 7:813–9. doi:10.1364/optica.391485

CrossRef Full Text | Google Scholar

3. Peyronel T, Firstenberg O, Liang QY, Hofferberth S, Gorshkov AV, Pohl T, et al. Quantum Nonlinear Optics with Single Photons Enabled by Strongly Interacting Atoms. Nature (2012) 488:57–60. doi:10.1038/nature11361

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Tiarks D, Baur S, Schneider K, Dürr S, Rempe G. Single-photon Transistor Using a Förster Resonance. Phys Rev Lett (2014) 113:053602. doi:10.1103/PhysRevLett.113.053602

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Jiao Y, Han X, Yang Z, Li J, Raithel G, Zhao J, et al. Spectroscopy of Cesium Rydberg Atoms in strong Radio-Frequency fields. Phys Rev A (2016) 94:1–7. doi:10.1103/PhysRevA.94.023832

CrossRef Full Text | Google Scholar

6. Jiao Y, Hao L, Han X, Bai S, Raithel G, Zhao J, et al. Atom-Based Radio-Frequency Field Calibration and Polarization Measurement Using Cesium nD_J Floquet States. Phys Rev Appl (2017) 8:1–7. doi:10.1103/PhysRevApplied.8.014028

CrossRef Full Text | Google Scholar

7. Jing M, Hu Y, Ma J, Zhang H, Zhang L, Xiao L, et al. Atomic Superheterodyne Receiver Based on Microwave-Dressed Rydberg Spectroscopy. Nat Phys (2020) 16:911–5. doi:10.1038/s41567-020-0918-5

CrossRef Full Text | Google Scholar

8. Hao L, Xue Y, Fan J, Bai J, Jiao Y, Zhao J. Precise Measurement of a Weak Radio Frequency Electric Field Using a Resonant Atomic Probe. Chin Phys B (2020) 29. doi:10.1088/1674-1056/ab6c49

CrossRef Full Text | Google Scholar

9. Sedlacek JA, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer JP. Microwave Electrometry with Rydberg Atoms in a Vapour Cell Using Bright Atomic Resonances. Nat Phys (2012) 8:819–24. doi:10.1038/nphys2423

CrossRef Full Text | Google Scholar

10. Bai J, Fan J, Hao L, Spong NL, Jiao Y, Zhao J. Measurement of the Near Field Distribution of a Microwave Horn Using a Resonant Atomic Probe. Appl Sci (Switzerland) (2019) 9:1–9. doi:10.3390/app9224895

CrossRef Full Text | Google Scholar

11. Vogt T, Viteau M, Zhao J, Chotia A, Comparat D, Pillet P. Dipole Blockade at Förster Resonances in High Resolution Laser Excitation of Rydberg States of Cesium Atoms. Phys Rev Lett (2006) 97:6–9. doi:10.1103/PhysRevLett.97.083003

CrossRef Full Text | Google Scholar

12. Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko Y, Grangier P, et al. Entanglement of Two Individual Neutral Atoms Using Rydberg Blockade. Phys Rev Lett (2010) 104:2–5. doi:10.1103/PhysRevLett.104.010502

CrossRef Full Text | Google Scholar

13. Mourachko I, Li W, Gallagher TF. Controlled many-body Interactions in a Frozen Rydberg Gas. Phys Rev A (2004) 70:1–4. doi:10.1103/PhysRevA.70.031401

CrossRef Full Text | Google Scholar

14. Gallagher TF, Gounand F, Kachru R, Tran NH, Pillet P. Perturbation of the Ba 6sng Series at n =24 by Zero-Field Spectroscopy and Forced Autoionization. Phys Rev A (1983) 27:2485–92. doi:10.1103/physreva.27.2485

CrossRef Full Text | Google Scholar

15. Renn MJ, Anderson WR, Gallagher TF. Resonant Collisions of K Rydberg Atoms. Phys Rev A (1994) 49:908–12. doi:10.1103/physreva.49.908

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pelle B, Faoro R, Billy J, Arimondo E, Pillet P, Cheinet P. Quasiforbidden Two-Body Förster Resonances in a Cold Cs Rydberg Gas. Phys Rev A (2016) 93:1–11. doi:10.1103/PhysRevA.93.023417

CrossRef Full Text | Google Scholar

17. Zhelyazkova V, Hogan SD. Electrically Tuned Förster Resonances in Collisions of NH₃ with Rydberg He Atoms. Phys Rev A (2017) 95:1–6. doi:10.1103/PhysRevA.95.042710

CrossRef Full Text | Google Scholar

18. Gurian JH, Cheinet P, Huillery P, Fioretti A, Zhao J, Gould PL, et al. Observation of a Resonant Four-Body Interaction in Cold Cesium Rydberg Atoms. Phys Rev Lett (2012) 108:1–5. doi:10.1103/PhysRevLett.108.023005

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Faoro R, Pelle B, Zuliani A, Cheinet P, Arimondo E, Pillet P. Borromean Three-Body FRET in Frozen Rydberg Gases. Nat Commun (2015) 6. doi:10.1038/ncomms9173

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Firstenberg O, Adams CS, Hofferberth S. Nonlinear Quantum Optics Mediated by Rydberg Interactions. J Phys B: At Mol Opt Phys (2016) 49:152003. doi:10.1088/0953-4075/49/15/152003

CrossRef Full Text | Google Scholar

21. Nipper J, Balewski JB, Krupp AT, Hofferberth S, Löw R, Pfau T. Atomic Pair-State Interferometer: Controlling and Measuring an Interaction-Induced Phase Shift in Rydberg-Atom Pairs. Phys Rev X (2012) 2:1–7. doi:10.1103/PhysRevX.2.031011

CrossRef Full Text | Google Scholar

22. Lukin MD, Fleischhauer M, Cote R, Duan LM, Jaksch D, Cirac JI, et al. Dipole Blockade and Quantum Information Processing in Mesoscopic Atomic Ensembles. Phys Rev Lett (2001) 87:37901. doi:10.1103/PhysRevLett.87.037901

CrossRef Full Text | Google Scholar

23. Isenhower L, Urban E, Zhang XL, Gill AT, Henage T, Johnson TA, et al. Demonstration of a Neutral Atom Controlled-Not Quantum Gate. Phys Rev Lett (2010) 104:8–11. doi:10.1103/PhysRevLett.104.010503

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Müller MM, Murphy M, Montangero S, Calarco T, Grangier P, Browaeys A. Implementation of an Experimentally Feasible Controlled-phase Gate on Two Blockaded Rydberg Atoms. Phys Rev A (2014) 89:1–8. doi:10.1103/PhysRevA.89.032334

CrossRef Full Text | Google Scholar

25. Wu X, Liang X, Tian Y, Yang F, Chen C, Liu YC, et al. A Concise Review of Rydberg Atom Based Quantum Computation and Quantum Simulation. Chin Phys B (2021) 30. doi:10.1088/1674-1056/abd76f

CrossRef Full Text | Google Scholar

26. Altman E, Brown KR, Carleo G, Carr LD, Demler E, Chin C. Quantum Simulators: Architectures and Opportunities. PRX Quan (2021) 2:1–19. doi:10.1103/prxquantum.2.017003

CrossRef Full Text | Google Scholar

27. Zimmerman M, Littman M, Kash M, Kleppner D. Stark Structure of the Rydberg States of Alkali-Metal Atoms. Phys Rev A (1979) 20. doi:10.1103/physreva.20.2251

CrossRef Full Text | Google Scholar

28. Tong D, Farooqi SM, Stanojevic J, Krishnan S, Zhang YP, Côté R, et al. Local Blockade of Rydberg Excitation in an Ultracold Gas. Phys Rev Lett (2004) 93:1–4. doi:10.1103/PhysRevLett.93.063001

CrossRef Full Text | Google Scholar

29. Safinya KA, Delpech JF, Gounand F, Sandner W, Gallagher TF. Resonant Rydberg-Atom-Rydberg-Atom Collisions. Phys Rev Lett (1981) 47:405–8. doi:10.1103/PhysRevLett.47.405

CrossRef Full Text | Google Scholar

30. Comparat D, Pillet P. Dipole Blockade in a Cold Rydberg Atomic Sample [Invited]. J Opt Soc America B (2010) 27:A208. doi:10.1364/josab.27.00a208

CrossRef Full Text | Google Scholar

31. Saffman M, Walker TG, Mølmer K. Quantum Information with Rydberg Atoms. Rev Mod Phys (2010) 82:2313–63. doi:10.1103/RevModPhys.82.2313

CrossRef Full Text | Google Scholar