- Department of Physics and Collaborative Innovation Center for Optoelectronic Semiconductors and Efficient Devices, Xiamen University, Xiamen, China
Quantum interferences of entangled photons have engendered tremendous intriguing phenomena that lack any counterpart in classical physics. Hitherto, owing to the salient properties of quantum optics, quantum interference has been widely studied and provides useful tools that ultimately broaden the path towards ultra-sensitive quantum metrology, ranging from sub-shot-noise quantum sensing to high-resolution optical spectroscopy. In particular, quantum interferometric metrology is an essential requisite for extracting information about the structure and dynamics of photon-sensitive biological and chemical molecules. This article reviews the theoretical and experimental progress of this quantum interferometric metrology technology along with their advanced applications. The scope of this review includes Hong–Ou–Mandel interferometry with ultrahigh timing resolution, entanglement-assisted absorption spectroscopy based on a Fourier transform, and virtual-state spectroscopy using tunable energy-time entangled photons.
1 Introduction
Quantum entanglement is a non-classical phenomenon that the quantum state of each individual particle cannot be described independently of the state of the others, whose nature reveals the most fascinating and unexpected aspects of the quantum world [1, 2]. For example, the non-classical correlation of such entangled particles would not be diminished even when they are spatially separated by arbitrary distances. Naturally, quantum entanglement is an essential prerequisite for a variety of quantum experiments in the field of fundamental tests of quantum physics, such as the investigation of the Einstein–Podolsky–Rosen (EPR) paradox and the violation of Bell’s inequalities [3–5], and practical applications, such as quantum information processing [6, 7]. The exploitation of quantum entanglement in these specific scenarios has great potential to outperform the schemes based on classical physics. As an example in metrology, while an individual particle exhibits an inherent uncertainty, the joint correlation between entangled photons can be exempt from such limitation. More specifically, the arriving time of the individual photons is completely random, but the entangled photons always arrive simultaneously. These myriad and significant implications of quantum entanglement make them compelling for use in quantum optical metrology [8–12].
Quantum interference of entangled photons leads to many counterintuitive results, which can be considered an absolute necessity in the quantum mechanic’s toolkit. Thereinto, Hong–Ou–Mandel (HOM) interference, the fact that two identical photons that arrive simultaneously on different input ports of a beam splitter would bunch into a common output port, is a prototypical example of quantum interference [13]. Its interference visibility, namely, the bunching probability, is directly related to photons’ level of indistinguishability. The definition of indistinguishability is on the bases of various parameters in all degrees of freedom, such as polarization, frequency, time, path, and orbital angular momentum. This quantum effect enables a wide range of quantum information processing tasks, in particular for the measurements of optical delays and spectroscopy with the requirements for ultrahigh resolution, precision and accuracy, and experimental robustness against detrimental noise [14–17].
In the context of the applications in both metrology and sensing, the precise and demanding measurements are most likely performed as optical interference, including but not limited to Ramsey interferometry in atomic spectroscopy [18], x-ray diffraction in crystallography [19], and optical interferometry in gravitational-wave studies [20, 21]. Quantum mechanics indicates that the fundamental shot noise limit of the phase uncertainty in optical metrology based on classical resources is
Additionally, while conventional spectroscopy based on classical light is limited by shot noise, absorption spectroscopy with single photons can achieve a precision that is beyond the shot-noise limit and even near the ultimate quantum limit [26]. Therefore, quantum light provides a powerful tool to extract the spectroscopic information of target materials by using a single-photon monochromator [27] or tunable frequency-correlated photons [26], which may be particularly relevant for photon-sensitive biological and chemical samples [25]. In order to tackle the experimental issues, quantum Fourier spectroscopy is presented as an alternative route [14, 28, 29]. In analogy to classical Fourier transform between time and frequency domains, the spectral and temporal degrees of freedom of biphoton wavefunction can also be connected by a Fourier transform [30]. Thus, quantum interferometric spectroscopy enables us to extract the spectroscopic information from the temporal pattern of quantum interference, but without the usual requirement for flexible single-photon monochromator or paired photons with tunable and narrow spectral distribution.
As an alternative route toward temporal measurement and spectroscopy, quantum interferometric metrology with entangled photons provides great advantages in resolution, precision, and time efficiency. Typically, the conventional interferometric approaches based on classical light, such as Mach–Zehnder interferometer, are known as first-order interference, which is extremely subject to environmental noise and photon loss. On the contrary, the HOM interference based on quantum light is not affected by variations in the optical phase, even when the fluctuations of path length difference are on the order of the wavelength [31]. This feature has resulted in proposals for quantum interferometric metrology with provable advantages in the robustness against noise and loss [32, 33], such as the cancellation of some deleterious dispersion effects [31, 34]. Although photon wave packets are generally broadened and delayed when they transmit through the dispersive optical elements, the corresponding dispersion is balanced in both arms of the HOM interferometer. Assisted by coincidence measurement made with entangled photon pairs, the observed interference pattern can be free of such dispersive behavior [35, 36]. These results may indicate a new direction toward fully harnessing quantum interference in practical quantum metrology.
In this review, our aim is to present the theoretical and experimental progress in the investigation of quantum interference with entangled photons and their applications in the field of quantum metrology. Emphasis is placed on the preparation of energy-time entanglement and its relevant applications in temporal measurement and spectroscopy.
This review is structured as follows: In Section 2, we discuss the creation of quantum entanglement, which is used as the probe in quantum interferometric metrology, in particular, the exploitation of energy-time entanglement. In Section 3, we review the experimental implementation and practical applications of HOM interferometry with ultrahigh timing resolution, regarding the enhancement of HOM interferometry by using discrete frequency entanglement and applications in the exploration of superluminal speeds of structured light and dephasing time of the molecular properties in biology and chemistry. In Section 4, we review the quantum interferometric spectroscopy with quantum entanglement and its applications in single-photon and two-photon absorption spectroscopy. Section 5 contains the conclusion and an outlook.
2 Entanglement source
Since this work focuses on the quantum interferometric metrology with entangled photons, we first introduce the concept and generation of quantum entanglement, whose specific properties enable the intriguing quantum interference that goes beyond the possibilities of classical physics.
In the set of a quantum system consisting of n subsystems, the Hilbert space of the whole system is the tensor product of the subsystem spaces, namely,
where |i1,…,n⟩ represents the specific state of the individual subsystems. We consider a more general case as a multipartite system A1, A2, …, Am. Typically, their many-body states can be divided into two classes: entangled states and separable states. One calls a state of m systems entangled if it cannot be written as a convex combination of product in the form of
In contrast, if the state can be decomposed into the tensor products of subsystems, one calls it separable [37–39]. Intuitively, the entangled state is a prototypical quantum phenomenon that lacks any counterpart in classical physics or simulation by classical correlations [1, 40–42]. This work focused on the two-photon entanglement in the bipartite systems with a Hilbert space H = H1 ⊗ H2. The complete Bell basis in this state space can be expressed by the well-known Bell states as
These Bell states have interesting properties [43–45].
This intriguing quantum entanglement is an enabling resource for a large number of practical applications, including but not limited to quantum information processing [46–51], quantum metrology [8–12], and quantum simulation [52–55]. Therefore, an efficient source of entangled photons has long been hailed as an essential prerequisite in the quantum mechanic’s toolkit. Among these available technologies, the spontaneous parametric down-conversion (SPDC) process in nonlinear materials is most commonly used in practice, which provides advantages in fiber coupling efficiency, entangled photon pair generation rates, and entanglement fidelity and flexibility [56–61]. In an SPDC process, a pump photon with high energy would spontaneously decay into signal and idler photons, which can be tailored to exhibit entanglement in various photonic degrees of freedom. For example, as the signal and idler photons are created simultaneously, the time entanglement is an inherent property of the down-converted photons generated by the SPDC process. The spontaneous down conversion ensures the time correlation between signal and idler photons, while the coherent temporal modes of pump lasers enable the nonlocal correlation. Thus, the time entanglement has been verified through the violation of Bell inequality by using the Franson interferometer [62, 63] and enabling the applications in quantum information processing [64–66]. In addition, since the frequency bandwidth of the pump laser is much narrower than that of the down-converted photons, the frequency entanglement arises quite naturally as a direct result of energy conservation. More specifically, the central frequencies of down-converted signal, idler, and pump photons satisfy the energy conservation as ωs + ωi = ωp, which directly indicates the spectral correlation of entangled photons. Backed by the coherent spectral modes of pump lasers that enable the nonlocal correlation, the violation of Bell inequality in the frequency domain has been verified [67].
2.1 Generation of quantum entanglement by spontaneous parametric down conversion
In particular, the quasi-phase matching in the SPDC process has a strict requirement for polarization states of pump, signal, and idler photons. Thus, polarization entanglement can be generated using elaborate configurations such as polarization Sagnac interferometer and crossed-crystal scheme. In order to implement a polarization entanglement source with ultrahigh brightness, we use the SPDC process with collinear type-0 quasi-phase matching, which has resulted in the highest photon pair generation rates reported to date [68]. However, the spatial modes of down-converted photons overlap completely, these type-0 sources typically require wavelength distinguishability to route photons into distinct spatial modes for independent manipulation. Consequently, these frequency-distinguishable signal and idler photons are inapplicable for quantum information process applications that require indistinguishable photons, such as HOM interference. This leads to a question of the utmost importance: How can we generate identical entangled photons that are separated in opposite spatial modes with ultrahigh brightness. By superimposing four pair-creation possibilities on a polarization beam splitter, pairs of identical photons are separated into two spatial modes as a direct result of time-reversed HOM interference and without the usual requirement for wavelength distinguishability or noncollinear emission angles [69]. More specifically, while the typical HOM interference states the fact that identical photons that arrive simultaneously on different input ports of a beam splitter would bunch into a common output port, time-reversed HOM interference states that the superposition of two-photon quantum states that arrive simultaneously on difference input ports of a beam splitter would deterministically anti-bunch into distinct output ports. This intriguing interference effect enables the deterministical separation of identical photons into distinct spatial modes without any requirement of photons’ distinguishability and phase stability. The resultant polarization entanglement is in the form of
where |H⟩ and |V⟩ represent the horizontal and vertical polarization, respectively. By combining the benefits of the phase-stable polarization Sagnac sources and highly-efficient crossed-crystal sources, we generate wavelength-degenerate photon pairs around the center wavelength of 810 nm with a Bell-state fidelity of 99.2% and detect a pair rate of 160 kcps per mW of pump power. Furthermore, we believe that our source can yield entangled photon rates in excess of 107 pairs per second for pump powers readily attainable using compact laser diodes. These polarization-entangled photons have been widely used in HOM interferometry, where polarization correlation is used to deterministically route paired photons into distinct spatial modes such that these identical photons can arrive on different input ports of a beam splitter.
To fulfill the requisites of specific applications, ultrabroadband biphotons can yield a high flux of nonoverlapping biphotons with ultrahigh brightness, which is essential for making quantum entanglement in nonclassical applications such as entangled-photon microscopy, quantum spectroscopy, and optical coherence tomography. To tackle this issue, adaptive modulation in quasi-phase-matched nonlinear gratings that have a linearly chirped wave vector is used to generate ultrabroadband biphotons with a spectral bandwidth of 300 nm, which results in the observation of ultranarrow HOM dip with a full width at half maximum of 7.1 fs [70]. Another approach to control the spectral structure of photon pairs is based on the SPDC process in microstructured fibers. Specifically, by fabricating fibers with design dispersion, the photons’ wavelengths, joint spectrum, and quantum entanglement can, thus, be manipulated [71]. In particularly, photon pairs with no spectral correlations are produced that allow direct heralding of single photons in pure-state wave packets without filtering. As the theoretical analysis and preliminary tests suggest that 94.5% purity is possible with a much longer fiber, an experimental purity of (85.9 ± 1.6)% has been achieved.
Additionally, photon pairs entangled in multiple properties have remarkable advantages, such as increasing the information capacity for quantum communication [72–74], implementing the complete Bell state measurements for superdense coding or larger quantum states can be transmitted in quantum teleportation [46, 75], enhancing the fidelity of mixed entangled states in entanglement purification [76, 77], and increasing the state space for multiphoton entanglement and quantum computing [78, 79]. Hence, it is of great significance to design wieldy and practical strategies to harness hyperentanglement. In analogy to polarization entanglement based on time-reversed HOM interference. we use the experimental configuration to generate and characterize the hyperentanglement in polarization and discrete frequency degrees of freedom [80], which can be written as
In the characterization process, we first measure two-photon correlation in two mutually orthogonal polarization bases, yielding visibilities that imply lower bounds on the Bell-state fidelity and concurrence as Fp ≥ 0.979 and Cp ≥ 0.958 in the polarization degree of freedom. However, as a result of the difficulty of a mutually unbiased measurement in the frequency domain, the verification of entanglement in the discrete frequency subspace is more elaborate. While the nonlocal measurement of the frequency-entangled states is difficult without the assistance of a nonlinear optical process and a time-resolved measurement, we use spatial beating in HOM interference to quantify the frequency entanglement. By scanning the time of arrival of one of the photons incident on the HOM interferometer, the interference pattern manifests itself in sinusoidal oscillations of the interference fringes within a Gaussian envelope as a function of relative time delay [81]. This coincidence probability can be modeled as
where Vω is the interference visibility, τ is the relative arrival time delay of two photons at the beam splitter, τc is the single-photon coherence time that equals the base-to-base envelope width, and μ = |ω1 − ω2| is the detuning of two well-separated frequency bins. Thus, under the assumption that energy is exactly conserved in the SPDC process, the lower bounds on the Bell-state fidelity and concurrence are Fp ≥ 0.971 and Cp ≥ 0.942 in the frequency degree of freedom. These measured high fidelities in both the polarization and frequency subspace indicate the presence of hyperentanglement, which allows proof that high-dimensional entanglement has indeed been produced in our setup via hyperentanglement. Different from the general HOM dip, quantum interference of frequency entangled photons exhibits periodic oscillation within the coherence time envelope. This feature provides an alternative route toward ultra-precise HOM interferometry using superpositions of two well-separated and entangled discrete frequency modes and coincidence detection on the bi-photon beat note [17].
2.2 Generation of quantum entanglement by atomic four-wave mixing
In addition to the widely used SPDC process, atomic four-wave mixing is an alternative route toward the creation of entanglement with high efficiency and brightness [82]. Up to date, a large wide range of theoretical research works and experimental implementations have been explored, including the generation and verification of biphotons entangled in polarization [83], orbital angular momentum [84], and time-frequency [85]. In this work, we focus on the energy-time entanglement of narrow-band biphotons that is used for quantum interferometric metrology. For example, the direct characterization of energy-time entanglement is produced from spontaneous four-wave mixing in cold atoms, where the Stokes and anti-Stokes two-photon temporal correlation is measured by using commercially available single-photon detectors with nanosecond temporal resolution, and their joint spectral intensity is characterized by using an optical cavity with a narrow linewidth of 72 KHz. As a direct result, the joint frequency-time uncertainty product of 0.063 ± 0.0044 is verified, which violates the separability criterion and satisfies the continuous variable Einstein–Podolsky–Rosen steering inequality [85]. Thus, the energy-time entanglement generated by using the atomic four-wave mixing can provide a significant advantage in enhancing the resolution, precision, and accuracy in quantum metrology.
Additionally, as a direct result of the ultranarrow bandwidth, the quantum entanglement generated by using the atomic four-wave mixing has the potential to be used in the storage of quantum qubits. For example, the entanglement of a 795 nm light polarization qubit and an atomic Rb spin-wave qubit for a storage time of 0.1 s is observed by measuring the violation of Bell’s inequality [86, 87]. On the other hand, these narrowband photons can be used in the measurement of absorption spectroscopy of biological and chemical molecules, and the detection of trace molecular species [88, 89].
2.3 High-dimensional entanglement by adaptive modulation
In addition to two-dimensional entanglement, high-dimensional entanglement is currently one of the most prolific fields in quantum information processing and quantum metrology [42, 72–74, 90, 91]. For example, photon pairs entangled in high dimensions provide the advantages of improving noise resilience and speeding up certain tasks in photonic quantum computation [65, 92, 93]. Although several physical properties of photons can be used to directly encode high-dimensional entanglement, such as orbital angular momentum, time-energy and path, the exploitation of high-dimensional spatial coding has strict requirements on the quality of optical wave-fronts and shaping for generation and measurement. In this work, we focus on time-energy entanglement because it is intrinsically suitable for long-distance transmission in fiber and free space and quantum spectroscopy. As an essential prerequisite, the versatile manipulation and characterization of frequency entanglement, however, poses an ongoing challenge. In particular, the required number of measurements for the task of full quantum state tomography of high-dimensional entanglement in a large state space would increase exponentially versus the dimensions, which is one of the fundamental but important problems concerning entanglement. We use spatial beating of HOM interference with polarization-frequency hyperentangled photons to discretize continuous and broadband spectra into a series of narrow frequency bins [94]. Since the incident entangled photons is in the form of polarization-frequency hyperentanglement, the HOM interference transforms the state into
where
where f(ω1, ω2) is the Gaussian spectral amplitude function that fulfills the normalized condition, it indicates that the anti-bunched photons are entangled in the frequency domain as
where m denotes the number of dimensions, Aj is a probability amplitude, ϕj is a phase-offset,
The generation, manipulation, and detection of photons that are entangled in frequency, time, and polarization degrees of freedom provide powerful tools for a variety of practical applications. Next, we present several prototypical applications in quantum metrology by using these entangled states.
3 Hong–Ou–Mandel interferometry with ultrahigh timing resolution
Hong–Ou–Mandel interference was first experimentally verified by Chunk Ki Hong, Zhe Yu OU, and Leonard Mandel in 1987 [13]. It shows a quantum phenomenon that identical photons arriving simultaneously on different input ports of a beam splitter would bunch into a common output port as a direct result of bosonic nature. We consider a basic model of two-photon HOM interference, as shown in Figure 1A. The incident two-photon state can be expressed as
where
Thus, the combined two-photon state interferes on the beam splitter, and the corresponding output state is
For a typically balanced beam splitter, η = 1/2, and the output state is transformed to
whose visualization is shown as Figure 1B. Since two photons are completely indistinguishable after the beam splitter, it indicates that the second and third terms in Eq. 13 can be cancelled out. Thus, Eq. 13 is simplified to
In the experimental implementation of HOM interference, we choose to detect the coincidence probability between the opposite spatial modes, which corresponds to the events that entangled photons bunched into different output ports of the beam splitter. Thus, quantum theory predicts that the coincidence probability of HOM interference would decrease to zeros when and only when the two incident photons are completely indistinguishable, i.e., the well-known HOM dip.
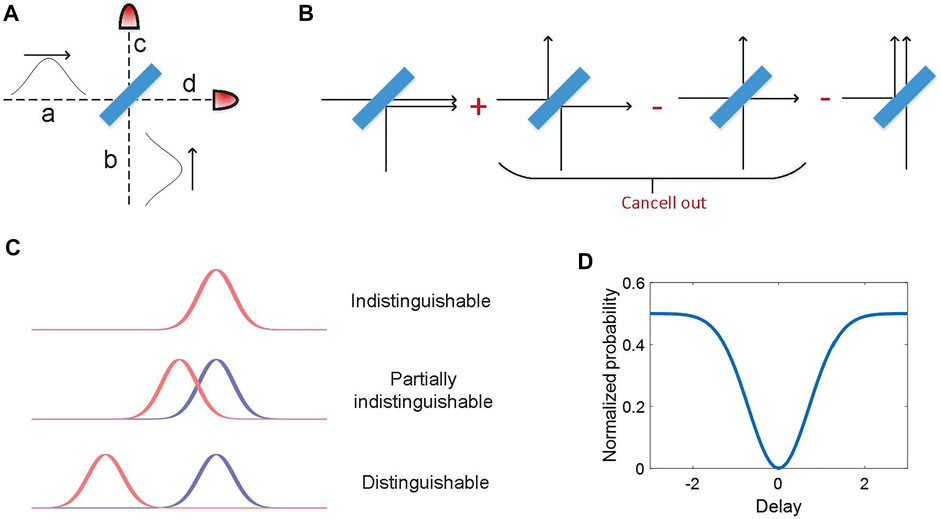
FIGURE 1. (A) Two photons interfere on a beam splitter. After the interaction on the beam splitter, the photons in opposite spatial modes are detected by single photon detectors. (B) Diagram showing four different cases for two photons to interact on a balanced beam splitter, wherein the relative phase is revealed by the signs. If these two photons are completely indistinguishable, the second and third terms can be cancelled out. (C) Taking temporal distinguishability into consideration, it is allowed to tune the level of distinguishability by changing the time delay between two photons with finite bandwidths. (D) The coincidence probability of HOM interference as a function of the relative time delay. Typically, the coincidence counts are identified by using two single-photon detectors at opposite spatial modes c and d, which can be normalized to fit Eq. 15.
Next, let us consider the distinguishability in the temporal degree of freedom. Since the distribution of single photons in the temporal domain is within a wavepacket, its coherence time refers to the time over which the photon may be considered coherent, which means that its average phase is predictable. By controlling the imbalance between two paths of the HOM interferometer, a relative time of arrival of one of the photons incidents on the beam splitter can be introduced and parameterized by the time delay τ. This manipulation of the temporal delay between the entangled photons is able to tune their level of distinguishability, which corresponds to two indistinguishable photons, partially distinguishable photons and distinguishable photons, as shown in Figure 1C. As a direct result of the coherence time of single photons, the HOM interference probability manifests itself as a Gaussian envelope, as a function of the relative time delay τ, where its coincidence probability can be modelled in the form of
where σ is relevant to single photon coherence time that equals to the base-to-base envelope width, as shown in Figure 1D [62, 81, 95–97].
3.1 Robust Hong–Ou–Mandel interferometry for measuring optical delays
Since the single-photon coherence time is in the order of subpicosecond, HOM interferometry has been widely used in the characterization of single photon source [98–101], quantum metrology [14, 15, 32], and quantum information processing [96, 102–104]. For example, while the speed of light in a vacuum is constant, the phase and group velocities of light beams have been changed because they have finite transverse sizes [24]. In other words, the modification of the axial component of the wave vector arises from the transverse spatial confinement of the field. Generally speaking, the magnitude of the wave vector for the light with center wavelength of λ is k0 = 2π/λ, which is related to its Cartesian components {kx, ky, kz} in the form of
It is obvious that the optical modes of finite transverse spatial extent have nonzero kx and ky, and the resultant kz < k0 leads to a corresponding modification of both the phase and group velocities of the light. Let us consider the Bessel beam with a description of a mode within a circular waveguide, which is a prototypical example of a structured beam. In free space, Bessel beams can be prepared by using an axicon that converts a plane wave into conical phase fronts, which is characterized by a single radial component of the wave vector as kr. As a direct result, the axial component of the wave vector is obtained as
By changing the beam’s transverse spatial structure, a relative delay in their arrival time is introduced. However, the reported superluminal speeds achieved with the various approaches in free space have been to data 1.00022c [105], 1.00012c [106], 1.00015c [107] and 1.111c in plasma [108]. Reports on measured subluminal speeds have been lacking and limited to delays to several micrometers over a propagation distance of
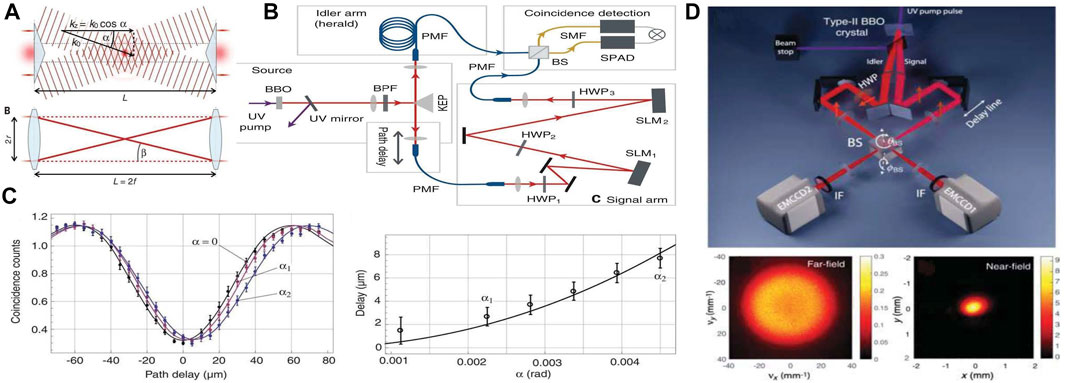
FIGURE 2. (A) Bessel beam can be created with an axicon, producing conical phase fronts of angle α. A ray entering a confocal telescope at radius r will travel an additional distance proportional to cos−1β. (B) Experimental setup for measuring the time delay arising from spatially structure of photons by using a ultra-precise HOM interferometry. (C) Experimental observation of the time delay for a Bessel beam. From ref. [24]. Reprinted with permission from AAAS.(D) Experimental setup for imaging spatiotemporal biphoton states with a HOM interferometer. Reprinted with permission from [109]. Copyright (2021) American Chemical Society.
In the context of quantum metrology, the simultaneous measurement of both the spatial and temporal degrees of freedom has long been hailed as an absolute necessity in quantum imaging. Since the quantum interference pattern is determined by photons’ level of distinguishability in all degrees of freedom, both the spatial and temporal properties can make contributions to the final measurement results. Inversely, it is allowed to extract the corresponding information from quantum interference results, which inspires various applications including but not limited to quantum imaging and sensing. In particular, with the combination of spatially-resolved detection implemented by single-photon cameras, quantum interference is a powerful tool for simultaneously measuring spatial and temporal information. For example, by detecting coincidence events with intensified scientific complementary metal-oxide-semiconductor cameras [109], spatiotemporal HOM interference of biphoton states is also experimentally observed, as shown in Figure 2D. Analogously, HOM interference in both spatial and temporal degrees of freedom enable us to implement a variety of applications in the field of quantum imaging, such as full-field quantum state tomography [110]. While this work focuses on the spectral and temporal domain in quantum interference, the overall scheme could also be extended to other degrees of freedom, such as orbital angular momentum, where the precise measurement of quantum information still poses a significant challenge.
In addition, the interference pattern of HOM interferometry is determined by the relative phase between two photons but is irrelevant to the global phase of single photons. Consequently, HOM interferometry can be used in applications with the requirements of dispersion cancellation, robustness against noise, and photon loss [31, 111]. For example, highly entangled states and N00N states are notoriously vulnerable to losses, which leads to the difficulty in sharing them between remote locations and recombining them for exploiting interference effects. In order to tackle this challenge, the reversed HOM interference effect is used to prepare a high-fidelity two-photon N00N state shared between two parties connected by a lossy optical medium [32]. Additionally, detector side channel attack is a notoriously hard problem in quantum key distribution. By using HOM interference between two photons coming from users, measurement device–independent quantum cryptography has been experimentally implemented. While this work focuses on the HOM interference of entangled photons created by using the SPDC process, the visibility of HOM interference is determined by the photons’ indistinguishability. In other words, if and only if the two-photon incident on a balanced beam splitter is indistinguishable in all degrees of freedom, quantum interference can be observed. The Bell state measurement based on quantum interference can passively reveal the information of the incident entanglement between the quantum state from users. Although the measurement device knows the public Bell state measurement results, it has no knowledge about the transmitted information such that the measurement device–independent quantum key distribution can be implemented. Backed by this technology, a long-distance quantum key distribution over, say, 400 km still has the potential to remain secure even with seriously flawed detectors [112–115].
3.2 Hong–Ou–Mandel interferometry on a biphoton beat note
In the context of applications in HOM interferometry for measuring the optical delays between different paths, the engineered attosecond resolution HOM interferometry by using statistical estimation theory has been experimentally implemented [16]. The ultimate limit on the precision of measurement by using quantum interference of two identical photons can be calculated as the quantum Cram
where N denotes the number of independent experimental trials [16, 116, 117]. Furthermore, backed by a measurement and estimation strategy based on Fisher information analysis, the precision of HOM interferometry achieves few-attosecond scale resolutions in a dual-arm geometry. It has also been proved that the HOM measurement can recover the quantum Cram
We embark on an alternative scheme for ultra-precise HOM interferometry by using two well-separated frequencies embedded in a quantum entanglement [17], namely, discrete color entanglement that can be written as
where
where
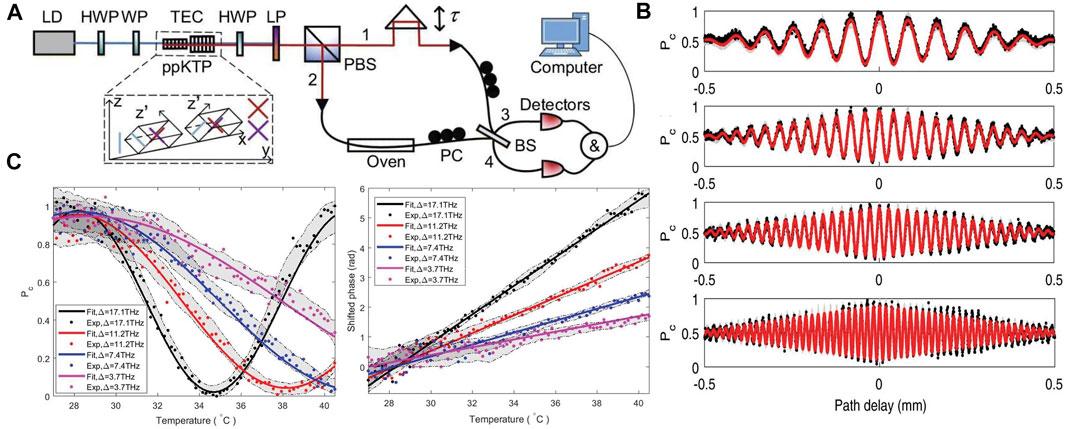
FIGURE 3. (A) Experimental setup for temperature sensor through the beating of frequency entanglement. (B) Two-photon HOM interference of frequency entanglement with various different frequency detunings such as 3.65 THz (7.98 nm) at a temperature of 30°C, 7.35 THz (16.08 nm) at a temperature of 50°C, 11.18 THz (24.45 nm) at a temperature of 70°C, and 17.08 THz (37.35 nm) at a temperature of 100°C. (C) Experimental demonstration of thermal characteristics of jacket optical fiber by using frequency-entangled photons with various different frequencies. Pc is the normalized probability of HOM interference as expressed in Eq. 6 [17].
3.3 Hong–Ou–Mandel interferometry for applications in biology and chemistry
In addition, since the quantum light with extremely low energy is suitable for interacting with those photon-sensitive samples, the HOM interferometry based on entangled photons can also provide a useful tool to study molecular properties such as dephasing time. Unlike other interferometric approaches based on first-order interference and simple measurement of intensity, HOM interference is not affected by variation in the relative optical phase and is strongly robust against experimental noise and channel loss. For example, a dephasing time of the organic molecular of as low as 102 fs upon coherent excitation and quantum interference with a path of entangled photons in the interferometer is extracted by using HOM interferometry as shown in Figure 4 [25]. Without inserting any molecular sample in the optical path, a well-known HOM interference pattern that agrees well with the theoretical prediction can be observed. By inserting a molecular sample IR-140 dye in the optical path, it is obvious that the observed HOM dip overall becomes narrower and gains an asymmetry on the right side, as shown in Figure 4B. Moreover, the center of the HOM dip with the sample is shifted to the left compared to the dip with the solvent. These measurement results allow extracting the information pertaining to the linear susceptibility and absorption of the studied sample. Additionally, HOM interference can be used to characterize the coherence properties of single photon source and the distinguishability of emitted single photons, which would pave the way toward quantum applications. Thereinto, single photons emitted by a single molecule are prepared for quantum networks. For example, single organic molecules that are optimized by an atomic Faraday filter are experimentally presented to create single photons whose properties have been verified by performing a number of nonclassical HOM interference measurements [119]. Thus, quantum interference has been proved to be an essential approach in the fields of biology and chemistry.
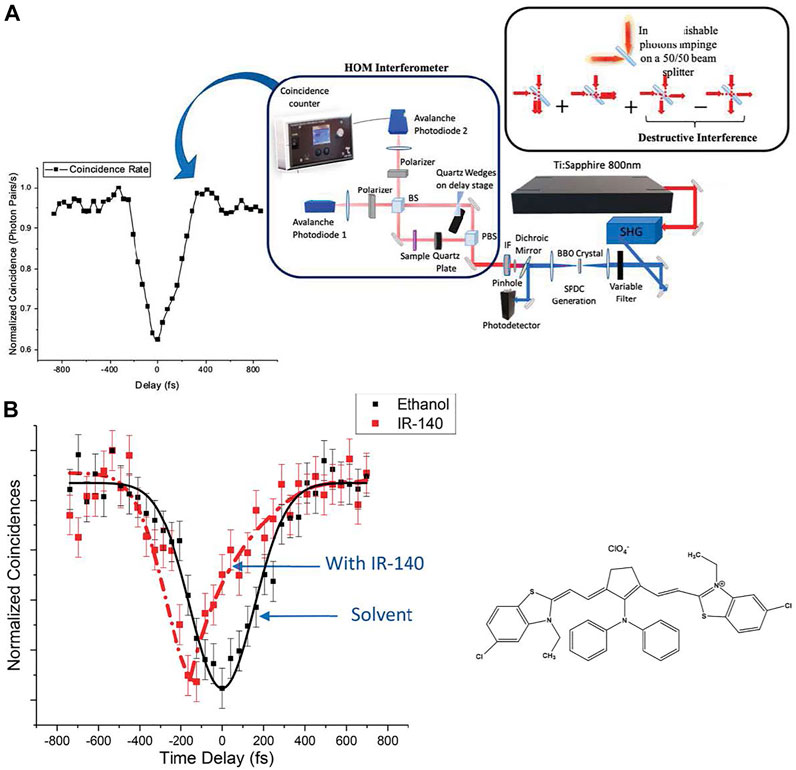
FIGURE 4. (A) Experimental setup for measuring the dephasing time of photons arising from its interaction with a molecular sample by using a HOM interferometer. (B) The presence of a simple refractive or birefringent material in the interferometer pathway can lead to polarization mode dispersion which degrades entanglement and causes temporal delays in the order of 100 fs. As a direct result, the normalized coincidence probability as a function of the scanning time is shifted by a time delay that corresponds to the dephasing time [25].
4 Entanglement-assisted quantum spectroscopy
Absorption spectroscopy has long been hailed as an essential prerequisite for characterizing the optical properties of materials, chemicals and biological samples [10, 28, 120, 121]. Typically, a sample’s absorption spectroscopy is obtained by comparing the spectrum and intensity of the incident light and those of the transmitted light after the interaction with the target sample. While absorption spectroscopy is generally implemented by using classical light, quantum light provides an alternative route toward quantum spectroscopy with high precision and robustness against deleterious noise.
4.1 Absorption spectroscopy using quantum light
While conventional laser absorption spectroscopy is significantly limited by shot-noise due to the fundamental Poisson-distribution of photon number in laser radiation [122, 123], quantum light provides an alternative route toward precise absorption spectroscopy. In addition, quantum spectroscopy with the assistance of coincidence detection can further enhance the measurement resolution as a direct result of a high signal-to-noise ratio. We consider a general case where paired photons are prepared by using the SPDC process. The down-converted photons are separated into opposite spatial modes, referring to signal and idler photons. After the interaction between one of the paired photons with the target sample, a single-photon monochromator is used to filter the photons at a specific frequency bin. The measured number of coincidence events corresponds to the intensity of absorption at this frequency. By scanning the monochromator, the whole absorption spectrum can be achieved. In this process, the single photon count is Ss,i = ηs,iP, where P is the number of photon pairs generated by the entanglement source, ηs,i represents the quantum efficiency of the detectors at signal and idler channel, respectively. Thus, the expected number of two-fold coincidence is proportional to the probability of joint detection in the opposite spatial modes as
The accidental coincidence counts arises from the overlap of uncorrelated photon counts within the coincidence window Δt, which can be calculated by
where Ns and Ni are the number of noise photon counts in the signal and idler channel. In conventional transmission spectroscopy, the transmission spectrum is obtained directly from single photon counts, and its signal-to-noise ratio for the transmission spectroscopy is given by SNRT = ηsP/Ns. For the quantum spectroscopy based on coincidence detection, the signal-to-noise ratio is given by SNRQ = R(ωs)/RN = ηsηiP/NsNiΔt, where it is assumed that NsNi ≫ SsNi or NsSi. The contrast of these two signal-to-noise ratios is written as SNRQ/SNRT = ηi/NiΔt, which indicates that quantum spectroscopy can provide provable advantages by using high-efficient, low-noise single-photon detectors, and the narrow coincidence window. This scheme has been used to measure the spectroscopic propertied of the YAG: Er3+ crystals [124] and plasmonic nanostructures [27], which proves the advantages of quantum spectroscopy based on coincidence detection in experiments as shown in Figure 5A. Since the entangled photons typically contain many frequencies, namely, a large bandwidth, a grating and spatial filter are used as a tunable monochromator to select out a specific frequency, which can enhance the spectral resolution. Thus, the dynamic range is limited by the frequency shape and bandwidth of entangled photons. As an alternative method, frequency-correlated and tunable entanglement sources are presented to perform quantum absorption spectroscopy with precision beyond the shot-noise limit and near the ultimate quantum limit, as shown in [26]. The use of type-II PPKTP crystal enables the generation of frequency-entangled photons with a narrow bandwidth, where the central frequency can be controlled by tuning the phase to match the temperature of the PPKTP crystal. Thus, by scanning the phase matching temperature, the absorption spectroscopy of the studied sample is achieved without any requirement of frequency filters. These theoretical and experimental investigations show that single photons are the optimal probes for absorption spectroscopy, and quantum-enhanced spectroscopy can achieve great performance that is beyond classical physics.
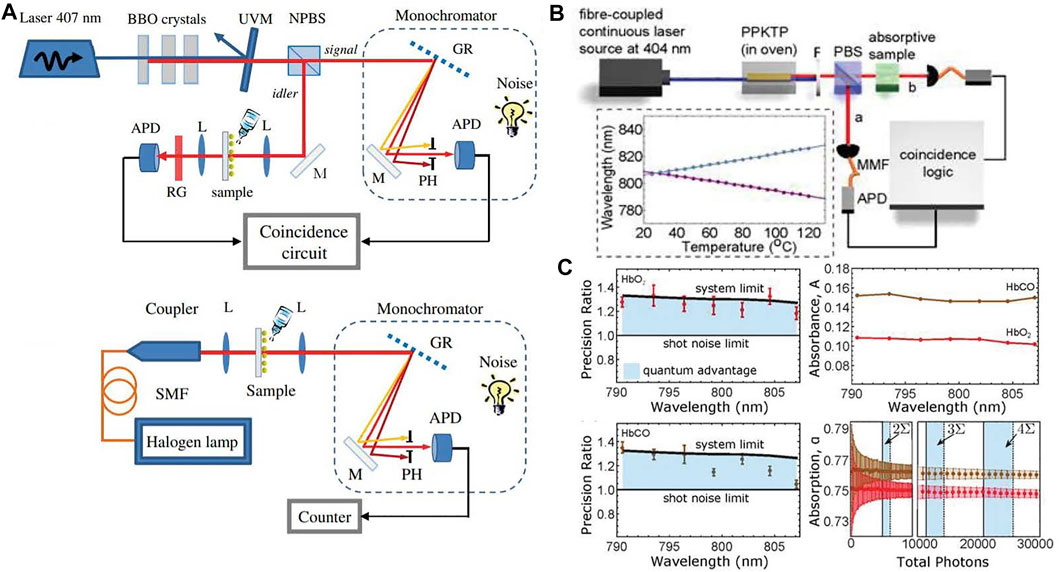
FIGURE 5. (A) Quantum spectroscopy setup based on coincidence detection of entangled photons and single photon monochromator for selecting out a specific frequency, and the conventional transmission spectroscopy by using classical light [27]. (B) Experimental setup for sub-shot-noise spectroscopy by using tunable frequency-entangled photons. (C) Sub-shot-noise absorbance spectra ofHbO2 and HbCO [26].
4.2 Entanglement-assisted absorption spectroscopy
However, the excess noise and thermal loss channel can make changes in the transmission ratio, the conventional method is susceptible to experimental imperfection, which limits its precision and resolution. In addition, since the resolution is determined by the bandwidth of down-converted photons, it has been a broad consensus that single photons with narrow frequency bandwidth enable us to obtain a higher spectral resolution. In contrast, generating spectrally narrow photons would reduce the brightness of the entanglement source, which inversely imposes an ultimate limit on the precision. In order to tackle this issue, entanglement-assisted absorption spectroscopy is presented [34]. It uses a source of multichromatic frequency-entangled photon pairs prepared by the SPDC process as the probe, and the photon detection after optical parametric amplification is used at the receiver side. Consequently, a maximum likelihood estimation strategy on the statistical analysis is sufficient for extracting the spectral distribution. This scheme has been theoretically proved that it can achieve an error probability orders of magnitude lower even than the optimal classical systems. In particular, it is also robust against noise and loss as a direct result of the optical parametric amplifier on entangled photons. Nevertheless, the complexity and efficiency in the experimental implementation of optical parametric amplifiers still face significant technological challenges.
Then, we present a robust and efficient entanglement-based absorption spectroscopy by using one of the entangled photons to interact with the target absorptive sample and exploiting the HOM interference at the detection side as shown in Figure 6 [125]. In our experiment, we use a pair of type-0 PPKTP crystals that are pumped with a ultra-narrow pump, broadband frequency entanglement arises quite naturally following the energy conservation. In order to tackle the issue of separating indistinguishable photons to distinct spatial modes, the two nonlinear crystals are placed in horizontal and vertical direction such that the emission |H⟩ → |HH⟩ in the first crystal and |V⟩ → |VV⟩ in the second crystal are generated with equal probability. Then, a half wave plate and a polarizing beam splitter are used to route paired photons into two input ports of a HOM interferometer. The nonclassical interference of frequency entanglement is observed by scanning the relative arriving time of paired photons. As shown in Eq. 6, the oscillation period in the interference pattern is determined by the frequency detuning. It is allowed to extract the spectral distribution from the HOM interference results by directly using nonlinear curve fitting. For an instructive means of understanding, this approach can be considered as a quantum version of spectral analysis, which decomposes the complex periodic vibration into a series of simple harmonic motions. Accordingly, the absorption spectra can be obtained from this spectral decomposition. As shown in Figure 6B, the observed HOM interference exhibits asymmetric patterns, which is relevant to the specific spectral distribution. By comparing the spectrum before and after inserting the studied samples (the black and red curves), it is able to extract the corresponding information about the absorptive spectroscopy. This entanglement-based absorption spectroscopy with the assistance of HOM interference has the potential to provide advantages in the robustness against detrimental noise and the measurement precision and accuracy.
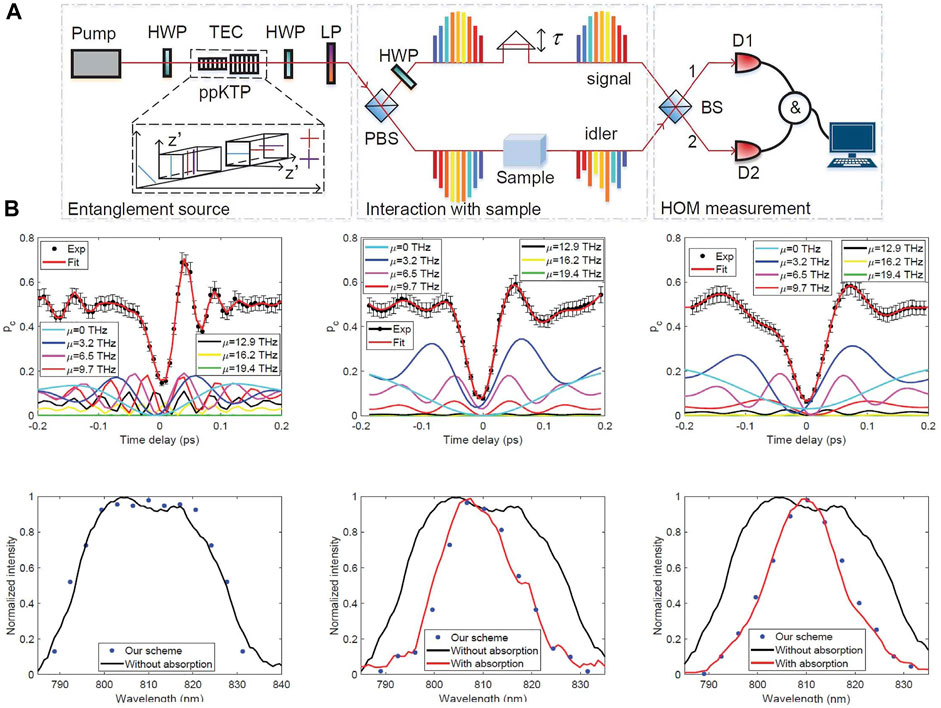
FIGURE 6. (A) Experimental setup for entanglement-assisted absorption spectroscopy by using HOM interference. (B) The experimental reconstruction of the spectra of two optical microcavities at resonance wavelengths of 806 and 810 nm. The colorful lines represent the interference patterns of sub-entanglement with various frequency detunings. Since the whole spectra are sampled by averaging them within each of m = 13 frequency bins, and they satisfy the strict energy conservation as a direct result of the exploitation of the pump with ultranarrow frequency linewidth, the resultant 7 pairs of subentanglement with frequency detunings μ = 0 THz, μ = 3.2THz, μ = 6.5 THz, μ = 9.7 THz, μ = 12.9 THz, μ = 16.2 THz and μ = 19.4 THz. Reprinted with permission from ref. [125]. Copyright (2022) by the American Physical Society.
Beyond its application appeal, our approach indicates a fundamental link between spectral and temporal degrees of freedom of biphoton wavefunction [94]. As the normalized coincidence probability of HOM interference is expressed as Eq. 8, which equals to
and it corresponds to the second-order correlation function in the form of
which can be considered as a two-photon temporal signal. The difference-frequency spectrum intensity of biphoton state can be defined as
It is obvious that the second-order temporal correlation and the difference-frequency spectrum intensity can be connected by performing a Fourier transform. As a direct result, this approach has a variety of potential applications, such as quantum interferometric spectroscopy [29, 30, 128] and spectral-domain quantum coherence tomography [97, 129].
4.3 Two-photon absorption by using entangled photons
Additionally, quantum interference with entangled photons also provides a powerful tool toward two-photon absorption spectroscopy, which has been widely used in many disciplines, including but not limited to photoluminescene polymer and light-harvesting photosynthetic complexes [130, 131]. While laser light is typically used in absorption spectroscopy, quantum light provides new and exciting avenues in this regime [34, 132–134]. Remarkably, as a prototypical example of quantum light that lacks any counterpart in classical physics, the exploitation of entangled photon pairs in two-photon absorption enables the observation of many fascinating phenomena, such as linear dependence of two-photon absorption rate on the photon flux [135, 136], inducing disallowed atomic transitions [137], manipulation of quantum pathways of matter [138, 139], and control in molecular processes [140]. However, the experimental implementation of entangled two-photon absorption spectroscopy has two major technical challenges. First, it has the requirement for performing multiple experiments with two-photon states bearing different temporal correlations. Second, it has the requirement for prior knowledge of the absorbing medium’s lowest-lying intermediate energy level. In order to tackle this issue, a tunable frequency entanglement source and a HOM interferometer with controllable delay are used to detect the two-photon absorption signal [126]. The central frequencies of down-converted photons prepared by the SPDC process can be tuned by changing the temperature for phase matching in the nonlinear crystal. As discussed in Section 2, the frequency entanglement used in this two-photon absorption spectroscopy is in the form of Eq. 5. One advantage of the exploitation of type-II PPKTP crystal in the process of entanglement generation is that the central frequencies of down-converted photons can be controlled by tuning the phase match temperature. Thus, the nondegeneracy of the signal and idler photons wavelengths is parameterized by the temperature as
where
This result indicates that the absorption properties of the sample can be tuned by appropriately controlling the time and frequency properties of the entangled photon pairs, as shown in Figure 7A. Up to date, the linear dependence of entangled two-photon absorption rate as a function of photon-pair rate has been experimentally proved, which enables the estimation for the concentration-dependent entangled two-photon absorption cross section for Rhodamine 6G [127, 136]. The signature of energy-time entanglement and polarization dependence in the fluorescence rate has also been investigated, which demonstrates a strong dependence of the signal on the interphoton delay that reflects the coherence time of the entangled biphoton wave packet, as shown in.
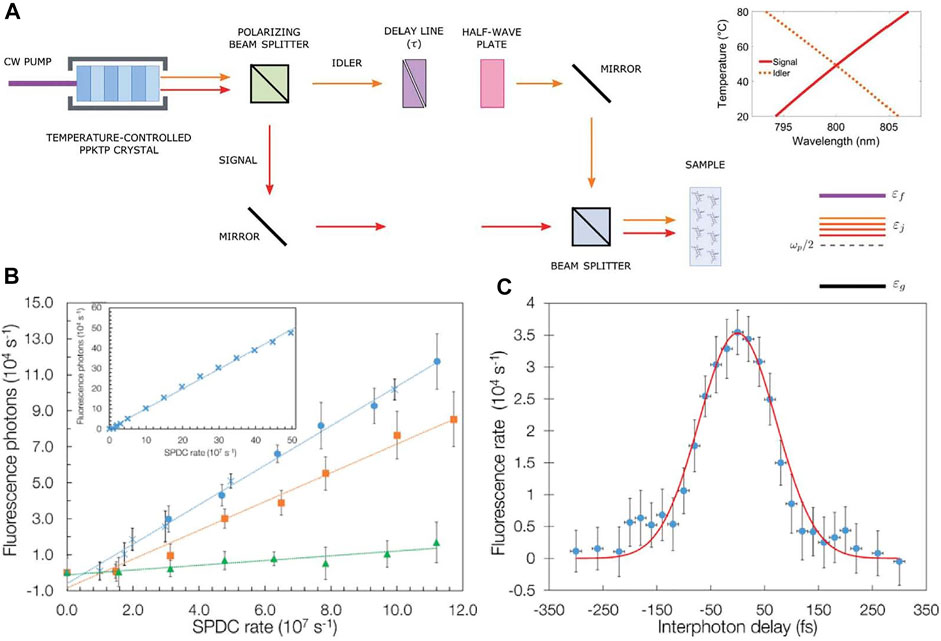
FIGURE 7. (A) Experimental illustration of temperature-controlled quantum nonlinear spectroscopy. Reprinted with permission from ref. [126]. Copyright (2022) by the American Physical Society. (B) Experimental measured fluorescence rate of entangled two-photon absorption as a function of the SPDC photon-pair flux for different Rh6G concentrations in ethanol: 110 mmol/L (blue circles); 4.5 mmol/L (orange squares), and 38 μ mol/l (green triangles). (C) Temporal dependence of fluorescence rate of entangled two-photon absorption for a 110 mmol/L Rh6G ethanol solution and an SPDC flux of 4.2 × 107 pairs/s, as a function of the inter-photon delay. Reprinted with permission from ref. [127]. Copyright (2022) by the American Physical Society.
5 Discussion
We have reviewed the non-classical phenomena as quantum interference of entangled photons, which has enabled a wide range of fundamental tests of quantum physics and pioneering applications such as quantum metrology. A number of important applications have been highlighted, such as HOM-based sensors for enhanced timing resolution and robust entanglement-assisted absorption spectroscopy. The scope of this review is limited to energy-time entanglement, which can be readily prepared by the SPDC process in a nonlinear crystal. Thus, the hyperentanglement in temporal and spectral degrees of freedom arises quite naturally as a direct result of energy conservation. Since the quantum interference pattern is determined by the level of photons’ distinguishability, the temporal and spectroscopic information can be extracted from interference patterns by using maximum likelihood estimation or Fourier transform. Additionally, the correlation of entangled photons has great potential to be used in studying the structure of complex molecular systems. By tuning the different frequencies and relative time delay between paired photons, both the spectral and temporal properties of two-photon absorption in a molecular sample are investigated. Therefore, quantum interferometric metrology with entangled photons provides a powerful tool to extract the temporal and spectroscopic information about the dynamics and structures of complex systems, ranging from spatially structured photons, optical materials, and biological and chemical samples, which is particularly relevant to those photon-sensitive samples.
Armed with quantum interferometric metrology based on entangled photons, these new techniques would inspire the development of quantum information processing and quantum metrology to reach a higher level. We also expect the techniques reviewed in this work can be applicable for more scenarios in future quantum applications and make near-term experimental demonstration possible.
Author contributions
YC and L H wrote the manuscript under the supervision of LC. All authors contributed to the final version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (NSFC) (12034016, 12004318, and 61975169), the Fundamental Research Funds for the Central Universities at Xiamen University (20720190057 and 20720210096), the Natural Science Foundation of Fujian Province of China (2020J05004), the Natural Science Foundation of Fujian Province of China for Distinguished Young Scientists (2015J06002), and the program for New Century Excellent Talents in University of China (NCET-13-0495).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor RL-M declared a shared affiliation with the authors YC and LC at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum entanglement. Rev Mod Phys (2009) 81:865–942. doi:10.1103/RevModPhys.81.865
2. Raimond JM, Brune M, Haroche S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev Mod Phys (2001) 73:565–82. doi:10.1103/RevModPhys.73.565
3. Giustina M, Mech A, Ramelow S, Wittmann B, Kofler J, Beyer J, et al. Bell violation using entangled photons without the fair-sampling assumption. Nature (2013) 497:227–30. doi:10.1038/nature12012
4. Rauch D, Handsteiner J, Hochrainer A, Gallicchio J, Friedman AS, Leung C, et al. Cosmic bell test using random measurement settings from high-redshift quasars. Phys Rev Lett (2018) 121:080403. doi:10.1103/PhysRevLett.121.080403
5. Chen L, Ma T, Qiu X, Zhang D, Zhang W, Boyd RW. Realization of the einstein-podolsky-rosen paradox using radial position and radial momentum variables. Phys Rev Lett (2019) 123:060403. doi:10.1103/PhysRevLett.123.060403
6. Pan JW, Chen ZB, Lu CY, Weinfurter H, Zeilinger A, Żukowski M. Multiphoton entanglement and interferometry. Rev Mod Phys (2012) 84:777–838. doi:10.1103/RevModPhys.84.777
7. Bennett CH, DiVincenzo DP. Quantum information and computation. nature (2000) 404:247–55. doi:10.1038/35005001
8. Giovannetti V, Lloyd S, Maccone L. Quantum metrology. Phys Rev Lett (2006) 96:010401. doi:10.1103/PhysRevLett.96.010401
9. Giovannetti V, Lloyd S, Maccone L. Advances in quantum metrology. Nat Photon (2011) 5:222–9. doi:10.1038/nphoton.2011.35
10. Taylor MA, Bowen WP. Quantum metrology and its application in biology. Phys Rep (2016) 615:1–59. doi:10.1016/j.physrep.2015.12.002
11. Joo J, Munro WJ, Spiller TP. Quantum metrology with entangled coherent states. Phys Rev Lett (2011) 107:083601. doi:10.1103/PhysRevLett.107.083601
12. Riedel MF, Böhi P, Li Y, Hänsch TW, Sinatra A, Treutlein P. Atom-chip-based generation of entanglement for quantum metrology. Nature (2010) 464:1170–3. doi:10.1038/nature08988
13. Hong CK, Ou ZY, Mandel L. Measurement of subpicosecond time intervals between two photons by interference. Phys Rev Lett (1987) 59:2044–6. doi:10.1103/PhysRevLett.59.2044
14. Su ZE, Li Y, Rohde PP, Huang HL, Wang XL, Li L, et al. Multiphoton interference in quantum fourier transform circuits and applications to quantum metrology. Phys Rev Lett (2017) 119:080502. doi:10.1103/PhysRevLett.119.080502
15. Georgi P, Massaro M, Luo KH, Sain B, Montaut N, Herrmann H, et al. Metasurface interferometry toward quantum sensors. Light Sci Appl (2019) 8:70–7. doi:10.1038/s41377-019-0182-6
16. Lyons A, Knee GC, Bolduc E, Roger T, Leach J, Gauger EM, et al. Attosecond-resolution hong-ou-mandel interferometry. Sci Adv (2018) 4:eaap9416. doi:10.1126/sciadv.aap9416
17. Chen Y, Fink M, Steinlechner F, Torres JP, Ursin R. Hong-ou-mandel interferometry on a biphoton beat note. Npj Quan Inf (2019) 5:43–6. doi:10.1038/s41534-019-0161-z
18. Ramsey NF. The method of successive oscillatory fields. Phys Today (1998) 21:25–30. doi:10.1063/1.2914161
19. Bragg WH, Bragg WL. “The reflection of x-rays by crystals,” Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathe-matical and Physical Character. The Royal Society London (1913) 88:428–38. doi:10.1098/rspa.1913.0040
20. Barish BC, Weiss R. Ligo and the detection of gravitational waves. Phys Today (1999) 52:44–50. doi:10.1063/1.882861
21. Abbott BP, Abbott R, Adhikari R, Ajith P, Allen B, Allen G, et al. Ligo: The laser interferometer gravitational-wave observatory. Rep Prog Phys (2009) 72:076901. doi:10.1088/0034-4885/72/7/076901
22. Holland M, Burnett K. Interferometric detection of optical phase shifts at the heisenberg limit. Phys Rev Lett (1993) 71:1355–8. doi:10.1103/PhysRevLett.71.1355
23. Zhou S, Zhang M, Preskill J, Jiang L. Achieving the heisenberg limit in quantum metrology using quantum error correction. Nat Commun (2018) 9:78. doi:10.1038/s41467-017-02510-3
24. Giovannini D, Romero J, Potoček V, Ferenczi G, Speirits F, Barnett SM, et al. Spatially structured photons that travel in free space slower than the speed of light. Science (2015) 347:857–60. doi:10.1126/science.aaa3035
25. Eshun A, Gu B, Varnavski O, Asban S, Dorfman KE, Mukamel S, et al. Investigations of molecular optical properties using quantum light and hong–ou–mandel interferometry. J Am Chem Soc (2021) 143:9070–81. doi:10.1021/jacs.1c02514
26. Whittaker R, Erven C, Neville A, Berry M, O’Brien J, Cable H, et al. Absorption spectroscopy at the ultimate quantum limit from single-photon states. New J Phys (2017) 19:023013. doi:10.1088/1367-2630/aa5512
27. Kalashnikov DA, Pan Z, Kuznetsov AI, Krivitsky LA. Quantum spectroscopy of plasmonic nanostructures. Phys Rev X (2014) 4:011049. doi:10.1103/PhysRevX.4.011049
28. De Oliveira N, Roudjane M, Joyeux D, Phalippou D, Rodier JC, Nahon L. High-resolution broad-bandwidth fourier-transform absorption spectroscopy in the vuv range down to 40 nm. Nat Photon (2011) 5:149–53. doi:10.1038/nphoton.2010.314
29. Mukai Y, Arahata M, Tashima T, Okamoto R, Takeuchi S. Quantum fourier-transform infrared spectroscopy for complex transmittance measurements. Phys Rev Appl (2021) 15:034019. doi:10.1103/PhysRevApplied.15.034019
30. Jin RB, Shimizu R. Extended wiener–khinchin theorem for quantum spectral analysis. Optica (2018) 5:93–8. doi:10.1364/OPTICA.5.000093
31. Okano M, Okamoto R, Tanaka A, Ishida S, Nishizawa N, Takeuchi S. Dispersion cancellation in high-resolution two-photon interference. Phys Rev A (Coll Park) (2013) 88:043845. doi:10.1103/PhysRevA.88.043845
32. Ulanov AE, Fedorov IA, Sychev D, Grangier P, Lvovsky A. Loss-tolerant state engineering for quantum-enhanced metrology via the reverse hong–ou–mandel effect. Nat Commun (2016) 7:11925–6. doi:10.1038/ncomms11925
33. Oszmaniec M, Augusiak R, Gogolin C, Kołodyński J, Acin A, Lewenstein M. Random bosonic states for robust quantum metrology. Phys Rev X (2016) 6:041044. doi:10.1103/PhysRevX.6.041044
34. Shi H, Zhang Z, Pirandola S, Zhuang Q. Entanglement-assisted absorption spectroscopy. Phys Rev Lett (2020) 125:180502. doi:10.1103/PhysRevLett.125.180502
35. Steinberg AM, Kwiat PG, Chiao RY. Dispersion cancellation in a measurement of the single-photon propagation velocity in glass. Phys Rev Lett (1992) 68:2421–4. doi:10.1103/PhysRevLett.68.2421
36. Larchuk TS, Teich MC, Saleh BEA. Nonlocal cancellation of dispersive broadening in mach-zehnder interferometers. Phys Rev A (Coll Park) (1995) 52:4145–54. doi:10.1103/PhysRevA.52.4145
37. Doherty AC, Parrilo PA, Spedalieri FM. Distinguishing separable and entangled states. Phys Rev Lett (2002) 88:187904. doi:10.1103/PhysRevLett.88.187904
38. Lewenstein M, Sanpera A. Separability and entanglement of composite quantum systems. Phys Rev Lett (1998) 80:2261–4. doi:10.1103/PhysRevLett.80.2261
39. Gao J, Qiao LF, Jiao ZQ, Ma YC, Hu CQ, Ren RJ, et al. Experimental machine learning of quantum states. Phys Rev Lett (2018) 120:240501. doi:10.1103/PhysRevLett.120.240501
41. Fickler R, Lapkiewicz R, Plick WN, Krenn M, Schaeff C, Ramelow S, et al. Quantum entanglement of high angular momenta. Science (2012) 338:640–3. doi:10.1126/science.1227193
42. Erhard M, Krenn M, Zeilinger A. Advances in high-dimensional quantum entanglement. Nat Rev Phys (2020) 2:365–81. doi:10.1038/s42254-020-0193-5
43. Terhal BM, DiVincenzo DP, Leung DW. Hiding bits in bell states. Phys Rev Lett (2001) 86:5807–10. doi:10.1103/PhysRevLett.86.5807
44. Tittel W, Brendel J, Zbinden H, Gisin N. Quantum cryptography using entangled photons in energy-time bell states. Phys Rev Lett (2000) 84:4737–40. doi:10.1103/PhysRevLett.84.4737
45. Ghosh S, Kar G, Roy A, Sen A, Sen U. Distinguishability of bell states. Phys Rev Lett (2001) 87:277902. doi:10.1103/PhysRevLett.87.277902
46. Hu XM, Guo Y, Liu BH, Huang YF, Li CF, Guo GC. Beating the channel capacity limit for superdense coding with entangled ququarts. Sci Adv (2018) 4:eaat9304. doi:10.1126/sciadv.aat9304
47. Harrow A, Hayden P, Leung D. Superdense coding of quantum states. Phys Rev Lett (2004) 92:187901. doi:10.1103/PhysRevLett.92.187901
48. Jennewein T, Simon C, Weihs G, Weinfurter H, Zeilinger A. Quantum cryptography with entangled photons. Phys Rev Lett (2000) 84:4729–32. doi:10.1103/PhysRevLett.84.4729
49. Ursin R, Tiefenbacher F, Schmitt-Manderbach T, Weier H, Scheidl T, Lindenthal M, et al. Entanglement-based quantum communication over 144 km. Nat Phys (2007) 3:481–6. doi:10.1038/nphys629
50. Yin J, Li YH, Liao SK, Yang M, Cao Y, Zhang L, et al. Entanglement-based secure quantum cryptography over 1, 120 kilometres. Nature (2020) 582:501–5. doi:10.1038/s41586-020-2401-y
51. Aspelmeyer M, Böhm HR, Gyatso T, Jennewein T, Kaltenbaek R, Lindenthal M, et al. Long-distance free-space distribution of quantum entanglement. Science (2003) 301:621–3. doi:10.1126/science.1085593
52. Georgescu IM, Ashhab S, Nori F. Quantum simulation. Rev Mod Phys (2014) 86:153–85. doi:10.1103/RevModPhys.86.153
54. Gerritsma R, Kirchmair G, Zähringer F, Solano E, Blatt R, Roos C. Quantum simulation of the Dirac equation. Nature (2010) 463:68–71. doi:10.1038/nature08688
55. Houck AA, Türeci HE, Koch J. On-chip quantum simulation with superconducting circuits. Nat Phys (2012) 8:292–9. doi:10.1038/NPHYS2251
56. Law C, Eberly J. Analysis and interpretation of high transverse entanglement in optical parametric down conversion. Phys Rev Lett (2004) 92:127903. doi:10.1103/PhysRevLett.92.127903
57. Zhang H, Jin XM, Yang J, Dai HN, Yang SJ, Zhao TM, et al. Preparation and storage of frequency-uncorrelated entangled photons from cavity-enhanced spontaneous parametric downconversion. Nat Photon (2011) 5:628–32. doi:10.1038/nphoton.2011.213
58. Eibl M, Gaertner S, Bourennane M, Kurtsiefer C, Żukowski M, Weinfurter H. Experimental observation of four-photon entanglement from parametric down-conversion. Phys Rev Lett (2003) 90:200403. doi:10.1103/PhysRevLett.90.200403
59. Zhong HS, Li Y, Li W, Peng LC, Su ZE, Hu Y, et al. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Phys Rev Lett (2018) 121:250505. doi:10.1103/PhysRevLett.121.250505
60. Wagenknecht C, Li CM, Reingruber A, Bao XH, Goebel A, Chen YA, et al. Experimental demonstration of a heralded entanglement source. Nat Photon (2010) 4:549–52. doi:10.1038/nphoton.2010.123
61. Guo X, Zou CL, Schuck C, Jung H, Cheng R, Tang HX. Parametric down-conversion photon-pair source on a nanophotonic chip. Light Sci Appl (2017) 6:e16249. doi:10.1038/lsa.2016.249
62. Xie Z, Zhong T, Shrestha S, Xu X, Liang J, Gong YX, et al. Harnessing high-dimensional hyperentanglement through a biphoton frequency comb. Nat Photon (2015) 9:536–42. doi:10.1038/nphoton.2015.110
63. Thew RT, Acín A, Zbinden H, Gisin N. Bell-type test of energy-time entangled qutrits. Phys Rev Lett (2004) 93:010503. doi:10.1103/PhysRevLett.93.010503
64. Steinlechner F, Ecker S, Fink M, Liu B, Bavaresco J, Huber M, et al. Distribution of high-dimensional entanglement via an intra-city free-space link. Nat Commun (2017) 8:15971–7. doi:10.1038/ncomms15971
65. Ecker S, Bouchard F, Bulla L, Brandt F, Kohout O, Steinlechner F, et al. Overcoming noise in entanglement distribution. Phys Rev X (2019) 9:041042. doi:10.1103/PhysRevX.9.041042
66. Jogenfors J, Elhassan AM, Ahrens J, Bourennane M, Åke Larsson J. Hacking the bell test using classical light in energy-time entanglement based quantum key distribution. Sci Adv (2015) 1:e1500793. doi:10.1126/sciadv.1500793
67. Guo X, Mei Y, Du S. Testing the bell inequality on frequency-bin entangled photon pairs using time-resolved detection. Optica (2017) 4:388–92. doi:10.1364/OPTICA.4.000388
68. Wengerowsky S, Joshi SK, Steinlechner F, Hübel H, Ursin R. An entanglement-based wavelength-multiplexed quantum communication network. Nature (2018) 564:225–8. doi:10.1038/s41586-018-0766-y
69. Chen Y, Ecker S, Wengerowsky S, Bulla L, Joshi SK, Steinlechner F, et al. Polarization entanglement by time-reversed hong-ou-mandel interference. Phys Rev Lett (2018) 121:200502. doi:10.1103/PhysRevLett.121.200502
70. Nasr MB, Carrasco S, Saleh BEA, Sergienko AV, Teich MC, Torres JP, et al. Ultrabroadband biphotons generated via chirped quasi-phase-matched optical parametric down-conversion. Phys Rev Lett (2008) 100:183601. doi:10.1103/PhysRevLett.100.183601
71. Cohen O, Lundeen JS, Smith BJ, Puentes G, Mosley PJ, Walmsley IA. Tailored photon-pair generation in optical fibers. Phys Rev Lett (2009) 102:123603. doi:10.1103/PhysRevLett.102.123603
72. Ding Y, Bacco D, Dalgaard K, Cai X, Zhou X, Rottwitt K, et al. High-dimensional quantum key distribution based on multicore fiber using silicon photonic integrated circuits. Npj Quan Inf (2017) 3:25–7. doi:10.1038/s41534-017-0026-2
73. Sit A, Bouchard F, Fickler R, Gagnon-Bischoff J, Larocque H, Heshami K, et al. High-dimensional intracity quantum cryptography with structured photons. Optica (2017) 4:1006–10. doi:10.1364/OPTICA.4.001006
74. Mirhosseini M, Magaña-Loaiza OS, O’Sullivan MN, Rodenburg B, Malik M, Lavery MP, et al. High-dimensional quantum cryptography with twisted light. New J Phys (2015) 17:033033. doi:10.1088/1367-2630/17/3/033033
75. Graham TM, Bernstein HJ, Wei TC, Junge M, Kwiat PG. Superdense teleportation using hyperentangled photons. Nat Commun (2015) 6:7185–9. doi:10.1038/ncomms8185
76. Hu XM, Huang CX, Sheng YB, Zhou L, Liu BH, Guo Y, et al. Long-distance entanglement purification for quantum communication. Phys Rev Lett (2021) 126:010503. doi:10.1103/PhysRevLett.126.010503
77. Ecker S, Sohr P, Bulla L, Huber M, Bohmann M, Ursin R. Experimental single-copy entanglement distillation. Phys Rev Lett (2021) 127:040506. doi:10.1103/PhysRevLett.127.040506
78. Deng FG, Ren BC, Li XH. Quantum hyperentanglement and its applications in quantum information processing. Sci Bull (Beijing) (2017) 62:46–68. doi:10.1016/j.scib.2016.11.007
79. Ciampini MA, Orieux A, Paesani S, Sciarrino F, Corrielli G, Crespi A, et al. Path-polarization hyperentangled and cluster states of photons on a chip. Light Sci Appl (2016) 5:e16064. doi:10.1038/lsa.2016.64
80. Chen Y, Ecker S, Bavaresco J, Scheidl T, Chen L, Steinlechner F, et al. Verification of high-dimensional entanglement generated in quantum interference. Phys Rev A (Coll Park) (2020) 101:032302. doi:10.1103/PhysRevA.101.032302
81. Ramelow S, Ratschbacher L, Fedrizzi A, Langford N, Zeilinger A. Discrete tunable color entanglement. Phys Rev Lett (2009) 103:253601. doi:10.1103/PhysRevLett.103.253601
82. Yun S, Wen J, Xu P, Xiao M, Zhu SN. Generation of frequency-correlated narrowband biphotons from four-wave mixing in cold atoms. Phys Rev A (Coll Park) (2010) 82:063830. doi:10.1103/PhysRevA.82.063830
83. Gulati GK, Srivathsan B, Chng B, Cerè A, Kurtsiefer C. Polarization entanglement and quantum beats of photon pairs from four-wave mixing in a cold87Rb ensemble. New J Phys (2015) 17:093034. doi:10.1088/1367-2630/17/9/093034
84. Pan X, Yu S, Zhou Y, Zhang K, Zhang K, Lv S, et al. Orbital-angular-momentum multiplexed continuous-variable entanglement from four-wave mixing in hot atomic vapor. Phys Rev Lett (2019) 123:070506. doi:10.1103/PhysRevLett.123.070506
85. Mei Y, Zhou Y, Zhang S, Li J, Liao K, Yan H, et al. Einstein-podolsky-rosen energy-time entanglement of narrow-band biphotons. Phys Rev Lett (2020) 124:010509. doi:10.1103/PhysRevLett.124.010509
86. Dudin YO, Radnaev AG, Zhao R, Blumoff JZ, Kennedy TAB, Kuzmich A. Entanglement of light-shift compensated atomic spin waves with telecom light. Phys Rev Lett (2010) 105:260502. doi:10.1103/PhysRevLett.105.260502
87. Ding DS, Jiang YK, Zhang W, Zhou ZY, Shi BS, Guo GC. Optical precursor with four-wave mixing and storage based on a cold-atom ensemble. Phys Rev Lett (2015) 114:093601. doi:10.1103/PhysRevLett.114.093601
88. Farrow RL, Rakestraw DJ. Detection of trace molecular species using degenerate four-wave mixing. Science (1992) 257:1894–900. doi:10.1126/science.257.5078.1894
90. Dada AC, Leach J, Buller GS, Padgett MJ, Andersson E. Experimental high-dimensional two-photon entanglement and violations of generalized bell inequalities. Nat Phys (2011) 7:677–80. doi:10.1038/nphys1996
91. Bavaresco J, Valencia NH, Klöckl C, Pivoluska M, Erker P, Friis N, et al. Measurements in two bases are sufficient for certifying high-dimensional entanglement. Nat Phys (2018) 14:1032–7. doi:10.1038/s41567-018-0203-z
92. Doda M, Huber M, Murta G, Pivoluska M, Plesch M, Vlachou C. Quantum key distribution overcoming extreme noise: Simultaneous subspace coding using high-dimensional entanglement. Phys Rev Appl (2021) 15:034003. doi:10.1103/PhysRevApplied.15.034003
93. Xu F, Shapiro JH, Wong FN. Experimental fast quantum random number generation using high-dimensional entanglement with entropy monitoring. Optica (2016) 3:1266–9. doi:10.1364/OPTICA.3.001266
94. Chen Y, Ecker S, Chen L, Steinlechner F, Huber M, Ursin R. Temporal distinguishability in hong-ou-mandel interference for harnessing high-dimensional frequency entanglement. Npj Quan Inf (2021) 7:167–7. doi:10.1038/s41534-021-00504-0
95. Legero T, Wilk T, Hennrich M, Rempe G, Kuhn A. Quantum beat of two single photons. Phys Rev Lett (2004) 93:070503. doi:10.1103/PhysRevLett.93.070503
96. Kobayashi T, Ikuta R, Yasui S, Miki S, Yamashita T, Terai H, et al. Frequency-domain hong-ou-mandel interference. Nat Photon (2016) 10:441–4. doi:10.1038/nphoton.2016.74
97. Vanselow A, Kaufmann P, Zorin I, Heise B, Chrzanowski HM, Ramelow S. Frequency-domain optical coherence tomography with undetected mid-infrared photons. Optica (2020) 7:1729–36. doi:10.1364/OPTICA.400128
98. Senellart P, Solomon G, White A. High-performance semiconductor quantum-dot single-photon sources. Nat Nanotechnol (2017) 12:1026–39. doi:10.1038/nnano.2017.218
99. He YM, He Y, Wei YJ, Wu D, Atatüre M, Schneider C, et al. On-demand semiconductor single-photon source with near-unity indistinguishability. Nat Nanotechnol (2013) 8:213–7. doi:10.1038/nnano.2012.262
100. Kim JH, Cai T, Richardson CJ, Leavitt RP, Waks E. Two-photon interference from a bright single-photon source at telecom wavelengths. Optica (2016) 3:577–84. doi:10.1364/OPTICA.3.000577
101. Ollivier H, Thomas S, Wein S, de Buy Wenniger IM, Coste N, Loredo J, et al. Hong-ou-mandel interference with imperfect single photon sources. Phys Rev Lett (2021) 126:063602. doi:10.1103/PhysRevLett.126.063602
102. Stobińska M, Buraczewski A, Moore M, Clements W, Renema JJ, Nam S, et al. Quantum interference enables constant-time quantum information processing. Sci Adv (2019) 5:eaau9674. doi:10.1126/sciadv.aau9674
103. Zhang Y, Roux FS, Konrad T, Agnew M, Leach J, Forbes A. Engineering two-photon high-dimensional states through quantum interference. Sci Adv (2016) 2:e1501165. doi:10.1126/sciadv.1501165
104. Zhang Y, Agnew M, Roger T, Roux FS, Konrad T, Faccio D, et al. Simultaneous entanglement swapping of multiple orbital angular momentum states of light. Nat Commun (2017) 8:632–7. doi:10.1038/s41467-017-00706-1
105. Bonaretti F, Faccio D, Clerici M, Biegert J, Di Trapani P. Spatiotemporal amplitude and phase retrieval of bessel-x pulses using a hartmann-shack sensor. Opt Express (2009) 17:9804–9. doi:10.1364/OE.17.009804
106. Bowlan P, Valtna-Lukner H, Lõhmus M, Piksarv P, Saari P, Trebino R. Measuring the spatiotemporal field of ultrashort bessel-x pulses. Opt Lett (2009) 34:2276–8. doi:10.1364/OL.34.002276
107. Kuntz K, Braverman B, Youn S, Lobino M, Pessina E, Lvovsky A. Spatial and temporal characterization of a bessel beam produced using a conical mirror. Phys Rev A (Coll Park) (2009) 79:043802. doi:10.1103/PhysRevA.79.043802
108. Alexeev I, Kim K, Milchberg H. Measurement of the superluminal group velocity of an ultrashort bessel beam pulse. Phys Rev Lett (2002) 88:073901. doi:10.1103/PhysRevLett.88.073901
109. Devaux F, Mosset A, Moreau PA, Lantz E. Imaging spatiotemporal hong-ou-mandel interference of biphoton states of extremely high schmidt number. Phys Rev X (2020) 10:031031. doi:10.1103/PhysRevX.10.031031
110. Ibarra-Borja Z, Sevilla-Gutiérrez C, Ramírez-Alarcón R, Cruz-Ramírez H, U’Ren AB. Experimental demonstration of full-field quantum optical coherence tomography. Photon Res (2020) 8:51–6. doi:10.1364/PRJ.8.000051
111. Aguilar G, Piera R, Saldanha P, de Matos Filho R, Walborn S. Robust interferometric sensing using two-photon interference. Phys Rev Appl (2020) 14:024028. doi:10.1103/PhysRevApplied.14.024028
112. Lo HK, Curty M, Qi B. Measurement-device-independent quantum key distribution. Phys Rev Lett (2012) 108:130503. doi:10.1103/PhysRevLett.108.130503
113. Liu Y, Chen TY, Wang LJ, Liang H, Shentu GL, Wang J, et al. Experimental measurement-device-independent quantum key distribution. Phys Rev Lett (2013) 111:130502. doi:10.1103/PhysRevLett.111.130502
114. Yin HL, Chen TY, Yu ZW, Liu H, You LX, Zhou YH, et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys Rev Lett (2016) 117:190501. doi:10.1103/PhysRevLett.117.190501
115. Curty M, Xu F, Cui W, Lim CCW, Tamaki K, Lo HK. Finite-key analysis for measurement-device-independent quantum key distribution. Nat Commun (2014) 5:3732–7. doi:10.1038/ncomms4732
116. Albarelli F, Friel JF, Datta A. Evaluating the holevo cramér-rao bound for multiparameter quantum metrology. Phys Rev Lett (2019) 123:200503. doi:10.1103/PhysRevLett.123.200503
117. Gammelmark S, Mølmer K. Fisher information and the quantum cramér-rao sensitivity limit of continuous measurements. Phys Rev Lett (2014) 112:170401. doi:10.1103/PhysRevLett.112.170401
118. Braunstein SL, Caves CM. Statistical distance and the geometry of quantum states. Phys Rev Lett (1994) 72:3439–43. doi:10.1103/PhysRevLett.72.3439
119. Rezai M, Wrachtrup J, Gerhardt I. Coherence properties of molecular single photons for quantum networks. Phys Rev X (2018) 8:031026. doi:10.1103/PhysRevX.8.031026
120. Van Loon JC. Analytical atomic absorption spectroscopy. New York: Elsevier (1980). doi:10.1016/B978-0-127-14050-6.X5001-3
121. Velasco-Velez JJ, Wu CH, Pascal TA, Wan LF, Guo J, Prendergast D, et al. The structure of interfacial water on gold electrodes studied by x-ray absorption spectroscopy. Science (2014) 346:831–4. doi:10.1126/science.1259437
122. Wolfgramm F, Vitelli C, Beduini FA, Godbout N, Mitchell MW. Entanglement-enhanced probing of a delicate material system. Nat Photon (2013) 7:28–32. doi:10.1038/nphoton.2012.300
123. Taylor MA, Janousek J, Daria V, Knittel J, Hage B, Bachor HA, et al. Biological measurement beyond the quantum limit. Nat Photon (2013) 7:229–33. doi:10.1038/nphoton.2012.346
124. Kalachev A, Kalashnikov D, Kalinkin A, Mitrofanova T, Shkalikov A, Samartsev V. Biphoton spectroscopy of yag: Er3+ crystal. Laser Phys Lett (2007) 4:722–5. doi:10.1002/lapl.200710061
125. Chen Y, Shen Q, Luo S, Zhang L, Chen Z, Chen L. Entanglement-assisted absorption spectroscopy by hong-ou-mandel interference. Phys Rev Appl (2022) 17:014010. doi:10.1103/PhysRevApplied.17.014010
126. León-Montiel RJ, Svozilík J, Torres JP, U’Ren AB. Temperature-controlled entangled-photon absorption spectroscopy. Phys Rev Lett (2019) 123:023601. doi:10.1103/PhysRevLett.123.023601
127. Tabakaev D, Montagnese M, Haack G, Bonacina L, Wolf JP, Zbinden H, et al. Energy-time-entangled two-photon molecular absorption. Phys Rev A (Coll Park) (2021) 103:033701. doi:10.1103/PhysRevA.103.033701
128. Barkai E, Jung Y, Silbey R. Time-dependent fluctuations in single molecule spectroscopy: A generalized wiener-khintchine approach. Phys Rev Lett (2001) 87:207403. doi:10.1103/PhysRevLett.87.207403
129. Yepiz-Graciano P, Martínez AMA, Lopez-Mago D, Cruz-Ramirez H, U’Ren AB. Spectrally resolved hong–ou–mandel interferometry for quantum-optical coherence tomography. Photon Res (2020) 8:1023–34. doi:10.1364/PRJ.388693
130. Hamm P. Principles of nonlinear optical spectroscopy: A practical approach or: Mukamel for dummies, 41. Zurich, Switzerland: University of Zurich (2005). p. 77.
131. Hamm P, Zanni M. Concepts and methods of 2D infrared spectroscopy. Cambridge, UK: Cambridge University Press (2011). doi:10.1017/cbo9780511675935
132. Schmidt PO, Rosenband T, Langer C, Itano WM, Bergquist JC, Wineland DJ. Spectroscopy using quantum logic. Science (2005) 309:749–52. doi:10.1126/science.1114375
133. Sánchez Muñoz C, Frascella G, Schlawin F. Quantum metrology of two-photon absorption. Phys Rev Res (2021) 3:033250. doi:10.1103/PhysRevResearch.3.033250
134. Prajapati N, Niu Z, Novikova I. Quantum-enhanced two-photon spectroscopy using two-mode squeezed light. Opt Lett (2021) 46:1800–3. doi:10.1364/OL.418398
135. Javanainen J, Gould PL. Linear intensity dependence of a two-photon transition rate. Phys Rev A (Coll Park) (1990) 41:5088–91. doi:10.1103/PhysRevA.41.5088
136. Landes T, Allgaier M, Merkouche S, Smith BJ, Marcus AH, Raymer MG. Experimental feasibility of molecular two-photon absorption with isolated time-frequency-entangled photon pairs. Phys Rev Res (2021) 3:033154. doi:10.1103/PhysRevResearch.3.033154
137. Muthukrishnan A, Agarwal GS, Scully MO. Inducing disallowed two-atom transitions with temporally entangled photons. Phys Rev Lett (2004) 93:093002. doi:10.1103/PhysRevLett.93.093002
138. Roslyak O, Mukamel S. Multidimensional pump-probe spectroscopy with entangled twin-photon states. Phys Rev A (Coll Park) (2009) 79:063409. doi:10.1103/PhysRevA.79.063409
139. Schlawin F, Dorfman KE, Fingerhut BP, Mukamel S. Suppression of population transport and control of exciton distributions by entangled photons. Nat Commun (2013) 4:1782–7. doi:10.1038/ncomms2802
Keywords: quantum entanglement, Hong–Ou–Mandel interference, spectral and temporal domains, biphoton wavefunction, quantum metrology, entanglement-assisted absorption spectroscopy
Citation: Chen Y, Hong L and Chen L (2022) Quantum interferometric metrology with entangled photons. Front. Phys. 10:892519. doi: 10.3389/fphy.2022.892519
Received: 09 March 2022; Accepted: 09 August 2022;
Published: 12 September 2022.
Edited by:
Roberto de J. León-Montiel, National Autonomous University of Mexico, MexicoReviewed by:
Yin Cai, Xi’an Jiaotong University, ChinaChe-Ming Li, National Cheng Kung University, Taiwan
Copyright © 2022 Chen, Hong and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuanyuan Chen, Y2hlbnl5QHhtdS5lZHUuY24=; Lixiang Chen, Y2hlbmx4QHhtdS5lZHUuY24=
 Yuanyuan Chen
Yuanyuan Chen Ling Hong
Ling Hong Lixiang Chen
Lixiang Chen