A Hybrid Norm for Guaranteed Tensor Recovery

Benefiting from the superiority of tensor Singular Value Decomposition (t-SVD) in excavating low-rankness in the spectral domain over other tensor decompositions (like Tucker decomposition), t-SVD-based tensor learning has shown promising performance and become an emerging research topic in computer vision and machine learning very recently. However, focusing on modeling spectral low-rankness, the t-SVD-based models may be insufficient to exploit low-rankness in the original domain, leading to limited performance while learning from tensor data (like videos) that are low-rank in both original and spectral domains. To this point, we define a hybrid tensor norm dubbed the “Tubal + Tucker” Nuclear Norm (T2NN) as the sum of two tensor norms, respectively, induced by t-SVD and Tucker decomposition to simultaneously impose low-rankness in both spectral and original domains. We further utilize the new norm for tensor recovery from linear observations by formulating a penalized least squares estimator. The statistical performance of the proposed estimator is then analyzed by establishing upper bounds on the estimation error in both deterministic and non-asymptotic manners. We also develop an efficient algorithm within the framework of Alternating Direction Method of Multipliers (ADMM). Experimental results on both synthetic and real datasets show the effectiveness of the proposed model.

1 Introduction

Thanks to the rapid progress of computer technology, data in tensor format (i.e., multi-dimensional array) are emerging in computer vision, machine learning, remote sensing, quantum physics, and many other fields, triggering an increasing need for tensor-based learning theory and algorithms [1–6]. In this paper, we carry out both theoretic and algorithmic research studies on tensor recovery from linear observations, which is a typical problem in tensor learning aiming to learn an unknown tensor when only a limited number of its noisy linear observations are available [7]. Tensor recovery finds applications in many industrial circumstances where the sensed or collected tensor data are polluted by unpredictable factors such as sensor failures, communication losses, occlusion by objects, shortage of instruments, and electromagnetic interferences [7–9], and is thus of both theoretical and empirical significance.

In general, reconstructing an unknown tensor from only a small number of its linear observations is hopeless, unless some assumptions on the underlying tensor are made [9]. The most commonly used assumption is that the underlying tensor possesses some kind of low-rankness which can significantly limit its degree of freedom, such that the signal can be estimated from a small but sufficient number of observations [7]. However, as a higher-order extension of matrix low-rankness, the tensor low-rankness has many different characterizations due to the multiple definitions of tensor rank, e.g., the CANDECOMP/PARAFAC (CP) rank [10], Tucker rank [11], Tensor Train (TT) rank [12], and Tensor Ring (TR) rank [13]. As has been discussed in [7] from a signal processing standpoint, the above exampled rank functions are defined in the original domain of the tensor signal and may thus be insufficient to model low-rankness in the spectral domain. The recently proposed tensor low-tubal-rankness [14] within the algebraic framework of tensor Singular Value Decomposition (t-SVD) [15] gives a kind of complement to it by exploiting low-rankness in the spectral domain defined via Discrete Fourier Transform (DFT), and has witnessed significant performance improvements in comparison with the original domain-based low-rankness for tensor recovery [6, 16, 17].

Despite the popularity of low-tubal-rankness, the fact that it is defined solely in the spectral domain also naturally poses a potential limitation on its usability to some tensor data that are low-rank in both spectral and original domains. To address this issue, we propose a hybrid tensor norm to encourage low-rankness in both spectral and original domains at the same time for tensor recovery in this paper. Specifically, the contributions of this work are four-fold:

• To simultaneously exploit low-rankness in both spectral and original domains, we define a new norm named T2NN as the sum of two tensor nuclear norms induced, respectively, by the t-SVD for spectral low-rankness and Tucker decomposition for original domain low-rankness.

• Then, we apply the proposed norm to tensor recovery by formulating a new tensor least squares estimator penalized by T2NN.

• Statistically, the statistical performance of the proposed estimator is analyzed by establishing upper bounds on the estimation error in both deterministic and non-asymptotic manners.

• Algorithmically, we propose an algorithm based on ADMM to compute the estimator and evaluate its effectiveness on three different types of real data.

The rest of this paper proceeds as follows. First, the notations and preliminaries of low-tubal-rankness and low-Tucker-rankness are introduced in Section 2. Then, we define the new norm and apply it to tensor recovery in Section 3. To understand the statistical behavior of the estimator, we establish an upper bound on the estimation error in Section 4. To compute the proposed estimator, we design an ADMM-based algorithm in Section 5 with empirical performance reported in Section 6.

2 Notations and Preliminaries

Notations. We use lowercase boldface, uppercase boldface, and calligraphy letters to denote vectors (e.g., v), matrices (e.g., M), and tensors (e.g., $\mathcal{T}$), respectively. For any real numbers a, b, let a ∨ b = max{a, b} and a ∧ b = min{a, b}. If the size of a tensor is not given explicitly, then it is in ${\mathbb{R}}^{d_1\times d_2\times d_3}$. We use c, c′, c₁, etc., to denote constants whose values can vary from line to line. For notational simplicity, let $\tilde{d}=(d_1+d_2)d_3$ and d_\k = d₁d₂d₃/d_k for k = 1, 2, 3.

Given a matrix $\mathbf{M}\in {\mathbb{C}}^{d_1\times d_2}$, its nuclear norm and spectral norm are defined as ‖M‖_∗≔∑_iσ_i and $\Vert \mathbf{M}\Vert ≔\underset{i}{\max }{\sigma }_i$, respectively, where {σ_i |i = 1, 2, … , d₁ ∧ d₂} are its singular values. Given a tensor $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$, define its l₁-norm and F-norm as $\Vert \mathcal{T}{\Vert }_1≔\Vert \text{vec}(\mathcal{T}){\Vert }_1,\Vert \mathcal{T}{\Vert }_{\text{F}}≔\Vert \text{vec}(\mathcal{T}){\Vert }_2$, respectively, where vec (⋅) denotes the vectorization operation of a tensor [18]. Given $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$, let ${\mathbf{T}}^{(i)}≔\mathcal{T}(:,:,i)$ denote its ith frontal slice. For any two (real or complex) tensors $\mathcal{A},\mathcal{B}$ of the same size, define their inner product as the inner product of their vectorizations $⟨\mathcal{A},\mathcal{B}⟩≔⟨\text{vec}(\mathcal{A}),\text{vec}(\mathcal{B})⟩$. Other notations are introduced at their first appearance.

2.1 Spectral Rankness Modeled by t-SVD

The low-tubal-rankness defined within the algebraic framework of t-SVD is a typical example to characterize low-rankness in the spectral domain. We give some basic notions about t-SVD in this section.

Definition 1 (t-product [15]). Given ${\mathcal{T}}_1\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ and ${\mathcal{T}}_2\in {\mathbb{R}}^{d_2\times d_4\times d_3}$, their t-product $\mathcal{T}={\mathcal{T}}_1\ast {\mathcal{T}}_2\in {\mathbb{R}}^{d_1\times d_4\times d_3}$ is a tensor whose (i, j)-th tube $\mathcal{T}(i,j,:)={\sum }_{k=1}^{d_2}{\mathcal{T}}_1(i,k,:)•{\mathcal{T}}_2(k,j,:)$, where • is the circular convolution [15].

Definition 2 (tensor transpose [15]). Let $\mathcal{T}$ be a tensor of size d₁ × d₂ × d₃, then ${\mathcal{T}}^{\top }$ is the d₂ × d₁ × d₃ tensor obtained by transposing each of the frontal slices and then reversing the order of transposed frontal slices 2 through d₃.

Definition 3 (identity tensor [15]). The identity tensor $\mathcal{I}\in {\mathbb{R}}^{d\times d\times d_3}$ is a tensor whose first frontal slice is the d × d identity matrix and all other frontal slices are zero.

Definition 4 (f-diagonal tensor [15]). A tensor is called f-diagonal if each frontal slice of the tensor is a diagonal matrix.

Definition 5 (Orthogonal tensor [15]). A tensor $\mathcal{Q}\in {\mathbb{R}}^{d\times d\times d_3}$ is orthogonal if ${\mathcal{Q}}^{\top }\ast \mathcal{Q}=\mathcal{Q}\ast {\mathcal{Q}}^{\top }=\mathcal{I}$.Then, t-SVD can be defined as follows.

Definition 6 (t-SVD, tubal rank [15]). Any tensor $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ has a tensor singular value decomposition as

$\begin{array}{c}\hfill \mathcal{T}=\mathcal{U}\ast \mathcal{S}\ast {\mathcal{V}}^{\top },\end{array}(1)$

where $\mathcal{U}\in {\mathbb{R}}^{d_1\times d_1\times d_3}$, $\mathcal{V}\in {\mathbb{R}}^{d_2\times d_2\times d_3}$ are orthogonal tensors and $\mathcal{S}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ is an f-diagonal tensor. The tubal rank of $\mathcal{T}$ is defined as the number of non-zero tubes of $\mathcal{T}$,

$\begin{array}{c}\hfill {\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{T})≔\#\left\{\left.i\right|\mathcal{S}(i,i,:)\ne \mathbf{0}\right\},\end{array}(2)$

where # counts the number of elements in a set.For convenience of analysis, the block diagonal matrix of 3-way tensors is also defined.

Definition 7 (block-diagonal matrix [15]). Let $\bar{\mathbf{T}}$ denote the block-diagonal matrix of the tensor $\tilde{\mathcal{T}}$ in the Fourier domain¹, i.e.,

$\begin{array}{c}\hfill \bar{\mathbf{T}}≔\left[\begin{array}{ccc}\hfill {\tilde{\mathbf{T}}}^{\left(1\right)}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\tilde{\mathbf{T}}}^{\left(d_3\right)}\hfill \end{array}\right]\in {\mathbb{C}}^{d_1{d}_3\times d_2{d}_3}.\end{array}(3)$

Definition 8 (tubal nuclear norm, tensor spectral norm [17]). Given $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$, let $\tilde{\mathcal{T}}$ be its Fourier version in ${\mathbb{C}}^{d_1\times d_2\times d_3}$. The Tubal Nuclear Norm (TNN) ‖⋅‖_tnn of $\mathcal{T}$ is defined as the averaged nuclear norm of frontal slices of $\tilde{\mathcal{T}}$,

$\begin{array}{c}\hfill \Vert \mathcal{T}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}≔\frac{1}{d_3}\sum _{i=1}^{d_3}\Vert {\tilde{\mathbf{T}}}^{(i)}{\Vert }_{\ast },\end{array}$

whereas the tensor spectral norm ‖⋅‖ is the largest spectral norm of the frontal slices,

$\begin{array}{c}\hfill \Vert \mathcal{T}\Vert ≔\underset{i\in [d_3]}{\max }\{\Vert {\tilde{\mathbf{T}}}^{(i)}\Vert \}.\end{array}$

We can see from Definition 8 that TNN captures low-rankness in the spectral domain and is thus more suitable for tensors with spectral low-rankness. As visual data (like images and videos) often process strong spectral low-rankness, it has achieved superior performance over many original domain-based nuclear norms in visual data restoration [6, 17].

2.2 Original Domain Low-Rankness Modeled by Tucker Decomposition

The low-Tucker-rankness is a classical higher-order extension of matrix low-rankness in the original domain and has been widely applied in computer vision and machine learning [19–21]. Given any K-way tensor $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$, its Tucker rank is defined as the following vector:

$\begin{array}{c}\hfill {\vec{\mathbf{r}}}_{\text{Tucker}}(\mathcal{T})≔{(\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{T}}_{(1)}),\cdots ,\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{T}}_{(K)}))}^{\top }\in {\mathbb{R}}^K,\end{array}(4)$

where ${\mathbf{T}}_{(k)}\in {\mathbb{R}}^{d_k\times {\prod }_{i\ne k}{d}_i}$ denotes the mode-k unfolding (matrix) of $\mathcal{T}$ [18] obtained by concatenating all the mode-k fibers of $\mathcal{T}$ as column vectors. We can see that the Tucker rank measures the low-rankness of all the mode-k unfoldings T_(k) in the original domain.

Through relaxing the matrix rank in Eq. 4 to its convex envelope, i.e., the matrix nuclear norm, we get a convex relaxation of the Tucker rank, called Sum of Nuclear Norms (SNN) [20], which is defined as follows:

$\begin{array}{c}\hfill \Vert \mathcal{T}{\Vert }_{\text{snn}}≔\sum _{k=1}^K{\alpha }_k\Vert {\mathbf{T}}_{(k)}{\Vert }_{\ast },\end{array}(5)$

where α_k’s are positive constants satisfying ∑_ka_k = 1. As a typical tensor low-rankness penalty in the original domain, SNN has found many applications in tensor recovery [19, 20, 22].

3 A Hybrid Norm for Tensor Recovery

In this section, we first define a new norm to exploit low-rankness in both spectral and original domains and then use it to formulate a penalized tensor least squares estimator.

3.1 The Proposed Norm

Although TNN has shown superior performance in many tensor learning tasks, it may still be insufficient for tensors which are low-rank in both spectral and original domains due to its definition solely in the spectral domain. Moreover, it is also unsuitable for tensors which have less significant spectral low-rankness than the original domain low-rankness. Thus, it is necessary to extend the vanilla TNN such that the original domain low-rankness can also be exploited for sounder low-rank modeling.

Under the inspiration of SNN’s impressive low-rank modeling capability in the original domain, our idea is quite simple: to combine the advantages of both TNN and SNN through their weighted sum. In this line of thinking, we come up with the following hybrid tensor norm.

Definition 9 (T2NN). The hybrid norm called “Tubal + Tucker” Nuclear Norm (T2NN) of any 3-way tensor $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ is defined as the weighted sum of its TNN and SNN as follows:

$\begin{array}{c}\hfill \Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}≔\gamma \Vert \mathcal{T}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\Vert \mathcal{T}{\Vert }_{\text{snn}},\end{array}(6)$

where γ ∈ (0, 1) is a constant balancing the low-rank modeling in the spectral and original domains.As can be seen from its definition, T2NN approximates TNN when γ → 1, and it degenerates to SNN as γ → 0. Thus, it can be viewed as an interpolation between TNN and SNN, which provides with more flexibility in low-rank tensor modeling. We also define the dual norm of T2NN (named the dual T2NN norm) which are frequently used in analyzing the statistical performance of the T2NN-based tensor estimator.

Lemma 1. The dual norm of the proposed T2NN defined as

$\begin{array}{c}\hfill \Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}^{\ast }≔\underset{\mathcal{T}}{\sup }⟨\mathcal{X},\mathcal{T}⟩,\text{s.t.\hspace{0.17em}}\Vert \mathcal{X}{\Vert }_{\text{t}2\text{nn}}\le 1,\end{array}(7)$

can be equivalently formulated as follows:

$\begin{array}{cc}\hfill \Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}^{\ast }& =\underset{\mathcal{A},\mathcal{B},\mathcal{C},\mathcal{D}}{\inf }\max \left\{\frac{1}{\gamma }\Vert \mathcal{A}\Vert ,\frac{1}{{\alpha }_1(1-\gamma )}\Vert {\mathbf{B}}_{(1)}\Vert ,\right.\hfill \\ \hfill & \left.\frac{1}{{\alpha }_2(1-\gamma )}\Vert {\mathbf{C}}_{(2)}\Vert ,\frac{1}{{\alpha }_3(1-\gamma )}\Vert {\mathbf{D}}_{(3)}\Vert \right\},\hfill \\ \hfill & \text{s.t.\hspace{0.17em}}\mathcal{A}+\mathcal{B}+\mathcal{C}+\mathcal{D}=\mathcal{T}.\hfill \end{array}(8)$

Proof of Lemma 1. Using the definition of T2NN, the supremum in Problem (7) can be equivalently converted to the opposite number of infimum as follows:

$\begin{array}{cc}\hfill -\Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}^{\ast }=& {\inf }_{\mathcal{T}}-⟨\mathcal{X},\mathcal{T}⟩,\hfill \\ \hfill & \text{s.t.\hspace{0.17em}}\gamma \Vert \mathcal{X}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+{\alpha }_1(1-\gamma )\Vert {\mathcal{X}}_{(1)}{\Vert }_{\ast }+{\alpha }_2(1-\gamma )\hfill \\ \hfill & \times \Vert {\mathcal{X}}_{(2)}{\Vert }_{\ast }+{\alpha }_3(1-\gamma )\Vert {\mathcal{X}}_{(3)}{\Vert }_{\ast }\le 1.\hfill \end{array}(9)$

By introducing a multiplier λ ≥ 0, we obtain the Lagrangian function of Problem (9),

$\begin{array}{cc}\hfill & L(\mathcal{X},\lambda )\hfill \\ \hfill & ≔-⟨\mathcal{X},\mathcal{T}⟩+\lambda \left(\gamma \Vert \mathcal{X}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+{\alpha }_1(1-\gamma )\Vert {\mathcal{X}}_{(1)}{\Vert }_{\ast }\right.\hfill \\ \hfill & \left.+{\alpha }_2(1-\gamma )\Vert {\mathcal{X}}_{(2)}{\Vert }_{\ast }+{\alpha }_3(1-\gamma )\Vert {\mathcal{X}}_{(3)}{\Vert }_{\ast }-1\right).\hfill \end{array}$

Since Slatter’s condition [23] is satisfied in Problem (9), strong duality holds, which means

$\begin{array}{c}\hfill -\Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}=\underset{\mathcal{X}}{\inf }\underset{\lambda }{\sup }L(\mathcal{X},\lambda )=\underset{\lambda }{\sup }\underset{\mathcal{X}}{\inf }L(\mathcal{X},\lambda ).\end{array}$

Thus, we proceed by computing ${\sup }_{\lambda }{\inf }_{\mathcal{X}}L(\mathcal{X},\lambda )$ as follows:

$\begin{array}{cc}\hfill & \underset{\lambda }{\sup }\underset{\mathcal{X}}{\inf }-⟨\mathcal{X},\mathcal{T}⟩+\lambda \left(\gamma \Vert \mathcal{X}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+{\alpha }_1(1-\gamma )\Vert {\mathcal{X}}_{(1)}{\Vert }_{\ast }\right.\hfill \\ \hfill & \left.+{\alpha }_2(1-\gamma )\Vert {\mathcal{X}}_{(2)}{\Vert }_{\ast }+{\alpha }_3(1-\gamma )\Vert {\mathcal{X}}_{(3)}{\Vert }_{\ast }-1\right)\hfill \\ \hfill & \stackrel{(i)}{=}\underset{\lambda }{\sup }\underset{\mathcal{X}}{\inf }-⟨\mathcal{X},\mathcal{A}+\mathcal{B}+\mathcal{C}+\mathcal{D}⟩\hfill \\ \hfill & +\lambda \left(\gamma \Vert \mathcal{X}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+{\alpha }_1(1-\gamma )\Vert {\mathcal{X}}_{(1)}{\Vert }_{\ast }+{\alpha }_2(1-\gamma )\Vert {\mathcal{X}}_{(2)}{\Vert }_{\ast }\right.\hfill \\ \hfill & \left.+{\alpha }_3(1-\gamma )\Vert {\mathcal{X}}_{(3)}{\Vert }_{\ast }-1\right)-\lambda ,\text{where}\hfill \\ \hfill & \mathcal{A}+\mathcal{B}+\mathcal{C}+\mathcal{D}=\mathcal{T},\hfill \\ \hfill & =\underset{\lambda }{\sup }\underset{\mathcal{X}}{\inf }-\lambda +\left(\lambda \gamma \Vert \mathcal{X}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-⟨\mathcal{X},\mathcal{A}⟩\right)+\left(\lambda {\alpha }_1(1-\gamma )\right.\hfill \\ \hfill & \left.\times \Vert {\mathbf{X}}_{(1)}{\Vert }_{\ast }-⟨\mathcal{X},\mathcal{B}⟩\right)+\left(\lambda {\alpha }_2(1-\gamma )\Vert {\mathbf{X}}_{(2)}{\Vert }_{\ast }-⟨\mathcal{X},\mathcal{C}⟩\right)\hfill \\ \hfill & +\left(\lambda {\alpha }_3(1-\gamma )\Vert {\mathbf{X}}_{(3)}{\Vert }_{\ast }-⟨\mathcal{X},\mathcal{D}⟩\right),\text{where}\hfill \\ \hfill & \mathcal{A}+\mathcal{B}+\mathcal{C}+\mathcal{D}=\mathcal{T},\hfill \\ \hfill & \stackrel{(ii)}{=}\underset{\lambda }{\sup }-\lambda +\left\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}\lambda \ge \frac{1}{\gamma }\Vert \mathcal{A}\Vert \hfill \\ \hfill -\infty \hfill & \hfill \text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill & +\left\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}\lambda \ge \frac{1}{{\alpha }_1(1-\gamma )}\Vert {\mathbf{B}}_{(1)}\Vert \hfill \\ \hfill -\infty \hfill & \hfill \text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill & +\left\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}\lambda \ge \frac{1}{{\alpha }_2(1-\gamma )}\Vert {\mathbf{C}}_{(2)}\Vert \hfill \\ \hfill -\infty \hfill & \hfill \text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill & +\left\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}\lambda \ge \frac{1}{{\alpha }_3(1-\gamma )}\Vert {\mathbf{D}}_{(3)}\Vert \hfill \\ \hfill -\infty \hfill & \hfill \text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill & \text{where}\mathcal{A}+\mathcal{B}+\mathcal{C}+\mathcal{D}=\mathcal{T},\hfill \\ \hfill & =-\underset{\mathcal{A}+\mathcal{B}+\mathcal{C}+\mathcal{D}=\mathcal{T}}{\inf }\max \left\{\frac{1}{\gamma }\Vert \mathcal{A}\Vert ,\frac{1}{{\alpha }_1(1-\gamma )}\right.\hfill \\ \hfill & \left.\times \Vert {\mathbf{B}}_{(1)}\Vert ,\frac{1}{{\alpha }_2(1-\gamma )}\Vert {\mathbf{C}}_{(2)}\Vert ,\frac{1}{{\alpha }_3(1-\gamma )}\Vert {\mathbf{D}}_{(3)}\Vert \right\},\hfill \end{array}$

where (i) is obtained by the trick of splitting $\mathcal{T}$ into four auxiliary tensors $\mathcal{A},\mathcal{B},\mathcal{C},\mathcal{D}$ for simpler analysis and (ii) holds because for any positive constant α, any norm f (⋅) with dual norm f*(⋅), we have the following relationship:

$\begin{array}{cc}\hfill & \underset{\mathcal{X}}{\inf }\lambda \alpha f(\mathcal{X})-⟨\mathcal{X},\mathcal{A}⟩\ge \underset{\mathcal{X}}{\inf }\lambda \alpha f(\mathcal{X})-\gamma f(\mathcal{X})\cdot \frac{1}{\alpha }{f}^{\ast }(\mathcal{A}),\hfill \\ \hfill & =\underset{\mathcal{X}}{\inf }\alpha f(\mathcal{X})\left(\lambda -\frac{1}{\alpha }{f}^{\ast }(\mathcal{A})\right),\hfill \\ \hfill & =\left\{\begin{array}{cc}\hfill 0,\hfill & \hfill \text{if}\lambda \ge \frac{1}{\gamma }{f}^{\ast }(\mathcal{A}),\hfill \\ \hfill -\infty ,\hfill & \hfill \text{otherwise}.\hfill \end{array}\right.\hfill \end{array}$

This completes the proof.Although an expression of the dual T2NN norm is given in Lemma 1, it is still an optimization problem whose optimal value cannot be straightforwardly computed from the variable tensor $\mathcal{T}$. Following the tricks in [22], we instead give an upper bound on the dual T2NN norm which is directly in terms of $\mathcal{T}$ in the following lemma:

Lemma 2. The dual T2NN norm can be upper bounded as follows:

$\begin{array}{cc}\hfill \Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}^{\ast }& \le \frac{1}{16}\left(\frac{1}{\gamma }\Vert \mathcal{T}\Vert +\frac{1}{{\alpha }_1(1-\gamma )}\Vert {\mathbf{T}}_{(1)}\Vert +\frac{1}{{\alpha }_2(1-\gamma )}\Vert {\mathbf{T}}_{(2)}\Vert \right.\hfill \\ \hfill & \left.+\frac{1}{{\alpha }_3(1-\gamma )}\Vert {\mathbf{T}}_{(3)}\Vert \right).\hfill \end{array}(10)$

Proof of Lemma 2. The proof is a direct application of the basic equality “harmonic mean ≤ arithmetic mean” with careful construction of auxiliary tensors $\mathcal{A},\mathcal{B},\mathcal{C},\mathcal{D}$ in Eq. 8 as follows:

$\begin{array}{cc}\hfill {\mathcal{A}}_0& =\frac{\gamma \Vert \mathcal{T}{\Vert }^{-1}}{M},{\mathcal{B}}_0=\frac{{\alpha }_1(1-\gamma )\Vert {\mathbf{T}}_{(1)}{\Vert }^{-1}}{M},\hfill \\ \hfill {\mathcal{C}}_0& =\frac{{\alpha }_2(1-\gamma )\Vert {\mathbf{T}}_{(2)}{\Vert }^{-1}}{M},{\mathcal{D}}_0=\frac{{\alpha }_3(1-\gamma )\Vert {\mathbf{T}}_{(3)}{\Vert }^{-1}}{M},\hfill \end{array}$

where the denominator M is given by

$\begin{array}{c}\hfill M=\gamma \Vert \mathcal{T}{\Vert }^{-1}+{\alpha }_1(1-\gamma )\Vert {\mathbf{T}}_{(1)}{\Vert }^{-1}+{\alpha }_2(1-\gamma )\Vert {\mathbf{T}}_{(2)}{\Vert }^{-1}+{\alpha }_3(1-\gamma )\Vert {\mathbf{T}}_{(3)}{\Vert }^{-1}.\end{array}$

It is obvious that ${\mathcal{A}}_0+{\mathcal{B}}_0+{\mathcal{C}}_0+{\mathcal{D}}_0=\mathcal{T}$. By substituting the particular setting $({\mathcal{A}}_0,{\mathcal{B}}_0,{\mathcal{C}}_0,{\mathcal{D}}_0)$ of $(\mathcal{A},\mathcal{B},\mathcal{C},\mathcal{D})$ into Eq. 8, we obtain

$\begin{array}{c}\hfill \Vert \mathcal{T}{\Vert }_{\text{t}2\text{nn}}^{\ast }\le \frac{1}{\begin{array}{c}\hfill \gamma \Vert \mathcal{T}{\Vert }^{-1}+{\alpha }_1(1-\gamma )\Vert {\mathbf{T}}_{(1)}{\Vert }^{-1}+{\alpha }_2(1-\gamma )\hfill \\ \hfill \Vert {\mathbf{T}}_{(2)}{\Vert }^{-1}+{\alpha }_3(1-\gamma )\Vert {\mathbf{T}}_{(3)}{\Vert }^{-1}\hfill \end{array}}.\end{array}(11)$

Then, by using “harmonic mean ≤ arithmetic mean” on the right-hand side of Eq. 11, we obtain

$\begin{array}{cc}\hfill & \frac{4}{\begin{array}{c}\hfill \gamma \Vert \mathcal{T}{\Vert }^{-1}+{\alpha }_1(1-\gamma )\Vert {\mathbf{T}}_{(1)}{\Vert }^{-1}+{\alpha }_2(1-\gamma )\hfill \\ \hfill \Vert {\mathbf{T}}_{(2)}{\Vert }^{-1}+{\alpha }_3(1-\gamma )\Vert {\mathbf{T}}_{(3)}{\Vert }^{-1}\hfill \end{array}}\hfill \\ \hfill & \le \frac{1}{4}\left(\frac{1}{\gamma }\Vert \mathcal{T}\Vert +\frac{1}{{\alpha }_1(1-\gamma )}\Vert {\mathbf{T}}_{(1)}\Vert +\frac{1}{{\alpha }_2(1-\gamma )}\Vert {\mathbf{T}}_{(2)}\Vert \right.\hfill \\ \hfill & \left.+\frac{1}{{\alpha }_3(1-\gamma )}\Vert {\mathbf{T}}_{(3)}\Vert \right),\hfill \end{array}(12)$

which directly leads to Eq. 10.

3.2 T2NN-Based Tensor Recovery

3.2.1 The observation Model

We use ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ to denote the underlying tensor which is unknown. Suppose one observes N ≪ d₁d₂d₃ scalars,

$\begin{array}{c}\hfill y_i=⟨{\mathcal{L}}^{\ast },{\mathcal{X}}_i⟩+\sigma {\xi }_i,\forall i\in [N],\end{array}(13)$

where ${\mathcal{X}}_i$’s are known (deterministic or random) design tensors, ξ_i’s are i. i.d. standard Gaussian noises, and σ is a known standard deviation constant measuring the noise level.

Let $\mathbf{y}={(y_1,\dots ,y_N)}^{\top }$ and $\xi ={({\xi }_1,\dots ,{\xi }_N)}^{\top }$ denote the collection of observations and noises. Define the design operator $\mathfrak{X}(\cdot )$ with adjoint operator ${\mathfrak{X}}^{\ast }(\cdot )$ as follows:

$\begin{array}{cc}\hfill & \forall \mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3},\mathfrak{X}(\mathcal{T})\hfill \\ \hfill & ≔{\left(⟨\mathcal{T},{\mathcal{X}}_1⟩,\cdots ,⟨\mathcal{T},{\mathcal{X}}_N⟩\right)}^{\top }\in {\mathbb{R}}^N,\hfill \\ \hfill \forall \mathbf{z}\in {\mathbb{R}}^N,{\mathfrak{X}}^{\ast }(\mathbf{z})& ≔\sum _{i=1}^N{z}_i{\mathcal{X}}_i\in {\mathbb{R}}^{d_1\times d_2\times d_3}.\hfill \end{array}(14)$

Then, the observation model (13) can be rewritten in the following compact form:

$\begin{array}{c}\hfill \mathbf{y}=\mathfrak{X}({\mathcal{L}}^{\ast })+\xi .\end{array}$

3.2.2 Two Typical Settings

With different settings of the design tensors $\{{\mathcal{X}}_i\}$, we consider two classical examples in this paper:

• Tensor completion. In tensor completion, the design tensors $\{{\mathcal{X}}_i\}$ are i. i.d. random tensor bases drawn from uniform distribution on the canonical basis in the space of d₁ × d₂ × d₃ tensors $\left\{{\mathbf{e}}_i◦{\mathbf{e}}_j◦{\mathbf{e}}_k,\forall (i,j,k)\in [d_1]\times [d_2]\times [d_3]\right\}$, where e_i denotes the vector whose ith entry is 1 with all the other entries 0 and ◦ denotes the tensor outer product [18].

• Tensor compressive sensing. When $\mathfrak{X}$ is a random Gaussian design, Model (13) is the tensor compressive sensing model with Gaussian measurements [24]. $\mathfrak{X}$ is named a random Gaussian design when $\{{\mathcal{X}}_i\}$ are random tensors with i. i.d. standard Gaussian entries [22].

3.2.3 The Proposed Estimator

The goal of this paper is to recover the unknown low-rank tensor ${\mathcal{L}}^{\ast }$ from noisy linear observations y satisfying the observation model (13).

Inspired by the capability of the newly defined T2NN in simultaneously modeling low-rankness in both spectral and original domains, we define the T2NN penalized least squares estimator $\widehat{\mathcal{L}}$ to estimate the unknown truth ${\mathcal{L}}^{\ast }$,

$\begin{array}{c}\hfill \widehat{\mathcal{L}}\in \underset{\mathcal{L}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2^2+\lambda \Vert \mathcal{L}{\Vert }_{\text{t}2\text{nn}},\end{array}(15)$

where the squared l₂-norm is adopted as the fidelity term for Gaussian noises, the proposed T2NN is used to impose both spectral and original low-rankness in the solution, and λ is a penalization parameter which balances the residual fitting accuracy and the parameter complicity (characterized by low-rankness) of the model.

Given the estimator $\widehat{\mathcal{L}}$ in Eq. 15, one may naturally ask how well it can estimate the truth ${\mathcal{L}}^{\ast }$ and how to compute it. In the following two sections, we first study the estimation performance of $\widehat{\mathcal{L}}$ by upper bounding its estimation error and then develop an ADMM-based algorithm to efficiently compute it.

4 Statistical Guarantee

In this section, we first come up with a deterministic upper bound of the estimation error and then establish non-asymptotic error bounds for the special cases of tensor compressive sensing with random Gaussian design and noisy tensor completion.

First, to describe the low-rankness of ${\mathcal{L}}^{\ast }$, we consider both its low-tubal-rank and low-Tucker-rank structures as follows:

• `Low-tubal-rank structure: Let $r_{\text{tb}}^{\ast }$ denote the tubal rank of ${\mathcal{L}}^{\ast }$. Suppose it has reduced t-SVD ${\mathcal{L}}^{\ast }=\mathcal{U}\ast \mathcal{S}\ast {\mathcal{V}}^{\top }$, where $\mathcal{U}\in {\mathbb{R}}^{d_1\times r_{\text{tb}}^{\ast }\times d_3},{\mathcal{V}}^{\top }\in {\mathbb{R}}^{d_2\times r_{\text{tb}}^{\ast }\times d_3}$ are orthogonal tensors and $\mathcal{S}\in {\mathbb{R}}^{r_{\text{tb}}^{\ast }\times r_{\text{tb}}^{\ast }\times d_3}$ is f-diagonal. Then, following [25], we define the following projections of any tensor $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$:

$\begin{array}{cc}\hfill & P^{\perp }(\mathcal{T})≔(\mathcal{I}-\mathcal{U}\ast {\mathcal{U}}^{\top })\ast \mathcal{T}\ast (\mathcal{I}-\mathcal{V}\ast {\mathcal{V}}^{\top })\text{and}P(\mathcal{T})=\mathcal{T}-P^{\perp }(\mathcal{T})\hfill \end{array}(16)$

where $\mathcal{I}$ denotes the identity tensor of appropriate dimensionality.

• Low-Tucker-rank structure: Let ${\mathbf{r}}_{\text{tk}}^{\ast }={(r_1^{\ast },r_2^{\ast },r_3^{\ast })}^{\top }$ denote the Tucker rank of ${\mathcal{L}}^{\ast }$, i.e., $r_k^{\ast }=\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{L}}_{(k)}^{\ast })$. Then, we have the reduced SVD factorization ${\mathbf{T}}_{(k)}={\mathbf{U}}_k{\mathbf{S}}_k{{\mathbf{V}}_k}^{\top }$, where ${\mathbf{U}}_k\in {\mathbb{R}}^{d_k\times r_k^{\ast }}$ and ${\mathbf{V}}_k\in {\mathbb{R}}^{(d_{\backslash k})\times r_k^{\ast }}$ are orthogonal and ${\mathbf{S}}_k\in {\mathbb{R}}^{r_k^{\ast }\times r_k^{\ast }}$ is diagonal. Let $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ be an arbitrary tensor. Similar to [22], we define the following two projections for any mode k = 1, 2, 3:

$\begin{array}{cc}\hfill P_k^{\perp }(\mathcal{T})& =(\mathbf{I}-{\mathbf{U}}_k{{\mathbf{U}}_k}^{\top }){\mathbf{T}}_{(k)}(\mathbf{I}-{\mathbf{V}}_k{{\mathbf{V}}_k}^{\top })\text{and}\hfill \\ \hfill P_k(\mathcal{T})& ={\mathbf{T}}_{(k)}-P_k^{\perp }(\mathcal{T}),\hfill \end{array}(17)$

where I denotes the identity matrix of appropriate dimensionality.

4.1 A Deterministic Bound on the Estimation Error

Before bounding the Frobenius-norm error $\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}$, the particularity of the error tensor $\mathrm{\Delta }≔\widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }$ is first characterized by a certain choice of regularization parameter λ involving the dual T2NN norm in the following proposition.

Proposition 1. By setting the regularization parameter $\lambda \ge 2\sigma \Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$, we have

(I) rank inequality:

$\begin{array}{cc}\hfill & {\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(P(\mathrm{\Delta }))\le 2r_{\text{tb}}^{\ast },\mathrm{a}\mathrm{n}\mathrm{d}\hfill \\ \hfill & \mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(P_k(\mathrm{\Delta }))\le 2r_k^{\ast },k=\mathrm{1,2,3},\hfill \end{array}(18)$

(II) sum of norms inequality:

$\begin{array}{cc}\hfill & \gamma \Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }\hfill \\ \hfill & \le 3\left(\gamma \Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right),\hfill \end{array}(19)$

(III) an upper bound on the “observed” error:

$\begin{array}{c}\hfill \Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2\le 3\left(\gamma \sqrt{2r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{2r_k^{\ast }}\right)\Vert \mathrm{\Delta }{\Vert }_{\text{F}}.\end{array}(20)$

Proof of Proposition 1. The proof is given as follows:Proof of Part (I): According to the definition of $P(\mathcal{T})$ in Eq. 16, we have

$\begin{array}{cc}\hfill P(\mathcal{T})=\mathcal{T}-P^{\perp }(\mathcal{T})& =\mathcal{U}\ast {\mathcal{U}}^{\top }\ast \mathcal{T}+\mathcal{T}\ast \mathcal{V}\ast {\mathcal{V}}^{\top }\hfill \\ \hfill & -\mathcal{U}\ast {\mathcal{U}}^{\top }\ast \mathcal{T}\ast \mathcal{V}\ast {\mathcal{V}}^{\top },\hfill \\ \hfill & =\mathcal{U}\ast {\mathcal{U}}^{\top }\ast \mathcal{T}+(\mathcal{I}-\mathcal{U}\ast {\mathcal{U}}^{\top })\hfill \\ \hfill & \ast \mathcal{T}\ast \mathcal{V}\ast {\mathcal{V}}^{\top }.\hfill \end{array}$

Due to the facts that ${\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{A}\ast \mathcal{B})\le \max \{{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{A}),{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{B})\}$, ${\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{A}+\mathcal{B})\le {\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{A})+{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{B})$ [26], and ${\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{U})={\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{V})=r_{\text{tb}}^{\ast }$, we have

$\begin{array}{c}\hfill {\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(P(\mathcal{T}))\le {\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{U}\ast {\mathcal{U}}^{\top }\ast \mathcal{T})+{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}((\mathcal{I}-\mathcal{U}\ast {\mathcal{U}}^{\top })\ast \mathcal{T}\ast \mathcal{V}\ast {\mathcal{V}}^{\top })\le 2r_{\text{tb}}^{\ast }.\end{array}$

Also, according to the definition of $P(\mathcal{T})$ in Eq. 17, we have

$\begin{array}{cc}\hfill P_k(\mathcal{T})={\mathbf{T}}_{(k)}-P_k^{\perp }(\mathcal{T})& ={\mathbf{U}}_k{\mathbf{U}}_k^{\top }{\mathbf{T}}_{(k)}+{\mathbf{T}}_{(k)}{\mathbf{V}}_k{\mathbf{V}}_k^{\top }\hfill \\ \hfill & -{\mathbf{U}}_k{\mathbf{U}}_k^{\top }{\mathbf{T}}_{(k)}{\mathbf{V}}_k{\mathbf{V}}_k^{\top }\hfill \\ ={\mathbf{U}}_k{\mathbf{U}}_k^{\top }{\mathbf{T}}_{(k)}+(\mathbf{I}-{\mathbf{U}}_k{\mathbf{U}}_k^{\top })\hfill \\ \times {\mathbf{T}}_{(k)}{\mathbf{V}}_k{\mathbf{V}}_k^{\top }.\hfill \end{array}$

Due to the facts that $\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{A}\mathbf{B})\le \max \{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{A}),\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{B})\}$, $\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{A}+\mathbf{B})\le \mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{A})+\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{B})$ [26], and $\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{U}}_k)=\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{V}}_k)=r_k^{\ast }$, we have

$\begin{array}{cc}\hfill & \mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(P_k(\mathcal{T}))\le \mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{U}}_k{\mathbf{U}}_k^{\top }\ast {\mathbf{T}}_{(k)})\hfill \\ \hfill & +\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}((\mathbf{I}-{\mathbf{U}}_k{\mathbf{U}}_k^{\top }){\mathbf{T}}_{(k)}{\mathbf{V}}_k{\mathbf{V}}_k^{\top })\le 2r_k^{\ast }.\hfill \end{array}$

Proof of Part (II) and Part (III): The optimality of $\widehat{\mathcal{L}}$ to Problem Eq. 15 indicates

$\begin{array}{c}\hfill \frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\widehat{\mathcal{L}}){\Vert }_2^2+\lambda \Vert \widehat{\mathcal{L}}{\Vert }_{\text{t}2\text{nn}}\le \frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}({\mathcal{L}}^{\ast }){\Vert }_2^2+\lambda \Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{t}2\text{nn}}.\end{array}$

By the definition of the error tensor $\mathrm{\Delta }≔\widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }$, we can get $\mathfrak{X}(\widehat{\mathcal{L}})=\mathfrak{X}({\mathcal{L}}^{\ast })+\mathfrak{X}(\mathrm{\Delta })$, which leads to

$\begin{array}{cc}\hfill & \frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}({\mathcal{L}}^{\ast })-\mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2-\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}({\mathcal{L}}^{\ast }){\Vert }_2^2\hfill \\ \hfill & \le \lambda \Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{t}2\text{nn}}-\lambda \Vert \widehat{\mathcal{L}}{\Vert }_{\text{t}2\text{nn}}.\hfill \end{array}$

The definition that $\sigma \xi =\mathbf{y}-\mathfrak{X}({\mathcal{L}}^{\ast })$ yields

$\begin{array}{cc}\hfill & \frac{1}{2}\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2\le ⟨\mathfrak{X}(\mathrm{\Delta }),\sigma \xi ⟩+\lambda (\Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{t}2\text{nn}}-\Vert \widehat{\mathcal{L}}{\Vert }_{\text{t}2\text{nn}})\hfill \\ \hfill & \le ⟨{\mathfrak{X}}^{\ast }(\xi ),\mathrm{\Delta }⟩+\lambda (\Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{t}2\text{nn}}-\Vert \widehat{\mathcal{L}}{\Vert }_{\text{t}2\text{nn}}),\hfill \end{array}$

where the last inequality holds due to the definition of the adjoint operator ${\mathfrak{X}}^{\ast }(\cdot )$.According to the definition and upper bound of the dual T2NN norm in Lemma 1 and Lemma 2, we obtain

$\begin{array}{c}\hfill \frac{1}{2}\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2\le \sigma \Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }\Vert \mathrm{\Delta }{\Vert }_{\text{t}2\text{nn}}+\lambda (\Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{t}2\text{nn}}^{\ast }-\Vert \widehat{\mathcal{L}}{\Vert }_{\text{t}2\text{nn}}).\end{array}(21)$

According to the decomposibility of TNN (see the supplementray material of [25]) and the decomposibility of matrix nuclear norm [27], one has

$\begin{array}{cc}\hfill \Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-\Vert \widehat{\mathcal{L}}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}& =\Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-\Vert {\mathcal{L}}^{\ast }+\mathrm{\Delta }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\hfill \\ \hfill & =\Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-‖\left({\mathcal{L}}^{\ast }+P^{\perp }(\mathrm{\Delta })\right)+P(\mathrm{\Delta })‖\hfill \\ \hfill & \le \Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-\left(\Vert {\mathcal{L}}^{\ast }+P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\right.\left.-\Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\right)\hfill \\ \hfill & =\Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-\left(\Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+\Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\right.\left.-\Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\right)\hfill \\ \hfill & =\Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}-\Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\hfill \end{array}$

and

$\begin{array}{cc}\hfill \Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }-\Vert {\widehat{\mathbf{L}}}_{(k)}{\Vert }_{\ast }& =\Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }-\Vert {\mathbf{L}}_{(k)}^{\ast }+{\widehat{\mathrm{\Delta }}}_{(k)}^{\ast }{\Vert }_{\ast }\hfill \\ \hfill & =\Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }-\Vert \left({\mathbf{L}}_{(k)}^{\ast }+P_k^{\perp }(\mathrm{\Delta })\right)+P_k(\mathrm{\Delta }){\Vert }_{\ast }\hfill \\ \hfill & \le \Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }-\left(\Vert {\mathbf{L}}_{(k)}^{\ast }+P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }\right.\left.-\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & =\Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }-\left(\Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }+\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }\right.\left.-\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & =\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }-\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }.\hfill \end{array}$

Then, we obtain

$\begin{array}{cc}\hfill & \Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{t}2\text{nn}}-\Vert \widehat{\mathcal{L}}{\Vert }_{\text{t}2\text{nn}}\hfill \\ \hfill & \le \left(\gamma \Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & -\left(\gamma \Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }\right).\hfill \end{array}(22)$

Using the definition of T2NN and triangular inequality yields

$\begin{array}{cc}\hfill & \Vert \mathrm{\Delta }{\Vert }_{\text{t}2\text{nn}}\hfill \\ \hfill & \le \left(\gamma \Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & +\left(\gamma \Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }\right).\hfill \end{array}(23)$

Further using the setting $\lambda \ge 2\sigma \Vert {\mathfrak{X}}^{\ast }(\mathbf{m}\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$ yields Part (III),

$\begin{array}{cc}\hfill & \frac{1}{2}\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2\hfill \\ \hfill & \stackrel{(i)}{\le }\frac{3\lambda }{2}\left(\gamma \Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & -\frac{\lambda }{2}\left(\gamma \Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & \le \frac{3\lambda }{2}\left(\gamma \Vert P(\mathrm{\Delta }){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k(\mathrm{\Delta }){\Vert }_{\ast }\right)\hfill \\ \hfill & \stackrel{(ii)}{\le }\frac{3\lambda }{2}\left(\gamma \sqrt{2r_{\text{tb}}^{\ast }}\Vert P(\mathrm{\Delta }){\Vert }_{\text{F}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{2r_k^{\ast }}\Vert P_k(\mathrm{\Delta }){\Vert }_{\text{F}}\right)\hfill \\ \hfill & \stackrel{(iii)}{\le }\frac{3\lambda }{2}\left(\gamma \sqrt{2r_{\text{tb}}^{\ast }}\Vert \mathrm{\Delta }{\Vert }_{\text{F}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{2r_k^{\ast }}\Vert \mathrm{\Delta }{\Vert }_{\text{F}}\right)\hfill \\ \hfill & =\frac{3\lambda }{2}\left(\gamma \sqrt{2r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{2r_k^{\ast }}\right)\Vert \mathrm{\Delta }{\Vert }_{\text{F}},\hfill \end{array}$

where by combing (i) and $\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2\ge 0$, Part (II) can be directly proved; inequality (ii) holds due to the compatible inequality of TNN and matrix nuclear norm, i.e., $\Vert \mathcal{T}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\le \sqrt{{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}(\mathcal{T})}\Vert \mathcal{T}{\Vert }_{\text{F}}$ [25] and $\Vert \mathbf{T}{\Vert }_{\ast }\le \sqrt{\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}(\mathbf{T})}\Vert \mathbf{T}{\Vert }_{\text{F}}$ [27], and Iiequality (iii) holds because one can easily verify the facts that $\Vert P(\mathrm{\Delta }){\Vert }_{\text{F}}^2=\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2-\Vert P^{\perp }(\mathrm{\Delta }){\Vert }_{\text{F}}^2\le \Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2$ [25] and $\Vert P_k(\mathrm{\Delta }){\Vert }_{\text{F}}^2=\Vert {\mathrm{\Delta }}_{(k)}{\Vert }_{\text{F}}^2-\Vert P_k^{\perp }(\mathrm{\Delta }){\Vert }_{\text{F}}^2\le \Vert {\mathrm{\Delta }}_{(k)}{\Vert }_{\text{F}}^2=\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2$ [27].Note that inequality (20) gives an upper bound on the $\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2$, which can be seen as the “observed” error. However, we are more concerned about upper bounds on the error itself ‖Δ‖_F rather than its observed version. The following assumption builds a bridge between $\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2$ and ‖Δ‖_F.

Assumption 1 (RSC condition). The observation operator $\mathfrak{X}(\cdot )$ is said to satisfy the Restricted Strong Convexity (RSC) condition with parameter κ if the following inequality holds:

$\begin{array}{c}\hfill \Vert \mathfrak{X}(\mathcal{T}){\Vert }_2^2\ge \kappa \Vert \mathcal{T}{\Vert }_{\text{F}}^2,\end{array}(24)$

for any $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ belong to the restricted direction set,

$\begin{array}{cc}\hfill \mathsf{C}& ≔\left\{\left.\mathcal{T}\right|\gamma \Vert P^{\perp }(\mathcal{T}){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k^{\perp }(\mathcal{T}){\Vert }_{\ast }\right.\hfill \\ \hfill & \left.\le 3\left(\gamma \Vert P(\mathcal{T}){\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert P_k(\mathcal{T}){\Vert }_{\ast }\right)\right\}.\hfill \end{array}(25)$

Then, a straightforward combination of Proposition 1 and Assumption 1 leads to an deterministic bound on the estimation error.

Theorem 1. By setting the regularization parameter $\lambda \ge 2\sigma \Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$, we have the following error bound for any solution $\widehat{\mathcal{L}}$ to Problem (15):

$\begin{array}{c}\hfill \Vert {\mathcal{L}}^{\ast }-\widehat{\mathcal{L}}{\Vert }_{\text{F}}\le \frac{3\sqrt{2}}{\kappa }\lambda \left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{r_k^{\ast }}\right).\end{array}(26)$

Note that we do not require information for distribution of the noise ξ in Theorem 1, which indicates that Theorem 1 provides a deterministic bound for general noise type. The bound on the right-hand side of Eq. 26 is in terms of the quantity,

$\begin{array}{c}\hfill \gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{r_k^{\ast }},\end{array}$

which serves as a measure of structure complexity, reflecting the natural intuition that more complex structure causes larger error. The result is in consistent with the results for sum-of-norms-based estimators in [5, 22, 24, 28]. A more general analysis in [24, 28] indicates that the performance of sum-of-norms-based estimators are determined by all the structural complexities for a simultaneously structured signal, just as shown by the proposed bound (26).

4.2 Tensor Compressive Sensing

In this section, we consider tensor compressive sensing from random Gaussian design where $\{{\mathcal{X}}_i\}$’s are random tensors with i. i.d. standard Gaussian entries [22]. First, the RSC condition holds in random Gaussian design as shown in the following lemma.

Lemma 3 (RSC of random Gaussian design). If $\mathfrak{X}(\cdot ):{\mathbb{R}}^{d_1\times d_2\times d_3}\to {\mathbb{R}}^N$ is a random Gaussian design, then a version of the RSC condition is satisfied with probability at least 1–2 exp(−N/32) as follows:

$\begin{array}{cccc}\hfill \Vert \mathfrak{X}(\mathrm{\Delta })\Vert & \ge \frac{\sqrt{N}}{4}\Vert \mathrm{\Delta }{\Vert }_{\text{F}}-\frac{1}{16}\left(\frac{\sqrt{d_1{d}_3}+\sqrt{d_2{d}_3}}{\gamma }\right.\hfill & \hfill & \left.+\sum _{k=1}^3\frac{\sqrt{d_k}+\sqrt{d_{\backslash k}}}{{\alpha }_k(1-\gamma )}\right)\Vert \mathrm{\Delta }{\Vert }_{\text{t}2\text{nn}},\hfill \end{array}(27)$

for any tensor $\mathrm{\Delta }\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ in the restricted direction set $\mathsf{C}$ whose definition is given in Eq. 25.Proof of Lemma 3. The proof is analogous to that of Proposition 1 in [27]. The difference lies in how we lower bound the right hand side of (H.7) in [27], i.e.,

$\begin{array}{c}\hfill \mathbb{E}\left[\underset{\mathrm{\Theta }\in \mathcal{R}(t)}{\inf }\underset{\mathbf{u}\in {\mathbb{S}}^{N-1}}{\sup }{Y}_{\mathbf{u},\mathrm{\Theta }}\right],\end{array}(\mathrm{27a})$

where ${\mathbb{S}}^{N-1}≔\left\{\left.\mathbf{v}\in {\mathbb{R}}^N\right|\Vert \mathbf{v}{\Vert }_2=1\right\}$, $\mathcal{R}(t)=\{\left.\mathrm{\Theta }\in {\mathbb{R}}^{d_1\times d_2\times d_3}\right|\Vert \mathrm{\Theta }{\Vert }_{\text{F}}=1,\Vert \mathrm{\Theta }{\Vert }_{\text{t}2\text{nn}}\le t\}$, and

$\begin{array}{c}\hfill Y_{\mathbf{u},\mathrm{\Theta }}≔⟨\mathbf{g},\mathbf{u}⟩+⟨\mathcal{G},\mathrm{\Theta }⟩,\end{array}$

where random vector $\mathbf{g}\in {\mathbb{R}}^N$ and random tensor $\mathcal{G}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ are independent with i. i.d. $\mathcal{N}(\mathrm{0,1})$ entries.We bound the quantity in Eq. 27 as follows:

$\begin{array}{cc}\hfill \mathbb{E}\left[\underset{\mathrm{\Theta }\in \mathcal{R}(t)}{\inf }\underset{\mathbf{u}\in {\mathbb{S}}^{N-1}}{\sup }{Y}_{\mathbf{u},\mathrm{\Theta }}\right]& =\mathbb{E}\left[\underset{\mathbf{u}\in {\mathbb{S}}^{N-1}}{\sup }⟨\mathbf{g},\mathbf{u}⟩\right]+\mathbb{E}\left[\underset{\mathrm{\Theta }\in \mathcal{R}(t)}{\inf }⟨\mathcal{G},\mathrm{\Theta }⟩\right]\hfill \\ \hfill & =\mathbb{E}\left[\Vert \mathbf{g}{\Vert }_2\right]-\mathbb{E}\left[\underset{\mathrm{\Theta }\in \mathcal{R}(t)}{\sup }⟨\mathcal{G},\mathrm{\Theta }⟩\right]\hfill \\ \hfill & =\frac{1}{2}\sqrt{N}-t\mathbb{E}\left[\Vert \mathcal{G}{\Vert }_{\text{t}2\text{nn}}^{\ast }\right],\hfill \end{array}(28)$

where $\Vert \mathcal{G}{\Vert }_{\text{t}2\text{nn}}^{\ast }$ can be bounded according to Lemma 4. The rest of the proof follows that of Proposition 1 in [27].The remaining bound on $\Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$ is shown in the following Lemma.

Lemma 4 (bound on $\Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$). Let $\mathfrak{X}:{\mathbb{R}}^{d_1\times d_2\times d_3}\to {\mathbb{R}}^N$ be a random Gaussian design. With high probability, the quantity $\Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$ is concentrated around its mean, which can be bounded as follows:

$\begin{array}{c}\hfill \mathbb{E}[\Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }]\le c\sqrt{N}\left(\frac{\sqrt{d_1{d}_3}+\sqrt{d_2{d}_3}}{\gamma }+\sum _{k=1}^3\frac{\sqrt{d_k}+\sqrt{d_k}}{{\alpha }_k(1-\gamma )}\right).\end{array}(29)$

Proof. Since ξ_m’s are i. i.d. $\mathcal{N}(\mathrm{0,1})$ variables, we have

$\begin{array}{c}\hfill \Vert \xi {\Vert }_2\le 2\sqrt{N}\end{array}(\mathrm{29a})$

with high probability according to Proposition 8.1 in [29].For k = 1, 2, 3, let X^∗(ξ) (_k) be the mode-k unfolding of random tensor ${\mathfrak{X}}^{\ast }(\xi )$. A direct use of Lemma C.1 in [27] leads to

$\begin{array}{c}\hfill \mathbb{E}\left[\Vert {\mathbf{X}}^{\ast }{(\xi )}_{(k)}\Vert \right]\le c_0\sqrt{N}\left(\sqrt{d_k}+\sqrt{d_{\backslash k}}\right)\end{array}(30)$

with high probability. A similar argument of Lemma C.1 in [27] also yields

$\begin{array}{c}\hfill \mathbb{E}\left[\Vert {\mathfrak{X}}^{\ast }(\xi )\Vert \right]\le c_1\sqrt{N}(\sqrt{d_1{d}_3}+\sqrt{d_2{d}_3})\end{array}(31)$

with high probability. Combining Eqs 30, 31, we can complete the proof.Then, the non-asymptotic error bound is obtained finally as follows.

Theorem 2 (non-asymptotic error bound). Under the random Gaussian design setup, there are universal constants c₃, c₄, and c₅ such that for a sample size N greater than

$\begin{array}{cc}\hfill & c_3{\left(\frac{\sqrt{d_1{d}_3}+\sqrt{d_2{d}_3}}{\gamma }+\sum _{k=1}^3\frac{\sqrt{d_k}+\sqrt{d_{\backslash k}}}{{\alpha }_k(1-\gamma )}\right)}^2\hfill \\ \hfill & \times {\left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{r_k^{\ast }}\right)}^2\hfill \end{array}$

and any solution to Problem (15) with regularization parameter

$\begin{array}{c}\hfill \lambda =c_4\sigma \sqrt{N}\left(\frac{\sqrt{d_1{d}_3}+\sqrt{d_2{d}_3}}{\gamma }+\sum _{k=1}^3\frac{\sqrt{d_k}+\sqrt{d_{\backslash k}}}{{\alpha }_k(1-\gamma )}\right),\end{array}$

then we have

$\begin{array}{cc}\hfill \Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2& \le c_5{\sigma }^2{\left(\frac{\sqrt{d_1{d}_3}+\sqrt{d_2{d}_3}}{\gamma }+\sum _{k=1}^3\frac{\sqrt{d_k}+\sqrt{d_{\backslash k}}}{{\alpha }_k(1-\gamma )}\right)}^2\hfill \\ \hfill & \frac{{\left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{r_k^{\ast }}\right)}^2}{N},\hfill \end{array}(32)$

which holds with high probability.To understand the proposed bound, we consider the three-way cubical tensor ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d\times d\times d}$ with regularization weights γ = (1 − γ)α₁ = (1 − γ)α₂ = (1 − γ)α₃ = 1/4. Then, the bound in Eq. 52 is simplified to the following element-wise error:

$\begin{array}{c}\hfill \frac{\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2}{d^3}\le O\left({\sigma }^2\cdot \frac{1}{N}\cdot {\left(\sqrt{\frac{r_{\text{tb}}^{\ast }}{d}}+\sum _{k=1}^3\sqrt{\frac{r_k^{\ast }}{d}}\right)}^2\right),\end{array}(33)$

which means the estimation error is controlled by the tubal rank and Tucker rank of ${\mathcal{L}}^{\ast }$ simultaneously. From the right-hand side of Eq. 33, it can be seen that the more observations (i.e., the larger N), the smaller the error; it is also reflected that larger tensors with more complex structures will lead to larger errors. The interpretation is consistent with our intuition.Equation 33 also indicates the sample size N should satisfy

$\begin{array}{c}\hfill N\ge \mathrm{\Omega }\left({\left(\sqrt{r_{\text{tb}}^{\ast }}+\sum _{k=1}^3\sqrt{r_k^{\ast }}\right)}^2{d}^2\right)\end{array}(34)$

for approximate tensor sensing.Another interesting result is that by setting the noise level σ = 0 in Eq. 33, the upper bound reaches 0, which means the proposed estimator can exactly recover the unknown truth ${\mathcal{L}}^{\ast }$ in the noiseless setting.

4.3 Noisy Tensor Completion

For noisy tensor completion, we consider a slightly modified estimator,

$\begin{array}{c}\hfill \widehat{\mathcal{L}}\in \underset{\Vert \mathcal{L}{\Vert }_{\infty }\le \mathsf{a}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2^2+\lambda \Vert \mathcal{L}{\Vert }_{\text{t}2\text{nn}},\end{array}(35)$

where $\mathbf{m}\mathsf{a}>0$ is a known constant constraining the magnitude of entries in ${\mathcal{L}}^{\ast }$. The constraint $\Vert \mathcal{L}{\Vert }_{\infty }\le \mathsf{a}$ is very mild because real signals are all of limited magnitude, e.g., the intensity of pixels in visual light images cannot be greater than 255. The constraint also provides with theoretical continence in excluding the “spiky” tensors while controlling the identifiability of ${\mathcal{L}}^{\ast }$. Similar “non-spiky” constraints are also considered in related work [6, 16, 30].

We consider noisy tensor completion under uniform sampling in this section.

Assumption 2 (uniform sampling scheme). The design tensors $\{{\mathcal{X}}_i\}$ are i.i.d. random tensor bases drawn from uniform distribution Π on the set,

$\begin{array}{c}\hfill \left\{{\mathbf{e}}_i◦{\mathbf{e}}_j◦{\mathbf{e}}_k:\forall (i,j,k)\in [d_1]\times [d_2]\times [d_3]\right\}.\end{array}$

Recall that Proposition 1 in Section 4.1 gives an upper bound on the “observed part” of the estimation error $\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_{\text{F}}$. As our goal is to establish a bound on ‖Δ‖_F, we then connect $\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_{\text{F}}$ with ‖Δ‖_F by quantifying the probability of the following RSC property of the sampling operator $\mathfrak{X}$:

$\begin{array}{c}\hfill \frac{1}{N}\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_{\text{F}}^2\ge \frac{1}{2d_1{d}_2{d}_3}\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2-\mathrm{a}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m},\end{array}$

when the error tensor Δ belongs to some set $\mathbf{m}\mathsf{C}(\beta ,\mathbf{m}r)$ defined as

$\begin{array}{cc}\hfill \mathsf{C}(\beta ,r)& ≔\{\left.\mathrm{\Delta }\in {\mathbb{R}}^{d_1\times d_2\times d_3}\right|\Vert \mathrm{\Delta }{\Vert }_{\infty }\le 1,\frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}\ge \beta ,\hfill \\ \hfill & \Vert \mathrm{\Delta }{\Vert }_{\text{t}2\text{nn}}\le \left(\gamma \sqrt{r}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{r_k}\right)\Vert \mathrm{\Delta }{\Vert }_{\text{F}}\},\hfill \end{array}(36)$

where $\beta =\sqrt{\frac{64\log \tilde{d}}{N\log (6/5)}}$ is an F-norm tolerance parameter and mr = (r, r₁, r₂, r₃) is a rank parameter whose values will be specified in the sequel.

Lemma 5 (RSC condition under uniform sampling). For any $\mathrm{\Delta }\in \mathsf{C}(\beta ,r)$, it holds with probability at least $1-{(d_1{d}_3+d_2{d}_3)}^{-1}$ that

$\begin{array}{cc}\hfill \frac{1}{N}\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_{\text{F}}^2& \ge \frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{2d_1{d}_2{d}_3}-\frac{44d_1{d}_2{d}_3}{N^2}\mathbb{E}{\left[\Vert {\mathfrak{X}}^{\ast }(ϵ){\Vert }_{\text{t}2\text{nn}}^{\ast }\right]}^2\hfill \\ \hfill & \times {\left(\gamma \sqrt{r}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{r_k}\right)}^2,\hfill \end{array}(37)$

where e is the base of the natural logarithm, and the entries ϵ_i of vector $ϵ\in {\mathbb{R}}^N$ are i. i.d. Rademacher random variables.Before proving Lemma 5, we first define a subset of $\mathsf{C}(\beta ,r)$ by upper bounding the F-norm of any element Δ in it,

$\begin{array}{c}\hfill \mathsf{B}(r,T)≔\left\{\mathrm{\Delta }:\mathrm{\Delta }\in \mathsf{C}(\beta ,r),\frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}\le T\right\},\end{array}$

and a quantity

$\begin{array}{c}\hfill Z_T≔\underset{\mathrm{\Delta }\in \mathsf{B}(r,T)}{\sup }\left|\frac{\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2}{N}-\frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}\right|,\end{array}$

which is the maximal absolute deviation of $N^{-1}\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2$ from its expectation ${(d_1{d}_2{d}_3)}^{-1}\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2$ in $\mathsf{B}(r,T)$. Lemma 6 shows the concentration behavior of Z_T.

Lemma 6 (concentration of Z_T). There exists a constant c₀ such that

$\begin{array}{cc}\hfill & \mathbb{P}\left[Z_T\ge \frac{5}{12}T-\frac{44d_1{d}_2{d}_3}{N^2}\mathbb{E}{\left[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert \right]}^2\left(\gamma \sqrt{r}+(1-\gamma )\right.\right.\hfill \\ \hfill & \left.{\left.\times {\sum }_k{\alpha }_k\sqrt{r_k}\right)}^2\right]\le \exp (-c_{0}N{T}^2).\hfill \end{array}$

Proof of Lemma 6. The proof is similar to that of Lemma 10 in [31]. The difference lies in the step of symmetrization arguments. Note that for any $\mathrm{\Delta }\in \mathsf{B}(r,T)$, it holds that

$\begin{array}{c}\hfill \Vert \mathrm{\Delta }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\le \sqrt{d_1{d}_2{d}_{3}T}\left(\gamma \sqrt{r}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k}\right),\end{array}$

which indicates

$\begin{array}{cc}\hfill \mathbb{E}[Z_T]& \le 8\mathbb{E}\left[\underset{\mathrm{\Delta }\in \mathsf{B}(r,T)}{\sup }⟨{\mathfrak{X}}^{\ast }(ϵ),\mathrm{\Delta }⟩\right]\hfill \\ \hfill & \le 8\mathbb{E}\left[\underset{\mathrm{\Delta }\in \mathsf{B}(r,T)}{\sup }\frac{1}{d_3}\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert \Vert \mathrm{\Delta }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\right]\hfill \\ \hfill & \le 8\sqrt{d_1{d}_2{d}_{3}T}\mathbb{E}[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]\left(\gamma \sqrt{r}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k}\right).\hfill \end{array}$

Then, Lemma 5 can be proved by using the peeling argument [30].Proof of Lemma 5. For any positive integer l, we define disjoint subsets of $\mathsf{C}(\beta ,r)$ as

$\begin{array}{c}\hfill \mathsf{D}(r,l)≔\{\mathrm{\Delta }:\mathrm{\Delta }\in \mathsf{C}(\beta ,r),\beta {\rho }^{l-1}\le \frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}\le \beta {\rho }^l\}\end{array}$

with constants $\rho =\frac{6}{5}$ and $\beta =\sqrt{\frac{64\log \tilde{d}}{N\log \rho }}$. Let D = d₁d₂d₃ for simplicity, and define the event

$\begin{array}{cc}\hfill \mathfrak{E}& ≔\left\{\exists \mathrm{\Delta }\in \mathsf{C}(\beta ,r),\mathrm{s}.\mathrm{t}.\left|\frac{\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2}{N}-\frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{D}\right|\ge \frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{2D}\right.\hfill \\ \hfill & \left.+\frac{44D}{N^2}{\mathbb{E}}^2[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]{\left(\gamma \sqrt{r}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k}\right)}^2\right\}\hfill \end{array}$

and its sub-events for any $l\in {\mathbb{N}}_{+}$,

$\begin{array}{cc}\hfill {\mathfrak{E}}_l& ≔\left\{\exists \mathrm{\Delta }\in \mathsf{D}(r,l),\mathrm{s}.\mathrm{t}.\left|\frac{\Vert \mathfrak{X}(\mathrm{\Delta }){\Vert }_2^2}{N}-\frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{D}\right|\ge \frac{5}{12}\beta {\rho }^l\right.\hfill \\ \hfill & \left.+\frac{44D}{N^2}{\mathbb{E}}^2[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]{\left(\gamma \sqrt{r}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k}\right)}^2\right\}.\hfill \end{array}$

Note that Lemma 6 implies that

$\begin{array}{cc}\hfill \mathbb{P}[{\mathfrak{E}}_l]& ={\mathbb{P}}_{\mathrm{\Delta }\in \mathsf{C}(r,l)}\left[Z_T\ge \frac{5}{12}\beta {\rho }^l+\frac{44D}{N^2}{\mathbb{E}}^2[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]\right.\hfill \\ \hfill & \left.\times {\left(\gamma \sqrt{r}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k}\right)}^2\right]\hfill \\ \hfill & \le \exp (-c_{0}N{\beta }^2{\rho }^{2l}).\hfill \end{array}$

Thus, we have

$\begin{array}{cc}\hfill \mathbb{P}[\mathfrak{E}]\le \sum _{l=1}^{\infty }\mathbb{P}[{\mathfrak{E}}_l]& \le \sum _{l=1}^{\infty }\exp (-c_{0}N{\beta }^2{\rho }^{2l})\hfill \\ \hfill & \le \sum _{l=1}^{\infty }\exp (-2c_{0}N{\beta }^{2}l\log \rho )\hfill \\ \hfill & \le \frac{\exp (-c_{0}p{\beta }^2\log \rho )}{1-\exp (-c_{0}p{\beta }^2\log \rho )}.\hfill \end{array}$

Recall that $\beta =\sqrt{\frac{64\log \tilde{d}}{\log (6/5)N}}$, then $\mathbb{P}[\mathfrak{E}]\le 2/\tilde{d}$, which leads to the result of Lemma 5.Based on the RSC condition in Lemma 5, we are able to give an upper bound on the estimation error ‖Δ‖_F in the following proposition.

Proposition 2. With parameter $\lambda \ge 2\sigma \Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$, the estimation error satisfies

$\begin{array}{cc}\hfill & \frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}\hfill \\ \hfill & \le \max \left\{c_1\frac{d_1{d}_3{d}_3}{N^2}\left({\lambda }^2+{\mathsf{a}}^2\mathbb{E}{[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]}^2\right)\times \left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma )\right.\right.\hfill \\ \hfill & \left.{\left.{\sum }_k{\alpha }_k\sqrt{r_k^{\ast }}\right)}^2,c_2{\mathsf{a}}^2\sqrt{\frac{\log \tilde{d}}{N}}\right\}\hfill \end{array}(38)$

with probability at least $1-2{(d_1{d}_3+d_2{d}_3)}^{-1}$.Proof of Proposition 2. A direct consequence of property (II) in Proposition 1 and the triangular inequality is that the error tensor Δ satisfies

$\begin{array}{c}\hfill \Vert \mathrm{\Delta }{\Vert }_{\text{t}2\text{nn}}\le \left(\gamma \sqrt{32r_{\text{tb}}^{\ast }}+(1-\gamma )\sum _{k=1}^3{\alpha }_k\sqrt{32r_k^{\ast }}\right)\Vert \mathrm{\Delta }{\Vert }_{\text{F}}.\end{array}(39)$

Since $\Vert \widehat{\mathcal{L}}{\Vert }_{\infty }<\mathsf{a}$ and $\Vert {\mathcal{L}}^{\ast }{\Vert }_{\infty }<\mathsf{a}$, we also have $\Vert \mathrm{\Delta }{\Vert }_{\infty }\le \Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\infty }\le \Vert \widehat{\mathcal{L}}{\Vert }_{\infty }+\Vert {\mathcal{L}}^{\ast }{\Vert }_{\infty }<2\mathsf{a}$.Let ${\mathbf{r}}^{\ast }={(r_{\text{tb}}^{\ast },r_1^{\ast },r_2^{\ast },r_3^{\ast })}^{\top }$ denote the rank complexity of the underlying tensor ${\mathcal{L}}^{\ast }$. By discussing whether tensor $\frac{\mathrm{\Delta }}{2\mathsf{a}}$ is in set $\mathsf{C}(\beta ,32{\mathbf{r}}^{\ast })$, we consider the following cases.Case 1: If $\frac{\mathrm{\Delta }}{2\mathsf{a}}\notin \mathsf{C}(\beta ,32{\mathbf{r}}^{\ast })$, then from the definition of set $\mathsf{C}(\beta ,r)$, we have

$\begin{array}{c}\hfill \frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}\le 4{\mathsf{a}}^2\sqrt{\frac{64\log \tilde{d}}{\log (6/5)N}}.\end{array}(40)$

Case 2: If $\frac{\mathrm{\Delta }}{2\mathbf{m}\mathsf{a}}\in \mathsf{C}(\beta ,32{\mathbf{r}}^{\ast })$, then by Proposition 1 and Lemma 5, we have

$\begin{array}{c}\frac{{‖\frac{\mathrm{\Delta }}{2\mathsf{a}}‖}_{\mathrm{F}}^{\mathrm{2}}}{2D}-\frac{44\cdot 32D}{N^2}{\mathbb{E}}^2\left[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert \right]\times {\left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k^{\ast }}\right)}^2\hfill \\ \hfill & \le \frac{3\sqrt{2}\lambda }{N}\left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k^{\ast }}\right){‖\frac{\mathrm{\Delta }}{2\mathsf{a}}‖}_{\mathrm{F}}\hfill \end{array}(41)$

with probability at least $1-2{(d_1{d}_3+d_2{d}_3)}^{-1}$.By performing some algebra (like the proof of Theorem 3 in [30]), we have

$\begin{array}{cc}\hfill \frac{\Vert \mathrm{\Delta }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}& \le C\frac{d_1{d}_2{d}_3}{N^2}\left({\lambda }^2+{\mathsf{a}}^2{\mathbb{E}}^2[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]\right)\hfill \\ \hfill & \times {\left(\gamma \sqrt{r_{\text{tb}}^{\ast }}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k^{\ast }}\right)}^2.\hfill \end{array}(42)$

Combining Case 1 and Case 2, we obtain the result of Proposition 2. According to Proposition 2 and Lemma 5, it remains to bound $\Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$ and $\mathbb{E}[\Vert {\mathfrak{X}}^{\ast }(ϵ){\Vert }_{\text{t}2\text{nn}}^{\ast }]$. The following lemmas give their bounds respectively. As the noise variables {ξ_i} are i. i.d. standard Gaussian, it belongs to the sub-exponential distribution [32], and thus, there exists a constant ϱ as the smallest number satisfying [30]

$\begin{array}{c}\hfill \underset{i\le N}{\max }\mathbb{E}\left[e^{\frac{|{\xi }_i|}{\varrho }}\right]\le e.\end{array}(43)$

Suppose the sample complexity N in noisy tensor completion satisfies

$\begin{array}{cc}\hfill N& \ge \max \{d_1{d}_3\vee d_2{d}_3,\underset{k}{\max }(d_k\vee d_{\backslash k})\}\hfill \\ \hfill N& \ge 2(d_1\wedge d_2){\varrho }^2{\log }^2(\varrho \sqrt{d_1\wedge d_2})\log (d_1{d}_3+d_2{d}_3)\hfill \\ \hfill N& \ge \underset{k\le 3}{\max }2(d_k\wedge d_{\backslash k}){\varrho }^2{\log }^2(\varrho \sqrt{d_k\wedge d_{\backslash k}})\log (d_k+d_{\backslash k})\hfill \\ \hfill N& \ge 2(d_1\wedge d_2){\log }^2(\sqrt{d_1\wedge d_2})\log (d_1{d}_3+d_2{d}_3)\hfill \\ \hfill N& \ge \underset{k\le 3}{\max }2(d_k\wedge d_{\backslash k}){\log }^2(\sqrt{d_k\wedge d_{\backslash k}})\log (d_k+d_{\backslash k}).\hfill \end{array}(44)$

Then, we have the following Lemma 7 and Lemma 8 to bound $\Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }$ and $\mathbb{E}[\Vert {\mathfrak{X}}^{\ast }(ϵ){\Vert }_{\text{t}2\text{nn}}^{\ast }]$.

Lemma 7. Under the sample complexity of noisy tensor completion in Eq. 44, it holds with probability at least $1-{(d_1{d}_3+d_2{d}_3)}^{-1}-{\sum }_k{(d_k+d_{\backslash k})}^{-1}$ that

$\begin{array}{cc}\hfill \Vert {\mathfrak{X}}^{\ast }(\xi ){\Vert }_{\text{t}2\text{nn}}^{\ast }& \le C_{\varrho }\sqrt{N}\left(\frac{1}{\gamma }\sqrt{\frac{\log (d_1{d}_3+d_2{d}_3)}{d_1\wedge d_2}}+\frac{1}{(1-\gamma )}\right.\hfill \\ \hfill & \left.\times \sum _{k=1}^3\frac{1}{{\alpha }_k}\sqrt{\frac{\log (d_k+d_{\backslash k})}{d_k\wedge d_{\backslash k}}}\right),\hfill \end{array}(45)$

where C_ϱ is a constant dependent on the ϱ that is defined in Eq. 43.Proof of Lemma 7. The proof can be straightforwardly obtained by adopting the upper bound of the dual T2NN norm in Lemma 2 and Lemma 5 in the supplementary material of [25], and Lemma 5 in [30] as follows:

• First, Lemma 5 in the supplementary material of [25] shows that letting N ≥ d₁d₃ ∨ d₂d₃ and $N\ge 2(d_1\wedge d_2){\varrho }^2{\log }^2(\varrho \sqrt{d_1\wedge d_2})\log (d_1{d}_3+d_2{d}_3)$, then it holds with probability at least $1-{(d_1{d}_3+d_2{d}_3)}^{-1}$ that

$\begin{array}{c}\hfill \Vert {\mathfrak{X}}^{\ast }(\xi )\Vert \le C_{\varrho }\sqrt{N{(d_1\wedge d_2)}^{-1}\log (d_1{d}_3+d_2{d}_3)}.\end{array}(46)$

• For k = 1, 2, 3, let X^∗(ξ) (_k) be the mode-k unfolding of random tensor ${\mathfrak{X}}^{\ast }(\xi )$. Then, Lemma 5 in [30] indicates that letting N ≥ d_k ∨ (d_\k) and $N\ge 2(d_k\wedge (d_{\backslash k})){\varrho }^2{\log }^2(\varrho \sqrt{d_k\wedge d_{\backslash k}})\log (d_k+d_{\backslash k})$, then it holds with probability at least $1-{(d_k+d_{\backslash k})}^{-1}$ that

$\begin{array}{c}\hfill \Vert {\mathbf{X}}^{\ast }{(\xi )}_{(k)}\Vert \le C_{\varrho }^{\prime }\sqrt{N{(d_k\wedge d_{\backslash k})}^{-1}\log (d_k+d_{\backslash k})}.\end{array}(47)$

Then, combining Eq. 46 and 47 and using union bound, Eq. 45 can be obtained.

Lemma 8. Under the sample complexity of noisy tensor completion in Eq. 44, it holds that

$\begin{array}{cc}\hfill \mathbb{E}[\Vert {\mathfrak{X}}^{\ast }(ϵ){\Vert }_{\text{t}2\text{nn}}^{\ast }]& \le C\sqrt{N}\left(\frac{1}{\gamma }\sqrt{\frac{\log (d_1{d}_3+d_2{d}_3)}{d_1\wedge d_2}}+\frac{1}{(1-\gamma )}\right.\hfill \\ \hfill & \left.\times \sum _{k=1}^3\frac{1}{{\alpha }_k}\sqrt{\frac{\log (d_k+d_{\backslash k})}{d_k\wedge d_{\backslash k}}}\right).\hfill \end{array}(48)$

Proof of Lemma 8. Similar to the proof of Lemma 7, the proof can be straightforwardly obtained by adopting the upper bound of the dual T2NN norm in Lemma 2 and Lemma 6 in the supplementary material of [25], and Lemma 6 in [30].

• First, Lemma 6 in the supplementary material of [25] shows that letting N ≥ d₁d₃ ∨ d₂d₃ and N ≥ 2 (d₁ ∧ d₂) log² (d₁ ∧ d₂) log (d₁d₃ + d₂d₃), then, the following inequality holds:

$\begin{array}{c}\hfill \mathbb{E}[\Vert {\mathfrak{X}}^{\ast }(ϵ)\Vert ]\le C_2\sqrt{N{(d_1\wedge d_2)}^{-1}\log (d_1{d}_3+d_2{d}_3)}.\end{array}(49)$

• For k = 1, 2, 3, let X∗(ϵ) (_k) be the mode-k unfolding of random tensor ${\mathfrak{X}}^{\ast }(ϵ)$. Then, Lemma 6 in [30] indicates that letting N ≥ d_k ∨ d_\k and N ≥ 2 (d_k ∧ d_\k) log² (d_k ∧ d_\,k) log (d_k + d_\k), then, the following inequality holds:

$\begin{array}{c}\hfill \mathbb{E}[\Vert {\mathbf{X}}^{\ast }{(ϵ)}_{(k)}\Vert ]\le C_2^{\prime }\sqrt{N{(d_k\wedge d_{\backslash k})}^{-1}\log (d_k+d_{\backslash k})}.\end{array}(50)$

Then, Eq. 48 can be obtained by combining Eqs. 49 and 50.Further combining Lemma 7, Lemma 8, and Proposition 2, we arrive at an upper bound on the estimation error in the follow theorem.

Theorem 3. Suppose Assumption 2 is satisfied and $\Vert {\mathcal{L}}^{\ast }{\Vert }_{\infty }\le \mathsf{a}$. Let the sample size N satisfies Eq. 44. By setting

$\begin{array}{cc}\hfill \lambda & =C_{\varrho }\sigma \sqrt{N}\left(\frac{1}{\gamma }\sqrt{\frac{\log (d_1{d}_3+d_2{d}_3)}{d_1\wedge d_2}}\right.\hfill \\ \hfill & \left.+\frac{1}{(1-\gamma )}\sum _{k=1}^3\frac{1}{{\alpha }_k}\sqrt{\frac{\log (d_k+d_{\backslash k})}{d_k\wedge d_{\backslash k}}}\right),\hfill \end{array}(51)$

the estimation error of any estimator $\widehat{\mathcal{L}}$ defined in Problem (35) can be upper bounded as follows:

$\begin{array}{cc}\hfill \frac{\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2}{d_1{d}_2{d}_3}& \le c_2\max \left\{{\mathsf{a}}^2\sqrt{\frac{\log \tilde{d}}{N}},\frac{d_1{d}_2{d}_3({\sigma }^2\vee {\mathsf{a}}^2)}{N}\right.\hfill \\ \hfill & \times {\left(\gamma \sqrt{r^{\ast }}+(1-\gamma ){\sum }_k{\alpha }_k\sqrt{r_k^{\ast }}\right)}^2\hfill \\ \hfill & \cdot \left(\frac{1}{\gamma }\sqrt{\frac{\log (d_1{d}_3+d_2{d}_3)}{d_1\wedge d_2}}+\frac{1}{(1-\gamma )}\right.\hfill \\ \hfill & \left.{\left.\times \sum _{k=1}^3\frac{1}{{\alpha }_k}\sqrt{\frac{\log (d_k+d_{\backslash k})}{d_k\wedge d_{\backslash k}}}\right)}^2\right\}.\hfill \end{array}(52)$

with probability at least $1-3{(d_1{d}_3+d_2{d}_3)}^{-1}-{\sum }_k{(d_k+d_{\backslash k})}^{-1}$.To understand the proposed bound in Theorem 3, we consider the three-way cubical tensor ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d\times d\times d}$ with regularization weights γ = (1 − γ)α₁ = (1 − γ)α₂ = (1 − γ)α₃ = 1/4. Then, the bound in Eq. 52 is simplified to the following element-wise error:

$\begin{array}{cc}\hfill & \frac{\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2}{d^3}\le O\left(\frac{d^3}{N}\cdot {(\sigma \vee \mathsf{a})}^2\cdot {\left(\sqrt{\frac{r^{\ast }}{d}}+\sum _{k=1}^3\sqrt{\frac{r_k^{\ast }}{d}}\right)}^2\log d\right),\hfill \end{array}(53)$

which means the estimation error is controlled by the tubal rank and Tucker rank of ${\mathcal{L}}^{\ast }$ simultaneously. Equation 53 also indicates that the sample size N should satisfy

$\begin{array}{c}\hfill N\ge \mathrm{\Omega }\left({\left(\sqrt{r^{\ast }}+\sum _{k=1}^3\sqrt{r_k^{\ast }}\right)}^2{d}^2\log d\right)\end{array}(54)$

for approximate tensor completion.

5 Optimization Algorithm

The ADMM framework [33] is applied to solve the proposed model. Adding auxiliary variables $\mathcal{K}$ and ${\mathcal{T}}^1,{\mathcal{T}}^2,{\mathcal{T}}^3$ to Problem (15) yields an equivalent formulation,

$\begin{array}{cc}\hfill \underset{\mathcal{L},\mathcal{K},{\{{\mathcal{T}}^k\}}_k}{\min }& \frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2^2+\lambda \gamma \Vert \mathcal{K}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+\lambda (1-\gamma )\hfill \\ \hfill & \times \sum _{k=1}^3{\alpha }_k\Vert {\mathbf{T}}_{(k)}^k{\Vert }_{\ast }\hfill \\ \hfill \text{s.t.\hspace{0.17em}}& \mathcal{K}=\mathcal{L};{\mathcal{T}}^k=\mathcal{L},k=\mathrm{1,2,3}.\hfill \end{array}(55)$

To solve Problem (55), an ADMM-based algorithm is proposed. First, the augmented Lagrangian is

$\begin{array}{cc}\hfill & L_{\rho }(\mathcal{L},\mathcal{K},{\{{\mathcal{T}}^k\}}_k,\mathcal{A},{\{{\mathcal{B}}^k\}}_k)=\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2^2+\lambda \gamma \Vert \mathcal{K}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\hfill \\ \hfill & +⟨\mathcal{A},\mathcal{K}-\mathcal{L}⟩+\frac{\rho }{2}\Vert \mathcal{K}-\mathcal{L}{\Vert }_{\text{F}}^2\hfill \\ \hfill & +\lambda (1-\gamma )\sum _{k=1}^3\left({\alpha }_k\Vert {\mathbf{T}}_{(k)}^k{\Vert }_{\ast }+⟨{\mathcal{B}}^k,{\mathcal{T}}^k-\mathcal{L}⟩\right.\left.+\frac{\rho }{2}\Vert {\mathcal{T}}^k-\mathcal{L}{\Vert }_{\text{F}}^2\right),\hfill \end{array}(56)$

where tensors $\mathcal{A}$ and ${\{{\mathcal{B}}^k\}}_k$ are the dual variables.

The primal variables $\mathcal{L},\mathcal{K}$, and ${\mathcal{T}}^k$ can be divided into two blocks: The first block has one tensor variable $\mathcal{L}$, whereas the second block consists of four variables $\mathcal{K}$ and ${\mathcal{T}}^k$’s. We use the minimization scheme of ADMM to update the two blocks alternatively after the tth iteration (t = 0, 1, ⋯):

Update the first block $\mathcal{L}$: We update $\mathcal{L}$ by solving following $\mathcal{L}$-subproblem with all the other variables fixed:

$\begin{array}{cc}\hfill & {\mathcal{L}}^{t+1}\hfill \\ \hfill & =\underset{\mathcal{L}}{\mathrm{argmin}}{L}_{\rho }(\mathcal{L},{\mathcal{K}}^t,{\{{({\mathcal{T}}^k)}^t\}}_k,{\mathcal{A}}^t,{\{{({\mathcal{B}}^k)}^t\}}_k)\hfill \\ \hfill & =\underset{\mathcal{L}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2^2+\frac{\rho }{2}\Vert {\mathcal{K}}^t+{\rho }^{-1}{\mathcal{A}}^t-\mathcal{L}{\Vert }_{\text{F}}^2\hfill \\ \hfill & +\sum _{k=1}^3\frac{\rho }{2}\Vert {({\mathcal{T}}^k)}^t+{\rho }^{-1}{({\mathcal{B}}^k)}^t-\mathcal{L}{\Vert }_{\text{F}}^2.\hfill \end{array}$

By taking derivative with respect to $\mathcal{L}$ and setting the derivative to zero, we obtain the following equation:

$\begin{array}{cc}\hfill & {\mathfrak{X}}^{\ast }(\mathfrak{X}(\mathcal{L})-\mathbf{y})+\rho \left(\mathcal{L}-{\mathcal{K}}^t-{\rho }^{-1}{\mathcal{A}}^t\right)\hfill \\ \hfill & +\sum _{k=1}^3\rho \left(\mathcal{L}-{({\mathcal{T}}^k)}^t-{\rho }^{-1}{({\mathcal{B}}^k)}^t\right)=\mathbf{0}.\hfill \end{array}$

Solving the above equation yields

$\begin{array}{cc}\hfill {\mathcal{L}}^{t+1}& ={({\mathfrak{X}}^{\ast }\mathfrak{X}+4\rho \mathbb{I})}^{-1}({\mathfrak{X}}^{\ast }(\mathbf{y})+\rho {\mathcal{K}}^t+{\mathcal{A}}^t\hfill \\ \hfill & \left.+\sum _{k=1}^3\left(\rho {({\mathcal{T}}^k)}^t+{({\mathcal{B}}^k)}^t\right)\right),\hfill \end{array}(57)$

where $\mathbb{I}(\cdot )$ is the identity operator.

Update the second block $(\mathcal{K},\{{\mathcal{T}}^k\})$: We update $\mathcal{K}$ and $\{{\mathcal{T}}^k\}$ in parallel by keeping all the other variables fixed. First, $\mathcal{K}$ is updated by solving the $\mathcal{K}$-subproblem,

$\begin{array}{cc}\hfill {\mathcal{K}}^{t+1}& =\underset{\mathcal{K}}{\mathrm{argmin}}{L}_{\rho }({\mathcal{L}}^{t+1},\mathcal{K},{\{{({\mathcal{T}}^k)}^t\}}_k,{\mathcal{A}}^t,{\{{({\mathcal{B}}^k)}^t\}}_k)\hfill \\ \hfill & =\underset{\mathcal{K}}{\mathrm{argmin}}\lambda \gamma \Vert \mathcal{K}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+⟨{\mathcal{A}}^t,\mathcal{K}-{\mathcal{L}}^{t+1}⟩+\frac{\rho }{2}\Vert \mathcal{K}-{\mathcal{L}}^{t+1}{\Vert }_{\text{F}}^2\hfill \\ \hfill & ={\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{x}}_{{\rho }^{-1}\lambda \gamma }^{\Vert \cdot \Vert \text{tnn}}({\mathcal{L}}^{t+1}-{\rho }^{-1}{\mathcal{A}}^t),\hfill \end{array}(58)$

where ${\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{x}}_{\tau }^{\Vert \cdot \Vert \text{tnn}}(\cdot )$ is the proximal operator of TNN given in Lemma 9.

Then, ${\mathcal{T}}^k$ is updated by solving the ${\mathcal{T}}^k$-subproblem (k = 1, 2, 3),

$\begin{array}{cc}\hfill & {({\mathcal{T}}^k)}^{t+1}=\underset{{\mathcal{T}}^k}{\mathrm{argmin}}{L}_{\rho }({\mathcal{L}}^{t+1},{\mathcal{K}}^t,{\{({\mathcal{T}}^k)\}}_k,{\mathcal{A}}^t,{\{{({\mathcal{B}}^k)}^t\}}_k)\hfill \\ \hfill & =\underset{{\mathcal{T}}^k}{\mathrm{argmin}}\lambda {\alpha }_k(1-\gamma )\Vert {\mathbf{T}}_{(k)}^k{\Vert }_{\ast }+⟨{({\mathcal{B}}^k)}^t,{\mathcal{T}}^k-{\mathcal{L}}^{t+1}⟩+\frac{\rho }{2}\Vert {\mathcal{T}}^k-{\mathcal{L}}^{t+1}{\Vert }_{\text{F}}^2\hfill \\ \hfill & ={\mathfrak{F}}_k\left({\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{x}}_{{\rho }^{-1}\lambda {\alpha }_k(1-\gamma )}^{\Vert \cdot {\Vert }_{\ast }}({\mathbf{L}}_{(k)}^{t+1}-{\rho }^{-1}{({\mathbf{B}}_{(k)}^k)}^t)\right),\hfill \end{array}(59)$

where ${\mathfrak{F}}_k(\cdot ):{\mathbb{R}}^{d_k\times d_{\backslash k}}\to {\mathbb{R}}^{d_1\times d_2\times d_3}$ is the folding function to reshape a mode-k matricazation to its original tensor format and ${\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{x}}_{\tau }^{\Vert \cdot {\Vert }_{\ast }}(\cdot )$ is the proximal operator of matrix nuclear norm given in Lemma 10.

Lemma 9 (proximal operator of TNN [34]). Let tensor ${\mathcal{T}}_0\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ with t-SVD ${\mathcal{T}}_0=\mathcal{U}\ast \mathcal{S}\ast {\mathcal{V}}^{\top }$, where $\mathcal{U}\in {\mathbb{R}}^{d_1\times r\times d_3}$ and $\mathcal{V}\in {\mathbb{R}}^{d_2\times r\times d_3}$ are orthogonal tensors and $\mathcal{S}\in {\mathbb{R}}^{r\times r\times d_3}$ is the f-diagonal tensor of singular tubes. Then, the proximal operator of function ‖⋅‖_tnn at point ${\mathcal{T}}_0$ with parameter τ can be computed as follows:

$\begin{array}{cc}\hfill {\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{x}}_{\tau }^{\Vert \cdot \Vert \text{tnn}}({\mathcal{T}}_0)& ≔\underset{\mathcal{T}}{\mathrm{argmin}}\frac{1}{2}\Vert {\mathcal{T}}_0-\mathcal{T}{\Vert }_{\text{F}}^2+\tau \Vert \mathcal{T}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}\hfill \\ \hfill & =\mathcal{U}\ast {\mathtt{i}\mathtt{f}\mathtt{f}\mathtt{t}}_3(\mathtt{m}\mathtt{a}\mathtt{x}({\mathtt{f}\mathtt{f}\mathtt{t}}_3(\mathcal{S})-\tau ,0))\ast {\mathcal{V}}^{\top },\hfill \end{array}$

where ${\mathtt{f}\mathtt{f}\mathtt{t}}_3(\cdot )$ and ${\mathtt{i}\mathtt{f}\mathtt{f}\mathtt{t}}_3(\cdot )$ denote the operations of fast DFT and fast inverse DFT on all the tubes of a given tensor, respectively.

Lemma 10 (proximal operator of the matrix nuclear norm [35]). Let tensor ${\mathbf{T}}_0\in {\mathbb{R}}^{d_1\times d_2}$ with SVD T₀ = USV^⊤, where $\mathbf{U}\in {\mathbb{R}}^{d_1\times r}$ and $\mathbf{V}\in {\mathbb{R}}^{d_2\times r}$ are orthogonal matrices and $\mathbf{S}\in {\mathbb{R}}^{r\times r}$ is a diagonal matrix of singular values. Then, the proximal operator of function ‖⋅‖_∗ at point T₀ with parameter τ can be computed as follows:

$\begin{array}{cc}\hfill {\mathtt{P}\mathtt{r}\mathtt{o}\mathtt{x}}_{\tau }^{\Vert \cdot {\Vert }_{\ast }}({\mathbf{T}}_0)≔& \underset{\mathcal{T}}{\mathrm{argmin}}\frac{1}{2}\Vert {\mathbf{T}}_0-\mathbf{T}{\Vert }_{\text{F}}^2+\tau \Vert \mathbf{T}{\Vert }_{\ast }\hfill \\ \hfill =& \mathbf{U}\text{max}(\mathbf{S}-\tau ,0){\mathbf{V}}^{\top }.\hfill \end{array}$

Update the dual variables $(\mathcal{A},\{{\mathcal{B}}^k\})$. We use dual ascending [33] to update $(\mathcal{A},\{{\mathcal{B}}^k\})$ as follows:

$\begin{array}{cc}\hfill {\mathcal{A}}^{t+1}& ={\mathcal{A}}^t+\rho ({\mathcal{K}}^{t+1}-{\mathcal{L}}^{t+1}),\hfill \\ \hfill {({\mathcal{B}}^k)}^{t+1}& ={({\mathcal{B}}^k)}^t+\rho \left({({\mathcal{T}}^k)}^{t+1}-{\mathcal{L}}^{t+1}\right),k=\mathrm{1,2,3}.\hfill \end{array}(60)$

Termination Condition. Given a tolerance ϵ > 0, check the termination condition of primal variables

$\begin{array}{c}\hfill \Vert {\mathcal{X}}^t-{\mathcal{X}}^t{\Vert }_{\infty }\le ϵ,\forall \mathcal{X}\in \left\{\mathcal{L},\mathcal{K},\{{\mathcal{T}}^k\}\right\},\end{array}(61)$

and convergence of constraints

$\begin{array}{cc}\hfill & \Vert {\mathcal{K}}^t-{\mathcal{L}}^t{\Vert }_{\infty }\le ϵ,\text{and}\Vert {({\mathcal{T}}^k)}^t-{\mathcal{L}}^t{\Vert }_{\infty }\le ϵ,k=\mathrm{1,2,3}.\hfill \end{array}(62)$

The ADMM-based algorithm is described in Algorithm 1.

Algorithm 1. ADMM for Problem(55)

Computational complexity analysis: We analyze the computational complexity as follows.

• By precomputing ${(\mathbb{I}+{\mathfrak{X}}^{\ast }\mathfrak{X}{\mathfrak{X}}^{\ast }\mathfrak{X})}^{-1}$ and ${\mathfrak{X}}^{\ast }\mathfrak{X}$, which costs $O(d_1^3{d}_2^3{d}_3^3+N{d}_1^2{d}_2^2{d}_3^2)$, the cost of updating $\mathcal{L}$ is $O(d_1^2{d}_2^2{d}_3^2)$.

• Updating $\mathcal{K}$ and ${\mathcal{T}}^k$ involves computing the proximal operator of TNN and NN, which costs $O\left(d_1{d}_2{d}_3(d_1\wedge d_2+\log d_3+{\sum }_{k=1}^3{d}_k\wedge d_{\backslash k})\right)$.

• Updating $\mathcal{A}$ and $\{{\mathcal{B}}^k\}$ (k = 1, 2, 3) costs O (d₁d₂d₃).

Overall, supposing the iteration number is T, the total computational complexity will be

$\begin{array}{cccc}\hfill & O(d_1^3{d}_2^3{d}_3^3+T{d}_1^2{d}_2^2{d}_3^2+T{d}_1{d}_2{d}_3(d_1\wedge d_2+\log d_3\hfill & \hfill & +\sum _{k=1}^3{d}_k\wedge d_{\backslash k})),\hfill \end{array}(63)$

which is very expensive for large tensors. In some special cases (like tensor completion) where $⟨{\mathcal{X}}_i,\mathcal{L}⟩$ operates on an element of $\mathcal{L}$, ${(\mathbb{I}+{\mathfrak{X}}^{\ast }\mathfrak{X}{\mathfrak{X}}^{\ast }\mathfrak{X})}^{-1}$ and ${\mathfrak{X}}^{\ast }\mathfrak{X}$ can be computed in O (d₁d₂d₃). Hence, the total complexity of Algorithm 1 will drop to

$\begin{array}{c}\hfill O\left(T{d}_1{d}_2{d}_3(\min \{d_1,d_2\}+\log d_3+\sum _{k=1}^3{d}_k\wedge d_{\backslash k})\right).\end{array}(64)$

Convergence analysis: We then discuss the convergence of Algorithm 1 as follows.

Theorem 4 (convergence of Algorithm 1). For any positive constant ρ, if the unaugmented Lagrangian function $L_0(\mathcal{L},\mathcal{K},\{{\mathcal{T}}^k\},\mathcal{A},\{{\mathcal{B}}^k\})$ has a saddle point, then the iterations $L_{\rho }({\mathcal{L}}^t,{\mathcal{K}}^t,\{{({\mathcal{T}}^k)}^t\},{\mathcal{A}}^t,\{{({\mathcal{B}}^k)}^t\})$ in Algorithm 1 satisfy the residual convergence, objective convergence, and dual variable convergence (defined in [33]) of Problem (55) as t → ∞.Proof of Theorem 4. The key idea is to rewrite Problem(55) into a standard two-block ADMM problem. For notational simplicity, let

$\begin{array}{cc}\hfill f(\mathbf{u})& =\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2^2,g(\mathbf{v})=\lambda \gamma \Vert \mathcal{K}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}+\lambda (1-\gamma )\sum _{k=1}^3{\alpha }_k\Vert {\mathbf{T}}_{(k)}^k{\Vert }_{\ast },\hfill \end{array}$

with u, v, w, and A defined as follows:

$\begin{array}{ccc}\hfill & \mathbf{u}≔\text{vec}(\mathcal{L})\in {\mathbb{R}}^{d_1{d}_2{d}_3},\hfill & \hfill \mathbf{v}≔\left[\begin{array}{c}\hfill \text{vec}(\mathcal{K})\hfill \\ \hfill \text{vec}({\mathcal{T}}^1)\hfill \\ \hfill \text{vec}({\mathcal{T}}^2)\hfill \\ \hfill \text{vec}({\mathcal{T}}^3)\hfill \end{array}\right]\in {\mathbb{R}}^{4d_1{d}_2{d}_3},\\ \hfill & \mathbf{w}≔\left[\begin{array}{c}\hfill \text{vec}(\mathcal{A})\hfill \\ \hfill \text{vec}({\mathcal{B}}^1)\hfill \\ \hfill \text{vec}({\mathcal{B}}^2)\hfill \\ \hfill \text{vec}({\mathcal{B}}^3)\hfill \end{array}\right]\in {\mathbb{R}}^{4d_1{d}_2{d}_3},\hfill & \hfill \mathbf{A}≔\left[\begin{array}{c}\hfill {\mathbf{I}}_D\hfill \\ \hfill {\mathbf{I}}_D\hfill \\ \hfill {\mathbf{I}}_D\hfill \\ \hfill {\mathbf{I}}_D\hfill \end{array}\right]\in {\mathbb{R}}^{4d_1{d}_2{d}_3\times d_1{d}_2{d}_3},\end{array}$

where vec (⋅) denotes the operation of tensor vectorization (see [18]).It can be verified that f (⋅) and g (⋅) are closed, proper convex functions. Then, Problem(55) can be re-written as follows:

$\begin{array}{cc}\hfill \underset{\mathbf{u},\mathbf{v}}{\min }& f(\mathbf{u})+g(\mathbf{v})\hfill \\ \hfill \text{s.t.\hspace{0.17em}\hspace{0.17em}}& \mathbf{A}\mathbf{u}-\mathbf{v}=\mathbf{0}.\hfill \end{array}$

According to the convergence analysis in [33], we have

$\begin{array}{cccc}\hfill & \text{objective\hspace{0.17em}convergence:}\hfill & \hfill & \underset{t\to \infty }{\lim }f({\mathbf{u}}^t)+g({\mathbf{v}}^t)=f^{\ast }+g^{\ast },\hfill \\ \hfill & \text{dual\hspace{0.17em}variable\hspace{0.17em}convergence:}\hfill & \hfill & \underset{t\to \infty }{\lim }{\mathbf{w}}^t={\mathbf{w}}^{\ast },\hfill \\ \hfill & \text{constraint\hspace{0.17em}convergence:}\hfill & \hfill & \underset{t\to \infty }{\lim }\mathbf{A}{\mathbf{u}}^t-{\mathbf{v}}^t=\mathbf{0},\hfill \end{array}$

where f ^∗, g^∗ are the optimal values of f(u), g(v), respectively. Variable w^∗ is a dual optimal point defined as

$\begin{array}{c}\hfill {\mathbf{w}}^{\ast }=\left[\begin{array}{c}\hfill \text{vec}({\mathcal{A}}^{\ast })\hfill \\ \hfill \text{vec}({\mathcal{B}}^{1\ast })\hfill \\ \hfill \text{vec}({\mathcal{B}}^{2\ast })\hfill \\ \hfill \text{vec}({\mathcal{B}}^{3\ast })\hfill \end{array}\right],\end{array}$

where $({\mathcal{A}}^{\ast },{\{{\mathcal{B}}^{k\ast }\}}_k)$ are the dual variables in a saddle point $({\mathcal{L}}^{\ast },{\mathcal{K}}^{\ast },\{{({\mathcal{T}}^k)}^{\ast }\},{\mathcal{A}}^{\ast },\{{({\mathcal{B}}^k)}^{\ast }\})$ of the unaugmented Lagrangian$L_0(\mathcal{L},\mathcal{K},\{{\mathcal{T}}^k\},\mathcal{A},\{{\mathcal{B}}^k\})$. Since there are only equality constraints in the convex problem(55), strong duality holds naturally as a corollary of Slater’s condition [23], which further indicates that the unaugmented Lagrangian $L_0(\mathcal{L},\mathcal{K},\{{\mathcal{T}}^k\},\mathcal{A},\{{\mathcal{B}}^k\})$ has a saddle point. Moreover, according to the analysis in [36], the convergence rate of general ADMM-based algorithms is O (1/T), where T denotes the iteration number. In this way, the convergence behavior of Algorithm 1 is analyzed.

6 Experimental Results

In this section, we first conduct experiments on synthetic datasets to validate the theory for tensor compressed sensing and then evaluate the effectiveness of the proposed T2NN on three types of real data for noisy tensor completion. MATLAB implementations of the algorithms are deployed on a PC running UOS system with an AMD 3 GHz CPU and a RAM of 40 GB.

6.1 Tensor Compressed Sensing

Our theoretical results on tensor compressed sensing are validated on synthetic data in this subsection. Motivated by [7], we consider a constrained T2NN minimization model that is equivalent to Model (15) for the ease of parameter selection. For performance evaluation, the proposed T2NN is also compared with TNN-based tensor compressed sensing [37]. First, the underlying tensor ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ and its compressed observations {y_i} are synthesized by the following tow steps, respectively:

• Step 1: Generate ${\mathcal{L}}^{\ast }$ that is low-rank in both spectral and original domains. Given positive integers d₁, d₂, d₃, and r ≤ min{d₁, d₂, d₃}, we first generate $\mathcal{T}\in {\mathbb{R}}^{d_1\times d_2\times r}$ by $\mathcal{T}={\mathcal{G}}_1\ast {\mathcal{G}}_2$, where ${\mathcal{G}}_1\in {\mathbb{R}}^{d_1\times 1\times r}$ and ${\mathcal{G}}_2\in {\mathbb{R}}^{1\times d_2\times r}$ are tensors with i. i.d. standard Gaussian entries. Then, let ${\mathcal{L}}^{\ast }=\mathcal{T}{\times }_3\mathbf{G}$ where ×₃ is the tensor mode-3 product [18], and $\mathbf{G}\in {\mathbb{R}}^{r\times d_3}$ is a matrix with i. i.d standard Gaussian entries. Our extensive numerical experimental results show that with high probability, the tubal rank and Tucker rank of ${\mathcal{L}}^{\ast }$ are all equal to r, that is, ${\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}}_{\mathrm{t}\mathrm{b}}({\mathcal{L}}^{\ast })=r$ and $\mathtt{r}\mathtt{a}\mathtt{n}\mathtt{k}({\mathbf{L}}_{(k)}^{\ast })=r,\forall k=\mathrm{1,2,3}$.

• Step 2: Generate N compressed observations {y_i}. Given a positive integer N ≪ D, we first generate N design tensors $\{{\mathcal{X}}_i\}$ with i. i.d. standard Gaussian entries. Then, N noise variables {ξ_i} are generated as i. i.d. standard Gaussian variables. The parameter of standard deviation σ is set by σ = cσ₀, where ${\sigma }_0=\Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{F}}/\sqrt{d_1{d}_2{d}_3}$, and we use c to denote the noise level. Finally, {y_i} are formed according to the observation model (13). The goal of tensor compressed sensing is to reconstruct the known ${\mathcal{L}}^{\ast }$ from its noisy compressed observations {y_i}.

For simplicity, we consider cubic tensors, i.e., d₁ = d₂ = d₃ = d, and choose the parameter of T2NN by γ = 1/4, α₁ = α₂ = α₃ = 1/3. Recall that the underlying tensor ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d\times d\times d}$ generated by the above Step 1 has the tubal rank and Tucker rank all equal to r with high probability. We consider tensors with dimensionality d ∈ {16, 20, 24} and rank proxy r ∈ {2, 3}. Then, if the proposed main theorem for tensor compressed sensing (i.e., Theorem 2) is correct, the following two phenomena should be observed:

(1) Phenomenon 1: In the noiseless setting, i.e., σ = 0, if the observation number N is larger than C₀rd² for a sufficiently large constant C₀, then the estimation error $\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2$ can be zero, which means exact recovery. Let N₀ = rd² as a unit measure of the sample complexity. Then, by increasing the observation number N gradually from 0, we will observe a phase transition point of the estimation error in the noiseless setting: If N/N₀ > C₀, the estimation error is relatively “large”; once N/N₀ ≤ C₀, the error will drop dramatically to 0.

(2) Phenomenon 2: In the noisy case, the estimation error $\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2$ scales linearly with the variance σ² of the random noises once the observation number N ≥ C₀N₀.

To check whether Phenomenon 1 occurs, we conduct tensor compressed sensing by setting the noise variance σ² = 0. We gradually increase the normalized observation number N/N₀ from 0.25 to 5. For each different setting of d, r, and N/N₀, we repeat the experiments 10 times and report the averaged estimation error $\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2$. For both TNN [37] and the proposed T2NN, we plot the curves of estimation error in logarithm versus the normalized observation number N/N₀ for ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d\times d\times d}$ with rank proxy r = 2 in Figure 1. It can be seen that Phenomenon 1 occurs for the proposed T2NN: When N/N₀ > 1.75, the estimation error is relatively “large”; once N/N₀ ≤ 1.75, the error will drop dramatically to 0. The same phenomenon also occurs for TNN with a phase transition point near 3.5. Thus, the sample complexity for exact tensor compressed sensing of T2NN is lower than that of TNN, indicating the superiority of the proposed T2NN. Since similar phenomena have also been observed for tensors of other sizes and rank proxies, we simply omit them.

FIGURE 1

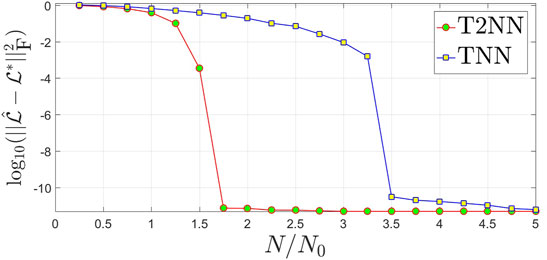
FIGURE 1. Estimation error in logarithm vs. the normalized observation number N/N₀ for tensor compressed sensing of underlying tensors of size 16×16×16 and rank proxy r =2. The proposed T2NN is compared with TNN [37].

For the validation of Phenomenon 2, we consider the noisy settings with normalized sample complexity N/N₀ = 3.5, which is nearly the phase transition point of TNN and much greater than that of T2NN. We gradually increase the noise level c = σ/σ₀ from 0.025 to 0.25. For each different setting of d, r, and c, we repeat the experiments 10 times and report the averaged estimation error $\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2$. For both TNN [37] and the proposed T2NN, we plot the curves of estimation error in logarithm versus the (squared) noise level ${\sigma }^2/{\sigma }_0^2$ for ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d\times d\times d}$ with rank proxy r = 2 in Figure 2. It can be seen that Phenomenon 2 also occurs for the proposed T2NN: The estimation error scales approximately linearly with the (squared) noise level. The same phenomenon can also be observed for TNN with a higher estimation error than T2NN, indicating T2NN is more accurate than TNN. We omit the results for tensors of other sizes and rank proxies because the error curves are so similar to Figure 2.

FIGURE 2

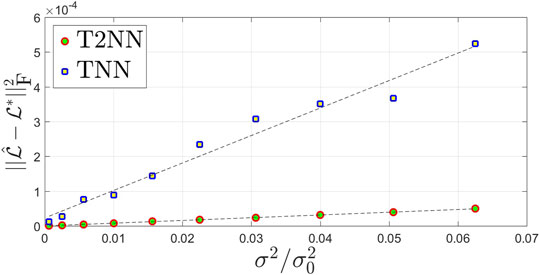
FIGURE 2. Estimation error vs. the (squared) noise level ${\sigma }^2/{\sigma }_0^2$ for tensor compressed sensing of underlying tensors of size 16×16×16 and rank proxy r =2. The proposed T2NN is compared with TNN [37].

6.2 Noisy Tensor Completion

This subsection evaluates effectiveness of the proposed T2NN through performance comparison with matrix nuclear norms (NN) [30], SNN [22], and TNN [25] by carrying out noisy tensor completion on three different types of visual data including video data, hyperspectral images, and seismic data.

6.2.1 Experimental Settings

Given the tensor data ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d_1\times d_2\times d_3}$, the goal is to recover it from its partial noisy observations. We consider uniform sampling with ratio p ∈ {0.05, 0.1, 0.15} for the tensors, that is, {95, 90, 85%} entries of a tensor are missing. The noise follows i. i.d. Gaussian $\mathcal{N}(0,{\sigma }^2)$ where σ = 0.05σ₀, where ${\sigma }_0=\Vert {\mathcal{L}}^{\ast }{\Vert }_{\text{F}}/\sqrt{d_1{d}_2{d}_3}$ is the rescaled magnitude of tensor ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d_1\times d_2\times d_3}$.

6.2.2 Performance evaluation

The effectiveness of algorithms is measured by the Peak Signal Noise Ratio (PSNR) and structural similarity (SSIM) [38]. Specifically, the PSNR of an estimator $\widehat{\mathcal{L}}$ is defined as

$\begin{array}{c}\hfill \mathtt{P}\mathtt{S}\mathtt{N}\mathtt{R}≔10{\log }_{10}\left(\frac{d_1{d}_2{d}_3\Vert {\mathcal{L}}^{\ast }{\Vert }_{\infty }^2}{\Vert \widehat{\mathcal{L}}-{\mathcal{L}}^{\ast }{\Vert }_{\text{F}}^2}\right),\end{array}$

for the underlying tensor ${\mathcal{L}}^{\ast }\in {\mathbb{R}}^{d_1\times d_2\times d_3}$. The SSIM is computed via

$\begin{array}{c}\hfill \mathtt{S}\mathtt{S}\mathtt{I}\mathtt{M}≔\frac{(2{\mu }_{{\mathcal{L}}^{\ast }}{\mu }_{\widehat{\mathcal{L}}}+{(0.01\bar{\omega })}^2)(2{\sigma }_{{\mathcal{L}}^{\ast },\widehat{\mathcal{L}}}+{(0.03\bar{\omega })}^2)}{({\mu }_{{\mathcal{L}}^{\ast }}^2+{\mu }_{\widehat{\mathcal{L}}}^2+{(0.01\bar{\omega })}^2)({\sigma }_{{\mathcal{L}}^{\ast }}^2+{\sigma }_{\widehat{\mathcal{L}}}^2+{(0.03\bar{\omega })}^2)},\end{array}$

where ${\mu }_{{\mathcal{L}}^{\ast }},{\mu }_{\widehat{\mathcal{L}}},{\sigma }_{{\mathcal{L}}^{\ast }},{\sigma }_{\widehat{\mathcal{L}}},{\sigma }_{{\mathcal{L}}^{\ast },\widehat{\mathcal{L}}}$, and $\bar{\omega }$ denote the local means, standard deviation, cross-covariance, and dynamic range of the magnitude of tensors ${\mathcal{L}}^{\ast }$ and $\widehat{\mathcal{L}}$. Larger PSNR and SSIM values indicate the higher quality of the estimator $\widehat{\mathcal{L}}$. In each setting, we test each tensor for 10 trials and report the averaged PSNR (in db) and SSIM values.

6.2.3 Parameter Setting

For NN [30], we set the parameter $\lambda ={\lambda }_{\iota }\sigma \sqrt{p(d_1\vee d_2)\log (d_1+d_2)}$. For SNN [22], we set the regularization parameter λ = λ_ι and chose the weight α by α₁: α₂: α₃ = 1 : 1: 1. For TNN [25], we set $\lambda ={\lambda }_{\iota }\sigma \sqrt{p{d}_3(d_1\vee d_2)\log (d_1{d}_3+d_2{d}_3)}$. For the proposed T2NN, we set the regularization parameter $\lambda ={\lambda }_{\iota }\sigma \sqrt{p{d}_3(d_1\vee d_2)\log (d_1{d}_3+d_2{d}_3)}$ and choose the weights γ = 0.5 and α with α₁: α₂: α₃ = 1 : 1: 10. The factor λ_ι is then tuned in {10^–3, 10^–2, … , 10³} for each norm, and we chose the one with highest PSNRs in most cases in the parameter tuning phase.

6.2.4 Experiments on Video Data

We first conduct noisy video completion on four widely used YUV videos: Akiyo, Carphone, Grandma, and Mother-daughter. Owing to computational limitation, we simply use the first 30 frames of the Y components of all the videos and obtain four tensors of size 144 × 17 × 30. We first report the averaged PSNR and SSIM values obtained by four norms for quantitative comparison in Table 1 and then give visual examples in Figure 3 when 95% of the tensor entries are missing for qualitative evaluation. A demo of the source code is available at https://github.com/pingzaiwang/T2NN-demo.

TABLE 1

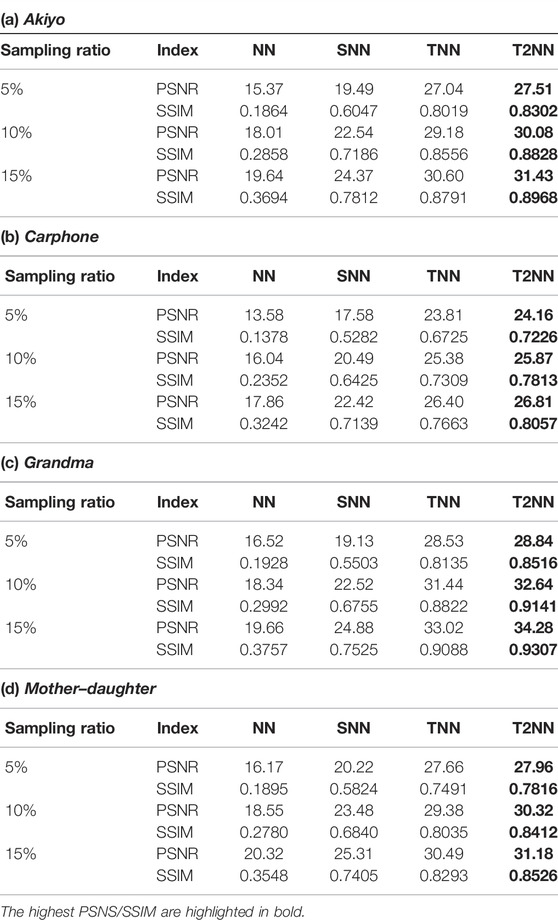
TABLE 1. PSNR and SSIM values obtained by four norms (NN [30], SNN [22], TNN [25], and our T2NN) for noisy tensor completion on the YUV videos.

FIGURE 3

FIGURE 3. Visual results obtained by four norms for noisy tensor completion with 95% missing entries on the YUV-video dataset. The first to fourth rows correspond to the video of Akiyo, Carphone, Grandman, and Mother-duaghter, respectively. The sub-plots from (A) to (F): (A) a frame of the original video, (B) the observed frame, (C) the frame recovered by NN [30], (D) the frame recovered by SNN [22], (E) the frame recovered by the vanilla TNN [25], and (F) the frame recovered by our T2NN.

6.2.5 Experiments on Hyperspectral Data

We then carry out noisy tensor completion on subsets of the two representative hyperspectral datasets described as follows:

• Indian Pines: The dataset was collected by AVIRIS sensor in 1992 over the Indian Pines test site in North-western Indiana and consists of 145 × 145 pixels and 224 spectral reflectance bands. We use the first 30 bands in the experiments due to the trade-off between the limitation of computing resources.

• Salinas A: The data were acquired by AVIRIS sensor over the Salinas Valley, California in 1998, and consists of 224 bands over a spectrum range of 400–2500 nm. This dataset has a spatial extent of 86 × 83 pixels with a resolution of 3.7 m. We use the first 30 bands in the experiments too.

The averaged PSNR and SSIM values are given in Table 2 for quantitative comparison. We also show visual examples in Figure 4 when 85% of the tensor entries are missing for qualitative evaluation.

TABLE 2

TABLE 2. PSNR and SSIM values obtained by four norms (NN [30], SNN [22], TNN [25], and our T2NN) for noisy tensor completion on the hyperspectral datasets.

FIGURE 4

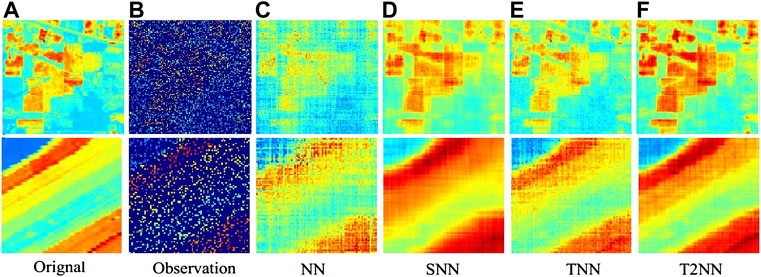
FIGURE 4. Visual results obtained by four norms for noisy tensor completion with 85% missing entries on the hyperspectral dataset (gray data shown with pseudo-color). The first and second rows correspond to Indian Pines and Salinas A, respectively. The sub-plots from (A) to (F): (A) a frame of the original data, (B) the observed frame, (C) the frame recovered by NN [30], (D) the frame recovered by SNN [22], (E) the frame recovered by the vanilla TNN [25], and (F) the frame recovered by our T2NN.

6.2.6 Experiments on Seismic Data

We use the seismic data tensor of size 512 × 512 × 3, which is abstracted from the test data “seismic.mat” of a toolbox for seismic data processing from Center of Geopyhsics, Harbin Institute of Technology, China. For quantitative comparison, we present the PSNR and SSIM values for two sampling schemes in Table 3.

TABLE 3

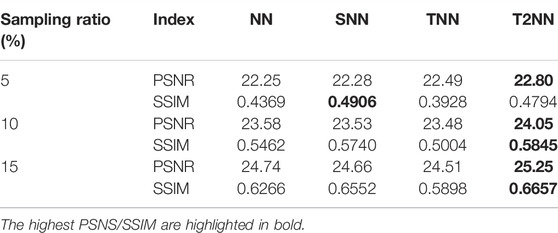
TABLE 3. PSNR and SSIM values obtained by four norms (NN [30], SNN [22], TNN [25], and our T2NN) for noisy tensor completion on the Seismic dataset.

6.2.7 Summary and Analysis of Experimental Results

According to the experimental results on three types of real tensor data shown in Table 1, Table 2, Table 3, and Figure 3, the summary and analysis are presented as follows:

1) In all the cases, tensor norms (SNN, TNN, and T2NN) perform better than the matrix norm (NN). It can be explained that tensor norms can honestly preserve the multi-way structure of tensor data such that the rich inter-modal and intra-modal correlations of the data can be exploited to impute the missing values, whereas the matrix norm can only handle two-way structure and thus fails to model the multi-way structural correlations of the tensor data.

2) In most cases, TNN outperforms SNN, which is in consistence with the results reported in [14, 17, 25]. One explanation is that the used video, hyperspectral images, and seismic data all possess stronger low-rankness in the spectral domain (than in the original domain), which can be successfully captured by TNN.

3) In most cases, the proposed T2NN performs best among the four norms. We owe the promising performance to the capability of T2NN in simultaneously exploiting low-rankness in both spectral and original domains.

7 Conclusion and Discussions

7.1 Conclusion

Due to its definition solely in the spectral domain, the popular TNN may be incapable to exploit low-rankness in the original domain. To remedy this weaknesses, a hybrid tensor norm named the “Tubal + Tucker” Nuclear Norm (T2NN) was first defined as the weighted sum of TNN and SNN to model both spectral and original domain low-rankness. It was further used to formulate a penalized least squares estimator for tensor recovery from noisy linear observations. Upper bounds on the estimation error were established in both deterministic and non-asymptotic senses to analyze the statistical performance of the proposed estimator. An ADMM-based algorithm was also developed to efficiently compute the estimator. The effectiveness of the proposed model was demonstrated through experimental results on both synthetic and real datasets.

7.2 Limitations of the Proposed Model and Possible Solutions

Generally speaking, the proposed estimator has the following two drawbacks due to the adoption of T2NN:

• Sample inefficiency: The analysis of [24, 28] indicates that for tensor recovery from a small number of observations, T2NN cannot provide essentially lower sample complexity than TNN.

• Computational inefficiency: Compared to TNN, T2NN is more time-consuming since it involves computing both TNN and SNN.

We list several directions that this work can be extended to overcome the above drawbacks.

• For sample inefficiency: First, inspired by the attempt of adopting the “best” norm (e.g., Eq. 8 in [28]), the following model can be considered:

$\begin{array}{cc}\hfill \underset{\mathcal{L}}{\min }& \max \left\{\frac{\Vert \mathcal{L}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}}{\Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}},\underset{k=\mathrm{1,2,3}}{\max }\frac{\Vert {\mathbf{L}}_{(k)}{\Vert }_{\ast }}{\Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }}\right\}\hfill \\ \hfill & \text{s.t.\hspace{0.17em}\hspace{0.17em}}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2\le ϵ\hfill \end{array}(65)$

for a certain noise level ϵ ≥ 0. Although Model (65) has a significantly higher accuracy and lower sample complexity according to the analysis in [28], it is impractical because it requires $\Vert {\mathcal{L}}^{\ast }{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}}$ and $\Vert {\mathbf{L}}_{(k)}^{\ast }{\Vert }_{\ast }$ (k = 1, 2, 3), which are unknown in advance. Motivated by [39], a more practical model is given as follows:

$\begin{array}{cc}\hfill \underset{\mathcal{L}}{\min }& \sum _{k=1}^3\text{exp}({\alpha }_k\Vert {\mathbf{L}}_{(k)}{\Vert }_{\ast })+\text{exp}(\beta \Vert \mathcal{L}{\Vert }_{\mathrm{t}\mathrm{n}\mathrm{n}})\hfill \\ \hfill & \text{s.t.\hspace{0.17em}\hspace{0.17em}}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}){\Vert }_2\le ϵ,\hfill \end{array}$

where β > 0 is a regularization parameter.

• For computational inefficiency: To improve the efficiency of the proposed T2NN-based models, we can use more efficient solvers of Problem (15) by adopting the factorization strategy [40, 41] or sampling-based approaches [42].

7.3 Extensions to the Proposed Model

In this subsection, we discuss possible extensions of the proposed model to general K-order (K > 3) tensors, general spectral domains, robust tensor recovery, and multi-view learning, respectively.

• Extensions to K-order (K > 3) tensors: Currently, the proposed T2NN is defined solely for 3-order tensors, and it cannot be directly applied to tensors of more than 3 orders like color videos. For general K-order tensors, it is suggested to replace the tubal nuclear norm in the definition of T2NN with orientation invariant tubal nuclear norm [5], which is defined to exploit multi-orientational spectral low-rankness for general higher-order tensors.

• Extensions to general spectral and original domains: This paper considers the DFT-based tensor product for spectral low-rank modeling. Recently, the DFT based t-product has been generalized to the *_L-product defined via any invertible linear transform [43], under which the tubal nuclear norm is also extended to *_L-tubal nuclear norm [44] and *_L-Spectral k-support norm [7]. It is natural to generalize the proposed T2NN by changing the tubal nuclear norm to *_L-tubal nuclear norm or *_L-Spectral k-support norm for further extensions. It is also interesting to consider other tensor decompositions for original domain low-rankness modeling such as CP, TT, and TR as future work.

• Extensions to robust tensor recovery: In many real applications, the tensor signal may also be corrupted by gross sparse outliers. Motivated by [5], the proposed T2NN can also be used in resisting sparse outliers for robust tensor recovery as follows:

$\begin{array}{c}\hfill \underset{\mathcal{L},\mathcal{S}}{\min }\frac{1}{2}\Vert \mathbf{y}-\mathfrak{X}(\mathcal{L}+\mathcal{S}){\Vert }_2+\lambda \Vert \mathcal{L}{\Vert }_{\text{t}2\text{nn}}+\mu \Vert \mathcal{S}{\Vert }_1,\end{array}$

where $\mathcal{S}\in {\mathbb{R}}^{d_1\times d_2\times d_3}$ denotes the tensor of sparse outliers, the tensor l₁-norm ‖⋅‖₁ is applied to encourage sparsity in $\mathcal{S}$, and μ > 0 is a regularization parameter.

• Extensions to multi-view learning: Due to its superiority in modeling multi-linear correlations of multi-modal data, TNN has been successfully applied to multi-view self-representations for clustering [45, 46]. Our proposed T2NN can also be utilized for clustering by straightforwardly replacing TNN in the formulation of multi-view learning models (e.g., Eq. 9 in [45]).

Data Availability Statement

Publicly available datasets were analyzed in this study. These data can be found here; https://sites.google.com/site/subudhibadri/fewhelpfuldownloads, https://engineering.purdue.edu/∼biehl/MultiSpec/hyperspectral.html, https://rslab.ut.ac.ir/documents/81960329/82035173/SalinasA_corrected.mat, https://github.com/sevenysw/MathGeo2018.

Author Contributions

Conceptualization and methodology—YL and AW; software—AW; formal analysis—YL, AW, GZ, and QZ; resources—YL, GZ, and QZ; writing: original draft preparation—YL, AW, GZ, and QZ; project administration and supervision—GZ, and QZ; and funding acquisition—AW, GZ, and QZ. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grants 61872188, 62073087, 62071132, 62103110, 61903095, U191140003, and 61973090, in part by the China Postdoctoral Science Foundation under Grant 2020M672536, and in part by the Natural Science Foundation of Guangdong Province under Grants 2020A1515010671, 2019B010154002, and 2019B010118001.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

AW is grateful to Prof. Zhong Jin in Nanjing University of Science and Technology for his long-time and generous support in both research and life. In addition, he would like to thank the Jin family in Zhuzhou for their kind understanding in finishing the project of tensor learning in these years.

Footnotes

¹The Fourier version $\tilde{\mathcal{T}}$ is obtained by performing 1D-DFT on all tubes of $\mathcal{T}$, i.e., $\tilde{\mathcal{T}}=\text{fft}(\mathcal{T},[],3)\in {\mathbb{C}}^{d_1\times d_2\times d_3}$ in MATLAB.

References

1. Guo C, Modi K, Poletti D. Tensor-Network-Based Machine Learning of Non-Markovian Quantum Processes. Phys Rev A (2020) 102:062414.

CrossRef Full Text | Google Scholar

2. Ma X, Zhang P, Zhang S, Duan N, Hou Y, Zhou M, et al. A Tensorized Transformer for Language Modeling. Adv Neural Inf Process Syst (2019) 32.

Google Scholar

3. Meng Y-M, Zhang J, Zhang P, Gao C, Ran S-J. Residual Matrix Product State for Machine Learning. arXiv preprint arXiv:2012.11841 (2020).

Google Scholar

4. Ran S-J, Sun Z-Z, Fei S-M, Su G, Lewenstein M. Tensor Network Compressed Sensing with Unsupervised Machine Learning. Phys Rev Res (2020) 2:033293. doi:10.1103/physrevresearch.2.033293

CrossRef Full Text | Google Scholar

5. Wang A, Zhao Q, Jin Z, Li C, Zhou G. Robust Tensor Decomposition via Orientation Invariant Tubal Nuclear Norms. Sci China Technol Sci (2022) 34:6102. doi:10.1007/s11431-021-1976-2

CrossRef Full Text | Google Scholar

6. Zhang X, Ng MK-P. Low Rank Tensor Completion with Poisson Observations. IEEE Trans Pattern Anal Machine Intelligence (2021). doi:10.1109/tpami.2021.3059299

CrossRef Full Text | Google Scholar

7. Wang A, Zhou G, Jin Z, Zhao Q. Tensor Recovery via *_L-Spectral k-Support Norm. IEEE J Sel Top Signal Process (2021) 15:522–34. doi:10.1109/jstsp.2021.3058763

CrossRef Full Text | Google Scholar

8. Cui C, Zhang Z. High-Dimensional Uncertainty Quantification of Electronic and Photonic Ic with Non-Gaussian Correlated Process Variations. IEEE Trans Computer-Aided Des Integrated Circuits Syst (2019) 39:1649–61. doi:10.1109/TCAD.2019.2925340

CrossRef Full Text | Google Scholar

9. Liu X-Y, Aeron S, Aggarwal V, Wang X. Low-Tubal-Rank Tensor Completion Using Alternating Minimization. IEEE Trans Inform Theor (2020) 66:1714–37. doi:10.1109/tit.2019.2959980

CrossRef Full Text | Google Scholar

10. Carroll JD, Chang J-J. Analysis of Individual Differences in Multidimensional Scaling via an N-Way Generalization of “Eckart-Young” Decomposition. Psychometrika (1970) 35:283–319. doi:10.1007/bf02310791

CrossRef Full Text | Google Scholar

11. Tucker LR. Some Mathematical Notes on Three-Mode Factor Analysis. Psychometrika (1966) 31:279–311. doi:10.1007/bf02289464

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Oseledets IV. Tensor-Train Decomposition. SIAM J Sci Comput (2011) 33:2295–317. doi:10.1137/090752286

CrossRef Full Text | Google Scholar

13. Zhao Q, Zhou G, Xie S, Zhang L, Cichocki A. Tensor Ring Decomposition. arXiv preprint arXiv:1606.05535 (2016).

Google Scholar

14. Zhang Z, Ely G, Aeron S, Hao N, Kilmer M. Novel Methods for Multilinear Data Completion and De-Noising Based on Tensor-Svd. In: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2014). p. 3842–9. doi:10.1109/cvpr.2014.485

CrossRef Full Text | Google Scholar

15. Kilmer ME, Braman K, Hao N, Hoover RC. Third-Order Tensors as Operators on Matrices: A Theoretical and Computational Framework with Applications in Imaging. SIAM J Matrix Anal Appl (2013) 34:148–72. doi:10.1137/110837711

CrossRef Full Text | Google Scholar

16. Hou J, Zhang F, Qiu H, Wang J, Wang Y, Meng D. Robust Low-Tubal-Rank Tensor Recovery from Binary Measurements. IEEE Trans Pattern Anal Machine Intelligence (2021). doi:10.1109/tpami.2021.3063527

CrossRef Full Text | Google Scholar

17. Lu C, Feng J, Chen Y, Liu W, Lin Z, Yan S. Tensor Robust Principal Component Analysis with a New Tensor Nuclear Norm. IEEE Trans Pattern Anal Mach Intell (2020) 42:925–38. doi:10.1109/tpami.2019.2891760

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kolda TG, Bader BW. Tensor Decompositions and Applications. SIAM Rev (2009) 51:455–500. doi:10.1137/07070111x

CrossRef Full Text | Google Scholar

19. Li X, Wang A, Lu J, Tang Z. Statistical Performance of Convex Low-Rank and Sparse Tensor Recovery. Pattern Recognition (2019) 93:193–203. doi:10.1016/j.patcog.2019.03.014

CrossRef Full Text | Google Scholar

20. Liu J, Musialski P, Wonka P, Ye J. Tensor Completion for Estimating Missing Values in Visual Data. IEEE Trans Pattern Anal Mach Intell (2013) 35:208–20. doi:10.1109/tpami.2012.39

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Qiu Y, Zhou G, Chen X, Zhang D, Zhao X, Zhao Q. Semi-Supervised Non-Negative Tucker Decomposition for Tensor Data Representation. Sci China Technol Sci (2021) 64:1881–92. doi:10.1007/s11431-020-1824-4

CrossRef Full Text | Google Scholar

22. Tomioka R, Suzuki T, Hayashi K, Kashima H. Statistical Performance of Convex Tensor Decomposition. In: Proceedings of Annual Conference on Neural Information Processing Systems (2011). p. 972–80.

Google Scholar

23. Boyd S, Boyd SP, Vandenberghe L. Convex Optimization. Cambridge: Cambridge University Press (2004).

Google Scholar

24. Mu C, Huang B, Wright J, Goldfarb D. Square Deal: Lower Bounds and Improved Relaxations for Tensor Recovery. In: International Conference on Machine Learning (2014). p. 73–81.

Google Scholar

25. Wang A, Lai Z, Jin Z. Noisy Low-Tubal-Rank Tensor Completion. Neurocomputing (2019) 330:267–79. doi:10.1016/j.neucom.2018.11.012

CrossRef Full Text | Google Scholar

26. Zhou P, Lu C, Lin Z, Zhang C. Tensor Factorization for Low-Rank Tensor Completion. IEEE Trans Image Process (2018) 27:1152–63. doi:10.1109/tip.2017.2762595

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Negahban S, Wainwright MJ. Estimation of (Near) Low-Rank Matrices with Noise and High-Dimensional Scaling. Ann Stat (2011) 2011:1069–97. doi:10.1214/10-aos850

CrossRef Full Text | Google Scholar

28. Oymak S, Jalali A, Fazel M, Eldar YC, Hassibi B. Simultaneously Structured Models with Application to Sparse and Low-Rank Matrices. IEEE Trans Inform Theor (2015) 61:2886–908. doi:10.1109/tit.2015.2401574

CrossRef Full Text | Google Scholar

29. Foucart S, Rauhut H. A Mathematical Introduction to Compressive Sensing, Vol. 1. Basel, Switzerland: Birkhäuser Basel (2013).

Google Scholar

30. Klopp O. Noisy Low-Rank Matrix Completion with General Sampling Distribution. Bernoulli (2014) 20:282–303. doi:10.3150/12-bej486

CrossRef Full Text | Google Scholar

31. Klopp O. Matrix Completion by Singular Value Thresholding: Sharp Bounds. Electron J Stat (2015) 9:2348–69. doi:10.1214/15-ejs1076

CrossRef Full Text | Google Scholar

32. Vershynin R. High-Dimensional Probability: An Introduction with Applications in Data Science, Vol. 47. Cambridge: Cambridge University Press (2018).

Google Scholar

33. Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations Trends® Machine Learn (2011) 3:1–122. doi:10.1561/2200000016

CrossRef Full Text | Google Scholar

34. Wang A, Wei D, Wang B, Jin Z. Noisy Low-Tubal-Rank Tensor Completion Through Iterative Singular Tube Thresholding. IEEE Access (2018) 6:35112–28. doi:10.1109/access.2018.2850324

CrossRef Full Text | Google Scholar

35. Cai J-F, Candès EJ, Shen Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J Optim (2010) 20:1956–82. doi:10.1137/080738970

CrossRef Full Text | Google Scholar

36. He B, Yuan X. On the $O(1/n)$ Convergence Rate of the Douglas-Rachford Alternating Direction Method. SIAM J Numer Anal (2012) 50:700–9. doi:10.1137/110836936

CrossRef Full Text | Google Scholar

37. Lu C, Feng J, Lin Z, Yan S. Exact Low Tubal Rank Tensor Recovery from Gaussian Measurements. In: Proceedings of the 28th International Joint Conference on Artificial Intelligence (2018). p. 1948–54. doi:10.24963/ijcai.2018/347

CrossRef Full Text | Google Scholar

38. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image Quality Assessment: from Error Visibility to Structural Similarity. IEEE Trans Image Process (2004) 13:600–12. doi:10.1109/tip.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Zhang X, Zhou Z, Wang D, Ma Y. Hybrid Singular Value Thresholding for Tensor Completion. In: Twenty-Eighth AAAI Conference on Artificial Intelligence (2014). p. 1362–8.

CrossRef Full Text | Google Scholar

40. Wang A-D, Jin Z, Yang J-Y. A Faster Tensor Robust Pca via Tensor Factorization. Int J Mach Learn Cyber (2020) 11:2771–91. doi:10.1007/s13042-020-01150-2

CrossRef Full Text | Google Scholar

41. Liu G, Yan S. Active Subspace: Toward Scalable Low-Rank Learning. Neural Comput (2012) 24:3371–94. doi:10.1162/neco_a_00369

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Wang L, Xie K, Semong T, Zhou H. Missing Data Recovery Based on Tensor-Cur Decomposition. IEEE Access (2017) PP:1.

Google Scholar

43. Kernfeld E, Kilmer M, Aeron S. Tensor-Tensor Products with Invertible Linear Transforms. Linear Algebra its Appl (2015) 485:545–70. doi:10.1016/j.laa.2015.07.021

CrossRef Full Text | Google Scholar

44. Lu C, Peng X, Wei Y. Low-Rank Tensor Completion with a New Tensor Nuclear Norm Induced by Invertible Linear Transforms. In: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2019). p. 5996–6004. doi:10.1109/cvpr.2019.00615

CrossRef Full Text | Google Scholar

45. Lu G-F, Zhao J. Latent Multi-View Self-Representations for Clustering via the Tensor Nuclear Norm. Appl Intelligence (2021) 2021:1–13. doi:10.1007/s10489-021-02710-x

CrossRef Full Text | Google Scholar

46. Liu Y, Zhang X, Tang G, Wang D. Multi-View Subspace Clustering Based on Tensor Schatten-P Norm. In: 2019 IEEE International Conference on Big Data (Big Data). Los Angeles, CA, USA: IEEE (2019). p. 5048–55. doi:10.1109/bigdata47090.2019.9006347

CrossRef Full Text | Google Scholar