Holographic Imaging Using an Imperfect Plane Wave Illumination With a Background Phase

Aberrations in the optical components and misalignments in the optical system cause a background phase in the coherent illumination. To reconstruct the object phase, the background phase illuminating the object must be measured and subtracted. For diffraction imaging and in-line holography, the traditional phase retrieval method reconstructs the phase diffracting from clear edges. However, it falls into stagnation when solving a background phase slowly varying in the spatial domain. In this study, we propose to solve the background phase using a modulation-based phase retrieval method. Alternative structured phase modulation (ASPM) can be the phase constraint to avoid stagnation when solving the background phase without clear edges. With ASPM, the background phase in the experiment can be efficiently retrieved when 16 phase patterns are employed. The ASPM acts as a phase grating to concentrate the intensities and provides robustness to noise. Compared to the conventional random phase modulations, the ASPM method had a smaller error value in the reconstruction iterations, which leads to a better reconstruction quality. After measuring and subtracting the background phase, the object phase was retrieved using a coherent diffraction imaging system. A phase plate can be accurately reconstructed under three different background phases.

Introduction

Aberrations and misalignments are inevitable in the optical setups of various phase imaging techniques, including interferometric methods [1–5] and diffraction-based methods [6–9]. To measure the complex amplitude, an object is illuminated with a coherent wave. The plane wave [10] or quasi-plane [11, 12] wave is widely used for illumination. With ideal plane-wave illumination, the transmitted wavefront represents the complex amplitude of the object. Typically, in the experiments, there are unavoidable aberrations and misalignments [13–15]. The illumination on the object has an undesirable background phase slowly varying in the spatial domain. The transmitted wavefront is the complex amplitude product of the object and illumination. To acquire the object phase, the background phase must be measured and subtracted.

Various methods have been proposed for the background phase compensation in the interferometric methods, such as off-axis holography techniques [16]. The compensation can be executed numerically during the reconstruction. The background phase can be compensated by generating a virtual phase from the hologram [17, 18] or using polynomial fitting [19, 20]. The aberration compensation can also be mimicked by the computation of a numerical parametric lens [21]. Apart from the numerical method, measuring and subtracting the background phase is a straightforward approach [22]. Complete information on system aberration is calculated from three laterally shifted phase images using spiral phase integration [23]. In angular scanning digital holography setup, pupil aberrations are recovered by utilizing the cross-spectral density between optical fields at various incident angles [24]. For off-axis digital holography, the background phase can be measured directly. The phase of an object is acquired after background elimination [25]. In phase-shifting methods, the background phase is measured directly [26] or eliminated by numerical methods [27]. The aberrations can also be compensated using Zernike polynomials [28].

In diffraction imaging methods, iterative phase retrieval methods are used to retrieve the phase [29, 30]. The basic procedure of the algorithm is the alternating propagation of the estimated wavefront between the planes of interest and the recorded intensity. There is conjugated noise while propagating the intensity. Traditional phase retrieval methods used constraints to eliminate the conjugated noise. The Gerchberg-Saxton (GS) algorithm [31] used the amplitude of the wavefront of interest to be a strong constraint. Then, Fienup modified the GS algorithm by using a loose non-negative constraint [32] or support constraint [33]. A support constraint was widely used as a priori information for phase retrieval [34, 35]. The support region was artificially created by coherently illuminating a finite region of an extended object or a large scene [36]. The wavefront inside the support region was reconstructed iteratively. The noise outside the support region was weakened or abandoned [37].

In a diffraction imaging setup, there is no reference beam while recording the diffracted hologram. The background phase compensation is hard to execute using the aforementioned numerical methods. The background phase needs to be measured. The traditional phase retrieval method performs well when solving the phase diffracting from clear edges. Using simulated data, the phase inside the support region can be rapidly reconstructed [37]. When solving the background phase without clear edges, the reconstruction algorithm stagnates [36]. In the experiment, the intensity data was with environmental noise. The background phase is unsolvable based on its intensity pattern with noise using traditional phase-retrieval methods. Diversities in the diffraction intensities need to be detected adequately for retrieving a smooth background phase [38, 39].

Modulations can also be used as modulation constraints to achieve successful phase retrieval. With multiple phase modulations, the wavefront can be fully reconstructed without finite support constraints [40]. Using shifting illumination, a large area of the specimen can be reconstructed at high resolution [41–43]. A novel topological modulation provides an effective dynamic range in the recorded intensities [44]. The two-dimensional circular grating array is designed for the simultaneous acquisition of scattering images in all possible directions using a single shot [45]. With a phase-stepping process, phase retrieval can be made with a high signal-to-noise ratio (SNR) with a low dose x-ray illumination [46]. Progress in holographic imaging is made with random phase modulation using metasurface. A reference-free holographic image sensor can be made with a random diffuser [47]. High-precision quantitative phase gradient imaging can be made with a single shot using two coded metasurface layers [48]. With phase modulations, phase retrieval methods can be applied to building a novel wavefront sensor. Traditional wavefront sensor such as the Shack-Hartmann wavefront sensor has a lateral resolution limited by the size of micro-lens [49]. The wavefront sensing is made with a 10-megapixel lateral resolution using random phase modulations (RPM) on a spatial light modulator (SLM) [50]. To reduce the modulation defects on an SLM [51], the alternative structured phase modulations (ASPM) were designed for providing a reliable phase modulation on the SLM and increasing the robustness of data acquisition [52]. The structured phase modulation can also be used to shift the high spatial frequency terms into the diffraction-limited imaging setup, which is an effective approach to enhance the resolution of holographic microscopy [53, 54] or phase-shifting interferometry [55, 56].

In this study, we propose to solve the background phase using a modulation-based phase retrieval method. The ASPM can be the phase constraint to avoid stagnation when solving the background phase slowly varying in the spatial domain. The structured phase modulation patterns consisted of periodic phase bars. Two adjacent patterns were orthogonally placed to form one pair of ASPM patterns. The measured wavefront was perturbed by the ASPM patterns, and the modulated intensities were recorded correspondingly. Then, a modified GS algorithm was performed for reconstruction. The modulated intensities are concentrated by the phase gratings, which makes the method robust to noise. The algorithm rapidly converged in 100 iterations when solving the background phase in an experimental setup. After background phase subtraction, the object phase can be reconstructed accurately. A phase plate was experimentally studied and reconstructed using illumination with three background phases. The RPM patterns in ref. 39 [50] were also evaluated by measuring a phase object in the same experimental setup. The root means square error (RMSE) curves showed that the ASPM method had a smaller error value in the reconstruction iterations, which leads to a better reconstruction quality. The ASPM method is reliable for background subtraction and measuring an object’s phase.

Retrieve the Object Phase in a Diffraction Imaging System

A schematic of the diffraction imaging setup used to measure the phase object is shown in Figure 1A. The investigated object had a complex amplitude, where $A_o$ and ${\varphi }_o$ represent the amplitude and phase component of the object, respectively, $x_o$, $y_o$ represent the Cartesian coordinates on the object plane and represent the complex function. When the illumination on the object is a coherent plane wave, it can be expressed as $\tilde{b}=1$. The wavefront emitted from the object is ${\tilde{u}}_o=\tilde{b}·\tilde{o}=\tilde{o}$.

FIGURE 1

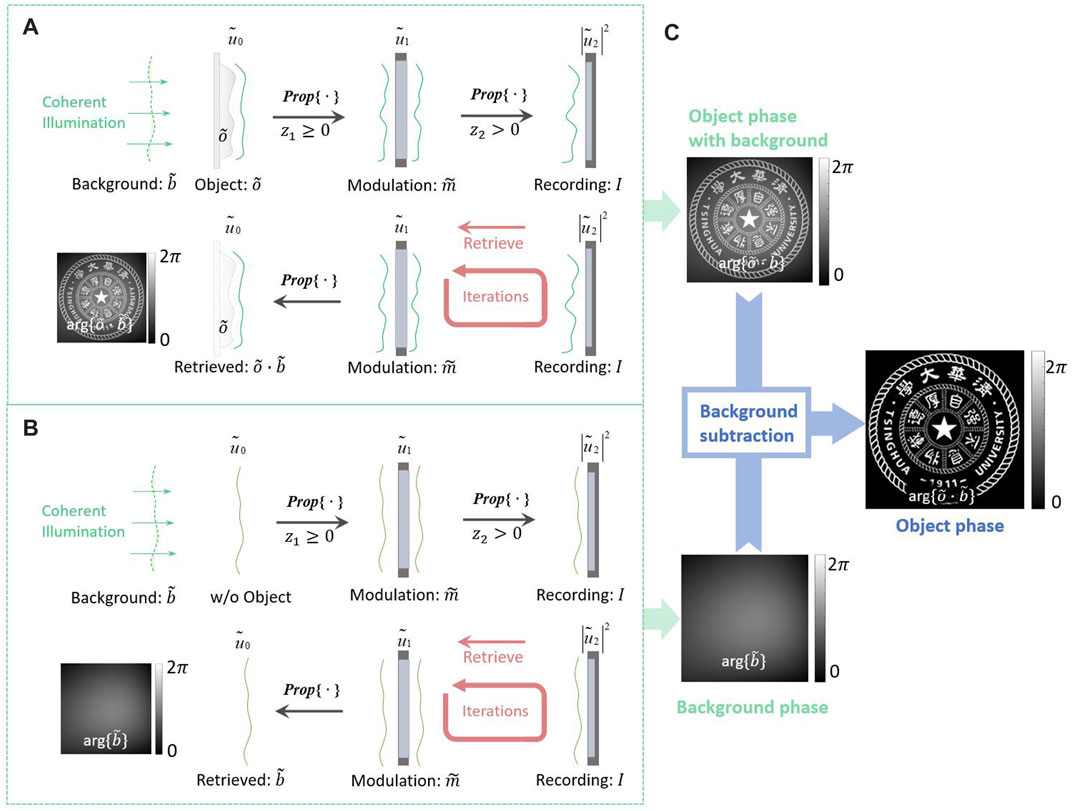
FIGURE 1. Schematic of the diffraction imaging technique when recording and retrieving. (A) Measuring and reconstructing the object phase with the background phase. (B) Measuring and reconstructing the background phase. $\tilde{m}$: modulation or support constraint. (C) Acquiring the object phase with background subtraction.

The illumination has a phase distribution, especially when there are some misalignments and aberrations in the setup. As shown in Figure 1A, the illumination on the object plane is $\tilde{b}=A_b\left(x_o, y_o\right)e^{i{\varphi }_b\left(x_o, y_o\right)}$ where $A_b$ and represents the amplitude and phase components of illumination, respectively. The wavefront emitted from the object is ${\tilde{u}}_o=\tilde{b}·\tilde{o}$. After freely propagating at a distance of z₁, the complex wavefront ${\tilde{u}}_1$ arriving at the modulation plane can be calculated based on the angular spectrum method (ASM) as follows:

${\tilde{u}}_o\left(x_1, y_1\right)=Prop{\left\{{\tilde{u}}_o\left(x_0, y_0\right)\right\}}_{z1}={\mathcal{F}}^{-1}\left\{\mathcal{F}\{{\tilde{u}}_o\left(x_0, y_0\right)\right\}\text{exp}\left[ikz\sqrt{1-{\left(\lambda f_x\right)}^2-{\left(\lambda f_y\right)}^2}\right]\}(1)$

where Prop{·} represents the propagation calculator, $\mathcal{F}${·}represents the Fourier transform $x_1$, $y_1$ represents the coordinates on the modulation plane, and $\lambda$ represents the wavelength of the illumination. On the modulation plane, modulation or support constraints were applied on ${\tilde{u}}_1$, which is ${\tilde{u}}_1·\tilde{m}$. Then, the constrained wavefront was propagated to the recording plane at a distance of z₂. The intensity of the propagated wavefront ${\tilde{u}}_2$ was recorded as the intensity constraint. Note that z₂ must be larger than zero and the phase terms can be coded into the diffraction intensity [57, 58].

A schematic of the retrieval of the object phase is shown in Figure 1A. In the reconstruction process, the phase-retrieval algorithm proceeded between the modulation plane and the recording plane. Using the support or modulation constraint and the recorded intensity constraint ${\left|{\tilde{u}}_2\right|}^2$, the wavefront ${\tilde{u}}_1$ was iteratively reconstructed using phase retrieval algorithms. Then, ${\tilde{u}}_o$ was retrieved by numerically propagating ${\tilde{u}}_1$ back to the object plane.

The background phase must be measured and subtracted from ${\tilde{u}}_o$ and the object phase can be reconstructed. In diffraction imaging, ${\tilde{u}}_1$ was retrieved from ${\left|{\tilde{u}}_2\right|}^2$. After propagating ${\tilde{u}}_o$ to ${\tilde{u}}_1$ and ${\tilde{u}}_2$, the object $\tilde{o}$ and illumination $\tilde{b}$ terms were convoluted with the additional terms, as shown in Eq. 1. $\tilde{b}$ could not be eliminated using a linear operation on ${\left|{\tilde{u}}_2\right|}^2$. The operation commonly used in in-line holography is ${\left|{\tilde{u}}_2\right|}^2/{\left|Prop{\left\{\tilde{b}\right\}}_{{\text{z}}_1+{\text{z}}_2}\right|}^2$. With the linear operation on the diffraction intensity, the reconstruction was performed with an enhancement of the object outline, instead of acquiring the object phase. The same is true for diffraction imaging. For proper reconstruction of $\tilde{o}$, the background $\tilde{b}$ also must be measured and reconstructed, as shown in Figure 1B. The investigated object can then be calculated as $\tilde{o}={\tilde{u}}_o/\tilde{b}$. In this study, the illumination background $\tilde{b}$ was reconstructed using the ASPM method.

Retrieving a Background Phase Using the Alternative Structured Phase Modulation Method

Reconstruct a Complex Wavefront Using the Alternative Structured Phase Modulation Method

A schematic of the ASPM method is shown in Figure 2A. A phase object was illuminated as $\tilde{b}$. Then, the emitted complex wavefront was freely propagated to a liquid crystal on silicon (LCoS), which is a reflective phase-only spatial light modulator. The ASPM patterns were uploaded to the LCoS for phase modulation. The intensities of the modulated wavefronts were recorded using a CMOS sensor. Multiple modulations and intensities were the modulation and intensity constraints for the reconstruction iterations. A modified GS algorithm was used for phase retrieval.

FIGURE 2

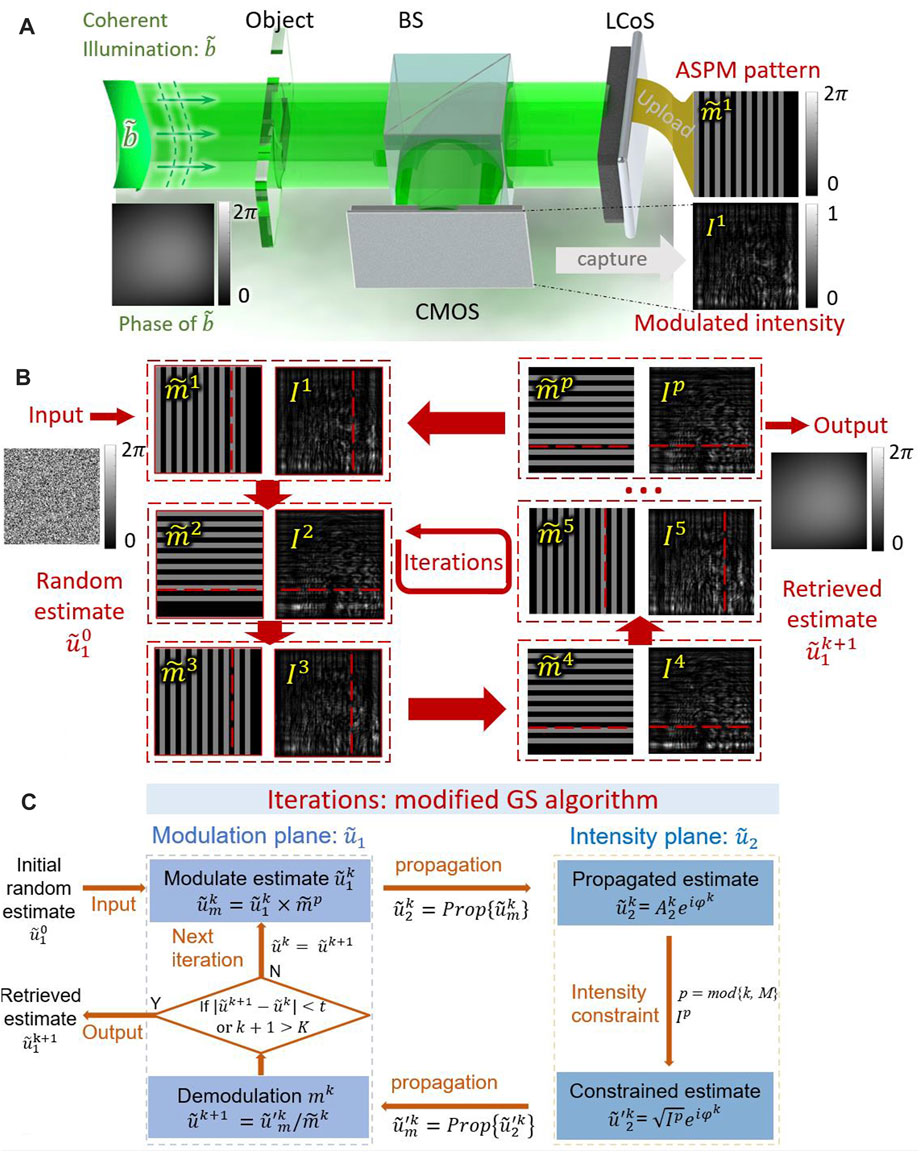
FIGURE 2. (A) Schematic of diffraction imaging using the ASPM method. (B) Uploaded ASPM patterns on the LCoS and corresponding modulated intensities. (C) Flowchart of the iterations using ASPM method. ${\tilde{m}}^1$: the first ASPM modulation pattern. $I^1$ : the first modulated intensity; k: number of iterations; p: number of modulations; M: total number of the constraints; mod{·} is the operator to calculate the remainder after division; t: the preferable value of the calculation error; K: a set maximum number of iterations.

As shown in Figure 2(and, an ASPM pattern is composed of bars and forms a structured phase modulation $\tilde{m}$ when uploaded on a phase-only LCOS. The modulated phase with phase bars is a binary-phase grating. For the ASPM in the x-direction, the normalized transmission function of the modulation is expressed as follows:

${\tilde{m}}_x\left(x, y\right)=\left[e^{i{\varphi }_g}-1\right]·rect\left(\frac{2x}{\text{Δ}}\right)\otimes comb\left(\frac{x+s}{\text{Δ}}\right)+1,(2)$

where ${\varphi }_g$ represents the modulated phase, $\text{Δ }$ represents the period of the phase grating, $\otimes$ represents the convolution operation, and s represents the shift factor after one modulation. For the ASPM in the x-direction, the amplitude and phase terms of the object were modulated in the x-direction. The modulation constraints were applied in the x-direction. To measure an object that covers the x- and y-directions, structured phase modulation was alternatively applied in both directions. After one modulation, the modulated wavefront ${\tilde{u}}_m={\tilde{u}}_1·\tilde{m}$ was propagated to the camera plane at a distance of z₂. The modulated wavefront after propagation is as follows:

${\tilde{u}}_2\left(x_2,y_2\right)=Prop{\left\{\tilde{m}\left(x_1,y_1\right)·{\tilde{u}}_1\left(x_1,y_1\right)\right\}}_{z_2},(3)$

The intensity ${\left|{\tilde{u}}_2\right|}^2$ is the intensity constraint recorded by the camera. As the modulation is a phase grating, the modulated wavefront is transmitted on the diffraction orders of the grating. Based on the principle of diffraction gratings, the diffraction angle $\alpha$ can be calculated from the period of the grating $\text{Δ}$, which is $\text{sin}\alpha =m\lambda /\text{Δ}$, where m is an integer representing the diffraction orders. The first order containing most of the diffraction energy is considered, and m is set to one. If the physical size of ${\tilde{u}}_1$ is $X_1·Y_1$, the size of ${\tilde{u}}_1$ after propagation is diffracted as $\left(X_1+z_2\text{tan}\alpha \right)·\left(Y_1+z_2\text{tan}\alpha \right)$. The physical size of the camera $X_c·Y_c$ should be sufficiently large to capture the modulated intensity.

$X_c\ge \left(X_1+z_2\text{tan}\alpha \right), Y_c\ge \left(Y_1+z_2\text{tan}\alpha \right),(4)$

A modified GS algorithm was used for the ASPM method. A flowchart of the algorithm is presented in Figure 2C. The algorithm alternately propagates the estimated wavefront between the modulation and intensity planes. Conjugate noise was eliminated by the constraints on the two planes. An initial random estimate of the measured wavefront ${\tilde{u}}_1^0$ was first modulated by the ASPM ${\tilde{m}}^0$. The modulation-constrained wavefront, ${\tilde{u}}_m^0={\tilde{u}}_1^0·{\tilde{m}}^0$, was propagated to the intensity plane. Then, the propagated wavefront ${\tilde{u}}_2^0$ was intensity-constrained by replacing its amplitude with the recorded intensity I⁰. The intensity-constrained wavefront $\tilde{u}{\prime }_2^0$ was back-propagated to the modulation plane and refresh the modulation-constrained wavefront $\tilde{u}{\prime }_m^0$. Demodulation was applied as ${\tilde{u}}_1^1=\tilde{u}{\prime }_m^0/{\tilde{m}}^k$ to acquire the estimated wavefront ${\tilde{u}}_1^1$, which is the input for the next iteration and correction. M pairs of modulations and intensity constraints were sequentially applied to the estimates. In the kth iteration, the pth pair of constraints were applied. p is decided as $p=mod\left\{k,M\right\}$, where mod{·} calculates the remainder after division.

After one iteration, the conjugated terms were suppressed with constraints. After k iterations, the refreshed estimated wavefront ${\tilde{u}}_1^k$ was closer to the ground truth of the ${\tilde{u}}_1$. The iterations could be terminated if the calculation error between two iterations is preferable or the maximum number of iterations is achieved. The error evaluation is performed on the phase component using the root mean square error (RMSE):

$RMSE=\sqrt{\frac{1}{X_1{Y}_1}{\displaystyle \sum }_{x,y}{\left|{\varphi }_1^{k+1}\left(x_1,y_1\right)-{\varphi }_1^k\left(x_1,y_1\right)\right|}^2} .(5)$

In the ASPM method, the multiple phase modulations are made by shifting and rotating the phase grating perpendicular to the optical axis. There is significant variance in the captured intensities from the modulations. The diversities in the multiple intensities provide sufficient constraints for good convergence of iterations. More constraints result in a solution closer to the ground truth.

Simulation of Retrieving a Background Phase Using the Alternative Structured Phase Modulation Method

A simulation was performed for retrieving a background phase using the ASPM method. A 200×200-pixel concave wavefront was measured as the ground truth, as shown in Figure 3A. The phase component had a maximum value of 0.5 $\pi$ rad, and the amplitude component had a uniform value of one. The illuminating wavelength was 532 nm. The measured wavefront was modulated using the ASPM method and then numerically propagated at a distance of 20 mm. The numerical propagation was calculated using the angular spectrum method (ASM) in the discrete form:

$Prop{\left\{u\left[\alpha ,\beta \right]\right\}}_{ASM}=DFT\left\{IDFT\left\{u\left[\alpha ,\beta \right]\right\}·\text{exp}\left[-iz\frac{2\pi }{\lambda }\sqrt{1-{\left(\frac{\lambda \xi }{\delta X_{\alpha }}\right)}^2-{\left(\frac{\lambda \eta }{\delta X_{\beta }}\right)}^2}\right]\right\},(6)$

where $\alpha$, $\beta$ and $\xi$, $\eta$ are the indices of the samples in spatial domain and Fourier domain. $X_{\alpha }$ and $X_{\beta }$ are the size of the wavefront, $X_{\alpha },X_{\beta }=200$. $\delta$ represents the sampling period of the numerical calculation, $\delta =3.8\mu m$. DFT{·} and IDFT{·} are the two-dimensional discrete Fourier transform and inverse discrete Fourier transform.

FIGURE 3

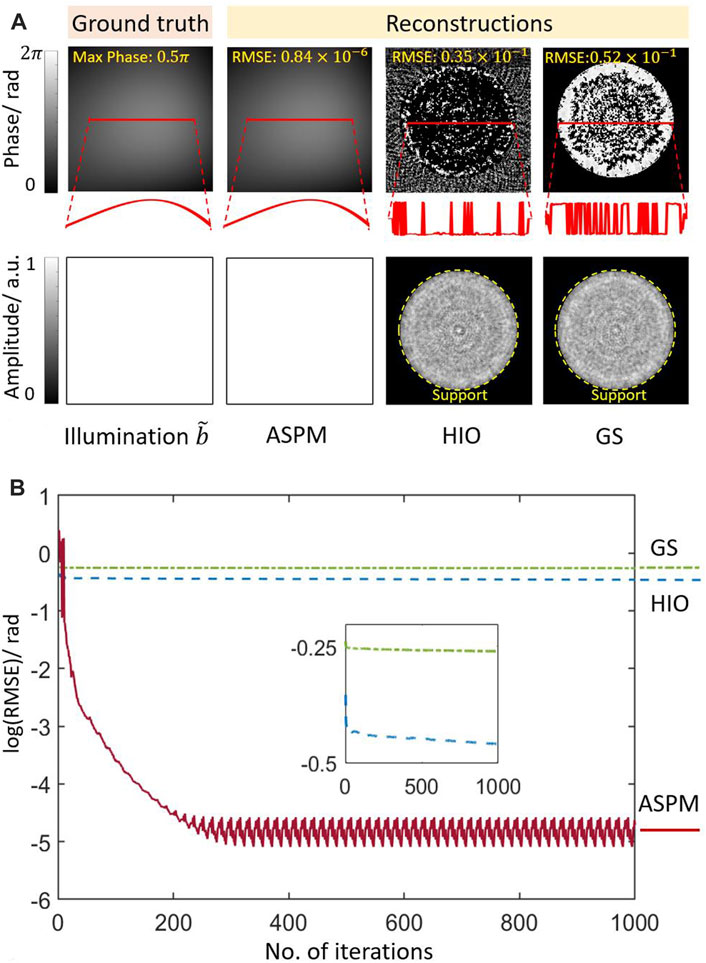
FIGURE 3. (A) Ground truth of the wavefront and reconstructed phase and amplitude components using the ASPM, HIO, and GS methods. (B) The logarithm of the RMSE of the ASPM, GS, and HIO methods with 1000 iterations. log(RMSE): logarithm of the RMSE of the calculated phase and the ground truth.

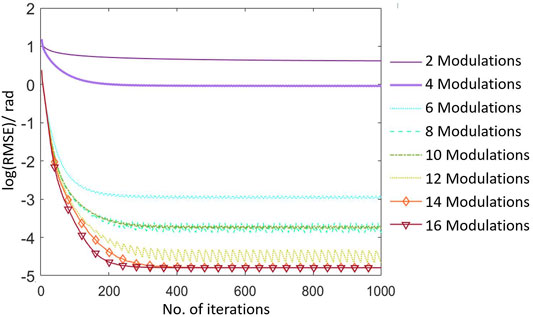
The concave smooth wavefront in Figure 3A was modulated with eight groups of ASPM patterns. The period of each group of the ASPM patterns was from 2 to 16 pixels, with a duty ratio of 50%. After the modulation in both the x- and y- directions, the pattern was shifted with one pixel. A modified GS algorithm was then used to work with the constraints for reconstruction. The logarithm of the RMSE between the ground truth and the calculated phase during the iterations is shown in Figure 4. A total of 1000 iterations were performed during the reconstruction process. When there are 2 or 4 modulations, the reconstruction cannot be made. There are three unknowns in the phase retrieval problem, which are the phase of the diffracted wavefront, phase and amplitude of the measured wavefront. At least three pairs of modulations in x- and y- directions are needed for reconstruction. As the number of modulations increases from 6, the concave smooth phase can be reconstructed successfully. Structured phase patterns are modulation constraints. The corresponding recorded modulated intensities were the intensity constraints. Multiple modulations provide sufficient constraints for noise elimination. The convergence of the iterations and the accuracy of the reconstruction are increased with the number of modulations. In the following simulations and experiments, 16 modulations are used for a good result.

FIGURE 4

FIGURE 4. The logarithm of the RMSE of the ASPM method using 2 to 16 modulations.

With 16 modulations, The ASPM pattern was shifted eight times in both the x- and y-directions. As shown in Figure 3B, during the first 100 iterations, the algorithm converges rapidly, which shows the efficiency of the ASPM method for error elimination. After 300 iterations, the algorithm converges to the final result. Compared to the ground truth, the RM phase component reached approximately 0.84 $\times {10}^{-6}$ after 300 iterations. The RMSE on the amplitude component is approximately 0.65 $\times {10}^{-5}$. In Figure 3B, the RMSE value of the ASPM is oscillatory. There are some residual errors in different iterations or using different constraints. As 16 modulations are sequentially used for reconstruction, the RMSE values oscillate at a period of 16.

The classical GS and hybrid-input-output (HIO) [13] algorithms were also used to measure the concave wavefront. The measured wavefront was the same as that in the ASPM method. To apply the GS and HIO method, the wavefront was constrained with a support region, which was a round central pass filter with a radius of 80 pixels. In the GS algorithm, the wavefront inside the support region was completely passed, and outside the region was blocked. In the HIO algorithm, the wavefront inside the support region was completely passed and outside the region was suppressed by a factor of 0.07 in every iteration. Both the GS and HIO algorithms failed to solve the background phase $\text{arg}\left\{\tilde{b}\right\}$. Compared to the efficient ASPM method, the convergence of the GS and HIO algorithms was marginal in this simulation, as shown in Figure 3B. The HIO algorithms performed better than the GS algorithm on the simulated intensity data. However, in the experiment, the intensity data were recorded with inevitable noise, which may lead to a failure when using the classical method for reconstructing the background wavefront.

In the classical GS and HIO method, the recording and retrieving can be described by Eqs. 7, 8. There is a support region C on the measured complex wavefront $\tilde{u}$. P is the propagation operator. After free propagation, one intensity pattern I is recorded. The retrieval is made by solving the optimization problem and searching for an optimal solution ${\tilde{u}}^{\ast }$ that minimize the error, as shown in Eq. 8. The GS method is based on alternatively propagating the estimation ${\tilde{u}}^{\text{'}}$ between the support C and intensity plane I. For a rough measured phase, there is effective diversity in the diffraction intensity during propagation. The conjugated noise falls out of the support region. In every propagation, the estimation is closer to the optimal solution with an effective support constraint. For a smooth background phase, there is insufficient diversity during the propagation. Support C fails to constrain the estimation in the iterations, which leads to low convergence or stagnation.

$I={\left|PC\tilde{u}\right|}^2,(7)$

${\tilde{u}}^{\ast }={\text{argmin}}_{{\tilde{u}}^{\prime }}\Vert I-{\left|PC\tilde{u}\prime \right|}^2{\Vert }_2.(8)$

In the ASPM method, the recording and retrieving can be described by Eqs. 9, 10. The measured complex wavefront $\tilde{u}$ is modulated by $M_n$ and then be recorded as $I_n$ after propagation. Multiple modulations and recordings provide redundant constraints to solve the optimization problem. As the recorded intensities vary with modulations, there is sufficient diversity for reconstruction. The smooth background phase can be retrieved with good convergence.

$I_n={\left|P{M}_n\tilde{u}\right|}^2,n=\mathrm{1,2,3}\dots ,(9)$

${\tilde{u}}^{\ast }={\text{argmin}}_{{\tilde{u}}^{\prime }}{\displaystyle \sum }_n\Vert I_n-{\left|P{M}_n\tilde{u}\prime \right|}^2{\Vert }_2 ,\text{ n}=1,2,3\dots .(10)$

Experiments on Reconstructing an Object Phase Using the Alternative Structured Phase Modulation

Calibrating the Phase Modulation of a Spatial Light Modulator

In the ASPM method, the designed phase patterns are the modulation constraints in the reconstruction iterations. The modulated phase is a priori information for eliminating conjugated terms. Quantitative phase modulation is required for successful reconstruction. In addition, the ASPM method requires multiple modulations and measurements to guarantee the convergence of the algorithm and robustness to noise. Phase calibration of the LCoS modulation benefits the acquisition of good experimental results.

In this study, phase modulations were made using an LCoS (Holoeye GAEA-2-vis). LCoS is a pixelated digital device that can quantitatively modulate the phase. Owing to the limited manufacturing process and nonlinear optical response of the liquid crystal [59], the LCoS must be calibrated before being used. Many calibration methods have been proposed [60–62]. In this study, the LCoS was calibrated using an efficient and convenient self-referenced calibration method [63, 64]. Using a blazed-grating pattern [65], the phase modulation was measured with an accuracy of 0.06 $\pi$ in the setup of diffraction imaging. The modulation curves before and after calibration are shown in Figure 5A. Using the cubic polynomial fitting method, the phase modulation of the LCoS can be predicted with an error less than the measurement error, as shown in Figure 5B. The modulated phase ${\varphi }_g$ related to the uploaded grayscale g can be predicted using cubic polynomial fitting as follows:

${\varphi }_g=\left(-1.75\times {10}^{-8}{g}^3+1.24\times {10}^{-5}{g}^2+5.32\times {10}^{-3}g-1.66\times {10}^{-2}\right)\times \pi .(11)$

FIGURE 5

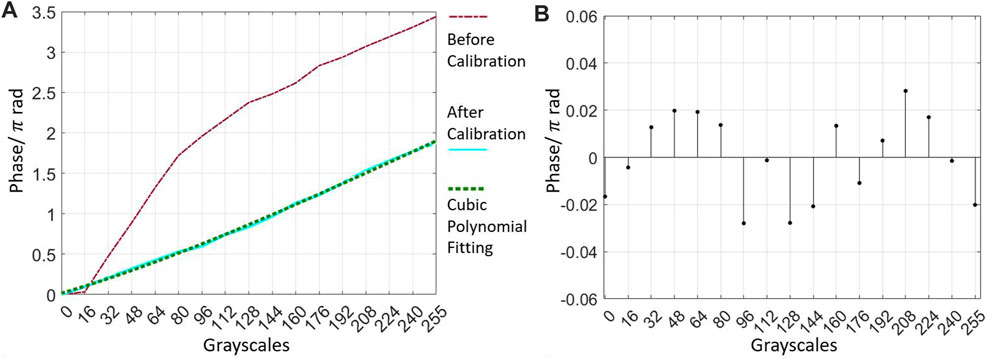
FIGURE 5. (A) Modulation curves of the LCoS before and after calibration and curve using the cubic polynomial fitting method. (B) Residuals of the fitted curve.

Measuring the object phase with background subtraction.

A phase plate was experimentally studied using the ASPM method. The setup was illuminated at 532 nm wavelength. The polarization of the laser was adjusted by a λ⁄2 wave plate. The illumination was experimentally adjusted to be collimated but it was still not a perfect plane wave. The interferogram of the illumination was measured using a shear interferometer (Thorlabs, SI254), as shown in Figure 6A. The fringe pattern shows that the illumination $\tilde{b}$ had a background phase. A phase plate was measured as the object. The intensity pattern of the diffracted wavefront from the object is shown in Figure 6E. The diffracted wavefront was modulated using the ASPM method to reconstruct the phase of the object. The ASPM patterns were uploaded to the calibrated LCoS (Holoeye GAEA-2, 3.a 8 $\mu m$) at 60 Hz refreshing rate. As the LCoS is a birefringent device and the polarization of the incident beam has a great impact on the modulation [66, 67]. The illumination was filtered by a linear polarizer to match the long display axis of the LCoS. The intensities of the modulated wavefront were captured with a CMOS camera (QHY 163, pixel size 3.8 $\mu m$) with 0.01 s exposure time. The period of the ASPM patterns was set to 40 pixels, and the modulated phase was $\pi$. After modulation in both directions, the pattern was shifted by five pixels for the next modulation. Sixteen modulations and captures were made for measuring a wavefront. Sixteen modulations and captures can be made in 0.27 s. Two of the modulation patterns and captured intensities are shown in Figures 6F–I.

FIGURE 6

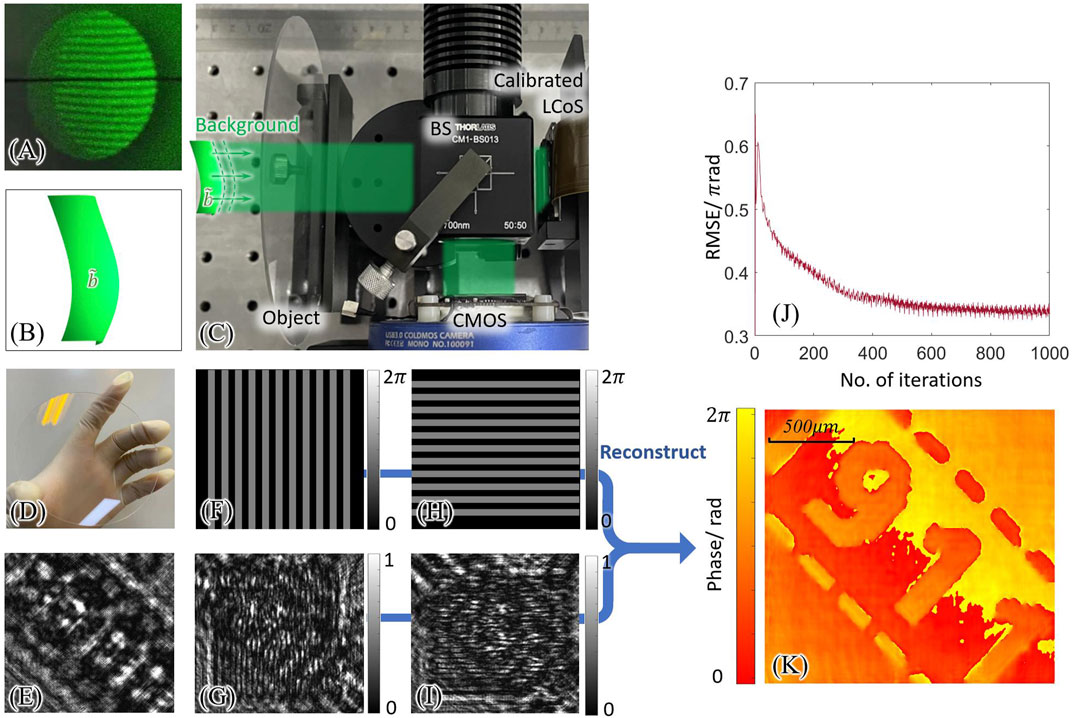
FIGURE 6. Measuring a phase object using illumination with background phase. (A) The fringe pattern on a shearing interferometer (Thorlabs SI254) for measuring the background wavefront. (B) Schematic of the illumination with a background phase. (C) Schematic of a coherent diffraction imaging setup. (D) Picture of the object, a phase plate. (E) Diffraction pattern of the measured object. (F,H): Two of the ASPM patterns in x- and y- direction. (G,F): Captured intensities of the modulated wavefront. (J) The curve of the RMSE between the calculated wavefronts of adjacent iterations. (K) The reconstructed phase of the object with distortion in the illumination.

The complex wavefront ${\tilde{u}}_1$ on the modulation plane was reconstructed using the ASPM method. The RMSEs of the adjacent iterations are shown in Figure 6J. The algorithm converged rapidly in 400 iterations and reached the final result after approximately 800 iterations. The complex wavefront ${\tilde{u}}_o$ emitted from the phase object was calculated by back-propagating ${\tilde{u}}_1$ to the object plane. As shown in Figure 6K, the phase can be distinguished as a character of ‘1911’, which is the founding year of Tsinghua University. However, the wavefront ${\tilde{u}}_o$ is the multiple products of $\tilde{o}$ and $\tilde{b}$, ${\tilde{u}}_o=\tilde{b}·\tilde{o}$.The phase of ${\tilde{u}}_o$ does not represent the object phase. The phase term of illumination $\tilde{b}$ must be measured and subtracted.

Using the ASPM method, illumination $\tilde{b}$ was measured individually during the experiment. As shown in Figure 7A, the phase of $\tilde{b}$ indicates that the illumination on the object was slightly oblique and nonuniform in the experiment. The RMSE values during the reconstruction iterations are shown in Figure 7B. The ASPM method has good convergence in solving the background phase using the experimental data with noise. To calculate $\tilde{o}$, the illumination $\tilde{b}$ must be subtracted from the measured ${\tilde{u}}_o$. The phase of the object after subtraction is shown in Figure 7D. The average phase difference of the character was measured to be approximately 2.9 rad, which matched the designed value of the phase plate.

FIGURE 7

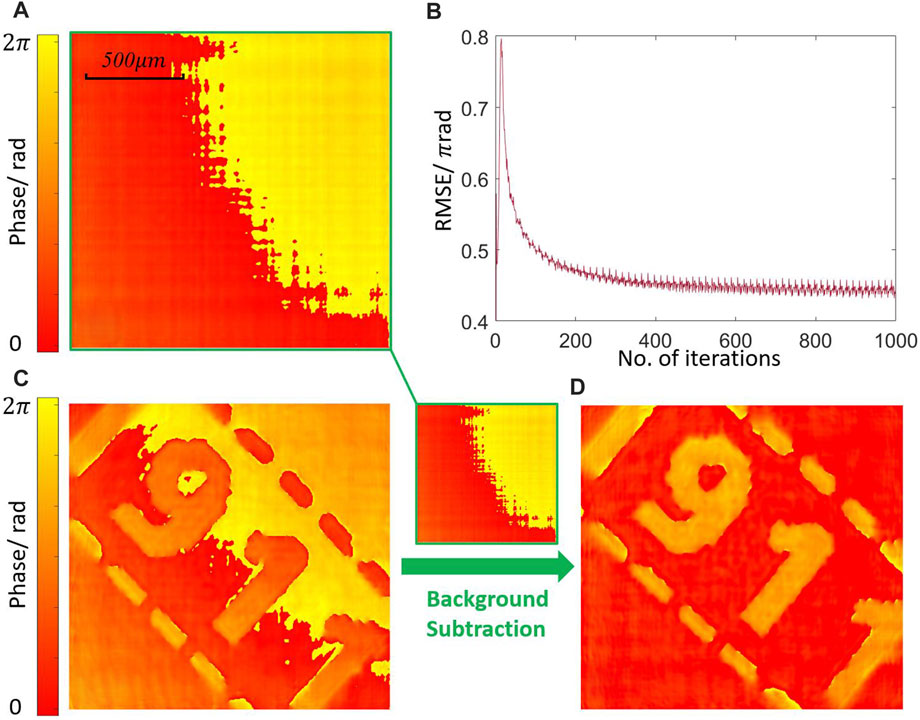
FIGURE 7. (A) Reconstructed phase of the illumination in the experiment using the ASPM method. (B) RMSE during reconstruction. (C) The reconstructed phase of the object with an illumination background. (D) Object phase with background subtraction.

In the experiment, the illumination was expanded, and a schematic of the phase profile of the illumination is shown in Figure 8A. The phase plate was measured experimentally using three sections of illumination. After modulations and captures using the central section of the illumination, the next sections at an interval of 250 pixels were used to illuminate the object. Using the ASPM method, the wavefronts of the three illumination sections were reconstructed. The background phases of the illumination sections are shown in Figure 8B. After subtracting the phase under illumination, the phase of the object was measured under the three illumination sections. The phase profiles before and after subtraction are shown in Figures 8C, D. The phase values along the dotted line in Figures 8C, D are plotted in Figures 9A, B. Before the subtraction, the phase was visually distinguished, but difficult to evaluate quantitatively. The strong background phases destroyed the investigated phase from the object. The phase profile of the reconstructed wavefront could not represent the object phase. After subtraction, the phase values along the line were quantitatively evaluated. The measured phase values under different illuminations matched well.

FIGURE 8

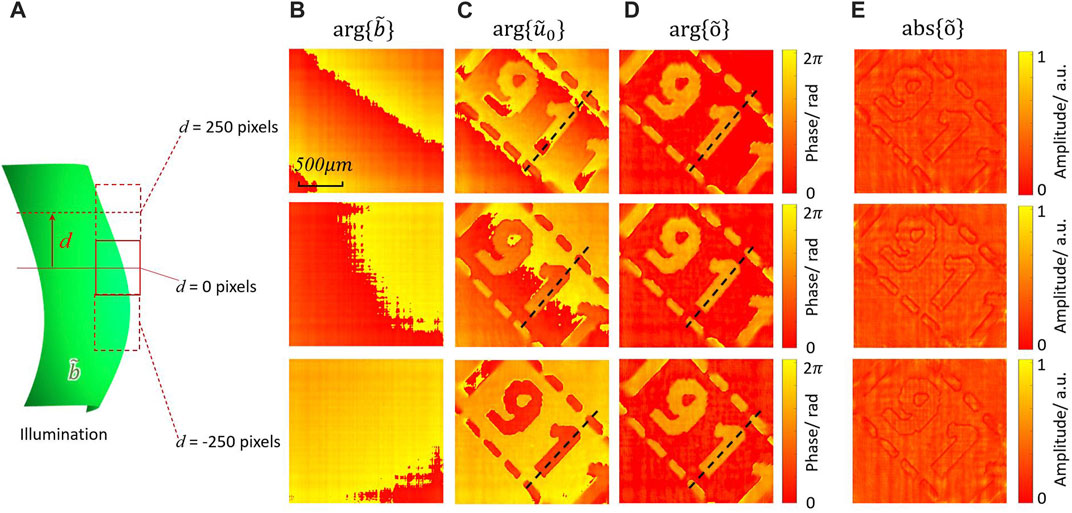
FIGURE 8. Measuring the phase object using three sections of the illumination. (A) Schematic of the illumination in the experiment. (B) The reconstructed phase of different sections of the illumination. (C) Reconstructed object phase without background subtraction. (D) Reconstructed object phase with background subtraction. (E) Reconstructed object amplitude with background subtraction.

FIGURE 9

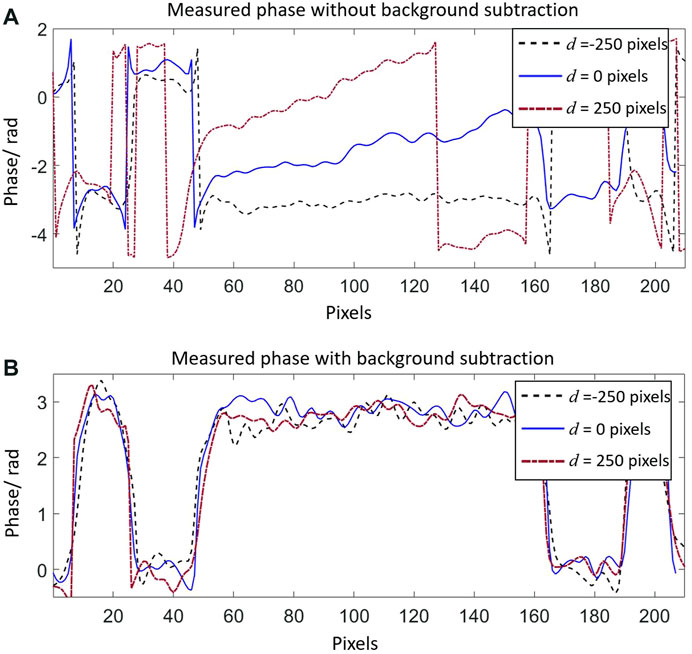
FIGURE 9. (A) Measured phase along the line of the object without background subtraction. (B) Measured phase along the line with background subtraction.

Evaluation of the Alternative Structured Phase Modulation and RPM Methods

The ASPM and RPM methods were experimentally evaluated. Sixteen ASPM patterns with a period of 40 pixels were used for modulation. For comparison, sixteen RPM patterns with a pitch size of 40 pixels were used for modulation. One of the RPM and ASPM patterns is shown in Figures 10A, B. Using the setup in Figures 6A, C phase object illuminated with a background phase was studied using the ASPM and RPM methods, respectively. Using the two methods, the phase of the background and object can be iteratively reconstructed, as shown in Figures 10C–H. The RMSEs curves of the two methods during iterations are shown in Figures 10I, J, which shows that the ASPM method has a smaller error during the reconstruction for a background phase and object phase. Compared to the RPM method, the ASPM method has a better reconstruction quality for the background phase and object phase.

FIGURE 10

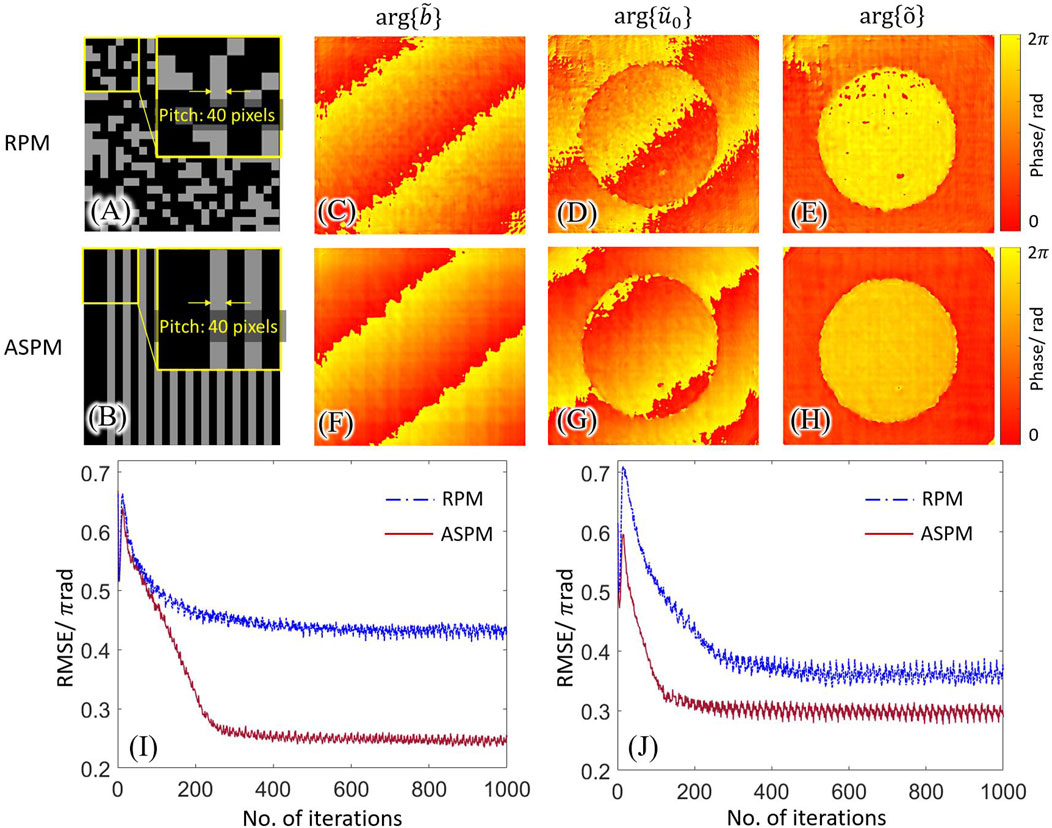
FIGURE 10. Evaluation of the ASPM and RPM methods. (A) One of the sixteen RPM patterns. (B) One of the sixteen ASPM patterns. (C–E) Reconstructed background phase, object phase without background subtraction, and object phase with background subtraction using RPM method. (F–H) Reconstructed background phase, object phase without background subtraction, and object phase with background subtraction using the ASPM method. (I) RMSE in the background reconstruction using the ASPM and RPM methods. (J) RMSE in the object phase reconstruction using the ASPM and RPM methods.

In the proposed method, the spatial light modulator is used for phase modulation. SLM is a digitalized device and has a limited modulation bandwidth. The phases in the RPM are randomly distributed in a high spatial complexity, which makes the RPM hard to be accurately modulated using an available SLM. The phases in the ASPM are the same in one direction and vary periodically in the other direction. Compared to the RPM, the ASPM have lower complexity and is friendly for SLM modulation. Besides, there us environmental noise during the experiment. The ASPM patterns act as the phase gratings and concentrate the modulated intensities, which provides robustness to noise.

Conclusion

In this study, the ASPM method was used to retrieve the background phase in the illumination. Three statics background phases were reconstructed in a diffraction imaging setup, which is difficult to use in traditional phase-retrieval methods. A phase plate was investigated under three background illuminations, and the object phase was reconstructed. The ASPM method can retrieve the complex wavefront gathered from a lens set. With the ASPM method, various wavefront sensing techniques can be used for quantitative phase imaging. The method is also capable of measuring an object with a phase slowly varying in the spatial domain. The background phases in various types of imaging setups, such as in-line holography, can be retrieved and compensated using the ASPM method. In this work, the modulations were made with an SLM working at a 60 Hz refreshing rate. Sixteen acquisitions for measuring a background phase can be made in 0.27 s. The acquisition time can be reduced by using a faster modulation device, such as ferroelectric SLM.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LC and FY conceived and supervised the project. RL performed experiments and data analysis. FY, RL, and LC contributed to data analysis. RL and LC wrote the draft of the manuscript; All the authors edited the manuscript.

Funding

National Nature Science Foundation of China (61775117).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhou W, Yu Y, Asundi A. Study on Aberration Suppressing Methods in Digital Micro-holography. Opt Lasers Eng (2009) 47(2):264–70. doi:10.1016/j.optlaseng.2008.04.026

CrossRef Full Text | Google Scholar

2. Javidi B, Carnicer A, Anand A, Barbastathis G, Chen W, Ferraro P, et al. Roadmap on Digital Holography [Invited]. Opt. Express (2021) 29(22):35078–118. doi:10.1364/OE.435915

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yan F, Yan H, Yu Y, Zhou W, Asundi A. The Suppression of Phase Error by Applying Window Functions to Digital Holography. Opt Lasers Eng (2016) 86:206–15. doi:10.1016/j.optlaseng.2016.05.022

CrossRef Full Text | Google Scholar

4. Sheridan JT, Kostuk RK, Gil AF, Wang Y, Lu W, Zhong H, et al. Roadmap on Holography. J Opt (2020) 22(12):123002. doi:10.1088/2040-8986/abb3a4

CrossRef Full Text | Google Scholar

5. Paturzo M, Pagliarulo V, Bianco V, Memmolo P, Miccio L, Merola F, et al. Digital Holography, a Metrological Tool for Quantitative Analysis: Trends and Future Applications. Opt Lasers Eng (2018) 104:32–47. doi:10.1016/j.optlaseng.2017.11.013

CrossRef Full Text | Google Scholar

6. Miao J, Charalambous P, Kirz J, Sayre D. Extending the Methodology of X-Ray Crystallography to Allow Imaging of Micrometre-Sized Non-crystalline Specimens. Nature (1999) 400(6742):342–4. doi:10.1038/22498

CrossRef Full Text | Google Scholar

7. Zuo C, Li J, Sun J, Fan Y, Zhang J, Lu L, et al. Transport of Intensity Equation: A Tutorial. Opt Lasers Eng (2020) 135:106187. doi:10.1016/j.optlaseng.2020.106187

CrossRef Full Text | Google Scholar

8. Latychevskaia T, Longchamp J-N, Fink H-W. When Holography Meets Coherent Diffraction Imaging. Opt. Express (2012) 20(27):28871–92. doi:10.1364/OE.20.028871

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wang K, Di J, Li Y, Ren Z, Kemao Q, Zhao J. Transport of Intensity Equation from a Single Intensity Image via Deep Learning. Opt Lasers Eng (2020) 134:106233. doi:10.1016/j.optlaseng.2020.106233

CrossRef Full Text | Google Scholar

10. Gao Y, Cao L. High-Fidelity Pixel-Super-Resolved Complex Field Reconstruction via Adaptive Smoothing. Opt. Lett. (2020) 45(24):6807–10. doi:10.1364/OL.409697

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ozcan A, McLeod E. Lensless Imaging and Sensing. Annu. Rev. Biomed. Eng. (2016) 18(1):77–102. doi:10.1146/annurev-bioeng-092515-010849

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Rivenson Y, Zhang Y, Günaydın H, Teng D, Ozcan A. Phase Recovery and Holographic Image Reconstruction Using Deep Learning in Neural Networks. Light Sci Appl (2018) 7(2):17141. doi:10.1038/lsa.2017.141

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Migukin A, Agour M, Katkovnik V. Phase Retrieval in 4f Optical System: Background Compensation and Sparse Regularization of Object with Binary Amplitude. Appl. Opt. (2013) 52(1):A269–A80. doi:10.1364/AO.52.00A269

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Min J, Yao B, Gao P, Ma B, Yan S, Peng F, et al. Wave-Front Curvature Compensation of Polarization Phase-Shifting Digital Holography. optik (2012) 123:1525–9. doi:10.1016/j.ijleo.2011.09.018

CrossRef Full Text | Google Scholar

15. He X, Tao H, Pan X, Liu C, Zhu J. High-Quality Laser Beam Diagnostics Using Modified Coherent Phase Modulation Imaging. Opt. Express (2018) 26(5):6239–48. doi:10.1364/OE.26.006239

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cuche E, Marquet P, Depeursinge C. Spatial Filtering for Zero-Order and Twin-Image Elimination in Digital off-Axis Holography. Appl. Opt. (2000) 39(23):4070–5. doi:10.1364/AO.39.004070

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Seo KW, Choi YS, Seo ES, Lee SJ. Aberration Compensation for Objective Phase Curvature in Phase Holographic Microscopy. Opt. Lett. (2012) 37(23):4976–8. doi:10.1364/OL.37.004976

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Di J, Zhao J, Sun W, Jiang H, Yan X. Phase Aberration Compensation of Digital Holographic Microscopy Based on Least Squares Surface Fitting. Opt Commun (2009) 282(19):3873–7. doi:10.1016/j.optcom.2009.06.049

CrossRef Full Text | Google Scholar

19. Yu H, Jia S, Dong J, Huang D, Xu S. Phase Curvature Compensation in Digital Holographic Microscopy Based on Phase Gradient Fitting and Optimization. J. Opt. Soc. Am. A (2019) 36(12):D1–D6. doi:10.1364/JOSAA.36.0000D1

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Miccio L, Alfieri D, Grilli S, Ferraro P, Finizio A, De Petrocellis L, et al. Direct Full Compensation of the Aberrations in Quantitative Phase Microscopy of Thin Objects by a Single Digital Hologram. Appl. Phys. Lett. (2007) 90(4):041104. doi:10.1063/1.2432287

CrossRef Full Text | Google Scholar

21. Colomb T, Montfort F, Kühn J, Aspert N, Cuche E, Marian A, et al. Numerical Parametric Lens for Shifting, Magnification, and Complete Aberration Compensation in Digital Holographic Microscopy. J. Opt. Soc. Am. A (2006) 23(12):3177–90. doi:10.1364/JOSAA.23.003177

CrossRef Full Text | Google Scholar

22. Jianglei D., Jianlin Z., Qi F., Hongzhen J., Weiwei S. Phase Correction of Wavefront Reconstruction in Digital Holographic Microscopy. Acta Optica Sinica (2008) 28(1):56–61. doi:10.3788/aos20082801.0056

CrossRef Full Text | Google Scholar

23. Choi I, Lee K, Park Y. Compensation of Aberration in Quantitative Phase Imaging Using Lateral Shifting and Spiral Phase Integration. Opt. Express (2017) 25(24):30771–9. doi:10.1364/OE.25.030771

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Baek Y, Hugonnet H, Park Y. Pupil-Aberration Calibration with Controlled Illumination for Quantitative Phase Imaging. Opt. Express (2021) 29(14):22127–35. doi:10.1364/OE.426080

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Stadelmaier A, Massig JH. Compensation of Lens Aberrations in Digital Holography. Opt. Lett. (2000) 25(22):1630–2. doi:10.1364/OL.25.001630

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Liu Q, Wang Y, He J, Ji F. Phase Shift Extraction and Wavefront Retrieval from Interferograms with Background and Contrast Fluctuations. J. Opt. (2015) 17(2):025704. doi:10.1088/2040-8978/17/2/025704

CrossRef Full Text | Google Scholar

27. Yatabe K, Ishikawa K, Oikawa Y. Simple, Flexible, and Accurate Phase Retrieval Method for Generalized Phase-Shifting Interferometry. J. Opt. Soc. Am. A (2017) 34(1):87–96. doi:10.1364/JOSAA.34.000087

PubMed Abstract | CrossRef Full Text | Google Scholar

28.RF Oliver, S Johannes, B Albrecht, and S Horst, editors. Measurement of the Wave Aberrations of Holographic Optical Lens Elements. Prague, Czech Republic: ProcSPIE (1993).

Google Scholar

29. Brady DJ, Choi K, Marks DL, Horisaki R, Lim S. Compressive Holography. Opt. Express (2009) 17(15):13040–9. doi:10.1364/OE.17.013040

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Huang Z, Memmolo P, Ferraro P, Cao L. Dual-Plane Coupled Phase Retrieval for Non-prior Holographic Imaging. PhotoniX (2022) 3(1):3. doi:10.1186/s43074-021-00046-w

CrossRef Full Text | Google Scholar

31. Gerchberg RWA. Practical Algorithm for the Determination of Phase from Image and Diffraction Plane Pictures. Optik (1971) 35(2):237

Google Scholar

32. Fienup JR. Reconstruction of an Object from the Modulus of its Fourier Transform. Opt. Lett. (1978) 3(1):27–9. doi:10.1364/OL.3.000027

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Fienup JR. Reconstruction of a Complex-Valued Object from the Modulus of its Fourier Transform Using a Support Constraint. J. Opt. Soc. Am. A (1987) 4(1):118–23. doi:10.1364/JOSAA.4.000118

CrossRef Full Text | Google Scholar

34. Zhang F, Chen B, Morrison GR, Vila-Comamala J, Guizar-Sicairos M, Robinson IK. Phase Retrieval by Coherent Modulation Imaging. Nat Commun (2016) 7(1):13367. doi:10.1038/ncomms13367

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wang B, Wang Q, Lyu W, Zhang F. Modulator Refinement Algorithm for Coherent Modulation Imaging. Ultramicroscopy (2020) 216:113034. doi:10.1016/j.ultramic.2020.113034

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Paxman RG, Fienup JR, Clinthorne JT. The Effects of Tapered Illumination and Fourier Intensity Errors on Phase Retrieval. Proc SPIE (1988) 0828. doi:10.1117/12.942098

CrossRef Full Text | Google Scholar

37. Fienup JR. Phase Retrieval Algorithms: A Comparison. Appl. Opt. (1982) 21(15):2758–69. doi:10.1364/AO.21.002758

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Almoro PF, Pham QD, Serrano-Garcia DI, Hasegawa S, Hayasaki Y, Takeda M, et al. Enhanced Intensity Variation for Multiple-Plane Phase Retrieval Using a Spatial Light Modulator as a Convenient Tunable Diffuser. Opt. Lett. (2016) 41(10):2161–4. doi:10.1364/OL.41.002161

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Almoro PF, Waller L, Agour M, Falldorf C, Pedrini G, Osten W, et al. Enhanced Deterministic Phase Retrieval Using a Partially Developed Speckle Field. Opt. Lett. (2012) 37(11):2088–90. doi:10.1364/OL.37.002088

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zhang F, Pedrini G, Osten W. Phase Retrieval of Arbitrary Complex-Valued Fields through Aperture-Plane Modulation. Phys. Rev. A (2007) 75(4):043805. doi:10.1103/PhysRevA.75.043805

CrossRef Full Text | Google Scholar

41. Rodenburg JM, Faulkner HML. A Phase Retrieval Algorithm for Shifting Illumination. Appl. Phys. Lett. (2004) 85(20):4795–7. doi:10.1063/1.1823034

CrossRef Full Text | Google Scholar

42. Zheng G, Horstmeyer R, Yang C. Wide-Field, High-Resolution Fourier Ptychographic Microscopy. Nat Phot (2013) 7(9):739–45. doi:10.1038/nphoton.2013.187

CrossRef Full Text | Google Scholar

43. Konda PC, Loetgering L, Zhou KC, Xu S, Harvey AR, Horstmeyer R. Fourier Ptychography: Current Applications and Future Promises. Opt. Express (2020) 28(7):9603–30. doi:10.1364/OE.386168

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Li R, Cao L. Complex Wavefront Sensing Based on Coherent Diffraction Imaging Using Vortex Modulation. Sci Rep (2021) 11(1):9019. doi:10.1038/s41598-021-88523-x

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Kagias M, Wang Z, Villanueva-Perez P, Jefimovs K, Stampanoni M. 2d-Omnidirectional Hard-X-Ray Scattering Sensitivity in a Single Shot. Phys. Rev. Lett. (2016) 116(9):093902. doi:10.1103/PhysRevLett.116.093902

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wang Z, Huang Z, Chen Z, Zhang L, Jiang X, Kang K, et al. Low-Dose Multiple-Information Retrieval Algorithm for X-Ray Grating-Based Imaging. Nucl Instrum Methods Phys Res Sect A Accel Spectrom Detect Assoc Equip (2011) 635(1):103–7. doi:10.1016/j.nima.2011.01.079

CrossRef Full Text | Google Scholar

47. Lee K, Park Y. Exploiting the Speckle-Correlation Scattering Matrix for a Compact Reference-free Holographic Image Sensor. Nat Commun (2016) 7(1):13359. doi:10.1038/ncomms13359

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Kwon H, Arbabi E, Kamali SM, Faraji-Dana M, Faraon A. Single-Shot Quantitative Phase Gradient Microscopy Using a System of Multifunctional Metasurfaces. Nat. Photonics (2020) 14(2):109–14. doi:10.1038/s41566-019-0536-x

CrossRef Full Text | Google Scholar

49. Platt BC, Shack R. History and Principles of Shack-Hartmann Wavefront Sensing. J Refract Surg (2001) 17(5):S573–7. Epub 2001/10/05. doi:10.3928/1081-597X-20010901-13

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Wu Y, Sharma MK, Veeraraghavan A. WISH: Wavefront Imaging Sensor with High Resolution. Light Sci Appl (2019) 8(1):44. doi:10.1038/s41377-019-0154-x

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Zhang Z, You Z, Chu D. Fundamentals of Phase-Only Liquid Crystal on Silicon (Lcos) Devices. Light Sci Appl (2014) 3:e213. doi:10.1038/lsa.2014.94

CrossRef Full Text | Google Scholar

52. Li R, Cao L. Complex Wavefront Sensing Based on Alternative Structured Phase Modulation. Appl. Opt. (2021) 60(4):A48–A53. doi:10.1364/AO.405630

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Gao P, Pedrini G, Osten W. Structured Illumination for Resolution Enhancement and Autofocusing in Digital Holographic Microscopy. Opt. Lett. (2013) 38(8):1328–30. doi:10.1364/OL.38.001328

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Zheng J, Gao P, Yao B, Ye T, Lei M, Min J, et al. Digital Holographic Microscopy with Phase-shift-free Structured Illumination. Phot. Res. (2014) 2(3):87–91. doi:10.1364/PRJ.2.000087

CrossRef Full Text | Google Scholar

55. Gao P, Pedrini G, Osten W. Phase Retrieval with Resolution Enhancement by Using Structured Illumination. Opt. Lett. (2013) 38(24):5204–7. doi:10.1364/OL.38.005204

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ma Y, Wen K, Liu M, Zheng J, Chu K, Smith ZJ, et al. Recent Advances in Structured Illumination Microscopy. J. Phys. Photonics (2021) 3(2):024009. doi:10.1088/2515-7647/abdb04

CrossRef Full Text | Google Scholar

57. Zhang J, Sun J, Chen Q, Zuo C. Resolution Analysis in a Lens-free On-Chip Digital Holographic Microscope. IEEE Trans. Comput. Imaging (2020) 6:697–710. doi:10.1109/TCI.2020.2964247

CrossRef Full Text | Google Scholar

58. Fan Y, Li J, Lu L, Sun J, Hu Y, Zhang J, et al. Smart Computational Light Microscopes (Sclms) of Smart Computational Imaging Laboratory (Scilab). PhotoniX (2021) 2(1):19. doi:10.1186/s43074-021-00040-2

CrossRef Full Text | Google Scholar

59. Cirtoaje C, Petrescu E. The Influence of Single-Walled Carbon Nanotubes on the Dynamic Properties of Nematic Liquid Crystals in Magnetic Field. Materials (2019) 12(24):4031. doi:10.3390/ma12244031

PubMed Abstract | CrossRef Full Text | Google Scholar

60. DeMars LA, Mikuła-Zdańkowska M, Falaggis K, Porras-Aguilar R. Single-Shot Phase Calibration of a Spatial Light Modulator Using Geometric Phase Interferometry. Appl. Opt. (2020) 59(13):D125–D30. doi:10.1364/AO.383610

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Arias A, Paniagua-Diaz AM, Prieto PM, Roca J, Artal P. Phase-Only Modulation with Two Vertical Aligned Liquid Crystal Devices. Opt. Express (2020) 28(23):34180–9. doi:10.1364/OE.410429

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Shen Y, Hu Z, Wu D, Ma C, Liu Y. An Open-Source, Accurate, and Iterative Calibration Method for Liquid-Crystal-Based Spatial Light Modulators. Opt Commun (2021) 495:127108. doi:10.1016/j.optcom.2021.127108

CrossRef Full Text | Google Scholar

63. Li R, Gao Y, Cao L. In Situ Calibration for a Phase-Only Spatial Light Modulator Based on Digital Holography. Opt. Eng. (2020) 59(5):1–10. doi:10.1117/1.OE.59.5.053101

CrossRef Full Text | Google Scholar

64. Gao Y, Li R, Cao L. Self-Referenced Multiple-Beam Interferometric Method for Robust Phase Calibration of Spatial Light Modulator. Opt. Express (2019) 27(23):34463–71. doi:10.1364/OE.27.034463

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Márquez A, Martínez-Guardiola F, Francés J, Neipp C, Ramírez M, Calzado E, et al. Analytical Modeling of Blazed Gratings on Two-Dimensional Pixelated Liquid Crystal on Silicon Devices. Opt Eng (2020) 59(4):041208. doi:10.1117/1.OE.59.4.041208

CrossRef Full Text | Google Scholar

66. Falldorf C, von Kopylow C, Bergmann RB. Wave Field Sensing by Means of Computational Shear Interferometry. J. Opt. Soc. Am. A (2013) 30(10):1905–12. doi:10.1364/JOSAA.30.001905

CrossRef Full Text | Google Scholar

67. Agour M, Falldorf C, Bergmann RB. Investigation of Composite Materials Using Slm-Based Phase Retrieval. Opt. Lett. (2013) 38(13):2203–5. doi:10.1364/OL.38.002203

PubMed Abstract | CrossRef Full Text | Google Scholar