- 1School of Science, China University of Geosciences, Beijing, China
- 2Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing, China
- 3Science and Technology on Solid-State Laser Laboratory, Beijing, China
- 4School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing, China
- 5Qilu Aerospace Information Research Institute, Jinan, China
A gradual edge-enhanced ghost imaging method with pseudo-thermal light is proposed in both the theory and experiment. In the experiment, a phase object and fractional spiral phase filter are placed symmetrically in the imaging plane of the pseudo-thermal light source in the distributed test and reference beams of the lensless ghost imaging system. The procedure of gradual edge-enhanced ghost imaging is carried out by modulating the fractional topological charge from 0 to 1. We observe that the brightness of the object edge increases with the increase of the fractional topological charge. It is also found that the intensity distribution is uniform and isotropic when the topological charge is an integer; otherwise, the intensity distribution is not uniform. Theoretical analysis is also provided. The proposed gradual edge-enhanced ghost imaging scenario releases the position limitation in the Fourier plane for the filter of the traditional phase filtering imaging process. The method is believed to have prospective applications in microscopic imaging and biomedical detection.
1 Introduction
As early as the 1930s, Zernike first proposed the phase contrast imaging method and won the Nobel Prize for employing this technology to observe the structure of living cells in 1953 [1]. Different from the traditional optical microscopy, the phase contrast method can convert the invisible phase distributions into visible optical field intensity [2–4] to highlight the edges of an object with phase changes, which is called edge enhancement [5–7]. Edge-enhanced imaging, a kind of image processing, can extract the contour features of an image, so that the boundary of the target can be displayed more clearly, and the position of the target can be determined. Since then, the phase contrast technology has been further developed to expand its applications from the initial differential interference phase contrast microscopy and interference reflection contrast microscopy to the later spiral phase contrast (SPC) microscopy [8, 9]. In the 1990s, researchers realized the imaging of one-dimensional (1D) and two-dimensional (2D) phase objects by employing the SPC technology [10, 11]. In 2006, the homogeneous enhancement of the amplitude and phase objects was achieved using SPC technology combined with optical microscopy [12]. In 2015, Prof. Lixiang Chen’s research group used a fractional spiral phase filter (SPF) in the Fourier plane of the lens to achieve the isotropic edge enhancement with laser [13, 14].
SPC was applied in quantum imaging in 2009 by Jack et al. [15]. The entangled two-photon was separated using a beam splitter (BS). The pure phase object and the SPF were symmetrically placed in the image plane of the entangled two photons. The phase objects can be recognized through edge enhancement through the two-photon coincident measurement. However, ghost imaging can not only be implemented with an entangled two-photon light source but also be achieved with incoherent thermal light [16–20]. The quantum entangled source behaves like a mirror, whereas the classical thermal source acts like a phase-conjugate mirror in the ghost imaging [21]. It has been demonstrated that intensity fluctuations give rise to the formation of correlations in the OAM components and angular positions of random light in [22]. It was then proved that the spatial signatures and phase information of an object with rotational symmetries can be identified using classical OAM correlations in random light [23]. Furthermore, an experimental scenario of distributed angular double-slit interference based on the OAM correlations of pseudo-thermal light was accomplished in [24]. In 2020, we proved the classical physical essence of the spatial dimension of the non-local edge-enhanced ghost imaging system by making use of orientated SPF [25]. Inspired by the previous research, we proposed the scenario here to observe the phase object edge-enhanced imaging with a fractional-order spiral phase filter based on the OAM components of incoherent random light. The experimental results proved that the enhanced edge intensity of the image increased with the increase of the topological charge from 0 to 1. The reason why the edge brightness increases with the increase of the fractional orbital angular momentum (OAM) is due to the pseudo-thermal light OAM correlation and eigenvalue decomposition of the fractional topological charge of the SPF. The theoretical analysis finds good agreement with the experimental results. The proposed scenario can accomplish the continuously modulated edge-enhanced ghost imaging even with the incoherent light source.
2 Experiment
A schematic diagram of the experimental setup is shown in Figure 1. The input light is a Gaussian beam derived from a 632.8 nm He–Ne laser (THORLABS, HNL225RB). The light beam illuminates a slowly rotating glass (RG) with the rotation angular velocity of 0.013 rad/s to produce a pseudo-thermal light beam. P1 and P2 are polarizers to modulate the intensity of the laser beam. N is a telescope (×2 magnification) to collimate and expand the transverse size of the laser beam. Radiation from a chaotic pseudo-thermal source via an Iris is then divided into two optical paths, namely, a test beam and a reference beam, by a 50:50 non-polarizing BS. The pseudo-thermal light source is imaged, by two convex lenses L1 and L2, to the transverse planes of the spatial light modulators (SLMs, HOLOEYE, PLUTO-2-VIS-016), a device with full high-definition resolutions of 1920 × 1080 square pixels. The focal length of the convex lens is 25 cm. Then, the SLM1 and SLM2, located at a distance of 50 cm from the biconvex lens, are re-imaged to the charge-coupled devices (CCDs, MTV-1881EX) with the resolution of 575 × 767 square pixels placed at the end of each light beam, respectively. Two beams are connected with a data acquisition card embedded in a personal computer, and the intensity correlation calculation can be carried out.
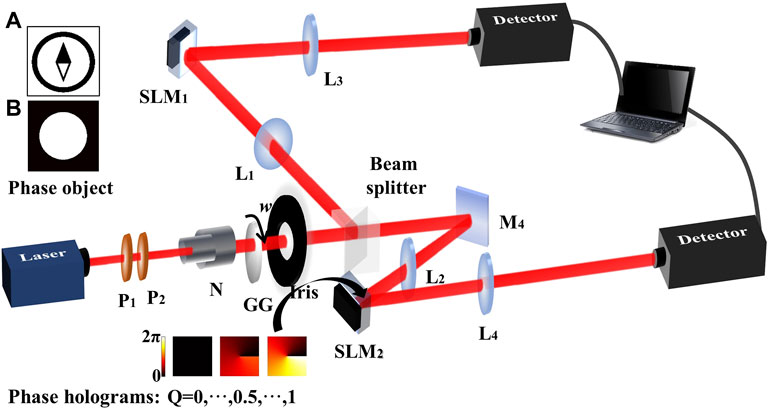
FIGURE 1. Schematic diagram of the experimental setup. Phase objects in the upper left corner are the sketch of a compass (A) and a circle (B) which are loaded by SLM1, and the dynamic phase hologram in the lower left corner is loaded by SLM2.
The role of the SLMs is loading phase objects and fractional SPF instead of the spiral phase plate, so that the gradual edge enhancement by varying the fractional OAM value from 0 to 1 with a step length of 0.1 can be observed conveniently. The phase object and the phase hologram are symmetrically loaded on SLM1 and SLM2 in the distributed beams. The size of the phase object compass is 150 × 150 square pixels. The phase mutation along the pointer and the dial is π. The black part of the phase object presents the phase of 0, and the white part presents the phase of π. The phase hologram placed on the SLM2 is 10 × 10 square pixels. Correspondingly, the black part of each phase filter presents the phase of 0, whereas the white part presents the phase of 2π. The correlation detection is carried out through scanning measurement. 10 × 10 square pixel points of the data obtained from CCD2 are taken as a unit to traverse line by line to implement the second-order correlation with the data of CCD1.
3 Results
The process of simulation calculation is as follows: first, a random thermal light field of Gaussian distribution in both the amplitude and phase is generated by a calculation program, which has the same size as the phase object to be detected. Then, the thermal light field is multiplied with the phase object and the vortex phase filter, respectively, in the reference and test beams to obtain the light field distributions in the detection planes. Finally, the correlation calculation is carried out to achieve the edge-enhanced imaging, as shown in Figure 2.
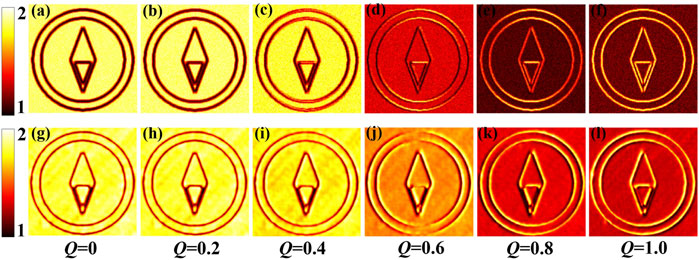
FIGURE 2. Simulation and experimental results of the non-local edge-enhanced imaging with a fractional spiral phase filter. (a–f) in the upper row show the simulation results, and (g–k) in the lower row show the experimental results.
We can find in Figure 2 that the intensity at the position where the phase gradient existed is lower than that where the phase gradient did not exist when the fractional OAM topological charge Q is lower than 0.5. It is because when Q is less than 0.5, the vortex has not formed yet, as shown in the lower right corner of each subgraph of Figure 3. However, when Q is greater than 0.5, a black hole at the center of the vortex appears. Thus, the contrast of the edge and background gradually reversed with the increase of Q. The intensity distribution of the fractional-order vortex light is not uniform along the radial direction, so the edge enhancement is not isotropic as the integer-order condition.
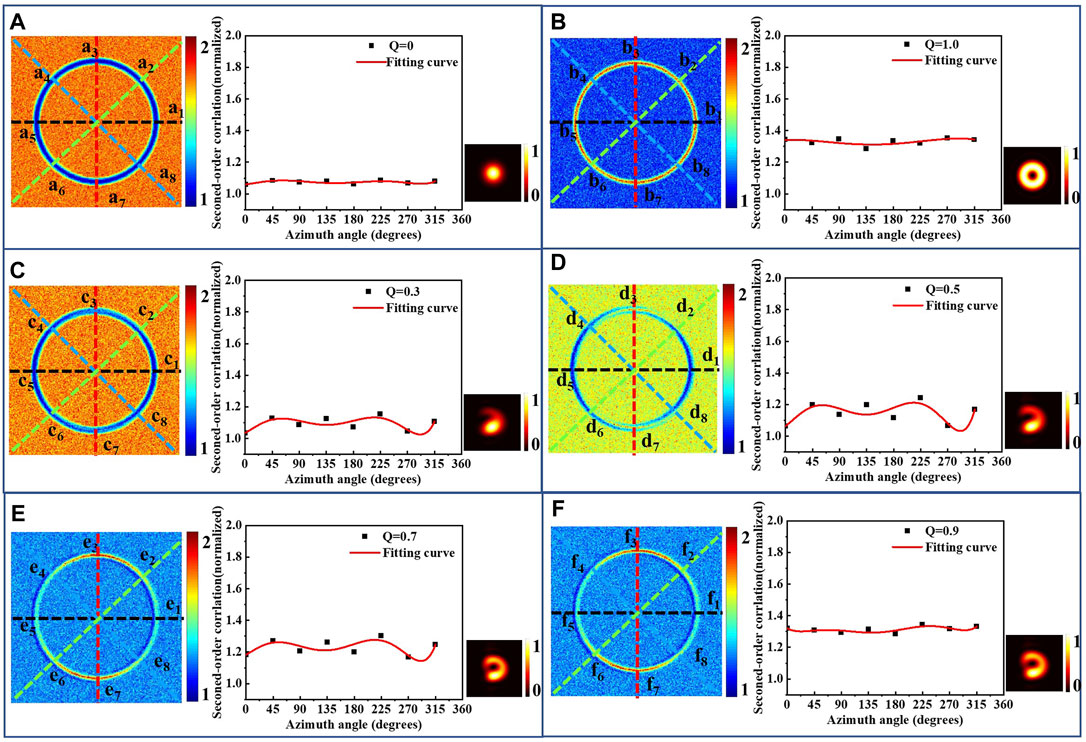
FIGURE 3. Experimental results of the circle phase with the integer and fractional vortex filters. (A–F) show the 2D edge-enhanced images and the fitted curves of some special azimuth corresponding to different Q.
Furthermore, we take a simple circular phase object as the detected phase object to analyze the isotropic feature of the SPC ghost imaging. The phase circle is shown in the upper left corner of Figure 1B, whose dimension is 200 × 200 pixels and diameter is 130 pixels. The black part of the circle presents the phase of 0, whereas the white part presents the phase of π. Figures 3A–F show the 2D edge-enhanced intensity distribution and the fitted edge-enhanced intensity curves of some special azimuth corresponding to the Q-value of 0, 1.0, 0.3, 0.5, 0.7, and 0.9. The lower right corner of each subgraph shows the vortex map of each fractional OAM. Figures 3C–F show that edge enhancement is non-isotropic of fractional Q.
4 Theoretical Analysis
The aforementioned experimental results are based on SPC imaging methods which are sensitive to the phase gradients by making use of SPF. SPF is a common device to generate helical wave fronts and vortex beams with an azimuthal structure exp (jlϕ), in which the topological charge l is an integer and 0⩽ϕ < 2π. Light with this phase structure carries OAM of lℏ per photon, and the most commonly used filter in the SPC imaging is the SPF with the integer topological charge of l = 1. All phase edges of a sample object can be enhanced isotropically as a result of the directional symmetry of an integer SPF.
In our case, Hi presents the impulse response functions during the free transmission in the reference beam between RG and D1 while i = 1 and in the test beam between RG and D2 while i = 2, respectively,
where k = ω/c is the wave number, f is the focal length of the convex lens, r0 is the 2D transverse plane position vector of the incident plane, and ri presents the 2D transverse plane position vector of the output plate of the reference and test beams.
Then, the SPF function of the polar coordinates (r, ϕ) is written as S (r1) = exp [jQϕ(r1)], where Q is a fraction varying from 0 to 1 and ϕ(r1) is an angular function of the filter. The amplitude transmittance of the input object is described by the function of T (r2) = exp [jϕ′(r2)]. Consequently, from the cascade relationship, the optical field in the transverse plane of the detectors D1 and D2 can be described as follows:
where Fi represents the SPF function S (r1) when the value of i is 1; otherwise, it represents the amplitude transmittance T (r2) of the object.
The second-order correlation function of the thermal light ghost imaging is given by [26].
where the cross-spectral density function is
The classical incoherent light source is characterized by the cross-spectral density function as
It was demonstrated that the integer OAM eigenstates form a complete and infinite basis [27–29]. A fractional vortex can be expressed in terms of the OAM eigenstates as
In the same way,
Hence, substituting the functions of the filter and object in Eq. 5, the second-order correlation function can be given as
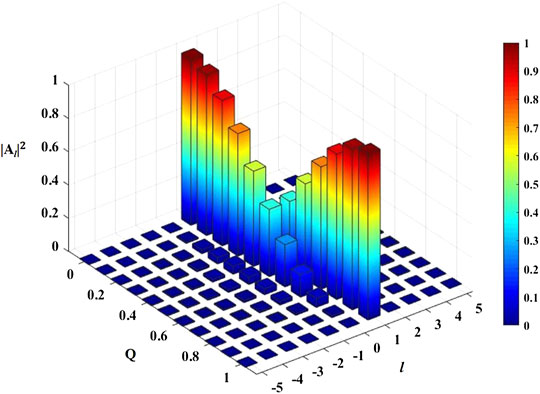
Equation 6 provides a clear understanding of the edge-enhanced effect of the fractional SPF. It indicates that the edge-enhanced image can be considered a coherent superposition of all images that are individually picked out by employing integer OAM filters. The OAM spectra of the phase platform of the object only have the composition of m = 0, so that the second-order correlation value represented by Eq. 6 will reach the maximum with l = 0 of the SPF and the minimum with l = 1. When the value of Q varies from 0 to 1, the OAM spectra composition of l = 0 decreases while l = 1 increases, as shown in Figure 4. Thus, the correlation value of the phase platform decreased as the value of Q increased. However, the situation of the edge part of the object is opposite to the phase platform. The second-order correlation value will reach the maximum with l = 1 and the minimum with l = 0, and the correlation value of the edge of the object increases as the value of Q increases.
5 Conclusion
In summary, a fractional phase filtering ghost imaging method with pseudo-thermal light is proposed. The experimental results show that the edge of the phase object can be gradually enhanced by the fractional SPF spatially distributed to the object with incoherent light beam illumination. The non-local gradual edge enhancement is also theoretically analyzed through correlation in the OAM components of the random fluctuations of the incoherent light beam. This effect is very important in a situation when entanglement is not required and when correlations in OAM suffice. The physical explanations of the gradual edge enhancement with the fractional topological charge change are the coherent superposition of the images filtered out by an integer vortex filter. The proposed scenario here provided a new edge enhancement imaging technology releasing the position of the filter in the Fourier plane with incoherent pseudo-thermal light. It is believed that the proposed non-locally fractional SPF imaging scenario may find potential applications in the field of micro-detection of quantum imaging and bioengineering.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.
Author Contributions
LG put forward the initial idea and supervised the project. HW further developed and confirmed the idea through analysis, experiment, and simulation. JM, ZY, and HD provided methodology and resources. HW analyzed the results with the assistance of JM, and ZY drew the figures. LG and HW wrote the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China (No. 12074350 and No. 62105341), the Fundamental Research Funds for the Central Universities (No. 2652021046), the National Science Foundation of Shandong Province, China (No. ZR2021QF126), and the National College Students Innovation and Entrepreneurship Training Program (No. S202111415184).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Hanquan Song for the meaningful advice and discussions.
References
1. Zernike F. Phase Contrast, a New Method for the Microscopic Observation of Transparent Objects Part Ii. Physica (1942) 9:974–86. doi:10.1016/s0031-8914(42)80079-8
2. Torre V, Poggio TA. On Edge Detection. IEEE Trans Pattern Anal Mach Intell (1986) PAMI-8:147–63. doi:10.1109/TPAMI.1986.4767769
3. Kohlmann K. Corner Detection in Natural Images Based on the 2-d hilbert Transform. Signal Process. (1996) 48:225–34. doi:10.1016/0165-1684(95)00138-7
4. Zhu T, Zhou Y, Lou Y, Ye H, Qiu M, Ruan Z, et al. Plasmonic Computing of Spatial Differentiation. Nat Commun (2017) 8:15391. doi:10.1038/ncomms15391
5. Zhou Y, Feng S, Nie S, Ma J, Yuan C. Image Edge Enhancement Using Airy Spiral Phase Filter. Opt Express (2016) 24:25258. doi:10.1364/OE.24.025258
6. Li D, Feng S, Nie S, Ma J, Yuan C. Scalar and Vectorial Vortex Filtering Based on Geometric Phase Modulation with a Q-Plate. J Opt (2019) 21:065702–5171. doi:10.1088/2040-8986/ab18e3
7. Han Y-J, Guo C-S, Rong Z-Y, Chen L-M. Radial hilbert Transform with the Spatially Variable Half-Wave Plate. Opt Lett (2013) 38:5169–71. doi:10.1364/OL.38.005169
8. Fürhapter S, Jesacher A, Bernet S, Ritsch-Marte M. Spiral Phase Contrast Imaging in Microscopy. Opt Express (2005) 13:689–94. doi:10.1364/OPEX.13.000689
9. Ritsch-Marte M. Orbital Angular Momentum Light in Microscopy. Phil Trans R Soc A (2017) 375:20150437. doi:10.1098/rsta.2015.0437
10. Khonina SN, Kotlyar VV, Shinkaryev MV, Soifer VA, Uspleniev GV. The Phase Rotor Filter. J Mod Opt (1992) 39:1147–54. doi:10.1080/09500349214551151
11. Jaroszewicz Z, Koo̵dziejczyk A. Zone Plates Performing Generalized Hankel Transforms and Their Metrological Applications. Opt Commun (1993) 102:391–6. doi:10.1016/0030-4018(93)90410-7
12. Bernet S, Jesacher A, Fürhapter S, Maurer C, Ritsch-Marte M. Quantitative Imaging of Complex Samples by Spiral Phase Contrast Microscopy. Opt Express (2006) 14:3792–805. doi:10.1364/oe.14.003792
13. Wang J, Zhang W, Qi Q, Zheng S, Chen L. Gradual Edge Enhancement in Spiral Phase Contrast Imaging with Fractional Vortex Filters. Sci Rep (2015) 5:15826. doi:10.1038/srep15826
14. Xu D, Ma T, Qiu X, Zhang W, Chen L. Implementing Selective Edge Enhancement in Nonlinear Optics. Opt Express (2020) 28:32377–85. doi:10.1364/OE.404594
15. Jack B, Leach J, Romero J, Franke-Arnold S, Ritsch-Marte M, Barnett SM, et al. Holographic Ghost Imaging and the Violation of a bell Inequality. Phys Rev Lett (2009) 103:083602. doi:10.1103/PhysRevLett.103.083602
16. Bennink RS, Bentley SJ, Boyd RW. "Two-Photon" Coincidence Imaging with a Classical Source. Phys Rev Lett (2002) 89:113601. doi:10.1103/PhysRevLett.89.113601
17. Valencia A, Scarcelli G, D'Angelo M, Shih Y. Two-photon Imaging with thermal Light. Phys Rev Lett (2005) 94:063601. doi:10.1103/PhysRevLett.94.063601
18. Scarcelli G, Berardi V, Shih Y. Can Two-Photon Correlation of Chaotic Light Be Considered as Correlation of Intensity Fluctuations? Phys Rev Lett (2006) 96:063602. doi:10.1103/PhysRevLett.96.063602
19. Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato LA. High-resolution Ghost Image and Ghost Diffraction Experiments with thermal Light. Phys Rev Lett (2005) 94:183602. doi:10.1103/PhysRevLett.94.183602
20. Zhang D-J, Tang Q, Wu T-F, Qiu H-C, Xu D-Q, Li H-G, et al. Lensless Ghost Imaging of a Phase Object with Pseudo-thermal Light. Appl Phys Lett (2014) 104:121113. doi:10.1063/1.4869959
21. Cao D-Z, Xiong J, Wang K. Geometrical Optics in Correlated Imaging Systems. Phys Rev A (2005) 71:013801. doi:10.1103/PhysRevA.71.013801
22. Magaña-Loaiza OS, Mirhosseini M, Cross RM, Rafsanjani SMH, Boyd RW. Hanbury Brown and Twiss Interferometry with Twisted Light. Sci Adv (2016) 2:e1501143. doi:10.1126/sciadv.1501143
23. Yang Z, Magaña-Loaiza OS, Mirhosseini M, Zhou Y, Gao B, Gao L, et al. Digital Spiral Object Identification Using Random Light. Light Sci Appl (2017) 6:e17013. doi:10.1038/lsa.2017.13
24. Gao L, Hashemi Rafsanjani SM, Zhou Y, Yang Z, Magaña-Loaiza OS, Mirhosseini M, et al. Distributed Angular Double-Slit Interference with Pseudo-thermal Light. Appl Phys Lett (2017) 110:071107. doi:10.1063/1.4976575
25. Song H, Zhang Y, Ren Y, Yuan Z, Zhao D, Zheng Z, et al. Non-local Edge Enhanced Imaging with Incoherent thermal Light. Appl Phys Lett (2020) 116:174001. doi:10.1063/5.0002069
26. Shirai T, Setälä T, Friberg AT. Ghost Imaging of Phase Objects with Classical Incoherent Light. Phys Rev A (2011) 84:2669–74. doi:10.1103/PhysRevA.84.041801
27. Götte JB, Franke-Arnold S, Zambrini R, Barnett SM. Quantum Formulation of Fractional Orbital Angular Momentum. J Mod Opt (2007) 54:1723–38. doi:10.1080/09500340601156827
28. Oemrawsingh SSR, Aiello A, Eliel ER, Nienhuis G, Woerdman JP. How to Observe High-Dimensional Two-Photon Entanglement with Only Two Detectors. Phys Rev Lett (2004) 92:217901. doi:10.1103/PhysRevLett.92.217901
29. Chen L, Lei J, Romero J. Quantum Digital Spiral Imaging. Light Sci Appl (2014) 3:e153. doi:10.1038/lsa.2014.34
Keywords: spiral phase contrast imaging, second-order correlation, edge enhancement, orbital angular momentum, fractional-order spiral filtering
Citation: Wang H, Ma J, Yang Z, Du H, Kang X, Su H, Gao L and Zhang Z (2022) Distributed Edge-Enhanced Imaging With a Fractional Spiral Phase Filter Using Random Light. Front. Phys. 10:878478. doi: 10.3389/fphy.2022.878478
Received: 18 February 2022; Accepted: 14 March 2022;
Published: 12 April 2022.
Edited by:
Omar Magana-Loaiza, Louisiana State University, United StatesReviewed by:
Chenglong You, Louisiana State University, United StatesYanfeng Bai, Hunan University, China
Copyright © 2022 Wang, Ma, Yang, Du, Kang, Su , Gao and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lu Gao, Z2FvbHVAY3VnYi5lZHUuY24=; Ze Zhang, emhhbmd6ZUBhaXJjYXMuYWMuY24=
 Huahua Wang
Huahua Wang Jian Ma1,2
Jian Ma1,2 Xingwang Kang
Xingwang Kang Lu Gao
Lu Gao