Collective States of Active Particles With Elastic Dipolar Interactions

Many types of animal cells exert active, contractile forces and mechanically deform their elastic substrate, to accomplish biological functions such as migration. These substrate deformations provide a mechanism in principle by which cells may sense other cells, leading to long-range mechanical inter–cell interactions and possible self-organization. Here, inspired by cell mechanobiology, we propose an active matter model comprising self-propelling particles that interact at a distance through their mutual deformations of an elastic substrate. By combining a minimal model for the motility of individual particles with a linear elastic model that accounts for substrate-mediated, inter–particle interactions, we examine emergent collective states that result from the interplay of motility and long-range elastic dipolar interactions. In particular, we show that particles self-assemble into flexible, motile chains which can cluster to form diverse larger-scale compact structures with polar order. By computing key structural and dynamical metrics, we distinguish between the collective states at weak and strong elastic interaction strength, as well as at low and high motility. We also show how these states are affected by confinement within a channel geometry–an important characteristic of the complex mechanical micro-environment inhabited by cells. Our model predictions may be generally applicable to active matter with dipolar interactions ranging from biological cells to synthetic colloids endowed with electric or magnetic dipole moments.

1 Introduction

Active matter typically comprises autonomous agents, biological or synthetic in origin, that harness internal energy sources to move [1, 2]. These agents often undergo complex interactions with each other and their surrounding media that influence their collective behavior [3]. Mammalian cells that move by crawling on elastic substrates such as tissue and constitute a canonical example of biological active matter in complex media, can cluster into persistently moving or rotating flocks [4]. These cells locomote by adhering to and exerting mechanical forces on their elastic extracellular substrate which they actively deform [5, 6]. The overall motility is guided by the cell’s interactions with its substrate as well as with other cells [7]. Cell-cell interactions can include mechanical interactions mediated by their mutual deformations of the surrounding elastic substrate [8, 9]. This is particularly the case in dilute cell cultures where cells are not in direct contact. On the other hand, in dense active matter systems such as in confluent epithelial cell monolayers, direct cell-cell interactions including steric interactions can dominate [10]. Mechanical interactions through a material medium are by their nature long-range and are expected to govern the collective states of active particles [11], and enrich the large–scale phenomena such as phase separation that arise purely from motility [12, 13].

Mechanobiology experiments with adherent cells cultured on elastic hydrogel substrates [14, 15], suggest that substrate elasticity may provide a robust route to long lived and long ranged cell-cell interactions. Indeed, cell culture experiments indicate that cells exert measurable forces on their neighbors, either through direct cell-cell contacts, or indirectly through mutual deformations of a compliant, extracellular substrate [16, 17]. The substrate-mediated elastic interactions between such cells has important implications for biological processes such as self-organization during blood vessel morphogenesis [18] and synchronization of beating cardiac muscle cells [19–22]. The overall motility of spatially separated cells is expected to depend on cell-cell mechanical interactions. This is revealed by experimental observations of substrate stiffness-dependent interactions of pairs of motile cells [23, 24].

In general, active particles endowed with a dipole moment are expected to interact at long range with each other while also propelling themselves. Passive dipolar particles such as ferromagnetic colloids at equilibrium will align end-to-end into linear structures such as chains or rings [25, 26]. At higher densities, the chains intersect to form gel-like network structures [27]. Topological defects in the networks such as junctions and rings are expected to affect the phases of passive dipolar fluids [28, 29]. When powered by chemical activity, dipolar colloidal systems exhibit self-assembly that depends on both the long-range, anisotropic interactions, as well as active motion, as revealed in recent experiments [30]. Such structures have also been studied in simulation in the context of active dipolar particles representing auto-phoretic colloids [31, 32], as well as swimming microorganisms [33] such as magnetotactic bacteria [34]. In related theoretical studies, constrained or bundled chains of self-propelling colloidal particles [35–38] have also been shown to exhibit collective instabilities. Elasticity mediated interactions are seen to play critical roles, with the competition between mechanical interactions, steric interactions and activity determining the eventual dynamical behavior.

Here we build a minimal model of interacting elastic dipoles that is inspired by the mechanobiology of animal cells that actively deform their elastic substrate, while also exhibiting persistent motility. The starting point is the observation and deduction that contractile deformations of the underlying substrate originate from the elastic dipolar nature of stresses exerted by the cell on the substrate [39]. We show that incorporation of these substrate-mediated interactions offers a robust way to the formation of compact, and relatively stable collective states. Our model combining active self-propulsion of the particles with their long-range dipolar interactions applies to a general class of experimentally realizable systems, including synthetic colloids endowed with permanent or induced magnetic or electric dipole moments [40]. By performing Brownian dynamics simulations on a collection of such dipolar active particles, we demonstrate the rich array of collective states that they can self-organize into. In particular, strong dipolar interactions promote end-to-end alignment of active particles, leading to self-assembled, motile chains. These chains can then further self-assemble into a hierarchy of larger-scale structures.

2 Model

Our model system consists of soft, repulsive, active Brownian particles (ABPs) [41, 42] in two dimensions (2D), that interact at long range through elastic dipolar interactions and strongly repel when they overlap. We have previously studied a simple isotropic interaction model valid in the limit where the propulsion direction was decoupled from the magnitude of cell-cell interactions [43]. Here, we analyze a more general model that accounts for the anisotropy of cell interactions, expected for the elongated shapes characteristic of migrating cells.

The basis of elastic interactions between model cells is illustrated in Figure 1. The schematic Figure 1A shows the typical scenario of an adherent cell on top of an elastic substrate. The internal cytoskeletal machinery of the cell comprising actin stress fibers and myosin II molecular motors generates contractile mechanical forces, that are communicated to the external substrate through cell-substrate focal adhesions [44]. In a minimal, coarse-grained description, the traction force distribution of an elongated cell with a long axis a and exerting a typical force F at the adhesion sites, can be modeled as a force dipole with dipole moment P_ij = F_ia_j. The theory of continuous elastic media then determines that the distribution of forces from multiple cells will lead to a restoring stress σ in the medium, that satisfies a force balance [45], ∂_jσ_ij = −∂_jp_ij, where the net dipole density, $p_{ij}(\mathbf{x})={\mathrm{\Sigma }}_{\alpha }{P}_{ij}^{\alpha }\delta (\mathbf{x}-{\mathbf{x}}^{\alpha })$ is the sum of traction forces exerted by each point-like cell dipole, here labeled by an index α. In modeling cells as point-like dipoles, we ignore their finite size, an assumption that is valid only at “far field”, i.e., at distances large compared to cell length. While this is not strictly the case in our simulations, a more general model accounting for finite separation of the cell forces is expected to lead to qualitatively similar interactions [22].

FIGURE 1

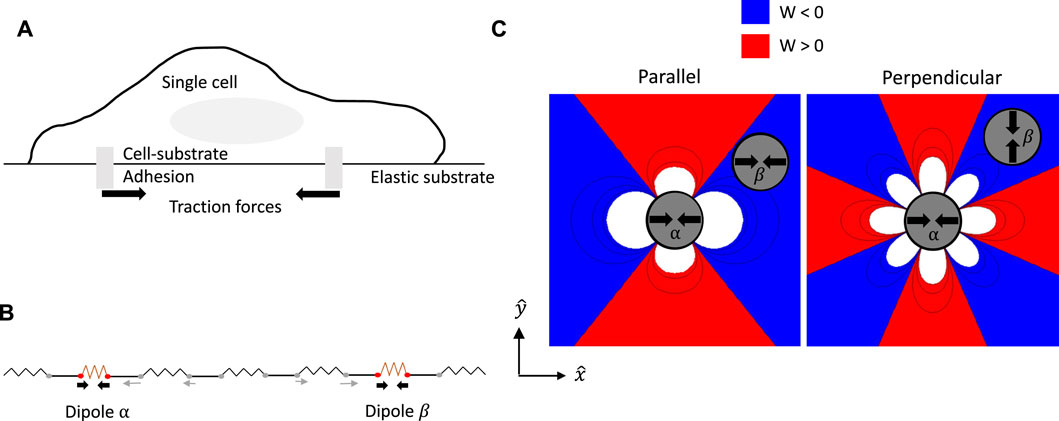
FIGURE 1. Elastic interactions between model cells on a substrate. (A) Schematic of adherent cell on an elastic substrate. (B) 1D spring model illustrating origin of elastic interaction potential between two contractile dipoles. The elastic energy stored in the medium corresponding to the deformation of springs depends on the relative placement of the dipoles. In particular, placing a contractile dipole in a region where the medium is already expanded by the other dipole can help to reduce the overall deformation of the medium. This leads to a strain-dependent interaction potential between the two dipoles. (C) Representative spatial maps of the interaction potential W^αβ between two dipoles, from the solution of the strain field for the full linear elastic problem of forces exerted on the surface of a semi-infinite medium are shown. The interaction potential corresponds to the work done by a point-like dipole in deforming the substrate in the presence of the strain created by the other. The potential maps shown here are for a pair of contractile force dipoles of fixed orientation. The second dipole is free to translate but held parallel (left) or perpendicular (right) to the central dipole which is placed at the origin and aligned along the x-axis. The contour lines show how the potential decays in space, whereas blue and red regions correspond to attractive (W^αβ < 0) and repulsive (W^αβ > 0) interactions, respectively.

By considering two dipoles P^α and P^β, we can show that the work done by a dipole β in deforming the elastic medium in the presence of the strain created by the other dipole α, is given by [46]: $W^{\alpha \beta }=P_{ij}^{\beta }{u}_{ij}^{\alpha }({\mathbf{x}}^{\beta })$. This minimal coupling between dipolar stress and medium strain represents the mechanical interaction energy between dipoles. The strain in the elastic medium created by dipole α at the position of the dipole β is given by the gradient of the displacement, $u_{ij}(x)=\frac{1}{2}(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})$ and can be calculated using standard methods in linear elastic theory [45]. This is detailed in the Methods section, where we follow the treatment introduced in Ref. [46]. The mechanical interaction between a pair of force dipoles is illustrated by the schematic in Figure 1B in the form of a 1D series of springs representing the effect of the elastic substrate. While the springs underlying the contractile dipoles are compressed, the springs between them are stretched. By moving to different positions in the medium for a given position of dipole α, the dipole β can reduce the net substrate deformation energy by compressing regions stretched by dipole α. This leads to a substrate deformation-mediated elastic force on the dipole β,

$f_{el}^{\beta }=-\frac{\partial W^{\alpha \beta }}{\partial {\mathbf{x}}^{\beta }}=-P_{ij}^{\beta }\frac{\partial u_{ij}^{\alpha }\left({\mathbf{x}}_{\beta }\right)}{\partial {\mathbf{x}}_j^{\beta }},(1)$

given by the gradient of the strain induced by the other dipole, where the strain therefore acts as a potential. While the expressions vary in detail, this physical interaction between elastic dipoles considered here is analogous to the interaction of an electric dipole with the electric field induced by another dipole. A similar reciprocal force results on dipole α, since the interactions are based on an elastic free energy. The physical origin of this force is the tendency of the passive elastic medium to minimize its deformations in response to the active, contractile forces generated by the cells. This generic mechanical interaction between dipoles is not limited to cells [46], but also occurs for passive inclusions in an elastic medium [47]. Experimentally, hydrogen atoms in metals were shown to diffuse and distribute themselves according to configurations dictated by these elastic interactions [48].

Pairwise dipolar interactions are anisotropic and depend on both the distance between and relative orientations of the two particles with respect to their separation axis. Insights into the nature of the elastic interaction potential between a pair of force dipoles, may be obtained from Figure 1C where we plot spatial maps of the interaction potential W^αβ for 2 cells with fixed orientation. To plot these functions, we choose a reference contractile force dipole α that is fixed at the origin with its axis along the − x direction, i.e., whose dipole moment has purely the P_xx component. A second dipole β interacts with the reference dipole according to its position and orientation. The red (blue) regions in the potential maps in Figure 1C represent repulsion (attraction) which arises from the substrate strain. Here, we use the convention that stretched (compressed) regions have positive (negative) strain, while compressive dipole moment is negative. While the map on the left corresponds to parallel alignment, that on the right maps the interaction potential for perpendicular alignment of the two dipoles. In this example, we fix the orientation of the second dipole to be either parallel or perpendicular, and therefore it couples to either the u_xx or the u_yy component of the strain according to Eq. 1. In general, the dipoles can also rotate and change their relative orientations. In particular, while the favorable parallel configuration shown here leads to end-to-end alignment of the dipoles, the unfavorable perpendicular configuration will lead to mutual torques that tend to orient them in the favorable parallel configuration. The elastic material comprising the substrate is treated as homogeneous and isotropic with shear and compression Moduli proportional to the Young’s modulus E, and a Poisson ratio ν that provides a measure of its compressibility [49]. While the Poisson’s ratio can in principle have the full range − 1 < ν < 1/2 in linear elasticity theory, the figures plotted here correspond to ν = 0.1¹.

The interaction potential and model dynamics are detailed in the Methods Section 4 in Eqs 4–7. As shown in Figure 2A, the ABPs–here termed particles–are modeled as circular disks of diameter σ, each particle being endowed with a dipole moment and a self-propulsion direction $\widehat{\mathbf{n}}$. The orientation of $\widehat{\mathbf{n}}$ is aligned with the dipole axis (shown as the bold black line). This assumption is reasonable for motile cells with elongated shape, but is not necessarily satisfied for all cell types, where higher force multipoles may be relevant [24]. Particles are assumed to self-propel with a speed v₀. This phenomenologically models the movement of cells which require internal cell forces arising from actomyosin activity as well as the remodeling dynamics of the cell-substrate adhesions, not explicitly modeled here. Additionally, the motion of each particle is subject to forces and torques arising from dipolar interactions with other particles, as well as a random stochastic force. The latter mimics the effect of the thermal environment surrounding the particles, and leads to diffusive effects in both orientation and spatial position of the ABPs.

FIGURE 2

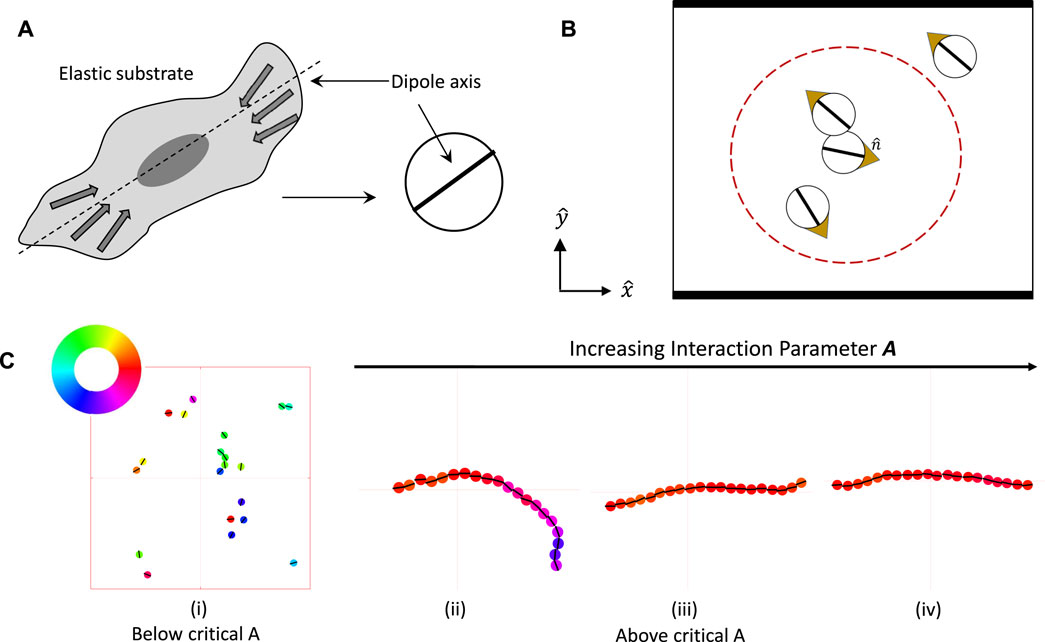
FIGURE 2. Overview of agent based simulations of active Brownian particles (ABPs) moving in the x-y plane and interacting mechanically via elastic deformations induced by contractile, active force dipoles. (A) An elongated cell with traction forces distributed around its long axis is modeled as a disk-like particle endowed with a dipole moment. (B) Each ABP has a dipole axis represented by the bold black line and an in-plane self-propulsion direction represented by the gold arrow. These particles move on a linearly elastic, thick, flat substrate, on which they exert contractile dipolar stresses. Substrate deformation due to one particle is sensed by neighboring particles. These dipole-dipole elastic interactions are confined to particles within a cutoff distance r_cut = 7σ (shown as the dashed red circle). Particle overlap is penalized by a short range steric repulsion. They are confined by steric repulsions along the top and bottom walls shown by the thick lines, while being free to move through periodic boundaries shown by the thin lines. (C) for figure (i) Simulation snapshot shows that weakly interacting particles do not stick to each other and move as independent entities. As the elastic dipolar interaction parameter A increases, the particles self-assemble into long chains ((ii)-(iv), zoomed view shown). The flexibility of the chains and fluctuations in the mean curvature both decrease with increasing values of the interaction parameter. The colors represent the self-propulsion direction of each particle, as indicated by the color wheel.

Since we are motivated by adherent cells on elastic substrates whose contractile traction forces act as elastic dipoles, a cutoff distance of r_cut = 7σ (red dashed circle in Figures 2B) is imposed on the long-range dipolar interactions. The choice of a cut-off length for interactions is consistent with experimental observations that cells can interact with one another via mechanical signalling at distances that are up to a few cell lengths away [8, 19]. In addition to the “long-range” interactions mediated by the elastic substrate, cells may also interact via “short-range” interactions. Here we introduce short-range steric repulsion using a mechanical model using compressive springs that discourage overlap between neighboring particles. Specifically, two particles in close-contact exert a repulsive elastic force on each other when the center-to-center distance is less than the rest length σ of these springs.

The ensuing dipolar interactions, when strong enough relative to the stochastic noise, cause end-to-end chaining of the particles along their dipole axis. Examples of this chaining process are seen to occur in our simulations and representative snapshots are shown in Figure 2C. As expected intuitively, increasing interaction gives rise to stronger alignment resulting in chains that are progressively less flexible. The effective elastic bending modulus of these chains that determines the fluctuations of the backbone contour of the chained ABPs is thus higher with increasing interaction strength.

To illustrate the bulk behavior of interacting ABPs as well as the effect of confinement on emergent collective patterns, we simulate a few hundred of these particles in a box confined in the y − direction, and periodic in the x − direction. The confining boundary is lined by repulsive springs of the same type used to penalize particle overlap, and keeps the ABPs from escaping the simulation box. This setup mimics a channel geometry typically used in cell motility experiments [51] and is used in other works on simulations of ABPs under confinement [52–54]. We focus on the physical barriers to cell motility and not interfaces in the elastic medium. In principle, such elastic interfaces can lead to additional elastic torques and forces on dipoles by inducing “image forces” [46], but this is outside the scope of the present work. One way to realize this type of confining boundary that does not induce stresses in the elastic medium is to culture cells on a large and thick slab of hydrogel with uniform elastic properties, but micropattern a specific region of the substrate with ligands to which the cells can adhere–a common technique in mechanobiological cell culture studies [14].

The important nondimensional control parameters in the model are the effective elastic interaction strength A, the active self-propulsion velocity characterized by a Péclet number, Pe, and the packing fraction, ϕ. The packing fraction used in simulations below is typically either ϕ = 0.08 or 0.25 corresponding to relatively dilute regimes, except in a narrow channel geometry where we go up to ϕ = 0.75. Definitions and physical interpretations of these parameters are provided in Section 4.

3 Results

3.1 Characteristic States of Active Dipolar Particles: Chains, Polar Bands, Clusters and Networks

We first explore the possible collective structures that result from the combination of active self-propulsion with dipolar attraction and alignment. We explore the parameter space of activity (given by the Péclet number, Pe) and strength of dipolar interactions (given by the effective elastic interaction parameter, A) for two representative systems: one dilute and the other semi-dilute. We show representative snapshots of the steady states of the simulations by coloring the particles according their orientation. Collections of these snapshots as well as the color wheel corresponding to particle orientations are shown in Figure 3, where the packing fraction ϕ ≈ 0.25, and Figure 4, where the packing fraction ϕ ≈ 0.08.

FIGURE 3

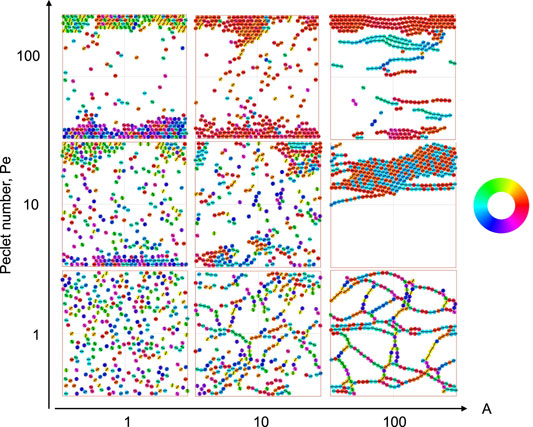
FIGURE 3. Simulation snapshots of active particles with short range steric repulsions and long-range elastic dipole-dipole interactions as a function of effective elastic interaction A ≡ P²/Eσ³k_BT_eff and Péclet number Pe ≡ σv₀/D_T. Particles are confined in the y-direction, while they experience periodic boundary conditions in the x-direction. They are colored according to their self-propulsion direction $\widehat{\mathbf{n}}$, and coded based on the color wheel. Motile particles at low effective elastic interaction collect into clusters at the boundaries. Strong elastic interactions promote network formation at low activity. Strong elastic interactions paired with high activity gives rise to active polymers and polar bands. The full movies corresponding to ABPs, networks, traveling cluster, and active polymers can be seen in Supplementary movies S1–S4, respectively.

FIGURE 4

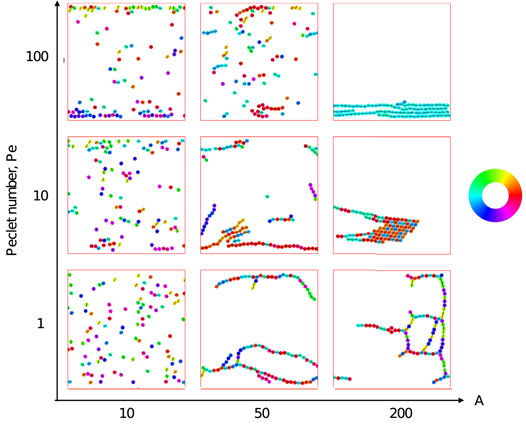
FIGURE 4. Simulation snapshots of active particles at low packing fraction. The interaction parameter A ≡ P²/Eσ³k_BT_eff and Péclet number Pe ≡ σv₀/D_T define the collective behavior of the particles. Particles are confined in the y-direction, while they experience periodic boundary conditions in the x-direction. They are colored based on the direction of $\widehat{\mathbf{n}}$, as indicated by the color wheel. At low interaction parameter A = 10, the particles remain isolated and diffuse (Supplementary Movie S6). At high Pe, more particles get collected at the confining boundary. At higher values of the interaction parameter, A, particles form chains. The typical length of the chains is seen to decrease with increasing Pe. At very high interaction parameter, A = 200, networks with multiple branches form at low Pe, while chains aggregate into polar clusters at Pe = 10 (Supplementary Movie S7). Although the particles in the cluster are oriented in opposite directions, the cluster is stable and moves in the direction given by its overall polarity. Again at very high Péclet, Pe = 100, the particles in the chains are oriented in the same direction.

We see from Figure 3 that at both low motility and weak elastic interactions (A = 1), particles do not form any ordered structures but are distributed uniformly in space, over the utilized simulation time. As motility is increased (Pe ≥ 10), particles are seen to clump up at the boundary with their orientation vectors facing the wall at which they are localized. This is a familiar result of confined active Brownian particles (ABPs) wherein these tend to point towards the wall until their orientation is sufficiently randomized by the rotational diffusion [55]. As elastic interactions are dialed up such that the motions resulting from the dipolar interactions are much stronger than the stochastic diffusion of the system, structures characteristic of dipolar interactions emerge. In the case of low particle motility (Pe = 1), and high elastic interactions, we see a branched network form. In the case of intermediate motility (Pe = 10), networks are broken down into a single traveling cluster. In the former case, the particles comprising any given chain can either be oriented parallel (0) or anti-parallel (π) with respect to one another as the dipolar interaction is head-tail symmetric. In the latter case, networks form at short time scales and are compressed into one motile cluster at long time scales. This motile cluster contains numerous defects (shown by their different color)–particles oriented anti-parallel to the direction of cluster motion–caused by the earlier stage of network formation. Lastly, in the case of high particle motility (Pe = 100), particles assemble into traveling flexible chains which predominantly move parallel to the confining boundary and undergo inter-chain collisions in the bulk. Much of our forthcoming analysis is focused on these highly ordered, yet highly dynamic, structures.

At low packing fraction (Figure 4), for A = 10 the elastic interaction between the particles is low and they diffuse around in the simulation space which is in contrast to what we see for higher packing fraction (Figure 3) where particles show alignment with weak attraction. Accumulation of the particles can be seen at the confining boundaries which is attributed to the activity of the particles. Upon increasing the elastic strength to A = 50, formation of chains is observed. At Pe = 1, long and branched chains of particles are formed. Increasing motility leads to a decrease in length of the chains and an increased polarity. At even higher elastic strength of A = 200, long chains with multiple branches are seen for Pe = 1. At increased activity, the chains stick to each other and form an ordered cluster that moves coherently in the direction determined by the net polarity of the constituent particles.

3.2 Pair Correlations Reveal Spatial Organization of Active Chains

To quantify the spatial distribution of particles around their neighbors, we calculate the pair correlation function, g(r, θ), the probability of finding a neighboring particle at a distance r in a direction θ from the central agent’s orientation axis. We calculate this quantity by averaging over the positions of all agents over time, and binning every other agent according to its separation vector (both distance and angle) from the current central agent. Finally the distribution is normalized such that g(r, θ) approaches 1 for distance r going to infinity. We then analyze the peaks in (r, θ) space. Figure 5 shows four such distance and angle dependent maps in the space of motility and elastic interaction. Elastic interactions localize the peaks of the pair correlation function. When motility is low, particles form branched networks and the primary configuration of particles is in straight chains. In this case, there exists two prominent peaks in the pair correlation function at (σ, 0) and (σ, π). When both motility and elastic interactions are high, particles form into flexible traveling chains that have a tendency to join one another in a parallel fashion with an offset - a configuration that is energetically favorable to the elastic interaction and can be seen prominently in the simulation snapshot corresponding to A = 100 and Pe = 100 in Figure 3. In this case, the primary peaks still occur at (σ, 0) and (σ, π), but secondary peaks are present at $(\sigma ,\frac{\pi }{3}\mathrm{m}\mathrm{o}\mathrm{d}\pi )$ and $(\sigma ,\frac{2\pi }{3}\mathrm{m}\mathrm{o}\mathrm{d}\pi )$, indicating the offset parallel band structure. Low elastic interactions constitute the more familiar case of collections of repulsive ABPs. In this regime, the head-tail symmetry characteristic of the elastic interactions is broken as particles are more likely to encounter other particles along their direction of propulsion [56]. There exists a single prominent peak at the head of the dipole that monotonically decreases on either side of the head axis. Increasing motility in the ABP system adds layers to the single peak function in integer multiples of particle size σ as collision frequency increases.

FIGURE 5

FIGURE 5. Angular dependent pair correlation function is affected by both motility and elastic interactions. Strong elastic interactions promote pair correlation peaks at (r, θ) = (σ, 0), (σ, π). At Pe = 1, these are the only prominent peaks in the pair correlation function. Motile activity gives rise to secondary peaks at roughly (r, θ) = ($\sigma ,\frac{\pi }{3}\mathrm{m}\mathrm{o}\mathrm{d}\pi$), ($\sigma ,\frac{2\pi }{3}\mathrm{m}\mathrm{o}\mathrm{d}\pi$) as the preeminent structures are bundles of offset traveling chains. Weak elastic interactions broaden the pair correlation distribution. In this case, motility breaks head-tail symmetry and peaks can be seen at multiple integers of particle diameter at the head (θ = 0 axis).

3.3 Activity and Elastic Interactions Promote Orientational Order

At higher interaction strength, A, and higher motility, Pe, we see chains that move parallel to each other forming polar bands at high density (top right of Figure 3). Since chains are elongated objects, a collection of them can give rise to orientational order, similar to active nematic and polar states that result from active, anisotropic particles [1]. This type of order is commonly seen in active matter comprising suspensions of cytoskeletal filaments and motors [57]. To quantify the orientational order in these cases and to distinguish from the individual ABPs under confinement, we measure the nematic and polar order for these states. The magnitude of the nematic order parameter is defined as an average over the orientation of all particles, S ≡ 2⟨ cos²θ⟩ − 1, where θ is the angle between a particle’s orientation and the average director. In this case, the global alignment direction is parallel to the confining boundaries given by the x − axis. The nematic order tells us how well the dipoles are aligned, without distinguishing between the head and tail and contains no information about the motility direction. To quantify the oriented motion, we calculate the polar order, whose magnitude is given by, $|p|\equiv \sqrt{{⟨n_x⟩}^2+{⟨n_y⟩}^2}$, where n_x and n_y are the x and y components of the orientation vector, $\widehat{\mathbf{n}}$, respectively. This quantity is higher if the particles are oriented in the same direction, in addition to being aligned. While nematic alignment is encouraged by the passive dipolar interactions, active motility induces polar order.

Figures 6A,C shows the global nematic order in time and Figures 6B,D shows the time averaged spatial map of the polar order parameter, calculated by subdividing the simulation box into regions of dimension 3.75σ × 3.75σ, for both ABPs and traveling flexible chains. In the ABP system, the global nematic order is small due to the tendency of particles at the walls to be oriented orthogonal to the wall and those in the bulk to be oriented parallel to the wall, as well as the presence of orientational fluctuations from rotational diffusion. Traveling flexible chains of dipolar particles exhibit a global nematic order close to unity as all particles in this system tend to point along a director parallel to the confined boundary. Spatially resolving the average of the magnitude of the polar order parameter gives us a picture of particle alignment at a smaller length scale. ABPs exhibit polar alignment at the boundary. This alignment quickly diminishes and no polar order is seen in the bulk. Traveling chains form bands at the boundary such that |p| > 0.7 up to 6σ away from the wall. The polar order of these flexible chains drops off far less drastically in the bulk than the ABP system.

FIGURE 6

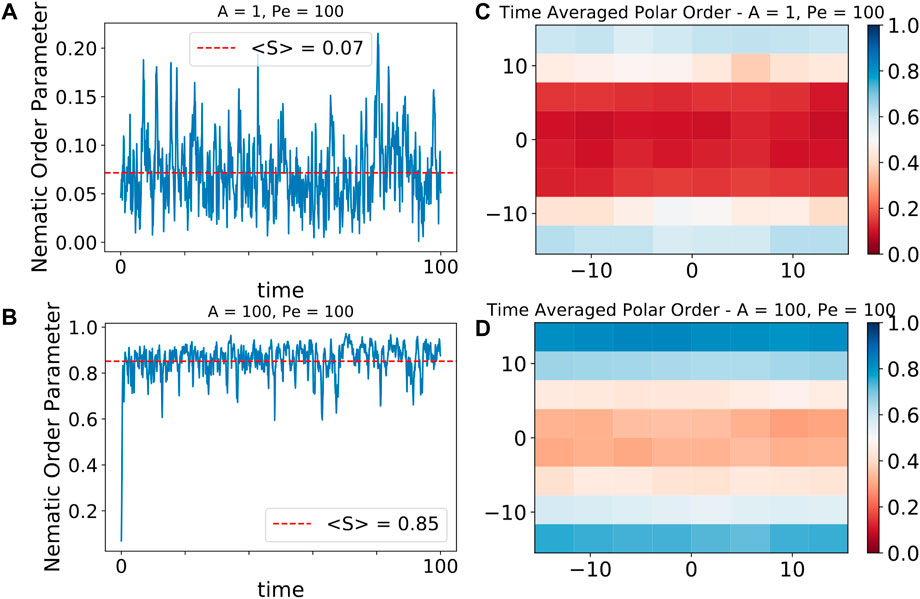
FIGURE 6. Elastic interactions promote global nematic order and local polar order. (A) Global nematic order, measuring the overall alignment of the particles’ dipole axes, vs. time for low effective elastic interaction and high activity. Average global nematic order is negligible for these parameters. (B) Global nematic order vs. time for high effective elastic interaction and high activity. The system quickly gains a persistent global nematic order parameter near unity because the chains align parallel to each other. (C) Spatial distribution of time averaged polar order, where grid size is 3.75σ × 3.75σ, measuring the overall orientation of motility for the particles, for a characteristic run at low effective elastic interaction and high activity. Particles accumulate at the boundary and exhibit polar order along that boundary. This order rapidly decays away from the boundary and there is virtually no polar order observed in the bulk. (D) Spatial distribution of time averaged polar order, where grid size is 3.75σ × 3.75σ, for a characteristic run at high effective elastic interaction and high activity. A polar order near unity is observed at the boundary and persists into the bulk where near the middle of the channel |p| ≈ 0.3.

3.4 Transport Properties of Active Chains Are Distinct From Single Particles

The mean-squared displacement, or MSD, is a typical metric that quantifies how motile entities cover space in time. In Figure 7, we report the MSD for simulations with a packing fraction ϕ ≈ 0.08 in a square box of size 30σ, corresponding to the structures shown in Figure 4. Given the confinement along one direction, we calculate the MSD separately for the confined (y-) and unconfined (x-) directions. The unconfined MSD, ⟨x²⟩, for particles with low elastic interaction e.g., at A = 10, shows similar trends to individual active Brownian particles [58]. At short time intervals, individual ABPs propel persistently in the direction of their orientation, leading to ballistic behavior. In Figure 7A, we see such behavior at very short time scales which gave way to super-diffusive behavior at intermediate time scales, where particles are slowed down by collisions with other particles. At sufficiently long time scales, the particles are diffusive as the rotational diffusion randomizes their orientation. Increasing Péclet number increases the time scale for superdiffusive behavior as the persistence time is longer.

FIGURE 7

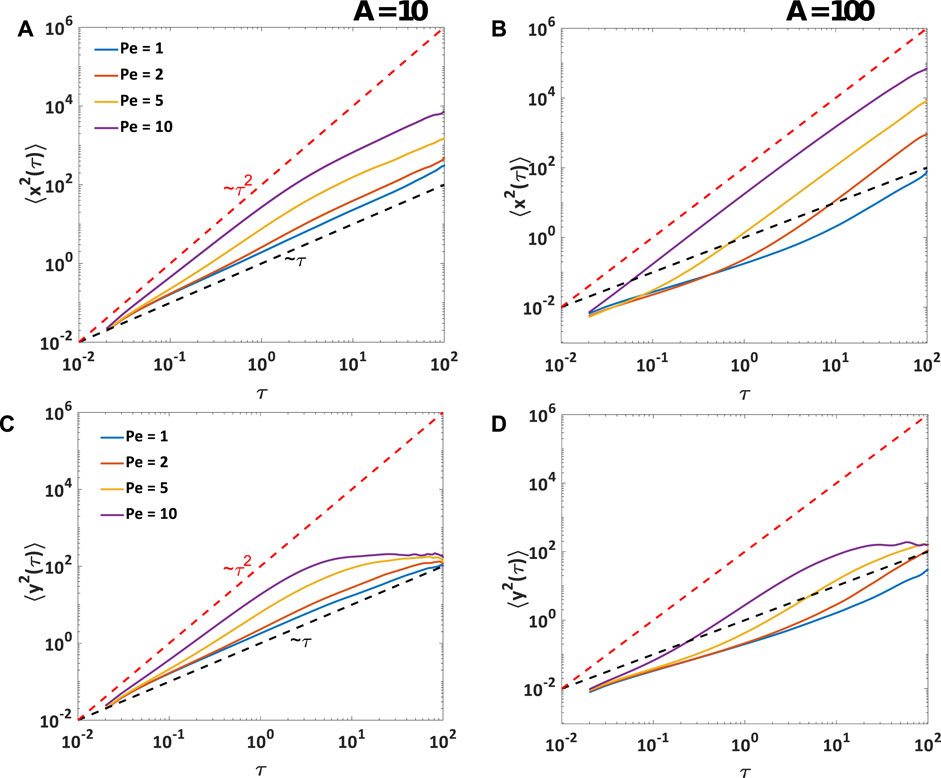
FIGURE 7. Mean-Squared Displacement, or MSD, vs. time interval, for 100 particles in a square simulation box of 30σ. Due to confinement of particles in y-direction, MSD is plotted separately for x and y components of displacement. (A), (B) MSD along unconfined direction: for A = 10, particles are super-diffusive at short time scale and diffusive at longer time scale, where the crossover time scale is determined by the Péclet number (Pe) of the particles. At A = 100, particles align themselves to form chains or clusters. At low Pe, the particles show sub-diffusive behavior at shorter times and ballistic behavior at longer times. At higher Pe, the ballistic behavior of particles is observed at all time scales. (C), (D) MSD along confined direction: particles reach the confining boundary at shorter times for high Pe number, and also at low elastic interactions A. At higher A, particles chain up and move predominantly parallel to the confining boundary.

We see qualitatively different regimes in the MSD for particles with stronger interaction in Figure 7B. At interaction strength A ≥ 100, which leads to formation of long, stable chains, we observe larger-scale structures such as branches, clusters and networks in the simulation snapshots shown in Figure 4. In this case, the particles show sub-diffusive behavior at shorter time scales when they are still moving individually in an uncorrelated manner and beginning to form these structures. On the other hand, at longer time scales, they cluster into larger scale structures that move coherently in a specific direction like polar flocks, giving rise to a ballistic behavior. The crossover from subdiffusive to nearly ballistic behavior occurs earlier for higher Péclet numbers. At higher particle motility, we obtain ballistic behavior for all time scales. The resulting behavior is thus qualitatively different from single ABP behavior, which shows a crossover from persistent to diffusive motion at time scales longer than the persistence time (∼ Pe). Here, on the other hand, the long time behavior is dictated by large-scale, polar structures that self-assemble irreversibly and move persistently at long times.

The MSD in the confined direction, ⟨y²⟩, plateaus at long times, both for the individual ABPs (Figure 7C) and the larger scale structures (Figure 7D). The time scale to reach a plateau in the MSD corresponds to the time it takes an entity to reach the confining walls from the bulk of the simulation box. Thus, ⟨y²⟩ reaches a plateau at a shorter time scale for highly motile particles, as compared to the less motile ones. Due to the confining wall in the y-direction and strong alignment with neighboring particles at A = 100, the particles line up into chains that orient and move parallel to the confining walls, and not as much in the y-direction. Thus, ⟨y²⟩ for A = 100 reaches the plateau later than for the A = 10 case, for corresponding values of Pe.

3.5 Collisions of Active Chains Reveal Stable, Mobile Structures

We observe from simulations at low packing fraction (Figure 4) that once particles self-assemble into chains, they can intersect to form junctions and get organized into larger-scale polar structures. We now explore in more detail the inter-chain interactions responsible for this self-organization. To do this, particles were initialized in an ordered chain and oriented in the same direction. Two such chains were oriented initially at different angles to control their approach direction, as shown in the insets in Figure 8.

FIGURE 8

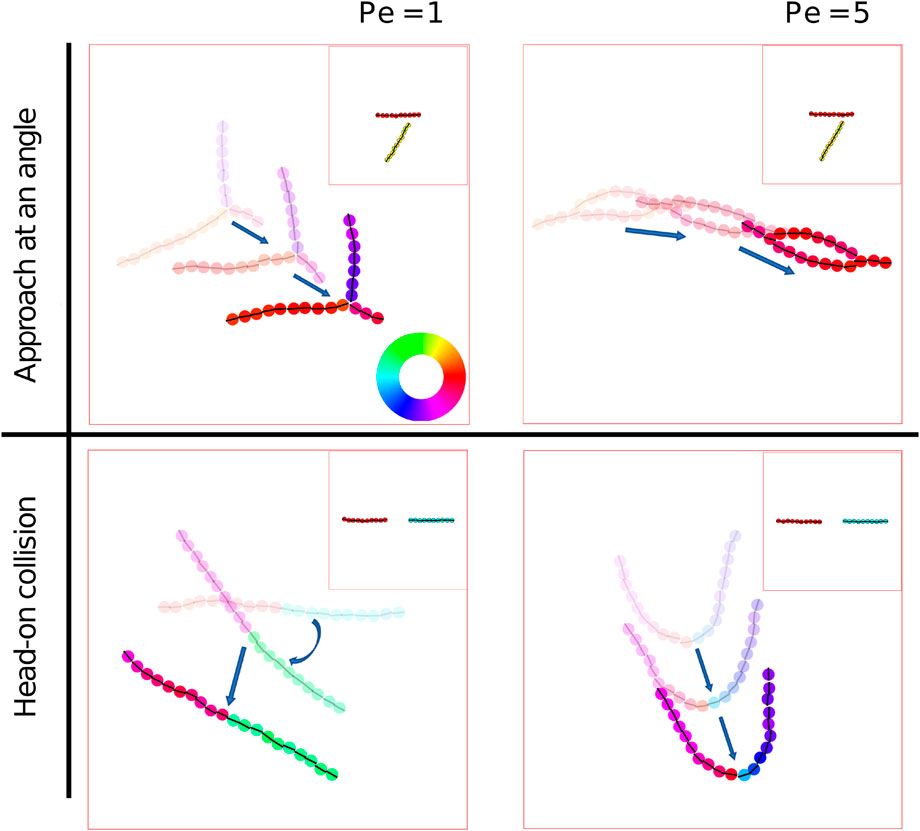
FIGURE 8. Interaction of two motile chains (Supplementary Movie (Supplementary Movie S8). Two straight chains of 10 particles each are initialized to approach each other at an angle of $\frac{\pi }{3}$ and also π (“head-on”) at Pe = 1 and 5. At Pe = 1, a “Y” junction forms for an approach angle of $\frac{\pi }{3}$ whereas at Pe = 5, an “eye” (two junctions) occurs. Upon head-on collision, a longer fluctuating chain with negligible net motility results at Pe = 1, and a propelling, buckled shape is observed at Pe = 5. Insets at the top corners represent the approach of the chains. Color represents angle of orientation of particles. The arrows indicate progression in time and suggest that the configurations are both stable and motile.

At A = 200 the junctions formed by chains depended on the Péclet number and the angle and position of approach. The “Y” junction was the most observed for all Péclet number, which is formed from when the second chain attaches itself at the middle of the first chain (Figure 8, top left). An “eye” (Figure 8, top right) is formed from two closely spaced “Y”s, which is observed for higher Péclet number, Pe = 5 and 10, and when the chains are oriented in the same direction. Again, at low particle motility (Pe = 1), the chains, upon colliding head on, form a longer and more rigid chain (Figure 8, bottom left). On the other hand, at Pe = 5, chains show buckling upon undergoing head on collision which leads to a propelling “necklace” (Figure 8, bottom right). At even higher Péclet number, the force between the particles is overpowered causing particles to detach from a chain and thereby creating defects. All these cases have been observed for A = 200. These junctions are also observed at lower elastic strength A = 50 and 100, but were unstable giving rise to many defects. Chains may interact with each other in a head-tail fashion which results in a stable longer chain. Chains with multiple defects have also been observed to form these “Y” and “eye” structures at A = 200 and Pe = 1 (Figure 4).

3.6 Stronger Confinement in Narrow Channels Reveals Polar Clustering Dynamics

In our system of traveling flexible chains comprised of strongly interacting and highly motile dipolar particles (A = 100, Pe = 100), bands that form along the confining boundary are relatively stable compared to those that form in the bulk. The latter are subject to more frequent collisions with other traveling chains. In order to gain understanding of these chain collision dynamics, we confine the same number of particles into a channel of width $L_y=\frac{L}{3}$, where L is the box size of our original simulation space, in order to induce more frequent and global chain-chain collisions. In this system we find a cyclic tripartite state dynamic. As shown in Figure 9A, at some point, the particles with orientations + x become well mixed with particles with orientations − x. The particles will then separate into lanes according to their polarity so that they can move unimpeded. These lanes will then collide which initializes another well mixed system and the cycle repeats.

FIGURE 9

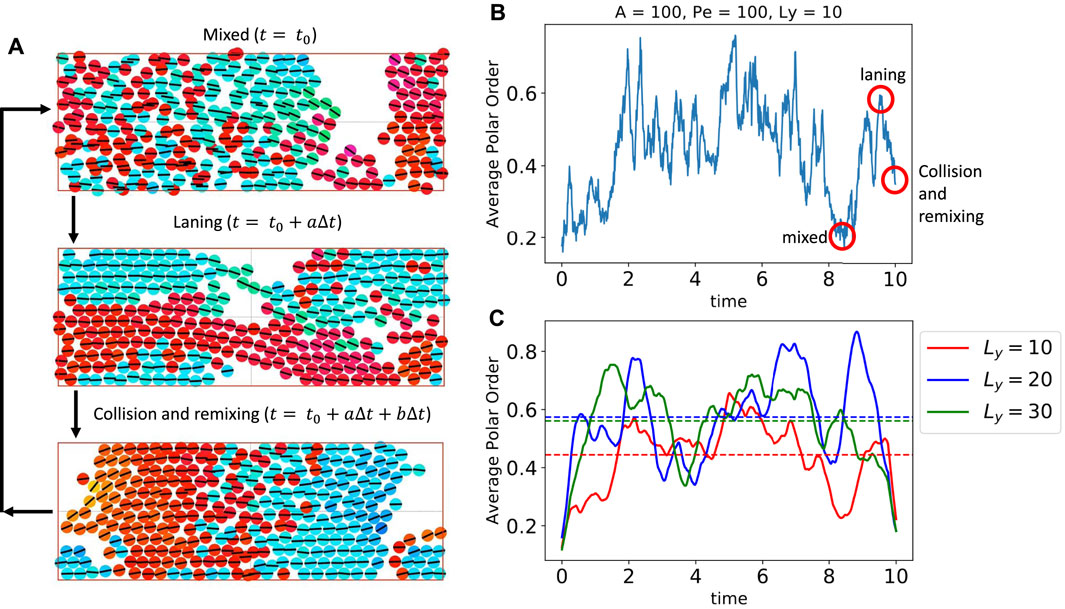
FIGURE 9. Traveling chains in a narrow channel exhibit cycles of mixing, laning, and collision and remixing. (A) Snapshots of a simulation where channel width has been decreased by a factor of 3. Dynamics of the system are encompassed by three cyclic states: A mixed state shown at an arbitrary initial time t₀, a phase separated laning state shown a short time after t₀, and a collision and remixing state shown a short time after the laning state. (B) Polar order averaged over boxes of width 3σ and height 2.5σ versus time is shown to elucidate the three states described in (A). The polar order for a mixed–laning–collision and remixing cycle are shown in the red circles. When the system is well mixed, the average polar order is small (p ≈ 0.2). When the particles separate into lanes, the polar order increases rapidly (p ≈ 0.6). When the lanes then collide and begin remixing, the remnants of the bulk of the lanes provide polar order while mixed particles and the interface between lanes decreases polar order (p ≈ 0.4). (C) Polar order averaged over boxes of width 3σ and height 2.5σ versus time for three channel widths. Time averaged polar order, shown in dashed horizontal lines, is similar for the L_y = 20 and L_y = 30 cases when collision dynamics occur in the bulk, but non-interacting traveling chains line the boundaries. Time averaged polar order is smaller for the L_y = 10 case as collision dynamics are global phenomena. The full movie corresponding to the narrow channel can be seen in Supplementary Movie S5.

This effect of colliding lanes can be seen quantitatively by tracking the magnitude of the polar order parameter averaged over boxes of width 3σ and height 2.5σ in time shown in Figure 9B. The well mixed system has an average polar order parameter of |p| ≈ 0.2. The system then phase separates into lanes with average polar order parameter $\approx 0.6$. The + x and − x lanes collide and the resultant combination has an average polar order parameter $\approx 0.4$. When the channel is sufficiently wide, collisions between opposite lanes is less common, and the average polar order is bolstered by persistent polar chains at the confining boundary as seen in Figure 9C. This time dependent formation and disbanding of polar structures is consistent with bead spring simulations of semiflexible filaments in the high activity regime [59].

4 Methods

Here, we present the equations governing the motion of the active motile particles discussed earlier and their interaction via the elastic substrate on which they move. In our model, we treat the particles as circular active Brownian particles (ABPs) that interact with other particles via long-range substrate modulated interactions and direct short-range particle-particle steric contact interactions. Long range interactions arise as each ABP exerts a contractile stress dipole P on the flat, semi-infinite, linearly elastic, isotropic substrate, thereby inducing strain fields which induce an effective force on nearby particles. For simplicity, we assume that the dipole axis is coincident with the direction of motion of the particle. For instance in an elongated cell, the force dipole axis coincides with the orientational axis of the cell, that is also the direction of self-propulsion.

In the derivation that follows we use Einstein summation convention over the Latin indices, while Greek indices are used to label the particles. Consider a particle α that deforms the substrate. The work done by the associated dipole, P^α in deforming the substrate in the presence of the strain created by a second dipole P^β (generated by a second particle β) is given by [46],

$W_{\alpha \beta }=P_{ij}^{\beta }{\partial }_j{\partial }_l{G}_{ik}^{\alpha \beta }\left({\mathbf{r}}_{\alpha \beta }\right)P_{kl}^{\alpha },(2)$

where r_αβ = r_β − r_α is the separation vector connecting the centers of particles α and β (Figure 10) (c.f [39, 49]). The elastic half space or Boussinesq Green’s function that gives the displacement field in the linearly elastic medium at the location of one particle caused by the application of a point force at the location of the other is given by [45],

$G_{ik}^{\alpha \beta }\left({\mathbf{r}}_{\alpha \beta }\right)=\frac{1+\nu }{\pi E}\left[\left(1-\nu \right)\frac{{\delta }_{ik}}{r_{\alpha \beta }}+\nu \frac{r_{\alpha \beta ,i}{r}_{\alpha \beta ,k}}{r_{\alpha \beta }^3}\right],(3)$

where E is the stiffness (Young’s modulus) and ν is Poisson’s ratio of the substrate. Given the linearity of the problem, superposition of strain fields, each of which is obtained by using the Green's function (1), appropriately provides the net displacement at a test position due to particles around it.

FIGURE 10

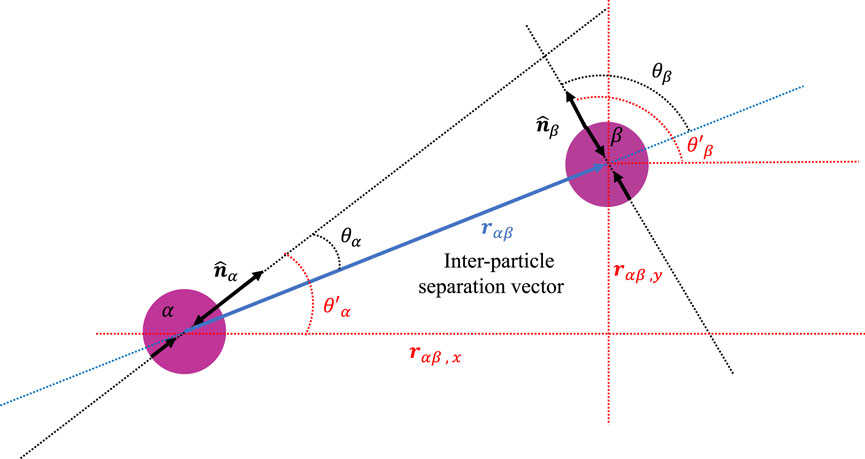
FIGURE 10. Schematic of two interacting particles with all relevant angles and vectors labeled. ${\widehat{\mathbf{n}}}_i$ are unit vectors of force dipoles. ${\theta }_i^{\prime }$ are angles of force dipoles with respect to the lab frame x-axis. θ_α and θ_β are angles of force dipoles with respect to their separation vector r_αβ which has components r_αβ,x and r_αβ,y.

Two particles in our model interact via a combination of pairwise long-range and short-range interactions. The long-range interaction forces originate from the substrate-mediated, elastic dipole-dipole interaction potential, W^αβ. The short-range interactions are steric in nature and prevent ABPs from overlapping. This functionality is achieved in the framework of our model by linear springs that only resist compression. Taken together, the total interaction potential between particles α and β can be written as,

$\begin{array}{ll}\hfill W^{\alpha \beta }& =\frac{1}{2}k{\left(\sigma -r_{\alpha \beta }\right)}^2,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}0\le r_{\alpha \beta }<\sigma \hfill \\ \hfill & =\frac{P^2}{E}\frac{f\left(\nu ,{\theta }_{\alpha },{\theta }_{\beta }\right)}{r_{\alpha \beta }^3},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\sigma \le r_{\alpha \beta }<r_{\text{cut}}\hfill \\ \hfill & =0,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}{r}_{\alpha \beta }\ge r_{\text{cut}},\hfill \end{array}(4)$

where k is the spring constant of the linear (repulsive) spring preventing overlap, σ is the particle diameter (kept constant in our simulations), and r_cut is a cutoff distance beyond which the dipolar interactions are neglected. The magnitude of each force dipole is taken to be the same value denoted by P. The dependence of the pairwise dipolar interactions on the orientations of the two dipoles with respect to their separation vectors, and on the Poisson ratio of the medium, ν, is expressed compactly in the expression [49],

$\begin{array}{ll}\hfill f\left(\nu ,{\theta }_{\alpha },{\theta }_{\beta }\right)& =\frac{\nu \left(\nu +1\right)}{2\pi }\left(3\left({\cos }^2{\theta }_{\alpha }+{\cos }^2{\theta }_{\beta }-5{\cos }^2{\theta }_{\alpha }{\cos }^2{\theta }_{\beta }-\frac{1}{3}\right)\right.\hfill \\ \hfill & \left.-\left(2-{\nu }^{-1}\right){\cos }^2\left({\theta }_{\alpha }-{\theta }_{\beta }\right)-3\left({\nu }^{-1}-4\right)\cos {\theta }_{\alpha }\cos {\theta }_{\beta }\cos \left({\theta }_{\alpha }-{\theta }_{\beta }\right)\right).\hfill \end{array}(5)$

where $\cos {\theta }_{\alpha }={\widehat{\mathit{n}}}_{\alpha }\cdot {\vec{\mathit{r}}}_{\alpha \beta }$ and $\cos {\theta }_{\beta }={\widehat{\mathit{n}}}_{\beta }\cdot {\vec{\mathit{r}}}_{\alpha \beta }$ are the orientations of particles, α and β, with respect to their separation vector, respectively (Figure 10).

Motivated by natural and synthetic systems to which our model is applicable, we assume that the particles are in an over-damped viscous environment, and the inertia of the ABPs can be ignored. We can then write the equations of motion governing the translation and rotation, respectively, of particle α as,

$\frac{d{\mathbf{r}}_{\alpha }}{dt}=v_0{\widehat{\mathbf{n}}}_{\alpha }-{\mu }_T\sum _{\beta }\frac{\partial W^{\alpha \beta }}{\partial {\mathbf{r}}_{\alpha }}+\sqrt{2D_{\text{T}}}{\mathit{\eta }}_{\mathrm{T},\alpha }\left(t\right)(6)$

and

$\frac{d{\widehat{\mathbf{n}}}_{\alpha }}{dt}=-{\mu }_R\sum _{\beta }{\widehat{\mathbf{n}}}_{\alpha }\times \frac{\partial W^{\alpha \beta }}{\partial {\widehat{\mathbf{n}}}_{\alpha }}+\sqrt{2D_{\text{R}}}{\mathit{\eta }}_{\mathrm{R},\alpha }\left(t\right),(7)$

where r_α and ${\widehat{\mathbf{n}}}_{\alpha }$ are the position and orientation of particle α, respectively. In the equations above D_T and D_R are the translational and rotational diffusivity quantifying the random motion of a single particle, respectively. The viscous environment results in the translational and rotational mobilities, μ_T and μ_R respectively. Random white noise terms η_T and η_R have components that satisfy ⟨η_T,i(t)η_T,j(t′)⟩ = δ(t − t′)δ_ij and ⟨η_R,i(t)η_R,j(t′)⟩ = δ(t − t′)δ_ij. Since the fluctuation dissipation theorem is not necessarily satisfied for a nonequilibrium system, the translational and rotational diffusivity are independent of each other. However, to reduce the number of free parameters and in the interest of simplicity, we assume that D_T = σ²D_R and μ_T = σ²μ_R. This allows the definition of an effective temperature, k_BT_eff = D_T/μ_T. Finally we emphasize that each particle is endowed with the same dipole strength, P, and self-propulsion velocity, v₀, both of which are constant.

We now choose the cell diameter σ, the diffusion time, σ²/D_T, and the effective thermal energy that quantifies the strength of stochastic fluctuations, D_T/μ_T, as physically relevant length, time, and energy scales in our model. Solutions to the scaled dynamical model are then dependent on three non-dimensional numbers,

$Pe=\frac{v_0\sigma }{D_{\text{T}}},A=\frac{{\mu }_T{P}^2}{E{\sigma }^3{D}_{\text{T}}},k^{*}=\frac{{\mu }_{\text{T}}k{\sigma }^2}{D_{\text{T}}}(8)$

where Pe is the Péclet number that is a measure of the self-propulsion in terms of the diffusion of motile particles, A is an effective elastic dipole-dipole interaction parameter, and k* is the nondimensional steric spring constant.

Nondimensional forms of the dynamical equations Eqs 6, 7 are discretized and numerically solved using the explicit half-order Euler-Maruyama method [60]. We use a time step of Δt = 10^–4 for a total of 10⁵ − 10⁶ timesteps corresponding to a total simulation time of 10 − 100. Each particle was initialized with a random position and orientation in our simulation box of size L_x = 30σ and 10σ ≤ L_y ≤ 30σ with periodic boundary conditions in x and confinement modeled by repulsive springs identical to those used for particle-particle steric repulsions, with a fixed spring constant, k* = 10⁴, placed along the top and bottom walls. In our simulations, we want particles near each other to interact via the elastic potential at every time step, and to ensure that the overlap of particles is minimized. Furthermore, to ensure that the particles are not subject to unphysical repulsive forces, we choose k* such that k*Δt = 1. We show in the Supplementary Figure S1 that the higher order structures formed by the particles at different k* are qualitatively similar when the timestep is appropriately rescaled. A and Pe are varied and analyzed in the Results section of the text.

5 Discussion

We have shown the typical collective behavior that emerges when active particles interact with each other as dipoles, using Brownian dynamics simulations. This minimal model is inspired by collective cell motility on elastic substrates where the cell-cell interaction is mediated by their mutual deformations of the passive substrate. While some of the emergent collective structures have analogs in cell culture experiments, such as the network organization of endothelial cells [61], our model is not intended to capture any specific biological behavior. We expect the first tests of our model to happen in dilute cell culture experiments that measure both pairwise cell interactions and substrate traction forces as in Ref. [23, 24].

The passive dipolar interactions lead to the end-to-end alignment of the particles into motile chains, which can be mutually aligned into polar bands and clusters because of their active motion. Polar chains that travel in opposite directions would be sorted into bands that get out of each others’ way. These basic implications of our model, while specifically demonstrated here for elastic dipoles, belong to a broader class of active particles with dipolar interactions [31, 32, 62], and may therefore also be experimentally realized in active colloids endowed with permanent or induced dipole moments [30, 63]. We note that the symmetry of the elastic dipolar interactions is modified at higher Poisson’s ratio [49], which is expected to result in structures such as active rings with rotational motion. This richer behavior with elastic interactions is a direct consequence of the tensorial, as opposed to vectorial nature of the elastic dipoles, in contrast with magnetic or electric dipoles, and will be the subject of future study. We further note that the mechanical interactions between cells in elastic media is in reality expected to include effects not considered here including from the nonlinear elastic properties of the substrate and nonlinear effects arising from the cells actively maintaining mechanical homeostasis at their boundaries, such as by regulating their shape [64]. We also ignore the elastic response of the cells themselves, which can give rise to additional interactions similar to that between rigid inclusions in soft media [65].

We focused on the strong elastic interaction cases in the dilute regime, where the self-assembly and dynamics of single chains can be studied. Since the chains are stable in this regime, they resemble other active polymer systems [57], that typically arise in gliding assays of biological filaments [66] or with synthetic colloids [26]. Polar bands are also seen at a higher density of active polymers [59]. However, in our system where these chains are self-assembled by dipolar interactions, multiple chains can stick to each other at higher interaction strength, while they can also fall apart, when colliding at high motility. By showing how a pair of chains interact with each other, we show the stable higher order structures that form and contribute to the polar clusters seen at higher density. Although not investigated in detail here, it will also be interesting to explore the bending dynamics of a single active polymer [67, 68] and characterize how the bending rigidity increases with dipolar interaction strength or decreases with particle motility.

To conclude, we note that our cell mechanobiology-inspired model also realizes a new class of active matter with long-range dipolar interactions. The emergent self-organization behavior distinct from the two typically studied pathways to the clustering of active particles: motility-induced phase separation [12], and Vicsek-style models [69]. In the latter, particle alignment is imposed in an agent-based manner, whereas here alignment emerges as a natural consequence of physical interactions.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

ArG, AjG, and KD conceived the study and the models. SB and PN performed the numeric simulations and analyses. All authors wrote the manuscript.

Funding

PN was supported by a graduate fellowship funding from the National Science Foundation: NSF-CREST: Center for Cellular and Biomolecular Machines (CCBM) at the University of California, Merced: NSF-HRD-1547848. ArG acknowledges funding from the National Science Foundation via the CAREER award NSF-CBET-2047210. AjG would like to acknowledge support from the National Science Foundation (NSF-DMS-1616926), NSF-CREST: Center for Cellular and Biomolecular Machines at UC Merced (NSF-HRD-1547848) and the NSF Center for Engineering Mechanobiology grant (CMMI-154857).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

PN and SB acknowledge computing time on the Multi-Environment Computer for Exploration and Discovery (MERCED) cluster at UC Merced (NSF-ACI-1429783). SB and PN acknowledge useful discussions with Farnaz Golnaraghi and Jimmy Gonzalez Nunez.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.876126/full#supplementary-material

Footnotes

¹This choice ensures end-to-end alignment of dipoles and provides interactions seen not just in cells but also in other types of active matter that feature particles with magnetic or electric dipole moments. The interactions at ν > 0.3 have a different symmetry and can result in more complex structures such as short rings without any electric or magnetic analogs [50].

References

1. Marchetti MC, Joanny JF, Ramaswamy S, Liverpool TB, Prost J, Rao M, et al. Hydrodynamics of Soft Active Matter. Rev Mod Phys (2013) 85:1143–89. doi:10.1103/RevModPhys.85.1143

CrossRef Full Text | Google Scholar

2. Gompper G, Winkler RG, Speck T, Solon A, Nardini C, Peruani F, et al. The 2020 Motile Active Matter Roadmap. J Phys Condensed Matter (2020) 32:193001. doi:10.1088/1361-648x/ab6348

CrossRef Full Text | Google Scholar

3. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active Particles in Complex and Crowded Environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/revmodphys.88.045006

CrossRef Full Text | Google Scholar

4. Copenhagen K, Malet-Engra G, Yu W, Scita G, Gov N, Gopinathan A. Frustration-Induced Phases in Migrating Cell Clusters. Sci Adv (2018) 4:eaar8483. doi:10.1126/sciadv.aar8483

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Ladoux B, Mège R-M. Mechanobiology of Collective Cell Behaviours. Nat Rev Mol Cel Biol (2017) 18:743–57. doi:10.1038/nrm.2017.98

CrossRef Full Text | Google Scholar

6. Alert R, Trepat X. Physical Models of Collective Cell Migration. Annu Rev Condens Matter Phys (2020) 11:77–101. doi:10.1146/annurev-conmatphys-031218-013516

CrossRef Full Text | Google Scholar

7. Angelini TE, Hannezo E, Trepat X, Fredberg JJ, Weitz DA. Cell Migration Driven by Cooperative Substrate Deformation Patterns. Phys Rev Lett (2010) 104:168104. doi:10.1103/PhysRevLett.104.168104

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Reinhart-King CA, Dembo M, Hammer DA. Cell-Cell Mechanical Communication through Compliant Substrates. Biophysical J (2008) 95:6044–51. doi:10.1529/biophysj.107.127662

CrossRef Full Text | Google Scholar

9. Schwarz US, Safran SA. Physics of Adherent Cells. Rev Mod Phys (2013) 85:1327–81. doi:10.1103/revmodphys.85.1327

CrossRef Full Text | Google Scholar

10. Henkes S, Kostanjevec K, Collinson JM, Sknepnek R, Bertin E. Dense Active Matter Model of Motion Patterns in Confluent Cell Monolayers. Nat Commun (2020) 11:1405. doi:10.1038/s41467-020-15164-5

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chaté H, Ginelli F, Grégoire G, Peruani F, Raynaud F. Modeling Collective Motion: Variations on the Vicsek Model. Eur Phys J B (2008) 64:451–6. doi:10.1140/epjb/e2008-00275-9

CrossRef Full Text | Google Scholar

12. Cates ME, Tailleur J. Motility-Induced Phase Separation. Annu Rev Condens Matter Phys (2015) 6:219–44. doi:10.1146/annurev-conmatphys-031214-014710

CrossRef Full Text | Google Scholar

13. Digregorio P, Levis D, Suma A, Cugliandolo LF, Gonnella G, Pagonabarraga I. Full Phase Diagram of Active Brownian Disks: From Melting to Motility-Induced Phase Separation. Phys Rev Lett (2018) 121:098003. doi:10.1103/PhysRevLett.121.098003

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Balaban NQ, Schwarz US, Riveline D, Goichberg P, Tzur G, Sabanay I, et al. Force and Focal Adhesion Assembly: A Close Relationship Studied Using Elastic Micropatterned Substrates. Nat Cel Biol (2001) 3:466–72. doi:10.1038/35074532

CrossRef Full Text | Google Scholar

15. Mandal K, Wang I, Vitiello E, Orellana LAC, Balland M. Cell Dipole Behaviour Revealed by Ecm Sub-Cellular Geometry. Nat Commun (2014) 5:5749. doi:10.1038/ncomms6749

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pelham RJ, Wang Y-L. Cell Locomotion and Focal Adhesions are Regulated by Substrate Flexibility. Proc Natl Acad Sci U.S.A (1997) 94:13661–5. doi:10.1073/pnas.94.25.13661

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Dembo M, Wang Y-L. Stresses at the Cell-To-Substrate Interface during Locomotion of Fibroblasts. Biophysical J (1999) 76:2307–16. doi:10.1016/S0006-3495(99)77386-8

CrossRef Full Text | Google Scholar

18. van Oers RFM, Rens EG, LaValley DJ, Reinhart-King CA, Merks RMH. Mechanical Cell-Matrix Feedback Explains Pairwise and Collective Endothelial Cell Behavior In Vitro. PLoS Comput Biol (2014) 10:e1003774. doi:10.1371/journal.pcbi.1003774

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tang X, Bajaj P, Bashir R, Saif TA. How Far Cardiac Cells Can See Each Other Mechanically. Soft Matter (2011) 7:6151–8. doi:10.1039/C0SM01453B

CrossRef Full Text | Google Scholar

20. Dasbiswas K, Majkut S, Discher DE, Safran SA. Substrate Stiffness-Modulated Registry Phase Correlations in Cardiomyocytes Map Structural Order to Coherent Beating. Nat Commun (2015) 6:6085. doi:10.1038/ncomms7085

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Nitsan I, Drori S, Lewis YE, Cohen S, Tzlil S. Mechanical Communication in Cardiac Cell Synchronized Beating. Nat Phys (2016) 12:472–7. doi:10.1038/nphys3619

CrossRef Full Text | Google Scholar

22. Cohen O, Safran SA. Elastic Interactions Synchronize Beating in Cardiomyocytes. Soft matter (2016) 12:6088–95. doi:10.1039/c6sm00351f

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Reinhart-King CA, Dembo M, Hammer DA. Endothelial Cell Traction Forces on Rgd-Derivatized Polyacrylamide Substrata. Langmuir (2003) 19:1573–9. doi:10.1021/la026142j

CrossRef Full Text | Google Scholar

24. Palmieri B, Scanlon C, Worroll D, Grant M, Lee J. Substrate Mediated Interaction between Pairs of Keratocytes: Multipole Traction Force Models Describe Their Migratory Behavior. PLoS One (2019) 14:e0212162. doi:10.1371/journal.pone.0212162

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Gennes PG, Pincus PA. Pair Correlations in a Ferromagnetic Colloid. Phys Kondens Materie (1970) 11:189–98. doi:10.1007/BF02422637

CrossRef Full Text | Google Scholar

26. Nishiguchi D, Iwasawa J, Jiang H-R, Sano M. Flagellar Dynamics of Chains of Active Janus Particles Fueled by an AC Electric Field. New J Phys (2018) 20:015002. doi:10.1088/1367-2630/aa9b48

CrossRef Full Text | Google Scholar

27. Ilg P, Del Gado E. Non-Linear Response of Dipolar Colloidal Gels to External Fields. Soft Matter (2011) 7:163–71. doi:10.1039/C0SM00592D

CrossRef Full Text | Google Scholar

28. Tlusty T, Safran SA. Defect-Induced Phase Separation in Dipolar Fluids. Science (2000) 290:1328–31. doi:10.1126/science.290.5495.1328

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Rovigatti L, Russo J, Sciortino F. No Evidence of Gas-Liquid Coexistence in Dipolar Hard Spheres. Phys Rev Lett (2011) 107:237801. doi:10.1103/physrevlett.107.237801

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sakaï N, Royall CP. Active Dipolar Colloids in Three Dimensions: Strings, Sheets, Labyrinthine Textures and Crystals. arXiv preprint arXiv:2010.03925 (2020).

Google Scholar

31. Kaiser A, Popowa K, Löwen H. Active Dipole Clusters: From Helical Motion to Fission. Phys Rev E (2015) 92:012301. doi:10.1103/PhysRevE.92.012301

CrossRef Full Text | Google Scholar

32. Liao G-J, Hall CK, Klapp SHL. Dynamical Self-Assembly of Dipolar Active Brownian Particles in Two Dimensions. Soft Matter (2020) 16:2208–23. doi:10.1039/c9sm01539f

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Guzmán-Lastra F, Kaiser A, Löwen H. Fission and Fusion Scenarios for Magnetic Microswimmer Clusters. Nat Commun (2016) 7:13519. doi:10.1038/ncomms13519

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Telezki V, Klumpp S. Simulations of Structure Formation by Confined Dipolar Active Particles. Soft Matter (2020) 16:10537–47. doi:10.1039/D0SM00926A

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Fatehiboroujeni S, Gopinath A, Goyal S. Nonlinear Oscillations Induced by Follower Forces in Prestressed Clamped Rods Subjected to Drag. J Comput Nonlinear Dyn (2018) 13:121005. doi:10.1115/1.4041681

CrossRef Full Text | Google Scholar

36. Sangani AS, Gopinath A. Elastohydrodynamical Instabilities of Active Filaments, Arrays, and Carpets Analyzed Using Slender-Body Theory. Phys Rev Fluids (2020) 5:083101. doi:10.1103/physrevfluids.5.083101

CrossRef Full Text | Google Scholar

37. Fily Y, Subramanian P, Schneider TM, Chelakkot R, Gopinath A. Buckling Instabilities and Spatio-Temporal Dynamics of Active Elastic Filaments. J R Soc Interf (2020) 17:20190794. doi:10.1098/rsif.2019.0794

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Chelakkot R, Hagan MF, Gopinath A. Synchronized Oscillations, Traveling Waves, and Jammed Clusters Induced by Steric Interactions in Active Filament Arrays. Soft Matter (2021) 17:1091–104. doi:10.1039/d0sm01162b

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Schwarz US, Safran SA. Elastic Interactions of Cells. Phys Rev Lett (2002) 88:048102. doi:10.1103/PhysRevLett.88.048102

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Yan J, Han M, Zhang J, Xu C, Luijten E, Granick S. Reconfiguring Active Particles by Electrostatic Imbalance. Nat Mater (2016) 15:1095–9. doi:10.1038/nmat4696

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Romanczuk P, Bär M, Ebeling W, Lindner B, Schimansky-Geier L. Active Brownian Particles. Eur Phys J Spec Top (2012) 202:1–162. doi:10.1140/epjst/e2012-01529-y

CrossRef Full Text | Google Scholar

42. Marchetti MC, Fily Y, Henkes S, Patch A, Yllanes D. Minimal Model of Active Colloids Highlights the Role of Mechanical Interactions in Controlling the Emergent Behavior of Active Matter. Curr Opin Colloid Interf Sci (2016) 21:34–43. doi:10.1016/j.cocis.2016.01.003

CrossRef Full Text | Google Scholar

43. Bose S, Dasbiswas K, Gopinath A. Matrix Stiffness Modulates Mechanical Interactions and Promotes Contact between Motile Cells. Biomedicines (2021) 9:428. doi:10.3390/biomedicines9040428

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Boal D. Mechanics of the Cell. 2 edn.. Cambridge: Cambridge University Press (2012). doi:10.1017/CBO9781139022217

CrossRef Full Text | Google Scholar

45. Landau LD, Lifshitz EM. Theory of Elasticity, Course of Theoretical Physics, 7. London: Pergamon Press (1959).

Google Scholar

46. Bischofs IB, Safran SA, Schwarz US. Elastic Interactions of Active Cells with Soft Materials. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 69:021911. doi:10.1103/PhysRevE.69.021911

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wagner H, Horner H. Elastic Interaction and the Phase Transition in Coherent Metal-Hydrogen Systems. Adv Phys (1974) 23:587–637. doi:10.1080/00018737400101401

CrossRef Full Text | Google Scholar

48. Zabel H, Peisl H. Sample-Shape-Dependent Phase Transition of Hydrogen in Niobium. Phys Rev Lett (1979) 42:511–4. doi:10.1103/physrevlett.42.511

CrossRef Full Text | Google Scholar

49. Bischofs IB, Schwarz US. Cell Organization in Soft media Due to Active Mechanosensing. Proc Natl Acad Sci U.S.A (2003) 100:9274–9. doi:10.1073/pnas.1233544100

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Bischofs I, Schwarz U. Collective Effects in Cellular Structure Formation Mediated by Compliant Environments: A Monte Carlo Study. Acta Biomater (2006) 2:253–65. doi:10.1016/j.actbio.2006.01.002

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Marel A-K, Zorn M, Klingner C, Wedlich-Söldner R, Frey E, Rädler JO. Flow and Diffusion in Channel-Guided Cell Migration. Biophysical J (2014) 107:1054–64. doi:10.1016/j.bpj.2014.07.017

CrossRef Full Text | Google Scholar

52. Ezhilan B, Alonso-Matilla R, Saintillan D. On the Distribution and Swim Pressure of Run-And-Tumble Particles in Confinement. J Fluid Mech (2015) 781, R4. doi:10.1017/jfm.2015.520

CrossRef Full Text | Google Scholar

53. Elgeti J, Gompper G. Run-And-Tumble Dynamics of Self-Propelled Particles in Confinement. EPL (Europhysics Letters) (2015) 109:58003. doi:10.1209/0295-5075/109/58003

CrossRef Full Text | Google Scholar

54. Yan W, Brady JF. The Force on a Boundary in Active Matter. J Fluid Mech (2015) 785, R1. doi:10.1017/jfm.2015.621

CrossRef Full Text | Google Scholar

55. Wagner CG, Hagan MF, Baskaran A. Steady-State Distributions of Ideal Active Brownian Particles under Confinement and Forcing. J Stat Mech (2017) 2017:043203. doi:10.1088/1742-5468/aa60a8

CrossRef Full Text | Google Scholar

56. Poncet A, Bénichou O, Démery V, Nishiguchi D. Pair Correlation of Dilute Active Brownian Particles: From Low-Activity Dipolar Correction to High-Activity Algebraic Depletion Wings. Phys Rev E (2021) 103, 012605. doi:10.1103/physreve.103.012605

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Winkler RG, Gompper G. The Physics of Active Polymers and Filaments. J Chem Phys (2020) 153:040901. doi:10.1063/5.0011466

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Volpe G, Gigan S, Volpe G. Simulation of the Active Brownian Motion of a Microswimmer. Am J Phys (2014) 82:659–64. doi:10.1119/1.4870398

CrossRef Full Text | Google Scholar

59. Vliegenthart GA, Ravichandran A, Ripoll M, Auth T, Gompper G. Filamentous Active Matter: Band Formation, Bending, Buckling, and Defects. Sci Adv (2020) 6:eaaw9975. doi:10.1126/sciadv.aaw9975

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford: Oxford University Press (2017).

Google Scholar

61. Califano JP, Reinhart-King CA. A Balance of Substrate Mechanics and Matrix Chemistry Regulates Endothelial Cell Network Assembly. Cel Mol Bioeng (2008) 1:122–32. doi:10.1007/s12195-008-0022-x

CrossRef Full Text | Google Scholar

62. Vutukuri HR, Lisicki M, Lauga E, Vermant J. Light-Switchable Propulsion of Active Particles with Reversible Interactions. Nat Commun (2020) 11:2628. doi:10.1038/s41467-020-15764-1

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Vutukuri HR, Bet B, Van Roij R, Dijkstra M, Huck WTS. Rational Design and Dynamics of Self-Propelled Colloidal Bead Chains: from Rotators to Flagella. Sci Rep (2017) 7:16758. doi:10.1038/s41598-017-16731-5

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Golkov R, Shokef Y. Shape Regulation Generates Elastic Interaction between Living Cells. New J Phys (2017) 19:063011. doi:10.1088/1367-2630/aa70ef

CrossRef Full Text | Google Scholar

65. Puljiz M, Huang S, Auernhammer GK, Menzel AM. Forces on Rigid Inclusions in Elastic Media and Resulting Matrix-Mediated Interactions. Phys Rev Lett (2016) 117:238003. doi:10.1103/PhysRevLett.117.238003

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Phillips R, Kondev J, Theriot J. Physical Biology of the Cell. New York: Garland Science, Taylor & Francis Group (2008).

Google Scholar

67. Eisenstecken T, Gompper G, Winkler R. Conformational Properties of Active Semiflexible Polymers. Polymers (2016) 8:304. doi:10.3390/polym8080304

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Liao X, Purohit PK, Gopinath A. Extensions of the Worm-Like-Chain Model to Tethered Active Filaments under Tension. J Chem Phys (2020) 153:194901. doi:10.1063/5.0025200

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys Rev Lett (1995) 75:1226–9. doi:10.1103/physrevlett.75.1226

PubMed Abstract | CrossRef Full Text | Google Scholar