Controlled Quantum Secure Direct Communication Based on Four-Qubit Cluster States and Quantum Search Algorithm

A controlled quantum secure direct communication protocol based on four-qubit cluster states and quantum search algorithm is put forward, in which four users, a sender, a receiver and two controllers, are involved in achieving the secure transmission of secret message. The four-qubit cluster state can ensure the feasibility and security of the protocol because of its large persistency of entanglement. Meanwhile, the idea of quantum search algorithm is used to accomplish the task of encoding and decoding secret message. The proposed protocol can successfully avoid the information leakage problem and resist some common attacks including the outsider attacks and the internal attacks, and its qubit efficiency is up to 20%. Furthermore, compared with the previous quantum secure direct communication protocols, it can effectively resist the attacks from the dishonest receiver.

1 Introduction

Quantum key distribution (QKD) protocol was first proposed by Bennett and Brassard in 1984, in which two remote authorized users can create a shared private key [1]. The security of QKD protocol was theoretically proven in [2, 3]. Afterwards, this topic has attracted the focus of many scholars so that some interesting branches of QKD have been built, such as quantum teleportation (QT) [4], quantum secret sharing (QSS) [5], and quantum secure direct communication (QSDC) [6], etc. Different from QKD, QSDC is to transmit the secret directly through a quantum channel without establishing a random key to encrypt and decrypt them beforehand. In 2000, Long and Liu proposed the first QSDC protocol (LL00 protocol), in which the strategy of quantum block transmission was exploited to settle the problem of information leakage for the first time [6]. In 2002, Boström and Felbinger put forward a ping-pong QSDC protocol employing EPR pairs as the information carriers [7], which was insecure in a noisy quantum channel as shown by Wójcik [8]. Deng et al. presented a two-step quantum direct communication protocol based on EPR pairs, which clearly stated the definition and basic requirements of QSDC [9]. Hereafter, a number of QSDC protocols have been constructed based on non-entangled quantum states [10, 11] or entangled quantum states [12–17]. To better control QSDC protocol, the first controlled QSDC (CQSDC) was proposed in 2005, where a controller is added to supervise the secure communication between a sender and a receiver [18]. Subsequently, some CQSDC protocols have been developed constantly, where the communication is controlled by at least one controller [19–25]. Quantitative security analysis of QSDC has completed using Wyner’s wiretap channel theory in Refs. [26, 27]. The previous protocols need the use of quantum memory [6–25]. Regretfully, no practical quantum memory exists, so the quantum-memory-free technique has been developed [28] to make QSDC protocols be implemented without quantum memory. To counter this adverse effect of high noise and high loss in a realistic environment, a classical coding scheme was presented, which causes the secure channel capacity to be small, and a practical prototype based on the DL04 protocol [10] has been established [27]. The issue of small channel capacity can be solved by INCUM technique [29]. Moreover, measurement-device-independent QSDC [30–32], device-independent QSDC [33, 34], detector-device-independent QSDC [35] and full Bell-basis QSDC [36] have further advanced the development of QSDC. Some progress has been made experimentally. Proof-of-principle experiments of the DL04 protocol was completed in 2016 [37], experimental demonstration of QSDC with state-of-the-art atomic quantum memory [38] and long-distance QSDC experiment [39] were presented in 2017. Recently, the applications of QSDC have been reported [40–42]. Reference [40] demonstrated the feasibility of QSDC over GEO satellite, and the application of QSDC in both 6G [41] and secure quantum network [42] were studied.

Nowadays, another research hotspot is quantum search algorithm (QSA), put forward by Grover in 1996, which can find a marked item with very high probability from an unsorted database with size $N$ with a quadratic speedup compared with other famous classical algorithms [43, 44]. QSA is mainly applied in computing, and it has been introduced into quantum cryptography in recent years, including quantum private comparison [45], quantum secret sharing [46], quantum key agreement (QKA) [47] and quantum secure direct communication [48–51]. In 2010, Wang et al. applied QSA to build a QSDC protocol, which was the first combination of QSDC and QSA [48]. Later, two CQSDC protocols based on QSA were proposed [49, 50]. In 2020, Yin et al. proposed a controlled bidirectional QSDC protocol with QSA [51]. The cluster states, first introduced by Briegel and Raussendorf, qualify some properties of robust against decoherence [52] and easily being processed by a one-way quantum computer [53]. Moreover, the four-qubit cluster state with large persistency of entanglement [52, 54] is a form of cluster states, which can be generated experimentally [55, 56]. So far, there has not been a combination of four-qubit cluster states and quantum search algorithm to achieve controlled quantum secure direct communication. To focus on the research of CQSDC with four-qubit cluster states and QSA can be worthwhile exploring.

In this paper, a novel controlled quantum secure direct communication protocol with four-qubit cluster states and quantum search algorithm is proposed. The sender Alice and the receiver Bob can successfully achieve the transmission of secret message with the qubit efficiency of 20% with the help of two controllers (Charlie 1, and Charlie 2) without any information leakage. Furthermore, the proposed protocol can not only resist some common attacks but also find the vicious behavior from the attackers. In addition, the proposed protocol outperforms the existing ones in terms of resisting the internal attacks.

The rest of the paper is organized as follows. Section 2 introduces QSA with two-qubit system briefly. An efficient CQSDC protocol based on four-particle cluster states and QSA is depicted in Sec.3. Section 4 analyzes the security of the proposed CQSDC protocol under various attacks. A performance comparison is shown in Section 5. Finally, the concluding remarks appear in Section 6.

2 Review of Grover’s Search Algorithm

We briefly review Grover’s search algorithm in this section [43, 44]. Assume that we want to search for a marked state $w$ belonging to the set $\left\{|00\rangle ,|01\rangle ,|10\rangle ,|11\rangle \right\}$. The database can be considered as a two-qubit quantum system, and its initial state is described as $|S\rangle =|+\rangle |+\rangle =1/2\left(|00\rangle +|01\rangle +|10\rangle +|11\rangle \right)$, where $|+\rangle =1/\sqrt{2}\left(|0\rangle +|1\rangle \right)$. QSA consists of two unitary operators $U_w$ and $U_S$, which can be expressed as follows:

$U_w=I-2|w\rangle \langle w|(1)$

$U_S=2|S\rangle \langle S|-I(2)$

Where $I$ means the identity operator.

Two operators in Eqs. 1, 2 are orderly conducted on initial state $|S\rangle$.

$U_S{U}_w|S\rangle =a|w\rangle (3)$

Where $\left|a\right|=1$. For example, assume that the marked state $w$ is $|11\rangle$. According to Eq. (3), $U_{11}$ is first operated on $|S\rangle$.

$|S^{\prime }\rangle =U_{11}|S\rangle =\frac{1}{2}\left(|00\rangle +|01\rangle +|10\rangle -|11\rangle \right)(4)$

Subsequently, the operator $U_S$ is performed on $|S^{\prime }\rangle$.

$U_S|S^{\prime }\rangle =|11\rangle .(5)$

Lastly, the marked state can be found with $Z$-basis $\left\{|0\rangle ,|1\rangle \right\}$ measurement with a 100% probability of success.

3 Description of the Proposed CQSDC Protocol

The CQSDC protocol, involving a honest sender Alice, a receiver Bob, and two controllers Charlie 1 and Charlie 2, employs four-particle cluster states and quantum search algorithm, which is presented in this section. If Alice is dishonest, the protocol doesn’t make any sense since the secret message is always known to Alice. Hence, let Alice be honest. Suppose that the secret message from Alice to Bob is a binary bit sequence $w=\left\{w_i|1\le i\le N\right\}$, where $w_{\text{i}}\in \left\{\mathrm{00,01,10,11}\right\}$. Simultaneously, Alice and Bob share a binary identity sequence $\text{ID}$ with length $N$ distributed through an absolutely secure QKD [57]. Here, we assume the quantum channel is ideal. The proposed CQSDC protocol is executed in the following steps and clearly illustrated in Figure 1.

FIGURE 1

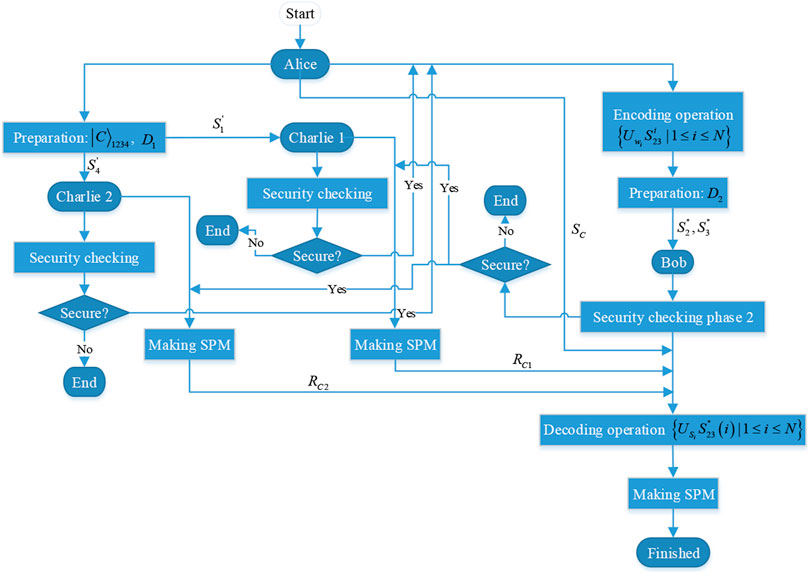
FIGURE 1. The executing process of the whole communication protocol. SPM denotes single-particle measurements with $Z$-basis.

3.1 Step 1 Preparation Phase

Alice generates $N$ ordered four-particle cluster states ${|C\rangle }_{1234}$ randomly in one of sixteen four-particle cluster states (see Eqn. 6), which can be denoted as$S_A=\left\{\left(P_1\left(1\right),P_1\left(2\right),P_1\left(3\right),P_1\left(4\right)\right),\left(P_2\left(1\right),P_2\left(2\right),P_2\left(3\right),P_2\left(4\right)\right),\dots ,\left(P_N\left(1\right),P_N\left(2\right),P_N\left(3\right),P_N\left(4\right)\right)\right\}$, where the subscripts denote the order of four-particle entanglement states. Subsequently, Alice selects the first photon from each cluster state ${|C\rangle }_{1234}$ to form an ordered sequence $S_1=\left\{P_1\left(1\right),P_2\left(1\right),\dots ,P_N\left(1\right)\right\}$ and the second and the third photons to construct sequence

$S_{23}=\left\{S_{23}^i|1\le i\le N\right\}=\left\{\left(P_1\left(2\right),P_1\left(3\right)\right),\left(P_2\left(2\right),P_2\left(3\right)\right),\dots ,\left(P_N\left(2\right),P_N\left(3\right)\right)\right\}$, and all the rest partner photons composes a sequence $S_4=\left\{P_1\left(4\right),P_2\left(4\right),\dots ,P_N\left(4\right)\right\}$. In the following, Alice prepares $2\mathrm{mN}$ decoy photons $D_1$ randomly selected from the set $\left\{|\text{0}\rangle \text{,}|1\rangle \text{,}|+\rangle \text{,}|-\rangle \right\}$, where $|\pm \rangle =1/\sqrt{2}\left(|0\rangle \pm |1\rangle \right)$, and inserts them in random positions into Sequences $S_1$ and $S_4$ obtaining two new Sequences $S_1^{\text{'}}$ and $S_4^{\text{'}}$, respectively, [58]. Alice records the initial state and corresponding position of each checking photon in Sequences $S_1^{\text{'}}$ and $S_4^{\text{'}}$. Finally, Alice sends $S_1^{\text{'}}$ and $S_4^{\text{'}}$ to Charlie 1 and Charlie 2 through a quantum channel, respectively.

$\begin{array}{l}|C_0\rangle =\frac{1}{2}\left(|0000\rangle +|0011\rangle +|1100\rangle -|1111\rangle \right)\\ |C_1\rangle =\frac{1}{2}\left(|0000\rangle -|0011\rangle +|1100\rangle -|1111\rangle \right)\\ |C_2\rangle =\frac{1}{2}\left(|0000\rangle +|0011\rangle -|1100\rangle -|1111\rangle \right)\\ |C_3\rangle =\frac{1}{2}\left(|0000\rangle -|0011\rangle -|1100\rangle -|1111\rangle \right)\\ |C_4\rangle =\frac{1}{2}\left(|0001\rangle +|0010\rangle -|1101\rangle +|1110\rangle \right)\\ |C_5\rangle =\frac{1}{2}\left(-|0001\rangle +|0010\rangle +|1101\rangle +|1110\rangle \right)\\ |C_6\rangle =\frac{1}{2}\left(|0001\rangle +|0010\rangle +|1101\rangle -|1110\rangle \right)\\ |C_7\rangle =\frac{1}{2}\left(-|0001\rangle +|0010\rangle -|1101\rangle -|1110\rangle \right)\\ |C_8\rangle =\frac{1}{2}\left(|0100\rangle -|0111\rangle +|1000\rangle +|1011\rangle \right)\\ |C_9\rangle =\frac{1}{2}\left(|0100\rangle +|0111\rangle +|1000\rangle -|1011\rangle \right)\\ |C_{10}\rangle =\frac{1}{2}\left(|0100\rangle -|0111\rangle -|1000\rangle -|1011\rangle \right)\\ |C_{11}\rangle =\frac{1}{2}\left(|0100\rangle +|0111\rangle -|1000\rangle +|1011\rangle \right)\\ |C_{12}\rangle =\frac{1}{2}\left(-|0101\rangle +|0110\rangle +|1001\rangle +|1010\rangle \right)\\ |C_{13}\rangle =\frac{1}{2}\left(|0101\rangle +|0110\rangle -|1001\rangle +|1010\rangle \right)\\ |C_{14}\rangle =\frac{1}{2}\left(-|0101\rangle +|0110\rangle -|1001\rangle -|1010\rangle \right)\\ |C_{15}\rangle =\frac{1}{2}\left(|0101\rangle +|0110\rangle +|1001\rangle -|1010\rangle \right).\left(6\right)\end{array}$

$|C_0\rangle$ can be evolved into any of four-qubit cluster states in Eqn. 6 if just two suitable unitary operations selected from Pauli matrix set $\left\{I,X,iY,Z\right\}$ are performed on particles 1 and 3 of $|C_0\rangle$, respectively, where $I=|0\rangle \langle 0|+|1\rangle \langle 1|$, $X=|0\rangle \langle 1|+|1\rangle \langle 0|$, $\mathrm{iY}=|0\rangle \langle 1|-|1\rangle \langle 0|$ and $Z=|0\rangle \langle 0|-|1\rangle \langle 1|$.

3.2 Step 2 Security Checking Phase 1

After confirming that Charlie 1 has received sequence $S_1^{\text{'}}$, Alice announces the positions and the preparation bases of all the decoy photons in sequence $S_1^{\text{'}}$ to Charlie 1 through a public classical channel. Charlie 1 measures each decoy photon based on the corresponding preparation basis published by Alice and tells the measurement results to Alice. Alice then computes the error rate by comparing the initial states with the measurement results of the decoy photons. If the error rate exceeds the limit they preset beforehand, they announce that the communication channels are not secure and terminate the communication protocol. Meanwhile, Charlie 2 will do an analogous security checking with Alice. When two security checking processes are secure, they continue with the protocol.

3.3 Step 3 Encoding Phase

After checking the security of transmission above, Alice then encodes the secret message $w_i$ into the $i$ th two-qubit state in $S_{23}$ by making the unitary operation $U_{w_i}$ based on the encoding rules shown in Table 1. The encoding process can be expressed as,

$S_{23}^{\text{'}}=\left\{U_{w_i}{S}_{23}^i|1\le i\le N\right\},(7)$

Where $S_{23}^{\text{'}}$ represents the encoded sequence. For simplicity, let the initial state and the secret $w$ be $|C_0\rangle$ and 10, respectively. The initial state $|C_0\rangle$ can be written in another form as follows:

$|C_0\rangle =\frac{1}{4}\left(\begin{array}{l}|+\rangle \left(|00\rangle +|01\rangle +|10\rangle -|11\rangle \right)|+\rangle +|+\rangle \left(|00\rangle -|01\rangle +|10\rangle +|11\rangle \right)|-\rangle +\\ |-\rangle \left(|00\rangle +|01\rangle -|10\rangle +|11\rangle \right)|+\rangle +|-\rangle \left(|00\rangle -|01\rangle -|10\rangle -|11\rangle \right)|-\rangle \end{array}\right)(8)$

TABLE 1

TABLE 1. Encoding rules.

After the effect of the encoding operator $U_{10}$ on the qubits 2 and 3 of $|C_0\rangle$, it becomes

$|C_0^{\prime }\rangle =\frac{1}{4}\left(\begin{array}{l}|+\rangle \left(|00\rangle +|01\rangle -|10\rangle -|11\rangle \right)|+\rangle +|+\rangle \left(|00\rangle -|01\rangle -|10\rangle +|11\rangle \right)|-\rangle +\\ |-\rangle \left(|00\rangle +|01\rangle +|10\rangle +|11\rangle \right)|+\rangle +|-\rangle \left(|00\rangle -|01\rangle +|10\rangle -|11\rangle \right)|-\rangle \end{array}\right)(9)$

Alice orderly picks out photon 2 from $S_{23}^{\text{'}}$ to form a new sequence $S_2^{\text{'}}$, and the remaining partner particles composes another sequence $S_3^{\text{'}}$. Afterwards, Alice generates two decoy photons sequences $D_2$ based on the values of $\text{ID}$. The rule is that, if the $i$ th bit of $\text{ID}$ is 0, she randomly prepares the decoy photon in the state $|0\rangle$ or $|1\rangle$, otherwise she randomly prepares one in the state $|+\rangle$ or $|-\rangle$ with a same probability 1/2. Later, Alice inserts them in random positions into Sequences $S_2^{\text{'}}$ and $S_3^{\text{'}}$ obtaining two new Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$, separately, and then retains $S_3^{\text{'}\text{'}}$ in her hand and transmits $S_2^{\text{'}\text{'}}$ to Bob.

3.4 Step 4 Security Checking Phase 2

Upon receiving sequence $S_2^{\text{'}\text{'}}$, he sends an acknowledgment to Alice. For the first round of security checking and identity authentication of Bob, Alice only tells Bob the position information of the decoy photons in $S_2^{\text{'}\text{'}}$. Bob then performs measurements on the decoy photons with the corresponding measurement bases. The rule of choosing the measurement bases is as follows: if the $i$ th bit of $\text{ID}$ is 0, Bob chooses $Z$-basis $\left\{|0\rangle ,|1\rangle \right\}$; if not, he selects $X$-basis $\left\{|+\rangle ,|-\rangle \right\}$. Similar to Ref. [59], he records the measurement results $\left\{|0\rangle ,|+\rangle \right\}$ and $\left\{|1\rangle ,|-\rangle \right\}$ as 0 and 1, respectively, and then announces the recorded result sequence $R_B$. Likewise, Alice can also obtain a classical bit sequence $R_A$ of the decoy states based on the recorded rule above. Finally, Alice computes the error rate by comparing $R_A$ with $R_B$ one by 1 bit. On condition that the error rate is lower than the security bound, Alice sends sequence $S_3^{\text{'}\text{'}}$ to Bob. Otherwise, the protocol will be terminated, and they repeat the communication procedure from the beginning. After finishing the transmission of $S_3^{\text{'}\text{'}}$, Alice and Bob collaborate to do the second round of security checking similar to the first round one.

3.5 Step 5 Decoding Phase

Upon confirming that security checking phase 2 is secure, Bob removes all the decoy photons from Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$ to obtain $S_2^{\text{'}}$ and $S_3^{\text{'}}$, respectively. Afterwards, Bob orderly picks out the particles in Sequences $S_2^{\text{'}}$ and $S_3^{\text{'}}$ to restore sequence $S_{23}^{\text{'}}$. It depends on Charlie 1, Charlie 2 and Alice to decode the secret message. If Charlie 1, Charlie 2 and Alice allow the communication between Alice and Bob, Charlie 1 and Charlie 2 measure their own particles with $X$-basis obtaining the measurement results $R_{C1}$ and $R_{C2}$, respectively, and announce them to Bob. Meanwhile, Alice broadcasts the initial state of each four-particle cluster state. According to the announced information of Charlie 1, Charlie 2 and Alice, Bob can deduce the state $S_i$ of 2 and 3, as listed in Supplementary Table S1 (For further details, please see Supplementary Table S1). Finally, Bob performs the corresponding operation $U_{S_i}$ on the $i$ th two-qubit quantum state in the collapsed state sequence $S_{23}^{\text{'}\text{'}}=\left\{S_{23}^{\text{'}\text{'}}\left(i\right)|1\le i\le N\right\}$ with encoded information,

$\begin{array}{l}{S}_F=\left\{U_{S_i}{S}_{23}^{″}\left(i\right)|1\le i\le N\right\}\\ =\left\{{\alpha }_i|w_i\rangle |1\le i\le N\right\}\end{array}(10)$

Where $\left|{\alpha }_i\right|=1$. Afterwards, Bob makes single-particle measurements on each particle in sequence $S_F$ with $Z$-basis to deduce the secret.

Both $R_{C1}$ and $R_{C2}$ have two possible values $\left\{|+\rangle ,|-\rangle \right\}$. For example, assume that the measurement results of Charlie 1 and Charlie 2 are $|+\rangle$ and $|-\rangle$, respectively, and the initial state is $|C_0\rangle$, then $|S\rangle =1/2\left(|00\rangle -|01\rangle +|10\rangle +|11\rangle \right)$ can be obtained from Supplementary Table S1 (For further details, please see Supplementary Table S1). The operator $U_S$ in Eqn. 2 is applied to decode the encoded particles, i.e., $U_S|S_{23}^{\text{'}\text{'}}\rangle =-|10\rangle$, where $|S_{23}^{\text{'}\text{'}}\rangle =1/2\left(|00\rangle -|01\rangle -|10\rangle +|11\rangle \right)$ from Eqn. 9. Finally, Bob performs single-particle measurement with $Z$-basis, and the secret “10” can be read out, as shown in Table 2.

TABLE 2

TABLE 2. Decoding table with the initial state$|C_0\rangle$.

Table 2 shows Charlie 1 and Charlie 2 have four possible measurement outcomes $\left\{|+\rangle ,|+\rangle ;|+\rangle ,|-\rangle ;|-\rangle ,|+\rangle ;|-\rangle ,|-\rangle \right\}$ corresponding to each encoding operation $U_{w_i}$ when the initial state is $|C_0\rangle$. If only the encoding operation keeps unchanged, the same secret message can be always obtained and do not vary with the measurement results of Charlie 1 and Charlie 2. Likewise, the remaining fifteen kinds of initial states can also establish their respective decoding tables.

4 Security Analysis

Since the crucial issue of a feasible quantum communication protocol is its security, it is essential to discuss the security of the proposed communication protocol. The security of the proposed protocol is discussed from the outsider attacks and the internal attacks, and the analysis makes clear that the proposed protocol can protect the transmitted message from leaking out under various attacks. Namely, it is a feasible protocol.

4.1 The Controllers

The decoding operation $U_S$ of the receiver Bob heavily depends on the announced information of Charlie 1, Charlie 2 and Alice. Without their help, Bob cannot determine state $S$ and perform $U_S$ on the encoded sequence. That is to say, the receiver Bob cannot recover Alice’s secret if any controller disapproves his request or announces the incorrect information. Furthermore, even if Eve captured two encoded Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$, she cannot read out the information either without the permissions of the controllers. Thus, the controllers are a must to make the communication protocol go well.

4.2 Outsider Attacks

4.2.1 Entangle-and-Measure Attack

The entangle-and-measure attack is also called auxiliary particle attack. If Eve wants to execute the entangle-measure attack, she intercepts the encoded particles in sequence $S_2^{\text{'}\text{'}}$ disseminated from Alice to Bob and entangles them with the prepared ancillary particles in state $|E\rangle$ beforehand by making a unitary operation, and then sends the entanglement results to Bob. Furthermore, she finishes an eavesdropping attack by performing measurements on the ancillary particles to deduce useful information. However, it can be shown that it is in vain for an eavesdropper to gain useful information and her vicious behavior will be found inevitably. In this proposed protocol, only one group of the encoded particles is transmitted in each communication round of two-step communication. Assume that Eve’s attack operation is $U_e$, its effect can be expressed as

$U_e|0,E\rangle \equiv U_e\left(|0\rangle |E\rangle \right)=\alpha |0\rangle |e_{00}\rangle +\beta |1\rangle |e_{01}\rangle (11)$

$U_e|1,E\rangle \equiv U_e\left(|1\rangle |E\rangle \right)=m|0\rangle |e_{10}\rangle +n|1\rangle |e_{11}\rangle (12)$

Where $U_e$ is a unitary operator, $|e_{i0}\rangle$ and $|e_{i1}\rangle$ ($i\in \left\{\mathrm{0,1}\right\}$) are the pure ancillary states uniquely determined by $U_e$. The above equations satisfy the conditions such that,

${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1(13)$

${\left|m\right|}^2+{\left|n\right|}^2=1(14)$

In our protocol, the decoy photons have four possible states $\left\{|0\rangle ,|1\rangle ,|+\rangle ,|-\rangle \right\}$. The states $|+\rangle$ and $|-\rangle$ after Eve’s entanglement actions become

$U_e|+,E\rangle \equiv U_e\left(|+\rangle |E\rangle \right)=\frac{1}{\sqrt{2}}\left[\begin{array}{l}|+\rangle \left(\alpha |e_{00}\rangle +\beta |e_{01}\rangle +m|e_{10}\rangle +n|e_{11}\rangle \right)+\\ |-\rangle \left(\alpha |e_{00}\rangle -\beta |e_{01}\rangle +m|e_{10}\rangle -n|e_{11}\rangle \right)\end{array}\right](15)$

$U_e|-,E\rangle \equiv U_e\left(|-\rangle |E\rangle \right)=\frac{1}{\sqrt{2}}\left[\begin{array}{l}|+\rangle \left(\alpha |e_{00}\rangle +\beta |e_{01}\rangle -m|e_{10}\rangle -n|e_{11}\rangle \right)+\\ |-\rangle \left(\alpha |e_{00}\rangle -\beta |e_{01}\rangle -m|e_{10}\rangle +n|e_{11}\rangle \right)\end{array}\right](16)$

Even though the transmitted particle states contain the secret information, Eve cannot read them out. Eqs. 11, 12 imply that the error rate introduced by the behavior of Eve’s eavesdropping will be ${\left|\beta \right|}^2$ or ${\left|m\right|}^2$ for one decoy photon if the state is $|0\rangle$ or $|1\rangle$, respectively. Similarly, if the checking qubit is in the state $|+\rangle$ or $|-\rangle$, the error rate in two cases is 1/2. The error rate will lead to Eve being detected in the eavesdropping check phase 2. To avoid being detected, Eve has to set $\beta =m=0$ which implies that $\alpha =\text{n}=1$, then it is very difficult for an eavesdropper to distinguish $|e_{00}\rangle$ from $|e_{11}\rangle$. Hence, the proposed protocol is secure from the entangle-and-measure attack.

4.2.2 Measure-Resend Attack

Eve may try to perform the measure-resend attack on the encoded particles in the transmission process to steal Alice’s useful message. Eve has to know the full information of the state and reproduce another same state without being detected. Eve intercepts the encoded Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$ sent by Alice and measures the particles to get useful information. Since the intercepted particles are part of the entangled states, any measurements on part of the state would destroy the entanglement. Meanwhile, since the positions, the states and the bases of these decoy states in Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$ are secret, Eve cannot forge exactly the same decoy states $D_2$ and insert into fake Sequences $F_2$ and $F_3$ to escape from the security checking and identity authentication in Step 4. Eve has to randomly choose the measurement bases from two sets of measurement bases $\left\{|0\rangle ,|1\rangle \right\}$ and $\left\{|+\rangle ,|-\rangle \right\}$ with the same probability 0.5. If Eve chooses the right measurement basis, which will not introduce any errors; however, she may select the wrong one with probability 1/2, which will bring the error rate of 1/2. Therefore, the error probability introduced by Eve will achieve 1/4 for one decoy photon, i.e., Eve passes the security checking between Alice and Bob for one decoy photon with probability 3/4. Let the number of the decoy photons for detecting this attack be $N$, then Eve’s vicious behavior will be detected in the first eavesdropping check process with probability $1-{\left(3/4\right)}^N$. If $N$ is sufficiently large, the probability will converge to 1. Therefore, the measure-resend attack cannot work in the proposed protocol.

4.2.3 Intercept-Resend Attack

As for the intercept-resend attack [60], Eve should replace the qubit sequence $S_{23}$ before encoding with the fake qubit sequence $F^{\prime }$ and send $F^{\prime }$ to Alice. However, the four-qubit entanglement state is generated by Alice, and sequence $S_{23}$ is always kept in Alice’s hand until it becomes the encoded sequence $S_{23}^{\text{'}}$ sent to Bob. Accordingly, it is impossible for Eve to perform the intercept-resend attack.

4.2.4 Trojan Horse Attacks

Reference [61] pointed out that two-way quantum communication protocols are vulnerable to the Trojan horse attacks which includes two types: invisible photon eavesdropping attack (IPE) [61] and multi-photon signal attack [62]. However, since both the preparation of qubit sequence $S_{23}$ and its encoding operation are completed by Alice, the proposed protocol is not a two-way quantum communication protocol. Therefore, it is in vain for Eve to perform the Trojan horse attacks, i.e., the proposed protocol is absolutely secure under the Trojan horse attacks.

4.3 Internal Attacks

Since the participants could possess more information than outsider eavesdroppers, the internal attacks are stronger than the outsider attacks. The internal attacks are made up of single attack and collusive attack [63, 64].

4.3.1 Single Attack

Single attack is a kind of eavesdropping from the dishonest Charlie 1, Charlie 2, or Bob. 1) If dishonest Charlie 1 (Charlie 2) wants to perform her single attack to extract the secret message, she needs to intercepts the encoded Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$. The single attack can be considered as the outsider attacks discussed in Section 4.2; 2) If Bob is dishonest, he cannot escape from the identity authentication between honest Alice and himself in Steps 3 and 4, i.e., her fake identity will be found. Even if he avoided the identity authentication, he also needs the assistances of two controllers and Alice to obtain Alice’s secret without being detected. Permissions $R_{C1}$, $R_{C2}$ and $S_C$ are always secret until published in public. If at least one controller disagrees with the communication, Bob cannot obtain the decoding operation $U_S$ related to $R_{C1}$, $R_{C2}$ and $S_C$ to decode Alice’s secret information accurately. If Bob insists on performing the eavesdropping action, he can only gain Alice’s secret message by guessing directly.

4.3.2 Collusive Attack

The collusive attack is the most powerful internal attack in which two or more dishonest participants collude together to steal secret information without revealing their vicious behavior. Since Alice is honest, the collusive attack can be divided into two scenarios: case (a) the collusive attack of two dishonest participants (Charlie 1 and Charlie 2, Charlie 1 and Bob, Charlie 2 and Bob); case (b) the collusive attack of three dishonest participants (Charlie 1, Charlie 2 and Bob). Since the honest Alice share identity sequence $\text{ID}$ with Bob, if Bob is dishonest, his illegal identity will be detected in Step 4 before he performs the collusive attack to extract information with other participants. Therefore, it is impossible for Bob to join in the collusive attack. The rest case is the collusive attack between two controllers. Since the encoded Sequences $S_2^{\text{'}\text{'}}$ and $S_3^{\text{'}\text{'}}$ carry secret message, it can also be considered as outsider attacks similar to case 1) of single attack above. In conclusion, the proposed protocol is immune to collusive attacks.

In the proposed protocol, the sender Alice must be honest and the ideal four-qubit entanglement resources are prepared by Alice. In real communication environment, due to inevitable imperfections of network nodes, every involved node maybe untrusted, that is, both trusted network nodes and untrusted network nodes exist in quantum communication networks [65]. The proposed communication scheme with four parties can be regarded as a mini quantum communication network, where the involved parties are equivalent to network nodes. Therefore, in a real scenario, the sender in our protocol maybe untrusted, which will cause the receiver to obtain fake message without being found. Fortunately, multipartite quantum correlations of graph states, a kind of strategy-independent physical resources, allow network nodes to create strong correlations before it performs distributed tasks, which is efficient and provides strong guarantees in quantum communication networks in the presence of untrusted network nodes [66]. Furthermore, multipartite EPR steering demonstrates that all the nodes in the quantum network can share entanglement even if the measurement devices of one party are untrusted, and even can count the number of untrusted nodes [65, 67, 68]. To put the presented scheme into practice, it is a good choice to use multipartite quantum correlations of graph states created by a graph state source to replace quantum entanglement resources generated by the honest sender for removing the adverse effect of untrusted parties.

5 Comparison

The definition of quantum efficiency suggested by Cabello [69], can be described as $\eta =\text{t}/\left(q_u+b\right)$, where $t$ represents the number of transmitted message bits, $q_u$ is the total number of the utilized qubits prepared and used in transmission and security checking, and $b$ is the number of classical bits exchanged for decoding the secret message in a protocol. In the presented communication protocol, $t=2N$, $q_u=6N+2\mathrm{mN}$ and $b=2N$, let us set $N=\mathrm{mN}$, then the qubit efficiency of the proposed protocol is $\eta =20\%$. Compared with QSDC protocols based on QSA [50, 51] and the existing CQSDC protocol without QSA [25], the proposed CQSDC protocol is only slightly less efficient than Ref. [51], but it is the only one who can detect the attack from dishonest receiver. These specific performance comparisons are indicated in Table 3.

TABLE 3

TABLE 3. Performance comparisons between the proposed protocol and other protocols.

6 Conclusion

This paper proposes a novel controlled quantum secure direct communication protocol based on a four-qubit cluster state and quantum search algorithm. It makes full use of the persistency property of the quantum resource, and two operators of QSA are used to achieve encoding operations and decoding operations, respectively. With the permissions of the controllers and Alice, the sender’s secret message can be successfully reconstructed by the receiver without any information leakage. Furthermore, the security of the proposed CQSDC protocol can be guaranteed and outperforms that of the existing protocol from the perspective of resisting the dishonest receiver, and its efficiency is as high as 20%.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Y-FY: Conceptualization, Methodology, Writing-Original Draft, Writing-Review and Editing. L-ZD: Data Curation, Writing-Review and Editing, Supervision. T-RQ: Conceptualization, Methodology, Writing-Review and Editing. X-MX: Conceptualization, Writing-Original Draft, Writing-Review and Editing.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 61871205).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.875441/full#supplementary-material

References

1. Bennett CH, Gilles B. Quantum Cryptography: Public-Key Distribution and coin Tossing. In Proceedings of the International Conference on Computers, systems and signal Processing, Bangalore, India, 9 December 1984. New York: Bangalore Press. p. 175–9.

Google Scholar

2. Shor PW, Preskill J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys Rev Lett (2000) 85(2):441–4. doi:10.1103/PhysRevLett.85.441

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Lo H-K, Chau HF. Unconditional Security of Quantum Key Distribution over Arbitrarily Long Distances. Science (1999) 283(5410):2050–6. doi:10.1126/science.283.5410.2050

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys Rev Lett (1993) 70(3):1895–9. doi:10.1103/PhysRevLett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Mark H, Vladimír B, André B. Quantum Secret Sharing. Phys Rev A (1999) 59(3):1829–34.

Google Scholar

6. GuiLu L, Liu XS. Theoretically Efficient High-Capacity Quantum-Key-Distribution Scheme. Phys Rev A (2002) 65(3):032302.

Google Scholar

7. Kim B, Timo F. Deterministic Secure Direct Communication Using Entanglement. Phys Rev Lett (2002) 89(18):187902.

PubMed Abstract | Google Scholar

8. Antoni W. Eavesdropping on the “Ping-pong” Quantum Communication Protocol. Phys Rev Lett (2003) 90(15):157901.

PubMed Abstract | Google Scholar

9. Deng FG, GuiLu L, Liu XS. Two-step Quantum Direct Communication Protocol Using the Einstein-Podolsky-Rosen Pair Block. Phys Rev A (2003) 68(4):042317. doi:10.1103/physreva.68.042317

CrossRef Full Text | Google Scholar

10. Deng FG, GuiLu L. Secure Direct Communication with a Quantum One-Time Pad. Phys Rev A (2004) 69(5):052319. doi:10.1103/physreva.69.052319

CrossRef Full Text | Google Scholar

11. Chang Y, Xu C, Zhang S, Yan L. Quantum Secure Direct Communication and Authentication Protocol with Single Photons. Chin Sci Bull (2013) 58(36):4571–6. doi:10.1007/s11434-013-6091-9

CrossRef Full Text | Google Scholar

12. Wang C, Deng F-G, Li Y-S, Liu X-S, Long GL. Quantum Secure Direct Communication with High-Dimension Quantum Superdense Coding. Phys Rev A (2005) 71(4):44305. doi:10.1103/physreva.71.044305

CrossRef Full Text | Google Scholar

13. Lu Y, Wu JW, Lin ZS, Yin LG, GuiLu L. Quantum Secure Direct Communication with Entanglement Source and Single-Photon Measurement. Sci China: Phys Mech Astron (2020) 63(11):110311.

Google Scholar

14. Farouk A, Zakaria M, Megahed A, Omara FA. A Generalized Architecture of Quantum Secure Direct Communication for N Disjointed Users with Authentication. Sci Rep (2015) 5:16080. doi:10.1038/srep16080

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Cao HJ, Song HS. Quantum Secure Direct Communication with W State. Chin Phys Lett (2006) 23(2):290–2.

Google Scholar

16. Cao W, Yang Y, Wen Q. Quantum Secure Direct Communication with Cluster States. Sci China Phys Mech Astron (2010) 53(7):1271–5. doi:10.1007/s11433-010-3210-3

CrossRef Full Text | Google Scholar

17. Liu Z, Chen H, Liu W, Xu J, Wang D, Li Z. Quantum Secure Direct Communication with Optimal Quantum Superdense Coding by Using General Four-Qubit States. Quan Inf Process (2013) 12(1):587–99. doi:10.1007/s11128-012-0404-9

CrossRef Full Text | Google Scholar

18. Gao T, Yan FL, Wang ZX. Controlled Quantum Teleportation and Secure Direct Communication. Chin Phys (2005) 14(5):892–7.

Google Scholar

19. Wang J, Zhang Q, Tang C-j. Multiparty Controlled Quantum Secure Direct Communication Using Greenberger-Horne-Zeilinger State. Opt Commun (2006) 266(2):732–7. doi:10.1016/j.optcom.2006.05.035

CrossRef Full Text | Google Scholar

20. Chen XB, Wang TY, Du JZ, Wen QY, Zhu FC. Controlled Quantum Secure Direct Communication with Quantum Encryption. Int J Quan Inf (2008) 6(3):543–51. doi:10.1142/s0219749908003566

CrossRef Full Text | Google Scholar

21. Kao SH, Tsai CW, Hwang T. Enhanced Multiparty Controlled QSDC Using GHZ State. Commun Theor Phys (2011) 55(6):1007–11.

Google Scholar

22. Li Y-h., Li X-l., Sang M-h., Nie Y-y., Wang Z-s. Bidirectional Controlled Quantum Teleportation and Secure Direct Communication Using Five-Qubit Entangled State. Quan Inf Process (2013) 12(12):3835–44. doi:10.1007/s11128-013-0638-1

CrossRef Full Text | Google Scholar

23. Zheng X-y., Long Y-x. Controlled Quantum Secure Direct Communication with Authentication Protocol Based on Five-Particle Cluster State and Classical XOR Operation. Quan Inf Process (2019) 18(5):129. doi:10.1007/s11128-019-2239-0

CrossRef Full Text | Google Scholar

24. FaezehMazloum K, Monireh H, NimaS A-N. Authenticated Controlled Quantum Secure Direct Communication Protocol Based on Five-Particle Brown States. Int J Theor Phys (2020) 59(5):1612–22.

Google Scholar

25. Pan H-M. Controlled Bidirectional Quantum Secure Direct Communication with Six-Qubit Entangled States. Int J Theor Phys (2021) 60(8):2943–50. doi:10.1007/s10773-021-04866-1

CrossRef Full Text | Google Scholar

26. Wu JW, Lin ZS, Yin LG, GuiLu L. Security of Quantum Secure Direct Communication Based on Wyner’s Wiretap Channel Theory. Quan Eng (2019) 1(4):e26. doi:10.1002/que2.26

CrossRef Full Text | Google Scholar

27. Qi R, Sun Z, Lin Z, Niu P, Hao W, Song L, et al. Implementation and Security Analysis of Practical Quantum Secure Direct Communication. Light Sci Appl (2019) 8(1):22–8. doi:10.1038/s41377-019-0132-3

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Sun Z, Song L, Huang Q, Yin L, Long G, Lu J, et al. Toward Practical Quantum Secure Direct Communication: a Quantum-memory-free Protocol and Code Design. IEEE Trans Commun (2020) 68(9):5778–92. doi:10.1109/tcomm.2020.3006201

CrossRef Full Text | Google Scholar

29. GuiLu L, Zhang HR. Drastic Increase of Channel Capacity in Quantum Secure Direct Communication Using Masking. Sci Bull (2021) 66(13):1267–9.

Google Scholar

30. Niu P-H, Zhou Z-R, Lin Z-S, Sheng Y-B, Yin L-G, Long G-L. Measurement-device-independent Quantum Communication without Encryption. Sci Bull (2018) 63(20):1345–50. doi:10.1016/j.scib.2018.09.009

CrossRef Full Text | Google Scholar

31. Zhou Z, Sheng Y, Niu P, Yin L, Long G, Hanzo L. Measurement-device-independent Quantum Secure Direct Communication. Sci China Phys Mech Astron (2020) 63(3):230362. doi:10.1007/s11433-019-1450-8

CrossRef Full Text | Google Scholar

32. Zou Z-K, Zhou L, Zhong W, Sheng Y-B. Measurement-device-independent Quantum Secure Direct Communication of Multiple Degrees of freedom of a Single Photon. Epl (2020) 131(4):40005. doi:10.1209/0295-5075/131/40005

CrossRef Full Text | Google Scholar

33. Zhou L, Sheng Y-B, Long G-L. Device-independent Quantum Secure Direct Communication against Collective Attacks. Sci Bull (2020) 65(1):12–20. doi:10.1016/j.scib.2019.10.025

CrossRef Full Text | Google Scholar

34. Zhou L, Sheng Y-B. One-step Device-independent Quantum Secure Direct Communication. Sci China Phys Mech Astron (2022) 65:250311. doi:10.1007/s11433-021-1863-9

CrossRef Full Text | Google Scholar

35. Tao L, GuiLu L. Quantum Secure Direct Communication Based on Single-Photon Bell-state Measurement. New J Phys (2020) 22(6):063017.

Google Scholar

36. Gao CY, Guo PL, Ren BC. Efficient Quantum Secure Direct Communication with Complete Bell-state Measurement. Quan Eng (2021) 3(4):e83. doi:10.1002/que2.83

CrossRef Full Text | Google Scholar

37. Hu J-Y, Yu B, Jing M-Y, Xiao L-T, Jia S-T, Qin G-Q, et al. Experimental Quantum Secure Direct Communication with Single Photons. Light Sci Appl (2016) 5(9):e16144. doi:10.1038/lsa.2016.144

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zhang W, Ding D-S, Sheng Y-B, Zhou L, Shi B-S, Guo G-C. Quantum Secure Direct Communication with Quantum Memory. Phys Rev Lett (2017) 118(22):220501. doi:10.1103/physrevlett.118.220501

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Zhu F, Zhang W, Sheng Y, Huang Y. Experimental Long-Distance Quantum Secure Direct Communication. Sci Bull (2017) 62(22):1519–24. doi:10.1016/j.scib.2017.10.023

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wang XF, Sun XJ, Liu YX, Wang W, Kan BX, Dong P, et al. Transmission of Photonic Polarization States from Geosynchronous Earth Orbit Satellite to the Ground. Quan Eng (2021) 3(3):e73. doi:10.1002/que2.73

CrossRef Full Text | Google Scholar

41. You X, Wang C-X, Huang J, Gao X, Zhang Z, Wang M, et al. Towards 6G Wireless Communication Networks: Vision, Enabling Technologies, and New Paradigm Shifts. Sci China Inf Sci (2021) 64(1):110301. doi:10.1007/s11432-020-2955-6

CrossRef Full Text | Google Scholar

42. GuiLu L, Pan D, Xue QK, Lajos H. An Evolutionary Pathway for the Quantum Internet Relying on Secure Classical Repeaters. Quan Commun Quan Signal Process (2022).

Google Scholar

43. Grover LK. A Fast Quantum Mechanical Algorithm for Database Search. Proceedings of the 28th Annual ACM Symposium on the Theory of Computing. Philadelphia Pennsylvania USA. 22 May 1996. Philadelphia: ACM. p. 212–9. doi:10.1145/237814.237866

CrossRef Full Text | Google Scholar

44. Grover LK. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys Rev Lett (1997) 79(2):325–8. doi:10.1103/physrevlett.79.325

CrossRef Full Text | Google Scholar

45. Zhang W-W, Li D, Song T-T, Li Y-B. Quantum Private Comparison Based on Quantum Search Algorithm. Int J Theor Phys (2013) 52(5):1466–73. doi:10.1007/s10773-012-1464-4

CrossRef Full Text | Google Scholar

46. Hsu LY. Quantum Secret-Sharing Protocol Based on Grover’s Algorithm. Phys Rev A (2003) 68(2):022306. doi:10.1103/physreva.68.022306

CrossRef Full Text | Google Scholar

47. Cao H, Ma W. Multiparty Quantum Key Agreement Based on Quantum Search Algorithm. Sci Rep (2017) 7:45046. doi:10.1038/srep45046

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Wang C, Liang H, Song SY, GuiLu L. Quantum Direct Communication Based on Quantum Search Algorithm. Int J Quan Inf (2010) 8(3):443–50. doi:10.1142/s0219749910006071

CrossRef Full Text | Google Scholar

49. Tseng H-Y, Tsai C-W, Hwang T. Controlled Deterministic Secure Quantum Communication Based on Quantum Search Algorithm. Int J Theor Phys (2012) 51(8):2447–54. doi:10.1007/s10773-012-1125-7

CrossRef Full Text | Google Scholar

50. Kao S-H, Hwang T. Multiparty Controlled Quantum Secure Direct Communication Based on Quantum Search Algorithm. Quan Inf Process (2013) 12(12):3791–805. doi:10.1007/s11128-013-0636-3

CrossRef Full Text | Google Scholar

51. Yin A, Lin W, He K, Han Z, Fan P. Controlled Bidirectional Quantum Secure Direct Communication Protocol Based on Grover's Algorithm. Mod Phys Lett A (2020) 35(28):2050228. doi:10.1142/s0217732320502284

CrossRef Full Text | Google Scholar

52. Briegel HJ, Raussendorf R. Persistent Entanglement in Arrays of Interacting Particles. Phys Rev Lett (2001) 86(5):910–3. doi:10.1103/PhysRevLett.86.910

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Raussendorf R, Briegel HJ. A One-Way Quantum Computer. Phys Rev Lett (2001) 86(22):5188–91. doi:10.1103/PhysRevLett.86.5188

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Hein M, Dür W, Briegel H-J. Entanglement Properties of Multipartite Entangled States under the Influence of Decoherence. Phys Rev A (2005) 71(3):32350. doi:10.1103/physreva.71.032350

CrossRef Full Text | Google Scholar

55. Kiesel N, Schmid C, Weber U, Tóth G, Gühne O, Ursin R, et al. Experimental Analysis of a Four-Qubit Photon Cluster State. Phys Rev Lett (2005) 95(21):210502. doi:10.1103/PhysRevLett.95.210502

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Lu C-Y, Zhou X-Q, Gühne O, Gao W-B, Zhang J, Yuan Z-S, et al. Experimental Entanglement of Six Photons in Graph States. Nat Phys (2007) 3(2):91–5. doi:10.1038/nphys507

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Wen K, Deng FG, GuiLu L. Secure Reusable Base-String in Quantum Key Distribution (2007). Available at: https://arxiv.org/abs/0706.3791 (Accessed October 8, 2021).

Google Scholar

58. Li CY, Zhou HY, Wang Y, Deng FG. Secure Quantum Key Distribution Network with Bell States and Local Unitary Operations. Chin Phys Lett (2007) 22(5):1049–52.

Google Scholar

59. Gao F, Qin S-J, Guo F-Z, Wen Q-Y. Cryptanalysis of Quantum Secure Direct Communication and Authentication Scheme via Bell States. Chin Phys. Lett. (2011) 28(2):020303. doi:10.1088/0256-307x/28/2/020303

CrossRef Full Text | Google Scholar

60. Man ZX, Zhang ZJ, Li Y. Quantum Dialogue Revisited. Chin Phys Lett (2005) 22(1):22–4.

Google Scholar

61. Cai Q-Y. Eavesdropping on the Two-Way Quantum Communication Protocols with Invisible Photons. Phys Lett A (2006) 351:23–5. doi:10.1016/j.physleta.2005.10.050

CrossRef Full Text | Google Scholar

62. Deng FG, Li XH, Zhou HY, Zhang ZJ. Improving the Security of Multiparty Quantum Secret Sharing against Trojan Horse Attack. Phys Rev A (2005) 72(4):440–50. doi:10.1103/physreva.72.044302

CrossRef Full Text | Google Scholar

63. Liu B, Xiao D, Jia H-Y, Liu R-Z. Collusive Attacks to "circle-type" Multi-Party Quantum Key Agreement Protocols. Quan Inf Process (2016) 15(5):2113–24. doi:10.1007/s11128-016-1264-5

CrossRef Full Text | Google Scholar

64. Ahmed E, Safia A, Hussein A, Safwat H. Improving the Security of Multi-Party Quantum Key Agreement with Five-Qubit Brown States. Comput Commun (2020) 159:155–60.

Google Scholar

65. Lu H, Huang C-Y, Li Z-D, Yin X-F, Zhang R, Liao T-L, et al. Counting Classical Nodes in Quantum Networks. Phys Rev Lett (2020) 124(18):180503. doi:10.1103/physrevlett.124.180503

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Huang CY, Lambert N, Li CM, Lu YT, Franco N. Securing Quantum Networking Tasks with Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev A (2019) 99(1):012302. doi:10.1103/physreva.99.012302

CrossRef Full Text | Google Scholar

67. He QY, Reid MD. Genuine Multipartite Einstein-Podolsky-Rosen Steering. Phys Rev Lett (250403201) 111(25):250403. doi:10.1103/PhysRevLett.111.250403

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Li CM, Chen K, Chen YN, Zhang Q, Chen YA, Pan JW. Genuine High-Order Einstein-Podolsky-Rosen Steering. Phys Rev Lett (2015) 115(1):010402. doi:10.1103/PhysRevLett.115.010402

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Cabello A. Quantum Key Distribution in the Holevo Limit. Phys Rev Lett (2000) 85(1):5635–8. doi:10.1103/PhysRevLett.85.5635

PubMed Abstract | CrossRef Full Text | Google Scholar