The Research of Long-Optical-Path Visible Laser Polarization Characteristics in Smoke Environment

The concentration of smoke in an environment can cause obvious interference to visible light intensity imaging, and it is a non-negligible factor in the polarized imaging of ground-based targets. Smoke particles cause severe scattering of photon intensity, resulting in polarization. In this case, low-visibility targets can be effectively identified by detecting the polarization dimension of targets. However, the polarization transmission of smoke in an environment is unclear, and the theoretical simulation lacks experimental reliability verification. To study this problem, this study constructs a polarization transmission model in a smoke environment and simulates and analyzes the scattering of visible polarized light at 450, 532, and 671 nm under different smoke densities. The optical thickness is determined to establish a reliable connection between the simulation and the external field long optical path test and verify the transmission of polarized light. Results show that the method has a 60% confidence in the polarization transmission model. With the increase in optical thickness, the degree of polarization (DOP) of the three wavelengths in the visible light band decreases, and the DOP of each polarized light decreases. No obvious difference is found between the DOPs of circularly polarized light at 450 nm and linearly polarized light. The DOP of circularly polarized light at 532 nm is 1–5% higher than that of linearly polarized light, 1–10% higher than that of the outdoor test, 1–5% higher than that of circularly polarized light at 671 nm, and 2–15% higher than that of the outdoor test. Therefore, the shorter the wavelength in the visible band, the higher the DOP. With the increase in wavelength, the polarization characteristics of circularly polarized light are gradually better than those of linearly polarized light.

Introduction

With the development of intelligent transportation and navigation, the demand for optical sensors that can penetrate a strong scattering environment has increased. At present, the low-visibility conditions caused by haze lead to frequent traffic accidents, abnormal airplane landings, and navigation ship accidents. Such scenarios have a significant economic impact, cause a huge waste of human, material, and time resources, and limit the development of transportation, aviation, navigation, and other fields [1, 2]. Haze poses a major safety challenge to the spatial perceptive ability in these fields and thus must be effectively detected in low-visibility environments, such as a car driving on a foggy road, a plane trying to land in the fog, or a ship in the sea fog [3–6].

The emission of a large number of fine particles can cause haze easily. Using the persistence and memory of visible polarized laser can effectively improve the action distance of the scattering environment, which has aroused the interest of researchers. Recently, polarimetric imaging has been widely exploited in target detection [7, 8], remote sensing [9, 10], and biomedical imaging [11, 12].

This study aims to characterize the propagation of polarized laser in different bands in a real haze long optical path environment. Our previous work simulated the polarization change of a short optical path linearly polarized laser in an oil mist particle environment and showed that linearly polarized laser in different bands is sensitive to concentration change. In the present work, we determine the characteristics of laser polarization with haze concentration change combined with numerical simulation and real long optical path haze environment test. In addition, we summarize the polarization transmission law of multiple band and polarization states.

Considering the lack of polarization characteristic tests in a real haze environment, few studies have shown the transmission law of polarized laser in haze environments with different concentrations. In addition, the influence of visibility on polarization characteristics in real haze weather remains unclear to date.

Most previous studies performed the numerical simulation of the polarization characteristics of fog particles or the indoor simulation of a fog environment with a short optical path and a single wavelength.

Wu analyzed the influence of a 550-nm laser on the polarization of dust particle and dig particle’s Muller matrix. The depolarization coefficient of dust particles was 0.6, and that of dig particles was 0.8. Dust particles have stronger depolarization than dig particles, which means that when illuminated by polarized light, dust particles produce scattered light with less polarization than dig particles. However, an analysis of the influence of the concentrations of dust and dig particles on polarization remains lacking [13]. John D. van der Laan simulated the evolution of circular and linear polarization in a polystyrene microsphere environment model with particle diameters of 0.1, 2.0, and 3.0 µm and an illuminating wavelength of 543.5 nm [14]. Xiangwei Zeng expressed the transmission distance by the relative distance of particles at the band of 0.5–4.2 μm. The circular linear polarization difference at a 0–1.5 relative distance of a single particle was numerically simulated [15]. Using the fog particle distribution model, D. Vander and J.B. Wright studied changes in the polarization degree (DOP) of 0.4- to 1.2-μm circularly polarized light with a wavelength under optical thicknesses of 5, 10, and 15 [16]. Ryan investigated the depolarization of a linearly polarized 514-nm wavelength beam through 1 m of laboratory-generated fog [17]. Their work was limited to a single fog concentration. Jinkui Chu et al. experimentally explored polarization state persistence through the polystyrene microsphere turbid liquid environments of 530-nm particles at varying concentrations. The scattering solution was held in a glass cubic cuvette at a length of 2.6 cm. At different concentrations, circularly polarized light had superior polarization state persistence to linearly polarized light [18]. Vanitha Sankaran analyzed the polarization discrimination of 632-nm coherently propagating light in polystyrene samples placed in a 1-cm path-length glass cuvette to simulate turbid media. The results indicated that polarization was maintained even after unpolarized irradiance through each sample had been extinguished by several orders of magnitude [19].

These studies produced a useful conclusion on polarized light propagation. However, polarization transmission characteristics in a real haze environment remain difficult to determine because they are carried out in well-established and well-controlled environments. In fact, the combined effects of changes in the density and size of particle scatterers in haze environments and changes in atmospheric conditions are difficult to model in the laboratory.

In the present study, we use the optical thickness to characterize and unify the haze concentration of the real ground haze environment and the simulated haze environment, obtain the variation law of laser polarization characteristics in different polarization states, find the detection laser wavelength and polarization state suitable for different concentration haze environments, establish the polarization transmission model around the optical thickness, and verify the model by performing a real field long path polarization test. These works are helpful to study the effects of different optical thicknesses on the transmission characteristics of different polarized lasers. The circular polarization and multiple linear polarizations of different wave bands are sensitive to the change in real haze concentration.

This article is organized as follows. Monte Carlo Method of Particle Swarm Optimization covers the background of polarization and the polarization-tracking Monte Carlo simulations. Numerical Results for Polarization Characteristics describes the smog environments of interest, including their particle distributions. Experiments presents general comments about the transmission results and details the results for each polarization at wavelengths ranging from 450 to 671 nm and over increasing optical thickness/range. Conclusion concludes that circularly polarized light maintains its signal better than linearly polarized light through the 450-, 532-, and 671-nm bands.

Monte Carlo Method of Particle Swarm Optimization

Concentration Characterization of Polarized Scattering of Smoke Particles

When visible light is transmitted in smoke particles, the Stokes parameter of reaction polarization characteristics is calculated as follows [20]:

$\left(\begin{array}{c}{I}_0\\ Q_0\\ U_0\\ V_0\end{array}\right)=\left(\begin{array}{cccc}{M}_1& M_2& 0& 0\\ M_2& M_1& 0& 0\\ 0& 0& S_{21}& -D_{21}\\ 0& 0& D_{21}& S_{21}\end{array}\right)\left(\begin{array}{c}{I}_1\\ Q_1\\ U_1\\ V_1\end{array}\right),(1)$

$M=\left(\begin{array}{cccc}{M}_1& M_2& 0& 0\\ M_2& M_1& 0& 0\\ 0& 0& S_{21}& -D_{21}\\ 0& 0& D_{21}& S_{21}\end{array}\right)=\frac{1}{k^2{r}^2}\left[\begin{array}{cccc}{F}_{11}& F_{12}& 0& 0\\ F_{12}& F_{22}& 0& 0\\ 0& 0& F_{33}& F_{34}\\ 0& 0& -F_{34}& F_{33}\end{array}\right].(2)$

The matrix element of the scattering phase function matrix of soot particles and its expression can be written as follows:

$\langle F_{ij}\rangle =\frac{{\displaystyle {\int }_{r_{\min }}^{r_{\max }}{Q}_{sca}\left(r\right)n\left(r\right)\pi r^2{P}_{ij}\left(r\right)dr}}{{\displaystyle {\int }_{r_{\min }}^{r_{\max }}{Q}_{sca}\left(r\right)n\left(r\right)\pi r^{2}dr}},(3)$

where $n\left(r\right)$ is the logarithmic particle spectrum distribution of transmission medium particles, and it can be expressed as follows:

$n\left(r\right)=\frac{N_0}{\sqrt{2\pi }\lg \sigma }\exp \left[-\frac{{\left(\lg r-\lg r_m\right)}^2}{2{\left(\lg \sigma \right)}^2}\right],(4)$

where $n\left(r\right)$ is the logarithmic particle spectrum distribution; $N_0$ is the number of aerosol particles per unit volume of air (number/ $c{m}^{-3}$ ), which represents the concentration of particles; $r_m$ is the geometric mean radius; and $\sigma$ is the geometric standard deviation. The relationship between particle concentration and Stokes parameter can be obtained; in other words, the relationship between particle concentration and polarization characteristics can be obtained. However, it is hard to obtain the number of aerosol particles in the actual environment. Thus, we hierarchically describe the transmission medium by optical thickness. The relationship among particle spectrum distribution, scattering coefficient, and absorption coefficient is shown as follows:

${\mu }_s=\pi {\displaystyle \underset{r_1}{\overset{r_2}{\int }}{r}^2{Q}_{sc}n\left(r\right)dr},{\mu }_a=\pi {\displaystyle \underset{r_1}{\overset{r_2}{\int }}{r}^2{\mathit{Q}}_{ab}n\left(r\right)dr},(5)$

where ${\mu }_s$ is the scattering coefficient, ${\mu }_a$ is the absorption coefficient, and ${\mu }_t$ is the extinction coefficient. The relationship between extinction coefficient and particle spectrum distribution is shown as follows:

${\mu }_t={\mu }_t+{\mu }_t=\pi {\displaystyle \underset{r_1}{\overset{r_2}{\int }}{r}^2\mathit{Q}n\left(r\right)dr}.(6)$

According to Beer’s law, the relationship between optical thickness $\tau$, transmission distance S, and extinction coefficient ${\mu }_t$ is shown as follows:

$\tau ={\mu }_{t}S=S\pi {\displaystyle \underset{r_1}{\overset{r_2}{\int }}{r}^2\mathit{Q}n\left(r\right)dr},(7)$

where Q is the extinction factor. The aforementioned formula shows that different concentrations of smoke can be represented by the optical thickness $\tau$, and Q is directly proportional to the optical thickness. The aforementioned formula can be achieved by changing the optical thickness in the Monte Carlo transmission model. The optical thickness can also be controlled in the experiment, and the extinction factor can be calculated by the Monte Carlo polarization transmission model of smoke particles. Therefore, using the optical thickness to characterize the concentration of smoke particles can connect the experiment with the simulation.

Relational Model Between Smoke Particle Concentration and Polarization Transmission Characteristics

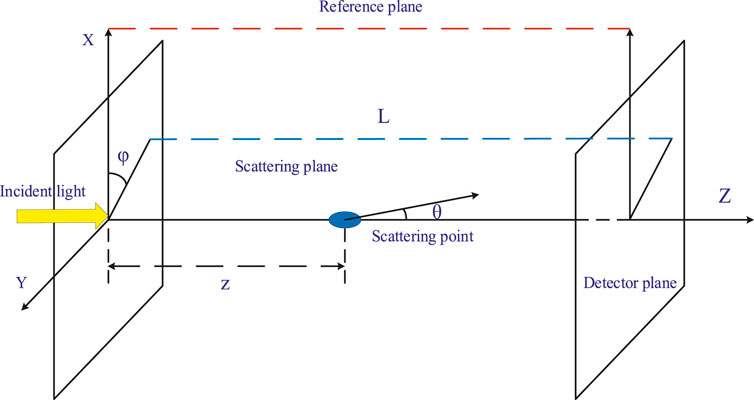
The reference plane is defined as shown in Figure 1. The yellow line and the direction of photons at the scattering point determine the propagation direction of photons. The included angle between them is the scattering angle. The X-axis, Z-axis, and scattering plane constitute the reference plane before and after scattering. For every scattering that occurs, the Stokes component must be adjusted to make the reference plane a new reference plane.

FIGURE 1

FIGURE 1. Definition of reference plane.

After defining the reference plane, we set the scattering coefficient ${\mu }_s$, absorption coefficient ${\mu }_a$, extinction coefficient of atmosphere ${\mu }_t={\mu }_s+{\mu }_a$, incident wavelength of laser $v$, particle diameter $r$, particle complex refractive index m, and initial values of Stokes parameters of light with different polarization states. Photons are incident in the positive direction of the z-axis. The initial position ${\mu }_0$ is (0, 0, 0), and the initial direction cosine D₀ is (0, 0, 1). The polarization reference plane is composed of an x-axis and a z-axis. We define the initial Stokes parameters of photons and set each Stokes parameter after scattering to 0.

The step length of particle transmission is the photon free path, and the relationship between optical thickness and photon free path is given as follows:

$S_1=\ln \left(\xi \right)\frac{\tau }{S}.(8)$

Once the photon free path is determined, the photons move. The current location $\left(x,y,z\right)$ and transmission direction $\left({\mu }_x,{\mu }_y,{\mu }_z\right)$ determine that the coordinate $\left(x^{\text{'}},y^{\text{'}},z^{\text{'}}\right)$ of the next scattering point reached by the photon is given as follows:

$\{\begin{array}{c}{x}^{\prime }=x+{\mu }_x{S}_1\\ y^{\prime }=y+{\mu }_y{S}_1\\ z^{\prime }=z+{\mu }_z{S}_1\end{array}.(9)$

Whether the photon emits the boundary determined by the reference plane is determined according to the coordinate position. If it emits the boundary determined by the reference plane, the Stokes parameter of the photon is calculated. By contrast, the Stokes component must be adjusted to make the reference plane a new meridional plane, and then the particle radius must be selected again.

After photons collide with particles, the sampling of the scattering angle $\alpha$ and azimuth angle $\beta$ is obtained from the joint probability density function (PDF), and the relationship between the function PDF and incident light’s Stokes component ${\left[I_0,Q_0,U_0,V_0\right]}^T$ is follows:

$\rho (\alpha ,\beta )=m_{11}\left(\alpha \right)+m_{12}\left(\alpha \right)[Q_0\cos \left(2\beta \right)+U_0\sin \left(2\beta \right)]/I_0,(10)$

where $m_{11}\left(\alpha \right)$ and $m_{12}\left(\alpha \right)$ are the corresponding elements in Mueller matrix $M\left(\alpha \right)$ of spherical particles:

$M\left(\alpha \right)=\left[\begin{array}{cccc}{m}_{11}\left(\alpha \right)& m_{12}\left(\alpha \right)& 0& 0\\ m_{12}\left(\alpha \right)& m_{11}\left(\alpha \right)& 0& 0\\ 0& 0& m_{33}\left(\alpha \right)& m_{34}\left(\alpha \right)\\ 0& 0& -m_{34}\left(\alpha \right)& m_{33}\left(\alpha \right)\end{array}\right].(11)$

$m_{11}\left(\alpha \right),m_{12}\left(\alpha \right),m_{33}\left(\alpha \right),\mathrm{and}{m}_{34}\left(\alpha \right)$ have the following relationship with scattering amplitude values $S_1$ and $S_2$:

$\begin{array}{l}{m}_{11}\left(\alpha \right)=\frac{1}{2}\left({\left|S_1\right|}^2+{\left|S_2\right|}^2\right),m_{12}\left(\alpha \right)=\frac{1}{2}\left({\left|S_1\right|}^2-{\left|S_2\right|}^2\right),\\ m_{33}\left(\alpha \right)=\frac{1}{2}\left(S_1{S}_2^{\ast }-S_1^{\ast }{S}_2\right),m_{44}\left(\alpha \right)=\frac{i}{2}\left(S_1{S}_2^{\ast }-S_2^{\ast }{S}_1\right).\end{array}(12)$

The energy weight of photos after n times of scattering becomes:

$W_n=W_{n-1}\times {\mu }_s/\left({\mu }_s+{\mu }_a\right).(13)$

When the photon energy weight is lower than a certain threshold (i.e., ${10}^{-4}$) or fly away from the boundary, the photon transmission is terminated. When a photon is emitted from the boundary of the polydisperse system, its Stokes vector must undergo the last rotation to ensure that the reference plane is the same as the plane where the detector is located, and the rotation angle is follows:

$\omega =\pm {\tan }^{-1}\left({\mu }_y/{\mu }_x\right).(14)$

The reflection mode takes a positive sign, and the transmission takes a negative sign. Due to different scattering paths, the time of photons arriving at the detector is different. For a beam whose polarization component is shaped like ${\left[I\left(t\right),Q\left(t\right),U\left(t\right),V\left(t\right)\right]}^T$, the time-domain polarization degree is defined as follows:

$DOP\left(t\right)=\frac{\sqrt{Q^2\left(t\right)+U^2\left(t\right)+V^2\left(t\right)}}{I\left(t\right)}.(15)$

The total polarization degree of the scattered beam is defined as Eq. 15, where $I$, $Q$, $U$, and $V$ represent the cumulative values of photon polarization components arriving at the detector at different times.

According to Eqs 7, 8, 13, and 15, after substituting the changes in the optical thickness τ and extinction factor Q into the Monte Carlo polarization simulation of smoke particles, the original free path, scattering angle and azimuth sampling, and photon energy weight also change. Finally, an improved relationship model between smoke particle concentration and polarization transmission characteristics can be obtained.

Numerical Results for Polarization Characteristics

Environments

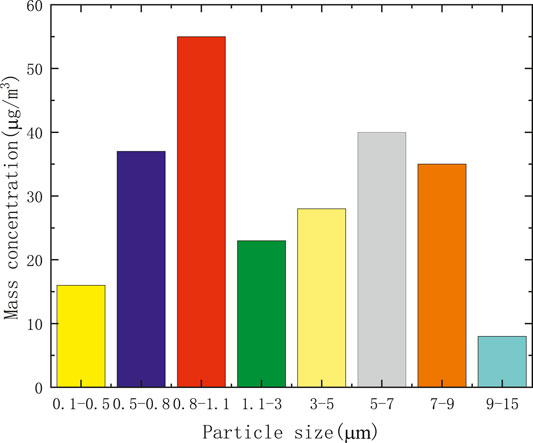
When winter comes in December, northern China starts heating, and the haze weather is the most serious. At this time, the climate is dry with minimal precipitation, which can almost eliminate the impact of humidity on aerosol particles. Soot particles are the main factor affecting visibility. The PM10 index is the highest in the whole year, and the particle content of 0.8–1.1 µm is the highest [21]. The relationship between particle size and concentration is displayed in Figure 2.

FIGURE 2

FIGURE 2. Distribution of PM10 particle size content in winter.

In this study, the physical parameter of optical thickness is used to unify the visibility of a real haze environment and the concentration of simulated haze. Thus, the two results can verify each other. The visibility of the real haze environment is tested as follows.

The relationship between visibility $V$ and transmittance $T$ is shown in Eq. 16:

$V=\frac{3.91\times \left(\frac{\lambda }{0.55}\right)}{-\ln T}.(16)$

The relationship between transmittance $T$ and optical thickness $\tau$ can be obtained according to the Beer–Lambert Law:

$T=\exp \left(-\tau \right).(17)$

Eqs 16, 17 are combined to obtain the conversion formula of visibility and optical thickness:

$V=\frac{3.91\times \left(\frac{\lambda }{0.55}\right)}{\tau }.(18)$

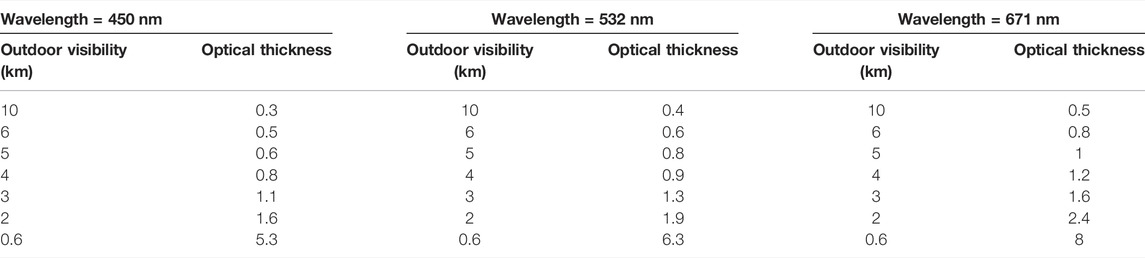
Thus, the relationship between outdoor visibility and optical thickness under different central wavelengths is shown in Table 1.

TABLE 1

TABLE 1. Comparison between outdoor visibility and optical thickness.

Simulation Results and Analysis

We simulate the polarization characteristics of six types of polarized light passing through the real smoke environment. PM 1 µm particle size with the largest distribution percentage in smoke particles is up to more than 50%, so we select the simulated smoke particle radius 1 µm, and the refractive index is 1.53 + 0.008i, and the number of particles set during simulation is 10⁶. The smoke particles adopt the logarithmic particle spectrum distribution, and the optical thickness is measured according to the real smoke environment. The polarization states of simulated polarized light are 0°, 45°, 90°, 135°, left-handed circular polarization, and right-handed circular polarization. The simulation results are shown in Figures 3, 4.

FIGURE 3

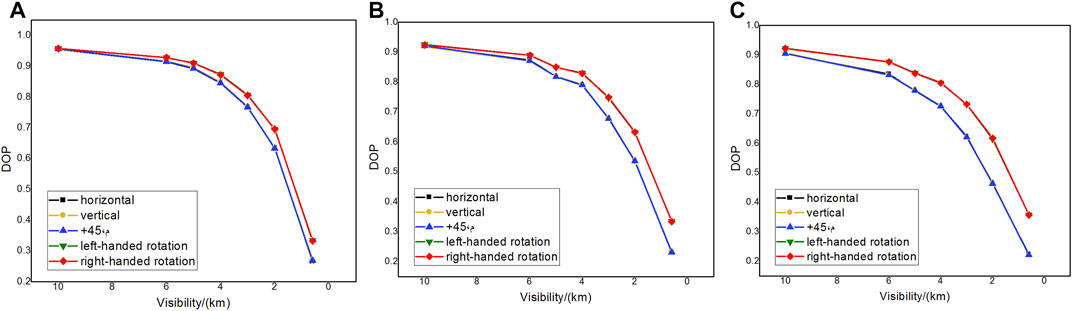
FIGURE 3. Simulation curves of polarization transmission characteristics at different wavelengths:(A) 450 nm, (B) 532 nm, and (C) 671 nm.

FIGURE 4

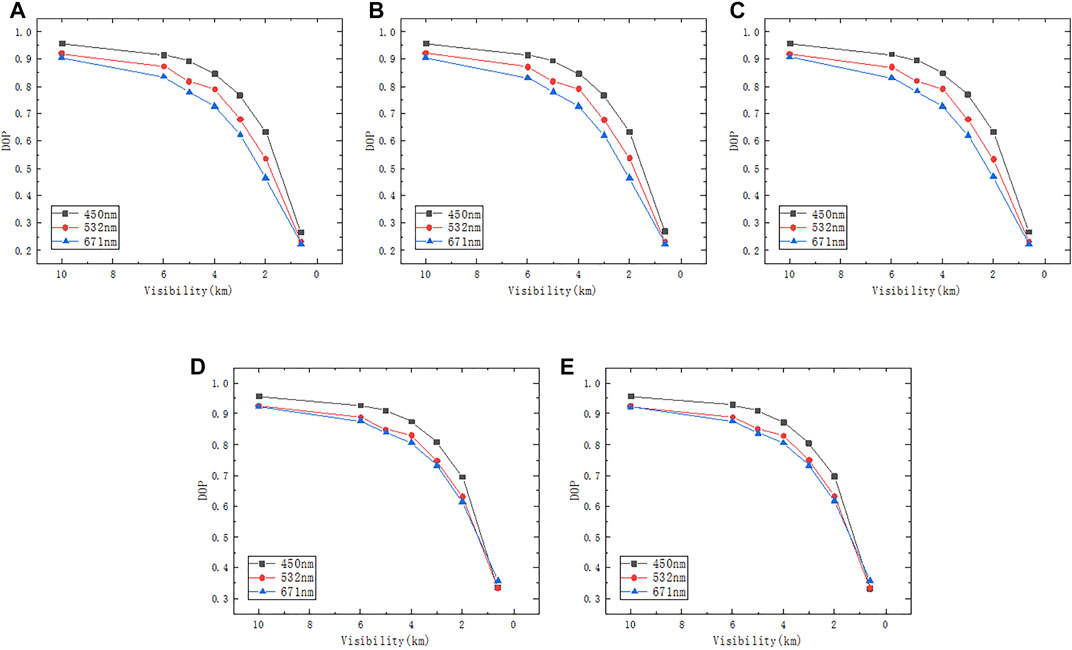
FIGURE 4. Simulation curves of polarization transmission characteristics of different polarization states:(A) 0°, (B) 45°, (C) 90°, (D) left-hand rotation, and (E) right-hand rotation.

As shown in Figures 3A–C, the DOP changes of left-handed and right-handed circularly polarized light are consistent, and the DOP changes of the three linearly polarized light are also consistent. It can be seen that because the DOP difference between left-handed circularly polarized light and right-handed circularly polarized light is less than 1%, the DOP curves of the two overlap; the DOP difference of 0°, 45°, and 90° linearly polarized light is less than 1%, resulting in the three DOP curves overlapping. The DOP difference between circularly polarized light and linearly polarized light in a thick smoke environment (the optical thickness after stabilization is greater than 1.0) is more obvious than that in a thin smoke environment (the optical thickness after stabilization is 0.3–1) because circularly polarized light has better polarization-maintaining ability. When the polarized light passed through the smoke, it would cause multiple scattering, and multiple scattering would cause depolarization. As the concentration increased, multiple scattering increased, then there would be more polarized light depolarized. With the increase in wavelength, the polarization characteristic of circularly polarized light is better than that of linearly polarized light. At 450 nm, the difference between circularly polarized light and linearly polarized light is not obvious; at 532 nm, the DOP of circularly polarized light is approximately 10% higher than that of linearly polarized light; at 671 nm, the DOP of circularly polarized light is approximately 20% higher than that of linearly polarized light. In the case of a long wavelength, the polarization-maintaining characteristic of circularly polarized light is better than that of linearly polarized light. However, with the increase in optical thickness, the DOP of the outgoing polarized light of the three wavelengths decreases gradually. When the concentration increases, the number of collisions of photons in the transmission medium increases, resulting in depolarization.

Figures 4A–E represent the variation curve of polarization with visibility when the incident polarized light is divided into 0° linear polarized light, 90° linear polarized light, 45° linear polarized light, left-handed circular polarized light, and right-handed circular polarized light. The DOP at 450-nm wavelength is higher than those at 532- and 671-nm wavelength. This result can be ascribed to the fact that the reflectivity of smoke increases with the increase in wavelength in the visible band [22], and the relationship between spectral reflectivity and spectral DOP is inversely proportional. Therefore, the DOP at 450-nm wavelength is higher than that at 671-nm wavelength. The aforementioned simulation results show that in the visible band, the shorter the wavelength, the higher the DOP, and the polarization-maintaining characteristic of circularly polarized light is more obvious when the wavelength is longer.

Experiments

Experimental Setup

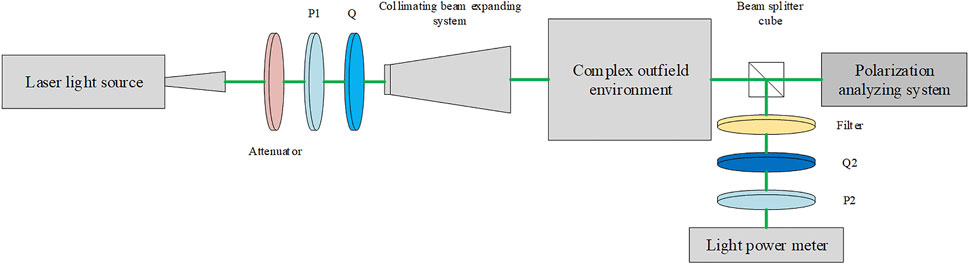
We designed a series of experiments to compare the polarization state change of parallel linearly and circularly polarized light interacting with scattering media. The experimental scheme is shown in Figure 5.

FIGURE 5

FIGURE 5. Experimental scheme.

The test in the real haze environment and experimental scenario is shown in Figure 6. Polarized light modulation is performed, and the distance between the transmitting and receiving ends is 1 km. A multiband laser beam (450, 532, 671 nm) is launched and polarized as the input to pass through scattering media and be collected by a detector. An attenuator and a quarter wave plate are sequentially placed in front of the laser source to produce uniformly circularly polarized light. A pass-through polarizer (labeled P1) and a quarter wave plate (labeled Q1) are placed in front of the laser source successively to obtain five types of stable polarized light, namely, 0° linear polarized light, 45° linear polarized light, 90° linear polarized light, left-handed circularly polarized light, and right-handed circularly polarized light. Linearly polarized (without using Q1) or right/left circularly polarized light is obtained by rotating them to different positions. The aforementioned six polarized lights pass through the smoke and dust atmospheric environment with a different visibility of 1 km. The prism at the receiving end divides the collected polarized scattered light into two channels. One channel records the changes in the polarization state and DOP through the polarization state-measuring instrument, and one channel reaches the optical power meter through a quarter wave plate, polarizer, and filter, which are used to calibrate and verify the accuracy of output light.

FIGURE 6

FIGURE 6. (A)Distance between field test sites is 1 km; (B) experimental scene light path diagram.

The transmission band of the polarizer is 400–700 nm, the transmittance of each wavelength can reach more than 80%, the extinction ratio is 1,000:1, and the actual output power of the laser is 49.99 mw (the output wavelengths are 450, 532, and 671 nm).

Measuring Method

The polarized light with different polarization states generated by the transmitting end is scattered by the real smoke environment and divided into two beams by the light splitting prism. One beam enters the polarization state-measuring instrument, and the other enters the optical power meter. The polarization information of a monochromatic plane wave can be characterized by four Stokes parameters: $I$, $Q$, $U$, and $V$. Full polarization information can be obtained using the rotation of polarizer and wave plate at different angles. $\beta$ is the included angle between the fast axis and the horizontal direction, and $\delta$ is the magnitude of the phase delay. The two are multiplied to obtain the actual Muller matrix of the polarizer, and then the final outgoing light intensity is multiplied by the incident Stokes vector as follows:

$I^{\prime }=\frac{1}{2}\left(\begin{array}{l}I+\left(\cos 2\theta \left({\cos }^{2}2\beta +{\sin }^{2}2\beta \cos \delta \right)+\sin 2\theta \cos 2\beta \sin 2\beta \left(1-\cos \delta \right)\right)Q\\ +\left(\cos 2\theta \cos 2\beta \sin 2\beta \left(1-\cos \delta \right)+\sin 2\theta \left({\sin }^{2}2\beta +{\cos }^{2}2\beta \cos \delta \right)\right)U\\ +\left(-\cos 2\theta \sin 2\beta \sin \delta +\sin 2\theta \cos 2\beta \sin \delta \right)V\end{array}\right).(19)$

The aforementioned formula indicates that the four Stokes vectors $I$, $Q$, $U$, and $V$ can be calculated by measuring the light intensity in any four directions. The angles selected in this study are 0°, 60°, and 120°. After calculation, the incident Stokes vector can be obtained as follows:

$\{\begin{array}{l}I=\frac{1}{2}(I^{\prime }(\mathrm{60,45},\frac{p}{,2})+I^{\prime }(\mathrm{120,45},\frac{p}{2})-3I^{\prime }(\mathrm{0,45},\frac{p}{2})),\hfill \\ Q=2I^{\prime }\left(\mathrm{0,0,0}\right)-\frac{1}{2}{I}^{\prime }\left(\mathrm{60,45,0}\right)-\frac{1}{2}{I}^{\prime }(\mathrm{120,45},\frac{p}{2})+\frac{3}{2}{I}^{\prime }(\mathrm{0,45},\frac{p}{2}),\hfill \\ U=\frac{2\sqrt{3}}{3}(I^{\prime }(\mathrm{60,45},\frac{p}{2})-I^{\prime }(\mathrm{120,45},\frac{p}{2})),\hfill \\ V=\frac{1}{2}(I^{\prime }(\mathrm{60,45},\frac{p}{2})+I^{\prime }(\mathrm{120,45},\frac{p}{2})-I^{\prime }(\mathrm{0,45},\frac{p}{,2})).\hfill \end{array}(20)$

The circular polarization component is added to the measurement method to realize the full polarization characteristic measurement of the target and compensate for the error caused by the previous polarization characteristic measurement only for the linear polarization component.

Experimental Results and Discussion

The transmission experiment of polarized light with three wavelengths and six polarization states is carried out under seven visibility environments. According to the relationship between optical thickness and outdoor visibility in Table 1, the researchers tested and recorded the polarization characteristics data under different visibility conditions. Figures 7, 8 data are the statistical results of the 1-month test on polarization characteristics in different visibilities. The experimental results are plotted, as shown in Figures 7, 8.

FIGURE 7

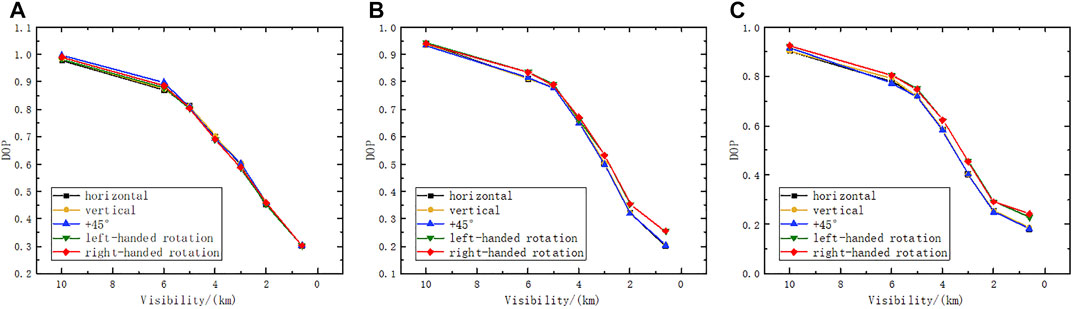
FIGURE 7. Field test curves of polarization transmission characteristics at different wavelengths:(A) 450 nm, (B) 532 nm, and (C) 671 nm.

FIGURE 8

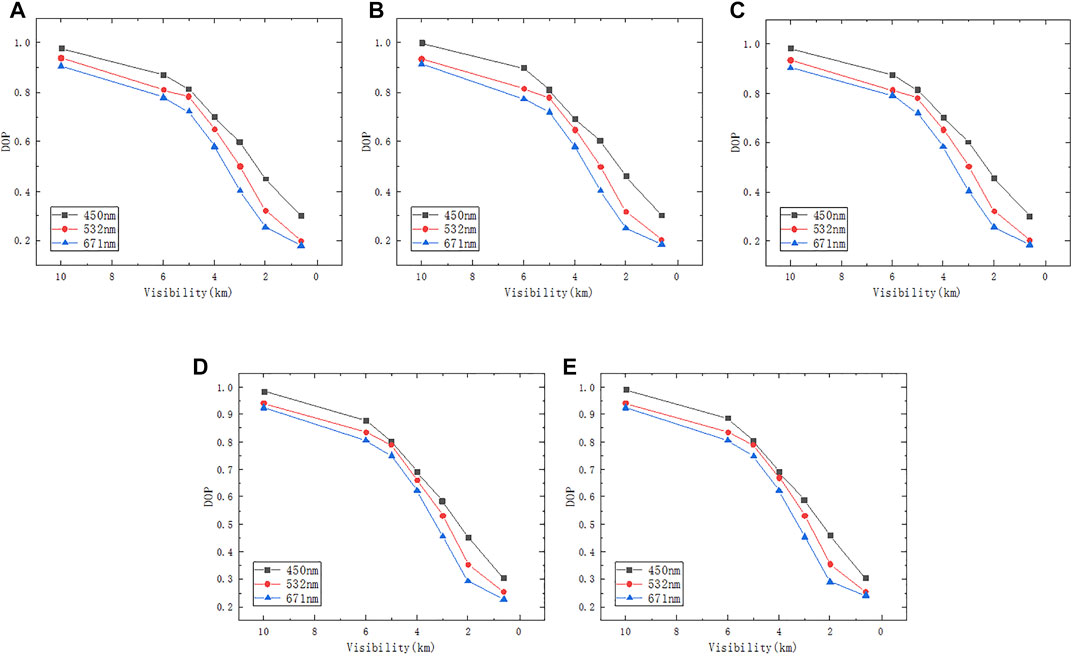
FIGURE 8. Field test curves of polarization transmission characteristics of different polarization states:(A) 0°, (B) 45°, (C) 90°, (D) left-hand rotation, and (E) right-hand rotation.

As shown in Figures 7A–C, the DOP changes of left-handed and right-handed circularly polarized light are consistent, and the DOP changes of the three linearly polarized light are also consistent. It can be seen that because the DOP difference between left-handed circularly polarized light and right-handed circularly polarized light is less than 3%, and the DOP curves of the two overlap; the DOP difference of 0°, 45°, and 90° linearly polarized light is less than 3%, resulting in the three DOP curves overlapping. With the increase in wavelength, the polarization characteristic of circularly polarized light is better than that of linearly polarized light. At 450 nm, the difference between circularly polarized light and linearly polarized light is not obvious. At 532 nm, the DOP of circularly polarized light is 1–10% higher than that of linearly polarized light. At 671 nm, the DOP of circularly polarized light is 2–15% higher than that of linearly polarized light.

The three groups of wavelength field test data in Figures 7A–C) show that for any polarized light of any wavelength, the DOP decreases gradually with the increase in transmission environment concentration. This result can be ascribed to the fact that the polarized light belongs to multiple scattering when passing through the smoke. In addition, the higher the smoke concentration, the higher the scattering times, the more the backscattering will increase, and the more the depolarization of polarized light occurs. When the concentration is low, the forward scattering of polarized light increases. Thus, the DOP will be greater than that when the concentration is high. In the visible light band at 450 nm, the DOP of circularly polarized light is close to that of linearly polarized light. The DOP of 532-nm circularly polarized light is slightly higher than that of linearly polarized light by 1–10%. Moreover, the higher the concentration, the more obvious the difference between the DOPs of circularly polarized light and linearly polarized light. The DOP of circularly polarized light is gradually higher than that of linearly polarized light. When the wavelength of polarized light increases to 671, the outgoing polarization degree of circularly polarized light is higher than that of linearly polarized light by 2–15% at all concentrations. This finding is consistent with the simulation results of concentration and polarized light transmission characteristics. With the increase in wavelength, the DOP of circularly polarized light is slightly higher than that of linear polarization. Therefore, if the polarization-maintaining characteristics of circularly polarized light are used, a long wavelength band must be used as much as possible because the polarization-maintaining characteristics of circularly polarized light of the same wavelength are better than those of linearly polarized light in this case.

Figures 8A–E show that in the smoke environment, the DOP at 450 nm of the five polarization states is higher than that at 532 and 671 nm. The simulation results of the change in DOP with dust concentration under different wavelength conditions are consistent.

The confidence between the test and simulation data is calculated as follows:

$M=1-\left({\displaystyle \sum _1^n\frac{\left|R-R_m\right|}{R_m}}\right)/n\times 100\%,(21)$

where $R$ and $R_m$ are the DOP values obtained by simulation and measurement under the same conditions. The simulation and measurement experiments are carried out for seven optical thicknesses, n = 7. Thus, the DOP confidence of five polarization states is calculated. The calculation results are as follows:

The confidence calculation results in Tables 2–4 show that in the visible band, the visibility is 0.6–10 km, the particle size is 0.7 µm, the particle refractive index is 1.53 + 0.008i, and the optical thickness is in the range of 0.3–8. The lowest confidence of the simulation model is 60.08%, and the highest is 83.58%. All confidence calculation results are greater than 60%, indicating that the results of the simulation model are reliable.

TABLE 2

TABLE 2. Calculation results of confidence of 450 nm polarized light simulation and test verification.

TABLE 3

TABLE 3. Calculation results of confidence of 532 nm polarized light simulation and test verification.

TABLE 4

TABLE 4. Calculation results of confidence of 671 nm polarized light simulation and test verification.

When testing the polarization characteristics in the field smoke environment, outdoor environmental factors such as wind force, temperature, and humidity will always affect the accuracy of the experimental measurement, resulting in inevitable errors in the data obtained from the field test. Therefore, in the subsequent experimental research, we should consider the outdoor environmental factors as variables to obtain the influence law of environmental factors on the experimental test to reduce errors. In addition, the simulation only focuses on the multiple polarization scattering characteristics of smoke particles with the same particle size. In the future, the external field and experimental research on the polarization characteristics of multiple particle sizes should be carried out.

Conclusion

In a smoke particle environment, the changes in polarization characteristics of visible polarized light transmitted through the medium are studied. By analyzing the size distribution of particles in a smoke environment, the polarization characteristic model of multiple scattering of polarized light in the visible band is established based on the Monte Carlo method, and the transmission characteristics of polarized light are studied by combining indoor and outdoor experiments. With the increase in optical thickness, the DOP at three wavelengths in the visible light band decreases, and the DOP of each polarized light decreases. No obvious difference exists between the DOP of circularly polarized light at 450 nm and linearly polarized light. The DOP of circularly polarized light at 532 nm is 1–5% higher than that of linearly polarized light, 1–10% higher than that of outdoor test, 1–5% higher than that of circularly polarized light at 671 nm, and 2–15% higher than that of outdoor test. Moreover, the DOP of the three wavelengths is always 450 nm > 532 nm > 671 nm. Therefore, the shorter the wavelength in the visible band, the higher the DOP. With the increase in wavelength, the polarization characteristics of circularly polarized light are slightly better than those of linearly polarized light. In the case of a long wavelength band, the polarization-maintaining characteristics of circularly polarized light at the same wavelength are better than those of linearly polarized light. In the follow-up work, we will carry out experimental research on the influence of particle size on polarization characteristics, expand the research scope to the near-infrared band, master the influence law of outdoor real environment on polarization characteristics, and provide a theoretical basis for the development of polarization imaging.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

ZJ conceived the project, conducted the experiment, and wrote the manuscript. All authors contributed to discussions during its preparation. ZJ supervised the project.

Funding

This research was funded by the National Natural Science Foundation of China (Nos. 61890963 and 61905025), Key project of Education Department of Jilin Province (JJKH20220738KJ and JJKH20220737KJ), and Project of Science and Technology Department of Jilin Province (Nos. 20210201093GX and 20200201261JC).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Evans KF, Stephens GL. A New Polarized Atmospheric Radiative Transfer Model. J Quantitative Spectrosc Radiative Transfer (1991) 46(5):413–23. doi:10.1016/0022-4073(91)90043-p

CrossRef Full Text | Google Scholar

2. Fade J, Panigrahi S, Carré A, Frein L, Hamel C, Bretenaker F, et al. Long-range Polarimetric Imaging through Fog. Appl Opt (2014) 53(18):3854–65. doi:10.1364/ao.53.003854

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Liu X, Qiao S, Ma Y. Highly Sensitive Methane Detection Based on Light-Induced Thermoelastic Spectroscopy with a 2.33 Μm Diode Laser and Adaptive Savitzky-Golay Filtering. Opt Express (2022) 30(2):1304–13. doi:10.1364/oe.446294

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ma Y, Hong Y, Qiao S, Lang Z, Liu X. H-shaped Acoustic Micro-resonator-based Quartz-Enhanced Photoacoustic Spectroscopy. Opt Lett (2022) 47(3):601–4. doi:10.1364/ol.449822

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Liu X, Ma Y. Sensitive Carbon Monoxide Detection Based on Light-Induced Thermoelastic Spectroscopy with a Fiber-Coupled Multipass Cell. Chin Opt Lett (2022) 20(3):031201. doi:10.3788/col202220.031201

CrossRef Full Text | Google Scholar

6. Ma Y, Hu Y, Qiao S, Lang Z, Liu X, He Y, et al. Quartz Tuning forks Resonance Frequency Matching for Laser Spectroscopy Sensing. Photoacoustics (2022) 25:100329. doi:10.1016/j.pacs.2022.100329

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chun CSL, Sadjadi FA. Polarimetric Laser Radar Target Classification. Opt Lett (2005) 30(14):1806–8. doi:10.1364/ol.30.001806

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Anna G, Goudail F, Dolfi D. Optimal Discrimination of Multiple Regions with an Active Polarimetric Imager. Opt Express (2011) 19(25):25367–78. doi:10.1364/oe.19.025367

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Tyo JS, Goldstein DL, Chenault DB, Shaw JA. Review of Passive Imaging Polarimetry for Remote Sensing Applications. Appl Opt (2006) 45(22):5453–69. doi:10.1364/ao.45.005453

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Tan S, Narayanan RM. Design and Performance of a Multiwavelength Airborne Polarimetric Lidar for Vegetation Remote Sensing. Appl Opt (2004) 43(11):2360–8. doi:10.1364/ao.43.002360

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Anastasiadou M, Martino AD, Clement D, Liège F, Laude-Boulesteix B, Quang N, et al. Polarimetric Imaging for the Diagnosis of Cervical Cancer. Phys Stat Sol(c). (2008) 5(5), 1423–6. doi:10.1002/pssc.200777805

CrossRef Full Text | Google Scholar

12. Baldwin AM, Chung JR, Baba JS, Spiegelman CH, Amoss MS, Cote GL. Mueller Matrix Imaging for Cancer Detection. Proc IEEE (2003) 1022:1027–30. doi:10.1109/iembs.2003.1279419

CrossRef Full Text | Google Scholar

13. Wu F, Yang Y, Jiang J, Zhang P, Li Y, Xiao X, et al. Classification between Digs and Dust Particles on Optical Surfaces with Acquisition and Analysis of Polarization Characteristics. Appl Opt (2019) 58(4):1073–83. doi:10.1364/ao.58.001073

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Van der Laan JD, Wright JB, Scrymgeour DA, Kemme SA, Dereniak EL. Evolution of Circular and Linear Polarization in Scattering Environments. Opt Express (2015) 23(25):31874–88. doi:10.1364/oe.23.031874

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zeng X, Chu J, Cao W, Kang W, Zhang R. Visible-IR Transmission Enhancement through Fog Using Circularly Polarized Light. Appl Opt (2018) 57(23):6817. doi:10.1364/ao.57.006817

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Van der Laan JD, Wright JB, Kemme SA, Scrymgeour DA. Superior Signal Persistence of Circularly Polarized Light in Polydisperse, Real-World Fog Environments. Appl Opt (2018) 57(19):5464–73. doi:10.1364/ao.57.005464

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ryan JS, Carswell AI. Laser Beam Broadening and Depolarization in Dense Fogs. J Opt Soc Am (1978) 68(7):900–8. doi:10.1364/josa.68.000900

CrossRef Full Text | Google Scholar

18. Chu J, Wu Q, Zeng X, Li Y. Forward Transmission Characteristics in Polystyrene Solution with Different Concentrations by Use of Circularly and Linearly Polarized Light. Appl Opt (2019) 58(25):6750–4. doi:10.1364/ao.58.006750

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sankaran V, Schönenberger K, Walsh JT, Maitland DJ. Polarization Discrimination of Coherently Propagating Light in Turbid media. Appl Opt (1999) 38(19):4252–61. doi:10.1364/ao.38.004252

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liao YB. Polarization Optics. China (2003).

Google Scholar

21. He SY. Particle Size Distribution Characteristics of Chemical Components of Atmospheric Particulate Matter in Nanjing. Nanjing: Nanjing University (2020).

Google Scholar

22. Hao L, Yang W, Wu TW, Zhao JQ, Shi GY. Optical Properties and Radiative Forcing Effects of Dust Aerosol. J Desert Res (2010) 30(06):1477–82.

Google Scholar