Numerical Simulation of Surface Dielectric Barrier Discharge With Functionally Graded Material

Atmospheric-pressure surface dielectric barrier discharge (SDBD) has drawn significant attention, and the influence on the SDBD characteristics of surface dielectric barrier materials has been widely studied. In this work, a two-dimensional self-consistent fluid model is built to investigate the effect of barrier material characteristics on SDBD by introducing a linear permittivity distribution. It is demonstrated that a dielectric barrier with graded permittivity can affect the SDBD by changing the electric field distribution near the surface and speeding up the propagation of the streamer. The graded permittivity along the layer of the dielectric barrier plays a significant role in improving the dynamic characteristics of the SDBD.

Introduction

Under conditions of low temperature, non-equilibrium, and atmospheric pressure, dielectric barrier discharge (DBD) shows great advantages in many applications, such as materials processing, environmental remediation, and flow control [1]. DBD has the advantage of generating stable and uniform plasma, helping to avoid the transition to a high temperature arc with a constricted channel [2]. The production of oxidizing species in the DBD application of activating water for sanification such as hydrogen peroxide and ozone is efficient, giving the plasma antiseptic properties [3]. It is found that the externally enforced electric potential is able to generate a drift of the heavy species and electrons, leading to a charge density distribution which in turn creates distortions of the electric potential distribution in the bulk of the plasma [4]. Compared with the DBD, the SDBD is more efficient than the parallel plate volume DBD in the intended application of fluid dynamic actuation [5]. The discharge propagates on the surface of the dielectric barrier, which is exposed to the ambient gas. During propagation, reactive species are formed; in which ions play the dominant role in flow control, such as controlling laminar to turbulent flow transitions [6–8]. As for the influence of parameters, SDBDs with positive and negative polarity have been investigated [9–11]. Several kinds of SDBDs with different geometries and voltage polarities of multi-electrodes have been studied to investigate the discharge dynamical characteristics [12]. For all voltage pulses, the discharge has a channeled structure, and the discharge length decreases with increased epsilon value [13]. The idea of using FGM for electric field optimization was proposed, and it was proved that the introduction of FGM could alleviate the local electric field concentration [14]. Considering the rapid development of 3D print technology, a non-linear functionally graded material (FGM) as a dielectric barrier may become a reality, creating a space-varying electric field on the dielectric surface [15]. The discharge becomes more intense [16, 17] and the surface charge density is much higher [18] with greater permittivity introduced into the dielectric. However, the issues of discharge uniformity and plasma propagation parameters have not received much attention in SDBD with functionally graded material. The use of graded permittivity material may provide a new way to control the SDBD plasma parameters. In this work, the influence mechanism of the graded permittivity dielectric barrier on SDBD is investigated in the light of both surface and space species accumulation. The spatiotemporal distributions of electron density and electric field are studied as streamers propagate along the dielectric surface. The aerodynamic characteristics are investigated and compared in permittivity to uniform and graded distributions as well.

Computational Model

Simulation Model and Governing Equations

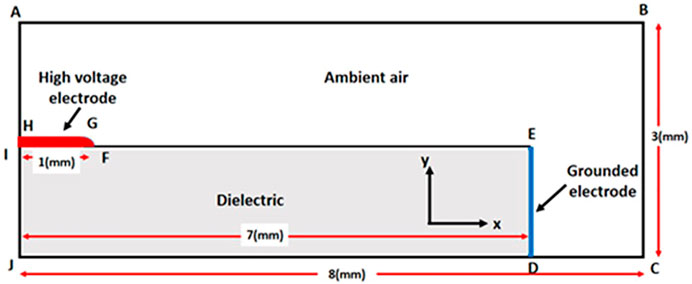
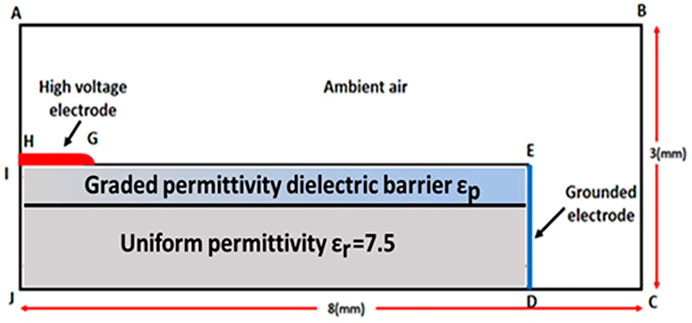
The surface dielectric barrier discharge in this work is simplified as a two-dimensional (2D) model, as depicted in Figure 1. The simulation domain is 8 mm (length) × 3 mm (height) in Cartesian x–y coordinates. The length of the ambient air and dielectric barrier are 8 and 7 mm, respectively. The thickness of the gas gap is 1.5 mm above the dielectric barrier and 3 mm above the rest. The grounded electrode was placed on the right side of the dielectric barrier, and the single exposed electrode with a high voltage is on the upper left surface of the dielectric barrier. The barrier dielectric is given a space-varying permittivity ${\epsilon }_r$ from 7.5 to 10.5, changed in linear or non-linear forms. The continuity equation for both charged and neutral species is Eq. 1. The drift-diffusion approximation for charged species is calculated by Eqs. 2, 3, and Eq. 4 is used to obtain diffusion flux for neutral species, where e, −, +, and m represent electrons, negative ions, positive ions, and neutral species. n is the number density, cm⁻³, and j is the flux, cm⁻² s⁻¹.

$\frac{\partial n_j}{\partial t}+\nabla \cdot {\mathit{j}}_j=S_j,(1)$

${\mathit{j}}_{e,-}=-{\mu }_{e,-}\mathit{E}{\mathit{n}}_{e,-}-D_{e,-}\nabla n_{e,-},(2)$

${\mathit{j}}_{+}={\mu }_{+}\mathit{E}{\mathit{n}}_{+}-D_{+}\nabla n_{+},(3)$

$j_m=-D_m\nabla n_m.(4)$

FIGURE 1

FIGURE 1. Two-dimensional model used for simulation.

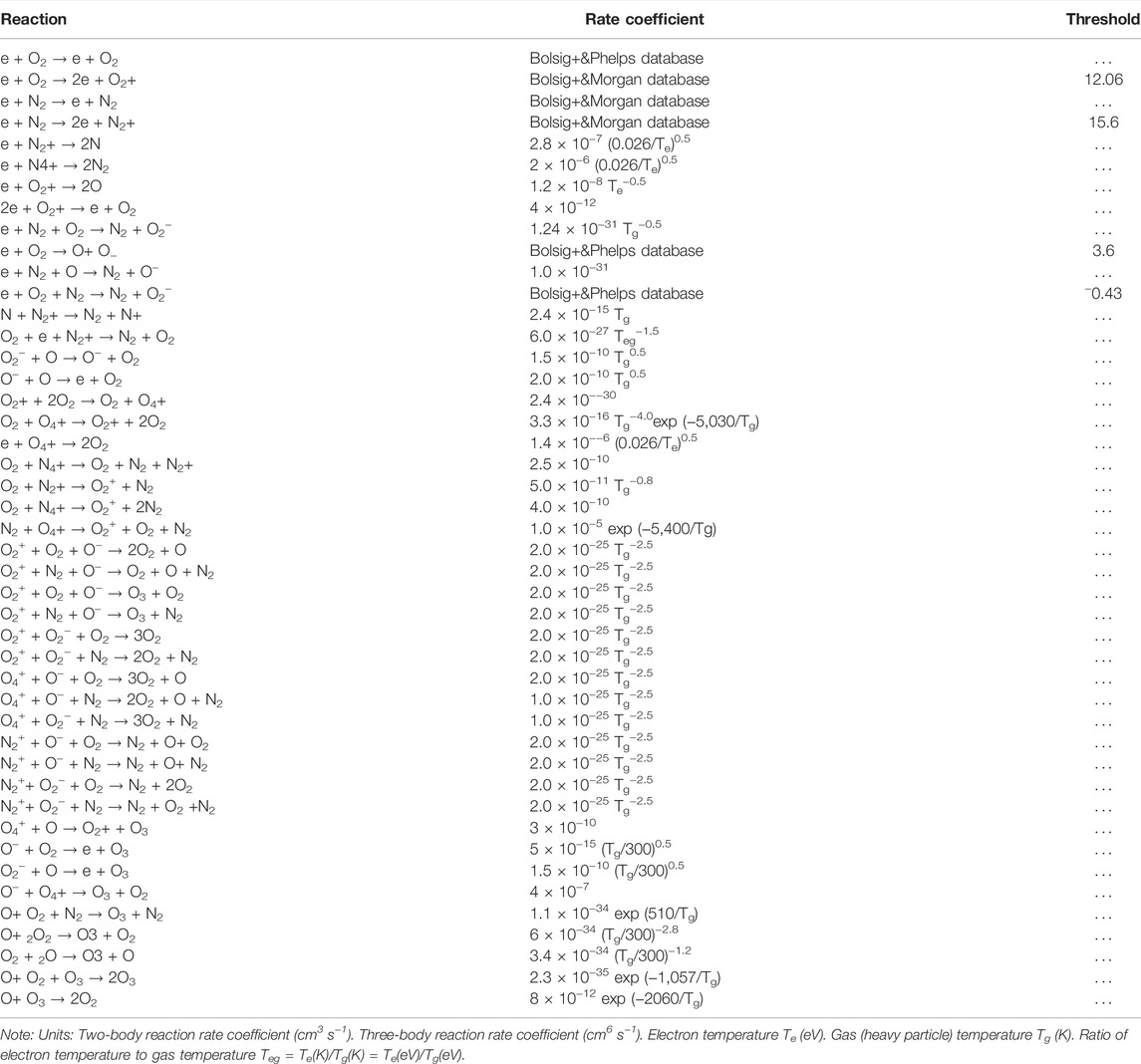
In the equations above, E is the electric field vector, µ is mobility, D is the diffusion coefficient, and S_j is the source of species of species j (j = e, −, +), which can be derived from the chemical reactions. The working gas is simplified as 80% N₂ and 20% O₂. The species and reactions in the model are given in Table 1. The rate coefficients of electron impact reactions are obtained by solving Boltzmann’s equation using BOLSIG+¹. Cross sections are taken from the Morgan, TRINITI, and Phelps databases^2–4. What’s more, the local field approximation is applied when calculating parameters, and the electron mean energy and electron transport coefficient are given as a function of reduced electric field. Transport coefficients for ions and neutrals were estimated following Ref. [19].

TABLE 1

TABLE 1. Species and reactions.

The electric potential is found by:

$\nabla \cdot \left({\epsilon }_r\nabla \phi \right)=-\rho /{\epsilon }_0,(5)$

where, $\phi$ and $\rho$ are the electric potential and space charge density, respectively, ${\epsilon }_0$ is the vacuum permittivity. ${\epsilon }_r$ is the relative permittivity of the dielectric barrier. The main plasma parameters, including dielectric surface charge, are calculated in this work.

$\frac{\partial {\sigma }_s}{\partial t}=-e\left[\left({\displaystyle \sum {\mathit{j}}_{+}}-{\displaystyle \sum {\mathit{j}}_{-}-{\mathit{j}}_{\mathit{e}}}\right)\cdot \mathit{n}\right],(6)$

${\mathit{j}}_e\cdot \mathit{n}=\left(-{\mu }_e\mathit{E}{\mathit{n}}_e-\gamma {\displaystyle \sum {\mathit{j}}_{+}}\right)\cdot \mathit{n},(7)$

where n is the unit vector perpendicular to the dielectric surface, $\gamma$ is the secondary emission coefficient, $\gamma =0.01$. The secondary emission electron energy is set at 2.5 eV, which is in the same as the surface reactions.

Graded Dielectric Permittivity and Boundaries

In a uniform electric field, the initial charged particle density is uniformly distributed. In a non-uniform distorted electric field, it is generally considered that the initial charged particle density obeys a Gaussian distribution. For the non-uniform field discharge of needle plate structure, it is often assumed that the initial charged particles (electrons and positive ions) follow the Gaussian distribution and that the negative ion density is zero [20–22]. The initial electron distribution is given by:

$N_{0\_e}=N_{max}exp\left(-\frac{{\left(x-x_0\right)}^2}{2{\sigma }^2}-\frac{{\left(y-y_0\right)}^2}{2{\sigma }^2}\right),(8)$

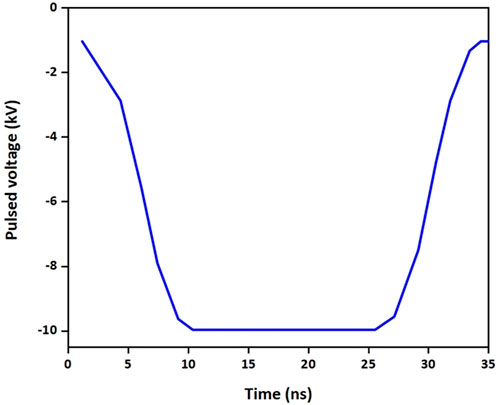
where N_max = 10¹⁶ m⁻³, (x₀, y₀) = (0, 2 mm), σ = 62.5 µm. (x₀, y₀) are the spatial coordinates of the needle electrode head. The negative voltage applied is shown in Figure 2.

FIGURE 2

FIGURE 2. Negative pulsed voltage applied to the electrode.

Considering the technical process and reliability of graded material in 3D printing, several dielectric permittivity distributions are proposed in the present work, as a function of x along the length of the dielectric barrier direction, as shown in Figure 3. Both ideal permittivity and practical permittivity distributions are depicted as in Figure 3, and the approximated function of ideal permittivity is ${\epsilon }_p=7.5+0.43x$. Obviously, non-linear distribution as a function of length along x direction is introduced, and to be a comparison of uniform distribution of dielectric permittivity, the case in the condition of ${\epsilon }_r=7.5$ is studied as well.

FIGURE 3

FIGURE 3. Dielectric permittivity distributions.

Boundary conditions are given in Table 2.

TABLE 2

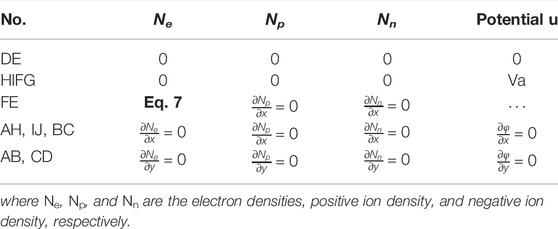
TABLE 2. Boundary conditions on potential $\phi$ and species density (N_e, N_p, N_n) in Figure 1A.

Results and Discussion

Species Density Distribution and Electric Field

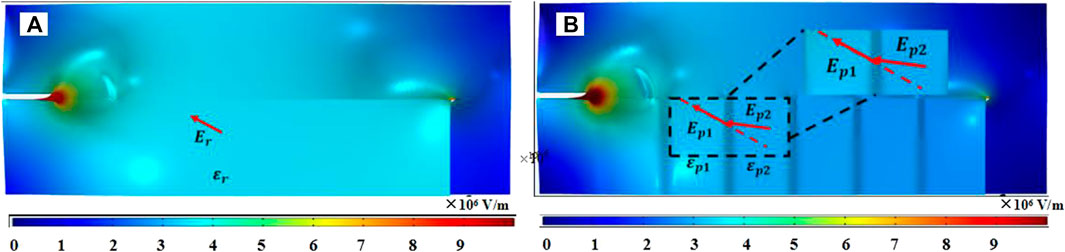
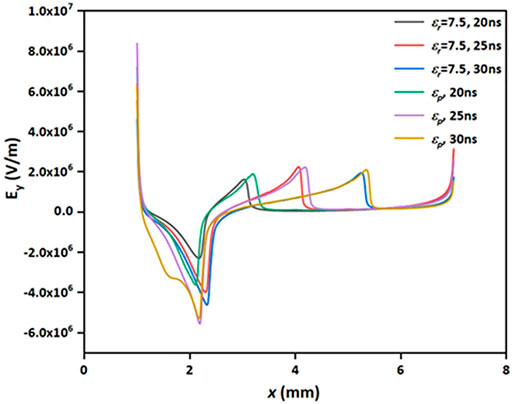
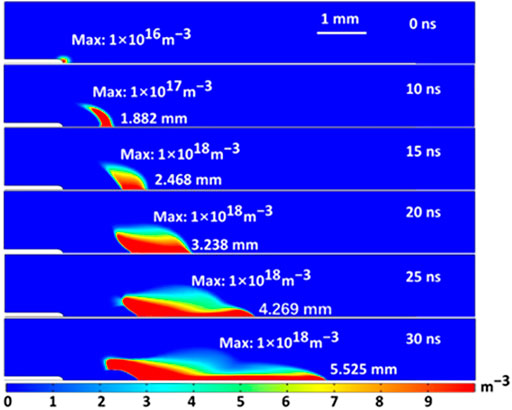
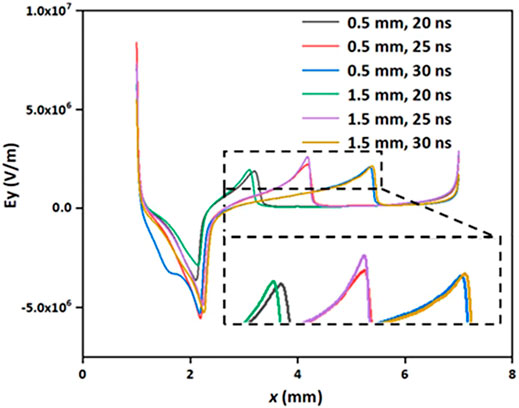
The spatial distribution of electron density with dielectric barrier permittivity ${\epsilon }_r=7.5$ and ${\epsilon }_p$ are shown in Figure 4. A streamer starts after the applied voltage rises to about −10 kV, at about 10 ns. Within the first 10 ns, the discharge transfers from a corona-like to a streamer-like discharge, mainly due to the upper side of the applied voltage. The negative discharge streamer propagates along the surface of the dielectric barrier, but the streamer starting positions with uniform permittivity ${\epsilon }_r=7.5$ seem to be farther than those with graded permittivity ${\epsilon }_p$. This also means that the streamer starts at an earlier time on the graded dielectric barrier in this case. Streamer approximately driven by high electric field, both of the direction and magnitude. The magnitude of electric field strength near the surface of the dielectric barrier has not changed greatly due to the graded permittivity. As a comparison, the direction of electric field strength is much different in graded dielectric than in the uniform distribution of permittivity, as is depicted in Figure 5B. Near the surface inside the dielectric with permittivity ${\epsilon }_{p1}$ and ${\epsilon }_{p2}$, there is ${\epsilon }_{p1}{E}_{p1}\cdot sin\left({\delta }_1\right)={\epsilon }_{p2}{E}_{p2}\cdot sin\left({\delta }_2\right)$, where ${\delta }_1\left({\delta }_2\right)$ are the angles between $E_{p1}\left(E_{p2}\right)$ and x direction. According to the given graded permittivity in Figure 3, the graded permittivity increases with the length of the dielectric barrier in the x-direction, thus, ${\epsilon }_{p2}>{\epsilon }_{p1}$. As a consequence, ${\delta }_2$ is smaller than ${\delta }_1$, which means the direction of electric field strength is concentrated on the streamer propagation direction, introducing functionally graded material. Besides, compared with Figure 5A, it shows a little rise in electric field magnitude in Figure 5B. At 25 ns, before the falloff of the negative voltage pulse, the streamer reaches 2.3 mm with uniform permittivity and almost 3 mm with graded permittivity. This may provide a longer propagation of streamer controlling without changing the electric field magnitude greatly.

FIGURE 4

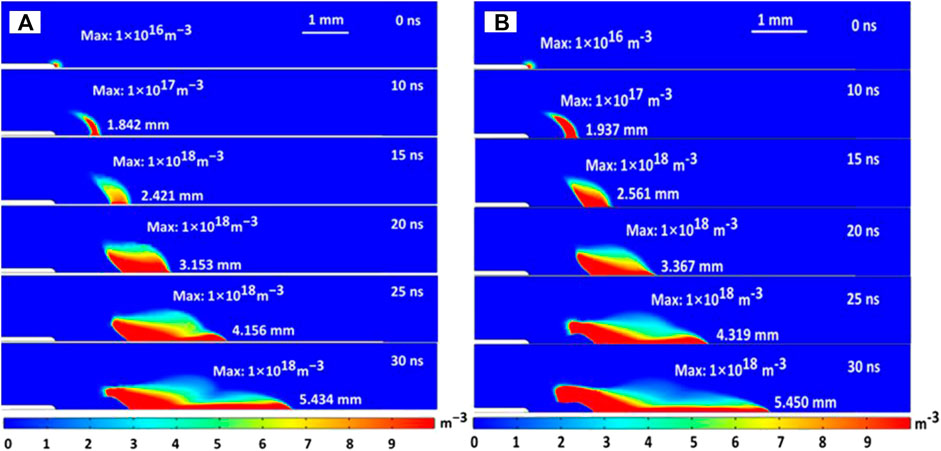
FIGURE 4. The spatial distribution of electron density with dielectric barrier ε_r =7.5 (A) and ε_p (B).

FIGURE 5

FIGURE 5. electric field distribution with uniform permittivity (A) and graded permittivity (B).

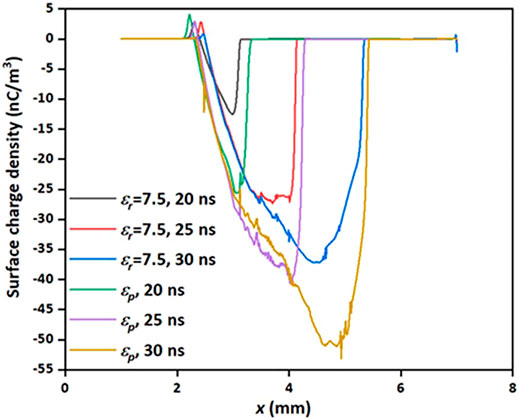
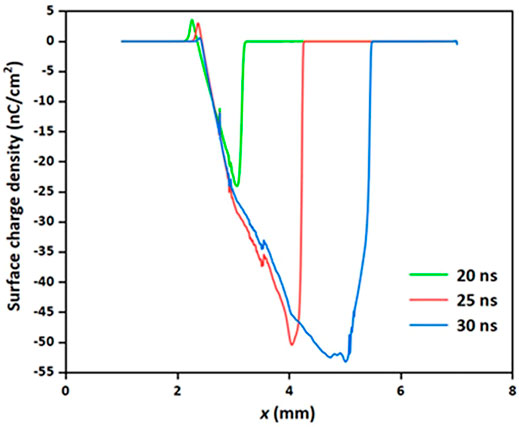
Figure 6 shows the spatial distribution of surface charge density with uniform and graded permittivity. The charge density along the dielectric barrier has a wider distribution range under the condition of graded permittivity. The $E_y$ component is shown in Figure 7, as the propagation of the streamer changes the sign and the surface charge decreases in accumulation when the $E_y$ component falls to zero. The slower-drifting ions, including,$N_4^{+}$, $N_2^{+}$ significantly change the charge polarity on the surface layer of the dielectric barrier. The charges on the surface generate a strong electric field, leading to the new ionization of the gas. The charge density keeps increasing during the falloff stage of applied voltage and corresponds to the propagation of the streamer. It can be found that surface charge density is much higher with the graded permittivity applied. As depicted in Figures 5B, 7, the usage of graded permittivity dielectric changes the electric field component softly, with almost no distortion of it. But the surface charge density is considerably increased; this may benefit some applications such as plasma catalysis [23], which create more intense reaction rates and reactive molecules.

FIGURE 6

FIGURE 6. Surface charge density.

FIGURE 7

FIGURE 7. E_y component.

What’s more, surface charge density increases with the graded permittivity, which is inflected by the length along the dielectric. With the development of discharge, the streamer slides over the surface of the dielectric barrier, driven by the increasing electric field caused by the graded permittivity in the form of step-rise. The graded permittivity applied in this case, as presented, is more obviously in a changing electric field. The tiny adjustment by the graded permittivity dielectric barrier may result in continuously extended discharge propagation and more surface charge density (Figure 6).

To understand the influence of graded permittivity on some reactive molecules, the spatiotemporal evolution of $N_4^{+}$, $N_2^{+}$ ion densities is shown in Figures 8, 9, respectively. It can be found that positive ions $N_2^{+}$ are always produced in regions of high electric fields. This is mainly due to the possible ionization. From Figures 8A, B, it shows a higher ionization rate where $N_2^{+}$ is relatively concentrated with the application of graded permittivity dielectric. Compared with the distribution of $N_2^{+}$, the density of reactive species $N_4^{+}$ shows a relatively uniform distribution along the streamer. $N_4^{+}$ is produced from the recombination and association reactions in which the species $N_2^{+}$ will be consumed, since $N_2^{+}$ is produced mainly in the head of the streamer. In the aspect of the early stage during the upper side of voltage, the distance between the concentration of $N_2^{+}\left(N_4^{+}\right)$ and the high voltage electrode is shorter with the graded dielectric barrier, and the density is higher. This indicates the production rates of two species are faster, the usage of graded permittivity dielectric may speed up the reaction rates. In the late stage of discharge development, a reversal density of $N_2^{+}$ and $N_4^{+}$ appears near the negative high voltage electrode, mainly due to the drift process.

FIGURE 8

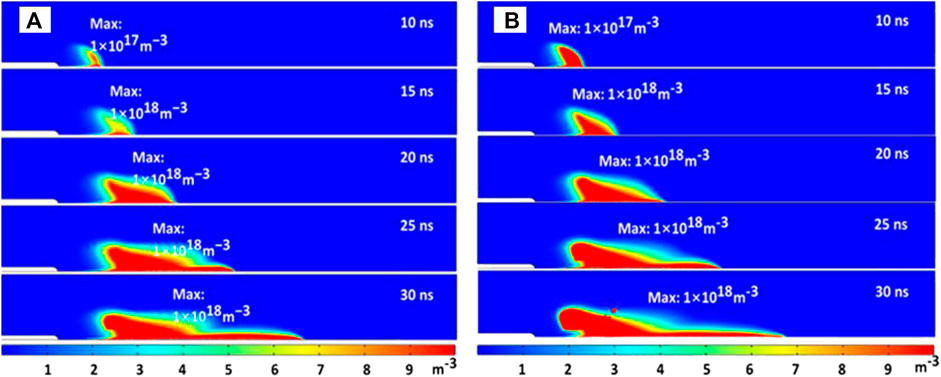
FIGURE 8. The spatiotemporal evolution of N₄⁺ density with uniform permittivity (A) and graded permittivity (B) dielectric barrier.

FIGURE 9

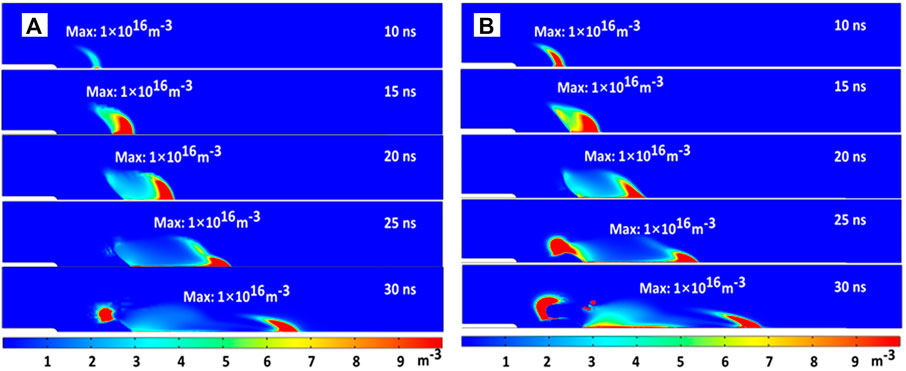
FIGURE 9. The spatiotemporal evolution of N₂⁺ density with uniform permittivity (A) and graded permittivity (B) dielectric barrier.

The higher density and producing rates of $N_2^{+}$ and $N_4^{+}$, caused by the introduction of graded permittivity, will benefit the plasma catalysis such as the application of synthesis of Ammonia [24]. Ni/ $\gamma$-Al₂O₃ enhance plasma-promoted NH₃ production and favors surface-adsorbed NH_x species. $N_2^{+}$ and $N_4^{+}$ on the surface of the catalyst Ni/ $\gamma$-Al₂O₃ can be regarded as the catalytic efficiency of plasma. As the dominant species, including $N_2^{+}$ and $N_4^{+}$, the introduction of graded permittivity to the solid catalyst will promote a faster synthesis rate of NH₃.

Contours of Momentum Sources (Body Force) With Uniform Permittivity and Graded Permittivity

As for the aerodynamic applications, the momentum source due to the charged particles’ collisions with neutral gas molecules (body force) is given by [10]

$F=e\left(n_i-n_{-}-n_e\right)E,(9)$

where $E$ is the electric field vector, e represents elementary charge, and n_i, n₋ and n_e are the positive ion density, negative ion density, and electron density, respectively. Figure 10 depicts the contours of a momentum source with uniform permittivity and one with graded permittivity. As is depicted in Figure 10A, the contours of the momentum source (volumetric force) show different signs inside and outside the streamer body, and are almost concentrated in the head of the streamer and a thin layer near the dielectric surface. In the thin layer near the surface, the sign of a body force is always in negative territory, and positive in the outer areas. This outcome is in accord with that in Ref. [10]. Compared with the gravity force in the atmospheric air, it is about ${10}^4$ times greater. Thus, the body force in the layer, which is perpendicular to the contours, drags the streamer slide along the dielectric surface. The non-linear structure of the contours of the momentum source is always accompanied by a complex vortex, and as the propagation of the streamer, this kind of vortex moves along the dielectric surface barrier. The flow conditions will be significantly changed due to the existence of the vortex.

FIGURE 10

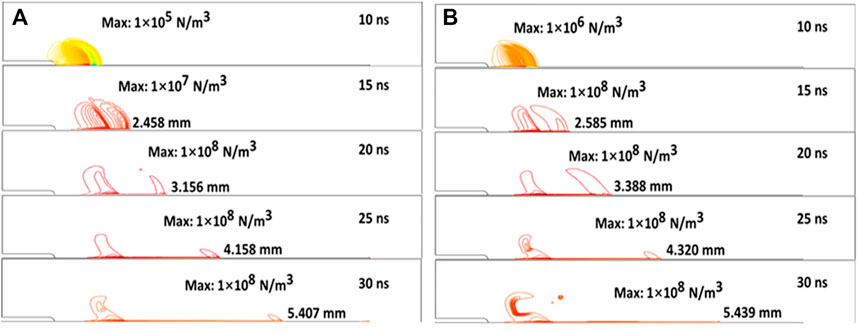
FIGURE 10. Contours of momentum source with dielectric barrier of uniform permittivity (A) and graded permittivity (B).

The numbers on the right side of the contours are the x-coordinates of the streamer head, as shown in Figure 10. It is obvious from Figure 10B that the contours cover a wider range on the dielectric surface and propagate at a faster speed. The graded permittivity introduced in the model shows an intense and speeded-up momentum exchange between charged ions, electrons, and neural molecules in the ambient air. Local vortex caused by body force is considered to be the possible way of cooling down of the temperature and a kind of diffusion effect to the streamer propagation. The longer propagation of vortex means that, with the same negative voltage pulse applied, the flow-field control along the dielectric surface seems to be more efficient. The “ionization wind” will slide faster and generate more thrust force on the surface of the functionally graded material dielectric barrier.

The Influence of Thickness on Graded Permittivity Dielectric Layer

The 2-D model of different dielectric barrier layer thickness is shown in Figure 11, in order to investigate the influence of thickness of linear permittivity dielectric layer on SDBD, the thickness of graded permittivity dielectric barrier is reduced to 0.5 mm, and the rest of the dielectric barrier is in the uniform permittivity${\epsilon }_r=7.5$. The 0.5 and 1.5 mm in the figure represent the thickness of the graded permittivity layer. The boundary conditions and negative voltage pulse applied to the model are the same as in Figure 1 and Figure 2. The graded permittivity applied here is still the ${\epsilon }_p$ as in Figure 3.

FIGURE 11

FIGURE 11. Different thickness of graded permittivity layer.

The number on the right side of the streamer head is the x coordinate of it. Figure 12 depicts the spatial distribution of electron density with a layer of thin thickness. Compared with Figure 4B, it depicts a shorter distance of propagation in Figure 12, but somewhat at 30 ns (falloff of the negative voltage pulse), in the similar position of the streamer head. But the reversal of electron density distribution pointing at the high voltage electrode is suppressed, which can be seen in Figure 12. As indicated in Figure 5B, the graded permittivity dielectric affects the streamer propagation by enhancing the electric field distribution, and it mainly takes place along the surface of the dielectric barrier. As a consequence, with the same voltage applied, the electric field would not be dramatically changed in the $E_y$ component, which can also be identified from Figure 13. Figure 13 shows the $E_y$ component of different layer thicknesses with graded permittivity. The magnitude of $E_y$ component is a little higher with the thickness of 1.5 mm of graded permittivity dielectric barrier than with the thickness of 0.5 mm. Figure 14 shows the instantaneous distribution of surface charge density at 20, 25, and 30 ns with a layer of very thin thickness. The $E_y$ component is negative over the surface with a high enough charge, as shown in Figure 14. This shows that the thickness of the graded permittivity dielectric layer will not significantly change the surface charge density along the barrier surface, of which is correlated with the $E_y$ component.

FIGURE 12

FIGURE 12. Electron density distribution on thinner layer of graded permittivity.

FIGURE 13

FIGURE 13. E_y component on the surface of thinner layer of graded permittivity.

FIGURE 14

FIGURE 14. Surface charge density thinner layer of graded permittivity.

Conclusion

In this work, a 2-D model was developed to study surface dielectric barrier discharge with functionally graded material under the condition of a single negative nanosecond voltage pulse being applied.

1) The dielectric layer with graded permittivity can influence SDBD characteristics by enhancing the electric field $E_x$ component, mainly in its direction, and changing of $E_y$ component which is correlated to the surface charge density. The thickness of the layer seems to have little influence on the electric field.

2) The propagation of streamer has a longer distance in step-rise graded permittivity dielectric barrier of all thickness of the layer, compared with that in uniform constant permittivity. The distribution of electrons and reactive species tends to be a wider range on the surface, which can provide a better application experience for the catalyst industry.

3) The contours of the momentum source are studied, and it predicts a more complex structure in the head of the streamer with a graded permittivity dielectric barrier surface and faster propagation. The direction of body force seems to point oppositely to the surface. It is enhanced in the propagation direction compared with the reported results for the positive voltage in the literature.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

ZZ contributed to the simulation model building, manuscript writing, and data collection.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹See http://www.bolsig.laplace.univ-tlse.fr/ for information about Bolsig+.

²See http://www.lxcat.net for Morgan database.

³See http://www.lxcat.net for TRINITI database.

⁴See http://www.lxcat.net for the Phelps database.

References

1. Adamovich I, Baalrud SD, Bogaerts A, Bruggeman PJ, Cappelli M, Colombo V, et al. The 2017 Plasma Roadmap: Low Temperature Plasma Science and Technology. J Phys D: Appl Phys (2017) 50(32):323001. doi:10.1088/1361-6463/aa76f5

CrossRef Full Text | Google Scholar

2. Zhang J, Wang Y, Wang D, Economou DJ. Numerical Simulation of Streamer Evolution in Surface Dielectric Barrier Discharge with Electrode-Array. J Appl Phys (2020) 128(9):093301. doi:10.1063/5.0013594

CrossRef Full Text | Google Scholar

3. Colonna G, Pintassilgo CD, Pegoraro F, Cristofolini A, Popoli A, Neretti G, et al. Theoretical and Experimental Aspects of Non-equilibrium Plasmas in Different Regimes: Fundamentals and Selected Applications. Eur Phys J D (2021) 75(6):183. doi:10.1140/epjd/s10053-021-00186-5

CrossRef Full Text | Google Scholar

4. Cristofolini A, Popoli A. A Multi-Stage Approach for DBD Modelling. J Phys Conf Ser (2019) 1243(1):012012. doi:10.1088/1742-6596/1243/1/012012

CrossRef Full Text | Google Scholar

5. Abdelaziz AA, Ishijima T, Seto T, Osawa N, Wedaa H, Otani Y. Characterization of Surface Dielectric Barrier Discharge Influenced by Intermediate Frequency for Ozone Production. Plasma Sourc Sci. Technol. (2016) 25(3):035012. doi:10.1088/0963-0252/25/3/035012

CrossRef Full Text | Google Scholar

6. Likhanskii AV, Shneider MN, Macheret SO, Miles RB. Modeling of Dielectric Barrier Discharge Plasma Actuator in Air. J Appl Phys (2008) 103(5):053305. doi:10.1063/1.2837890

CrossRef Full Text | Google Scholar

7. Boeuf JP, Pitchford LC. Electrohydrodynamic Force and Aerodynamic Flow Acceleration in Surface Dielectric Barrier Discharge. J Appl Phys (2005) 97(10):103307. doi:10.1063/1.1901841

CrossRef Full Text | Google Scholar

8. Likhanskii AV, Shneider MN, Macheret SO, Miles RB. Modeling of Dielectric Barrier Discharge Plasma Actuators Driven by Repetitive Nanosecond Pulses. Phys Plasmas (2007) 14(7):073501. doi:10.1063/1.2744227

CrossRef Full Text | Google Scholar

9. Soloviev VR, Krivtsov VM, Shcherbanev SA, Starikovskaia SM. Evolution of Nanosecond Surface Dielectric Barrier Discharge for Negative Polarity of a Voltage Pulse. Plasma Sourc Sci Tech (2017) 26(1):014001. doi:10.1088/1361-6595/aae63e

CrossRef Full Text | Google Scholar

10. Soloviev VR, Krivtsov VM. Surface Barrier Discharge Modelling for Aerodynamic Applications. J Phys D: Appl Phys (2009) 42:125208. doi:10.1088/0022-3727/42/12/125208

CrossRef Full Text | Google Scholar

11. Babaeva NY, Tereshonok DV, Naidis GV. Fluid and Hybrid Modeling of Nanosecond Surface Discharges: Effect of Polarity and Secondary Electrons Emission. Plasma Sourc Sci. Technol. (2016) 25(4):044008. doi:10.1088/0963-0252/25/4/044008

CrossRef Full Text | Google Scholar

12. Zhang J, Wang Y, Wang D. Modeling of Surface Dielectric Barrier Discharge with Multi-Electrode at Atmospheric Pressure. IEEE Trans Plasma Sci (2021) 49(10):3059–69. doi:10.1109/tps.2021.3108814

CrossRef Full Text | Google Scholar

13. Sokolova MV, Voevodin VV, Malakhov JI, Aleksandrov NL, Anokhin EM, Soloviev VR. Barrier Properties Influence on the Surface Dielectric Barrier Discharge Driven by Single Voltage Pulses of Different Duration. J Phys D: Appl Phys (2019) 52(32):324001. doi:10.1088/1361-6463/ab20ef

CrossRef Full Text | Google Scholar

14. Watanabe S, Hayashi N, Takeuchi H, Uchida Y, Dykes D, Touchard G, et al. Electrical Applications of Titanium-Based FGMs Manufactured by Progressive Lamination. In: Proceedings of the IEEE 6th International Conference on Conduction and Breakdown in Solid Dielectrics; 22-25 June 1998; Vasteras, Sweden (1998). p. 539–42.

Google Scholar

15. Zhang G-J, Su G-Q, Song B-P, Mu H-B. Pulsed Flashover across a Solid Dielectric in Vacuum. IEEE Trans Dielect Electr Insul (2018) 25(6):2321–39. doi:10.1109/tdei.2018.007133

CrossRef Full Text | Google Scholar

16. Golubovskii YB, Maiorov VA, Li P, Lindmayer M. Effect of the Barrier Material in a Townsend Barrier Discharge in Nitrogen at Atmospheric Pressure. J Phys D: Appl Phys (2006) 39(8):1574–83. doi:10.1088/0022-3727/39/8/016

CrossRef Full Text | Google Scholar

17. Li R, Tang Q, Yin S, Sato T. Investigation of Dielectric Barrier Discharge Dependence on Permittivity of Barrier Materials. Appl Phys Lett (2007) 90(13):131502. doi:10.1063/1.2716848

CrossRef Full Text | Google Scholar

18. Tschiersch R, Nemschokmichal S, Bogaczyk M, Meichsner J. Surface Charge Measurements on Different Dielectrics in Diffuse and Filamentary Barrier Discharges. J Phys D: Appl Phys (2017) 50(10):105207. doi:10.1088/1361-6463/aa5605

CrossRef Full Text | Google Scholar

19. Murakami T, Niemi K, Gans T, O' Connell D, Graham WG. Chemical Kinetics and Reactive Species in Atmospheric Pressure Helium–Oxygen Plasmas with Humid-Air Impurities. Plasma Sourc Sci Tech (2013) 22(1):015003. doi:10.1088/0963-0252/22/4/045010

CrossRef Full Text | Google Scholar

20. Morrow R, Lowke JJ. Streamer Propagation in Air. J Phys D: Appl Phys (1997) 30(4):614–27. doi:10.1088/0022-3727/30/4/017

CrossRef Full Text | Google Scholar

21. Woo Seok Kang WS, Jin Myung Park J, Yongho Kim Y, Sang Hee Hong S. Numerical Study on Influences of Barrier Arrangements on Dielectric Barrier Discharge Characteristics. IEEE Trans Plasma Sci (2003) 31(4):504–10. doi:10.1109/tps.2003.815469

CrossRef Full Text | Google Scholar

22. Tran TN, Golosnoy IO, Lewin PL, Georghiou GE. Numerical Modelling of Negative Discharges in Air with Experimental Validation. J Phys D: Appl Phys (2011) 44(1):015203. doi:10.1088/0022-3727/44/1/015203

CrossRef Full Text | Google Scholar

23. Cheng H, Fan J, Zhang Y, Liu D, Ostrikov K. Nanosecond Pulse Plasma Dry Reforming of Natural Gas. Catal Today (2020) 351:103–12. doi:10.1016/j.cattod.2018.11.026

CrossRef Full Text | Google Scholar

24. Winter LR, Ashford B, Hong JM, Murphy AB, Chen JGG. Identifying Surface Reaction Intermediates in Plasma Catalytic Ammonia Synthesis. ACS CATALYSIS (2021) 10:14763–74. doi:10.1021/acscatal.0c03166

CrossRef Full Text | Google Scholar