- 1Ocean Intelligence Technology Center, Shenzhen Institute of Guangdong Ocean University, Shenzhen, China
- 2College of Ocean Engineering, Guangdong Ocean University, Zhanjiang, China
- 3School of Engineering and Information Technology, University of New South Wales, Canberra, ACT, Australia
Efficient navigation in complex flows is of crucial importance for robotic applications. This work presents a numerical study of the point-to-point navigation of a fish-like swimmer in a time-varying vortical flow with a hybrid method of deep reinforcement learning (DRL) and immersed boundary–lattice Boltzmann method (IB-LBM). The vortical flow is generated by placing four stationary cylinders in a uniform flow. The swimmer is trained to discover effective navigation strategies that could help itself to reach a given destination point in the flow field, utilizing only the time-sequential information of position, orientation, velocity and angular velocity. After training, the fish can reach its destination from random positions and orientations, demonstrating the effectiveness and robustness of the method. A detailed analysis shows that the fish utilizes highly subtle tail flapping to control its swimming orientation and take advantage of the reduced streamwise flow area to reach it destination, and in the same time avoiding entering the high flow velocity area.
1 Introduction
To find the timely optimal path between two given points in a complex flow is known as Zermelo’s navigation problem [1]. This problem is a key issue for many robotic and engineering applications, including micro-swimmers [2,3], fish-like underwater vehicles [4], unmanned drones [5], and weather balloons [6]. In realistic environments, different structures interact with disturbances like wind, waves and currents, generating abundant vortices that could significantly effect the operation of these robotics [7], making the predefined control algorithms ineffective. In this work, we tackle the Zermelo’s problem for the point-to-point navigation of a fish-like swimmer in a vortical flow environment. Typical application scenarios include oceanic supervision [8], fishery conservation and intervention on offshore structures [9].
Naive control strategies are usually ineffective or inefficient in vortical environments [10], since the vortices could easily deviate the vehicles away from their desired path [11]. Numerous methods have been trying to design a customized optimal path for a given environment, ranging from the classical optimal control theory [12] to modern optimization approaches [13,14]. An important feature of these methods is that they require the knowledge of the dynamics of the background flow [15]. However, in real world applications, it is impractical to measure the entire flow environment in advance, as ocean and air currents are too variable to be fully measured [15]. In addition, the vehicles themselves can also significantly alter the surrounding flow fields, making them more unpredictable [15].
Reinforcement learning (RL) offers a promising alternative for solving Zermelo’s navigation problem in complex time-varying environments. Compared to the classical methods, RL possesses two main advantages. The first advantage is that it does not require any prior knowledge of the environment [16]. Instead, it automatically develops an understanding of the dynamics of the environment through trial and error. The other advantage is that the influence of the historical states can be easily taken into consideration [17]. Therefore, the correlation between action and its effect can be accurately captured even when there is a delay between them and there are measurable impacts from the historical actions. Colabrese et al. [3] first demonstrated that reinforcement learning is an efficient way to address Zermelo’s Problem. They adopted this method to train a point-like swimmer in an Arnold-Beltrami-Childress (ABC) flow to navigate vertically as quickly as possible. The swimmer was assumed to swim with constant speed and its direction was decided by the combined effect of a shear-induced viscous torque and a torque applied by the swimmer to orient itself to a desired direction. And a torque on the swimmer was designed by measuring its instantaneous swimming direction and the local flow vorticity. The authors found that smart swimmer can take advantage of upwelling flows to accelerate upward navigation and avoid being trapped in the vortices. This work motivated a series of studies, investigating the point-to-point navigation in different flows, as well as different actions [7,10,15,18–26].
The above studies demonstrated the potential of reinforcement learning in solving the navigation problems in complex flows. However, several simplifications are used for a better comparison with the traditional control methods. Firstly, most of these studies adopted simplified flow models to avoid the actual complexity and unpredictability of a time-varying fluid flow. Secondly, idealized model of the swimmer and their actions are utilized. In most of studies, the swimmers are considered to be an infinitely small point, which has negligible influence on the background flow. Moreover, the propellers of those swimmers are not modeled. Instead, it is assumed that the swimmers have full control of their own velocities. Those assumptions neglect the complex interaction between the swimmers and the environmental flows, such as time delays between sensing, actions and rewards. In this work, we investigate the point-to-point navigation of a fish-like swimmer in a vortical flow with a hybrid method of deep reinforcement learning (DRL) and immersed boundary–lattice Boltzmann method (IB-LBM). Compared with previous works, the present work utilizes a full model of both the flow and the swimmer. Specifically, the vortical flow is numerically generated with IB-LBM by putting four cylinders in a uniform flow, and the fish-like swimmer propels itself by periodically undulating its fish-like body to push the surrounding flow afterwards. This setup retains the complex nonlinear interaction between the swimmer and the flow.
The rest of the paper is organized as follows. Numerical methods are simply introduced in Section 2. The results of the simulation are discussed in Section 3. The conclusions are provided in Section 4.
2 Methodology
The methodology used here is almost the same as that in our previous work [27]. Here briefly describe it for complicity. More details of the method and its validations can be found in our previous work.
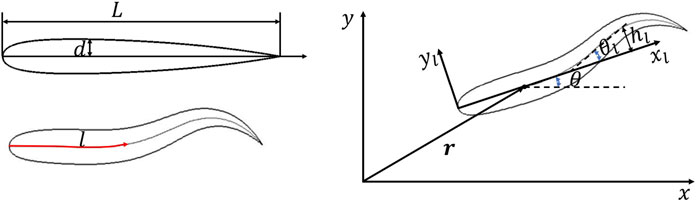
2.1 Kinematic Model of the Fish
The half thickness of the body is mathematically approximated by
where l is the arc length along the mid-line of the body, and L is the body length which is a constant during the swimming [28].
The motion of the fish body is composed of the translation of the mass center, the body rotation around the mass center and the body undulation in the local coordinate system (Figure 1). The translational and rotational motion of the fish are determined by the FSI in the global coordinate system according to the Newton’s laws of motion. The FSI equations are solved by an explicit FSI coupling method as in Ref. [27,30]. The undulatory motion is controlled by the fish itself, which can be taken as the superposition of different waves propagating from head to tail. A polynomial-based waveform is adopted for each wave and the kinematics of the newest generated waves can be changed every half cycle. In the nth half cycle, the mid-line lateral displacement is determined by
where θl is the deflection angle of the mid-line with respect to axis xl as shown in Figure 1, λn is the wavelength, Tn is the period, t is the time, t0n = 0 for n = 1 and
where c0−5 can be determined by
2.2 Immersed Boundary–Lattice Boltzmann Method
The lattice Boltzmann method (LBM) is used to simulate the fluid dynamics [31,32]. Instead of solving the Navier-Stokes equations, the LBM solves the discrete lattice Boltzmann equation which governs the kinematics of the mesoscopic particles,
where f is the particle density distribution function, r = (x, y) is the space coordinate, ci is the discrete lattice velocity, Δt is time step, Ωi is the collision operator, and Gi is the source term representing the body force. A detailed description of this equation can be found in Ref. [33]. f in the whole flow field can be acquired from a well-defined boundary condition, such as the no-slip velocity condition on the boundary of the swimmer model. Once f is known, the macroscopic physical quantity such as fluid density, pressure and velocity can be computed from
where cs is the lattice speed of sound in the fluid, and g is the body force. Then the force and torque on the swimmer model can be computed from those macroscopic physical quantity.
In addition, a diffusion immersed boundary method (IBM) [32,34–36] is utilized to handle the boundary condition at the fluid-structure interface. In this method, the influence of the boundary on the fluid is represented by a distribution of body force on the background Eulerian mesh nodes. Compared to body conformal methods [37–39], the grid generation in IBM is much easier for complicated shapes [32,40,41]. And a multi-block geometry-adaptive Cartesian grid is coupled with the IB–LBM to accelerate the computation. A detailed description of this numerical scheme and its validation can be found in Refs. [27,31,34,42–44]. The current method is first-order in accuracy.
2.3 Deep Reinforcement Learning
DRL is a machine learning method combining reinforcement learning with an artificial neural network. DRL has gained extensive attention due to its success in complex real-world problems [45]. In this study, a specific DRL method called deep recurrent Q-network (DRQN) [46] is adopted, in which a long-short-term-memory recurrent neural network (LSTM-RNN) is used to process time-sequential data. The method includes two basic elements: a learning agent and its environment [3]. The agent interacts with the environment in a trial-and-error fashion to collect observation of the environment state (denoted by s), control actions (denoted by a), and rewards (denoted by rd) [47]. The goal of the agent is learning to find a control policy (denoted by π(s, a)) that enables it to collect highest rewards in a single try.
The interaction procedure between the environment (IB-LBM) and the agent (DRL) is shown in Figure 2. The interaction is divided into a sequence of discrete steps n = 0, 1, 2, 3, …. At steps n, the agents detect state sn, and select action an, based on policy
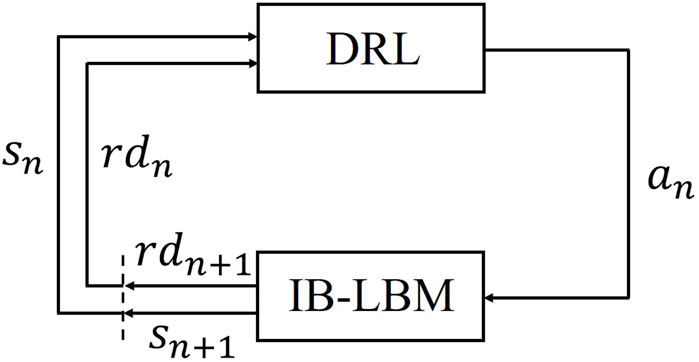
FIGURE 2. The interaction procedure between IB-LBM and DRL (Adapted from Ref. [29]).
3 Results and Discussion
3.1 The Hydrodynamics of a Uniform Flow Over Four Stationary Cylinders
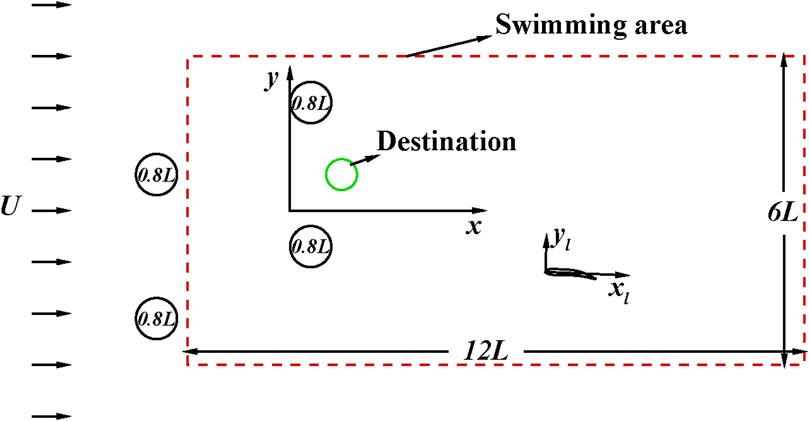
A uniform flow over four stationary cylinders is conducted to produce a large-scale vortical flow environment as an initial flow for the fish to swim in. The diameter of the cylinders is D = 0.8L, which is slightly smaller than the body length of the fish. The centers of the cylinders are respectively placed at (−3L, 0.7L), (−3L, − 2.1L), (0L, − 0.7L) and (0L, 2.1L), as shown in Figure 3. Such arrangement is used in order to generate a complex vortical flow via the interaction of the vortices shedding from the leading two cylinder with the trailing cylinders.
The simulation is performed for a Reynolds number of Re = ρUL/μ = 400 or Recylinder = ρUD/μ = 320, where ρ is the density of the fluid, U is the incoming fluid velocity, and μ is the dynamic viscosity of the fluid. This Reynold number is used because it is able to generate sufficiently complex flows with reasonably low computational costs. The computational domain of 50L × 50L is divided into seven blocks with 98,373 grids. The minimum nondimensional grid spacing is Δx/L = Δy/L = 0.01 near the inner boundaries and the nondimensional time step size is ΔtU/L = 0.0004. Validation has been performed to ensure the numerical results are independent of mesh size, domain size and time step size.
Figure 4 shows the vorticity contour and flow velocity distribution behind the cylinders at four different instants (the animation of the movement of the vortices can be found in the Supplementary Materials). It can be seen that abundant vortices are generated in the wake flow of the cylinders, and the strength and moving velocity of the vortices are diversified. Those vortices interact with each other and the trailing cylinders, forming a highly dynamic and unpredictable flow field. Two basic types of vortices are identified: clockwise vortices (blue) and counter-clockwise vortices (red). The clockwise vortices accelerate the flow above it and decelerate the flow below it, and induce upward flow in its left side and downward flow in its right side. On the contrary, the counter-clockwise vortices accelerate the flow below it and decelerate the flow above it, and induce upward flow in its right side and downward flow in its left side. As a result, the flow velocity in the field is vastly altered. In next section, tL/U = 50 is used as an initial flow field for the swimming training.
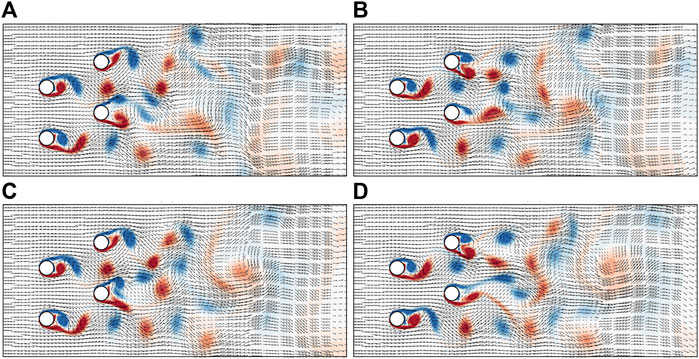
FIGURE 4. Vorticity contour and flow velocity distribution behind the cylinders at four different instants: (A) tU/L = 22.7, (B) tU/L = 24.7, (C) tU/L = 26.7, and (D) tU/L = 28.7.
3.2 Learning to Navigate in the Vortical Flow
In this section, a fish is trained to navigate in a flow field as in the last section. The cases are conducted with four computational cores on a workstation with Intel Xeon CPU E5-2678 and OpenMP. The computational domain of 50L × 50L is divided into seven blocks with about 120,000 grids. The simulation requires about 21.0 s of CPU time per nondimensional time unit t/T = 1.0. For simplicity, the fish is restricted to swim in a rectangular area of 12L × 6L, as shown in Figure 3. The goal of the fish is to swim towards a given destination at (1L, 0.7L) from different initial positions. The goal is reflected by defining a reward as
where xtip and ytip are the space coordinates of the head tip of the fish. In addition, if the fish swims out of the boundary of the confined area, it is given a strong penalty of rd = −100.
The swimmer propels itself by generating a travelling wave propagating from head to tail, as defined by Eq. 2. In order to achieve high maneuverability, the swimmer can change the wave amplitude every half swimming cycle. Each selected set of parameters is considered as an action. In this case, the period is fixed at TU/L = 0.4; the amplitude action base is defined as θlmax = 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70° and 80°; and the wavelength is fixed at λ = L. This parameter set forms an action base of nine components.
A comprehensive representation of the environment state is very important for the accurate motion control. Specifically, the historical evolution of the sensory information should be considered throughly. Zhu et al. [27] conducted tests with different environment information and found that only considering the actions and body kinematics in the last four periods could provide environmental information with enough accuracy for motion control. Therefore, a similar way to consider the environment information is adopted here, in which the state is defined by a tuple.
where x, y and θ are respectively the space coordinates and orientation angle of the fish, and
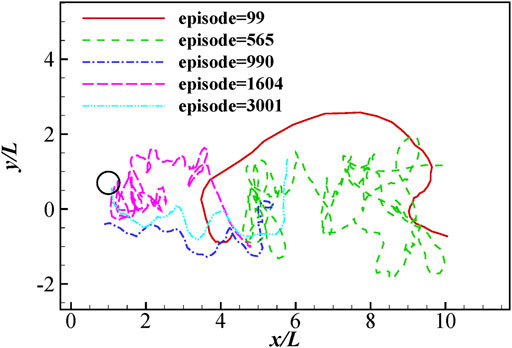
The learning process is divided into a series of episodes. In each episode, the initial x coordinate x0 is randomly chosen between 3 and 7L, the initial y coordinate y0 is randomly chosen between −1.5 and 1.5L, and the initial orientation angle θ0 randomly varies between −30° and 30°. The subsequent positions and orientations of the swimmer are then determined by the FSI with the actions. Once the swimmer exceeds the confined area or reaches a small circle area near the destination with radius 0.3L, the episode ends and another starts. The fish is trained for 3,000 episodes and 126,893 periods. Figure 5 shows the traces of the head tip during different learning stages. In episode 99, the fish is not able to maintain in the vortical flow area for a prolonged time and swims out of the confined area quickly. Nevertheless, after a trial-and-error exploration period (episode 565), it learns to hold position in the area for longer time instead of being washed away. At last, it has learned how to directly swim towards its destination. After learning for 990 episodes, it successfully finds a path leading it to close area of the destination, but ending up with a collision with one of the cylinders. Then it struggles and learns to reach the destination without hitting the cylinders (episode 1,604). Finally, after learning for about 3,000 episodes, it could accurately reach the destination.
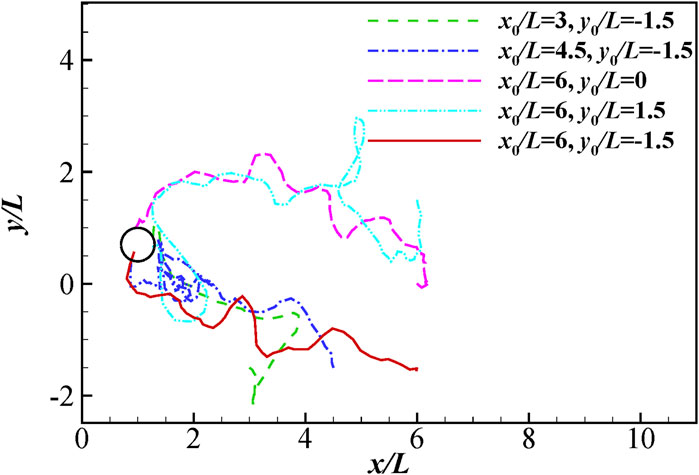
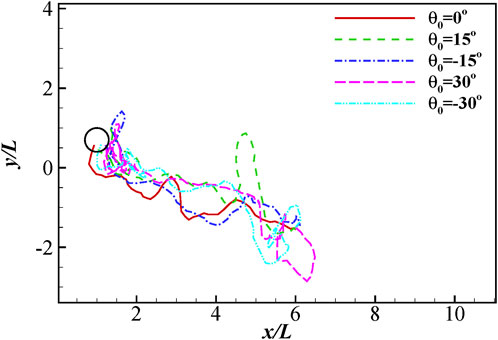
In order to test the robustness of the control strategy, we investigated 100 different cases with different initial positions and orientation angles using the same control strategy after learning for 3,000 episodes. In 9 of the 100 tests, the fish loses its balance and eventually swam out of the confined area. In those cases, the relative angle of the fish with respective to the incoming flow grows so large that the fish could not restore its orientation in time. In 15 of the 100 tests, the fish ends up with a collision with the cylinders. In those cases, the fish could not resist the strong suction force behind the cylinders. In the other 76 cases, the fish successfully reach the destination. Figure 6 presents the traces when the fish swims to its destination with different initial positions. 5 cases are studied, in which the initial orientation angle is fixed at 0° while the initial position of the head tip
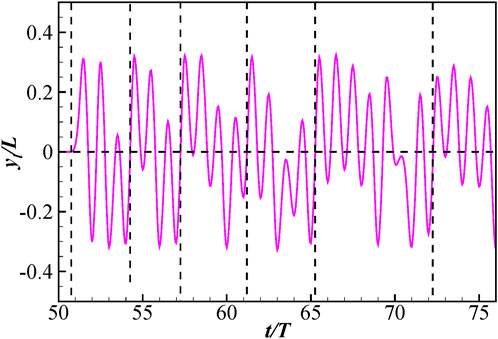
In order to understand the hydrodynamics underlying the behaviors, we investigate a typical case in details, in which the initial orientation angle is 0° and the initial position is (6L, − 1.5L). The time change of the lateral tail tip movement is shown in Figure 8. The vorticity contour and flow velocity distribution in several typical instants are shown in Figure 9 (the animation of the fish swimming can be found in the Supplementary Materials). It is noted that the fish is forced to hold still in the flow field for 50 periods until the vortex street is fully developed. Then it is allowed to swim freely in the flow. Its goal is to swim upstream and reach its destination (green circle in Figure 9). Figure 9A shows the body gesture of the fish and the ambient flow field at instant t/T = 50. It can be seen that an area of reduced streamwise flow (denoted as RSF in the figure) is formed in the right side of the fish. It will be easier if the fish can take advantage of this area to move upstream. However, the surrounding flow is trying to push the fish leftwards to the high flow velocity area. Without active control, the fish will be washed downstream quickly. Therefore, the fish adopts a large-amplitude right flapping to turn right towards the reduced flow area (Figure 9B). At instants t/T = 53 and t/T = 54 (Figures 9C,D), the fish is oriented at the reduced streamwise flow area. Meanwhile, the clockwise flow induced by Vortex 1 (denoted by V1 in the figure) has a tendency to turn it right (rotating clockwise) and draw it backwards to the downstream area. And large-amplitude right flapping will accelerate this process. Therefore, the fish adopts a large-amplitude left flapping to resist this tendency and restore its swimming orientation. In the following several periods, a similar strategy is adopted by the swimmer to take advantage of the reduced streamwise flow area and keep balance (see details in the Supplementary Video S6). From instant t/T = 61.5 to t/T = 65.0 (Figures 9E–H), a strong counter-clockwise vortex (V2) is at the right side of the fish, inducing strong rightward flow and reduce streamwise flow in the right side of the fish. Therefore, the fish adopts two large-amplitude right flapping motions to swim rightwards and three compensate left flapping motions to hold stability. Those motions are of crucial importance for the fish to make the most use of the flow to swim upstream while keeping perfect balance. From instant t/T = 72.5 to t/T = 75.9 (Figures 9I–L), the fish is very close to the destination and located in a strong streamwise flow that could wash it away from the destination. Therefore, the fish adopts a sequence of high-amplitude right flapping motions to fast reach the destination. It is noted that the fish chooses to approach the destination from the counterflow direction instead of the downstream direction, since the high flow velocity makes it extremely hard to swim upstream.
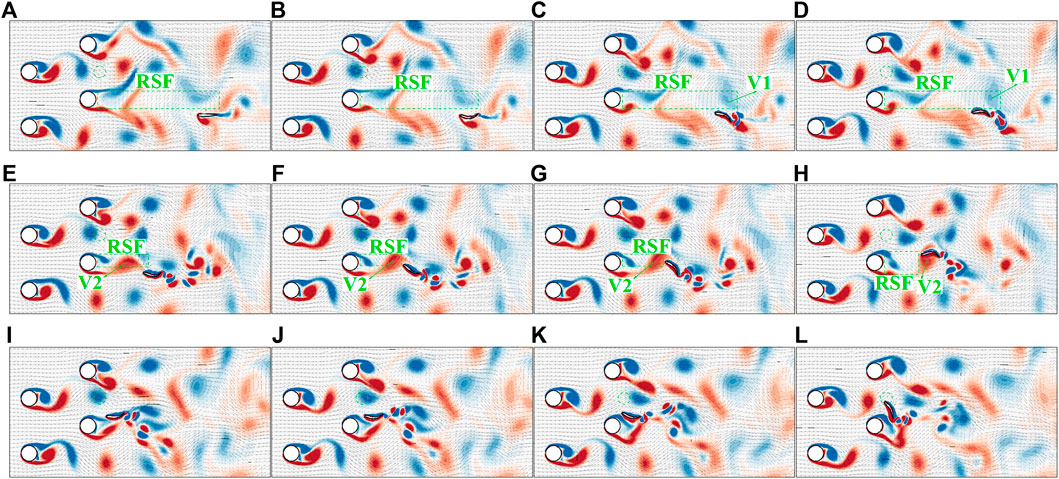
FIGURE 9. Vorticity contour and flow velocity distribution at 12 different instants: (A) t/T = 50, (B) t/T = 51.5, (C) t/T = 53, (D) t/T = 54, (E) t/T = 61.5, (F) t/T = 62.5, (G) t/T = 63, (H) t/T = 65, (I) t/T = 72.5, (J) t/T = 73.5, (K) t/T = 74.5 and (L) t/T = 75.9.
4 Conclusion
The point-to-point navigation of a fish-like swimmer in a vortical flow is numerically studied with a hybrid method of deep reinforcement learning and immersed boundary–lattice Boltzmann method. The goal of the swimmer is to swim upstream through the vortical area to its destination. The vortical area is generated by placing four stationary cylinders in a uniform flow. The function of the vortices is twofold. It not only induces reduced streamwise flow to make swimming upstream easier, but also induces strong streamwise and lateral flow to deviate the swimmer from its desired path. The swimmer utilizes only the time-sequential information of position, orientation, velocity and angular velocity to learn to navigate to its destination. By considering the time-sequential information, the swimmer learns to reach its destination from different initial positions and orientations, demonstrating the effectiveness and robustness of the method. A detailed analysis shows that the fish utilizes highly subtle tail flapping motions to control its swimming orientation and take advantage of the reduced streamwise flow area to reach it destination, and in the same time avoiding entering the high flow velocity area.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
YZ has made contributions to methodology, software development, data analysis and interpolation, and writing of the work. F-BT has made contributions to the conception of the work, methodology, and revising of the work. J-HP has made contribution to the conception and revising of the work.
Funding
This work was partially supported by the Australian Research Council (project number DE160101098).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
YZ acknowledges Shenzhen Institute of Guangdong Ocean University and Dalian Maritime University during the pursuit this study.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.870273/full#supplementary-material
References
1. Zermelo E. Über das Navigationsproblem bei ruhender oder veränderlicher Windverteilung. Z Angew Math Mech (1931) 11:114–24. doi:10.1002/zamm.19310110205
2. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active Particles in Complex and Crowded Environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/revmodphys.88.045006
3. Colabrese S, Gustavsson K, Celani A, Biferale L. Flow Navigation by Smart Microswimmers via Reinforcement Learning. Phys Rev Lett (2017) 118:158004. doi:10.1103/physrevlett.118.158004
4. Yu J, Wang M, Dong H, Zhang Y, Wu Z. Motion Control and Motion Coordination of Bionic Robotic Fish: A Review. J Bionic Eng (2018) 15:579–98. doi:10.1007/s42235-018-0048-2
5. Guerrero JA, Bestaoui Y. UAV Path Planning for Structure Inspection in Windy Environments. J Intell Robot Syst (2013) 69:297–311. doi:10.1007/s10846-012-9778-2
6. Bellemare MG, Candido S, Castro PS, Gong J, Machado MC, Moitra S, et al. Autonomous Navigation of Stratospheric Balloons Using Reinforcement Learning. Nature (2020) 588:77–82. doi:10.1038/s41586-020-2939-8
7. Buzzicotti M, Biferale L, Bonaccorso F, Di Leoni PC, Gustavsson K. Optimal Control of point-to-point Navigation in Turbulent Time Dependent Flows Using Reinforcement Learning. In: International Conference of the Italian Association for Artificial Intelligence. Berlin, Germany: Springer (2020). p. 223–34.
8. Zhang W, Inanc T, Ober-Blobaum S, Marsden JE. Optimal Trajectory Generation for a Glider in Time-Varying 2D Ocean Flows B-Spline Model. In: 2008 IEEE International Conference on Robotics and Automation. Pasadena, CA, USA: IEEE (2008). p. 1083–8. doi:10.1109/robot.2008.4543348
9. Insaurralde CC, Cartwright JJ, Petillot YR. Cognitive Control Architecture for Autonomous marine Vehicles. In: 2012 IEEE International Systems Conference SysCon. Vancouver, BC, Canada: IEEE (2012). p. 1–8. doi:10.1109/syscon.2012.6189542
10. Colabrese S, Gustavsson K, Celani A, Biferale L. Smart Inertial Particles. Phys Rev Fluids (2018) 3:084301. doi:10.1103/physrevfluids.3.084301
11. Salumäe T, Kruusmaa M. Flow-relative Control of an Underwater Robot. Proc R Soc A: Math Phys Eng Sci (2013) 469:20120671.
12. Techy L. Optimal Navigation in Planar Time-Varying Flow: Zermelo's Problem Revisited. Intel Serv Robotics (2011) 4:271–83. doi:10.1007/s11370-011-0092-9
13. Kularatne D, Bhattacharya S, Hsieh MA. Going with the Flow: a Graph Based Approach to Optimal Path Planning in General Flows. Auton Robot (2018) 42:1369–87. doi:10.1007/s10514-018-9741-6
14. Panda M, Das B, Subudhi B, Pati BB. A Comprehensive Review of Path Planning Algorithms for Autonomous Underwater Vehicles. Int J Autom Comput (2020) 17:321–52. doi:10.1007/s11633-019-1204-9
15. Gunnarson P, Mandralis I, Novati G, Koumoutsakos P, Dabiri JO. Learning Efficient Navigation in Vortical Flow fields. arXiv preprint arXiv:2102.10536 (2021). doi:10.1038/s41467-021-27015-y
16. Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Cambridge, MA, USA: MIT press (2018).
17. Verma S, Novati G, Koumoutsakos P. Efficient Collective Swimming by Harnessing Vortices through Deep Reinforcement Learning. Proc Natl Acad Sci U.S.A (2018) 115:5849–54. doi:10.1073/pnas.1800923115
18. Gustavsson K, Biferale L, Celani A, Colabrese S. Finding Efficient Swimming Strategies in a Three-Dimensional Chaotic Flow by Reinforcement Learning. Eur Phys J E Soft Matter (2017) 40:110–6. doi:10.1140/epje/i2017-11602-9
19. Biferale L, Bonaccorso F, Buzzicotti M, Clark Di Leoni P, Gustavsson K. Zermelo's Problem: Optimal point-to-point Navigation in 2D Turbulent Flows Using Reinforcement Learning. Chaos (2019) 29:103138. doi:10.1063/1.5120370
20. Alageshan JK, Verma AK, Bec J, Pandit R. Machine Learning Strategies for Path-Planning Microswimmers in Turbulent Flows. Phys Rev E (2020) 101:043110. doi:10.1103/PhysRevE.101.043110
21. Qiu J, Huang W, Xu C, Zhao L. Swimming Strategy of Settling Elongated Micro-swimmers by Reinforcement Learning. SCIENCE CHINA Phys Mech Astron (2020) 63:1–9. doi:10.1007/s11433-019-1502-2
22. Daddi-Moussa-Ider A, Löwen H, Liebchen B. Hydrodynamics Can Determine the Optimal Route for Microswimmer Navigation. Commun Phys (2021) 4:1–11. doi:10.1038/s42005-021-00522-6
23. Qiu J, Mousavi N, Gustavsson K, Xu C, Mehlig B, Zhao L. Navigation of Micro-swimmers in Steady Flow: the Importance of Symmetries. J Fluid Mech (2022) 932. doi:10.1017/jfm.2021.978
24. Yan L, Chang X, Tian R, Wang N, Zhang L, Liu W. A Numerical Simulation Method for Bionic Fish Self-Propelled Swimming under Control Based on Deep Reinforcement Learning. Proc Inst Mech Eng C: J Mech Eng Sci (2020) 234:3397–415. doi:10.1177/0954406220915216
25. Yan L, Chang X-h., Wang N-h., Tian R-y., Zhang L-p., Liu W. Computational Analysis of Fluid-Structure Interaction in Case of Fish Swimming in the Vortex Street. J Hydrodyn (2021) 33:747–62. doi:10.1007/s42241-021-0070-4
26. Yan L, Chang X, Wang N, Tian R, Zhang L, Liu W. Learning How to Avoid Obstacles: A Numerical Investigation for Maneuvering of Self‐propelled Fish Based on Deep Reinforcement Learning. Int J Numer Meth Fluids (2021) 93:3073–91. doi:10.1002/fld.5025
27. Zhu Y, Tian F-B, Young J, Liao JC, Lai JC. A Numerical Study of Fish Adaption Behaviors in Complex Environments with a Deep Reinforcement Learning and Immersed Boundary–Lattice Boltzmann Method. Scientific Rep (2021) 11:1–20. doi:10.1038/s41598-021-81124-8
28. Tian F-B. A Numerical Study of Linear and Nonlinear Kinematic Models in Fish Swimming with the DSD/SST Method. Comput Mech (2015) 55:469–77. doi:10.1007/s00466-014-1116-z
29. Zhu Y, Pang J-H, Tian F-B. Stable Schooling Formations Emerge from the Combined Effect of the Active Control and Passive Self-Organization. Fluids (2022) 7:41. doi:10.3390/fluids7010041
30. Zhou CH, Shu C. Simulation of Self-Propelled Anguilliform Swimming by Local Domain-free Discretization Method. Int J Numer Meth Fluids (2012) 69:1891–906. doi:10.1002/fld.2670
31. Xu L, Tian F-B, Young J, Lai JCS. A Novel Geometry-Adaptive Cartesian Grid Based Immersed Boundary-Lattice Boltzmann Method for Fluid-Structure Interactions at Moderate and High Reynolds Numbers. J Comput Phys (2018) 375:22–56. doi:10.1016/j.jcp.2018.08.024
32. Huang W-X, Tian F-B. Recent Trends and Progress in the Immersed Boundary Method. Proc Inst Mech Eng Part C: J Mech Eng Sci (2019) 233:7617–36. doi:10.1177/0954406219842606
33. Krüger T, Kusumaatmaja H, Kuzmin A, Shardt O, Silva G, Viggen EM. The Lattice Boltzmann Method. Berlin, Germany: Springer (2017).
34. Ma J, Wang Z, Young J, Lai JCS, Sui Y, Tian F-B. An Immersed Boundary-Lattice Boltzmann Method for Fluid-Structure Interaction Problems Involving Viscoelastic Fluids and Complex Geometries. J Comput Phys (2020) 415:109487. doi:10.1016/j.jcp.2020.109487
35. Xu Y-Q, Tang X-Y, Tian F-B, Peng Y-H, Xu Y, Zeng Y-J. IB–LBM Simulation of the Haemocyte Dynamics in a Stenotic Capillary. Comput Methods Biomech Biomed Eng (2014) 17:978–85.
36. Huang Q, Tian F-B, Young J, Lai JC. Transition to Chaos in a Two-Sided Collapsible Channel Flow. J Fluid Mech (2021) 926. doi:10.1017/jfm.2021.710
37. Tian F-B, Bharti RP, Xu Y-Q. Deforming-Spatial-Domain/Stabilized Space-Time (DSD/SST) Method in Computation of Non-newtonian Fluid Flow and Heat Transfer with Moving Boundaries. Comput Mech (2014) 53:257–71. doi:10.1007/s00466-013-0905-0
38. Tian F-B. FSI Modeling with the DSD/SST Method for the Fluid and Finite Difference Method for the Structure. Comput Mech (2014) 54:581–9. doi:10.1007/s00466-014-1007-3
39. Tian F-B, Wang Y, Young J, Lai JCS. An FSI Solution Technique Based on the DSD/SST Method and its Applications. Math Models Methods Appl Sci (2015) 25:2257–85. doi:10.1142/s0218202515400084
40. Mittal R, Iaccarino G. Immersed Boundary Methods. Annu Rev Fluid Mech (2005) 37:239–61. doi:10.1146/annurev.fluid.37.061903.175743
41. Sotiropoulos F, Yang X. Immersed Boundary Methods for Simulating Fluid-Structure Interaction. Prog Aerospace Sci (2014) 65:1–21. doi:10.1016/j.paerosci.2013.09.003
42. Xu L, Wang L, Tian F-B, Young J, Lai JCS. A Geometry-Adaptive Immersed Boundary-Lattice Boltzmann Method for Modelling Fluid-Structure Interaction Problems. In: IUTAM Symposium on Recent Advances in Moving Boundary Problems in Mechanics. Berlin, Germany: Springer (2019). p. 161–71. doi:10.1007/978-3-030-13720-5_14
43. Young J, Tian F-B, Liu Z, Lai JC, Nadim N, Lucey AD. Analysis of Unsteady Flow Effects on the Betz Limit for Flapping Foil Power Generation. J Fluid Mech (2020) 902. doi:10.1017/jfm.2020.612
44. Tian F-B, Luo H, Zhu L, Liao JC, Lu X-Y. An Efficient Immersed Boundary-Lattice Boltzmann Method for the Hydrodynamic Interaction of Elastic Filaments. J Comput Phys (2011) 230:7266–83. doi:10.1016/j.jcp.2011.05.028
45. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level Control through Deep Reinforcement Learning. Nature (2015) 518:529–33. doi:10.1038/nature14236
46. Hausknecht M, Stone P. Deep Recurrent Q-Learning for Partially Observable MDPs. In: 2015 AAAI Fall Symposium Series (2015).
47. Jiao Y, Ling F, Heydari S, Kanso E, Heess N, Merel J. Learning to Swim in Potential Flow. Phys Rev Fluids (2021) 6:050505. doi:10.1103/physrevfluids.6.050505
Keywords: vortical flow, immersed boundary-lattice Boltzmann method, deep reinforcement learning, point-to-point navigation, robotic fish, target-directed swimming, fish swimming
Citation: Zhu Y, Pang J-H and Tian F-B (2022) Point-to-Point Navigation of a Fish-Like Swimmer in a Vortical Flow With Deep Reinforcement Learning. Front. Phys. 10:870273. doi: 10.3389/fphy.2022.870273
Received: 06 February 2022; Accepted: 07 March 2022;
Published: 09 May 2022.
Edited by:
Haibo Huang, University of Science and Technology of China, ChinaReviewed by:
Chengwen Zhong, Northwestern Polytechnical University, ChinaCharles Reichhardt, Los Alamos National Laboratory (DOE), United States
Copyright © 2022 Zhu, Pang and Tian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian-Hua Pang, cGFuZ2ppYW5odWFAZ2RvdS5lZHUuY24=; Fang-Bao Tian, Zi50aWFuQGFkZmEuZWR1LmF1
 Yi Zhu
Yi Zhu Jian-Hua Pang
Jian-Hua Pang Fang-Bao Tian
Fang-Bao Tian