- 1Departamento de Fsica, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Ciudad Universitaria, Buenos Aires, Argentina
- 2CONICET-Universidad de Buenos Aires, Instituto de Fisica de Buenos Aires (IFIBA), Ciudad Universitaria, Buenos Aires, Argentina
We propose a method for generation of entangled photonic states in high dimensions, the so-called qudits, by exploiting quantum correlations of Orbital Angular Momentum (OAM) entangled photons, produced via Spontaneous Parametric Down Conversion. Diffraction masks containing N angular slits placed in the path of twin photons define a qudit space of dimension N2, spanned by the alternative pathways of OAM-entangled photons. We quantify the high-dimensional entanglement of path-entangled photons by the Concurrence, using an analytic expression valid for pure states. We report numerical results for the Concurrence as a function of the angular aperture size for the case of high-dimensional OAM entanglement and for the case of high-dimensional path entanglement, produced by N × M angular slits. Our results provide additional means for preparation and characterization of entangled quantum states in high-dimensions, a fundamental resource for quantum simulation and quantum information protocols.
1 Introduction
In recent years, Spontaneous Parametric Down Conversion (SPDC) has become a fundamental process for generation of entangled photonic states, allowing for preparation of quantum states entangled in several degrees of freedom, such as position and momentum, time and energy, polarization or angular position and Orbital Angular Momentum (OAM), thus providing for a key resource in fundamentals of quantum physics and quantum information. Quantum correlations of SPDC photons in a given domain give rise to interference phenomena resulting from two-photon coherence [1–8]. These phenomena are routinely used in fundamental tests of quantum physics [9–11] and are a key ingredient for the implementation of quantum communication and information protocols, including quantum teleportation and quantum cryptography [12–14]. Fourier relations link angular position and OAM of photons, leading to angular interference in the OAM-mode distribution, as photons diffract through angular apertures, resulting in two-photon quantum interference [15–22].
In this article, we quantify entanglement of such high-dimensional angular qudits, in a scheme in which OAM-entangled photons produced by SPDC are transmitted through multiple angular apertures, in the form of N × M angular slits in the path of signal and idler photons, which results in path entanglement in a space of dimension D = N × M. Using this scheme, we demonstrate high-dimensional entanglement based on angular-position correlations of down-converted photons. Our results suggest that violations of Bell’s inequalities in even higher dimensions could in principle be achieved. Moreover, in contrast to previous approaches [16, 17] relying on the Fourier limit only, our results shine light on the quantum interpretation, providing new insights. Adding to the novelty of our work, we consider the case of asymmetric angular slits N and M for signal and idler, which can lead to high-dimensional angular interference phenomena. We note that linear qudits have previously been proposed [24]. Here we propose and characterize angular qudits, which due to their shape can enable generation of entanglement in a larger Hilbert space than linear qudits. In order to quantify entanglement, we derive an analytic expression for calculation of the Concurrence, valid for pure states. The results reported here extend the notion of angular qudits to an arbitrary number of angular slits N × M, which not only demonstrates two-photon coherence effects in the angular domain but also provide additional means for preparation and characterization of entangled quantum states in a high-dimensional Hilbert space. This is a fundamental resource for quantum communication [23–40] and quantum information protocols [12, 16, 19, 41–57].
The article is organized as follows: In Section 2 we introduce the concept of high-dimensional path-entanglement of angular qudits [56]. Next, in Section 3 we present an overview of angular diffraction in the position basis [57] and we derive an analytic expression for the Concurrence of high-dimensional qudits, valid for pure states. In Section 4 we present numerical results in two specific scenarios, (IVA) high-dimensional OAM entanglement and (IVB) high-dimensional path entanglement. Finally, in Section 5 we outline the conclusions.
2 High-Dimensional Angular Qudits
Consider the experimental scheme depicted in Figure 1. A Gaussian pump beam produces signal (s) and idler (i) entangled twin photons by the non-linear process of SPDC. In the simplest scenario of a Gaussian pump beam with zero OAM (l = 0), phase matching conditions determine the two-photon down-converted state |ψ0⟩, which can be expressed in the following form [56]:
where s and i label signal and idler photons, |l⟩ refers to the OAM eigen-mode of order l, and D = 2ν + 1 is the dimension of the OAM Hilbert space under consideration. Such OAM modes are characterized by an helical phase front typically expressed as eilϕ. For |ψ0⟩ to represent a quantum state, the normalization condition imposes
where n = 0, … , N − 1 is the angular slit label, α represents the aperture of the angular slits, and β represents the separation between consecutive angular slits. For the simplest case N = 2 slits, we recover the results reported in [49]. Considering N slits in both arms, there are in principle N2 alternative pathways by which the down-converted photons can pass through the apertures and get detected in coincidence at single-photon avalanche detectors Ds and Di. The N2 alternative paths, here labelled by the sub-index q = 1, … , N2, can be expressed as the outer product of the sub-spaces corresponding to each photon (s, i) passing through the slits n = 0, … , N − 1, respectively, in the following form [56]:
Spatial quantum correlations between the twin photons can be controlled so that only paths of the form |i, n⟩|s, n⟩ will have a significant contribution. We note there is a one to one mapping between the path-way basis and the OAM-mode basis. For a given path n, the two-photon state can be written in the OAM-mode basis as [49]:
In this notation, the single-photon quantum state with OAM of order l diffracted by the k-th slit, with OAM momentum l, can be expressed as [56]:
where
where
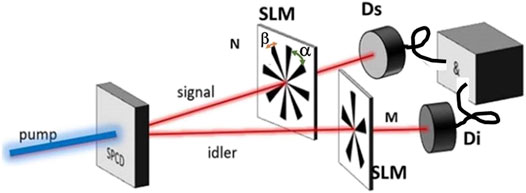
FIGURE 1. Proposed experimental scheme for generation of high-dimensional OAM-entangled photon pairs via SPDC. Spatial Light Modulators (SLMs) containing (N, M) angular slits are placed in the path of signal and idler photons, generating high-dimensional angular qudits. Further details are in the text. The figure was modified from Ref. [56].
For the simple case of a single slit, we have j = k = 1, the mode overlap ⟨ψm|ψl⟩ can be expressed as:
3 High-Dimensional Spatial Mode Entanglement and Diffraction
In this Section we derive expressions for twin photons angular diffracted states in the position basis. As already anticipated in Section 2, we focus on D − dimensional (D = 2ν + 1) entangled biphoton pure states of the form [57].
where
are single photon states in the spatial modes defined by the orthonormal transverse functions ul(r), i.e.,
We are interested in how the entanglement of such states is modified by diffraction of the two photons on two independent opaque screens of different shapes and forms. Moreover, we focus on the case where both photons are detected after the diffracting screens. In this post-selection scenario, entanglement is only modified by the change of the spatial profile of the modes occupied by the photons due to diffraction on the screens. Under these assumptions, the quantum state of the diffracted photons can be written [57, 58].
with
where the modes ψl(r) are the images of the modes ul(r) that can be computed using standard diffraction theory [57], and
with
the mutual overlaps between pairs of diffracted modes [57]. We note that since the single photon states |ψl⟩ are fully determined by the modes they occupy, we also have that ⟨ψl|ψk⟩ = blk.
We now set to characterize the entanglement of such states developing a high-dimensional generalization of the method presented in [56, 57]. Following this path, we quantify the entanglement of the diffracted state using the Concurrence, that for pure states in arbitrary dimensions can be expressed as a function of the purity Tr [ρ2] of the reduced density matrix ρ = Tr2 [|ψ⟩⟨ψ|] [57].
The reduced density matrix can be computed using the expression (11) for the quantum state of single photons in the diffracted modes and the mutual overlap (13)
In a similar fashion, we can determine the purity of the reduced density matrix
which fully determines the Concurrence Eq. 14. From Eq. 16, we see that the entanglement of diffracted biphoton states is fully characterized by the entanglement of the input state (encoded in the coefficients cl), and by the diffraction induced overlaps of the states |ψl⟩ (quantified by the coefficients blk).
We note that the goal of the scheme presented in Figure 1 is to provide an alternative means for generation of entangled quantum states in high dimensions, using only two photons. It should be mentioned that the operations introduced by the SLMs are local and cannot increase the total amount of entanglement, which is given by the entanglement content present in the initial state generated by the SPDC process, as quantified by the Concurrence (Eq. 14). In particular, for a maximally entangled pure input state in D-dimensions, the Concurrence is given
4 Examples
In the following, we will apply the theoretical framework presented in Sections 2, 3 to two particular examples. In particular, in Section 4A, we will consider high-dimensional OAM-entangled biphotons diffracted on screens containing a single angular aperture, while in Section 4B we will consider initial biphotons entangled in few OAM modes impinging on screens containing multiple apertures.
A. High-Dimensional OAM Entanglement on Angular Apertures
We now specialize to the study of maximally entangled states, i.e., we set
where
Using Eq. 18, we can calculate the mutual overlaps (13) which results into
Combining Eqs 19, 20 into Eq. 14 we can compute the concurrence of the diffracted state, which is plotted in Figure 2.
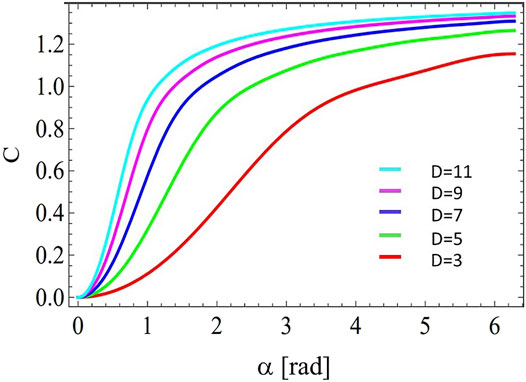
FIGURE 2. Concurrence vs. angular aperture size for different OAM subpsace dimension (D = 2ν + 1) as indicated in the label, considering a single angular slit for both signal and idler photons (M = N = 1). Details are in the text.
B. High-Dimensional Path-Entanglement on Angular Apertures
We now consider an alternative scenario for generation of high-dimensional entanglement relying on path-entangled modes generated by multiple angular apertures in the path of signal and idler photons (s, i). For simplicity, we consider twin photons initially prepared in a OAM qubit state of the form:
When masks with (N, M) angular slits for (s, i) photons are placed in each spatial mode (seen Figure 1), the biphoton state immediately after the apertures can be expressed as [36]:
where xs,i denote the position of signal and idler photons at the crystal plane (z). ϕ(xs, xi, z) indicates the biphoton amplitude at z, which can be regarded as a product of the pump transverse amplitude and phase matching function [36]. For simplicity, in what follows we consider the biphoton amplitude to be approximately constant. |ψk,k′⟩ describe the quantum state of signal and idler photons diffracted by angular apertures (k, k′), respectively.
In the notation introduced in Section 2, for an initial state of the form |l0⟩s| − l0⟩i, the quantum state of (s, i) photons diffracted by angular apertures (k, k′), respectively, can be expressed as:
The biphoton path-entangled state diffracted by N × M angular slits results in:
A compact expression for the biphoton diffracted state can be cast in the form:
where the coefficients in the summation
The Concurrence for the path-entangled biphoton states can be derived considering the generalized overlap (blm) of the form:
where Ak,k′ describe the angular aperture functions introduced in Section 2.
Figures 3–5 present numerical simulations of the Concurrence (C) vs. Aperture Size (in radians), for different angular slit dimensions M × N for signal and idler photons, respectively. For the case of N and M angular slits the maximum angular aperture size per slit is 2π/N and 2π/M, respectively. Taking this limit into consideration, we performed numerical simulations for aperture sizes in the range 2π/Nmax, where Nmax is the maximum number of slits between the values of N and M considered in the specific numerical simulations. All angular dimensions considered are experimentally feasible in view of the resolution of state-of-the-art Spatial Light Modulators (SLMs) [56]. Different curves in Figure 3 correspond to symmetric path-dimensions M × N given by 2 × 2, 3 × 3, 4 × 4, 5 × 5, and 6 × 6 angular silts, for aperture sizes in the range [0, 2π/Nmax], with Nmax = 6. Different curves in Figure 4 correspond to asymmetric path-dimensions M × N given by 2 × 2, 2 × 4, 2 × 5, 3 × 4, 3 × 5 and 4 × 5 angular silts, for aperture sizes in the range [0, 2π/Nmax], with Nmax = 5. Different curves in Figure 5 correspond to asymmetric path-dimensions M × N given by 5 × 6, 5 × 7, 5 × 8, 6 × 7, 6 × 8 and 7 × 8 angular silts, for aperture sizes in the range [0, 2π/Nmax], with Nmax = 8. Interestingly, within our approximation, for a sufficiently large number of angular apertures (M × N) it is possible to reach the same amount of entanglement as with high-dimensional OAM.
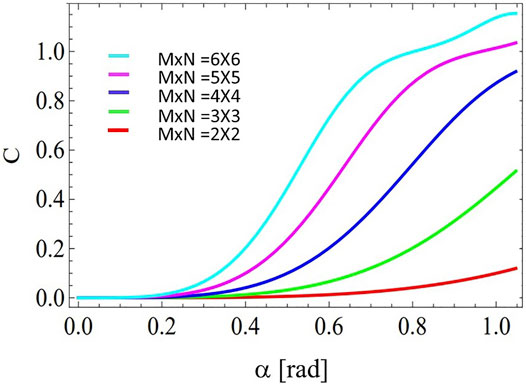
FIGURE 3. Concurrence vs. angular aperture size for different path dimensions (M × N) and aperture sizes in the range [0, 2π/Nmax] with Nmax = 6. Details are in the text.
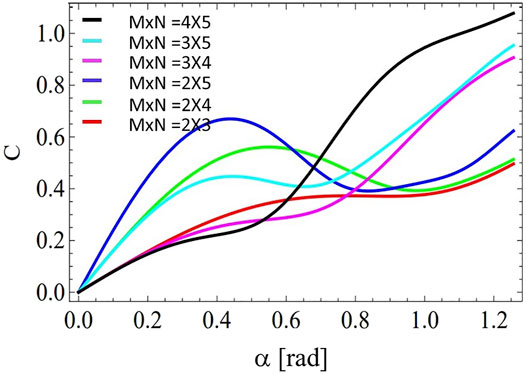
FIGURE 4. Concurrence vs. angular aperture size for different path dimensions (M × N) and aperture sizes in the range [0, 2π/Nmax] with Nmax = 5. Details are in the text.
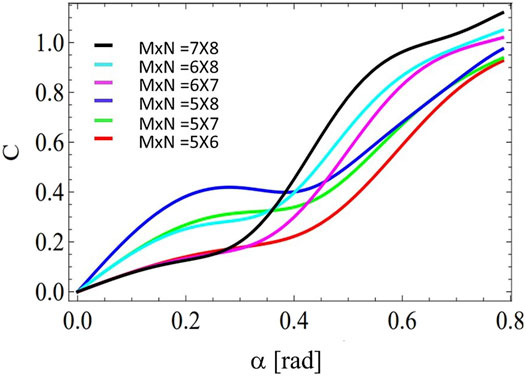
FIGURE 5. Concurrence vs. angular aperture size for different path dimensions (M × N) and aperture sizes in the range [0, 2π/Nmax] with Nmax = 8. Details are in the text.
Figure 2 indicates that for the case of OAM-entangled modes in D-dimensions, it is possible to reach the maximal amount of entanglement present in the initial state for a sufficiently large angular aperture size (nearly equal to 2π). On the other hand, a similar amount of entanglement can be achieved with path-entangled states using smaller angular apertures, by introducing a sufficiently large number of angular slits (Figures 3–5). Therefore, we can conclude that the advantage of high-dimensional path-entangled states is that they can enable to achieve the maximal entanglement present in the initial state at reduced angular aperture sizes, by increasing the number of angular slits.
Close inspection of Figures 2–5 reveals that the monotonicity in the Concurrence is directly linked to a symmetric slit configuration (M = N), as depicted in Figures 2, 3. While non-monotonicity can be ascribed to high-dimensional interference phenomena associated with an asymmetric slit configurations (M ≠ N), as depicted in Figures 4, 5. Therefore, a tunable slit configuration can be regarded as an alternative means for tailoring the entanglement content in the angular qudit state. This could prove a promising solution for instance for improving the performance of next generation function-integrated quantum circuits, among other relevant applications [50–57].
5 Experimental Implementation
The proposed experimental scheme envisioned to characterize high-dimensional entanglement using (N, M) angular slits is depicted in Figure 1. It is based on the experimental setup described in Ref. [49]. In this experimental scenario, a Gaussian pump laser beam with zero OAM is customarily prepared by spatial filtering using single-mode fibers. The pump power is typically in the range of 100 mW and typical operational wavelength is at λ = 413 nm. Degenerate down-converted photons at λ = 826 nm are created by the non-linear process of Spontaneous Parametric Down Conversion (SPDC), where a pump beam is normally incident on a non-linear crystal, for either type-I or type-II phase matching conditions. Conservation of OAM for the twin photons is granted by the SPDC process itself, for the given pump and phase matching conditions [49]. The novel element introduced in the setup is given by the angular masks containing (N, M) angular slits, for signal and idler photons, respectively. Such angular slits are programmed using state-of-the-art Spatial Light Modulators (SLMs). The OAM spectrum of the diffracted states can be analyzed in terms of OAM spiral harmonics, typically over a range from l = 12 to l = 12. This is routinely accomplished in the laboratory using diffraction holograms, which for ease of implementation can be programmed in the same SLM used for the angular masks (Figure 6). Such OAM projective measurements are registered via Coincidence Counts (Rsi), in the (ls, li) OAM basis. The Coincidence Count (CC) rate Rsi of single-photon detectors Ds(i) gives the probability that signal(idler) photons are detected at single-photon detector Ds(i) in mode |ls(i)⟩, in a given fixed-time coincidence window. Specifically, the CC rate is given by Rsi = ⟨ li|⟨ls‖ρ‖li|⟩ls| [49].
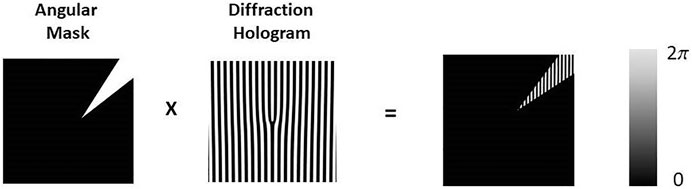
FIGURE 6. Angular masks used to create path-entanglement and diffraction holograms used to analyze the OAM spectrum. Both the angular mask and the diffraction hologram can be programmed using the same Spatial Light Modulator. Details are in the text.
An alternative, more exciting, detection approach would consist of implementing a detection scheme that could resolve the angular slits taken by the photons and enable to reconstruct the density matrix directly in the path-way basis. We envision that such complex detection schemes could in principle be implemented by means of N-arm interferometers in combination with spatial multiplexing techniques. More specific, spatial multiplexing could enable active stabilization of such complex interferometers, which is a key experimental challenge in the context [59].
As mentioned, SLMs are used both for preparation of angular masks, and for analysis of the transmitted state in the OAM basis via diffraction holograms. As it is well known in the literature, SLMs are programmable refractive elements which enable full control of the amplitude of the diffracted beams. In the standard technique, if the index of the analysis l-forked hologram is opposite to that of the incoming mode, planar wave-fronts with on-axis intensity are generated in the first diffraction order. The on-axis intensity can be coupled to single-mode fibers with high efficiency, and can be measured with single-photon detectors Ds,i, using a coincidence count circuit (Figure 1). The maximum number of angular slits that can be implemented in a realistic experimental situation will be fundamentally limited by the finite spatial and angular correlation width of signal and idler photons, as well as by the resolution of the SLM itself [56].
6 Discussion
We presented a method to generate entangled photonic states in high-dimensional quantum systems, the so-called qudits, by exploiting quantum correlations of OAM-entangled photons produced by the non-linear process of Spontaneous Parametric Down Conversion. Diffraction masks containing N angular slits in the path of twin photons define a qudit space of dimension N2, spanned by the alternative pathways of the entangled photons. We quantify the entanglement of path-entangled photons by an explicit calculation of the Concurrence, valid for pure states. We reported numerical results for the Concurrence as a function of the angular aperture size for the case of high-dimensional OAM-entangled photons and for the case the case of high-dimensional entanglement produced by N × M angular slits. Interestingly, within our approximation, it is possible to reach the same amount of entanglement using either high-dimensional OAM-entangled photons or path-entangled photons. Our results shine light into the fundamental quantum aspects of two-photon angular interference, and provide alternative means for preparation of entangled quantum states in high-dimensions, a fundamental resource for quantum information and quantum simulation protocols [12, 16, 19, 25–57].
Data Availability Statement
Data supporting the conclusion of this article will be made available by the authors upon request.
Author Contributions
GP conceived the idea, developed the theory, performed numerical simulations, and wrote the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors gratefully acknowledge Giacomo Sorelli for the derivation of Eq. 15. GP acknowledges Sonja Franke-Arnold, Antonio Zelaquett-Khoury, and Leonardo Neves for helpful discussions. GP acknowledges financial support via PICT Startup.
References
1. Hong CK, Ou ZY, Mandel L. Measurement of Subpicosecond Time Intervals between Two Photons by Interference. Phys Rev Lett (1987) 59:2044–6. doi:10.1103/physrevlett.59.2044
2. Brendel J, Gisin N, Tittel W, Zbinden H. Pulsed Energy-Time Entangled Twin-Photon Source for Quantum Communication. Phys Rev Lett (1999) 82:2594–7. doi:10.1103/physrevlett.82.2594
3. Thew RT, Tanzilli S, Tittel W, Zbinden H, Gisin N. Experimental Investigation of the Robustness of Partially Entangled Qubits Over 11 km. Phys Rev A (2002) 66:062304. doi:10.1103/physreva.66.012303
4. Herzog TJ, Rarity JG, Weinfurter H, Zeilinger A. Frustrated Two-Photon Creation via Interference. Phys Rev Lett (1994) 72:629–32. doi:10.1103/physrevlett.72.629
5. Jha AK, O’Sullivan MN, Clifford Chan KW, Boyd RW. Temporal Coherence and Indistinguishability in Two-Photon Interference Effects. Phys Rev A (2008) 77:021801(R). doi:10.1103/physrevc.77.045801
6. Neves L, Lima G, Aguirre Gómez JG, Monken CH, Saavedra C, Pádua S, et al. Generation of Entangled States of Qudits Using Twin Photons. Phys Rev Lett (2005) 94:100501.
7. Fonseca EJS, Machado da Silva JC, Monken CH, Pádua S. Generation of Entangled States of Qudits using Twin Photons. Phys Rev A (2000) 61:023801. doi:10.1103/physreve.61.1550
8. Neves L, Lima G, Fonseca EJS, Davidovich L, Pádua S. Characterizing Entanglement in Qubits Created With Spatially Correlated Twin Photons. Phys Rev A (2007) 76:032314. doi:10.1103/physreva.76.032314
9. Aspect A, Grangier P, Roger G. Experimental Realization of Einstein-Podolsky-Rosen-BohmGedankenexperiment: A New Violation of Bell's Inequalities. Phys Rev Lett (1982) 49:91–4. doi:10.1103/physrevlett.49.91
10. Mandel L. Quantum Effects in One-Photon and Two-Photon Interference. Rev Mod Phys (1999) 71:S274–S282. doi:10.1103/revmodphys.71.s274
11. Zeilinger A. Experiment and the Foundations of Quantum Physics. Rev Mod Phys (1999) 71:S288–S297. doi:10.1103/revmodphys.71.s288
12. Ekert AK. Quantum Cryptography Based on Bell's Theorem. Phys Rev Lett (1991) 67:661–3. doi:10.1103/physrevlett.67.661
13. Bennett CH, Wiesner SJ. Communication via One- and Two-Particle Operators on Einstein-Podolsky-Rosen States. Phys Rev Lett (1992) 69:2881–4. doi:10.1103/physrevlett.69.2881
14. Jack B, Padgett MJ, Franke-Arnold S. Angular Diffraction. New J Phys (2008) 10:103013. doi:10.1088/1367-2630/10/10/103013
15. Jha AK, Mishra H. Constraints on Nuclear Matter Parameters of an Effective Chiral Model. Phys Rev A (2008) 78:043810. doi:10.1103/physrevc.78.065802
16. Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/physrevlett.70.1895
17. Barnett SM, Pegg DT. Quantum Theory of Rotation Angles. Phys Rev A (1990) 41:3427–35. doi:10.1103/physreva.41.3427
18. Franke-Arnold S, Barnett SM, Yao E, Leach J, Courtial J, Padgett M. Uncertainty Principle for Angular Position and Angular Momentum. New J Phys (2004) 6:103. doi:10.1088/1367-2630/6/1/103
19. Vaziri A, Weihs G, Zeilinger A. Experimental Two-Photon, Three-Dimensional Entanglement for Quantum Communication. Phys Rev Lett (2002) 89:240401. doi:10.1103/physrevlett.89.240401
20. Langford NK, Harvey MD, O’Brien JL, Pryde GJ, Gilchrist A, Bartlett SD, et al. Measuring Entangled Qutrits and Their Use for Quantum Bit Commitment. Phys Rev Lett (2004) 93:053601.
21. Leach J, Jack B, Romero J, Ritsch-Marte M, Boyd RW, Jha AK, et al. Violation of a Bell Inequality in Two-Dimensional Orbital Angular Momentum State-Spaces. Opt Express (2009) 17:8287. doi:10.1364/oe.17.008287
22. Dadda A, Leach J, Buller GS, Padgett MJ, Andersson E. Experimental Highdimensional Two-Photon Entanglement and Violations of Generalized Bell Inequalities. Nat Phys (2011) 7:677–80.
23. Kwiat PG, Mattle K, Weinfurter H, Zeilinger A, Sergienko AV, Shih Y. New High-Intensity Source of Polarization-Entangled Photon Pairs. Phys Rev Lett (1995) 75:4337–41. doi:10.1103/physrevlett.75.4337
24. Ramelow S, Ratschbacher L, Fedrizzi A, Langford NK, Zeilinger A. Discrete Tunable Color Entanglement. Phys Rev Lett (2009) 103:253601. doi:10.1103/physrevlett.103.253601
25. Rarity JG, Tapster PR. Experimental Violation of Bell's Inequality Based on Phase and Momentum. Phys Rev Lett (1990) 64:2495–8. doi:10.1103/physrevlett.64.2495
26. O’Sullivan-Hale MN, Ali Khan I, Boyd RW, Howell JC. Pixel Entanglement: Experimental Realization of Optically Entangled d=3 and d=6 Qudits. Phys Rev Lett (2005) 94:220501.
27. Walborn SP, de Oliveira AN, Thebaldi RS, Monken CH. Entanglement and Conservation of Orbital Angular Momentum in Spontaneous Parametric Down-Conversion. Phys Rev A (2004) 69:023811. doi:10.1103/physreva.69.023811
28. Franke-Arnold S, Barnett SM, Padgett MJ, Allen L. Two-photon Entanglement of Orbital Angular Momentum States. Phys Rev A (2002) 65:033823. doi:10.1103/physreva.65.033823
29. Torres JP, Alexandrescu A, Torner L. Phys Rev A (2003) 68:050301(R). doi:10.1103/physreva.68.050301
30. Wootters WK. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys Rev Lett (1998) 80:2245–8. doi:10.1103/physrevlett.80.2245
31. Jack B, Leach J, Ritsch H, Barnett SM, Padgett MJ, Franke-Arnold S. Precise Quantum Tomography of Photon Pairs with Entangled Orbital Angular Momentum. New J Phys (2009) 11:103024. doi:10.1088/1367-2630/11/10/103024
32. Molina-Terriza G, Torres JP, Torner L. Orbital Angular Momentum of Photons in Noncollinear Parametric Downconversion. Opt Commun (2003) 228:155–60. doi:10.1016/j.optcom.2003.09.071
33. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the Orbital Angular Momentum States of Photons. Nature (2001) 412:313–6. doi:10.1038/35085529
34. Leach J, Dennis MR, Courtial J, Padgett MJ. Vortex Knots in Light. New J Phys (2005) 7:55. doi:10.1088/1367-2630/7/1/055
35. Tyler GA, Boyd RW. Influence of Atmospheric Turbulence on the Propagation of Quantum States of Light Carrying Orbital Angular Momentum. Opt Lett (2009) 34:142. doi:10.1364/ol.34.000142
36. Machado P, Slooter RJ, Blanter YM. Quantum Signatures in Quadratic Optomechanics. Phys Rev A (2019) 99:063839. doi:10.1103/physreva.99.053801
38. Ling A, Han PY, Lamas-Linares A, Kurtsiefer C. Preparation of bell States with Controlled white Noise. Laser Phys (2006) 16:1140–4. doi:10.1134/s1054660x06070206
39. Wei T-C, Altepeter JB, Branning D, Goldbart PM, James DF, Jeffrey E, et al. Synthesizing Arbitrary Two-Photon Mixed States. Phys Rev A (2005) 71:032329. doi:10.1103/physreva.71.032329
40. Kaslikowski D, Gnaciński P, Żukowski M, Miklaszewski W, Zeilinger A. Violations of Local Realism by Two Entangled N-Dimensional Systems Are Stronger than for Two Qubits. Phys Rev Lett (2000) 85:4418.
41. Collins D, Gisin N, Linden N, Massar S, Popescu S. Bell Inequalities for Arbitrarily High-Dimensional Systems. Phys Rev Lett (2002) 88:040404.
42. Bechmann-Pasquinucci H, Peres A. Quantum Cryptography with 3-State Systems. Phys Rev Lett (2000) 85:3313–6. doi:10.1103/physrevlett.85.3313
43. Durt T, Cerf NJ, Gisin N, Zukowski M. Phys Rev A (2003) 67:012311. doi:10.1103/physreva.67.012311
45. Cerf NJ, Bourennane M, Karlsson A, Gisin N. Security of Quantum Key Distribution Usingd-Level Systems. Phys Rev Lett (2002) 88:127902. doi:10.1103/physrevlett.88.127902
47. Thew RT, Acın A, Zbinden H, Gisin N. Phys Rev Lett (2004) 93:010503. doi:10.1103/physrevlett.93.010503
48. de Riedmatten H, Marcikic I, Zbinden H, Gisin N. Creating High-Dimensional Time-Bin Entanglement Using Mode-Locked Lasers. Qic (2002) 2:425–33. doi:10.26421/qic2.6-1
49. Kumar Jha A, Leach J, Jack B, Franke-Arnold S, Barnett S, Boyd R, et al. Phys Rev Lett (2010) 104:010501. doi:10.1103/physrevlett.104.010501
50. Puentes G, Datta A, Feito A, Eisert J, Plenio MB, Walmsley IA. Entanglement Quantification from Incomplete Measurements: Applications Using Photon-Number-Resolving Weak Homodyne Detectors. New J Phys (2010) 12:033042. doi:10.1088/1367-2630/12/3/033042
51. Puentes G, Waldherr G, Neumann P, Balasubramanian G, Wrachtrup J. Scientific Rep (2014) 4:1–6. doi:10.1038/srep04677
52. Puentes G, Aiello A, Voigt D, Woerdman JP. Phys Rev A (2007) 75:032319. doi:10.1103/physreva.75.032319
53. Puentes G, Colangelo G, Sewell RJ, Mitchell MW. Planar Squeezing by Quantum Non-demolition Measurement in Cold Atomic Ensembles. New J Phys (2013) 15:103031. doi:10.1088/1367-2630/15/10/103031
54. Takayama O, Sukham J, Malureanu R, Lavrinenko AV, Puentes G. Photonic Spin Hall Effect in Hyperbolic Metamaterials at Visible Wavelengths. Opt Lett (2018) 43:4602–5. doi:10.1364/ol.43.004602
55. Moulieras S, Lewenstein M, Puentes G. Entanglement Engineering and Topological protection by Discrete-Time Quantum Walks. J Phys B: Mol Opt Phys (2013) 46:104005. doi:10.1088/0953-4075/46/10/104005
56. Puentes G. High-dimensional Angular Two-Photon Interference and Angular Qudit States. OSA Continuum (2020) 3:1616. doi:10.1364/osac.392178
57. Sorelli G, Shatokhin VN, Buchleitner A. Universal Entanglement Loss Induced by Angular Uncertainty. J Opt (2020) 22:024002. doi:10.1088/2040-8986/ab66d0
Keywords: parametric down conversion, orbital angular momentum, qudits, entanglement, angular diffraction, quantum optics
Citation: Puentes G (2022) High-Dimensional Entanglement of Photonic Angular Qudits. Front. Phys. 10:868522. doi: 10.3389/fphy.2022.868522
Received: 02 February 2022; Accepted: 09 March 2022;
Published: 26 April 2022.
Edited by:
Mario Alan Quiroz-Juarez, Autonomous Metropolitan University, MexicoReviewed by:
Nicolò Spagnolo, Sapienza University of Rome, ItalyAlfred U’Ren, National Autonomous University of Mexico, Mexico
Copyright © 2022 Puentes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Graciana Puentes, Z3B1ZW50ZXNAZGYudWJhLmFy
 Graciana Puentes
Graciana Puentes