Optical Fingerprints of Nematicity in Iron-Based Superconductors

Nematicity, which refers to a phase of broken rotational but preserved translational symmetry, is underlined by the appearance of anisotropic properties and leaves remarkable fingerprints in all measurable physical quantities upon crossing the structural tetragonal-orthorhombic transition at T_s in several iron-based materials. Here, we review part of our own broadband optical investigations, addressing the impact of nematicity on the charge dynamics, as a function of temperature and of tunable applied stress, the latter acting as an external symmetry breaking field. We shall first focus our attention on FeSe, which undergoes a nematic (structural) transition without any subsequent onset of magnetic ordering below T_s. FeSe thus provides an opportunity to study nematicity without the limitations due to the reconstruction of the Fermi surface because of the spin-density-wave collective state in the orthorhombic phase, typical for several other iron-based superconductors. Our data reveal an astonishing anisotropy of the optical response in the mid-infrared-to-visible spectral range, which bears testimony of an important polarization of the underlying electronic structure in agreement with angle-resolved-photoemission-spectroscopy results. Our findings at high energy scales support models for the nematic phase resting on an orbital-ordering mechanism, supplemented by orbital selective band renormalization. The optical results at energies close to the Fermi level furthermore emphasize scenarios relying on scattering by anisotropic spin-fluctuations and shed new light on the origin of nematicity in FeSe. Moreover, the composition at which the associated Weiss temperature of the nematic susceptibility extrapolates to zero is found to be close to optimal doping (i.e., in coincidence with the largest superconducting transition temperature), boosting the debate to what extent nematic fluctuations contribute to the pairing-mechanism and generally affect the electronic structure of iron-based superconductors. The present review then offers a discussion of our optical data on the optimally hole-doped Ba_0.6K_0.4Fe₂As₂. We show that the stress-induced optical anisotropy in the infrared spectral range is reversible upon sweeping the applied stress and occurs only below the superconducting transition temperature. These findings demonstrate that there is a large electronic nematicity at optimal doping which extends right under the superconducting dome.

Introduction

Nematicity lately arose to a key concept in solid state physics, because of its intimate relationship to the onset of superconductivity at high temperature [1–3]. It was soon recognised that this is a hallmark of iron-based superconductors, which are deemed to be unconventional and set new paradigms for superconductivity [4]. Nematicity, for which the electronic system breaks a discrete rotational symmetry of the crystal lattice without altering the existing translational symmetry, was originally brought into action in order to justify the anisotropy in the dc transport properties of the 122-materials Ba(Fe_1−xCo_x)₂As₂ below their structural tetragonal-to-orthorhombic phase transition at T_s [5, 6]. Since the anisotropy of any measurable physical quantity is considerably larger than any reasonable expectations by solely pondering the lattice distortion, it has been conjectured that nematicity is electronic in nature. A central quantity is the nematic susceptibility in the tetragonal phase, for instance as evinced by elastoresistance measurements (i.e., measurements of the induced resistivity anisotropy due to anisotropic strain) [7, 8], which incidentally turns out to diverge in a Curie-like fashion. Such an astonishing divergence of the nematic susceptibility was also inferred by Raman [9–11] and elastic moduli [12] investigations.

In a broader perspective, electronic nematicity is not only a topic of relevance for the iron-based superconductors but its far-reaching consequences affect several cuprates and some heavy-fermion compounds, just to quote a few examples of other unconventional superconductors, which in fact provide signatures for strongly anisotropic electronic phases [13], as well.

Another basic ingredient of unconventional superconductors is the interplay of structural, magnetic and orbital order, which cannot be considered apart and disconnected from the onset of the nematic phase [4, 14–16]. Being here the focus on iron-based superconductors, it is well established that in almost all of them a structural transition at T_s coincides with or precedes a magnetic transition at T_N and the related stripe-type magnetic order is coupled to the orthorhombic lattice distortion. The anticipated anisotropy of all physical quantities implicit in the nematic phase will be also experienced, because of symmetry, by all structural, magnetic as well as orbital properties. This thus hampers the determination of the driving mechanism and microscopic origin of nematicity [16]. In this context, FeSe lately acquired a prominent role within the panorama of iron-based materials, since it harbors a tetragonal-to-orthorhombic structural phase transition at T_s ≃ 90 K, where the lattice breaks the C4 rotational symmetry, in the absence of any subsequent, ambient pressure long-range magnetic order, prior the onset of superconductivity at T_c = 8 K [17, 18]. Therefore, FeSe is an ideal playground for the study of nematicity, since the absence of the Fermi surface folding due to the spin-density-wave-like antiferromagnetic order allows circumventing its concomitant coupling to the lattice structural transition.

Furthermore, the divergent nematic susceptibility, as observed in the strained-dependent dc transport properties, is empirically established in several iron-based superconductors even up to optimally doped compositions [19]. It is then a generic property spanning the great part of the phase diagram and led to speculate about scenarios for which nematic quantum criticality could perhaps enhance the pairing interaction [16, 20, 21]. Such an opportunity is intriguing and could open novel perspectives towards the onset of superconductivity in iron-based superconductors, as it has been already envisaged for the cuprates [22, 23]. There is an ongoing theoretical debate about the relationship between superconductivity and nematicity [13]. Equally, there is still the quest to better experimentally scrutinise the influence of nematic fluctuations on the electronic properties over a large energy range and at temperatures (T) extending under the superconducting dome, which are not accessible by elastoresistive technique. This motivated us to address the hole-doped Ba_1−xK_xFe₂As₂, which displays a nematic state up to x ∼ 0.3, when the antiferromagnetic phase boundary is reached [24]. We specifically choose the optimally-doped x = 0.4 compound (T_c = 38.5 K), which is an ideal composition in order to address the impact of the nematic fluctuations and their alleged relationship to superconductivity. Indeed, the nematic order fully disappears (i.e., T_s = 0) at this doping.

Here, we review data of our thorough broadband optical investigations of FeSe and Ba_0.6K_0.4Fe₂As₂, consisting in the measurement of the optical reflectivity as a function of T for samples experiencing a tunable symmetry breaking field, given by uniaxial stress. We ultimately extract the optical conductivity from the far-infrared up to the ultraviolet. This review, based on our publications in Refs. [25–27], is organised as follows: first an ample presentation of the experiment and then a thorough display of the data on both selected materials, together with their own dedicated discussion. An overall summary and a future outlook will conclude this paper.

Experiment

Any phase transition that breaks a point group symmetry naturally leads to domain formation. In the case of a ferroelastic-like tetragonal-to-orthorhombic transition, as exhibited by underdoped iron-arsenide superconductors as well as by FeSe, a spontaneous strain at low T can be oriented in one of two possible directions, and a twin domain structure forms to minimize the elastic energy [5, 6]. Therefore, a tunable applied stress acts as a conjugate field to the orthorhombic distortion and enforces an adjustable population of domains oriented along a preferential direction, effectively bypassing sample twinning below T_s. Our mechanical device for applying stress, and thus detwinning the samples, is shown in Figure 1 [28, 29] and consists of a spring bellows, which is made of stainless steel and it is mounted at the oxygen-free Cu cold finger of the cryostat. The bellows can be extended/retracted in order to exert and release in − situ uniaxial stress (generally abbreviated by p) on the lateral side of the sample. This is undoubtedly a major technical progress, since the capability to control the symmetry breaking field grants more experimental opportunities than in the original, yet pioneering optical work based on a mechanical clamp enabling a fixed and mostly unknown amount of compressive stress [5, 30, 31].

FIGURE 1

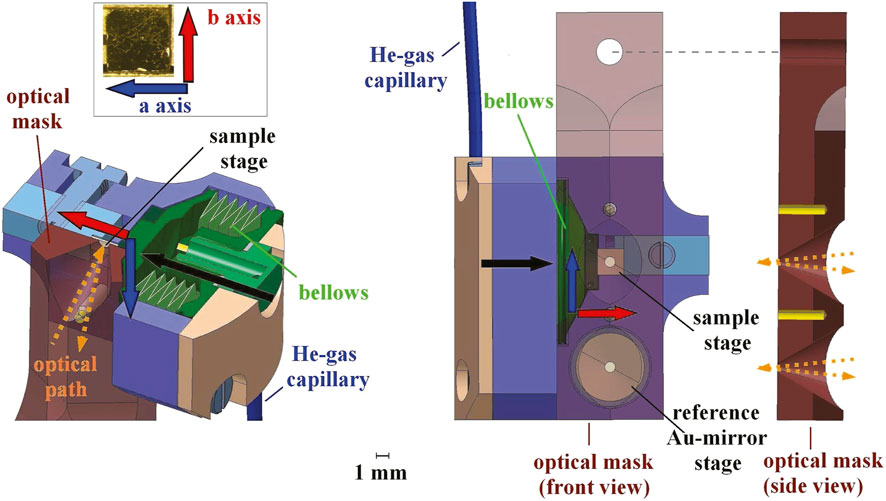
FIGURE 1. (color online) (left) Three-dimensional schematic view of the stress device with a cross-section along the plane of the incident/reflected optical path. (right) Front view along the light path. By flushing He-gas into the spring bellows and evacuating its volume, one can exert and release stress, respectively, along the direction corresponding to the (shorter) orthorhombic b-axis, as indicated by the black arrow. The optical mask, placed on top of the stress device, defines equal spots of the sample and reference Au-mirror surface, which are exposed to the electromagnetic radiation polarized along the a- and b-axis (blue and red arrow, respectively). Reproduced from Ref. [29].

The stress device (Figure 1), with the specimens mounted into it, is then placed inside an Oxford SM 4000 cryostat coupled to a Fourier-transform infrared interferometer (Bruker Vertex 80v). This permits measurements of the frequency (ω) dependence of the reflectivity (R(ω)) at nearly normal incidence [32] at different T and as a function of p in the spectral range from the far-infrared (FIR) up to the near-infrared (NIR), i.e. between 30 and 6,000 cm⁻¹. Room-temperature and stress-free data were complementary collected from NIR up to the ultra-violet (UV) range, i.e. 3200–48000 cm⁻¹. The electromagnetic radiation in all spectrometers was polarized along the a and b axes (Figure 1); in the following the measured reflectivity will be defined as R_a and R_b, respectively [28].

In displaying the data, we refer to the pressure of the He-gas flushed inside the volume of the bellows (p_bellows) in order to extend it: the effective stress felt by the sample (p_sample) depends on its size and thickness, so that p_bellows = 0.1 bar corresponds to an effective uniaxial stress of about p_sample ∼ 1.5–2 MPa on our crystals. It has been widely established that an effective p of at least 10 MPa is enough to fully detwin the specimen and thus reveal the underlying symmetry-breaking [5]. The released p data are achieved upon retracting the bellows, thus by evacuating its volume (Figure 1). We report results obtained from zero-pressure-cooled (ZPC) ‘pressure-loop’ experiments: we reach the selected T without applying stress and at that fixed T we measure R(ω) at progressively increasing p_bellows (i.e., tunable degree of detwinning) from 0 up to a material-dependent maximum pressure ranging between 0.8 and 1.2 bar. We subsequently collect R(ω) when stepwise releasing stress back to 0 bar, thus completing the p-loop.

Finally, the real part σ₁(ω) of the optical conductivity was obtained via the Kramers–Kronig (KK) transformation of R(ω) by applying suitable extrapolations at low and high frequencies. For the ω → 0 extrapolation, we made use of the Hagen-Rubens formula $(R(\omega )=1-2\sqrt{\frac{\omega }{{\sigma }_{dc}}})$, inserting the dc conductivity values (σ_dc) consistent with the relative T dependence of the samples transport data, while above the upper frequency limit R(ω) ∼ ω^−s (2⩽s⩽4) [32].

Our original publications and their Supplemental Material [25–29] cited along this work should be consulted for more details on the experimental technique and set-up as well as samples growth.

Results and Discussion

FeSe

We commence our data survey by the measured stress dependence of R(ω) in FeSe [25, 26], of which representative data in the FIR and mid-infrared (MIR) spectral range (i.e., for ω < 7,000 cm⁻¹) are shown in the main panel of Figure 2A at 10 K. The stress applied by the spring bellows of p_bellows = 1.2 bar corresponds to the situation for a fully detwinned specimen (i.e., at saturation). We can immediately recognise the overall (optical) metallicity of FeSe (inset of Figure 2A), identified by the increase of R(ω) below 2 × 10⁴ cm⁻¹ (i.e., plasma edge). The raw data explicitly convey the anisotropy of R(ω) between the two polarization directions at FIR-MIR frequencies. Such an anisotropy indeed develops from R(ω) at zero stress (see below), which shares the same trend over the whole investigated spectral range as in a previous work [33].

FIGURE 2

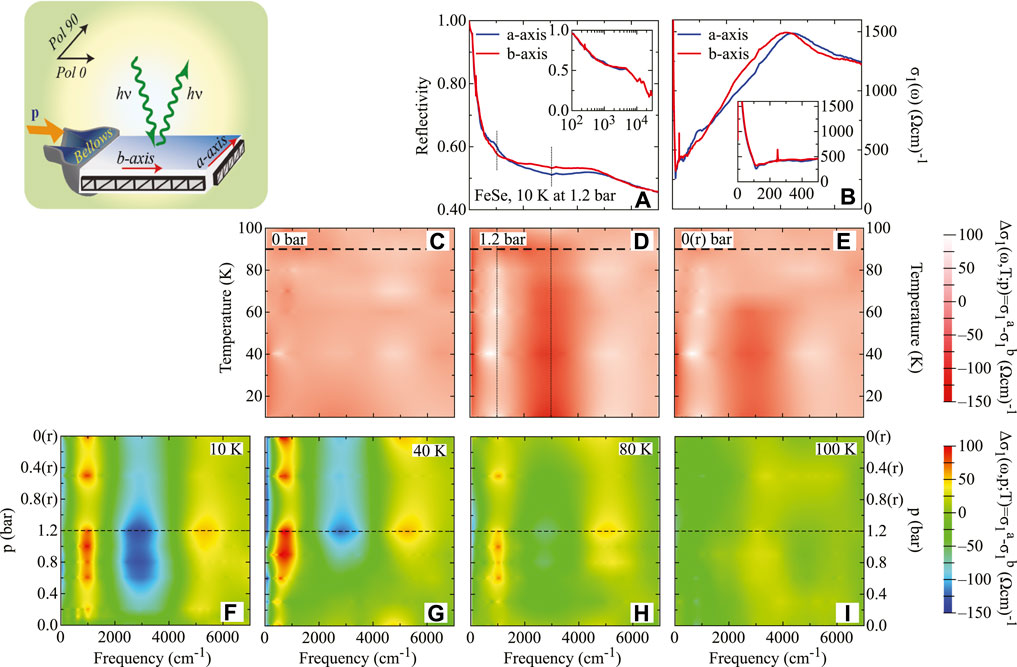
FIGURE 2. (color online) Experimental setup as well as T and p dependence of the optical anisotropy in FeSe: The upper-left panel schematically shows a sample inside the mechanical device and emphasizes the orientation of its a- and b-axis with respect to the direction of the applied stress p. Polarized light parallel to the orthorhombic (elongated) a- and (short) b-axis (in our experimental set-up Pol 90 and Pol 0, respectively) illuminates the sample (see details in Figure 1). (A) Representative data of the optical reflectivity (R(ω)) of FeSe at 10 K and 1.2 bar (i.e., at saturation) after a ZPC experiment; it emphasizes the optical anisotropy at MIR frequencies (1 eV = 8.06548 × 10³ cm⁻¹) [25]. The inset shows R_a(ω) and R_b(ω) from the FIR up to the UV range with a logarithmic frequency scale. (B) Real part σ₁(ω) of the optical conductivity and its blow up pertinent to the FIR range (inset) at 10 K and 1.2 bar. (C–E) T dependence of the dichroism defined as $\mathrm{\Delta }{\sigma }_1(\omega )={\sigma }_1^a(\omega )-{\sigma }_1^b(\omega )$ at 0, 1.2 and released 0 bar after the ZPC p-loop experiment. The thick horizontal dashed line marks T_s. The thin vertical dotted lines in panels (A) and (D) mark the frequencies 1,000 and 3,000 cm⁻¹. (F–I) Δσ₁(ω) at selected T below and above T_s within each ZPC p-loop experiment. The thin horizontal dashed line marks p at saturation. A first-neighbor interpolation procedure is used in order to generate the color maps. Released p is denoted by “(r)”. Reproduced from Ref. [26].

The polarisation dependence of R(ω) is also reflected in the excitation spectrum, represented by σ₁(ω), as shown at saturation in Figure 2B. An alternative illuminating quantity, in order to emphasise the optical anisotropy, is the so-called dichroism $\mathrm{\Delta }{\sigma }_1(\omega )={\sigma }_1^a(\omega )-{\sigma }_1^b(\omega )$, which is shown at three selected p of 0, 1.2 and released 0 bar after the p-loop experiment within the ZPC protocol in Figures 2C–E. The optical anisotropy is evident below T_s and is particularly well identified by the change of sign of Δσ₁(ω) around 1,000, 3,000 and 5,000 cm⁻¹ at saturation. The evolution of the optical anisotropy at T < T_s upon sweeping p can be equally recognised in Δσ₁(ω) at selected T within each p-loop experiment (Figures 2F–I). Furthermore, the anisotropy at dc (i.e., ω → 0) and for T < T_s (inset of Figure 2B) is such that ${\sigma }_1^b(\omega )>{\sigma }_1^a(\omega )$ for fully detwinned specimens (i.e., Δσ₁(ω) < 0, Figure 2D). This is consistent with the measured dc transport anisotropy and is reminiscent of the situation encountered in the hole-doped iron-pnictides [34].

Before going any further, we focus our attention on the hysteretic behavior of the optical anisotropy. To this goal, we shed light on the p dependence of ΔR_ratio(ω) = (R_a(ω)/R_b(ω)) - 1 at 1,000 and 3,000 cm⁻¹ (dashed vertical lines in Figure 2A) for the ZPC p-loop measurements, shown in Figure 3 for several representative T [25]. A clear half-hysteresis in the p dependence of ΔR_ratio is encountered for T < T_s and at both frequencies, though with opposite sign. We claim that this startling hysteretic occurrence is likely due to twin boundary motion. A quite rapid enhancement in |ΔR_ratio| at low T shapes the so-called virgin curve of the hysteretic behaviour. Afterwards, the optical anisotropy starts to saturate for larger p (Figures 3A,B,F,G). Therefore, a relatively modest uniaxial stress of p_sample ∼ 6 MPa is able to detwin the sample in the orthorhombic phase. The saturation of ΔR_ratio at T ≪ T_s presumably reflects complete detwinning of the sample, and any subsequent p dependence arises from the intrinsic response to p of the orthorhombic structure. The optical anisotropy is achieved more gradually for T ≤ T_s (Figures 3C,H), at which indeed the initial curve increases smoothly. At T_s (Figures 3D,I), the half-hysteresis loop has essentially collapsed and for T ≥ T_s (Figures 3E,J) the material is tetragonal and no half-hysteresis is observed so that the optical anisotropy totally vanishes at 3,000 cm⁻¹ and is weakly negative at 1,000 cm⁻¹.

FIGURE 3

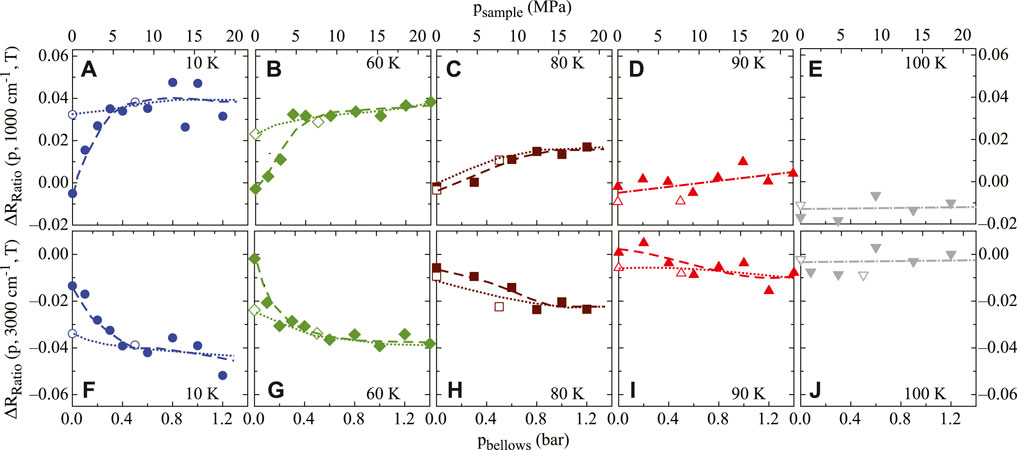
FIGURE 3. (color online) Optical anisotropy given by ΔR_ratio (see text) read at (A–E) 1,000 and (F–J) 3,000 cm⁻¹ (dashed vertical lines in Figure 2A) of FeSe as a function of applied stress p at representative T: full and open symbols denote increasing and decreasing p, respectively, for p-loop measurements following an initial ZPC protocol. Lower x-axis denotes He-gas p in the spring bellows (p_bellows) and upper x-axis the effective stress felt by the sample (p_sample). Dashed (increasing p) and dotted (releasing p) lines are drawn to guide the eye. Reproduced from Ref. [25].

We expect that the imbalance of the two twin orientations remains frozen in place at low T. This can be probed by the remanent optical anisotropy upon releasing p back to 0 [28]. At 10 K, the material barely shows changes in the optical anisotropy when p is released, indicating in fact that the sample remains in a near-single domain state. The intrinsic optical anisotropy of a fully detwinned but stress-free material is therefore given by ΔR_ratio at released p = 0. For increasing T, the thermally assisted domain-wall motion suppresses the anisotropy at released p = 0 [28]. Such a hysteretic behavior of ΔR_ratio(ω) is equivalently mapped onto Δσ₁(ω), since its saturation value tends to persist at low T, while it vanishes for T → T_s, upon releasing p (Figures 2D,E as well as Figures 2F–I).

Figure 4 summarizes the T dependence of ΔR_ratio for FeSe at 1,000 and 3,000 cm⁻¹ read at fixed p_bellows = 1.2 bar (i.e., at saturation (sat), $\mathrm{\Delta }{R}_{ratio}^{sat}$) from the p-loop experiments within the ZPC procedure (Figure 3), normalized by this quantity at 5 K. $\mathrm{\Delta }{R}_{ratio}^{sat}$ at both energy scales undergoes a quite sharp onset at T_s and tends to flatten out below T_s/2. We reiterate that at 1,000 ${\mathrm{c}\mathrm{m}}^{-1}\mathrm{\Delta }{R}_{ratio}^{sat}<$ 0 slightly above T_s, anticipating an incipient optical anisotropy at infrared frequencies, consistent in the ω → 0 limit with the measured dc one for detwinned samples [34]. The T dependence of $\mathrm{\Delta }{R}_{ratio}^{sat}$ is at variance with other experimental findings in FeSe, which attest local nematicity up to 300 K in x-ray atomic pair distribution function measurements [37] and dc transport anisotropy exhibiting a significant stress-induced tail above T_s [34]. Moreover, as shown in Figure 4, $\mathrm{\Delta }{R}_{ratio}^{sat}$ remains constant at T < T_c, which is compatible with our previous results on Co-doped 122-materials [29]. Even though the impact of superconductivity on the excitation spectrum generally occurs at much lower energy scales, the high energy optical anisotropy, addressed here at T < T_c, indicates that the superconducting state develops within a polarized electronic structure. Similarly, the orthorhombic lattice distortion is barely affected by superconductivity in FeSe [34]. However, the most astonishing outcome from the T dependence of ΔR_ratio (Figure 4) is that the optical anisotropy at MIR energies seems to act as a proxy for a mean-field-like order parameter of nematicity [25].

FIGURE 4

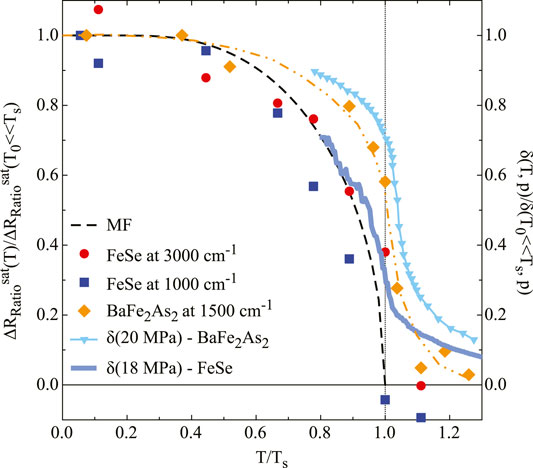
FIGURE 4. (color online) T dependence of $\mathrm{\Delta }{R}_{ratio}^{sat}$ (i.e., optical anisotropy at saturation, see text): at 1,000 and 3,000 cm⁻¹ in FeSe for p_bellows = 1.2 bar (i.e., p_sample ≈ 18.5 MPa), read from Figure 3. $\mathrm{\Delta }{R}_{ratio}^{sat}$ is normalized by its value at T₀ = 5 K. The same quantity at 1,500 cm⁻¹ for BaFe₂As₂ [28], normalized at T₀ = 10 K, is shown with dashed-double dot line as guide to the eyes. With respect to the normalized view of $\mathrm{\Delta }{R}_{ratio}^{sat}$ in FeSe, it is worth reminding that as shown in Figures 2A, 3 ΔR_ratio > 0 and ΔR_ratio < 0 at 1,000 cm⁻¹ and at 3,000 cm⁻¹, respectively. $\mathrm{\Delta }{R}_{ratio}^{sat}$ at FeSe is compared to the T dependence of the mean-field order parameter (dashed line). The stressed-induced orthorhombicity (δ) at typical stress for fully detwinned specimens (i.e., at saturation) is reproduced from Ref. [35] for BaFe₂As₂ and estimated for FeSe [36], respectively. The T axis has been normalized by T_s ∼ 90 and 135 K for FeSe and BaFe₂As₂ (vertical dotted line), respectively. Reproduced from Ref. [25].

When comparing FeSe (Figure 3) and Ba(Fe_1−xCo_x)₂As₂ [28, 29], we identify some distinct features of the hysteretic p dependence of their optical anisotropy at equivalent effectively felt uniaxial stress. First of all, the hysteretic behavior of the optical anisotropy in Co-doped BaFe₂As₂, while qualitatively reminiscent of FeSe, is clearly established only at frequencies below 2000 cm⁻¹ with R_a(ω) > R_b(ω) and without any sign change over the whole spectral range. Moreover the anisotropy at saturation was found to display a broad crossover through T_s (Figure 4), similar to the T dependence of the dc transport anisotropy for fully detwinned specimens [5] as well as of the magneto-torque signal [38] and directly comparable to the stress-induced orthorhombicity ($\delta =\frac{a-b}{a+b}$, being a and b the lattice constant of the corresponding axes) [35], replicated in Figure 4. This is rather different to the above-mentioned sudden onset of $\mathrm{\Delta }{R}_{ratio}^{sat}$ at T ≤ T_s in FeSe, despite its anticipated stress-induced δ above T_s (Figure 4) [36]. Such a distinct T dependence of the optical anisotropy across T_s between FeSe and 122-materials was also encountered in quantities from other experimental probes. For instance, the recent investigation of the linear dichroism with laser-photoemission electron microscope maps out the nematic parameter, which disappears at T_s in FeSe while it persists with a tail extending above T_s in BaFe₂(As_0.87P_0.13)₂ [39]. To which extent the magnetic transition at T_N in the underdoped regime of 122-materials may be the dominant aspect governing these differences still remains to be figured out. It is certainly safe to conclude that, at least at the energy scales addressed here, δ in FeSe may be less strongly or not obviously bound to the electronic structure as in other iron-based superconductors.

The key role of the anisotropic electronic structure with respect to the nematic phase transition in FeSe (see Ref. [40] for the most recent, comprehensive review) is underscored by our optical data, which also highlight the central significance of the orbital degrees of freedom, affecting the band structure in an extended energy interval [41–47]. The optical anisotropy indeed occurs within the frequency range 0–6,000 cm⁻¹ (Figure 2A), which is fairly consistent with the extent from the Fermi level of the correlated and weakly dispersing 3d iron bands [45, 48, 49]. However, there is an ongoing debate about the detailed nature of the nematic state in FeSe. Nuclear-magnetic-resonance (NMR) studies [50–52] initially promote a so-called on-site ferro-orbital ordering. Investigations of the electronic band structure in the reciprocal space force to revise the conclusions unbent from NMR, so that the purely on-site ferro-orbital order needs to be reconsidered within momentum-dependent scenarios. In fact, angle-resolved-photoemission-spectroscopy (ARPES) results [40, 45, 49, 53–61] indicate that the electronic band structure in FeSe undergoes a rather intricate momentum-dependent behavior, possibly consistent with either the bond-type ordering of the iron d_xy, d_xz and d_yz orbitals when crossing T_s [40, 56, 60, 62], the non-trivial energy splitting between the Γ and M point of the Brillouin zone [53, 59], leading to a band shift reversion [59], or finally the orbital-dependent Fermi-surface shrinking [45]. These scenarios demonstrate a nematicity-driven band reconstruction [33, 63], which is likely reflected in the optical anisotropy in FeSe and could account for its extension in energy and the change of sign in ΔR_ratio, as observed between 1,000 and 3,000 cm⁻¹ (Figures 2A, 3). The optical anisotropy further implies an important reshuffling of spectral weight, occurring at larger energy scales than the characteristic ones set by the critical (structural) transition temperatures. This latter observation is another manifestation of the strong orbital-selective electronic correlations in FeSe [48, 49, 64–66]. In this context, recent ARPES results [67] imply that the d_xz orbital has a larger quasi-particle spectral weight and a smaller spectral weight in the Hubbard band compared to the d_yz orbital. This may be interpreted in terms of a more coherent d_xz orbital than the d_yz orbital inside the nematic phase; a result which further highlights the importance of electronic correlations in the description of nematicity [67].

The optical conductivity allows accessing all parameters, which determine the transport properties; the scattering rate and the plasma frequency of the itinerant charge carriers. They can be extracted phenomenologically within the well-established Drude–Lorentz fit procedure [32], which we did successfully apply in the past for the 122-materials [68, 69]. By recalling that the complex optical conductivity relates to the complex dielectric function as $\widetilde{ϵ}={ϵ}_1+i{ϵ}_2={ϵ}_{\infty }+4\pi i({\sigma }_1-i{\sigma }_2)/\omega$, we can summarize our Drude–Lorentz fit as follows [32]:

$\widetilde{ϵ}={ϵ}_{\infty }-\frac{{\omega }_{pN}^2}{{\omega }^2+i\omega {\mathrm{\Gamma }}_N}-\frac{{\omega }_{pB}^2}{{\omega }^2+i\omega {\mathrm{\Gamma }}_B}+\sum _{j=3}^8\frac{S_j^2}{{\omega }_{0,j}^2-{\omega }^2-i\omega {\gamma }_j}(1)$

Besides several Lorentz harmonic oscillators (h.o.) for the finite frequency excitations we consider two Drude terms, a narrow (N) and a broad (B) one, accounting for the multi-band nature of iron-based superconductors [70]. Γ_N/B and ω_pN/B are respectively the width at half-maximum (scattering rate) and the plasma frequency $({\omega }_p=\sqrt{\frac{4\pi e^{2}n}{m^{*}}})$ of the itinerant charge carriers, with charge e, density n and effective mass m*. The parameters for each h. o. at finite frequency are the strength (S), the center-peak frequency (ω₀) and the width (γ). In Eq. 1, ϵ_∞ is the optical dielectric constant (close to one for all our fits [26]). Within this phenomenological approach we simultaneously fit both R(ω) and σ₁(ω), achieving a good reproduction of the optical functions [26].

Here, we will argue on the Drude parameters only (for additional informations on the overall fit results, please consult Ref. [26]), since the link to the (anisotropic) dc transport properties [34] is at the center of our interest. We consider the ratio of the fit parameters between the a- and b-axis, in order to shed light on their own anisotropy. Figure 5 then shows the anisotropy of ${\mathrm{\Gamma }}_{N,B}^{a,b}$ (Figures 5A,B) for both Drude terms and of the total Drude weight ($S{W}_D^{a,b}={\omega }_{pN}^2+{\omega }_{pB}^2$, Figure 5C) as a function of T within the p-loop. The resulting anisotropy in the relevant Drude parameters develops upon progressively detwinning the specimen, particularly in the T interval between 40 and 80 K, and vanishes upon releasing p back to zero. The cut of the color maps in Figures 5A–C at saturation indicates that the anisotropy of all Drude quantities for fully detwinned samples is weak just above T_s, reaches its maximum value around 60–70 K and substantially drops upon further lowering T to 10 K (i.e. just above T_c). A recent approach resting upon orbital-selective spin fluctuations [45, 71, 72] can explain the emergence of the orbital ordering, as well as of the anisotropy in the scattering rate and plasma frequency. Besides being in broad qualitative agreement with our findings, those theoretical thoughts reveal the importance of the spin-orbital interplay.

FIGURE 5

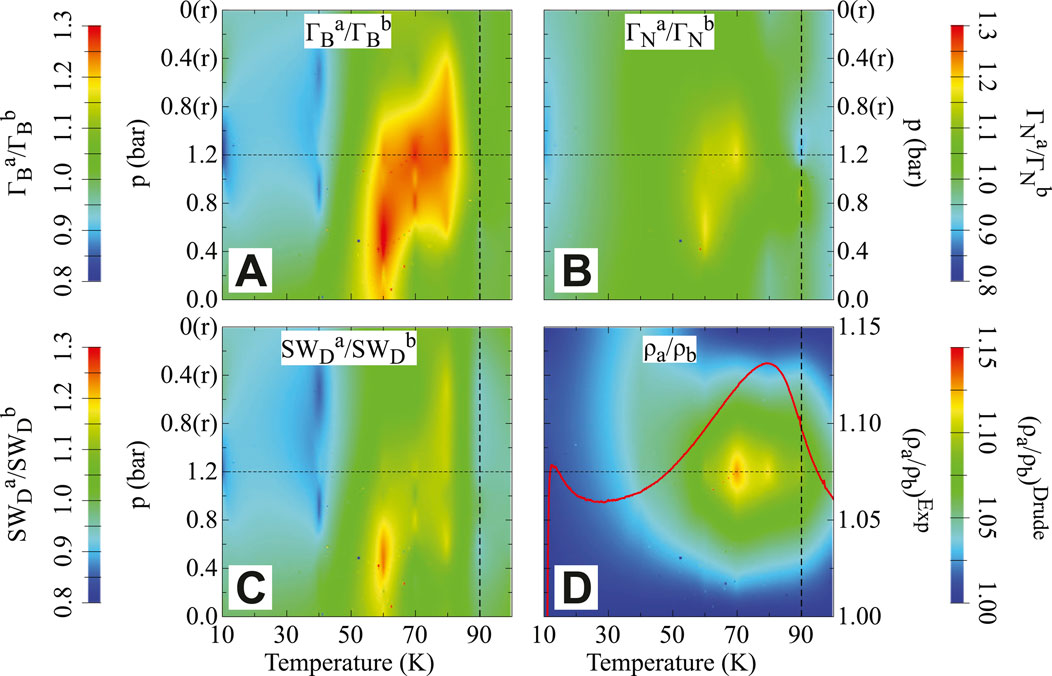
FIGURE 5. (color online) (A–C) T and p dependence of the anisotropy of both scattering rates $({\mathrm{\Gamma }}_{N,B}^a/{\mathrm{\Gamma }}_{N,B}^b)$ for the broad (B) and narrow (N) Drude components and of the total Drude weight $(S{W}_D^a/S{W}_D^b)$ from the phenomenological fit (Eq. 1) of the p-loop experiments after the ZPC protocol (see text) in FeSe. (D) T and p (left scale) dependence of the dc anisotropy (ρ_a/ρ_b) calculated within the Drude model. A first-neighbor interpolation procedure is used in order to generate the color maps. Released p is denoted by “(r)”. The thick vertical dashed line marks T_s, while the thin horizontal dashed line indicates p = 1.2 bar (i.e., at saturation). The red curve in panel (D) corresponds to the experimental ρ_a/ρ_b (right scale) for fully detwinned specimen [34]. Reproduced from Ref. [26].

The dc resistivity can be directly reconstructed within the Drude approach and by exploiting the corresponding parameters $(1/\rho (T)={\sigma }_1(\omega =0,T)=\frac{{\omega }_{pB}^2}{4\pi {\mathrm{\Gamma }}_B}+\frac{{\omega }_{pN}^2}{4\pi {\mathrm{\Gamma }}_N})$. The resulting anisotropy ρ_a/ρ_b, shown in Figure 5D, gets stronger upon applying p, specifically in the T interval 40 K$<T\le T_s$. From our investigations, it turns out that both scattering rates and total Drude weight consistently cooperate in order to recover the measured dc anisotropy [34]. By the way, this is similar to the findings in the 122-materials [68, 69] and also provides a reliability check of our analysis (Figure 5D). Since the anisotropy in the scattering rate (Γ_a > Γ_b) does coincide with the measured dc anisotropy (ρ_a > ρ_b) [34], as expected within the Drude model (i.e., ρ(T) ∼Γ [32]), the advanced interplay among the Drude parameters with respect to the dc properties is even more stringent. Conversely and interestingly enough, the anisotropy of the total Drude weight $(S{W}_D^a>S{W}_D^b)$ is opposite and unexpected within the Drude model for which $\rho (T)\sim 1/{\omega }_p^2$ [32].

Figure 6 presents the results of our analysis from a slightly different perspective, with the aim to elaborate on possible ingredients for nematicity in FeSe. In fact, it displays the T dependence of the anisotropic Drude parameters at saturation, compared to the average dc resistivity [34]. It is worth remembering that the anisotropy in all Drude quantities is mostly evident around 60–70 K, consistent with the anisotropy of the dc transport properties for the strained sample (Figure 5D). Being at odds with early conclusions drawn from our optical results in 122-materials [68, 69], Figure 6 suggests that the Drude weight has a less strong impact on the T dependence of the dc resistivity (Figure 6C) than the scattering rates for both narrow and broad Drude terms. Stated more specifically, we can convincingly affirm that the scattering rates closely follow the dc resistivity as a function of T (Figures 6A,B). Previous conjectures [73], that inelastic scattering of electrons (e.g., off magnetic fluctuations) would mainly affect the dc transport properties, find here a unique support, as given by the dominant role of our phenomenological Drude scattering rates.

FIGURE 6

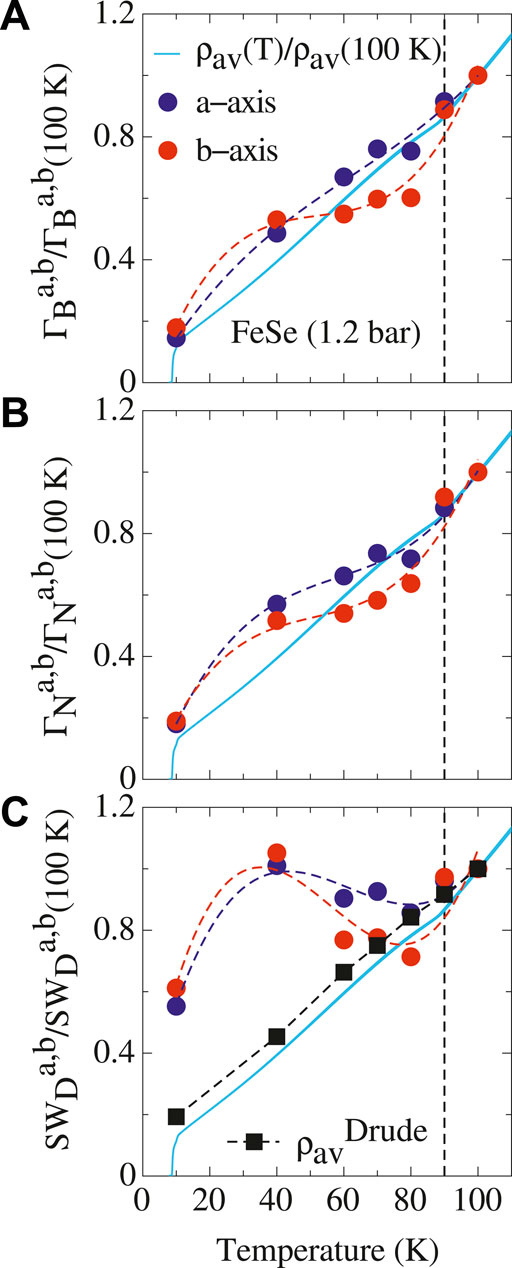
FIGURE 6. (color online) (A–C) T dependence of the anisotropic scattering rates $({\mathrm{\Gamma }}_{N,B}^{a,b})$ for the narrow (N) and broad (B) Drude term as well as of the total Drude spectral weight $S{W}_D^{a,b}$ (see text), at p = 1.2 bar (i.e., for fully detwinned samples) along both orthorhombic a- and b-axis. The measured, average dc resistivity between the two axes is replicated from Ref. [34] as comparison. Panel (C) also reproduces the average dc resistivity $({\rho }_{av}^{Drude})$, calculated within the Drude model from the fit parameters, as alternative reliability check of our analysis. All quantities are normalized by their respective values at 100 K. The thick vertical dashed line in all panels marks T_s. Reproduced from Ref. [26].

Ideas for nematicity underpinned by magnetic interactions even when nematic order precedes the magnetic one were motivated by the frequently observed intimate coupling between structure and magnetism in iron-based materials [14, 73, 74]. Magnetic fluctuations at T > T_N would then cause the tetragonal-to-orthorhombic transition in iron-pnictides (e.g., the 122-materials). Likewise, FeSe with (and despite) T_N ∼ 0 may dissimulate the same mechanism. Interestingly, the dc resistivity anisotropy Δρ = ρ_a − ρ_b in FeSe could arise from the convolution of two functions: the order parameter of the nematic phase transition (Figure 4), which breaks the same symmetry as Δρ and therefore it is proportional to it, and a proportionality factor monotonically decreasing in T [34], so that an overall dome-like T dependence peaked at ∼ 70 K (Figure 5D) would arise. A natural explanation for the T dependence of the proportionality factor derives from inelastic scattering, for instance by anisotropic magnetic excitations [34]. Indeed, the electronic scattering rates in Figures 6A,B exhibit such a T dependence. In conjunction with the nematic order parameter (Figure 4) the scattering rate then conspires in order to reproduce the resistivity anisotropy (Figure 5D). We thus speculate that the low-energy charge dynamics of FeSe is a quite direct fingerprint of a scenario for which the spin fluctuations together with the high-energy orbital ordering apparently assume a rather dominant role in connection with the onset of nematicity. Recent resonant inelastic x-ray scattering data below T_s underline a matchless strong spin-excitations anisotropy, which suggests a primarily spin-driven nematic phase transition [75]. Spin fluctuations are also an important ingredient as driving force for superconductivity [76], as advanced from recent NMR measurements [77], ARPES data [40] as well as inelastic neutron scattering investigations [78, 79].

Ba_0.6K_0.4Fe₂As₂

We start off this section with a comprehensive view of the collected R(ω) data within the p-loop experiment at 10 K (Figures 7A,B) [27]. The chosen T is well within the superconducting state and the displayed data were collected after a ZPC protocol. There is an obvious metallic behaviour of the overall R(ω) spectra along the a- and b-axis. The measured quantity along both axes approaches total reflection at finite frequencies below ν_g ∼ 180 cm⁻¹, as expected at T < T_c [32]. We note the great agreement of our data at p = 0 (averaged between the two axes) and for all T with those in Refs. [80–85], which comprehensively address the electrodynamic response both above and below T_c in un-stressed Ba_1−xK_xFe₂As₂ samples. We encounter a reversible anisotropy of R(ω) upon sweeping p, which can be further emphasized by the calculation of the reflectivity ratio R_Ratio = R_a/R_b, shown in Figure 7C. In the FIR range around 600 cm⁻¹, R_Ratio drops below 1 (i.e., the isotropic situation) upon reaching 1.2 bar (i.e., corresponding to the saturation limit for this sample). R_Ratio reconverts then to unity when p is released back to zero. From the measured R(ω) we achieve σ₁(ω), as shown in Figures 7D,E, and consequently the already introduced dichroism $\mathrm{\Delta }{\sigma }_1(\omega )={\sigma }_1^a(\omega )-{\sigma }_1^b(\omega )$ (see above our discussion for the FeSe material). Δσ₁(ω) for the p-loop experiment at 10 K is depicted in Figure 7F. The optical anisotropy in the range between 300 and 1,000 cm⁻¹ for the stressed specimen is clearly resolved and further implies an anisotropy in the spectral weight distribution at FIR frequencies [27]. It is historically well established that σ₁(ω) in the superconducting state allows in principle the determination of the so-called superconducting gap. This is the characteristic energy scale of the superconducting collective state and is supposed to correspond to a sharp onset of the absorption spectrum at least for s-wave like superconducting materials [32]. The drop of σ₁(ω) to almost zero below ν_g, as illustrated in Figures 7D,E as well as Figure 8B, is the most clear signature of the superconducting gap at 10 K for every p. We conclude that Ba_0.6K_0.4Fe₂As₂ is a fully gapped superconducting material. Moreover, the residual, unpaired charge carriers (i.e., activated across the gap because of the thermal pair-breaking effect) at finite T lead to the upturn of σ₁(ω) at frequencies towards zero [32].

FIGURE 7

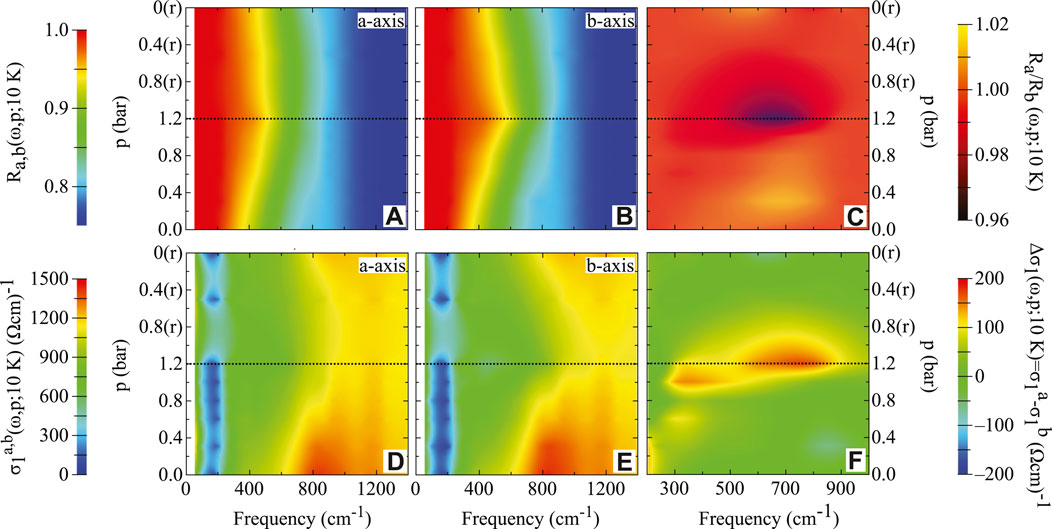
FIGURE 7. (color online) (A,B) Representative data of the optical reflectivity (R(ω)) of Ba_0.6K_0.4Fe₂As₂ at 10 K for the p-loop experiment after a ZPC protocol along the a- and b-axis (R_a and R_b, respectively, upper-left panel of Figure 2) in the spectral range below 1,400 cm⁻¹. (C) The reflectivity ratio R_Ratio = R_a/R_b. (D,E) Real part σ₁(ω) of the optical conductivity, achieved through KK transformation of the data in panels (A,B). (F) The dichroism $\mathrm{\Delta }{\sigma }_1(\omega )={\sigma }_1^a(\omega )-{\sigma }_1^b(\omega )$ at 10 K within the p-loop experiment. Panels (C,F) focus the attention to the FIR energy interval 200–1,000 cm⁻¹, where the reversible optical anisotropy upon sweeping p is discovered. A first-neighbor interpolation procedure is used in order to generate the color maps. Released p is denoted by “(r)”. The thick dotted line in all panels marks p = 1.2 bar (i.e., at saturation). Reproduced from Ref. [27].

FIGURE 8

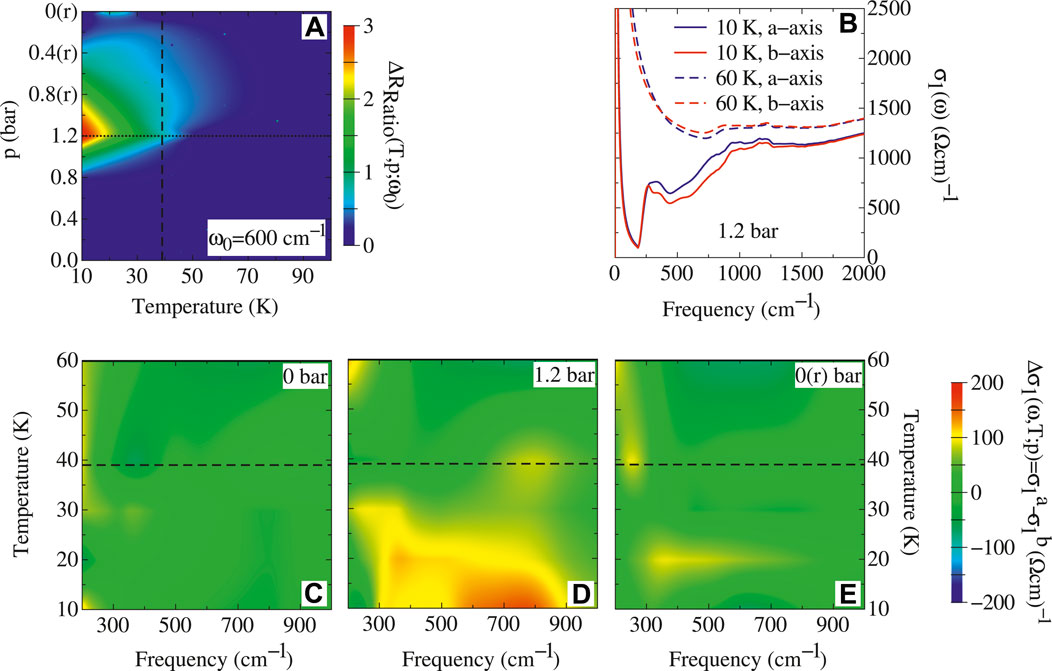
FIGURE 8. (color online) (A) T dependence of the quantity ΔR_Ratio (ω₀) (see text) of Ba_0.6K_0.4Fe₂As₂ within the p-loop experiment after a ZPC protocol, which emphasizes the T evolution of the p-induced optical anisotropy. We choose ω₀ = 600 cm⁻¹. The thick dotted line marks p = 1.2 bar (i.e., at saturation). (B) Measured σ₁(ω) at 10 K (i.e., T < T_c) and 60 K (i.e., T > T_c) for p = 1.2 bar along both crystallographic axes. (C,E) T dependence of Δσ₁(ω) at the selected p of 0, 1.2 and released 0 bar. These panels focus the attention to the FIR energy interval 200–1,000 cm⁻¹, thus emphasising the reversible optical anisotropy upon sweeping p. The thick dashed line in panels (A) and (C–E) indicates T_c. A first-neighbor interpolation procedure is used in order to generate the color maps. Released p is denoted by “(r)”. Reproduced from Ref. [27].

So far, we could provide a clear-cut evidence for an optical anisotropy, which is p-induced in the tetragonal structure of Ba_0.6K_0.4Fe₂As₂ at T = 10 K $<T_c$. The question then arises about its T dependence and its relationship to the overall phase diagram of iron-based superconductors. The quantity $\mathrm{\Delta }{R}_{Ratio}({\omega }_0)=\frac{R_{Ratio}(p=0,T)-R_{Ratio}(p,T)}{R_{Ratio}(p=0,T)}\times 100$ is very instrumental to this goal. It amplifies the relative change of the optical anisotropy during the p-loop experiments at each T with respect to the p = 0 initial situation (i.e., the isotropic limit since R_Ratio (p = 0, T) ∼ 1 at all T). We made the argument that ΔR_Ratio (ω₀) truly helps pointing out the variation of the optical anisotropy beyond the experimental data noise [27]. Figure 8A therefore pictures ΔR_Ratio (ω₀) at the fixed frequency ω₀ = 600 cm⁻¹, chosen because the largest anisotropy occurs at that frequency (Figure 7C). The nematic susceptibility in the normal state (i.e., at T > T_c) from elastoresistive investigation [19] images a substantial Curie-like behaviour, which is however not seen or reproduced by our own optical data above T_c. It seems that our experiment does not have enough resolution in this respect and a possible optical evidence for nematicity above T_c must be vanishingly small, if any. From our data, it follows that only upon entering the superconducting state there is a p-induced anisotropy; large enough applied p can cause a polarization dependence of the excitation spectrum. This is mostly and better seen at saturation (thick horizontal dotted line at p = 1.2 bar in the color map of Figure 8A), where an indisputable pronounced increase of the optical anisotropy is discernible at T < T_c. The established hardening occurring below T_c [12] and the mild reduction at low T of the Raman susceptibilities [10] for dopings across the whole phase diagram would presage an opposite behaviour, instead of the growing of the p-induced nematicity in the superconducting state as evidenced from optics. This latter aspect calls for additional studies and it remains to be seen how this apparent controversy may be solved. Nonetheless, we stress here the T evolution of the optical anisotropy with Δσ₁(ω), shown in Figures 8C–E. We limit our view to the energy interval between 200 and 1,000 cm⁻¹ at three selected p, which again highlight the p-induced as well as p-reversible optical anisotropy below T_c in the FIR range. This is the most important aspect of these findings, signalling the presence of electronic nematicity at T deep into the superconducting dome yet in the purely tetragonal phase and that the band structure is responding to nematic fluctuations, since here T_s = 0. It is worth recalling (see above, Figure 4) that the optical anisotropy of Co-underdoped 122-materials and FeSe persists even at T < T_c, and reiterating the idea that their superconductivity develops in an electronically polarized state [25, 26, 68, 69].

Our present data of Ba_0.6K_0.4Fe₂As₂ bear testimony to a p-induced anisotropy of the excitation spectrum, which mirrors nematicity and seems to be a generic feature in 122 iron-based superconductors [28, 29, 68, 69] even into the optimally-doped regime, similar to the dc transport properties [19]. We discover that the optical anisotropy in the optimally K-doped 122-compound occurs at the low FIR energy scales, relevant to the superconducting gap(s) (Figure 7F and Figure 8C–E). This is peculiar with respect to the previously investigated underdoped 122-materials and FeSe [25, 26, 28, 29, 68, 69], for which the optical anisotropy extends up to high energy scales. Our findings in Ba_0.6K_0.4Fe₂As₂ thus tend to exclude the involvement of bands deep into the electronic structure and potentially imply a less prominent impact of orbital ordering in the optimally doped than in the underdoped regime. Ergo, the p-induced optical anisotropy in Ba_0.6K_0.4Fe₂As₂ elucidates the response of the conduction bands to an external symmetry breaking field. For instance, the deployed optical response and its p dependence flag the imprint of (anisotropic) scattering, uncovering some kind of spin-orbital interplay, so that the p-induced nematicity is caused by spin fluctuations and is vestigial to stripe magnetism [16]. This would directly influence the energy scales close to the Fermi level, ultimately of relevance for the transport properties as well as superconductivity. Moreover and beyond nematicity, Raman results equally make a strong case for a pairing mechanism for superconductivity mediated by spin fluctuations [86]. In addition, a so-called differentiation of the orbital effective masses and related anisotropy, which is further enhanced by the presence of strong electronic correlations above all in hole-doped materials [46], can be alike installed by uniaxial stress, as applied here in our experiment. This impairs the optical response of the conduction bands as well and could be also reflected in an anisotropic reshuffling of spectral weight at T < T_c between the superconducting collective mode and the FIR energies (Figures 8C–E) [87].

Conclusion and Outlook

We conclude this review by summarising the major outcomes of our optical studies in selected iron-based superconductors and projecting the treated topics into possible future directions.

First of all, within one single experiment we disclose all relevant ingredients (order parameter and Drude quantities, Figures 4, 5), which were shown to fully determine the anisotropy in the charge dynamics as well as in the dc transport properties of FeSe. It is worth warning the readership that the interplay between the orbital order [25, 28, 29] and the intertwined anisotropy of the Drude parameters (Figure 5) cannot be neglected when addressing the complete excitation spectrum [45, 68, 69, 71]. Having said that, the inelastic scattering by magnetic fluctuations rather than the Fermi surface parameters seems to shape the nematic anisotropy in the dc limit (Figure 6). Proposals advocating a close connection between spin fluctuations, nematicity (i.e., orbital order) and superconductivity [15, 16] would be reasonably promoted by our findings, since they give ample support for the role played by magnetic interactions. In a broader context and looking ahead, it could be of interest to systematically compare our results with data collected across the whole T versus doping phase diagram of representative iron-based superconductors, and to exploit the broadband optical anisotropy, addressed here, in order to precisely test the impact of doping-induced disorder [88], thus expanding at finite frequencies the debate already addressed by dc transport investigations [89–91].

Second, the p-induced optical anisotropy in (optimally doped) Ba_0.6K_0.4Fe₂As₂ only at T < T_c (Figure 8A) is an astonishing fingerprint that the electronic structure is extremely susceptible to symmetry breaking stress below T_c. In Ref. [87], we additionally discover that our findings (Figure 7) imply the presence of p-induced anisotropic gaps between both axes at T ≪ T_c. Chasing the implications of the gap anisotropy with respect to the debate on the dominant pairing symmetry [86, 92, 93] goes beyond the scope of this work. Nonetheless, the unprecedented anisotropic charge dynamics deep into the superconducting dome is contingently consistent with recent observations of nematic superconductivity in compounds with similar doping [94–96] as well as in LiFeAs [97]. This is a pretty strong speculation, which needs to be challenged with adhoc ascertainments. As outlook, it remains to be seen whether an orbital-selective pairing, eventually supplemented by the guiding principle of spin fluctuations as proposed for FeSe [76, 98–101], may explain the anisotropy of the superconducting gap. This would also shed new light on the putative relationship between quantum critical nematic fluctuations and unconventional superconductivity [21, 22]. In this respect, interrogating the exact extent to which uniaxial stress couple to nematic fluctuations will be of paramount importance and is a task left to the future.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author wishes to thank C. Mirri, M. Chinotti and A. Pal for the data collection and analysis, as reported in the original, quoted references, as well as R. Fernandes, M. Schütt, L. Benfatto, L. Fanfarillo, B. Valenzuela, E. Bascones, M. Watson, R. Lobo, A. Chubukov, P. Hirschfeld, W. Ku and D. Lu for fruitful discussions. This work was supported by the Swiss National Foundation for the Scientific Research.

References

1. Fradkin E, Kivelson SA, Lawler MJ, Eisenstein JP, Mackenzie AP. Nematic Fermi Fluids in Condensed Matter Physics. Annu Rev Condens Matter Phys (2010) 1:153–78. doi:10.1146/annurev-conmatphys-070909-103925

2. Fradkin E, Kivelson SA. Electron Nematic Phases Proliferate. Science (2010) 327:155–6. doi:10.1126/science.1183464

3. Fradkin E, Kivelson SA. Ineluctable Complexity. Nat Phys (2012) 8:864–6. doi:10.1038/nphys2498

4. Fernandes RM, Coldea AI, Ding H, Fisher IR, Hirschfeld PJ, Kotliar G. Iron Pnictides and Chalcogenides: a New Paradigm for Superconductivity. Nature (2022) 601:35–44. doi:10.1038/s41586-021-04073-2

5. Fisher IR, Degiorgi L, Shen ZX. In-plane Electronic Anisotropy of Underdoped '122' Fe-Arsenide Superconductors Revealed by Measurements of Detwinned Single Crystals. Rep Prog Phys (2011) 74:124506. doi:10.1088/0034-4885/74/12/124506

6. Tanatar MA, Kreyssig A, Nandi S, Ni N, Bud’ko SL, Canfield PC, et al. Direct Imaging of the Structural Domains in the Iron Pnictides AFe₂As₂ (A=Ca,Sr,Ba). Phys Rev B (2009) 79:180508. doi:10.1103/physrevb.79.180508

7. Chu J-H, Kuo H-H, Analytis JG, Fisher IR. Divergent Nematic Susceptibility in an Iron Arsenide Superconductor. Science (2012) 337:710–2. doi:10.1126/science.1221713

8. Kuo H-H, Shapiro MC, Riggs SC, Fisher IR. Measurement of the Elastoresistivity Coefficients of the Underdoped Iron Arsenide Ba(Fe_0.975Co_0.025)₂As₂. Phys Rev B (2013) 88:085113. doi:10.1103/physrevb.88.085113

9. Gallais Y, Fernandes RM, Paul I, Chauvière L, Yang Y-X, Méasson M-A, et al. Observation of Incipient Charge Nematicity in Ba(Fe_1−XCo_X)₂As₂. Phys Rev Lett (2013) 111:267001. doi:10.1103/physrevlett.111.267001

10. Wu S-F, Richard P, Ding H, Wen H-H, Tan G, Wang M, et al. Superconductivity and Electronic Fluctuations in Ba_1−xK_xFe₂As₂ Studied by Raman Scattering. Phys Rev B (2017) 95:085125. doi:10.1103/PhysRevB.95.085125

11. Wu SF, Zhang WL, Li L, Cao HB, Kung HH, Sefat AS, et al. (2017) arXiv:1712.06066 [cond-mat.supr-con]. Available at: https://arxiv.org/abs/1712.06066.

12. Böhmer AE, Burger P, Hardy F, Wolf T, Schweiss P, Fromknecht R, et al. Nematic Susceptibility of Hole-Doped and Electron-Doped BaFe₂As₂ Iron-Based Superconductors from Shear Modulus Measurements. Phys Rev Lett (2014) 112:047001. doi:10.1103/PhysRevLett.112.047001

13. Fradkin E, Kivelson SA, Tranquada JM. Colloquium: Theory of Intertwined Orders in High Temperature Superconductors. Rev Mod Phys (2015) 87:457–82. doi:10.1103/revmodphys.87.457

14. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors? Nat Phys (2014) 10:97–104. doi:10.1038/nphys2877

15. Glasbrenner JK, Mazin II, Jeschke HO, Hirschfeld PJ, Fernandes RM, Valentí R. Effect of Magnetic Frustration on Nematicity and Superconductivity in Iron Chalcogenides. Nat Phys (2015) 11:953–8. doi:10.1038/nphys3434

16. Chubukov AV, Khodas M, Fernandes RM. Magnetism, Superconductivity, and Spontaneous Orbital Order in Iron-Based Superconductors: Which Comes First and Why?. Phys Rev X (2016) 6:041045. doi:10.1103/physrevx.6.041045

17. Hsu F-C, Luo J-Y, Yeh K-W, Chen T-K, Huang T-W, Wu PM, et al. Superconductivity in the PbO-type Structure -FeSe. Proc Natl Acad Sci (2008) 105:14262–4. doi:10.1073/pnas.0807325105

18. McQueen TM, Williams AJ, Stephens PW, Tao J, Zhu Y, Ksenofontov V, et al. Tetragonal-to-Orthorhombic Structural Phase Transition at 90 K in the Superconductor Fe_1.01Se. Phys Rev Lett (2009) 103:057002. doi:10.1103/physrevlett.103.057002

19. Kuo H-H, Chu J-H, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous Signatures of Nematic Quantum Criticality in Optimally Doped Fe-Based Superconductors. Science (2016) 352:958–62. doi:10.1126/science.aab0103

20. Metlitski MA, Mross DF, Sachdev S, Senthil T. Cooper Pairing in Non-fermi Liquids. Phys Rev B (2015) 91:115111. doi:10.1103/physrevb.91.115111

21. Lederer S, Schattner Y, Berg E, Kivelson SA. Enhancement of Superconductivity Near a Nematic Quantum Critical Point. Phys Rev Lett (2015) 114:097001. doi:10.1103/physrevlett.114.097001

22. Nie L, Tarjus G, Kivelson SA. Quenched Disorder and Vestigial Nematicity in the Pseudogap Regime of the Cuprates. Proc Natl Acad Sci (2014) 111:7980–5. doi:10.1073/pnas.1406019111

23. Fujita K, Kim CK, Lee I, Lee J, Hamidian MH, Firmo IA, et al. Simultaneous Transitions in Cuprate Momentum-Space Topology and Electronic Symmetry Breaking. Science (2014) 344:612–6. doi:10.1126/science.1248783

24. Böhmer AE, Hardy F, Wang L, Wolf T, Schweiss P, Meingast C. Superconductivity-Induced Re-Entrance of the Orthorhombic Distortion in Ba_1−xK_xFe₂As₂. Nat Commun (2015) 6:7911. doi:10.1038/ncomms8911

25. Chinotti M, Pal A, Degiorgi L, Böhmer AE, Canfield PC. Optical Anisotropy in the Electronic Nematic Phase of FeSe. Phys Rev B (2017) 96:121112. doi:10.1103/physrevb.96.121112

26. Chinotti M, Pal A, Degiorgi L, Böhmer AE, Canfield PC. Ingredients for the Electronic Nematic Phase in FeSe Revealed by its Anisotropic Optical Response. Phys Rev B (2018) 98:094506. doi:10.1103/physrevb.98.094506

27. Pal A, Chinotti M, Chu J-H, Kuo H-H, Fisher IR, Degiorgi L. Optical Anisotropy in Optimally Doped Iron-Based Superconductor. Npj Quant Mater (2019) 4:3. doi:10.1038/s41535-018-0140-1

28. Mirri C, Dusza A, Bastelberger S, Chu J-H, Kuo H-H, Fisher IR, et al. Hysteretic Behavior in the Optical Response of the Underdoped Fe-Arsenide Ba(Fe_1–xCo_x)₂As₂ in the Electronic Nematic Phase. Phys Rev B (2014) 89:060501. doi:10.1103/physrevb.89.060501

29. Mirri C, Dusza A, Bastelberger S, Chu J-H, Kuo H-H, Fisher IR, et al. Nematic-driven Anisotropic Electronic Properties of Underdoped detwinned Ba(Fe_1−xCo_x)₂As₂ Revealed by Optical Spectroscopy. Phys Rev B (2014) 90:155125. doi:10.1103/physrevb.90.155125

30. Dusza A, Lucarelli A, Pfuner F, Chu J-H, Fisher IR, Degiorgi L. Anisotropic Charge Dynamics in Detwinned Ba(Fe_1−xCo_x)₂As₂. Epl (2011) 93:37002. doi:10.1209/0295-5075/93/37002

31. Nakajima M, Liang T, Ishida S, Tomioka Y, Kihou K, Lee CH, et al. Unprecedented Anisotropic Metallic State in Undoped Iron Arsenide BaFe₂As₂ Revealed by Optical Spectroscopy. Proc Natl Acad Sci (2011) 108:12238–42. doi:10.1073/pnas.1100102108

32. Dressel M, Gruner G. Electrodynamics of Solids. Cambridge: Cambridge University Press (2002).

33. Wang H, Ye Z, Zhang Y, Wang N. Band Structure Reconstruction across Nematic Order in High Quality FeSe Single crystal as Revealed by Optical Spectroscopy Study. Sci Bull (2016) 61:1126–31. doi:10.1007/s11434-016-1102-2

34. Tanatar MA, Böhmer AE, Timmons EI, Schütt M, Drachuck G, Taufour V, et al. Origin of the Resistivity Anisotropy in the Nematic Phase of FeSe. Phys Rev Lett (2016) 117:127001. doi:10.1103/physrevlett.117.127001

35. Lu X, Tseng K-F, Keller T, Zhang W, Hu D, Song Y, et al. Impact of Uniaxial Pressure on Structural and Magnetic Phase Transitions in Electron-Doped Iron Pnictides. Phys Rev B (2016) 93:134519. doi:10.1103/physrevb.93.134519

36.The stress-induced orthorhombicity in FeSe above T_s can be reasonably estimated for effectively applied stress of about 18 MPa (i.e., at saturation) from the elastic constant and x-ray diffraction data [102, 103]. It is comparable to values measured in BaFe₂As₂ [35].

37. Koch RJ, Konstantinova T, Abeykoon M, Wang A, Petrovic C, Zhu Y, et al. Room Temperature Local Nematicity in FeSe Superconductor. Phys Rev B (2019) 100:020501. doi:10.1103/physrevb.100.020501

38. Kasahara S, Shi HJ, Hashimoto K, Tonegawa S, Mizukami Y, Shibauchi T, et al. Electronic Nematicity above the Structural and Superconducting Transition in BaFe₂(As_1−xP_x)₂. Nature (2012) 486:382–5. doi:10.1038/nature11178

39. Shimojima T, Motoyui Y, Taniuchi T, Bareille C, Onari S, Kontani H, et al. Discovery of Mesoscopic Nematicity Wave in Iron-Based Superconductors. Science (2021) 373:1122–5. doi:10.1126/science.abd6701

40. Rhodes LC, Eschrig M, Kim TK, Watson MD, (2022), and references therein, arXiv:2201.11702 [cond-mat.supr-con]. Available at: https://arxiv.org/abs/2201.11702.

41. Chen C-C, Maciejko J, Sorini AP, Moritz B, Singh RRP, Devereaux TP. Orbital Order and Spontaneous Orthorhombicity in Iron Pnictides. Phys Rev B (2010) 82:100504. doi:10.1103/physrevb.82.100504

42. Lee C-C, Yin W-G, Ku W. Ferro-Orbital Order and Strong Magnetic Anisotropy in the Parent Compounds of Iron-Pnictide Superconductors. Phys Rev Lett (2009) 103:267001. doi:10.1103/physrevlett.103.267001

43. Lv W, Krüger F, Phillips P. Orbital Ordering and Unfrustrated (π,0) Magnetism from Degenerate Double Exchange in the Iron Pnictides. Phys Rev B (2010) 82:045125. doi:10.1103/physrevb.82.045125

44. Daghofer M, Luo Q-L, Yu R, Yao DX, Moreo A, Dagotto E. Orbital-weight Redistribution Triggered by Spin Order in the Pnictides. Phys Rev B (2010) 81:180514. doi:10.1103/physrevb.81.180514

45. Fanfarillo L, Mansart J, Toulemonde P, Cercellier H, Le Fèvre P, Bertran F, et al. Orbital-dependent Fermi Surface Shrinking as a Fingerprint of Nematicity in FeSe. Phys Rev B (2016) 94:155138. doi:10.1103/physrevb.94.155138

46. Fanfarillo L, Giovannetti G, Capone M, Bascones E. Nematicity at the Hund's Metal Crossover in Iron Superconductors. Phys Rev B (2017) 95:144511. doi:10.1103/physrevb.95.144511

47. Benfatto L, Cappelluti E. Effects of the Fermi-Surface Shrinking on the Optical Sum Rule in Pnictides. Phys Rev B (2011) 83:104516. doi:10.1103/physrevb.83.104516

48. Watson MD, Backes S, Haghighirad AA, Hoesch M, Kim TK, Coldea AI, et al. Formation of Hubbard-Like Bands as a Fingerprint of Strong Electron-Electron Interactions in FeSe. Phys Rev B (2017) 95:081106. doi:10.1103/physrevb.95.081106

49. Evtushinsky DV, Aichhorn M, Sassa Y, Liu ZH, Maletz J, Wolf T, et al. (2016), arXiv:1612.02313 [cond-mat.supr-con]. Available at: https://arxiv.org/abs/1612.02313.

50. Baek S-H, Efremov DV, Ok JM, Kim JS, van den Brink J, Büchner B. Orbital-driven Nematicity in FeSe. Nat Mater (2015) 14:210–4. doi:10.1038/nmat4138

51. Böhmer AE, Arai T, Hardy F, Hattori T, Iye T, Wolf T, et al. Origin of the Tetragonal-to-Orthorhombic Phase Transition in FeSe: A Combined Thermodynamic and NMR Study of Nematicity. Phys Rev Lett (2015) 114:027001. doi:10.1103/PhysRevLett.114.027001

52. Cao RX, Hu J, Dong J, Zhang JB, Ye XS, Xu YF, et al. Observation of Orbital Ordering and Origin of the Nematic Order in FeSe. New J Phys (2019) 21:103033. doi:10.1088/1367-2630/ab4927

53. Nakayama K, Miyata Y, Phan GN, Sato T, Tanabe Y, Urata T, et al. Reconstruction of Band Structure Induced by Electronic Nematicity in an FeSe Superconductor. Phys Rev Lett (2014) 113:237001. doi:10.1103/physrevlett.113.237001

54. Zhang P, Qian T, Richard P, Wang XP, Miao H, Lv BQ, et al. Observation of Two Distinctdxz/dyzband Splittings in FeSe. Phys Rev B (2015) 91:214503. doi:10.1103/physrevb.91.214503

55. Suzuki Y, Shimojima T, Sonobe T, Nakamura A, Sakano M, Tsuji H, et al. Momentum-dependent Sign Inversion of Orbital Order in Superconducting FeSe. Phys Rev B (2015) 92:205117. doi:10.1103/physrevb.92.205117

56. Watson MD, Kim TK, Rhodes LC, Eschrig M, Hoesch M, Haghighirad AA, et al. Evidence for Unidirectional Nematic Bond Ordering in FeSe. Phys Rev B (2016) 94:201107. doi:10.1103/physrevb.94.201107

57. Fedorov A, Yaresko A, Kim TK, Kushnirenko Y, Haubold E, Wolf T, et al. Effect of Nematic Ordering on Electronic Structure of FeSe. Sci Rep (2016) 6:36834. doi:10.1038/srep36834

58. Pustovit YV, Kordyuk AA. Metamorphoses of Electronic Structure of FeSe-Based Superconductors (Review Article). Low Temperature Phys (2016) 42:995–1007. doi:10.1063/1.4969896

59. Zhang Y, Yi M, Liu Z-K, Li W, Lee JJ, Moore RG, et al. Distinctive Orbital Anisotropy Observed in the Nematic State of a FeSe Thin Film. Phys Rev B (2016) 94:115153. doi:10.1103/physrevb.94.115153

60. Watson MD, Haghighirad AA, Rhodes LC, Hoesch M, Kim TK. Electronic Anisotropies Revealed by Detwinned Angle-Resolved Photo-Emission Spectroscopy Measurements of FeSe. New J Phys (2017) 19:103021. doi:10.1088/1367-2630/aa8a04

61. Coldea AI, Watson MD. The Key Ingredients of the Electronic Structure of FeSe. Annu Rev Condens Matter Phys (2018) 9:125–46. doi:10.1146/annurev-conmatphys-033117-054137

62. Jiang K, Hu J, Ding H, Wang Z. Interatomic Coulomb Interaction and Electron Nematic Bond Order in FeSe. Phys Rev B (2016) 93:115138. doi:10.1103/physrevb.93.115138

63. Yi M, Pfau H, Zhang Y, He Y, Wu H, Chen T, et al. Nematic Energy Scale and the Missing Electron Pocket in FeSe. Phys Rev X (2019) 9:041049. doi:10.1103/physrevx.9.041049

64. Yu R, Zhu J-X, Si Q. Orbital Selectivity Enhanced by Nematic Order in FeSe. Phys Rev Lett (2018) 121:227003. doi:10.1103/physrevlett.121.227003

65. Yi M, Zhang Y, Shen Z-X, Lu D. Role of the Orbital Degree of freedom in Iron-Based Superconductors. Npj Quant Mater (2017) 2:57. doi:10.1038/s41535-017-0059-y

66. Huang J, Yu R, Xu Z, Zhu JX, Oh JS, Jiang Q, et al. Correlation-Driven Electronic Reconstruction in FeTe_1−xSe_x. Communications Physics (2022) 5 (1):29. doi:10.1038/s42005-022-00805-6

67. Pfau H, Yi M, Hashimoto M, Chen T, Dai P-C, Shen Z-X, et al. Quasiparticle Coherence in the Nematic State of FeSe. Phys Rev B (2021) 104:L241101. doi:10.1103/physrevb.104.l241101

68. Mirri C, Dusza A, Bastelberger S, Chinotti M, Degiorgi L, Chu J-H, et al. Origin of the Resistive Anisotropy in the Electronic Nematic Phase of BaFe₂As₂ Revealed by Optical Spectroscopy. Phys Rev Lett (2015) 115:107001. doi:10.1103/physrevlett.115.107001

69. Mirri C, Dusza A, Bastelberger S, Chinotti M, Chu J-H, Kuo H-H, et al. Electrodynamic Response in the Electronic Nematic Phase of BaFe₂As₂. Phys Rev B (2016) 93:085114. doi:10.1103/physrevb.93.085114

70. Wu D, Barišić N, Kallina P, Faridian A, Gorshunov B, Drichko N, et al. Optical Investigations of the normal and Superconducting States Reveal Two Electronic Subsystems in Iron Pnictides. Phys Rev B (2010) 81:100512. doi:10.1103/physrevb.81.100512

71. Fanfarillo L, Benfatto L, Valenzuela B. Orbital Mismatch Boosting Nematic Instability in Iron-Based Superconductors. Phys Rev B (2018) 97:121109. doi:10.1103/physrevb.97.121109

72. Fernández-Martín R, Fanfarillo L, Benfatto L, Valenzuela B. Anisotropy of the dc Conductivity Due to Orbital-Selective Spin Fluctuations in the Nematic Phase of Iron Superconductors. Phys Rev B (2019) 99:155117. doi:10.1103/PhysRevB.99.155117

73. Schütt M, Schmalian J, Fernandes RM. Origin of DC and AC Conductivity Anisotropy in Iron-Based Superconductors: Scattering Rate Versus Spectral Weight Effects. Phys Rev B (2016) 94:075111. doi:10.1103/PhysRevB.94.075111

74. Böhmer AE, Kreisel A. Nematicity, Magnetism and Superconductivity in FeSe. J Phys Condensed Matter (2017) 30:023001. doi:10.1088/1361-648x/aa9caa

75. Lu X, Zhang W, Tseng Y, Liu R, Tao Z, Paris E, et al. (2021), arXiv:2108.04484 [cond-mat.supr-con]. Available at: https://arxiv.org/abs/2108.04484.

76. Benfatto L, Valenzuela B, Fanfarillo L. Nematic Pairing from Orbital-Selective Spin Fluctuations in FeSe. Npj Quant Mater (2018) 3:56. doi:10.1038/s41535-018-0129-9

77. Baek S-H, Ok JM, Kim JS, Aswartham S, Morozov I, Chareev D, et al. Separate Tuning of Nematicity and Spin Fluctuations to Unravel the Origin of Superconductivity in FeSe. Npj Quan Mater. (2020) 5:8. doi:10.1038/s41535-020-0211-y

78. Wang Q, Shen Y, Pan B, Hao Y, Ma M, Zhou F, et al. Strong Interplay between Stripe Spin Fluctuations, Nematicity and Superconductivity in FeSe. Nat Mater (2016) 15:159–63. doi:10.1038/nmat4492

79. Chen T, Chen Y, Kreisel A, Lu X, Schneidewind A, Qiu Y, et al. Anisotropic Spin Fluctuations in Detwinned FeSe. Nat Mater (2019) 18:709–16. doi:10.1038/s41563-019-0369-5

80. Li G, Hu WZ, Dong J, Li Z, Zheng P, Chen GF, et al. Probing the Superconducting Energy Gap from Infrared Spectroscopy on a Ba_0.6K_0.4Fe₂As₂ Single Crystal with T_c=37 K. Phys Rev Lett (2008) 101:107004. doi:10.1103/physrevlett.101.107004

81. Charnukha A, Dolgov OV, Golubov AA, Matiks Y, Sun DL, Lin CT, et al. Eliashberg Approach to Infrared Anomalies Induced by the Superconducting State of Ba_0.68K_0.32Fe₂As₂ Single Crystals. Phys Rev B (2011) 84:174511. doi:10.1103/physrevb.84.174511

82. Charnukha A, Popovich P, Matiks Y, Sun DL, Lin CT, Yaresko AN, et al. Superconductivity-induced Optical Anomaly in an Iron Arsenide. Nat Commun (2011) 2:219. doi:10.1038/ncomms1223

83. Dai YM, Xu B, Shen B, Xiao H, Wen HH, Qiu XG, et al. Hidden T-Linear Scattering Rate in Ba_0.6K_0.4Fe₂As₂ Revealed by Optical Spectroscopy. Phys Rev Lett (2013) 111:117001. doi:10.1103/physrevlett.111.117001

84. Dai YM, Xu B, Shen B, Wen HH, Qiu XG, Lobo RPSM. Optical Conductivity of Ba_0.6K_0.4Fe₂As₂: The Effect of In-Plane and Out-Of-Plane Doping in the Superconducting gap. Epl (2013) 104:47006. doi:10.1209/0295-5075/104/47006

85. Xu B, Dai YM, Xiao H, Shen B, Wen HH, Qiu XG, et al. Infrared Probe of the gap Evolution across the Phase Diagram of Ba_1−xK_xFe₂As₂. Phys Rev B (2017) 96:115125. doi:10.1103/physrevb.96.115125

86. Kretzschmar F, Muschler B, Böhm T, Baum A, Hackl R, Wen H-H, et al. Raman-Scattering Detection of Nearly Degenerate s-Wave and d-Wave Pairing Channels in Iron-Based Ba_0.6K_0.4Fe₂As₂ and Rb_0.8Fe_1.6Se₂ Superconductors. Phys Rev Lett (2013) 110:187002. doi:10.1103/physrevlett.110.187002

87. Pal A, Chinotti M, Chu J-H, Kuo H-H, Fisher IR, Degiorgi L. Anisotropic Superconducting Gap in Optimally Doped Iron-Based Material. J Supercond Nov Magn (2020) 33:2313–8. doi:10.1007/s10948-019-05390-4

88. Carlson EW, Dahmen KA. Using Disorder to Detect Locally Ordered Electron Nematics via Hysteresis. Nat Commun (2011) 2:379. doi:10.1038/ncomms1375

89. Kuo H-H, Fisher IR. Effect of Disorder on the Resistivity Anisotropy Near the Electronic Nematic Phase Transition in Pure and Electron-Doped BaFe₂As₂. Phys Rev Lett (2014) 112:227001. doi:10.1103/physrevlett.112.227001

90. Ishida S, Nakajima M, Liang T, Kihou K, Lee CH, Iyo A, et al. Anisotropy of the In-Plane Resistivity of Underdoped Ba(Fe_1−xCo_x)₂As₂ Superconductors Induced by Impurity Scattering in the Antiferromagnetic Orthorhombic Phase. Phys Rev Lett (2013) 110:207001. doi:10.1103/physrevlett.110.207001

91. Nakajima M, Ishida S, Tomioka Y, Kihou K, Lee CH, Iyo A, et al. Effect of Co Doping on the In-Plane Anisotropy in the Optical Spectrum of Underdoped Ba(Fe_1−xCo_x)₂As₂. Phys Rev Lett (2012) 109:217003. doi:10.1103/physrevlett.109.217003

92. Christianson AD, Goremychkin EA, Osborn R, Rosenkranz S, Lumsden MD, Malliakas CD, et al. Unconventional Superconductivity in Ba_0.6K_0.4Fe₂As₂ from Inelastic Neutron Scattering. Nature (2008) 456:930–2. doi:10.1038/nature07625

93. Böhm T, Kemper AF, Moritz B, Kretzschmar F, Muschler B, Eiter H-M, et al. Balancing Act: Evidence for a Strong Subdominant d-Wave Pairing Channel in Ba_0.6K_0.4Fe₂As₂. Phys Rev X (2014) 4:041046. doi:10.1103/PhysRevX.4.041046

94. Li J, Pereira PJ, Yuan J, Lv Y-Y, Jiang M-P, Lu D, et al. Nematic Superconducting State in Iron Pnictide Superconductors. Nat Commun (2017) 8:1880. doi:10.1038/s41467-017-02016-y

95. Chen L, Han TT, Cai C, Wang ZG, Wang YD, Xin ZM, et al. Orbital-dependent Modulation of the Superconducting gap in Uniaxially Strained Ba_0.6K_0.4Fe₂As₂. Phys Rev B (2021) 104:L060502. doi:10.1103/physrevb.104.l060502

96. Dong Y, Lv Y, Xu Z, Abdel-Hafiez M, Vasiliev AN, Zhu H, et al. Observation of a Ubiquitous (π, π)-Type Nematic Superconducting Order in the Whole Superconducting Dome of Ultra-thin BaFe_2−xNi_xAs₂ Single Crystals. Chin Phys. Lett. (2021) 38:097401. doi:10.1088/0256-307x/38/9/097401

97. Kushnirenko YS, Evtushinsky DV, Kim TK, Morozov I, Harnagea L, Wurmehl S, et al. Nematic Superconductivity in LiFeAs. Phys Rev B (2020) 102:184502. doi:10.1103/physrevb.102.184502

98. Sprau PO, Kostin A, Kreisel A, Böhmer AE, Taufour V, Canfield PC, et al. Discovery of Orbital-Selective Cooper Pairing in FeSe. Science (2017) 357:75–80. doi:10.1126/science.aal1575

99. She J-H, Lawler MJ, Kim E-A. Quantum Spin Liquid Intertwining Nematic and Superconducting Order in Fese. Phys Rev Lett (2018) 121:237002. doi:10.1103/physrevlett.121.237002

100. Liu D, Li C, Huang J, Lei B, Wang L, Wu X, et al. Orbital Origin of Extremely Anisotropic Superconducting Gap in Nematic Phase of FeSe Superconductor. Phys Rev X (2018) 8:031033. doi:10.1103/physrevx.8.031033

101. Hu H, Yu R, Nica EM, Zhu J-X, Si Q. Orbital-selective Superconductivity in the Nematic Phase of FeSe. Phys Rev B (2018) 98:220503. doi:10.1103/physrevb.98.220503

102. Zvyagina GA, Gaydamak TN, Zhekov KR, Bilich IV, Fil VD, Chareev DA, et al. Acoustic Characteristics of FeSe Single Crystals. EPL (2013) 101:56005. doi:10.1209/0295-5075/101/56005

103. Kothapalli K, Boöhmer AE, Jayasekara WT, Ueland BG, Das P, Sapkota A, et al. Strong Cooperative Coupling of Pressure-Induced Magnetic Order and Nematicity in FeSe. Nat Commun (2016) 7:12728. doi:10.1038/ncomms12728