Topological Phase Transitions and Evolution of Boundary States Induced by Zeeman Fields in Second-Order Topological Insulators

Second-order topological insulators (SOTIs) are a class of materials hosting gapless bound states at boundaries with dimension lower than the bulk by two. In this work, we investigate the effect of Zeeman field on two- and three-dimensional time-reversal invariant SOTIs. We find that a diversity of topological phase transitions can be driven by the Zeeman field, including both boundary and bulk types. For boundary topological phase transitions, we find that the Zeeman field can change the time-reversal invariant SOTIs to time-reversal symmetry breaking SOTIs, accompanying with the change of the number of robust corner or hinge states. Relying on the direction of Zeeman field, the number of bound states per corner or chiral states per hinge can be either one or two in the resulting time-reversal symmetry breaking SOTIs. Remarkably, for bulk topological phase transitions, we find that the transitions can result in Chern insulator phases with chiral edge states and topological semimetal phases with sharply-localized corner states in two dimensions, and hybrid-order Weyl semimetal phases with the coexistence of surface Fermi arcs and gapless hinge states in three dimensions. Our study reveals that the Zeeman field can induce very rich physics in higher-order topological materials.

1 Introduction

In the last few years, higher-order topological phases have attracted tremendous interest owing to the emergence of novel boundary physics beyond the description of conventional bulk-boundary correspondence [1–27]. Roughly speaking, a mth-order topological phases in n dimensions (n ≥ m) harbors robust gapless states at boundaries with dimensions lower than the bulk by m [28]. For instance, a second-order topological insulator (SOTI) will harbor robust bound states at the sample corners in two dimensions and chiral or helical propagating states on the sample hinges in three dimensions. From a boundary perspective, the higher-order topology can be intuitively understood as the existence of certain forms of Dirac domain walls on the boundary [29, 30]. If the Dirac domain walls are symmetry-enforced, the corresponding higher-order topological phases are commonly categorized to the intrinsic class, otherwise they are categorized to the extrinsic class.

The higher-order topology greatly extends the freedom of bound states on the boundary. On one hand, the positions of bound states may be highly tunable by some external fields if they are not pinned due to symmetry constraints [31, 32]. Such tunability may benefit the design of devices based on higher-order topological materials for applications [33–35]. On the other hand, bound states with different dimensions can coexist in the same system [36], which may result in novel responses absent in conventional topological phases. The higher-order topology also enriches the possibility of topological phase transitions [37–42]. With the advent of higher-order topology, topological phase transitions can happen not only between the different topological sectors of a topological phase following Z or Z₂ classification [43, 44], but also between phases with different orders in topology [37].

Higher-order topological insulators and semimetals have already been implemented in a great amount of platforms [45–56], while the experimental progress in higher-order topological superconductors is slow as the superconductivity is an intrinsic quantum phenomena without classical counterparts [57]. Thus far, the experimental studies on higher-order topological insulators and semimetals have also been mainly done in metamaterial systems owing to their great advantages in controllability in design and measurements [58]. In comparison, in spite of the accumulation in quantum material candidates for higher-order topological insulator and semimetals [59–72], related experiments on quantum materials remain relatively rare due to the much higher complexity in material growth and detecting the expected signatures of higher-order topology [73–77].

While higher-order topological insulators and semimetals have been intensively studied in experiments in metamaterial systems, we notice that the response of higher-order topological phases to external fields remains poorly explored [78–85]. In this work, we systematically investigate the effects of Zeeman field on time-reversal invariant SOTIs, with a particular focus on the possible topological phase transitions and the associated evolution of boundary states. It is worth noting that while the Zeeman field in a quantum material can be induced by an external magnetic field or the proximity-induced exchange field from magnetic materials in contact, the Zeeman field in metamaterials cannot be implemented in the same way as the underlying spin degrees of freedom are not real spin. Nevertheless, effective Zeeman fields in metamaterials can also be generated by appropriately designing the on-site potentials and couplings between sites [86]. In a quantum material, if the Zeeman field is generated by an external out-of-plane magnetic field, it is known that orbital effect also needs to be taken into account. However, if the Zeeman field is generated by an in-plane magnetic field or exchange interaction in a quantum material, the orbital effect is absent. Moreover, the effective Zeeman field in matematerials is not tied with an orbital effect as the spin is pseudo. With these in mind, in this work we will only focus on the Zeeman field and not consider the orbit effect.

The main findings of our work can be summarized as follows. In two dimensions, when the concerned time-reversal invariant SOTI with each corner harboring two zero-energy bound states is subjected to the Zeeman field, we find that the fate of the zero-energy corner states depends on the direction, the strength, and the type of Zeeman field. When the Zeeman field is a layer-independent ferromagnetic type and in the out-of-plane direction, we find that the two zero-energy bound states per corner are robust in the weak-field regime even though the time-reversal symmetry and chiral symmetry are broken. With the increase of Zeeman field, a bulk topological phase transition will happen at a critical value, and the system will enter a Chern insulator phase [87]. The topological phase transition is accompanied with the disappearance of corner modes and the emergence of chiral edge states. When the ferromagnetic-type Zeeman field is changed to lie in the lattice plane, we find that the number of zero-energy bound states per corner also does not change in the weak-field regime. With the increase of field strength, we find that the system can first undergo a boundary topological phase transition and enter a new SOTI phase with the number and the locations of zero-energy bound states depend on the direction of Zeeman field. Remarkably, we find that corner states can still exist even when the system is driven into a topological semimetal phase with flat-band edge states. When the Zeeman field changes to be an antiferromagnetic type, we find that the number of zero-energy bound states per corner does not change in the weak-field regime if the Zeeman field is along the out-of-plane direction. With the increase of field strength, the system will undergo a bulk topological phase transition and enter a new SOTI with each corner only hosting one zero-energy bound state. When the antiferromagnetic-type Zeeman field lies in the lattice plane, we find that the energies of the corner states will in general be shifted away from zero. Only when the Zeeman field is along certain special direction, the corner states can accidentally be pinned at zero energy. In three dimensions, we focus on the ferromagnetic-type Zeeman field as it is more realistic than the antiferromagnetic one in a bulk system. Similar to the situations in two dimensions, we find that the helical states on the hinges are robust in the weak-field regime. Interestingly, when the field is strong enough to drive the system into a Weyl semimetal phase [88], we find that the resulting Weyl semimetal can host hybrid-order topological properties. That is, first-order topological surface Fermi arcs and second-order topological helical or chiral hinge states can coexist on the boundary.

The paper is organized as follows. In Section 2, we start with a minimal model of time-reversal invariant SOTI and systematically study what kind of topological phase transitions can be induced by Zeeman fields. In Section 3, we generalize the study to three dimensions and investigate what kind of novel topological phases can be achieved. We discuss the results and conclude the paper in Section 4.

2 Topological Phase Transitions Induced by Zeeman Field in Two-Dimensional SOTIs

As an important consequence of the presence of Zeeman field is the breaking of time-reversal symmetry, in this paper we will start with a time-reversal invariant SOTI so that the effect of Zeeman field can be fully appreciated. While theoretically time-reversal invariant SOTIs allow a lot of model realizations, the essential physics is similar. Without loss of generality, here we consider the following minimal Hamiltonian [4],

$\begin{array}{ccc}\hfill H\left(\mathit{k}\right)& =\hfill & \left(m-t\cos k_x-t\cos k_y\right){\rho }_0{\sigma }_z{s}_0+\mathrm{\lambda }\sin k_x{\rho }_0{\sigma }_x{s}_x\hfill \\ \hfill & \hfill & +\mathrm{\lambda }\sin k_y{\rho }_0{\sigma }_x{s}_y+\eta \left(\cos k_x-\cos k_y\right){\rho }_y{\sigma }_y{s}_0\hfill \\ \hfill & \hfill & +{\rho }_0{\sigma }_0\mathit{B}\cdot \mathbf{s},\hfill \end{array}(1)$

where ρ_i, σ_i and s_i are Pauli matrices acting on layer, orbital and spin degrees of freedom, respectively. For notational simplicity, the lattice constants are set to unity throughout this paper. If the Hamiltonian only has the first three terms, the Hamiltonian simply describes two layers of decoupled topological insulators when 0 < |m| < 2t and λ ≠ 0 [89]. Accordingly, there are two pairs of helical edge states on the boundary. Since time-reversal invariant insulators in two dimensions follow a Z₂ classification if there is no additional crystalline symmetry [90], the two pairs of helical edge states are not topologically protected and can be gapped out by perturbations respecting time-reversal symmetry. The fourth term couples the two layers and leads to the hybridization of the edge states to open a gap. Interestingly, because of the existence of line nodes along the directions k_x = ±k_y, this term results in a time-reversal invariant SOTI with doubly-degenerate zero-energy bound states appearing at the intersecting corners of x-normal and y-normal edges [4]. The last term represents the Zeeman field which breaks time-reversal symmetry. Here we first consider that the two layers have the same Zeeman field, corresponding to a ferromagnetic type.

When the Zeeman field is along the z direction, i.e., B = (B_x, B_y, B_z) = (0, 0, B_z), besides the time-reversal symmetry, one can find that the chiral symmetry is also broken. As a result, one should expect that the doubly-degenerate bound states per corner of the time-reversal invariant SOTI are not stable against the Zeeman field. However, counterintuitively, this is not the case. To see this, the most evident way is to derive the boundary Hamiltonian explicitly since the corner states are a result of the formation of Dirac domain walls on the boundary [12]. Without loss of generality, let us first derive the low-energy Hamiltonian describing the left x-normal edge. Assuming that the minimum of the band gap is located at the time-reversal invariant momentum Γ = (0, 0), we expand the lattice Hamiltonian around Γ to obtain the low-energy bulk Hamiltonian. Keeping momentum up to the second order, it takes the form

$\begin{array}{ccc}\hfill H\left(\mathit{k}\right)& =\hfill & \left[\tilde{m}+\frac{t}{2}\left(k_x^2+k_y^2\right)\right]{\rho }_0{\sigma }_z{s}_0+\mathrm{\lambda }{k}_x{\rho }_0{\sigma }_x{s}_x\hfill \\ \hfill & \hfill & +\mathrm{\lambda }{k}_y{\rho }_0{\sigma }_x{s}_y-\frac{\eta }{2}\left(k_x^2-k_y^2\right){\rho }_y{\sigma }_y{s}_0\hfill \\ \hfill & \hfill & +B_z{\rho }_0{\sigma }_0{s}_z.\hfill \end{array}(2)$

where $\tilde{m}=m-2t$ is assumed to be negative so that the Hamiltonian is in the SOTI phase when B_z = 0. For the convenience of discussion, below we consider that coefficients {t, λ, η, B_z} are all positive. When focusing on the left x-normal edge, we can assume that the system occupies the half-infinity plane 0 ≤ x < + ∞. Because of the breaking of translation symmetry along the x direction, the momentum k_x needs to be replaced by − i∂_x. Next we divide the Hamiltonian into two parts, H = H₁ + H₂, where

$\begin{array}{ccc}\hfill H_1\left(-i{\partial }_x,k_y\right)& =\hfill & \left[\tilde{m}+\frac{t}{2}{k}_y^2-\frac{t}{2}{\partial }_x^2\right]{\rho }_0{\sigma }_z{s}_0-i\mathrm{\lambda }{\partial }_x{\rho }_0{\sigma }_x{s}_x,\hfill \\ \hfill H_2\left(-i{\partial }_x,k_y\right)& =\hfill & \mathrm{\lambda }{k}_y{\rho }_0{\sigma }_x{s}_y-\frac{\eta }{2}\left(k_x^2-k_y^2\right){\rho }_y{\sigma }_y{s}_0\hfill \\ \hfill & \hfill & +B_z{\rho }_0{\sigma }_0{s}_z.\hfill \end{array}(3)$

By solving the eigenvalue equation H₁ (−i∂_x, k_y)ψ(x) = Eψ(x) under the boundary conditions ψ(0) = ψ(+∞) = 0, one finds the existence of four zero-energy bound states as long as $\tilde{m}+t{k}_y^2/2<0$. The wave functions for the four zero-energy bound states can be compactly written in the form [12].

${\psi }_{\rho \sigma }\left(x\right)=\mathcal{N}\sin \left({\kappa }_{1}x\right)e^{-{\kappa }_{2}x}{e}^{i{k}_{y}y}{\chi }_{\rho \sigma },(4)$

where ${\chi }_{\rho \sigma }=|{\rho }_z=\rho ,{\sigma }_y=\sigma ,s_x=\bar{\sigma }\rangle$ with ρ = ±1, σ = ±1 and $\bar{\sigma }=-\sigma$, the normalization constant $\mathcal{N}=2\sqrt{{\kappa }_2({\kappa }_1^2+{\kappa }_2^2)/{\kappa }_1^2}$ with ${\kappa }_1=\sqrt{-2\tilde{m}/t-k_y^2-{(\mathrm{\lambda }/t)}^2}$ and κ₂ = λ/t. The effect of H₂ on these zero-energy bound states can be determined by projecting H₂ onto the four-dimensional subspace spanned by the four orthogonal wave functions of the zero-energy bound states. Since the bound states from H₁ have zero energy, this projection directly determines the low-energy boundary Hamiltonian. Put it explicitly, the low-energy Hamiltonian is given by

$H_{x_L;\rho \sigma ,{\rho }^{\prime }{\sigma }^{\prime }}\left(k_y\right)={\int }_0^{+\infty }{\psi }_{\rho \sigma }^{†}\left(x\right)H_2\left(-i{\partial }_x,k_y\right){\psi }_{{\rho }^{\prime }{\sigma }^{\prime }}\left(x\right)dx.(5)$

Simple algebra calculations reveal that under the basis ${({\chi }_{11},{\chi }_{1-1},{\chi }_{-11},{\chi }_{-1-1})}^T$, the low-energy boundary Hamiltonian can be expressed in terms of the Pauli matrices as

$H_{x_L}\left(k_y\right)=-\mathrm{\lambda }{k}_y{\rho }_0{\sigma }_x-\frac{\eta \tilde{m}}{t}{\rho }_y{\sigma }_z.(6)$

The second term on the right hand side corresponds to the Dirac mass induced by the η term. Remarkably, one can find that the Zeeman field does not enter the boundary Hamiltonian. In other words, the Zeeman field does not have a direct effect on the boundary Hamiltonian, so the corner modes, even though both time-reversal symmetry and chiral symmetry are broken. Using the lattice Hamiltonian, we have numerically verified that the doubly-degenerate zero-energy bound states per corner are indeed robust against the Zeeman field in the weak-field regime, as shown in Figure 1.

FIGURE 1

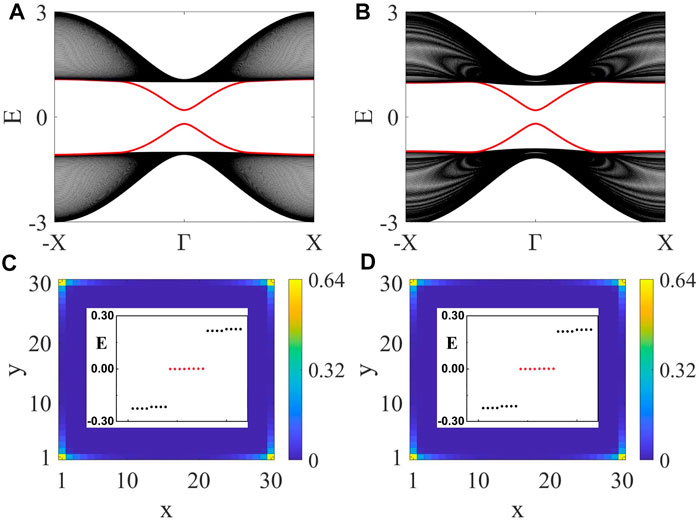
FIGURE 1. (Color online) The response of edge states (red lines) and corner states (red dots) to an out-of-plane ferromagnetic-type Zeeman field. Chosen parameters are: t = 1, m = 1, λ = 1, η = 0.2. In (A) and (C), B_z = 0. In (B) and (D), B_z = 0.1. In (A) and (B), periodic and open boundary conditions are considered in the x and y directions, respectively. The system size in the y direction is N_y = 100. In (A) and (B), Γ and X denote k_x = 0 and π, respectively. In (C) and (D), both x and y directions take open boundary conditions, and the probability density files of the zero-energy eigenstates (red dots in the inset) show that they are strongly localized at the lattice corners. A comparison of (A) and (C) with (B) and (D) reveals that the out-of-plane Zeeman field has negligible effects on the edge states and corner states in the weak-field regime.

Although the out-of-plane Zeeman field does not directly enter the boundary Hamiltonian, it affects the boundary through the bulk indirectly. To be more specific, the Zeeman field will affect the boundary states by reducing the bulk energy gap. To see this, let us diagonalize the Hamiltonian and obtain the energy spectrum, which reads

$E\left(\mathit{k}\right)=\pm \sqrt{{\left[M\left(\mathit{k}\right)\pm B_z\right]}^2+{\mathrm{\lambda }}^2\left({\sin }^2{k}_x+{\sin }^2{k}_y\right)},(7)$

where $M(\mathit{k})=\sqrt{m^2(\mathit{k})+{\eta }^2(\mathit{k})}$ with m(k) = (m − t cos k_x − t cos k_y) and η(k) = η(cos k_x − cos k_y) is introduced to shorten the expression. Apparently, the Zeeman field will directly change the bulk energy gap. In fact, it is easy to find that the bulk energy gap will vanish at one or two of the four time-reversal invariant momentums, Γ = (0, 0), X = (π, 0), Y = (0, π), M = (π, π), when B_z takes any one of the follow-up values, ± (m ± 2t) and $\pm \sqrt{m^2+4{\eta }^2}$. To see what kind of new topological phases can be induced by the out-of-plane Zeeman field, let us assume that m is close to 2t and η is much smaller than t, then the bulk energy gap undergoes the first closing-and-reopening transition when B_z is increased to the value B_c,Γ ≡|m − 2t|, and the last transition when B_z is increased to the value B_c,M ≡|m + 2t|. Let us first consider that B_z is approaching to B_c,Γ. Near this critical value, the band-gap minimum is located at Γ. To simplify the follow-up discussions, we keep momentum only up to the linear order in the low-energy bulk Hamiltonian. Accordingly, we have

$\begin{array}{ccc}\hfill H\left(\mathit{k}\right)& =\hfill & \tilde{m}{\rho }_0{\sigma }_z{s}_0+\mathrm{\lambda }{k}_x{\rho }_0{\sigma }_x{s}_x\hfill \\ \hfill & \hfill & +\mathrm{\lambda }{k}_y{\rho }_0{\sigma }_x{s}_y+B_z{\rho }_0{\sigma }_0{s}_z\hfill \\ \hfill & =\hfill & H_{{\rho }_z=1}\left(\mathit{k}\right)\oplus H_{{\rho }_z=-1}\left(\mathit{k}\right).\hfill \end{array}(8)$

Since $H_{{\rho }_z=\pm 1}$ are the same, we can focus on just one of them, e.g., $H_{{\rho }_z=1}$. Interestingly, $H_{{\rho }_z=1}$ itself takes a block diagonal form, i.e., $H_{{\rho }_z=1}=H_{+}\oplus H_{-}$ with

$\begin{array}{ccc}\hfill H_{+}\left(\mathit{k}\right)& =\hfill & \left(\tilde{m}+B_z\right){\sigma }_z+\mathrm{\lambda }{k}_x{\sigma }_x+\mathrm{\lambda }{k}_y{\sigma }_y,\hfill \\ \hfill H_{-}\left(\mathit{k}\right)& =\hfill & \left(\tilde{m}-B_z\right){\sigma }_z+\mathrm{\lambda }{k}_x{\sigma }_x-\mathrm{\lambda }{k}_y{\sigma }_y.\hfill \end{array}(9)$

It is worth noting that although the mathematical forms of Pauli matrices are same, the physical interpretation of the Pauli matrices σ_i in H_± is distinct to that in Eq. 1 as their underlying bases are different. However, here we are only interested in the topological property hiding in the mathematical structure of the Hamiltonian. When B_z is approaching to B_c,Γ, the energy gap for H₊(k) will undergo a closing-and-reopening transition while the one for H₋(k) remains open. Therefore, only H₊(k) will undergo a topological phase transition. Because neither time-reversal symmetry nor chiral symmetry is conserved, the first-order topology of H₊(k) is characterized by the first-class Chern number [91]. For a two-band model, the Chern number can be simply determined by the formula [92].

$C=-\frac{1}{4\pi }\int \frac{\mathit{d}\cdot \left(\frac{\partial \mathit{d}}{\partial k_x}\times \frac{\partial \mathit{d}}{\partial k_y}\right)}{d^3}{d}^{2}k,(10)$

where d = (d_x, d_y, d_z) with d_i being the coefficient before the Pauli matrix σ_i and the integral is over the whole two-dimensional momentum space. A simple calculation reveals that the Chern number for H₊(k) is C₊ = sgn (−B_c,Γ + B_z)/2. It indicates that the Chern number has a jump ΔC = 1 when B_z is changed from B_z < B_c,Γ to B_z > B_c,Γ. As the Chern number is forced to be zero by time-reversal symmetry when B_z = 0 [93], the change of Chern number indicates that the system enters a Chern insulator phase with the total Chern number C = 2 after taking into account the contributions from two layers. In other words, an out-of-plane Zeeman field can induce a topological phase transition from a SOTI to a Chern insulator with the increase of its strength. We have numerically demonstrated this topological phase transition, as shown in Figure 2. After the topological phase transition, the zero-dimensional corner states disappear and one-dimensional chiral edge states emerge on the boundary. It is known that higher-order topology can naturally descend from symmetry-protected first-order topology by appropriately lifting the protecting symmetry [7, 8]. The above result indicates that the reverse is also true. As a final remark of this part, we point out that increasing the Zeeman field will drive the system from the Chern insulator phase back to the trivial insulator phase. This is easy to see since the system will go to the topologically trivial atomic limit when the strength of Zeeman field goes to infinity.

FIGURE 2

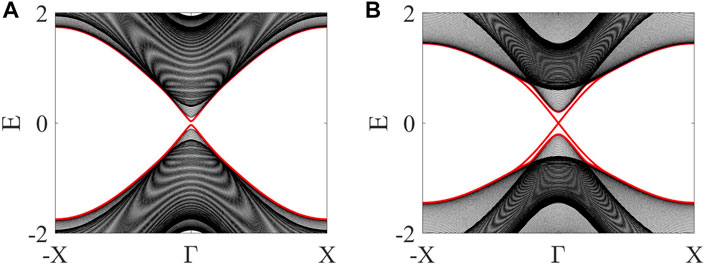
FIGURE 2. (Color online) Bulk topological phase transitions induced by an out-of-plane Zeeman field. Chosen parameters are: t = 1, m = 1.8, λ = 1, η = 0.2, N_y = 100. (A) B_z = 0.1, the edge spectrum remains gapped as B_z is smaller than the critical value B_c,Γ = 0.2. (B) B_z = 0.4, with B_z beyond the critical value, the edge spectrum becomes gapless, indicating the occurrence of a topological phase transition from a SOTI with corner states to a Chern insulator with chiral edge states.

Let us now turn our attention to the case with the Zeeman field lying in the xy plane, i.e., B = (B_x, B_y, 0). Unlike the out-of-plane Zeeman field, the in-plane Zeeman field does not break the chiral symmetry. It is worth noting that due to the simplicity of the Hamiltonian, there are two chiral symmetry operators, ρ_yσ_xs_z and ρ₀σ_xs_z. Since the time-reversal symmetry is broken and the chiral symmetry is preserved, the Hamiltonian falls into the symmetry class AIII. In two dimensions, this symmetry class does not support nontrivial first-order topological insulator phases [43, 44].

To see what kind of new topological phases can be induced by the in-plane Zeeman field, we follow previous procedures and firstly study the effect of Zeeman field on the boundary Hamiltonian. Let us still focus on the left x-normal edge for illustration. Similarly, the contribution from the Zeeman field to the boundary Hamiltonian is determined by

$\begin{array}{ccc}\hfill {\left(H_Z\right)}_{\rho \sigma ,{\rho }^{\prime }{\sigma }^{\prime }}& =\hfill & {\int }_0^{+\infty }{\psi }_{\rho \sigma }^{†}\left(x\right)\left[{\rho }_0{\sigma }_0\left(B_x{s}_x+B_y{s}_y\right)\right]{\psi }_{{\rho }^{\prime }{\sigma }^{\prime }}\left(x\right)dx\hfill \\ \hfill & =\hfill & -B_x{\left({\rho }_0{\sigma }_z\right)}_{\rho \sigma ,{\rho }^{\prime }{\sigma }^{\prime }}.\hfill \end{array}(11)$

Adding this contribution, the boundary Hamiltonian on the left x-normal edge becomes

$H_{x_L}\left(k_y\right)=-\mathrm{\lambda }{k}_y{\rho }_0{\sigma }_x-\frac{\eta \tilde{m}}{t}{\rho }_y{\sigma }_z-B_x{\rho }_0{\sigma }_z.(12)$

Since $[{\rho }_y,H_{x_L}]=0$, the Hamiltonian can be decomposed as the direct sum of two parts, $H_{x_L}=H_{{\rho }_y=1}\oplus H_{{\rho }_y=-1}$, where

$H_{{\rho }_y=\pm 1}\left(k_y\right)=-\mathrm{\lambda }{k}_y{\sigma }_x-\left(B_x\pm \frac{\eta \tilde{m}}{t}\right){\sigma }_z.(13)$

Apparently, the x-component of the in-plane Zeeman field directly changes the boundary Dirac mass on the x-normal edges. Similar analysis can also find that the y-component of the in-plane Zeeman field directly changes the boundary Dirac mass on the y-normal edges in the same way. According to Eq. 13, it is easy to find that the Dirac mass of one of the branches vanishes when $B_x=\pm \eta \tilde{m}/t$. This means that increasing the field strength from zero will induce a closing-and-reopening transition in the boundary energy gap, leading to the occurrence of a boundary topological phase transition [94]. Since the Zeeman field neither breaks the chiral symmetry nor changes the sign of Dirac mass when its value is smaller than the critical value $(|\eta \tilde{m}/t|)$, the doubly-degenerate corner states are also expected to be robust in the weak-field regime as long as the system size is sufficiently large so that the wave functions of corner states remain well separated in real space. When the Zeeman field is strong enough to induce a closing-and-reopening transition in the boundary energy gap, the sign change of Dirac mass will change the topological property of the domain walls at the corners. Accordingly, the number of corner states will change and the locations of corner states will depend on the direction of Zeeman field.

To show the evolution of boundary physics with respect to Zeeman field more explicitly, we numerically diagonalize the Hamiltonian under different boundary conditions. In Figures 3A–C, the energy spectra correspond to a cylindrical geometry with periodic boundary condition in the x direction and open boundary condition in the y direction. It is readily seen that the boundary energy gap undergoes a closing-and-reopening transition with the increase of Zeeman field, in agreement with the above analytical analysis. In Figures 3D–F, the number and locations of corner states are shown. The parameters in Figures 3D–F are respectively the same as Figures 3A–C, what is different is that open boundary conditions are adopted in both the x and y directions. It is readily found that the eight zero-energy corner states do remain robust in the weak-field regime. After the boundary topological phase transition, the number of zero-energy corner states is reduced by half. Interestingly, the remaining four zero-energy bound states are found to appear only at two of the four corners, with each one of the two corners hosting two zero-energy bound states. In Figures 3C,F, as B_x = − B_y is considered, the result indicates that the zero-energy bound states appear at the two corners whose connecting line is perpendicular to the direction of Zeeman field, implying that the positions of corner states can be manipulated by controlling the direction of Zeeman field.

FIGURE 3

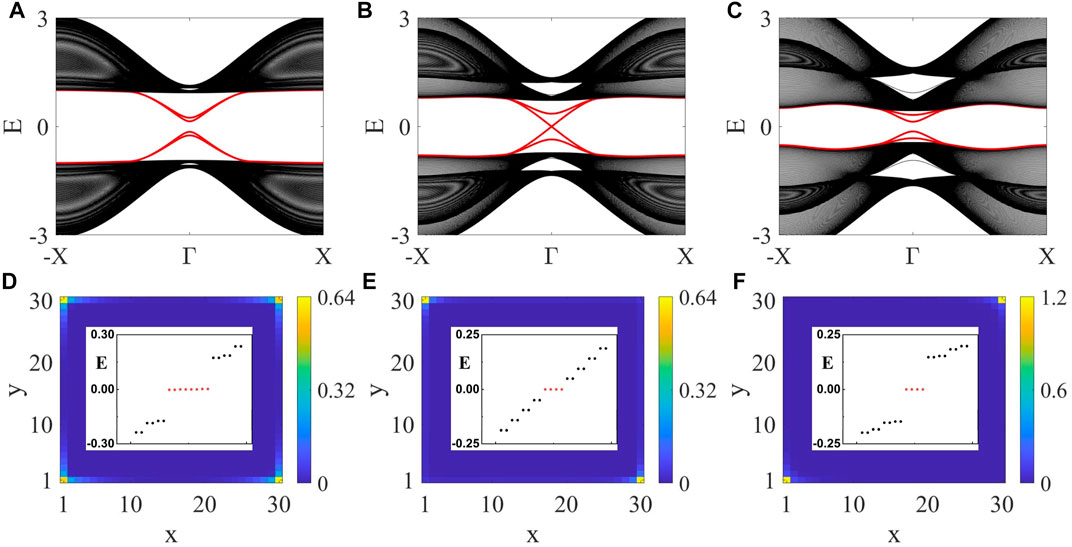
FIGURE 3. (Color online) Boundary topological phase transitions induced by an in-plane ferromagnetic-type Zeeman field. Chosen parameters are: t = 1, m = 1, λ = 1, η = 0.2. For the chosen set of parameters, the critical value for the boundary topological phase transition is $B_c=|\eta \tilde{m}/t|=0.2$. In (A) and (D), B_x = B_y = 0.05. As both B_x and B_y are smaller than B_c, the eight zero-energy corner states remain robust (the observable energy splitting for four corner states originates from the enhancement of finite-size effects as a result of the decrease in the boundary energy gap). In (B) and (E), B_x = B_y = 0.2, the boundary energy spectrum becomes gapless at this critical point. In (C) and (F), B_x = − B_y = 0.4. The boundary spectrum becomes gapped again, but the number of zero-energy bound states is reduced by half, indicating the realization of a new SOTI phase. In (A–C), periodic and open boundary conditions are considered in the x and y directions, respectively, with N_y = 100. In (D–F), both x and y directions take open boundary conditions.

Since the Dirac mass on the x(y)-normal edge is affected by the x(y)-component of the in-plane Zeeman field, the evolutions of the corner modes can be briefly described as follows. For the convenience of discussion, we also consider B_x and B_y to be positive and define $M_{\eta }=|\eta \tilde{m}/t|$. When B_x < M_η and B_y < M_η, each corner of the square-lattice sample harbors two zero-energy bound states as the Zeeman field is not strong enough to induce a boundary topological phase transition. When B_x < M_η < B_y or B_y < M_η < B_x, a sign change in Dirac mass has occurred on the y-normal or x-normal edges. As a result, the number of Dirac domain walls per corner will reduce from two to one, resulting in a new SOTI with one zero-energy bound state per corner. When M_η < B_x and M_η < B_y, the sign change in Dirac mass has occurred on both x-normal and y-normal edges. As we have illustrated in Figure 3F, for this case, two of the four corners harbor zero-energy bound states, and the positions of corner states are determined by the direction of Zeeman field. In Figure 4, the number and locations of zero-energy bound states are shown for the case with B_y < M_η < B_x. One can find that each corner does harbor one zero-energy bound state, in agreement with the above analysis.

FIGURE 4

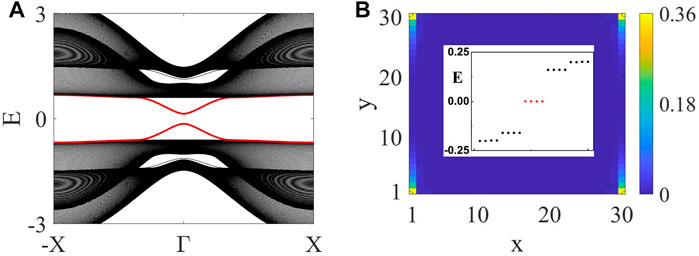
FIGURE 4. (Color online) Chosen parameters are: t = 1, m = 1, λ = 1, η = 0.2, B_x = 0.4, B_y = 0. (A) N_y = 100, the edge spectrum (red lines) on the y-normal edges does not split as the y-component of the Zeeman field is chosen to be zero. (B) Each corner of the open-square geometric lattice harbors one zero-energy bound state.

For the in-plane Zeeman field, so far we have only investigated its effect on the boundary. When the in-plane Zeeman field is strong enough, we find that the system will be driven into a topological semimetal phase. To see this, let us consider that the Zeeman field is in the x direction. Accordingly, the bulk energy spectrum is

$E\left(\mathit{k}\right)=\pm \sqrt{{\left[\sqrt{M^2\left(\mathit{k}\right)+{\mathrm{\lambda }}^2{\sin }^2{k}_x}\pm B_x\right]}^2+{\mathrm{\lambda }}^2{\sin }^2{k}_y}.(14)$

If we assume that the value of m is close to 2t so that the minimum of band gap is located at Γ, then the system becomes a topological semimetal when B_x becomes larger than B_c,Γ = |m − 2t|, with two nodal points appearing on the k_y = 0 axis. As the chiral symmetry is conserved, the topological properties of these nodal points are characterized by the winding number defined along a closed contour enclosing the nodal point [95]. Due to this topological protection, the nodal points are robust against perturbations respecting chiral symmetry and can only be annihilated pairwise.

If one views the system as a one-dimensional system by taking one of the momentum as a parameter, then the nodal points can also be viewed as critical points across which the winding number has a discrete change. Since a one-dimensional insulator with nontrivial winding number harbors zero-energy bound states on its two ends, this implies that the two-dimensional topological semimetal harbors flat-band edge states, as shown in Figure 5A. Remarkably, we find that even though the system becomes a semimetal, sharply-localized corner states can still appear if the Zeeman field is applied along the diagonal direction of the square geometric sample, as shown in Figures 5B–D.

FIGURE 5

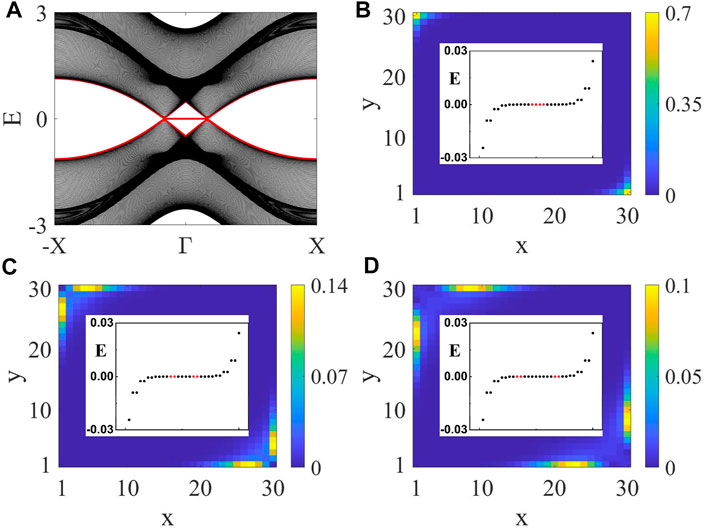
FIGURE 5. (Color online) Topological semimetal phases induced by an in-plane ferromagnetic-type Zeeman field. Chosen parameters are: t = 1, m = 1.8, λ = 1, η = 0.2, B_x = B_y = 0.5. (A) N_y = 100, the energy spectrum under a cylindrical geometry shows the existence of flat-band edge states. Under an open-square geometry, (B) shows that the probability density profiles of the four middle eigenstates (the four red dots in the inset) are sharply localized at the corners even though the bulk is gapless. (C) and (D) show the probability density profiles of some other eigenstates (also highlighted by red dots) with energies close to zero.

Above the Zeeman field has been assumed to be same in the two layers, corresponding to a ferromagnetic type, in the following we extend the study to the antiferromagnetic case for which the Zeeman fields in the two layers are opposite. Accordingly, the Hamiltonian takes the form

$\begin{array}{ccc}\hfill H\left(\mathit{k}\right)& =\hfill & \left(m-t\cos k_x-t\cos k_y\right){\rho }_0{\sigma }_z{s}_0+\mathrm{\lambda }\sin k_x{\rho }_0{\sigma }_x{s}_x\hfill \\ \hfill & \hfill & +\mathrm{\lambda }\sin k_y{\rho }_0{\sigma }_x{s}_y+\eta \left(\cos k_x-\cos k_y\right){\rho }_y{\sigma }_y{s}_0\hfill \\ \hfill & \hfill & +{\rho }_z{\sigma }_0\mathit{B}\cdot \mathbf{s}.\hfill \end{array}(15)$

Similarly, let us first focus on the out-of-plane case. It is easy to find that the chiral symmetry remains for this case, with the remaining chiral symmetry operator being ρ_yσ_xs_z. According to our previous discussion, the existence of chiral symmetry implies that the antiferromagnetic Zeeman field cannot drive the Hamiltonian into a Chern insulator phase. As the chiral symmetry still remains, the doubly-degenerate corner states are robust in the weak-field regime. By projecting the Zeeman field onto the subspace spanned by boundary states, one can find that it still does not enter the Hamiltonian. In other words, the out-of-plane antiferromagnetic Zeeman field cannot induce boundary topological phase transitions. Nevertheless, the topological property of the Hamiltonian can be changed with the increase of Zeeman field. This can be simply inferred from the bulk energy spectrum which reads

$E\left(\mathit{k}\right)=\pm \sqrt{{\left[m\left(\mathit{k}\right)\pm B_z\right]}^2+{\eta }^2\left(\mathit{k}\right)+{\mathrm{\lambda }}^2\left({\sin }^2{k}_x+{\sin }^2{k}_y\right)}.(16)$

With the increase of Zeeman field, the bulk energy gap will undergo closing-and-reopening transitions. To be specific, let us again assume the value of m to be close to 2t so that the minimum of band energy gap is located at Γ. Accordingly, with the increase of Zeeman field, the first transition occurs at B_z = B_c,Γ = |m − 2t|. When B_z > B_c,Γ, the Hamiltonian enters a new SOTI phase with each corner harboring one zero-energy bound state, as shown in Figure 6.

FIGURE 6

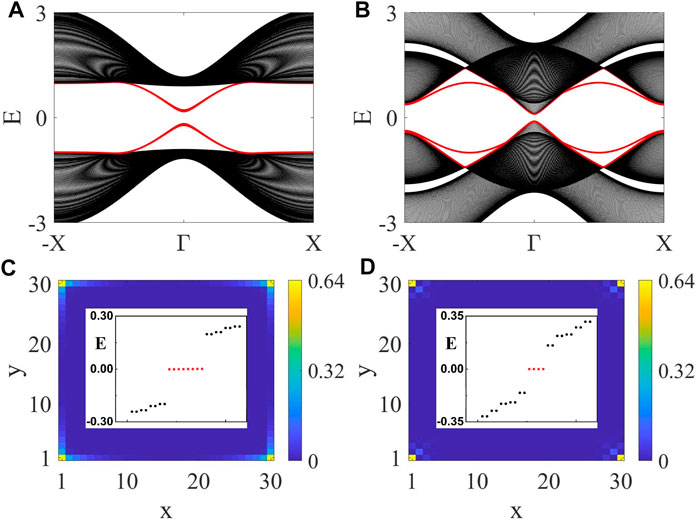
FIGURE 6. (Color online) Bulk topological phase transitions induced by an out-of-plane antiferromagnetic-type Zeeman field. Chosen parameters are: t = 1, m = 1, λ = 1, η = 0.2. For the chosen set of parameters, B_c,Γ = 1. In (A) and (C), B_z = 0.1 < B_c,Γ. The probability density profiles of the middle eight eigenstates and their eigenvalues (red dots) show that the eight zero-energy corner states are robust in the weak-field regime. In (B) and (D), B_z = 1.1 > B_c,Γ. The number of zero-energy corner states indicates that the system enters a new SOTI phase with one bound state per corner. N_y = 100 in (A) and (B).

When the antiferromagnetic-type Zeeman field lies in the xy plane, similar to the ferromagnetic-type case, the chiral symmetry also remains. However, now the Zeeman field will directly enter the boundary Hamiltonian. For instance, using the same derivation, we find that the low-energy boundary Hamiltonian for the left x-normal edge becomes

$H_{x_L}\left(k_y\right)=-\mathrm{\lambda }{k}_y{\rho }_0{\sigma }_x-\frac{\eta \tilde{m}}{t}{\rho }_y{\sigma }_z-B_x{\rho }_z{\sigma }_z.(17)$

A remarkable feature of the above Hamiltonian is that the Dirac masses induced by the η term and the Zeeman field become anticommutative. As the presence of an additional anticommutative term induces an overall mass on the boundary, the corner states are thus expected to be split away from zero energy. Through numerical calculations, we find that in general this is indeed the case, as shown in Figures 7A,C. However, when the Dirac masses induced by the Zeeman field and the η term are fine-tuned to have the same ratio on two near-neighboring edges, then their intersecting corner will harbor zero-energy bound states, as shown in Figures 7B,D. This result can be simply understood by noting that when the two Dirac masses with different origins have the same ratio on two near-neighboring edges, in fact we can redefine the Pauli matrices while maintaining their anticommutative relationship. By such a procedure, the boundary Hamiltonian reduces to the standard Dirac-Hamiltonian form with only one mass term which is known to support zero-energy bound states when the mass term has a domain-wall configuration in real space [96].

FIGURE 7

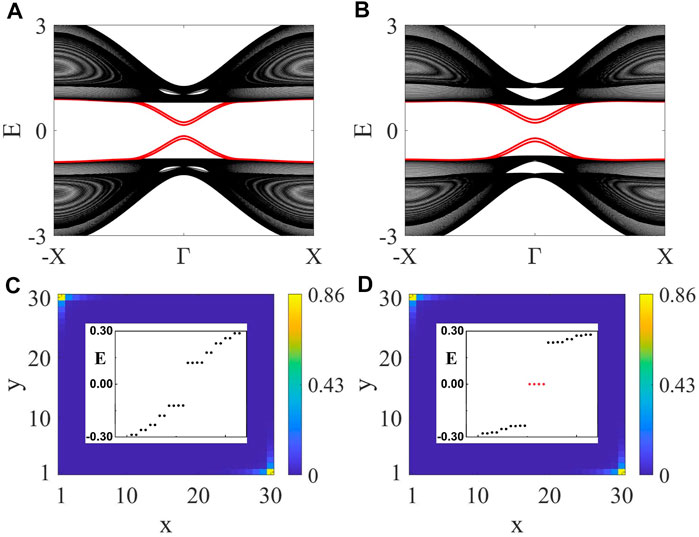
FIGURE 7. (Color online) The effect of an in-plane antiferromagnetic-type Zeeman field on the corner states. Chosen parameters are: t = 1, m = 1, λ = 1, η = 0.2. In (A) and (C), B_x = 0.2, B_y = 0. The Zeeman field shifts the energies of the corner states away from zero. In (B) and (D), B_x = B_y = 0.2. There are four corner states with energies accidentally pinned to zero due to the special choice of the Zeeman field. N_y = 100 in (A) and (B).

Since without fine tuning the zero-energy bound states are immediately gapped by the antiferromagnetic-type in-plane Zeeman field, the evolution of boundary physics is less interesting compared to the case with ferromagnetic-type in-plane Zeeman field. In addition, we find that the antiferromagnetic-type in-plane Zeeman field cannot drive the system into a topological semimetal phase. The increase of the field strength only drives the system to another trivial insulator phase, therefore, from the perspective of topology, the bulk physics is also less interesting compared to the case with ferromagnetic-type in-plane Zeeman fields.

3 Topological Phase Transitions Induced by Zeeman Field in Three-Dimensional SOTIs

As the increase of dimension enriches the allowed types of boundary states, it is natural to expect that the Zeeman field can induce a diversity of topological phases transitions and exotic patterns of boundary states in a three-dimensional SOTI. To generalize the study, we also follow the minimal-model approach as adopted in two dimensions. To be specific, we consider that the minimal Hamiltonian takes the form

$\begin{array}{ccc}\hfill H\left(\mathit{k}\right)& =\hfill & \left(m-t\sum _{i=x,y}\cos k_i-t_z\cos k_z\right){\rho }_0{\sigma }_z{s}_0\hfill \\ \hfill & \hfill & +\mathrm{\lambda }\sum _{i=x,y,z}\sin k_i{\rho }_0{\sigma }_x{s}_i\hfill \\ \hfill & \hfill & +\eta \left(\cos k_x-\cos k_y\right){\rho }_y{\sigma }_y{s}_0+{\rho }_0{\sigma }_0\mathit{B}\cdot \mathbf{s}.\hfill \end{array}(18)$

In this part, we will focus on the ferromagnetic-type Zeeman field as the study in two dimensions tells us that it can induce more interesting physics than the antiferromagnetic type. For this Hamiltonian, it realizes a time-reversal invariant SOTI when the last term representing the time-reversal symmetry breaking Zeeman field is absent and the parameters satisfy λ ≠ 0 and η ≠ 0, and |2t − t_z| < |m| < 2t + t_z. If open boundary conditions are taken in both the x and y directions, the second-order topology is manifested through the appearance of a pair of helical states on each of the z-direction hinges [3]. It is worth noting that when the open boundary condition is only applied in the z direction, the top and bottom surfaces still harbor gapless Dirac cones since the η term cannot open a gap at the time-reversal invariant momentum at which the Dirac cones are located.

In parallel to the two-dimensional case, we first consider that the Zeeman field is along the z direction. In the weak-field regime, the main effect of the Zeeman field is to open a gap on the top and bottom surfaces. Following the same analysis as done in two dimensions, it is easy to figure out that the Zeeman field has little impact on the helical states on the z-direction hinges even though the time-reversal symmetry is broken. To be more explicit, note that the three-dimensional Hamiltonian can be viewed as the stacking of an infinite number of two-dimensional layers in momentum space. In particular, the Hamiltonians at the two high-symmetry planes with k_z = 0 and π just reduce to the form of the previously studied two-dimensional Hamiltonian. According to the results in two dimensions, an out-of-plane Zeeman field does not directly affect the corner states in the weak-field regime, for the same reason, the helical states propagating on the z-direction hinges will remain stable in the weak-field regime. Because of the opening of a gap on the top and bottom surfaces and the stability of the helical states on the z-direction hinges against the z-direction Zeeman field, the helical states will no longer flow in the whole surface when they flow towards the top and bottom surfaces as the low-energy channels on these two surfaces have been emptied by the Zeeman field, instead they will be confined to flow along the x-direction or y-direction hinges so that the low-energy transport channels can form closed paths along the hinges.

With the increase of Zeeman field, we have shown that in two dimensions a Chern insulator with chiral edge states will be realized after the bulk energy gap undergoes a closing-and-reopening transition. For the Hamiltonian in Eq. 18, because of the increase in dimension, we find that the bulk energy gap does not immediately reopen when it is reduced to zero by the Zeeman field. Instead, the system enters a Weyl semimetal phase for a broad range of parameters, with the Weyl points located at some high-symmetry k_z axes. It is known that a hallmark of the Weyl semimetal is the Fermi arcs connecting the projections of Weyl points in the surface Brillouin zone [88]. Furthermore, if one treats the momentum k_z as a parameter, the Weyl points correspond to critical points separating regions with C (k_z) = 0 from the ones with C (k_z) ≠ 0. Interestingly, this raises the possibility of the coexistence of helical hinge states characterizing second-order topology and surface Fermi arcs characterizing first-order topology. In other words, hybrid-order topology is possible in this system. To see this, without loss of generality, let us assume that H (k_x, k_y, k_z = 0) realizes a SOTI with zero-energy corner states and H (k_x, k_y, k_z = π) realizes a trivial insulator. If the energy gap of H (k_x, k_y, k_z = π) is smaller than that of H (k_x, k_y, k_z = 0), then H (k_x, k_y, k_z = π) can first underdo a topological phase transition and enter a Chern insulator phase. Accordingly, it is clear that there exists a window within which H (k_x, k_y, k_z = 0) remains to be a SOTI due to its stability against the Zeeman field and H (k_x, k_y, k_z = π) becomes a Chern insulator with chiral edge states. In Figure 8, we have numerically demonstrated the above picture. It is worth noting that this class of hybrid-order Weyl semimetal phase is distinct to those so-called higher-order Weyl semimetals in which the hinge states are neither helical nor chiral [97, 98].

FIGURE 8

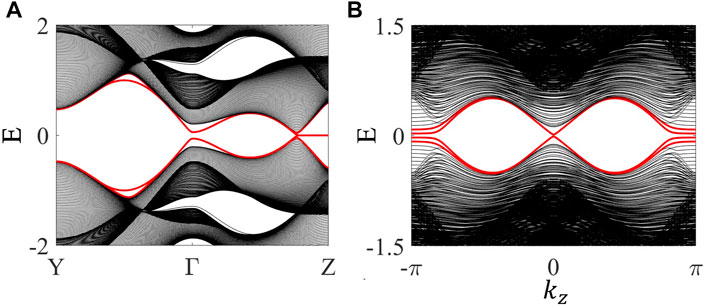
FIGURE 8. (Color online) Hybrid-order Weyl semimetal phases. Chosen parameters are: t = 1, t_z = 0.5, m = 1.6, λ = 1, η = 0.2. (a) The energy spectrum is for a geometry with open boundary condition in the x direction (N_x = 100) and periodic boundary conditions in both the y and z directions. The energy spectrum is plot along two high symmetry lines in the surface Brillouin zone. Y, Γ, Z denote the time-reversal invariant momentums (k_y, k_z) = (π, 0) (0, 0) (0, π), respectively. The zero-energy flat bands in red in (A) indicate the appearance of surface Fermi arcs on the x-normal surfaces. (B) The energy spectrum for a geometry with periodic boundary condition only in the z direction. The system size in the x and y directions is N_x = N_y = 20. The crossing of the red lines at k_z = 0 is a manifestation of the existence of helical hinge states.

When the Zeeman field becomes aligned in the xy plane, according to the study in two dimensions one can simply infer that the helical hinge states are stable against the Zeeman field when its strength is smaller than a critical value, and they will transform into chiral hinge states when the strength of the Zeeman field goes beyond the critical value at which the energy gaps on the x-normal or y-normal surfaces get closed. In Figures 9A–C, we have numerically demonstrated this expected evolution. Similar findings have also been obtained based on low-energy boundary theories in Ref. [78].

FIGURE 9

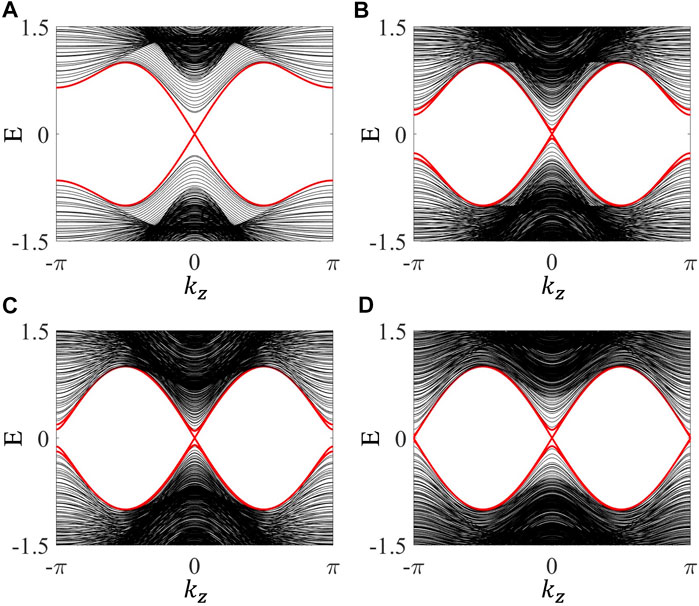
FIGURE 9. (Color online) The evolution of gapless hinge states with respect to Zeeman field. Chosen parameters are: t = 1, m = 1.6, λ = 1, η = 0.2. In (A–D), all energy spectra are for a geometry with periodic boundary condition only in the z direction. The system size in the x and y directions is fixed to N_x = N_y = 20. (A) t_z = 1, B_x = B_y = 0, the four-fold degeneracy of the crossing red lines reveals that each z-direction hinge harbors a pair of helical states. (B) t_z = 1, B_x = B_y = 0.28, the surface energy gap vanishes at this critical value. (C) t_z = 1, B_x = B_y = 0.4, the degeneracy of the crossing red lines is reduced by half, corresponding to the transition from helical hinge states to chiral hinge states. (D) t_z = 0.5, B_x = B_y = 0.25, chiral hinge states remain even though the energy spectrum at the k_z = π plane becomes gapless.

Apparently, because chiral hinge states can exist in the strong-field regime, Weyl semimetal phases with hybrid-order topology can also be realized when the parameters satisfy appropriate conditions. For an in-plane Zeeman field, according to the energy spectrum of the Hamiltonian one can infer that the Weyl points are located at the k_z = 0 or π plane when the Zeeman field is strong enough to drive the system into a gapless phase, as shown in Figure 9D. Accordingly, Fermi arcs will appear on the top and bottom z-normal surfaces, indicating a different pattern of the distribution of the boundary states compared to the case with a z-direction Zeeman field.

4 Discussions and Conclusion

For first-order topological phases protected by time-reversal symmetry, the one-dimensional lower boundary states are generally gapped by the Zeeman field due to the breaking of time-reversal symmetry [7, 8]. However, this picture cannot be simply generalized to time-reversal invariant higher-order topological phases. The underlying reason is that the gapless bound states in a higher-order topological phases live in a subspace of the total Hilbert space of the bulk Hamiltonian. While the Zeeman field directly breaks the time-reversal symmetry of the bulk Hamiltonian, in general it cannot induce direct couplings between different sectors (e.g., for two corner states, two sectors with spin-up polarization and spin-down polarization) of the subspace [99], so the gapless bound states remain stable. Nevertheless, the Zeeman field will change the localization length of the wave functions for bound states either through the reduction in boundary energy gap or through the reduction in bulk energy gap. When the boundary or bulk energy gap vanishes, the overlap of wave functions will lead to the annihilation of some or all of the bound states, corresponding to the occurrence of boundary or bulk topological phase transitions.

In this work, we have systematically investigated the possible topological phase transitions and the associated evolution of boundary bound states when a time-reversal invariant SOTI is subjected to a Zeeman field. In both two and three dimensions, we find that the bound states characterizing the second-order topology are generally stable in the weak-field regime. With the increase in field strength, both bulk and boundary topological phase transitions can be induced. Depending on the direction, the strength, as well as the type of Zeeman field, the boundary bound states will change their total number or the type across the topological phase transitions. Remarkably, we find that corner states can exist even when the system becomes a topological semimetal in two dimensions. In addition, in three dimensions we find that the Zeeman field can induce hybrid-order Weyl semimetal phases in which surface Fermi arcs and gapless hinge states coexist. Our study reveals that the Zeeman field can induce very rich physics in higher-order topological materials, and the results are applied to both quantum materials and metamaterials.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

Z-YZ performed the calculations and prepared the figures. ZY conceived and supervised the project and wrote the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos.11904417 and No. 12174455) and the Natural Science Foundation of Guangdong Province (Grant Nos. 2021B1515020026).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Benalcazar WA, Bernevig BA, Hughes TL. Quantized Electric Multipole Insulators. Science (2017) 357:61–6. doi:10.1126/science.aah6442

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Benalcazar WA, Bernevig BA, Hughes TL. Electric Multipole Moments, Topological Multipole Moment Pumping, and Chiral Hinge States in Crystalline Insulators. Phys Rev B (2017) 96:245115. doi:10.1103/physrevb.96.245115

CrossRef Full Text | Google Scholar

3. Schindler F, Cook AM, Vergniory MG, Wang Z, Parkin SSP, Bernevig BA, et al. Higher-order Topological Insulators. Sci Adv (2018) 4:eaat0346. doi:10.1126/sciadv.aat0346

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Song Z, Fang Z, Fang C. (d−2) -Dimensional Edge States of Rotation Symmetry Protected Topological States. Phys Rev Lett (2017) 119:246402. doi:10.1103/physrevlett.119.246402

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Langbehn J, Peng Y, Trifunovic L, von Oppen F, Brouwer PW. Reflection-symmetric Second-Order Topological Insulators and Superconductors. Phys Rev Lett (2017) 119:246401. doi:10.1103/physrevlett.119.246401

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Liu F, Wakabayashi K. Novel Topological Phase with a Zero berry Curvature. Phys Rev Lett (2017) 118:076803. doi:10.1103/PhysRevLett.118.076803

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sitte M, Rosch A, Altman E, Fritz L. Topological Insulators in Magnetic Fields: Quantum Hall Effect and Edge Channels with a NonquantizedθTerm. Phys Rev Lett (2012) 108:126807. doi:10.1103/physrevlett.108.126807

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Zhang F, Kane CL, Mele EJ. Surface State Magnetization and Chiral Edge States on Topological Insulators. Phys Rev Lett (2013) 110:046404. doi:10.1103/PhysRevLett.110.046404

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Ezawa M. Higher-order Topological Insulators and Semimetals on the Breathing Kagome and Pyrochlore Lattices. Phys Rev Lett (2018) 120:026801. doi:10.1103/PhysRevLett.120.026801

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Geier M, Trifunovic L, Hoskam M, Brouwer PW. Second-order Topological Insulators and Superconductors with an Order-Two Crystalline Symmetry. Phys Rev B (2018) 97:205135. doi:10.1103/physrevb.97.205135

CrossRef Full Text | Google Scholar

11. Khalaf E. Higher-order Topological Insulators and Superconductors Protected by Inversion Symmetry. Phys Rev B (2018) 97:205136. doi:10.1103/physrevb.97.205136

CrossRef Full Text | Google Scholar

12. Yan Z, Song F, Wang Z. Majorana Corner Modes in a High-Temperature Platform. Phys Rev Lett (2018) 121:096803. doi:10.1103/PhysRevLett.121.096803

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang Q, Liu C-C, Lu Y-M, Zhang F. High-temperature Majorana Corner States. Phys Rev Lett (2018) 121:186801. doi:10.1103/physrevlett.121.186801

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Franca S, van den Brink J, Fulga IC. An Anomalous Higher-Order Topological Insulator. Phys Rev B (2018) 98:201114. doi:10.1103/physrevb.98.201114

CrossRef Full Text | Google Scholar

15. Van Miert G, Ortix C. Higher-order Topological Insulators Protected by Inversion and Rotoinversion Symmetries. Phys Rev B (2018) 98:081110. doi:10.1103/physrevb.98.081110

CrossRef Full Text | Google Scholar

16. Lin M, Hughes TL. Topological Quadrupolar Semimetals. Phys Rev B (2018) 98:241103. doi:10.1103/physrevb.98.241103

CrossRef Full Text | Google Scholar

17. You Y, Devakul T, Burnell FJ, Neupert T. Higher-order Symmetry-Protected Topological States for Interacting Bosons and Fermions. Phys Rev B (2018) 98:235102. doi:10.1103/physrevb.98.235102

CrossRef Full Text | Google Scholar

18. Călugăru D, Juričić V, Roy B. Higher-order Topological Phases: A General Principle of Construction. Phys Rev B (2019) 99:041301.

Google Scholar

19. Liu T, Zhang YR, Ai Q, Gong Z, Kawabata K, Ueda M, et al. Second-order Topological Phases in Non-hermitian Systems. Phys Rev Lett (2019) 122:076801. doi:10.1103/PhysRevLett.122.076801

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Kudo K, Yoshida T, Hatsugai Y. Higher-order Topological mott Insulators. Phys Rev Lett (2019) 123:196402. doi:10.1103/physrevlett.123.196402

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Huang B, Liu WV. Floquet Higher-Order Topological Insulators with Anomalous Dynamical Polarization. Phys Rev Lett (2020) 124:216601. doi:10.1103/physrevlett.124.216601

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen R, Chen CZ, Gao JH, Zhou B, Xu DH. Higher-order Topological Insulators in Quasicrystals. Phys Rev Lett (2020) 124:036803. doi:10.1103/PhysRevLett.124.036803

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Wieder BJ, Wang Z, Cano J, Dai X, Schoop LM, Bradlyn B, et al. Strong and Fragile Topological Dirac Semimetals with Higher-Order Fermi Arcs. Nat Commun (2020) 11:627. doi:10.1038/s41467-020-14443-5

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Liu Z-R, Hu L-H, Chen C-Z, Zhou B, Xu D-H. Topological Excitonic Corner States and Nodal Phase in Bilayer Quantum Spin Hall Insulators. Phys Rev B (2021) 103:L201115. doi:10.1103/physrevb.103.l201115

CrossRef Full Text | Google Scholar

25. Li C-A, Fu B, Hu Z-A, Li J, Shen S-Q. Topological Phase Transitions in Disordered Electric Quadrupole Insulators. Phys Rev Lett (2020) 125:166801. doi:10.1103/physrevlett.125.166801

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Yang Y-B, Li K, Duan L-M, Xu Y. Higher-order Topological anderson Insulators. Phys Rev B (2021) 103:085408. doi:10.1103/physrevb.103.085408

CrossRef Full Text | Google Scholar

27. Peng T, Hua C-B, Chen R, Liu Z-R, Xu D-H, Zhou B. Higher-order Topological anderson Insulators in Quasicrystals. Phys Rev B (2021) 104:245302. doi:10.1103/physrevb.104.245302

CrossRef Full Text | Google Scholar

28. Trifunovic L, Brouwer PW. Higher-order Bulk-Boundary Correspondence for Topological Crystalline Phases. Phys Rev X (2019) 9:011012. doi:10.1103/physrevx.9.011012

CrossRef Full Text | Google Scholar

29. Yan Z-B. Higher-order Topological Insulators and Superconductors. Acta Phys Sin (2019) 68:226101. doi:10.7498/aps.68.20191101

CrossRef Full Text | Google Scholar

30. Schindler F. Dirac Equation Perspective on Higher-Order Topological Insulators. J Appl Phys (2020) 128:221102. doi:10.1063/5.0035850

CrossRef Full Text | Google Scholar

31. Zhu X. Tunable Majorana Corner States in a Two-Dimensional Second-Order Topological Superconductor Induced by Magnetic fields. Phys Rev B (2018) 97:205134. doi:10.1103/physrevb.97.205134

CrossRef Full Text | Google Scholar

32. Zhu D, Li B-X, Yan Z. Sublattice-sensitive Majorana Modes. arXiv e-prints, arXiv:2112.00761 (2021). arXiv:2112.00761 [cond-mat.supr-con].

Google Scholar

33. Zhang SB, Rui WB, Calzona A, Choi SJ, Schnyder AP, Trauzettel B. Topological and Holonomic Quantum Computation Based on Second-Order Topological Superconductors. Phys Rev Res (2020) 2:043025. doi:10.1103/physrevresearch.2.043025

CrossRef Full Text | Google Scholar

34. LapaLapa MF, Cheng M, Wang Y. Symmetry-protected gates of Majorana Qubits in a high-$T_c$ Higher-Order Topological Superconductor Platform. Scipost Phys (2021) 11:86. doi:10.21468/scipostphys.11.5.086

CrossRef Full Text | Google Scholar

35. Pan X-H, Luo X-J, Gao J-H, Liu X. Braiding Higher-Order Majorana Corner States through Their Spin Degree of freedom. arXiv:2111.12359 (2021).

Google Scholar

36. Yang Y, Lu J, Yan M, Huang X, Deng W, Liu Z. Hybrid-order Topological Insulators in a Phononic crystal. Phys Rev Lett (2021) 126:156801. doi:10.1103/physrevlett.126.156801

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Niu J, Yan T, Zhou Y, Tao Z, Li X, Liu W, et al. Simulation of Higher-Order Topological Phases and Related Topological Phase Transitions in a Superconducting Qubit. Sci Bull (2021) 66:1168–75. doi:10.1016/j.scib.2021.02.035

CrossRef Full Text | Google Scholar

38. Kheirkhah M, Yan Z, Nagai Y, Marsiglio F. First- and Second-Order Topological Superconductivity and Temperature-Driven Topological Phase Transitions in the Extended hubbard Model with Spin-Orbit Coupling. Phys Rev Lett (2020) 125:017001. doi:10.1103/PhysRevLett.125.017001

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Peng C, Zhang L, Lu Z-Y. Deconfined Quantum Phase Transition of a Higher-Order Symmetry-Protected Topological State. Phys Rev B (2021) 104:075112. doi:10.1103/physrevb.104.075112

CrossRef Full Text | Google Scholar

40. Wang C, Wang XR. Disorder-induced Quantum Phase Transitions in Three-Dimensional Second-Order Topological Insulators. Phys Rev Res (2020) 2:033521. doi:10.1103/physrevresearch.2.033521

CrossRef Full Text | Google Scholar

41. Wang C, Wang XR. Robustness of Helical Hinge States of Weak Second-Order Topological Insulators. Phys Rev B (2021) 103:115118. doi:10.1103/physrevb.103.115118

CrossRef Full Text | Google Scholar

42. Wu Y-B, Guo G-C, Zheng Z, Zou X-B. Multiorder Topological Superfluid Phase Transitions in a Two-Dimensional Optical Superlattice. Phys Rev A (2021) 104:013306. doi:10.1103/physreva.104.013306

CrossRef Full Text | Google Scholar

43. Schnyder AP, Ryu S, Furusaki A, Ludwig AWW. Classification of Topological Insulators and Superconductors in Three Spatial Dimensions. Phys Rev B (2008) 78:195125. doi:10.1103/physrevb.78.195125

CrossRef Full Text | Google Scholar

44. Kitaev A. Periodic Table for Topological Insulators and Superconductors. AIP Conf Proc (2009) 1134:22–30. doi:10.1063/1.3149495

CrossRef Full Text | Google Scholar

45. Peterson CW, Benalcazar WA, Hughes TL, Bahl G. A Quantized Microwave Quadrupole Insulator with Topologically Protected Corner States. Nature (2018) 555:346–50. doi:10.1038/nature25777

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Imhof S, Berger C, Bayer F, Brehm J, Molenkamp LW, Kiessling T, et al. Topolectrical-circuit Realization of Topological Corner Modes. Nat Phys (2018) 14:925–9. doi:10.1038/s41567-018-0246-1

CrossRef Full Text | Google Scholar

47. Serra-Garcia M, Peri V, Süsstrunk R, Bilal OR, Larsen T, Villanueva LG, et al. Observation of a Phononic Quadrupole Topological Insulator. Nature (2018) 555:342–5. doi:10.1038/nature25156

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Xue H, Yang Y, Gao F, Chong Y, Zhang B. Acoustic Higher-Order Topological Insulator on a Kagome Lattice. Nat Mater (2019) 18:108–12. doi:10.1038/s41563-018-0251-x

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Chen X-D, Deng W-M, Shi F-L, Zhao F-L, Chen M, Dong J-W. Direct Observation of Corner States in Second-Order Topological Photonic crystal Slabs. Phys Rev Lett (2019) 122:233902. doi:10.1103/physrevlett.122.233902

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Ni X, Weiner M, Alù A, Khanikaev AB. Observation of Higher-Order Topological Acoustic States Protected by Generalized Chiral Symmetry. Nat Mater (2019) 18:113–20. doi:10.1038/s41563-018-0252-9

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Zhang X, Wang H-X, Lin Z-K, Tian Y, Xie B, Lu M-H, et al. Second-order Topology and Multidimensional Topological Transitions in Sonic Crystals. Nat Phys (2019) 15:582–8. doi:10.1038/s41567-019-0472-1

CrossRef Full Text | Google Scholar

52. Mittal S, Orre VV, Zhu G, Gorlach MA, Poddubny A, Hafezi M. Photonic Quadrupole Topological Phases. Nat Photon (2019) 13:692–6. doi:10.1038/s41566-019-0452-0

CrossRef Full Text | Google Scholar

53. Wei Q, Zhang X, Deng W, Lu J, Huang X, Yan M, et al. Higher-order Topological Semimetal in Acoustic Crystals. Nat Mater (2021) 20:812–7. doi:10.1038/s41563-021-00933-4

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Luo L, Wang H-X, Lin Z-K, Jiang B, Wu Y, Li F, et al. Observation of a Phononic Higher-Order Weyl Semimetal. Nat Mater (2021) 20:794–9. doi:10.1038/s41563-021-00985-6

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Qiu H, Xiao M, Zhang F, Qiu C. Higher-order Dirac Sonic Crystals. Phys Rev Lett (2021) 127:146601. doi:10.1103/physrevlett.127.146601

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Zhang W, Zou D, Pei Q, He W, Bao J, Sun H, et al. Experimental Observation of Higher-Order Topological anderson Insulators. Phys Rev Lett (2021) 126:146802. doi:10.1103/physrevlett.126.146802

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Gray MJ, Freudenstein J, Zhao SYF, O’Connor R, Jenkins S, Kumar N, et al. Evidence for Helical Hinge Zero Modes in an Fe-Based Superconductor. Nano Lett (2019) 19:4890–6. doi:10.1021/acs.nanolett.9b00844

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Xie B, Wang H-X, Zhang X, Zhan P, Jiang J-H, Lu M, et al. Higher-order Band Topology. Nat Rev Phys (2021) 3:520–32. doi:10.1038/s42254-021-00323-4

CrossRef Full Text | Google Scholar

59. Xu Y, Song Z, Wang Z, Weng H, Dai X. Higher-Order Topology of the Axion Insulator EuIn2As2. Phys Rev Lett (2019) 122:256402. doi:10.1103/physrevlett.122.256402

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Yue C, Xu Y, Song Z, Weng H, Lu Y-M, Fang C, et al. Symmetry-enforced Chiral Hinge States and Surface Quantum Anomalous Hall Effect in the Magnetic Axion Insulator Bi2-Xsmxse3. Nat Phys (2019) 15:577–81. doi:10.1038/s41567-019-0457-0

CrossRef Full Text | Google Scholar

61. Wang Z, Wieder BJ, Li J, Yan B, Bernevig BA. Higher-Order Topology, Monopole Nodal Lines, and the Origin of Large Fermi Arcs in Transition Metal Dichalcogenides XTe2 ( X=Mo,W ). Phys Rev Lett (2019) 123:186401. doi:10.1103/physrevlett.123.186401

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Park MJ, Kim Y, Cho GY, Lee S. Higher-order Topological Insulator in Twisted Bilayer Graphene. Phys Rev Lett (2019) 123:216803. doi:10.1103/physrevlett.123.216803

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Sheng X-L, Chen C, Liu H, Chen Z, Yu Z-M, Zhao YX, et al. Two-dimensional Second-Order Topological Insulator in Graphdiyne. Phys Rev Lett (2019) 123:256402. doi:10.1103/physrevlett.123.256402

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Lee E, Kim R, Ahn J, Yang B-J. Two-dimensional Higher-Order Topology in Monolayer Graphdiyne. Npj Quan Mater. (2020) 5:1. doi:10.1038/s41535-019-0206-8

CrossRef Full Text | Google Scholar

65. Zhang R-X, Wu F, Das Sarma S. Möbius Insulator and Higher-Order Topology in MnBi2nTe3n+1. Phys Rev Lett (2020) 124:136407. doi:10.1103/physrevlett.124.136407

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Yoon C, Liu C-C, Min H, Zhang F. Quasi-One-Dimensional Higher-Order Topological Insulators. arXiv e-prints, arXiv:2005.14710 (2020). arXiv:2005.14710 [cond-mat.mes-hall].

Google Scholar

67. Fang Y, Cano J. Higher-order Topological Insulators in Antiperovskites. Phys Rev B (2020) 101:245110. doi:10.1103/physrevb.101.245110

CrossRef Full Text | Google Scholar

68. Chen C, Song Z, Zhao JZ, Chen Z, Yu ZM, Sheng XL, et al. Universal Approach to Magnetic Second-Order Topological Insulator. Phys Rev Lett (2020) 125:056402. doi:10.1103/PhysRevLett.125.056402

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Qian S, Liu C-C, Yao Y. Second-order Topological Insulator State in Hexagonal Lattices and its Abundant Material Candidates. Phys Rev B (2021) 104:245427. doi:10.1103/physrevb.104.245427

CrossRef Full Text | Google Scholar

70. Liu B, Xian L, Mu H, Zhao G, Liu Z, Rubio A, et al. Higher-Order Band Topology in Twisted Moiré Superlattice. Phys Rev Lett (2021) 126:066401. doi:10.1103/PhysRevLett.126.066401

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Luo A, Song Z, Xu G. Fragile Topologically Flat Band in the Checkerboard Antiferromagnetic Monolayer FeSe. arXiv e-prints, arXiv:2107.05433 (2021). arXiv:2107.05433 [cond-mat.mtrl-sci].

Google Scholar

72. Zhao G, Mu H, Zhang H, Wang ZF. Higher-Order Topology in Monolayer FeSe. arXiv e-prints, arXiv:2107.05910 (2021). arXiv:2107.05910 [cond-mat.mes-hall].

Google Scholar

73. Schindler F, Wang Z, Vergniory MG, Cook AM, Murani A, Sengupta S, et al. Higher-order Topology in Bismuth. Nat Phys (2018) 14:918–24. doi:10.1038/s41567-018-0224-7

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Choi Y-B, Xie Y, Chen C-Z, Park J, Song S-B, Yoon J, et al. Evidence of Higher-Order Topology in Multilayer Wte2 from Josephson Coupling through Anisotropic Hinge States. Nat Mater (2020) 19:974–9. doi:10.1038/s41563-020-0721-9

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Noguchi R, Kobayashi M, Jiang Z, Kuroda K, Takahashi T, Xu Z, et al. Evidence for a higher-order topological insulator in a three-dimensional material built from van der waals stacking of bismuth-halide chains. Nat Mater (2021) 20:473–9. doi:10.1038/s41563-020-00871-7

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Aggarwal L, Zhu P, Hughes TL, Madhavan V. Evidence for Higher Order Topology in Bi and bi0.92sb0.08. Nat Commun (2021) 12:4420. doi:10.1038/s41467-021-24683-8

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Shumiya N, Hossain MS, Yin J-X, Wang Z, Litskevich M, Yoon C, et al. Room-temperature Quantum Spin Hall Edge State in a Higher-Order Topological Insulator Bi₄Br₄. arXiv e-prints, arXiv:2110.05718 (2021). arXiv:2110.05718 [cond-mat.mes-hall].

Google Scholar

78. Queiroz R, Stern A. Splitting the Hinge Mode of Higher-Order Topological Insulators. Phys Rev Lett (2019) 123:036802. doi:10.1103/PhysRevLett.123.036802

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Pozo O, Repellin C, Grushin AG. Quantization in Chiral Higher Order Topological Insulators: Circular Dichroism and Local Chern Marker. Phys Rev Lett (2019) 123:247401. doi:10.1103/physrevlett.123.247401

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Levitan BA, Pereg-Barnea T. Second-order Topological Insulator under strong Magnetic Field: Landau Levels, Zeeman Effect, and Magnetotransport. Phys Rev Res (2020) 2:033327. doi:10.1103/physrevresearch.2.033327

CrossRef Full Text | Google Scholar

81. De SJ, Khanna U, Rao S. Magnetic Flux Periodicity in Second Order Topological Superconductors. Phys Rev B (2020) 101:125429. doi:10.1103/physrevb.101.125429

CrossRef Full Text | Google Scholar

82. Luo K, Geng H, Sheng L, Chen W, Xing DY. Aharonov-bohm Effect in Three-Dimensional Higher-Order Topological Insulators. Phys Rev B (2021) 104:085427. doi:10.1103/physrevb.104.085427

CrossRef Full Text | Google Scholar

83. Li CA, Zhang SB, Li J, Trauzettel B. Higher-Order Fabry-Pérot Interferometer from Topological Hinge States. Phys Rev Lett (2021) 127:026803. doi:10.1103/PhysRevLett.127.026803

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Chen R, Liu T, Wang CM, Lu HZ, Xie XC. Field-tunable One-Sided Higher-Order Topological Hinge States in Dirac Semimetals. Phys Rev Lett (2021) 127:066801. doi:10.1103/PhysRevLett.127.066801

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Li S, Yan X-X, Gao J-H, Hu Y. Circuit QED Simulator of Two-Dimensional Su-Schrieffer-Hegger Model: Magnetic Field Induced Topological Phase Transition in High-Order Topological Insulators. arXiv e-prints, arXiv:2109.12919 (2021). arXiv:2109.12919 [quant-ph].

Google Scholar

86. Huang X, Lu J, Yan Z, Yan M, Deng W, Chen G, et al. Acoustic Higher-Order Topology Derived from First-Order with Built-In Zeeman-like fields. Sci Bull (2022) 67:488. doi:10.1016/j.scib.2021.11.020

CrossRef Full Text | Google Scholar

87. Haldane FDM. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly". Phys Rev Lett (1988) 61:2015–8. doi:10.1103/physrevlett.61.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological Semimetal and Fermi-Arc Surface States in the Electronic Structure of Pyrochlore Iridates. Phys Rev B (2011) 83:205101. doi:10.1103/physrevb.83.205101

CrossRef Full Text | Google Scholar

89. Bernevig BA, Hughes TL, Zhang S-C. Quantum Spin Hall Effect and Topological Phase Transition in Hgte Quantum wells. Science (2006) 314:1757–61. doi:10.1126/science.1133734

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Kane CL, Mele EJ. Z2Topological Order and the Quantum Spin Hall Effect. Phys Rev Lett (2005) 95:146802. doi:10.1103/physrevlett.95.146802

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Chiu C-K, Teo JCY, Schnyder AP, Ryu S. Classification of Topological Quantum Matter with Symmetries. Rev Mod Phys (2016) 88:035005. doi:10.1103/revmodphys.88.035005

CrossRef Full Text | Google Scholar

92. Qi X-L, Wu Y-S, Zhang S-C. Topological Quantization of the Spin Hall Effect in Two-Dimensional Paramagnetic Semiconductors. Phys Rev B (2006) 74:085308. doi:10.1103/physrevb.74.085308

CrossRef Full Text | Google Scholar

93. Xiao D, Chang M-C, Niu Q. Berry Phase Effects on Electronic Properties. Rev Mod Phys (2010) 82:1959–2007. doi:10.1103/revmodphys.82.1959

CrossRef Full Text | Google Scholar

94. Yan Z. Majorana Corner and Hinge Modes in Second-Order Topological Insulator/superconductor Heterostructures. Phys Rev B (2019) 100:205406. doi:10.1103/physrevb.100.205406

CrossRef Full Text | Google Scholar

95. Chiu C-K, Schnyder AP. Classification of Reflection-Symmetry-Protected Topological Semimetals and Nodal Superconductors. Phys Rev B (2014) 90:205136. doi:10.1103/physrevb.90.205136

CrossRef Full Text | Google Scholar

96. Jackiw R, Rebbi C. Solitons with Fermion Number ½. Phys Rev D (1976) 13:3398–409. doi:10.1103/physrevd.13.3398

CrossRef Full Text | Google Scholar

97. Wang H-X, Lin Z-K, Jiang B, Guo G-Y, Jiang J-H. Higher-order Weyl Semimetals. Phys Rev Lett (2020) 125:146401. doi:10.1103/physrevlett.125.146401

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Ghorashi SAA, Li T, Hughes TL. Higher-order Weyl Semimetals. Phys Rev Lett (2020) 125:266804. doi:10.1103/physrevlett.125.266804

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Kheirkhah M, Yan Z, Marsiglio F. Vortex-line Topology in Iron-Based Superconductors with and without Second-Order Topology. Phys Rev B (2021) 103:L140502. doi:10.1103/physrevb.103.l140502

CrossRef Full Text | Google Scholar