Modeling of a retarding potential analyzer and comparison with Express-A in-flight measurements

In-flight data from the retarding potential analyzers (RPAs) on the Russian geostationary telecommunication satellite Express-A #3 are used to validate electric thruster plume simulations. The RPAs placed on the solar array have made it possible to measure ion properties, current densities, and ion energy distribution functions (IEDFs) at different distances and field-of-view configurations with regard to the thrusters. The present work shows that the conventional probe theory used to interpret measurements is only valid if the probe is oriented toward the thruster. In most Express-A #3 measurements, this is not the case, and it leads to incorrect interpretations. In this study, a new RPA probe model is presented. It enables the physics of a tilted probe to be described more accurately, taking into account the view angle between the RPA entrance surface normal relative to the incoming flux direction, the flux direction nonaligned with the collection surface normal, the internal RPA electric fields, and masking effects due to RPA walls. This probe model is coupled with a simple model for ion transport from an electric thruster source to the probe to allow a comparison with in-flight data. The comparison between Express-A #3 RPA collected currents and calculations from the new model discriminates true ion energy shift from probe misorientation effects. It also shows that highly tilted RPA measurements that were previously never interpreted can be understood and analyzed.

1 Introduction

To understand and predict erosion and electrostatic discharges (ESDs) on spacecrafts in the presence of a plasma thruster, it is necessary to properly represent the electrostatic coupling between the plume of the thruster and the surfaces of the spacecraft. Several works have shown that this coupling has a significant impact on the charging mechanism [1] and can increase the risk of ESDs on solar arrays [2, 3]. Erosion and contamination due to charge exchange ions created by the thruster device on sensitive components such as solar cell interconnectors can also lead to premature termination of the mission [4]. As the demand for higher power plasma thrusters and higher solar-array bus voltages increases, these issues are magnified and become a limiting factor for power upscaling [5].

Plume models aim to represent the primary ion beam dynamics and the coupling with the environment. Thus, a numerical plume simulation usually includes the transport of charged particles and neutral atoms (using full particle-in-cell (PIC) [6] or hybrid fluid–PIC [1, 7, 8] approaches), solves the Poisson equation, and computes collisions between particles. To validate the thruster plume and spacecraft interaction models, experimental data are needed.

Although large ground-based vacuum chambers permit the study of plasma thruster far fields [9, 10], the conditions are different from space. The environment in the vacuum facility is denser [11], leading to a greater charge exchange collision rate between the primary ion beam and the residual $X{e}^{+}$ ions in the chamber. The study of the backflow (i.e., the $X{e}^{+}$ created from charge exchange collisions) is therefore biased. Moreover, due to the presence of walls, the radial potential drop in the vacuum chamber is also altered. In-flight experiments make it possible to have a representative measurement for model comparisons.

An in-flight experiment has been conducted on SMART-1 [12], but few data are available in the literature, and the plasma diagnostic package position only makes it possible to study the backflow at a single point in space. On the other hand, the Russian geostationary telecommunication satellite Express-A #3 (launched in June 2000) provides a large number of retarding potential analyzer (RPA) measurements, at various locations with respect to the thruster firing axis, enabling a unique in-flight experimental setup to study the plasma plume. However, the RPA data processing is nonconventional due to the oblique incidence of the plasma beam coming from the thruster. The probe tilt-angle with respect to the plasma drift vector (i.e., the angle between the probe normal axis and the probe–thruster axis) is within the range of $\mathit{2}-\mathit{45}°$ , and, therefore, the RPA theory allowing for the ion energy distribution function (IEDF) to be obtained is no longer valid. Thus, Express-A RPA results are underexploited due to the lack of interpretability of the measurements when the probe tilt-angle is significantly high.

In this study, the setup of the RPA probes onboard Express-A is presented. Then, the modeling approach for RPA measurements prediction is described, introducing a new RPA model. It makes it possible to take into account the geometry of the RPA, an oblique incidence of the plasma beam with respect to the probe normal axis, the effects of the axial electric field in the RPA on ion trajectories, and to consider grid transparency. Then, the coupling between the RPA model and a simple transport model taking into input a thruster IEDF derived from a hybrid simulation code is detailed. Finally, the comparison between the model and Express-A data is shown and discussed.

2 Express-A mission and in-flight data

Express-A #3 is equipped with 8 Fakel SPT-100, a well-documented hall thruster used for station keeping and two RPAs mounted on solar panels (DRT1, DRT2), as shown in Figure 1. The RPA positions allow for a scan of ion current and ion energy distribution function (IEDF) as the solar arrays rotate. This unique setup is often compared to thruster plume simulation in space vacuum [14, 15, and references therein].

FIGURE 1

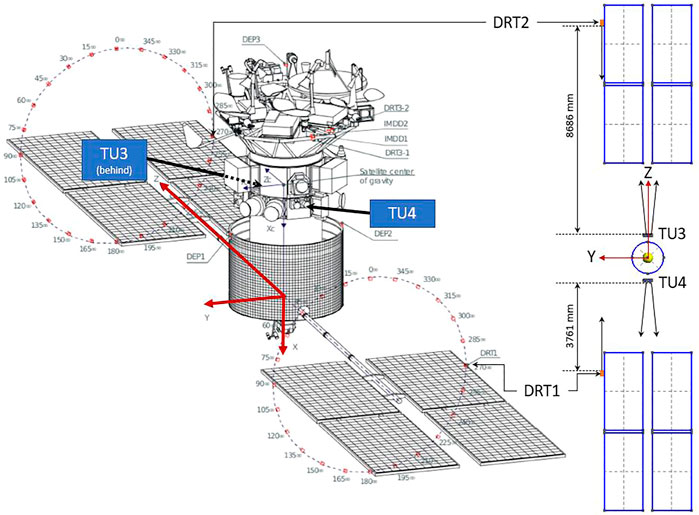
FIGURE 1. Express-A thruster and RPA locations [13].

The spacecraft is also equipped with electric field and pressure sensors, along with torque measurements induced by the thruster plume studied in other works [8, 16]. However, in the scope of this study, only RPA data will be investigated.

RPA data have previously been used and compared with simulation [16, 17]. However, we demonstrate that taking ion current measurements and IEDF without an RPA response model leads to significant errors. This approach may be used in future works to obtain plume measurements on unexploited Express-A data.

On Express-A, the RPA collector surface normal is along + Z for DRT1 and along -Z for DRT2. The DRT1 probe measures the ion current from the thruster unit TU4 and DRT2 measurements concern the TU3. It is to be noted that each thruster unit TUX consists of two SPT-100 Hall thrusters, designated as TX and RTX.

To be able to analyze and interpret the RPA measurements without biases, the probe needs to be oriented toward the studied ion source. However, regarding the position of the thruster units, TU3 and TU4, the probe tilt-angle ${\beta }_{RPA}$ (angle formed by the incoming ion flux and the RPA collector surface normal) can be up to 45°, leading to a complicated measurement analysis.

The Express-A RPA data have previously been used in two ways: first, as an ion current density probe and, second, to measure IEDF. Previous articles seem to take some precautions with the IEDF analysis and only consider RPA data when the probe tilt-angle is close to 0° [16]. But few cases are available. For the ion current analysis, raw RPA data are directly used despite the varying tilt-angle ${\beta }_{RPA}$.

This study aims to analyse the effect of probe misorientation over Express-A RPA measurements (over 170 angle/distance configurations from 3.82 to 9.26 m with an angle relative to the thruster varying from 2° to 45°, as shown in Figure 2) and to identify whether the data provide information about thruster IEDF only or if more information can be extracted such as electrostatic effects or collision effects inside the plume.

FIGURE 2

FIGURE 2. (A) Express-A firing angles for data configurations/. (B) Diagram for angle definition.

Previously, an analytical model has been developed [18] to take into account the shading effect due to the geometry of the tilted-RPA. It allows to apply a correcting factor on each RPA current measurement. In this study, a more advanced analytical RPA model is presented, allowing us to consider the RPA axial electrostatic effects as well and to study the effect of the tilted-RPA on IEDF measurements. The new RPA model is presented in Section 3.

3 Transfer function model for RPA measurement prediction

This section introduces the model used in this study. First, in Section 3.1, the RPA theory is recalled, detailing the issue with tilted RPA measurements. Then, Section 3.2, Section 3.3, and Section 3.4 present the approach used to predict Express-A RPA measurements. To do so, the subsections successively focus on the modeling of the inside of the RPA, using a transfer function approach, then, on the input distribution function used to model the thruster ion source, and finally, on the modeling of the ion motion from the thruster to the RPA. In Section 3.5, the effect of the RPA tilt-angle on probe measurements is analyzed using the model previously described.

3.1 Elementary theory of RPA

A retarding potential analyzer is an electrostatic hollow cylindrical probe consisting of three to four polarized grids. First, a screen grid is polarized to the probe floating body potential ${\varphi }_S$, restraining plasma perturbation. Then, the cut-off grid, negatively polarized to ${\varphi }_{CO}$, repels the electrons, and, finally, the analyzing grid is polarized to ${\varphi }_A$ sweeping from the floating potential to a chosen positive potential, repelling all of the ions. The latter acts like a high-pass energy filter for ions. The collector potential is also set to the probe floating body potential.

Let us consider a beam of singly charged ions of charge $q$ and mass $m$ whose distribution function along the axial z direction is noted $f\left(v_z\right)$ and an RPA with nonpolarized grids is used. All of the ions whose energy of the motion in the z direction is ${\epsilon }_z\ge q\left({\varphi }_A-{\varphi }_S\right)$ are collected by the RPA. We can easily calculate the collected current $I_c=Sq\tau {\int }_{\mathit{0}}^{+\infty }{v}_{z}f\left(v_z\right)d{v}_z=Sq\tau /m{\int }_{\mathit{0}}^{+\infty }f\left(\sqrt{2{\epsilon }_z/m}\right)d{\epsilon }_z$, where $S$ is the collection surface area, $\tau$ the product of grid transparencies, and $m$ the mass of an ion.

If a positive value of the analyzer potential ${\varphi }_A$ is considered, then the collected current becomes:

$\begin{array}{c}{I}_c\left({\mathrm{\varphi }}_A\right)=\frac{Sq\tau }{m}{{\displaystyle \int }}_{q{\mathrm{\varphi }}_A}^{+\infty }f\left(\sqrt{\frac{2{\epsilon }_z}{m}}\right)d{\epsilon }_z=\frac{Sq\tau }{m}\bullet \left[F\left({\epsilon }_z\to +\infty \right)-F\left(q{\varphi }_A\right)\right]\end{array}[1]$

The derivative of the collected current by the analyzing potential ${\varphi }_A$ of Eq. 1 gives:

$\frac{d{I}_c\left({\mathrm{\varphi }}_A\right)}{d{\mathrm{\varphi }}_A}=\frac{Sq\tau }{m}\frac{d\left(F\left({\epsilon }_z\to +\infty \right)-F\left(q{\mathrm{\varphi }}_A\right)\right)}{d{\mathrm{\varphi }}_A}=-\frac{Sq\tau }{m}\bullet \frac{d\left(F\left(q{\mathrm{\varphi }}_A\right)\right)}{d\left(q{\mathrm{\varphi }}_A\right)}\bullet \frac{d\left(q{\mathrm{\varphi }}_A\right)}{d{\mathrm{\varphi }}_A}=-\frac{S{q}^2\tau }{m}f\left(\sqrt{\frac{2q{\mathrm{\varphi }}_A}{m}}\right)=-\frac{S{q}^2\tau }{m}f\left(v_z\right)$

We finally obtain the proportionality relationship: $f\left(v_z\right)\propto -\frac{d{I}_c}{d{\mathrm{\varphi }}_A}\left[2\right]$

This equation relies on the initial hypothesis that if an ion has an axial energy ${\epsilon }_z\ge q\left({\varphi }_A-{\varphi }_S\right)$, it is collected, but as soon as the ion axial energy is not high enough to get through the potential barrier imposed by the analyzer grid, it is repelled and therefore not collected. This hypothesis is valid when $\frac{{\epsilon }_z}{{\epsilon }_r}\gg 1$, where ${\epsilon }_z$ and ${\epsilon }_r$, respectively, are the axial and radial energy of the ion. For an untilted probe (i.e., directed toward the ion source), assuming that most of the ions are coming directly from the source in a straight line, this relationship holds. However, if the tilt-angle ${\beta }_{RPA}$ increases, this assumption is no longer valid. It must also be noted that the $-dI/d{\varphi }_A$ curve is in fact a measurement of the axial component of the velocity. For a perfectly oriented probe, it corresponds to the velocity vector norm, but for a tilted-RPA, the velocity vector norm is obtained by performing a velocity shift, such that the ion velocity is $v=v_z/{\cos }^2\left({\beta }_{RPA}\right)$.

Figure 3 shows the trajectory of an $X{e}^{+}$ entering the RPA with an energy $\frac{\epsilon }{q}=250eV$, leading to a velocity $v=\sqrt{2\epsilon /m_{X{e}^{+}}}$ and a tilt-angle ${\beta }_{RPA}=40°$. Therefore, the energy along the axial and radial directions is:

$\begin{array}{c}\{\begin{array}{c}\frac{{\epsilon }_z}{q}=\frac{m_{X{e}^{+}}\bullet v_z^2}{2q}=\frac{m_{X{e}^{+}}\bullet {\left(v\bullet \cos \left({\beta }_{RPA}\right)\right)}^2}{2q}=\epsilon \bullet {\cos }^2\left({\beta }_{RPA}\right)\approx 147\mathrm{e}\mathrm{V}\\ {\epsilon }_r=\epsilon \bullet {\sin }^2\left({\beta }_{RPA}\right)\approx 103eV\end{array}\end{array}[3]$

FIGURE 3

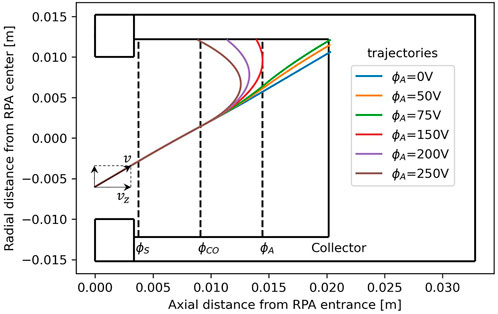
FIGURE 3. Trajectories of an ion $\mathit{X}{\mathit{e}}^{+}$ (total energy of 250 eV and a tilt-angle ${\mathit{\beta }}_{\mathit{R}\mathit{P}\mathit{A}}=\mathit{40}°$) in Express-A RPA for different values of analyzer grid potential. The grid potentials are ${\mathit{\varphi }}_{\mathit{S}}=\mathit{0}\mathit{V}$ and ${\mathit{\varphi }}_{\mathit{C}\mathit{O}}=-\mathit{30}\mathit{V}$ , and ${\mathit{\varphi }}_{\mathit{A}}$ varies between 0 and 250 V.

This simple simulation of the motion of a single ion shows that when ${\epsilon }_z\approx {\epsilon }_r$, a significant part of the ion flux can reach the RPA walls before being collected. For example, in Figure 3, the ion has an axial energy $\frac{{\epsilon }_z}{q}\approx 147eV$ , but it is intercepted by the walls as soon as the analyzer potential reaches ${\varphi }_A\approx 75V$. As Eq. 2 states, any change in the ion current at the collector between two values of ${\varphi }_A$ is interpreted as the presence of ions in this energy range. Therefore, in this example, the ion will be considered as an ion of $75eV$ of axial energy. This effect needs to be modeled to correct this probe measurement bias.

As the ${\beta }_{RPA}$ increases, the proportion of the ion flux deviated toward the walls increases and becomes a function of the analyzer potential.

3.2 Modeling of the RPA: Transfer function approach

The expression of the collected current introduced earlier can be completed by the introduction of a transfer function $H\left(\overrightarrow{v},\dots \right)$, dependent on the velocity vector and other parameters. The collected current in the RPA as a function of the IEDF at the probe entrance can be obtained. Considering $\overrightarrow{n_{RPA}}$ colinear to $-\overrightarrow{z}$, the collector surface $S$, the product of grid transparencies $\tau$, the axial velocity $v_z$, the velocity distribution function $f\left(v_x,v_y,v_z\right)$ , and a transfer function $H$, the current at the collector can be expressed as:

$\begin{array}{c}{I}_C=Sq\tau \stackrel{+\infty }{\underset{-\infty }{\iint }}{\int }_0^{+\infty }{v}_{z}f\left(v_x,v_y,v_z\right)H\left(v_x,v_y,v_z,\dots \right)d{v}_{z}d{v}_{y}d{v}_x\end{array}[4]$

where $H$ is defined as the product of different transfer functions representing different phenomena, such as the effects of the axial electric fields on ion trajectories and the presence of walls. In principle, $H$ could also include space charge effects. Nevertheless, for typical conditions considered in this study, the electron temperature $T_e\sim 2eV$ and electron density $n_e\sim {10}^{11}{m}^{-3}$, the Debye length ${\lambda }_D$ is approximately $0.03m$, which is larger than the characteristic length of the probe with its diameter $d_{RPA}\approx 0.02m$. Regarding the fact that ${\lambda }_D>d_{RPA}$, the hypothesis of no space charge effects can be reasonably made in the RPA. Thus, $H=E_f\bullet W_f$ with $E_f$ being the high-pass energy filter and $W_f$ being the filter induced by ion losses at the RPA walls.

The objective of the following approach is to express the collected current $I_c$ as a function of the ion velocity distribution function at the source exit and other constant parameters related to the RPA geometry, such as the radius, length, grid transparency, and grid potentials.

Other RPA modeling approaches, for example, using PIC simulation, exist [19]. However, the duration time of the simulation is much larger than that of the pseudoanalytical approach due to the large number of macroparticles needed to capture the shape of the energy distribution on the collector surface with good accuracy. The misoriented RPA case has never been studied using the PIC models. In the end, the coupling between this fast analytical approach with a plasma-spacecraft solver (already time-consuming due to the description of the charged particle transport and interactions with the spacecraft) will be performed.

We will now detail the expression of $H$ in Eq. 4. First, the high-pass energy filter (Eq. 5) is simply a Heaviside step function derived from the conservation of energy, considering an initial velocity $\overrightarrow{v}$ and a purely axial electric field in the RPA (derived from the electric potential). To be collected, the initial ion energy divided by the charge must be higher than the potential barrier resulting from the analyzer grid and the plasma potential. Otherwise, the incoming ion will be repelled and will not reach the collector:

$\begin{array}{c}{E}_f\left(\Vert \overrightarrow{v}\Vert ,{\beta }_{RPA},{\varphi }_A\right)=\{\begin{array}{c}1if{\left(\Vert \overrightarrow{v}\Vert \bullet \mathit{cos}\left({\beta }_{RPA}\right)\right)}^2>\frac{2Zq\left({\varphi }_A-{\varphi }_{plasma}\right)}{m}\\ 0otherwise\end{array}\end{array}[5]$

In this study, only singly charged ions are considered. Therefore, $Z=1.$

Second, the effect of the wall filter being less straightforward is taken into account. Considering only the particles with $E_f=1$, for a given $\overrightarrow{v},{\beta }_{RPA}$ and ${\varphi }_A$, due to a nonzero initial radial velocity, the particles are shifted by a fixed value in the radial direction, regardless of their initial positions. This shift $d_s$ can be computed with the piecewise application of the fundamental principle of dynamics in regions of isoelectric field (i.e., between each intergrid space). The integrated transfer function over all of the initial positions can be obtained (Eq. 6) by computing the intersection between two disks: the entry disk, representing all of the possible initial positions, and the collector disk shifted by distance $d_s$, representing all of the final positions, as shown in Figure 4.

FIGURE 4

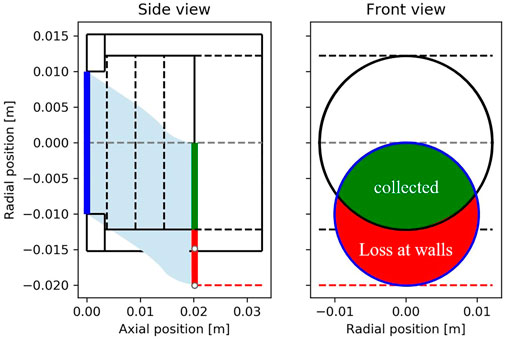
FIGURE 4. Integration over initial positions for a given velocity vector (axial kinetic energy greater than retarding potential energy).

The surface of the intersection of the disks becomes the effective collection surface $S_{eff}=S_{entry}\cap {shifted(S}_{collector},d_s)$ and the filter is defined as

$\begin{array}{c}{W}_f\left(v,{\beta }_{RPA},{\varphi }_A\right)=\frac{S_{eff}}{S_{entry}}\end{array}[6]$

The transfer function $H$ is plotted in Figure 5 for several values of the analyzer grid potential ${\varphi }_A$. The left plot shows the 2D transfer function. The energy filter $E_f$ is responsible for the high-pass filter above ${\varphi }_A$. The right plot in Figure 5 shows the effect of ${\varphi }_A$ on the value of $H$ for $\frac{{\epsilon }_s}{q}=250eV$. The energy filter induces a cut-off tilt-angle, above which no more current is collected and the wall filter leads to a decrease of $H$, as the analyzer potential increases, describing ion deflection due to the increasing axial electrostatic field between the cut-off and the analyzer grids. The effect of the wall filter magnifies as ${\beta }_{RPA}$ increases.

FIGURE 5

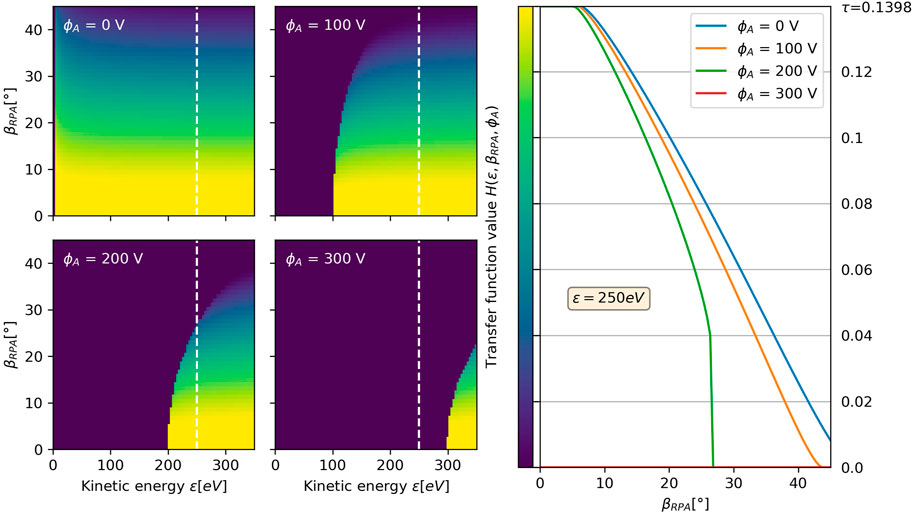
FIGURE 5. Transfer function $\mathit{H}$ of the RPA for $\mathit{X}{\mathit{e}}^{+}$ as a function of the kinetic energy and the RPA tilt-angle plotted for different values of the analyzer grid potential. The higher bound of the scale correspond to the grid transparency product $\mathit{\tau }$. The ${\mathit{\beta }}_{\mathit{R}\mathit{P}\mathit{A}}$ dependency of the transfer function at 250eV is shown on the right. Parameter: ${\mathit{\varphi }}_{\mathit{C}\mathit{O}}=-\mathit{30}\mathit{V}.$

At this point, the IEDF at the thruster exit (i.e., the model input) needs to be specified. The transfer function between the thruster and the RPA entrance is also needed. They are described, respectively, in Sections 3.3 and 3.4.

3.3 Modeling of the thruster IEDF

The model presented in Section 3.2 makes it possible to compute the transfer function of the RPA. The IEDF at the RPA entrance depends on the IEDF at the thruster exit and how this distribution varies between the thruster and the RPA locations. This section presents the approach used to model the IEDF at the thruster exit.

Figure 6 illustrates an $X{e}^{+}$ ion current distribution function at the cathode line boundary fitted from calculations using a hybrid Hall thruster model for the nominal conditions of SPT-100 [20].

FIGURE 6

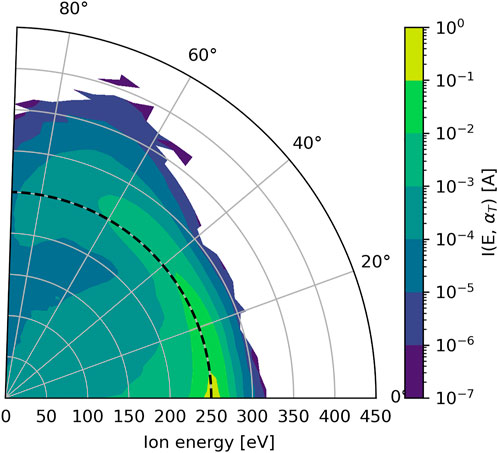
FIGURE 6. Radial ion current distribution function at the thruster cathode line boundary from the hybrid model [20]. The angle is ${\mathit{\alpha }}_{\mathit{T}}$, relative to the thruster surface normal (in degrees), and the radius represents the energy (in eV).

As shown in Figure 6, the emitted current decreases with the angle, but the shape of the current energy distribution function between 0° and 45° evolves with very little change. Therefore, the IEDF can be approximated using the separation of variables in spherical coordinates with $r,\theta ,\varphi$, which are, respectively, the radial position, the polar angle (equal to ${\alpha }_T$), and the azimuthal angle, such that $f_T\left(v_r,\theta \right)=f_{sm}\left(v_r\right)\cdot g\left(\theta \right)$. As the thruster is considered to emit ions homogeneously and with a symmetry axis along $z$ (independent of $\varphi$), spherical coordinates are well-suited. They allow for simplifying the numerical integration. Therefore, this coordinate system will be used in the rest of the study.

The velocity distribution function is defined accurately by a fitted Gaussian distribution $f\left(v_r\right)$, with the velocity expressed in spherical coordinates and its parameters $\mu =v_s=\sqrt{2{\epsilon }_s/m_{X{e}^{+}}}$, where $\frac{{\epsilon }_s}{q}\approx 250eV$ and $\sigma =v_T=\sqrt{2q{T}_i/m_{X{e}^{+}}}$, with $T_i\approx 0.2eV$. It looks like a shifted Maxwellian distribution but in spherical coordinates. The ${\alpha }_T$-dependency is modeled by the function $g\left(\theta \right)$ also fitted on the hybrid model as a first approach. Figure 7 shows the fitted $f_{sm}\left(v_r\right)$ and $g\left(\theta \right)$ compared to the hybrid model.

$\begin{array}{c}{f}_T\left(v_r,\theta \right):\{\begin{array}{c}{f}_T\left(v_r,\theta \right)=f_{sm}\left(v_r\right)\bullet g\left(\theta \right)\\ f_{sm}\left(v_r\right)={\left(\frac{m_{X{e}^{+}}}{2\pi q{T}_i}\right)}^{1/2}\bullet \exp \left(-\frac{{\left(v_r-v_s\right)}^2}{v_T^2}\right)\end{array}\end{array}[7]$

FIGURE 7

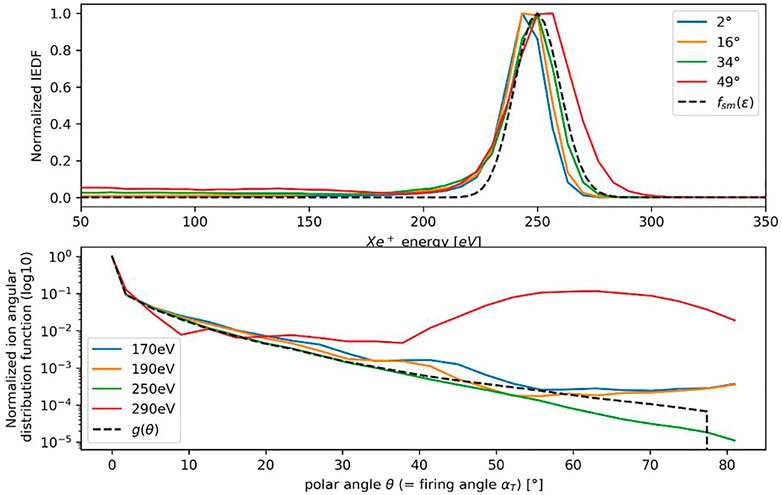
FIGURE 7. Top: normalized velocity distribution for various $\mathit{\theta }$ angles. Bottom: normalized angular distribution for various kinetic energies (log10). In black, the ${\mathit{f}}_{\mathit{s}\mathit{m}}\left({\mathit{v}}_{\mathit{r}}\right)$ and $\mathit{g}\left(\mathit{\theta }\right)$ derived from the hybrid model fit.

3.4 Ion transport model

To obtain the distribution function at the RPA location, the transport has to be modeled between the source and the RPA entrance. In this section, we detailed the expression of the ion distribution function as a function of the position and the velocity $f(r,\theta ,\varphi ,v_r,v_{\theta },v_{\varphi }$).

First, we assume that there are no collisions and no plasma effects in the plume. This strong approximation will be discussed in Section 4.3. Second, the RPAs on Express-A #3 are far from the thrusters (in-flight data, the distance is at least $r\sim 3.8m$), and the thruster exit and RPA are small devices (diameters of $d_T\sim 10cm$ and $d_{RPA}\sim 2cm$ respectively). This leads to $\frac{r}{d_{RPA}}\gg 1$ and $\frac{r}{d_T}\gg 1$. Therefore, we have made the hypothesis that there is no geometrical factor neither due to the annular shape of the thruster nor due to the disk shape of the RPA entrance. They are treated, respectively, as a point source and a point target. These two hypotheses combined lead to a purely radial motion for ions. This implies that the ion density and ion current must follow an inverse square law. This also means that the $v_{\theta }$ and $v_{\varphi }$ components of the velocity vector are always zero; therefore, the distribution function is independent of these variables.

$f\left(r,\theta ,\varphi ,v_r\right)=\frac{r_0^2}{r^2}\cdot f\left(r_0,{\alpha }_T,\varphi ,v_r\right)$

The hypothesis that the velocity distribution of the thruster is independent of the firing angle ${\alpha }_T$ has been made (Section 3.3). Thus, the velocity distribution at any RPA location is independent of ${\alpha }_T$. So, the shape of the velocity distribution function at the RPA location is always $f_{sm}\left(v_r\right)$. Moreover, the thruster distribution is independent of $\varphi$, and it is consequently the same for the distribution function in volume. Thus, the expression of the distribution function is:

$f\left(r,\theta ,v_r\right)=\frac{C}{r^2}\cdot f_T\left(v_r,\theta \right)=\frac{C}{r^2}\cdot g\left(\theta \right)\cdot f_{sm}\left(v_r\right)$

With $C$, a constant such that the current of the thruster source $I_T$ is conserved:

$I_T=3.1A=I\left(r\right)=\frac{qC}{r^2}{\iint }_{\Sigma }g\left(\theta \right)dS\cdot {\int }_0^{+\infty }{v}_r\cdot f_{sm}\left(v_r\right)d{v}_r$

With $dS=r^2\sin \left(\theta \right)d\theta d\varphi$, the surface element of $\mathrm{\Sigma }$, the hemisphere collects all of the emitted ions. Finally, the current collected by the RPA is expressed as:

$\begin{array}{c}{I}_c\left(r,{\alpha }_T,{\beta }_{RPA},{\varphi }_A\right)=S_{coll}{\int }_0^{+\infty }{v}_r\cdot \cos \left({\beta }_{RPA}\right)\cdot f\left(r,{\alpha }_T,v_r\right)\cdot H\left(v_r,{\alpha }_T,{\beta }_{RPA},{\varphi }_A,\dots \right)d{v}_r\end{array}[8]$

3.5 RPA measurement prediction: Effect of the RPA tilt-angle

As mentioned in Section 2, the RPA measurements can be analyzed in two interesting ways. First, the derivative of the collected current with respect to the analyzer potential $-d{I}_c/d{\varphi }_A$ can give information about the ion IEDF, and second, the absolute value of $I_{{\varphi }_A=0}$ can give information about the ion current density. The effect of the RPA tilt-angle on both is analyzed in the following sections.

3.5.1 Effect of the RPA tilt-angle on ${\mathit{d}\mathit{I}}_{\mathit{c}}/\mathit{d}{\mathit{\varphi }}_{\mathit{A}}$

In Figure 8, the effect of the RPA tilt-angle ${\beta }_{RPA}$ is studied. The predicted $-dI/d{\varphi }_A$ curves shown are obtained in Eq. 8, using the transfer function described in Section 3.2, the input distribution from Section 3.3, and the transport model in Section 3.4. The derivative of the collected current $-dI/d{\varphi }_A$ has been normalized to allow for a comparison with the IEDF. The light gray areas represent the IEDF that an RPA without walls should measure (such that the transfer function $H=E_f$). It corresponds to a shifted Maxwellian distribution ($v_s=\sqrt{2{\epsilon }_{shift}/m_{Xe}^{+}}$ with ${\epsilon }_{shift}={\epsilon }_s\bullet {\cos }^2\left({\beta }_{RPA}\right)$, as Eq. 3 state), with from left to right, ${\beta }_{RPA}=40°,30°,20°$. The blue area is the true input velocity distribution, $f_{sm}$.

FIGURE 8

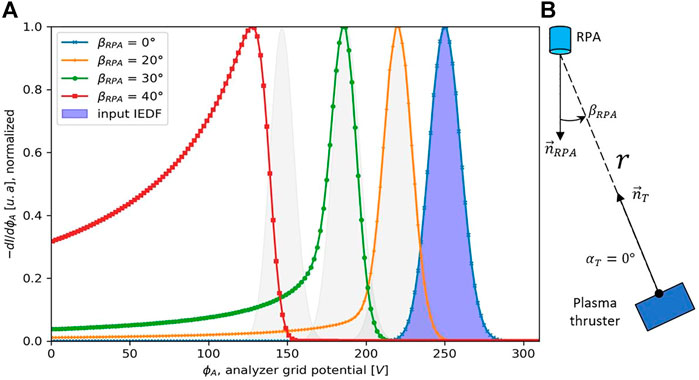
FIGURE 8. (A) $-\mathbf{d}\mathbf{I}/\mathbf{d}{\mathbf{\varphi }}_{\mathbf{A}}$ computed at different RPA tilt-angles, (B) Model diagram. The input distribution is a shifted Maxwellian with ${\mathit{\epsilon }}_{\mathit{s}}=\mathit{250}\mathit{e}\mathit{V}$ and ${\mathit{T}}_{\mathit{i}}=\mathit{0.2}\mathit{e}\mathit{V}$.

When the tilt-angle ${\beta }_{RPA}$ is near $0°$ (i.e., the perfectly oriented RPA case), the measure fits the injected IEDF, as expected. In terms of the transfer function, it means that $W_f\left({\varphi }_A\right)$ is constant. As the ${\beta }_{RPA}$ increases, the loss at wall effects described with $W_f\left({\varphi }_A\right)$ appears in the $-dI/d{\varphi }_A$ curves. For ${\beta }_{RPA}=20°$, the model computation of the RPA $-dI/d{\varphi }_A$ curve is shifted, with a peak corresponding to the expected value $\frac{{\epsilon }_{\mathit{peak}}}{q}\approx {\epsilon }_s/q\cdot {\cos }^2({\beta }_{RPA})\approx 221eV$. We can see that the shape of the curve changes slightly at low energy due to the collection at walls described in $W_f$. The curve is no longer symmetric compared to the case where ${\beta }_{RPA}=0°$.

Figure 5 shows that the effect of the tilt-angle becomes more pronounced as ${\beta }_{RPA}$ increases. At ${\beta }_{RPA}=30°$, the value of $-dI/d{\varphi }_A$ reaches 10% of the maximum value at ${\varphi }_A\approx 125V$, but the peak is still around the expected energy. However, for high ${\beta }_{RPA}$ values, as can be seen when ${\beta }_{RPA}=40°$, the predicted peak is before the gray-area peak (${\varphi }_A\sim 127V$ instead of $146V)$. This means that the loss of collected ions due to the combined effects of wall collection and analyzer potential filtering is the strongest at this energy. Thus, for ${\beta }_{RPA}>30°$, the energy peak cannot be predicted easily without modeling the RPA transfer function.

For the study of the Express-A plasma thruster, the effect of wall collection on the $-dI/d{\varphi }_A$ curve is an issue. In the plume, charge exchange $X{e}^{+}$ ions can be created and can be found at a large firing angle ${\alpha }_T$, with an energy of the order of tens of $eV$ [12]. As shown in Figure 2, large ${\alpha }_T$ leads to large tilt angle ${\beta }_{RPA}$. Therefore, it is important to model the transfer function accurately to discriminate the real low-energy ions from high-energy ions.

3.5.2 Effect of the RPA tilt-angle on ${\mathit{I}}_{{\mathit{\varphi }}_{\mathit{A}}=\mathbf{0}}$

It is possible to deduce the ion current at the RPA location from the RPA current measurement at ${\varphi }_A=0$V but only if the transfer function of the RPA is known. Figure 9 shows the collected current for the shifted Maxwellian distribution $f_{sm}$ described in Section 3.3. It shows that the decrease of the current as a function of the tilt-angle is much steeper than a simple cosine (as if it was a disk surface). The wall effect on the measured ion current stays negligible while the tilt-angle ${\beta }_{RPA}$ is below $\approx 10°$, but it quickly becomes important. Indeed, at ${\beta }_{RPA}=26°$, the probe collects half the ion current compared to a perfectly oriented RPA. For ${\beta }_{RPA}>45°$, no more current is collected. For the range of probe tilt-angle of the Express-A RPA, the drop of the collected current can be strong. It must be taken into account to study the dependency of the emitted current on the firing angle ${\alpha }_T$.

FIGURE 9

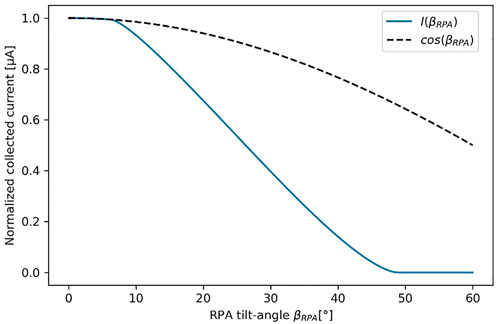
FIGURE 9. Normalized collected current as a function of the RPA tilt-angle ${\mathit{\beta }}_{\mathit{R}\mathit{P}\mathit{A}}$ for ${\mathit{\varphi }}_{\mathit{A}}=\mathit{0}\mathit{V}$. The velocity distribution is sampled from a shifted Maxwellian with ${\mathbf{T}}_{\mathbf{i}}=\mathbf{0.2}\mathbf{e}\mathbf{V}$, ${\mathbf{E}}_{\mathbf{s}\mathbf{h}\mathbf{i}\mathbf{f}\mathbf{t}}=\mathbf{250}\mathbf{e}\mathbf{V}$, $\mathit{X}{\mathit{e}}^{+}$ ions.

4 Comparisons between Express-A data and RPA modeling

4.1 Express-A data filtering

All of the available RPA curves were processed using the following procedure. To analyze the curves, a data cleaning-based method on the following simple criterion was applied: the probe has to collect a current $I_c>0A$, and data have to be acquired while the thruster is firing. The data selected in this study have been processed to get a single I–V curve for each operational point. To obtain a single curve for each configuration, the first mean is computed among all of the selected curves. To exclude extreme curves and to reduce the dispersion, when possible, the following processing was applied: if the RPA configuration has more than 10 acquisitions, only the five closest to the mean curve (computed by the residual sum of squares) are kept to compute the final averaged measurement. If the RPA configuration has between five and nine curves, the two worst curves are omitted to compute the final averaged measurement, and, finally, if the RPA configuration has less than five curves, all data are kept.

An RPA provides two useful types of measurement for thruster characterization. The first is the shape of the $-dI/d{\varphi }_A$ curve, which provides information on the ion-energy distribution function. The second is the absolute value of the collected current when ${\varphi }_A=0V$, making it possible to obtain the current density at the RPA location but only if the transfer function of the probe is known. The collected current can be plotted as a function of ${\alpha }_T$ to obtain information on the angular distribution of the emitted current of ions.

In the remainder of the section, we compare the introduced transfer function model to Express-A measurements on the two kinds of measurements from an RPA probe: on one hand, the study of the ion energy distribution function and on the other hand, the analysis of the ion current at ${\varphi }_A=0V$.

4.2 Comparison between the model prediction of the $-\mathit{d}\mathit{I}/\mathit{d}{\mathit{\varphi }}_{\mathit{A}}$ curve and Express-A RPA measurements

In this section, several curves obtained from Express data are shown in Figure 10. We have decided to focus on four configurations corresponding to the DRT1 (near probe) measurements with RT4 firing with the solar array angle of (10.a) 45° and (10.c) 58°, and T4 firing with the solar array angle of (10.b) 75° and (10.d) 92° (as shown in Figure 2). All probe tilt-angles ${\beta }_{RPA}$ are greater than $25°$, making it possible to highlight cases where misorientation effects are significant (see Figure 8). For every configuration, three curves are shown: the Express data, the IEDF imposed by the model at the RPA entrance, and the $-dI/d{\varphi }_A$ RPA curve prediction obtained from the transfer function model computation described in Section 3.

FIGURE 10

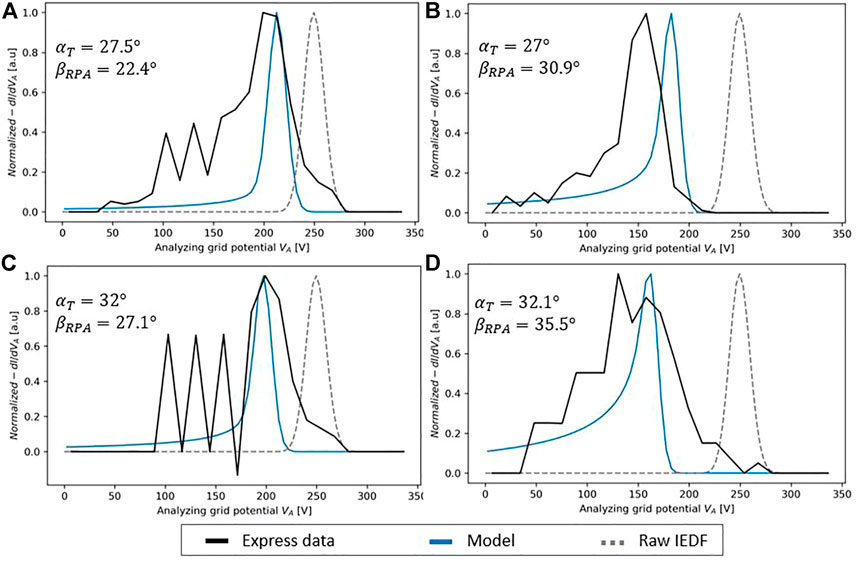
FIGURE 10. Normalized $-\mathit{d}\mathit{I}/\mathit{d}\mathit{V}$ curves as a function of the analyzer potential. The processed Express-A data are compared to the model prediction and to the raw IEDF at the RPA location applied by the simulation. Shown for four configurations.

In Figure 10, the firing angle ${\alpha }_T$ and the distance stay approximately the same on each row, allowing us to highlight the tilt-angle effects. On the first row, Figures 10A,B, the $-dI/d{\varphi }_A$ curves from the Express data (in black) show an energy peak shifted from 200 eV (for ${\beta }_{RPA}=22.4°$) to 160 eV (for ${\beta }_{RPA}=30.9°$). The transfer function model, taking into account the tilt-angle and losses to the RPA walls, also predicts an energy shift of the same order of magnitude, from 210 to 180 eV.

Comparing Figures 10C,D, the energy peak also shifts when ${\beta }_{RPA}$ increases. Thus, the peak shifts from 200 eV (${\beta }_{RPA}=27.1°$) to 150eV with a wider distribution (${\beta }_{RPA}=35.5°$). Here, the model is closer to the energy peak value. In addition, the model manages to predict the widening of the shape of the $-dI/d{\varphi }_A$ curves at low energy when ${\beta }_{RPA}$ increases, also visible in the Express-A data.

It should be noted that there is good agreement between the simulation results and the in-flight measurements, considering that all of the model inputs are completely theoretical (the only input of the RPA model is the distribution function at the thruster exit and the latter is taken from the hybrid model). The sources of discrepancy between the model and measurements can be due to the approximations in our modeling approach, and only primary singly charged ions are taken into account and neither collision nor plasma effects are considered. It can also come from the considered input thruster IEDF or any Express-A measurement error.

4.3 Comparison between the model prediction of the absolute value of the collected current ${\mathit{I}}_{{\mathit{\varphi }}_{\mathit{A}}=\mathit{0}}\left({\mathit{\alpha }}_{\mathit{T}}\right)$ and Express-A measurements

The previous section presented the bias due to a misoriented RPA on the shape of the IEDF. This section focuses on the consequences on the collected currents (in absolute values) and, therefore, on the measurement of the angular distribution function of the emitted ion current.

To fit plasma parameters in simulation from the experimental data, Manzella [15] and Sang-Wook Kim [21] used a normalization to reconstruct the ${\alpha }_T$ dependency of the emitted current from the probe-collected currents. For Express, this is obtained by gathering all of the collected current values for ${\varphi }_A=0V$ for all of the data points. To eliminate the dependency on the varying distance between the thruster and the probe, the data are normalized 1 m downstream of the thruster location using the $1/r^2²$ decrease law. This gives a point cloud representing $I_{{\varphi }_A}=f\left({\alpha }_T\right)$. However, in this method, the effects of the tilt-angle on the collected current are not considered. This is a bias because the tilt-angle varies for each data point.

Figure 11 shows the comparison between the transfer function model as described in Section 3 and the processed Express-A RPA measurements.

FIGURE 11

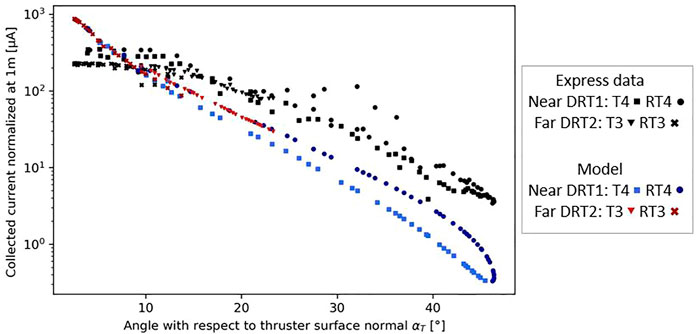
FIGURE 11. Collected current normalized at 1 m from the thruster using a $\mathit{1}/{\mathit{r}}^{\mathit{2}}$ law as a function of the firing angle. Comparison of the processed Express-A data and model results (using input IEDF from the hybrid Hall-thruster code). The near and far probes are, respectively, ‘DRT1’ and ‘DRT2’.

Each point represents the collected current for a configuration (a unique set of thruster, probe, and solar array rotation angle). These configurations are summarized in Figure 2. The RPA data are presented in black and the transfer function model predictions for a misoriented RPA, with the loss at the RPA walls, are in red and blue. The model prediction splits into two curves as the firing angle ${\alpha }_T$ increases. This highlights the relationship between ${\beta }_{RPA}$ and ${\alpha }_T$ , as shown in Figure 2. Each thruster unit consists of two thrusters, one firing in the Y+ direction and the other in the Y- direction (see Figure 1). Therefore, the RPA tilt-angle is maximized when the firing thruster is on the opposite side of the RPA (T4 for near probe and RT3 for far probe), leading to the bottom branch. On the same principle, the probe tilt-angle is minimized when the thruster and the probe are on the same side (RT4 for near probe and T3 for far probe), leading to the top branch.

The comparison between the transfer function model prediction and the Express-A measurements shows that the model overestimates the collected current at low angles ($1-2\bullet {10}^2\mu A$ for Express-A data vs. ${10}^3\mu A$ for model prediction at ${\alpha }_T\sim 2-3°$). Regarding the ${\alpha }_T$ dependency of the current, we can see that the model predicts a steeper decrease than the measured one. This leads to an underestimation of the current at larger angles (factor of 10 at ${\alpha }_T\approx 45°$).

These observations indicate that the beam at the RPA location seems too focalized. The beam divergence is too low compared to what the Express measurements show. The difference between measurements and the model prediction can be attributed to several plume effects. First, electrostatic effects and second, collisions. Considering the electrostatic effects, ion transport from the thruster exit to the probe is not purely radial due to the plasma effects. In particular, a radial electric field builds up in the plume due to electron pressure. High-velocity ions are then attracted outside of the main beam modifying the velocity vector. These plasma effects can be seen in the measurements by comparing the near RPA measurements (∼4 m) to the far ones (∼9 m). Once normalized at 1 m (Figure 11), we can see in Figure 11 that the normalized RPA collected current at small angles (<15°) do not overlap for the near and far RPA (nearly a difference of a factor of 2), as it should be if the $1/r^2$ law was correct. This implies that divergence must build up in the plume. This was already mentioned and also computed by Boyd [14].

Moreover, the results in Figure 11 only consider the primary ion beam. However, charge exchange collisions (CEX) take place in the plume, and fast ions can exchange their charge with slow neutrals, creating slow ions. These slow ions are also attracted in the radial direction and may increase the measured current at large ${\alpha }_T$. The energy of CEX is relatively low (order of 50eV) and cannot be discriminated from the main beam at a large ${\alpha }_T$ (as shown in Figure 10).

In addition to plume effects and collisions, the gap between the measurements and model could also be due to the modeling of the thruster. Indeed, only singly charged ions are modeled, while a significant proportion of the emitted current is doubly or triply charged (respectively, $11-16\%$ and $2-5\%$ [22]). Their high charge leads to a stronger deviation due to electrostatic effects in the plume and therefore to a higher current at a large angle.

4.4 Comparison between the model prediction of the absolute value of the collected current ${\mathit{I}}_{{\mathit{\varphi }}_{\mathit{A}}=\mathit{0}}\left({\mathit{\alpha }}_{\mathit{T}}\right)$ and Express-A measurements with a modified thruster beam as input

Section 4.3 shows that the model is not able to predict the shape of the emitted current measured by the RPA. To highlight the tilt-angle effects in Express-A RPA measurements, it is necessary to change the modeling approach. Figure 10 shows that the velocity distribution $f_{sm}\left(v_r\right)$ fitted from the hybrid model gives good results. However, the measured angular distribution is far from the predicted one. Therefore, to highlight the tilt-angle effect, the function $g\left(\theta \right)$, describing the angular dependency of the emitted current (Eq.7), is fitted from the measurements in Figure 12.

FIGURE 12

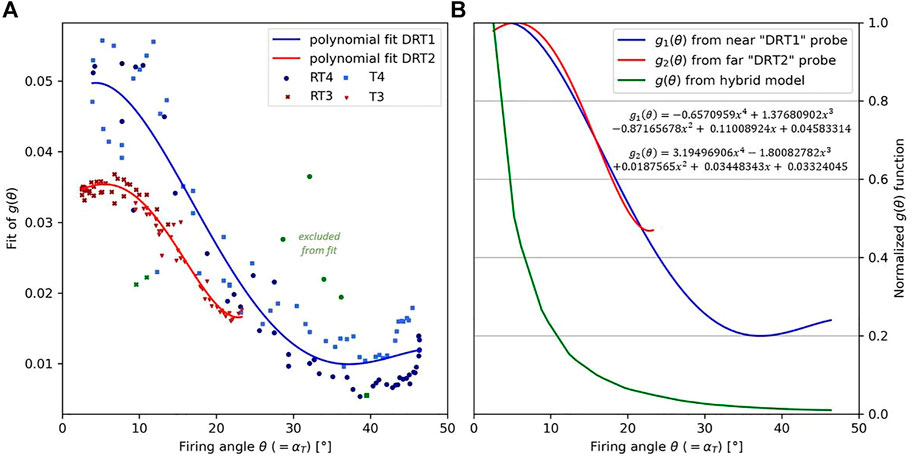
FIGURE 12. (A) Fit of the ion angular distribution function $\mathit{g}\left(\mathit{\theta }\right)$ from the Express-A measurements. (B) Comparison between the normalized ion angular distribution function from experimental fits and thruster hybrid model results. The ion energy distribution function is a shifted Maxwellian (${\mathit{\epsilon }}_{\mathit{s}}=\mathit{250}\mathit{e}\mathit{V}$, ${\mathit{T}}_{\mathit{i}}$ = 0.2 eV).

The experimental results of $g\left(\theta \right)$ in Figure 12A are obtained by inverting the expression of the current collected by the RPA (Eq. 8), such that:

$g\left(\theta \right)=\frac{I_c\left(r,\theta ,{\beta }_{RPA},{\varphi }_A=0\right)\cdot r^2}{S_{coll}\cdot \mathit{cos}\left({\beta }_{RPA}\right)\cdot C\cdot {\int }_0^{+\infty }{v}_r\cdot \cdot f_{sm}\left(v_r\right)\cdot H\left(v_r,\theta ,{\beta }_{RPA},{\varphi }_A,\dots \right)d{v}_r}$

Then, a fit is performed using a fourth-order polynomial. The function is normalized to match the Express-A measurements at a very low firing angle. Ideally (i.e., if the model assumptions were true), the Express-A data in Figure 12 and Figure 11A should be on a unique curve. However, this is not the case and can be due to the dispersion in Express-A measurements on one side and strong model hypotheses on the other side. In Figure 11, the normalization at 1 m shows that the normalized measurements of the near probe were twice the normalized measurements of the far probe, suggesting that the divergence increases in the plume between the probes and invalidating the $1/r^2$ current law. However, this is not a certainty and could be also due to a partially blocked far probe. The only way to discriminate between these two causes would be to compute the current conservation. Unfortunately, this is not possible, as the range of the angle of the far probe does not permit the evaluation of the emitted current at high angles.

In conclusion, without taking into account the plasma effects in the plume, this approach is not able to give the $g\left(\theta \right)$ function at the thruster exit from the RPA measurements. But, the two fits can be used to study the effect of the RPA tilt-angle on the current measurements of Express-A.

Figure 13 shows the comparison between the collected current normalized at 1 m (for ${\varphi }_A=0V$) of the near and far probes to the value predicted by the model using the fits of $g\left(\theta \right)$ , as described previously.

FIGURE 13

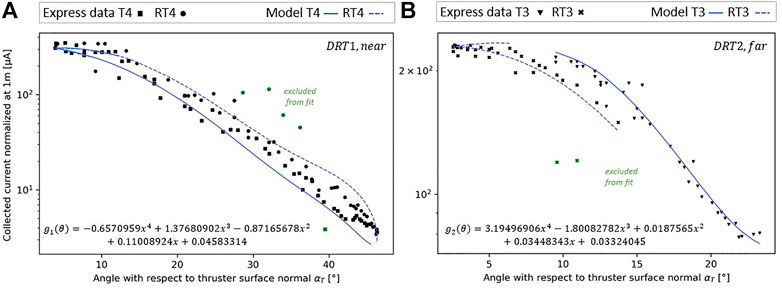
FIGURE 13. Collected current normalized at 1 m from the thruster exit as a function of the firing angle. Comparison of the processed Express-A data and model results. (A) Near probe and (B) far probe. The input IEDF is a shifted Maxwellian distribution for energy (${\mathit{\epsilon }}_{\mathit{s}}=\mathit{250}\mathit{e}\mathit{V}$, ${\mathit{T}}_{\mathit{i}}$ = 0.2 eV) and a fitted angular function $\mathit{g}\left(\mathit{\theta }\right)$.

First, the far probe results (Figure 13B) show that the Express-A data follow two distinct tendencies between ${\alpha }_T=10°$ and $15°$. In this range, the normalized current values while T3 is firing are above the measured values with the RT3 on. This is predicted by the transfer function model as well and is due to the RPA tilt-angle being different in the T3 vs. the RT3 configuration (Figure 2 shows that in the range $10°<{\alpha }_T<15°$, the tilt-angle ${\beta }_{RPA}$ in the RT3 case is $10°$ above the T3 case).

Second, the experimental data and model prediction for the near probe ‘DRT1’ are compared in Figure 13A. As for the far probe, the predicted collected current is different depending on the firing thruster, due to the same tilt-angle effect. The prediction made with the T4 thruster configuration led to the bottom branch and the RT4 thruster configuration to the top one. The Express-A measurements are more dispersed with ‘DRT1’ than ‘DRT2’. However, the measurements for ${\alpha }_T>20°$, especially at very large angles (${\alpha }_T>40°$), also split in two, as predicted. Moreover, although the measurements in the mid ${\alpha }_T$ range, between 10° and 35°, are dispersed, the measured values when RT4 is firing seem generally higher than those made with T4 on. This is also in good agreement with the prediction.

To conclude, both the far and near probe analyses demonstrate that the effects of the tilt-angle are noticeable on the Express-A RPA absolute current measurements and that plotting the current normalized at 1 m as a function of the thruster firing angle ${\alpha }_T$ leads to a bias induced by the varying RPA tilt-angle. The predictions are in good agreement with the data, showing that the model performs well with a corrected $g\left(\theta \right)$ function. Doing so permits us to correct the RPA measurement and to deduce the absolute value of the collected current at the probe location. Furthermore, as the collected current values can be corrected for the tilt-angle, the coupling of this model with a more advanced ion transport should allow deducing the angular distribution of the emitted current at the thruster exit.

5 Conclusion

The new model presented in this study makes it possible to predict the RPA response for cases where the tilt-angle is significant. The new RPA model uses a transfer function formalism, describing the motion of ions inside the RPA. It considers the RPA geometry (with boundary effects, grid transparency, and the field of view with respect to the source) and the ion deflection due to the axial electrostatic fields between each grid. The space charge effects that can appear in the dense plasma are not taken into account in this model. To be able to compare this RPA model to the Express-A measurements, the plasma thruster has been modeled as a point source, using a realistic SPT-100 IEDF from the existing simulation results, considering only the primary singly charged ions. The ion propagation model used between the thruster exit and the RPA entrance assumes no space charge effects and no collisions in the plume.

The analysis of the RPA transfer function theoretically suggests that the tilt-angle effects are significant in Express-A configurations. Comparing these predictions to the actual RPA measurements, it has been shown that RPA misorientation effects are indeed visible on both the $-dI/{\varphi }_A$ curves and on the absolute value of the collected current, affecting both the IEDF analysis and the analysis of angular dependency of the collected ion current.

For the IEDF analysis, the results from the model are in good agreement with the Express-A measurements. It demonstrates that the probe misorientation induces two biases. First, the measured ion energies are shifted toward lower values. Second, the $-dI/d{\varphi }_A$ curves can become nonzero at low energies due to the ions being deflected toward the RPA walls as the analyzer potential increases. This must be taken into account as it can lead to the underestimation of primary ion energy and overestimation of low-energy ion density. Previously, only the Express-A $-dI/d{\varphi }_A$ curves that were studied were when the tilt-angle was near 0°. This work shows that the tilted-RPA measurements can also be understood if this new RPA model is used.

Concerning the angular dependency of the collected current $I_{{\varphi }_A=0}\left({\alpha }_T\right)$ analysis, the comparison between the transfer function model and the Express-A data shows that the model prediction overestimates the collected current at low firing angles and underestimates it at larger angles. The reasons for these discrepancies can be attributed to plasma effects in the plume (electrostatic effects and collisions). Indeed, the Express-A RPA measurements show that the measured thruster beam divergence increases with the distance to the thruster, indicating that the plasma effects created by the electron pressure in the plume tend to widen the beam. To still be able to highlight the tilt-angle effects in $I_{{\varphi }_A=0}\left({\alpha }_T\right)$ measurements, the angular distribution of the emitted current has been fitted to match the Express-A measurements. This allowed us to demonstrate that the tilt-angle effects are also visible on the absolute value of the collected current and that the decrease of the measured current with respect to the firing angle is much steeper than in reality. The previous work [14] results from modeling were directly compared to the raw Express-A tilted RPA measurements. It can induce an overestimation of the thruster beam divergence or an overestimation of plasma effects and collisions in the plume, leading to erroneous conclusions about plasma properties.

The simple ion transport model has shown some limitations and underlines the necessity to model the plasma effects in the plume to more accurately predict the shape of $I_{{\varphi }_A=0}\left({\alpha }_T\right)$. One solution would be to integrate this model into a software such as SPIS (or another plume model) solving plasma effects and plasma-surface interactions so as to obtain more accurate results. This will fall within the scope of future work.

The present probe model can also be applied in vacuum facilities, where it is not always possible to have a perfectly oriented RPA due to the shape of the chamber. This could be interesting to acquire more precise backflow measurements. The distance between the plasma source and the RPA needs to be large enough to consider a point source and point RPA. Moreover, the simplicity of this kind of probe model (with respect to much more sophisticated codes using the hybrid or particle-in-cell methods) means it can be integrated into other numerical tools or used to solve the inverse problem. For example, the probe model can be combined with an optimization code and a more advanced plasma model to extract the IEDF parameters using RPA data as input.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LN, PS, and LG performed the conceptual design of the study. LN and PS designed the calculation model and wrote the simulation codes. LN performed the simulations. The data were analyzed by LN and discussed by PS, LG, SH, and MV. The first draft of the manuscript was written by LN and revised by PS, LG, SH, and MV.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Sarrailh P, Hess SL, Mateo-Velez J-C. 2015, Simulations of plasma thruster effect on the electrostatic behavior of spacecrafts in GEO. In: Proceeding AIAA SPACE 2015 Conference and Exposition; 28 Aug 2015; Pasadena, CA. AIAA-2015-4640. doi:10.2514/6.2015-4640

CrossRef Full Text | Google Scholar

2. Wright KH, Schneider TA, Vaughn JA, Hoang B, Funderburk VV, Wong FK, et al. Electrostatic discharge testing of multijunction solar array coupons after combined space environmental exposures. IEEE Trans Plasma Sci IEEE Nucl Plasma Sci Socieee Trans Plasma Sci (2012) 40(2):334–44. doi:10.1109/TPS.2011.2174447

CrossRef Full Text | Google Scholar

3. Likar JJ, Bogorad AL, Malko TR, Goodzeit NE, Galofaro JT, Mandell MJ. Interaction of charged spacecraft with electric propulsion plume: On orbit data and ground test results. IEEE Trans Nucl Sci (2006) 53:3602–6. doi:10.1109/TNS.2006.885107

CrossRef Full Text | Google Scholar

4. Yan L, Wang P-Y, Ou Y-H, Kang X-L. (2012) Numerical study of Hall thruster plume and sputtering erosion. J Appl Math 2020 1–16. doi:10.1155/2012/327021

CrossRef Full Text | Google Scholar

5. Reza M, Faraji F, Andreussi T. Characterization of a high-power Hall thruster operation in direct drive. Acta Astronautica (2021) 178:392–405. doi:10.1016/j.actaastro.2020.09.008

CrossRef Full Text | Google Scholar

6. Shan K, Chu Y, Li Q, Zheng L, Cao Y. Numerical simulation of interaction between Hall thruster CEX ions and SMART-1 spacecraft. In: NR Junuthula, editor. Mathematical problems in engineering (2015). p. 1–8. doi:10.1155/2015/418493

CrossRef Full Text | Google Scholar

7. Muranaka T, Inanaga Y. Development of a numerical tool for Hall thruster plume and spacecraft interaction analysis. AEROSPACE TECHNOLOGY JAPAN (2018) 16:366–73. doi:10.2322/tastj.16.366

CrossRef Full Text | Google Scholar

8. Mikellides IG, Jongeward GA, Gardner BM, Katz I, Mandell MJ, Davis VA. A Hall-effect thruster plume and spacecraft interactions modeling package. In: Proceeding 27th International Electric Propulsion Conference; 15-19 October, 2001; Pasadena, CA. IEPC-01-251 (2001).

Google Scholar

9. Giono G, Gudmundsson JT, Ivchenko N, Mazouffre S, Dannenmayer K, Loubère D, et al. Non-Maxwellian electron energy probability functions in the plume of a SPT-100 Hall thruster. Plasma Sourc Sci Technol (2017) 27:015006. doi:10.1088/1361-6595/aaa06b

CrossRef Full Text | Google Scholar

10. Kim S-W, Gallimore AD. Plume study of a 1.35-kW SPT-100 using an ExB probe. J Spacecraft Rockets (2002) 39:904–9. doi:10.2514/2.3897

CrossRef Full Text | Google Scholar

11. Passaro A, Vicini A, Biagioni L. Plasma thruster plume simulation: Effect of vacuum chamber environment. In: Proceeding 35th AIAA Plasmadynamics and Lasers Conference; Portland. paper AIAA-2004-2357 (2004). doi:10.2514/6.2004-2357

CrossRef Full Text | Google Scholar

12. Di Cara DM, Estublier D. Smart-1: An analysis of flight data. Acta Astronautica (2005) 57:250–6. doi:10.1016/j.actaastro.2005.03.036

CrossRef Full Text | Google Scholar

13. Sitnikova N, Volkov D, Maximov I, Petrusevich V, Allen D. "Hall effect thruster interactions data from the Russian express-A2 and express-A3 satellites - task 27A," (2003). Available at: https://ntrs.nasa.gov/citations/20030062907.

Google Scholar

14. Boyd I. 2020, Hall thruster far field plume modeling and comparison to Express flight data. In: Proceeding 40th AIAA Aerospace Sciences Meeting & Exhibit (2002); 14 January 2002 - 17 January 2002; NV Reno. AIAA. doi:10.2514/6.2002-487

CrossRef Full Text | Google Scholar

15. Manzella D, Jankovsky R, Elliott F, Mikellides IG, Jongeward GA, Allen D. Hall thruster plume measurements on-board the Russian express satellites. In: Proceeding 27th International Electric Propulsion Conference; October 14-19, 2001; Pasadena, CA. IEPC (2001). Available at: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=505965F4BFAC7A689E0E7A4C589B9ADC?doi=10.1.1.618.6148&rep=rep1&type=pdf.

Google Scholar

16. Mikellides IG, Jongeward GA, Katz I, Manzella DH. Plume modeling of stationary plasma thrusters and interactions with the express-A spacecraft. J Spacecraft Rockets (2002) 39:894–903. doi:10.2514/2.3896

CrossRef Full Text | Google Scholar

17. Boyd ID, Dressler RA. Far field modeling of the plasma plume of a Hall thruster. J Appl Phys (2002) 92:1764–74. doi:10.1063/1.1492014

CrossRef Full Text | Google Scholar

18. Korsun AG, Tverdokhlebova EM, Gabdullin FF. The distinction between the ep plume expansion in space and in vacuum chamber. In: Proceeding 29th International Electric Propulsion Conference. Princeton, NJ: Central Research Institute of Machine Building (TsNIIMASH)Pionerskaya str (2005). paper IEPC-2005-073. Available at: https://www.researchgate.net/profile/Ekaterina-Tverdokhlebova/publication/236171538_The_Distinction_between_the_EP_Plume_Expansion_in_Space_and_in_Vacuum_Chamber/data/0deec516d1b0e0b0e2000000/IEPC-2005-073.pdf.

Google Scholar

19. Chao CK, Su S-Y. Charged particle motion inside the retarding potential analyzer. Phys Plasmas (2000) 7:101–7. doi:10.1063/1.873817

CrossRef Full Text | Google Scholar

20. Garrigues L, Hagelaar GJM, Boniface C, Boeuf JP. Anomalous conductivity and secondary electron emission in Hall effect thrusters. J Appl Phys (2006) 100:123301. doi:10.1063/1.2401773

CrossRef Full Text | Google Scholar

21. Kim S-W, Foster J, Gallimore A. Very-near-field plume study of a 1.35 kW SPT-100. In: Proceeding 32nd Joint Propulsion Conference and Exhibit; 22 Aug 2012; Lake Buena Vista, FL. AIAA (1996). doi:10.2514/6.1996-2972

CrossRef Full Text | Google Scholar

22. Kim S-W. Experimental investigations of plasma parameters and species-dependent ion energy distribution in the plasma exhaust plume of a Hall thruster, United States: Aerospace EngineeringUniversity of Michigan (1999). Ph.D. Dissertation.

Google Scholar