Topological Corner States in Non-Unitary Coinless Discrete-Time Quantum Walks

Meng, Ya

doi:10.3389/fphy.2022.861125

ORIGINAL RESEARCH article

Front. Phys., 03 May 2022

Sec. Condensed Matter Physics

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.861125

This article is part of the Research Topic Higher-Order Topological Matter View all 4 articles

Topological Corner States in Non-Unitary Coinless Discrete-Time Quantum Walks

Ya Meng*

Department of Physics, Xinzhou Teachers University, Xinzhou, China

The discrete-time quantum walk provides a versatile platform for exploring abundant topological phenomena due to its intrinsic spin-orbit coupling. In this work, we study the non-Hermitian second-order topology in a two-dimensional non-unitary coinless discrete-time quantum walk, which is realizable in the three-dimensional photonic waveguides. By adding the non-unitary gain-loss substep operators into the one-step operator of the coinless discrete-time quantum walk, we find the appearance of the four-degenerate zero-dimensional corner states at ReE = 0 when the gain-loss parameter of the system is larger than a critical value. This intriguing phenomenon originates from the nontrivial second-order topology of the system, which can be characterized by a second-order topological invariant of polarizations. Finally, we show that the exotic corner states can be observed experimentally through the probability distributions during the multistep non-unitary coinless discrete-time quantum walks. Our work potentially pave the way for exploring exotic non-Hermitian higher-order topological states of matter in coinless discrete-time quantum walks.

1 Introduction

Due to the unique bulk-boundary correspondence, topological phases of matter have attracted great attention in recent years [1–3]. The standard bulk-boundary correspondence generates the emergence of robust gapless eigenstates localized at the boundary of the nontrivial topological sample. However, in 2017, Benalcazar et al extend the concept of the topological phases of matter by introducing the higher-order topological insulators, which obey a generalized bulk-boundary correspondence [4, 5]. Specifically, for a d-dimensional nth nontrivial topological system, the robust gapless eigenstates localized at (d − n)-dimensional boundary of the system will appear [6–8]. Generally speaking, the nontrivial topological phases can be generated through engineering specific hoppings in lattice models [9, 10]. In addition, more exotic topological properties can arise due to other characteristics of the system, such as periodic driving [11–13], non-Hermiticity [14–18], and disorder [19–22], to mention a few.

As a typical time-periodic driving (Floquet) system, the discrete-time quantum walk (DTQW), which is a dynamical evolution process of particles (called walkers) in discrete position space at discrete points in time, exhibits abundant topological properties [23, 24] and has been realized experimentally in systems of cold atoms [25, 26], trapped ions [27, 28], photons [29–32], superconducting circuits [33], and nuclear magnetic resonance [34]. Although the intriguing first-order topological phenomena in unitary [35–49] and non-unitary [50–59] DTQWs have been widely studied both in theory and experiment, little attention has been paid to the connection between the DTQWs and the higher-order topology [60]. As the quantum counterpart of classical random walk, the walker’s internal degree of freedom (IDF) of the DTQW plays the role of a quantum coin [61]. Thus, the walker’s internal state is also called the coin state. According to the coin state, DTQW can be divided into the coined DTQW (IDF $>$ 1) and the coinless DTQW (IDF = 1) [62]. Here we study the second-order topology in two-dimensional non-unitary coinless DTQWs. Compared with the coined DTQW, in which the walker’s direction of motion depends on its coin states, the research of the coinless one without coin states is still lack [63, 64], especially its topological properties [57, 60, 65, 66]. However, the coinless DTQW can be directed constructed from the static Hamiltonian and thus can easily simulate rich physical phenomena originate from the static Hamiltonian. Furthermore, novel phenomena beyond the static Hamiltonian can emerge in coinless DTQW, such as the emergence of the topological boundary states at energy π, which is unique for the Floquet systems.

In this paper, we construct a non-unitary one-step operator of a two-dimensional coinless DTQW, which can be realized using three-dimensional photonic waveguides. Through the quasi-energy spectrum and the collective distributions of the eigenstates, we observe four energy-degenerate corner-localized eigenstates induced solely by the gain-loss term in our proposed non-unitary coinless DTQW. The existence of such corner states originate from the nontrivial second-order topology of the system. To characterize the topological properties of the system, we calculate numerically a second-order topological invariant of polarizations through constructing the biorthogonal nested Wilson loops and give the topological phase diagram. Moreover, we numerically demonstrate that the corner states governed by the nontrivial second-order topology can be experimentally observed through the probability distributions in multistep coinless non-unitary DTQWs. Our work potentially pave the way for studying exotic non-Hermitian higher-order topological states of matter in coinless discrete-time quantum walks.

The structure of this paper is organized as follows. In Section 2, the one-step operator of a two-dimensional coinless non-unitary DTQW is constructed. In Section 3, we numerically calculate the quasienergy spectra and observe the second-order topological corner states. In Section 4, we show the topological phase diagram characterized by a topological invariant of polarizations. In Section 5, we illustrate how to observe the corner states in such system. Discussion and conclusion are finally drawn in Section 6.

2 Non-Unitary Coinless Discrete-Time Quantum Walk

Based on the point that the coinless DTQW can be constructed by dividing the static Hamiltonian, we first introduce an extended Benalcazar-Bernevig-Hughes (BBH) Hamiltonian with on-site gain and loss

{\hat{H}}_{total} = {\hat{H}}_{BBH} + {\hat{H}}_{gl} . (1)

The first term in Eq. 1 is exactly the BBH Hamiltonian [4, 5].

{\hat{H}}_{BBH} = \sum_{y = 1}^{N_{y}} \sum_{x = 1}^{N_{x}} (t_{x} {\hat{a}}_{x + 1, y}^{†} {\hat{a}}_{x, y} + {(- 1)}^{x} t_{y} {\hat{a}}_{x, y + 1}^{†} {\hat{a}}_{x, y}) + H.c., (2)

where ${\hat{a}}_{x, y}^{†}$ $({\hat{a}}_{x, y})$ is the creation (annihilation) operator of a spinless particle at the site (x, y), t_x(y) = t + (−1)^x(y)δt are the hopping amplitudes in the x (y) direction respectively, and H.c. is the Hermitian conjugate. N_x and N_y are the numbers of the lattice sites in the x and y directions, respectively. We can see that there are two types of hopping amplitudes t − δt and t + δt. To simplify the writing in the following paper, we relabel these two types of hopping amplitudes as t − δt = J₁ and t + δt = J₂. Furthermore, the on-site gain-loss Hamiltonian ${\hat{H}}_{gl}$ is introduced as

\begin{align} {\hat{H}}_{gl} & = i γ \sum_{y = 1}^{N_{y} / 4} \sum_{x = 1}^{N_{x} / 4} \\ ({\hat{a}}_{4 x - 3,4 y - 3}^{†} {\hat{a}}_{4 x - 3,4 y - 3} - {\hat{a}}_{4 x - 2,4 y - 3}^{†} {\hat{a}}_{4 x - 2,4 y - 3} - {\hat{a}}_{4 x - 1,4 y - 3}^{†} {\hat{a}}_{4 x - 1,4 y - 3} + {\hat{a}}_{4 x, 4 y - 3}^{†} {\hat{a}}_{4 x, 4 y - 3} \\ - {\hat{a}}_{4 x - 3,4 y - 2}^{†} {\hat{a}}_{4 x - 3,4 y - 2} + {\hat{a}}_{4 x - 2,4 y - 2}^{†} {\hat{a}}_{4 x - 2,4 y - 2} + {\hat{a}}_{4 x - 1,4 y - 2}^{†} {\hat{a}}_{4 x - 1,4 y - 2} - {\hat{a}}_{4 x, 4 y - 2}^{†} {\hat{a}}_{4 x, 4 y - 2} \\ - {\hat{a}}_{4 x - 3,4 y - 1}^{†} {\hat{a}}_{4 x - 3,4 y - 1} + {\hat{a}}_{4 x - 2,4 y - 1}^{†} {\hat{a}}_{4 x - 2,4 y - 1} + {\hat{a}}_{4 x - 1,4 y - 1}^{†} {\hat{a}}_{4 x - 1,4 y - 1} - {\hat{a}}_{4 x, 4 y - 1}^{†} {\hat{a}}_{4 x, 4 y - 1} \\ + {\hat{a}}_{4 x - 3,4 y}^{†} {\hat{a}}_{4 x - 3,4 y} - {\hat{a}}_{4 x - 2,4 y}^{†} {\hat{a}}_{4 x - 2,4 y} - {\hat{a}}_{4 x - 1,4 y}^{†} {\hat{a}}_{4 x - 1,4 y} + {\hat{a}}_{4 x, 4 y}^{†} {\hat{a}}_{4 x, 4 y}), \end{align} (3)

where γ is the gain-loss parameter. ${\hat{H}}_{gl}$ has a period of four lattice sites (gain-loss-loss-gain) both in x and y directions. Since the previous work [67, 68] have demonstrated that such gain-loss-loss-gain typed non-Hermitian term occurring in one-dimensional lattice system can dramatically affect the topology of the system, its two-dimensional extension ${\hat{H}}_{gl}$ are also expected to bring some novel topological phenomena.

In order to construct a coinless discrete-time quantum walk, we first divide the Hamiltonian (1) into five parts

{\hat{H}}_{total} = {\hat{H}}_{2 y} + {\hat{H}}_{1 y} + {\hat{H}}_{2 x} + {\hat{H}}_{1 x} + {\hat{H}}_{gl} (4)

where ${\hat{H}}_{1 x}$ $({\hat{H}}_{2 x})$ and ${\hat{H}}_{1 y}$ $({\hat{H}}_{2 y})$ represent the sum of the hoppings with parameter J₁ (J₂) along the x and y directions, respectively. Thus, in the Hilbert space |x⟩ ⊗|y⟩ (or |x, y⟩) with x ∈ {1, N_x} and y ∈ {1, N_y}, an one-step operator of the coinless DTQW can be constructed as

\begin{align} {\hat{U}}_{step} & = e^{- i \frac{{\hat{H}}_{gl} Δ T}{4 ℏ}} e^{- i \frac{{\hat{H}}_{2 y} Δ T}{ℏ}} e^{- i \frac{{\hat{H}}_{gl} Δ T}{4 ℏ}} e^{- i \frac{{\hat{H}}_{1 y} Δ T}{ℏ}} e^{- i \frac{{\hat{H}}_{gl} Δ T}{4 ℏ}} e^{- i \frac{{\hat{H}}_{2 x} Δ T}{ℏ}} e^{- i \frac{{\hat{H}}_{gl} Δ T}{4 ℏ}} e^{- i \frac{{\hat{H}}_{1 x} Δ T}{ℏ}} \\ = {\hat{U}}_{gl} {\hat{U}}_{4} {\hat{U}}_{gl} {\hat{U}}_{3} {\hat{U}}_{gl} {\hat{U}}_{2} {\hat{U}}_{gl} {\hat{U}}_{1} \end{align} (5)

Other alternative one-step operators will also be discussed in the next section. For simplicity, we use the units ΔT = ℏ = 1 hereafter. By directly calculating the matrix exponential, we can write these four unitary substep operators as

\begin{align} {\hat{U}}_{1} & = \sum_{x = 0}^{N_{x} / 2 - 1} {\hat{V}}_{2 x + 1} (J_{1}) \otimes {\hat{I}}_{y}, \end{align} (6)

\begin{align} {\hat{U}}_{2} & = \sum_{x = 1}^{N_{x} / 2 - 1} {\hat{V}}_{2 x} (J_{2}) \otimes {\hat{I}}_{y} + (| 1 〉 〈 1 | + | N_{x} 〉 〈 N_{x} |) \otimes {\hat{I}}_{y}, \end{align} (7)

\begin{align} {\hat{U}}_{3} & = \sum_{x = 1}^{N_{x}} \sum_{y = 0}^{N_{y} / 2 - 1} | x 〉 〈 x | \otimes {\hat{V}}_{2 y + 1} (J_{1}), \end{align} (8)

\begin{align} {\hat{U}}_{4} & = \sum_{x = 1}^{N_{x}} \sum_{y = 1}^{N_{y} / 2 - 1} | x 〉 〈 x | \otimes {\hat{V}}_{2 y} (J_{2}) + {\hat{I}}_{x} \otimes (| 1 〉 〈 1 | + | N_{y} 〉 〈 N_{y} |) \end{align} (9)

with the coupling operators defined as

\begin{align} {\hat{V}}_{x} (r) & = \cos (r) [| x 〉 〈 x | + | x + 1 〉 〈 x + 1 |] - i \sin (r) [| x + 1 〉 〈 x | + | x 〉 〈 x + 1 |], \end{align} (10)

\begin{align} {\hat{V}}_{y} (r) & = \cos (r) [| y 〉 〈 y | + | y + 1 〉 〈 y + 1 |] - i \sin (r) [e^{i x π} | y + 1 〉 〈 y | + e^{- i x π} | y 〉 〈 y + 1 |] . \end{align} (11)

The operator ${\hat{I}}_{x (y)}$ denotes a N_x × N_x (N_y × N_y) identity matrix in the sub-Hilbert space |x⟩ (|y⟩).

Similarly, the non-unitary substep operator can be written in the following form

\begin{align} {\hat{U}}_{gl} & = \sum_{y = 1}^{N_{y} / 4} \sum_{x = 1}^{N_{x} / 4} (e^{\frac{γ}{4}} | 4 x - 3,4 y - 3 〉 〈 4 x - 3,4 y - 3 | + e^{- \frac{γ}{4}} | 4 x - 2,4 y - 3 〉 〈 4 x - 2,4 y - 3 | \\ + e^{- \frac{γ}{4}} | 4 x - 1,4 y - 3 〉 〈 4 x - 1,4 y - 3 | + e^{\frac{γ}{4}} | 4 x, 4 y - 3 〉 〈 4 x, 4 y - 3 | \\ + e^{- \frac{γ}{4}} | 4 x - 3,4 y - 2 〉 〈 4 x - 3,4 y - 2 | + e^{\frac{γ}{4}} | 4 x - 2,4 y - 2 〉 〈 4 x - 2,4 y - 2 | \\ + e^{\frac{γ}{4}} | 4 x - 1,4 y - 2 〉 〈 4 x - 1,4 y - 2 | + e^{- \frac{γ}{4}} | 4 x, 4 y - 2 〉 〈 4 x, 4 y - 2 | \\ + e^{- \frac{γ}{4}} | 4 x - 3,4 y - 1 〉 〈 4 x - 3,4 y - 1 | + e^{\frac{γ}{4}} | 4 x - 2,4 y - 1 〉 〈 4 x - 2,4 y - 1 | \\ + e^{\frac{γ}{4}} | 4 x - 1,4 y - 1 〉 〈 4 x - 1,4 y - 1 | + e^{- \frac{γ}{4}} | 4 x, 4 y - 1 〉 〈 4 x, 4 y - 1 | \\ + e^{\frac{γ}{4}} | 4 x - 3,4 y 〉 〈 4 x - 3,4 y | + e^{- \frac{γ}{4}} | 4 x - 2,4 y 〉 〈 4 x - 2,4 y | \\ + e^{- \frac{γ}{4}} | 4 x - 1,4 y 〉 〈 4 x - 1,4 y | + e^{\frac{γ}{4}} | 4 x, 4 y 〉 〈 4 x, 4 y |) . \end{align} (12)

By applying the one-step operator in Eq. 5 many times, a multiple non-unitary coinless DTQW can be realized, as shown schematically in Figure 1. Furthermore, when the gain-loss parameter γ = 0, the substep operator ${\hat{U}}_{gl}$ is exactly a (N_x ⋅ N_y) × (N_x ⋅ N_y) identity matrix and the corresponding one-step operator ${\hat{U}}_{step}$ will become unitary.

FIGURE 1

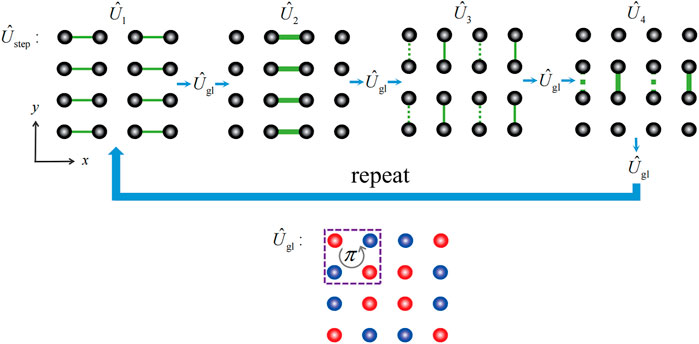
FIGURE 1. Up: Schematic of the eight-step non-unitary coinless DTQW in a two-dimensional lattice. For the four unitary substep operators ${\hat{U}}_{i}$ in Eqs 6–9, the couplings between the different lattice sites are represented by the different thicknesses of the green lines. The two kinds of green lines with different thicknesses represent two types of coupling strengths J₁ (thin) and J₂ (thick), respectively. And the dashed green lines in the y direction indicate the required phases of ± π in the coupling process. Bottom: Schematic of the non-unitary substep operator ${\hat{U}}_{gl}$ of Eq. 12. The color of red (blue) indicates the on-site gain (loss). Due to the emergent phases in the y direction, a π-flux will be induced when a walker goes through a closed loop of four sites anticlockwise.

Based on recent experimental progress of quantum walks in waveguides [66, 69–73], the realization of Eq. 5 is accessible under the flexible control of the three-dimensional photonic waveguides. Specifically, the above discussed coinless DTQW except the gain-loss term ${\hat{U}}_{gl}$ can be realized by the directional coupling of two waveguides [60, 66, 70, 74]. And the alternative gain or loss can be introduced in a single waveguide [57, 75].

3 Spectra and Corner States

In order to illustrate the effect of the gain-loss term ${\hat{U}}_{gl}$ on the topological features of this non-unitary coinless DTQW, in this section we fix the coupling parameter J₁/J₂ = 1.1, which corresponds to a trivial phase when the gain-loss parameter γ is zero [60]. Since the one-step operator ${\hat{U}}_{step}$ is non-unitary, its effective Hamiltion ${\hat{H}}_{eff} = i \ln {\hat{U}}_{step}$ is non-Hermitian with complex energy. In Figure 2A, we plot the real part of the quasi-energy spectrum, obtained from diagonalizing ${\hat{H}}_{eff}$ , as a function of γ under the open boundary condition in both directions. We find that when the gain-loss parameter γ is large than a critical value γ_c, four energy-degenerate states will emerge at ReE = 0. The value of γ_c is related to the specific form of the one-step operator except the value of the coupling parameter J₁/J₂. The one-step operator ${\hat{U}}_{step}$ of Eq. 5 contains four unitary operators, each of which is followed by a non-unitary gain-loss operator ${\hat{U}}_{gl}$ . However, the one-step operator can also be constructed as ${\hat{U}}_{step}^{'} = {\hat{U}}_{4} {\hat{U}}_{gl} {\hat{U}}_{3} {\hat{U}}_{2} {\hat{U}}_{gl} {\hat{U}}_{1}$ , which consists of only six substep operators. In Figure 2B, we show the real part of the quasi-energy spectrum of ${\hat{H}}_{eff}^{'} = i \ln {\hat{U}}_{step}^{'}$ varying with γ. Similarly, we observe the existence of four energy-degenerate states at ReE’ = 0 when the gain-loss parameter γ is large than a critical value $γ_{c}^{'}$ . Compared with the critical value γ_c for ${\hat{U}}_{step}$ , the critical value $γ_{c}^{'}$ for ${\hat{U}}_{step}^{'}$ is larger since the latter contains less gain-loss operators ${\hat{U}}_{gl}$ . Since the numerical methods used to analyse the topological features of the systems generated by the above two one-step operators are similar, we only discuss the former in the following paper. We notice that no four energy-degenerate states will emerge at ReE = 0 in the real part of the quasi-energy varying with γ when the system is generated by another one-step operator ${\hat{U}}_{step}^{''} = {\hat{U}}_{gl} {\hat{U}}_{4} {\hat{U}}_{3} {\hat{U}}_{2} {\hat{U}}_{1}$ . Furthermore, we do not show the imag part of the quasi-energy varying with γ since no more valuable information can be obtained.

FIGURE 2

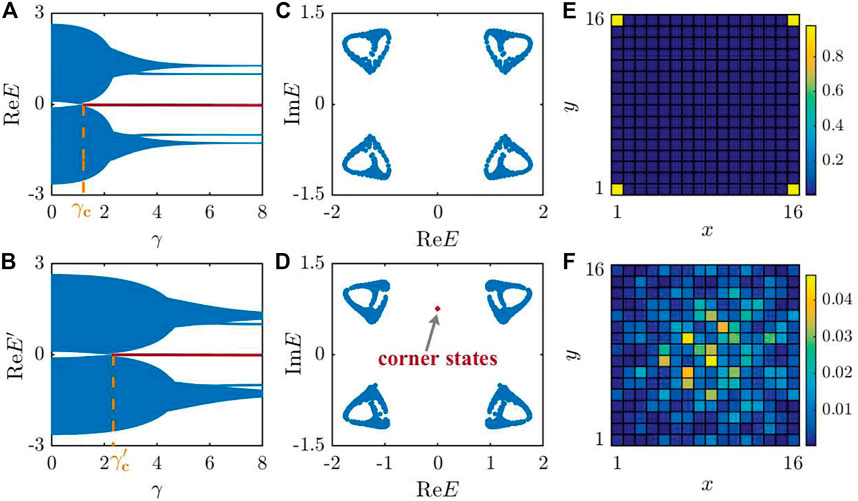
FIGURE 2. (A,B) Real part of the quasi-energy spectrum obtained from the effective Hamiltonian ${\hat{H}}_{eff} = i \ln {\hat{U}}_{step}$ (A) or ${\hat{H}}_{eff}^{'} = i \ln {\hat{U}}_{step}^{'}$ (B), as a function of γ under the open boundary condition. The bulk energy gap begin to close at γ = γ_c ≈ 1.2 (A) or $γ = γ_{c}^{'} \approx 2.4$ (B), where a topological phase transition occurs and in-gap corner states (red line with fourfold degeneracy) emerge when γ > γ_c (A) or $γ > γ_{c}^{'}$ (B). The lattice size is chosen as 60, ×, 60. (C,D) Typical quasi-energy spectrum of the system under the periodic boundary condition (C) or the open boundary condition (D). The gain-loss parameter is γ = 2.5 and the lattice size is same with (A,B). (E,F) Collective density distributions $Σ_{i} | Ψ_{i}^{R} (x, y) |^{2}$ of the four-degenerate corner states with state numbers {127, 128, 129, 130} (E) and two-degenerate bulk states with state numbers {161, 162} (F). The eigenstates are sorted by the value of the real part of the quasi-energy. The gain-loss parameter is chosen as γ = 3.5 and the lattice size is 16 × 16. Here the coupling parameter is fixed at J₁/J₂ = 1.1.

A unique phenomenon in non-Hermitian systems is the appearance of the skin effects [14], which means that all of the eigenstates will be localized near the boundary under the open boundary conditions. However, the skin effects will not emerge in all of the non-Hermitian systems [16]. A major consequence of non-Hermitian systems with the skin effects is that the bulk bands of the system under the open boundary conditions are considerably different from those of the system under the periodic boundary conditions. Thus, we show the complete quasi-energy spectrum under the open and periodic boundary conditions in Figures 2C,D, respectively. We find that the bulk bands under the different boundary conditions are consistent except the emergence of the four energy-degenerate states at ReE = 0 when we consider the open boundary conditions. Figures 2C,D strongly demonstrate that our system does not suffer from the skin effects and therefore it does not matter whether the right and/or left eigenstates are used to calculate the density distribution. In Figure 2E, we show the collective density distributions of these four energy-degenerate gapless states at ReE = 0, which are localized at the four corners of the lattice. And the remaining two energy-degenerate gapped states at ReE ≠ 0 are indeed extended in the bulk of the lattice, as shown in Figure 2F.

4 Topological Phase Diagram

The emergence of the exotic four energy-degenerate corner states at ReE = 0 can be attributed to the second-order bulk topology, which corresponds a kind of topological phase supporting lower-dimensional corner or hinge states, induced by the gain-loss term ${\hat{U}}_{gl}$ in Eq. 12. The nontrivial second-order bulk topology in non-Hermitian systems can be characterized by introducing the non-Bloch winding numbers or the biorthogonal nested Wilson loops [76–81]. In addition, due to the intrinsic 2π period of quasi-energy, a pair of topological invariants are required to predict the appearance of zero-energy and π-energy corner states in the Floquet second-order topological systems [82–87]. Specifically for the second-order topological characterisation of our model, only one invariant of polarizations (the quadrupole moments) constructed by the biorthogonal nested Wilson loops is enough since the C₄ symmetry and the absence of the π-energy corner states.

The second-order topological invariant of polarizations are constructed in momentum space. Thus, we first need to renumber the lattice sites in terms of the unit cell, each of which contains 16 sublattices, as shown in Figure 3. Using the Fourier transformation, the one-step operator can be written in momentum space as ${\hat{ψ}}_{k}^{†} {\hat{U}}_{step} (k) {\hat{ψ}}_{k}$ , where ${\hat{ψ}}_{k} = {({\hat{a}}_{(i = 1,2,3,4), k}, {\hat{b}}_{(i = 1,2,3,4), k}, {\hat{c}}_{(i = 1,2,3,4), k}, {\hat{d}}_{(i = 1,2,3,4), k})}^{T}$ and ${\hat{U}}_{step} (k)$ is a 16 × 16 matrix in the basis of ${\hat{ψ}}_{k}$ . Then, we consider the right and left eigenstates of the effective Hamiltonian ${\hat{H}}_{eff} (k) = i \ln {\hat{U}}_{step} (k)$ ,

\begin{align} {\hat{H}}_{eff} (k) | u_{α, k}^{R} 〉 & = E_{α} (k) | u_{α, k}^{R} 〉, \\ {\hat{H}}_{eff}^{†} (k) | u_{α, k}^{L} 〉 & = E_{α}^{*} (k) | u_{α, k}^{L} 〉, \end{align} (13)

which satisfies the biorthogonal normalization $〈 u_{α, k}^{L} | u_{β, k}^{R} 〉 = δ_{α, β}$ with the band indices α and β. Alternatively, one can write the matrix of the effective Hamiltonian as H_eff = VDV⁻¹, where D is a diagonal matrix of quasi-energies and the columns of the matrixes V and ${(V^{- 1})}^{†}$ are corresponding right and left eigenstates, respectively. Because of the absence of the non-Hermitian skin effects, the bulk-boundary correspondence based on the ordinary Bloch band theory is valid here. Thus, we can determine the topological phase transition points with the gapless real quasi-energy spectrum ReE(k), see Figures 4A–C. When the system is in the topological trivial or nontrivial phases, the real quasi-energy spectrum ReE(k) is all gapped.

FIGURE 3

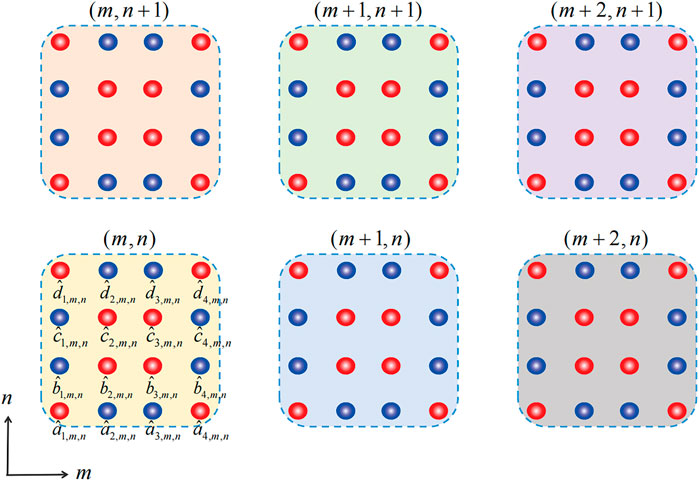
FIGURE 3. The unit cells, labeled with (m, n), of our coinless DTQW in the two-dimensional lattice. Each unit cell has 16 sublattices, which are labeled as ${{\hat{a}}_{(i = 1,2,3,4), m, n}, {\hat{b}}_{(i = 1,2,3,4), m, n}, {\hat{c}}_{(i = 1,2,3,4), m, n}, {\hat{d}}_{(i = 1,2,3,4), m, n}}$ , respectively. Here six unit cells are shown for a simple graphical representation.

FIGURE 4

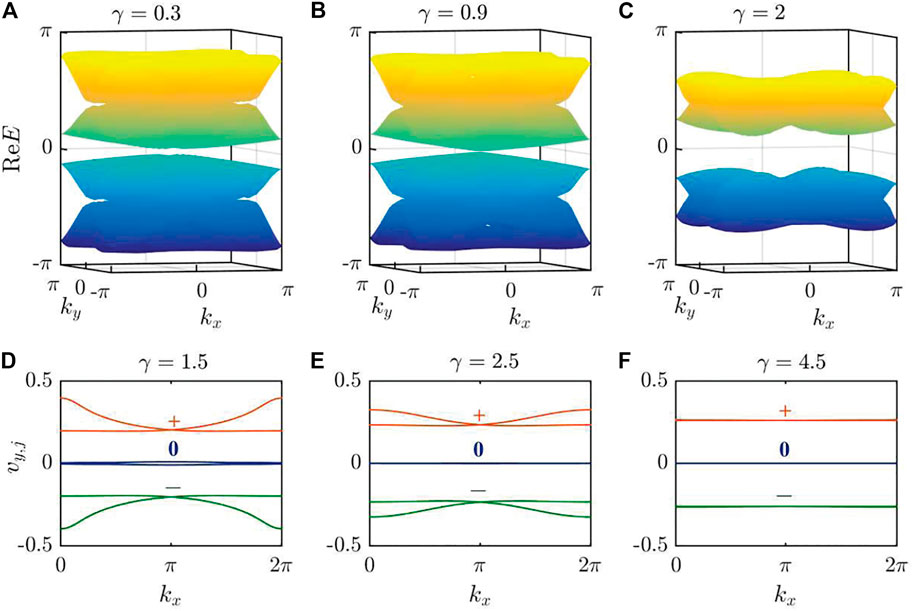
FIGURE 4. (A–C) Real quasi-energy spectrum in momentum space of the effective Hamiltonian ${\hat{H}}_{eff} (k)$ with different gain-loss parameters. For the trivial (A) and topological (C) phases, the real spectrums are gapped. While at the phase transition point (B), the real spectrum is gapless. (D–F) Wannier bands structures v_y,j (k_x) with different gain-loss parameters. The imaginary parts are always zero. Here the coupling parameter is fixed at J₁ = 1.1.

To characterize the gapped phases using polarizations, we consider the case of half filling and define the biorthogonal Wilson loop operator along y direction as

{\hat{W}}_{y, k} = {\hat{F}}_{y, k + (N_{y} - 1) Δ k_{y} e_{y}} \cdot \cdot \cdot {\hat{F}}_{y, k + Δ k_{y} e_{y}} {\hat{F}}_{y, k}, (14)

where ${\hat{F}}_{y, k}$ is a 8 × 8 matrix with elements ${[{\hat{F}}_{y, k}]}^{α β} = 〈 u_{α, k + Δ k_{y} e_{y}}^{L} | u_{β, k}^{R} 〉 (α, β = 1,2, \dots, 8)$ , e_y is the unit vector in the y direction, and Δk_y = 2π/N_y. The two-dimensional Brillouin zone is discretized by using the interval (2π/N_x, 2π/N_y), such that there are (N_x + 1) (N_y + 1) k-points in total. Due to the non-Hermiticity of the effective Hmiltonian ${\hat{H}}_{eff} (k)$ , the constructed operator ${\hat{W}}_{y, k}$ is a non-unitary operator and corresponds to a non-Hermitian Wannier Hamiltonian ${\hat{H}}_{W_{y}} (k) = - i \ln {\hat{W}}_{y, k}$ . With the periodic boundary conditions, $| u_{α, k}^{R} 〉 = | u_{α, k + 2 π e_{y}}^{R} 〉$ and $| u_{α, k}^{L} 〉 = | u_{α, k + 2 π e_{y}}^{L} 〉$ , we can obtain the right and left Wannier states by diagonalizing Eq. 14 as

\begin{align} {\hat{W}}_{y, k} | v_{y, j, k}^{R} 〉 & = e^{i 2 π v_{y, j} (k_{x})} | v_{y, j, k}^{R} 〉, \\ {({\hat{W}}_{y, k}^{- 1})}^{†} | v_{y, j, k}^{L} 〉 & = e^{i 2 π v_{y, j}^{*} (k_{x})} | v_{y, j, k}^{L} 〉, \end{align} (15)

where j is the Wannier band index and $〈 v_{y, j, k}^{L} | v_{y, j^{'}, k}^{R} 〉 = δ_{j, j^{'}}$ . These eight Wannier bands v_y,j (j = 1, 2, … 8) can be divided into three Wannier sectors (labeled by ς = 0, ±) with finite gaps, see Figures 4D–F. Especially, all Wannier bands will tend to be flat when γ is pretty large. Each Wannier sector can carry their own biorthogonal topological invariants, which can be evaluated by constructing the biorthogonal nested Wilson loops. Utilizing eigenstates $| u_{α, k}^{R (L)} 〉$ and $| v_{y, j, k}^{R (L)} 〉$ , we can construct the biorthogonal Wannier states as

| w_{y, j, k}^{R (L)} 〉 = \sum_{α = 1}^{8} {[v_{y, j, k}^{R (L)}]}^{α} | u_{α, k}^{R (L)} 〉, (16)

where ${[v_{y, j, k}^{R (L)}]}^{α}$ denotes the αth element of the 8-component state vector $| v_{y, j, k}^{R (L)} 〉$ and $〈 w_{y, j, k}^{L} | w_{y, j^{'}, k}^{R} 〉 = δ_{j, j^{'}}$ . For each Wannier sector ς, with the periodic boundary conditions, $| w_{y, j, k}^{R} 〉 = | w_{y, j, k + 2 π e_{x}}^{R} 〉$ and $| w_{y, j, k}^{L} 〉 = | w_{y, j, k + 2 π e_{x}}^{L} 〉$ , the elements of the constructed nested Wilson loop operator along x direction are

{[{\hat{\tilde{W}}}_{x, k}^{ς}]}^{l, l^{'}} = 〈 w_{y, l, k + N_{x} Δ k_{x} e_{x}}^{L} | w_{y, r, k + (N_{x} - 1) Δ k_{x} e_{x}}^{R} 〉 〈 w_{y, r, k + (N_{x} - 1) Δ k_{x} e_{x}}^{L} | \dots | w_{y, s, k + Δ k_{x} e_{x}}^{R} 〉 〈 w_{y, s, k + Δ k_{x} e_{x}}^{L} | w_{y, l^{'}, k}^{R} 〉, (17)

where e_x is the unit vector in the x direction and Δk_x = 2π/N_x, the indices l, l′ ∈ 1 … N_W with N_W the number of the Wanner bands in sector ς. In Eq. 17, summation is implied over repeated indices r, … , s ∈ 1 … N_W over all Wannier bands in sector ς. After that, we can obtain the polarizations along x direction as

p_{x}^{ς} = - \frac{i}{2 π} \frac{1}{N_{y}} \sum_{k_{y}} \log \det [{\hat{\tilde{W}}}_{x, k}^{ς}] . (18)

In a similar way, we can directly obtain the Wannier bands v_x,j and polarizations along y direction $p_{y}^{ς}$ by constructing the biorthoganal Wilson and nested Wilson loop operator along x and y directions, respectively. Due to the C₄ symmetry, we have v_y,j ≡ v_x,j and $p_{x}^{ς} \equiv p_{y}^{ς}$ .

Using the above procedure, we numerically calculate the polarizations $p_{x (y)}^{ς}$ and find that the polarizations $p_{x (y)}^{0} \equiv 0$ and $p_{x (y)}^{+} \equiv p_{x (y)}^{-}$ . In Figure 5A, we show the polarizations $p_{x (y)}^{-}$ varying with γ, which equal to 0.5 (0) for topological (trivial) phases with (without) corner states. It means strongly that the polarizations here are good candidates for characterizing the second-order topology of this system. Thus, we define the topological invariant with the polarizations $p_{x}^{-}$ and $p_{y}^{-}$ ,

W = 4 p_{x}^{-} p_{y}^{-} . (19)

The topological invariant W has two possible quantized values: 0 and 1, which corresponds to the trivial and topological phases, respectively. In Figure 5B, we show the topological phase diagram of the topological invariant P versus the coupling parameter J₁ and the gain-loss parameter γ. When J₁ ∈ (0.5, 1), the system with γ = 0 is in the topological phase and will still remain topological as γ is incremented from zero. However, the system with γ = 0 is in the trivial phase with J₁ ∈ (1, 1.5) and will become topological when γ > γ_c. Furthermore, the value of γ_c will increase sharply as we increase J₁.

FIGURE 5

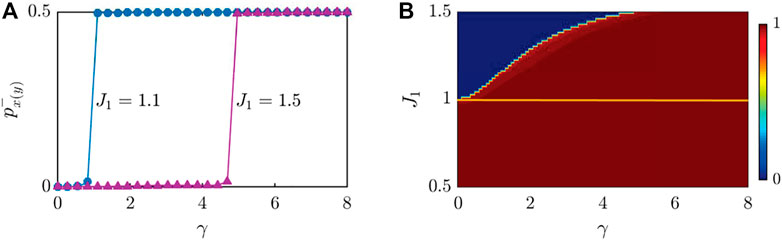
FIGURE 5. (A) Polarizations $p_{x}^{-}$ (lines) and $p_{y}^{-}$ (symbols) versus the gain-loss parameter γ with different coupling parameters J₁. The color blue (magenta) indicates the coupling parameter is fixed at J₁ = 1.1 (J₁ = 1.5). (B) Topological phase diagram of eight-step non-unitary coinless DTQWs characterized by the topological invariant $W = 4 p_{x}^{-} p_{y}^{-}$ versus the gain-loss parameter γ and the coupling parameter J₁. The crimson (blue) filled region corresponds to the topological (trivial) phase with W = 1(W = 0). In the crimson filled region, the part above the yellow line indicates the topological phase induced by the gain-loss term of Eq. 12.

5 Observation of Corner States

Experimentally, the exotic corner states can be observed through the localization of probability distributions in multi-step non-unitary coinless DTQWs. Without the existence of the local states, such as the above discussed corner states, the typical transfer behavior of the coinless DTQW is ballistic [63]. In this section, we demonstrate the existence of the corner states by showing the numerical results of probability distributions of multistep non-unitary coinless DTQWs with different gain-loss parameters and initial states. We fix the coupling parameter at J₁ = 1.1 and tune the gain-loss parameter γ.

First, we tune the gain-loss parameter at γ = 3.5, which corresponds to a topological phase with the emergence of localized corner states, and initialize the walker at one corner (x, y) = (1, 16) of the lattice. As shown in Figure 6A, since the initial state has a large overlap with the corner state, the most part of the walker’s wave packet remains localized near the same corner as increasing the step of the quantum walk. Then, we tune the gain-loss parameter at γ = 0.5, which corresponds to a trivial phase. Since the absence of the localized corner states, the probability distributions of the walker spread ballistically into the bulk with increasing the step of the quantum walk, see Figure 6B. When the initial states are prepared at other three corners of the lattice, the numerical results are similar and thus are not shown here. Finally, we retune the gain-loss parameter at γ = 3.5 and initial the walker at the bulk (x, y) = (8, 8) of the lattice. Similiar to the second case, the walker’s wave packet extends into the bulk as increasing the step of the quantum walk, which further confirms the absence of the non-Hermitian skin effects with the nonlocalization of the bulk states, see Figure 6C.

FIGURE 6

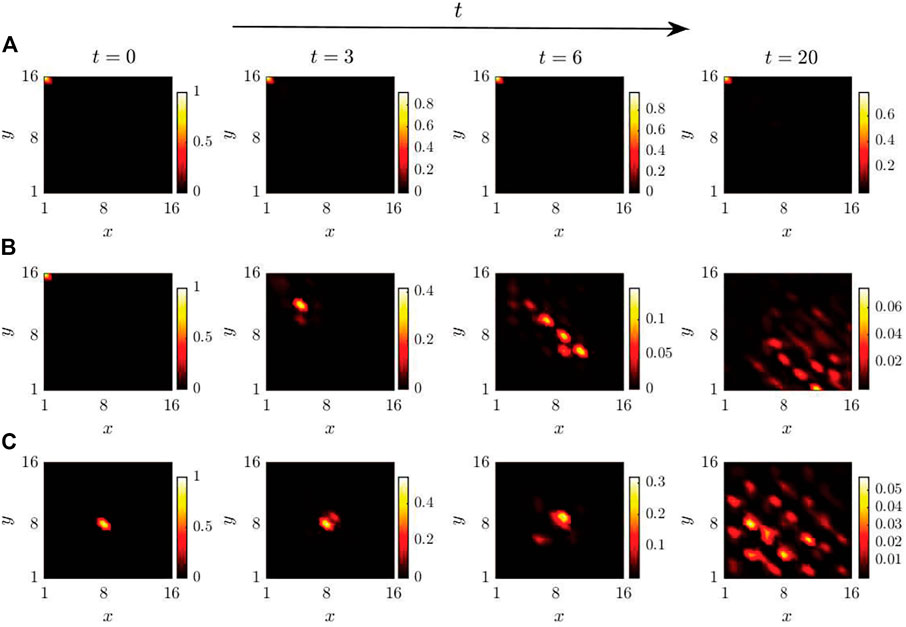
FIGURE 6. Probability distributions $P (x, y, t) = | 〈 x, y | \tilde{ψ} (t) 〉 |^{2}$ of multi-step non-unitary coinless DTQWs on a 16 × 16 lattice. After each step of this DTQW, the state of the walker $| ψ (t) 〉 = {\hat{U}}_{step} | \tilde{ψ} (t - 1) 〉$ will be normalized as $| \tilde{ψ} (t) 〉$ with $〈 \tilde{ψ} (t) | \tilde{ψ} (t) 〉 = 1$ . The walker is initialized at the upper-left corner (x, y) = (1, 16) (A,B) or bulk (x, y) = (8, 8) (C) of the lattice. The gain-loss parameter is chosen as γ = 3.5 (A,C) or γ = 0.5 (B), which correspond to the topological or trivial phase, respectively. The steps are chosen as t = 0, 3, 6, 20. Here the coupling parameter is fixed at J₁ = 1.1.

6 Discussion and Conclusion

We first give a more detailed illustration of the topological phase diagram. In Section 4, we only show part of the complete topological phase diagram for simplicity. Actually, the complete phase diagram has a period of π in the J₁ direction, see Figure 7. Moreover, when the coupling parameter J₁ converges to qπ/2 (q is an integer), the value of γ_c will go to infinity. Especially, when the coupling parameter is exactly fixed at J₁ = qπ/2, a 100%-coupling is present for each unitary sub-evolutionary process governed by ${\hat{U}}_{i}$ (i = 1, 2, 3, 4). In such a case, a single walker does not feel the gain or loss after one step of the eight-step non-unitary coinless DTQW. Thus, the system with 100%-coupling is always trivial without corner states no matter the value of the gain-loss parameter γ.

FIGURE 7

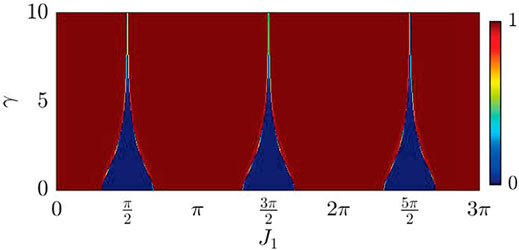
FIGURE 7. Complete topological phase diagram of eight-step non-unitary coinless DTQWs characterized by the topological invariant W versus the coupling parameter J₁ and the gain-loss parameter γ.

In summary, we have constructed a two-dimensional non-unitary coinless DTQW which exhibits nontrivial second-order non-Hermitian topology. We have shown second-order non-Hermitian topological phase diagram characterized by polarizations. Finally, we have shown that the corner states can be observed through the probability distributions. Our work suggests that the coinless DTQW is a potential platform to explore novel non-Hermitian higher-order topological quantum phases, and may shed light on the ongoing exploration of topologically protected quantum information processing.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YM: theory and writing.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hasan MZ, Kane CL. Colloquium: Topological Insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/revmodphys.82.3045