Effects of Ablation Regimes on the Formation and Evolution of Femtosecond Laser-Induced Periodic Structures on Titanium

The formation and evolution of laser-induced periodic structures (LIPSS) have attracted much attention due to their broad applications and rich physics. The literature has shown that excessive laser energy accumulation, such as increasing single pulse energy or cumulative pulse number on a sample, leads to a final fuzzy LIPSS period or even disappearance of the period. This article discovers a new phenomenon by increasing the laser fluence; the periodic structure appears blurred and disappears in the middle of the laser fluence region. Two contrary evolution tendencies of the period’s disappearance are observed for the first time. This phenomenon can be attributed to femtosecond ablation regimes in different fluence regions. The experimental results and discussion provide a powerful guarantee for the high-quality preparation of structures by controlling the experimental parameters for future practical applications. The findings of this study play a significant role in regulating the LIPSS period and provide ideas for avoiding the hidden danger of the cycle structure disappearing during the creation of the LIPSS structure, which has practical implications for future LIPSS applications.

Introduction

Recently, laser-induced periodic structures (LIPSS) induced by femtosecond laser irradiation on metal surfaces have been intensively studied. A distinct feature of LIPSS is a periodic ripple structure with a combination of microscale period and nanostructures. The LIPSS morphological feature has been found to be applicable in diverse fields, such as nanograting [1], metal surface colorization [2–4], surface-enhanced Raman scattering [5], surface wettability [6], and biomedical application [7]. The optimization and control of LIPSS surface topography, especially the period, are the key factors in enhancing the surface function characteristics. Therefore, it is important to conduct further research on LIPSS with an inquiry into the surface microstructure period regulation.

Experimental results from the literature show that the preparation of LIPSS by femtosecond laser on Au, Pt, Ti, and other metal surfaces is dependent on the laser fluence [8–12] and the cumulative pulse number [13–17]. Further findings in the literature also show that when the parameters reach a certain threshold and the laser fluence increases or the cumulative pulse number decreases, LIPSS transforms and transitions from high spatial frequency (HSFL) to low spatial frequency (LSFL), where the period of HSFL is Λ < 2/λ, and the period of LSFL is λ > Λ > λ/2 [18, 19]. Extensive research has also been conducted on LIPSS due to its unique application value for titanium metal in aviation and biomedicine [18–23]. Researchers have prepared and optimized the subwavelength periodic structure (HSFL) on the metal titanium surface by adjusting various laser parameters such as the laser fluence, pulse number, wavelength, and pulse duration. Relevant research works from the literature have shown the dependency between the period of LIPSS and various laser parameters. The dependency effect shows whether LIPSS on the titanium surface is prepared in water or air, and the formed HSFL is always parallel to the laser polarization direction, whereas LSFL is the opposite [18]. Furthermore, when the laser fluence and the cumulative number of pulses are low or exceed a particular threshold, the surface does not create LIPSS or cause damage to the formed LIPSS. Instead, a random nanostructure, below or above surface growth mounds, deep pits, and other structures, is formed on the surfaces [19–21].

In terms of LIPSS structure formation and evolution of semiconductor and metal materials, the general attention is focused on the use of the surface plasmon polarization (SPP) model which takes into account laser-induced changes in the dielectric environment, as well as which is often used to explain the period evolution of LIPSS in semiconductors due to the grating-assisted SP–laser coupling model under the cumulative number of pulses for the physical explanation of the formation and evolution of periodic structures [15, 24–27]. Also, the current experimental phenomenon shows that the ablation and melting caused by the thermal effect will have a certain negative impact on the formation of LIPSS [24, 25]. Researchers have concluded that an excessive accumulation of laser energy will eventually cause LIPSS to become fuzzy, if not to completely disappear, because the surface structure is more likely to be destroyed under greater laser fluence irradiation. The work of revealing new mechanisms related to LIPSS optimization and preparation is ongoing. Whether LIPSS can be formed stably in the optimization and preparation process has always been a developing tendency. However, the formation of this structure is inseparable from the laser ablation process. Unfortunately, the laser ablation mechanism as an important factor affecting the periodic evolution of LIPSS has not been systematically studied.

This study optimized and regulated the LPSS period on the Ti surface under different laser fluences and pulse numbers. It was discovered that the dependence of the LIPSS period on laser fluence or pulse number under the single parameter change was consistent with previous Ti results in the literature [16, 17, 20, 21]. Furthermore, with a low number (N) of laser pulse irradiation (30 ≤ N ≤ 90), the LIPSS period enlarges gradually with the increase in the laser fluence, abiding by the same periodic evolution law as previous studies [13–17]. However, in more pulse number (N ≥ 120) irradiation conditions, the structure period blurs or even disappears with the increase in the laser fluence in the middle of the laser fluence parameter region. To the best of our knowledge, these experimental phenomena are first experienced in the proposed study. The proposed study combines the SPP model with the grating-assisted SP–laser coupling model and conducts numerical simulation research on the periodic evolution law using the rigorous coupled-wave analysis (RCWA) and the finite-difference time-domain (FDTD) methods. The formation of LIPSS on the titanium surface was systematically analyzed by combining the femtosecond laser’s non-thermal ablation and thermal ablation mechanisms. This phenomenon can be attributed to two different ablation regimes of femtosecond laser pulse with varied laser energy deposition, leading to different period evolution phenomena between the high and low regions of laser fluence. The findings of this study play a significant role in regulating the LIPSS period and provide ideas for avoiding the hidden danger of the cycle structure disappearing during the creation of the LIPSS structure, which has practical implications for future LIPSS applications.

Experimental Details

A commercial regenerative Ti:sapphire femtosecond laser system used in the experiment is shown in Figure 1A. The system provides linearly polarized light in the horizontal direction at a central wavelength of 800 nm with a pulse width of 50 fs, a repetition rate of 1 kHz, and maximum laser energy of 3 mJ. The titanium (99.9% purity) with a size of 20 × 20 mm² was selected as a sample in the experiment.

FIGURE 1

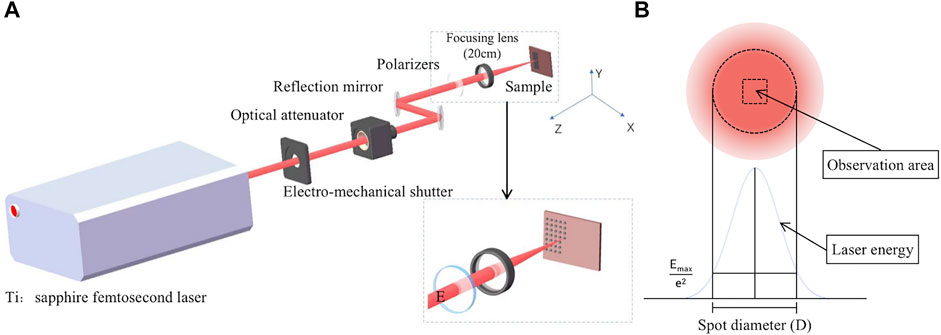
FIGURE 1. (A) Schematic diagram of titanium sapphire femtosecond laser machining system. (B) Schematic diagram of laser intensity distribution and data observation area.

The energy attenuator is used during the experiment to adjust the laser energy continuously, as shown in Figure 1A; the laser energy E is measured by the laser energy meter, the laser fluence is calculated by F = E/π(D/2)², and D represents the diameter of the laser beam. The output’s vertically polarized laser is focused on the sample through a convex lens (f = 200 mm) with a beam spot of 240 µm in diameter by adjusting the translation platform where the sample is located along the laser incident direction. The number of laser pulses can be selected by reducing the repetition rate of the laser to 100 Hz and setting the electro-mechanical shutter by controlling the platform displacement to change a new position for each experimental parameter combination (laser fluence and pulse number) prepared.

The surface structure of the irradiated laser samples was characterized using scanning electron microscopy (SEM). However, due to the Gaussian distribution of the laser beam, the non-uniform distribution of laser focal spot energy was excluded from studying the influence of laser energy density on the structure. As shown in Figure 1B, this study only observes the central region’s structure of laser ablation. The LIPSS period was analyzed by 30 points randomly distributed in the ablation region of the selected laser center.

Results and Discussions

At the beginning of the experiment, we studied the effect of femtosecond laser fluence on the LIPSS of the titanium surface near the ripple formation threshold under two experimental conditions, respectively, low pulse number (N = 30) and multi-pulse number (N = 150). As shown in Figure 2A, the LIPSS is formed in the laser fluence ranging from 23.4 to 52.6 mJ/cm² with a low pulse number (N = 30) by laser irradiation. Through the measurement and characterization of LIPSS, with the increase in laser fluence, LIPSS structure gradually transits from HSFL to LSFL. Its direction is always perpendicular to the direction of laser polarization, which is different from the phenomenon that LIPSS on the Ti surface changes from parallel to the polarization direction (HSFL) to perpendicular to the polarization direction (LSFL) with the increase in laser fluence in previous studies [18, 19]. However, as shown in Figure 2B, under the condition of laser irradiation with multi-pulse (N = 150), we found an interesting and unexpected experimental phenomenon. Although the changing trend and regular LIPSS period with incident laser fluence under this condition are generally consistent with those under the condition of fewer pulses (N = 30), in the medium laser fluence region (26.3, 29.2, and 32.2 mJ/cm²), the LIPSS becomes fuzzy and disappears. The surface of the obvious structure of LSFL reappeared when the laser fluence exceeded 35.1 mJ/cm².

FIGURE 2

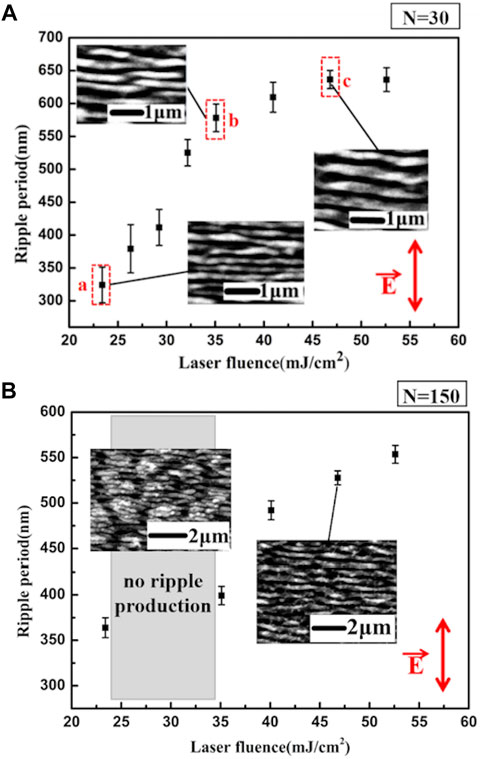
FIGURE 2. Dependence of the LIPSS period produced by fs-laser pulses on the laser fluence. The number of laser pulses in the experiment is (A) N = 30 and (B) N = 150, and the images inserted in the picture show the typical SEM morphology photos. The red arrow in the figure shows the direction of laser polarization. Error bars show the standard deviation of the periods.

The SPP model theory was used to systematically analyze the formation and periodic evolution of LIPSS caused by a single variable, laser fluence, to explore the causes of the above unexpected experimental phenomena. The interference between the linearly polarized laser and SPPs creates a periodic spatial modulation of the energy deposited on the irradiated material, generally recognized as the production mechanism of LIPSS on metal surfaces [28]. This leads to a spatially modulated intensity distribution and the formation of the periodic structure. The period of the LIPSS will depend entirely on the wavelength of the SPPs, and the following Equation 1 must be satisfied [29]:

$\mathrm{\Lambda }={\lambda }_L/(\frac{{\lambda }_L}{{\lambda }_{SPP}}\pm \sin \theta ).(1)$

Here, ${\lambda }_L$, ${\lambda }_{SPP}$, and $\theta$ are the incident laser (vacuum) wavelength, the surface plasmon wavelength, and the incident angle; and $\Lambda$ is the observed LIPSS period. In this experiment, the laser is incident to the surface of the sample ($\theta =0^{\circ }$) and deduced that the period of LIPSS is equal to the wavelength of the SPPs.

${\lambda }_{SPP}={\lambda }_L{\left[\frac{\left({\epsilon }^{\prime }+{\epsilon }_{\text{d}}\right)}{{\epsilon }^{\prime }{\epsilon }_{\text{d}}}\right]}^{\frac{1}{2}},(2)$

$\epsilon \left(\omega \right)={\epsilon }_{\text{c}}-\frac{{\omega }_P^2}{\omega \left(\omega +\text{i}\mathrm{\Gamma }\right)},(3)$

${\omega }_P={\left[\frac{{\text{e}}^2{\text{n}}_{\text{e}}}{\left({\text{m}}_{\text{ef}}{\epsilon }_0\right)}\right]}^{\frac{1}{2}}.(4)$

On one hand, the permittivity of the excited state of the laser-irradiated material can be described by the Drude model represented in Eqs. 2–4; ε_d is the dielectric constant of the dielectric material, ε_c is the dielectric constant of the normal state, ω_p is the plasma frequency, Γ = 1/τ is the electron collision frequency, and ε’ is the real part of ε [15]. Under femtosecond laser irradiation, many free electrons near the surface of metal materials are excited. The free electrons absorb laser energy through the inverse Bremsstrahgen process, leading to electron temperature increases and the formation of hot electrons. Meanwhile, the density of free electrons (n_e) increases rapidly with the increase in laser fluence [11, 12, 15]. Then, free electrons through the electron–phonon and electron–electron scattering processes gain momentum, increasing the electron collision frequency (Γ). The collision frequency is directly proportional to the square of the laser fluence; simultaneously, the change of collision frequency causes the change of the dielectric constant of the excited state, causing the real part of the constant dielectric to increase with the increase in laser fluence. However, the change in the dielectric constant modulates the wavelength of SPPs. Therefore, with the change of laser fluence, the LIPSS period will change correspondingly [10, 21]. This analysis is consistent with the phenomena observed in our experiment (Figure 2), such that the LIPSS disappearance phenomenon of the middle fluence region (Figure 2B) can be ignored. Therefore, it is concluded that the accumulation of the number of pulses may lead to the disappearance of the structure period.

Specific laser fluence at positions A, B, and C in Figure 2A was selected to analyze the influence of accumulated pulse number as a single variable on the LIPSS period to better understand the mechanism of LIPSS disappearance. According to the experimental results shown in Figure 3, point A corresponds to the initial fluence threshold F = 23.4 mJ/cm² that forms the LIPSS; point B corresponds to the region F = 35.1 mJ/cm², where the LIPSS period increases with the laser fluence; point C with F = 46.8 mJ/cm² corresponds to the area where the ripple period variation is slower. The evolution rules of the LIPSS period impacted by the cumulative pulse number are obtained under various fluence situations; the variation of the LIPSS period caused by the cumulative pulse number is diverse under different irradiated laser fluences related to the fluence of the single laser pulse. As shown in Figure 3A, the LIPSS period is near 370 nm under a laser fluence of 23.4 mJ/cm² and does not change significantly with the increase in the accumulated pulse number. However, the LIPSS disappears when the pulses are increased to approximately 220 shots. The LIPSS period decreases with the pulse number increase when the laser fluence increases to 35.1 mJ/cm² (as shown in Figure 3B). When the cumulative irradiated pulses are 1 ≤ N ≤ 90, the period does not change obviously with the increase in the cumulative number of laser pulses. When N ≥ 120, the number of pulses increases, the LIPSS becomes unclear, and the period disappears. As shown in Figure 3C, the LIPSS period variation tendency is similar to the condition where the laser fluence is 35.1 mJ/cm², but there are more irradiation pulses with a clear surface structure period until the number of pulses reaches 400. This means that due to excessive laser ablation, higher laser fluence does not result in a faster reduction of surface fringe.

FIGURE 3

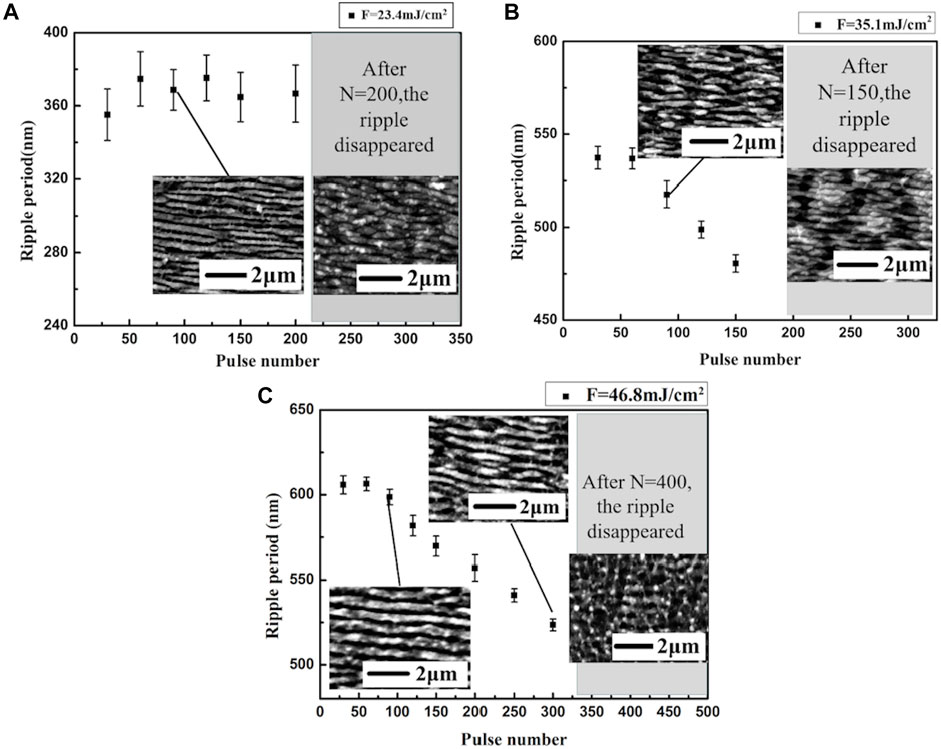
FIGURE 3. Dependence of the LIPSS period induced by fs-laser pulses on the accumulated pulses of laser irradiation, when laser fluence is (A) F = 23.4 mJ/cm², (B) F = 35.1 mJ/cm², and (C) F = 46.8 mJ/cm². The SEM images inserted in the figure are the topography of typical LIPSS under various conditions, and the surface structure topographies disappear when the cumulative pulse number is too large.

In addition, the formation of the LIPSS is a process determined by accumulated laser pulses, and grating-assisted SP–laser coupling caused by the grating type LIPSS must be taken into account. Previous research on LIPSS semiconductor surfaces has demonstrated that as the pulse number (N) and groove depth grow, the LIPSS periods change and evolve further under the condition that surface plasmon excitation is satisfied and the usage of a grating-assisted SP–laser coupling mechanism [15, 20, 27]. Therefore, numerical modeling studies were performed to determine the impact of the structural depth change caused by pulse accumulation on the LIPSS of the Ti surface. First, an RCWA was used to obtain the full-period (Λ = 0–800 nm) coverage grating reflectivity images at different depths (H) to focus on the SP band. This is because the titanium surface itself has a high reflectivity; when the SP mode is excited on the grating, the surface’s reflectivity should decrease significantly due to the energy transfer of the incident light. In the reflectivity map for titanium surfaces, the low reflectivity band usually corresponds to the SP band [27]. Hence, a suitable free electron density (n_e = 1 × 10²⁹/m³) was selected according to the n_e-Λ map and applied FDTD to obtain near-field distribution images of the grating surface at different depths, as shown in Figure 4A.

FIGURE 4

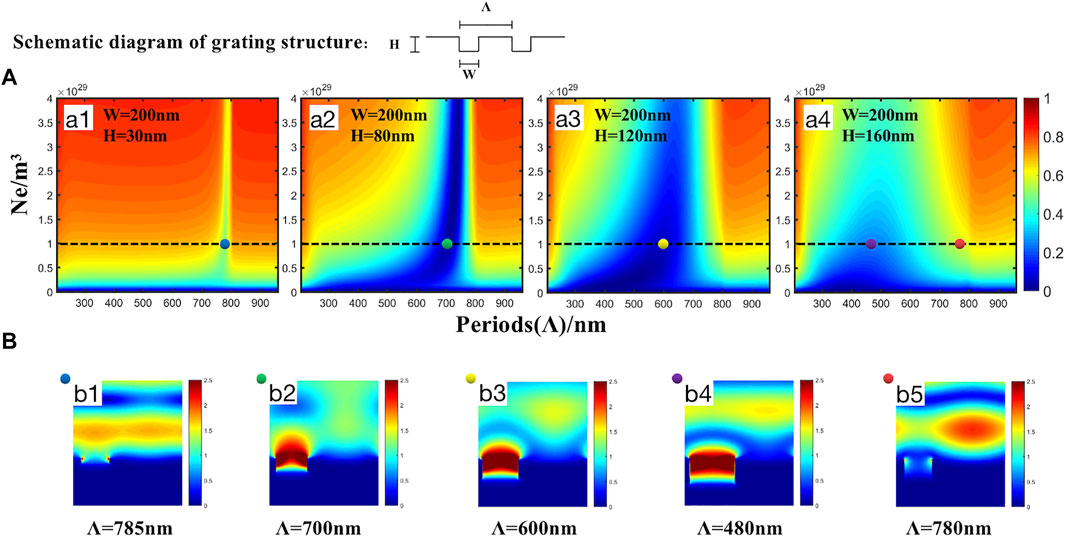
FIGURE 4. (A) n_e-Λ reflectance map of the highly excited titanium surface grating with a groove width of 200 nm at different depths is numerically simulated. The grating contour parameters are marked in the corresponding image. (B) Ex-field distributions of points b1–b5 correspond to different SP modes in the n_e-Λ reflectance maps denoted by the same color points.

According to the structural scale of the titanium surface LIPSS obtained from the SEM images, its width (w) under different laser fluences and pulse numbers in the simulation is approximately 120–210 nm. Therefore, in Figure 4, a width of 200 nm was selected before performing a numerical simulation of reflectivity in the parameter space of full electron density for different depths (H). As shown in Figures 4A1–A4, the increase in the depth of the grating groove makes it easier for the plasmon to resonate with a smaller period than the depth of the LIPSS groove changes. While the near-field distribution diagrams in Figures 4B2–B4 show that the evolution of LIPSS to a smaller period makes it easier for the groove to continue to deepen as the number of pulses increases, resulting in higher positive feedback of near-field enhancement inside the groove. It is worth mentioning that the near-field amplification effect in the groove is significantly weaker when the groove is shallow (H = 30 nm, as shown in Figure 4B1) than when H is greater (as shown in Figures 4B2–B4). Meanwhile, a strongly near-field distribution is formed between the grooves (as shown in Figure 4B5) when out of the non-resonant state of the resonant frequency.

Furthermore, simulation images of grating reflectivity under depth and period variations were obtained by selecting three groove widths (W = 100, 150, and 200 nm) that are consistent with the experimental results to eliminate the possible influence of the groove width on the near-field distribution of the grating surface under a fixed electron density (n_e = 1 × 10²⁹/m³). Although the W varies, there is a positive feedback of LIPSS evaluation toward a smaller period, as described in Figure 4, with increasing depth to achieve near-field enhancement inside the grooves and retain the SP–laser resonance mode illustrated in Figure 5. Similarly, only when the groove reaches a certain depth does an obvious positive feedback effect of near-field enhancement occur inside the grooves. However, as the depth increases and surpasses a particular range, the plasmonic resonance deteriorates. Therefore, based on the simulation mentioned earlier, it is ideal to conclude that within a certain width variation range (100–200 nm), a deeper groove is likely to promote the near-field enhancement formed inside the groove due to the reduction of the LIPSS period. When the depth H is small, the resonance frequency is near the frequency of the incident light, and the period range in which the resonance can be achieved is also narrower than when the depth H is larger.

FIGURE 5

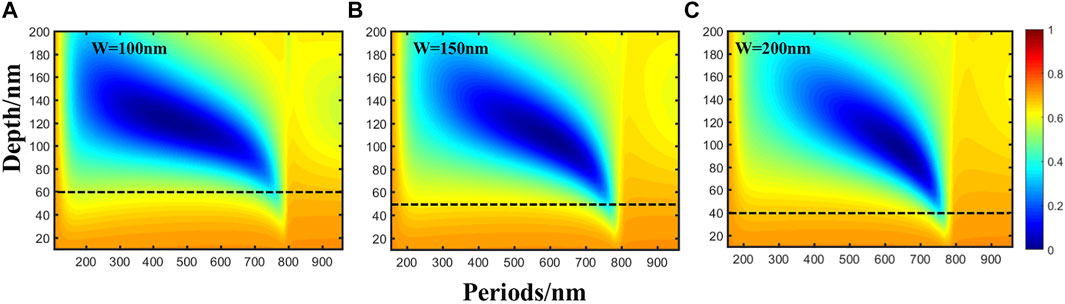
FIGURE 5. (A–C) Depth-Λ reflectance maps of highly excited titanium surfaces with groove depth evolution at different groove widths (W = 100, 150, and 200 nm).

Based on the previous simulation results, the phenomena of the period decrease with the increase in incident pulse number under the condition of high laser fluence (F = 35.1 or 46.8 mJ/cm², as shown in Figures 3B, C). This can be interpreted as follows: the post-sequence pulse will produce local enhancement in the grooves of the initial periodic structure, and the ablation of the enhanced field will further deepen the groove. The periodic structure’s depth will steadily deepen as the number of pulse accumulations grows, changing the SPP’s formation conditions. This forms a period of smaller light field distribution because the corrugated structure needs to reduce the period to continue to meet the new excitation model of grating-assisted SP–laser coupling. A similar phenomenon is also found in the related study of LIPSS on the ZnO surface [15, 27]. It should also be mentioned that no such pattern was observed in Figure 3A under the condition of low laser fluence (F = 23.4 mJ/cm²). The evolution mechanism of the period is related to laser fluence with other factors that affect the depth of ablation because the accumulation of pulse numbers at low laser fluence does not form an evolutionary trend of period reduction brought about by deepening depth.

To explore this physical process, we further zoom in on the SEM pictures of the periodic disappearing regions in Figure 3. As shown in Figure 6, when the laser fluence is low, few re-deposited materials are deposited on the sample’s surface (marked as a red dotted line in Figure 6A). Similarly, when the laser fluence is F = 35.1 or 46.8 mJ/cm² (as shown in Figures 6B and C, red dotted line marks), the solidification after melting on the sample’s surface is not seen in Figure 6A. By comparing Figures 6A, B, and C, the higher laser fluence can cause a more significant surface thermal effect. Generally, the microstructure formation cannot be separated from the ablation process of a pulsed laser. According to the current research, femtosecond lasers correspond to two ablation mechanisms under different laser fluences [30], and there are qualitative differences between them. The lower laser fluence usually corresponds to the ultrafast non-thermal ablation process of the femtosecond laser. The laser-induced hot electron density is low. The energy transfer from the skin depth to the target structure is negligible; hence, no obvious traces of material melting were observed in Figure 6A. Under the higher laser fluence, corresponding to the thermal ablation process of the femtosecond laser, the effect of electronic heat conduction in the formation of the structure is more significant; therefore, the melting of the microstructure is caused by the higher penetration depth and thermal effect (as shown in Figures 6B and C).

FIGURE 6

FIGURE 6. (A–C) Magnified SEM images of the surface topography at F = 23.4, 35.1, and 46/8 mJ/cm² and N = 300, respectively.

The distribution of LIPSS periods is presented on different fluences and several laser pulse conditions to further analyze the influence of the laser fluence on the formation and disappearance of the LIPSS periods between the two different ablation regimes, as shown in Figure 7A. The experimental results show that the periodic evolution of the LIPSS is divided into two regions (as shown in Figures 7A1 and A2) by the two ablation regimes. In these two regions, the different ablation mechanisms caused by the laser fluence under the accumulation of several pulses lead to the difference in the evolution law of the LIPSS period in the two regions. In contrast, the LIPSS disappearance law is diametrically opposite. Meanwhile, for the LIPSS period evolution, the period does not evolve significantly in the non-thermal ablation region; however, in the thermal ablation region, the period of LIPSS evolves to a smaller period with the cumulative pulse number under different laser fluxes. Furthermore, according to the LIPSS disappearance law, the larger the laser fluence is in the non-thermal ablation region, the faster the LIPSS disappears under the continuous accumulation of pulses (as shown in the overlap area of Figures 7A1 and A3). In contrast, in the thermal ablation region, the LIPSS disappears faster with the pulse number accumulation at a relatively smaller laser fluence (as shown in the overlap area of Figures 7A2 and A3). The observed phenomenon in Figure 2B is directly caused at the junction of the two ablation regions, as shown in Figure 7A, and the disappearance of LIPSS in the middle of the laser fluence region when the cumulative number of pulses is 120, 150, and 200, respectively, according to the opposite evolution laws caused by the influence of two different ablation mechanisms. To explain the reasons for the previous phenomena, we will analyze them in detail in the following sections.

FIGURE 7

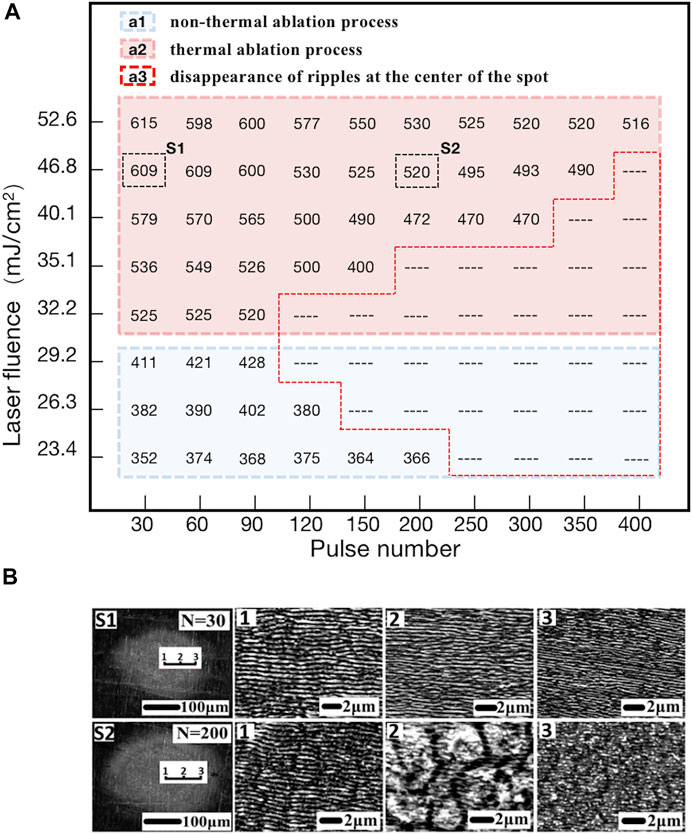
FIGURE 7. (A) Period distribution of LIPSS within different laser fluences and pulse number ranges; “--” represents the disappearance of ripples at the center of the spot here; the value of the ripple period in the figure is the mean value. (B) S1 and S2 are the examples in figure (A), which correspond to laser fluence of 46.8 mJ/cm², and the number of pulses (N) is 30 and 200, respectively. Therefore, 1, 2, and 3 correspond to the magnified SEM images of the structures at different spot positions in S1 and S2, respectively.

When the laser fluence is in the range of 23.4–29.2 mJ/cm² (near the fluence threshold for generating the LIPSS and work in the first regime, as shown in Figure 7A1), the laser energy influence depth is about the optical penetration depth that is calculated to be approximately 20 nm by the optical penetration depth formula d = 1/α (where α is the decay index). The depth of the energy range where the skin depth layer can exist to achieve the ablation threshold will decay exponentially due to the interaction between the material surface and the laser, so the penetration depth of the longitudinally generated ablation effect will also be much smaller than this value. Therefore, the groove depth evolves extremely slowly under the continuous accumulation of the number of pulses. The simulation results in Figure 4A show that the positive feedback of the near-field enhancement generated inside the groove is very weak at a depth of 30 nm. While Figure 5 shows that within the experimental range, the minimum groove depth that can cause SP–laser resonance is approximately 40–60 nm. Thus, when the grooves are shallow, the grating-assisted SP–laser coupling mechanism cannot effectively excite the SP and generate a near-field enhanced positive feedback inside the grooves (as shown in Figures 4A1 and B1). Generally, the initial laser pulses can induce a nanometric roughness surface. Under this condition, the interference between the subsequent incident laser and the SPPs caused by the surface roughness plays a dominant role in the formation of the LIPSS. Hence, the period of the LIPSS under this condition completely depends on the wavelength of the SPP. Therefore, it is believed that this is the reason why the period does not evolve significantly in the region of the non-thermal ablation mechanism. In addition, LIPSS will eventually disappear due to excessive ablation for the higher cumulative pulse number or larger single pulse fluence (as shown in the overlap area of Figures 7A2 and A3).

When the laser fluence is within the range of 32.2–52.6 mJ/cm² (as shown in Figure 7A2), the influence of electronic heat conduction becomes significant, and the second ablation regime appears (femtosecond laser thermal ablation process). Compared with the non-thermal ablation process, it is characterized by a higher energy penetration depth that is not limited to the optical skin depth. Therefore, in the thermal ablation process, with the participation of trace thermal effects, the average ablation depth will rapidly increase under relatively larger laser fluence due to the continuous accumulation of the number of pulses [20]. According to the simulation in Figure 5, it is beneficial to promote the evolution of LIPSS to a smaller period when the groove depth continues to deepen within a certain range. However, to achieve this evolution process, a specific condition is required; the thermodynamic feedback must keep up with the optical feedback to obtain the near-field enhanced positive feedback [27]. In other words, each pulse’s thermal ablation of the surface should be strong enough to cause the depth of the grooves to deepen as the pulse number accumulates, causing LIPSS to evolve toward smaller periods under the grating-assisted SP–laser coupling mechanism and further satisfying the SP–laser resonance condition (as shown in Figures 4B2–B4). Higher laser fluence will certainly result in a deeper heat-affected zone while satisfying the conditions described earlier [20]. Enhancing the near field inside the grooves as laser pulses accumulate will cause them to develop deeper, maintaining the periodic evolution of LIPSS. As seen in Figure 7A2 region, increased laser fluence also necessitates additional pulses to complete the LIPSS period evolution. In thermal ablation, it is worth noting that the dynamic balance between thermodynamic and optical feedback will be broken when the groove depth increases beyond a certain range under the continuous accumulation of laser fluence and pulse number, which ultimately affect the formation of SPP. Under such a condition, non-resonant SP–laser modes are generated on the surface of LIPSS (as shown in Figure 4B5), which makes the formed LIPSS fuzzy or even disappear, as shown in the overlapping area of Figures 7A2 and A3.

On the other hand, according to previous research reports, the formation of LIPSS is the result of the competition between energy deposition caused by SPP excitation and the thermal effect, and the thermal effect has both favorable and negative effects on the formation of LIPSS. Under the participation of excessive thermal effect, excessive melting will cause the disappearance of LIPSS even if plasmon resonance is formed on the material’s surface [24, 25]. The enhanced longitudinal ablation capability of the laser propagation direction caused by the higher energy penetration depth is beneficial for the stable formation of the excitation model of grating-assisted SP–laser coupling under multiple laser pulses, which is beneficial for the formation and periodic evolution of LIPSS. However, the melting caused by horizontal thermal diffusion is the main component of the negative influence factors of thermal effect on the formation of LIPSS. Therefore, another reason for the fuzzy or even disappearance of LIPSS is that the melting occurs under the influence of horizontal thermal diffusion when the period of LIPSS evolves to a smaller value with the accumulation of pulse numbers. In addition, as shown in Figure 7B, at N = 30 and N = 200 of 46.8 mJ/cm², this kind of experimental phenomenon of a laser ablation mechanism can be observed within the affected area of a focused spot due to the spot of the non-uniform energy distribution of the Gaussian laser. Therefore, in the future application process, the abrupt changes in the periodic evolution law caused by the ablation mechanism should be paid attention to better avoid the potential threat in the preparation and optimization of LIPSS.

Conclusion

Various laser fluences and pulse number combination parameters were employed in this study to fabricate LIPSS on metal surfaces. The experimental results show that when the number of cumulative pulses is low, the influence of laser fluence on the period disappearance is not noticeable, and the LIPSS period can be controlled by altering the laser fluence. The evolution of the LIPSS period is divided into two opposite stages according to the laser fluence when the pulse number is large. It is believed that the different ablation regimes determine it for femtosecond lasers, which are ultrafast non-thermal and thermal ablation processes caused by different laser fluences. Under various mechanism conditions, the LIPSS period can be optimized in various ways. More importantly, it should effectively avoid the risk of the LIPSS period disappearing during preparation. The findings from the study are crucial for developing LIPSS with controllable periods by using femtosecond lasers in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

SL was responsible for the formal analysis and experimental verification of the preliminary work and wrote the original draft according to the preliminary investigation and the collation of experimental data. WS was responsible for the preliminary formal analysis and data curation. TH was responsible for the concept extraction of the article and the supervision of the writing of the original manuscript, as well as the project management and fund acquisition of the team. LJ was responsible for the concept elaboration of the article, review and editing of the article writing, supervision of the originality of the article, and acquisition of resources and funds within the group.

Funding

This work was supported by the National Natural Science Foundation of China (51976015, 61605017), funds from the Science and Technology Department of Jilin Province (20200201250JC), 111 Project (D17017), Key Laboratory of Ultrafast and Extreme Ultraviolet Optics of Jilin Province (YDZJ202102CXJD028), and the Ministry of Education Key Laboratory for Cross-Scale Micro and Nano Manufacturing, Changchun University of Science and Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Miyazaki K, Miyaji G, Inoue T. Nanograting Formation on Metals in Air with Interfering Femtosecond Laser Pulses. Appl Phys Lett (2015) 107:071103. doi:10.1063/1.4928670

CrossRef Full Text | Google Scholar

2. Vorobyev AY, Guo C. Colorizing Metals with Femtosecond Laser Pulses. Appl Phys Lett (2008) 92:041914. doi:10.1063/1.2834902

CrossRef Full Text | Google Scholar

3. Dusser B, Sagan Z, Soder H, Faure N, Colombier JP, Jourlin M, et al. Controlled Nanostructrures Formation by Ultra Fast Laser Pulses for Color Marking. Opt Express (2010) 18:2913–24. doi:10.1364/oe.18.002913

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Ionin AA, Kudryashov SI, Makarov SV, Seleznev LV, Sinitsyn DV, Golosov EV, et al. Femtosecond Laser Color Marking of Metal and Semiconductor Surfaces. Appl Phys A (2012) 107:301–5. doi:10.1007/s00339-012-6849-y

CrossRef Full Text | Google Scholar

5. Jiang L, Ying D, Li X, Lu Y. Two-step Femtosecond Laser Pulse Train Fabrication of Nanostructured Substrates for Highly Surface-Enhanced Raman Scattering. Opt Lett (2012) 37:3648–50. doi:10.1364/ol.37.003648

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wu B, Zhou M, Li J, Ye X, Li G, Cai L. Superhydrophobic Surfaces Fabricated by Microstructuring of Stainless Steel Using a Femtosecond Laser. Appl Surf Sci (2009) 256:61–6. doi:10.1016/j.apsusc.2009.07.061

CrossRef Full Text | Google Scholar

7. Shinonaga T, Tsukamoto M, Kawa T, Chen P, Nagai A, Hanawa T. Formation of Periodic Nanostructures Using a Femtosecond Laser to Control Cell Spreading on Titanium. Appl Phys B (2015) 119:493–6. doi:10.1007/s00340-015-6082-4

CrossRef Full Text | Google Scholar

8. Okamuro K, Hashida M, Miyasaka Y, Ikuta Y, Tokita S, Sakabe S. Laser Fluence Dependence of Periodic Grating Structures Formed on Metal Surfaces under Femtosecond Laser Pulse Irradiation. Phys Rev B (2010) 82:165417. doi:10.1103/physrevb.82.165417

CrossRef Full Text | Google Scholar

9. Liu D, Chen C, Man B, Meng X, Sun Y, Li F. Evolution and Mechanism of the Periodical Structures Formed on Ti Plate under Femtosecond Laser Irradiation. Appl Surf Sci (2016) 378:120–9. doi:10.1016/j.apsusc.2016.03.229

CrossRef Full Text | Google Scholar

10. Sakabe S, Hashida M, Tokita S, Namba S, Okamuro K. Mechanism for Self-Formationof Periodic Grating Structures on a Metal Surface by a Femtosecond Laser Pulse. Phys Rev B (2009) 79:033409. doi:10.1103/physrevb.79.033409

CrossRef Full Text | Google Scholar

11. Shimotsuma Y, Kazansky PG, Qiu J, Hirao K. Self-Organized Nanogratings in Glass Irradiated by Ultrashort Light Pulses. Phys Rev Lett (2003) 91:247405. doi:10.1103/physrevlett.91.247405

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Chakravarty U, Naik PA, Chakera JA, Upadhyay A, Gupta PD. Estimation of Electron Density and Temperature of Semiconductor Surfaces Excited by Ultra-short Laser Pulses. Appl Phys A (2014) 115:1457–67. doi:10.1007/s00339-013-8063-y

CrossRef Full Text | Google Scholar

13. Vorobyev AY, Makin VS, Guo C. Periodic Ordering of Random Surface Nanostructures Induced by Femtosecond Laser Pulses on Metals. J Appl Phys (2007) 101:034903. doi:10.1063/1.2432288

CrossRef Full Text | Google Scholar

14. Hou S, Huo Y, Xiong P, Zhang Y, Zhang S, Jia T, et al. Formation of Long- and Short-Periodic Nanoripples on Stainless Steel Irradiated by Femtosecond Laser Pulses. J Phys D: Appl Phys (2011) 44:505401. doi:10.1088/0022-3727/44/50/505401

CrossRef Full Text | Google Scholar

15. Huang M, Zhao F, Cheng Y, Xu N, Xu Z. Origin of Laser-Induced Near-Subwavelength Ripples: Interference between Surface Plasmons and Incident Laser. ACS Nano (2009) 3:4062–70. doi:10.1021/nn900654v

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Feng P, Jiang L, Li X, Zhang K, Shi X, Li B, et al. Femtosecond Laser-Induced Subwavelength Ripples Formed by Asymmetrical Grating Splitting. Appl Surf Sci (2016) 372:52–6. doi:10.1016/j.apsusc.2016.02.195

CrossRef Full Text | Google Scholar

17. Hong L, Rusli X, Wang XC, Zheng HY, Wang H, Yu HY. Femtosecond Laser Fabrication of Large-Area Periodic Surface Ripple Structure on Si Substrate. Appl Surf Sci (2014) 297:134–8. doi:10.1016/j.apsusc.2014.01.100

CrossRef Full Text | Google Scholar

18. Mudasir HD, Kuladeep R, Saikiran V, Narayana RD. Femtosecond Laser Nanostructuring of Titanium Metal Towards Fabrication of Low‐reflflective Surfaces Over Broad Wavelength Range. Appl Surf Sci (2016) 371:0169–4332.

Google Scholar

19. Nathala CSR, Ajami A, Ionin AA, Kudryashov SI, Makarov SV, Ganz T, et al. Experimental Study of Fs-Laser Induced Sub-100-nm Periodic Surface Structures on Titanium. Opt Express (2015) 23:5915–29. doi:10.1364/oe.23.005915

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Peng E, Bell R, Zuhlke CA, Wang M, Alexander DR, Gogos G, et al. Growth Mechanisms of Multiscale, mound-like Surface Structures on Titanium by Femtosecond Laser Processing. J Appl Phys (2017) 122:133108. doi:10.1063/1.4990709

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xu S, Chen Y, Liu H, Miao X, Yuan X, Jiang X. Femtosecond Laser Ablation of Ti Alloy and Al Alloy. Optik (2020) 164628:0030–4026.

CrossRef Full Text | Google Scholar

22. Gnilitskyi I, Derrien JY, Levy Y, Bulgakova NM, Mocek T, Orazi L. High-speed Manufacturing of Highly Regular Femtosecond Laser-Induced Periodic Surface Structures: Physical Origin of Regularity. Scientific Rep (2017) 7(1). doi:10.1038/s41598-017-08788-z

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Bonse J, Höhm S, Rosenfeld A, Krüger J. Sub-100-nm Laser-Induced Periodic Surface Structures upon Irradiation of Titanium by Ti:sapphire Femtosecond Laser Pulses in Air. Appl Phys A (2013) 110(3):547–51. doi:10.1007/s00339-012-7140-y

CrossRef Full Text | Google Scholar

24. Zhou K, Jia X, Jia T, Cheng K, Cao K, Zhang S, et al. The Influences of Surface Plasmons and thermal Effects on Femtosecond Laser-Induced Subwavelength Periodic Ripples on Au Film by Pump-Probe Imaging. J Appl Phys (2017) 121:104301. doi:10.1063/1.4978375

CrossRef Full Text | Google Scholar

25. Yang M, Wu Q, Chen Z, Zhang B, Tang B, Yao J, et al. Generation and Erasure of Femtosecond Laser-Induced Periodic Surface Structures on Nanoparticle-Covered Silicon by a Single Laser Pulse. Opt Lett (2014) 39:343–6. doi:10.1364/ol.39.000343

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Cheng K, Liu J, Cao K, Chen L, Zhang Y, Jiang Q, et al. Ultrafast Dynamics of Single-Pulse Femtosecond Laser-Induced Periodic Ripples on the Surface of a Gold Film. Phys Rev B (2018) 98:184106. doi:10.1103/physrevb.98.184106

CrossRef Full Text | Google Scholar

27. Huang M, Cheng Y, Zhao F, Xu Z. The Significant Role of Plasmonic Effects in Femtosecond Laser-Induced Grating Fabrication on the Nanoscale. Ann Phys (Berlin) (2012) 1–13. doi:10.1002/andp.201200136

CrossRef Full Text | Google Scholar

28. Vorobyev AY, Guo C. Direct Femtosecond Laser Surface Nano/microstructuring and its Applications. Laser Photon Rev (2013) 7:385–407. doi:10.1002/lpor.201200017

CrossRef Full Text | Google Scholar

29. Garrelie F, Colombier J-P, Pigeon F, Tonchev S, Faure N, Bounhalli M, et al. Evidence of Surface Plasmon Resonance in Ultrafast Laser-Induced Ripples. Opt Express (2011) 19:9035–43. doi:10.1364/oe.19.009035

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Nolte S, Momma C, Jacobs H, Tünnermann A, Chichkov BN, Wellegehausen B, et al. Ablation of Metals by Ultrashort Laser Pulses. J Opt Soc Am B (1997) 14:2716–22. doi:10.1364/josab.14.002716

CrossRef Full Text | Google Scholar