Plasma-Surface Interactions Within Helicon Plasma Sources

Helicon plasma sources do not require electrodes or grids directly immersed in the plasma, and also present an axial magnetic field confining the plasma discharge. These factors are believed to provide them with long operational lifetimes because of the reduced potential for surface etching. The physics of helicon waves, cylindrical magnetized plasmas, sheaths, and plasma-surface interactions are discussed in the context of this claim. Practical implementation aspects are also reviewed, along with relevant experimental results. It is shown that understanding the distribution of ion density within the source, the presence of induced potentials in its surfaces, and the physics of low-energy sputtering reactions is essential to properly model erosion phenomena within helicons, and consequently predict their performance in practical applications.

1 Introduction

Helicon plasma sources (HPS) have attracted attention in recent decades because of their ability to produce high-density plasmas at low or moderate power levels and magnetic field intensities. For example, electron densities of more than 10¹² cm⁻³ can be produced on helicon plasma sources operating at input power levels of around 1 kW_e [1]. These properties make them suitable for practical applications in several fields. Within the research of plasma-material interactions at fusion-relevant conditions, HPSs have been used as a part of test facilities where candidate wall materials are subjected to the typical operating conditions in projected fusion devices [2, 3], up to heat flux levels exceeding 20 MW/m² [4]. Helicons have also been used in the plasma-processing of commercial materials and products [5, 6]. Within the field of electric space propulsion, helicon plasma thrusters have been actively developed in recent years [7–11]; helicons are also essential components of more advanced electric propulsion systems such as the VASIMR engine [12]. Figure 1 shows some examples of devices based on helicon plasma sources.

FIGURE 1

FIGURE 1. Examples of applications of Helicon Plasma Sources. (A) The Proto-MPEX linear device for the study of plasma-material interactions at fusion-relevant conditions [3]. Courtesy of Oak Ridge National Laboratory, U.S. Dept. of Energy. (B) The VX-CR research helicon plasma source [61]. Courtesy of Ad Astra Rocket Company Costa Rica, Liberia, Costa Rica. (C) The VASIMR VX-200SS high-power propulsion engine [12]. Courtesy of Ad Astra Rocket Company, Webster, TX, United States.

Another key feature of HPSs is that they typically do not have electrodes or cathodes in direct contact with the plasma, but rely instead on external radio frequency (RF) systems to launch and couple the corresponding waves within the medium and excite the discharge. This differs from other common plasma sources such as glow or DC discharges, where the plasma risks contamination from the release of electrode material or the source may fail if this element erodes sufficiently. Avoiding direct contact between the plasma and such elements is particularly useful where a long operating lifetime is desired for the plasma source, either because long duty cycles will be required in the application (as in commercial plasma-processing devices), high power densities are required (as in linear devices used for the research of suitable materials for fusion-relevant conditions), or because these previous conditions combine with the impossibility to access the device in the case of component failure (as in electric space thrusters).

Despite this advantage particular to the discharge excitation mechanism, practical implementations of HPSs do contain other confinement surfaces which are in direct contact with the plasma. The performance of helicon sources depends on the specific properties of these surfaces as well, and their ability to withstand the conditions they are subjected to throughout the operating lifetime of the source. These issues are therefore also important when considering the long-term viability of helicon plasma sources in their intended applications, and are the subject of the present review.

This article is structured as follows. Section 2 discusses the physics behind helicon plasma waves and recent results on the modeling of cylindrical magnetized plasmas. Section 3 then reviews the theory of plasma-surface interactions as it applies to helicon plasma sources. Section 4 describes practical aspects of helicon plasma source design and implementation, as they relate to the plasma-surface interaction phenomena. Finally, section 5 summarizes this review’s findings and offers perspectives for the advancement of the research and design of reliable, robust helicon plasma sources with long operational lifespans.

2 Physics of Helicon Plasma Sources

2.1 Helicon Plasma Waves

Helicon waves are a category of right-hand polarized (RHP) plasma waves which propagate along DC magnetic fields in bounded systems. They are related to so-called whistler waves, which have been studied in atmospheric physics since the early twentieth century. Whistlers and helicon waves belong to the group of right-hand polarized (RHP) waves propagating parallel to a magnetic field, in the frequency range ω_ci ≪ ω ≪ ω_ce (where ω_ci is the ion cyclotron frequency and ω_ce is the electron cyclotron frequency), together with electron cyclotron waves. Figure 2 shows the location of whistlers and helicon plasma waves within a ω-k diagram representing RHP cold plasma waves.

FIGURE 2

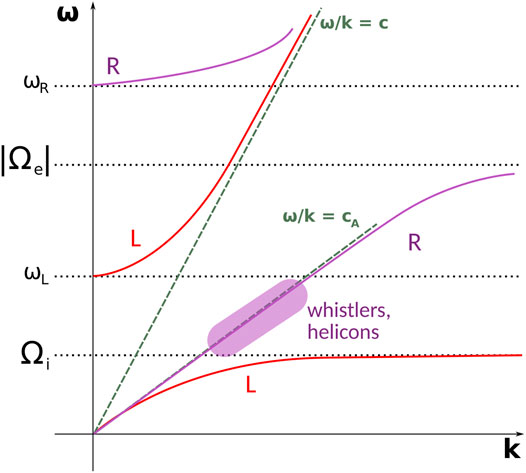
FIGURE 2. Location of whistlers and helicon plasma waves, among cold plasma waves propagating parallel to the externally-applied magnetic field.

A historical perspective for the first twenty years of helicon research has been given by Chen and Boswell [13, 14]. The following twenty-year period has been covered in more recent reviews by Chen [15] and Shinohara [1]. Theoretical treatments of the physics behind helicon waves have been produced, among others, by Klozenberg et al. [16], Chen [17], and Chen and Arnush [18, 19].

A basic dispersion relation can be obtained for helicon plasma waves from simplifying the Appleton-Hartree expression for quasi-longitudinal right-handed cold plasma waves [20, 21], propagating at an angle θ from an axial, static magnetic field $\mathbf{B}=B_0{\widehat{\mathbf{e}}}_{\mathbf{z}}$,

$\beta =\frac{\omega }{k}\frac{n_{0}e{\mu }_0}{B_0}(1)$

where ${\beta }^2=k^2+k_{\perp }^2$ is the total wave number, k = β cos θ and k_⊥ are the parallel and perpendicular components of the wave number, and n₀ is the plasma density. This expression, despite being a simplification, provides an intuitive insight on the relationship between the magnetic field B₀, the density n₀, the wave frequency ω, and the wave number β, and can be used as a starting point when designing or analyzing a HPS.

A more detailed description of helicon waves can be obtained from Maxwell’s equations by neglecting ion motions and the displacement current, as originally shown by Klozenberg et al. [16]. When the effects of electron inertia are retained within the analysis [14, 18, 22] two solutions are obtained for the dispersion relation,

${\beta }_{\mathrm{1,2}}=\frac{k}{2\delta }\left[1\mp {\left(1-\frac{4\delta k_{\omega }^2}{k^2}\right)}^{1/2}\right](2)$

where δ = ω/ω_ce is the ratio between the wave frequency and the electron cyclotron frequency ω_ce = eB₀/m_e, and $k_{\omega }^2=\omega {\omega }_p^2/{\omega }_c{c}^2=\omega n_{0}e{\mu }_0/B_0\equiv \alpha k$ is the wavenumber for low-frequency whistler waves along B₀ in free space, with α = β the wave number previously described in Eq. 1. ω_p is the electron plasma frequency at density n₀. δ is neglected when the effects of the electron mass are omitted or for frequencies ω ≪ ω_ce.

Eq. 2 describes two solutions for the wave dispersion relation, which can be simplified as shown in Eq. 3.

${\beta }_{\mathrm{1,2}}\approx \frac{k}{2\delta }\left[1\mp \left(1-\frac{2\delta k_{\omega }^2}{k^2}\right)\right]\approx \left\{\begin{array}{c}\hfill k_{\omega }^2/k\hfill \\ \hfill k/\delta \hfill \end{array}\right.(3)$

Solution β₁ corresponds to the zero electron mass limit, and describes the helicon wave (“H”) from Eq. 1. The second solution β₂ = β₂  cos θω_ce/ω describes a wave with frequency ω = ω_ce  cos θ, which is an electron cyclotron wave propagating at an angle to the magnetic field. This is the Trivelpiece-Gould mode (“TG”), first described in bounded systems by Trivelpiece and Gould [23]. The TG mode co-exists with the H mode, and becomes relevant at lower values of B₀. The TG mode is thought to play a relevant role in the damping mechanism of helicon plasma sources and to contribute to its high ionization efficiency via mode-conversion processes [24].

Eq. 3 describes the dispersion relation for both the H-mode and the TG mode. Expressions for the magnetic and electric fields (B, E) have been derived for different geometries as described in the early works on helicons [16, 25] as well as in more recent literature [14, 17, 22]. These expressions depend as well on the boundary conditions chosen for the analysis and on whether these boundaries are modelled as conductors or not [18]. Practical implementations of HPSs are typically linear devices implemented as cylindrical enclosures made of dielectric materials, as will be described in section 4.

The expressions obtained from Eqs. 1, 3, as well as the detailed derivations of the B and E fields that can be obtained for a particular configuration and geometry, can be used as an initial approximation to understand the regimes of H and TG modes that can be propagated in a given configuration, and establish a baseline estimation of the expected density distribution in a given HPS device.

One particular advantage of HPSs stemming from the fundamental physics of helicon waves is the ability of these devices to couple RF waves at the core of dense plasmas, enabled by the presence of the axial magnetic field and the propagation of the H-mode. This fact presents an advantage over other types of plasma sources, such as inductively-coupled plasmas (ICPs) where the penetration of RF waves into the plasma is limited by its skin-depth, or electron-cyclotron sources (ECR), where microwaves cannot propagate below the O-mode cutoff frequency (the electron plasma frequency ω_pe).

An investigation on the mechanisms which enable the initiation of the high-density helicon mode (the H-mode), based on modeling and experimental work, has been carried out by Carter et al. [26], including indirect evidence of the deposition of RF power at the high-density core in a helicon plasma source.

2.2 Cylindrical Magnetized Plasmas

Section 2.1 described helicon plasma waves and derived their dispersion relation in various scenarios. The general behavior of magnetized plasmas in cylindrical geometries will now be analyzed, which is relevant to the characterization of practical HPSs as described in section 4.

The problem of describing the bulk behavior of a plasma discharge has been addressed since the early stages of the development of plasma physics. In the classical paper by Tonks and Langmuir [27], expressions were derived for the distribution of the electric potential in an arc discharge, for various geometries including cylindrical coordinates. Scenarios were analyzed for different regimes of ion collisionality and ionization rates. This work also contains a treatment of the plasma-material boundary at the edge of the plasma discharge, pointing to the discontinuity of the bulk model within the plasma sheath.

In a later paper, Tonks [28] studied the effects of the magnetic field in an arc plasma. One of the cases described was the positive column plasma immersed within a longitudinal magnetic field, the same typical configuration applied nowadays to most helicon plasma sources. A radial model is developed based on classical diffusion theory. More recent models for cylindrical magnetized plasmas have been developed by Fruchtman et al. [29] and Sternberg et al. [30]. These works introduced the use of 2D fluid models in cylindrical coordinates (with the assumption of azimuthal symmetry), the separation of variables in order to decouple the expressions for the radial and axial coordinates, and the analysis of different degrees of magnetization. Differences between these authors rely on the assumptions chosen to simplify their models. The previous works were further adapted and extended by Ahedo et al. [31, 32], who developed a 2D model for cylindrical magnetized plasmas as part of their work on describing the plasma dynamics within helicon plasma thrusters. The properties of these models have been summarized in Table 1.

TABLE 1

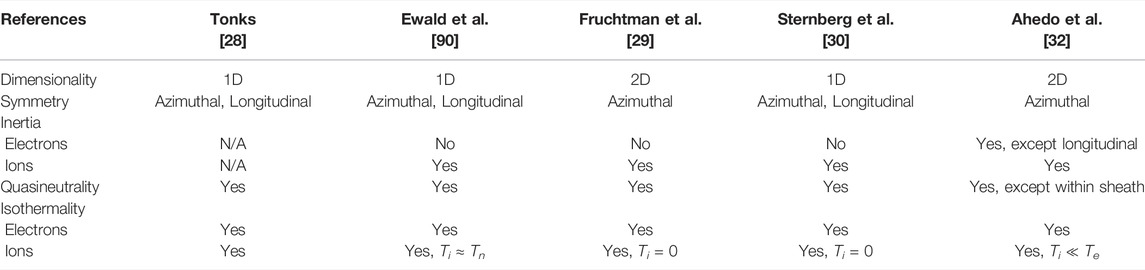
TABLE 1. Relevant models developed for cylindrical magnetized plasmas which are applicable to the study of Helicon Plasma Sources.

These descriptions of cylindrical magnetized plasmas can be used to approximate the distribution of key parameters within the discharge, such as the density distribution, the velocity of ions and electrons, and the plasma potential. As an example, the complete model developed by Ahedo et al. [31, 32] is described by a set of four radial equations and five more for the axial dimension. These take as inputs information regarding the ion species taking part in the discharge, collisional rates related to the ionization and interactions between ions, electrons and neutrals, and constant parameters such as the magnitude of the axial magnetic field B₀ and the isothermal electron temperature T_e.

The dispersion relations found for helicon plasma waves in section 2.1 can be used to obtain reference values for parameters such as the peak density value in the discharge. This information can be coupled with the description obtained from a 2D fluid model in order to project the distribution of plasma density, kinetic energy, and plasma potential throughout the discharge. Understanding the values of these parameters at the boundaries of the system, where the plasma comes into contact with solid materials, is essential to describe the interaction phenomena taking place in this region. Figure 3 shows an example of the models from Refs. [31, 32] being used to estimate the 2D plasma distribution within a particular HPS, the VX-CR device. Data from these models can be used to obtain the plasma conditions at the radial (r → R) and axial (z → − L) boundaries, which then enable the analysis of the interaction between the plasma discharges and the physical confinement materials.

FIGURE 3

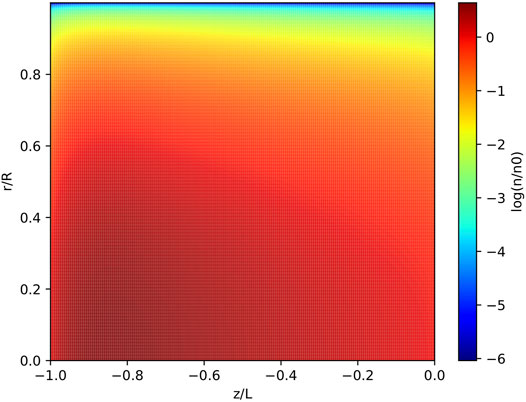
FIGURE 3. Estimation of 2D plasma density distribution in the VX-CR research HPS, obtained through the model developed by Ahedo et al. [31, 32]. Geometry and plasma parameters were obtained from [61, 88, 91]. Density values are normalized with respect to the background neutral Argon density, n_n0 ≈ 2 × 1020 m⁻³. The VX-CR source is composed of a dielectric ceramic tube with R = 0.045 m and L = 0.226 m.

3 Plasma-Surface Phenomena in HPS

Solid materials often constitute the physical boundaries of plasmas, and the interaction between the surface atoms and the bulk plasma can have a significant effect on the behaviour of the latter. In the case of typical HPSs, the dielectric containment surfaces are the only regions of direct interaction between the plasma and material surfaces. This is a particular advantage over other plasma generation technologies in which electrodes or cathodes have to be immersed within the plasma discharge, as they constitute additional regions of potential failure limiting the operational lifetime of the device. It is therefore relevant to understand the fundamental principles behind the most typical plasma-surface interactions within HPSs, in order to characterize them and to design strategies for their control or mitigation.

3.1 Plasma Sheaths

3.1.1 DC Sheaths

Sheath is the region near a material boundary in contact with a plasma where the bulk quasineutrality breaks due to the buildup of charge at the surface. In low-temperature plasmas, such as those typically found in HPSs, the more mobile electrons produce a negative charge at the surface and, therefore, a positive sheath where the ion density is larger than the electron density, n_i > n_e. Sheaths typically have a scale in the order of the Debye length, ${\lambda }_D={\left({ϵ}_0{T}_e/e{n}_0\right)}^{1/2}$. Sheaths have been studied since the early days of plasma physics, with the term originally coined by Irving Langmuir [33].

The process by which the quasineutrality in the bulk plasma transitions into the sheath is gradual, and three distinct regions can be identified as shown in Figure 4. The quasineutral density within the bulk plasma (n_i = n_e = n₀) begins to decrease in the vicinity of the boundary, in a region called the pre-sheath where the bulk density and the plasma potential both decrease. The scale of the pre-sheath is of the order of the ion mean free path (λ_i). The plasma then enters the sheath proper, at which point the quasineutrality does break and the electron density diminishes at a much faster rate than the ion density. The plasma potential decreases until reaching the wall potential, which is typically lower than the bulk plasma potential.

FIGURE 4

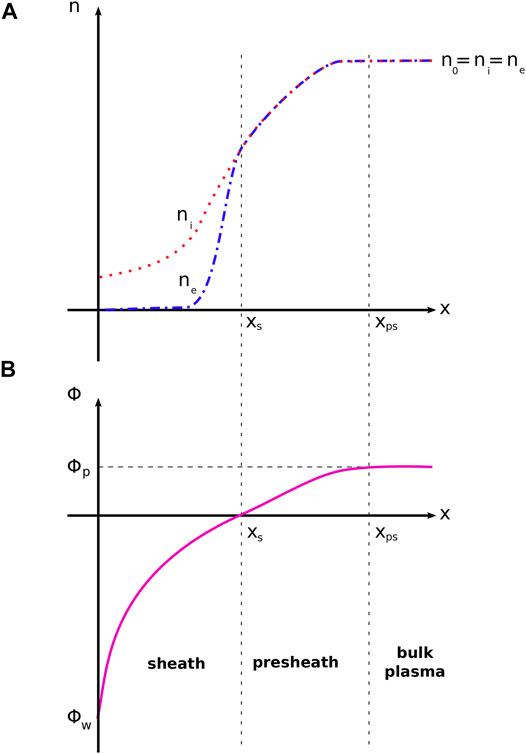
FIGURE 4. Regions in the transition between the bulk plasma and a surface in contact with a plasma, such as the inner confinement surfaces in a HPS or the surface of an electrostatic probe immersed in the plasma. Graph (A) shows the behavior of the electron and ion density, while graph (B) shows the electric potential. The surface is located at x = 0. The bulk plasma region is located at x > x_ps, where the plasma is quasineutral and its potential is the plasma potential Φ_p. The presheath is the region x_s < x < x_ps where both the plasma density and potential decrease gradually as x → x_s. The sheath properly begins at the point x = x_s ≈ λ_De, where the ions acquire the Bohm velocity $u_i=u_B=-{\left(k_B{T}_e/m_i\right)}^{1/2}$. Quasineutrality is broken, the electron density quickly decreases to zero and the potential drops gradually towards the wall potential Φ_w at x = 0.

An important property of the transition from the plasma to the sheath is the Bohm Sheath Criterion, which establishes a condition on the minimum energy of the ions as they enter the sheath. The derivation of this criterion is based upon the assumptions of negligible ionization within the sheath itself, negligible electric field at the plasma edge, Maxwellian electrons with a density given by the Boltzmann relation, and cold ions with constant temperature [34, 35]. Its expression is provided by Eq. 4 and states that the energy of the ions within the sheath is comparable to that of the electrons in the bulk plasma, and that their thermal velocities surpass the Bohm velocity $u_B^2=(k_B{T}_e)/m_i$.

$e{V}_0\ge \frac{T_e}{2}\Rightarrow v_i\ge u_B(4)$

It is possible to find expressions for the potential obtained by the surface wall due to the formation of the sheath. For the case of collisionless sheaths, Eq. 5 describes the wall potential with respect to the plasma potential at the sheath-presheath point of transition for the case of floating surfaces immersed within the plasma [35], a condition typical of certain types of probes as well as the boundary surfaces of HPSs.

${\mathrm{\Phi }}_w=-\left(\frac{k_B{T}_e}{e}\right)\ln \sqrt{\frac{m_i}{2\pi m_e}}(5)$

This value is directly proportional to the electron temperature, and a constant factor related to the ion/electron mass ratio. It is also possible to obtain expressions for the approximate width of the sheath, as well as expressions for these values when the sheath is collisional or the material surface is biased with a particular voltage [35].

The behavior of the plasma as it enters and traverses the sheath is critical to the understanding of the phenomena occurring at the boundary surfaces, as these depend on the energy of the ions and electrons reaching it.

3.1.2 RF or Capacitive Sheaths

In devices where radiofrequency (RF) waves, plasmas, and materials coexist, the RF wave field dominates the formation and properties of the sheath near the boundary surfaces, allowing the appearance of potentials that surpass those typical of DC sheaths dominated by thermal effects. This phenomenon is defined as an RF plasma sheath, and it presents specific implications in the design of capacitive plasma sources, in material processing applications and within RF subsystems in fusion devices. An early treatise on this subject was presented by Butler and Kino [36], and a more recent review on this topic has been presented by Myra [37] with a particular emphasis on magnetically confined fusion systems.

RF sheaths present several features not found in the previously described DC sheaths. Plasmas interact with electrodes driven by oscillating currents I_rf, characterized by a frequency ω_rf. The sheaths created in the boundary region between the bulk plasma and these electrodes have a time-varying thickness correlated to the oscillation in the driving electrical parameters. Similar to the DC case, quasineutrality breaks within the sheath with the electron density becoming very low or even negligible. Lieberman and Lichtenberg [35] show simplified models for the case of simple, plane-parallel capacitive discharges, where assumptions help to gain a better understanding on the phenomena involved.

For idealized cases where the driving frequency is larger than the ion plasma frequency, ${\omega }_{\text{rf}}^2\gg {\omega }_{pi}^2$, the ions react to the time-averaged potentials in the bulk plasma and not to the driving RF frequency. On the other hand, electrons do respond to the driving RF current, given the particular condition ${\omega }_{pe}^2\gg {\omega }_{\text{rf}}^2(1+{\nu }_m^2/{\omega }_{\text{rf}}^2)$, with ν_m being the electron-neutral collision frequency. The current travelling through the RF sheaths is then mostly displacement current produced by the time-varying electric field (given the very low electron density within the sheaths), unlike inside the bulk plasma where electrons react to the RF field and are able to carry the current through conduction. The analysis of an RF sheath depends on several factors, including the geometry of the problem, whether collisions are present within the sheath (when the ion mean free path, λ_i is smaller than the sheath thickness), and the frequency applied by the RF source. For the very high frequency (VHF) range, high (n_e ≈ 10¹⁷m⁻³) plasma densities can be achieved with moderate power input, and this has been exploited in commercial devices used for materials processing [22].

In the particular case where ω_rf < ω_i, with ω_i = 2π/τ_i and τ_i being the ion transit time through the sheath, the ions within the sheath are able to respond to the time-varying RF field and a low-frequency RF sheath is formed [35]. These differ from the high-frequency case since current conduction through the sheath is dominated by resistive effects and not by the displacement of the time-varying electric potential. Besides, the voltage at the capacitive electrodes becomes rectified within portions of the RF cycle, losing its sinusoidal character. In this low-frequency regime, ions react to the sheath as in the case of a high-voltage DC sheath, and the energy they obtain is a non-linear function of the time-varying voltage within the RF cycle [35].

RF sheaths are relevant to HPSs since they are present in the regions near the conductors of the antenna system used to produce the helicon discharge, where the plasma reacts to the time-varying field of the RF cycle. Despite the advantage presented by the fact that the antenna can be located outside of the discharge chamber, these RF sheaths are able to accelerate ions traversing the RF sheath with energies that can surpass those obtained in the boundary DC sheaths present in other regions within the source. This fact has critical implications for the subsequent analysis of plasma-material interactions within HPSs.

3.2 Plasma-Surface Interactions

Plasma-surface interactions (PSIs) or plasma-material interactions (PMIs) comprehend the different phenomena that occur when ions, electrons, and neutrals within a plasma reach a material boundary. These interactions might produce effects on both the plasma itself as well as on the boundary. PSIs are essential in the field of plasma materials processing, and are also critical to the successful development of practical fusion devices [38, 39], as most designs include open magnetic flux surfaces where the plasma directly impinges the physical boundaries. They are also crucial in the advancement of electric propulsion technologies, where the lifetime of the thrusters directly depends on the erosion rate of those critical surfaces directly in contact with the plasma discharge or the plume of the thruster [40, 41].

Several processes can occur at the physical boundaries of a helicon plasma. Positive ions traversing the sheath typically become neutralized, in a process that either produces an excited neutral, or a neutral plus the emission of a secondary electron (Auger emission [35]). Secondary electron emission has been found to play a role in the sheath dynamics of certain types of low-energy plasma discharges, such as capacitively-coupled plasmas [42].

Another fundamental process is sputtering, the removal of material from a solid surface material due to the impact of an energetic impinging particle, typically ions in the case of plasma discharges. It is one of the most relevant phenomena occurring at the boundary surfaces of plasma discharges, since it can be responsible for significant erosion of said surfaces if the adequate conditions are met. Figure 5 depicts the basic mechanisms behind the most relevant PSI phenomena encountered in the study of HPSs.

FIGURE 5

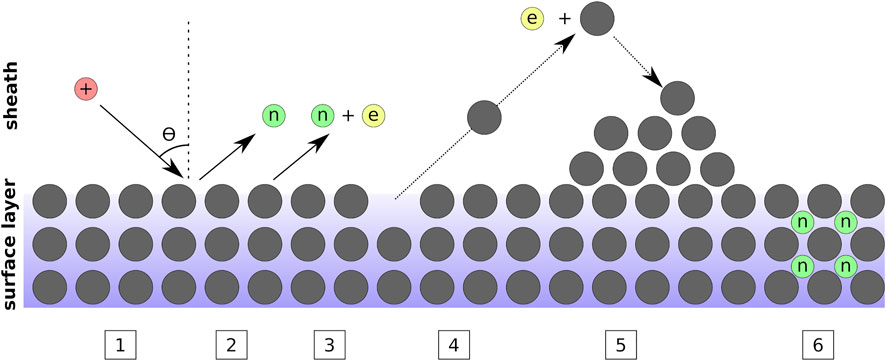
FIGURE 5. Simplified diagram of the plasma-surface interaction phenomena most relevant to the study of HPSs. The plasma sheath region is depicted at the top of the diagram, while the top layers of the plasma-facing surface lattice are represented at its bottom, where the surface atoms are represented by solid circles. (1) represents the impacting ion, approaching the surface at an angle θ with respect to its normal, and with an energy E₀. When the ion energy does not surpass the threshold energy for sputtering E₀ < E_thr, the ion may become neutralized by a surface electron releasing a reflected neutral as shown in (2). In some cases, an additional electron may be released [secondary or Auger emission, (3)]. When E₀ > E_thr, collisional cascades within the top surface lattice are sufficient to expel a surface atom and sputtering occurs (4). The sputtered surface atoms might become ionized as they traverse the sheath, in which case they will be accelerated by the sheath potential back towards the surface and redeposition of material may occur (5). If the ion impact energy is sufficiently large, E₀ ≫ E_thr, the ions may become neutralized and implanted within the surface lattice (6).

Theoretical treatments of the phenomenon of sputtering are provided by Sigmund [43], Bohdansky [44], Yamamura [45], Eckstein [46], and Behrisch et al. [47]. Most models describe the process as the result of collisional cascades in the surface layer of the target material, in which the momentum of the impacting ion is transferred to an atom in the target material’s lattice through elastic collisions. The random arrangement of the position of both particles implies that an oblique collision is likely. The impacted target atom, in turn, collides with other neighboring particles triggering the cascade. With sufficient energy in the original impacting ion, eventually the collisional cascade will provide one of the atoms in the surface layer with an energy level surpassing the surface binding energy of the material [48], and a momentum directed outside of the surface. The atom will then be sputtered from the surface.

Simulation of the sputtering process based on the first principles from classical mechanics is possible, by using the technique of Molecular Dynamics [49, 50]. Other popular simulation packages are based on the Monte Carlo statistical method, such as TRIM. SP [51] and SRIM [52]. Sputtering yield estimations obtained by the use of these software packages are strongly dependent on the chosen input parameters, and have been shown to differ from experimental values in certain ranges [53].

The fundamental parameter in sputtering models is the sputtering yield, Y_sputt, defined as the number of surface atoms sputtered off the surface per incident impacting ion. Y_sputt is mainly a function of the ion species and surface material, the ion energy, and the angle of incidence between the surface normal and the ion’s velocity vector. Below a particular threshold energy level, E_thr, ion impacts are not able to sputter surface atoms and Y_sputt = 0.

Several models have been developed to produce estimations for the sputtering yield, each particular to the species involved in the process, and the angle of incidence and energy E₀. Lieberman and Lichtenberg [35] report expressions valid for large atomic species within certain boundaries of their atomic number ratio. Eckstein and Preuss [46] proposed the model shown on Eq. 6, which is valid for ions impacting the surface at a normal angle of incidence.

$Y\left(E_0\right)=q{s}_n^{KrC}\left(E_0\right)\frac{{\left(\frac{E_0}{E_{thr}}-1\right)}^{\mu }}{\lambda +{\left(\frac{E_0}{E_{thr}}-1\right)}^{\mu }}(6)$

where the krypton-carbon interaction potential $s_n^{KrC}$ [46, 54] is used as an adequate mean value for different participating species and describes the nuclear stopping cross section. This parameter is defined as follows,

$s_n^{KrC}\left(\epsilon \right)=\frac{0.5\ln \left(1+1.2288\epsilon \right)}{\epsilon +0.1728\sqrt{\epsilon }+0.008{\epsilon }^{0.1504}}(7)$

The reduced energy ɛ is obtained as follows,

$\epsilon =E_0\frac{M_t}{M_i+M_t}\frac{a_L}{Z_i{Z}_t{e}^2}(8)$

where the subindexes i and t are used to describe the atomic numbers Z and atomic masses M of the projectile ion and target surface atoms, respectively. a_L is the Lindhard screening length [55],

$a_L={\left(\frac{9{\pi }^2}{128}\right)}^{1/3}{a}_B{\left(Z_i^{2/3}+Z_t^{2/3}\right)}^{-1/2}(9)$

where a_B is the Bohr atomic radius.

The remaining free parameters q and λ from Eq. 6 can be found in [47] for a variety of impacting ions, target materials, and ion energies.

When ions impact on a boundary surface not in a perpendicular direction, but instead at an angle α with respect to the surface normal, the calculation of the sputtering yield needs to take this geometry into account. Eckstein and Preuss [46] proposed the formula in Eq. 10,

$Y\left(E_0,\alpha \right)=Y\left(E_0,0\right){\left\{\cos \left[{\left(\frac{\alpha }{{\alpha }_0}\frac{\pi }{2}\right)}^c\right]\right\}}^{-f}\exp \left\{b\left(1-\frac{1}{\cos \left[{\left(\frac{\alpha }{{\alpha }_0}\frac{\pi }{2}\right)}^c\right]}\right)\right\}(10)$

where

${\alpha }_0=\pi -\arccos \sqrt{\frac{1}{1+\left(E_0/E_{sp}\right)}}\ge \frac{\pi }{2}(11)$

E_sp is a binding energy characteristic of impacting ions, and c and f are fitting parameters. Behrisch and Eckstein [47] have compiled tables for these formulae for the most common ions and target materials.

For the case of surface materials consisting of alloys or compounds of different elements, the sputtering yield will be different for each different species present in the target surface. For the steady state with a sufficiently high flux of incident ions, the sputtering yields will distribute according to the stochiometric concentration of each species within the target compound. However, this distribution is not kept for small fluences of impinging ions, and the phenomenon of preferential sputtering occurs.

For binary target materials, containing two elemental species i and j, the sputter preferentiality δ can be defined [47] as a ratio of the elemental sputtering yields Y_i, Y_j and their stochiometric concentrations c_i, c_j,

$\delta =\frac{Y_i}{Y_j}\frac{c_j}{c_i}(12)$

δ can also be estimated as follows,

$\delta ={\left(\frac{M_j}{M_i}\right)}^{2m}{\left(\frac{U_j}{U_i}\right)}^{1-2m}(13)$

where M_i, M_j are the atomic masses, U_i, U_j the surface binding energies, and m is a power exponent describing the interaction potential.

When a plasma encounters a solid surface, such as at the boundaries provided by the containment surfaces of a HPS, a sheath will be formed and ions will be accelerated according to the potential present at the wall. If the ions are able to increase their energy beyond the threshold energy E_thr, sputtering will occur and the surface will be modified. Combining this information with the density distribution obtained through experimental measurements or simulations, such as the fluid models described in section 2.2, an etch rate or erosion rate can be calculated for the surface. This value can be used to project the behavior of the HPS and establish limits to its useful lifetime in a particular practical application.

In practical applications, the etch rate E of a surface bombarded with energetic ions, measured as a ratio of the etch depth per unit of time, is calculated as a function of the incident ion flux Γ_i, the particular sputtering yield Y, and the mass density of the target surface ρ_t as shown in Eq. 14,

$E=\frac{{\mathrm{\Gamma }}_{i}Y{M}_{m,t}}{{\rho }_t{N}_A}(14)$

where M_m,t is the molar mass of the target surface and N_A is Avogadro’s constant. The calculation of the sputtering yield would take into account all the considerations discussed in this section. The incident ion flux Γ_i is determined by the particular conditions of the plasma discharge near the surface; for example, it can be approximated by applying the Bohm Sheath Criterion and specifying that Γ_i = n_su_B where n_s is the ion density at the entrance of the sheath and u_B the ion Bohm velocity.

4 Relevant Engineering Aspects

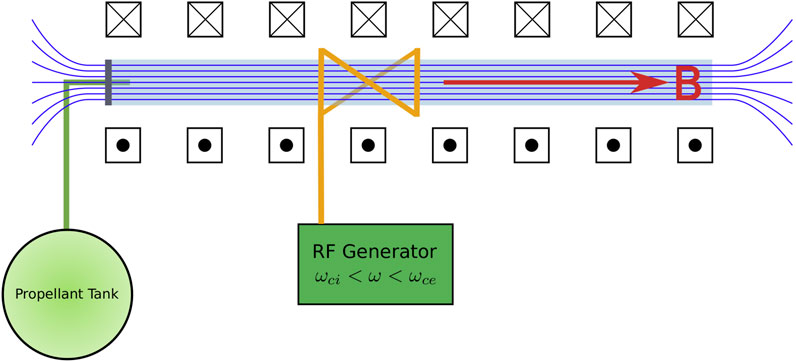
Figure 6 shows a simplified 2-D cross section of a typical HPS built in a cylindrical geometry (excluding auxiliary vacuum vessels, diagnostics or nozzle elements which may exist in laboratory or thruster applications). A cylindrical dielectric tube is sealed at one of its ends by an endcap or barrier. Neutral gas is fed inside the cylinder from an external source. An axial magnetic field, parallel to the dielectric cylinder axis, is created by using solenoid coils or permanent magnets. An antenna is used to launch the helicon waves into the neutral medium; this antenna is typically placed outside of the exterior surface of the dielectric tube. The open end of the cylinder is commonly attached to an external chamber and a gas extraction system capable of maintaining the vacuum pressure within the source at the required limits. Considerations for the design and implementation of practical HPSs are discussed in detail in [22].

FIGURE 6

FIGURE 6. Simplified representation of a typical implementation of a Helicon Plasma Source.

Given the fact that the antenna used to launch the helicon waves can be placed outside the plasma medium, surrounding the external surface of the dielectric cylinder, the plasma-facing surfaces of the endcap, the dielectric cylinder and any other purposely-designed limiter inner walls are the only material boundaries in direct contact with the plasma, and therefore the only ones potentially subject to plasma-material interactions. The axial magnetic field limits the diffusion of particles toward the cylinder’s inner surfaces. The upstream section of typical HPSs, shown at the left of Figure 6, will usually contain another boundary surface and is a common location for the injection of the neutral gas required to sustain the plasma discharge. Depending on the specific geometry of a particular device, this section might be located in the vicinity of the helicon antenna or away from it, and the magnetic field might remain parallel to the axis of the source or diverge instead. The density of neutrals is usually higher in this region, promoting more frequent interactions with ions and removing momentum from them, which in turn has an effect on the energy they carry towards the boundary surfaces.

The careful selection of these materials interacting with the plasma discharge, as well as an adequate design of the HPS geometry, magnetic field, and antenna, can reduce the plasma density and particle energies near the inner surfaces of these elements and therefore mitigate their erosion due to material sputtering. This in turn provides HPSs with the potential of long operational lifetimes. This is a critical property in fields such as in-space electric propulsion, where thrusters based on HPSs are among the leading candidate technologies within electrode-less thrusters [56].

4.1 Plasma-Facing Materials in HPSs

Materials used for the construction of HPSs must comply with a number of often conflicting properties. RF-transparent materials are commonly used to manufacture the cylindrical tube, allowing for the efficient transmission of the RF waves produced by the external antenna to the plasma medium. This requires materials with a low dissipation of RF energy, which is usually measured in terms of the loss tangent (tan δ). The amount of thermal energy dissipated by the boundary material is directly proportional to this loss tangent parameter, which is in itself proportional to the material temperature [57]. This can potentially create a positive feedback loop of RF energy losses within the boundary material, showing the importance of the material selection in practical HPSs.

From a practical engineering point of view, HPS materials should feature a high thermal conductivity, enabling the distribution and extraction of the heat loads produced by the inherent inefficiencies of the RF transmission and the ionization process within the source. Materials with a high thermal conductivity will allow the heat loads present in the material to spread axially and azimuthally, promoting the creation of a more even temperature distribution and reducing the appearance of thermal hotspots. This in turn contributes to the reduction of the amount of thermal energy dissipated as the RF energy traverses the boundary material. Thermal management of HPSs is a critical issue in practical implementations [58–62] and is essential for the development of high-power systems relying on HPSs, such as the VASIMR engine [63], the Proto-MPEX PMI research device [64], and the PISCES-RF steady-state helicon device [2].

De Faoite et al. [65] compiled a thorough review of the available data on the most relevant thermal and mechanical properties of dielectric technical ceramics commonly used in HPSs, focusing on those aspects relevant to the thermal management issues described above. The materials included in the analysis included alumina, aluminum nitride, berylia, quartz, sialon, and silicon nitride. A later work [66] presents linear regressions of these properties as a function of temperature, where adequate fits were found for some of them while also highlighting the limits of the publicly available data sets.

In order to assess the reliability of these dielectric materials under the boundary conditions present in inner confinement surfaces of HPSs, their sputtering parameters would have to be evaluated under similar conditions, using the models and techniques discussed in section 3.2. As an example, Figure 7 compiles experimental and simulated data for the sputtering yields of singly charged argon ions impacting some of these dielectric materials commonly used in HPSs, as a function of the impacting ion energy and at normal incidence. These choices are typical for the materials used in the VX-CR research HPS [61].

FIGURE 7

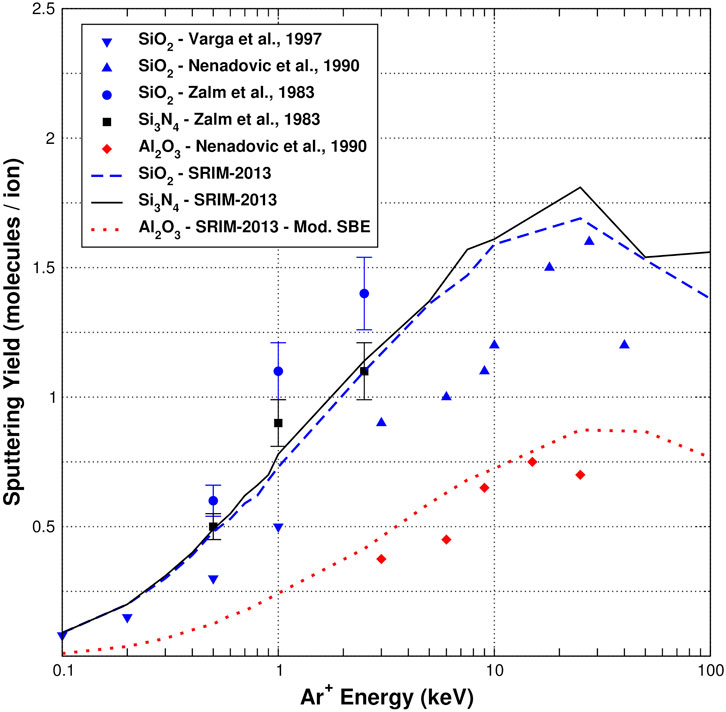
FIGURE 7. Sputtering yields for Ar⁺ ions impacting perpendicularly onto some of the compounds commonly used in the construction of HPSs. Experimental data is shown for SiO₂ [92–94], Al₂O₃ [93], and Si₃N₄ [92]; as well as computational results obtained with the SRIM-2013 package.

As an indicative example, erosion phenomena will be estimated for a typical HPS operating with an electron temperature of T_e ≈ 5 eV and a density n ≈ 2 × 10¹⁸ m⁻³ in the regions near the surface of a floating dielectric confinement wall [67]. Eq. 5 estimates that the wall potential becomes Φ_w = − 23.5 V. If the ions enter the sheath with negligible kinetic energy, it can be assumed this will be the incident energy at the wall, slightly larger than the corresponding threshold energy for sputtering E_thr ≈ 19 eV. If the wall material is alumina, Eq. 6 produces a value of Y ≈ 0.06 atoms/ion for the case of normal incidence to the surface and Eq. 14 produces an approximate etch rate of E = 17.62 nm/s. If the wall thickness of this material is t = 2.5 mm, this means it would take Δt = 141.9 × 10³ s = 39.4 h for the wall to erode (in a scenario where all conditions remain constant). If the confinement surface is made of quartz glass (silicon dioxide), the wall potential Φ_w would be below the threshold energy for sputtering for argon ions impinging on SiO₂, E₀ < E_thr ≈ 35 eV, and no sputtering would occur.

If these conditions exist in the vicinity of the antenna straps of the HPS, where the RF energy is transmitted as a 13.56 MHz signal with a peak-to-peak voltage amplitude of V_pp = 1 kV (and therefore a peak voltage of V_p = 500 V), the methods described by Berisford et al. [68] can be used to estimate an average sputtering rate given the ion energy distribution function for low-frequency RF sheaths [35]. In this particular case, an average sputtering yield of Y_avg = 0.08 is obtained for the case of Argon ions impacting the alumina surface. The corresponding etch rate would then be E = 23.5 nm/s, and it would take Δt = 106,400 s = 29.56 h for the wall to erode. If the material is quartz, the RF sheath would be able to produce sputtering, with an average yield of Y_avg = 0.06, an etch rate of E = 18.85 nm/s, and the surface would be eroded in Δt = 132,600 s = 36.84 h. These are extremely simplified estimations, where conditions remain constant during the whole process, and no variations in the sputtering yield are introduced due to surface modification or deviations from normal incidence as the surface degrades.

4.2 Relevant Experimental Work Regarding PSI Within HPSs

HPSs have been used as part of plasma processing devices since early in their development [5, 10]), generating plasmas with the adequate parameters in order to modify the surfaces of samples or substrates subjected to their discharge. However, few studies have been conducted on the effects of the plasma discharge itself upon the inner confinement surfaces of HPSs.

Among these, Aanesland et al. [69] reported on the effects of an additional, floating copper antenna immersed within the discharge itself. They describe the sputtering of copper atoms from this additional antenna, which are then redeposited on the inner surface of the dielectric discharge tube. At high power levels, they describe how the areas in this dielectric tube located under the straps of the external helicon antenna remain clean due to the re-sputtering of the deposited copper layer. They suggest this is an effect of the RF sheath created on the plasma-surface boundary, as previously discussed in section 3.1.2.

This same mechanism was observed by Berisford et al. [60], when researching the power distribution and erosion within the dielectric tube of a linear helicon device. These authors developed expressions to estimate the etch rates observed at these regions under the straps of the extenal helicon antenna, modelling the sheath present in these areas as a low-frequency RF scenario (refer to section 3.1.2) and averaging the sputtering yield according to the ion energy distribution throughout the RF cycle [35]. These findings were validated through experimental observations of the actual erosion in the dielectric cylinder used in their experiment. These authors were able to estimate the required particle flux at the regions under the helicon antenna conductor from the measured etch rates, and also by analyzing IR thermal data measured at the same location; both estimations agreed within a factor of two.

Barada et al. [70] investigated this phenomenon more thoroughly, experimentally confirming the existence of an increased negative DC bias under the straps of the external antenna in the inner surfaces of a HPS, and investigating how this wall potential is affected by variations in the helicon discharge parameters. Infra-red (IR) thermography measurements taken on the inner surface of the dielectric ceramic window of the PISCES-RF device [2] also provided indirect evidence of this phenomena, showing increased values of the plasma heat flux under the straps of the helicon antenna, particularly the conductor connected to the live (non-grounded) terminal of the RF power supply.

The use of Faraday shields has been explored as a means to mitigate the effect of capacitive coupling within inductively-coupled plasmas (ICPs), and their application to HPSs has been suggested for the same purpose [71]. The Faraday shield has been implemented as a cylindrical jacket made of conducting material, installed between the dielectric plasma confinement surface and the helical antenna used in the ICP reactor [72]. Longitudinal slits have to be cut along this shield, to enable the inductive fields to penetrate the discharge. Specific experiments applying this technique to HPSs have yet to be performed. This method could potentially improve the performance of HPSs by reducing the erosion rate due to capacitive coupling under the antenna straps; however, its effects on other aspects of the source such as thermal management, and discharge efficiency, have to be investigated.

Recent experiments by Beers et al. [73, 74] describe the analysis of the helicon discharge section of the Proto-MPEX device, where they combined a finite-element model describing the helicon discharge, an ad-hoc sheath model, and a transport code in order to analyze the production of impurities due to sputtering at the material boundaries. Their results confirm the experimental findings of Berisford et al. [60] and Barada et al. [70], showing the importance of the electrostatic potentials near the helicon antenna straps as a source of energetic ions impacting the radial boundaries. They also showed the difference between the operation in non-magnetized and magnetized regimes, as was also discussed by Ahedo et al. [32].

The effect of the strength and geometry of the magnetic field on the performance of HPSs has also been researched. The magnetic field has an effect on the density profile within the source. Lafleur et al. [75] show that its intensity affects the peak value of the plasma density in the helicon mode, and they show the existence of optimal configurations for given values of input RF power and magnetic field intensity. The axial magnetic configuration is also able to modify the performance of an HPS. Takahashi et al. [76–78] have described the distribution of momentum transfer between the plasma and different elements of the source, its relationship with the magnetic field configuration, and how it can affect the total thrust of a helicon plasma thruster. These experiments describe how the ions are able to impart an axial momentum to the inner wall of the dielectric confinement material, due to the fact that their velocity vector is not completely normal to the wall surface [78]. This method could be used to indirectly estimate the incident angle with the confinement surface as the ions traverse the sheath, a critical factor in the calculation of the sputtering yield, although it is shown how the radial component is responsible of the energy transfer towards the wall.

The profile of the magnetic field within a HPS can be designed to mitigate the consequences of plasma-wall interactions within the source. Caneses et al. [79] describe experiments where two configurations of the magnetic field within the Proto-MPEX high-power helicon device were used to demonstrate the usefulness of controlling where the last uninterrupted magnetic flux surface (LUFS) makes contact with the inner confinement surfaces of the source. They relocated this contact point away from the dielectric ceramic window towards a purposely-designed stainless steel cylindrical limiter surface, an element with a function analog to that of divertors in fusion devices. This design change reduced the thermal heat loads under the dielectric window associated with direct impingement of the plasma, since the magnetic geometry maintains the LUFS at a minimum distance of approximately 1 cm away from the boundary surfaces. The plasma density decays rapidly beyond this point, as the magnetic lines intersect the material boundaries more often. This technique of magnetic field shaping allows the Proto-MPEX to reduce the heat loads on the dielectric window, but its effects on the sputtering and erosion related to plasma-surface interaction have not been thoroughly investigated. However, the careful design of magnetic geometries is commonly used for this purpose on electric propulsion devices [80, 81].

Figure 8 summarizes the findings of these experiments with regard to the appearance of sputtering phenomena within the internal dielectric confinement surfaces of HPSs. Region (1) in the figure represents areas within these internal surfaces in direct contact with the plasma, where a sheath forms and the dielectric surface obtains a negative electric potential Φ_w as described by Eq. 5. The positive ions are then accelerated towards the wall with a surface flux determined by the product of the bulk plasma density n₀ and the Bohm velocity u_B they obtain when entering the sheath. The effect of the impinging ions on the dielectric surface can then be analyzed according to the sputtering models discussed in subsection 3.2, and effective surface etch rates may be computed. Region (2) in Figure 8 describes the particular phenomena observed by Berisford et al. [60], Aanesland et al. [69], Barada et al. [70], and Beers et al. [73, 74], where the creation of RF sheaths on the internal surfaces directly under the helical antenna straps may create the conditions for high-voltage DC sheaths in the negative part of the cycle. In this scenario, average sputtering yields can be computed through the ion energy distribution within the negative portion of the RF cycle [35], and hence etch rates can be computed as well.

FIGURE 8

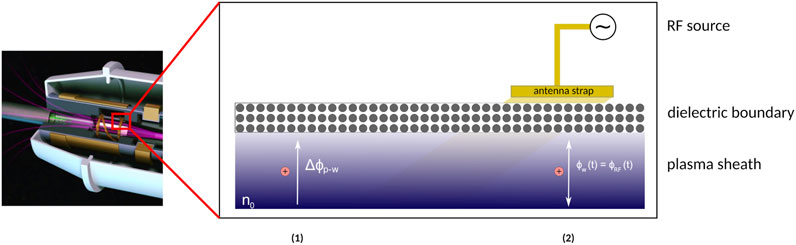
FIGURE 8. Representation of the two main sputtering regimes present in helicon plasma sources, as previously reported in literature. (1) shows the conditions present at the boundary between the bulk plasma, with density n₀, and the internal dielectric boundaries within an HPS. Parameters such as this density and the electron temperature T_e define the conditions present within the plasma sheath, which accelerate the positive ions towards the wall through the plasma-wall potential ΔΦ_p−w [35]. If the energy obtained by the ions at the material boundary surpasses the threshold energy E_thr, sputtering will then occur. (2) describes the situation particular to the areas under the antenna straps, which may be subjected to high capacitive voltages driven by the external RF subsystem [60, 70, 73]. Given sufficiently large voltages, the negative part of the antenna’s RF cycle will accelerate the ions towards the surface with enough time to traverse the sheath, essentially behaving as a high-voltage DC sheath [60]. Once again, if the energy obtained by the ions surpasses the threshold limit, sputtering will occur.

5 Summary and Conclusion

Helicon plasma sources (HPSs) hold great potential for the development of efficient, high-density plasma sources. One of their widely quoted advantages is the absence of cathodes or electrodes directly in contact with the plasma discharge. This fact limits any plasma-surface interactions to the inner surfaces of the dielectric confinement surfaces, where the diffusion of the plasma is limited by the action and geometry of the axial magnetic field, thus reducing the expected material erosion rates and providing these devices with a potentially long operational lifetime. This proposed advantage of HPSs, among others, is still the subject of debate [82, 83].

The present review summarized the theory describing these interactions, beginning with the physics of helicon waves and cylindrical magnetized plasmas (section 2), followed by a description of the most relevant plasma-surface interaction phenomena within HPSs (section 3). Practical implementation aspects and relevant experimental results were presented in section 4.

Current research results point towards the existence of two main modes of plasma-surface interaction within HPSs. The first one is the diffusion of plasma towards the inner surfaces of these material boundaries, where the ions are then accelerated through DC sheaths and sputtering may occur if they are able to become energized above the corresponding threshold energy level. The eventual etch rate experienced by particular devices will depend on the plasma parameters near the boundaries, the species present in the plasma and the wall material, and the geometry of the magnetic field at each region. The second mode of interaction appears in the regions of the helicon dielectric window directly under the conductor straps of the antenna, where capacitive RF sheaths are created and accelerate the ions. Direct (profilometry and surface analysis) and indirect (IR thermography) evidence has confirmed the existence of this phenomenon, and it has also been investigated through modeling and simulations. Experimental results suggest that these RF sheaths appearing under the helicon antenna straps are responsible for the appearance of thermal hot spots and regions of concentrated erosion patterns in the inner surface of the dielectric windows of HPSs.

Despite recent advances in the description and understanding of these plasma-material interactions within helicon plasma sources, several topics are still open for research and experimentation. Current modeling efforts integrate different specific tools to simulate the interactions between the plasma discharge, the transport and diffusion of the plasma species throughout the simulation domain, the creation of DC and RF sheaths, and the interaction phenomena occurring at the material boundaries. As usual within the simulation of plasma phenomena, varying timescales, lengths and energy levels are involved. Integrated simulation efforts for the specific purpose of studying sputtering and impurity transport within HPSs are recent, and they could benefit from the development of purposely-designed integrated simulation tools for this task.

Specific models for sputtering phenomena on the dielectric ceramics commonly used in HPSs should be developed and validated through experimentation. Additionally, the interaction between the sputtered species, the original plasma, external impurities, and the boundary surfaces, including the formation of new compounds and molecules, appears to be a topic of relevance, as shown in the results obtained in the Proto-MPEX device [74] where these relationships were taken into account to better explain the observed experimental results.

The magnetic field geometry can be designed in order to displace the contact points between the plasma and its boundary surfaces and also to create a separation between the magnetic flux surface enveloping the plasma and the confinement materials. This strategy appears to have a potential effect in reducing the erosion phenomena within the HPS, as suggested by the effect it has shown in modifying and reducing the heat flux distribution in the Proto-MPEX experiment [79]. Yet this claim has not been thoroughly investigated. This experiment also demonstrated how cylindrical liners can be placed at the locations where the plasma does contact the boundary surfaces; when this occurs outside of the section where the helicon antenna is located, the requirement for an RF-transparent dielectric window can be removed and other materials with lower sputtering yields can be selected. However, the exact interactions between these liner materials, the plasma, and the sputtered impurities have to be investigated. This technique could offer some critical advantages for the creation of impurity-free plasmas in high-power helicon devices used to research fusion-relevant material interactions; however, they might introduce new unwanted issues in other applications where the physical lifetime of the hardware is the priority, such as in electric propulsion devices.

From an experimental perspective, the diagnostics able to measure the above-mentioned parameters can be improved. Given the linear nature of most helicon devices, access to the critical regions near the dielectric ceramic window and the RF antenna region is complex. High power density devices, such as the Proto-MPEX and Pisces-RF devices, or the VASIMR VX-200SS engine, create a hostile environment for most physical probes. Measurements have been done of the inner wall potential [70], the radial heat flux, and the UV radiation [60], yet these experiments were not conducted inside high-power, steady-state devices.

Measurements of the effects of sputtering within the inner surface of helicon confinement surfaces have been studied through profilometry [60] and x-ray photoelectron spectroscopy [74]. Extensive experience in this particular field has been obtained in the simulation and execution of long-duration experimental runs of electric propulsion devices [40, 84–86], but not in those which employ HPSs. Diagnostics such as optical profilometry [87] and coordinate-measuring machines [88] could also be applied to HPSs, particularly for the measurement of surface erosion after long-duration tests in high-power devices.

The engineering problem of managing the heat fluxes transferred by the plasma onto the inner confinement surfaces of HPSs is partially related to the plasma-surface interaction issues discussed throughout this review, since the direct impingement of energetic ions onto these surfaces is one of the mechanisms of heat transfer present in the sources. Some mitigation techniques previously discussed, such as shaping the magnetic field to control the points of direct contact between the plasma and these inner surfaces, can be applied to both phenomena. The role of the temperature on the erosion rate of these surfaces in contact with the plasma has not been investigated in the particular case of HPSs. The formation of nanostructures has been studied in the case of candidate materials for the divertors of projected fusion devices [89]; similar conditions might be achievable in high-power HPSs operating at steady-state for long periods of time, and whether these phenomena affect the sputtering of these inner confinement surfaces remains to be investigated.

The physics concepts presented here can be combined to establish a framework for analyzing the impact of plasma-material interactions within HPSs, and explore mitigation strategies suited for the development of high-power helicon sources, particularly for those applications where an extended operational lifetime of the system is a critical requirement. These concepts can be used to model the density distribution within the HPS and the existence of induced RF or DC bias voltages on its inner surfaces, which appear to be a significant factor in the appearance of local sputtering and deposition phenomena. A sufficient understanding of these phenomena will be required as the application of high-power, steady-state helicon sources continues to grow in the fields of materials processing, fusion research, and in-space electric propulsion.

Author Contributions

JDV conceptualized the review and figures, and wrote the first draft of the manuscript. FCD and VG critically revised the manuscript. All authors read and approved the final submitted version of the article.

Funding

This research work was funded by Ad Astra Rocket Company Costa Rica. Financial support for the open-access publishing of this manuscript was provided by Universidad Nacional de Costa Rica (UNA). The authors declare that this study received funding from Ad Astra Rocket Company Costa Rica. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Conflict of Interest

Authors JDV, FCD, and VG were employed by the company Ad Astra Rocket Company Costa Rica.

The remaining author declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors wish to acknowledge the contribution of Juan Francisco Caneses, who reviewed a draft of this manuscript and provided critical feedback and comments.

References

1. Shinohara S. Helicon High-Density Plasma Sources: Physics and Applications. Adv Phys X (2018) 3:1420424. doi:10.1080/23746149.2017.1420424

CrossRef Full Text | Google Scholar

2. Thakur SC, Simmonds MJ, Caneses JF, Chang F, Hollmann EM, Doerner RP, et al. PISCES-RF: a Liquid-Cooled High-Power Steady-State Helicon Plasma Device. Plasma Sourc Sci. Technol (2021) 30:055014. doi:10.1088/1361-6595/abef19

CrossRef Full Text | Google Scholar

3. Rapp J, Biewer TM, Bigelow TS, Caughman JBO, Duckworth RC, Ellis RJ, et al. The Development of the Material Plasma Exposure experiment. IEEE Trans Plasma Sci (2016) 44:3456–64. doi:10.1109/tps.2016.2628326

CrossRef Full Text | Google Scholar

4. Caneses JF, Lau C, Goulding RH, Bigelow TS, Biewer TM, Caughman JB, et al. Power Transport Efficiency during O-X-B 2nd Harmonic Electron Cyclotron Heating in a Helicon Linear Plasma Device. Plasma Phys Controlled Fusion (2021) 64:025005 (21pp). doi:10.1088/1361-6587/ac4525

CrossRef Full Text | Google Scholar

5. Perry AJ, Vender D, Boswell R. The Application of the Helicon Source to Plasma Processing. J Vac Sci Technol B (1991) 9:310–7. doi:10.1116/1.585611

CrossRef Full Text | Google Scholar

6. Wang S-B, Wendt AE. Control of Ion Energy Distribution at Substrates during Plasma Processing. J Appl Phys (2000) 88:643–6. doi:10.1063/1.373715

CrossRef Full Text | Google Scholar

7. Charles C, Boswell R, Alexander P, Costa C, Sutherland O, Pfitzner L, et al. Operating the Helicon Double Layer Thruster in a Space Simulation Chamber. IEEE Trans Plasma Sci (2008) 36:1196–7. doi:10.1109/tps.2008.924425

CrossRef Full Text | Google Scholar

8. Shabshelowitz A, Gallimore AD. Performance and Probe Measurements of a Radio-Frequency Plasma Thruster. J Propulsion Power (2013) 29:919–29. doi:10.2514/1.b34720

CrossRef Full Text | Google Scholar

9. Shinohara S, Nishida H, Tanikawa T, Hada T, Funaki I, Shamrai KP. Development of Electrodeless Plasma Thrusters with High-Density Helicon Plasma Sources. IEEE Trans Plasma Sci (2014) 42:1245–54. doi:10.1109/tps.2014.2313633

CrossRef Full Text | Google Scholar

10. Chen FF. A Compact Permanent-Magnet Helicon Thruster. IEEE Trans Plasma Sci (2015) 43:195–7. doi:10.1109/tps.2014.2361476

CrossRef Full Text | Google Scholar

11. Takahashi K. Magnetic Nozzle Radiofrequency Plasma Thruster Approaching Twenty Percent Thruster Efficiency. Scientific Rep (2021) 11:1–12. doi:10.1038/s41598-021-82471-2

CrossRef Full Text | Google Scholar

12. Chang Diaz F, Squire JP, Carter M, Corrigan A, Dean L, Farrias J, et al. An Overview of the VASIMR^® Engine. In: 2018 Joint Propulsion Conference; 2018 July 9-11; Cincinnati, OH, USA. (2018). p. 4416.

Google Scholar

13. Boswell RW, Chen FF. Helicons-the Early Years. IEEE Trans Plasma Sci (1997) 25:1229–44. doi:10.1109/27.650898

CrossRef Full Text | Google Scholar

14. Chen FF, Boswell RW. Helicons-the Past Decade. IEEE Trans Plasma Sci (1997) 25:1245–57. doi:10.1109/27.650899

CrossRef Full Text | Google Scholar

15. Chen F. Helicon Discharges and Sources: a Review. Plasma Sourc Sci Tech (2015) 24:014001 (25 pp). doi:10.1088/0963-0252/24/1/014001

CrossRef Full Text | Google Scholar

16. Klozenberg JP, McNamara B, Thonemann PC. The Dispersion and Attenuation of Helicon Waves in a Uniform Cylindrical Plasma. J Fluid Mech (1965) 21:545–63. doi:10.1017/s0022112065000320

CrossRef Full Text | Google Scholar

17. Chen FF. Plasma Ionization by Helicon Waves. Plasma Phys Control Fusion (1991) 33:339–64. doi:10.1088/0741-3335/33/4/006

CrossRef Full Text | Google Scholar

18. Chen F, Arnush D. Generalized Theory of Helicon Waves - I - normal Modes. Phys Plasmas (1998) 4:3411. doi:10.1063/1.872483

CrossRef Full Text | Google Scholar

19. Arnush D, Chen F. Generalized Theory of Helicon Waves - II - Excitation and Absorption. Phyisics of Plasmas (1998) 5(5):1239–1254. doi:10.1063/1.872782

CrossRef Full Text | Google Scholar

20. Stix TH. Waves In Plasmas. New York, NY, USA: Springer Science & Business Media (1992).

Google Scholar

21. Goldston RJ, Rutherford PH. Introduction to Plasma Physics. Bristol, UK: CRC Press (1995).

Google Scholar

22.OA Popov ed. High Density Plasma Sources: Design, Physics and Performance. Park Ridge, NJ, USA: Noyes Publications (1995).

Google Scholar

23. Trivelpiece AW, Gould RW. Space Charge Waves in Cylindrical Plasma Columns. J Appl Phys (1959) 30:1784–93. doi:10.1063/1.1735056

CrossRef Full Text | Google Scholar

24. Shamrai KP, Taranov VB. Volume and Surface Rf Power Absorption in a Helicon Plasma Source. Plasma Sourc Sci. Technol. (1996) 5:474–91. doi:10.1088/0963-0252/5/3/015

CrossRef Full Text | Google Scholar

25. Legéndy CR. Macroscopic Theory of Helicons. Phys Rev (1964) 135:A1713–A1724. doi:10.1103/physrev.135.a1713

CrossRef Full Text | Google Scholar

26. Carter MD, Baity FW, Barber GC, Goulding RH, Mori Y, Sparks DO, et al. Comparing Experiments with Modeling for Light Ion Helicon Plasma Sources. Phys Plasmas (2002) 9:5097–110. doi:10.1063/1.1519539

CrossRef Full Text | Google Scholar

27. Tonks L, Langmuir I. A General Theory of the Plasma of an Arc. Phys Rev (1929) 34:876–922. doi:10.1103/physrev.34.876

CrossRef Full Text | Google Scholar

28. Tonks L. Theory of Magnetic Effects in the Plasma of an Arc. Phys Rev (1939) 56:360–73. doi:10.1103/physrev.56.360

CrossRef Full Text | Google Scholar

29. Fruchtman A, Makrinich G, Ashkenazy J. Two-dimensional Equilibrium of a Low Temperature Magnetized Plasma. Plasma Sourc Sci. Technol. (2005) 14:152–67. doi:10.1088/0963-0252/14/1/017

CrossRef Full Text | Google Scholar

30. Sternberg N, Godyak V, Hoffman D. Magnetic Field Effects on Gas Discharge Plasmas. Phys Plasmas (2006) 13:063511. doi:10.1063/1.2214537

CrossRef Full Text | Google Scholar

31. Ahedo E. Parametric Analysis of a Magnetized Cylindrical Plasma. Phys Plasmas (2009) 16:113503. doi:10.1063/1.3262529

CrossRef Full Text | Google Scholar

32. Ahedo E, Navarro-Cavallé J. Helicon Thruster Plasma Modeling: Two-Dimensional Fluid-Dynamics and Propulsive Performances. Phys Plasmas (2013) 20:043512. doi:10.1063/1.4798409

CrossRef Full Text | Google Scholar

33. Langmuir I. Oscillations in Ionized Gases. Proc Natl Acad Sci (1928) 14:627–37. doi:10.1073/pnas.14.8.627

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Allen J. The Plasma-Sheath Boundary: its History and Langmuir’s Definition of the Sheath Edge. Plasma Sourc Sci Tech (2009) 18:014004. doi:10.1088/0963-0252/18/1/014004

CrossRef Full Text | Google Scholar

35. Lieberman M, Lichtenberg A. Principles of Plasma Discharges and Materials Processing. Hoboken, NJ, USA: Wiley-Interscience (2005).

Google Scholar

36. Butler HS, Kino GS. Plasma Sheath Formation by Radio-Frequency fields. Phys Fluids (1963) 6:1346–55. doi:10.1063/1.1706905

CrossRef Full Text | Google Scholar

37. Myra J. A Tutorial on Radio Frequency Sheath Physics for Magnetically Confined Fusion Devices. J Plasma Phys (2021) 87:905870504. doi:10.1017/s0022377821000878

CrossRef Full Text | Google Scholar

38. Rapp J, Biewer TM, Bigelow TS, Caneses JF, Caughman JBO, Diem SJ, et al. Developing the Science and Technology for the Material Plasma Exposure experiment. Nucl Fusion (2017) 57:116001. doi:10.1088/1741-4326/aa7b1c

CrossRef Full Text | Google Scholar

39. Linsmeier C, Unterberg B, Coenen J, Doerner R, Greuner H, Kreter A, et al. Material Testing Facilities and Pprogram for Plasma-Facing Component Testing. Nucl Fusion (2017) 59(9):092012. doi:10.1088/1741-4326/aa4feb

CrossRef Full Text | Google Scholar

40. Pérez-Grande D, Fajardo P, Ahedo E. Evaluation of Erosion Reduction Mechanisms in a Hall Effect Thruster. In: Joint Conference of 30th International Symposium on Space Technology and Science, 34th International Electric Propulsion Conference and 6th Nano-satellite Symposium; 2015 July 4-10; Hyogo-Kobe, Japan. (2015).

Google Scholar

41. Brown NP, Walker MLR. Review of Plasma-Induced Hall Thruster Erosion. Appl Sci (2020) 10:3775. doi:10.3390/app10113775

CrossRef Full Text | Google Scholar

42. Horváth B, Daksha M, Korolov I, Derzsi A, Schulze J. The Role of Electron Induced Secondary Electron Emission from SiO2surfaces in Capacitively Coupled Radio Frequency Plasmas Operated at Low Pressures. Plasma Sourc Sci. Technol. (2017) 26:124001. doi:10.1088/1361-6595/aa963d

CrossRef Full Text | Google Scholar

43. Sigmund P. Theory of Sputtering. I. Sputtering Yield of Amorphous and Polycrystalline Targets. Phys Rev (1969) 184:383–416. doi:10.1103/physrev.184.383

CrossRef Full Text | Google Scholar

44. Bohdansky J. A Universal Relation for the Sputtering Yield of Monatomic Solids at normal Ion Incidence. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (1984) 2:587–91. doi:10.1016/0168-583x(84)90271-4

CrossRef Full Text | Google Scholar

45. Yamamura Y, Tawara H. Energy Dependence of Ion-Induced Sputtering Yields from Monoatomic Solids at normal Incidence (1995). Technical report. Japan: National Institute for Fusion Science.

Google Scholar

46. Eckstein W, Preuss R. New Fit Formulae for the Sputtering Yield. J Nucl Mater (2003) 320:209–13. doi:10.1016/s0022-3115(03)00192-2

CrossRef Full Text | Google Scholar

47.R Behrisch, and W Eckstein eds. Sputtering by Particle Bombardment: Experiments and Computer Calculations from Threshold to MeV Energies. Berlin, Germany: Springer-Verlag (2007).

Google Scholar

48. Kelly R. The Surface Binding Energy in Slow Collisional Sputtering. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (1986) 18:388–98. doi:10.1016/s0168-583x(86)80063-5

CrossRef Full Text | Google Scholar

49. Urbassek HM. Molecular-dynamics Simulation of Sputtering. Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (1997) 122:427–41. doi:10.1016/s0168-583x(96)00681-7

CrossRef Full Text | Google Scholar

50. Kubota NA, Economou DJ, Plimpton SJ. Molecular Dynamics Simulations of Low-Energy (25-200 eV) Argon Ion Interactions with Silicon Surfaces: Sputter Yields and Product Formation Pathways. J Appl Phys (1998) 83:4055–63. doi:10.1063/1.367225

CrossRef Full Text | Google Scholar

51. Biersack JP, Eckstein W. Sputtering Studies with the Monte Carlo Program TRIM.SP. Appl Phys A (1984) 34:73–94. doi:10.1007/bf00614759

CrossRef Full Text | Google Scholar

52. Ziegler JF, Ziegler MD, Biersack JP. SRIM - the Stopping and Range of Ions in Matter (2010). Nucl Instr Methods Phys Res Section B: Beam Interactions Mater Atoms (2010) 268:1818–23. doi:10.1016/j.nimb.2010.02.091

CrossRef Full Text | Google Scholar

53. Wittmaack K. Reliability of a Popular Simulation Code for Predicting Sputtering Yields of Solids and Ranges of Low-Energy Ions. J Appl Phys (2004) 96:2632–7. doi:10.1063/1.1776318

CrossRef Full Text | Google Scholar

54. García-Rosales C, Eckstein W, Roth J. Revised Formulae for Sputtering Data. J Nucl Mater (1995) 218:8–17. doi:10.1016/0022-3115(94)00376-9

CrossRef Full Text | Google Scholar

55. Lindhard J, Scharff M. Energy Dissipation by Ions in the Kev Region. Phys Rev (1961) 124:128–30. doi:10.1103/physrev.124.128

CrossRef Full Text | Google Scholar

56. Charles C. Plasmas for Spacecraft Propulsion. J Phys D: Appl Phys (2009) 42:163001. doi:10.1088/0022-3727/42/16/163001

CrossRef Full Text | Google Scholar

57. Caughman J, Baity F, Bigelow T, Gardner W, Hoffman D, Forrester S, et al. Non-fusion Applications of Rf and Microwave Technology. In: The 11th Topical Conference on Radio Frequency Power in Plasmas; 1995 17–19 May; Palm Springs, California (USA), 355 (1996). p. 449–58.

Google Scholar

58. Berisford DF, Bengtson RD, Raja LL, Cassady LD, Chancery WJ. Heat Flow Diagnostics for Helicon Plasmas. Rev Sci Instrum (2008) 79:10F515. doi:10.1063/1.2955710

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Mulcahy JM, Browne DJ, Stanton KT, Chang Diaz FR, Cassady LD, Berisford DF, et al. Heat Flux Estimation of a Plasma Rocket Helicon Source by Solution of the Inverse Heat Conduction Problem. Int J Heat Mass Transfer (2009) 52:2343–57. doi:10.1016/j.ijheatmasstransfer.2008.10.031

CrossRef Full Text | Google Scholar

60. Berisford D, Bengston R, Raja L. Power Balance and wall Erosion Measurements in a Helicon Plasma, Sputtering. Phys Plasmas (2010) 17:033503. doi:10.1063/1.3304184

CrossRef Full Text | Google Scholar

61. Del Valle Gamboa J, Cortés S, Fonseca L, Oguilve-Araya J, Valverde J, Martínez C, et al. The VX-CR experiment: A thermal and Lifetime Testbed for the VASIMR^TM Engine. In: 32nd International Electric Propulsion Conference; 2011 September 11-15; Wiesbaden, Germany. IEPC-2011-155 (2011).

Google Scholar

62. De Faoite D, Browne DJ, Del Valle Gamboa JI, Stanton KT. Inverse Estimate of Heat Flux on a Plasma Discharge Tube to Steady-State Conditions Using Thermocouple Data and a Radiation Boundary Condition. Int J Heat Mass Transfer (2014) 77:564–76. doi:10.1016/j.ijheatmasstransfer.2014.04.069

CrossRef Full Text | Google Scholar

63. Squire JP, Carter M, Chang Diaz FR, Corrigan A, Dean L, Farrias J, et al. Steady-state Testing at 100 kW in the VASIMR® VX-200SS Project. In: AIAA Propulsion and Energy 2019 Forum; 2019 August 19-22; Indianapolis, IN, USA. (2019). p. 3810.

Google Scholar

64. Showers M, Piotrowicz PA, Beers CJ, Biewer TM, Caneses J, Canik J, et al. Power Accounting of Plasma Discharges in the Linear Device Proto-Mpex. Plasma Phys Control Fusion (2018) 60:065001. doi:10.1088/1361-6587/aab7c8

CrossRef Full Text | Google Scholar

65. De Faoite D, Browne D, Chang-Diaz F, Stanton K. A Review of the Processing, Composition and Temperature-dependent Mechanical and thermal Properties of Dielectric Technical Ceramics. J Mater Sci (2011) 47:4211–4235. doi:10.1007/s10853-011-6140-1

CrossRef Full Text | Google Scholar

66. De Faoite D, Browne D, Stanton K. Regression Analysis of Temperature-dependent and thermal Properties of Dielectric Technical Ceramics. J Mater Sci (2012) 48:451–461. doi:10.1007/s10853-012-6759-6

CrossRef Full Text | Google Scholar

67. Lee CA, Chen G, Arefiev AV, Bengtson RD, Breizman BN. Measurements and Modeling of Radio Frequency Field Structures in a Helicon Plasma. Phys Plasmas (2011) 18:013501. doi:10.1063/1.3533273

CrossRef Full Text | Google Scholar

68. Berisford D. Thermal Phenomena and Power Balance in a Helicon Plasma. [Ph.D. thesis]. Austin (TX): University of Texas at Austin (2009).

Google Scholar

69. Aanesland A, Charles C, Boswell RW, Fredriksen A. Sputtering Effects in a Helicon Plasma with an Additional Immersed Antenna. Plasma Sourc Sci. Technol. (2003) 12:85–8. doi:10.1088/0963-0252/12/1/311

CrossRef Full Text | Google Scholar

70. Barada KK, Chattopadhyay PK, Ghosh J, Saxena YC, Bora D. Wall Charging of a Helicon Antenna Wrapped Plasma Filled Dielectric Tube. Phys Plasmas (2015) 22:013507. doi:10.1063/1.4906360

CrossRef Full Text | Google Scholar

71. Takahashi K. Helicon-type Radiofrequency Plasma Thrusters and Magnetic Plasma Nozzles. Rev Mod Plasma Phys (2019) 3:1–61. doi:10.1007/s41614-019-0024-2

CrossRef Full Text | Google Scholar

72. Hopwood J. Review of Inductively Coupled Plasmas for Plasma Processing. Plasma Sourc Sci. Technol. (1992) 1:109–16. doi:10.1088/0963-0252/1/2/006

CrossRef Full Text | Google Scholar

73. Beers CJ, Green DL, Lau C, Myra JR, Rapp J, Younkin TR, et al. Rf Sheath Induced Sputtering on Proto-Mpex. I. Sheath Equivalent Dielectric Layer for Modeling the Rf Sheath. Phys Plasmas (2021) 28:093503. doi:10.1063/5.0054074

CrossRef Full Text | Google Scholar

74. Beers CJ, Lau C, Rapp J, Younkin TR, Biewer TM, Bigelow T, et al. Rf Sheath Induced Sputtering on Proto-Mpex Part 2: Impurity Transport Modeling and Experimental Comparison. Phys Plasmas (2021) 28:103508. doi:10.1063/5.0065464

CrossRef Full Text | Google Scholar

75. Lafleur T, Charles C, Boswell RW. Characterization of a Helicon Plasma Source in Low Diverging Magnetic fields. J Phys D: Appl Phys (2011) 44:055202. doi:10.1088/0022-3727/44/5/055202

CrossRef Full Text | Google Scholar

76. Takahashi K, Chiba A, Komuro A, Ando A. Axial Momentum Lost to a Lateral wall of a Helicon Plasma Source. Phys Rev Lett (2015) 114:195001. doi:10.1103/physrevlett.114.195001

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Takahashi K, Ando A. Enhancement of Axial Momentum Lost to the Radial wall by the Upstream Magnetic Field in a Helicon Source. Plasma Phys Control Fusion (2017) 59:054007. doi:10.1088/1361-6587/aa626f

CrossRef Full Text | Google Scholar

78. Takahashi K, Sugawara T, Ando A. Spatially- and Vector-Resolved Momentum Flux Lost to a wall in a Magnetic Nozzle Rf Plasma Thruster. Sci Rep (2020) 10:1061–11. doi:10.1038/s41598-020-58022-6

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Caneses JF, Beers C, Thakur SC, Simmonds MJ, Goulding RH, Lau C, et al. Characterizing the Plasma-Induced thermal Loads on a 200-kW Light-Ion Helicon Plasma Source via Infra-red Thermography. Plasma Sourc Sci Tech (2021) 30:075022. doi:10.1088/1361-6595/abf814

CrossRef Full Text | Google Scholar

80. Mikellides IG, Katz I, Hofer RR, Goebel DM. Magnetic Shielding of a Laboratory Hall Thruster. I. Theory and Validation. J Appl Phys (2014) 115:043303. doi:10.1063/1.4862313

CrossRef Full Text | Google Scholar

81. Hofer RR, Goebel DM, Mikellides IG, Katz I. Magnetic Shielding of a Laboratory Hall Thruster. II. Experiments. J Appl Phys (2014) 115:043304. doi:10.1063/1.4862314

CrossRef Full Text | Google Scholar

82. Godyak V. On Helicon Thrusters: Will They Ever Fly? J Appl Phys (2020) 127:103301. doi:10.1063/1.5139998

CrossRef Full Text | Google Scholar

83. Takahashi K, Charles C, Boswell RW, Takao Y, Fruchtman A, Navarro-Cavallé J, et al. Commentary: On Helicon Thrusters: Will They Ever Fly? Front Phys (2020) 8:277. doi:10.3389/fphy.2020.00277

CrossRef Full Text | Google Scholar

84. Boyd I, Falk M. A Review of Spacecraft Material Sputtering by Hall Thruster Plumes. In: AIAA 37th Joint Propulsion Conference; 2001 July 8–11; Salt Lake City, Utah (USA) (2001). doi:10.2514/6.2001-3353

CrossRef Full Text | Google Scholar

85. Eagle W, Boyd I, Trepp S, Sedwick R. The Erosion Prediction Impact on Current Hall Thruster Model Development. In: 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit; 2008 July 21-23; Hartford, CT. (2008). doi:10.2514/6.2008-5087

CrossRef Full Text | Google Scholar

86. Shastry R, Herman D, Soulas G, Patterson M. NASA’s Evolutionary Xenon Thruster (NEXT) Long-Duration Test as of 736 Kg of Propellant Throughput. In: 48th AIAA/AME/SAE/ASEE Joint Propulsion Conference and Exhibit; 2012 July 30 - August 01; Atlanta, GA. (2012). doi:10.2514/6.2012-4023

CrossRef Full Text | Google Scholar

87. Gildea S, Matlock T. Martinez-sanchez WJ Mand Hargus. Erosion Measurements in a Diverging Cusped-Field Thruster. In: 32nd International Electric Propulsion Conference; 2011 September 11-15; Wiesbaden, Germany. IEPC-2011-149 (2011).

Google Scholar

88. Del Valle Gamboa J, Castro J, Arce N, Chinchilla E, Echeverría E, Lezama D, et al. Measurement of the Dielectric wall Erosion in Helicon Plasma Thrusters: an Application to the VASIMR VX-CR experiment. In: 33rd International Electric Propulsion Conference; 2013 October 6-10; Washington, DC, USA. (2013).

Google Scholar

89. Kajita S, Sakaguchi W, Ohno N, Yoshida N, Saeki T. Formation Process of Tungsten Nanostructure by the Exposure to Helium Plasma under Fusion Relevant Plasma Conditions. Nucl Fusion (2009) 49:095005. doi:10.1088/0029-5515/49/9/095005

CrossRef Full Text | Google Scholar

90. Ewald HN, Crawford FW, Self SA. Steady‐State Theory of an Intermediate‐Pressure Discharge Column in a Magnetic Field. J Appl Phys (1967) 38:2753–61. doi:10.1063/1.1710000

CrossRef Full Text | Google Scholar

91. Castro J, Del Valle J, Arce N, Chinchilla E, Echeverría E, Lezama D, et al. VASIMR VX-CR experiment: Status, Diagnostics and Plasma Plume Characterization. In: The 33rd International Electric Propulsion Conference; 2013 October 6-10; Washington, DC, USA. IEPC-2013-202. USA: The George Washington University (2013).

Google Scholar

92. Zalm PC, Beckers LJ, Sanders FHM. On the Pole of Physical Sputtering in Reactive Ion Beam Etching. Nucl Instr Methods Phys Res (1983) 209-210:561–5. doi:10.1016/0167-5087(83)90853-0

CrossRef Full Text | Google Scholar

93. Nenadovic T, Perraillon B, Bogdanov Z, Djordjevic Z, Milic M. Sputtering and Surface Topography of Oxides. Nucl Instr Methods Phys Res B (1990) 48:538–43.

Google Scholar

94. Varga P, Neidhart T, Sporn M, Libiseller G, Schmid M, Aumayr F, et al. Sputter Yields of Insulators Bombarded with Hyperthermal Multiply Charged Ions. Phys Scr (1997) T73:307–10. doi:10.1088/0031-8949/1997/t73/100

CrossRef Full Text | Google Scholar