Linear Seesaw in A5′ Modular Symmetry With Leptogenesis

In this study, we investigate the implication of modular ${\mathrm{\Gamma }}_5^{\prime }\simeq A_5^{\prime }$ symmetry on neutrino oscillation phenomenology in the linear seesaw framework. In order to achieve the well-defined mass structure for the light active neutrinos as dictated by the linear seesaw mechanism, we introduce six heavy fermion fields along with a pair of weightons to retain the holomorphic nature of the superpotential. The notable feature of modular symmetry is that it reduces the usage of flavon fields significantly. In addition, the Yukawa couplings transform non-trivially under the flavor symmetry group and are expressed in terms of the Dedekind eta functions, the q expansion of which renders numerical simplicity in calculations. We demonstrate that the model framework diligently accommodates all the neutrino oscillation data. Alongside, we also investigate the effect of CP asymmetry generated from the decay of lightest heavy fermions to explain the observed baryon asymmetry through the phenomenon of leptogenesis.

1 Introduction

There are several unsolved knots in the realm of particle physics, for example, the baryon asymmetry of the universe, the dark matter content, the origin of neutrino masses and mixing, and the understanding of these issues is one of the prime objectives of the present-day research. In the last couple of decades, several diligent attempts have been made towards comprehending and resolving the issue of the dynamical origin of fermion masses and their mixing. The present scenario has taken us a few steps ahead in terms of getting a convincing explanation of the origin of mass through the Higgs mechanism while being within the domain of the standard model (SM). However, it does not provide proper grounds to explain the origin of the observed neutrino masses and their mixing. Rather, very diverse approaches are made in order to gain an insightful resolution toward the aforementioned existing problems, and obviously, the answer lies in going beyond standard model (BSM) physics. It should be emphasized that certain well-defined patterns are observed in quark masses and mixing, the appreciation of which is still an enigma. Nonetheless, there is ample amount of research work present, which makes an attempt to grasp their fundamental origin. In addition, perplexity to the problem has increased due to the observation of the neutrino masses and their sizeable mixing. The reason is the order of magnitude of the observed neutrino masses are approximately twelve orders smaller than that of the EW scale. Also, there is an immense difference in the pattern of leptonic and quark mixings, with the former having large mixing angles and the latter having smaller mixing angles. Numerous experiments [1–4] have confirmed the tininess of the neutrino mass and other parameters with high accuracy. The best-fit values of the neutrino oscillation parameters are furnished in References [5, 6].

It is well-known that in the SM framework, the neutrino mass generation cannot be explained through the standard Higgs mechanism due to the absence of the right-handed (RH) components. Still, if we could manage to add the RH neutrinos into SM by hand and allow Dirac mass terms, the values of the required Yukawa couplings would be around $\mathcal{O}(10^{-12})$, which appear aberrant. In contrast, there exist many BSM scenarios that help generate tiny neutrino masses through the conventional seesaw mechanism. Some of the prominent seesaw mechanisms are categorized as type I [7–10], type II [11–16], and type III [17–22], and all of them require additional heavy fermions or scalars beyond the SM particle content. Literature survey shows there are many flavor symmetries either discrete A₄ [23–25], S₃ [26–29], S₄ [30–32], etc. or continuous U(1)_B−L [33–37], U(1)_H [38–40], $U{(1)}_{L_e-L_{\tau }}$ [41, 42], etc., which can generate the tiny neutrino masses and also accommodate the observed neutrino oscillation data with the help of some additional scalars and perturbation (wherever required). As aforesaid, the inclusion of flavons affects the neatness of the model, and the predictability of the model is hampered because of the higher dimensional operators. These drawbacks can be eliminated through the recent approach of modular symmetry [43–65], where the Yukawa couplings transform non-trivially under the discrete flavor symmetry group and have a certain modular weight.

The modular group ${\mathrm{\Gamma }}_5^{\prime }\simeq A_5^{\prime }$ is a new and promising candidate, which corresponds to the specific case of N = 5. People have done extensive research on the basic properties of this finite group $A_5^{\prime }$ [66–68], so here we mention only the important points regarding $A_5^{\prime }$ modular symmetry. The $A_5^{\prime }$ group consists of 120 elements, which are likely to be produced by the generators S, T, and R gratifying the identities for N = 5 [69]. So, categorization of these 120 elements are done into nine conjugacy classes which are represented by nine well-defined irreducible representations, symbolized as 1, $\widehat{\mathbf{2}}$, ${\widehat{\mathbf{2}}}^{\prime }$, 3, 3′, 4, $\widehat{\mathbf{4}}$, 5, and $\widehat{\mathbf{6}}$. Additionally, the conjugacy classes and character table of $A_5^{\prime }$, as well as the representation matrices of all three generators S, T, and R, are presented in Supplementary Appendix [69]. It ought to be noticed that the 1, 3, 3′, 4, and 5 representations with $R=\mathbb{I}$ coincide with those for A₅, while $\widehat{\mathbf{2}}$, ${\widehat{\mathbf{2}}}^{\prime }$, $\widehat{\mathbf{4}}$, and $\widehat{\mathbf{6}}$ are unique for $A_5^{\prime }$ with $R=-\mathbb{I}$. As we are working in the modular space of γ(5), its dimension is 5k + 1, where k is the modular weight. A brief discussion concerning the modular space of γ( 5) is presented in Supplementary Appendix SA. For k = 1, the modular space M₁ [Γ(5)] will have six basis vectors, that is, (${\widehat{e}}_i$, where i = 1, 2, 3, 4, 5, 6), whose q-expansion are given in the following, and they are used in expressing the Yukawa coupling $Y_{\widehat{\mathbf{6}}}^{(1)}$, as shown in Supplementary Appendix SB:

$\begin{array}{ccc}\hfill {\widehat{e}}_1& =\hfill & 1+3q+4q^2+2q^3+q^4+3q^5+6q^6+4q^7-q^9+\cdots ,\hfill \\ \hfill {\widehat{e}}_2& =\hfill & q^{1/5}\left(1+2q+2q^2+q^3+2q^4+2q^5+2q^6+q^7+2q^8+2q^9+\cdots \right),\hfill \\ \hfill {\widehat{e}}_3& =\hfill & q^{2/5}\left(1+q+q^2+q^3+2q^4+q^6+q^7+2q^8+q^9+\cdots \right),\hfill \\ \hfill {\widehat{e}}_4& =\hfill & q^{3/5}\left(1+q^2+q^3+q^4-q^5+2q^6+2q^8+q^9+\cdots \right),\hfill \\ \hfill {\widehat{e}}_5& =\hfill & q^{4/5}\left(1-q+2q^2+2q^6-2q^7+2q^8+q^9+\cdots \right),\hfill \\ \hfill {\widehat{e}}_6& =\hfill & q\left(1-2q+4q^2-3q^3+q^4+2q^5-2q^6+3q^8-2q^9+\cdots \right),\hfill \end{array}(1)$

where q ≡ e^2iπτ, with τ as a complex modulus parameter. The significance of the modulus τ is that the modular group Γ is generated by performing the linear fractional transformation on τ as follows:

$\gamma :\tau \to \gamma \left(\tau \right)\to \frac{a\tau +b}{c\tau +d},\left\{a,b,c,d\in Z:ad-bc=0,\mathrm{I}\mathrm{m}\left(\tau \right)>0\right\}.(2)$

Our aim is to utilize the expediency of $A_5^{\prime }$ modular symmetry by employing it to the linear seesaw mechanism in the context of supersymmetry as we are quite familiar with the dynamics of TeV-scale seesaw frameworks from numerous [70, 71] studies. The deciding factor whether it will be linear seesaw or inverse seesaw is the position of the zero elements in the mass matrix under the basis of (ν, $N_{R_i}$, $S_{L_i}$). It is quite evident when 11 and 33 elements of the mass matrix are zero; it gives the structure of a linear seesaw. As mentioned before, the introduction of three left-handed neutral fermion superfields $S_{L_i}$ alongside three-right handed ones $N_{R_i}(i=\mathrm{1,2,3})$ validates and produces the neutrino mass matrix structure of a linear seesaw, which is intricate enough, and has been studied in the context of discrete A₄ flavor symmetry in [72–74]. In this work, we are implementing it under $A_5^{\prime }$ modular symmetry. For this purpose, the heavy fermions S_Li and N_Ri are assigned as 3′ under $A_5^{\prime }$ symmetry, and the modular form of the Yukawa couplings leads to a constrained structure. After that, we perform the numerical analysis to look for the region which is acceptable in order to fit the neutrino data. Hence, prediction for the neutrino sector is done after fixing the allowed parameter space.

The structure of this article is as follows. In Section 2, we discuss the layout of the familiar linear seesaw framework with $A_5^{\prime }$ modular symmetry and its alluring feature, which leads to a simple mass structure for the charged leptons and neutral leptons, utilizing the product rules of $A_5^{\prime }$ symmetry. We thereafter briefly discuss the phenomena of light neutrino masses and mixing in this framework. The numerical analysis pertaining to different observables of the neutrino sector and the input model parameters is presented in Section 3. We also briefly comment on the non-unitarity effect in Section 4. The discussion on leptogenesis within the context of the proposed model is furnished in Section 5, and our results are summarized in Section 6.

2 Model Framework

Here, we have built a model under a linear seesaw scenario in the context of supersymmetry (SUSY), where Table 1 expresses the particle content and their respective group charges. For exploring the neutrino sector beyond standard model (BSM), we extend it with the discrete $A_5^{\prime }$ modular symmetry and a local U(1)_B−L gauge symmetry. However, the local U(1)_B−L becomes the auxiliary symmetry, which has been added to avoid certain undesirable terms in the superpotential. The advantage of using BSM is that we can add right-handed neutrinos and extra fields, and hence, we have included three extra right-handed SM singlet superfields (N_Ri), three left-handed singlet superfields (S_Li), and a pair weightons (ζ, ζ′) in the particle gamut. The transformation of extra added superfields is taken as 3′ under the $A_5^{\prime }$ modular group. The $A_5^{\prime }$ and U(1)_B−L symmetries are broken at a very high scale, much greater than the scale of electroweak symmetry breaking [75]. Mass acquisition by the extra singlet superfields is done by allocating non-zero vacuum expectation values (VEVs) to the weightons ζ and ζ′. The modular weight assigned to various particles is denoted by k_I. One of the significant points of introducing the modular symmetry is the curtailment of flavon (weighton) fields, which otherwise are traditionally required while using BSM with discrete symmetries, since the Yukawa couplings have non-trivial group transformation under the $A_5^{\prime }$ modular symmetry group, and their transformation are present in [69].

TABLE 1

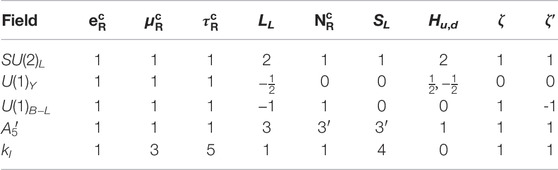
TABLE 1. Particle spectrum and their charges under the symmetry groups $SU{(2)}_L\times U{(1)}_Y\times U{(1)}_{B-L}\times A_5^{\prime }$, while k_I represents the modular weight.

The complete superpotential is given as follows:

$\begin{array}{ccc}\hfill \mathcal{W}& =\hfill & A_{M_l}\left[{\left(L_L{l}_R^c\right)}_{\mathbf{3}}{Y}_{\mathbf{3}}^{k_Y}\right]H_d+\mu H_u{H}_d+G_D\left[{\left(L_L{N}_R^c\right)}_{\mathbf{5}}{Y}_{\mathbf{5}}^{\left(2\right)}\right]H_u+\hfill \\ \hfill & \hfill & G_{LS}\left[{\left(L_L{S}_L\right)}_{\mathbf{4}}{H}_u\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right]\frac{\zeta }{\mathrm{\Lambda }}+B_{M_{RS}}\left[{\left(S_L{N}_R^c\right)}_{\mathbf{5}}\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right]{\zeta }^{\prime },\hfill \end{array}(3)$

where $A_{{\mathcal{M}}_l}=({\alpha }_{{\mathcal{M}}_l},{\beta }_{{\mathcal{M}}_l},{\gamma }_{{\mathcal{M}}_l})$, $l_R^c=(e_R^c,{\mu }_R^c,{\tau }_R^c)$, k_Y = (2, 4, 6), and $G_D=\mathrm{diag}\{g_{D_1},g_{D_2},g_{D_3}\}$, $G_{LS}=\mathrm{diag}\{{\mathrm{g}}_{{\mathrm{L}\mathrm{S}}_1},{\mathrm{g}}_{{\mathrm{L}\mathrm{S}}_2},{\mathrm{g}}_{{\mathrm{L}\mathrm{S}}_3}\}$, and $B_{M_{RS}}=\mathrm{diag}\{{\alpha }_{R{S}_1},{\alpha }_{R{S}_2},{\alpha }_{R{S}_3}\}$ represent the coupling strengths of various interaction terms.

2.1 Mass Terms for the Charged Leptons (M_ℓ)

In order to have a clear and simplified structure for the charged lepton mass matrix, we consider the three families of left-handed lepton doublets (L_L) to transform as 3 under the $A_5^{\prime }$ symmetry with U(1)_B−L charge −1. The right-handed charged leptons $l_R^c$ transform as singlets under $A_5^{\prime }$ symmetry and have U(1)_B−L charge +1. However, $e_R^c$, ${\mu }_R^c$, and ${\tau }_R^c$ are given the modular weight as 1, 3, and 5, respectively. The Higgsinos H_u,d are given charges 0 and 1 under the U(1)_B−L and $A_5^{\prime }$ symmetries with zero modular weights. The VEVs of these Higgsinos H_u and H_d are given as $v_u/\sqrt{2}$ and $v_d/\sqrt{2}$, respectively. Moreover, Higgsinos VEVs are associated to SM Higgs VEV as $v_H=\frac{1}{2}\sqrt{v_u^2+v_d^2}$, and the ratio of their VEVs is expressed as tan β = (v_u/v_d); we use its value as 5 in our analysis. The relevant superpotential terms for charged leptons obtained from Eq. 3 are given as follows:

${\mathcal{W}}_{M_l}={\alpha }_{M_l}\left[{\left(L_L{e}_R^c\right)}_{\mathbf{3}}{Y}_{\mathbf{3}}^{\left(2\right)}\right]H_d+{\beta }_{M_l}\left[{\left(L_L{\mu }_R^c\right)}_{\mathbf{3}}{Y}_{\mathbf{3}}^{\left(4\right)}\right]H_d+{\gamma }_{M_l}\left[{\left(L_L{\tau }_R^c\right)}_{\mathbf{3}}\left\{\sum _{i=1}^2{Y}_{\mathbf{3},i}^{\left(6\right)}\right\}\right]H_d.(4)$

In the $A_5^{\prime }$ modular group, its Kronecker product (as provided in Supplementary Appendix SC) leaves us with a non-diagonal charged lepton mass matrix after the spontaneous symmetry breaking. The mass matrix takes the following form:

$M_l=\frac{v_d}{\sqrt{2}}{\left[\begin{array}{ccccc}\hfill {\left(Y_{\mathbf{3}}^{\left(2\right)}\right)}_1\hfill & \hfill \hfill & \hfill {\left(Y_{\mathbf{3}}^{\left(4\right)}\right)}_1\hfill & \hfill \hfill & \hfill {\left(\sum _{i=1}^2{Y}_{\mathbf{3},i}^{\left(6\right)}\right)}_1\hfill \\ \hfill {\left(Y_{\mathbf{3}}^{\left(2\right)}\right)}_3\hfill & \hfill \hfill & \hfill {\left(Y_{\mathbf{3}}^{\left(4\right)}\right)}_3\hfill & \hfill \hfill & \hfill {\left(\sum _{i=1}^2{Y}_{\mathbf{3},i}^{\left(6\right)}\right)}_3\hfill \\ \hfill {\left(Y_{\mathbf{3}}^{\left(2\right)}\right)}_2\hfill & \hfill \hfill & \hfill {\left(Y_{\mathbf{3}}^{\left(4\right)}\right)}_2\hfill & \hfill \hfill & \hfill {\left(\sum _{i=1}^2{Y}_{\mathbf{3},i}^{\left(6\right)}\right)}_2\hfill \end{array}\right]}_{LR}\cdot \left[\begin{array}{ccc}\hfill {\alpha }_{M_l}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_{M_l}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\gamma }_{M_l}\hfill \end{array}\right].(5)$

The charged lepton mass matrix M_l can be diagonalized by the unitary matrix U_l, resulting in the physical masses m_e, m_μ, and m_τ as follows:

$U_l^{†}{M}_l{M}_l^{†}{U}_l=\mathrm{diag}\left(m_e^2,m_{\mu }^2,m_{\tau }^2\right).(6)$

In addition, it also satisfies the following identities, which will be used for numerical analysis in Section 3:

$\begin{array}{ccc}\hfill \mathrm{Tr}\left(M_l{M}_l^{†}\right)& =\hfill & m_e^2+m_{\mu }^2+m_{\tau }^2,\hfill \\ \hfill \mathrm{D}\mathrm{e}\mathrm{t}\left(M_l{M}_l^{†}\right)& =\hfill & m_e^2{m}_{\mu }^2{m}_{\tau }^2,\hfill \\ \hfill \frac{1}{2}{\left[\mathrm{Tr}\left(M_l{M}_l^{†}\right)\right]}^2-\frac{1}{2}\mathrm{Tr}\left[{\left(M_l{M}_l^{†}\right)}^2\right]& =\hfill & m_e^2{m}_{\mu }^2+m_{\mu }^2{m}_{\tau }^2+m_{\tau }^2{m}_e^2.\hfill \end{array}(7)$

2.2 Dirac and Pseudo-Dirac Mass Terms for the Light Neutrinos

In addition to lepton doublets transformation, hitherto, the heavy fermion superfields, that is, $N_{R_i}$ $(S_{L_i})$, transform as triplet 3′ under the $A_5^{\prime }$ modular group with U(1)_B−L charge of −1 (0) along with modular weight 1 (4), respectively. As discussed in Ref. [69], the choice of Yukawa couplings depends on the equation $k_Y=k_{I_1}+k_{I_2}+\cdots +k_{I_n}$, where k_Y is the modular weight of Yukawa couplings and ${\mathrm{\Sigma }}_{i=1}^{I_n}{k}_{I_n}$ is the sum of the modular weights of all other particles present in the definition of superpotential terms. These Yukawa couplings are expressed in terms of Dedekind eta function η(τ) and thus have q-expansion forms, in order to avoid the complexity in calculations. The relevant superpotential term involving the active and right-handed neutrinos can be expressed as follows:

${\mathcal{W}}_D=G_D\left[{\left(L_L{N}_R^c\right)}_{\mathbf{5}}{Y}_{\mathbf{5}}^{\left(2\right)}\right]H_u,(8)$

where G_D is the diagonal matrix containing the free parameters and the modular weight of the Yukawa coupling is equal to the sum of the modular weights of all other particles present in Eq. 8. The choice of the Yukawa coupling is made based on the Kronecker product rules for $A_5^{\prime }$ modular symmetry such that superpotential remains invariant. The resulting Dirac neutrino mass matrix is found to be as follows:

$M_D=\frac{v_u}{\sqrt{3}0}{G}_D{\left[\begin{array}{ccc}\hfill \sqrt{3}{\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_1\hfill & \hfill {\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_4\hfill & \hfill {\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_3\hfill \\ \hfill {\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_5\hfill & \hfill -\sqrt{2}{\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_3\hfill & \hfill -\sqrt{2}{\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_2\hfill \\ \hfill {\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_2\hfill & \hfill -\sqrt{2}{\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_5\hfill & \hfill -\sqrt{2}{\left(Y_{\mathbf{5}}^{\left(2\right)}\right)}_4\hfill \end{array}\right]}_{LR}.(9)$

As the transformation of the sterile fermion superfield S_L is same as N_R under $A_5^{\prime }$ modular symmetry, it allows us to define a pseudo-Dirac mass term for the light neutrinos, and the corresponding interaction superpotential is expressed as follows:

${\mathcal{W}}_{LS}=G_{LS}\left[{\left(L_L{S}_L\right)}_{\mathbf{4}}\sum _2^{i=1}{Y}_{\mathbf{4},i}^{\left(6\right)}\right]H_u\left(\frac{\zeta }{\mathrm{\Lambda }}\right),(10)$

where G_LS is a diagonal matrix containing three free parameters and the choice of Yukawa coupling depends on the idea of keeping the superpotential singlet. Thus, we obtain the structure for the pseudo-Dirac neutrino mass matrix of the following form:

$M_{LS}=\frac{v_u}{2\sqrt{6}}\left(\frac{v_{\zeta }}{\sqrt{2}\mathrm{\Lambda }}\right)G_{LS}{\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -\sqrt{2}{\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_3\hfill & \hfill -\sqrt{2}{\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_2\hfill \\ \hfill \sqrt{2}{\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_4\hfill & \hfill -{\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_2\hfill & \hfill {\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_1\hfill \\ \hfill {\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_1\hfill & \hfill {\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_4\hfill & \hfill -{\left(\sum _{i=1}^2{Y}_{\mathbf{4},i}^{\left(6\right)}\right)}_3\hfill \end{array}\right]}_{LR}.(11)$

2.3 Mixing Between the Heavy Fermions N_Ri and S_Li

Introduction of extra symmetries helps to allow the mixing of heavy superfields but forbids the usual Majorana mass terms. Hence, we exhibit the mixing of these extra superfields, that is, (N_R, S_L) as follows:

${\mathcal{W}}_{M_{RS}}=B_{M_{RS}}\left[{\left(S_L{N}_R^c\right)}_{\mathbf{5}}\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right]{\zeta }^{\prime },(12)$

where $B_{M_{RS}}$ is the free parameter and $⟨{\zeta }^{\prime }⟩=v_{{\zeta }^{\prime }}/\sqrt{2}$ is the VEV of ζ′, and the superpotential is singlet under the $A_5^{\prime }$ modular symmetry product rule. Thus, considering v_ζ′ ≈ v_ζ, one can obtain the mass matrix as follows:

$M_{RS}=\frac{v_{\zeta }}{\sqrt{6}0}{B}_{M_{RS}}{\left[\begin{array}{ccc}\hfill 2{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_1\hfill & \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_4\hfill & \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_3\hfill \\ \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_4\hfill & \hfill \sqrt{6}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_2\hfill & \hfill -{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_1\hfill \\ \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_3\hfill & \hfill -{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_1\hfill & \hfill \sqrt{6}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(6\right)}\right)}_5\hfill \end{array}\right]}_{LR}.(13)$

The masses for the heavy superfields can be found in the basis ${(N_R,S_L)}^T$ as

$M_{hf}=\left(\begin{array}{cc}\hfill 0\hfill & \hfill M_{RS}\hfill \\ \hfill M_{RS}^T\hfill & \hfill 0\hfill \end{array}\right).(14)$

Hence, one can have three doubly degenerate mass eigenstates for the heavy superfields upon diagonalization.

2.4 Linear Seesaw Framework for the Light Neutrino Masses

In the present scenario of $A_5^{\prime }$ modular symmetry, the light neutrino masses can be generated in the framework of linear seesaw. Thus, the mass matrix in the flavor basis of ${\left({\nu }_L,N_R^c,S_L\right)}^T$ can be manifested as

The mass formula for the light neutrinos in the framework of linear seesaw is governed by the assumption that M_RS ≫ M_D, M_LS and is given as follows:

$m_{\nu }=M_D{M}_{RS}^{-1}{M}_{LS}^T+\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}.(16)$

In addition to the light neutrino masses, other related parameters in the leptonic sector are the Jarlskog invariant, which signifies the measure of CP violation and the effective neutrino mass parameter m_ee that plays a key role in the neutrinoless double beta decay process. These parameters can be obtained from the PMNS matrix elements through the following relations:

$\begin{array}{ccc}\hfill & \hfill & J_{CP}=\text{Im}\left[U_{e1}{U}_{\mu 2}{U}_{e2}^{*}{U}_{\mu 1}^{*}\right]=s_{23}{c}_{23}{s}_{12}{c}_{12}{s}_{13}{c}_{13}^2\sin {\delta }_{CP},\hfill \end{array}(17)$

$\begin{array}{ccc}\hfill & \hfill & m_{ee}=|m_1{\cos }^2{\theta }_{12}{\cos }^2{\theta }_{13}+m_2{\sin }^2{\theta }_{12}{\cos }^2{\theta }_{13}{e}^{i{\alpha }_{21}}+m_3{\sin }^2{\theta }_{13}{e}^{i\left({\alpha }_{31}-2{\delta }_{CP}\right)}|.\hfill \end{array}(18)$

Tremendous experimental efforts are being undertaken to measure the effective Majorana mass parameter m_ee, and it is expected to be measured by the KamLAND-Zen experiment in the near future [76].

3 Numerical Analysis

For numerical analysis, we use the neutrino oscillation parameters from the global-fit results [77–79] obtained from various experiments, as given in Table 2. The numerical diagonalization of the light neutrino mass matrix given in Eq. 16 is done through $U_{\nu }^{†}\mathcal{M}{U}_{\nu }=\mathrm{diag}(m_1^2,m_2^2,m_3^2)$, where $\mathcal{M}=m_{\nu }{m}_{\nu }^{†}$ and U_ν is an unitary matrix. Thus, the lepton mixing matrix is given as $U=U_l^{†}{U}_{\nu }$, from which the mixing angles can be excerpted using the standard relations:

${\sin }^2{\theta }_{13}=|U_{13}{|}^2,{\sin }^2{\theta }_{12}=\frac{|U_{12}{|}^2}{1-|U_{13}{|}^2},{\sin }^2{\theta }_{23}=\frac{|U_{23}{|}^2}{1-|U_{13}{|}^2}.(19)$

To fit to the current neutrino oscillation data, we use the following ranges for the model parameters:

$\begin{array}{ll}\hfill & \mathrm{R}\mathrm{e}\left[\tau \right]\in \left[\mathrm{0,0.5}\right],\mathrm{I}\mathrm{m}\left[\tau \right]\in \left[\mathrm{1,3}\right],G_D\in \left[10^{-7},10^{-6}\right],G_{LS}\in \left[10^{-4},10^{-3}\right]v_{\zeta }\in \left[\mathrm{10,100}\right]\mathrm{T}\mathrm{e}\mathrm{V},\hfill \\ \hfill & B_{M_{RS}}\in \left[10^{-3},10^{-2}\right],\mathrm{\Lambda }\in \left[10^4,10^5\right]\mathrm{T}\mathrm{e}\mathrm{V}.\hfill \end{array}(20)$

The input parameters are varied randomly in the ranges as provided in Eq. 20 and constrained by imposing the 3σ bounds on neutrino oscillation data, that is, the solar and atmospheric mass-squared differences and the mixing angles, as presented in Table 2, as well as the sum of active neutrino masses Σm_i < 0.12 eV [80, 81]. The typical range of the modulus τ is found to be: 0 ≲ Re [τ] ≲ 0.5 and 1 ≲ Im [τ] ≲ 3 for normal ordered neutrino masses. In Figure 1, we show the variation of the sum of active neutrino masses (Σm_i) with the reactor mixing angle sin²θ₁₃ in the left panel, while the right panel demonstrates Σm_i versus sin²θ₁₂ and sin²θ₂₃. From these figures, it can be observed that the model predictions for the sum of neutrino masses as 0.058 eV ≤ Σm_i ≤ 0.062 eV for the allowed 3σ ranges of the mixing angles.

TABLE 2

TABLE 2. Global-fit values of the oscillation parameters along with their 1σ, 2σ, and 3σ ranges [77–79].

FIGURE 1

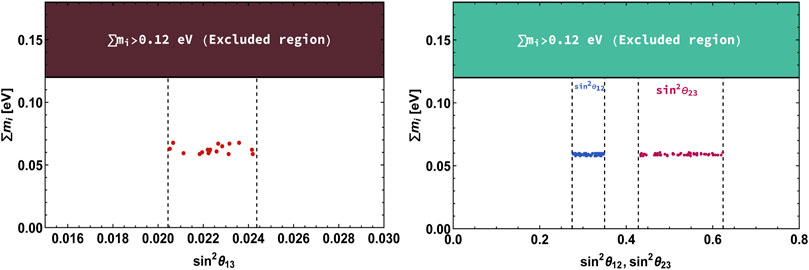
FIGURE 1. Left (right) panel displays the correlation between sin²θ₁₃ (sin²θ₁₂ and sin²θ₂₃) with the sum of active neutrino masses. The vertical lines represent 3σ allowed ranges of the mixing angles.

The variation of the effective neutrinoless double beta decay mass parameter m_ee with Σm_i is displayed in Figure 2, from which the upper limit on m_ee is found to be 0.025 eV satisfying KamLAND-Zen bound. Furthermore, we display the variation of δ_CP and J_CP in the left and right panels of Figure 3, respectively, where 100° ≤ δ_CP ≤ 250° and |J_CP| ≤ 0.004.

FIGURE 2

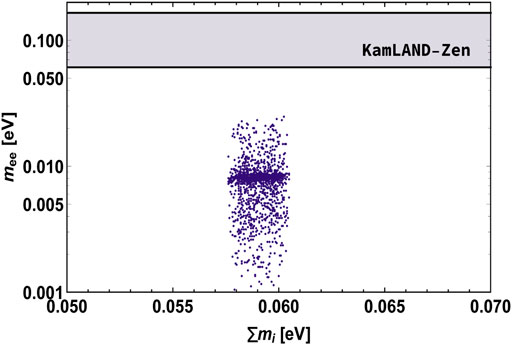
FIGURE 2. Correlation plot between the effective neutrino mass m_ee of neutrinoless double beta decay and the sum of active neutrino masses.

FIGURE 3

FIGURE 3. Left (right) panel shows the plot of δ_CP (J_CP) with sin²θ₁₃ within its 3σ bound.

4 Comment on Non-Unitarity of Leptonic Mixing Matrix

Here, we present a brief discussion on the non-unitarity of the neutrino mixing matrix $U_{\text{PMNS}}^{\prime }$ in the context of the present model. Due to the mixing between the light and heavy fermions, there will be a small deviation from the unitarity of the leptonic mixing matrix, which can be expressed as follows [82]:

$U_{\text{PMNS}}^{\prime }\equiv \left(1-\frac{1}{2}F{F}^{†}\right)U_{\text{PMNS}}.(21)$

Here, U_PMNS denotes the leptonic mixing matrix that diagonalizes the light neutrino mass matrix and F represents the mixing of active neutrinos with the heavy fermions, approximated as $F\equiv {(M_{NS}^T)}^{-1}{M}_D\approx \frac{g_{D}v}{{\alpha }_{RS}{v}_{\zeta }}$, and is a Hermitian matrix. The local constraints on the non-unitarity parameters [83–85] are obtained through various experimental results on electroweak parameters, for example, the mass of W boson (M_W), the Weinberg mixing angle (θ_W), several ratios of fermionic Z boson decays as well as its invisible decay, bounds from CKM unitarity, and lepton flavor violations. In the context of the present model, we presume the following approximated normalized order for the Dirac, pseudo-Dirac, and heavy fermion masses for correctly generating the observed solar and atmospheric mass-squared differences, as well as the sum of active neutrino masses of desired order as follows:

$\left(\frac{m_{\nu }}{0.1\mathrm{e}\mathrm{V}}\right)\approx \left(\frac{M_D}{10^{-3}\mathrm{G}\mathrm{e}\mathrm{V}}\right){\left(\frac{M_{RS}}{10^3\mathrm{G}\mathrm{e}\mathrm{V}}\right)}^{-1}\left(\frac{M_{LS}}{10^{-4}\mathrm{G}\mathrm{e}\mathrm{V}}\right).(22)$

With these chosen order masses, we obtain an approximated non-unitary mixing for the present model as follows:

$|F{F}^{†}|\le \left[\begin{array}{ccc}\hfill 4.5\times 10^{-13}\hfill & \hfill 2.3\times 10^{-13}\hfill & \hfill 6.2\times 10^{-13}\hfill \\ \hfill 2.3\times 10^{-13}\hfill & \hfill 2.08\times 10^{-12}\hfill & \hfill 4.5\times 10^{-12}\hfill \\ \hfill 6.2\times 10^{-13}\hfill & \hfill 4.5\times 10^{-12}\hfill & \hfill 5.6\times 10^{-12}\hfill \end{array}\right].(23)$

As the mixing between the active light and heavy fermions in our model is quite small, it leads to a negligible contribution for the non-unitarity.

5 Leptogenesis

The present universe is clearly seen to be baryon-dominated, with the ratio of the measured over-abundance of baryons over anti-baryons to the entropy density is found to be

$Y_B=\left(8.56\pm 0.22\right)\times 10^{-11}.(24)$

If the universe had started from an initially symmetric state of baryons and antibaryons, the following three conditions have to be fulfilled for generating a non-zero baryon asymmetry. According to Sakharov [86], the three criteria are Baryon number violation, C and CP violation, and departure from equilibrium during the evolution of the universe. Although the SM assures all these criteria for an expanding universe are akin to ours, the extent of CP violation found in the SM is quite small to accommodate the observed baryon asymmetry of the universe. Therefore, additional sources of CP violation are absolutely essential for explaining this asymmetry. The most common new sources of CP violation possibly could arise in the lepton sector, which is however not yet firmly established experimentally. Leptogenesis is the phenomenon that furnishes a minimal setup to correlate the CP violation in the lepton sector to the observed baryon asymmetry, as well as imposes indirect constraints on the CP phases from the requirement that it would yield the correct baryon asymmetry. It is seen that the scale of CP asymmetry generated from the heavy neutral fermion decays can come down to as low as TeV [87–90] due to resonant enhancement. However, the present scenario is realized by involving six heavy states, which comprise three pairs of heavy neutrinos with doubly degenerate masses (Eq. 14). Nevertheless, introduction of higher dimensional mass terms for the Majorana fermions (N_R) can be made through the following superpotential:

${\mathcal{W}}_{M_R}=-G_R\left[\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}{N}_R^c{N}_R^c\right]\frac{{{\zeta }^{\prime }}^2}{\mathrm{\Lambda }},(25)$

which gives rise to a petty mass splitting between the heavy neutral fermions and hence provides an enhancement in the CP asymmetry for generating the required lepton asymmetry [91, 92]. Thus, from Eq. 25, one can construct the Majorana mass matrix for the right-handed neutrinos N_R as follows:

$M_R=\frac{G_R{v}_{\zeta }^2}{2\mathrm{\Lambda }\sqrt{30}}{\left[\begin{array}{ccc}\hfill 2{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_1\hfill & \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_4\hfill & \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_3\hfill \\ \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_4\hfill & \hfill \sqrt{6}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_2\hfill & \hfill -{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_1\hfill \\ \hfill -\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_3\hfill & \hfill -{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_1\hfill & \hfill \sqrt{6}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{\left(4\right)}\right)}_5\hfill \end{array}\right]}_{LR}.(26)$

The coupling G_R is considered as extremely small to preserve the linear seesaw texture of the neutrino mass matrix (Eq. 15), that is, M_D, M_LS ≫ M_R, and hence, inclusion of such additional term does not alter the previous results. However, this added term generates a small mass splitting. Hence, the 2 × 2 submatrix of Eq. 15 in the basis of (N_R, S_L) becomes

$M=\left(\begin{array}{cc}\hfill M_R\hfill & \hfill M_{RS}\hfill \\ \hfill M_{RS}^T\hfill & \hfill 0\hfill \end{array}\right),(27)$

which can be block diagonalized by the unitary matrix $\frac{1}{\sqrt{2}}\left(\begin{array}{cc}\hfill I\hfill & \hfill -I\hfill \\ \hfill I\hfill & \hfill I\hfill \end{array}\right)$ as follows:

$M^{\prime }=\left(\begin{array}{cc}\hfill M_{RS}+\frac{M_R}{2}\hfill & \hfill -\frac{M_R}{2}\hfill \\ \hfill -\frac{M_R}{2}\hfill & \hfill -M_{RS}+\frac{M_R}{2}\hfill \end{array}\right)\approx \left(\begin{array}{cc}\hfill M_{RS}+\frac{M_R}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -M_{RS}+\frac{M_R}{2}\hfill \end{array}\right).(28)$

Thus, one can express the mass eigenstates (N^±) in terms of the flavor states (N_R, S_L) as follows:

$\left(\begin{array}{c}\hfill S_{Li}\hfill \\ \hfill N_{Ri}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill \\ \hfill \sin \theta \hfill & \hfill \cos \theta \hfill \end{array}\right)\left(\begin{array}{c}\hfill N_i^{+}\hfill \\ \hfill N_i^{-}\hfill \end{array}\right).(29)$

Assuming the mixing to be maximal, one can have

$N_{Ri}=\frac{\left(N_i^{+}+N_i^{-}\right)}{\sqrt{2}},S_{Li}=\frac{\left(N_i^{+}-N_i^{-}\right)}{\sqrt{2}}.(30)$

Hence, the interaction superpotential (Eq. 8) can be manifested in terms of the new basis. The mass eigenvalues of the new states N⁺ and N⁻ can be obtained by diagonalizing the block diagonal form of the heavy fermion masses and are found as $\frac{M_R}{2}+M_{RS}$ and $\frac{M_R}{2}-M_{RS}$ (Eq. 28).

The Dirac (Eq. 10) and pseudo-Dirac (Eq. 11) terms are now modified as follows:

${\mathcal{W}}_D=G_D{L}_L{H}_u\left[Y_{\mathbf{5}}^{\left(2\right)}\left(\frac{\left(N_i^{+}+N_i^{-}\right)}{\sqrt{2}}\right)\right],(31)$

and

${\mathcal{W}}_{LS}=G_{LS}{L}_L{H}_u\left[\sum _2^{i=1}{Y}_{\mathbf{4},i}^{\left(6\right)}\left(\frac{\left(N_i^{+}-N_i^{-}\right)}{\sqrt{2}}\right)\right]\frac{\zeta }{\mathrm{\Lambda }}.(32)$

Thus, one can symbolically express the block diagonal matrix for the heavy fermions (Eq. 28) as follows:

$M_{RS}\pm \frac{M_R}{2}=\frac{v_{\zeta }}{\sqrt{6}0}{B}_{M_{RS}}{\left[\begin{array}{ccc}\hfill 2a\hfill & \hfill d\hfill & \hfill e\hfill \\ \hfill d\hfill & \hfill b\hfill & \hfill f\hfill \\ \hfill e\hfill & \hfill f\hfill & \hfill c\hfill \end{array}\right]}_{LR}\pm \frac{G_R{v}_{\zeta }^2}{2\mathrm{\Lambda }\sqrt{30}}{\left[\begin{array}{ccc}\hfill 2a^{\prime }\hfill & \hfill d^{\prime }\hfill & \hfill e^{\prime }\hfill \\ \hfill d^{\prime }\hfill & \hfill b^{\prime }\hfill & \hfill f^{\prime }\hfill \\ \hfill e^{\prime }\hfill & \hfill f^{\prime }\hfill & \hfill c^{\prime }\hfill \end{array}\right]}_{LR},(33)$

where the different matrix elements are defined as follows:

$\begin{array}{ccc}\hfill a\left(a^{\prime }\right)={\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{6\left(4\right)}\right)}_1,b\left(b^{\prime }\right)=\sqrt{6}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{6\left(4\right)}\right)}_2,c\left(c^{\prime }\right)=\sqrt{6}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{6\left(4\right)}\right)}_5,& \hfill & \hfill \end{array}(34)$

$\begin{array}{ccc}\hfill d\left(d^{\prime }\right)=-\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{6\left(4\right)}\right)}_4,e\left(e^{\prime }\right)=-\sqrt{3}{\left(\sum _{i=1}^2{Y}_{\mathbf{5},i}^{6\left(4\right)}\right)}_3,f\left(f^{\prime }\right)=-a\left(a^{\prime }\right).& \hfill & \hfill \end{array}(35)$

One can obtain the diagonalized mass matrix from Eq. 33 through rotation to the mass eigenbasis as ${(M^{\pm })}_{\mathrm{diag}}=U_{\text{TBM}}{U}_R\left(M_{RS}\pm \frac{M_R}{2}\right)U_R^T{U}_{\text{TBM}}^T$, and thus, three sets of nearly degenerate mass states can be obtained upon diagonalization. We further presume that the lightest pair among them with mass in the TeV range contributes predominantly to the CP asymmetry. The small mass difference between the lightest pair demonstrates that the CP asymmetry generated from the one-loop self-energy contribution of heavy particle decay dominates over the vertex part. Thus, the CP asymmetry can be expressed as follows [87, 93]:

${ϵ}_{N_i^{-}}\approx \frac{1}{32{\pi }^2{A}_{N_i^{-}}}\mathrm{I}\mathrm{m}{\left[{\left(\frac{{\tilde{M}}_D}{v}-\frac{{\tilde{M}}_{LS}}{v}\right)}^{†}{\left(\frac{{\tilde{M}}_D}{v}+\frac{{\tilde{M}}_{LS}}{v}\right)}^2{\left(\frac{{\tilde{M}}_D}{v}-\frac{{\tilde{M}}_{LS}}{v}\right)}^{†}\right]}_{ii}\frac{r_N}{r_N^2+4A_{N_i^{-}}^2},(36)$

where ${\tilde{M}}_{D(LS)}=M_{D(LS)}{U}_{\text{TBM}}{U}_R$, $\mathrm{\Delta }M=M_i^{+}-M_i^{-}\approx M_R$, and the parameters r_N and $A_{N^{-}}$ are given as follows:

$\begin{array}{ccc}\hfill & \hfill & r_N=\frac{{\left(M_i^{+}\right)}^2-{\left(M_i^{-}\right)}^2}{M_i^{+}{M}_i^{-}}=\frac{\mathrm{\Delta }M\left(M_i^{+}+M_i^{-}\right)}{M_i^{+}{M}_i^{-}},\hfill \\ \hfill & \hfill & A_{N^{-}}\approx \frac{1}{16\pi }{\left[\left(\frac{{\tilde{M}}_D}{v}-\frac{{\tilde{M}}_{LS}}{v}\right)\left(\frac{{\tilde{M}}_D}{v}+\frac{{\tilde{M}}_{LS}}{v}\right)\right]}_{ii}.\hfill \end{array}(37)$

In Figure 4, we depict the behavior of CP asymmetry with r_N, which satisfies both neutrino oscillation data and the CP asymmetry required for leptogenesis [94–95], which will be discussed in the next subsection.

FIGURE 4

FIGURE 4. Correlation plot demonstrating the dependence of CP asymmetry with the parameter r_N.

5.1 Boltzmann Equations

Boltzmann equations are invoked to solve for the lepton asymmetry. It should be reiterated that the Sakharov criteria [86] require the decay of the parent heavy fermion which ought to be out of equilibrium for generating the lepton asymmetry. In order to implement this condition, one has to confront the Hubble rate to the decay rate as follows:

$K_{N_i^{-}}=\frac{{\mathrm{\Gamma }}_{N_i^{-}}}{H\left(T=M_i^{-}\right)}.(38)$

Here, $H=\frac{1.67\sqrt{g_{\star }}{T}^2}{M_{\text{Pl}}}$ is the Hubble expansion rate, with g_⋆ = 106.75 is the number of relativistic degrees of freedom in the thermal bath and M_Pl = 1.22 × 10¹⁹ GeV is the Planck mass. Coupling strength becomes the deciding factor that guarantees inverse decay does not come into thermal equilibrium. For instance, if the strength is below 10^–7, it gives $K_{N^{-}}\sim 1$. The Boltzmann equations associated with the evolution of the number densities of right-handed fermion field and lepton, articulated in terms of yield parameter (ratio of number density to entropy density), are given by the following expression [96–99]:

$\begin{array}{ccc}\hfill & \hfill & \frac{d{Y}_{N^{-}}}{dz}=-\frac{z}{sH\left(M_{N^{-}}\right)}\left[\left(\frac{Y_{N^{-}}}{Y_{N^{-}}^{\text{eq}}}-1\right){\gamma }_D+\left({\left(\frac{Y_{N^{-}}}{Y_{N^{-}}^{\text{eq}}}\right)}^2-1\right){\gamma }_S\right],\hfill \\ \hfill & \hfill & \frac{d{Y}_{B-L}}{dz}=-\frac{z}{sH\left(M_{N^{-}}\right)}\left[2\frac{Y_{B-L}}{Y_{\ell }^{\text{eq}}}{\gamma }_{Ns}-{ϵ}_{N^{-}}\left(\frac{Y_{N^{-}}}{Y_{N^{-}}^{\text{eq}}}-1\right){\gamma }_D\right],\hfill \end{array}(39)$

where, s denotes the entropy density, $z=M_i^{-}/T$ and $Y_{\mathcal{L}}=Y_{\ell }-Y_{\bar{\ell }}$, and the equilibrium number densities are given as follows [94]:

$Y_{N^{-}}^{\text{eq}}=\frac{135g_{N^{-}}}{16{\pi }^4{g}_{\star }}{z}^2{K}_2\left(z\right),Y_{\ell }^{\text{eq}}=\frac{3}{4}\frac{45\zeta \left(3\right)g_{\ell }}{2{\pi }^4{g}_{\star }}.(40)$

Here, K_1,2 are the modified Bessel functions, g_ℓ = 2 and $g_{N^{-}}=2$ represent the degrees of freedom of lepton and RH fermions, and γ_D is the decay rate and is given as follows:

${\gamma }_D=s{Y}_{N^{-}}^{\text{eq}}{\mathrm{\Gamma }}_{N^{-}}\frac{K_1\left(z\right)}{K_2\left(z\right)}.(41)$

While γ_S represents the scattering rate of N⁻N⁻ → ζζ [99] and γ_Ns denotes the scattering rate of ΔL = 2 process. One can keep away the delicacy of the asymmetry being produced even when N⁻ is in thermal equilibrium by subtracting the contribution arising from on-shell N⁻ exchange: $(\frac{{\gamma }_D}{4})$ from the total rate γ_Ns, given as ${\gamma }_{Ns}^{\text{sub}}={\gamma }_{Ns}-\frac{{\gamma }_D}{4}$ [97]. The solution of Boltzmann (Eq. 39) is displayed in Figure 5. For large coupling strength, $Y_{N^{-}}$ (green thick curve) almost traces $Y_{N^{-}}^{\text{eq}}$ (black solid curve), and the lepton asymmetry (red dashed curve) is generated. The obtained lepton asymmetry can be converted to the baryon asymmetry through the process of sphaleron transition given as follows [96]:

$Y_B=-\left(\frac{8N_f+4N_H}{22N_f+13N_H}\right)Y_{\mathcal{L}},(42)$

where N_f represents the number of fermion generations and N_H denotes the number of Higgs doublets. The observed baryon asymmetry can be expressed in terms of baryon to photon ratio as follows [81]:

$\eta =\frac{{\eta }_b-{\eta }_{\bar{b}}}{{\eta }_{\gamma }}=6.08\times 10^{-10}.(43)$

The current bound on the baryon asymmetry can be procured from the relation Y_B = η/7.04 as Y_B ∼ 8.6 × 10^–11. Using the asymptotic value of $Y_{\mathcal{L}}$ as (8.77 × 10^–10) from Figure 5, the obtained baryon asymmetry is $Y_B=-\frac{28}{79}{Y}_{\mathcal{L}}\sim 10^{-10}$.

FIGURE 5

FIGURE 5. Evolution of the yield parameters Y_N and $Y_{\mathcal{L}}$ as a function of $z=M_{N^{-}}/T$.

5.2 A Note on Flavor Consideration

In leptogenesis, one flavor approximation is sufficient when (T > 10¹² GeV), meaning all the Yukawa interactions are out of equilibrium. But for temperatures T ≪ 10⁸ GeV, several charged lepton Yukawa couplings come into equilibrium, making flavor effects an important consideration for generating the final lepton asymmetry. For temperatures below 10⁶ GeV, all the Yukawa interactions are in equilibrium and the asymmetry is stored in the individual lepton flavor. The detailed investigation of flavor effects in type I leptogenesis can be seen in myriads of studies [100–105].

The Boltzmann equation for generating the lepton asymmetry in each flavor is given as follows [101]:

$\frac{d{Y}_{B-L_{\alpha }}^{\alpha }}{dz}=-\frac{z}{sH\left(M_1^{-}\right)}\left[{ϵ}_{N^{-}}^{\alpha }\left(\frac{Y_{N^{-}}}{Y_{N^{-}}^{eq}}-1\right){\gamma }_D-\left(\frac{{\gamma }_D^{\alpha }}{2}\right)\frac{A_{\alpha \alpha }{Y}_{\text{B}-{\mathrm{L}}_{\alpha }}^{\alpha }}{Y_{\ell }^{eq}}\right],(44)$

where, ${ϵ}_{N^{-}}^{\alpha }$ (α = e, μ, τ) represents the CP asymmetry in each lepton flavor.

${\gamma }_D^{\alpha }=s{Y}_{N^{-}}^{eq}{\mathrm{\Gamma }}_{N^{-}}^{\alpha }\frac{K_1\left(z\right)}{K_2\left(z\right)},{\gamma }_D=\sum _{\alpha }{\gamma }_D^{\alpha }.$

The matrix A is given by the following expression [102]:

$A=\left(\begin{array}{ccccc}\hfill -\frac{221}{711}\hfill & \hfill \hfill & \hfill \frac{16}{711}\hfill & \hfill \hfill & \hfill \frac{16}{711}\hfill \\ \hfill \frac{16}{711}\hfill & \hfill \hfill & \hfill -\frac{221}{711}\hfill & \hfill \hfill & \hfill \frac{16}{711}\hfill \\ \hfill \frac{16}{711}\hfill & \hfill \hfill & \hfill \frac{16}{711}\hfill & \hfill \hfill & \hfill -\frac{221}{711}\hfill \end{array}\right).$

From the benchmark considered in Table 3, we estimate the B− L yield with flavor consideration in the left panel of Figure 6. It is quite obvious to notice that the enhancement in B − L asymmetry is obtained in the case of flavor consideration (blue line) over the one flavor approximation (red line), as displayed in the right panel. This is because in one flavor approximation, the decay of the heavy fermion to a particular lepton flavor final state can get washed away by the inverse decays of any flavor unlike the flavored case [103].

TABLE 3

TABLE 3. CP asymmetries and mass splitting obtained from the allowed range of model parameters which satisfy neutrino oscillation data.

FIGURE 6

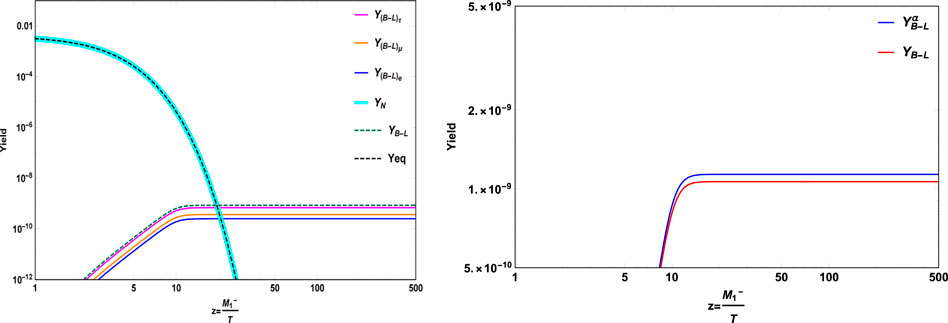
FIGURE 6. After including the flavor effects, the yield is shown in the left panel, whereas the right panel shows the enhancement in the yield due to flavor effects.

6 Summary and Conclusion

In this work, we have investigated the implications of $A_5^{\prime }$ modular symmetry on neutrino phenomenology. The important feature of modular flavor symmetry is that it reduces the complications of accommodating multiple flavons, which are usually associated with the use of discrete flavor symmetries. In the present model, we consider the SM to be extended by the $A_5^{\prime }$ modular symmetry along with a U(1)_B−L local gauge symmetry. It encompasses three right-handed and three left-handed heavy fermion superfields to explore the neutrino phenomenology within the context of the linear seesaw. In addition, it contains a pair of singlet weightons, which play a vital role in the spontaneous breaking of U(1)_B−L local symmetry and provide masses to the heavy fermions. The Yukawa couplings are considered to transform non-trivially in the modular $A_5^{\prime }$ group, which replace the role of conventional flavon fields. This, in turn, leads to a specific flavor structure for the neutrino mass matrix and helps in exploring the phenomenology of neutrino mixing. We numerically diagonalized the neutrino mass matrix to obtain the allowed regions for the model parameters, compatible with the current 3σ limit of oscillation data. Furthermore, our model predicts the CP-violating phase δ_CP to be in the range of (100°–250°) and the Jarlskog invariant to be $\mathcal{O}(10^{-3})$. The sum of active neutrino masses is found to be in the range 0.058 eV ≤ Σm_i ≤ 0.062 eV and the value of effective neutrinoless double beta decay mass parameter m_ee as (0.001–0.025) eV, which is quite below the current upper limits from KamLAND-Zen experiment, that is, $<(61-165)\mathrm{m}\mathrm{e}\mathrm{V}$. In addition, the flavor structure of heavy fermions gives rise to three sets of doubly degenerate mass eigenstates, and hence, to incorporate leptogenesis, we introduced a higher dimension mass term for the right-handed neutrinos for generating a small mass splitting. We then obtained a non-zero CP asymmetry from the lightest heavy fermion decay where the self-energy contribution is partially enhanced due to the small mass splitting between the two lightest heavy fermions. Utilizing a particular benchmark of model parameters consistent with oscillation data, we tackled coupled Boltzmann equations to get the evolution of lepton asymmetry at TeV scale that emerges to be of the order ≃ 10^–10, which is adequate to explain the present baryon asymmetry of the universe. In addition, we have shed light on the increase in asymmetry due to flavor consideration.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

RM conceptualized the research and wrote the manuscript. MK contributed to the numerical analysis and wrote the manuscript.

Funding

This study was funded by the Science and Engineering Research Board, government of India (Grant No: EMR/2017/001448), and the University of Hyderabad, IoE Project (Grant No: RC1-20-012).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

MK wishes to acknowledge DST for its financial help. RM acknowledges the support from SERB, government of India (Grant No. EMR/2017/001448), and the University of Hyderabad IoE project (Grant No. RC1-20-012).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.854595/full#supplementary-material

References

1. Bronner C. Details of T2K Oscillation Analysis. PoS NuFact2019 (2020) 037. doi:10.22323/1.369.0037

CrossRef Full Text | Google Scholar

2. Pac MY. Recent Results from RENO. PoS NuFact2017 (2018) 038. doi:10.22323/1.295.0038

CrossRef Full Text | Google Scholar

3. Yu Z. Recent Results from the Daya Bay Experiment. J Phys Conf Ser (2017) 888:012011. doi:10.1088/1742-6596/888/1/012011

CrossRef Full Text | Google Scholar

4. Abrahao T, Almazan H, dos Anjos JC, Appel S, Barriere JC, Bekman I. Double Chooz θ13 Measurement via Total Neutron Capture Detection. Nat Phys (2020) 16:558–64. doi:10.1038/s41567-020-0831-y

CrossRef Full Text | Google Scholar

5. de Salas PF, Forero DV, Gariazzo S, Martínez-Miravé P, Mena O, Ternes CA, et al. 2020 Global Reassessment of the Neutrino Oscillation Picture. JHEP (2021) 02:071. doi:10.1007/JHEP02(2021)071

CrossRef Full Text | Google Scholar

6. Esteban I, Gonzalez-Garcia MC, Maltoni M, Schwetz T, Zhou A. The Fate of Hints: Updated Global Analysis of Three-Flavor Neutrino Oscillations. J High Energ Phys (2020) 2020:178. doi:10.1007/JHEP09(2020)178

CrossRef Full Text | Google Scholar

7. Mohapatra RN, Senjanovic G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys Rev Lett (1980) 44:912. doi:10.1103/PhysRevLett.44.912

CrossRef Full Text | Google Scholar

8. Brdar V, Helmboldt AJ, Iwamoto S, Schmitz K. Type I Seesaw Mechanism as the Common Origin of Neutrino Mass, Baryon Asymmetry, and the Electroweak Scale. Phys Rev D (2019) 100:075029. doi:10.1103/PhysRevD.100.075029

CrossRef Full Text | Google Scholar

9. Branco GC, Penedo JT, Pereira PMF, Rebelo MN, Silva-Marcos JI. Type-I Seesaw with eV-Scale Neutrinos. J High Energ Phys (2020) 2020:164. doi:10.1007/JHEP07(2020)164

CrossRef Full Text | Google Scholar

10. Bilenky S. Introduction to the Physics of Massive and Mixed Neutrinos. (2010) 817. doi:10.1007/978-3-642-14043-3

CrossRef Full Text | Google Scholar

11. Gu P-H, Zhang H, Zhou S. A Minimal Type II Seesaw Model. Phys Rev D (2006) 74:076002. doi:10.1103/physrevd.74.076002

CrossRef Full Text | Google Scholar

12. Luo S, Xing Z-z. The Minimal Type-II Seesaw Model and Flavor-Dependent Leptogenesis. Int J Mod Phys A (2008) 23:3412–5. doi:10.1142/S0217751X08042225

CrossRef Full Text | Google Scholar

13. Antusch S, King SF. Type II Leptogenesis and the Neutrino Mass Scale. Phys Lett B (2004) 597:199–207. doi:10.1016/j.physletb.2004.07.009

CrossRef Full Text | Google Scholar

14. Rodejohann W. Type II Seesaw Mechanism, Deviations from Bimaximal Neutrino Mixing and Leptogenesis. Phys Rev D (2004) 70:073010. doi:10.1103/PhysRevD.70.073010

CrossRef Full Text | Google Scholar

15. Gu P-H. Double Type II Seesaw Mechanism Accompanied by Dirac Fermionic Dark Matter. Phys Rev D (2020) 101:015006. doi:10.1103/PhysRevD.101.015006

CrossRef Full Text | Google Scholar

16. McDonald J, Sahu N, Sarkar U. Type-II Seesaw at Collider, Lepton Asymmetry and Singlet Scalar Dark Matter. JCAP (2008) 04:037. doi:10.1088/1475-7516/2008/04/037

CrossRef Full Text | Google Scholar

17. Liao Y, Liu J-Y, Ning G-Z. Radiative Neutrino Mass in Type III Seesaw Model. Phys Rev D (2009) 79:073003. doi:10.1103/PhysRevD.79.073003

CrossRef Full Text | Google Scholar

18. Ma E. Pathways to Naturally Small Neutrino Masses. Phys Rev Lett (1998) 81:1171–4. doi:10.1103/physrevlett.81.1171

CrossRef Full Text | Google Scholar

19. Foot R, Lew H, He X-G, Joshi GC. See-Saw Neutrino Masses Induced by a Triplet of Leptons. Z Phys C - Particles Fields (1989) 44:441–4. doi:10.1007/BF01415558

CrossRef Full Text | Google Scholar

20. Doršner I, Pérez PF. Upper Bound on the Mass of the Type III Seesaw Triplet in an SU(5) Model. J High Energ Phys. (2007) 2007:029. doi:10.1088/1126-6708/2007/06/029

CrossRef Full Text | Google Scholar

21. Franceschini R, Hambye T, Strumia A. Type-III See-Saw at LHC. Phys Rev D (2008) 78:033002. doi:10.1103/physrevd.78.033002

CrossRef Full Text | Google Scholar

22. He X-G, Oh S. Lepton FCNC in Type III Seesaw Model. JHEP (2009) 09:027. doi:10.1088/1126-6708/2009/09/027

CrossRef Full Text | Google Scholar

23. King SF, Malinsky M. A(4) Family Symmetry and Quark-Lepton Unification. Phys Lett B (2007) 645:351–7. doi:10.1016/j.physletb.2006.12.006

CrossRef Full Text | Google Scholar

24. Kalita R, Borah D. Constraining a Type I Seesaw Model with A₄ Flavor Symmetry from Neutrino Data and Leptogenesis. Phys Rev D (2015) 92:055012. doi:10.1103/PhysRevD.92.055012

CrossRef Full Text | Google Scholar

25. Altarelli G. Lectures on Models of Neutrino Masses and Mixings. Soryushiron Kenkyu Electron (2008) 116:A29–A55. doi:10.24532/soken.116.1_A29

CrossRef Full Text | Google Scholar

26. Kimura T. The Minimal S(3) Symmetric Model. Prog Theor Phys (2005) 114:329–58. doi:10.1143/PTP.114.329

CrossRef Full Text | Google Scholar

27. Mishra S. Majorana Dark Matter and Neutrino Mass with S₃ Symmetry. Eur Phys J Plus (2020) 135:485. doi:10.1140/epjp/s13360-020-00461-1

CrossRef Full Text | Google Scholar

28. Meloni D, Morisi S, Peinado E. Fritzsch Neutrino Mass Matrix from S₃ Symmetry. J Phys G (2011) 38:015003. doi:10.1088/0954-3899/38/1/015003

CrossRef Full Text | Google Scholar

29. Pramanick S. Scotogenic S₃ Symmetric Generation of Realistic Neutrino Mixing. Phys Rev D (2019) 100:035009. doi:10.1103/PhysRevD.100.035009

CrossRef Full Text | Google Scholar

30. Krishnan R, Harrison PF, Scott WG. Simplest Neutrino Mixing from S4 Symmetry. JHEP (2013) 04:087. doi:10.1007/JHEP04(2013)087

CrossRef Full Text | Google Scholar

31. Chakraborty M, Krishnan R, Ghosal A. Predictive S₄ Flavon Model with TM₁ Mixing and Baryogenesis Through Leptogenesis. JHEP (2020) 09:025. doi:10.1007/JHEP09(2020)025

CrossRef Full Text | Google Scholar

32. Vien VV. Lepton Mass and Mixing in a Neutrino Mass Model Based on S₄ Flavor Symmetry. Int J Mod Phys A (2016) 31:1650039. doi:10.1142/S0217751X16500391

CrossRef Full Text | Google Scholar

33. Ma E, Srivastava R. Dirac or Inverse Seesaw Neutrino Masses with B − L Gauge Symmetry and S₃ Flavor Symmetry. Phys Lett B (2015) 741:217–22. doi:10.1016/j.physletb.2014.12.049

CrossRef Full Text | Google Scholar

34. Kanemura S, Matsui T, Sugiyama H. Neutrino Mass and Dark Matter from Gauged U(1)_B−L Breaking. Phys Rev D (2014) 90:013001. doi:10.1103/PhysRevD.90.013001

CrossRef Full Text | Google Scholar

35. Kanemura S, Nabeshima T, Sugiyama H. Radiative Type-I Seesaw Model with Dark Matter via U(1)_B−L Gauge Symmetry Breaking at Future Linear Colliders. Phys Rev D (2013) 87:015009. doi:10.1103/physrevd.87.015009

CrossRef Full Text | Google Scholar

36. Mishra S, Singirala S, Sahoo S. Scalar Dark Matter, Neutrino Mass, Leptogenesis and Rare B Decays in a U(1)_B−L Model. J. Phys. G (2021) 48 (7):075003. doi:10.1088/1361-6471/abd83f

CrossRef Full Text | Google Scholar

37. Singirala S, Mohanta R, Patra S, Rao S. Majorana Dark Matter in a New B − L Model. JCAP (2018) 11:026. doi:10.1088/1475-7516/2018/11/026

CrossRef Full Text | Google Scholar

38. Cai H, Nomura T, Okada H. A Neutrino Mass Model with Hidden U(1) Gauge Symmetry. Nucl Phys B (2019) 949:114802. doi:10.1016/j.nuclphysb.2019.114802

CrossRef Full Text | Google Scholar

39. Nomura T, Okada H, Sanyal P. A Radiatively Induced Inverse Seesaw Model with Hidden U(1) Gauge Symmetry (2021). arXiv.

Google Scholar

40. Dey UK, Nomura T, Okada H. Inverse Seesaw Model with Global U(1)H Symmetry. Phys Rev D (2019) 100:075013. doi:10.1103/PhysRevD.100.075013

CrossRef Full Text | Google Scholar

41. Esmaili A, Farzan Y. Explaining the ANITA Events by a L_e − L_τ Gauge Model. J Cosmol Astropart Phys (2019) 2019:017. doi:10.1088/1475-7516/2019/12/017

CrossRef Full Text | Google Scholar

42. Behera MK, Panda P, Mishra P, Singirala S, Mohanta R. Exploring Neutrino Masses and Mixing in the Seesaw Model with L_e − L_τ Gauged Symmetry. (2021). arXiv.

Google Scholar

43. Kobayashi T, Tanaka K, Tatsuishi TH. Neutrino Mixing from Finite Modular Groups. Phys Rev D (2018) 98:016004. doi:10.1103/PhysRevD.98.016004

CrossRef Full Text | Google Scholar

44. Feruglio F. Are Neutrino Masses Modular Forms? (2018) 227–66. doi:10.1142/9789813238053_0012

CrossRef Full Text | Google Scholar

45. de Adelhart Toorop R, Feruglio F, Hagedorn C. Finite Modular Groups and Lepton Mixing. Nucl Phys B (2012) 858:437–67. doi:10.1016/j.nuclphysb.2012.01.017

CrossRef Full Text | Google Scholar

46. Dudas E, Pokorski S, Savoy CA. Soft Scalar Masses in Supergravity with Horizontal U(1)x Gauge Symmetry. Phys Lett B (1996) 369:255–61. doi:10.1016/0370-2693(95)01536-1

CrossRef Full Text | Google Scholar

47. Leontaris GK, Tracas ND. Modular Weights, U(1)’s and Mass Matrices. Phys Lett B (1998) 419:206–10. doi:10.1016/S0370-2693(97)01412-3

CrossRef Full Text | Google Scholar

48. Du X, Wang F. SUSY Breaking Constraints on Modular Flavor S3 Invariant SU(5) GUT Model. J High Energ Phys (2021) 2021:221. doi:10.1007/JHEP02(2021)221

CrossRef Full Text | Google Scholar

49. Mishra S. Neutrino Mixing and Leptogenesis with Modular S₃ Symmetry in the Framework of Type III Seesaw (2020). arXiv.

Google Scholar

50. Okada H, Orikasa Y. Modular S₃ Symmetric Radiative Seesaw Model. Phys Rev D (2019) 100:115037. doi:10.1103/PhysRevD.100.115037

CrossRef Full Text | Google Scholar

51. Penedo J, Petcov S. Lepton Masses and Mixing from Modular S₄ Symmetry. Nucl Phys B (2019) 939:292–307. doi:10.1016/j.nuclphysb.2018.12.016

CrossRef Full Text | Google Scholar

52. Novichkov P, Penedo J, Petcov S, Titov A. Modular S₄ Models of Lepton Masses and Mixing. JHEP (2019) 04:005. doi:10.1007/JHEP04(2019)005

CrossRef Full Text | Google Scholar

53. Okada H, Orikasa Y. Neutrino Mass Model with a Modular S₄ Symmetry (2019). arXiv.

Google Scholar

54. Abbas M. Modular A₄ Invariance Model for Lepton Masses and Mixing. Phys Atom Nuclei (2020) 83:764–9. doi:10.1134/S1063778820050038

CrossRef Full Text | Google Scholar

55. Nagao KI, Okada H. Lepton Sector in Modular A₄ and Gauged U(1)_R Symmetry (2020). arXiv.

Google Scholar

56. Asaka T, Heo Y, Yoshida T. Lepton Flavor Model with Modular A₄ Symmetry in Large Volume Limit. Phys Lett B (2020) 811:135956. doi:10.1016/j.physletb.2020.135956

CrossRef Full Text | Google Scholar

57. Nomura T, Okada H. A Linear Seesaw Model with A₄-Modular Flavor and Local U(1)_B−L Symmetries (2020).

Google Scholar

58. Okada H, Shoji Y. A Radiative Seesaw Model with Three Higgs Doublets in Modular A₄ Symmetry. Nucl Phys B (2020) 961:115216. doi:10.1016/j.nuclphysb.2020.115216

CrossRef Full Text | Google Scholar

59. Behera MK, Singirala S, Mishra S, Mohanta R. A Modular A₄ Symmetric Scotogenic Model for Neutrino Mass and Dark Matter. J Phys G (2022) 49 (3):035002. doi:10.1088/1361-6471/ac3cc2

CrossRef Full Text | Google Scholar

60. Behera MK, Mishra S, Singirala S, Mohanta R. Implications of A₄ Modular Symmetry on Neutrino Mass, Mixing and Leptogenesis with Linear Seesaw (2020). arXiv.

Google Scholar

61. Ding G-J, King SF, Liu X-G. Modular A₄ Symmetry Models of Neutrinos and Charged Leptons. JHEP (2019) 09:074. doi:10.1007/JHEP09(2019)074

CrossRef Full Text | Google Scholar

62. Altarelli G, Feruglio F. Tri-bimaximal Neutrino Mixing, and the Modular Symmetry. Nucl Phys B (2006) 741:215–35. doi:10.1016/j.nuclphysb.2006.02.015

CrossRef Full Text | Google Scholar

63. Novichkov P, Penedo J, Petcov S, Titov A. Modular A₅ Symmetry for Flavour Model Building. JHEP (2019) 04:174. doi:10.1007/JHEP04(2019)174

CrossRef Full Text | Google Scholar

64. Kashav M, Verma S. Broken Scaling Neutrino Mass Matrix and Leptogenesis Based on A₄ Modular Invariance. JHEP (2021) 09:100. doi:10.1007/JHEP09(2021)100

CrossRef Full Text | Google Scholar

65. Yao C-Y, Liu X-G, Ding G-J. Fermion Masses and Mixing from the Double Cover and Metaplectic Cover of the A₅ Modular Group. Phys Rev D (2021) 103:095013. doi:10.1103/PhysRevD.103.095013

CrossRef Full Text | Google Scholar

66. Everett LL, Stuart AJ. The Double Cover of the Icosahedral Symmetry Group and Quark Mass Textures. Phys Lett B (2011) 698:131–9. doi:10.1016/j.physletb.2011.02.054

CrossRef Full Text | Google Scholar

67. Hashimoto K, Okada H. Lepton Flavor Model and Decaying Dark Matter in the Binary Icosahedral Group Symmetry (2011). arXiv.

Google Scholar

68. Chen C-S, Kephart TW, Yuan T-C. Binary Icosahedral Flavor Symmetry for Four Generations of Quarks and Leptons. Prog Theor Exp Phys (2013) 2013:103B01. doi:10.1093/ptep/ptt071

CrossRef Full Text | Google Scholar

69. Wang X, Yu B, Zhou S. Double Covering of the Modular A₅ Group and Lepton Flavor Mixing in the Minimal Seesaw Model. Phys Rev D (2021) 103:076005. doi:10.1103/PhysRevD.103.076005

CrossRef Full Text | Google Scholar

70. Grimus W. Theory of Neutrino Masses and Mixing. Phys Part Nucl (2011) 42:566–76. doi:10.1134/S1063779611040083

CrossRef Full Text | Google Scholar

71. Ma E. Neutrino Mass: Mechanisms and Models (2009). arXiv.

Google Scholar

72. Sruthilaya M, Mohanta R, Patra S. A₄ Realization of Linear Seesaw and Neutrino Phenomenology. Eur Phys J C (2018) 78:719. doi:10.1140/epjc/s10052-018-6181-6

CrossRef Full Text | Google Scholar

73. Borah D, Karmakar B. Linear Seesaw for Dirac Neutrinos with A4 Flavour Symmetry. Phys Lett B (2019) 789:59–70. doi:10.1016/j.physletb.2018.12.006

CrossRef Full Text | Google Scholar

74. Borah D, Karmakar B. A4 Flavour Model for Dirac Neutrinos: Type I and Inverse Seesaw. Phys Lett B (2018) 780:461–70. doi:10.1016/j.physletb.2018.03.047

CrossRef Full Text | Google Scholar

75. Dawson S. Electroweak Symmetry Breaking and Effective Field Theory. In: Theoretical Advanced Study Institute in Elementary Particle Physics: Anticipating the Next Discoveries in Particle Physics (2017). p. 1–63. doi:10.1142/9789813233348n0001

CrossRef Full Text | Google Scholar

76. Gando A, Hachiya T, Hayashi A, Hayashida S, Ikeda H, Inoue K. Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys Rev Lett (2016) 117:082503. [Addendum: Phys.Rev.Lett. 117, 109903 (2016)]. doi:10.1103/PhysRevLett.117.082503

PubMed Abstract | CrossRef Full Text | Google Scholar

77. de Salas PF, Forero DV, Ternes CA, Tórtola M, Valle JWF. Status of Neutrino Oscillations 2018: 3σ Hint for normal Mass Ordering and Improved CP Sensitivity. Phys Lett B (2018) 782:633–40. doi:10.1016/j.physletb.2018.06.019

CrossRef Full Text | Google Scholar

78. Gariazzo S, Archidiacono M, de Salas P, Mena O, Ternes C, Tórtola M. Neutrino Masses and Their Ordering: Global Data, Priors and Models. JCAP (2018) 03:011. doi:10.1088/1475-7516/2018/03/011

CrossRef Full Text | Google Scholar

79. Esteban I, Gonzalez-Garcia MC, Hernandez-Cabezudo A, Maltoni M, Schwetz T. Global Analysis of Three-Flavour Neutrino Oscillations: Synergies and Tensions in the Determination of θ23, δCP, and the Mass Ordering. J High Energ Phys (2019) 2019:106. doi:10.1007/JHEP01(2019)106

CrossRef Full Text | Google Scholar

80. Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, Banday AJ. Planck 2018 Results. V. CMB Power Spectra and Likelihoods. Astron Astrophys (2020) 641:A5. doi:10.1051/0004-6361/201936386

CrossRef Full Text | Google Scholar

81. Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, Banday AJ. Planck 2018 Results. VI. Cosmological Parameters. Astron Astrophys (2020) 641:A6. [Erratum: Astron.Astrophys. 652, C4 (2021)]. doi:10.1051/0004-6361/201833910

CrossRef Full Text | Google Scholar

82. Forero DV, Morisi S, Tórtola M, Valle JWF. Lepton Flavor Violation and Non-unitary Lepton Mixing in Low-Scale Type-I Seesaw. J High Energ Phys (2011) 2011:142. doi:10.1007/JHEP09(2011)142

CrossRef Full Text | Google Scholar

83. Antusch S, Fischer O. Non-unitarity of the Leptonic Mixing Matrix: Present Bounds and Future Sensitivities. JHEP (2014) 10:094. doi:10.1007/JHEP10(2014)094

CrossRef Full Text | Google Scholar

84. Blennow M, Coloma P, Fernandez-Martinez E, Hernandez-Garcia J, Lopez-Pavon J. Non-Unitarity, Sterile Neutrinos, and Non-Standard Neutrino Interactions. J High Energ Phys (2017) 2017:153. doi:10.1007/JHEP04(2017)153

CrossRef Full Text | Google Scholar

85. Fernandez-Martinez E, Hernandez-Garcia J, Lopez-Pavon J. Global Constraints on Heavy Neutrino Mixing. JHEP (2016) 08:033. doi:10.1007/JHEP08(2016)033

CrossRef Full Text | Google Scholar

86. Sakharov A. Violation of CP Invariance, C Asymmetry, and Baryon Asymmetry of the Universe. Sov Phys Usp (1991) 34:392–3. doi:10.1070/PU1991v034n05ABEH002497

CrossRef Full Text | Google Scholar

87. Pilaftsis A. CP Violation and Baryogenesis Due to Heavy Majorana Neutrinos. Phys Rev D (1997) 56:5431–51. doi:10.1103/PhysRevD.56.5431

CrossRef Full Text | Google Scholar

88. Bambhaniya G, Bhupal Dev PS, Goswami S, Khan S, Rodejohann W. Naturalness, Vacuum Stability, and Leptogenesis in the Minimal Seesaw Model. Phys Rev D (2017) 95:095016. doi:10.1103/PhysRevD.95.095016

CrossRef Full Text | Google Scholar

89. Pilaftsis A, Underwood TE. Resonant Leptogenesis. Nucl Phys B (2004) 692:303–45. doi:10.1016/j.nuclphysb.2004.05.029

CrossRef Full Text | Google Scholar

90. Abada A, Arcadi G, Domcke V, Drewes M, Klaric J, Lucente M. Low-Scale Leptogenesis with Three Heavy Neutrinos. J High Energ Phys (2019) 2019:164. doi:10.1007/JHEP01(2019)164

CrossRef Full Text | Google Scholar

91. Pilaftsis A, Underwood TE. Electroweak-Scale Resonant Leptogenesis. Phys Rev D (2005) 72:113001. doi:10.1103/physrevd.72.113001

CrossRef Full Text | Google Scholar

92. Asaka T, Yoshida T. Resonant Leptogenesis at TeV-Scale and Neutrinoless Double Beta Decay. JHEP (2019) 09:089. doi:10.1007/JHEP09(2019)089

CrossRef Full Text | Google Scholar

93. Gu P-H, Sarkar U. Leptogenesis with Linear, Inverse or Double Seesaw. Phys Lett B (2011) 694:226–32. doi:10.1016/j.physletb.2010.09.062

CrossRef Full Text | Google Scholar

94. Davidson S, Nardi E, Nir Y. Leptogenesis. Phys Rep (2008) 466:105–77. doi:10.1016/j.physrep.2008.06.002

CrossRef Full Text | Google Scholar

95. Buchmüller W, Di Bari P, Plümacher M. Leptogenesis for Pedestrians. Ann Phys (2005) 315:305–51. doi:10.1016/j.aop.2004.02.003

CrossRef Full Text | Google Scholar

96. Plumacher M. Baryogenesis and Lepton Number Violation. Z Phys C (1997) 74:549–59. doi:10.1007/s002880050418

CrossRef Full Text | Google Scholar

97. Giudice G, Notari A, Raidal M, Riotto A, Strumia A. Towards a Complete Theory of Thermal Leptogenesis in the SM and MSSM. Nucl Phys B (2004) 685:89–149. doi:10.1016/j.nuclphysb.2004.02.019

CrossRef Full Text | Google Scholar

98. Strumia A. Baryogenesis via Leptogenesis. In: Les Houches Summer School on Theoretical Physics: Session 84: Particle Physics Beyond the Standard Model (2006). p. 655–80. doi:10.1016/s0924-8099(06)80032-6

CrossRef Full Text | Google Scholar

99. Iso S, Okada N, Orikasa Y. Resonant Leptogenesis in the Minimal B-L Extended Standard Model at TeV. Phys Rev D (2011) 83:093011. doi:10.1103/PhysRevD.83.093011

CrossRef Full Text | Google Scholar

100. Pascoli S, Petcov ST, Riotto A. Leptogenesis and Low Energy CP Violation in Neutrino Physics. Nucl Phys B (2007) 774:1–52. doi:10.1016/j.nuclphysb.2007.02.019

CrossRef Full Text | Google Scholar

101. Antusch S, King SF, Riotto A. Flavour-Dependent Leptogenesis with Sequential Dominance. J Cosmol Astropart Phys (2006) 2006:011. doi:10.1088/1475-7516/2006/11/011

CrossRef Full Text | Google Scholar

102. Nardi E, Nir Y, Roulet E, Racker J. The Importance of Flavor in Leptogenesis. JHEP (2006) 01:164. doi:10.1088/1126-6708/2006/01/164

CrossRef Full Text | Google Scholar

103. Abada A, Davidson S, Ibarra A, Josse-Michaux F-X, Losada M, Riotto A. Flavour Matters in Leptogenesis. J High Energ Phys. (2006) 2006:010. doi:10.1088/1126-6708/2006/09/010

CrossRef Full Text | Google Scholar

104. Granelli A, Moffat K, Petcov ST. Flavoured Resonant Leptogenesis at Sub-TeV Scales. Nucl Phys B (2021) 973:115597. doi:10.1016/j.nuclphysb.2021.115597

CrossRef Full Text | Google Scholar

105. Dev PSB, Di Bari P, Garbrecht B, Lavignac S, Millington P, Teresi D. Flavor Effects in Leptogenesis. Int J Mod Phys A (2018) 33:1842001. doi:10.1142/S0217751X18420010

CrossRef Full Text | Google Scholar

106. Schultz D. Notes on Modular Forms (2015).

Google Scholar

107. Ding G-J, King SF, Liu X-G. Neutrino Mass and Mixing with A5 Modular Symmetry. Phys Rev D (2019) 100:115005. doi:10.1103/PhysRevD.100.115005

CrossRef Full Text | Google Scholar