- 1Fakultät für Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, Wuppertal, Germany
- 2Leibniz-Institute for Solid State and Materials Research (IFW-Dresden), Dresden, Germany
- 3Institute for Theoretical Physics and Würzburg-Dresden Cluster of Excellence ct.qmat, Technische Universität Dresden, Dresden, Germany
- 4Dipartimento di Fisica, University of Genoa, Genoa, Italy
- 5Consiglio Nazionale Delle Ricerche (CNR)-SPIN, Genova, Italy
- 6Department of Chemistry, Lomonosov Moscow State University, Moscow, Russia
- 7Tsung-Dao Lee Institute, Shanghai Jiao Tong University, Shanghai, China
- 8Institute of Solid State and Materials Physics and Würzburg-Dresden Cluster of Excellence ct.qmat, Technische Universität Dresden, Dresden, Germany
- 9National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Japan
Nematicity in heavily hole-doped iron pnictide superconductors remains controversial. Sizeable nematic fluctuations and even nematic orders far from magnetic instability were declared in RbFe2As2 and its sister compounds. Here, we report a systematic elastoresistance study of a series of isovalent- and electron-doped KFe2As2 crystals. We found divergent elastoresistance on cooling for all the crystals along their [110] direction. The amplitude of elastoresistivity diverges if K is substituted with larger ions or if the system is driven toward a Lifshitz transition. However, we conclude that none of them necessarily indicates an independent nematic critical point. Instead, the increased nematicity can be associated with another electronic criticality. In particular, we propose a mechanism for how elastoresistivity is enhanced at a Lifshitz transition.
1 Introduction
The “122” family, an abbreviation coined for BaFe2As2 and its substituted sister compounds, played a central role in the study of iron-based superconductors [1]. Those tetragonal ThCr2Si2-type structured compounds have the advantage that sizeable single crystals with continuous tunable doping can be prepared in a wide range, which is a crucial merit for the systematic investigation of various ordered states. Within the extended phase diagram of 122 compounds, the heavily hole-doped region, including the end-members K/Rb/CsFe2As2,, is of particular interest. The superconducting transition temperature Tc of Ba1−xKxFe2As2 peaks at optimal doping x = 0.4 and continuously decreases toward the overdoped (larger x) region. Tc remains finite in the end-member x = 1, while a change of the Fermi surface topology (Lifshitz transition) exists around x = 0.6 ∼ 0.8 [2]. Although the Tc vs. x trend seems to be smooth across the Lifshitz transition, there are quite a lot of things happening here. Vanishing electron pockets for x > 0.8 destroy the basis of the interpocket scattering induced-S± pairing symmetry which is generally believed as a feature of most iron-based superconductors. As a result, a change in the superconducting gap structure across the Lifshitz transition was observed experimentally [2–4]. Comparable pairing strength at the transition can foster a complex pairing state that breaks the time-reversal symmetry. Such an exotic state was also demonstrated to exist around the Lifshitz transition [5, 6]. Very recently, a so-called “Z2 metal state” above Tc at the Lifshitz transition has been unveiled, with an astonishing feature of spontaneous Nernst effect [7].
Electronic nematicity, a strongly correlated electronic state of electrons breaking the underlying rotational symmetry of their lattice but preserving translation symmetry, has been a wave of research in unconventional superconductors, particularly in iron-based superconductors [8, 9]. Consistent experimental efforts have identified nematicity in all the different iron-based superconductor families [10–15], accompanied by theoretical proposals of the intimate relationship between nematicity and superconducting pairing [16–19]. However, according to the previous background, we should not simply extend what is known in the under- and optimal-doped 122s to the over-doped region. Whether nematicity exists and how it develops in this region needs independent censoring.
Indeed, nematicity in the heavily hole-doped 122 turns out to be more elusive. Heavily hole-doped 122s stand out as a featured series because of their peculiar Fermi surface topology, isostructural phase transition, and possible novel pairing symmetries [20–23]. Nematically ordered states were suggested by nuclear magnetic resonance spectroscopy and scanning tunneling microscopy on CsFe2As2 and RbFe2As2, and they were found to develop in different wave vectors other than the underdoped 122s [24, 25]. Such a nematic state far away from magnetic ordering challenges the prevailing idea that nematicity is some kind of vestigial order of magnetism [26]. An elastoresistance study further claims that a tantalizing isotropic (or XY-) nematicity is realized in the crossover region from dominating [100] nematicity in RbFe2As2 to [110] nematicity at the optimal doping [27]. However, many works pointed out that elastoresistance in K/Rb/CsFe2As2 is actually contributed by the symmetric A1g channel, having little to do with the B1g or B2g channels which are related to nematicity [28, 29]. Overall, the debate is still on for this topic.
In this brief report, we will not touch upon the nature of the possible nematicity of K/Rb/CsFe2As2. Instead, we confirm phenomenologically the existence of elastoresistance (χer) in K/Rb/CsFe2As2 and find that its amplitude diverges exponentially with growing substituted ion size. Moreover, we present χer data on a series of Ba1−xKxFe2As2 crystals crossing the Lifshitz transition. We observe, unexpectedly, a clear enhancement of χer from both sides of the Lifshitz point. Although a presumptive nematic quantum critical point (QCP) might be of relevance, here we propose a rather more conventional explanation based on a small Fermi pocket effect. Our results add a novel phenomenon to the Lifshitz transition of the Ba1−xKxFe2As2 system and highlight another contributing factor of elastoresistance which has been almost ignored so far.
2 Experimental Details
Single crystals of heavily hole-doped Ba1−xKxFe2As2 were grown by the self-flux method [30–32]. The actual doping level x was determined by considering their structural parameters and Tc values. Elastoresistance measurements were performed as described in Ref. s [10–12]. Thin stripe-shaped samples were glued on the surface of piezo actuators. The strain gauge were glued on the other side of the piezo actuators to monitor the real strain generated. In most cases, the samples were mounted to let the electric current flow along the polar direction of the piezo actuators (Rxx), along which direction the strain was measured by the gauge. For one sample (x = 0.68), an additional crystal was mounted at 90° rotated according to the polar direction (Ryy). More details are described in Section 3.3. The sample resistance was collected with a combination of a high-precision current source and a nanovoltage meter. Because of the very large RRR (R300K/R0) values of the samples, special care was taken to avoid a temperature drift effect, and the electric current was set in an alternating positive/negative manner to avoid artifact.
We point out that noisy and irreproducible elastoresistance results can be acquired if DuPontⓇ 4922N silver paint is used for making contacts to the samples. On the other hand, samples contacted with EPO-TEKⓇ H20E epoxy or directly tin-soldering gave perfectly overlapping results. Given that DuPontⓇ 4922N silver paint is widely used for transport measurements and is indeed suitable for elastoresistance experiments of other materials (for example) the LaFe1−xCoxAsO series [12], we have no idea why it does not work for heavily hole-doped Ba1−xKxFe2As2 crystals. In this work, the presented data were collected by using the H20E epoxy. To avoid sample degradation, the epoxy was cured inside an Ar-glove box. A similar silver paint contact problem of K/Rb/CsFe2As2 crystals was also noticed by another group [29].
3 Results and Discussions
3.1 Elastoresistance Measurement
The elastoresistance measured along the [110] direction of the KFe2As2 single crystal is shown in Figure 1. The sample resistance closely followed the strain change of the piezo actuator when the voltage across the piezo actuator is tuned. As presented in Figure 1B, the relationship between resistance change (ΔR/R) and strain (ΔL/L) is linear. This fact ensures that our experiments were performed in the small strain limit. In such a case, the elastoresistance χer, defined as the ratio between ΔR/R and the strain, acts as a measurement of the nematic susceptibility [10]. It is worthwhile to note that χer in KFe2As2 is positive (sample under tension yields higher resistance), consistent with the previous reports [27, 28] and opposite to that of BaFe2As2 [10]. It is to be noted that sign reversal of the elastoresistance was reported to occur in the underdoped region [33].
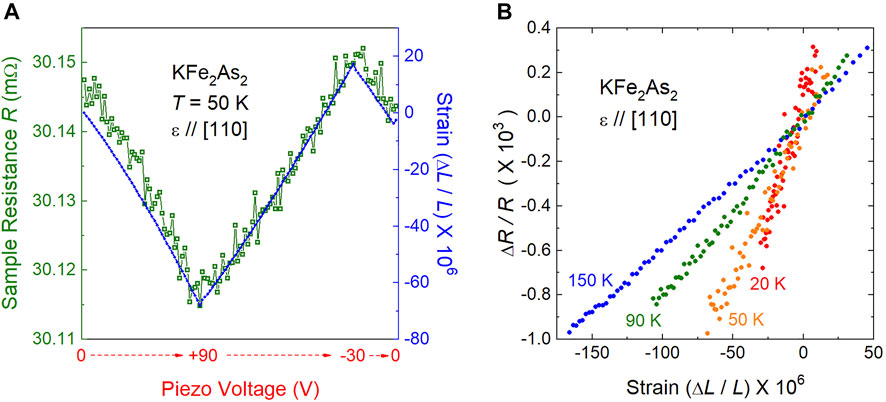
FIGURE 1. Representative example of elastoresistance under strain for KFe2As2. (A) Resistance and strain change according to the voltage applied across the piezo actuator at a fixed temperature T = 50 K. The strain was applied along the [110] direction. (B) Change of resistance ΔR/R as a function of strain ΔL/L at several temperatures.
3.2 Elastoresistance of K/Rb/CsFe2As2
We start by showing our χer(T) data measured along the [110] direction (
can record the data. A slight deviation can be discriminated at low temperature, which is typical for elastoresistance data and is understood as a disorder effect [13]. It is to be noted that the amplitude of the elastoresistance grows substantially from KFe2As2 to CsFe2As2, nearly 5-fold at 30 K. The extracted parameters from the CW fit are shown in Figures 2E,F. While the amplitude term shows a diverging trend, the Tnem of all four samples is of a very small negative value, which practically remains unchanged if experimental and fit uncertainties are taken into account, which is at odds with a possible nematic criticality in this isovalent-doping direction. The enhanced
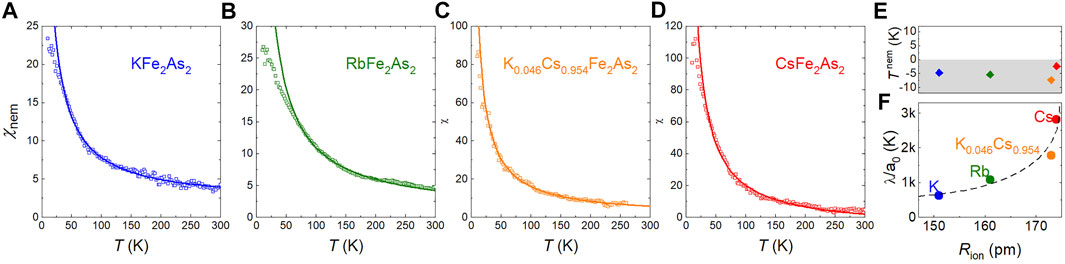
FIGURE 2. Temperature dependence of elastoresistance
3.3 Elastoresistance of Overdoped Ba1−xKxFe2As2
Next, we present a set of χer(T) data of five overdoped Ba1−xKxFe2As2 (0.55 ≤ x ≤ 1) across the Lifshitz point. The elastoresistance, measured only for the Rxx direction, as has been performed regularly in many reports [10, 12, 14], has been argued to be inconclusive for the end members (K/Rb/Cs)Fe2As2, as a result of the dominating A1g contribution, instead of a B2g (or B1g) component which is related to nematicity [28, 29]. However, such complexities are ruled out by taking Ryy into account for calculating χer(T) for one representative example x = 0.68 (Figure 3B). The χer(T) curves calculated by the two different methods match well.
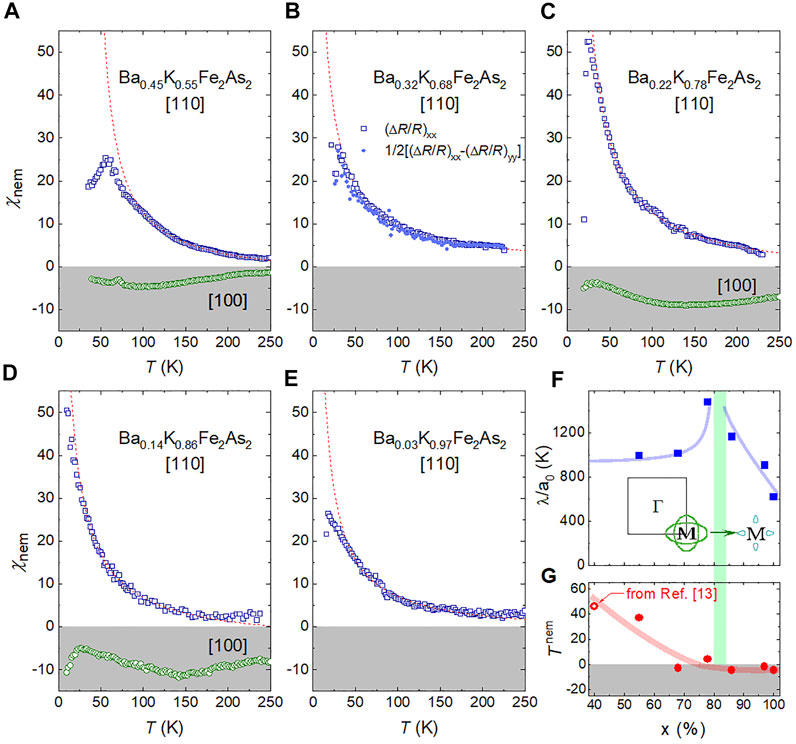
FIGURE 3. Doping evolution of the elastoresistance in overdoped Ba1−xKxFe2As2. χer measured along the [110] direction is presented in the upper panels for Ba1−xKxFe2As2 single crystals with (A) x = 0.55, (B) x = 0.68, (C) x = 0.78, (D) x = 0.86, and (E) x = 0.97. The red dashed lines are CW-fit to the data. χer was also measured along the [100] direction for three of the samples. The data are presented in the lower panels of (A) and (C,D). In panel (B), χer extracted by using both (ΔR/R)xx and (ΔR/R)yy (filled light blue circles) and (ΔR/R)xx (open blue squares) shows indistinguishable results. A doping dependence of the fit parameters is displayed in (F) λ/a0 and (G) Tnem of the [110]
After checking the potential A1g contribution to χer for a doping level close to the Lifshitz transition, we turn now to the data. As shown in Figure 3, the
On the other hand, we measured χer along the [100] direction
One remarkable feature, however, that can be safely concluded is that the amplitude of
3.4 Theory for Enhanced Elastoresistance at the Lifshitz Transition
To study the effect of a Lifshitz transition to elastoresistance, we have calculated this quantity based on a minimal model of iron-based superconductors [41] with a very small Fermi surface. The corresponding dispersion which was used is shown in Figure 4A for the normal state along a cut (π, ky). We considered the two orbital models in Ref. [41] with the same hopping matrix elements but having set the nematic interaction equal to a very small value. Thus, the nematic interaction accounts here only for the temperature dependence of the susceptibility according to the Curie–Weiss law. Moreover, we introduced a very small lattice distortion in the x direction which is coupled with the electron system. Using the first-order perturbation theory with respect to this coupling (linear response), we then calculated the elastoresistivity. We have considered two different cases of the coupling between distortion and electrons (strength g): (i) The conventional coupling with the local electron density (electron–phonon coupling), where we denote the corresponding response with χph. (ii) A direct coupling of the distortion with the hopping matrix element tx in the x direction. The corresponding response is denoted by χt.
Here, tx is the hopping matrix element in the x direction and σxx, σyy are the conductivities in the x and y directions [41]. The phonon energy ω in
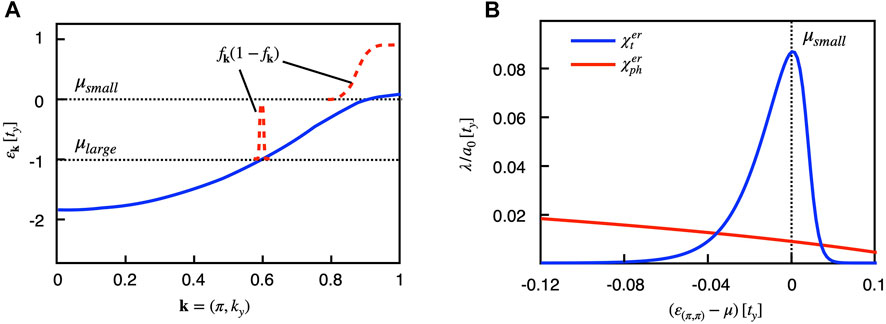
FIGURE 4. Theoretical consideration of the elastoresisitivity. (A) Dispersion of the hole-like band leading to a very small hole pocket around the point (π, π) when the chemical potential μsmall (upper dotted line) is placed near the Lifshitz point. The range of momentum vectors contributing to the elastoresisitivity arising from the Fermi function is schematically shown by the dashed lines. A much larger hole pocket is indicated by a lower value of the chemical potential μlarge (lower dotted line). (B) Calculated parts of the elastoresistivity according to Eq. 3. Around the Lifshitz point μsmall the first-order part
Figure 4B shows the two parts
The enhancement of
we find that at low temperature, if the Fermi surface is small, the momentum range k, where fk(1 − fk) is non-zero, is much larger because of the tendency of the band to rapidly change the Fermi surface topology near the Lifshitz transition (compare the red dashed lines in Figure 4A) than for a usual Fermi surface.
4 Conclusion
To summarize, we reported that a CW-like χer(T) is observed for all kinds of heavily hole-doped 122s. There is an unexpected enhancement of the elastoresistance around the Lifshitz transition. We explained it as a small Fermi pocket effect on the nematicity. We expect that our explanation of an alternative contribution to the enhanced elastoresistance other than a nematic QCP will be considered in other systems, in particular for those with small Fermi pockets.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
IM, SA, VG, KK, and C-HL prepared the samples. XH, FC, and MB performed the experiments. SS proposed the theoretical model. CH and BB supervised the study. XH, SS, FC, and CH analyzed the data and wrote the manuscript with input from all authors.
Funding
This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) through SFB 1143 (Project No. 247310070), through the Research Projects CA 1931/1-1 (FC) and SA 523/4-1 (SA). SS acknowledges funding by the Deutsche Forschungs gemeinschaft via the Emmy Noether Program ME4844/1-1 (project id 327807255). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Program (grant agreement No. 647276-MARS-ERC-2014-CoG).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank Anna Böhmer, Ian Fisher, Suguru Hosoi, Rüdiger Klingeler, Christoph Meingast, Jörg Schmalian, Christoph Wuttke, Paul Wiecki, and Liran Wang for helpful discussions. We would like to thank Christian Blum and Silvia Seiro for their technical support.
References
1. Chen X, Dai P, Feng D, Xiang T, Zhang FC. Iron-based High Transition Temperature Superconductors. Natl.Sci.Rev. (2014) 1:371–95. doi:10.1093/nsr/nwu007
2. Xu N, Richard P, Shi X, van Roekeghem A, Qian T, Razzoli E. Possible Nodal Superconducting gap and Lifshitz Transition in Heavily Hole-Doped Ba0. 1K0.9Fe2As2 Phys.Rev.B (2013) 88:220508. doi:10.1103/PhysRevB.88.220508
3. Malaeb W, Shimojima T, Ishida Y, Okazaki K, Ota Y, Ohgushi K, et al. Abrupt Change in the Energy gap of Superconducting Ba1−xKxFe2As2 Single Crystals with Hole Doping. Phys.Rev.B (2012) 86:165117. doi:10.1103/PhysRevB.86.165117
4. Hong XC, Wang AF, Zhang Z, Pan J, He LP, Luo XG, et al. Doping Evolution of the Superconducting Gap Structure in Heavily Hole-Doped Ba1−xKxFe2As2: a Heat Transport Study. Chin.Phys.Lett. (2015) 32:127403. doi:10.1088/0256-307X/32/12/127403
5. Grinenko V, Materne P, Sarkar R, Luetkens H, Kihou K, Lee CH, et al. Superconductivity with Broken Time-Reversal Symmetry in Ion-Irradiated Ba0.27K0.73Fe2As2 Single Crystals. Phys.Rev.B (2017) 95:214511. doi:10.1103/PhysRevB.95.214511
6. Grinenko V, Sarkar R, Kihou K, Lee CH, Morozov I, Aswartham S, et al. Superconductivity with Broken Time-Reversal Symmetry inside a Superconducting S-Wave State. Nat.Phys. (2020) 16:789. doi:10.1038/s41567-020-0886-9
7. Grinenko V, Weston D, Caglieris F, Wuttke C, Hess C, Gottschall T, et al. State with Spontaneously Broken Time-Reversal Symmetry above the Superconducting Phase Transition. Nat.Phys. (2021) 17:1254. doi:10.1038/s41567-021-01350-9
8. Fisher IR, Degiorgi L, Shen ZX. In-plane Electronic Anisotropy of Underdoped ’122’ Fe-Arsenide Superconductors Revealed by Measurements of Detwinned Single Crystals. Rep.Prog.Phys. (2011) 74:124506. doi:10.1088/0034-4885/74/12/124506
9. Fernandes RM, Chubukov AV, Schmalian J. What Drives Nematic Order in Iron-Based Superconductors? Nat.Phys. (2014) 10:97. doi:10.1038/nphys2877
10. Chu JH, Kuo HH, Aanlytis JG, Fisher IR. Divergent Nematic Susceptibility in an Iron Arsenide Superconductor. Science (2012) 337:710. doi:10.1126/science.1221713
11. Hosoi S, Matsuura K, Ishida K, Wang H, Mizukami Y, Watashige T, et al. Nematic Quantum Critical point without Magnetism in FeSe1−xSx Superconductors. Proc.Natl.Acad.Sci.U.S.A. (2016) 113:8139. doi:10.1073/pnas.1605806113
12. Hong XC, Caglieris F, Kappenberger R, Wurmehl S, Aswartham S, Scaravaggi F, et al. Evolution of the Nematic Susceptibility in LaFe1−xCoxAsO. Phys.Rev.Lett. (2020) 125:067001. doi:10.1103/PhysRevLett.125.067001
13. Kuo HH, Chu JH, Palmstrom JC, Kivelson SA, Fisher IR. Ubiquitous Signatures of Nematic Quantum Criticality in Optimally Doped Fe-Based Superconductors. Science (2016) 52:958. doi:10.1126/science.aab0103
14. Gu YH, Liu ZY, Xie T, Zhang WL, Gong DL, Hu D, et al. Unified Phase Diagram for Iron-Based Superconductors. Phys.Rev.Lett. (2017) 119:157001. doi:10.1103/PhysRevLett.119.157001
15. Terashima T, Matsushita Y, Yamase H, Kikugawa N, Abe H, Imai M, et al. Elastoresistance Measurements on CaKFe4As4 and KCa2Fe4As4F2 with the Fe Site of C2v Symmetry. Phys.RevB (2020) 102:054511. doi:10.1103/PhysRevB.102.054511
16. Fernandes RM, Schmalian J. Manifestations of Nematic Degrees of freedom in the Magnetic, Elastic, and Superconducting Properties of the Iron Pnictides. Supercond.Sci.Technol. (2012) 25:084005. doi:10.1088/0953-2048/25/8/084005
17. Lederer S, Schattner Y, Berg E, Kivelson SA. Enhancement of Superconductivity Near a Nematic Quantum Critical Point. Phys.Rev.Lett. (2015) 114:097001. doi:10.1103/PhysRevLett.114.097001
18. Labat D, Paul I. Pairing Instability Near a Lattice-Influenced Nematic Quantum Critical point. Phys.Rev.B (2017) 96:195146. doi:10.1103/PhysRevB.96.195146
19. Maslov DL, Chubukov AV. Fermi Liquid Near Pomeranchuk Quantum Criticality. Phys.Rev.B (2010) 81:045110. doi:10.1103/PhysRevB.81.045110
20. Tafti FF, Juneau-Fecteau A, Delage M-E, René de Cotret S, Reid J-P, Wang AF, et al. Sudden Reversal in the Pressure Dependence of Tc in the Iron-Based Superconductor KFe2As2. Nat.Phys. (2013) 9:349. doi:10.1038/nphys2617
21. Wang YQ, Lu PC, Wu JJ, Liu J, Wang XC, Zhao JY, et al. Phonon Density of States of Single-crystal SrFe2As2 across the Collapsed Phase Transition at High Pressure. Phys.Rev.B (2016) 94:014516. doi:10.1103/PhysRevB.94.014516
22. Ptok A, Sternik M, Kapcia KJ, Piekarz P. Structural, Electronic, and Dynamical Properties of the Tetragonal and Collapsed Tetragonal Phases of KFe2As2. Phys.Rev.B (2019) 99:134103. doi:10.1103/PhysRevB.99.134103
23. Ptok A, Kapcia KJ, Cichy A, Oleś AM, Piekarz P. Magnetic Lifshitz Transition and its Consequences in Multi-Band Iron-Based Superconductors. Sci.Rep. (2017) 7:41979. doi:10.1038/srep41979
24. Li J, Zhao D, Wu YP, Li SJ, Song DW, Zheng LX, et al. Reemergeing Electronic Nematicity in Heavily Hole-Doped Fe-Based Superconductors (2016). arXiv:1611.04694.
25. Liu X, Tao R, Ren MQ, Chen W, Yao Q, Wolf T, et al. Evidence of Nematic Order and Nodal Superconducting gap along [110] Direction in RbFe2As2. Nat.Commun. (2019).
26. Fernandes RM, Orth PP, Schmalian J. Intertwined Vestigial Order in Quantum Materials: Nematicity and beyond. Annu.Rev.Condens.MatterPhys. (2019) 10:133. doi:10.1146/annurev-conmatphys-031218-013200
27. Ishida K, Tsujii M, Hosoi S, Mizukami Y, Ishida S, Iyo A, et al. Novel Electronic Nematicity in Heavily Hole-Doped Iron Pnictide Superconductors. Proc.Natl.Acad.Sci.U.S.A. (2020) 117:6424. doi:10.1073/pnas.1909172117
28. Wiecki P, Haghighirad AA, Weber F, Merz M, Heid R, Böhmer AE. Dominant In-Plane Symmetric Elastoresistance in CsFe2As2. Phys.Rev.Lett. (2020) 125:187001. doi:10.1103/PhysRevLett.125.187001
29. Wiecki P, Frachet M, Haghighirad AA, Wolf T, Meingast C, Heid R, et al. Emerging Symmetric Strain Response and Weakening Nematic Fluctuations in Strongly Hole-Doped Iron-Based Superconductors. Nat.Commun. (2021) 12:4824. doi:10.1038/s41467-021-25121-5
30. Aswartham S, Abdel-Hafiez M, Bombor D, Kumar M, Wolter AUB, Hess C, et al. Hole Doping in BaFe2As2: The Case of Ba1−xNaxFe2As2 Single Crystals. Phys.Rev.B (2012) 85:224520. doi:10.1103/PhysRevB.85.224520
31. Abdel-Hafiez M, Aswartham S, Wurmehl S, Grinenko V, Hess C, Drechsler S-L, et al. Specific Heat and Upper Critical fields in KFe2As2 Single Crystals. Phys.Rev.B (2012) 85:134533. doi:10.1103/PhysRevB.85.134533
32. Moroni M, Prando G, Aswartham S, Morozov I, Bukowski Z, Büchner B, et al. Charge and Nematic Orders in AFe2As2 (A = Rb, Cs) Superconductors. Phys.Rev.B (2019) 99:235147. doi:10.1103/PhysRevB.99.235147
33. Blomberg EC, Tanatar MA, Fernandes RM, Mazin II, Shen B, Wen HH, et al. Sign-reversal of the In-Plane Resistivity Anisotropy in Hole-Doped Iron Pnictides. Nat.Commun. (2013) 4:1914. doi:10.1038/ncomms2933
34. Eilers F, Grube K, Zocco DA, Wolf T, Merz M, Schweiss P, et al. Strain-Driven Approach to Quantum Criticality in AFe2As2 with A=K, Rb, and Cs. Phys.Rev.Lett. (2016) 116:237003. doi:10.1103/PhysRevLett.116.237003
35. Zhang ZT, Dmytriieva D, Molatta S, Wosnitza J, Khim S, Gass S, et al. Increasing Stripe-type Fluctuations in AFe2As2 (A=K, Rb, Cs) Superconductors Probed by 75As NMR Spectroscopy. Phys.Rev.B (2018) 97:115110. doi:10.1103/PhysRevB.97.115110
36. Hardy F, Böhmer AE, Aoki D, Burger P, Wolf T, Schweiss P, et al. Evidence of Strong Correlations and Coherence-Incoherence Crossover in the Iron Pnictide Superconductor KFe2As2. Phys.Rev.Lett. (2013) 111:027002. doi:10.1103/PhysRevLett.111.027002
37. Onari S, Kontani H. Origin of Diverse Nematic Orders in Fe-Based Superconductors: 45° Rotated Nematicity in AFe2As2 (A=Cs,Rb). Phys.Rev.B (2019) 100:020507. doi:10.1103/PhysRevB.100.020507
38. Borisov V, Fernandes RM, Valentí R. Evolution from B2g Nematics to B1g Nematics in Heavily Hole-Doped Iron-Based Superconductors. Phys.Rev.Lett. (2019) 123:146402. doi:10.1103/PhysRevLett.123.146402
39. Böhmer AE, Burger P, Hardy F, Wolf T, Schweiss P, Fromknecht R, et al. Nematic Susceptibility of Hole-Doped and Electron-Doped BaFe2As2 Iron-Based Superconductors from Shear Modulus Measurements. Phys.Rev.Lett. (2014) 112:047001. doi:10.1103/PhysRevLett.112.047001
40. Fernandes RM, VanBebber LH, Bhattacharya S, Chandra P, Keppens V, Mandrus D, et al. Effects of Nematic Fluctuations on the Elastic Properties of Iron Arsenide Superconductors. Phys.Rev.Lett. (2010) 105:157003. doi:10.1103/PhysRevLett.105.157003
41. Wuttke C, Caglieris F, Sykora S, Steckel F, Hong X, Ran S, et al. Ubiquitous Enhancement of Nematic Fluctuations across the Phase Diagram of Iron Based Superconductors Probed by the Nernst Effect. arXiv:2202.00485.
42. Sykora S, Hübsch A, Becker KW. Dominant Particle-Hole Contributions to the Phonon Dynamics in the Spinless One-Dimensional Holstein Model. Europhys.Lett. (2006) 76:644. doi:10.1209/epl/i2006-10327-x
Keywords: elastoresistance, nematicity, Lifshitz transition, iron-based superconductors, quantum criticality
Citation: Hong X, Sykora S, Caglieris F, Behnami M, Morozov I, Aswartham S, Grinenko V, Kihou K, Lee C-, Büchner B and Hess C (2022) Elastoresistivity of Heavily Hole-Doped 122 Iron Pnictide Superconductors. Front. Phys. 10:853717. doi: 10.3389/fphy.2022.853717
Received: 12 January 2022; Accepted: 21 March 2022;
Published: 20 April 2022.
Edited by:
Anna Böhmer, Ruhr-University Bochum, GermanyReviewed by:
Konrad Jerzy Kapcia, Adam Mickiewicz University, PolandMarcin Matusiak, Institute of Physics (PAN), Poland
Copyright © 2022 Hong, Sykora, Caglieris, Behnami, Morozov, Aswartham, Grinenko, Kihou, Lee, Büchner and Hess. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaochen Hong, eGhvbmdAdW5pLXd1cHBlcnRhbC5kZQ==; Steffen Sykora, c3RlZmZlbi5zeWtvcmFAdHUtZHJlc2Rlbi5kZQ==; Federico Caglieris, ZmVkZXJpY28uY2FnbGllcmlzQHNwaW4uY25yLml0; Christian Hess, Yy5oZXNzQHVuaS13dXBwZXJ0YWwuZGU=
 Xiaochen Hong
Xiaochen Hong Steffen Sykora
Steffen Sykora Federico Caglieris
Federico Caglieris Mahdi Behnami
Mahdi Behnami Igor Morozov2,6
Igor Morozov2,6 Saicharan Aswartham
Saicharan Aswartham Chul-Ho Lee
Chul-Ho Lee Bernd Büchner
Bernd Büchner Christian Hess
Christian Hess