Ultra Fast Switching of DFLC Based Dynamic Metasurfaces

Dielectric metasurfaces give rise to very interesting optical and photonic properties such as Huygens lens, absolute transmission and absorption, directional scattering, etc. Liquid crystal based dynamic metasurfaces are being increasingly explored due to their excellent tunability of polarization, phase and amplitude modulations, enabling applications in spatial light modulators (SLM’s), holography, AR and VR and flat optics. We investigate the effect of geometry of dielectric microstructures on electromagnetic response and switching of Dual frequency liquid crystal based metasurfaces in the mid-IR range of frequencies. Scattering response, near-field profiles and far-field radiation show significant dependence on the alignment and geometry of the microstructures. At selected frequencies switching between different polarization directions and variable phase modulations are observed simultaneously. Response times calculated theoretically show switching times of the order of milliseconds paving way for ultrafast multifunctional active metasurfaces.

1 Introduction

Metasurfaces are artificial materials comprising of periodic or non-periodic arrangement of constituent sub-wavelength structures, called “meta-atoms” and give rise to effective properties which do not exist in nature. Due to their remarkable electromagnetic responses to the incident light, they find applications as negative refractive index materials [1,2], Huygen’s lens [3], perfect absorbers [4], sub-diffraction imaging [5], etc [1,6,7]. As an alternative to the metallic constituents, high refractive index dielectric metasurfaces such as Si, TiO₂ are being increasingly investigated in the recent years as they give rise to lesser dissipative losses mainly in visible and infrared frequencies [8]. Dielectric metasurfaces have the distinct advantage over plasmonics as they give rise to Mie-type resonances and excite both magnetic as well as electric resonant modes with comparable intensities. Further, very recently dielectric metasurfaces are observed to exhibit novel resonant states such as anapoles [9–11], quasi-BIC states [12,13], etc, with giant localisation of fields [14]. Dielectric metasurfaces find many applications in energy harvesting, wavefront shaping, multifunctional metadevices, etc. [15].

While most of these applications have been achieved using static optical responses, tunability of electromagnetic responses give rise to dynamic or reconfigurable metasurfaces and have significant advantages in dynamic beam steering, spatial light modulators (SLM’s), combined phase and amplitude modulations, polarization controllers, etc [16–19]. Tunability of metasurfaces are typically achieved via electric, optical, mechanical or thermal tuning parameters [17]. One of such versatile materials which can be tuned via optical, thermal or electric means are liquid crystals.

Liquid crystals (LC’s) are highly birefringent anisotropic materials which respond very well to external parameters such as temperature and applied voltage. In nematic phase, LC’s are liquid-like and possess only orientational order. These are the most studied phases among metasurfaces based on liquid crystals and is the focus of our present work. Metasurfaces infiltrated with liquid crystal (LC) give rise to highly tunable resonant spectra [20–25] and are being investigated recently in non-display applications such as phase manipulation [26], polarization converters [27,28], perfect absorbers [22] and flat optics [29]. The reorientations of LC due to presence of micro or nano structures has potential applications in AR/VR technologies, SLM’s, holography, etc.

Microstructures induce suppression of orientational order in the surrounding nematic medium and give rise to deformations in the director field, director being the average orientation of a statistically large number of molecules. These deformations are particularly significant for structures in nano and micro length scales as they are comparable with the size of LC molecules. These molecules undergo reorientations in the presence of aligning fields, surface anchoring and temperature and hence give rise to inhomogeneous director fields. There has been very few studies of the effect of these geometry-induced inhomogeneous director fields on the optical response of the dielectric metasurfaces [30] and forms the subject of interest in the current work.

It is known that LC devices suffer from large decay times due to the slow relaxation of the LC molecules when the external field is switched off. The response times in LC’s can be reduced to some extent by using thinner films, pre-tilt angles at the substrates, weak anchoring and high driving potentials. In the current work, we investigate the effect of geometry-induced LC alignment on the switching times as well as the phase and polarization modulations. Further to drive the switching response in both rise τ_rise and decay τ_decay times we employ dual-frequency liquid crystals (DFLC’s) [31–34]. DFLC’s are a mixture of frequency-dependent highly anisotropic materials operated at two frequencies and exhibit positive dielectric anisotropy below a certain threshold frequency (f_L) and negative dielectric anisotropy above the threshold (f_H).‘Due to this the LC molecules orient parallel to the aligning field at lower frequencies and normal to the external aligning field at higher frequency above a threshold frequency. The driving voltages to induce switching transition between these two frequencies are typically in the range 1–10 V and depend on the rotational viscosity γ and Frank’s elastic constants K₁₁, K₂₂ and K₃₃ of the liquid crystal medium. In DFLC the response times can be reduced by application of high voltages to drive the reorientations at both the frequencies f_L and f_H giving rise to ultrafast response times while exhibiting tunable optical responses [35–37]. However application of higher voltages is not feasible for the flat optics based devices and one would ideally like to operate LC devices with smaller voltages. In the present work we investigate the geometry-induced switching in DFLC-based metasurfaces and the effect of LC orientations surrounding the dielectric microstructures on the electromagnetic spectra opening up further possibilities in designing LC based fast light manipulation such as beam steering and phase modulations.

2 Results and Discussion

2.1 Director Configurations and Layer-Wise Angles

According to Landau-de Gennes formalism, the free energy of a liquid crystal medium can be written as a function of order parameter tensor, Q_ij in terms of temperature dependent bulk energy (f_T), Frank’s elastic energy (f_E) and surface-induced energy written in Rapini-Papoular form (f_S) as shown below [38].

$\begin{array}{ccc}\hfill f& =\hfill & \frac{1}{2}a\left(T-T_{NI}^{*}\right)Q_{ij}{Q}_{ji}+\frac{1}{3}B{Q}_{ij}{Q}_{jk}{Q}_{ki}+\frac{1}{4}C{\left(Q_{ij}{Q}_{ji}\right)}^2\hfill \\ \hfill +& \hfill & \frac{1}{2}W{\left(Q_{ij}-{Q°}_{ij}\right)}^2+\frac{1}{2}K\frac{\partial Q_{ij}}{\partial x_k}\frac{\partial Q_{ij}}{\partial x_k}\hfill \end{array}(1)$

where a, B and C are temperature dependent constants, $T_{NI}^{*}$ is the nematic-isotropic transition temperature, W is the surface-induced anchoring strength, K represents the Frank’s elastic constant under single elastic constant approximation (K₁₁ = K₂₂ = K₃₃) and Q_ij° is the surface-preferred order. The total free energy f is minimized using Euler-Langrangian formalism and explicit finite difference scheme is employed to arrive at the stable configurations.

Periodic arrays of cylinders (radius a = 1 μm, thickness t = 300 nm) and cylindrical rings (inner radius r = 600 nm, outer radius R = 1.0 μm and thickness t = 300 nm) made of dielectric material TiO₂ with periodicity p = 2.5 μμm are placed on the bottom glass substrate coated with ITO as shown in the Figure 1. DFLC mixture is introduced in the cell of thickness d = 2.5 μm. The unit cells of cylindrical and cylindrical ring periodic arrays with lattice constant 3 μm are shown in Figures 2A,B,D,E. At low frequency f_L (“ON” state), the equilibrium director configurations exhibit vertically aligned configuration as shown in Figures 2A,B) for cylinders and cylindrical rings, respectively. Microstructures induce distortion in the surrounding director field leading to suppression of the orientational order, S and hence variation in the optical properties as shown in Figures 2A–E). In the case of complex geometry like cylindrical rings, the director field is also influenced within the inner ring as shown in the Figures 2B,E). Inset in Figure 2E) shows that the director orients parallel to the walls of the inner rings to reduce the elastic energy. The layer-wise director angles-polar angle θ and azimuth angle ϕ averaged in each layer along the Z-direction, $\bar{n}(x,z)$ are plotted as a function of layer number in the Figures 2C,F). In the “ON” state, LC molecules undergo maximum distortion due to contradicting aligning conditions- 1) by the external voltage induced vertical alignment and 2) the surface anchoring at the glass and microstructures. The plot of $\bar{n}(x,z)$ as a function of the layer number, Figure 2C), shows decrease in value of θ from the surface induced planar alignment at bottom substrate till the height of microstructure (indicated by the shaded region) after which θ = 0. Azimuthal angle ϕ increases from 0° (X-direction) at the bottom substrate to 90° (Y-direction) at the top substrate giving rise to twisted structure. From Figure 2C) it is clear that distortion in θ and ϕ is more pronounced and complex near the cylindrical rings. In the case of planar alignment (“OFF” state) θ and ϕ undergo maximum distortion near the microstructures (shaded region) from X-axis (θ = 90°, ϕ = 0°) at bottom and top substrates due to the geometry-preferred alignment as shown in the Figure 2F). The distortion is higher for cylindrical rings compared to the cylinders as in the case of “ON” state.

FIGURE 1

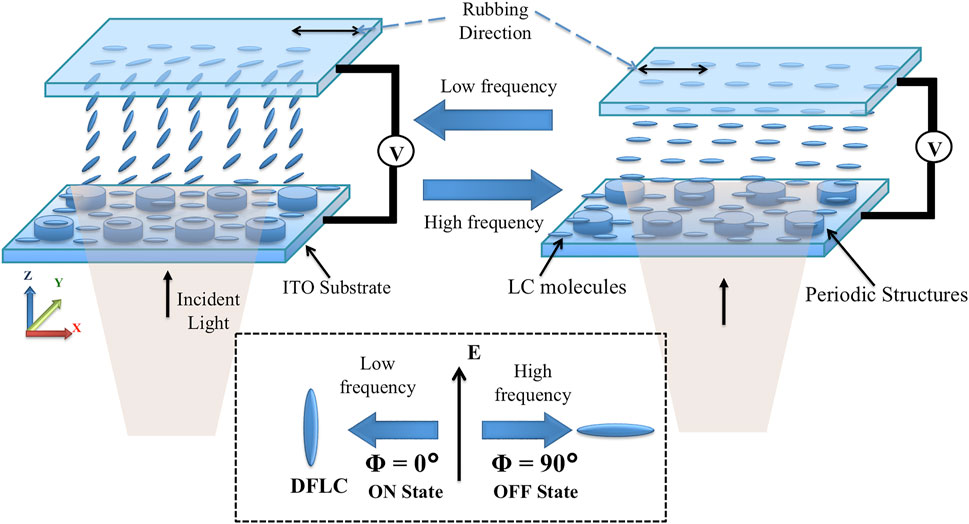
FIGURE 1. Schematic of metasurface device with DFLC operated between low frequency, f_L (left) and high frequency, f_H (right).

FIGURE 2

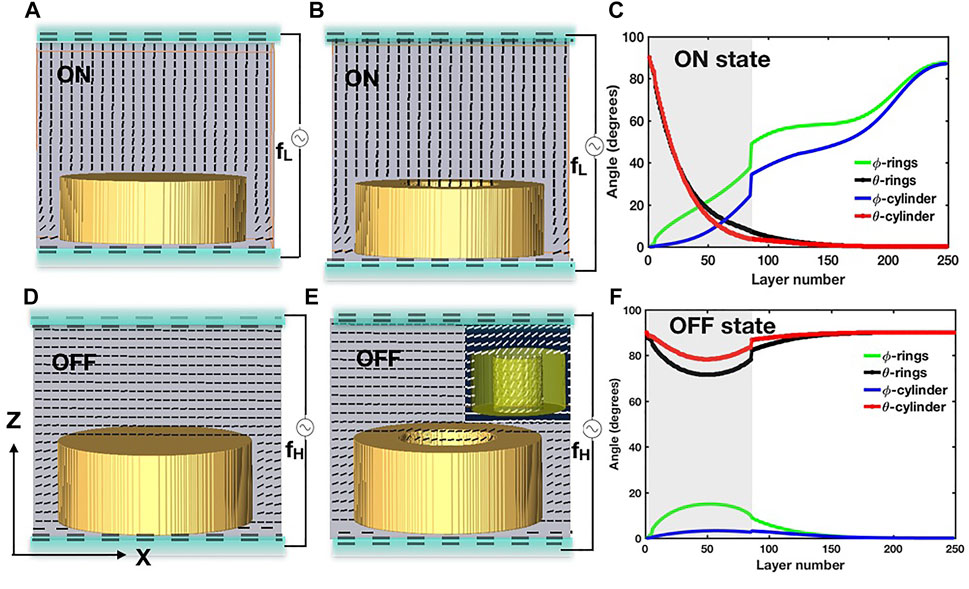
FIGURE 2. Director configurations of DFLC cell embedded with cylinders and cylindrical rings: (A,B). Vertically aligned configuration (ON state) of DFLC cell with cylinders and cylindrical rings at f_L = 10 KHz (V = 0). (C) Layer wise averaged director angles $\bar{n}(x,z)$ as a function of layer number for ON state. (D,E) Planar aligned configuration (OFF state) of DFLC cell with cylinders and cylindrical rings at f_H = 100 KHz (V = 0). (F) Layer wise averaged director angles $\bar{n}(x,z)$ as a function of layer number for OFF state. Shaded areas in (C,F) represent the layers occupied by microstructures.

Once the equilibrium director configurations are obtained from free-energy minimization method, we investigate the light-matter interactions of the microstructure embedded LC cell using commercial software CST Microwave studio. The electric and magnetic fields are discretized on a cubic lattice and full wave electromagnetic calculations using FEM method are performed to investigate the electromagnetic response of the microstructures present in the LC cell. Layer-wise averaged director orientations of the LC, $\bar{n}(x,y)$ are considered for the electromagnetic calculations along the thickness of the cell.

2.2 Electromagnetic Response of Microstructure Arrays

Dual frequency liquid crystal (DFLC) is filled within the glass substrates coated with ITO. A periodic array of TiO₂ structures is placed on the glass substrate as shown in the Figure 2A. The glass substrates induce planar alignment with weak anchoring strength, W = 10⁻⁵N/m² along X-axis and the TiO₂ structures induce random anchoring of strength W = 10⁻⁴N/m². Standard DFLC mixture CPEP (3F)-5NCS [31] which exhibits a birefringence, Δn = 0.224 at 25°C and γ/K₁₁ = 23.5/msμm² in the mid-wavelength infrared frequencies is considered for the simulations. DFLC cell embedded with microstructures is operated between f_L = 10 KHz with dielectric anisotropy, Δϵ = 20 and f_H = 100 KHz with Δϵ = −2.0. Liquid crystal molecules orient parallel to the applied field (Z-direction) at low frequency, f_L and rotate perpendicular to the field (X-axis) at high frequency, f_H as shown in the Figure 1. We investigate the electromagnetic response of LC device operated with weak anchoring on both substrates and at the microstructures.

Incorporating the director orientations averaged in each layer along Z-axis $\bar{n}(x,z)$ as shown in the Figures 2C,F), we perform electromagnetic simulations based on FEM method using commercial software CST. Linearly polarized light is incident along Z-axis and incident polarization direction is along Y-axis. Scattering parameters (S-parameters) are defined by S₁₁ = R and $S_{12}=T{e}^{i{k}_{0}d}$, where “d” is the thickness of the metasurface, k₀ is the wavenumber of the incident light in vacuum, R and T are the reflection and transmission coefficients.

Scattering response of cylinders for both the layer-wise averaged director angles $(\bar{n}(x,z))$ and average director of the cell $\bar{n}$ (does not consider the geometry-induced director distortions) are shown in Figures 3A,B). Here $\bar{n}=z$ for “ON” state and $\bar{n}=x$ for “OFF” state. In the sub-wavelength regime exhibited above 30 THz for both the alignments, vertically aligned state (“ON” state) gives rise to multiple narrow bands as shown in Figure 3A, while the planar alignment (“OFF” state) exhibits a single broad transmission band in the range 30, −,44 THz. The transmission band in the “OFF” state is observed to have fano resonance type of characteristic with prominent peaks at selected frequencies. As observed from the Figures 3A,B), the shift in the response frequencies and the characteristics of the spectra for $\bar{n}$ and $\bar{n}(x,z)$ differ more significantly for the “ON” state compared to the “OFF” state. Scattered light further undergoes a gradual phase variation within the transmission band (29, −,37.5 THz for “ON” state and 30.5–38 THz for “OFF” state) as shown in the Figures 3C,D) and hence acts as tunable phase retarder within this broad frequency range. However abrupt shifts in frequencies are observed for “ON” state as shown in the Figure 3C). Interestingly variation in phase of the scattered light between $\bar{n}$ and $\bar{n}(x,z)$ is more prominent in the “OFF” state. While the $\bar{n}$ case shows a variation of 2π in transmission band in both “ON” and “OFF” states, a more realistic consideration of $\bar{n}(x,z)$ gives rise to lesser phase variation. At some of these resonance frequencies, complex hybrid and higher order modes are observed as can be seen from the near-field electric field profiles along XY- and YZ-planes in the Figure 3E). Significantly, “ON” state exhibits radiating hybrid modes at the frequencies indicated while “OFF” state gives rise to toroidal resonances (31 and 46.76 THz) and higher order modes (43.7 THz) with near-zero transmission in the propagation direction as shown in the Figure 3E).

FIGURE 3

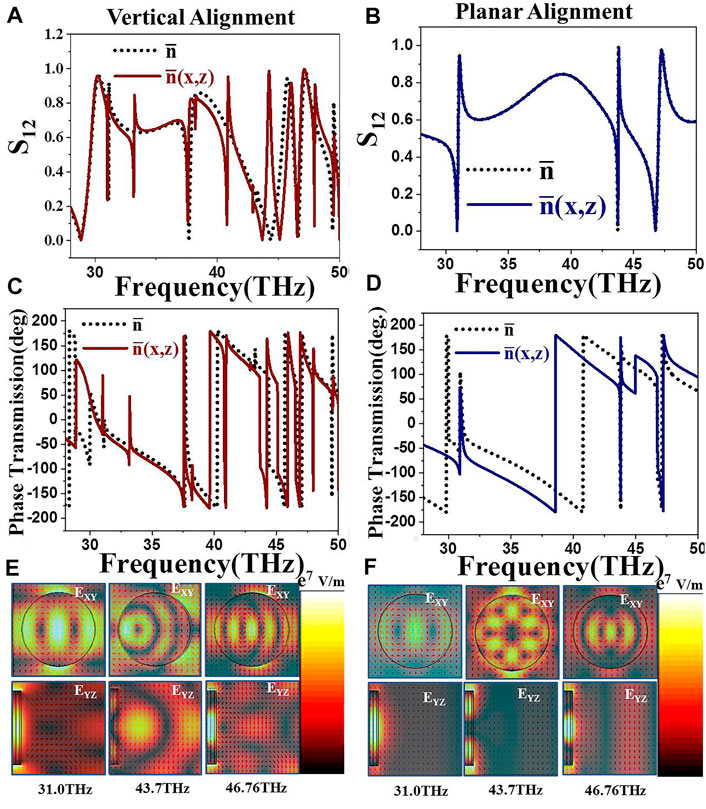
FIGURE 3. Electromagnetic response of DFLC with cylindrical microstructures: (A,B). S₁₂ parameters for vertical (ON state, f_L) and planar aligned configuration (OFF state, f_H) of DFLC cell respectively. (C,D). Phase of transmitted light at f_L and f_H respectively. (E,F). Near-field profiles of electric field components in XY plane (top) and scattered electric field profiles in YZ plane (bottom) at f_L and f_H respectively.

Scattering parameters for cylindrical rings show similar behavior of multiple sharp responses in “ON” state and broad asymmetric transmission bands characteristic of fano resonance in “OFF” state as shown in the Figures 4A,B. As observed in the case of cylinders, the characteristics of the responses are quite similar for $\bar{n}$ and $\bar{n}(x,z)$ in the case of planar alignment. Phase variation in the case of “ON” state is sharper for cylindrical rings (at a single frequency) compared to cylinders while the “OFF” state exhibits a smooth variation of 2π for both $\bar{n}$ and $\bar{n}(x,z)$ cases in the frequency range 50, −, 56 THz as observed in Figures 4C,D. Figure 4D further shows that cylindrical rings in planar alignment exhibit efficient phase retardation compared to the solid cylinders. Near-field profiles of the cylindrical rings show presence of hybrid modes in both “ON” and “OFF” states. It is observed that the ring structures do not support non-radiating toroidal modes unlike cylinders. A detailed multipole analysis will help in further identifying the dominant resonant modes in all the above cases.

FIGURE 4

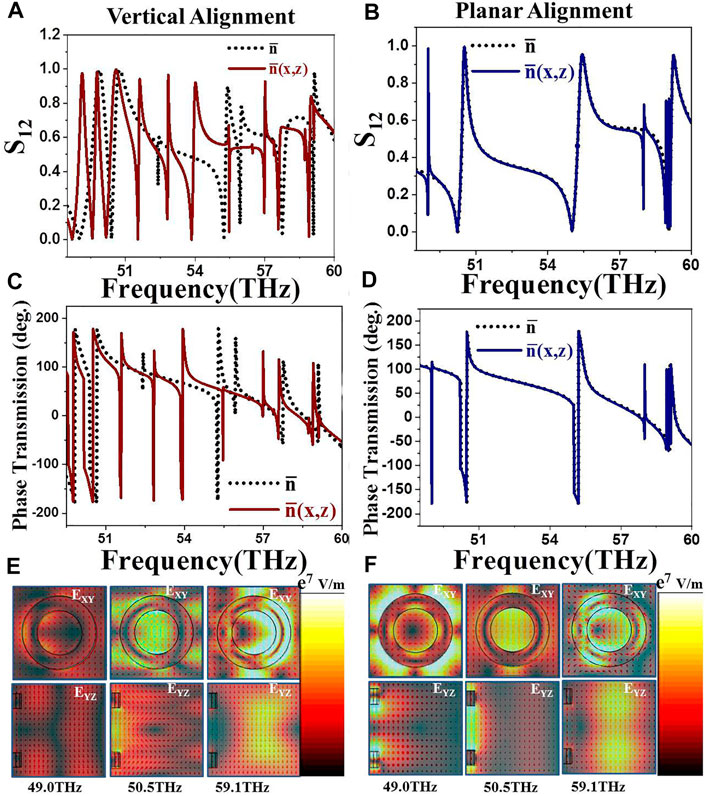
FIGURE 4. Electromagnetic response of DFLC with cylindrical ring microstructures: (A,B). S₁₂ parameters for vertical (ON state, f_L) and planar aligned configuration (OFF state, f_H) of DFLC cell, respectively. (C,D). Phase of transmitted light at f_L and f_H respectively. (E,F). Near-field profiles of electric field components in XY plane (top) and scattered electric field profiles in YZ plane (bottom) at f_L and f_H respectively.

Far-field radiation (XZ plane) and angular distribution of electric and magnetic far-field profiles (XY plane) are plotted for cylinders and cylindrical rings incorporating $\bar{n}(x,z)$ at selected resonance frequencies in the Figures 5, 6, respectively. In the case of cylinders (Figure 5), far-field radiation at 31.1 THz in “ON” and, “OFF” states are complimentary to each other. This is due to the excitation of electric dipole mode in the “OFF” state in addition to magnetic dipole (observed in both the states) along Y-direction resulting in destructive interference along forward propagation. Hence the metasurface mediated DFLC cell acts as a polarization converter and switches from forward to backward propagation of scattered light at this frequency. Further one can also observe transition from magnetic dipole modes to hybrid modes (magnetic quadrupole + magnetic dipole in this case) and vice versa as observed at 43.7 and 46.76 THz, respectively.

FIGURE 5

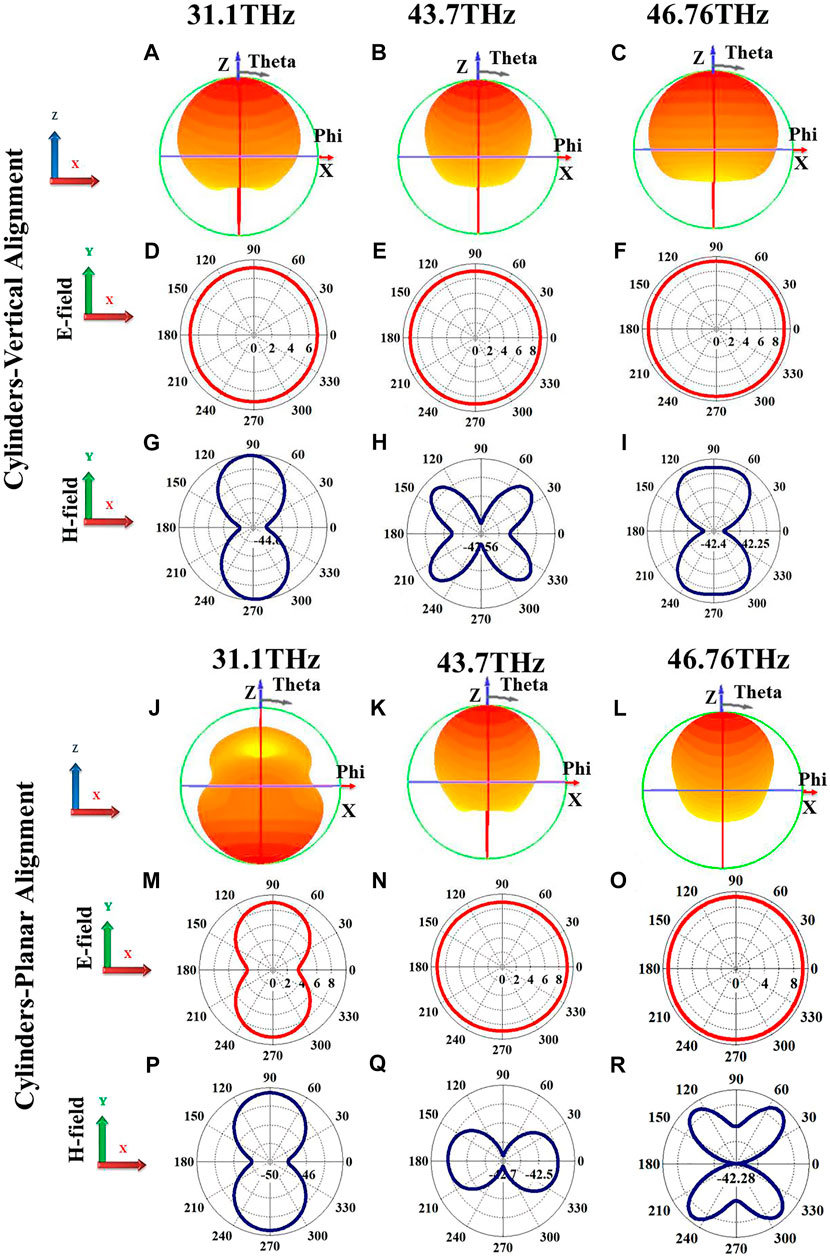
FIGURE 5. Far-field radiation and angular distribution of electric and magnetic fields for cylinders: (A–C). Far-field radiation in XZ plane at f_L, (D–F). corresponding angular distribution of electric field profiles (polarization) in XY plane and (G–I). Corresponding angular distribution of magnetic field profiles in XY plane; (J–L). Far-field radiation in XZ plane at f_H, (M–O). corresponding angular distribution of electric field profiles (polarization) in XY plane and (P–R). Corresponding angular distribution of magnetic field profiles in XY plane, respectively.

FIGURE 6

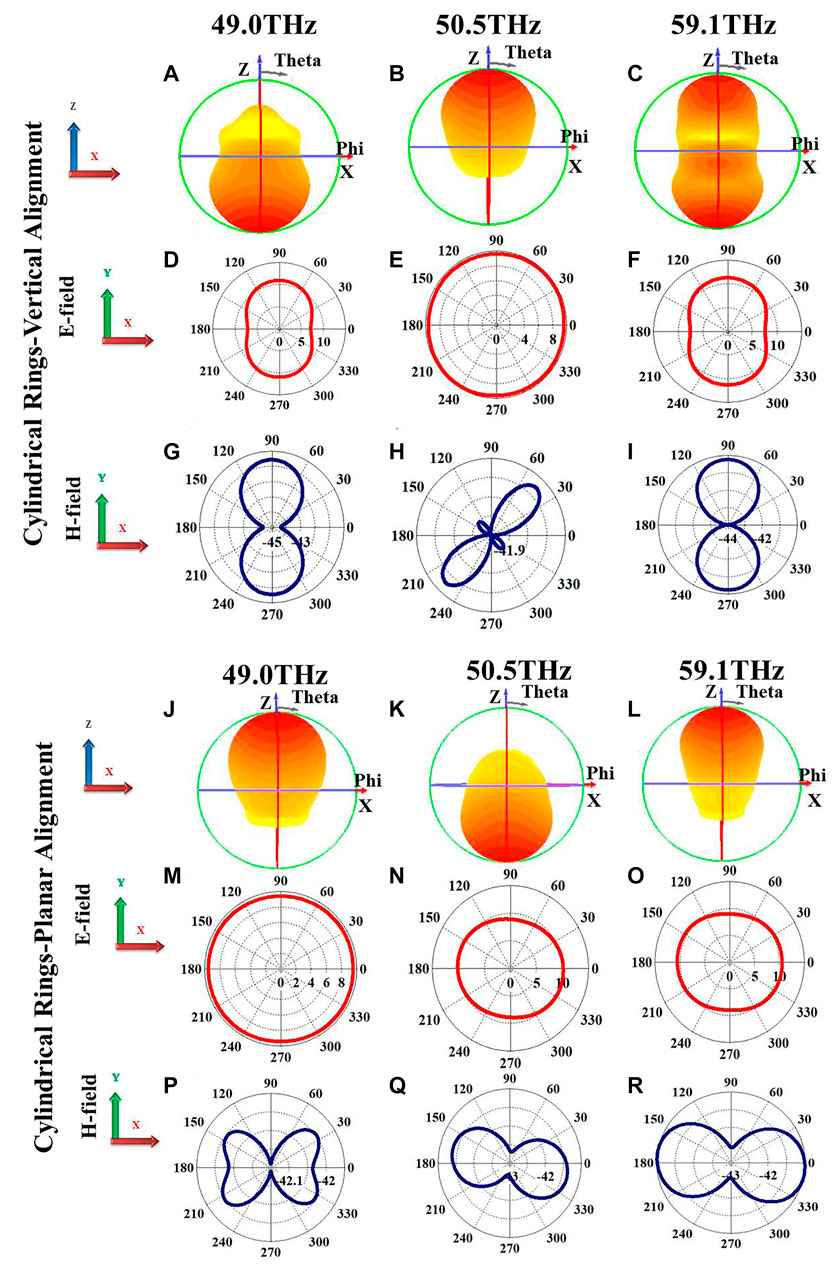
FIGURE 6. Far-field radiation and angular distribution of electric and magnetic fields for cylindrical rings: (A–C). Far-field radiation in XZ plane at f_L, (D–F). corresponding angular distribution of electric field profiles (polarization) in XY plane and (G–I). Corresponding angular distribution of magnetic field profiles in XY plane; (J–L). Far-field radiation in XZ plane at f_H, (M–O). corresponding angular distribution of electric field profiles (polarization) in XY plane and (P–R). Corresponding angular distribution of magnetic field profiles in XY plane, respectively.

Cylindrical rings exhibit more complex response spectra and near-field profiles compared to the cylinders which is also reflected in the far-field behaviour. For example, at one of the resonant frequencies, 49 THz the far-field radiation switches between backward to forward propagation at “ON” and “OFF” states. “ON” state exhibits both electric and magnetic dipoles while “OFF” state exhibits magnetic dipole + quadrupole hybrid mode. At 50.5 THz (Figure 6), “ON” state shows onset of magnetic quadrupole mode along with magneitc dipole at an angle 45° while the “OFF” state shows both electric dipole and magnetic dipole oriented at an angle 15° from X-axis giving rise to backward propagation. At 59.1 THz, the electric and magnetic dipole modes orient normal to each other for “ON” and “OFF” states hence the incident polarization vector shifts from Y-axis to X-axis as we switch the DFLC cell from vertical alignment (“ON”) to planar alignment (“OFF”) and vice versa. Far-field radiation at this frequency shows scattering along both forward and backward directions for “ON” state while the “OFF” state exhibits strong forward propagation. Cylindrical rings hence give rise to rich near- and far-field responses compared to cylinders in both “OFF” and “ON” states with versatile functionality as dynamic metasurfaces.

2.3 Optical Response Times

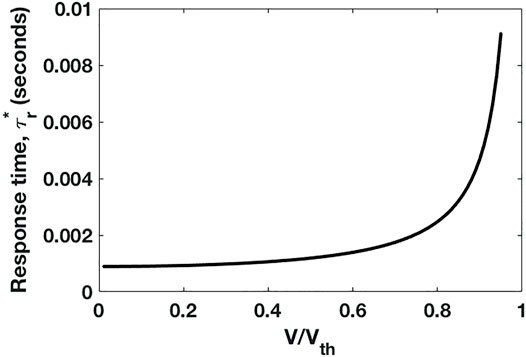
The response times of a typical liquid crystal under the influence of an aligning field can be estimated as a function of the applied voltage. The rise time of the LC molecules to orient along the aligning direction is given by [33,39]:

${\tau }_r=\frac{\gamma d^2}{K{\pi }^2\left({\frac{V}{V_{th}}}^2-1\right)},(2)$

where V_th is the threshold voltage, V is the voltage applied to drive the LC molecules, γ is the rotational viscosity of the LC material, d is the thickness of the cell and K is the elastic constant (bend constant K₃₃ in the present case of VA cell). The relaxation time or the decay time, τ_d or τ₀ of the LC molecules depends on the LC reorientations and hence on the elastic properties of the medium as

${\tau }_d=\frac{\gamma d^2}{K{\pi }^2}(3)$

In DFLC since both the “ON” and “OFF” states are driven by high voltages the response times can be written in terms of the decay time,τ₀ and voltage amplitudes as

$\begin{array}{ccc}\hfill {\tau }_{ON}=\frac{{\tau }_0}{{\left(\frac{V_l}{V_{t{h}_l}}\right)}^2-1}& \hfill & \hfill \end{array}(4)$

$\begin{array}{ccc}\hfill {\tau }_{OFF}=\frac{{\tau }_0}{{\left(\frac{V_h}{V_{t{h}_h}}\right)}^2-1}& \hfill & \hfill \end{array}(5)$

where V_h and V_l are the corresponding driving voltages at f_H and f_L, respectively. $V_{t{h}_h}$ and $V_{t{h}_l}$ are the corresponding threshold voltages. Using the above equations, one can calculate the response times of the microstructure embedded DFLC cell as a function of V/V_th as shown in the Figure 7. It is observed from the figure that the rise time τ_ON ≤ 1 ms for V < 0.5V_th. As the applied voltage approaches V_th, ${\tau }_r^{*}$ diverges. The decay time calculated from the above equation show a similar behaviour as a function of V/V_th. Threshold voltage V_th can be approximated theoretically from the elastic properties of LC as given below:

$V_{th}=\pi \sqrt{\frac{K_{33}}{{ϵ}_0|\mathrm{\Delta }ϵ|}}(6)$

FIGURE 7

FIGURE 7. Response time ${\tau }_r^{*}$ as a function of V/V_th.

From the above equation, threshold voltage for reorientations of LC molecules is given by V_th = 0.9 V at f_L (ON) and V_th = 8 V at f_H (OFF), respectively. From this we show that the response times of the LC orientations to the external driving voltages falls in the range of 1 ms and hence switching between electromagnetic responses at “ON” and “OFF” states as discussed in the earlier sections can be performed in ultrafast times. This opens up possibilities to design multifunctional devices that can be operated in ultrafast times, with some of the functionalities demonstrated in the present work with cylindrical and cylindrical ring microstructures in IR frequencies.

3 Conclusion

In the present work cylindrical and cylindrical ring microstructures are introduced in DFLC to investigate the effect of geometry and hence the near-field director orientations on the electromagnetic response and switching times. Simulations based on free-energy minimizaiton are performed to obtain inhomogeneous director field in the presence of microstructures at both vertical and planar aligned configurations. Layer-wise averaged angles along the thickness of the cell show that cylindrical rings give rise to complex variation of the director angles compared to the simple cylindrical geometry. We show that such a complex variation in director profile at micro scales has a significant effect on the electromagnetic responses due to comparable length scales with the LC molecular orientations. In the present work we incorporate layer-wise averaged director angles into the FEM based electromagnetic simulations to include the director orientations near the microstructures. We observe significant effect on the scattering responses such as shift in the response spectra and phase modulations which is more visible in the vertical alignment (“OFF” state) for both the geometries. From far-field radiation and electric and magnetic field profiles (both near-field and far-field) it is observed that cylindrical rings are more versatile multifunctional devices exhibiting amplitude, polarization and phase modulations over a range a frequencies. Cylindrical rings exhibited simultaneous polarization and phase modulations in the frequency range 50, −, 60 THz and both the geometries exhibited complex switching between different resonant modes. A more realistic electromagnetic response can be obtained by including full director profile using FDTD based simulations. Switching times between “ON” and “OFF” states are estimated theoretically as a function of the driving voltages of DFLC. These calculations predicted rise and delay response times for both cylinders and cylindrical rings to be approximately $\le 1$ms giving rise to ultrafast multifunctional dynamic metasurfaces. We hope that our work opens up possibilities in designing DFLC based dynamic metasurfaces with applications in polarization modulators, variable phase modulators, SLM’s, etc.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JD has conceived the idea and led the work. PS and JD performed the simulations. JD contributed in analysing the results and writing the manuscript.

Funding

JD and PS acknowledge financial support by the DST-SERB EMR (CR) Grant EMR/2017/004045 by Government of India.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a past co-authorship with one of the authors JD.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Smith DR, Pendry JB, Wiltshire MCK. Metamaterials and Negative Refractive index. Science (2004) 305:788–92. doi:10.1126/science.1096796

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Shalaev VM. Optical Negative-index Metamaterials. Nat Photon (2007) 1:41–8. doi:10.1038/nphoton.2006.49

CrossRef Full Text | Google Scholar

3. Yu N, Capasso F. Flat Optics with Designer Metasurfaces. Nat Mater (2014) 13:139–50. doi:10.1038/nmat3839

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Hajian H, Ghobadi A, Butun B, Ozbay E. Active Metamaterial Nearly Perfect Light Absorbers: a Review [Invited]. J Opt Soc Am B (2019) 36:F131–F143. doi:10.1364/josab.36.00f131

CrossRef Full Text | Google Scholar

5. Liu Y, Zhang X. Metamaterials: a New Frontier of Science and Technology. Chem Soc Rev (2011) 40:2494–507. doi:10.1039/c0cs00184h

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zheludev NI, Kivshar YS. From Metamaterials to Metadevices. Nat Mater (2012) 11:917–24. doi:10.1038/nmat3431

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Hsiao H-H, Chu CH, Tsai DP. Fundamentals and Applications of Metasurfaces. Small Methods (2017) 1:1600064. doi:10.1002/smtd.201600064

CrossRef Full Text | Google Scholar

8. Kivshar Y. All-dielectric Meta-Optics and Non-linear Nanophotonics. Natl Sci Rev (2018) 5:144–58. doi:10.1093/nsr/nwy017

CrossRef Full Text | Google Scholar

9. Miroshnichenko AE, Evlyukhin AB, Yu YF, Bakker RM, Chipouline A, Kuznetsov AI, et al. Nonradiating Anapole Modes in Dielectric Nanoparticles. Nat Commun (2015) 6:8069. doi:10.1038/ncomms9069

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Baryshnikova KV, Smirnova DA, Luk'yanchuk BS, Kivshar YS. Optical Anapoles: Concepts and Applications. Adv Opt Mater. (2019) 7:1801350. doi:10.1002/adom.201801350

CrossRef Full Text | Google Scholar

11. Amanaganti SR, Ravnik M, Dontabhaktuni J. Collective Photonic Response of High Refractive index Dielectric Metasurfaces. Sci Rep (2020) 10:15599–8. doi:10.1038/s41598-020-72675-3

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Koshelev K, Favraud G, Bogdanov A, Kivshar Y, Fratalocchi A. Nonradiating Photonics with Resonant Dielectric Nanostructures. Nanophotonics (2019) 8:725–45. doi:10.1515/nanoph-2019-0024

CrossRef Full Text | Google Scholar

13. Koshelev K, Bogdanov A, Kivshar Y. Meta-optics and Bound States in the Continuum. Sci Bull (2019) 64:836–42. doi:10.1016/j.scib.2018.12.003

CrossRef Full Text | Google Scholar

14. Jahani S, Jacob Z. All-dielectric Metamaterials. Nat Nanotech (2016) 11:23–36. doi:10.1038/nnano.2015.304

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Liu W, Li Z, Cheng H, Chen S. Dielectric Resonance-Based Optical Metasurfaces: From Fundamentals to Applications. iScience (2020) 23:101868. doi:10.1016/j.isci.2020.101868

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zahra S, Ma L, Wang W, Li J, Chen D, Liu Y, et al. Electromagnetic Metasurfaces and Reconfigurable Metasurfaces: A Review. Front Phys (2021) 8:615. doi:10.3389/fphy.2020.593411

CrossRef Full Text | Google Scholar

17. He Q, Sun S, Zhou L. Tunable/Reconfigurable Metasurfaces: Physics and Applications. Research (2019) 2019:1–16. doi:10.34133/2019/1849272

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Nemati A, Wang Q, Hong M, Teng J. Tunable and Reconfigurable Metasurfaces and Metadevices. Opto-Electronic Adv (2018) 1:180009. doi:10.29026/oea.2018.180009

CrossRef Full Text | Google Scholar

19. Shalaginov MY, Campbell SD, An S, Zhang Y, Ríos C, Whiting EB, et al. Design for Quality: Reconfigurable Flat Optics Based on Active Metasurfaces. Nanophotonics (2020) 9:3505–34. doi:10.1515/nanoph-2020-0033

CrossRef Full Text | Google Scholar

20. Xu J, Yang R, Fan Y, Fu Q, Zhang F. A Review of Tunable Electromagnetic Metamaterials with Anisotropic Liquid Crystals. Front Phys (2021) 9:67. doi:10.3389/fphy.2021.633104

CrossRef Full Text | Google Scholar

21. Atorf B, Mühlenbernd H, Muldarisnur M, Zentgraf T, Kitzerow H. Electro-optic Tuning of Split Ring Resonators Embedded in a Liquid crystal. Opt Lett (2014) 39:1129–32. doi:10.1364/ol.39.001129

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Kowerdziej R, Jaroszewicz L. Tunable Dual-Band Liquid crystal Based Near-Infrared Perfect Metamaterial Absorber with High-Loss Metal. Liquid Crystals (2019) 46:1568–73. doi:10.1080/02678292.2019.1618935

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zografopoulos DC, Beccherelli R. Tunable Terahertz Fishnet Metamaterials Based on Thin Nematic Liquid crystal Layers for Fast Switching. Sci Rep (2015) 5:13137–11. doi:10.1038/srep13137

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kowerdziej R, Olifierczuk M, Parka J. Thermally Induced Tunability of a Terahertz Metamaterial by Using a Specially Designed Nematic Liquid crystal Mixture. Opt Express (2018) 26:2443–52. doi:10.1364/oe.26.002443

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Komar A, Paniagua-Domínguez R, Miroshnichenko A, Yu YF, Kivshar YS, Kuznetsov AI, et al. Dynamic Beam Switching by Liquid crystal Tunable Dielectric Metasurfaces. ACS Photon (2018) 5:1742–8. doi:10.1021/acsphotonics.7b01343

CrossRef Full Text | Google Scholar

26. Li S-Q, Xu X, Maruthiyodan Veetil R, Valuckas V, Paniagua-Domínguez R, Kuznetsov AI. Phase-only Transmissive Spatial Light Modulator Based on Tunable Dielectric Metasurface. Science (2019) 364:1087–90. doi:10.1126/science.aaw6747

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Yu P, Li J, Liu N. Electrically Tunable Optical Metasurfaces for Dynamic Polarization Conversion. Nano Lett (2021) 21:6690–5. doi:10.1021/acs.nanolett.1c02318

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hu Y, Ou X, Zeng T, Lai J, Zhang J, Li X, et al. Electrically Tunable Multifunctional Polarization-dependent Metasurfaces Integrated with Liquid Crystals in the Visible Region. Nano Lett (2021) 21:4554. doi:10.1021/acs.nanolett.1c00104

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Lininger A, Zhu AY, Park J-S, Palermo G, Chatterjee S, Boyd J, et al. Optical Properties of Metasurfaces Infiltrated with Liquid Crystals. Proc Natl Acad Sci USA (2020) 117:20390–6. doi:10.1073/pnas.2006336117

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Dolan JA, Cai H, Delalande L, Li X, Martinson ABF, de Pablo JJ, et al. Broadband Liquid crystal Tunable Metasurfaces in the Visible: Liquid crystal Inhomogeneities across the Metasurface Parameter Space. ACS Photon (2021) 8:567–75. doi:10.1021/acsphotonics.0c01599

CrossRef Full Text | Google Scholar

31. Xianyu H, Wu S-T, Lin C-L. Dual Frequency Liquid Crystals: a Review. Liquid Crystals (2009) 36:717–26. doi:10.1080/02678290902755598

CrossRef Full Text | Google Scholar

32. Melnyk O, Garbovskiy Y, Bueno-Baques D, Glushchenko A. Electro-optical Switching of Dual-Frequency Nematic Liquid Crystals: Regimes of Thin and Thick Cells. Crystals (2019) 9:314. doi:10.3390/cryst9060314

CrossRef Full Text | Google Scholar

33. Hsieh CT, Huang CY, Lin CH. In-plane Switching Dual-Frequency Liquid crystal Cell. Opt Express (2007) 15:11685. doi:10.1364/OE.15.011685

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Xianyu H, Zhao Y, Gauza S, Liang X, Wu ST. High Performance Dual Frequency Liquid crystal Compounds. Liquid Crystals (2008) 35:1129–35. doi:10.1080/02678290802389589

CrossRef Full Text | Google Scholar

35. Shang X, Cuypers D, Chen F, Xu C, Li Q, Wu C, et al. Dual-frequency Liquid crystal-polymer Grating for Fast Response Optical Beam Steering. Smart Mater Struct (2019) 28:105036. doi:10.1088/1361-665x/ab3b2e

CrossRef Full Text | Google Scholar

36. Li B-X, Xiao R-L, Paladugu S, Shiyanovskii SV, Lavrentovich OD. Dye-doped Dual-Frequency Nematic Cells as Fast-Switching Polarization-independent Shutters. Opt Express (2019) 27:3861–6. doi:10.1364/OE.27.003861

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Mangelinckx G, Beeckman J, Chojnowska O, Shin J, Kim JDK, Dąbrowski R, et al. Fast Polarisation-Insensitive Optical Shutter Supported by Backflow in Dichroic Dye-Doped Dual-Frequency Liquid crystal. Liquid Crystals (2014) 41:1553–8. doi:10.1080/02678292.2014.934307

CrossRef Full Text | Google Scholar

38. Ravnik M. Colloidal Structures in Confined Nematic Liquid Crystals. Liquid Crystals Today (2011) 20:77–84. doi:10.1080/1358314x.2011.589162

CrossRef Full Text | Google Scholar

39. Wang H, Wu TX, Zhu X, Wu S-T. Correlations between Liquid crystal Director Reorientation and Optical Response Time of a Homeotropic Cell. J Appl Phys (2004) 95:5502–8. doi:10.1063/1.1707210

CrossRef Full Text | Google Scholar