- 1Graduate School of Science and Engineering, Yamagata University, Yamagata, Japan
- 2Faculty of Science, Yamagata University, Yamagata, Japan
Collective cell migration (CCM) is a universal process that is responsible for various biological phenomena in living organisms. Therefore, unraveling the mechanism of CCM is critical for understanding the principles underlying such processes and for their application in biomaterials and biomedical science. Among these phenomena, unjamming/jamming transitions are particularly intriguing as they are controlled by three factors: cell motility, cell density, and cell–cell adhesion. However, there is no experimental system to independently demonstrate and control these effects. In this study, we added 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) to a nitrobenzene droplet containing KI and I2 to develop a prototype system that shows self-propelled motion in an aqueous trimethylstearylammonium chloride (TSAC) solution. First, we explored the relationship between the motility of the droplet and experimental parameters, namely, the concentrations of TSAC, I2, and DMPC and droplet size. The droplet showed directional motion driven by Marangoni convection owing to a solubilization promoted by the formation of mixed micelles filled with oil between DMPC and TSA+; notably, droplet motility could be controlled by each parameter. Furthermore, the interfacial tension (γ) at the oil–water interface, measured using the pendant drop method, indicated that each parameter contributed to changes in γ. Based on our experimental results, we inferred that the dynamics of the insertion of TSA+ in the aqueous phase into the self-assembled DMPC membrane covering the nitrobenzene droplet, as well as the solubilization, are important factors that trigger Marangoni convection and lead to controlled droplet motility. Furthermore, the developed droplets remained stable in a confluent state, wherein they were in contact with each other and exhibited various polygonal shapes depending on their size and density because they were protected by a robust self-assembled DMPC membrane layer. The results indicated that the density and the morphology of the droplets are controllable in this system, and that they indirectly altered droplet adhesion. Thus, we procured a prototype system that could be controlled independently using three parameters to elucidate phase transition for CCM. This system can be biomodified through the combination of phospholipids with any biomolecule and can enable a more precise evaluation of the CCM exhibited by living cells.
Introduction
Cell migration plays a central role in the development and maintenance of the morphologies and functions of cells in multicellular organisms, wherein cells move toward and between tissue compartments either individually or collectively [1, 2]. In particular, it has been reported that collective cell migration (CCM) [3, 4] is involved in embryo development [5], wound healing [6], and cancer infiltration and metastasis [7, 8]. Therefore, elucidating the mechanism underlying CCM would not only lead to a better understanding of the basis of life science phenomena but also to a wide range of applications, including the development of drugs that utilize this mechanism. However, it is difficult to study the underlying mechanism of CCM because interactions during this process are usually complex. Previous studies of single cell migration have provided fundamental insights into cell migration. According to these studies, the motion of a cell is induced by the following factors: the generation of differences in intracellular tensions for directed movement (cell polarization) through competitive actin polymerization and formation of actomyosin networks [9–11], and the development of chemical and/or physical factor gradients [12–14]. Therefore, the mechanism of single cell migration has been clarified sufficiently. On the other hand, cell–cell interactions, namely, adhesion and interaction through fields, should be considered in CCM, in addition to the above-mentioned factors [3–5, 15–17]. With the recent developments in measurement technologies [15, 18, 19], biological studies have become much more effective for understanding single cell migration. However, it is difficult to investigate the complex interactions between cells using only biological studies for understanding CCM. To solve this issue, experimental studies and mathematical modeling are crucial, because by using this approach each interaction can be investigated independently.
Unjamming/jamming transitions are one of the most important phenomena in CCM under confluent conditions for cells such as epithelial cells [8, 20–22]. The unjamming phase is a fluid phase in which cell motility is guaranteed and individual cells can alter their positions, while the jamming phase is a solid phase in which cell motility is lost and the positions of individual cells are locked. Some previous biological experiments and numerical simulations have suggested that mutual relationships among single cell motility, cell density in an ensemble of cells, and cell–cell adhesion dominate the unjamming/jamming transitions [23–25]. However, there is a lack of methods that can control these factors to demonstrate their effects independently; therefore, the involvement of these factors in CCM remains speculative. However, as such transitions are also observed in spherical colloidal particle systems [26, 27], these systems have been used as models [28]. However, movements in such systems are randomly governed by Brownian motion, unlike the directional motion of cells, and these systems do not exhibit the polygonal adhesion morphology of cells [5, 29] owing to the robustness of their spherical morphology. Therefore, the development of soft matter showing spontaneous self-propelled motion, namely, active soft matter, is important for developing a practical experimental system to demonstrate the unjamming/jamming transitions in CCM.
This study focused on a self-propelled oil droplet of nitrobenzene containing I− and I2 in a water phase containing trimethylstearylammonium chloride (TSAC) as the surfactant, as an attractive experimental system that satisfies the above-mentioned requirements [30–33]. This oil droplet shows self-propelled motion driven by Marangoni convection on a glass substrate due to symmetry breaking of interfacial tension owing to the competition between the adsorption of TSA+ onto the glass surface and its uptake by the droplet. Although other self-propelled oil droplets have been reported, some of them move at the air–water interface [34]. In contrast, self-propelled oil droplets developed in this study can move on a glass substrate in a manner similar to the two-dimensional movement of cells on the extracellular matrix. This is because the density of the oil phase is higher than that of the water phase. Furthermore, as the related mechanism has been studied well both experimentally and numerically [33], it is feasible to consider and control the motility of the droplet. Therefore, this system could potentially serve as a practical model for CCM. However, when droplets meet each other in the same batch, they immediately coalesce; that is, they are very unstable in collectivity. This is because these droplets are not covered with a robust self-assembled membrane, as in the case of cells enclosed by a phospholipid bilayer membrane.
To improve the stability of oil droplets in contact, previously, silicon oil droplets in which the water–oil interface contained a monolayer of a self-assembled lipid and surfactant, were prepared by emulsifying the phospholipid-containing oil phase with a surfactant-containing aqueous solution [35, 36]. In these studies, two types of lipids, egg l-α-phosphatidylcholine lipids and polyethylene glycol (PEG) biotinylated lipids, were used, and then streptavidin was added to the system with emulsion droplets. This resulted in biotin–streptavidin–biotin complex bridging, leading to crosslinking of the droplets with streptavidin [37, 38], resulting in the development of adhesive properties similar to the molecular crosslinking mechanism of cells. Therefore, combining a self-propelled droplet with a phospholipid could not only improve the stability of droplets in collectivity but also result in the creation of a practical model with cell-like adhesiveness upon further biomodification (for example, using the above biotin–streptavidin interaction).
The objective of this study was to develop a prototype experimental system using a self-propelled active soft matter with independently controllable motility, density, and adhesiveness as a model of CCM; this system is suitable for further biomodification in the future. For developing this system, we included 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) as a phospholipid in the aforementioned self-propelling nitrobenzene oil droplet. This study is based on two considerations: 1) exploring the factors controlling droplet motility and probing the mechanism of self-propelled motion in the presence of the phospholipid, and 2) investigating whether droplets maintain their form in collectivity without coalescing and whether their density is controllable. For consideration 1), we explored the dependence of the motion speed (V) of the droplet on the experimental parameters (the concentrations of TSAC, I2, and DMPC, and droplet diameter). We found that the motion was driven by Marangoni convection induced in a droplet by a solubilization of the oil droplet promoted by a formation of mixed DMPC/TSA+ micelle filled with oil and symmetry breaking of interfacial tension (γ) owing to their departure from the oil–water interface. Furthermore, V could be controlled by changing these parameters, and the results are discussed from the perspective of changes in the γ of a droplet. In addition, for consideration 2), the droplet stability was evaluated. The droplets existed stably in collectivity without coalescing for ∼200 s, and they showed unique morphology depending on confluency and density.
Materials and Methods
Reagents
TSAC (>98.0%) and iodine (I2, >98.0%) were purchased from Tokyo Chemical Industry (Tokyo, Japan). Nitrobenzene and potassium iodide (KI) were purchased from FUJIFILM Wako Pure Chemical Industries (Osaka, Japan). DMPC (25 mg/ml in chloroform) was purchased from Sigma-Aldrich Co. LLC (St. Louis, MS, United States). All reagents were used without further purification.
Exploration of the Self-Propelled Motion of a Nitrobenzene Droplet in an Aqueous TSAC Solution
The lipid DMPC (5 mg) was first dried by blowing Ar gas and then dried overnight under vacuum. Subsequently, 1.0 ml of nitrobenzene saturated with KI was added to the dried lipid. The resulting mixture was sonicated for 60 min and then heated at 50°C for 3 h to dissolve the lipid in nitrobenzene. Subsequently, I2 was dissolved in this mixture to a predetermined concentration (0–10 mM) through sonication, followed by heating at 50°C. The concentration of DMPC was changed by mixing DMPC-containing nitrobenzene with DMPC-free nitrobenzene, both containing the same [I2]. Before the self-propelled motion experiment, 10 ml of an aqueous TSAC solution of known concentration (0–1.0 mM) was prepared in a glass Petri dish (Ø = 47 mm). Subsequently, a known volume of DMPC-containing nitrobenzene was pipetted (2.0–15.0 μl per droplet) into the TSAC solution. This motion experiment was carried out at room temperature (26 ± 0.4°C). The droplet motion was monitored and the corresponding images were captured using a digital camera.
Measurement of Interfacial Tension (γ) at the Oil–Water Interface Using the Pendant Drop Method
The interfacial tension, γ, at the oil–water interface (oil droplet surface) was measured using the pendant drop method [39]. The aqueous TSAC solution was poured into a glass cell (10 × 10 mm) used for spectrophotometry. Subsequently, a microsyringe (710N PST-5, Hamilton Company, Reno, NV, United States) was used to form a droplet at the tip of the needle in the aqueous solution such that it did not touch wall surface. The droplets were formed at the largest size that allowed them to adhere to the needle tip. The value of γ was calculated using the following equations:
Here, ∆ρ, g, and D are the density difference between the water and oil phases, gravitational acceleration, and maximum diameter of a droplet, respectively. H is a correction factor calculated using the characteristic coefficients (Bn) in Eq. 2; these coefficients are determined depending on the ratio (S) between D and the diameter at a distance D from the bottom of a droplet (d) [39]. The value of ∆ρ was calculated from the average of three measurements of the weight per milliliter of the aqueous TSAC solution and DMPC-containing nitrobenzene, respectively, at room temperature (26 ± 0.4°C). γ was evaluated under the same condition.
Demonstration of Droplet Stability in Collectivity
First, we prepared DMPC-containing nitrobenzene saturated with 5.0 mg/ml DMPC and 10 mM I2 as the oil phase, according to the above-described procedures. Then, 5.0 ml of water was added to a glass Petri dish (Ø = 21 mm). Subsequently, a silicon ring (Ø = 10 mm) was submerged in the water. Subsequently, the oil phase, nitrobenzene mixture was pipetted into the silicon ring several times with 5.0 or 10.0 μl per droplet. After multiple droplets were pipetted, pipetting was stopped, and the coalescence behavior of the droplets was observed.
Statistical Analysis
All error bars of experimental results in this study were obtained from replicates of at least three times, which were calculated using p-values < 0.05.
Results and Discussion
Self-Propelled Motion of a Single Droplet
Figure 1A shows the self-propelled locomotion under the typical conditions of [DMPC] = 1.0 mg/ml, [I2] = 10 mM, and [TSAC] = 1.0 mM. After the nitrobenzene droplet was dispensed (t = 0 s) into the aqueous phase, it exhibited a random spontaneous movement for a few seconds, and then the motion was stabilized, i.e., the droplet showed self-propelled directional motion from the center of the Petri dish to its edge (t ∼ 20 s). The direction of motion was different for each droplet and not controllable. In addition, as shown later, this directed motion was also observed for droplets with much smaller diameters (∼1.8 mm) than the height of the aqueous phase (∼5.4 mm). Therefore, this motion is independent of meniscus effects, and the driving force originates from the droplet itself. To investigate the principle of this self-propulsion, we carefully observed the droplets under magnification (Figure 1B). Immediately after it was dispensed (t = 0 s), there was no change in the droplet appearance and it did not move. However, after a few seconds, the droplet ejected brown aggregates from several parts of its surface (regions enclosed by pink circles in Figure 1B) and began to move concurrently. This aggregate ejection event occurred repeatedly, and the droplet showed random motion during this period. However, after a certain time, the weak ejection point (dashed pink circle) moved along the interface toward a strong ejection point (solid pink circle), and the ejection points began to converge to one position. After several repetitions of this concentrating event, the ejection point was completely fixed in one position (yellow circle). During this period, the motion was maintained in the direction opposite to this strong ejection point; that is, the random motion switched to directional motion. We could observe that Marangoni convection (blue arrow) occurred inside the droplet because ejection points were transported along the interface. Therefore, we inferred that this convection, which has been identified as the primary driving force in many self-propelled droplet systems, was the cause of the self-propulsion of the droplet in this system [40–46]. In general, Marangoni convection occurs when the interfacial tension γ at the droplet interface becomes unbalanced. Figure 1C shows an enlarged image of the ejected aggregates, which consisted of many microemulsion units. Therefore, the emergence of droplet motility, which was attributed to Marangoni convection, can be linked to the ejection of aggregates. It was found that the ejection of such emulsion units induced a change in γ, suggesting that the emulsion was formed by the desorption of materials that can alter γ, namely, DMPC and TSA+. Some previous studies have shown that the formation and ejection of molecular aggregates of the surfactant induce unbalanced γ, following which Marangoni convection occurs and propels the motion of the droplet [42, 43]. In these systems, aggregates were suggested to form by the aggregation of products generated by the hydrolysis of surfactant molecules at the droplet interface with unhydrolyzed surfactant molecules. However, our system does not contain hydrolysable surfactants. On the other hand, it has been reported that phospholipids and surfactants form aggregates, in a process that is well known as the solubilization of lipid membranes by surfactants into the solution [47]. In this phenomenon, surfactant molecules first enter the lipid membrane with an increasing surfactant concentration, and aggregates of the surfactant and lipid molecules are formed as surfactant concentration is increased further. Furthermore, another study showed that solubilization, namely micellization of surfactants with oil, and ejection of solubilized emulsions proceed when the concentration of the surfactant at the droplet interface exceeds a threshold value [46]. Therefore, we infer that, in this study, TSA+ is first inserted into the self-assembled DMPC monolayer surrounding the droplet, and aggregated emulsions are formed and ejected them owing to the solubilization promoted by the micellization among TSA+, DMPC, and nitrobenzene oil when the concentration of the inserted TSA+ exceeds a threshold value. Accordingly, we assume that Marangoni convection is generated inside the droplet due to the unbalanced γ between the solubilized and non-solubilized regions, and finally the droplet shows self-propelled motion.
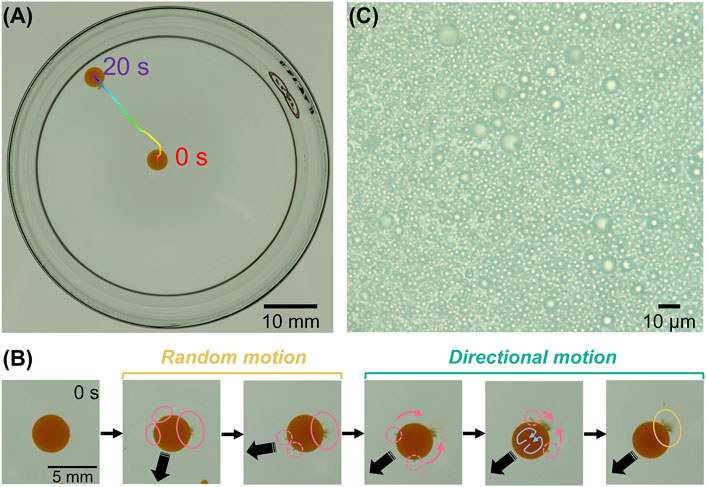
FIGURE 1. (A) Top-view image illustrating the self-propelled locomotion of a droplet for 20 s ([DMPC] = 1.0 mg/ml, [I2] = 10 mM, and [TSAC] = 1.0 mM). (B) Successive snapshots of a self-propelled droplet under the same condition as in (A). Pink and yellow circles show ejection points of aggregates at the beginning and final stages, respectively. Blue arrows represent Marangoni convection inside the droplet. (C) Enlarged image of an ejected aggregate.
If our system follows the above-mentioned mechanism, TSAC plays an important role because the solubilization might depend on a concentration of TSA+. We therefore explored the effect of TSAC concentration on the motility of the droplet. Figure 2A shows the droplet locomotion for 30 s at different initial TSAC concentrations in the range of 0–1.0 mM. At [TSAC] = 0 mM, the droplets did not exhibit motility. Although the droplet moved slightly at [TSAC] = 0.20 and 0.30 mM, the final position was almost anchored at the center. However, droplet motility improved remarkably when TSAC concentration was increased further. With an increase in TSAC concentration from 0.40 to 1.0 mM, the droplet moved toward the edge of the glass Petri dish, and the total path length of movement during this observation (L) increased. In particular, the sudden change in direction after ∼20 s at [TSAC] = 1.0 mM indicated that the droplet collided with the glass wall and continued its motion along the wall. To clarify the effect of TSAC concentration, we evaluated the relationship between L and time from the initiation of their locomotion (Figure 2B). Note that L was evaluated from 0 s (pipetting a droplet) until after 20 s to eliminate the effect of collision on the glass wall. For [TSAC] = 0–0.30 mM, L was almost the same during the entire period, without any significant differences in the changes in L. However, L increased significantly from 15 to 35 mm with an increase in [TSAC] from 0.40 to 1.0 mM. Furthermore, the increasing trend of L with time was noted for each condition. Although L increased immediately after the dispensation of the droplet in the case of [TSAC] = 1.0 mM, the increase in L began after a certain duration in the cases of [TSAC] = 0.40 and 0.80 mM, indicating an induction period (τ) for the propulsion of this system. Then, we evaluated the dependence of the mean motion speed (V) and τ as a function of TSAC concentration (Figure 2C); in this evaluation, τ was defined as the time taken until L became greater than 5 mm, and V was calculated from the slope of the L vs. time plot obtained after τ. Similar to the above-mentioned results, V increased remarkably at [TSAC] ≥ 0.30 mM (black circle). The value of τ decreased from 20 to 2 s with an increase in [TSAC] (green triangle). Thus, we found that TSAC not only controlled the emergence of motility but also improved the motility of the droplet. Furthermore, the critical micellar concentration (CMC) of TSAC is ∼0.3 mM at room temperature [48]. Although solubilization could occur at TSAC concentrations lower than the CMC, the motility of the droplet only emerged when the TSAC concentration approached the CMC of our system. Therefore, this strongly suggests that the solubilization process that induces droplet motility is related to the micellization of TSA+.
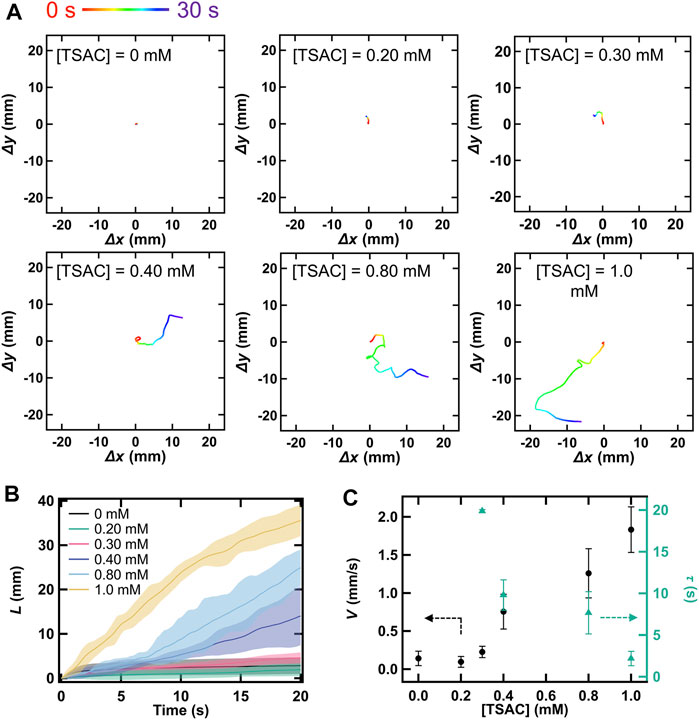
FIGURE 2. (A) Locomotion of a droplet over 20 s owing to its self-propelled motion at different TSAC concentrations in the range of 0–1.0 mM ([DMPC] = 2.0 mg/ml and [I2] = 10 mM). Quantity of motion with respect to the x- or y-direction is calculated as a displacement value with respect to an initial pipetted position. (B) Relationship between time and the total path length of droplet movement during 20 s (L) at different TSAC concentrations, where t = 0 represents the time of pipetting. (C) Variation in the mean motion speed of the droplet (V) and induction period (τ) at different TSAC concentrations.
To further investigate the influence of TSAC concentration on droplet motility, we measured the changes in γ with time using the pendant drop method. Figures 3A,B present the changes in the appearance of droplets at [TSAC] = 0 and 0.20 mM. Under both conditions, the appearance of the droplets was almost the same immediately after their formation (t = 0 s). However, some differences were observed in their evolution with time. Whereas the droplet stretched slightly and then simply broke off and fell after 60 s in the absence of TSAC, apparent aggregates were formed at the bottom of the droplet in addition to the above-mentioned changes in the presence of TSAC (0.20 mM). Therefore, it is clear that γ changed with the formation of aggregates in the presence of TSA+. Furthermore, Figure 3C shows the changes in γ with time at different TSAC concentrations; in this evaluation, γ was calculated using Eqs. 1–3, and the measurement was continued until the droplets fell from the tip of the needle. In the absence of TSAC, γ decreased with time (data represented by •). This could be ascribed to the self-assembly of DMPC at the oil–water interface. Then, the droplet fell when γ decreased below ∼1.8 mN/m. Under all the conditions, the droplets fell at this critical value of γ. However, the rate of decrease in γ was different in the presence of TSA+ (data represented by▲–▼). At [TSAC] = 0.20 mM, the droplets fell after 50 s following their formation, and the time taken for their fall shortened with increasing TSAC concentration. Finally, the droplets fell immediately after being formed at [TSAC] = 0.60 mM. These results indicated that a higher TSAC concentration promoted faster TSA+ insertion into the droplet interface and the solubilization. Marangoni convection in this study is triggered by the unbalancing of γ between the front (direction of motion) and rear parts of the droplet owing to the increase in γ at the rear where TSA+ and DMPC leave the interface (owing to the solubilization). As shown clearly by the above-described experiments, a higher TSAC concentration led to the faster formation of aggregates and their ejection. That is, the time required for γ imbalance was shortened with increasing TSAC concentration; thus, τ decreased with increasing TSAC concentration, leading to self-propelled motion. Therefore, we can analyze the improvement in motility from the perspective of the change in the equilibrium γ value. In general, the distribution ratio between surfactant molecules in the water phase and lipid membrane depends on the concentration of the surfactant in the water phase [49–51]. It is also known that the value of γ at equilibrium at the air–water interface decreases with an increase in the amount of the adsorbed surfactant [52, 53], which is generally observed in the cases of oil–water interfaces. Therefore, the increase in TSAC concentration caused a decrease in γ at equilibrium, in addition to affecting the kinetics of the solubilization. The possible scenarios are as follows: although the equilibrium γ value could not be measured with the pendant drop method because the droplet fell, the equilibrium γ at the oil (nitrobenzene-DMPC)–water (aqueous TSAC solution) interface decreased with increasing TSAC concentration because the surfactant distribution ratio increased. Owing to the lowered equilibrium γ value, the difference between γ (Δγ) before and after the ejection DMPC/TSA+/oil aggregates increase. This enhances the Marangoni convection, and improves the motility.
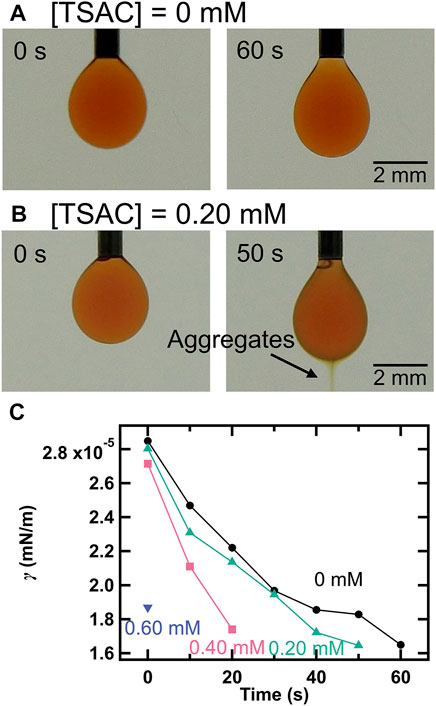
FIGURE 3. Snapshots of the droplet at the tip of a needle when (A) [TSAC] = 0 mM and (B) [TSAC] = 0.20 mM ([DMPC] = 0.25 mg/ml and [I2] = 10 mM). (C) Variation in the interfacial tension (γ) with time at different TSAC concentrations (the concentrations of DMPC and I2 were the same as those in the cases of (A) and (B)).
According to a previous study [33, 54], anionic I3− generated by the complexation of I2 and I− made ion pairs with cationic TSA+ both at the oil–water interface and in the oil phase, and thus the incorporation (dissolution) of TSA+ into the oil phase is promoted, leading to improved droplet motility. The authors suggested that I2 is the primary source of self-propelled energy. Therefore, we explored the role of I2 in droplet motility (Figure 4A). Interestingly, while V was almost 0 at [I2] = 0 and 2.0 mM (i.e., no motion), the motility emerged abruptly at [I2] exceeding 4.0 mM and then V increased linearly with increasing I2 concentration. This result suggests that a certain amount of I2 present in the droplet is required for the emergence of self-propelled motion. To investigate this aspect, we evaluated the changes in γ with iodine concentration (Figures 4B–D). In the absence of I2, the surface of the droplet, which was clear immediately after droplet formation, became cloudy after 20 s (Figure 4B). This is probably due to structural disruption and the formation of small aggregates owing to TSA+ insertion into the DMPC layer. In contrast, yellow aggregates, which were similar to those observed in earlier experiments, were formed and ejected from the droplet after 20 s at [I2] = 10 mM (Figure 4C). Furthermore, γ decreased rapidly in the case of [I2] = 10 mM, compared to that in the case of [I2] = 0 mM (Figure 4D). This behavior is similar to that observed with an increase in TSAC concentration. Thus, we found that I2 promoted the insertion of TSA+ into the DMPC membrane and thus aided the solubilization process. That is, I2 played an important role in the dissolution of more TSA+ into the droplet and TSA+ insertion at the interface to overcome the energy barrier required to break the stable DMPC membrane structure and promote the solubilization depending on the micelle formation.

FIGURE 4. (A) Effects of I2 concentration (0–10 mM) on V ([DMPC] = 1.0 mg/ml and [TSAC] = 1.0 mM). Snapshots of the droplet when (B) [I2] = 0 mM and (C) [I2] = 10 mM. (D) Changes in γ with time at different I2 concentrations (the concentrations of DMPC and I2 were the same as those in the cases of (B) and (C)).
Furthermore, we explored the influence of DMPC concentration on droplet motility (Figure 5A). V increased substantially with DMPC concentration between 0.50 and 1.0 mg/ml and then increased gently until DMPC concentration reached 5.0 mg/ml. In addition, we studied the variation in γ value in water with the changes in DMPC concentration (Figure 5B). The value of γ decreased exponentially with an increase in DMPC concentration. Thus, the increase in V can be explained based on the change in γ, as in the case of TSAC concentration. That is, Δγ increases as the concentration of DMPC increases. In addition, we studied the effect of droplet diameter, another factor that affects droplet motility in this system (Figure 5C), by changing the pipetted liquid volume for tuning the diameter. At both [DMPC] = 1.0 and 2.0 mg/ml, V increased with an increase in droplet diameter, as observed in other studies [45, 55, 56]. In some of the previous studies, the motion behavior was found to change, for example, from random to directional motion; however, our system did not show such a transition. The effect of droplet diameter on V in our system can be explained by following reason: As the diameter of the droplet decreases, the distinction between front and rear parts of the droplet becomes blurred. Therefore, Δγ became smaller and V decreased.
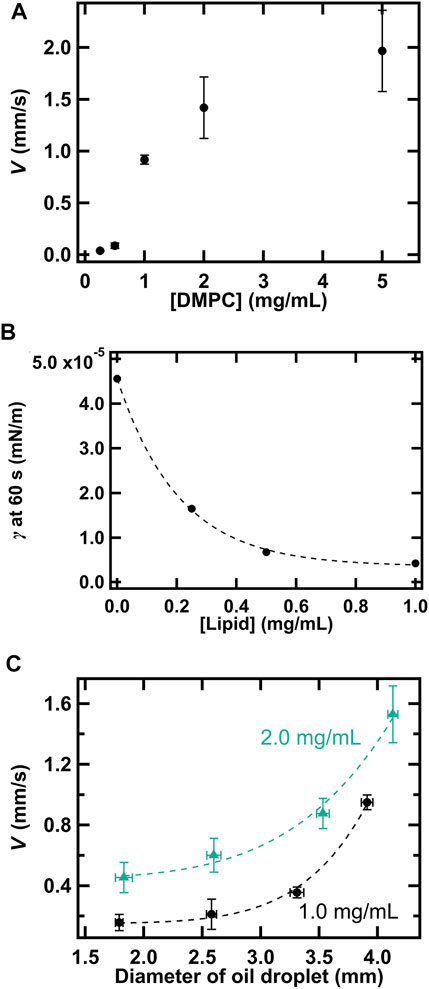
FIGURE 5. (A) Effects of DMPC concentration (0–5.0 mg/ml) on V ([I2] = 1.0 mM and [TSAC] = 1.0 mM). (B) Measured γ at 60 s for droplets with different DMPC concentrations ([I2] = 1.0 mM and [TSAC] = 0 mM). (C) Variation in V with the diameter of the droplet at [DMPC] = 1.0 and 2.0 mg/ml.
According to the results of the dependence of droplet motility on TSAC, I2, and DMPC concentrations and droplet diameter, the complete mechanism of the self-propelled motion of the droplet is depicted in Figure 6. Immediately after the oil phase (DMPC-containing nitrobenzene) is dispensed into the water phase, a droplet covered with a self-assembled DMPC monolayer membrane is formed on the glass substrate (step 1). At this time, TSA+ present in the water phase is adsorbed on the glass surface and exists both in molecular and micellar forms in the solution. Subsequently, TSA+ enters the self-assembled layer and dissolves in the oil phase, assisted by ion pairing between TSA+ and I3−, a complex formed between I− and I2 (step 2). The concentration of TSA+ in the self-assembled layer increases because of this process. When the concentration finally exceeds the CMC of TSAC, the solubilization process is promoted drastically, which is combination of the formation of emulsions formation among TSA+, DMPC, and nitrobenzene followed by the ejection of their aggregates. In the beginning, ejection points exist all over the surface of the droplet, and each point induces an increase in γ. Therefore, the Marangoni effect is induced, and the droplet exhibits random self-propelled motion. After a certain duration, the scattered points that proceed the solubilization eventually coalesce into a single point (this final point depends on the initial fluctuation of γ) owing to Marangoni convection. That is, complete symmetry breaking occurs and a unified Marangoni convection is induced in the droplet (step 3). Thus, the mode of movement (random) switches to directional motion. Furthermore, because TSA+ is adsorbed to the glass surface in the forward part of the droplet in the direction of motion, γ is always maintained at a low value in the front of the droplet owing to TSA+ insertion from the surface of a glass substrate (step 4). In addition, the direct insertion of TSA+ from the solution plays the same role in maintaining a lower γ. Furthermore, the oil–water interface of the entire droplet is continuously supplied with DMPC molecules because DMPC continues to self-assemble from the inside of the droplet. This process (step 4) causes the droplet to recover to step 3, and the directional self-propelled motion continues; that is, step 4 provides positive feedback for this mechanism. Therefore, the motility of the droplet can be rationalized from the perspective of the change in γ, droplet motility, which is one of the important parameters that govern the unjamming/jamming phase transition, can be controlled by controlling these experimental parameters.
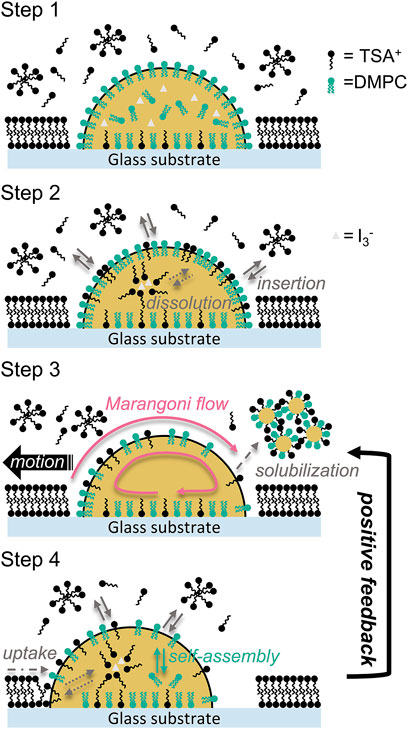
FIGURE 6. Mechanism of the self-propelled motion of the nitrobenzene droplet observed in this study. Step 1: Initial state of the oil phase (the droplet) and water phase containing TSAC, corresponding to the situation immediately after the droplet was dispensed. Step 2: Insertion of TSAC into the DMPC membrane layer and dissolution of TSAC in the oil phase assisted by I3−. Step 3: Symmetry breaking of the interfacial tension at the oil–water interface owing to the solubilization by the formation and ejection of DMPC/TSA+/nitrobenzene aggregates, and then the self-propelled motion. Step 4: Recovery of the droplet condition owing to following processes: the uptake of TSA+ from the front of the droplet and from the solution (reinsertion), and the self-assembly of DMPC at the interface.
Stability of Droplets in Collectivity
Figure 7 shows the variation in the number of droplets (N) with time in cases where the pipetted volume per droplet was 10.0 μl (Figure 7A) and 5.0 μl (Figure 7B). The confluency was calculated from the ratio between the total area occupied by all the droplets and the area surrounded by the silicon ring, wherein the vertical axis corresponding to confluency has been inverted for comparison with N. The droplet boundaries required for this calculation were determined by segmentation image processing using an arbitrary color threshold. In these figures, the increase in N indicates that droplets were added within the silicon ring by pipetting, and the time when the increase stops indicates that the addition of droplets was stopped. Furthermore, Figures 7C,D shows a collection of actual droplets under several N conditions; their state can be distinguished into two types: non-confluent and confluent. At 10.0 μl/droplet, N increased monotonically with the regular addition of droplets (•), and the confluency decreased accordingly (▲), reaching the confluent state at N = 9 (confluency is ∼100%) (Figure 7A). Thereafter, N increased with the addition of droplets, while maintaining the confluent state, and the addition was continued until the maximum N of 14 was reached. The monotonic increase in N with each addition indicated that the droplets did not coalesce and maintained their individual morphologies. That is, the droplets remained stable with an increase in N, which suggests that they maintained their stability with an increase in droplet density. This result indicates that droplet density, which is another important parameter for CCM, is controllable. On the other hand, N decreased at t = 150 s because of droplet coalescence, which began after 50 s following the termination of addition. Subsequently, intermittent droplet coalescence finally reduced the N to 11 at t = 300 s. However, this instability was not an issue in our experiments because the time taken for this coalescence process to start (∼50 s) was less compared to the observation time of the self-propelled motion (∼30 s). Furthermore, the morphology of each droplet in the ensemble was also observed, as shown in Figure 7C. Under non-confluent conditions (N = 3), each droplet had a clear spherical morphology because the droplets did not contact each other. On the other hand, linear contact surfaces were formed under confluent conditions (N = 9) because the droplets contacted each other, and each droplet showed a characteristic polygonal shape depending on the number of surface contacts. As the density increased (N = 14), the area occupied by each droplet decreased, while the polygonal shape remained intact. As the droplets coalesced (★ in N = 11), the morphology of each droplet changed slightly. The observed polygonal morphology is similar to the cell morphologies of confluent cells, such as epithelial cells. In most previous studies that examined the collective motion of self-collective droplets, each droplet had a relatively small specific surface area, thus maintaining a small contact area and a spherical shape [34, 57]. Therefore, our results are superior to those of previous studies because the droplets could stably adopt a characteristic polygonal shape. Although the details are not provided here, we have also experimentally confirmed that these droplets exhibit self-propelled motion in collectivity. In addition, the same experiment was also conducted under the condition of 5.0 μl/droplet (Figures 7B,D). In contrast to that in the case of 10.0 μl/droplet, the maximum N increased significantly to 22 and the droplets were highly stable (without coalescing over the entire period), but the confluency saturated at ∼80% (Figure 7B). This is because of two reasons: 1) many miniscule droplets were formed due to pipetting when the droplets were added and 2) each droplet had a high spherical retention and large vacancy between contacting points because the droplets were smaller than those created with 10.0 μl/droplet (Figure 7D). Thus, we found that it is possible to alter the adhesion of droplets in terms of the size of the contact area depending on the rigidity by adjusting the droplet size, which is different from the adhesion mechanism in cells. As such, this control of adhesiveness is considered indirect. However, this droplet system has potential to be possibility of biomodification in order to further improve the controllability of adhesion, as mentioned in the introduction section. These results clarify the second consideration of this study, which is the stability of the droplets in collectivity. Thus, we succeeded in developing a prototype experimental self-propelled droplet system for demonstrating the unjamming/jamming phase transition in CCM.
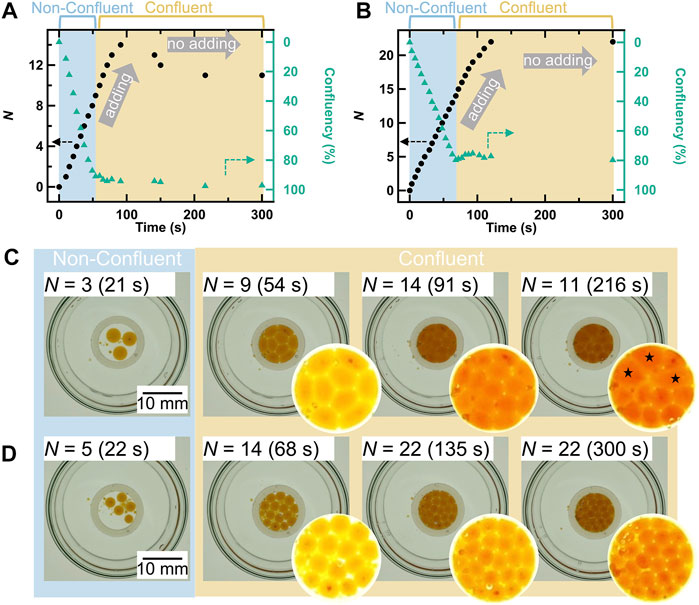
FIGURE 7. Changes in the total number of droplets within the silicon ring (N) and confluency with time in the cases of (A) 10.0 μl/droplet and (B) 5.0 μl/droplet. Confluency was calculated as the ratio between the total area occupied by all the droplets and the area surrounded by the silicon ring. The axis of confluency is inverted. The increasing N indicates that droplets were added, and stopping means that droplet addition was stopped. Top-view snapshots of the droplets and enlarged images showing the interior of the silicon ring in the cases of (C) 10.0 μl/droplet and (D) 5.0 μl/droplet. The ★ symbol represents coalescing droplets.
Conclusion
In this study, we developed an improved prototype of a self-propelled droplet system by combining self-propelling nitrobenzene oil on a glass surface with a robust self-assembled DMPC membrane. This system can potentially be used for demonstrating the unjamming/jamming phase transitions in CCM. The main driving force of the self-propelled motility of this system is the Marangoni convection induced by the following processes: The insertion of TSAC into the DMPC membrane layer and the solubilization promoted by the combination of DMPC/TSA+/nitrobenzene aggregate formation. The controllability of motility was explored in terms of the concentrations of TSAC, I2, and DMPC, as well as the droplet size. Furthermore, the effects of these parameters were discussed based on the changes in the interfacial tension and its unbalancing owing to the chemical dynamics at the oil–water surface under each condition because the change in interfacial tension was the main factor driving the Marangoni convection. We found that droplet motility could be controlled well by altering these conditions, and the related mechanism was explained adequately. In addition, the developed system showed high stability in collectivity, regardless of the conditions (non-confluent or confluent conditions). Therefore, the cell density could also be controlled for this system. Furthermore, each droplet in collectivity showed characteristic polygonal shapes depending on the droplet size because of the difference in the contact area between the droplets owing to their rigidity. Thus, the adhesive force could be controlled experimentally. In fact, this controlling mechanism is different from the molecular adhesion mechanism operating in living cells. This issue can be overcome by modifying the system for implementing interactions such as those between biomodified lipid molecules and proteins as in the case of biotin–streptavidin–biotin complex bridging. As described above, the developed system is highly attractive because it can control three important aspects of CCM: the motility, density, and adhesion of cells. The CCM exhibited by cells is unique, but the underlying mechanisms are extremely complex. Therefore, a simple understanding of this phenomenon through experiments and mathematical modeling is essential. The system developed in this study has the potential to address this challenge. Accordingly, we expect that this prototype experimental model can be applied in various modeling studies of the unjamming/jamming phase transitions in CCM, and that it can bridge the gap between modeling studies and real biochemical phenomena.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
In this study, all experiments and data analyses were performed by MI. Both the authors contributed to the preparation of the final manuscript.
Funding
This work was supported by JSPS KAKENHI (Grant Number 19H02668) and JSPS Fellows (Grant Number 19J23178).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
CCM, collective cell migration; DMPC, 1,2-dimyristoyl-sn-glycero-3-phosphocholine; TSAC, trimethylstearylammonium chloride; CMC, critical micellar concentration; PEG, polyethylene glycol; potassium iodide, KI.
References
1. Lauffenburger DA, Horwitz AF. Cell Migration: A Physically Integrated Molecular Process. Cell (1996) 84:359–69. doi:10.1016/s0092-8674(00)81280-5
2. Ridley AJ, Schwartz MA, Burridge K, Firtel RA, Ginsberg MH, Borisy G, et al. Cell Migration: Integrating Signals from Front to Back. Science (2003) 302:1704–9. doi:10.1126/science.1092053
3. Friedl P, Gilmour D. Collective Cell Migration in Morphogenesis, Regeneration and Cancer. Nat Rev Mol Cel Biol (2009) 10:445–57. doi:10.1038/nrm2720
4. Haeger A, Wolf K, Zegers MM, Friedl P. Collective Cell Migration: Guidance Principles and Hierarchies. Trends Cel Biol (2015) 25:556–66. doi:10.1016/j.tcb.2015.06.003
5. Montell DJ. Morphogenetic Cell Movements: Diversity from Modular Mechanical Properties. Science (2008) 322:1502–5. doi:10.1126/science.1164073
6. Staddon MF, Bi D, Tabatabai AP, Ajeti V, Murrell MP, Banerjee S. Cooperation of Dual Modes of Cell Motility Promotes Epithelial Stress Relaxation to Accelerate Wound Healing. Plos Comput Biol (2018) 14:e1006502. doi:10.1371/journal.pcbi.1006502
7. Friedl P, Wolf K. Tumour-cell Invasion and Migration: Diversity and Escape Mechanisms. Nat Rev Cancer (2003) 3:362–74. doi:10.1038/nrc1075
8. Spatarelu C-P, Zhang H, Nguyen DT, Han X, Liu R, Guo Q, et al. Biomechanics of Collective Cell Migration in Cancer Progression: Experimental and Computational Methods. ACS Biomater Sci Eng (2019) 5:3766–87. doi:10.1021/acsbiomaterials.8b01428
9. Rappel W-J, Edelstein-Keshet L. Mechanisms of Cell Polarization. Curr Opin Syst Biol (2017) 3:43–53. doi:10.1016/j.coisb.2017.03.005
11. Ananthakrishnan R, Ehrlicher A. The Forces behind Cell Movement. Int J Biol Sci (2007) 3:303–17. doi:10.7150/ijbs.3.303
12. Van Haastert PJM, Devreotes PN. Chemotaxis: Signalling the Way Forward. Nat Rev Mol Cel Biol (2004) 5:626–34. doi:10.1038/nrm1435
13. Cai P, Layani M, Leow WR, Amini S, Liu Z, Qi D, et al. Bio-Inspired Mechanotactic Hybrids for Orchestrating Traction-Mediated Epithelial Migration. Adv Mater (2016) 28:3102–10. doi:10.1002/adma.201505300
14. Chen Y-C, Allen SG, Ingram PN, Buckanovich R, Merajver SD, Yoon E. Single-cell Migration Chip for Chemotaxis-Based Microfluidic Selection of Heterogeneous Cell Populations. Sci Rep (2015) 5:9980. doi:10.1038/srep09980
15. Trepat X, Wasserman MR, Angelini TE, Millet E, Weitz DA, Butler JP, et al. Physical Forces during Collective Cell Migration. Nat Phys (2009) 5:426–30. doi:10.1038/nphys1269
16. Pegoraro AF, Fredberg JJ, Park J-A. Problems in Biology with many Scales of Length: Cell-Cell Adhesion and Cell Jamming in Collective Cellular Migration. Exp Cel Res (2016) 343:54–9. doi:10.1016/j.yexcr.2015.10.036
17. Angelini TE, Hannezo E, Trepat X, Fredberg JJ, Weitz DA. Cell Migration Driven by Cooperative Substrate Deformation Patterns. Phys Rev Lett (2010) 104:168104. doi:10.1103/physrevlett.104.168104
18. Hu B, Leow WR, Cai P, Li Y-Q, Wu Y-L, Chen X. Nanomechanical Force Mapping of Restricted Cell-To-Cell Collisions Oscillating between Contraction and Relaxation. ACS Nano (2017) 11:12302–10. doi:10.1021/acsnano.7b06063
19. Brugués A, Anon E, Conte V, Veldhuis JH, Gupta M, Colombelli J, et al. Forces Driving Epithelial Wound Healing. Nat Phys (2014) 10:683–90. doi:10.1038/nphys3040
20. Szabó B, Szöllösi GJ, Gönci B, Jurányi Z, Selmeczi D, Vicsek T. Phase Transition in the Collective Migration of Tissue Cells: Experiment and Model. Phys Rev E (2006) 74:061908. doi:10.1103/PhysRevE.74.061908
21. Sadati M, Taheri Qazvini N, Krishnan R, Park CY, Fredberg JJ. Collective Migration and Cell Jamming. Differentiation (2013) 86:121–5. doi:10.1016/j.diff.2013.02.005
22. Park JA, Atia L, Mitchel JA, Fredberg JJ, Butler JP. Collective Migration and Cell Jamming in Asthma, Cancer and Development. J Cel Sci (2016) 129:3375–83. doi:10.1242/jcs.187922
23. Doxzen K, Vedula SRK, Leong MC, Hirata H, Gov NS, Kabla AJ, et al. Guidance of Collective Cell Migration by Substrate Geometry. Integr Biol (2013) 5:1026–35. doi:10.1039/c3ib40054a
24. Bi D, Yang X, Marchetti MC, Manning ML. Motility-Driven Glass and Jamming Transitions in Biological Tissues. Phys Rev X (2016) 6:021011. doi:10.1103/PhysRevX.6.021011
25. Bi D, Lopez JH, Schwarz JM, Manning ML. A Density-independent Rigidity Transition in Biological Tissues. Nat Phys (2015) 11:1074–9. doi:10.1038/nphys3471
26. Liu AJ, Nagel SR. The Jamming Transition and the Marginally Jammed Solid. Annu Rev Condens Matter Phys (2010) 1:347–69. doi:10.1146/annurev-conmatphys-070909-104045
27. Pusey PN, Van Megen W. Phase Behaviour of Concentrated Suspensions of Nearly Hard Colloidal Spheres. Nature (1986) 320:340–2. doi:10.1038/320340a0
28. Zhou EH, Trepat X, Park CY, Lenormand G, Oliver MN, Mijailovich SM, et al. Universal Behavior of the Osmotically Compressed Cell and its Analogy to the Colloidal Glass Transition. Proc Natl Acad Sci (2009) 106:10632–7. doi:10.1073/pnas.0901462106
29. Kim S, Pochitaloff M, Stooke-Vaughan GA, Campàs O. Embryonic Tissues as Active Foams. Nat Phys (2021) 17:859–66. doi:10.1038/s41567-021-01215-1
30. Magome N, Yoshikawa K. Nonlinear Oscillation and Ameba-like Motion in an Oil/Water System. J Phys Chem (1996) 100:19102–5. doi:10.1021/jp9616876
31. Sumino Y, Magome N, Hamada T, Yoshikawa K. Self-Running Droplet: Emergence of Regular Motion from Nonequilibrium Noise. Phys Rev Lett (2005) 94:068301. doi:10.1103/PhysRevLett.94.068301
32. Sumino Y, Kitahata H, Yoshikawa K, Nagayama M, Nomura SM, Magome N, et al. Chemosensitive Running Droplet. Phys Rev E Stat Nonlin Soft Matter Phys (2005) 72:041603. doi:10.1103/PhysRevE.72.041603
33. Sumino Y, Yoshikawa K. Self-motion of an Oil Droplet: A Simple Physicochemical Model of Active Brownian Motion. Chaos (2008) 18:026106. doi:10.1063/1.2943646
34. Kichatov B, Korshunov A, Sudakov V, Gubernov V, Yakovenko I, Kiverin A. Crystallization of Active Emulsion. Langmuir (2021) 37:5691–8. doi:10.1021/acs.langmuir.1c00630
35. Pontani L-L, Jorjadze I, Viasnoff V, Brujic J. Biomimetic Emulsions Reveal the Effect of Mechanical Forces on Cell-Cell Adhesion. Proc Natl Acad Sci (2012) 109:9839–44. doi:10.1073/pnas.1201499109
36. Golovkova I, Montel L, Pan F, Wandersman E, Prevost AM, Bertrand T, et al. Adhesion as a Trigger of Droplet Polarization in Flowing Emulsions. Soft Matter (2021) 17:3820–8. doi:10.1039/d1sm00097g
37. Fattaccioli J, Baudry J, Henry N, Brochard-Wyart F, Bibette J. Specific Wetting Probed with Biomimetic Emulsion Droplets. Soft Matter (2008) 4:2434. doi:10.1039/b806635c
38. Bourouina N, Husson J, Waharte F, Pansu RB, Henry N. Formation of Specific Receptor-Ligand Bonds between Liquid Interfaces. Soft Matter (2011) 7:9130–9. doi:10.1039/c1sm05659j
40. Suematsu NJ, Saikusa K, Nagata T, Izumi S. Interfacial Dynamics in the Spontaneous Motion of an Aqueous Droplet. Langmuir (2019) 35:11601–7. doi:10.1021/acs.langmuir.9b01866
41. Suematsu NJ, Mori Y, Amemiya T, Nakata S. Spontaneous Mode Switching of Self-Propelled Droplet Motion Induced by a Clock Reaction in the Belousov-Zhabotinsky Medium. J Phys Chem Lett (2021) 12:7526–30. doi:10.1021/acs.jpclett.1c02079
42. Toyota T, Maru N, Hanczyc MM, Ikegami T, Sugawara T. Self-Propelled Oil Droplets Consuming "Fuel" Surfactant. J Am Chem Soc (2009) 131:5012–3. doi:10.1021/ja806689p
43. Banno T, Kuroha R, Toyota T. pH-Sensitive Self-Propelled Motion of Oil Droplets in the Presence of Cationic Surfactants Containing Hydrolyzable Ester Linkages. Langmuir (2012) 28:1190–5. doi:10.1021/la2045338
44. Banno T, Asami A, Ueno N, Kitahata H, Koyano Y, Asakura K, et al. Deformable Self-Propelled Micro-object Comprising Underwater Oil Droplets. Sci Rep (2016) 6:31292. doi:10.1038/srep31292
45. Ban T, Yamagami T, Nakata H, Okano Y. pH-Dependent Motion of Self-Propelled Droplets Due to Marangoni Effect at Neutral pH. Langmuir (2013) 29:2554–61. doi:10.1021/la3047164
46. Babu D, Scanes RJH, Plamont R, Ryabchun A, Lancia F, Kudernac T, et al. Acceleration of Lipid Reproduction by Emergence of Microscopic Motion. Nat Commun (2021) 12:2959. doi:10.1038/s41467-021-23022-1
47. Aguirre-Ramírez M, Silva-Jiménez H, Banat IM, Díaz De Rienzo MA. Surfactants: Physicochemical Interactions with Biological Macromolecules. Biotechnol Lett (2021) 43:523–35. doi:10.1007/s10529-020-03054-1
48. Sumino Y, Kitahata H, Seto H, Nakata S, Yoshikawa K. Spontaneous Deformation of an Oil Droplet Induced by the Cooperative Transport of Cationic and Anionic Surfactants through the Interface. J Phys Chem B (2009) 113:15709–14. doi:10.1021/jp9037733
49. Ueno M. Partition Behavior of a Nonionic Detergent, Octyl Glucoside, between Membrane and Water Phases, and its Effect on Membrane Permeability. Biochemistry (1989) 28:5631–4. doi:10.1021/bi00439a044
50. Levy D, Gulik A, Seigneuret M, Rigaud JL. Phospholipid Vesicle Solubilization and Reconstitution by Detergents. Symmetrical Analysis of the Two Processes Using Octaethylene Glycol Mono-N-Dodecyl Ether. Biochemistry (1990) 29:9480–8. doi:10.1021/bi00492a022
51. Schurtenberger P, Mazer N, Kaenzig W. Micelle to Vesicle Transition in Aqueous Solutions of Bile Salt and Lecithin. J Phys Chem (1985) 89:1042–9. doi:10.1021/j100252a031
52. Chang H-C, Hsu C-T, Lin S-Y. Adsorption Kinetics of C10E8 at the Air−Water Interface. Langmuir (1998) 14:2476–84. doi:10.1021/la970923g
53. Touhami Y, Rana D, Neale GH, Hornof V. Study of Polymer-Surfactant Interactions via Surface Tension Measurements. Colloid Polym Sci (2001) 279:297–300. doi:10.1007/s003960000455
54. Yoshikawa K, Matsubara Y. Spontaneous Oscillation of pH and Electrical Potential in an Oil-Water System. J Am Chem Soc (1983) 105:5967–9. doi:10.1021/ja00357a001
55. Ueno N, Banno T, Asami A, Kazayama Y, Morimoto Y, Osaki T, et al. Self-Propelled Motion of Monodisperse Underwater Oil Droplets Formed by a Microfluidic Device. Langmuir (2017) 33:5393–7. doi:10.1021/acs.langmuir.7b00092
56. Suga M, Suda S, Ichikawa M, Kimura Y. Self-propelled Motion Switching in Nematic Liquid crystal Droplets in Aqueous Surfactant Solutions. Phys Rev E (2018) 97:062703. doi:10.1103/PhysRevE.97.062703
Keywords: nonlinear science, active matter, phospholipid, self-propelled motion, oil droplet, surface chemistry
Citation: Itatani M and Nabika H (2022) Self-Propelled Motion of an Oil Droplet Containing a Phospholipid and its Stability in Collectivity. Front. Phys. 10:849111. doi: 10.3389/fphy.2022.849111
Received: 05 January 2022; Accepted: 21 February 2022;
Published: 07 March 2022.
Edited by:
Nobuhiko J. Suematsu, Meiji University, JapanReviewed by:
Taisuke Banno, Keio University, JapanRyan McGorty, University of San Diego, United States
Copyright © 2022 Itatani and Nabika. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hideki Nabika, bmFiaWthQHNjaS5rai55YW1hZ2F0YS11LmFjLmpw
 Masaki Itatani
Masaki Itatani Hideki Nabika
Hideki Nabika