
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 25 February 2022
Sec. Optics and Photonics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.846718
This article is part of the Research TopicOptical Vortices: Generation and DetectionView all 13 articles
 Naitao Song1,2
Naitao Song1,2 Nianxi Xu1
Nianxi Xu1 Jinsong Gao2,3*
Jinsong Gao2,3* Xiaonan Jiang1
Xiaonan Jiang1 Dongzhi Shan1,2
Dongzhi Shan1,2 Yang Tang1
Yang Tang1 Qiao Sun1
Qiao Sun1 Hai Liu1
Hai Liu1 Xin Chen1
Xin Chen1Optical vortex (OV) beams are ideal carriers for high-capacity optical communication, and long-wave infrared (LWIR) is the ideal wavelength band for long-range optical communication. Here, we propose a method for the achromatic generation of focused optical vortex (FOV) beams with arbitrary homogenous polarization states in the LWIR using a single all-germanium metasurface. The chromatic aberration and polarization sensitivity are eliminated by superimposing a polarization-insensitive geometric phase and a dispersion-engineered dynamic phase. The method is validated using two broadband FOV generators with the same diameter and focal length but different topological charges. The results indicate that the FOV generators are broadband achromatic and polarization insensitive. The proposed method may pave the way for chip-scale optical communication devices.
Optical vortex (OV) beams characterized by the Hilbert factor
Metasurfaces are two-dimensional metamaterials that possess powerful light modulation capabilities and can manipulate the phase, amplitude, and polarization of light locally, making them highly promising as a powerful platform for integrated optics. To date, a wide range of metasurfaces with sophisticated features have been demonstrated, such as beam deflector [13], metalens [14–20], cloak [21–23], polarizer [24], information encryption [25–29], analog computation [30–32], metasurface interferometry [33], and meta-holograms [34], covering a wide spectrum from visible to terahertz frequencies. Yu [35] et al. were the first to demonstrate the generation of OV beams via a metasurface consisting of a V-shaped plasmonic antenna. Owing to the intrinsic absorption loss of metals in the visible region, the efficiency of such metasurfaces is highly limited. To overcome this, all-dielectric metasurfaces composed of high-refractive-index materials have been proposed to achieve high efficiency in generating OV beams [36, 37]. Zhan [38] et al. proposed an OV generator based on a silicon nitride metasurface with an efficiency much higher than its plasmonic counterparts. By superimposing hyperbolic and helical phase profiles, Tang [39] further reduced the bulk of the optical system by generating FOV beams using only a single metasurface. Sroor et al. [40] integrated the metasurface into the laser cavity, which increased the mode purity of the generated OV beam to 92%. Although a wide variety of FOV generator metasurfaces have been developed, most of them are monochromatic. Considering the needs of practical applications, it is clear that broadband achromatic FOV generators are more desirable owing to their powerful functionalities. Recently, Ou et al. [41, 42] proposed a broadband achromatic FOV generator based on silicon metasurface in the mid-infrared region. However, such silicon metasurfaces are highly sensitive to the state of polarization (SOP) of incident light. The longwave infrared (LWIR) corresponds to an atmospheric transparent window, which makes it an ideal spectrum for optical wireless communications. However, to the best of our knowledge, no achromatic flat FOV generator for LWIR has been reported thus far.
In this study, we demonstrate a general method to achromatically generate FOV beams via a single germanium metasurface with high efficiency and high mode purity in the LWIR band. It should be noted that our metasurface is polarization-insensitive and can transform plane waves with arbitrary SOP to FOV with an arbitrary OAM state. The proposed metasurface is composed of anisotropic nanostructures, and each nanostructure behaves as a quasi-ideal half-wave plate that flips the chirality of the incident circularly polarized (CP) light. A polarization-insensitive geometric phase is imparted on the metasurface by limiting the rotation angle of each nanostructure to 0° or 90° [43]. The anisotropic geometry also allows us to finely regulate the dispersion of the dynamic phase [44, 45]. By combining the polarization-insensitive geometric phase and dispersion-engineered dynamic phase, the desired group delay and phase profile are simultaneously imparted on the metasurface, resulting in good polarization insensitivity and achromatic performance.
To validate our method, we designed and simulated two broadband achromatic flat-FOV generators. The two FOV generators have the same diameter of 200 μm, the same focal length of 300 μm, and different topological charge numbers (
For most applications, intrinsic divergence of the OV beam is not preferred, and lenses are used to control the beam radius and increase the light intensity. The functionality of generating and focusing OV beams can be integrated on a single metasurface by superimposing radially hyperbolic and azimuthally linear phase profiles as follows:
Where
where
Formula [3] and Formula [4] show the group delay condition and phase condition, respectively, that need to be fulfilled by the achromatic FOV generator.
To precisely modulate the dispersion of meta-atoms, anisotropic nanopillar combinations were chosen as the archetypes of the meta-atom, as shown in the inset of Figure 2A. Moreover, each nanostructure on the metasurface is designed to be a miniature half-wave plate, which can flip the chirality of the incident CP wave. When RCP light is incident from the substrate, the metasurface converts it into an LCP converged vortex beam with a topological charge of
where
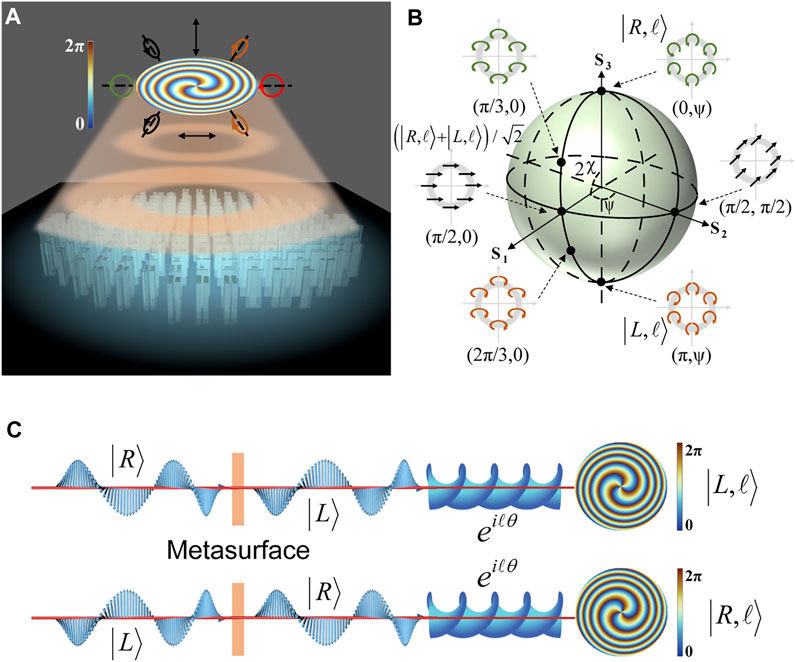
FIGURE 1. Schematic of the flat FOV generator. (A) Schematic of the metasurface consisting of anisotropic nanostructures for generating FOV beams with arbitrary SOP. (B) Schematic illustration of
For incident light with a more general SOP
The SOP corresponding to any point on the high-order Poincaré sphere (HOP) can be decomposed into a linear combination of the SOP corresponding to the north and south poles, as shown in Figure 1B. For all possible scalar SOPs of the vortex beam, we can find the corresponding points on the corresponding
In addition, the Jones matrix of the metasurface can be expressed as
Formula [10] implies that a metasurface with only one wavelength thickness integrates the functions of a half-wave plate, spiral phase plate, and lens. Considering that the metasurface also has the ability to eliminate chromatic aberration, we can see that the entire optical system is highly integrated.
Although it is counterintuitive to utilize anisotropic nanostructures to form polarization-insensitive metasurfaces, this can be understood in terms of the geometric phase. For the anisotropic meta-atom shown in Figure 2A, its transmittance properties after a rotation angle α can be described by the Jones matrix as follows:
where
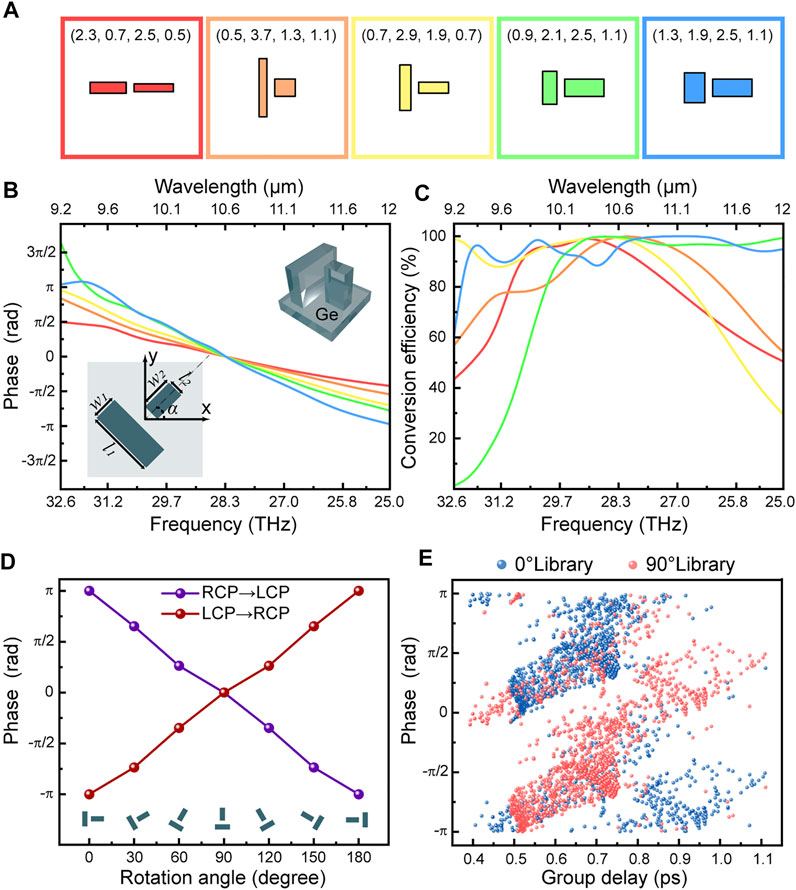
FIGURE 2. Numerical results of the meta-atoms. (A) Schematic of the five selected meta-atoms. (B,C) Phase and polarization conversion efficiency of the five selected meta-atoms. The five meta-atoms with different geometrical dimensions satisfy the screening conditions mentioned in the text, i.e. linear phase versus frequency and high polarization conversion efficiency within the designed bandwidth, but different group delays (the slope of phase with respect to the frequency). Each color curve corresponds to a meta-atom in the same colored box in (A). The parameters in the colored boxes correspond to the geometric parameters (l1, w1, l2, w2) of the nanopillars shown in the inset of (B) in microns, and the gap between nanopillars is g = 0.5 μm. (D) Geometric phase with respect to rotation angle for the same meta-atom under LCP and RCP incidence. The meta-atom has the same geometrical parameters as that in the yellow box in (A). (E) The phase and group delay for all meta-atoms in the library. Each meta-atom is represented by a blue and red point in the plot because a 90° rotation can impart a phase change of πwithout changing the group delay.
The properties of meta-atoms are also fundamentally determined by the constituent materials. Due to mature fabrication methods, silicon is widely used as the base material for metasurfaces. However, in the LWIR band, germanium has smaller absorption and higher refractive index than silicon, so the nanostructures composed of germanium materials can modulate light more efficiently. Therefore, germanium was selected as the constituent material for the meta-atom. Currently, it is still very challenging to deposit tens of microns of germanium on other materials due to material stress, so we also chose germanium as a substrate material so that in the future, we can inexpensively process metasurfaces on a single germanium wafer. We built up a meta-atoms library, and there were multiple mutually parallel nanopillars in a single meta-atom. Figure 2A shows the case of two nanopillars in one meta-atom, and a detailed discussion on the meta-atoms library is included in Supplementary Material. The nanopillars in every unit cell have the same height H = 10 μm and the same gap g = 0.5 µm, and the finest structure size is forced to be larger than 1 μm. The lattice constant P of the unit cell was chosen to be 6.2 μm to satisfy both the Nyquist law and the requirement to suppress higher-order diffraction [48].
To obtain the phase spectrum of each nanostructure, we conducted simulations using a finite-difference time-domain (FDTD) solver from Lumerical [49]. Periodic conditions were applied in the transverse direction, and the perfect matched layer (PML) condition was applied in the longitudinal direction with respect to the propagation of light, and CP illumination was applied from the substrate. After obtaining the phase spectra of all meta-atoms, we screened the meta-atoms suitable for constituting the achromatic FOV metasurface according to Formula [2]. We used a homemade linear regression program to screen the meta-atoms in the library, with an R-squared number greater than 0.98 and an avaverage conversion efficiency greater than 80%. The phase spectra and conversion efficiency spectra of the five meta-atoms meeting the above screening conditions are shown in Figure 2B,C. As shown in Figure 2E, nanostructure rotation does not affect the dispersion (group delay) of meta-atoms, but nanostructures with 0° and 90° rotation angles have a phase difference of π, which enriches the number of combinations of phase and group delays that can be implemented in our library, allowing us to meet the requirements of more achromatic FOV metasurface designs.
When the topological charge
To validate our method, we designed and simulated an achromatic metalens with a diameter of 200 μm and a numerical aperture (NA) of 0.32. We calculated the phase distribution and group delay distribution required for the achromatic metalens according to Formula [3] and Formula [4], respectively. We then discretized the required phase profile and group delay profile and selected the meta-atom in the library that best matched the required phase and group delay pairs, as shown in Figures 3B,C. Figure 3A shows the layout of a quarter of the designed metalens. Figure 4A shows the simulated intensity profile in the x-z plane under RCP, LCP, and XLP illumination. The metalens can focus light over a wide range of wavelengths, and the focal point does not shift with wavelength, indicating good achromatic performance. The metalens has the same intensity profile under three polarized incidences, which indicates good polarization insensitivity performance. We extracted the focal length of the metalens at the selected wavelengths by analyzing the intensity distribution in the x–z plane, where the focal point is defined as the position corresponding to the maximum intensity on the z-axis. Figure 5A shows the relative focal shift of the metalens, and the relative focal shift is defined as
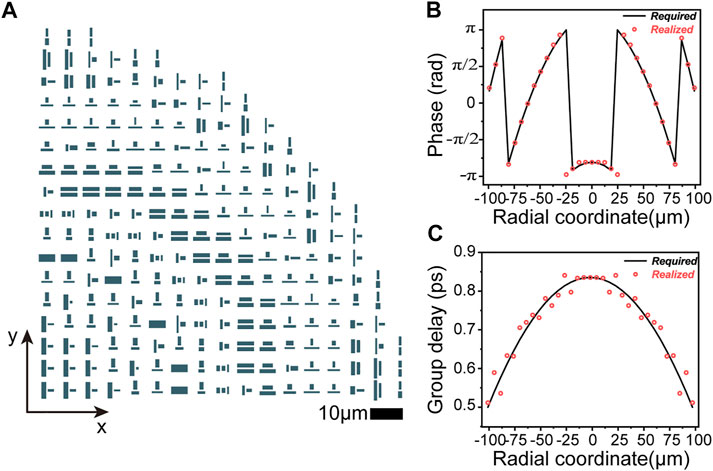
FIGURE 3. Design result of the broadband achromatic metalens. (A) Layout of the quarter of the metalens. (B,C) Realized (red circles) and required (black curves) phase and group delay at each radial coordinate on the metalens.
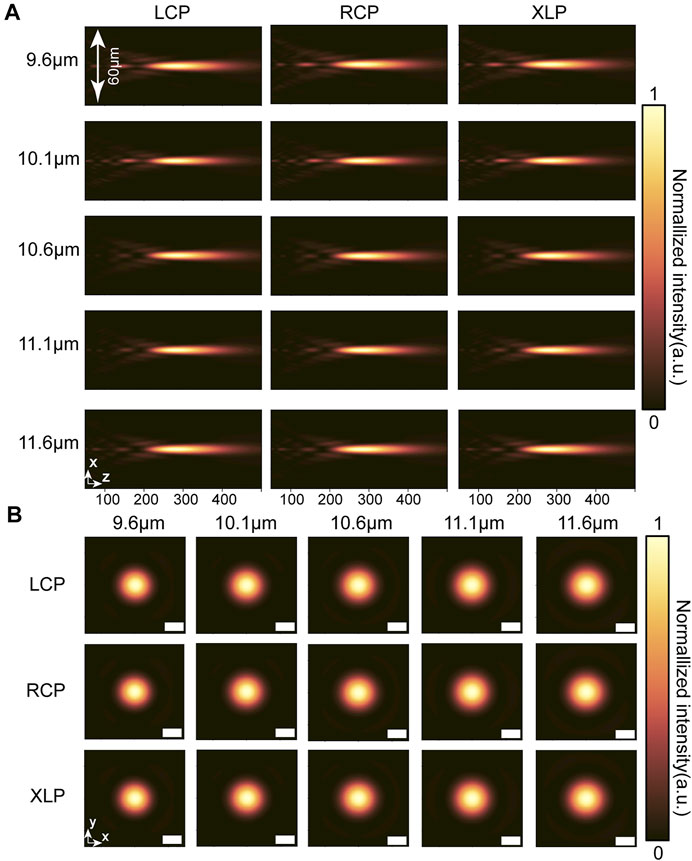
FIGURE 4. Intensity distribution of the broadband achromatic metalens. (A) Intensity profiles in the x-z plane at selected wavelengths. From left to right, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. (B) Intensity distribution at the focal plane at selected wavelengths. From top to bottom, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. Scale bar is 10 µm.
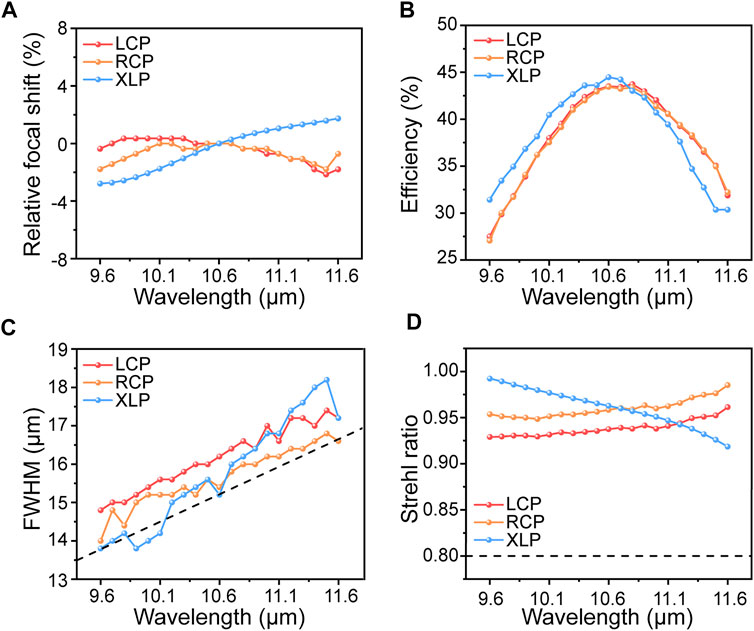
FIGURE 5. Performance characterization of the metalens. (A) Relative focal shift of the metalens. (B) Efficiency of the metalens. (C)Full-width-half-maximum of the intensity at the focal plane. (D) Strehl ratio of the metalens. The black dashed lines in (C) and (D) represent the diffraction limit.
Figure 4B shows the point spread function (PSF) of the metalens in the focal plane under RCP, LCP, and XLP illumination. The symmetric focal spot was clear, and no focal spot diffusion caused by defocusing and spherical aberration was evident at any wavelength [50]. Based on the intensity distribution in the focal plane, we extracted some metrics to quantify the performance of the metalens, such as full width half maximum (FWHM), Strehl ratio, and efficiency. Figure 5C shows the FWHM of the metalens, where the black dashed line indicates the FWHM corresponding to the ideal Airy disk. Figure 5D shows the Strehl ratio of the metalens. The Strehl ratio is defined as in Ref. [51], and the black dashed line in Figure 5D indicates the diffraction limit criterion referred to by Marehal. From the FWHM and Strehl ratio, we can conclude that our metalens is capable of diffraction-limited focusing in the continuous wavelength band. Figure 5B illustrates the efficiency of the metalens, which is defined as the power in the focal spot (circles of radius three times the FWHM spanning the center of the focal spot) compared to the power of the incident light. The efficiency of the metalens is highest around the design wavelength
We designed and simulated an FOV generator based on the method proposed above. The FOV generator has a diameter of 200 μm, focal length of 300 μm, design wavelength of 10.6 μm, topological number of −2, and design operating bandwidth of 2 μm. Figure 6A shows the layout of the metasurface, which consists of mutually parallel or perpendicular nanopillars arranged in a square lattice. The design process of the FOV generator was the same as that of the metalens. First, we calculated the desired phase and group delay profiles using Formula [2] and Formula [3]. Then, we discretized the group delay and phase profiles according to the lattice constant and selected a meta-atom at each coordinate that provided the best match to the desired group delay and phase pair in the library. Figures 6B,C illustrate the group delay and phase required for the ideal achromatic FOV generator, as well as the group delay and phase that can be realized by the metasurface. The required group delay and phase exhibit small inconsistencies with the realized ones.
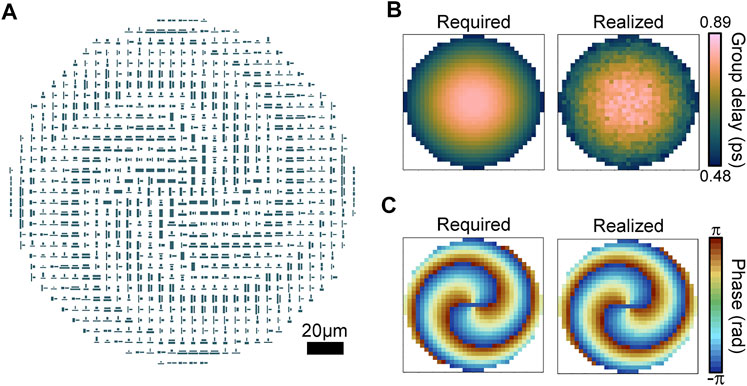
FIGURE 6. Design of the broadband achromatic and polarization insensitive flat FOV generator. (A) Layout of the flat FOV generator. (B) Required group delay (left) and realized group delay (right) of the flat FOV generator at each coordinate. (C) Required phase (left) and realized phase (right) of the flat FOV generator at each coordinate.
Figure 7A shows the intensity distribution in the x-z plane for the FOV generator under LCP, RCP, and XLP illumination. The focal length of the FOV generator is constant at all selected wavelengths, which indicates that the FOV generator has good achromatic performance, and a similar intensity distribution under LCP, RCP, and XLP incidence confirms that the FOV generator is polarization-insensitive. Figure 7B shows the intensity and phase distributions of the FOV generator in the focal plane. The donut-shaped intensity distribution and the spiral-shaped phase distribution are clear in the focal plane, both of which confirm the existence of OV at the origin. The phase distribution confirms that the transmitted beams carry an OAM of
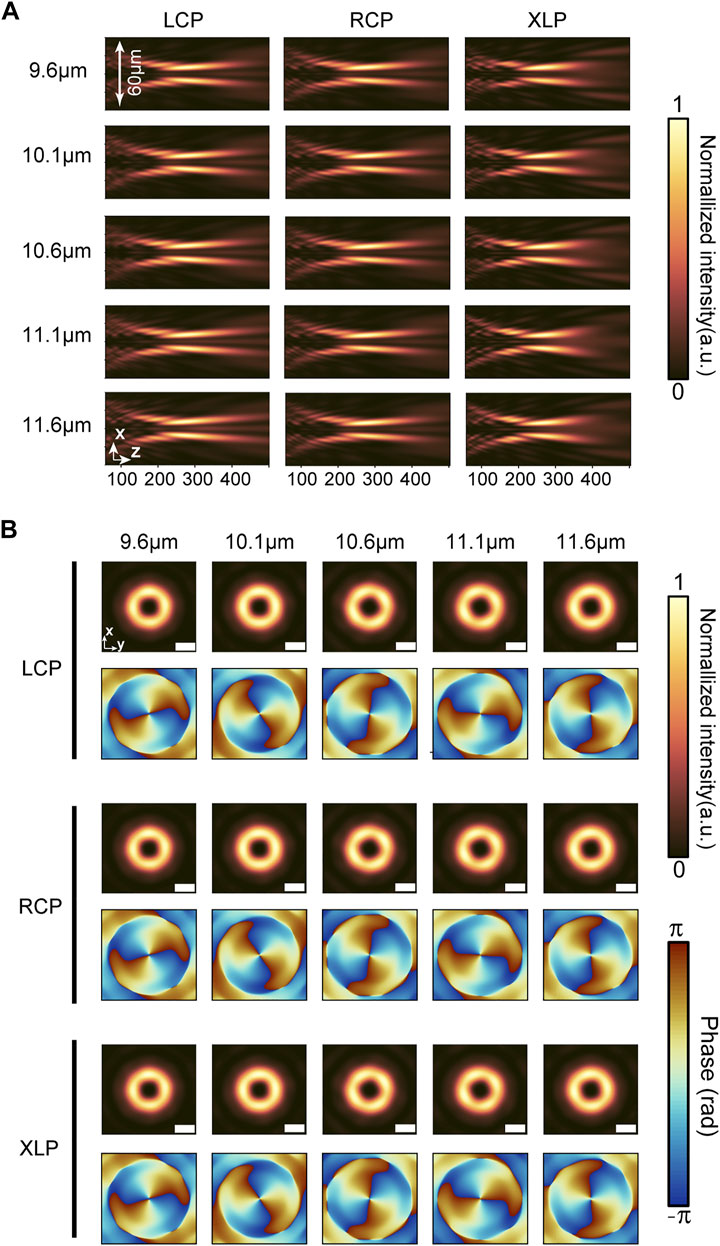
FIGURE 7. Intensity and phase distributions for the FOV generator. (A) Intensity profiles in the x-z plane at selected wavelengths. From left to right, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. (B) Intensity profiles and phase profiles at the focal plane at selected wavelengths. From top to bottom, each column corresponds to LCP incidence, RCP incidence, and XLP incidence. Scale bar is 10 µm.
Figure 8D shows the efficiency of the FOV generator. Efficiency is defined as the power inside the donut ring divided by the power of the incident light, which can be expressed as follows:
where
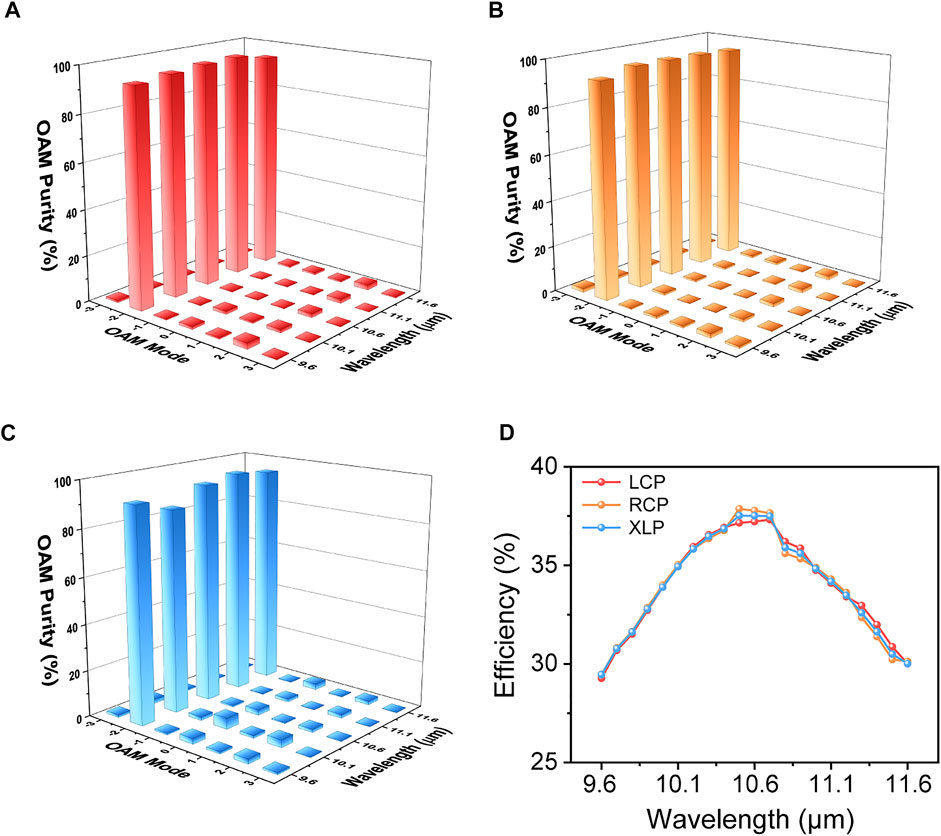
FIGURE 8. Efficiency and mode purity of the FOV generator. (A,B,C) Mode purity of the generated OV under LCP incidence, RCP incidence, and XLP incidence, respectively. (D) Efficiency of the flat FOV generator under LCP, RCP, and XLP incidence.
To quantitatively describe the modal purity of the OV beams, we performed a modal decomposition analysis of the phase in the focal plane [53]. The Fourier relationship between the OAM mode and the phase distribution can be expressed as
where
We proposed a general method to implement a metasurface for generating FOV beams with arbitrary scalar SOPs in a broad continuous wavelength range. Although the proposed FOV generator works in the LWIR band, this design principle can be applied to arbitrary regions of the electromagnetic spectrum.
The average efficiency of the metasurfaces demonstrated in the main text is approximately 44% (metasurface Ⅰ with
A comparison between this study and previously reported flat FOV generators is presented in Table 1. Compared to previously reported works, our metasurfaces have the advantage of broadband achromatic, high mode purity and polarization insensitivity.
In summary, we theoretically proposed two broadband achromatic polarization-insensitive FOV generators in the LWIR range based on an all-germanium metasurface. Metasurface Ⅰ with
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
JG and XJ proposed the idea and supervised the entire work. NS and NX performed the simulation and wrote the original manuscript. HL and XC deduced the theory method. QS conducted the design work and reviewed the manuscript. YT and DS discussed the results and analyzed the data.
This research was funded by the National Natural Science Foundation of China (NSFC), grant number 61901437.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.846718/full#supplementary-material
1. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical Communications Using Orbital Angular Momentum Beams. Adv Opt Photon (2015) 7(1):66–106. doi:10.1364/AOP.7.000066
2. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical Vortices 30 Years on: OAM Manipulation from Topological Charge to Multiple Singularities. Light Sci Appl (2019) 8:90. doi:10.1038/s41377-019-0194-2
3. He H, Friese MEJ, Heckenberg NR, Rubinsztein-Dunlop H. Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity. Phys Rev Lett (1995) 75(5):826–9. doi:10.1103/PhysRevLett.75.826
4. Fang X, Ren H, Gu M. Orbital Angular Momentum Holography for High-Security Encryption. Nat Photon (2020) 14(2):102–8. doi:10.1038/s41566-019-0560-x
5. Zhuang X. Unraveling DNA Condensation with Optical Tweezers. Science (2004) 305(5681):188–90. doi:10.1126/science.1100603
6. Stav T, Faerman A, Maguid E, Oren D, Kleiner V, Hasman E, et al. Quantum Entanglement of the Spin and Orbital Angular Momentum of Photons Using Metamaterials. Science (2018) 361(6407):1101–4. doi:10.1126/science.aat9042
7. Tamburini F, Anzolin G, Umbriaco G, Bianchini A, Barbieri C. Overcoming the Rayleigh Criterion Limit with Optical Vortices. Phys Rev Lett (2006) 97(16):163903. doi:10.1103/PhysRevLett.97.163903
8. Sueda K, Miyaji G, Miyanaga N, Nakatsuka M. Laguerre-Gaussian Beam Generated with a Multilevel Spiral Phase Plate for High Intensity Laser Pulses. Opt Express (2004) 12(15):3548–53. doi:10.1364/OPEX.12.003548
9. Turnbull GA, Robertson DA, Smith GM, Allen L, Padgett MJ. The Generation of Free-Space Laguerre-Gaussian Modes at Millimetre-Wave Frequencies by Use of a Spiral Phaseplate. Opt Commun (1996) 127(4):183–8. doi:10.1016/0030-4018(96)00070-3
10. Karimi E, Piccirillo B, Nagali E, Marrucci L, Santamato E. Efficient Generation and Sorting of Orbital Angular Momentum Eigenmodes of Light by Thermally Tuned Q-Plates. Appl Phys Lett (2009) 94(23):231124. doi:10.1063/1.3154549
11. Wang X, Nie Z, Liang Y, Wang J, Li T, Jia B. Recent Advances on Optical Vortex Generation. Nanophotonics (2018) 7(9):1533–56. doi:10.1515/nanoph-2018-0072
12. Liu J, Wang J. Demonstration of Polarization-Insensitive Spatial Light Modulation Using a Single Polarization-Sensitive Spatial Light Modulator. Sci Rep (2015) 5(1):9959. doi:10.1038/srep09959
13. Wang D, Hwang Y, Dai Y, Si G, Wei S, Choi DY, et al. Broadband High‐Efficiency Chiral Splitters and Holograms from Dielectric Nanoarc Metasurfaces. Small (2019) 15(20):1900483. doi:10.1002/smll.201900483
14. McClung A, Mansouree M, Arbabi A. At-will Chromatic Dispersion by Prescribing Light Trajectories with Cascaded Metasurfaces. Light Sci Appl (2020) 9:93. doi:10.1038/s41377-020-0335-7
15. Zhao M, Chen MK, Zhuang Z-P, Zhang Y, Chen A, Chen Q, et al. Phase Characterisation of Metalenses. Light Sci Appl (2021) 10(1):52. doi:10.1038/s41377-021-00492-y
16. Chung H, Miller OD. High-NA Achromatic Metalenses by Inverse Design. Opt Express (2020) 28(5):6945–65. doi:10.1364/OE.385440
17. She A, Zhang S, Shian S, Clarke DR, Capasso F. Large Area Metalenses: Design, Characterization, and Mass Manufacturing. Opt Express (2018) 26(2):1573–85. doi:10.1364/OE.26.001573
18. Huang L, Coppens Z, Hallman K, Han Z, Böhringer KF, Akozbek N, et al. Long Wavelength Infrared Imaging under Ambient thermal Radiation via an All-Silicon Metalens. Opt Mater Express (2021) 11(9):2907–14. doi:10.1364/OME.434362
19. Zhou H, Chen L, Shen F, Guo K, Guo Z. Broadband Achromatic Metalens in the Midinfrared Range. Phys Rev Appl (2019) 11(2):024066. doi:10.1103/PhysRevApplied.11.024066
20. Ding X, Kang Q, Guo K, Guo Z. Tunable GST Metasurfaces for Chromatic Aberration Compensation in the Mid-infrared. Opt Mater (2020) 109:110284. doi:10.1016/j.optmat.2020.110284
21. Chu H, Li Q, Liu B, Luo J, Sun S, Hang ZH, et al. A Hybrid Invisibility Cloak Based on Integration of Transparent Metasurfaces and Zero-index Materials. Light Sci Appl (2018) 7(1):50. doi:10.1038/s41377-018-0052-7
22. Xu H-X, Hu G, Wang Y, Wang C, Wang M, Wang S, et al. Polarization-insensitive 3D Conformal-Skin Metasurface Cloak. Light Sci Appl (2021) 10(1):75. doi:10.1038/s41377-021-00507-8
23. Wang C, Yang Y, Liu Q, Liang D, Zheng B, Chen H, et al. Multi-frequency Metasurface Carpet Cloaks. Opt Express (2018) 26(11):14123–31. doi:10.1364/OE.26.014123
24. Wang S, Deng Z-L, Wang Y, Zhou Q, Wang X, Cao Y, et al. Arbitrary Polarization Conversion Dichroism Metasurfaces for All-In-One Full Poincaré Sphere Polarizers. Light Sci Appl (2021) 10(1):24. doi:10.1038/s41377-021-00468-y
25. Cui T-J, Liu S, Li L-L. Information Entropy of Coding Metasurface. Light Sci Appl (2016) 5(11):e16172. doi:10.1038/lsa.2016.172
26. Deng Y, Wang M, Zhuang Y, Liu S, Huang W, Zhao Q. Circularly Polarized Luminescence from Organic Micro-/nano-structures. Light Sci Appl (2021) 10(1):76. doi:10.1038/s41377-021-00516-7
27. Jang J, Badloe T, Rho J. Unlocking the Future of Optical Security with Metasurfaces. Light Sci Appl (2021) 10(1):144. doi:10.1038/s41377-021-00589-4
28. Zhao R, Sain B, Wei Q, Tang C, Li X, Weiss T, et al. Multichannel Vectorial Holographic Display and Encryption. Light Sci Appl (2018) 7(1):95. doi:10.1038/s41377-018-0091-0
29. Deng ZL, Tu QA, Wang Y, Wang ZQ, Shi T, Feng Z, et al. Vectorial Compound Metapixels for Arbitrary Nonorthogonal Polarization Steganography. Adv Mater (2021) 33(43):2103472. doi:10.1002/adma.202103472
30. Mohammadi Estakhri N, Edwards B, Engheta N. Inverse-designed Metastructures that Solve Equations. Science (2019) 363(6433):1333–8. doi:10.1126/science.aaw2498
31. Silva A, Monticone F, Castaldi G, Galdi V, Alù A, Engheta N. Performing Mathematical Operations with Metamaterials. Science (2014) 343(6167):160–3. doi:10.1126/science.1242818
32. Qian C, Lin X, Lin X, Xu J, Sun Y, Li E, et al. Performing Optical Logic Operations by a Diffractive Neural Network. Light Sci Appl (2020) 9(1):59. doi:10.1038/s41377-020-0303-2
33. Georgi P, Massaro M, Luo K-H, Sain B, Montaut N, Herrmann H, et al. Metasurface Interferometry toward Quantum Sensors. Light Sci Appl (2019) 8(1):70. doi:10.1038/s41377-019-0182-6
34. Overvig AC, Shrestha S, Malek SC, Lu M, Stein A, Zheng C, et al. Dielectric Metasurfaces for Complete and Independent Control of the Optical Amplitude and Phase. Light Sci Appl (2019) 8(1):92. doi:10.1038/s41377-019-0201-7
35. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science (2011) 334(6054):333–7. doi:10.1126/science.1210713
36. Yan C, Li X, Pu M, Ma X, Zhang F, Gao P, et al. Generation of Polarization-Sensitive Modulated Optical Vortices with All-Dielectric Metasurfaces. ACS Photon (2019) 6(3):628–33. doi:10.1021/acsphotonics.8b01119
37. Zhang F, Zeng Q, Pu M, Wang Y, Guo Y, Li X, et al. Broadband and High-Efficiency Accelerating Beam Generation by Dielectric Catenary Metasurfaces. Nanophotonics (2020) 9(9):2829–37. doi:10.1515/nanoph-2020-0057
38. Zhan A, Colburn S, Trivedi R, Fryett TK, Dodson CM, Majumdar A. Low-Contrast Dielectric Metasurface Optics. ACS Photon (2016) 3(2):209–14. doi:10.1021/acsphotonics.5b00660
39. Tang S, Ding F. High-efficiency Focused Optical Vortex Generation with Geometric gap-surface Plasmon Metalenses. Appl Phys Lett (2020) 117(1):011103. doi:10.1063/5.0014822
40. Sroor H, Huang Y-W, Sephton B, Naidoo D, Vallés A, Ginis V, et al. High-purity Orbital Angular Momentum States from a Visible Metasurface Laser. Nat Photon (2020) 14(8):498–503. doi:10.1038/s41566-020-0623-z
41. Ou K, Yu F, Li G, Wang W, Miroshnichenko AE, Huang L, et al. Mid-infrared Polarization-Controlled Broadband Achromatic Metadevice. Sci Adv (2020) 6(37):eabc0711. doi:10.1126/sciadv.abc0711
42. Ou K, Yu F, Li G, Wang W, Chen J, Miroshnichenko AE, et al. Broadband Achromatic Metalens in Mid‐Wavelength Infrared. Laser Photon Rev (2021) 15:2100020. doi:10.1002/lpor.202100020
43. Chen WT, Zhu AY, Sisler J, Bharwani Z, Capasso F. A Broadband Achromatic Polarization-Insensitive Metalens Consisting of Anisotropic Nanostructures. Nat Commun (2019) 10(1):355. doi:10.1038/s41467-019-08305-y
44. Wang S, Wu PC, Su V-C, Lai Y-C, Hung Chu C, Chen J-W, et al. Broadband Achromatic Optical Metasurface Devices. Nat Commun (2017) 8(1):187. doi:10.1038/s41467-017-00166-7
45. Chen WT, Zhu AY, Sanjeev V, Khorasaninejad M, Shi Z, Lee E, et al. A Broadband Achromatic Metalens for Focusing and Imaging in the Visible. Nat Nanotech (2018) 13(3):220–6. doi:10.1038/s41565-017-0034-6
46. Devlin RC, Ambrosio A, Rubin NA, Mueller JPB, Capasso F. Arbitrary Spin-To-Orbital Angular Momentum Conversion of Light. Science (2017) 358(6365):896–901. doi:10.1126/science.aao5392
47. Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-Order Poincaré Sphere, Stokes Parameters, and the Angular Momentum of Light. Phys Rev Lett (2011) 107(5):053601. doi:10.1103/PhysRevLett.107.053601
48. Khorasaninejad M, Shi Z, Zhu AY, Chen WT, Sanjeev V, Zaidi A, et al. Achromatic Metalens over 60 Nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett (2017) 17(3):1819–24. doi:10.1021/acs.nanolett.6b05137
49.Lumerical. Lumerical Is Now Part of the Ansys Family (2022). Available from: https://www.lumerical.com/ (Accessed January 31, 2022).
50. Song N, Xu N, Shan D, Zhao Y, Gao J, Tang Y, et al. Broadband Achromatic Metasurfaces for Longwave Infrared Applications. Nanomaterials (2021) 11(10):2760. doi:10.3390/nano11102760
51. Aieta F, Kats MA, Genevet P, Capasso F. Multiwavelength Achromatic Metasurfaces by Dispersive Phase Compensation. Science (2015) 347(6228):1342–5. doi:10.1126/science.aaa2494
52. Fan Q, Liu M, Yang C, Yu L, Yan F, Xu T. A High Numerical Aperture, Polarization-Insensitive Metalens for Long-Wavelength Infrared Imaging. Appl Phys Lett (2018) 113(20):201104. doi:10.1063/1.5050562
53. Jack B, Padgett MJ, Franke-Arnold S. Angular Diffraction. New J Phys (2008) 10(10):103013. doi:10.1088/1367-2630/10/10/103013
54. Zhao Y, Belkin MA, Alù A. Twisted Optical Metamaterials for Planarized Ultrathin Broadband Circular Polarizers. Nat Commun (2012) 3:870. doi:10.1038/ncomms1877
55. Karimi E, Schulz SA, De Leon I, Qassim H, Upham J, Boyd RW. Generating Optical Orbital Angular Momentum at Visible Wavelengths Using a Plasmonic Metasurface. Light Sci Appl (2014) 3(5):e167. doi:10.1038/lsa.2014.48
56. Shi Z, Khorasaninejad M, Huang Y-W, Roques-Carmes C, Zhu AY, Chen WT, et al. Single-Layer Metasurface with Controllable Multiwavelength Functions. Nano Lett (2018) 18(4):2420–7. doi:10.1021/acs.nanolett.7b05458
57. Zhou T, Liu Q, Liu Y, Zang X. Spin-independent Metalens for Helicity-Multiplexing of Converged Vortices and Cylindrical Vector Beams. Opt Lett (2020) 45(21):5941–4. doi:10.1364/OL.404436
Keywords: broadband achromatism, optical vortex, germanium metasurface, polarization insensitive, orbital angular momentum, modal purity, anisotropic nanostructure, longwave infrared
Citation: Song N, Xu N, Gao J, Jiang X, Shan D, Tang Y, Sun Q, Liu H and Chen X (2022) Broadband Achromatic and Polarization Insensitive Focused Optical Vortex Generator Based on Metasurface Consisting of Anisotropic Nanostructures. Front. Phys. 10:846718. doi: 10.3389/fphy.2022.846718
Received: 31 December 2021; Accepted: 31 January 2022;
Published: 25 February 2022.
Edited by:
Pei Zhang, Xi’an Jiaotong University, ChinaReviewed by:
Arka Majumdar, University of Washington, United StatesCopyright © 2022 Song, Xu, Gao, Jiang, Shan, Tang, Sun, Liu and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jinsong Gao, Z2FvanM5OTlAMTYzLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.