Near-Optimal Variance-Based Uncertainty Relations

Learning physical properties of a quantum system is essential for the developments of quantum technologies. However, Heisenberg’s uncertainty principle constrains the potential knowledge one can simultaneously have about a system in quantum theory. Aside from its fundamental significance, the mathematical characterization of this restriction, known as ‘uncertainty relation’, plays important roles in a wide range of applications, stimulating the formation of tighter uncertainty relations. In this work, we investigate the fundamental limitations of variance-based uncertainty relations, and introduce several ‘near optimal’ bounds for incompatible observables. Our results consist of two morphologically distinct phases: lower bounds that illustrate the uncertainties about measurement outcomes, and the upper bound that indicates the potential knowledge we can gain. Combining them together leads to an uncertainty interval, which captures the essence of uncertainties in quantum theory. Finally, we have detailed how to formulate lower bounds for product-form variance-based uncertainty relations by employing entropic uncertainty relations, and hence built a link between different forms of uncertainty relations.

1 Introduction

Uncertainty principle, originally introduced by Heisenberg [1], clearly sets quantum theory apart from our classical world. Formally, it states that it is impossible to predict the outcomes of incompatible measurements simultaneously, such as the position and momentum of a particle. The corresponding mathematical formulation for position and momentum are given by Kennard in Ref. [2] (see also Ref. [3]). Later, a general form of uncertainty relation has been established by Robertson [4], and has been further improved by Schrödinger in Ref. [5], which is expressed in terms of commutator and anticommutator of obserables:

$V\left(A\right)V\left(B\right)\ge |\frac{1}{2}\langle \left[A,B\right]\rangle {|}^2+|\frac{1}{2}\langle \left\{\bar{A},\bar{B}\right\}\rangle {|}^2,(1)$

where the quantity $V(A)=⟨{\bar{A}}^2⟩$ (resp. V(B)) stands for the variance of observable A (resp. B), the operator $\bar{A}$ is defined as A− ⟨A⟩, and the expectation value ⟨ ⟩ is over the quantum state |Ψ⟩. Another way to demonstrate the joint uncertainty associated with incompatible observables is through the summation, namely V(A) + V(B) [6–9], which highlights an advantage in the parameter estimation of quantum system [10–13].

Riding the waves of information theory, entropies have been used to quantify the uncertainties associated with quantum measurements [14]. For instance, the entropies of probability distributions of canonically conjugate variables obey Białynicki-Birula-Mycielski uncertainty relation [15]. It is noteworthy that Heisenberg’s uncertainty relation follows from Ref. [15] as a special case. The entropic uncertainty relation for any pair of bounded observables is established by Deutsch in Ref. [16]. An improved expression was subsequently conjectured by Kraus [17] and then had been proved by Maassen and Uffink [18]. With access to a memory system, the conventional entropic uncertainty relations have been further generalized to entanglement-assisted formalism [19]. Soon afterwards, several improvements and extensions, including the cases of multiple measurements, universal uncertainty regions and quantum processes, have been proposed in Refs. [20–25]. Recently, beyond inertial frames, the uncertainty trade-off occurred near the event horizon of a Schwarzschild black hole [26] and the relativistic protocol of an uncertainty game in the presence of localized fermionic quantum fields inside cavities [27] have also been demonstrated.

Aside from their theoretical significance [28], these uncertainty relations support a variety of applications and have been widely used in current quantum technologies, such as analyzing the security of quantum key distribution protocols [19], witnessing quantum correlations [29–32], and even inferring causality from quantum dynamics [33]. Thus, pushing the boundary of uncertainty relation will not only deepen our understanding of quantum foundations, but also has impact on practical applications.

In this work, we focus on the case of variance-based uncertainty relations, with the forms of both product and summation, and introduce the concept of uncertainty interval. The formulation of such an interval can of course be subdivided into two, namely finding the lower bound and upper bounds for joint uncertainties. To do so, we establish the partial Cauchy-Schwarz inequality, which generalizes the standard Cauchy-Schwarz inequality, and use this toolkit to construct near-optimal bounds for variance-based uncertainty relations. Numerical results highlight the advantages of our framework.

2 Product-Form Variance-Based Uncertainty Relations

Throughout this paper, we consider quantum systems acting on finite-dimensional Hilbert space. Let us start with a pair of incompatible observables A and B, and denote their spectral decompositions as A = ∑_ia_i|a_i⟩⟨a_i| and B = ∑_ib_i|b_i⟩⟨b_i| respectively. On the other hand, assume the alternative observable $\bar{A}$ and $\bar{B}$ have the following spectral decompositions; that are $\bar{A}={\sum }_i{a}_i^{\prime }|a_i\rangle \langle a_i|$ and $\bar{B}={\sum }_i{b}_i^{\prime }|b_i\rangle \langle b_i|$. Remark that, here all the eigenvalues are real numbers, i.e. $a_i,a_i^{\prime },b_i,b_i^{\prime }\in \mathbb{R}$. Now for any given orthonormal basis {|ψ_i⟩}, we can re-express $\bar{A}|\mathrm{\Psi }\rangle$ and $\bar{B}|\mathrm{\Psi }\rangle$ as ∑_iα_i|ψ_i⟩ and ∑_iβ_i|ψ_i⟩ respectively. It is worth mentioning that in general both $\bar{A}|\mathrm{\Psi }\rangle$ and $\bar{B}|\mathrm{\Psi }\rangle$ are unnormalized, and hence the vectors (α_i) and (β_i) do not forms probability distributions. Then, by defining the absolute value of α_i and β_i as x_i and y_i respectively, the variance of observables A and B can be rewritten as

$V\left(A\right)=|\vec{x}{|}^2,V\left(B\right)=|\vec{y}{|}^2,(2)$

and thus we have

$V\left(A\right)V\left(B\right)=|\vec{x}{|}^2\cdot |\vec{y}{|}^2.(3)$

It now follows from Cauchy-Schwarz inequality immediately that

$V\left(A\right)V\left(B\right)\ge {\left(\sum _i{x}_i{y}_i\right)}^2.(4)$

We note that such a choice of x_i and y_i leads directly to the main results presented in a recent formulation of strong uncertainty relation [34]. Clearly, this is not the only choice of x_i and y_i. By setting x_i as $|a_i^{\prime }|\sqrt{⟨\mathrm{\Psi }|a_i⟩⟨a_i|\mathrm{\Psi }⟩}$ and y_i as $|b_i^{\prime }|\sqrt{⟨\mathrm{\Psi }|b_i⟩⟨b_i|\mathrm{\Psi }⟩}$, we re-obtain another part of results constructed in Ref. [34]. Here, for simplicity, we further denote the Uhlmann’s fidelity between |Ψ⟩ and |a_i⟩ (|b_i⟩) as $F_i^a$ $(F_i^b)$, which are

$F_i^a=\langle \mathrm{\Psi }|a_i\rangle \langle a_i|\mathrm{\Psi }\rangle ,F_i^b=\langle \mathrm{\Psi }|b_i\rangle \langle b_i|\mathrm{\Psi }\rangle .(5)$

A key observation in this work is that any improvement over the well-known Cauchy-Schwarz inequality will give us a better bound of variance-based uncertainty relation, with the same amount of information required in Eq. (4). To this end, we investigate the intrinsic connection between the arithmetic-geometric mean (AM-GM) inequality and the Cauchy-Schwarz inequality. We start by writing down the product of $|\vec{\alpha }{|}^2$ and $|\vec{\beta }{|}^2$,

$\begin{array}{ll}\hfill |\vec{\alpha }{|}^2|\vec{\beta }{|}^2=\sum _{ij}{x}_i^2{y}_j^2& =\sum _{i<j}\left(x_i^2{y}_j^2+x_j^2{y}_i^2\right)+\sum _i{x}_i^2{y}_i^2\hfill \\ \hfill & \ge \sum _{i<j}\left(2x_i{x}_j{y}_j{y}_i\right)+\sum _i{x}_i^2{y}_i^2\hfill \\ \hfill & ={\left(\sum _i{x}_i{y}_i\right)}^2.\hfill \end{array}(6)$

Above inequality is a result of n (n − 1)/2 rounds of AM-GM inequalities for $x_i^2{y}_j^2+x_j^2{y}_i^2\ge 2x_i{y}_j{x}_j{y}_i$ with different indexes. Therefore, the equality condition holds if and only if x_iy_j = x_jy_i for all i ≠ j. By defining the quantity I_k as

$\sum _{1\le i<j\le k}\left(2x_i{x}_j{y}_j{y}_i\right)+\sum _{\begin{array}{c}1\le i<j\le n\\ k<j\end{array}}\left(x_i^2{y}_j^2+x_j^2{y}_i^2\right)+\sum _{1\le i\le n}{x}_i^2{y}_i^2,(7)$

we can write the left-hand-side of Eq. 4 as

$I_0=|\vec{x}{|}^2|\vec{y}{|}^2=V\left(A\right)V\left(B\right),(8)$

which is precisely the product-form joint uncertainty. On the other hand, the previous known bound in Ref. [34], i.e. right-hand-side quantity of Eq. 4, can be reformatted as

$I_n={\left(\sum _i{x}_i{y}_i\right)}^2.(9)$

Now we introduce a chain of inequalities that outperform Cauchy-Schwarz inequality. More precisely, we have.

Theorem 1. For any n-dimensional real vectors $\vec{x}$, $\vec{y}$ with non-negative components, and I_k defined in Eq. 7, we have

$I_0\ge I_2\ge \dots ,\ge I_{n-1}\ge I_n.(10)$

Actually, for any index k it follow from the AM-GM inequality that

$I_{k+1}=I_k+\sum _{i=1}^k\left(2x_i{x}_{k+1}{y}_i{y}_{k+1}-x_i^2{y}_{k+1}^2-x_{k+1}^2{y}_i^2\right)\le I_k,(11)$

as required. Algebraically, the inequality $|\vec{x}{|}^2|\vec{y}{|}^2\ge I_k$ is obtained by applying AM-GM inequality to the first k components of both $\vec{x}$ and $\vec{y}$, and hence can be viewed as a partial Cauchy-Schwarz inequality. More importantly, such a partial Cauchy-Schwarz inequality, see Eq. 10, provides n − 2 tighter lower bounds for V(A)V(B) compared with the main result of [34], namely I₀ = V(A)V(B) ≥ I_n. In particular, we can insert more terms in the above descending chain by selecting arbitrary $x_i^2{y}_j^2+x_j^2{y}_i^2$ (i < j). For example, the inequality I₀ ≥ I_n−1 obtained from our Thm. One immediately leads to a tighter bound. More precisely, Eq. 4 can be improved to

$\begin{array}{ll}\hfill V\left(A\right)V\left(B\right)\ge & \frac{1}{4}{\left(\sum _{i=1}^{n-1}\left|\langle \left[\bar{A},{\bar{B}}_n\right]\rangle +\langle \left\{\bar{A},{\bar{B}}_n\right\}\rangle \right|\right)}^2\hfill \\ \hfill +& {\left|\langle \mathrm{\Psi }|\bar{A}|{\psi }_n\rangle \right|}^2\left(\sum _{i=1}^n{\left|\langle \mathrm{\Psi }|\bar{B}|{\psi }_n\rangle \right|}^2\right)\hfill \\ \hfill +& {\left|\langle \mathrm{\Psi }|\bar{B}|{\psi }_n\rangle \right|}^2\left(\sum _{i=1}^n{\left|\langle \mathrm{\Psi }|\bar{A}|{\psi }_n\rangle \right|}^2\right)\hfill \\ \hfill -& {\left|\langle \mathrm{\Psi }|\bar{A}|{\psi }_n\rangle \right|}^2{\left|\langle \mathrm{\Psi }|\bar{B}|{\psi }_n\rangle \right|}^2≔{\mathcal{L}}_1,\hfill \end{array}(12)$

which offers a stronger bound than that of

${\mathcal{L}}_1\ge \frac{1}{4}{\left(\sum _{i=1}^n\left|⟨\left[\bar{A},{\bar{B}}_n\right]⟩+⟨\left\{\bar{A},{\bar{B}}_n\right\}⟩\right|\right)}^2\ge {\left|⟨\bar{A}\bar{B}⟩\right|}^2.(13)$

Note that the method of constructing bounds presented here for variance-based uncertainty relations requires the same amount of information, i.e. the fidelity between quantum state and the eigenvector of observables, needed in previous works, such as the one considered in Ref. [34], but provable tighter.We now move on to further strengthening the bounds of uncertainty relations by considering the action of symmetric group ${\mathfrak{S}}_n$. For any two permutations ${\pi }_1,{\pi }_2\in {\mathfrak{S}}_n$, we define

$\begin{array}{ll}\hfill \left({\pi }_1,{\pi }_2\right)I_k=& \sum _{1\le {\pi }_1\left(i\right)<{\pi }_2\left(j\right)\le k}\left(2x_{{\pi }_1\left(i\right)}{x}_{{\pi }_2\left(j\right)}{y}_{{\pi }_2\left(j\right)}{y}_{{\pi }_1\left(i\right)}\right)\hfill \\ \hfill +& \sum _{\begin{array}{c}1\le {\pi }_1\left(i\right)<{\pi }_2\left(j\right)\le n\\ k<{\pi }_2\left(j\right)\end{array}}\left(x_{{\pi }_1\left(i\right)}^2{y}_{{\pi }_2\left(j\right)}^2+x_{{\pi }_2\left(j\right)}^2{y}_{{\pi }_1\left(i\right)}^2\right)\hfill \\ \hfill +& \sum _{{\pi }_1\left(i\right)={\pi }_2\left(j\right)}{x}_{{\pi }_1\left(i\right)}^2{y}_{{\pi }_2\left(j\right)}^2.\hfill \end{array}(14)$

It is straightforward to check that the quantity I₀ is stable under the action of ${\mathfrak{S}}_n\times {\mathfrak{S}}_n$. Writing everything out explicitly, we have.

Theorem 2. For any permutations ${\pi }_1,{\pi }_2\in {\mathfrak{S}}_n$, we have

$I_0\ge \left({\pi }_1,{\pi }_2\right)I_2\ge \dots ,\ge \left({\pi }_1,{\pi }_2\right)I_{n-1}\ge \left({\pi }_1,{\pi }_2\right)I_n.(15)$

Optimizing over the symmetric group ${\mathfrak{S}}_n$, a stronger version of the variance-based uncertainty relations is obtained.

Theorem 3. For any permutations ${\pi }_1,{\pi }_2\in {\mathfrak{S}}_n$, we have

$I_0\ge \underset{{\pi }_1,{\pi }_2\in {\mathfrak{S}}_n}{\max }\left({\pi }_1,{\pi }_2\right)I_2\ge \dots ,\ge \underset{{\pi }_1,{\pi }_2\in {\mathfrak{S}}_n}{\max }\left({\pi }_1,{\pi }_2\right)I_n.(16)$

Mathematically, above inequalities are tighter than the result in Thm. 1, since $\underset{{\pi }_1,{\pi }_2\in {\mathfrak{S}}_n}{\max }({\pi }_1,{\pi }_2)I_k\ge I_k$ holds for any permutations. Physically, the action of symmetric group works well since the overlaps between quantum state and the eigenvectors of observables are not uniformly distributed.

3 Sum-Form Variance-Based Uncertainty Relations

In this section we turn our attention to the sum-form variance-based uncertainty relations. Before doing so, let us recall the rearrangement inequality first. Let (x_i) and (y_i) be two n-tuple of real positive numbers arranged in non-increasing order, namely x_i ≥ x_i+1 and y_i ≥ y_i+1, with their direct sum, random sum and reverse sum between x_i and y_i being defined as

$\begin{array}{ll}\hfill Di≔& x_1{y}_1+x_2{y}_2+\cdots +x_n{y}_n,\hfill \\ \hfill Ra≔& x_1{y}_{\pi \left(1\right)}+x_2{y}_{\pi \left(2\right)}+\cdots +x_n{y}_{\pi \left(n\right)},\pi \in {\mathfrak{S}}_n\hfill \\ \hfill Re≔& x_1{y}_n+x_2{y}_{n-1}+\cdots +x_n{y}_1.\hfill \end{array}(17)$

Then the following lemma characterizes the relationship among these quantities; that is.

Lemma. (Rearrangement inequality) For any two non-increasing n-tuples x and y of nonnegative numbers, we have

$Di\ge Ra\ge \mathrm{R}\mathrm{e}.(18)$

From the parallelogram law, the summation of variances can be re-expressed as

$V\left(A\right)+V\left(B\right)=\frac{1}{2}\sum _i{\left(x_i+y_i\right)}^2+\frac{1}{2}\sum _i{\left(x_i-y_i\right)}^2.(19)$

Combining with the rearrangement inequality we obtain the following result.

Theorem 4. For any two permutations ${\pi }_1,{\pi }_2\in {\mathfrak{S}}_n$, we have

$\begin{array}{ll}\hfill V\left(A\right)+V\left(B\right)\ge & \frac{1}{2}\sum _i\left(x_i+y_i\right)\left(x_{{\pi }_1\left(i\right)}+y_{{\pi }_1\left(i\right)}\right)\hfill \\ \hfill +& \frac{1}{2}\sum _i\left|x_i-y_i\right|\left|x_{{\pi }_2\left(i\right)}-y_{{\pi }_2\left(i\right)}\right|.\hfill \end{array}(20)$

Remark that, by setting π₁ = (1), our newly constructed uncertainty relation outperforms similar results of sum-form variance-based uncertainty relation considered in Ref. [34]. We denote by ${\mathcal{L}}_2$ the bound of Thm. Four corresponding to the choice of π₁ = (1), π₂ = (1 2 … n), $x_i=\left|{\alpha }_i\right|$, $y_i=\left|{\beta }_i\right|$, which will be used in Sec. V.

4 Uncertainty Intervals

Quantum theory does not only impose restrictions on the lower bounds of uncertainties, but also sets limitations on the upper bounds of uncertainties [34], which are known as reverse uncertainty relations in the literature. In this section, we investigate the reverse uncertainty relations for both the product-form and sum-form uncertainty relations, and introduce several tighter bounds. Consequently, our lower bounds presented in previous sections together with the results obtained in this section lead to intervals for joint uncertainty, which are referred as uncertainty intervals.

For index 1 ≤ i ≤ n, we define

$\begin{array}{ll}\hfill X& =\underset{i}{\max }\left\{x_i\right\},x=\underset{i}{\min }\left\{x_i\right\},\hfill \\ \hfill Y& =\underset{i}{\max }\left\{y_i\right\},y=\underset{i}{\min }\left\{y_i\right\}.\hfill \end{array}(21)$

Using the rearrangement inequality, we thus see that

$\begin{array}{ll}\hfill \frac{{\left(xy+XY\right)}^2}{4xyXY}{\left(\sum _i{x}_i{y}_i\right)}^2& \ge \frac{{\left(xy+XY\right)}^2}{4xyXY}{\left(\sum _i{x}_i{y}_{\pi \left(i\right)}\right)}^2\hfill \\ \hfill & \ge V\left(A\right)V\left(B\right).\hfill \end{array}(22)$

By taking minimum over all permutations $\pi \in {\mathfrak{S}}_n$, we obtain a tighter upper bound for V(A)V(B):

$V\left(A\right)V\left(B\right)\le \underset{\pi \in {\mathcal{S}}_n}{\min }\frac{{\left(xy+XY\right)}^2}{4xyXY}{\left(\sum _i{x}_i{y}_{\pi \left(i\right)}\right)}^2≔{\mathcal{U}}_1,(23)$

which proves that the joint uncertainty of incompatible observables A and B (for the product-form) is restricted within the interval $[{\mathcal{L}}_1,{\mathcal{U}}_1]$, i.e. $V(A)V(B)\in [{\mathcal{L}}_1,{\mathcal{U}}_1]$. In other words, $[{\mathcal{L}}_1,{\mathcal{U}}_1]$ is an uncertainty interval for V(A)V(B).

On the other hand, using the fact $V(A)=|\vec{\alpha }{|}^2$ and $V(B)=|\vec{\beta }{|}^2$, one derive an upper bound on the sum of variances of incompatible observables A and B as

$V\left(A\right)+V\left(B\right)=\sum _i\left(x_i^2+y_i^2\right)\le \sum _i{\left(x_i+y_i\right)}^2.(24)$

Recalling the definitions $x_i=\left|{\alpha }_i\right|$ and $y_i=\left|{\beta }_i\right|$, we have that

$V\left(A\right)+V\left(B\right)\le \sum _i{\left(\left|\langle {\psi }_n|\bar{A}|\mathrm{\Psi }\rangle \right|+\left|\langle {\psi }_n|\bar{B}|\mathrm{\Psi }\rangle \right|\right)}^2.(25)$

Denote the right-hand (RHS) of (25) by ${\mathcal{U}}_2$. Thus we have obtained a uncertainty interval for V(A) + V(B): $[{\mathcal{L}}_2,{\mathcal{U}}_2]$. We remark that ${\mathcal{U}}_2$ is not always better than the bound obtained by [34], but it provides a complementary one. The comparison will be discussed by examples in the next section.

5 Numerical Examples and Conclusion

In this section we provide numerical examples to show how the bounds obtained in this work outperform previous strong results [34]. First of all, let us consider the spin-1 particle with the state |Ψ(θ)⟩ = cos θ|1⟩ − sin θ|0⟩, where the state |0⟩ and |1⟩ are eigenstates of the angular momentum L_z. We investigate the uncertainty associated with angular momentum operators for spin-1 particle, namely A = L_x and B = L_y. To formulate bounds for uncertainty relations, we choose $x_i=\left|{\alpha }_i\right|$ and $y_i=\left|{\beta }_i\right|$ (similar for $x_i=|a_i^{\prime }|\sqrt{⟨\mathrm{\Psi }(\theta )|a_i⟩⟨a_i|\mathrm{\Psi }(\theta )⟩}$ and $y_i=|b_i^{\prime }|\sqrt{⟨\mathrm{\Psi }(\theta )|b_i⟩⟨b_i|\mathrm{\Psi }(\theta )⟩}$).

In Figure 1, our bound ${\mathcal{L}}_1$ has been compared with that of [34] in the product-form for the family of spin-1 particles |Ψ(θ)⟩. As shown in our numerical results, the bound ${\mathcal{L}}_1$ (in blue) provides the best estimation and is almost optimal. As a supplement, we also compare our result with Schrödinger’s uncertainty relation (in orange). In Figure 2, we plot lower bounds for the sum-form variance-based uncertainty relation for the family of the spin-1 particles |Ψ(θ)⟩, which highlights the advantage of our method.

FIGURE 1

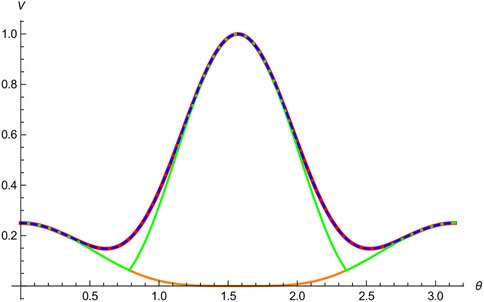
FIGURE 1. Lower bounds of V(A)V(B) for a family of spin-1 particles |Ψ(θ)⟩: the product-form uncertainty relation V(A)V(B), the bound ${\mathcal{L}}_1$ of Eq. 12, the bound of Ref. [34], and the bound of Schrödinger uncertainty relation [5] are depicted in red, blue, green, and orange respectively.

FIGURE 2

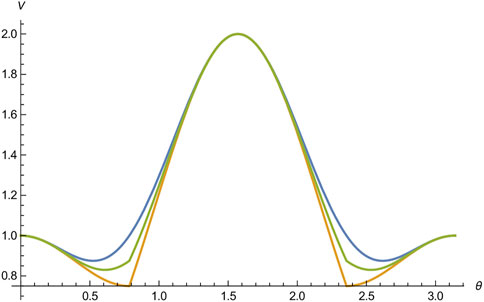
FIGURE 2. Lower bounds of V(A) + V(B) for a family of spin-1 particles |Ψ(θ)⟩: the sum-form uncertainty relation V(A) + V(B), our bound ${\mathcal{L}}_2$ of Eq. 20, and the bound of Ref. [34] are depicted in blue, green, and yellow respectively.

Let us move on to considering the spin-$\frac{1}{2}$ particle with the following density matrix

$\rho \left(\theta \right)=\frac{1}{2}\left(Id+\cos \frac{\theta }{2}{\sigma }_x+\frac{\sqrt{3}}{2}\sin \frac{\theta }{2}{\sigma }_y+\frac{1}{2}\sin \frac{\theta }{2}{\sigma }_z\right),(26)$

where the two incompatible observables are taken as A = σ_x and B = σ_z. In Figure 3, it has been shown that our upper bound ${\mathcal{U}}_1$ provides the best estimation for the product of two variances and typically outperforms the upper bound from Ref. [34]. Note that our bound is almost optimal, as it is almost identical to the optimal value. However, our upper bound ${\mathcal{U}}_2$ for the sum of variances V(A) + V(B) for states ρ(θ) is not always tighter than that of Ref. [34]. Nevertheless, it still provides an improvements for most of the time. See Figure 4 for an illustration.

FIGURE 3

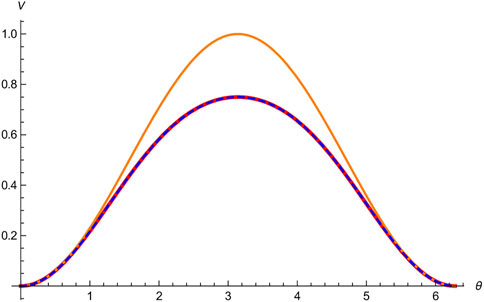
FIGURE 3. Upper bounds of V(A)V(B) for a family of spin-1/2 particles ρ(θ): the product-form uncertainty relation V(A)V(B), our bound ${\mathcal{U}}_1$ of Eq. 23, and the bound of Ref. [34] are depicted in red, blue, and orange respectively.

FIGURE 4

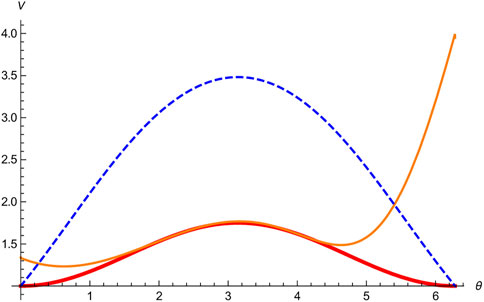
FIGURE 4. Upper bounds of V(A) + V(B) for a family of spin-1/2 particles ρ(θ): the sum-form uncertainty relation V(A)V(B), our bound ${\mathcal{U}}_2$ of Eq. 25, and the bound of Ref. [34] are depicted in red, blue, and orange respectively.

Apart from constructing stronger uncertainty relations, our method introduced in Sec. II also helps to fill up the gap between product-form variance-based uncertainty relations and entropic uncertainty relations. Following Ref. [35], we have

$V\left(A\right)+V\left(B\right)\ge H\left(A\right)+H\left(B\right)+c,(27)$

where H (⋅) stands for the Shannon entropy and c is a state-independent constant. Using Thm. 1, it is straightforward to check that

$V\left(A\right)V\left(B\right)\ge \frac{1}{4}{\left(\sum _{i=1}^{n-1}{x}_i{y}_i\right)}^2+x_n^{2}V\left(B\right)+y_n^{2}V\left(A\right)-x_n^2{y}_n^2.(28)$

On the one hand, the term $x_n^{2}V(B)+y_n^{2}V(A)$ appeared above forms a so-called weighted uncertainty relation [7]. Notice that we can always assume $x_n^2=y_n^2$ in the numerical calculation, since V (rA)V(B) = r²V(A)V(B). Thus, Eq. 28 can be bounded as

$V\left(A\right)V\left(B\right)\ge \frac{1}{4}{\left(\sum _{i=1}^{n-1}{x}_i{y}_i\right)}^2+x_n^2\left(H\left(A\right)+H\left(B\right)+c\right)-x_n^4.(29)$

Therefore both the incompatibility between observables and mixness of the quantum state will affect the variance-based uncertainty relations. Moreover, any entropic uncertainty relation can be employed to construct a lower bound for product-form variance-based uncertainty relation.

To summarize, we have introduced several variance-based uncertainty relations both in the sum and product forms. Our results contain both the lower bounds and the upper bounds, which leads to the concept of uncertainty intervals. Numerical experiments illustrate the advantages of our bounds, and in some cases our bounds are near optimal. Quite remarkable, our method in deriving stronger variance-based uncertainty relations also fills the gap between the product-form variance-based uncertainty relations and the entropic uncertainty relations. Beside the results present here, our framework can also be used in formulating unitary uncertainty relations. For more details, see our follow-up work [36].

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YX and NJ conceived the original idea and developed the theory. YX designed the numerical experiments and performed the numerical calculations. YX and NJ wrote the first draft of the paper and YX contributed to the final version. All authors analysed the results and reviewed the manuscript.

Funding

YX is supported by the Natural Sciences, the National Research Foundation (NRF). Singapore, under its NRFF Fellow programme (Grant No. NRF-NRFF2016-02), Singapore Ministry of Education Tier 1 Grants RG162/19 (S), the Quantum Engineering Program QEP-SF3, and No FQXi-RFP-1809 (The Role of Quantum Effects in Simplifying Quantum Agents) from the Foundational Questions Institute and Fetzer Franklin Fund (a donor-advised fund of Silicon Valley Community Foundation). BY acknowledges the support of Startup Funding of Guangdong Polytechnic Normal University No. 2021SDKYA178, and Guangdong Basic and Applied Basic Research Foundation No. 2020A1515111007. S-MF acknowledges the support of National Natural Science Foundation of China (NSFC) under Grant Nos. 12075159 and 12171044; Beijing Natural Science Foundation (Grant No. Z190005); the Academician Innovation Platform of Hainan Province. The work is supported by National Natural Science Foundation of China (grant Nos. 12126351, 12126314 and 11531004), Natural Science Foundation of Hubei Province grant No. 2020CFB538, China Scholarship Council and Simons Foundation grant No. 523868. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not reflect the views of National Research Foundation or Ministry of Education, Singapore.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Heisenberg W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z Physik (1927) 43:172–98. doi:10.1007/BF01397280

CrossRef Full Text | Google Scholar

2. Kennard EH. Zur Quantenmechanik Einfacher Bewegungstypen. Z Physik (1927) 44:326–52. doi:10.1007/BF01391200

CrossRef Full Text | Google Scholar

3. Weyl H. Quantenmechanik und Gruppentheorie. Z Physik (1927) 46:1–46. doi:10.1007/BF02055756

CrossRef Full Text | Google Scholar

4. Robertson HP. The Uncertainty Principle. Phys Rev (1929) 34:163–4. URL https://link.aps.org/doi/10.1103/PhysRev.34.163. doi:10.1103/physrev.34.163

CrossRef Full Text | Google Scholar

5. Schrödinger E. About Heisenberg Uncertainty Relation. Ber Kgl Akad Wiss Berlin (1930) 24:296.

Google Scholar

6. Pati AK, Sahu PK. Sum Uncertainty Relation in Quantum Theory. Phys Lett A (2007) 367:177–81. ISSN 0375-9601, URL https://www.sciencedirect.com/science/article/pii/S0375960107003696. doi:10.1016/j.physleta.2007.03.005

CrossRef Full Text | Google Scholar

7. Xiao Y, Jing N, Li-Jost X, Fei S-M. Weighted Uncertainty Relations. Sci Rep (2016) 6:23201. doi:10.1038/srep23201

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Xiao Y. A Framework for Uncertainty Relations. Leipzig, Germany: Leipzig University (2017). Ph.D. thesis. URL https://ul.qucosa.de/landing-page/?tx_dlf[id]=https%3A%2F%2Ful.qucosa.de%2Fapi%2Fqucosa%253A15366%2Fmets

9. Xiao Y, Guo C, Meng F, Jing N, Yung M-H. Incompatibility of Observables as State-independent Bound of Uncertainty Relations. Phys Rev A (2019) 100:032118. URL https://link.aps.org/doi/10.1103/PhysRevA.100.032118. doi:10.1103/physreva.100.032118

CrossRef Full Text | Google Scholar

10. Giovannetti V, Lloyd S, Maccone L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science (2004) 306:1330–6. URL https://www.science.org/doi/abs/10.1126/science.1104149.doi:10.1126/science.1104149

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Giovannetti V, Lloyd S, Maccone L. Quantum Metrology. Phys Rev Lett (2006) 96:010401. URL https://link.aps.org/doi/10.1103/PhysRevLett.96.010401. doi:10.1103/PhysRevLett.96.010401

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Roy SM, Braunstein SL. Exponentially Enhanced Quantum Metrology. Phys Rev Lett (2008) 100:220501. URL https://link.aps.org/doi/10.1103/PhysRevLett.100.220501. doi:10.1103/physrevlett.100.220501

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Giovannetti V, Lloyd S, Maccone L. Advances in Quantum Metrology. Nat Photon (2011) 5:222–9. doi:10.1038/nphoton.2011.35

CrossRef Full Text | Google Scholar

14. Wehner S, Winter A. Entropic Uncertainty Relations-A Survey. New J Phys (2010) 12:025009. doi:10.1088/1367-2630/12/2/025009

CrossRef Full Text | Google Scholar

15. Białynicki-Birula I, Mycielski J. Uncertainty Relations for Information Entropy in Wave Mechanics. Commun.Math Phys (1975) 44:129–32. doi:10.1007/BF01608825

CrossRef Full Text | Google Scholar

16. Deutsch D. Uncertainty in Quantum Measurements. Phys Rev Lett (1983) 50:631–3. URL https://link.aps.org/doi/10.1103/PhysRevLett.50.631. doi:10.1103/physrevlett.50.631

CrossRef Full Text | Google Scholar

17. Kraus K. Complementary Observables and Uncertainty Relations. Phys Rev D (1987) 35:3070–5. URL https://link.aps.org/doi/10.1103/PhysRevD.35.3070. doi:10.1103/physrevd.35.3070

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Maassen H, Uffink JBM. Generalized Entropic Uncertainty Relations. Phys Rev Lett (1988) 60:1103–6. URL https://link.aps.org/doi/10.1103/PhysRevLett.60.1103. doi:10.1103/physrevlett.60.1103

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Berta M, Christandl M, Colbeck R, Renes JM, Renner R. The Uncertainty Principle in the Presence of Quantum Memory. Nat Phys (2010) 6:659–62. doi:10.1038/nphys1734

CrossRef Full Text | Google Scholar

20. Coles PJ, Piani M. Improved Entropic Uncertainty Relations and Information Exclusion Relations. Phys Rev A (2014) 89:022112. URL https://link.aps.org/doi/10.1103/PhysRevA.89.022112.doi:10.1103/PhysRevA.89.022112

CrossRef Full Text | Google Scholar

21. Xiao Y, Jing N, Fei S-M, Li T, Li-Jost X, Ma T, et al. Strong Entropic Uncertainty Relations for Multiple Measurements. Phys Rev A (2016) 93:042125. URL https://link.aps.org/doi/10.1103/PhysRevA.93.042125. doi:10.1103/PhysRevA.93.042125

CrossRef Full Text | Google Scholar

22. Xiao Y, Jing N, Fei S-M, Li-Jost X. Improved Uncertainty Relation in the Presence of Quantum Memory. J Phys A: Math Theor (2016) 49:49LT01. doi:10.1088/1751-8113/49/49/49lt01

CrossRef Full Text | Google Scholar

23. Xiao Y, Jing N, Li-Jost X. Uncertainty under Quantum Measures and Quantum Memory. Quan Inf Process (2017) 16:104. doi:10.1007/s11128-017-1554-6

CrossRef Full Text | Google Scholar

24. Xiao Y, Fang K, Gour G. The Complementary Information Principle of Quantum Mechanics (2019). 1908.07694. URL https://arxiv.org/abs/1908.07694.

Google Scholar

25. Xiao Y, Sengupta K, Yang S, Gour G. Uncertainty Principle of Quantum Processes. Phys Rev Res (2021) 3:023077. URL https://link.aps.org/doi/10.1103/PhysRevResearch.3.023077. doi:10.1103/physrevresearch.3.023077

CrossRef Full Text | Google Scholar

26. Huang J-L, Gan W-C, Xiao Y, Shu F-W, Yung M-H. Holevo Bound of Entropic Uncertainty in Schwarzschild Spacetime. Eur Phys J C (2018) 78:545. doi:10.1140/epjc/s10052-018-6026-3

CrossRef Full Text | Google Scholar

27. Qian C, Wu Y-D, Ji J-W, Xiao Y, Sanders BC. Multiple Uncertainty Relation for Accelerated Quantum Information. Phys Rev D (2020) 102:096009. URL https://link.aps.org/doi/10.1103/PhysRevD.102.096009. doi:10.1103/PhysRevD.102.096009

CrossRef Full Text | Google Scholar

28. Candes EJ, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Trans Inform Theor (2006) 52:489–509. doi:10.1109/tit.2005.862083

CrossRef Full Text | Google Scholar

29. Hofmann HF, Takeuchi S. Violation of Local Uncertainty Relations as a Signature of Entanglement. Phys Rev A (2003) 68:032103. URL https://link.aps.org/doi/10.1103/PhysRevA.68.032103. doi:10.1103/PhysRevA.68.032103

CrossRef Full Text | Google Scholar

30. Rutkowski A, Buraczewski A, Horodecki P, Stobińska M. Quantum Steering Inequality with Tolerance for Measurement-Setting Errors: Experimentally Feasible Signature of Unbounded Violation. Phys Rev Lett (2017) 118:020402. URL https://link.aps.org/doi/10.1103/PhysRevLett.118.020402. doi:10.1103/PhysRevLett.118.020402

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Xiao Y, Xiang Y, He Q, Sanders BC. Quasi-fine-grained Uncertainty Relations. New J Phys (2020) 22:073063. doi:10.1088/1367-2630/ab9d57

CrossRef Full Text | Google Scholar

32. Coles PJ, Berta M, Tomamichel M, Wehner S. Entropic Uncertainty Relations and Their Applications. Rev Mod Phys (2017) 89:015002. URL https://link.aps.org/doi/10.1103/RevModPhys.89.015002. doi:10.1103/RevModPhys.89.015002

CrossRef Full Text | Google Scholar

33. Xiao Y, Yang Y, Wang X, Liu Q, Gu M. Under preparation (2022).

34. Mondal D, Bagchi S, Pati AK. Tighter Uncertainty and Reverse Uncertainty Relations. Phys Rev A (2017) 95:052117. URL https://link.aps.org/doi/10.1103/PhysRevA.95.052117. doi:10.1103/PhysRevA.95.052117

CrossRef Full Text | Google Scholar

35. Huang Y. Variance-based Uncertainty Relations. Phys Rev A (2012) 86:024101. URL https://link.aps.org/doi/10.1103/PhysRevA.86.024101. doi:10.1103/PhysRevA.86.024101

CrossRef Full Text | Google Scholar

36. Yu B, Jing N, Li-Jost X. Strong Unitary Uncertainty Relations. Phys Rev A (2019) 100:022116. URL https://link.aps.org/doi/10.1103/PhysRevA.100.022116. doi:10.1103/PhysRevA.100.022116

CrossRef Full Text | Google Scholar