Hermitian and Non-Hermitian Dirac-Like Cones in Photonic and Phononic Structures

Accidental degeneracy plays an important role in the generation of novel band dispersions. Photonic structures that exhibit an accidental Dirac-like conical dispersion at the center of the Brillouin zone can behave like a zero-index material at the Dirac-point frequency, leading to a number of unique features, such as invariant phase in space, wave tunneling, photonic doping and anti-doping, etc. Such a phenomenon has been explored in on-chip structures or three dimensions recently. The introduction of non-Hermiticity into the system via loss or gain could transform the accidental Dirac-like cone into a spawning ring of exceptional points, a complex Dirac-like cone or other unique dispersions. Similar Dirac-like cones and related physics are also observed in phononic structures. This review presents an overview of the accidental-degeneracy-induced Dirac-like cones at the center of the Brillouin zone in both photonic and phononic structures, including the fundamental physics, effective-medium description and experimental demonstration, as well as current challenges and future directions.

Introduction

Dirac cones or conical dispersions are unique features in some electronic band structures that describe unusual electron transport properties of materials like graphene. The electronic band structure of graphene near the Fermi level can be described by the massless Dirac equation near the six corners of the two-dimensional (2D) hexagonal Brillouin zone at the $\text{K}$ and $\text{K'}$ points [1, 2]. The linear dispersion can be visualized as two cones meeting at the Fermi level at the Dirac point, and the conical dispersion near the Dirac point is usually referred to as Dirac cones. Due to this unusual conical dispersion, graphene exhibits intriguing transport properties [1, 2], such as abnormal quantum Hall effect, Zitterbewegung, Klein tunneling, anti-localization, etc.

Dirac cone dispersions can also be observed in classical wave periodic structures such as photonic crystals (PhCs) [3, 4] and phononic crystals (PnCs) [5–8]. As photonic/acoustic analogue of graphene, 2D triangular/honeycomb PhCs [9–24] and PnCs [23, 25–28] have been demonstrated to possess Dirac cones near the $\text{K}$ and $\text{K'}$ points. This type of Dirac cones of double degeneracy are usually stable to the material parameters as long as the system exhibits the perfect symmetry (e.g., ${\text{C}}_{3\left(v\right)}$ and ${\text{C}}_{6\left(v\right)}$, and time reversal) [28].

Besides the structural symmetry, Dirac cones can also be created by accidental degeneracy through engineering the material and geometrical parameters [29–31]. In 2011, Huang et al. demonstrated a Dirac cone at the center of the Brillouin zone, i.e., the $\text{Γ}$ point with $\mathbf{k}=0$, of a square lattice of 2D dielectric PhC [32]. The physical origin of this Dirac cone is different from the symmetry-protected Dirac cones occurring at high-symmetry points (i.e., $\text{K}$ and $\text{K'}$ points of a triangular/honeycomb lattice). The symmetry-protected Dirac cone is a result of double degeneracy and carries a $\pi$ Berry phase. While the Dirac cone at the center of the Brillouin zone is a result of triple degeneracy, i.e., accidental degeneracy of a doubly degenerate mode and a single mode. The linear dispersions created by triply degenerate modes cannot be mapped into the Dirac Hamiltonian and carry no Berry phase. Therefore, the conical linear dispersions with triple degeneracy at the Brillouin zone center induced by accidental degeneracy instead of structural symmetry is called Dirac-like cones [23].

The presence or absence of Dirac-like cones is determined by the combination of mode symmetries [33, 34]. We should emphasize that accidental degeneracy can also lead to Dirac cones of double degeneracy in periodic systems without structural symmetry and at almost any k point in the Brillouin zone [35], i.e. beyond the Brillouin zone center, edges and high-symmetry lines. Such accidental-degeneracy-induced Dirac cones in general can be achieved by closing band gaps at a desired k point with a band engineering method [35] or other optimization techniques [36–40].

The PhC possessing a Dirac-like cone at the $\text{Γ}$ point is of particular interest, because it offers an effective refractive index of zero at the Dirac-point frequency. It was discovered that such a PhC behaves like an impedance-matched zero index material (ZIM) [41–43] with ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$ at the Dirac-point frequency, and the linear dispersions could be understood from the effective medium perspective [32]. In this sense, this type of PhCs is an important class of dielectric metamaterials [44]. Possessing an infinite effective wavelength and zero spatial phase change, ZIMs exhibit extraordinary physical properties that enable many applications including directive emission [45–47], tunneling waveguides [48–50], energy flux control [51–56], photonic doping [57–61], cloaking and anti-doping [62–65], transmission and scattering manipulation [65–74], perfect absorption [59, 60, 75–80] and nonlinearity enhancement [81–85], etc. To date, the ZIMs have become an important class of artificial electromagnetic materials with potential applications in the wide spectrum from microwaves to optical frequencies. The dielectric PhCs with a Dirac-like cone at the center of the Brillouin zone provide a feasible and promising route towards ultralow-loss ZIMs.

The PhC with a Dirac-like cone has attracted significant research interest [23, 33, 35, 40, 59, 60, 64, 86–121]. Extensive investigations revealed many unique and interesting features. For instance, double Dirac cones, as a pair of two identical and overlapping Dirac cones, were observed at the $\text{Γ}$ point of by utilizing a fourfold accidental degeneracy in triangular PhCs [100, 122, 123]. The double Dirac cones can also be obtained through folding the Dirac cones at the $\text{K}$ and $\text{K'}$ points in a honeycomb PhC to the $\text{Γ}$ point [124–126]. Dual-polarization Dirac-like cones, i.e., the existence of Dirac-like cones for both transverse electric and magnetic polarizations in 2D PhC, have been proposed [39, 127, 128]. Semi-Dirac cones, which exhibit linear-parabolic dispersion, were created by the accidental degeneracy of two modes with a linear dispersion in one direction but a quadratic dispersion in the other direction [129–134]. The PhC with a semi-Dirac cone behaves as an intriguing class of anisotropic ZIM with ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$ along only one direction.

The Dirac cone system has been extended from the original 2D to on-chip platform or the bound state in continuum (BIC) [22, 135–147] and three-dimension (3D) [148–150], and from the original Hermitian (lossless) to non-Hermitian (lossy or gain) ones [136, 151–155]. It was discovered that the Dirac degeneracy can be straightforwardly linked to exceptional points (EPs) through the introduction of non-Hermiticity, i.e., material loss, gain, or open boundaries. The EP is a singularity in a non-Hermitian system where two or more eigenvalues and their associated eigenfunctions collapse into one eigenvalue or eigenfunction [156–158]. Besides photonic structures, the concept of Dirac-like cones has also been applied to other kinds of classical wave structures, including acoustic and elastic structures [23, 28, 148, 159–174].

This review presents an overview of Dirac-like cones from Hermitian and non-Hermitian systems in both photonic and phononic structures. We will introduce the fundamental physics, effective-medium description and experimental demonstration, as well as current challenges and potential directions of future research.

Photonic Crystals With a Dirac-like Cone as Zero Index Materials

Figure 1A shows an example of a 2D PhC that exhibits a Dirac-like cone at the center of the Brillouin zone. The PhC consists of a square lattice of dielectric cylinders. The polarization is transverse-magnetic polarization, with electric field parallel to the cylinder axis. A Dirac-like cone, i.e., the triply-degenerate point, occurs at the $\text{Γ}$ point. It comprises two linear bands that generate conical dispersions and an additional flat band. The two linear bands correspond to the accidental degeneracy of the electric monopole and magnetic dipole modes, whereas the flat band corresponds to the magnetic dipole mode in a rotated orientation, as shown by the right panel of Figure 1A. The doubly degenerate dipole modes correspond to the fields rotated by $90°$ with the wave vector perpendicular or parallel to the dipole moment (i.e., transverse or longitudinal dipole mode), as the result of ${\text{C}}_{4v}$ symmetry of the PhC. The flat band is the consequence of the longitudinal dipole mode whose magnetic field is parallel to the wave vector, which is inaccessible from normal incidence.

FIGURE 1

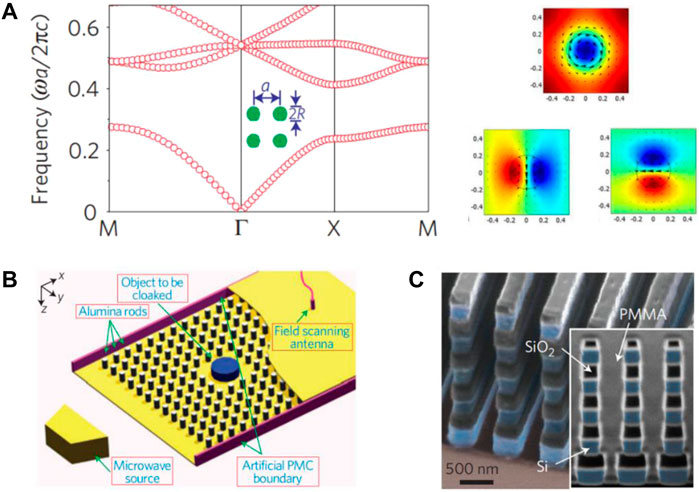
FIGURE 1. (A) The band structure of a PhC consisting of a square lattice of dielectric rods. Two branches with linear dispersion intersect at a triply-degenerate point at the $\text{Γ}$ point, forming a Dirac-like cone. The right panel shows the distributions of out-of-plane electric fields (color) and in-plane magnetic fields (arrows) of the eigenstates near the Dirac-like point. (B) The PhC with a Dirac-like cone was experimentally demonstrated in the microwave regime using a square array of alumina rods. Reproduced with permission from Ref. [32]. (C) A PhC consisting of horizontal square array of silicon bars was demonstrated to exhibit the Dirac-like cone in the infrared regime. Reproduced with permission from Ref. [91].

In the vicinity of the $\text{Γ}$ point where the in-plane wave vector $\mathbf{k}$ is small, the band structure of the PhC can be described by an effective Hamiltonian given by first-order degenerate perturbation theory [33, 136].

$H_{\text{eff}}=\left(\begin{array}{ccc}{\omega }_D& v_g \left|\mathbf{k}\right|& 0\\ v_g \left|\mathbf{k}\right|& {\omega }_D& 0\\ 0& 0& {\omega }_D\end{array}\right)(1)$

where ${\omega }_D$ is the Dirac-point frequency, $v_g$ is the group velocity of the linear Dirac dispersion. The effective Hamiltonian has three eigenvalues as

${\mathit{\omega }}_{\mathrm{1}}\mathrm{=}{\mathit{\omega }}_{\mathit{D}}\mathrm{+}{\mathit{v}}_{\mathit{g}}\mathbf{|k|,}{\mathit{\omega }}_{\mathrm{2}}\mathrm{=}{\mathit{\omega }}_{\mathit{D}}\mathrm{-}{\mathit{v}}_{\mathit{g}}\mathbf{|k|,}{\mathit{\omega }}_{\mathrm{3}}\mathrm{=}{\mathit{\omega }}_{\mathit{D}}(2)$

The first two eigenvalues indicate the conical linear dispersion in the vicinity of Dirac-point frequency, while third one is related to the intersecting flat band.

The experimental observation of the Dirac-like cone was realized in the microwave regime by Huang et al in 2011 [32] using a square array of alumina rods embedded within a parallel-plate waveguide, as schematically shown in Figure 1B. In the experimental implementation, the alumina rods have a finite height of 16 mm. To realize effective 2D PhC with infinite height, aluminum plates, as perfect electric conductor boundaries, are utilized to form a parallel plate waveguide. At the Dirac-point frequency, the PhC was found to behave like an impedance-matched ZIM with ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$. Experimental observation has clearly verified the ZIM-enabled cloaking and lensing effect with this PhC.

The optical PhC with a Dirac-like cone was demonstrated by Moitra et al in 2013 [91]. We note that the implementation at microwave frequencies cannot be directly transplanted to the optical frequencies because the dissipation loss of metal plates is dramatic. Therefore, an out-of-plane configuration by patterning horizontal square array of silicon bars was proposed instead (Figure 1C). The measured spectrum shows a ZIM-induced transmission peak at the wavelength of 1,409 nm, corresponding to the Dirac-like point. Furthermore, ZIM-enabled applications including angular selectivity of transmission and directional quantum dot emission were experimentally demonstrated.

It is noteworthy that the Dirac-like cone is a consequence of accidental degeneracy rather than structural symmetry. When the system parameters (e.g., cylinder radius or relative permittivity) are changed, the triple degenerate modes at the Dirac point will split into a single monopole mode and doubly degenerate dipole modes, forming a photonic band gap [32]. The band edge points at the $\text{Γ}$ point are related to the zero effective parameters, because the phase accumulation on adjacent unit cell boundaries is zero. It is found that the zero permittivity, i.e., ${\epsilon }_{\text{eff}}=0$, originates from the electric monopole resonance, while the zero permeability, i.e., ${\mu }_{\text{eff}}=0$, originates from the doubly degenerate magnetic dipole resonance [47]. However, due to the quadratic dispersions at band edges, the zero parameter leads to zero group velocity. Interestingly, the accidental degeneracy of the monopole and dipole modes turns the quadratic dispersion into a linearly conical dispersion with ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$, but with a non-zero group velocity. In addition, due to the ultralow-loss of the dielectric materials, the PhCs with a Dirac-like cone are excellent candidates for the ultralow-loss ZIMs.

ZIMs with a Dirac-like cone and a finite group velocity enable many intriguing applications. In the following, we give three examples of unique applications. The first one is the hybrid invisibility cloak based on the integration of metasurfaces and ZIM (Figure 2A) [64]. The key functionalities of wavefront tailoring with the metasurfaces and wave energy tunneling with the ZIM are combined together to achieve the invisibility cloak. The second one is a geometry-invariant coherent perfect absorber via doping an impedance-matched ZIM with absorptive defects (Figure 2B) [59]. The behavior of coherent perfect absorption is independent of the size and shape of the ZIM and the position of the doping defects, because of the zero spatial phase change and uniform electric fields inside the ZIM. The third one is a plane-concave lens made of ZIM at near-infrared wavelengths (Figure 2C) [139]. Due to the zero spatial phase change across the ZIM, such a plane-concave lens can focus the incident plane wave with ultralow spherical aberration.

FIGURE 2

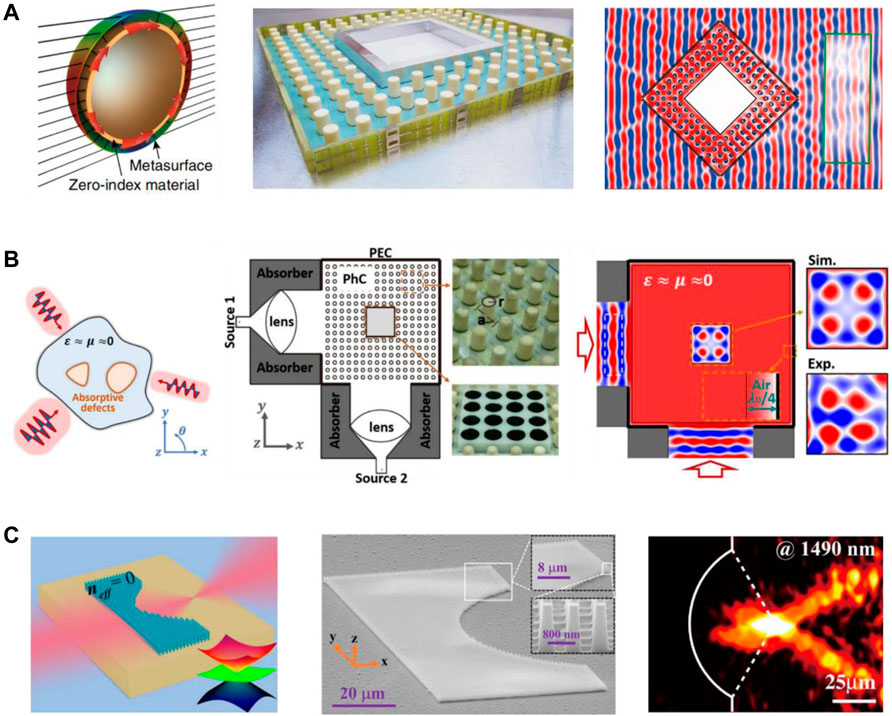
FIGURE 2. (A) Left: schematic graph of a hybrid invisibility cloak based on the integration of metasurfaces and ZIM. Middle: picture of the fabricated microwave cloaking shell, which consists of a metasurface and a PhC with a Dirac-like cone. Right panel shows the electric-field distribution. The part inside the region marked by the green rectangle is measured in the experiment, and the other part is obtained by simulations. Reproduced with permission from Ref. [64]. (B) Left: illustration of the geometry-invariant coherent perfect absorber by using impedance-matched ZIM doped with absorptive defects. Middle panel shows the microwave experimental setup. A dielectric PhC with a Dirac-like cone is utilized to work as an effective impedance-matched ZIM. Right panel shows the measured electric-field distribution at the Dirac-point frequency. Reproduced with permission from Ref. [59]. (C) Left: schematic view of a plane-concave lens made of ZIM. Middle: scanning electron microscopy image of the fabricated lens consisting of silicon nanopillars on a silicon substrate. Right: optical microscope images of two incoherent beams passing through the lens, showing the focusing behavior at 1490 nm. Reproduced with permission from Ref. [139].

Non-Hermitian Dirac-Like Cones and Effective Medium Description

The abovementioned Dirac-like cone is based on the assumption of Hermitian PhC. It is reasonable, as the PhC are composed of low-loss dielectric materials. It is interesting to point out the band dispersion of the PhC could be drastically deformed if there exists loss/gain [24, 80, 136, 151–155, 175]. In 2015, Zhen et al experimentally demonstrated that in a photonic crystal slab the radiative loss-induced non-Hermitian perturbation can deform the Dirac-like cone into a 2D flat band enclosed by a ring of EPs [136]. The EP is a singularity in a non-Hermitian system where two or more eigenvalues and their associated eigenfunctions collapse into one eigenvalue or eigenfunction [156–158]. In the absence of loss, a Dirac-like cone as the result of accidental degeneracy of a doubly degenerate dipole mode and a single quadrupole mode dipole can be obtained at the $\text{Γ}$ point. While in the presence of radiative loss, the Dirac-like cone is deformed into a flat band enclosed by a ring of EPs. As shown in Figure 3A, inside the ring of EPs, the real parts of the eigen-frequencies have degenerate flat dispersions, while the imaginary parts split into two branches. Outside the ring of EPs, the situations are just the opposite. The real parts split, while the imaginary parts tend to degeneracy.

FIGURE 3

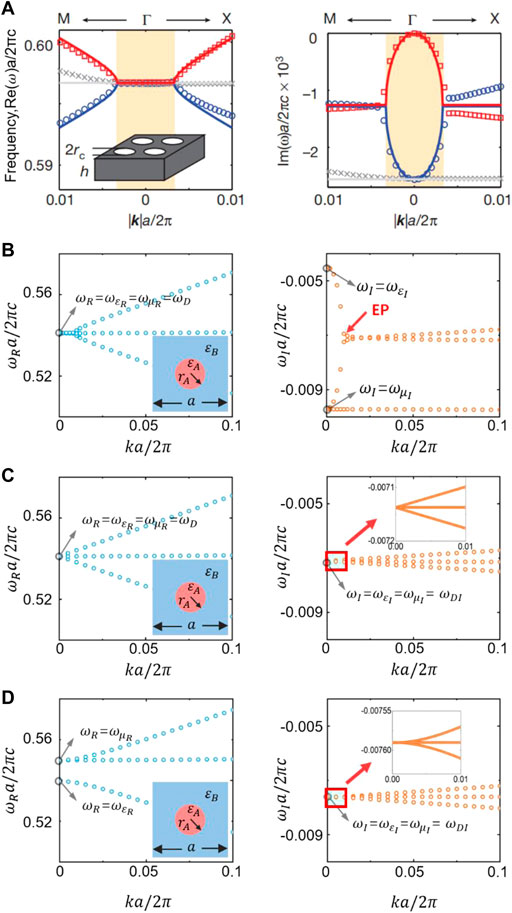
FIGURE 3. (A) The real (left panel) and imaginary (right panel) parts of the eigen-frequencies of a PhC slab with finite thickness. By tuning the radius, accidental degeneracy in the real part can be achieved, but the Dirac-like cone is deformed into a 2D flat band enclosed by a ring of EPs. Reproduced with permission from Ref. [136] [(B–D)] The real (left) and imaginary (right) parts of the eigen-frequencies of a 2D non-Hermitian PhC consisting of a square lattice of cylindrical rods, showing (B) the ring of EPs, (C) complex Dirac-like cone with conical dispersions in both real and imaginary frequency spectra, and (D) the quadratic degeneracy. The relative permittivities of the rods (or background medium) are $12.5+0.5i$ (or 1) in (B), $12.5+0.33i$ (or $1+0.0264i$ ) in (C), and $12+0.33i$ (or $1.04+0.02978i$ ) in (D). Reproduced with permission from Ref. [155].

These unique dispersion characteristics of the non-Hermitian PhC can also be described by an effective Hamiltonian as [33, 136].

$H_{\text{eff}}=\left(\begin{array}{ccc}{\omega }_D& v_g \left|\mathbf{k}\right|& 0\\ v_g \left|\mathbf{k}\right|& {\omega }_D-i{\gamma }_d& 0\\ 0& 0& {\omega }_D-i{\gamma }_d\end{array}\right)(3)$

with complex eigenvalues

${\mathit{\omega }}_{\mathrm{1}}\mathrm{=}{\mathit{\omega }}_{\mathit{D}}\mathrm{-}\mathit{i}\frac{{\mathit{\gamma }}_{\mathit{d}}}{\mathrm{2}}\mathrm{+}{\mathit{v}}_{\mathit{g}}\sqrt{{\left|\mathbf{k}\right|}^{\mathrm{2}}\mathrm{-}{\left({\mathit{\gamma }}_{\mathit{d}}/\mathrm{2}{\mathit{v}}_{\mathit{g}}\right)}^{\mathrm{2}}}\mathrm{,}{\mathit{\omega }}_{\mathrm{2}}\mathrm{=}{\mathit{\omega }}_{\mathrm{1}}\mathrm{=}{\mathit{\omega }}_{\mathit{D}}\mathrm{-}\mathit{i}\frac{{\mathit{\gamma }}_{\mathit{d}}}{\mathrm{2}}\mathrm{-}{\mathit{v}}_{\mathit{g}}\sqrt{{\left|\mathbf{k}\right|}^{\mathrm{2}}\mathrm{-}{\left({\mathit{\gamma }}_{\mathit{d}}/\mathrm{2}{\mathit{v}}_{\mathit{g}}\right)}^{\mathrm{2}}}\mathrm{,}{\mathit{\omega }}_{\mathrm{3}}\mathrm{=}{\mathit{\omega }}_{\mathrm{D}}\mathrm{-}\mathit{i}{\mathit{\gamma }}_{\mathit{d}}(4)$

where ${\gamma }_d$ is induced by the radiative loss of the dipole modes. It is noted that the quadrupole mode does not radiate owing to its symmetry mismatch with plane waves in free space [136]. The first two eigenvalues indicate a ring of EPs appears at $\left|\mathbf{k}\right|={\gamma }_d/2v_g$. Inside the ring, the real parts of eigenvalues are dispersionless and degenerate. While outside the ring, the imaginary parts are dispersionless and degenerate.

We note that the radiative loss from the PhC slab can be considered equivalent to the material loss in a 2D PhC. This provides us a simple way to investigate the non-Hermitian properties through engineering the losses in different constituents of the PhC. In 2021, Luo et al proposed a non-Hermitian 2D PhC composed of a square lattice of cylindrical rods [155]. The background medium and/or cylindrical rods contain material loss/gain. Through engineering the material loss/gain, it was discovered that besides the ring of EPs (Figure 3B), complex Dirac-like cone with conical dispersions in both real and imaginary frequency spectra (Figure 3C), and the quadratic degeneracy (Figure 3D) can be realized in non-Hermitian PhCs [155]. Such phenomena show the unique consequences of introducing loss/gain to the PhCs with Dirac-like cones.

Moreover, it was found that these non-Hermitian properties can be well explained from the effective medium point of view [155]. In a non-Hermitian PhC involving loss and/or gain, the eigen-frequency becomes a complex value as $\mathit{\omega =}{\mathit{\omega }}_{\mathit{R}}\mathit{+i}{\mathit{\omega }}_{\mathit{I}}$, and the effective permittivity $\mathit{\epsilon }\left(\mathit{\omega }\right)$ and permeability $\mu \left(\mathit{\omega }\right)$ are generally complex and dispersive, which can be expressed as $\mathit{\epsilon }\left(\mathit{\omega }\right)\mathit{=}{\mathit{\epsilon }}_{\mathit{R}}\left(\mathit{\omega }\right)\mathit{+i}{\mathit{\epsilon }}_{\mathit{I}}\left(\mathit{\omega }\right)$ and $\mathit{\mu }\left(\mathit{\omega }\right)\mathit{=}{\mathit{\mu }}_{\mathit{R}}\left(\mathit{\omega }\right)\mathit{+i}{\mathit{\mu }}_{\mathit{I}}\left(\mathit{\omega }\right)$. In a small frequency regime near the Γ point, linear relations between the effective parameters and the eigen-frequency can be assumed as:

$\{\begin{array}{c}{\epsilon }_R\left({\omega }_R\right)=A_{{\epsilon }_R}\times \left({\omega }_R-{\omega }_{{\epsilon }_R}\right)\\ {\mu }_R\left({\omega }_R\right)=A_{{\mu }_R}\times \left({\omega }_R-{\omega }_{{\mu }_R}\right)\\ {\epsilon }_I\left({\omega }_I\right)=A_{{\epsilon }_I}\times \left({\omega }_I-{\omega }_{{\epsilon }_I}\right)\\ {\mu }_I\left({\omega }_I\right)=A_{{\mu }_I}\times \left({\omega }_I-{\omega }_{{\mu }_I}\right)\end{array}(5)$

where $A_{{\epsilon }_R}$, $A_{{\mu }_R}$, $A_{{\epsilon }_I}$ and $A_{{\mu }_I}$ are unknown coefficients to be determined. When the loss/gain is small, we have ${\mathit{\omega }}_{{\mathit{\epsilon }}_{\mathit{I}}}\approx {\mathit{\omega }}_{{\mathit{\mu }}_{\mathit{I}}}\approx \mathrm{0}$ and ${\mathit{\omega }}_{{\mathit{\epsilon }}_{\mathit{R}}}\approx {\mathit{\omega }}_{{\mathit{\mu }}_{\mathit{R}}}\approx {\mathit{\omega }}_{\mathit{D}}$ with ${\omega }_D$ being the Dirac-point frequency in absence of loss/gain. In the complex frequency space, the dispersion relation can be expressed as,

${\left({\omega }_R+i{\omega }_I\right)}^2\left({\epsilon }_R+i{\epsilon }_I\right)\left({\mu }_R+i{\mu }_I\right)=c^2{\mathbf{k}}^2(6)$

where $\mathbf{k}$ is the in-plane wave vector, and $c$ is the speed of light in free space. Based on the effective medium model with parameters and dispersion relation, besides the well explanation of the occurrence of the EP ring, other unique non-Hermitian phenomena like complex Dirac-like cone with conical dispersions in both real and imaginary frequency spectra, as well as the quadratic degeneracy were predicted [155], as summarized in Table 1. Moreover, we note that the flat band induced by the longitudinal electromagnetic mode in all scenarios can also be accurately predicted by using this non-Hermitian effective medium theory [155].

TABLE 1

TABLE 1. Features of band structures of non-Hermitian PhCs.

On-Chip Applications With Cladding and BIC Techniques

For on-chip applications, the PhCs with a Dirac-like cone would suffer from large radiative losses in the out-of-plane direction, because the Dirac-cone dispersion resides above the light line and the transverse dipole mode forming the Dirac-like cone can couple to extended plane waves in free space [30, 31]. This would turn the PhC to be non-Hermitian, and hence the Dirac-like cone would disappear, hindering its applications as the ultralow-loss ZIM. In this sense, it is very important to solve the issue of radiative loss from real PhC chip structures with finite pillar height [22, 135–147]. In order to eliminate the out-of-plane radiative loss, two important classes of approaches have been proposed, that is, the utilization of claddings and BIC techniques.

A mirror cladding can reflect the leaky wave back down into the PhC slab, so as to eliminate the out-of-plane radiation. In 2015 Li et al fabricated an on-chip PhC slab cladded with gold films to avoid out-of-plane radiation, and a Dirac-like cone was observed at the wavelength of 1,590 nm (Figure 4A) [138]. However, such an implementation suffers propagation loss due to the conduction loss originating from the gold films. To reduce the conduction loss from the mirror, a dielectric Bragg reflector was proposed (Figure 4B) [30]. The Bragg reflector can reflect the leaky wave back down into the pillars, where it destructively interferes with the leaky wave below the array, thus eliminating the radiative loss.

FIGURE 4

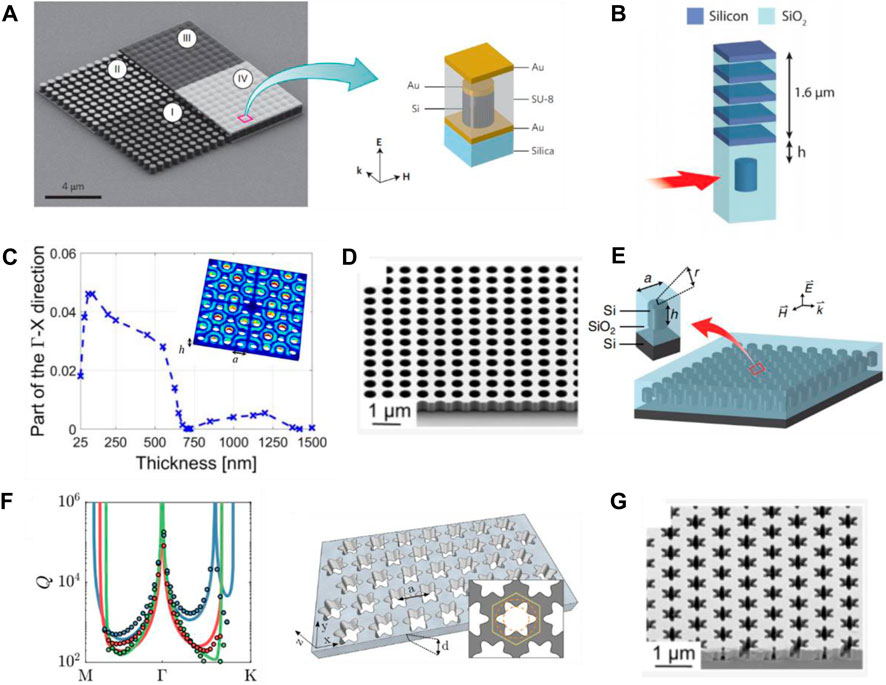
FIGURE 4. (A) Scanning electron microscopy image of an on-chip PhC with a Dirac-like cone, and the schematic of unit cell. The cladding gold films are used to eliminate the out-of-plane radiation. Reproduced with permission from Ref. [138]. (B) Schematic of Bragg reflector design used to reflect the leaky wave back down into the pillars, where it destructively interferes with the leaky wave below the array. Reproduced with permission from Ref. [30]. (C) Extent of the ring of EPs in the $\text{ΓX}$ direction versus the thickness of the PhC slab, which is illustrated by the inset. The radiative losses can be reduced using resonance-trapped BIC. Reproduced with permission from Ref. [140]. (D) Scanning electron microscopy images of a PhC slab with resonance-trapped BIC. A Dirac-like cone is formed due to the accidental degeneracy of a pair of dipole modes and a single quadrupole mode. Reproduced with permission from Ref. [147]. (E) Schematic of an on-chip PhC with resonance-trapped BIC. A Dirac-like cone is formed due to the accidental degeneracy of a single monopole mode and doubly degenerate dipole modes. Reproduced with permission from Ref. [146]. (F) Radiative quality factors for three photonic bands of a PhC slab illustrated by the right panel. A Dirac-like cone dispersion is obtained via symmetry-protected BIC without out-of-plane radiation. Reproduced with permission from Ref. [144]. (G) Scanning electron microscopy images of the PhC slab with symmetry-protected BIC. Reproduced with permission from Ref. [147].

Another technique is based on the concept of BIC, which is the photonic mode in the radiation continuum above the light line but is confined with an infinite quality factor [176]. With the BIC, it is possible to create resonances in a PhC slab with a Dirac-like cone that do not radiate [177]. Specifically, through engineering the height of the PhC slab, all the upward/downward out-of-plane radiation destructively interferes, thus forming a resonance-trapped BIC with a high quality factor (Figure 4C) [140]. Consequently, the radiative loss-induced EP ring would shrink into a Dirac-like cone [140, 145–147], which has been experimentally demonstrated at near-infrared wavelengths (Figure 4D) [147]. The Dirac-like cone is the consequence of the accidental degeneracy of a pair of dipole modes and a single quadrupole mode at the $\text{Γ}$ point in [140, 147], while is formed due to the accidental degeneracy of a single monopole mode and doubly degenerate dipole modes in [145, 146] (Figure 4E). The low-order mode-based design can be better treated as a homogeneous ZIM.

We note that the monopole and higher-order modes besides the dipole modes at the $\text{Γ}$ point do not have out-of-plane radiative loss because of their intrinsic mode symmetry. This suggests that it is possible to realize Dirac-like cone through harnessing the mode symmetry of the degenerate modes at the Dirac point. In 2018 minkov et al theoretically proposed a PhC slab with a hexagonal lattice described by the ${\text{C}}_{6v}$ point group, in which a Dirac-like cone at the $\text{Γ}$ point is achieved via the symmetry-protected BIC (Figure 4F) [144]. For a PhC slab with the ${\text{C}}_{6v}$ symmetry, at the at the $\text{Γ}$ point, modes that belong to the ${\text{E}}_2$ 2D irreducible representation or a one-dimensional irreducible representation do not couple to plane waves in free space, that is, these modes are symmetry-protected BICs. Through engineering the structural parameters of the PhC slab, a Dirac-like cone as the result of accidental degeneracy of modes in the ${\text{E}}_2$ and the ${\text{B}}_1$ or ${\text{B}}_2$ irreducible representations can be obtained [144]. This theoretical prediction was experimentally demonstrated at near-infrared wavelengths recently (Figure 4G) [147].

Three-Dimensional Dirac-Like Cone and the Electromagnetic Void Space

Previously, Dirac-like cones due to accidental degeneracy are mostly investigated in 2D systems. 3D Dirac-like cones and ZIMs were rarely explored. Actually, the wave behaviors in 2D and 3D ZIM are inherently different as the former obey scalar wave equations while the latter follow vector wave equations. As a result, some physical effects observed in 2D ZIM, such as photonic doping [57–61], are absent in 3D ZIM. Instead, when a 3D impedance-matched ZIM contains random defects, unusual percolation of electromagnetic waves could appear [62]. In 2015 Luo et al theoretically demonstrated that there exists an unusual type of percolation threshold which, unlike normal percolation theory, is induced by the long-range connectivity of the defects in the transverse direction [62] (Figure 5A). It was discovered that below the percolation threshold, the transmittance is always unity, irrespective of the material, shape and size of the embedded inclusions. The electromagnetic waves can squeeze through the gaps between random defects. While beyond the threshold, the transmittance will generally suffer a sharp reduction, and become strongly dependent on the configuration of defects (Figure 5B).

FIGURE 5

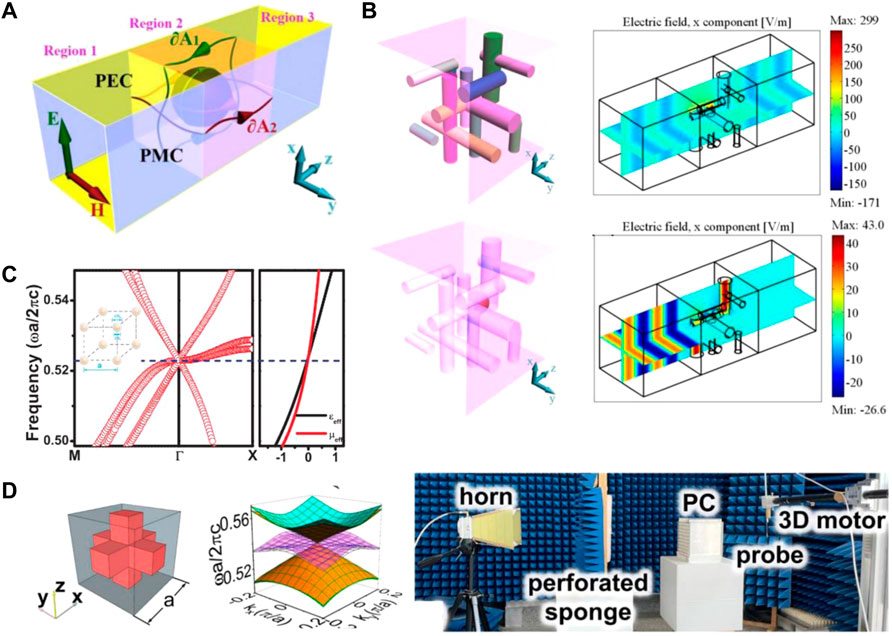
FIGURE 5. (A) Schematic of unusual percolation of electromagnetic waves in a 3D impedance-matched ZIM host with defects. (B) Upper: schematic diagram of a 3D ZIM host embedded with random dielectric cylinders below the percolation threshold (left), and the simulated electric-field distribution, showing perfect transmission of electromagnetic waves (right). Lower: schematic diagram of the case beyond the percolation threshold (left), and the simulated electric-field distribution, showing near-zero transmission (right). Reproduced with permission from Ref. [62]. (C) A theoretical design of 3D ZIM using a 3D PhC consisting of a simple cubic lattice of core-shell spheres. A Dirac-like cone composed of sixfold degenerate modes is observed at the $\text{Γ}$ point, and the effective parameters satisfy ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$ at the Dirac-point frequency. Reproduced with permission from Ref. [148]. (D) A microwave experimental realization of the 3D PhC with a Dirac-like cone for 3D ZIM. The PhC is composed of dielectric meshes. Reproduced with permission from Ref. [150].

The 3D PhC with a Dirac-line cone dispersion offers a platform to explore the intriguing features of 3D ZIM. A theoretical design was investigated by Chan in 2012 [148]. The PhC consists of a simple cubic lattice of core-shell spheres. The core is a perfect electric conductor, and the shell is dielectric. From Figure 5C Dirac-like cone as the consequence of sixfold degenerate modes is observed at the $\text{Γ}$ point. Both the effective permittivity and permeability are zero, i.e., ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$, at the Dirac-point frequency. However, the design is sensitive to the parameters and the fabrication is quite challenging. In 2021, Xu et al [150] experimentally realized the Dirac-like cone by employing another design of a 3D PhC composed of dielectric meshes. The dielectric meshes are orthogonally aligned along the $x$, $y$, and $z$ directions, and intersect at the center of the unit cell (Figure 5D). At the $\text{Γ}$ point, a sixfold accidental degeneracy of electric and magnetic dipole modes results in a Dirac-like cone. The microwave experiment demonstrated the near-perfect transmission of electromagnetic waves when there exist defects inside the PhC (i.e., effective 3D impedance-matched ZIM) below the percolation threshold. Such an extraordinary phenomenon that the transmission through an impedance-matched ZIM is independent of the embedded impurities may be referred to as an impurity-immunity or anti-doping effect [63, 150]. We emphasize that the 3D PhC of ${\epsilon }_{\text{eff}}={\mu }_{\text{eff}}=0$ represents an interesting electromagnetic void space that is generated by expanding an infinitesimal point to a finite volume of space using transformation optics [178–180]. Such an electromagnetic void space has many interesting features that are absent in any other electromagnetic media.

Dirac-Like Cones in Acoustic and Elastic Structures

The concept of Dirac-like cones has also been developed in other kinds of classical wave structures including acoustic and elastic structures [23, 28, 148, 159–174].

In acoustics, the two key physical parameters that are essential for the propagation of the sound wave in materials are mass density and bulk modulus. Through carefully designing the two key physical parameters, microstructure and dimension parameters of PnCs, the Dirac-like cones at the center of the Brillouin zone can be obtained, also showing the effective zero refraction index property (i.e., simultaneous zero mass density and zero reciprocal bulk modulus). An experimental visualization of the Dirac-like cone in a 2D PnC was realized by Dubois et al in 2017 [166]. The PnC is a square lattice of blind holes (Figure 6A). Three bands are degenerate at the Dirac point, which correspond to a monopole mode and doubly degenerate dipole modes. Through measuring pressure field radiated by acoustic point source embedded in PnC, the directive emission enabled by zero refractive index was observed at the Dirac-point frequency. The 3D PnC exhibiting a Dirac-like cone was experimentally demonstrated by Xu et al in 2020 (Figure 6B) [174]. The unit cell of the PnC comprises three aluminum rods in air. A Dirac-like cone composed of fourfold degenerate modes occurs at the $\text{Γ}$ point. The effective zero refractive index property at the Dirac-point frequency was demonstrated through investigating of wave tunneling effect in bending waveguides in both simulations and experiments, which is referred to as an acoustic “periscope”.

FIGURE 6

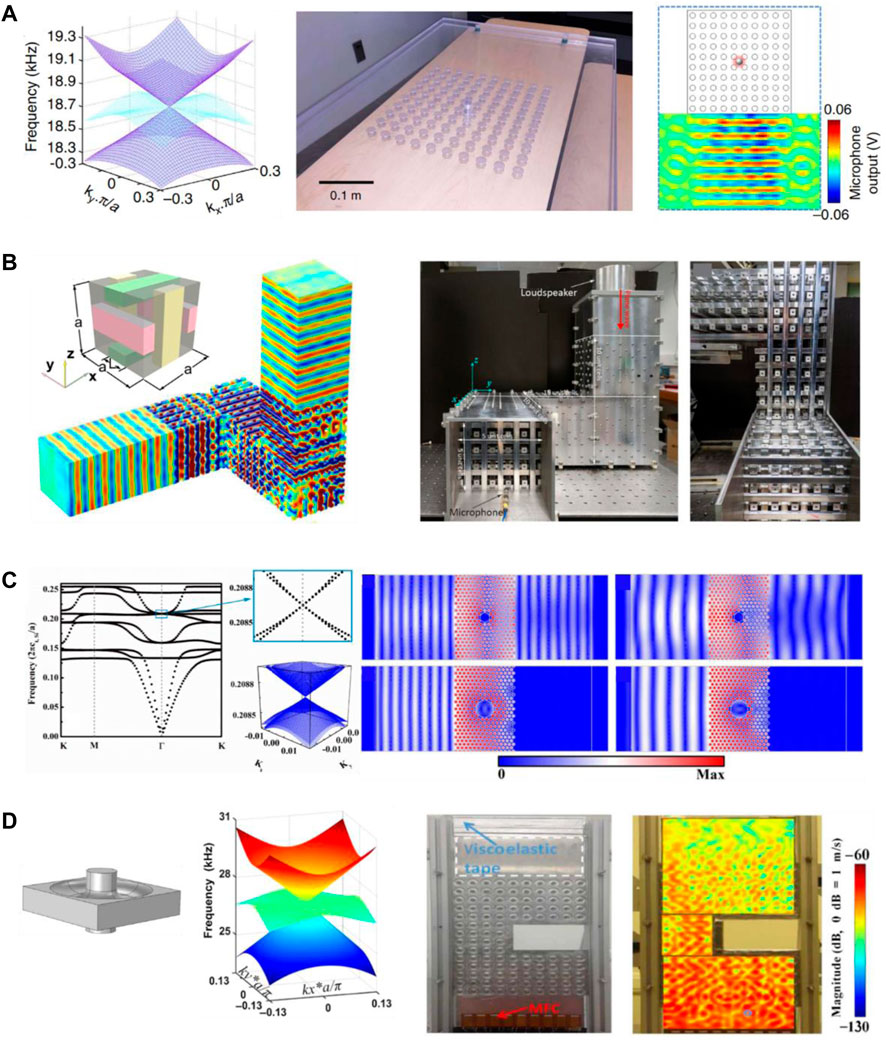
FIGURE 6. (A) Left: enlarged view of dispersion surfaces near the Dirac-like cone of the PnC consisting of a square lattice of blind holes. Middle: photograph of the fabricated sample. Right: measured pressure field radiated by an acoustic point source embedded in PnC, showing the directive emission behavior at the Dirac-point frequency. Reproduced with permission from Ref. [166]. (B) Left: simulated pressure-field distribution when a bending waveguide is filled with 3D cubic-lattice PnC with a Dirac-like cone. The inset shows the unit cell comprising three aluminum rods in air. Right: photograph of the fabricated bending waveguide. Reproduced with permission from Ref. [174]. (C) Left: band structure for in-plane modes of a 2D triangular-lattice PnC consisting of rubber cylinders embedded in silicon host, and the enlarged view of the double Dirac cone. Right: simulated displacement-field distributions for the 2D PnC embedded with the steel cylinders to achieve transmission preserving plane wave characteristic (upper) and total reflection (lower). Different columns represent the incident longitudinal and transverse waves, respectively. Reproduced with permission from Ref. [163]. (D) Left: schematic of the tapered unit cell of a square-lattice PnC. Middle: enlarged view of dispersion surfaces near the Dirac-like cone. Right: photograph of U-shaped waveguide channel filled with the PnC, and measured amplitude of out-of-plane velocity at the Dirac-point frequency. Reproduced with permission from Ref. [165].

In solids, both longitudinal and transverse waves exist, and the wave propagation properties are characterized by more parameters, such as the shear modulus. Through engineering the characteristic and dimension parameters, it is also possible to obtain Dirac cones in a PnC supporting both longitudinal and transverse waves. For example, Liu et al designed a 2D triangular-lattice PnC consisting of rubber cylinders embedded in silicon host, exhibiting a double Dirac cone at the $\text{Γ}$ point as the consequence of fourfold degenerate modes (Figure 6C) [163]. Such a PnC possesses simultaneous zero effective refractive indices for both longitudinal and transverse waves at the Dirac cone frequency, which can be utilized to prohibit the longitudinal-transverse mode conversion even in the presence of scattering objects. In 2017 Zhu et al experimentally realized simultaneous zero mass density and zero reciprocal shear modulus in an elastic waveguide filled with a square-lattice PnC with a Dirac-like cone. The unit cell consists of a square plate having an embedded elliptic torus-like taper and a resonating center mass (Figure 6D) [165]. Threefold degenerate modes result in a Dirac-like cone at the $\text{Γ}$ point. Numerical and experimental results confirmed the zero-refractive-index-enabled cloaking and super-coupling effects at the Dirac-point frequency.

Summary and Outlook

We have reviewed the study of Dirac-like cones in both PhCs and PnCs, from Hermitian to non-Hermitian systems and from 2D to 3D. PhCs/PnCs with a Dirac-like cone at the center of the Brillouin zone behave as effective ZIM at the Dirac-point frequency, providing a remarkable platform for the ultralow-loss ZIMs and the ZIM-based applications. Due to this unique feature, the Dirac-like cones have attracted considerable attention from theoretical investigation of underlying physics to experimental verification and application exploration.

Despite the above advances, there are some remaining important open questions are worth exploring. For instance, the fast inverse design of Dirac-like cones at will is an interesting question. The inverse design problem, meaning the direct retrieval of the proper structure for the desired optical performance, requires exploration of a large degree of freedom in the design space, and hence is very challenging and time-consuming [36, 181]. Recently, topology optimization, as a large-scale computational technique employing powerful gradient-based numerical algorithms, has been applied to inversely design Dirac-like cones [36–40]. The topology optimization is a rule-based approach containing iterative searching steps in a case-by-case manner, usually relying on numerical simulations in each step to produce intermediate results that help to modify the searching strategy [181]. This process would be very time-consuming especially when dealing with complicated 3D structures. Deep learning, as a data-driven methodology, could overcome complicated design problems with growth of structural complexity and higher degree of freedom through training the artificial neural network [36, 181]. A trained neural network can be used as a fast, general purpose predictor of optical and electromagnetic responses of complicated 3D structures, and is particularly efficient in solving notoriously difficult inverse problems in nanophotonics [182–185]. Another way is the utilization of the systematic band engineering method that has realized Dirac cones at arbitrary k point in the Brillouin zone of PhCs without symmetry [35]. With such advanced designing techniques, customized Dirac and Dirac-like cones can realized in complex PhCs/PnCs.

Another interesting topic is the realization of Dirac-like cones or ZIMs at the deep-subwavelength scale. One of the most important features of PhCs/PnCs with Dirac-like cones is that they can mimic effective ZIM. However, most of the PhCs/PnCs are composed of periodic structures, whose lattice constant is in the half-wavelength scale. Such a bulky size hinders many applications that require deep-wavelength ZIM, including tunneling effect in deep-subwavelength channels [48–50] and arbitrary control of energy flux in the deep-subwavelength scale [52], etc. The realization of PhCs/PnCs with Dirac-like cones in the deep-subwavelength scale is important to expand their application scenarios.

Author Contributions

YL and JL conceived the idea and wrote the draft of this review.

Funding

This work was supported by the National Key R&D Program of China (Grant Nos 2020YFA0211300, 2020YFA0211400, 2017YFA0303702) National Natural Science Foundation of China (Grant Nos 11974176, 12174188), China Postdoctoral Science Foundation (2021M702401), the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Geim AK, Novoselov KS. The Rise of Graphene. Nat Mater (2007) 6:183–91. doi:10.1038/nmat1849

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Castro Neto AH, Guinea F, Peres NMR, Novoselov KS, Geim AK. The Electronic Properties of Graphene. Rev Mod Phys (2009) 81:109–62. doi:10.1103/revmodphys.81.109

CrossRef Full Text | Google Scholar

3. John S. Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Phys Rev Lett (1987) 58:2486–9. doi:10.1103/physrevlett.58.2486

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yablonovitch E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys Rev Lett (1987) 58:2059–62. doi:10.1103/physrevlett.58.2059

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Sigalas MM, Economou EN. Elastic and Acoustic Wave Band Structure. J Sound Vibration (1992) 158:377–82. doi:10.1016/0022-460x(92)90059-7

CrossRef Full Text | Google Scholar

6. Kushwaha MS, Halevi P, Dobrzynski L, Djafari-Rouhani B. Acoustic Band Structure of Periodic Elastic Composites. Phys Rev Lett (1993) 71:2022–5. doi:10.1103/physrevlett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Martínez-Sala R, Sancho J, Sánchez JV, Gómez V, Llinares J, Meseguer F. Sound Attenuation by Sculpture. Nature (1995) 378:241. doi:10.1038/378241a0

CrossRef Full Text | Google Scholar

8. Page JH, Sheng P, Schriemer HP, Jones I, Jing X, Weitz DA. Group Velocity in Strongly Scattering Media. Science (1996) 271:634–7. doi:10.1126/science.271.5249.634

CrossRef Full Text | Google Scholar

9. Plihal M, Maradudin AA. Photonic Band Structure of Two-Dimensional Systems: The Triangular Lattice. Phys Rev B (1991) 44:8565–71. doi:10.1103/physrevb.44.8565

CrossRef Full Text | Google Scholar

10. Peleg O, Bartal G, Freedman B, Manela O, Segev M, Christodoulides DN. Conical Diffraction and Gap Solitons in Honeycomb Photonic Lattices. Phys Rev Lett (2007) 98:103901. doi:10.1103/physrevlett.98.103901

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sepkhanov RA, Bazaliy YB, Beenakker CWJ. Extremal Transmission at the Dirac point of a Photonic Band Structure. Phys Rev A (2007) 75:063813. doi:10.1103/physreva.75.063813

CrossRef Full Text | Google Scholar

12. Raghu S, Haldane FDM. Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys Rev A (2008) 78:033834. doi:10.1103/physreva.78.033834

CrossRef Full Text | Google Scholar

13. Sepkhanov RA, Nilsson J, Beenakker CWJ. Proposed Method for Detection of the Pseudospin-1/2 Berry Phase in a Photonic crystal with a Dirac Spectrum. Phys Rev B (2008) 78:045122. doi:10.1103/physrevb.78.045122

CrossRef Full Text | Google Scholar

14. Zhang X. ObservingZitterbewegungfor Photons Near the Dirac Point of a Two-Dimensional Photonic Crystal. Phys Rev Lett (2008) 100:113903. doi:10.1103/physrevlett.100.113903

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Haldane FD, Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys Rev Lett (2008) 100:013904. doi:10.1103/PhysRevLett.100.013904

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ochiai T, Onoda M. Photonic Analog of Graphene Model and its Extension: Dirac Cone, Symmetry, and Edge States. Phys Rev B (2009) 80:155103. doi:10.1103/physrevb.80.155103

CrossRef Full Text | Google Scholar

17. Ao X, Lin Z, Chan C. One-way Edge Mode in a Magneto-Optical Honeycomb Photonic crystal. Phys Rev B (2009) 80:033105. doi:10.1103/physrevb.80.033105

CrossRef Full Text | Google Scholar

18. Diem M, Koschny T, Soukoulis CM. Transmission in the Vicinity of the Dirac point in Hexagonal Photonic Crystals. Physica B: Condensed Matter (2010) 405:2990–5. doi:10.1016/j.physb.2010.01.020

CrossRef Full Text | Google Scholar

19. Bittner S, Dietz B, Miski-Oglu M, Oria Iriarte P, Richter A, Schäfer F. Observation of a Dirac point in Microwave Experiments with a Photonic crystal Modeling Graphene. Phys Rev B (2010) 82:014301. doi:10.1103/physrevb.82.014301

CrossRef Full Text | Google Scholar

20. Zandbergen SR, de Dood MJ. Experimental Observation of strong Edge Effects on the Pseudodiffusive Transport of Light in Photonic Graphene. Phys Rev Lett (2010) 104:043903. doi:10.1103/PhysRevLett.104.043903

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yu S-Y, Sun X-C, Ni X, Wang Q, Yan X-J, He C, et al. Surface Phononic Graphene. Nat Mater (2016) 15:1243–7. doi:10.1038/nmat4743

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Collins MJ, Zhang F, Bojko R, Chrostowski L, Rechtsman MC. Integrated Optical Dirac Physics via Inversion Symmetry Breaking. Phys Rev A (2016) 94:063827. doi:10.1103/physreva.94.063827

CrossRef Full Text | Google Scholar

23. Mei J, Wu Y, Chan CT, Zhang Z. First-principles Study of Dirac and Dirac-like Cones in Phononic and Photonic Crystals. Phys Rev B (2012) 86:035141. doi:10.1103/physrevb.86.035141

CrossRef Full Text | Google Scholar

24. Szameit A, Rechtsman MC, Bahat-Treidel O, Segev M. PT-symmetry in Honeycomb Photonic Lattices. Phys Rev A (2011) 84:021806(R). doi:10.1103/physreva.84.021806

CrossRef Full Text | Google Scholar

25. Zhang X, Liu Z. Extremal Transmission and Beating Effect of Acoustic Waves in Two-Dimensional Sonic Crystals. Phys Rev Lett (2008) 101:264303. doi:10.1103/physrevlett.101.264303

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Torrent D, Sánchez-Dehesa J. Acoustic Analogue of Graphene: Observation of Dirac Cones in Acoustic Surface Waves. Phys Rev Lett (2012) 108:174301. doi:10.1103/physrevlett.108.174301

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Torrent D, Mayou D, Sánchez-Dehesa J. Elastic Analog of Graphene: Dirac Cones and Edge States for Flexural Waves in Thin Plates. Phys Rev B (2013) 87:115143. doi:10.1103/physrevb.87.115143

CrossRef Full Text | Google Scholar

28. Lu J, Qiu C, Xu S, Ye Y, Ke M, Liu Z. Dirac Cones in Two-Dimensional Artificial Crystals for Classical Waves. Phys Rev B (2014) 89:134302. doi:10.1103/physrevb.89.134302

CrossRef Full Text | Google Scholar

29. Chan CT, Hang ZH, Huang X. Dirac Dispersion in Two-Dimensional Photonic Crystals. Adv OptoElectronics (2012) 2012:1–11. doi:10.1155/2012/313984

CrossRef Full Text | Google Scholar

30. Vulis DI, Reshef O, Camayd-Muñoz P, Mazur E. Manipulating the Flow of Light Using Dirac-Cone Zero-index Metamaterials. Rep Prog Phys (2019) 82:012001. doi:10.1088/1361-6633/aad3e5

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Li Y, Chan CT, Mazur E. Dirac-like Cone-Based Electromagnetic Zero-index Metamaterials. Light Sci Appl (2021) 10:203. doi:10.1038/s41377-021-00642-2

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Huang X, Lai Y, Hang ZH, Zheng H, Chan CT. Dirac Cones Induced by Accidental Degeneracy in Photonic Crystals and Zero-Refractive-index Materials. Nat Mater (2011) 10:582–6. doi:10.1038/nmat3030

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Sakoda K. Proof of the Universality of Mode Symmetries in Creating Photonic Dirac Cones. Opt Express (2012) 20:25181–94. doi:10.1364/oe.20.025181

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Sakoda K. Optical Properties of Photonic Crystals. New York, USA: Springer (2005).

Google Scholar

35. Chu H, Zhang Y, Luo J, Xu C, Xiong X, Peng R, et al. Band Engineering Method to Create Dirac Cones of Accidental Degeneracy in General Photonic Crystals without Symmetry. Opt Express (2021) 29:18070. doi:10.1364/oe.427389

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Li W, Meng F, Chen Y, Li YF, Huang X. Topology Optimization of Photonic and Phononic Crystals and Metamaterials: A Review. Adv Theor Simul. (2019) 2:1900017. doi:10.1002/adts.201900017

CrossRef Full Text | Google Scholar

37. Chen Y, Meng F, Jia B, Li G, Huang X. Inverse Design of Photonic Topological Insulators with Extra-wide Bandgaps. Phys Status Solidi RRL (2019) 13:1900175. doi:10.1002/pssr.201900175

CrossRef Full Text | Google Scholar

38. Chen Y, Meng F, Li G, Huang X. Topology Optimization of Photonic Crystals with Exotic Properties Resulting from Dirac-like Cones. Acta Materialia (2019) 164:377–89. doi:10.1016/j.actamat.2018.10.058

CrossRef Full Text | Google Scholar

39. Lin Z, Christakis L, Li Y, Mazur E, Rodriguez AW, Lončar M. Topology-optimized Dual-Polarization Dirac Cones. Phys Rev B (2018) 97:081408(R). doi:10.1103/physrevb.97.081408

CrossRef Full Text | Google Scholar

40. Lin Z, Pick A, Lončar M, Rodriguez AW. Enhanced Spontaneous Emission at Third-Order Dirac Exceptional Points in Inverse-Designed Photonic Crystals. Phys Rev Lett (2016) 117:107402. doi:10.1103/physrevlett.117.107402

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Liberal I, Engheta N. Near-zero Refractive index Photonics. Nat Photon (2017) 11:149–58. doi:10.1038/nphoton.2017.13

CrossRef Full Text | Google Scholar

42. Liberal I, Engheta N. The Rise of Near-Zero-index Technologies. Science (2017) 358:1540–1. doi:10.1126/science.aaq0459

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Niu X, Hu X, Chu S, Gong Q. Epsilon-near-zero Photonics: A New Platform for Integrated Devices. Adv Opt Mater (2018) 6:1701292. doi:10.1002/adom.201701292

CrossRef Full Text | Google Scholar

44. Jahani S, Jacob Z. All-dielectric Metamaterials. Nat Nanotech (2016) 11:23–36. doi:10.1038/nnano.2015.304

CrossRef Full Text | Google Scholar

45. Enoch S, Tayeb G, Sabouroux P, Guérin N, Vincent P. A Metamaterial for Directive Emission. Phys Rev Lett (2002) 89:213902. doi:10.1103/physrevlett.89.213902

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Luo J, Xu P, Gao L. Directive Emission Based on One-Dimensional Metal Heterostructures. J Opt Soc Am B (2012) 29:35–9. doi:10.1364/josab.29.000035

CrossRef Full Text | Google Scholar

47. Luo J, Lai Y. Epsilon-near-zero or Mu-Near-Zero Materials Composed of Dielectric Photonic Crystals. Sci China Inf Sci (2013) 56:1–10. doi:10.1007/s11432-013-5029-9

CrossRef Full Text | Google Scholar

48. Silveirinha M, Engheta N. Tunneling of Electromagnetic Energy through Subwavelength Channels and Bends Usingε-Near-Zero Materials. Phys Rev Lett (2006) 97:157403. doi:10.1103/physrevlett.97.157403

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Liu R, Cheng Q, Hand T, Mock JJ, Cui TJ, Cummer SA, et al. Experimental Demonstration of Electromagnetic Tunneling through an Epsilon-Near-Zero Metamaterial at Microwave Frequencies. Phys Rev Lett (2008) 100:023903. doi:10.1103/PhysRevLett.100.023903

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Edwards B, Alù A, Young ME, Silveirinha M, Engheta N. Experimental Verification of Epsilon-Near-Zero Metamaterial Coupling and Energy Squeezing Using a Microwave Waveguide. Phys Rev Lett (2008) 100:033903. doi:10.1103/PhysRevLett.100.033903

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Luo J, Xu P, Chen H, Hou B, Gao L, Lai Y. Realizing Almost Perfect Bending Waveguides with Anisotropic Epsilon-Near-Zero Metamaterials. Appl Phys Lett (2012) 100:221903. doi:10.1063/1.4723844

CrossRef Full Text | Google Scholar

52. Luo J, Lu W, Hang Z, Chen H, Hou B, Lai Y, et al. Arbitrary Control of Electromagnetic Flux in Inhomogeneous Anisotropic media with Near-Zero index. Phys Rev Lett (2014) 112:073903. doi:10.1103/PhysRevLett.112.073903

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Li Y, Jiang HT, Liu WW, Ran J, Lai Y, Chen H. Experimental Realization of Subwavelength Flux Manipulation in Anisotropic Near-Zero index Metamaterials. Epl (2016) 113:57006. doi:10.1209/0295-5075/113/57006

CrossRef Full Text | Google Scholar

54. Luo J, Lai Y. Anisotropic Zero-index Waveguide with Arbitrary Shapes. Sci Rep (2014) 4:5875. doi:10.1038/srep05875

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Zhang X, Wu Y. Effective Medium Theory for Anisotropic Metamaterials. Sci Rep (2015) 5:7892. doi:10.1038/srep07892

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Ji W, Luo J, Lai Y. Extremely Anisotropic Epsilon-Near-Zero media in Waveguide Metamaterials. Opt Express (2019) 27:19463–73. doi:10.1364/oe.27.019463

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Liberal I, Mahmoud AM, Li Y, Edwards B, Engheta N. Photonic Doping of Epsilon-Near-Zero media. Science (2017) 355:1058–62. doi:10.1126/science.aal2672

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Liberal I, Li Y, Engheta N. Reconfigurable Epsilon-Near-Zero Metasurfaces via Photonic Doping. Nanophotonics (2018) 7:1117–27. doi:10.1515/nanoph-2018-0012

CrossRef Full Text | Google Scholar

59. Luo J, Liu B, Hang ZH, Lai Y. Coherent Perfect Absorption via Photonic Doping of Zero-index media. Laser Photon Rev. (2018) 12:1800001. doi:10.1002/lpor.201800001

CrossRef Full Text | Google Scholar

60. Wang D, Luo J, Sun Z, Lai Y. Transforming Zero-index media into Geometry-Invariant Coherent Perfect Absorbers via Embedded Conductive Films. Opt Express (2021) 29:5247. doi:10.1364/oe.416632

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Coppolaro M, Moccia M, Castaldi G, Engheta N, Galdi V. Non-Hermitian Doping of Epsilon-Near-Zero media. Proc Natl Acad Sci USA (2020) 117:13921–8. doi:10.1073/pnas.2001125117

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Luo J, Hang ZH, Chan CT, Lai Y. Unusual Percolation Threshold of Electromagnetic Waves in Double-Zero Medium Embedded with Random Inclusions. Laser Photon Rev (2015) 9:523–9. doi:10.1002/lpor.201500083

CrossRef Full Text | Google Scholar

63. Luo J, Li J, Lai Y. Electromagnetic Impurity-Immunity Induced by Parity-Time Symmetry. Phys Rev X (2018) 8:031035. doi:10.1103/physrevx.8.031035

CrossRef Full Text | Google Scholar

64. Chu H, Li Q, Liu B, Luo J, Sun S, Hang ZH, et al. A Hybrid Invisibility Cloak Based on Integration of Transparent Metasurfaces and Zero-index Materials. Light Sci Appl (2018) 7:50. doi:10.1038/s41377-018-0052-7

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Hao J, Yan W, Qiu M. Super-reflection and Cloaking Based on Zero index Metamaterial. Appl Phys Lett (2010) 96:101109. doi:10.1063/1.3359428

CrossRef Full Text | Google Scholar

66. Silveirinha M, Engheta N. Design of Matched Zero-index Metamaterials Using Nonmagnetic Inclusions in Epsilon-Near-Zero media. Phys Rev B (2007) 75:075119. doi:10.1103/physrevb.75.075119

CrossRef Full Text | Google Scholar

67. Tagviashvili M. ε→ 0 Limits in the Mie-Scattering Theory. Phys Rev A (2010) 81:045802. doi:10.1103/physreva.81.045802

CrossRef Full Text | Google Scholar

68. Nguyen VC, Chen L, Halterman K. Total Transmission and Total Reflection by Zero index Metamaterials with Defects. Phys Rev Lett (2010) 105:233908. doi:10.1103/physrevlett.105.233908

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Luo J, Xu P, Gao L, Lai Y, Chen H. Manipulate the Transmissions Using index-near-zero or Epsilon-Near-Zero Metamaterials with Coated Defects. Plasmonics (2012) 7:353–8. doi:10.1007/s11468-011-9314-4

CrossRef Full Text | Google Scholar

70. Xu Y, Chen H. Total Reflection and Transmission by Epsilon-Near-Zero Metamaterials with Defects. Appl Phys Lett (2011) 98:113501. doi:10.1063/1.3565172

CrossRef Full Text | Google Scholar

71. Wang T, Luo J, Gao L, Xu P, Lai Y. Hiding Objects and Obtaining Fano Resonances in index-near-zero and Epsilon-Near-Zero Metamaterials with Bragg-fiber-like Defects. J Opt Soc Am B (2013) 30:1878–84. doi:10.1364/josab.30.001878

CrossRef Full Text | Google Scholar

72. Wang T, Luo J, Gao L, Xu P, Lai Y. Equivalent Perfect Magnetic Conductor Based on Epsilon-Near-Zero media. Appl Phys Lett (2014) 104:211904. doi:10.1063/1.4876918

CrossRef Full Text | Google Scholar

73. Song J, Luo J, Lai Y. Side Scattering Shadow and Energy Concentration Effects of Epsilon-Near-Zero media. Opt Lett (2018) 43:1738–41. doi:10.1364/ol.43.001738

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Yang Y, Jia Z, Xu T, Luo J, Lai Y, Hang ZH. Beam Splitting and Unidirectional Cloaking Using Anisotropic Zero-index Photonic Crystals. Appl Phys Lett (2019) 114:161905. doi:10.1063/1.5088837

CrossRef Full Text | Google Scholar

75. Feng S, Halterman K. Coherent Perfect Absorption in Epsilon-Near-Zero Metamaterials. Phys Rev B (2012) 86:165103. doi:10.1103/physrevb.86.165103

CrossRef Full Text | Google Scholar

76. Luo J, Li S, Hou B, Lai Y. Unified Theory for Perfect Absorption in Ultrathin Absorptive Films with Constant Tangential Electric or Magnetic fields. Phys Rev B (2014) 90:165128. doi:10.1103/physrevb.90.165128

CrossRef Full Text | Google Scholar

77. Zhong S, Ma Y, He S. Perfect Absorption in Ultrathin Anisotropic ε-near-zero Metamaterials. Appl Phys Lett (2014) 105:023504. doi:10.1063/1.4890397

CrossRef Full Text | Google Scholar

78. Bai P, Ding K, Wang G, Luo J, Zhang Z, Chan CT, et al. Simultaneous Realization of a Coherent Perfect Absorber and Laser by Zero-index media with Both Gain and Loss. Phys Rev A (2016) 94:063841. doi:10.1103/physreva.94.063841

CrossRef Full Text | Google Scholar

79. Rensberg J, Zhou Y, Richter S, Wan C, Zhang S, Schöppe P, et al. Epsilon-near-zero Substrate Engineering for Ultrathin-Film Perfect Absorbers. Phys Rev Appl (2017) 8:014009. doi:10.1103/physrevapplied.8.014009

CrossRef Full Text | Google Scholar

80. Xu C, Farhat M, Wu Y. Non-Hermitian Electromagnetic Double-Near-Zero index Medium in a Two-Dimensional Photonic crystal. Appl Phys Lett (2021) 119:224102. doi:10.1063/5.0073391

CrossRef Full Text | Google Scholar

81. Vincenti MA, de Ceglia D, Ciattoni A, Scalora M. Singularity-driven Second- and Third-Harmonic Generation at ε-near-zero Crossing Points. Phys Rev A (2011) 84:063826. doi:10.1103/physreva.84.063826

CrossRef Full Text | Google Scholar

82. Suchowski H, O’Brien K, Wong ZJ, Salandrino A, Yin X, Zhang X. Phase Mismatch-free Nonlinear Propagation in Optical Zero-index Materials. Science (2013) 342:1223–6. doi:10.1126/science.1244303

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Alam MZ, De Leon I, Boyd RW. Large Optical Nonlinearity of Indium Tin Oxide in its Epsilon-Near-Zero Region. Science (2016) 352:795–7. doi:10.1126/science.aae0330

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Alam MZ, Schulz SA, Upham J, De Leon I, Boyd RW. Large Optical Nonlinearity of Nanoantennas Coupled to an Epsilon-Near-Zero Material. Nat Photon (2018) 12:79–83. doi:10.1038/s41566-017-0089-9

CrossRef Full Text | Google Scholar

85. Reshef O, De Leon I, Alam MZ, Boyd RW. Nonlinear Optical Effects in Epsilon-Near-Zero media. Nat Rev Mater (2019) 4:535–51. doi:10.1038/s41578-019-0120-5

CrossRef Full Text | Google Scholar

86. Bittner S, Dietz B, Miski-Oglu M, Richter A. Extremal Transmission through a Microwave Photonic crystal and the Observation of Edge States in a Rectangular Dirac Billiard. Phys Rev B (2012) 85. doi:10.1103/physrevb.85.064301

CrossRef Full Text | Google Scholar

87. Sakoda K. Universality of Mode Symmetries in Creating Photonic Dirac Cones. J Opt Soc Am B (2012) 29:2770. doi:10.1364/josab.29.002770

CrossRef Full Text | Google Scholar

88. Fang K, Zhang Y, Li F, Jiang H, Li Y, Wang W, et al. Microwave Collimation Based on Zero index Metamaterials with Dirac point. Opt Lett (2012) 37:4654–6. doi:10.1364/ol.37.004654

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Antonakakis T, Craster RV, Guenneau S. High-frequency Homogenization of Zero-Frequency Stop Band Photonic and Phononic Crystals. New J Phys (2013) 15:103014. doi:10.1088/1367-2630/15/10/103014

CrossRef Full Text | Google Scholar

90. Mattiucci N, Bloemer MJ, D’Aguanno G. All-optical Bistability and Switching Near the Dirac point of a 2-D Photonic crystal. Opt Express (2013) 21:11862. doi:10.1364/oe.21.011862

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Moitra P, Yang Y, Anderson Z, Kravchenko II, Briggs DP, Valentine J. Realization of an All-Dielectric Zero-index Optical Metamaterial. Nat Photon (2013) 7:791–5. doi:10.1038/nphoton.2013.214

CrossRef Full Text | Google Scholar

92. D Aguanno G, Mattiucci N, Conti C, Bloemer MJ. Field Localization and Enhancement Near the Dirac point of a Finite Defectless Photonic crystal. Phys Rev B (2013) 87:085135.

Google Scholar

93. Sakoda K. Polarization-dependent Continuous Change in the Propagation Direction of Dirac-Cone Modes in Photonic-crystal Slabs. Phys Rev A (2014) 90:013835. doi:10.1103/physreva.90.013835

CrossRef Full Text | Google Scholar

94. Mattiucci N, Bloemer MJ, D’Aguanno G. Phase-matched Second Harmonic Generation at the Dirac point of a 2-D Photonic crystal. Opt Express (2014) 22:6381. doi:10.1364/oe.22.006381

PubMed Abstract | CrossRef Full Text | Google Scholar

95. He W-Y, Chan CT. The Emergence of Dirac Points in Photonic Crystals with Mirror Symmetry. Sci Rep (2015) 5:8186. doi:10.1038/srep08186

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Yu S-Y, Wang Q, Zheng L-Y, He C, Liu X-P, Lu M-H, et al. Acoustic Phase-Reconstruction Near the Dirac point of a Triangular Phononic crystal. Appl Phys Lett (2015) 106:151906. doi:10.1063/1.4918651

CrossRef Full Text | Google Scholar

97. Ashraf MW, Faryad M. Dirac-like Cone Dispersion in Two-Dimensional Core-Shell Dielectric Photonic Crystals. J Nanophoton (2015) 9:093057. doi:10.1117/1.jnp.9.093057

CrossRef Full Text | Google Scholar

98. Wang X, Jiang H, Li Y, Yan C, Deng F, Sun Y, et al. Transport Properties of Disordered Photonic Crystals Around a Dirac-like point. Opt Express (2015) 23:5126. doi:10.1364/oe.23.005126

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Dong J-W, Chang M-L, Huang X-Q, Hang ZH, Zhong Z-C, Chen W-J, et al. Conical Dispersion and Effective Zero Refractive index in Photonic Quasicrystals. Phys Rev Lett (2015) 114:163901. doi:10.1103/physrevlett.114.163901

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Li Y, Mei J. Double Dirac Cones in Two-Dimensional Dielectric Photonic Crystals. Opt Express (2015) 23:12089. doi:10.1364/oe.23.012089

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Zhang P, Fietz C, Tassin P, Koschny T, Soukoulis CM. Numerical Investigation of the Flat Band Bloch Modes in a 2D Photonic crystal with Dirac Cones. Opt Express (2015) 23:10444. doi:10.1364/oe.23.010444

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Ashraf MW, Faryad M. On the Mapping of Dirac-like Cone Dispersion in Dielectric Photonic Crystals to an Effective Zero-index Medium. J Opt Soc Am B (2016) 33:1008. doi:10.1364/josab.33.001008

CrossRef Full Text | Google Scholar

103. Dong G, Zhou J, Yang X, Meng X. Precise Identification of Dirac-like point through a Finite Photonic crystal Square Matrix. Sci Rep (2016) 6:36712. doi:10.1038/srep36712

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Nagai S, Sanada A. Γ-point Group Velocity of Lossy Dirac Cone Composite Right/left-Handed Metamaterials. IEICE Electron Express (2016) 13:20160281. doi:10.1587/elex.13.20160281

CrossRef Full Text | Google Scholar

105. Xu C, Lai Y. Configurable Dirac-like Conical Dispersions in Complex Photonic Crystals. Phys Rev B (2017) 95:045124. doi:10.1103/physrevb.95.045124

CrossRef Full Text | Google Scholar

106. Qiu P, Qiu W, Lin Z, Chen H, Ren J, Wang J-X, et al. Investigation of Beam Splitter in a Zero-Refractive-index Photonic crystal at the Frequency of Dirac-like point. Sci Rep (2017) 7:9588. doi:10.1038/s41598-017-10056-z

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Gao H, Zhou YS, Zheng ZY, Chen SJ, Dong JJ. Is the Photonic crystal with a Dirac Cone at its Г point a Real Zero-index Material. Appl Phys B (2017) 123:165. doi:10.1007/s00340-017-6738-3

CrossRef Full Text | Google Scholar

108. Lou Q, Zhang Y, Poo Y, Ma H, Wu R. Realization of Unidirectional Transmission under Accidental Degenerated Dirac point. Opt Commun (2017) 389:58–62. doi:10.1016/j.optcom.2016.12.013

CrossRef Full Text | Google Scholar

109. Xu T, Fang A, Jia Z, Ji L, Hang ZH. Realization of a complementary medium using dielectric photonic crystals. Opt. Lett. (2017) 42:4909. doi:10.1364/ol.42.004909

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Dong G, Li Z, Zhou J, Qiao P, Yang X, Meng X. Precise Displacement Measurement in Single-Beam Interferometry Employing Photonic Metamaterial with Effective Zero-index. Opt Express (2017) 25:31509. doi:10.1364/oe.25.031509

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Yves S, Berthelot T, Fink M, Lerosey G, Lemoult F. Measuring Dirac Cones in a Subwavelength Metamaterial. Phys Rev Lett (2018) 121:267601. doi:10.1103/physrevlett.121.267601

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Xu B, Li T, Zhu S. Simulation of Massless Dirac Dynamics in Plasmonic Waveguide Arrays. Opt Express (2018) 26:13416. doi:10.1364/oe.26.013416

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Hu L, Xie K, Hu Z, Mao Q, Xia J, Jiang H, et al. Experimental Observation of Wave Localization at the Dirac Frequency in a Two-Dimensional Photonic crystal Microcavity. Opt Express (2018) 26:8213. doi:10.1364/oe.26.008213

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Reddy IVAK, Sukhotskiy V, Baev A, Liu K, Haus JW, Sakoda K, et al. Quasi-triply-degenerate States and Zero Refractive index in Two-Dimensional All-Dielectric Photonic Crystals. Opt Express (2020) 28:5548. doi:10.1364/oe.383589

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Xu T, Zhu D, Hang ZH. Pulse Reshaping in Double-Zero-index Photonic Crystals with Dirac-Like-Cone Dispersion. Sci Rep (2020) 10:8416. doi:10.1038/s41598-020-65461-8

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Xu C, Fang A, Chu H, Luo J, Chan CT, Hang ZH, et al. Angular Selection of Incident Waves by Photonic Crystals with Position-Varying Dirac Points at the Brillouin Zone Boundary. Phys Rev B (2016) 93:245116. doi:10.1103/physrevb.93.245116

CrossRef Full Text | Google Scholar

117. Kim J, Yu S, Park N. Universal Design Platform for an Extended Class of Photonic Dirac Cones. Phys Rev Appl (2020) 13:044015. doi:10.1103/physrevapplied.13.044015

CrossRef Full Text | Google Scholar

118. Hajian H, Ozbay E, Caglayan H. Enhanced Transmission and Beaming via a Zero-index Photonic crystal. Appl Phys Lett (2016) 109:031105. doi:10.1063/1.4959085

CrossRef Full Text | Google Scholar

119. Li Y, Wu Y, Chen X, Mei J. Selection Rule for Dirac-like Points in Two-Dimensional Dielectric Photonic Crystals. Opt Express (2013) 21:7699. doi:10.1364/oe.21.007699

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Indaleeb MM, Banerjee S. Simultaneous Dirac-like Cones at Two Energy States in Tunable Phononic Crystals: An Analytical and Numerical Study. Crystals (2021) 11:1528. doi:10.3390/cryst11121528

CrossRef Full Text | Google Scholar

121. Shankhwar N, Kalra Y, Sinha RK. All Dielectric Zero-index Metamaterial for TE/TM Polarization. J Opt (2018) 20:115101. doi:10.1088/2040-8986/aae31c

CrossRef Full Text | Google Scholar

122. Sakoda K. Double Dirac Cones in Triangular-Lattice Metamaterials. Opt Express (2012) 20:9925–39. doi:10.1364/oe.20.009925

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Kim S, Kim S, Kee C. Photonic Crystals Composed of Virtual Pillars with Magnetic walls: Photonic Band Gaps and Double Dirac Cones. Phys Rev B (2016) 94: 085118. doi:10.1103/physrevb.94.085118

CrossRef Full Text | Google Scholar

124. Wu L-H, Hu X. Scheme for Achieving a Topological Photonic crystal by Using Dielectric Material. Phys Rev Lett (2015) 114:223901. doi:10.1103/physrevlett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Yang Y, Xu YF, Xu T, Wang H-X, Jiang J-H, Hu X, et al. Visualization of a Unidirectional Electromagnetic Waveguide Using Topological Photonic Crystals Made of Dielectric Materials. Phys Rev Lett (2018) 120:217401. doi:10.1103/physrevlett.120.217401

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Lei L, Yu T, Liu W, Wang T, Liao Q. Dirac Cones with Zero Refractive Indices in Phoxonic Crystals. Opt Express (2022) 30:308. doi:10.1364/oe.446356

CrossRef Full Text | Google Scholar

127. Wang J-R, Chen X-D, Zhao F-L, Dong J-W. Full Polarization Conical Dispersion and Zero-Refractive-Index in Two-Dimensional Photonic Hypercrystals. Sci Rep (2016) 6:22739. doi:10.1038/srep22739

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Rodríguez JA, Wang B, Cappelli MA. Dual-polarization Dirac Cones in a Simple 2D Square Lattice Photonic crystal. Opt Lett (2020) 45:2486. doi:10.1364/ol.389163

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Wu Y. A Semi-dirac point and an Electromagnetic Topological Transition in a Dielectric Photonic crystal. Opt Express (2014) 22:1906–17. doi:10.1364/oe.22.001906

PubMed Abstract | CrossRef Full Text | Google Scholar

130. He X-T, Zhong Y-N, Zhou Y, Zhong Z-C, Dong J-W. Dirac Directional Emission in Anisotropic Zero Refractive index Photonic Crystals. Sci Rep (2015) 5:13085. doi:10.1038/srep13085

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Vertchenko L, DeVault C, Malureanu R, Mazur E, Lavrinenko A. Near-Zero Index Photonic Crystals with Directive Bound States in the Continuum. Laser Photon Rev (2021) 15:2000559. doi:10.1002/lpor.202000559

CrossRef Full Text | Google Scholar

132. Yasa UG, Turduev M, Giden IH, Kurt H. Full Utilization of Semi-dirac Cones in Photonics. Phys Rev B (2018) 97:195131. doi:10.1103/physrevb.97.195131

CrossRef Full Text | Google Scholar

133. Bor E, Turduev M, Yasa UG, Kurt H, Staliunas K. Asymmetric Light Transmission Effect Based on an Evolutionary Optimized Semi-dirac Cone Dispersion Photonic Structure. Phys Rev B (2018) 98:245112. doi:10.1103/physrevb.98.245112

CrossRef Full Text | Google Scholar

134. Bor E, Gorkem Yasa U, Kurt H, Turduev M. Demonstration of Carpet Cloaking by an Anisotropic Zero Refractive index Medium. Opt Lett (2020) 45:2423. doi:10.1364/ol.388432

PubMed Abstract | CrossRef Full Text | Google Scholar

135. Chua S-L, Lu L, Bravo-Abad J, Joannopoulos JD, Soljačić M. Larger-area Single-Mode Photonic crystal Surface-Emitting Lasers Enabled by an Accidental Dirac point. Opt Lett (2014) 39:2072. doi:10.1364/ol.39.002072

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Zhen B, Hsu CW, Igarashi Y, Lu L, Kaminer I, Pick A, et al. Spawning Rings of Exceptional Points Out of Dirac Cones. Nature (2015) 525:354–8. doi:10.1038/nature14889

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Memarian M, Eleftheriades GV. Dirac Leaky-Wave Antennas for Continuous Beam Scanning from Photonic Crystals. Nat Commun (2015) 6:5855. doi:10.1038/ncomms6855

PubMed Abstract | CrossRef Full Text | Google Scholar

138. Li Y, Kita S, Muñoz P, Reshef O, Vulis DI, Yin M, et al. On-chip Zero-index Metamaterials. Nat Photon (2015) 9:738–42. doi:10.1038/nphoton.2015.198

CrossRef Full Text | Google Scholar

139. He X-T, Huang Z-Z, Chang M-L, Xu S-Z, Zhao F-L, Deng S-Z, et al. Realization of Zero-Refractive-Index Lens with Ultralow Spherical Aberration. ACS Photon (2016) 3:2262–7. doi:10.1021/acsphotonics.6b00714

CrossRef Full Text | Google Scholar

140. Kamiński PM, Taghizadeh A, Breinbjerg O, Mørk J, Arslanagić S. Control of Exceptional Points in Photonic crystal Slabs. Opt Lett (2017) 42:2866–9. doi:10.1364/OL.42.002866

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Vulis DI, Li Y, Reshef O, Camayd-Muñoz P, Yin M, Kita S, et al. Monolithic CMOS-Compatible Zero-index Metamaterials. Opt Express (2017) 25:12381–99. doi:10.1364/oe.25.012381

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Kita S, Li Y, Camayd-Muñoz P, Reshef O, Vulis DI, Day RW, et al. On-chip All-Dielectric Fabrication-Tolerant Zero-index Metamaterials. Opt Express (2017) 25:8326. doi:10.1364/oe.25.008326

PubMed Abstract | CrossRef Full Text | Google Scholar

143. Reshef O, Camayd-Muñoz P, Vulis DI, Li Y, Lonc̆ar M, Mazur E. Direct Observation of Phase-free Propagation in a Silicon Waveguide. ACS Photon (2017) 4:2385–9. doi:10.1021/acsphotonics.7b00760

CrossRef Full Text | Google Scholar

144. Minkov M, Williamson IAD, Xiao M, Fan S. Zero-index Bound States in the Continuum. Phys Rev Lett (2018) 121:263901. doi:10.1103/physrevlett.121.263901

PubMed Abstract | CrossRef Full Text | Google Scholar

145. Peng Y, Liao S. ZIM Laser: Zero-Index-Materials Laser. IEEE J Multiscale Multiphys Comput Tech (2019) 4:133–42. doi:10.1109/jmmct.2019.2905368

CrossRef Full Text | Google Scholar

146. Dong T, Liang J, Camayd-Muñoz S, Liu Y, Tang H, Kita S, et al. Ultra-low-loss On-Chip Zero-index Materials. Light Sci Appl (2021) 10:10. doi:10.1038/s41377-020-00436-y

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Tang H, DeVault C, Camayd-Muñoz SA, Liu Y, Jia D, Du F, et al. Low-Loss Zero-Index Materials. Nano Lett (2021) 21:914–20. doi:10.1021/acs.nanolett.0c03575

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Chan CT, Huang X, Liu F, Hang ZH. Dirac Dispersion and Zero-index in Two Dimensional and Three Dimensional Photonic and Phononic Systems. Prog Electromagn Res B (2012) 44:164–90. doi:10.2528/pierb12082103

CrossRef Full Text | Google Scholar

149. Sakoda K. Dirac Cone in Two- and Three-Dimensional Metamaterials. Opt Express (2012) 20:3898–917. doi:10.1364/oe.20.003898

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Xu C, Chu H, Luo J, Hang ZH, Wu Y, Lai Y. Three-dimensional Electromagnetic Void Space. Phys Rev Lett (2021) 127:123902. doi:10.1103/physrevlett.127.123902

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Cui X, Ding K, Dong J-W, Chan CT. Realization of Complex Conjugate media Using Non-PT-symmetric Photonic Crystals. Nanophotonics (2019) 9:195–203. doi:10.1515/nanoph-2019-0389

CrossRef Full Text | Google Scholar

152. Wang H, Xie B, Gupta SK, Zhu X, Liu L, Liu X, et al. Exceptional Concentric Rings in a Non-hermitian Bilayer Photonic System. Phys Rev B (2019) 100:165134. doi:10.1103/physrevb.100.165134

CrossRef Full Text | Google Scholar

153. Xue H, Wang Q, Zhang B, Chong YD. Non-Hermitian Dirac Cones. Phys Rev Lett (2020) 124:236403. doi:10.1103/physrevlett.124.236403

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Wang N, Zhang R, Chan CT, Wang GP. Effective Medium Theory for a Photonic Pseudospin-1/2 System. Phys Rev B (2020) 102:094312. doi:10.1103/physrevb.102.094312

CrossRef Full Text | Google Scholar

155. Luo L, Shao Y, Li J, Fan R, Peng R, Wang M, et al. Non-Hermitian Effective Medium Theory and Complex Dirac-like Cones. Opt Express (2021) 29:14345. doi:10.1364/oe.425862

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Miri MA, Alù A. Exceptional Points in Optics and Photonics. Science (2019) 363:eaar7709. doi:10.1126/science.aar7709

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Özdemir SK, Rotter S, Nori F, Yang L. Parity-time Symmetry and Exceptional Points in Photonics. Nat Mater (2019) 18:783–98. doi:10.1038/s41563-019-0304-9

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Gupta SK, Zou Y, Zhu XY, Lu MH, Zhang LJ, Liu XP, et al. Parity-Time Symmetry in Non-hermitian Complex Optical Media. Adv Mater (2019) 2019:1903639. doi:10.1002/adma.201903639

CrossRef Full Text | Google Scholar

159. Liu F, Lai Y, Huang X, Chan CT. Dirac Cones at k=0 in Phononic Crystals. Phys Rev B (2011) 84:224113. doi:10.1103/physrevb.84.224113

CrossRef Full Text | Google Scholar

160. Liu F, Huang X, Chan CT. Dirac Cones at k=0 in Acoustic Crystals and Zero Refractive index Acoustic Materials. Appl Phys Lett (2012) 100:071911. doi:10.1063/1.3686907

CrossRef Full Text | Google Scholar

161. Chen Z-G, Ni X, Wu Y, He C, Sun X-C, Zheng L-Y, et al. Accidental Degeneracy of Double Dirac Cones in a Phononic crystal. Sci Rep (2014) 4:4613. doi:10.1038/srep04613

PubMed Abstract | CrossRef Full Text | Google Scholar

162. Li Y, Wu Y, Mei J. Double Dirac Cones in Phononic Crystals. Appl Phys Lett (2014) 105:014107. doi:10.1063/1.4890304

CrossRef Full Text | Google Scholar

163. Liu F, Liu Z. Elastic Waves Scattering without Conversion in Metamaterials with Simultaneous Zero Indices for Longitudinal and Transverse Waves. Phys Rev Lett (2015) 115:175502. doi:10.1103/physrevlett.115.175502

PubMed Abstract | CrossRef Full Text | Google Scholar

164. Wu S, Mei J. Flat Band Degeneracy and Near-Zero Refractive index Materials in Acoustic Crystals. AIP Adv (2016) 6:015204. doi:10.1063/1.4939847

CrossRef Full Text | Google Scholar

165. Zhu H, Semperlotti F. Double-zero-index Structural Phononic Waveguides. Phys Rev Appl (2017) 8:064031. doi:10.1103/physrevapplied.8.064031

CrossRef Full Text | Google Scholar

166. Dubois M, Shi C, Zhu X, Wang Y, Zhang X. Observation of Acoustic Dirac-like Cone and Double Zero Refractive index. Nat Commun (2017) 8:14871. doi:10.1038/ncomms14871

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Dai H, Xia B, Yu D. Dirac Cones in Two-Dimensional Acoustic Metamaterials. J Appl Phys (2017) 122:065103. doi:10.1063/1.4998438

CrossRef Full Text | Google Scholar

168. Dai H, Liu T, Jiao J, Xia B, Yu D. Double Dirac Cone in Two-Dimensional Phononic Crystals beyond Circular Cells. J Appl Phys (2017) 121:135105. doi:10.1063/1.4979852

CrossRef Full Text | Google Scholar

169. Zhao W, Yang Y, Tao Z, Hang ZH. Tunable Transmission and Deterministic Interface States in Double-Zero-index Acoustic Metamaterials. Sci Rep (2018) 8:6311. doi:10.1038/s41598-018-24773-6

PubMed Abstract | CrossRef Full Text | Google Scholar

170. Hyun J, Choi W, Wang S, Park C-s., Kim M. Systematic Realization of Double-Zero-index Phononic Crystals with Hard Inclusions. Sci Rep (2018) 8:7288. doi:10.1038/s41598-018-25696-y

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Indaleeb MM, Banerjee S, Ahmed H, Saadatzi M, Ahmed R. Deaf Band Based Engineered Dirac Cone in a Periodic Acoustic Metamaterial: A Numerical and Experimental Study. Phys Rev B (2019) 99:024311. doi:10.1103/physrevb.99.024311

CrossRef Full Text | Google Scholar

172. Li B, Li Z, Christensen J, Tan KT. Dual Dirac Cones in Elastic Lieb-like Lattice Metamaterials. Appl Phys Lett (2019) 114:081906. doi:10.1063/1.5085782

CrossRef Full Text | Google Scholar

173. Indaleeb MM, Ahmed H, Saadatzi M, Banerjee S. Deaf Band-Based Prediction of Dirac Cone in Acoustic Metamaterials. J Appl Phys (2020) 127:064903. doi:10.1063/1.5122297

CrossRef Full Text | Google Scholar

174. Xu C, Ma G, Chen ZG, Luo J, Shi J, Lai Y, et al. Three-dimensional Acoustic Double-Zero-index Medium with a Fourfold Degenerate Dirac-like point. Phys Rev Lett (2020) 124:074501. doi:10.1103/PhysRevLett.124.074501

PubMed Abstract | CrossRef Full Text | Google Scholar

175. Makris KG, El-Ganainy R, Christodoulides DN, Musslimani ZH. Beam Dynamics in PT Symmetric Optical Lattices. Phys Rev Lett (2008) 100:103904. doi:10.1103/physrevlett.100.103904

PubMed Abstract | CrossRef Full Text | Google Scholar

176. Hsu CW, Zhen B, Stone AD, Joannopoulos JD, Soljačić M. Bound States in the Continuum. Nat Rev Mater (2016) 1:16048. doi:10.1038/natrevmats.2016.48

CrossRef Full Text | Google Scholar

177. Hsu CW, Zhen B, Lee J, Chua S-L, Johnson SG, Joannopoulos JD, et al. Observation of Trapped Light within the Radiation Continuum. Nature (2013) 499:188–91. doi:10.1038/nature12289

PubMed Abstract | CrossRef Full Text | Google Scholar

178. Pendry JB, Schurig D, Smith DR. Controlling Electromagnetic fields. Science (2006) 312:1780–2. doi:10.1126/science.1125907

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Leonhardt U. Optical Conformal Mapping. Science (2006) 312:1777–80. doi:10.1126/science.1126493

PubMed Abstract | CrossRef Full Text | Google Scholar

180. Schurig D, Mock JJ, Justice BJ, Cummer SA, Pendry JB, Starr AF, et al. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science (2006) 314:977–80. doi:10.1126/science.1133628

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Ma W, Liu Z, Kudyshev ZA, Boltasseva A, Cai W, Liu Y. Deep Learning for the Design of Photonic Structures. Nat Photon (2020) 15:77–90. doi:10.1038/s41566-020-0685-y

CrossRef Full Text | Google Scholar

182. Peurifoy J, Shen Y, Jing L, Yang Y, Cano-Renteria F, DeLacy BG, et al. Nanophotonic Particle Simulation and Inverse Design Using Artificial Neural Networks. Sci Adv (2018) 4:eaar4206. doi:10.1126/sciadv.aar4206

PubMed Abstract | CrossRef Full Text | Google Scholar

183. Malkiel I, Mrejen M, Nagler A, Arieli U, Wolf L, Suchowski H. Plasmonic Nanostructure Design and Characterization via Deep Learning. Light Sci Appl (2018) 7:60. doi:10.1038/s41377-018-0060-7

PubMed Abstract | CrossRef Full Text | Google Scholar

184. Liu Z, Zhu D, Rodrigues SP, Lee K-T, Cai W. Generative Model for the Inverse Design of Metasurfaces. Nano Lett (2018) 18:6570–6. doi:10.1021/acs.nanolett.8b03171

PubMed Abstract | CrossRef Full Text | Google Scholar

185. Luo J, Li X, Zhang X, Guo J, Liu W, Lai Y, et al. Deep-learning-enabled Inverse Engineering of Multi-Wavelength Invisibility-To-Superscattering Switching with Phase-Change Materials. Opt Express (2021) 29:10527. doi:10.1364/oe.422119

PubMed Abstract | CrossRef Full Text | Google Scholar