A Novel 3D Image Encryption Based on the Chaotic System and RNA Crossover and Mutation

In this paper, a novel 3D image encryption based on the memristive chaotic system and RNA crossover and mutation is proposed. Firstly, the dynamic characteristics of the nonlinear system with two memristors are analyzed, including phase diagrams, Lyapunov exponential spectrums, and bifurcation diagrams. According to the merged image of three 3D images, the initial values of the memristive chaotic system are generated by SHA-256. Then the vertex coordinates are scrambled and diffused by 3D Arnold matrix and chaotic sequences. Finally, according to the dynamical encoding and decoding rules, crossover and RNA mutation are designed to confuse and diffuse the vertex coordinates. Throughout the encryption process, the Arnold matrix, RNA encoding and decoding rules, and crossover and mutation algorithms are determined by the memristive chaotic system. The experimental results verify that the proposed cryptosystem could encrypt three 3D images at the same time and resist various attacks effectively, and has good security performance.

Introduction

With the development of wireless network and multimedia technology, more images are transmitted on the network. Among them, 3D printing has been widely used in medical, military, marine, and many other fields due to its available price. It can be predicted that the 3D images will be as popular as color images and videos in the future [1–3]. However, the 3D images can be downloaded easily, and 3D objects can be printed out without permission from the original providers. In order to prevent the attacks by unauthorized users, the 3D images should be encrypted before being stored and transmitted. Unlike the traditional files, the 3D image files have enormous data and special storage format, so the traditional encryption algorithms such as DES and AES cannot protect them efficiently [4–8]. Therefore, it is necessary to research high-level encryption technology for 3D images, and there are few researches on this field at present.

In the era of big data, some traditional image cryptosystems can be easily cracked by cloud computing. Therefore, it is necessary to propose a more secure image cryptosystem to meet the current requirements and protect the privacy of users. Chaotic systems have many significant features, including ergodicity, randomness, and sensitivity to initial values, which make them suitable for image encryption [9–22]. It is important to point out that the nonlinearity of memristor element enables the memristor circuits to generate chaotic signal and various chaotic attractors and exhibit abundant nonlinear phenomena [11, 23, 24]. Peng et al. [25] presented a dimensional chaotic map based on the discrete memristor, which can enlarge the hyperchaotic region and enhance complexity. Chen et al. [26] proposed a pseudorandom number generator by three kinds of four-wing memristive hyperchaotic systems, the dynamical characteristics are sensitive and complex. Ma et al. [27] proposed a chaotic circuit based on two memristors, which has rich dynamical behaviors and is suitable for image encryption and secure communication.

With the development of the chaos theory, the fusion of chaotic system and cryptography has become an important solution to ensure image security [28–32]. Based on the chaotic systems, many image encryption schemes are designed by optical transformation [33, 34], compressive sensing [35], DNA and RNA computing [36–41], cellular automata [42], etc. Among them, RNA computing can increase information density, improve parallelism, and reduce energy consumption, so it has become a research hotspot recently [43–45]. Abbasi et al. [46] proposed a cryptosystem based on amino acid, RNA codons, and evolutionary chaotic model, and the performance of the cryptosystem is improved by biomolecules and the imperialist competition algorithm. Jarjar et al. [47] presented a method that uses several genetic and biological features of DNA and RNA to encrypt color images and model mathematical problems as biological ones. Zhang et al. [48] proposed an image cryptosystem based on hyperchaotic system and RNA operation, which could resist various attacks. However, all the researches above are based on the RNA encoding/decoding law; the calculation results between the RNA bases are easy to predict, increasing the risk of cracking. Therefore, the traditional RNA scheme could be improved.

Based on the above analyses, a novel 3D image cryptosystem is proposed in this paper. The rest of the parts are organized as follows. In Preprocessing of the 3D Model, the preprocessing of 3D model data is described. In Chaotic System, the memristive chaotic system is introduced and its dynamical characteristics are illustrated. In Encryption Scheme, the SHA-256 algorithm, improved 3D Arnold algorithm, and RNA level encryption algorithm are described. In Performance Analysis, the security performance and experimental results are evaluated through the key analysis, statistical analysis, information entropy, and robust security analysis. In Section Conclusion, some important conclusions are obtained.

Preprocessing of the 3D Model

Stereolithography (STL) is the standard technology file of current 3D printing technology, which is used to describe the triangulated surface geometry of a 3D model by vertices, faces, and unit normal. The format of the STL file is shown in Table 1. The x, y, and z coordinates of the vertices determine the shape of the 3D model, just like the RGB pixels of a color image file. Therefore, 3D images could be transformed into 2D objects, and the coordinates of the vertices are a protected object.

TABLE 1

TABLE 1. The format of the STL file

Each vertex consists of x, y, and z coordinates (floating point value of at least 96 bit). To enable fast processing with accurate results, all data should be normalized first. Considered the efficiency requirement, the Min–Max Normalization is used to normalize the coordinate data, and the scale criterion is used to rescale the coordinate data, as follows:

$V^{\prime }=R_{\min }+\frac{V-V_{\min }}{V_{\max }-V_{\min }}\times \left(R_{\max }-R_{\min }\right)(1)$

where V^′ is the normalized coordinate, V is the original coordinate, V_min and V_max are minimum and maximum original coordinates, and R_min and R_max are the selected range, ranging from −255 to 255.

After extracting the symbol matrix from the floating point number matrix, the positive array is obtained. Then, it is decomposed into integer matrix V_i and fractional matrix V_f.

Chaotic System

Recently, a chaotic circuit based on two memristors was proposed, which has multiple attractor coexistence and state transition, defined as

$\{\begin{array}{l}\dot{x}=\frac{1}{L}\cdot y-\frac{1}{L{a}_1}\cdot \frac{x}{z}\\ \dot{y}=-\frac{1}{C}\cdot x-\frac{a_2}{C}\cdot wy\\ \dot{z}={\left(\frac{x}{a_{1}z}\right)}^2-b_1\\ \dot{w}=y^2-b_2\end{array}(2)$

where x, y, z, and w represent the system states variables; L, C, a₁, a₂, b₁, and b₂ are system parameters. With the variation of parameters, the system has seven types of attractors. Set L = 0.025, C = 0.025, a₁ = 5.8, a₂ = 0.825, b₁ = 1.85, b₂ = 10, and the initial values are (1, 3, 1, −0.7). Figure 1 shows the phase diagrams. The Lyapunov exponential spectrums and bifurcation diagrams are presented in Figure 2.

FIGURE 1

FIGURE 1. The phase diagrams. (A) x-z plane, (B) x-w plane, (C) y-z plane.

FIGURE 2

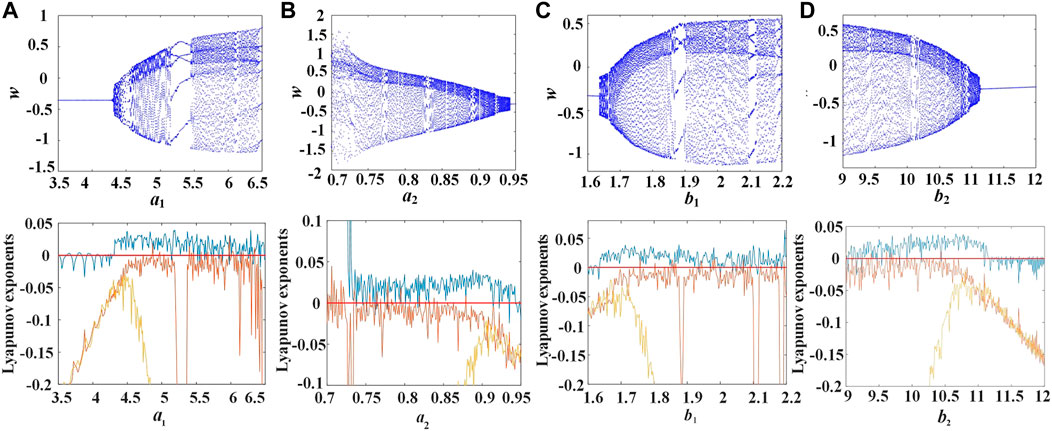
FIGURE 2. Lyapunov exponent spectrums and bifurcation diagrams. (A) a₁∈(3.5,6.5), (B) a₂∈(0.7,0.95), (C) b₁∈(1.6,2.2), (D) b₂∈(9,12).

When a₁∈(4.5,6.5), a₂∈(0.7,0.9), b₁∈(1.7,2.2), and b₂∈(9,11), the bifurcation diagram shows that the system changes from periodic to chaotic, the chaotic states are widely distributed, and the system has complex dynamic characteristics, which can also be verified by the Lyapunov exponential spectrum. At least one Lyapunov exponent in a chaotic system is greater than zero, and the largest Lyapunov exponent in a Lyapunov diagram is always positive, that is, the system is in the chaotic state. These characteristics of the chaotic system make it suitable for image encryption.

Encryption Scheme

The encryption process is described, including the SHA-256 algorithm, improved 3D Arnold algorithm, and RNA operations. The flowchart is shown in Figure 3.

FIGURE 3

FIGURE 3. The flowchart of encryption algorithm.

SHA-256 Algorithm

To improve the security, the SHA-256 is used in the encryption algorithm. Three 3D images are merged together by the method of 3D stereo arrangement. Therefore, different images and different orders will generate different hash values and then obtain different initial conditions, thus producing different chaotic sequences.

Step 1: Based on the merged image I, the 256-bit hash value is generated by the SHA-256 algorithm and divided into eight-bit blocks (total 64 group bit blocks). Thus, the stream key is obtained by XOR operation:

$H\left(i\right)=h\left(2i\right)\oplus h\left(2i-1\right)(3)$

where $i\in \left(\mathrm{1,32}\right)$. The slight disturbance is generated as follows

$\{\begin{array}{l}{k}_1={10}^{-15}\times \text{sum}\left(H\left(1:8\right)\oplus H\left(9:16\right)\right)\\ k_2={10}^{-15}\times \text{sum}\left(H\left(17:24\right)\oplus H\left(25:32\right)\right)\\ k_3={10}^{-15}\times \text{sum}\left(H\left(1:8\right)\oplus H\left(25:32\right)\right)\\ k_4={10}^{-15}\times \text{sum}\left(H\left(9:16\right)\oplus H\left(17:24\right)\right)\\ k_5={10}^{-15}\times \text{sum}\left(V\right)\end{array}(4)$

Step 2: Input the initial condition as the key. Then, the adjusted initial conditions are generated.

$\{\begin{array}{l}x=x_0+\left(k_1+k_2\right)\\ y=y_0+\left(k_2+k_3\right)\\ z=z_0+\left(k_3+k_4\right)\\ w=w_0+\left(k_4+k_5\right)\end{array}(5)$

where x, y, z, and w are adjusted initial values; x₀, y₀, z₀, and w₀ are given values without disturbance. Suppose the plaintext size is M×N, according to the adjusted initial conditions, the chaotic system is iterated (n + M × N) times. To increase the sensitivity of initial values, discard the front n times values. The sequences X, Y, Z and W are generated.

$\{\begin{array}{l}X=\mathrm{mod}\left(\text{floor}\left(\text{abs}\left(x\times {10}^{15}\right)\right),256\right)\\ Y=\mathrm{mod}\left(\text{floor}\left(\text{abs}\left(y\times {10}^{15}\right)\right),256\right)\\ Z=\mathrm{mod}\left(\text{floor}\left(\text{abs}\left(z\times {10}^{15}\right)\right),256\right)\\ W=\mathrm{mod}\left(\text{floor}\left(\text{abs}\left(w\times {10}^{15}\right)\right),256\right)\end{array}(6)$

Thus, the chaotic sequences are affected by hash value of plaintext, which can improve the random adaptive ability.

Improved 3D Arnold Algorithm

On the basis of chaotic sequence, irrelevant vertices are added to ensure security, and then, an improved 3D Arnold cat map is performed for scrambling and diffusion. In the encryption scheme, the integer matrix is confused and diffused. In order to save the encryption time, the fractional matrix is only treated by diffusion.

Step 1: In the 3D Arnold matrix, the calculation principle of control parameters depends on the chaotic sequence, as shown in the formula:

$\{\begin{array}{l}{S}_A=\lfloor a\cdot x+c\cdot y-y\cdot z\rfloor \\ S_B=\lfloor z\cdot \left(x-1\right)-b\cdot y\rfloor \\ S_C=\lfloor a\cdot y+c\cdot z-x\cdot z\rfloor \\ S_D=\lfloor x\cdot \left(y-1\right)-b\cdot z\rfloor \\ S_E=\lfloor a\cdot z+c\cdot x-x\cdot y\rfloor \\ S_F=\lfloor y\cdot \left(z-1\right)-b\cdot x\rfloor \end{array}(7)$

where a, b, and c are specified parameters.

Step 2: The 3D Arnold matrix is obtained by multiplication of cubic matrices, as follows:

$A=\left[\begin{array}{ccc}1& 0& S_A\\ 0& 1& 0\\ S_B& 0& S_A\times S_B+1\end{array}\right]\cdot \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& S_C\\ 0& S_D& S_C\times S_D+1\end{array}\right]\cdot \left[\begin{array}{ccc}1& S_E& 0\\ S_F& S_E\times S_F+1& 0\\ 0& 0& 1\end{array}\right](8)$

Step 3: The integer matrix and fractional matrix are scrambled by the 3D Arnold matrix. The scrambled coordinate positions are generated as follows:

$\left[\begin{array}{c}{i}_A\\ j_A\\ k_A\end{array}\right]=A\cdot \left[\begin{array}{c}i\\ j\\ k\end{array}\right]\mathrm{mod}\left[\begin{array}{c}{N}_{\text{row}}\\ N_{\text{column}}\\ N_{\text{graph}}\end{array}\right]+\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right](9)$

where (i, j, k) is the original position; N_row, N_column, and N_gragh are the number of rows, columns, and graphs. (i_A, j_A, k_A) is the scrambled position. After each vertex coordinate is shifted with the replacement vertex, the scrambled image is obtained.

Step 4: The integer matrix is diffused by the 3D Arnold matrix, as follows:

$\left[\begin{array}{c}A{V}_i\left(i,j,k\right)\\ A{V}_i\left(i_A,j_A,k_A\right)\\ A{V}_i\left(i^{\text{'}},j^{\text{'}},k^{\text{'}}\right)\end{array}\right]=A\cdot \left[\begin{array}{c}{V}_i\left(i,j,k\right)\\ V_i\left(i_A,j_A,k_A\right)\\ V_i\left(i^{\text{'}},j^{\text{'}},k^{\text{'}}\right)\end{array}\right]\mathrm{mod}\left[\begin{array}{c}256\\ 256\\ 256\end{array}\right](10)$

where V_i(i, j, k) and V_i(i_A, j_A, k_A) are scrambled values of the previous step, and V_i(i′, j′, k′) is the diffused value of the previous round. AV_i(i, j, k), AV_i(i_A, j_A, k_A), and AV_i(i′, j′, k′) are the values after diffusion. After each coordinate in the matrix is transformed, the diffused image matrix I₁ is obtained.

With the improved 3D Arnold algorithm, the matrix can be scrambled and diffused simultaneously, which could save the encryption time and reduce the computational complexity.

RNA Encryption Algorithm

The RNA encryption algorithm aims to confuse and diffuse the vertex coordinates completely. The bio-inspired chaotic encryption algorithm can be divided into encoding, diffusion, crossover, mutation, and decoding stages.

Step 1: RNA coding rules. The RNA sequence is constructed by four nitrogen bases, namely, Adenine (A), Guanine (G), Uracil (U), and Cytosine (C). The complementary coding rules are shown in Table 2. Besides, Table 3 shows the RNA operation rules.

TABLE 2

TABLE 2. The RNA encoding rules

TABLE 3

TABLE 3. The RNA operation rules

Step 2: RNA diffusion. The rules of coding and operation are both determined by chaotic sequences. Convert the matrix I₁ and chaotic sequence to a binary matrix of size M × N × 8. Then, according to the dynamic coding rules, the plaintext is transformed into an RNA sequence of size M × N × 4. The disorder sequence is obtained by substituting base pairs under the complementary rule. Then, the diffused cipher sequence P is obtained.

Step 3: Gene crossover. Crossover, also known as gene recombination or hybridization, is the exchange of genetic material at the same location of two chromosomes to generate two new recombinant chromosomes. In 3D image encryption algorithm, the vertex coordinates are exchanged to accomplish the crossover, similar to the chromosome swapping in biology. The sequence P is divided into two sequences P₁ and P₂ of equal length. Transform the chaotic sequence (x⊕w) into a binary sequence that determines the crossover position of the unit: 1 means exchange, 0 means non-exchange, as shown in Figure 4. When the crossover is complete, merge the two sequences.

FIGURE 4

FIGURE 4. Crossover process. (A) Before crossover. (B) After crossover.

Step 4: RNA mutation. Codon refers to a triplet sequence of nucleotide residues in RNA that encodes a specific amino acid during protein synthesis. Mutations are certain replication errors that occur during replication, leading to the formation of new chromosomes. In 3D image cryptosystem, the changes in vertex coordinates correspond to mutation in biology. According to the chaotic sequence, two mutation units are found and defined in RNA sequence, as shown in Figure 5. According to the chaotic sequence, mutation units [AUC] at position 2 and [UCG] at position 4 are selected by (z⊕w). If the mutation units selected are the same, the selection will continue according to the subsequent chaotic sequence.

FIGURE 5

FIGURE 5. Selection of mutant genomes.

The codons mutated accordingly, as shown in Figure 6. The red and green codons convert to each other.

FIGURE 6

FIGURE 6. Mutation process. (A) Before mutation. (B) After mutation.

Step 5: RNA decoding rules. Based on chaotic sequence, decoding rules are selected, and binary matrix is obtained. Then convert it into decimal matrix, which is the final ciphertext C.

According to the RNA coding theory, each RNA gene carries certain information of the images. Dynamic RNA encoding rules and RNA decoding rules could increase the randomness of ciphertext and the resistance to statistical attacks. Crossover and mutation based on chaotic sequences could increase the unpredictability of the encryption algorithm. Therefore, a different ciphertext can be obtained by using different crossover and mutation rules and different encoding and decoding rules.

Decryption Scheme

Due to the symmetrical image cryptosystem, the cipher matrix can be decrypted and the original images can be restored using the reverse process of the encryption process, as shown in Figure 7. After the reverse mutation and crossover of RNA operation and the reverse scrambling and diffusion of 3D Arnold algorithm, the added random points were removed and the image was decomposed, and three original images could be obtained.

FIGURE 7

FIGURE 7. The flowchart of decryption algorithm.

Performance Analysis

Simulation Results

In order to verify the performance of the designed cryptosystem, several experiments were carried out on 3D images. The experiments were tested on a computer: Intel Core i7 CPU 2.9GHz, RAM 32 GB. The operating system is Windows 10. The simulation software is Matlab 2016b. Set the parameters as follows: L = 0.025, C = 0.025, a₁ = 5.8, a₂ = 0.825, b₁ = 2, b₂ = 10, and the initial values are (1, 3, 1, −0.7). To test the encryption performance, three 3D images Car $\left(39888\times 3\right)$, Jet $\left(25896\times 3\right)$, and Rocket $\left(51310\times 3\right)$ are used as encryption models. The simulation results of cryptosystem are shown in Figure 8. The encrypted images can completely hide the original images, and decryption process can successfully restore the original images with the keys. Based on the characteristics of 3D images, it is considered as a special color image. Therefore, the performance analysis methods of color images cryptosystem can be applied to 3D images encryption.

FIGURE 8

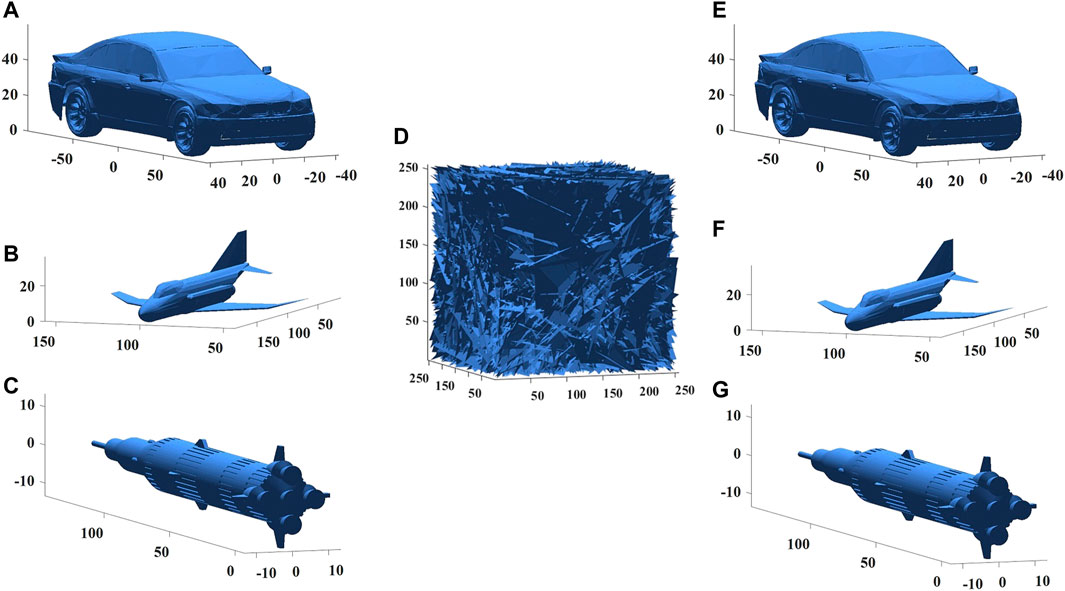
FIGURE 8. The simulation results. (A) Car image. (B) Jet image. (C) Rocket image. (D) Cipher image. (E) Decrypted Car image. (F) Decrypted Jet image. (G) Decrypted Rocket image.

Key Space Analysis

In cryptosystem, the key space must be large enough, which is critical to the encryption algorithm. The secret key consists of 1) system parameters L, C, a₁, a₂, b₁, and b₂; 2) initial value of the chaotic system (x, y, z, w); 3) SHA-256 hash value k₁, k₂, k₃, k₄; and 4) parameter of vertex matrix k₅. With the calculation accuracy of 10⁻¹⁵, the key space will reach 2⁷⁴⁷, which exceeds the minimum requirement of 2¹⁰⁰, and could resist brute force attacks [49]. Table 4 shows the test results of key space. Compared with other literatures, key space of this cryptosystem is larger.

TABLE 4

TABLE 4. Key space for different algorithms

Key Sensitivity Analysis

Key sensitivity is an important feature of encryption algorithm. An effective cryptosystem should be extremely sensitive to the key. The cipher matrix obtained by encrypting the same plaintext matrix should be significantly different when there is a small change in the key. In the key sensitivity test, a slight change in the key during the decryption results in three restored images that are completely different from originals, as shown in Figure 9.

FIGURE 9

FIGURE 9. The key sensitivity test. (A) a₁+10⁻¹⁵, (B) a₂+10⁻¹⁵, (C) b₁+10⁻¹⁵, (D) b₂+10⁻¹⁵, (E) L+10⁻¹⁵, (F) C+10⁻¹⁵.

Histogram Analysis

In order to hide the information about vertex coordinates, the ciphertext histograms should be flat and evenly distributed. The histogram results are plotted in Figure 10. In the figure, the plaintext and ciphertext histograms are completely different. There is a clear coordinate aggregation interval in the plaintext matrix, while the coordinates in the cipher matrix are uniformly distributed.

FIGURE 10

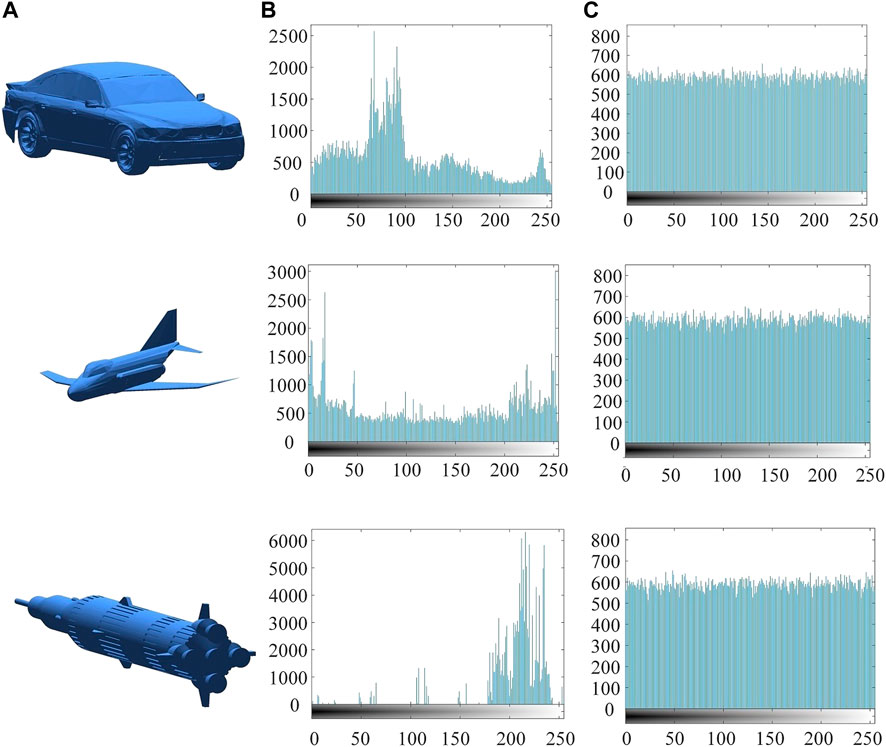
FIGURE 10. The histogram analysis results. (A) Plaintext images. (B) Histograms of plaintext images. (C) Histograms of cipher images.

Moreover, the χ² test results can be used to quantitatively analyze whether vertex coordinates are evenly distributed. In Table 5, the χ² test results of plaintexts and ciphertexts are presented. The measured results of the proposed algorithm are less than the critical values of different probabilities (10%, 5%, and 1%), indicating that the encryption algorithm could overwrite the statistics of vertex coordinates and resist statistical attacks.

TABLE 5

TABLE 5. Results of the χ²-value test

Correlation Analysis

To protect vertex coordinate information, the statistics needs to be hidden, and the correlation between adjacent vertices coordinates needs to be reduced. The relevant equations are given below:

${\gamma }_{\text{xy}}=\frac{E\left\{\left[x-E\left(x\right)\right]-\left[y-E\left(y\right)\right]\right\}}{\sqrt{D\left(x\right)D\left(y\right)}}(11)$

$E\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i}(12)$

$D\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[x_i-E\left(x\right)\right]}^2}(13)$

Figures 11A,C,E show the correlation of plaintexts; the coordinate distribution is intensive, and the vertex coordinates are highly correlated. On the contrary, Figures 11B,D,F demonstrated that the correlation of the encryption model is low, which means that the algorithm could reduce the correlations between adjacent vertices in each direction and resist statistical attacks.

FIGURE 11

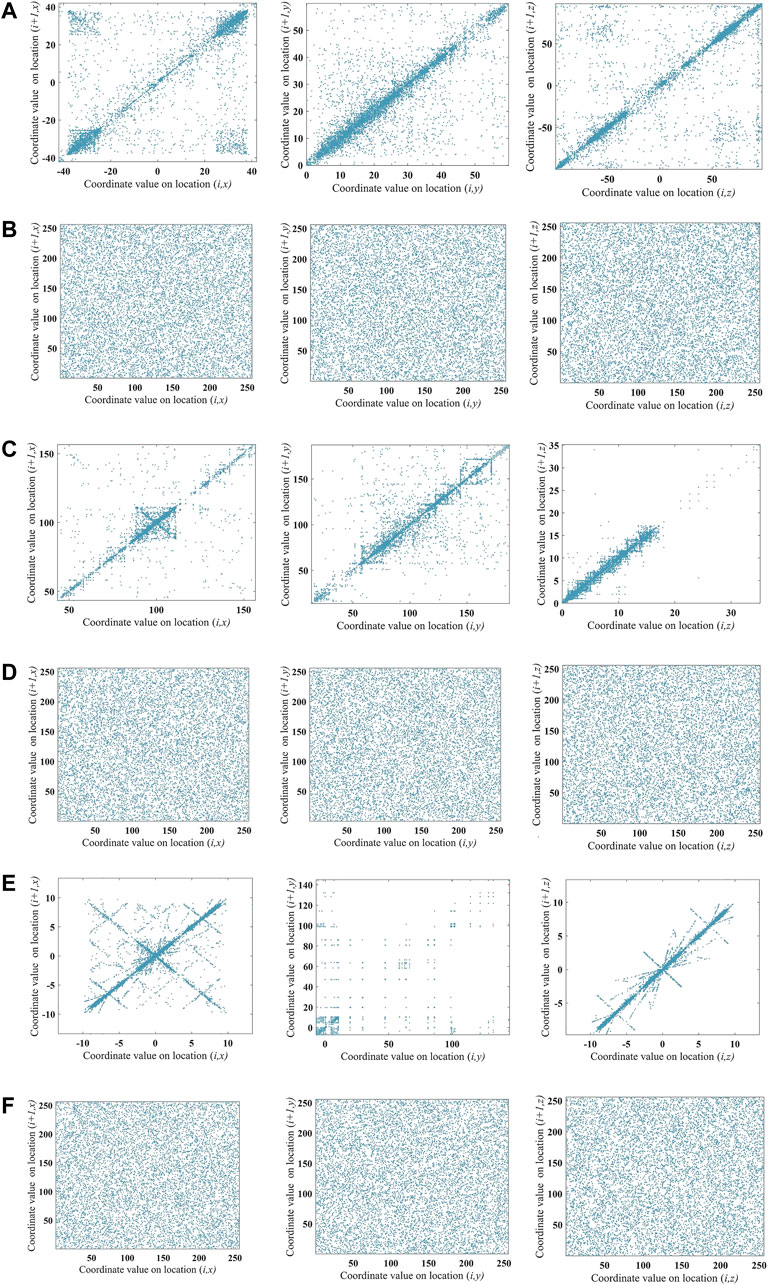
FIGURE 11. The correlation analysis of different images. (A) Car plaintext. (B) Car ciphertext. (C) Jet plaintext. (D) Jet ciphertext. (E) Rocket plaintext. (F) Rocket ciphertext.

When the absolute value of the correlation coefficient is close to 1, it means that the coordinate values of the large region in the vertex matrix are small. On the contrary, if it is close to 0, the cryptosystem could confuse coordinate positions effectively. The correlation coefficient between adjacent coordinates are shown in Table 6. In each direction, the adjacent coordinates of the plaintexts are highly correlated and the correlation between adjacent coordinates of ciphertexts is low.

TABLE 6

TABLE 6. The correlation coefficients between the plain images and cipher images

Randomness Analysis

In order to ensure the uniform distribution of cipher coordinate values, a variety of 3D images are adopted to measure the security of cipher. SP (Special Publications) 800-22 is a randomness standard test published by NIST, which contains 15 sub-tests that identify the randomness of the encryption algorithm. NIST test uses p-value magnitude and the pass rate to reflect the bit sequence randomness property of the encryption algorithm. When the p-value is greater than or equal to 0.01, it is considered that the bit sequence has passed the NIST test, that is, the bit sequence has randomness. The pass rate reflected the number of sample sequences that pass the randomness test.

With different test samples and different initial conditions, several cryptographic matrixes are obtained. Then, the cipher matrix is converted to binary sequence. The value of each cipher matrix is represented by eight bits. Thus, the length of test sample is 86,400,000 bits. The randomness test results are present in Table 7, with the worst set of data. The test sample can pass all 15 sub-tests, indicating that the cipher matrix has high randomness.

TABLE 7

TABLE 7. NIST test results

Information Entropy Analysis

Information entropy is used to measure the average amount of information in the whole image, and its theoretical value is 8. The more evenly coordinate values are distributed, the less effective information the information source has. The coordinates in the vertex matrix are floating-point numbers. Therefore, the positive integer less than or equal to the coordinates in vertex matrix is taken. Thus, for the vertex matrix with 256 levels, information entropy can be expressed as:

$H\left(x\right)={\displaystyle \sum _{i=0}^{N}p\left(x_i\right)}{\log }_2\frac{1}{p\left(x_i\right)}(14)$

Table 8 gives the information entropy of plaintexts and ciphertexts. The information entropy of original images Car, Jet, and Rocket of different sizes are 7.7123, 7.8348, and 5.929, and the information entropy of ciphertexts are significantly improved to 7.9988, 7.9988, and 7.9987, respectively. The information entropies of ciphertexts are larger than that of the plaintexts and close to the theoretical value. Compared with other algorithms, the proposed algorithm could confuse the coordinate information successfully and resist statistical attacks.

TABLE 8

TABLE 8. The information entropy test for different algorithms

Differential Attack Analysis

When one of the original images is changed in a slight way, the encrypted images should be significantly different. NPCR and UACI could reflect the sensitivity of the original 3D images, as shown in the following formula:

$\text{NPCR}=\frac{{\displaystyle {\sum }_{i,j}D\left(i,j\right)}}{M\times N}\times 100\%(15)$

$\text{UACI}=\frac{1}{M\times N}\left[{\displaystyle {\sum }_{i,j}\frac{\left|C_1\left(i,j\right)-C_2\left(i,j\right)\right|}{255}}\right]\times 100\%(16)$

$D\left(i,j\right)=\{\begin{array}{l}1,C_1\left(i,j\right)\ne C_2\left(i,j\right)\\ 0,C_1\left(i,j\right)=C_2\left(i,j\right)\end{array}(17)$

where C₁ and C₂ represent ciphertexts before and after a coordinate value of plaintext changes by 1. When the NPCR is close to 1 and the UACI is about 0.3346, the algorithm is considered to have passed the test.

The idea values of NPCR and UACI are given [51, 52]. According to Table 9 and Table 10, the mean value of NPCR and UACI of the three images is 99.6154% and 33.35%. Figure 12 shows the NPCR and UACI calculated by randomly varying the vertex matrix values in different test model. The test results of NPCR and UACI are greater than the theoretical values with a confidence level of 0.05. A comparison of NPCR and UACI with different algorithms is shown in Table 11, which proves the ability to resist differential attack.

TABLE 9

TABLE 9. The NPCR results for different images

TABLE 10

TABLE 10. The UACI results for different images

FIGURE 12

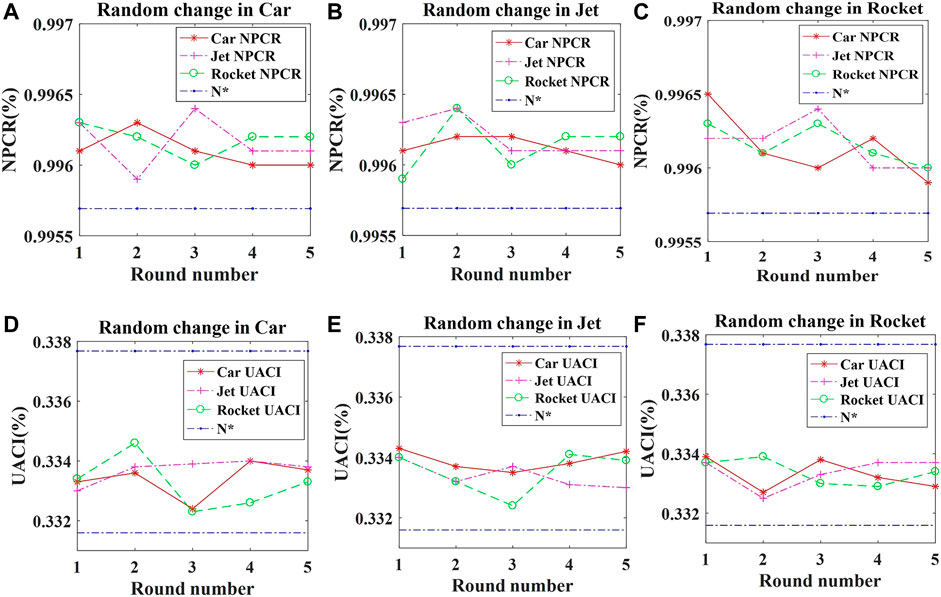
FIGURE 12. The test results of differential attacks. (A) NPCR of Car change. (B) NPCR of Jet change. (C) NPCR of Rocket change. (D) UACI of Car change. (E) UACI of Jet change. (F) UACI of Rocket change.

TABLE 11

TABLE 11. Comparison of NPCR and UACI with different algorithms

Time Analysis

The image cryptosystem mainly includes three processes: chaotic system iteration, 3D Arnold algorithm and DNA encryption. The encryption time of images with 348,282 vertex coordinates is 30.1795 s. In Ref. [36], the encryption time of 89,271 data is 0.261795 s. In Ref. [40], the encryption time of the $256\times 256$ gray image is 7.59 s. The proposed cryptosystem sacrifices the encryption time to ensure the encryption effect.

Conclusion

A novel 3D image encryption based on the memristive chaotic system and RNA crossover and mutation is proposed. Firstly, the chaotic system based on two memristors is analyzed by bifurcation diagrams and Lyapunov exponential spectrums. It is shown that the chaotic system has complex dynamical behaviors and large parameter space, which are suitable for image encryption. Secondly, the initial values are generated by SHA-256, so different plaintexts and merge orders will generate different keys and chaotic sequences. Besides, an improved 3D Arnold algorithm is used to confuse the vertex positions and convert coordinates. Based on dynamic RNA encoding and decoding rules, the RNA crossover and mutation algorithms are given to directly exchange codons. In addition, the cryptosystem can encrypt multiple images at the same time, which improves security and effectiveness. Finally, experimental results indicate that the cryptosystem could ensure the security of three 3D images simultaneously, and the security analysis verifies that it could resist various attacks effectively.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

RC provided the idea of algorithm, carried out the simulations, arranged the architecture and drafted the manuscript. SZ and XG supervised the work and revised the manuscript. Both authors read and approved the final manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (No. 61231006 and No. 61501078).

Conflict of Interest

XG was employed by the company Tokai Carbon Dalian Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a shared affiliation with one of the authors RC at time of review.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Jiang R, Zhou H, Zhang W, Yu N. Reversible Data Hiding in Encrypted Three-Dimensional Mesh Models. IEEE Trans Multimedia (2018) 20(1):55–67. doi:10.1109/tmm.2017.2723244

CrossRef Full Text | Google Scholar

2. Peng Y, He S, Sun K. A Higher Dimensional Chaotic Map with Discrete Memristor. AEU - Int J Elect Commun (2021) 129:153539–7. doi:10.1016/j.aeue.2020.153539

CrossRef Full Text | Google Scholar

3. Joshi AB, Kumar D, Gaffar A, Mishra DC. Triple Color Image Encryption Based on 2D Multiple Parameter Fractional Discrete Fourier Transform and 3D Arnold Transform. Opt Lasers Eng (2020) 133:106139–13. doi:10.1016/j.optlaseng.2020.106139

CrossRef Full Text | Google Scholar

4. Pham G, Lee S-H, Kwon K-R. Interpolating Spline Curve-Based Perceptual Encryption for 3D Printing Models. Appl Sci (2018) 8(2):242–54. doi:10.3390/app8020242

CrossRef Full Text | Google Scholar

5. Xu J, Zhao C, Mou J. A 3D Image Encryption Algorithm Based on the Chaotic System and the Image Segmentation. IEEE Access (2020) 8(99):145995–6005. doi:10.1109/access.2020.3005925

CrossRef Full Text | Google Scholar

6. Pham N-G, Lee S-H, Lee S-H, Kwon O-H, Kwon K-R. 3D Printing Model Random Encryption Based on Geometric Transformation. Int J Machine Learn Comput (2018) 8(2):186–90. doi:10.18178/ijmlc.2018.8.2.685

CrossRef Full Text | Google Scholar

7. Jin X, Zhu S, Xiao C, Sun H, Li X, Zhao G, et al. 3D Textured Model Encryption via 3D Lu Chaotic Mapping. Sci China Inf Sci (2017) 60(12):1–9. doi:10.1007/s11432-017-9266-1

CrossRef Full Text | Google Scholar

8. Wang X, Xu M, Li Y. Fast Encryption Scheme for 3D Models Based on Chaos System. Multimed Tools Appl (2019) 78(23):33865–84. doi:10.1007/s11042-019-08171-2

CrossRef Full Text | Google Scholar

9. An X, Qiao S. The Hidden, Period-Adding, Mixed-Mode Oscillations and Control in a HR Neuron under Electromagnetic Induction. Chaos, Solitons & Fractals (2021) 143:110587–18. doi:10.1016/j.chaos.2020.110587

CrossRef Full Text | Google Scholar

10. Qiao S, An X-L. Dynamic Expression of a HR Neuron Model under an Electric Field. Int J Mod Phys B (2020) 35(02):2150024–3. doi:10.1142/s0217979221500247

CrossRef Full Text | Google Scholar

11. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100(3):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

12. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. Dynamics Analysis, Hardware Implementation and Engineering Applications of Novel Multi-Style Attractors in a Neural Network under Electromagnetic Radiation. Chaos, Solitons & Fractals (2021) 152:111350–14. doi:10.1016/j.chaos.2021.111350

CrossRef Full Text | Google Scholar

13. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Jin J, et al. Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic Radiation. Front Phys (2021) 9:1–15. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

14. Ma C, Mou J, Xiong L, Banerjee S, Liu T, Han X. Dynamical Analysis of a New Chaotic System: Asymmetric Multistability, Offset Boosting Control and Circuit Realization. Nonlinear Dyn (2021) 103(3):2867–80. doi:10.1007/s11071-021-06276-8

CrossRef Full Text | Google Scholar

15. Liu T, Yan H, Banerjee S, Mou J. A Fractional-Order Chaotic System with Hidden Attractor and Self-Excited Attractor and its DSP Implementation. Chaos, Solitons & Fractals (2021) 145(2):110791–12. doi:10.1016/j.chaos.2021.110791

CrossRef Full Text | Google Scholar

16. Liu T, Banerjee S, Yan H, Mou J. Dynamical Analysis of the Improper Fractional-Order 2D-SCLMM and its DSP Implementation. Eur Phys J Plus (2021) 136(5):1–17. doi:10.1140/epjp/s13360-021-01503-y

CrossRef Full Text | Google Scholar

17. Liu H, Zhang Y, Kadir A, Xu Y. Image Encryption Using Complex Hyper Chaotic System by Injecting Impulse into Parameters. Appl Maths Comput (2019) 360:83–93. doi:10.1016/j.amc.2019.04.078

CrossRef Full Text | Google Scholar

18. Liu H, Kadir A, Liu J. Color Pathological Image Encryption Algorithm Using Arithmetic over Galois Field and Coupled Hyper Chaotic System. Opt Lasers Eng (2019) 122:123–33. doi:10.1016/j.optlaseng.2019.05.027

CrossRef Full Text | Google Scholar

19. Liu H, Kadir A, Xu C. Cryptanalysis and Constructing S-Box Based on Chaotic Map and Backtracking. Appl Maths Comput (2020) 376:125153. doi:10.1016/j.amc.2020.125153

CrossRef Full Text | Google Scholar

20. Liu H, Kadir A, Xu C. Color Image Encryption with Cipher Feedback and Coupling Chaotic Map. Int J Bifurcation Chaos (2020) 30(12):2050173. doi:10.1142/s0218127420501734

CrossRef Full Text | Google Scholar

21. Si Y, Liu H, Chen Y. Constructing Keyed strong S-Box Using an Enhanced Quadratic Map. Int J Bifurcation Chaos (2021) 31(10):2150146. doi:10.1142/s0218127421501467

CrossRef Full Text | Google Scholar

22. Liu H, Wang X, Kadir A. Constructing Chaos-Based Hash Function via Parallel Impulse Perturbation. Soft Comput (2021) 25(16):11077–86. doi:10.1007/s00500-021-05849-4

CrossRef Full Text | Google Scholar

23. Ma C, Mou J, Li P, Liu T. Dynamic Analysis of a New Two-Dimensional Map in Three Forms: Integer-Order, Fractional-Order and Improper Fractional-Order. Eur Phys J Spec Top (2021) 230(7-8):1945–57. doi:10.1140/epjs/s11734-021-00133-w

CrossRef Full Text | Google Scholar

24. Yu F, Li L, He B, Liu L, Qian S, Zhang Z, et al. Pseudorandom Number Generator Based on a 5D Hyperchaotic Four-wing Memristive System and its FPGA Implementation. Eur Phys J Spec Top (2021) 230(7-8):1763–72. doi:10.1140/epjs/s11734-021-00132-x

CrossRef Full Text | Google Scholar

25. Peng Y, He S, Sun K. Chaos in the Discrete Memristor-Based System with Fractional-Order Difference. Results Phys (2021) 24:104106–7. doi:10.1016/j.rinp.2021.104106

CrossRef Full Text | Google Scholar

26. Chen X, Qian S, Yu F, Zhang Z, Shen H, Huang Y, et al. Pseudorandom Number Generator Based on Three Kinds of Four-Wing Memristive Hyperchaotic System and its Application in Image Encryption. Complexity (2020) 2020:1–17. doi:10.1155/2020/8274685

CrossRef Full Text | Google Scholar

27. Ma X, Mou J, Xiong L, Banerjee S, Cao Y, Wang J. A Novel Chaotic Circuit with Coexistence of Multiple Attractors and State Transition Based on Two Memristors. Chaos, Solitons & Fractals (2021) 152:111363–11. doi:10.1016/j.chaos.2021.111363

CrossRef Full Text | Google Scholar

28. Yang F, Mou J, Ma C, Cao Y. Dynamic Analysis of an Improper Fractional-Order Laser Chaotic System and its Image Encryption Application. Opt Lasers Eng (2020) 129:106031–16. doi:10.1016/j.optlaseng.2020.106031

CrossRef Full Text | Google Scholar

29. Li X, Mou J, Xiong L, Wang Z, Xu J. Fractional-order Double-Ring Erbium-Doped Fiber Laser Chaotic System and its Application on Image Encryption. Opt Laser Tech (2021) 140:107074–18. doi:10.1016/j.optlastec.2021.107074

CrossRef Full Text | Google Scholar

30. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. A New Multi-Scroll Chua's Circuit with Composite Hyperbolic tangent-cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011

CrossRef Full Text | Google Scholar

31. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Du S. FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys. B (2021) 31(2):20505–020505. doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

32. Mou J, Yang F, Chu R, Cao Y. Image Compression and Encryption Algorithm Based on Hyper-Chaotic Map. Mobile Netw Appl (2019) 26(5):1849–61. doi:10.1007/s11036-019-01293-9

CrossRef Full Text | Google Scholar

33. Yang F, Mou J, Luo C, Cao Y. An Improved Color Image Encryption Scheme and Cryptanalysis Based on a Hyperchaotic Sequence. Phys Scr (2019) 94(8):085206–9. doi:10.1088/1402-4896/ab0033

CrossRef Full Text | Google Scholar

34. Ravichandran D, Praveenkumar P, Balaguru Rayappan JB, Amirtharajan R. Chaos Based Crossover and Mutation for Securing DICOM Image. Comput Biol Med (2016) 72:170–84. doi:10.1016/j.compbiomed.2016.03.020

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Chai X, Bi J, Gan Z, Liu X, Zhang Y, Chen Y. Color Image Compression and Encryption Scheme Based on Compressive Sensing and Double Random Encryption Strategy. Signal Process. (2020) 176:107684–18. doi:10.1016/j.sigpro.2020.107684

CrossRef Full Text | Google Scholar

36. Zhang X, Hu Y. Multiple-image Encryption Algorithm Based on the 3D Scrambling Model and Dynamic DNA Coding. Opt Laser Tech (2021) 141(441):107073–16. doi:10.1016/j.optlastec.2021.107073

CrossRef Full Text | Google Scholar

37. Chai X, Chen Y, Broyde LA Novel Chaos-Based Image Encryption Algorithm Using DNA Sequence Operations. Opt Lasers Eng (2017) 88:197–213. (Complete). doi:10.1016/j.optlaseng.2016.08.009

CrossRef Full Text | Google Scholar

38. Chai X, Fu X, Gan Z, Lu Y, Chen Y. A Color Image Cryptosystem Based on Dynamic DNA Encryption and Chaos. Signal Process. (2019) 155(FEB.):44–62. doi:10.1016/j.sigpro.2018.09.029

CrossRef Full Text | Google Scholar

39. Wang X-Y, Zhang Y-Q, Zhao Y-Y. A Novel Image Encryption Scheme Based on 2-D Logistic Map and DNA Sequence Operations. Nonlinear Dyn (2015) 82(3):1269–80. doi:10.1007/s11071-015-2234-7

CrossRef Full Text | Google Scholar

40. Chai X, Gan Z, Lu Y, Chen Y, Han D. A Novel Image Encryption Algorithm Based on the Chaotic System and DNA Computing. Int J Mod Phys C (2017) 28(05):1750069–24. doi:10.1142/S0129183117500693

CrossRef Full Text | Google Scholar

41. Hao J, Li H, Yan H, Mou J. A New Fractional Chaotic System and its Application in Image Encryption with DNA Mutation. IEEE Access (2021) 9:52364–77. doi:10.1109/ACCESS.2021.3069977

CrossRef Full Text | Google Scholar

42. Martín del Rey A. A Method to Encrypt $$3$$ 3 D Solid Objects Based on Three-Dimensional Cellular Automata. In: E Onieva, I Santos, E Osaba, H Quintián, and E Corchado, editors. Lecture Notes in Computer Science, 9121. Cham: Springer (2015). p. 427–38. doi:10.1007/978-3-319-19644-2_36

CrossRef Full Text | Google Scholar

43. Devi RS, Aravind ARN, Vishal JC, Amritha D, Thenmozhi K, Rayappan JBB, et al. Image Encryption through RNA Approach Assisted with Neural Key Sequences. Multimed Tools Appl (2020) 79(17-18):12093–124. doi:10.1007/s11042-019-08562-5

CrossRef Full Text | Google Scholar

44. Wang X, Liu L. Application of Chaotic Josephus Scrambling and RNA Computing in Image Encryption. Multimed Tools Appl (2021) 80(15):23337–58. doi:10.1007/s11042-020-10209-9

CrossRef Full Text | Google Scholar

45. Wang X, Guan N. A Novel Chaotic Image Encryption Algorithm Based on Extended Zigzag Confusion and RNA Operation. Opt Laser Tech (2020) 131(6):106366–17. doi:10.1016/j.optlastec.2020.106366

CrossRef Full Text | Google Scholar

46. Abbasi AA, Mazinani M, Hosseini R. Chaotic Evolutionary-Based Image Encryption Using RNA Codons and Amino Acid Truth Table. Opt Laser Tech (2020) 132(12):106465–13. doi:10.1016/j.optlastec.2020.106465

CrossRef Full Text | Google Scholar

47. JarJar A. Two Advanced Classics Exploiting DNA and RNA Characteristics to Encrypt a Color Image. Multimed Tools Appl (2021) 80(16):24603–29. doi:10.1007/s11042-021-10658-w

CrossRef Full Text | Google Scholar

48. Zhang D, Chen L, Li T. Hyper-Chaotic Color Image Encryption Based on Transformed Zigzag Diffusion and RNA Operation. Entropy (2021) 23(3):361–23. doi:10.3390/e23030361

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Zhu C, Gan Z, Lu Y, Chai X. An Image Encryption Algorithm Based on 3-D DNA Level Permutation and Substitution Scheme. Multimed Tools Appl (2019) 79(11-12):7227–58. doi:10.1007/s11042-019-08226-4

CrossRef Full Text | Google Scholar

50. Jin X, Wu Z, Song C, Zhang C, Li X. 3D Point Cloud Encryption through Chaotic Mapping. In: Pacific Rim Conference on Multimedia, 9916 (2016). p. 119–29. doi:10.1007/978-3-319-48890-5_12

CrossRef Full Text | Google Scholar

51. Hua Z, Zhou Y, Huang H. Cosine-transform-based Chaotic System for Image Encryption. Inf Sci (2019) 480:403–19. doi:10.1016/j.ins.2018.12.048

CrossRef Full Text | Google Scholar

52. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022). doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar